四年级思维训练幻方与数阵图(试卷+解析)
小学四年级逻辑思维学习—数阵图与幻方

⼩学四年级逻辑思维学习—数阵图与幻⽅⼩学四年级逻辑思维学习—数阵图与幻⽅”知识定位⼀、什么是数阵图?在神奇的数学王国中,有⼀类⾮常有趣的数学问题,它变化多端,引⼈⼊胜,奇妙⽆穷。
它就是数阵,⼀座真正的数字迷宫,它对喜欢探究数字规律的⼈有着极⼤的吸引⼒,以⾄有些⼈留连其中,⽤毕⽣的精⼒来研究它的变化,就连⼤数学家欧拉对它都有着浓厚的兴趣。
那么,到底什么是数阵呢?我们先观察上⾯两个图:右图(1)中有3个⼤圆,每个圆周上都有四个数字,有意思的是,每个圆周上的四个数字之和都等于13。
右图(2)就更有意思了,1~9九个数字被排成三⾏三列,每⾏的三个数字之和与每列的三个数字之和,以及每条对⾓线上的三个数字之和都等于15,不信你就算算。
上⾯两个图就是数阵图。
准确地说,数阵图是将⼀些数按照⼀定要求排列⽽成的某种图形,有时简称数阵。
要排出这样巧妙的数阵图,可不是⼀件容易的事情。
我们还是先从如何来填好数阵图开始。
如何填好数阵图?数阵图问题千变万化,这⼀类问题要求数阵中填⼊了⼀些数以后,能保证数阵中特定关系线(或关系区域)上的数的和相等,解决这⼀类问题可以按以下步骤解决问题:第⼀步:区分数阵图中的普通点(或⽅格),和交叉点(⽅格)第⼆步:在数阵图的少数关键点(⼀般是交叉点)上设置未知数,计算各个点与该点被重复计算次数之积的和的代数式,即数阵图关系线(关系区域)上和的总和,这个和是关系线(关系区域)的个数的整数倍.第三步:判断少数关键点上可以填⼊的数的余数性质,并得出相应的数阵图关系线(关系区域)和.第四步:运⽤已经得到的信息进⾏尝试:数阵图还有⼀类题型⽐较少见,解决这⼀类问题需要理清数阵中数与数之间的相关关系,找出问题关键.【授课批注】数阵图问题千变万化,⼀般没有特定的解法,往往需要综合运⽤掌握的各种数学知识来解决问题. 本讲出了要讲授填数阵图的主要技巧,还有以下注意点:1.引导学⽣从整体到局部对问题进⾏观察和判断;2.教授巧妙利⽤容斥原理、余数的性质、整除性质的数学⽅法;3.锻炼学⽣利⽤已知信息枚举,尝试的能⼒;4.培养学⽣综合运⽤各种数学知识,分析问题,找问题关键,解决问题的能⼒.⼆、什么是幻⽅?同学们是否知道我国古代有关“洛书”的神话传说?传说在⼤禹治⽔的年代,陕西的洛⽔经常⼤肆泛滥,⽆论怎样祭祀河神都⽆济于事,每年⼈们摆好祭品之后,河中都会爬出⼀只⼤乌龟,乌龟壳有九⼤块,横着数是3⾏,竖着数是3列,每块乌龟壳上都有⼏个点点,正好凑成1⾄9的数字,可是谁也弄不清这些⼩点点是什么意思.⼀次,⼤乌龟⼜从河⾥爬上来,⼀个看热闹的⼩孩惊叫起来:“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于⼗五!”于是⼈们赶紧把⼗五份祭品献给河神,说来也怪,河⽔果然从此不再泛滥了.这个神奇的图案叫做“幻⽅”,由于它有3⾏3列,所以叫做“三阶幻⽅”,这个相等的和叫做“幻和”.“洛书”就是幻和为15的三阶幻⽅.如下图:三、如何解决幻⽅问题?幻⽅是指横⾏、竖列、对⾓线上数的和都相等的数的⽅阵,具有这⼀性质的3×3的数阵称作三阶幻⽅,4×4的数阵称作四阶幻⽅,5×5的称作五阶幻⽅……如图为三阶幻⽅、四阶幻⽅的标准式样,三阶幻⽅的中⼼位置上的数等于所有所填数的平均数,也等于横⾏、竖列、对⾓线上数和的三分之⼀.解决数表类问题中,⾸先要找出数填写的规律,再从规律中找到数表的数量关系,从⽽找出解决问题的关键.知识梳理987653421987654321(⼀)封闭型数阵问题(⼆)辐射型数阵(三)其它类型的数阵图(四)幻⽅例题精讲【试题来源】【题⽬】将1~6填⼊左下图的六个○中,使三⾓形每条边上的三个数之和都等于k,请指出k的取值范围.k=9 k=10 k=11 k=12【题⽬】⼩猴聪聪有⼀天捡到像左下图的模具,它试着将1~10分别填⼊图中,使得每个⼩三⾓形3个顶点上的数字之和为图中所表⽰的数值,你能做到吗?【题⽬】图中的6条线分别连接着9个圆圈,其中⼀个圆圈⾥的数是6.请你选9个连续⾃然数(包括6在内)填⼈圆圈内,使每条线上各数的和都等于23.6543216543216543216543216【题⽬】⼩兔⼦在森林玩耍,遇到⼀个画着奇怪图形的树桩,上⾯写着:把10⾄20这11个数分别填⼊下图的各圆圈内,使每条线段上3个圆内所填数的和都相等.如果中⼼圆内填的数相等,那么就视为同⼀种填法,请写出所有可能的填法,⼩兔⼦发了愁,你能帮它吗?【题⽬】海豚是很聪明的动物,它能将1~9填⼊右下图的九个○内,并且使得每个圆周和每条直线上的三数之和都相等,并且7,8,9依次位于⼩、中、⼤圆周上,你能做到吗?【题⽬】在下图中的10个○内填⼊0~9这10个数字,使得循环式成⽴:【题⽬】请在图中的每个圆圈内填⼊不同的⾃然数,使得图中每个圆圈中所填的数都是上⼀⾏与它相邻的两个圆圈中所填数的和,最下⾯的数是20.+=====----20【题⽬】请你将2~10这九个⾃然数填⼊图中的空格内每⾏、每列、每条对⾓线上的三数之和相等.【题⽬】请你将1~25这⼆⼗五个⾃然数填⼊图中的空格内每⾏、每列、每条对⾓线上的五数之和相等.【题⽬】将九个数填⼊左下图的九个空格中,使得任⼀⾏、任⼀列以及两条对⾓线上的三个数之和都等于定数k,则中⼼⽅格中的数必为k÷3【题⽬】在下图的九个⽅格中填⼊不⼤于12且互不相同的九个⾃然数(其中已填好⼀个数),使得任⼀⾏、任⼀列及两条对⾓线上的三个数之和都等于21.【题⽬】将前9个⾃然数填⼊右图的9个⽅格中,使得任⼀⾏、任⼀列以及两条对⾓线上的三个数之和互不相同,并且相邻的两个⾃然数在图中的位置也相邻.【题⽬】将1、2、3、4、5、6、7、8、9这九个数字,分别填⼊3×3阵列中的九个⽅格,使第⼆⾏组成的三位数是第⼀⾏组成的三位数的2倍,第三⾏组成的三位数是第⼀⾏组成的三位数的3倍.【题⽬】在⼀个3×3的⽹格中填⼊9个数使得每⼀横⾏、竖⾏、对⾓线上三个数的乘积相等.习题演练【题⽬】将1~7这七个数分别填⼊图中的○⾥,使每条直线上的三个数之和都等于12。
四年级数学竞赛秋季班-第12讲-数阵图与幻方
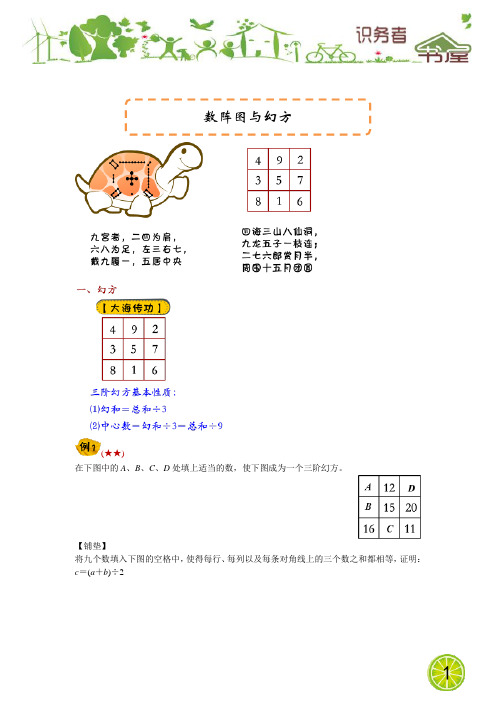
(★★)
在下图中的A、B、C、D处填上适当的数,使下图成为一个三阶幻方。
【铺垫】
将九个数填入下图的空格中,使得每行、每列以及每条对角线上的三个数之和都相等,证明:c=(a+b)÷2
数阵图与幻方
(★★★)
在下图的空格里填入七个自然数,使每一行、每一列及每一条对角线上的三个数的和都等于90。
(★★★★)
在一个乘法幻方中,每一行、每一列、对角线上的数之积都相等。
如果在图中的空格中填上正整数,构成一个乘法幻方,那么x的值是多少?
(★★★)
⑴把10~20这11个数分别填入下图的各圆圈内,使每条线段上3个圆内所填数的和都等于45。
⑵将1~6填入下图的六个○中,使三角形每条边上的三个数之和都等于9。
四年级计算幻方与数表教师版

知识要点幻方与数表一、 如果一个n n ⨯的方阵中,每一横行、每一竖列以及两条对角线上数的和都相等,那么这个方阵称为n 阶幻方。
二、 在n 阶幻方中,其每一行、每一列、两条对角线上的数字之和都相等,这个和称为幻和。
对于n 行或者n 列,其和为幻和乘以n ,也等于所有2n 个数的和;所以,幻和2n S n=个数。
用1、2、……、2n 这2n 个数构造n 阶幻方,其幻和为2212(1)2n n n n ++++=……; 用1、2、3、4、5、6、7、8、9这9个数构造3阶幻方, 其幻和为21234567893(13)1532++++++++⨯+==。
三、 对于n 阶幻方,当n 分别为奇数或偶数时,幻方有一个明显的不同,即奇数阶幻方有一个中心方格,而偶数阶幻方则没有;奇数阶幻方这个中心方格上的数称为中心数。
中心数等于幻方中所有2n 个数的平均数,也等于任意一行、一列、一条对角线中n 个数的平均数,也等于任意两个关于中心对称的空格中的数的平均数;中心数22n S n =个数n=幻和。
用1、2、……、2n 这2n 个数构造n 阶幻方,其中心数为212n +。
用1、2、3、4、5、6、7、8、9这9个数构造3阶幻方,其中心数为21352+=。
四、在3阶幻方中,2222a i b h c g d f e ++++====,2f h a +=、2d h c +=、2b f g +=、2b di +=。
ihgf e d c b a幻方【例1】 请将2009、2010、2011、2012、2013、2014、2015、2016、2017这9个自然数填入图中的空格内,使每行、每列、两条对角线上的3个数之和相等。
(只要构造出一种)200920102011201220132014201520162017201620092014201520132011201220172010201420152010201720132009201620112012201020172012201120132015201420092016201620112012201720132009201420152010201020152014200920132017201220112016201420092016201120132015201020172012201220172010201520132011201620092014【分析】 (方法一)第一步——求幻和:幻和为(200920102011201220132014201520162017)36039++++++++÷=;第二步——求中心数:中心数为603932013÷=;第三步——确定4个角上的数:用尝试法,可推出4个角上的数只能为偶数; 第四步——求出幻方:根据幻和求出各边中点的数,求出1个基本解; 以基本解为基础,可通过旋转或镜像变换得到其它各解,共8解。
小学四年级奥数第10课数阵图试题附答案-精品

小学四年级上册数学奥数知识点讲解第10课《数阵图》试题附答案第十二讲数阵图把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图,即封闭型数阵图、辐射型数阵图和复合型数阵图.为了让同学们学会解数阵图的分析思考方法,我们举例说明.例1将1〜8这八个自然数分别填入下图中的八个。
内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上,应如何填?例2请你把1〜7这七个自然数,分别填在下图Q)的圆圈内,使每条直线上的三个数的和都相等.应怎样填?例3如下图Q)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈上三个数的和.例4请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等,应怎样填?例5将1~16分别填入下图(1)中圆圈内,要求每个扇形上四个数之和及中间正方形的四个数之和都为34,图中已填好八个数,请将其余的数填完.答案第十二讲数阵图把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图,即封闭型数阵图、辐射型数阵图和复合型数阵图.为了让同学们学会解数阵图的分析思考方法,我们举例说明.例1将1~8这八个自然数分别填入下图中的八个O内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?分析为了叙述方便,先在各圆圈内填上字母,如上图(2).由条件得出以下四个算式:a+b+c=14(1)c+d+e=14(2)e+f+g=14(3)a+h+g=14(4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h)-(d+h)=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8,又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h与b+f只能有2+6和3+5两种填法.又由对称性,不妨设b=2,f=6,d=3,h=5.a,c,e,g可取到1,4,7,8若a=l,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=l,则a=14-(1+2)=11,不行, 若81,则c=14-(1+3)=10,不行. 若g=l,则a=8,c=4,e=7.填的飘嘉踊畿篇分析思考过程可以看出‘确定各边顶点所应例2请你把1〜7这七个自然数,分别填在下图(1)的圆圈内,使每条直线上的三个数的和都相等.应怎样填?分析为叙述方便,先在圆圈中标上字母,如上图(2)・设a+b+e=a+c+f=a+d+g=k,则(a+b+e)+(a+c+f)+(a+d+g)=3k3a+b+c+d+e+f+3k2a+(a+b+c+d+e+f+g)=3k2a+(1+2+3+4+5+6+7)=3k2a+28=3ka为1、4或7.若a=l,则k=10,直线上另外两个数的和为9.在2、3、4、5、6、7中, 2+7=3+6=44-5=9,因此得到一个解为:a=l,b=2,c=3,d=4,e=7,f=6,g=5.若平4,则k=12,直线上另外两个数的和为8.在1、2、3、5、6、7中,117=2+6=3+5=8,因此得到第二个解为:a=4,b=l,c=2,d=3,e=7,f=6,g=5.若a=7,则k=若,直线上另外两个数的和为7•在1、2、3、4、5、6中,1+6=2+5=3+47,因此得到第三个解为:a=7,b=l,c=2,d=3,e=6,f=5, g=4.解:共得到三个解:如下图.上几霜翳疆胪,填辐射型数阵图的关键在于确定中心数用每条直线例3如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三 个数的和都等于大圆圈上三个数的和.分析为叙述方便,先在每个圆圈内标上字母,如图(2)则有a+4+9=a+b+c (1)b+8+9=a+b+c (2)c+17+9=a+b+c (3)⑴+(2)+(3) (a+b+c )+56=3(a+b+c )a+b+c=28贝Ua=28-(4+9)=15 b=28-(8+9)=11 c=28-(17+9)=2解:见图. H 892例4请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等,应怎样填?分析为了叙述方便,将各圆圈内先填上字母,如图(2)所示.设A+B+C=A+F+G-A+D+E=B+D+F=C+E+G=k(A+B+C)+(A+F+G)+(A+D+E)+(B+D+F)+(C+E+G)=5k,3A+2B+2c+2D+2E+2F+2G=5k,2(A+B+C+D+E+F+G)+A=5k,2(1+2+3+4+5+6+7)+A=5k,56+A=5k.因为56+A为5的倍数,得A=4,进而推出k=12.因为在1、2、3、5、6、7中,1+5+6=7+3+2=12,不妨设B=l,F=5,D=6,则012-(4+1)=7,G=12-(4+5)=3,E=12-(4+6)=2.解:得到一个基本解为:(见图)例5将1―16分别填入下图(1)中圆圈内,要求每个扇形上四个数之和及中间正方形的四个数之和都为34,图中己填好八个数,请将其余的数填完.分析为了叙述方便,将圆圈内先填上字母,如图(2)所示.9+15+a+c=34,5+10+e+g=34,7+14+b+d=34,ll+8+f+h=34,c+d+e+f=34,化简得:a+c=104+6=10.e+g=193+16=19,6+13=19b+d=131+12=13,f+h=152+13=15,3+12=15.a,b,c,d,e,f,g,啦分别从1,2,3,4,6,12,13,16中选取.因为a+c=10,所以只能选a+c=4+6;b+d=13,只能选b+d=13;e+g=19,只能选e+g=3+16;f+h=15,只能选£+11=2+13若d=l,c=4,则e+f=34-1-4=29,有巳=16,f=13.若#1,c=6,则e+f=34-1-6=27,那么e、f无值可取,使其和为27.若d=12,c=4,则e+f=34-12-4=18,有巳=16,f=2.若#12,c=6,则e+若34-12-6=16,有『3,f=13.解:共有三个解(见图).习题十二L如果把例1的条件改为“使四边形每条边上的三个数之和都等于121其他条件不变,又应如何填?2.请在下图(1)中圆圈内填入1〜9这九个数,其中6,8已填好,要求A、B、C、D四个小三角形边上各数字之和全都相等.3,将1-10这十个数填入如上图(2)的圆圈内,使每个正方形的四个数字之和都等于23,应怎样填?和四个正方形.若想打电话,必须首先将1〜12这十二个数填入其中,使四个椭圆、四个圆形、四个正方形以及四条直线上的四个数之和都为26,假如你要打电话,那么你将怎样填数?5 .请在下图的空格内填入1〜46这四十六个自然数,使每一笔直线上各数之 和都等于93.应怎样填?6 .把1〜8这八个数字分别填入下图Q )中的圆圈内,使每个圆周上与每条 直线上四个数之和都相等,给出一种具体的填法.,下图(2)中,内部四个交点上已填好数,请你在四周方格里填上适当的 数,使交点上的数恰好等于四周四个方格内的数的和.应怎样填?四年级奥数上册:第十二讲数阵图习题中间的十二个键分别为四个圆形、四个椭圆形4.右图是一部古怪的电话, 0管/§习题十二1.如果把例1的条件改为“使四边形每条边上的三个数之和都等于12”,其 他条件不变,又应如何填?2,请在下图Q )中圆圈内填入1~9这九个数,其中6,8已填好,要求A 、B 、C 、D 四个小三角形边上各数字之和全都相等.3,将1~10这十个数填入如上图(2)的圆圈内,使每个正方形的四个数字 之和都等于23,应怎样填?和四个正方形.若想打电话,必须首先将1〜12这十二个数填入其中,使四个椭圆、四个圆形、四个正方形以及四条直线上的四个数之和都为26,假如你要打 电话,那么你将怎样填数?5.请在下图的空格内填入1〜46这四十六个自然数,使每一笔直线上各数之 和都等于93.应怎样填? 中间的十二个键分别为四个圆形、四个椭圆形 4.右图是一部古怪的电话, Q4率由(1)6.把1〜8这八个数字分别填入下图Q)中的圆圈内,使每个圆周上与每条直线上四个数之和都相等,给出一种具体的填法.7,下图(2)中,内部四个交点上已填好数,请你在四周方格里填上适当的数,使交点上的数恰好等于四周四个方格内的数的和.应怎样填?附:奥数技巧分享分享四个奥数小技巧。
小学奥数:数阵图(二).专项练习及答案解析

1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格); 第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.复合型数阵图【例 1】 由数字1、2、3组成的不同的两位数共有9个,老师将这9个数写在一个九宫格上,让同学选数,每个同学可以从中选5个数来求和.小刚选的5个数的和是120,小明选的5个数的和是111.如果两人选的数中只有一个是相同的,那么这个数是_____________.313233212223131211【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】迎春杯,中年级,决赛,3题 【分析】 这9个数的和:111213212223313233++++++++10203031233198=++⨯+++⨯=()()由小刚和小明选的数中只有一个是相同的,可知他们正好把这9个数全部都取到了,且有一个数取了两遍.所以他们取的数的总和比这9个数的和多出来的部分就例题精讲知识点拨教学目标5-1-3-2.数阵图是所求的数.那么,这个数是12011119833+-=.【答案】33【例 2】 如图1,圆圈内分别填有1,2,……,7这7个数。
如果6个三角形的顶点处圆圈内的数字的和是64,那么,中间圆圈内填入的数是 。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】希望杯,五年级,复赛,第5题,5分 【解析】 2 【答案】2【例 3】 如下图(1)所示,在每个小圆圈内填上一个数,使得每一条直线上的三个数的和都等于大圆圈上三个数的和.(1)17894【考点】复合型数阵图 【难度】3星 【题型】填空 【解析】 为叙述方便,先在每个圆圈内标上字母,如图(2),(2)a cb49817则有a+4+9=a+b+c (1)b+8+9=a+b+c (2)c+17+9=a+b+c (3) (1)+(2)+(3):(a+b+c )+56=3(a+b+c ),a+b+c=28,则 a=28-(4+9)=15,b=28-(8+9)=11,c=28-(17+9)=2解:见图.1789411215【答案】1789411215【例 4】请你将数字1、2、3、4、5、6、7填在下面图(1)所示的圆圈内,使得每个圆圈上的三个数之和与每条直线上的三个数之和相等.应怎样填?【考点】复合型数阵图【难度】3星【题型】填空【解析】为了叙述方便,将各圆圈内先填上字母,如图(2)所示.设A+B+C=A+F+G=A+D+E=B+D+F=C+E+G=k(A+B+C)+(A+F+G)+(A+D+E)+(B+D+F)+(C+E+G)=5k,3A+2B+2C+2D+2E+2F+2G=5k,2(A+B+C+D+E+F+G)+A=5k,2(1+2+3+4+5+6+7)+A=5k,56+A=5k.,因为56+A为5的倍数,得A=4,进而推出k=12,因为在1、2、3、5、6、7中,1+5+6=7+3+2=12,不妨设B=1,F=5,D=6,则C=12-(4+1)=7,G=12-(4+5)=3,E=12-(4+6)=2.,解:得到一个基本解为:(见图)7654321【答案】7654321【例 5】在左下图的每个圆圈中填上一个数,各数互不相等,每个圆圈有3个相邻(即有线段相连的圆圈)的圆圈。
小学奥数 数阵与幻方 知识点+例题+练习 (分类全面)

拓展、把1~5这五个数分别填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于8和10。
例2、将1—7七个自然数分别填入图中的圆圈里,使每条线上三个数的和相等。
拓展、将1~7这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都等于10。
例3、把1~5这五个数填入下图中的○里(已填入5),使两条直线上的三个数之和相等。
拓展、将 10~20填入下图的○内,其中15已填好,使得每条边上的三个数字之和都相等。
例4、将1—10这十个数填入下图小圆中,使每个大圆上六个数的和是30。
拓展、将1~8个数分别填入图中,使每个圆圈上五个数和分别为20,22。
例5、把1—10这十个数分别填入下图的○内,使每个四边形顶点的○内四个数的和都相等,且和最大。
拓展、将1~11这十一个数分别填入下图的○里,使每条直线上的三个数之和相等,并且尽可能大。
例6、将1—6六个数分别填入下图的○内,使每边上的三个○内数的和相等。
拓展、将1—8八个数分别填入下图的○内,使每条边上三个数的和相等。
例7、将1—8这八个数分别填入下图○内,使外圆四个数的和,内圆四个数的和以及横行、竖行上四个数的和都等于18。
拓展、将1—8八个数填入下图方格里,使上面四格、下面四格、左四格、右四格、中间四格以及对角线四格内四个数的和都是18。
例8、将1—9九个数分别填入下图○内,使外三角形边上○内数之和等于里面三角形边上○内数之和。
拓展、将1—9填入下图的○中,使横、竖行五个数相加的和都等于25。
例9、如下图,将1~9这九个数字填在方格里,使每行、每列、每条对角线上的三个数之和都相等。
拓展、将1—9九个自然数分别填入下图的九个小三角形中,使靠近大三角形每条边上五个数的和相等,并且尽可能大。
这五个数之和最大是多少?例10、将4~12这九个数字填在下图所示的3×3的方格中,使每行、每列及两条对角线上的三个数的和都相等。
拓展、下图的每个空格中,填入不大于12且互不相同的九个自然数,使每行、每列、每条对角线上的三个数之和都等于21。
小学思维数学讲义:幻方(一)-带详解

⼩学思维数学讲义:幻⽅(⼀)-带详解幻⽅(⼀)1. 会⽤罗伯法填奇数阶幻⽅2. 了解偶数阶幻⽅相关知识点3. 深⼊学习三阶幻⽅⼀、幻⽅起源也叫纵横图,也就是把数字纵横排列成正⽅形,因此纵横图⼜叫幻⽅.幻⽅起源于我国,古⼈还为它编撰了⼀些神话.传说在⼤禹治⽔的年代,陕西的洛⽔经常⼤肆泛滥,⽆论怎样祭祀河神都⽆济于事,每年⼈们摆好祭品之后,河中都会爬出⼀只⼤乌龟,乌龟壳有九⼤块,横着数是3⾏,竖着数是3列,每块乌龟壳上都有⼏个点点,正好凑成1⾄9的数字,可是谁也弄不清这些⼩点点是什么意思.⼀次,⼤乌龟⼜从河⾥爬上来,⼀个看热闹的⼩孩惊叫起来:“瞧多有趣啊,这些点点不论横着加、竖着加还是斜着加,结果都等于⼗五!”于是⼈们赶紧把⼗五份祭品献给河神,说来也怪,河⽔果然从此不再泛滥了.这个神奇的图案叫做“幻⽅”,由于它有3⾏3列,所以叫做“三阶幻⽅”,这个相等的和叫做“幻和”.“洛书”就是幻和为15的三阶幻⽅.如下图:987654321我国北周时期的数学家甄鸾在《算数记遗》⾥有⼀段注解:“九宫者,⼆四为肩,六⼋为⾜,左三右七,戴九履⼀,五居中央.”这段⽂字说明了九个数字的排列情况,可见幻⽅在我国历史悠久.三阶幻⽅⼜叫做九宫图,九宫图的幻⽅民间歌谣是这样的:“四海三⼭⼋仙洞,九龙五⼦⼀枝连;⼆七六郎赏⽉半,周围⼗五⽉团圆.”幻⽅的种类还很多,这节课我们将学习认识了解它们.⼆、幻⽅定义幻⽅是指横⾏、竖列、对⾓线上数的和都相等的数的⽅阵,具有这⼀性质的33?的数阵称作三阶幻⽅,44?的数阵称作四阶幻⽅,55?的称作五阶幻⽅……如图为三阶幻⽅、四阶幻⽅的标准式样,98765432113414151612978105113216三、解决这幻⽅常⽤的⽅法⑴适⽤于所有奇数阶幻⽅的填法有罗伯法.⼝诀是:⼀居上⾏正中央,后数依次右上连.上出框时往下填,右出框时往左填.排重便在下格填,右上排重⼀个样.⑵适⽤于三阶幻⽅的三⼤法则有:①求幻和:所有数的和÷⾏数(或列数)②求中⼼数:我们把幻⽅中对⾓线交点的数叫“中⼼数”,中⼼数=幻和÷3.③⾓上的数=与它不同⾏、不同列、不同对⾓线的两数和÷2.四、数独知识点拨教学⽬标数独简介:(⽇语:数独すうどく)是⼀种源⾃18世纪末的瑞⼠,后在美国发展、并在⽇本得以发扬光⼤的数学智⼒拼图游戏。
小学思维数学讲义:数阵图(一)-含答案解析

数阵图(一)1. 了解数阵图的种类2. 学会一些解决数阵图的解题方法3. 能够解决和数论相关的数阵图问题.一、数阵图定义及分类:1. 定义:把一些数字按照一定的要求,排成各种各样的图形,这类问题叫数阵图.2. 数阵是一种由幻方演变而来的数字图.数阵图的种类繁多,这里只向大家介绍三种数阵图:即封闭型数阵图、辐射型数阵图和复合型数阵图. 3.二、解题方法:解决数阵类问题可以采取从局部到整体再到局部的方法入手: 第一步:区分数阵图中的普通点(或方格)和关键点(或方格);第二步:在数阵图的少数关键点(一般是交叉点)上设置未知数,计算这些关键点与相关点的数量关系,得到关键点上所填数的范围;第三步:运用已经得到的信息进行尝试.这个步骤并不是对所有数阵题都适用,很多数阵题更需要对数学方法的综合运用.模块一、封闭型数阵图【例 1】 把1~8的数填到下图中,使每个四边形中顶点的数字和相等。
【考点】复合型数阵图 【难度】3星 【题型】填空 【关键词】学而思杯,3年级,第6题 【解析】87654321【答案】例题精讲知识点拨教学目标87654321【例 2】 将1~8这八个自然数分别填入下图中的八个○内,使四边形每条边上的三个数之和都等于14,且数字1出现在四边形的一个顶点上.应如何填?(1)【考点】封闭型数阵图 【难度】2星 【题型】填空 【解析】 为了叙述方便,先在各圆圈内填上字母,如下图(2).由条件得出以下四个算式:(2)h gf ed c baa+b+c=14(1)c+d+e=14 (2) e+f+g=14 (3)a+h+g=14 (4)由(1)+(3),得:a+b+c+e+f+g=28,(a+b+c+d+e+f+g+h )-(d+h )=28,d+h=(1+2+3+4+5+6+7+8)-28=8,由(2)+(4),同样可得b+f=8, 又1,2,3,4,5,6,7,8中有1+7=2+6=3+5=8.又1要出现在顶点上,d+h 与b+f 只能有2+6和3+5两种填法. 又由对称性,不妨设b=2,f=6,d=3,h=5. a ,c ,e ,g 可取到1,4,7,8若a=1,则c=14-(1+2)=11,不在1,4,7,8中,不行.若c=1,则a=14-(1+2)=11,不行. 若e=1,则c=14-(1+3)=10,不行. 若g=1,则a=8,c=4,e=7.说明:例题为封闭型数阵,由它的分析思考过程可以看出,确定各边顶点所应填的数为封闭型数阵的解题突破口.【答案】【例 3】 在如图6所示的○内填入不同的数,使得三条边上的三个数的和都是12,若A 、B 、C 的和为18,则三个顶点上的三个数的和是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级思维训练18 幻方与数阵图1.在幻方中.每行、每列和每条对角线上的数的和都相同,那么在下图所示的未完成的幻方中该是____。
2.幻方是将n2个数(不重复)排列成纵、横各有n个数的方阵,使其每行、每列和两条对角线上n个数相加的和都相等.请问下图3×3的幻方中丁是多少?3.在下图所示的O内填入不同的数,使得三条边上的三个数的和都是12.若A、B、C的和为18,则三个顶点上的三个数的和是________。
4.下图3×3正方形的每个方格内的字母都代表一个数,已知其每行,每列以及两条对角线上三个数之和都相等,若“a=4,d=19,l=22,那么6=_______ ,h=______。
5.在图1、图2的空格中分别填人适当的数,使得横、竖及对角线上的三个数之和都相等,那么“?”处的数字分别为多少?.6.在下图中每个小方格中填人一个数,使每一行每一列都有1、2、3、4、5,那么,右上角小方格内填人的数字,应该是________。
7.下图是一个3×3幻方,满足每行、每列及两条对角线上三数之和都相等,那么其中“★代表的数是__________。
8.下边的一排方格中,除9、8外,每个方格中的汉字都表示一个数(不同的汉字可表示相同的数),已知其中任意3个连续方格巾的数加起来都为22,则“走”+“进”+“数”+“学”+“花”+“园”=__________9. 所谓“三阶乘法幻方”是指在3×3的方格中填入9个不等于0的整数,使得每行、每列及每条对角线上的三个数之积都相等,请将下图的“乘法幻方”补充完整,则其中的“”所代表的数是___________。
10.将1至8这八个自然数分别填入下图中的正方体的八个顶点处的o内,并使每个面上的四个O内的数字之和都相等,求与填人数字1的O有线段相连的三个O内的数的和的最大值.11.将从8开始的1 1个连续自然数填入下图中的圆圈内,要使每边上的三个数之和都相等,中间数共有__________ 种填法.12.将1--12这十二个自然数分别填人下图的12个圆圈内,使得每条直线上的四个数之和都相等,这个相等的和为___________。
13.麦斯将9个不同的自然数填入下图的9个空格内,使每行、每列、每条对角线上3个数的和都相等.已知A和B的差为14,B和C的差也为14,那么D和E的差是__________。
14.将1~8这8个自然数分别填人下图数阵中的8个圆圈,使得数阵中各条直线上的三个数之和都相等,那么A和B两个圆圈中所填的数之差(大数减小数)是________。
15.在下图的每个圆圈中,各填入一个不为0的数字,使得所有有线段连接的相邻两个圆圈内数的差至少为2,且每个数字都恰好出现两次.那么A×B的值是____________。
16.从1、2、3、…、20这20个数中选出9个不同的数放人3×3的方格表中,使得每行、每列、每条对角线上的三个数的和都相等.这9个数中最多有____个质数。
17.在下图的空格中填上不同的自然数,使每行、每列和两条对角线的四个数之和都等于264.求A +B -C+D+E- F+G-H的和是多少?18.A、B、C、D、E、F、G、H、M各代表一个互不相同的非零数字,其中A-B=14,M÷G=M-F=H-C,D×F=24.B+E=16,那么H代表_________。
19.如下图所示,A、B、C、D、E、F、G、H、J、J表示10个各不相同的数字,表中的数为所在行与列的对应字母的和,例如“G+C=14”.请将表中其他的数全部填好.20.将1、2、3、…、15、16填入下图的1 6个方格中,并满足下列条件。
(1)A+C+F=10; (2)B+H=R:(3) D-C= 13; (4) E X M=126;(5)F+G=21; (7)G÷J=2;(7)H XM=36: (8)J XP=80;(9)K-N=Q.那么L=___________。
21.如下图所示,在每个圆圈中填入一个数,使每条直线上所有圆圈中数的和都234,那么,标有★的圆圈中所填的数是_________。
22.如下表所示,请将1个1、2个2、3个3、…、7个7、8个8填入6×6的表格中,使得相同的数所在的方格都连在一起(相连的两个方格必须有公共边);现在已经给出了其中8个方格中的数,并且知道A、B、C、D、E、F各不相同;那么,六位数是__________。
四年级思维训练18 幻方与数阵图参考答案1.在幻方中.每行、每列和每条对角线上的数的和都相同,那么在下图所示的未完成的幻方中该是____。
【答案】12【分析】正中间填(5+15)÷2 -10,那么幻和为10×3=30,所以=30 -13 -5=122.幻方是将n2个数(不重复)排列成纵、横各有n个数的方阵,使其每行、每列和两条对角线上n个数相加的和都相等.请问下图3×3的幻方中丁是多少?【答案】194【分析】左下角的数为35+89 -1=123所以中间的数为(123+89)÷2-106故幻和为106×3—318所以= 318- 35 - 89 -194.3.在下图所示的O内填入不同的数,使得三条边上的三个数的和都是12.若A、B、C的和为18,则三个顶点上的三个数的和是________。
【答案】9【分析】设三个顶点为D,E,F.观察容易发现,三条边的和为36即D+A+E+E+C:-I-F+F+B+D=3618+2(D+E+F)=36所以D+E+F=9.4.下图3×3正方形的每个方格内的字母都代表一个数,已知其每行,每列以及两条对角线上三个数之和都相等,若“a=4,d=19,l=22,那么b=_______ ,h=______。
【答案】b=25,h=1【分析】由h+l=a+d,得h=1,b+h=a+l,b+1=4+22,所以b=25.5.在图1、图2的空格中分别填人适当的数,使得横、竖及对角线上的三个数之和都相等,那么“?”处的数字分别为多少?.【答案】 (1)9;(2)6【分析】在幻方中.有重要结论:每一行之和或每一列之和或对角线之和均为中间方格数的3倍。
(1)给下图中空白处标上字母.8+12+a=11+a+b,.则应为:8+12 - 11=9.则a+20=3a.所以a=10.每行每列每条对角线上的和是30,对应的?处应填30 -12 -9=9.(2)给下图中空白处标上字母.根据幻方的性质有2×?=3+9.所以?处应填6。
6.在下图中每个小方格中填人一个数,使每一行每一列都有1、2、3、4、5,那么,右上角小方格内填人的数字,应该是________。
【答案】 1【分析】每一行每一列中1、2、3、4、5分别出现1次,从左到右来看,第一行的第一个数不能填1,第4个数也不能填1,所以=1.7.下图是一个3×3幻方,满足每行、每列及两条对角线上三数之和都相等,那么其中“★代表的数是__________。
【答案】21【分析】有下图知,2+a=8+10,所以a=16,又8+b=2a,得b—24,同理2+8 =2c,c=5, ★+5=10+16,所以★=21.8.下边的一排方格中,除9、8外,每个方格中的汉字都表示一个数(不同的汉字可表示相同的数),已知其中任意3个连续方格巾的数加起来都为22,则“走”+“进”+“数”+“学”+“花”+“园”=__________。
【答案】40【分析】9+数十学一数十学十花,所以花=9;同理,走=数=8进=学=园=22-9-8=5综上,走十进十数+学+花+园=8+5+8+5+9+5=409. 所谓“三阶乘法幻方”是指在3×3的方格中填入9个不等于0的整数,使得每行、每列及每条对角线上的三个数之积都相等,请将下图的“乘法幻方”补充完整,则其中的“”所代表的数是___________。
【答案】 8【分析】第3行第3列的数为20×16÷4—80,第2行第3列的数为80×20÷16 =100,第1行第2列的数为100×80÷20一400,所以由20×400= 16×100×第2行第2列的数=4×80×第3行第1列的数,得到第2行第2列的数=5,第3行第1列的数=25,这样就有20×400=×5×25,故20×400=5×25,解得 =8.10.将1至8这八个自然数分别填入下图中的正方体的八个顶点处的o内,并使每个面上的四个O内的数字之和都相等,求与填人数字1的O有线段相连的三个O内的数的和的最大值.【答案】 21【分析】如下图所示,因为1到8的和为36,而上面四个数的和等于下面四个数的和,所以都为18.因为每个面的数字和相等,所以一个面上应当大小数搭配,也就是说,和最小的数字1在同一个面上的应该有较大的数.尝试最大的三个数8,7,6,则和1,8,7在同一个面上的数应该是18—1-8 -7=2,和1,8,6在同一个面上的数应该是18 -1-8 -6 =3,和1,7,6在同一个面上的数应该是在同一个面上的数应该是18—1—7-6=4,剩下一个5填在剩下的O 中,经检验,符合题意.8+7+6=21.11.将从8开始的1 1个连续自然数填入下图中的圆圈内,要使每边上的三个数之和都相等,中间数共有__________ 种填法.【答案】3【分析】设中间的数为a,则除去以后剩下的所有数的和为(8+9+10+…+18) –a= 143 -a由题意知此和必须被5整除,因此a只能为8、13或18.所以a共有3种填法.12.将1--12这十二个自然数分别填人下图的12个圆圈内,使得每条直线上的四个数之和都相等,这个相等的和为___________。
【答案】26【分析】将图中6条直线上所有的数相加,相当于每个圆圈中的数算两次,和为2×(1+2+…+12) =156.另一方面,这正是每条直线上四个数之和的6倍,所以相等的和为156÷6=26.13.麦斯将9个不同的自然数填入下图的9个空格内,使每行、每列、每条对角线上3个数的和都相等.已知A和B的差为14,B和C的差也为14,那么D和E的差是__________。
【答案】 49【分析】根据幻方性质,2A =C+E,2D=B+C.因为B和C的差为14.则B与D、C构成公差为7的等差数列,D为等差中项.A和B的差为14,则A和C的差为28,C、A、E构成公差为28的等差数列,A为等差中项.A、B、C构成公差为14的等差数列,B为等差中项,故C和E差56.而五个数按顺序排列应为E、A、I3、D、C,所以D和E的差是56-7=49.14.将1~8这8个自然数分别填人下图数阵中的8个圆圈,使得数阵中各条直线上的三个数之和都相等,那么A和B两个圆圈中所填的数之差(大数减小数)是________。
