《频率的稳定性》频率与概率PPT课件(1)
合集下载
频率的稳定性(优秀经典公开课课件)
这 100 个品牌的食用油可能有 20 个不合格，对吗？ [提示] 对．
以你对合格率的理解，这 100 个品牌的食用油，不合格的应有多少 个？
[提示] 可能有 20 个，也可能一个也没有．
◎结论形成 1．频率的稳定性 一般地，随着试验次数 n 的增大，频率偏离概率的幅度会缩小，即事件 A 发 生的频率 fn(A)会逐渐___稳__定__于___事件 A 发生的概率 P(A)，我们称频率的这个性 质为频率的稳定性． 2．频率稳定性的作用 可以用频率 fn(A)估计概率 P(A)．
题型三 游戏的公平性(一题多变) [例 3] 某校高二年级(1)(2)班准备联合举办晚会，组织者欲使晚会气氛热烈、 有趣，策划整场晚会以转盘游戏的方式进行，每个节目开始时，两班各派一人先 进行转盘游戏，胜者获得一件奖品，负者表演一个节目．(1)班的文娱委员利用分 别标有数字 1,2,3,4,5,6,7 的两个转盘(如图所示)，设计了一种游戏方案：两人同时 各转动一个转盘一次，将转到的数字相加，和为偶数时(1)班代表获胜，否则(2) 班代表获胜．该方案对双方是否公平？为什么？
【思考】 频率和概率有什么区别和联系？
[提示] 区别： (1)在相同的条件下重复 n 次试验，观察某一事件 A 是否出现，称 n 次试验中 事件 A 出现的次数 nA 为事件 A 出现的频数，称事件 A 出现的比例 fn(A)＝nnA为事 件 A 出现的频率． (2)概率是度量随机事件发生的可能性大小的量．
(2)为了保证游戏的公平性，应当选择方案 A，这是因为方案 A 是猜“是奇 数”和“是偶数”的概率均为 0.5，从而保证了该游戏的公平性．
[规律方法] 游戏公平性的标准及判断方法
(1)游戏规则是否公平，要看对游戏的双方来说，获胜的可能性或概率是否相 同．若相同，则规则公平，否则就是不公平的．
课件 频率与概率(1)
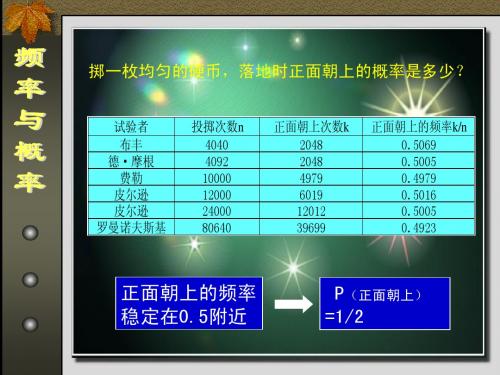
掷一枚均匀的硬币，落地时正面朝上的概率是多少？
试验者 布丰 德·摩根 费勒 皮尔逊 皮尔逊 罗曼诺夫斯基 投掷次数n 4040 4092 10000 12000 24000 80640 正面朝上次数k 2048 2048 4979 6019 12012 39699 正面朝上的频率k/n 0.5069 0.5005 0.4979 0.5016 0.5005 0.4923
六个同学组成一组，根据原来的试验分别 汇总其中两人、三人、四人、五人、六人的试验 数据，相应得到试验60次、90次、120次、150次、 180次时两枚棋子数字和等于2的频率，并制作相 应的统计图表，你能估计两枚棋子数字和等于2的 概率大约是多少吗？ 试验次数n 两枚棋子数字和是 2的频数m 两枚棋子数字和是 2的频率m/n 60 90 120 150 180
谈谈你在这节课中的收获
弄清了一种关系：频率与概率的关系
了解了一种方法：用多次试验频率去估计概率
加深了一点体会：互相合作交流的重要性
作业
完成课本161页
P（正面朝上） =1/2
试验规则：
在纸杯中放进一黑一白两枚棋子， 先从杯中随机摸出一枚棋子，记住颜 色后又放回杯中，摇晃一下杯子后再 从杯中随机摸出一枚棋子…… 规定：黑棋表示1 白棋表示2 规定：黑棋表示1，白棋表示2；连
续摸两回记为一次试验。 续摸两回记为一次试验。 一次试验
试验目的： 一次试验中两枚棋子表示的数字和可能有哪些值？ 通过试验，估计两枚棋子数字和等 于3的概率。
每人做30次试验，并在表中作好数据记 录，然后计算出相应的频率。 =1 =2
两枚棋子数字和 频数m 频率m/30 请你根据自己的试验结果估计两枚棋子数字和等 于3的概率是多少? 2 3 4
做一做：
试验者 布丰 德·摩根 费勒 皮尔逊 皮尔逊 罗曼诺夫斯基 投掷次数n 4040 4092 10000 12000 24000 80640 正面朝上次数k 2048 2048 4979 6019 12012 39699 正面朝上的频率k/n 0.5069 0.5005 0.4979 0.5016 0.5005 0.4923
六个同学组成一组，根据原来的试验分别 汇总其中两人、三人、四人、五人、六人的试验 数据，相应得到试验60次、90次、120次、150次、 180次时两枚棋子数字和等于2的频率，并制作相 应的统计图表，你能估计两枚棋子数字和等于2的 概率大约是多少吗？ 试验次数n 两枚棋子数字和是 2的频数m 两枚棋子数字和是 2的频率m/n 60 90 120 150 180
谈谈你在这节课中的收获
弄清了一种关系：频率与概率的关系
了解了一种方法：用多次试验频率去估计概率
加深了一点体会：互相合作交流的重要性
作业
完成课本161页
P（正面朝上） =1/2
试验规则：
在纸杯中放进一黑一白两枚棋子， 先从杯中随机摸出一枚棋子，记住颜 色后又放回杯中，摇晃一下杯子后再 从杯中随机摸出一枚棋子…… 规定：黑棋表示1 白棋表示2 规定：黑棋表示1，白棋表示2；连
续摸两回记为一次试验。 续摸两回记为一次试验。 一次试验
试验目的： 一次试验中两枚棋子表示的数字和可能有哪些值？ 通过试验，估计两枚棋子数字和等 于3的概率。
每人做30次试验，并在表中作好数据记 录，然后计算出相应的频率。 =1 =2
两枚棋子数字和 频数m 频率m/30 请你根据自己的试验结果估计两枚棋子数字和等 于3的概率是多少? 2 3 4
做一做：
《频率与概率》课件
$P(A|B) = frac{P(B|A) cdot P(A)}{P(B)}$，其中$P(A|B)$表示在 事件B发生的条件下，事件A发生的概率。
贝叶斯定理应用
贝叶斯定理在统计学、机器学习、决策理论等领域有广泛应用， 尤其是在处理不确定性和主观概率方面。
全概率公式
全概率公式定义
全概率公式用于计算一个复杂事件发生的概率，该复杂事件可以分 解为若干个互斥且完备的子事件。
市场调查
在市场调查中，全概率公式可以用于计算某个事件发生的概率，例如消费者购买某产品的概率，可以通过考虑不 同市场细分和购买行为的条件概率来计算。
感谢您的观看
THANKS
概率的乘法性质是指一个事件发生后，另一个事件接着发生的概率等于前一事 件的概率乘以后一事件的概率。
详细描述
如果事件A和事件B有因果关系，即B的发生依赖于A的发生，那么 P(AB)=P(A)P(B)。如果事件A和事件B没有因果关系，那么P(AB)=P(A)P(B)。
条件概率与独立性
总结词
条件概率是指在某个已知条件下，一个事件发生的概率。独立性是指两个事件之 间没有相互影响。
中心极限定理的实例
在投掷骰子实验中，随着投掷次数的增加，出现3.5次朝上的频率 逐渐接近正态分布。
大数定律与中心极限定理的应用
在统计学中的应用01 Nhomakorabea大数定律和中心极限定理是统计学中的基本原理，用于估计样
本均值和方差，以及进行假设检验和置信区间的计算。
在金融领域的应用
02
大数定律和中心极限定理用于金融风险管理和资产定价，例如
方差
方差是随机变量取值与其期望的差的 平方的平均值，表示随机变量取值的 离散程度。
05
大数定律与中心极限定理
贝叶斯定理应用
贝叶斯定理在统计学、机器学习、决策理论等领域有广泛应用， 尤其是在处理不确定性和主观概率方面。
全概率公式
全概率公式定义
全概率公式用于计算一个复杂事件发生的概率，该复杂事件可以分 解为若干个互斥且完备的子事件。
市场调查
在市场调查中，全概率公式可以用于计算某个事件发生的概率，例如消费者购买某产品的概率，可以通过考虑不 同市场细分和购买行为的条件概率来计算。
感谢您的观看
THANKS
概率的乘法性质是指一个事件发生后，另一个事件接着发生的概率等于前一事 件的概率乘以后一事件的概率。
详细描述
如果事件A和事件B有因果关系，即B的发生依赖于A的发生，那么 P(AB)=P(A)P(B)。如果事件A和事件B没有因果关系，那么P(AB)=P(A)P(B)。
条件概率与独立性
总结词
条件概率是指在某个已知条件下，一个事件发生的概率。独立性是指两个事件之 间没有相互影响。
中心极限定理的实例
在投掷骰子实验中，随着投掷次数的增加，出现3.5次朝上的频率 逐渐接近正态分布。
大数定律与中心极限定理的应用
在统计学中的应用01 Nhomakorabea大数定律和中心极限定理是统计学中的基本原理，用于估计样
本均值和方差，以及进行假设检验和置信区间的计算。
在金融领域的应用
02
大数定律和中心极限定理用于金融风险管理和资产定价，例如
方差
方差是随机变量取值与其期望的差的 平方的平均值，表示随机变量取值的 离散程度。
05
大数定律与中心极限定理
《频率的稳定性》概率初步
03
频率的稳定性的计算方法
频率的稳定性的计算公式
频率稳定性计算公式
频率稳定度通常用频率偏移与标称频率的比 值表示，即 Δf/f。其中，Δf是实际频率与标 称频率的偏差，f是标称频率。频率稳定度 越高，意味着频率偏差越小，信号质量越佳 。
频率稳定度的单位
频率稳定度的单位通常是赫兹（Hz），也 可以用百分比表示。在用百分比表示时，频
在物理学、经济学、工程学等领域中，频率的稳定性被广泛应用于信号处理、数据分析、模型预测等 方面。
频率的稳定性的重要性
频率的稳定性是时间序列数据的一个重 要特征，它可以反映出一个系统的内在 规律和性质。
在数据分析中，频率的稳定性对于预测未来 的趋势和变化具有重要意义，因为稳定的频 率可以提供更可靠和精确的预测结果。
THANKS
感谢观看
率稳定度 = (Δf/f) × 100%。
频率的稳定性的计算实例
要点一
例子1
一个10 MHz的信号源，其频率稳定度为10 Hz，那么 它的频率偏差为 Δf = 10 Hz，标称频率 f = 10 MHz 。根据频率稳定度的计算公式，其频率稳定度为 (Δf/f) × 100% = (10 Hz/10 MHz) × 100% = 0.01%。
03
风险管理模型
频率稳定性对于构建风险管理模型也 至关重要。这些模型通常基于历史数 据和分析，以预测和减轻潜在的市场 风险。
在气象预报中的应用
气候预测
频率稳定性在气候预测中发挥重要作用。通过对历史气象数据的频率分析，可以预测未来一段时间内 的天气趋势，为农业、交通和能源等行业提供决策依据。
天气预报
06
频率的稳定性在概率初步中的应 用
在金融风险管理中的应用
25.2.2《频率与概率》ppt课件
2. 频率与概率
观看图片
复习导入
（一）什么是概率？ 表示一个事件发生的可能性大小的数， 叫做该事件的概率(probability). P （事件 A ） 事件A发生的概率表示方法为: 例：你投掷手中的一枚普通的六面体骰 子，“出现数字1”的概率是多少？ 解：Ｐ（出现数字1）=1/6 读作：“出现数字1”的概率为 1/6
n Ｐ( Ａ) ＝ m
2、怎样计算事件发生的概率？
计算事件的概率时要弄清以下两 点：
① 要清楚关注的是发生哪个或哪些结果个数； ② 要清楚所有机会均等的结果的个数； 以上两种结果个数之比就是关注的结果发生的概 率. 简单事件的概率公式为： 关注的结果的个数 P（事件发生）＝ 所有机会均等的结果的个数
解： P（取出取出两枚硬币总值小于1.5元） =
3 = 6
1 2
课堂小结
通过本节课的学习，对本章的知识你 有哪些新的认识和体会？ 获得哪些分析概率的方法？你还有哪 些问题？请与同伴交流.
课后作业
1.从教材习题中选取， 2.完成练习册本课时的习题.
学习的敌人是自己的满足，要认真学习 一点东西，必须从不自满开始。对自己， “学而不厌”，对人家，“诲人不倦”， 我们应取这种态度。 —— 毛泽东
0.857
0.892
0.910
0.913
0.893
0.903
0.905
当试验的油菜籽的粒数很多时,油菜籽发芽的频 率 接近于常数0.9,在它附近摆动.
m 在大量重复进行同一试验时,事件A发生的频率 总是接近于 n 某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记做
P(A)
注： (1)求一个事件的概率的基本方法是通过大量的重复试验; (2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A的 概率; (3)概率是频率的稳定值,而频率是概率的近似值;
《概率》统计与概率PPT(频率与概率)
人教版高中数学B版必修二
第五章 统计与概率
5.3 概率
5.3.4
频率与概率
- .
-1-
课标阐释
思维脉络
1.在具体情境中,了
解随机事件发生的
不确定性和频率的
稳定性.
2.正确理解概率的
意义,利用概率知
识正确理解现实生
活中的实际问题.
3.理解概率的意义
以及频率与概率的
区别.
4.通过该内容的学
习,培养逻辑推
700÷0.95≈1 789.
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
概率的应用——数学建模
典例为了估计水库中鱼的尾数,可以使用以下的方法:先从水库
中捕出2 000尾鱼,给每尾鱼做上记号,不影响其存活,然后放回水库.
经过适当的时间,让其和水库中的其他鱼充分混合,再从水库中捕
出500尾,查看其中有记号的鱼,有40尾,试根据上述数据,估计水库
194
500
470
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率.
1 000
954
2 000
1 902
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
解:
抽取球数
优等品数
优等品出
现的频率
50
45
100
92
200
194
500
470
1 000
954
2 000
1 902
0.9
0.92
0.97
A.事件 C 发生的概率为
1
10
1
B.此次检查事件 C 发生的频率为10
第五章 统计与概率
5.3 概率
5.3.4
频率与概率
- .
-1-
课标阐释
思维脉络
1.在具体情境中,了
解随机事件发生的
不确定性和频率的
稳定性.
2.正确理解概率的
意义,利用概率知
识正确理解现实生
活中的实际问题.
3.理解概率的意义
以及频率与概率的
区别.
4.通过该内容的学
习,培养逻辑推
700÷0.95≈1 789.
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
概率的应用——数学建模
典例为了估计水库中鱼的尾数,可以使用以下的方法:先从水库
中捕出2 000尾鱼,给每尾鱼做上记号,不影响其存活,然后放回水库.
经过适当的时间,让其和水库中的其他鱼充分混合,再从水库中捕
出500尾,查看其中有记号的鱼,有40尾,试根据上述数据,估计水库
194
500
470
(1)在上表中填上优等品出现的频率;
(2)估计该批乒乓球优等品的概率.
1 000
954
2 000
1 902
课堂篇探究学习
探究一
探究二
思维辨析
当堂检测
解:
抽取球数
优等品数
优等品出
现的频率
50
45
100
92
200
194
500
470
1 000
954
2 000
1 902
0.9
0.92
0.97
A.事件 C 发生的概率为
1
10
1
B.此次检查事件 C 发生的频率为10
人教A版(2019)高中数学必修第二册教学课件：第十章 10.3 频率与概率(共20张PPT)
常考题型
题型一 频率与概率意义的理解
例1.下列关于概率和频率的叙述中正确的有
.（把符合
条件的所有答案的序号填在横线上）
①随机事件的频率就是概率；②随机事件的概率是一个确定的
数值，而频率不是一个确定的数值；③频率是客观存在的，与
试验次数无关；④概率是随机的，在试验前不能确定；
⑤概率可以看作频率在理论上的期望值，它从数量上反映了随
解：（1）这种鱼卵的孵化概率为
7 645 10 000
＝0.764
5.
（2）由（1）知，30 000个鱼卵大约能孵化出
30 000×0.764 5＝22 935（尾）鱼苗.
（3）要孵化出5
000尾鱼苗，需准备
5 000 0.764 5
≈6
540个鱼卵.
题型四 利用随机模拟法估计概率
例4 已知某运动员每次投篮命中的概率低于40%，现采用随机模 拟的方法估计该运动员三次投篮恰有两次命中的概率：先由计 算器产生0到9之间取整数值的随机数，指定1，2，3，4表示命 中，5，6，7，8，9，0表示不命中；再以每三个随机数为一组 ，代表三次投篮的结果.经随机模拟产生了20组随机数： 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989据此估计，该 运动员三次投篮恰有两次命中的概率为 （ ）
【变式训练2】［2019·西藏林芝一中高三模拟］某超市为了解顾客的购物量
及结算时间等信息，安排一名员工随机收集了在该超市购物的100名顾客的相
关数据，如下表所示：已知这100位顾客中一次性购物超过8件的顾客占55%.
一次性购物数量
1至 4件
(苏科版)八年级数学下册《8.3频率与概率》ppt课件
初中数学 八年级(下册)
8.3 频率与概率
昭阳湖初级中学八年级数学备课组
8.3 频率与概率（1）
一个随机事件发生的可能性有大有小
飞机失事会给旅客造成意外伤害．一家保险公 司要为购买机票的旅客进行保险，应该向旅客收 取多少保费呢？
我们通常用一个数值来表示一个事件发生的可 能性的大小， 这个数值称为这个事件的概率。
在实际生活中，人们常把试验次数很大时，事件发生 的频率作为其概率的估计值
在硬地上掷1枚图钉,通常会出现两种情况： 钉尖着地,钉尖不着地； （1）任意掷1枚图钉，你认为是“钉尖着地”的可 能性大，还是“钉尖不着地”的可能性大？ （2）做“掷图钉试验”，每人掷1枚图钉20次，分别 汇总5人、10人、15人、„、50人„„的试验结果，并 将试验数据填入下表：
你能根据实验数 据估计钉尖不着 地的概率吗？
课堂练习： 课本48页
作业：
《个事件， 则我们就用P(A)表示事件发生的概率． 若用A表示一个必然事件，则P(A)=1 若用A表示一个不可能事件，则P(A)=0 若用A表示一个随机事件，则 。
做抛掷硬币试验，记录正面朝上的 次数及总次数。
正面 反面
抛掷次数n
50
m n
100 150 200 250 300 350 400 450 500
试验数据如下：
抛掷次数n 钉尖不着地的频数 m 钉尖不着地的频率 100 200 300 400 500 600 700 800 900 1000 „
64 0.64
118
189
252
310
360 434 488 549 610
0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61
8.3 频率与概率
昭阳湖初级中学八年级数学备课组
8.3 频率与概率（1）
一个随机事件发生的可能性有大有小
飞机失事会给旅客造成意外伤害．一家保险公 司要为购买机票的旅客进行保险，应该向旅客收 取多少保费呢？
我们通常用一个数值来表示一个事件发生的可 能性的大小， 这个数值称为这个事件的概率。
在实际生活中，人们常把试验次数很大时，事件发生 的频率作为其概率的估计值
在硬地上掷1枚图钉,通常会出现两种情况： 钉尖着地,钉尖不着地； （1）任意掷1枚图钉，你认为是“钉尖着地”的可 能性大，还是“钉尖不着地”的可能性大？ （2）做“掷图钉试验”，每人掷1枚图钉20次，分别 汇总5人、10人、15人、„、50人„„的试验结果，并 将试验数据填入下表：
你能根据实验数 据估计钉尖不着 地的概率吗？
课堂练习： 课本48页
作业：
《个事件， 则我们就用P(A)表示事件发生的概率． 若用A表示一个必然事件，则P(A)=1 若用A表示一个不可能事件，则P(A)=0 若用A表示一个随机事件，则 。
做抛掷硬币试验，记录正面朝上的 次数及总次数。
正面 反面
抛掷次数n
50
m n
100 150 200 250 300 350 400 450 500
试验数据如下：
抛掷次数n 钉尖不着地的频数 m 钉尖不着地的频率 100 200 300 400 500 600 700 800 900 1000 „
64 0.64
118
189
252
310
360 434 488 549 610
0.59 0.63 0.63 0.62 0.60 0.62 0.61 0.61 0.61