129951133054687500直线与平面、两平面之间的相对位置PPT课件
合集下载
空间直线与平面平面与平面之间的位置关系PPT课件

1.两个平面平行—— 没有一条公共直线.
a
第10页/共20页
练习:
若M∈平面α,M∈平面β,则不同平面α与β
的
B
位置关系是 ( )
A.平行
B.相交
【C.解重析合】由公理3知D,.α不与确β相定交.
第11页/共20页
例2 如果三个平面两两相交,那么它们的交线有多少条? 画出图形表示你的结论.
判断直线与平面的位置关系关键在于——判断 直线与平面的公共点的个数.
第2页/共20页
a α
a a
A
α
α
直线在平面α内 直线与平面α相交
直线与平面α平行
有无数个交点 a⊂α
有且只有一个交点 a ∩ α= A
无交点 a∥α
第3页/共20页
下面画法错误的是:
a
α
α
a a
α
直线应画在面内
第4页/共20页
答:有可能1条交线,也有可能3条交线.
(1)
(2)
第12页/共20页
(3)
1.若直线a不平行于平面α,且 立的是( B )
A.α内所有直线与a异面 B.α内不存在与a平行的直线 C.α内存在唯一的直线与a平行 D.α内的直线与a都相交
则下列结论成
第13页/共20页
2.平面α//平面β,且直线a在平面α内,下列四个 命题: ①a与β内的所有直线都平行; ②a与β内的无数条直线平行; ③a与β内的任一直线都不垂直; ④a与β无公共点. 其中错误命题的序号为__①___③_____.
直线与平面的位置关系
位置 关系
a在α内
a与α相交 a与α平行
公共点 符号表示
有无数个公共 点
高中数学《空间中直线与平面之间的位置关系 平面与平面之间的位置关系 》课件

知识点一 空间中直线与平面的位置关系
3
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
知识点二 两个平面的位置关系 1.位置关系:有且只有两种:
①两个平面平行—— □1 没有公共点 ; ②两个平面相交—— □2 有一条公共直线.
2.符号表示:两个平面 α,β 平行,记为 α∥β;两个平
直线与平面平行直线与平面没有公共点
1按点公的共个直线与平直有线唯与一平公面共相点交直线与平面
数分类面不平行直线在平面内直线与平面有
无数个公共点
6
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
按是否直线在平面内 (2)在内平分面类直线在平面外直直线线与与平平面面相平交行 2.判断直线与平面及平面与平面的位置关系常用定义 法和反证法.
7
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
1.(教材改编,P49,例 4)判一判(正确的打“√”,错 误的打“×”)
(1)若直线 a 在平面 α 外,则 a∥α.( × ) (2)若直线与平面不相交,则直线与平面平行.( × ) (3)若 a∥b,b⊂α,则 a 平行于 α 内的无数条直线.( √ )
13
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
拓展提升 直线与平面位置关系的判断方法
(1)空间中直线与平面只有三种位置关系:直线在平面 内、直线与平面相交、直线与平面平行.
(2)在判断直线与平面的位置关系时,这三种情形都要 考虑到,避免疏忽或遗漏.另外,我们可以借助空间几何图 形,把要判断关系的直线、平面放在某些具体的空间图形中, 以便于正确作出判断,避免凭空臆断.
3
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
知识点二 两个平面的位置关系 1.位置关系:有且只有两种:
①两个平面平行—— □1 没有公共点 ; ②两个平面相交—— □2 有一条公共直线.
2.符号表示:两个平面 α,β 平行,记为 α∥β;两个平
直线与平面平行直线与平面没有公共点
1按点公的共个直线与平直有线唯与一平公面共相点交直线与平面
数分类面不平行直线在平面内直线与平面有
无数个公共点
6
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
按是否直线在平面内 (2)在内平分面类直线在平面外直直线线与与平平面面相平交行 2.判断直线与平面及平面与平面的位置关系常用定义 法和反证法.
7
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
1.(教材改编,P49,例 4)判一判(正确的打“√”,错 误的打“×”)
(1)若直线 a 在平面 α 外,则 a∥α.( × ) (2)若直线与平面不相交,则直线与平面平行.( × ) (3)若 a∥b,b⊂α,则 a 平行于 α 内的无数条直线.( √ )
13
课前自主预习
课堂互动探究
课堂达标自测
课后课时精练
数学 ·必修2
拓展提升 直线与平面位置关系的判断方法
(1)空间中直线与平面只有三种位置关系:直线在平面 内、直线与平面相交、直线与平面平行.
(2)在判断直线与平面的位置关系时,这三种情形都要 考虑到,避免疏忽或遗漏.另外,我们可以借助空间几何图 形,把要判断关系的直线、平面放在某些具体的空间图形中, 以便于正确作出判断,避免凭空臆断.
《工程制图》精品课件—2-3直线、平面与平面的相对位置:平行问题、相交问题
● ●
⑵ 直线为特殊位置
b m
k
a
●
●
n
1(2)
c
b
k● 2 m(n) ● 1
●
a
c
空间及投影分析 直线MN为铅垂线,其 水平投影积聚成一个点, 故交点K的水平投影也积聚 在该点上。 作图 用面上取点法 ① 求交点 ② 判别可见性 点Ⅰ位于平面上,在前; 点Ⅱ位于MN上,在后。故 k 2为不可见。
a f
c
① 求交线 ② 判别可见性 点Ⅰ在FH上,点Ⅱ在BC上, 点Ⅰ在上,点Ⅱ在下,故fh可 见,n2不可见。
•
V
直线与特殊位置平面相交
b
N n
a
P m
k
B
K a b k M c n k
A PH a
c
C H
m
b
c
由于特殊位置平面的某些投影有积聚性,交点可直接求出。
•
V
判断直线的可见性
a
P m
b
n
N
k
B
K
A PH M a
c a n k b
b k c
C H
m
c
特殊位置线面相交,根据平面的积聚性投影,能直接判别直线的可见性。
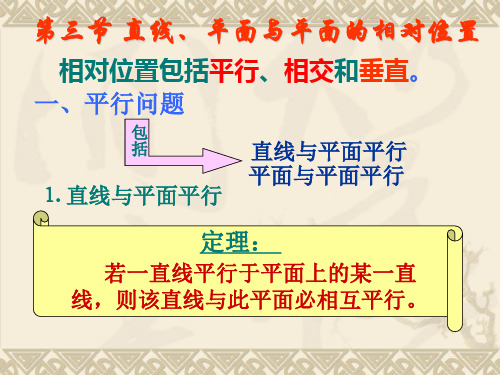
第三节 直线、平面与平面的相对位置
相对位置包括平行、相交和垂直。 一、平行问题
包 括
⒈ 直线与平面平行
直线与平面平行 平面与平面平行
定理:
若一直线平行于平面上的某一直 线,则该直线与此平面必相互平行。
例1:过M点作直线MN平行于平面△ABC。
b
有无数解
n
c m
●
a
b
n a
●
c
⑵ 直线为特殊位置
b m
k
a
●
●
n
1(2)
c
b
k● 2 m(n) ● 1
●
a
c
空间及投影分析 直线MN为铅垂线,其 水平投影积聚成一个点, 故交点K的水平投影也积聚 在该点上。 作图 用面上取点法 ① 求交点 ② 判别可见性 点Ⅰ位于平面上,在前; 点Ⅱ位于MN上,在后。故 k 2为不可见。
a f
c
① 求交线 ② 判别可见性 点Ⅰ在FH上,点Ⅱ在BC上, 点Ⅰ在上,点Ⅱ在下,故fh可 见,n2不可见。
•
V
直线与特殊位置平面相交
b
N n
a
P m
k
B
K a b k M c n k
A PH a
c
C H
m
b
c
由于特殊位置平面的某些投影有积聚性,交点可直接求出。
•
V
判断直线的可见性
a
P m
b
n
N
k
B
K
A PH M a
c a n k b
b k c
C H
m
c
特殊位置线面相交,根据平面的积聚性投影,能直接判别直线的可见性。
第三节 直线、平面与平面的相对位置
相对位置包括平行、相交和垂直。 一、平行问题
包 括
⒈ 直线与平面平行
直线与平面平行 平面与平面平行
定理:
若一直线平行于平面上的某一直 线,则该直线与此平面必相互平行。
例1:过M点作直线MN平行于平面△ABC。
b
有无数解
n
c m
●
a
b
n a
●
c
空间直线与平面平面与平面之间的位置关系课件

它通过将几何问题转化为代数问 题,利用代数工具进行求解,再
将其结果转换回几何意义。
解析法的基础是坐标系和坐标轴 的设置,通过坐标表示点、线、
面的位置和关系。
解析法的应用实例
1 2
确定点在空间中的位置
通过设定三维坐标系,将点的坐标表示为(x, y, z) ,进而确定其在空间中的位置。
计算两点之间的距离
缺点
解析法需要设定坐标系和坐标轴,对于某些不规则或抽象的几何形状可能难以应用。此外,解析法在处理复杂的 几何问题时可能较为繁琐,需要较高的数学技巧和计算能力。
05
CATALOGUE
空间几何问题几何法解析
几何法的基本概念
01
几何法是一种通过图形和空间想 象来解析问题的方法,它利用点 、线、面等几何元素之间的关系 来解决问题。
详细描述
直线与平面平行意味着直线不在 平面内,并且直线与平面没有交 点。在几何学中,这表示为直线 与平面平行或线面平行。
直线与平面相交
总结词
当直线与平面有且仅有一个公共点时 ,直线与平面相交。
详细描述
直线与平面相交意味着直线与平面有 一个共同的点,即交点。除了交点之 外,直线与平面上其他点不重合。
几何法的优缺点分析
优点
几何法直观易懂,可以通过图形和空间想象来帮助理解问题,对于一些直观的问题,几何法可以快速 找到解决方案。
缺点
对于一些复杂的问题,几何法可能会比较繁琐,需要花费较多的时间和精力,而且有时候难以找到合 适的几何元素和关系来解决。
THANKS
感谢观看
03
CATALOGUE
空间几何定理及其应用
直线与平面的定理
直线与平面平行
如果一条直线与平面内无数条直 线平行,则这条直线与该平面平
直线与平面平面与平面的相对关系PPT课件

作X1 平行于a' b'
a1
d1 b1
c1 e1
f1 作X2轴垂直于a1b1
θ
f'2
d'2
第61页/共76页
(四) 把一般位置平面变为投影面垂直面 [例题8] 求平面与H面的夹角α [例题9] 求平面与V面的夹角β [例题10] 求平面ABC与直线DE的交点 [例题11] 求两平行平面A BC与 DFE的距离 [例题12] 求平面ABC与平面DEF的交线 [例题13] 求平面ABC与平面DEF的交线
§2.5.1 直线与平面、平面与平面的平行
一、直线与平面相互平行 二、平面与平面相互平行
第1页/共76页
一、直线与平面相互平行
1. 直线与一般面相互平行 2. 直线与投影面垂直面相互平行
第2页/共76页
1. 直线与一般面相互平行
(1)直线与一般面相互平行 直线与平面平行的几何条件:当平面
外一直线平行于平面内一已知直线时, 则直线与该平面平行。 (2) [例题1]
二、一般位置直线与投影面垂直面相交
1. 直线与投影面垂直面相交 2. [例题3] 求四棱锥与正垂面Q的截交线
第14页/共76页
1. 一般位置直线与投影面垂直面相交
c'
c 一般位置直线与投影面垂直面相交时,该面的积聚投影与直线的同面投影的交点, 就是所求交点的同面投影。
第15页/共76页
2. [例题3] 求四棱锥与正垂面Q的截交线。
a1 b1
第52页/共76页
a1 b1
(三) 把一般位置直线变为投影面垂直线
[例题3] 把一般位置直线变为投影面垂直线 [例题4] 求两平行线的距离 [例题5] 求点C到直线AB的距离 [例题6] 求两直线AB与CD的公垂线 [例题7] 求两相邻斗壁的夹角
a1
d1 b1
c1 e1
f1 作X2轴垂直于a1b1
θ
f'2
d'2
第61页/共76页
(四) 把一般位置平面变为投影面垂直面 [例题8] 求平面与H面的夹角α [例题9] 求平面与V面的夹角β [例题10] 求平面ABC与直线DE的交点 [例题11] 求两平行平面A BC与 DFE的距离 [例题12] 求平面ABC与平面DEF的交线 [例题13] 求平面ABC与平面DEF的交线
§2.5.1 直线与平面、平面与平面的平行
一、直线与平面相互平行 二、平面与平面相互平行
第1页/共76页
一、直线与平面相互平行
1. 直线与一般面相互平行 2. 直线与投影面垂直面相互平行
第2页/共76页
1. 直线与一般面相互平行
(1)直线与一般面相互平行 直线与平面平行的几何条件:当平面
外一直线平行于平面内一已知直线时, 则直线与该平面平行。 (2) [例题1]
二、一般位置直线与投影面垂直面相交
1. 直线与投影面垂直面相交 2. [例题3] 求四棱锥与正垂面Q的截交线
第14页/共76页
1. 一般位置直线与投影面垂直面相交
c'
c 一般位置直线与投影面垂直面相交时,该面的积聚投影与直线的同面投影的交点, 就是所求交点的同面投影。
第15页/共76页
2. [例题3] 求四棱锥与正垂面Q的截交线。
a1 b1
第52页/共76页
a1 b1
(三) 把一般位置直线变为投影面垂直线
[例题3] 把一般位置直线变为投影面垂直线 [例题4] 求两平行线的距离 [例题5] 求点C到直线AB的距离 [例题6] 求两直线AB与CD的公垂线 [例题7] 求两相邻斗壁的夹角
空间中直线与平面之间的位置关系PPT完美课件

空间中直线与平面之间的位置关系
04.09.2020
思考?(一)
线段A′B所在直线与长方
体ABCD-A′B′C′D′
的六个面所在平面有几种
位置关系?
D′
A′
D
A
C′ B′
C B
【目标导学】
学习目标:
1.直线与平面的三种位置关系
【主体自学】 :看书P53至54 限时5分钟
思考下面问题: 1.直线与平面有哪三种位置关系? 2.如何表示直线与平面的三种位置关系?
//
•l
l
空间中直线与平面之间的位置关系PPT 完美课 件
切割长方体
• 一个长方体切一刀可以分成多少块?2 • 一个长方体切两刀可以分成多少块?3或4 • 一个长方体切三刀可以分成多少块?
4或6或7或8 D′
A′ D
B′ C
空间中直线与平面之间的位置关系PPT 完美课 件
A
B
空间中直线与平面之间的位置关系PPT 完美课 件
空间中直线与平面之间的位置关系PPT 完美课 件
不妨再思考一题?
1、一个平面把空间分为几部分? 2 2、二个平面把空间分为几部分? 3或4 3、三个平面把空间分为几部分? 4或6或7或8
了解一下: n个平面最多可将空间分为 (n3 + 5n + 6)/6个部分
空间中直线与平面之间的位置关系PPT 完美课 件
空间中直线与平面之间的位置关系PPT 完美课 件
•
2对教育来说,阅读是最基础的教学 手段, 教育里 最关键 、最重 要的基 石就是 阅读。
•
3但是现在,我们的教育在一定程度 上,还 不够重 视阅读 ,尤其 是延伸 阅读和 课外阅 读。
04.09.2020
思考?(一)
线段A′B所在直线与长方
体ABCD-A′B′C′D′
的六个面所在平面有几种
位置关系?
D′
A′
D
A
C′ B′
C B
【目标导学】
学习目标:
1.直线与平面的三种位置关系
【主体自学】 :看书P53至54 限时5分钟
思考下面问题: 1.直线与平面有哪三种位置关系? 2.如何表示直线与平面的三种位置关系?
//
•l
l
空间中直线与平面之间的位置关系PPT 完美课 件
切割长方体
• 一个长方体切一刀可以分成多少块?2 • 一个长方体切两刀可以分成多少块?3或4 • 一个长方体切三刀可以分成多少块?
4或6或7或8 D′
A′ D
B′ C
空间中直线与平面之间的位置关系PPT 完美课 件
A
B
空间中直线与平面之间的位置关系PPT 完美课 件
空间中直线与平面之间的位置关系PPT 完美课 件
不妨再思考一题?
1、一个平面把空间分为几部分? 2 2、二个平面把空间分为几部分? 3或4 3、三个平面把空间分为几部分? 4或6或7或8
了解一下: n个平面最多可将空间分为 (n3 + 5n + 6)/6个部分
空间中直线与平面之间的位置关系PPT 完美课 件
空间中直线与平面之间的位置关系PPT 完美课 件
•
2对教育来说,阅读是最基础的教学 手段, 教育里 最关键 、最重 要的基 石就是 阅读。
•
3但是现在,我们的教育在一定程度 上,还 不够重 视阅读 ,尤其 是延伸 阅读和 课外阅 读。
人教版新课标高中数学第二章空间中直线与平面之间的位置关系 (共30张PPT)教育课件

B'
D
C
A
B
结论: 两个平面之间的关系有且只有两种:
(1)两个平面平行――没有公共点; (2)两个平面相交――有一条公共直线。 想一想:两个平面平行应怎样画?相交又怎样画?
画两个互相平行的平面时,要注意使表示 平面的两个平行四边形的对应边平行
图1
图2
√
×
小结:空间中面与面的位置关系
图形
文字语言(读法)
符号语言
两个平面无公共点
b
两个平面平行
α∥β
β
两个平面有一公共直线 两个平面相交
b l
α
例2:已知 ∥β, a b b
则直线a和直线b的位置关系如何?
a
b
bb
探究:
1.直线与直线,直线与平面,平面与平面之间 没有公共点就平行,平行就没有公共点,这句 话对吗?为什么?
2.直线与直线,直线与平面,平面与平面之间 有两个公共点时,它们的位置关系如何?
不同在任何一个平面内的两条直线叫做异面直线
一、研探新知
(1)一支笔所在直线与一个作业本所在 的平面,可能有几种位置关系?
(2)如图,线段A´B所在直线与长方体 ABCD-A´B´C´D´的六个面所在平面有几 种位置关系?
D´
C´
A´
B´
D A
C B
二、新课
1、交流归纳:直线与平面的位置关系有且只有三种:
例3 已知直线a在平面α外,则 ( D) (A)a∥α (B)aα=A (C)直线a与平面α至少有一个公共点 (D)直线a与平面α至多有一个公共点。
巩固练习: 新疆 王新敞 奎屯
1.选择题
(1)以下命题(其中a,b表示直线,表示平面) ①若a∥b,b,则a∥ ②若a∥,b∥,则 a∥b ③若a∥b,b∥,则a∥ ④若a∥, b,则a∥b 其中正确命题的个数是 ( A )
机械制图CAI课件 第03章直线、平面的相对位置

第三章 直线、平面的相对位置
本章主要介绍直线、平面的相对位 置,包括平行关系、相交关系和垂直关 系,以及点、线、面综合题及其解法。
第三章 直线、平面的相对位置
§3.1 平行关系 §3.2 相交关系 §3.3 垂直关系 §3.4 点、线、面综合题及其解法
§3.1 平行关系
§3.1.1 直线与平面平行
求△ABC与DE、FG两平面交线的正投影图
选通过点A、E 的
正垂面P 为辅助面, 求出一个三面共点K ;
又选过点A、F
的铅垂面Q为辅助面, 求出另一个三面共点 L;
连接K、L ,则
KL即为所求的交线。
(a)
(b)
P、Q 两平面都用迹线给出,且其同面迹线相交,即 PH∩QH=M,PV∩QV=N,则交点M、N是P、Q 两平面交线
c
k′l′∥a′d′,
b
则直线KL为所求。
d
l
c
a
k
[例2]试过K 点作一正平线,使之平行于P
平面。
因PV 是P 平面上特 殊的正平线,所以过点K
作KL∥PV, 即作k′l′∥PV,kl∥X
轴,则直线KL为所求。
[例3]试过K点作一铅垂面P (用迹线表示) ,使之平行于AB直线 。
作铅垂面平行于AB 直 线,则PH必平行于ab 。
直线与平面平行的几何条件是:如果平面外 的一直线和这个平面上的一直线平行,则此直线 平行于该平面。
由于EF∥BD,且 BD 是ABC 平面上的一 直线,所以,直线EF 平行于ABC 平面。
[例1]试过K点作一水平线,使之平行于
△ABC 。
b
先在△ABC上
a
d k
l
作一水平线AD; 再
本章主要介绍直线、平面的相对位 置,包括平行关系、相交关系和垂直关 系,以及点、线、面综合题及其解法。
第三章 直线、平面的相对位置
§3.1 平行关系 §3.2 相交关系 §3.3 垂直关系 §3.4 点、线、面综合题及其解法
§3.1 平行关系
§3.1.1 直线与平面平行
求△ABC与DE、FG两平面交线的正投影图
选通过点A、E 的
正垂面P 为辅助面, 求出一个三面共点K ;
又选过点A、F
的铅垂面Q为辅助面, 求出另一个三面共点 L;
连接K、L ,则
KL即为所求的交线。
(a)
(b)
P、Q 两平面都用迹线给出,且其同面迹线相交,即 PH∩QH=M,PV∩QV=N,则交点M、N是P、Q 两平面交线
c
k′l′∥a′d′,
b
则直线KL为所求。
d
l
c
a
k
[例2]试过K 点作一正平线,使之平行于P
平面。
因PV 是P 平面上特 殊的正平线,所以过点K
作KL∥PV, 即作k′l′∥PV,kl∥X
轴,则直线KL为所求。
[例3]试过K点作一铅垂面P (用迹线表示) ,使之平行于AB直线 。
作铅垂面平行于AB 直 线,则PH必平行于ab 。
直线与平面平行的几何条件是:如果平面外 的一直线和这个平面上的一直线平行,则此直线 平行于该平面。
由于EF∥BD,且 BD 是ABC 平面上的一 直线,所以,直线EF 平行于ABC 平面。
[例1]试过K点作一水平线,使之平行于
△ABC 。
b
先在△ABC上
a
d k
l
作一水平线AD; 再
