晶体结构的计算
常见晶体模型及晶胞计算
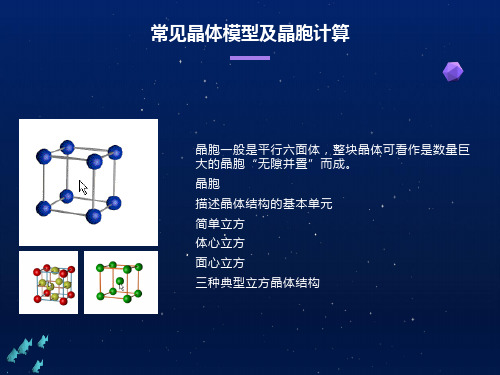
晶胞中微粒个数的计算,求化学式
小结:高考常见题型
1、(2013·江苏,21A(1)) 元素X 位于第四周期,其基态原子的内层轨道全部排满电子,且最外层电子数为2。元素Y基态原子的3p 轨道上有4个电子。
X与Y所形成化合物晶体的晶胞如右图所示。 ①在1个晶胞中,X离子的数目为 。 ②该化合物的化学式为 。
Mg、Zn、Ti 每个晶胞含 个原子 六方最密堆积的配位数 =12 2
④面心立方最密堆积(铜型)
Cu、Ag、Au 面心立方堆积的配位数 =12 每个晶胞含 个原子 4
面心立方最密堆积的空间占有率
=74%
金属晶体的四种堆积模型对比
堆积模型
采纳这种堆积的典型代表
(3)若NaCl晶体的密度为ρg/cm3,则 NaCl晶体中Na+与Na+间的最短距离是多少?
a/2
a/2
=
练习
CsCl的晶体结构
(1)每个Cs+( Cl-)周围等距且紧邻的Cl- (Cs+)有 个, Cs+( Cl-)的配位数为 。
8
8×1/8=1
6
——晶胞为体心立方体
8
(2)每个Cs+ ( Cl-)周围 等距且紧邻的Cs+ ( Cl-)有 个。
1
3
6
4
2
A
5
密置层
配位数为4
配位数为6
返
A
B
A
B
A
返
第三层的另一种排列方式,是将球对准第一层的 2,4,6 位,不同于 AB 两层的位置,这是 C 层。
1
2
3
4
5
6
1
2
3
晶体结构计算范文

晶体结构计算范文一、晶体结构计算的原理和方法晶体结构是由一个个原子或离子组成的有序排列,这种有序排列在结晶体中呈现出周期性的空间分布。
晶体结构计算的主要目标是确定晶体中原子的准确位置和其之间的相互作用,以及晶格参数等信息。
晶体结构计算的方法主要有实验方法、理论计算方法和模拟方法等。
实验方法包括X射线衍射、电子衍射、中子衍射等,通过分析衍射的图样可以确定晶体的结构。
理论计算方法主要是基于量子力学原理,包括密度泛函理论、分子力学等,通过计算得到晶体的能量、晶格参数和原子位置等信息。
模拟方法主要有分子动力学模拟、蒙特卡洛模拟等,模拟系统的原子运动和相互作用,从而得到晶体的结构和性质。
二、晶体结构计算的应用晶体结构计算在材料科学、物理化学等领域具有广泛的应用。
首先,晶体结构计算可以用于研究材料的物理和化学性质。
通过计算分析可以预测材料的电子能带结构、光学性质、磁性等,为材料的设计和应用提供理论基础。
其次,晶体结构计算可以用于材料的合成和工艺优化。
通过计算和模拟可以预测材料的晶体生长行为,优化合成工艺,提高材料的质量和性能。
此外,晶体结构计算还可以用于研究材料的相变过程、相图和微观性质变化等,对材料的相变机制和性质变化规律进行深入研究。
三、晶体结构计算的实际案例展示为了更好地展示晶体结构计算的应用,我们以典型的半导体材料硅Sio2为例进行分析。
硅是一种广泛应用于电子器件中的材料,其结构具有平面型和空间型两种。
通过晶体结构计算可以得到硅的结构参数、晶体中原子的位置等信息。
首先,通过X射线衍射实验可以得到硅的晶胞结构和晶格参数。
然后,利用密度泛函理论和分子动力学模拟等方法进行计算分析,得到硅晶体中原子的位置以及相互作用等信息。
通过计算和模拟可以发现硅晶体中的晶格缺陷、晶界和表面等问题,并对其进行优化和修复,得到具有优异性能的硅晶体材料。
在实际应用中,硅晶体的结构计算可以用于电子器件的设计和性能优化。
通过模拟和计算可以预测材料的电子能带结构,优化器件的导电性能和光学特性,提高器件的效率和可靠性。
晶体结构的分析与计算题和答案

晶体结构的分析与计算1.常见共价晶体结构的分析2.常见分子晶体结构的分析3.常见离子晶体结构的分析684F-:8;Ca2+:41.AB型化合物形成的晶体结构多种多样。
下图所示的几种结构所表示的物质最有可能是分子晶体的是()A.①③B.②⑤C.⑤⑥D.③④⑤⑥2.如图为几种晶体或晶胞的示意图:请回答下列问题:(1)上述晶体中,微粒之间以共价键结合形成的晶体是________。
(2)冰、金刚石、MgO、CaCl2、干冰5种晶体的熔点由高到低的顺序为______________________。
(3)NaCl晶胞与MgO晶胞相同,NaCl晶体的离子键________(填“大于”或“小于”)MgO 晶体的离子键,原因是___________________________________________________________。
(4)CaCl2晶体中Ca2+的配位数________。
(5)冰的熔点远高于干冰,除H2O是极性分子、CO2是非极性分子外,还有一个重要的原因是_______________________________________________________________________________。
3.[2017·全国卷Ⅲ,35(5)]MgO具有NaCl型结构(如图),其中阴离子采用面心立方最密堆积方式,X射线衍射实验测得MgO的晶胞参数为a=0.420 nm,则r(O2-)为________nm。
MnO 也属于NaCl型结构,晶胞参数为a′=0.448 nm,则r(Mn2+)为________nm。
4.Li2O具有反萤石结构,晶胞如图所示。
已知晶胞参数为0.466 5 nm,阿伏加德罗常数的值为N A,则Li2O的密度为________________________________________g·cm-3(列出计算式)。
5.[2018·全国卷Ⅱ,35(5)]FeS2晶体的晶胞如图所示。
几种常见的晶体模型及晶胞的计算

几种常见的晶体结构模型和晶胞的计算
知识建构
晶体结构与性质
氨的转化与生成氨晶的体转结化构与与生性成质
知识建构
一、 密置层
一、金属晶体
二维空间 非密置层
密置层
配位数(直接相切) 4
6
堆积方式
简单立方堆积 体心立方密堆积
面心立方最密堆积
结构示意图
六方最密堆积
晶胞
配位数
6
8
每个晶胞完整
拥有微粒数
1
2
R与a的关系
2R=a
12
12
4
2
2R=a
氨晶的体转结化构与与生性成质 知识建构 一、金属晶体
堆积方式
简单立方堆积 体心立方密堆积(A2) 面心立方最密堆积(A1) 六方最密堆积(A3 )
结构示意图
晶胞
每个晶胞完整拥
1
2
有微粒数
R与a的关系
2R=a
空间利用率
4
2
2R=aHale Waihona Puke b知识建构NaCl型
CsCl型
ZnS型
CaF2型
晶胞
F-
Ca2+
配位数
每个晶胞完整 拥有微粒数
Na+:6 Cl-:6 Na+:4 Cl-:4
Cs+:8 Cl-:8 Cs+:1 Cl-:1
Zn2+:4 S2-:4 Zn2+:4 S2-:4
Ca2+:8 F-:4 Ca2+:4 F-:8
符合物质
BaF2、PbF2、CeO2等
思考:1.NaCl晶胞中,距离最近且相等的Cl-的数目是多少?ZnS中的S2-?CaF2中的Ca2+? 12 思考:2. CsCl晶胞中,距离最近且相等的Cl-的数目是多少?Cs+? CaF2中的F-? 6
晶体结构的分析和计算

一、晶胞对组成晶胞的各质 点的占有率
立方晶胞
体心: 1 面心: 1/2 棱边: 1/4 顶点: 1/8
有关晶体的计算
1、当题给信息为晶体中最小重 复单元——晶胞(或平面结构)中 的微粒排列方式时,要运用空间想 象力,将晶胞在三维空间内重复延 伸,得到一个较完整的晶体结构, 形成求解思路。
例1:
因C60分子含30个双键,与极活泼的F2发生加成反应即可生成C60F60 (只 要指__出__“___C_6_0_含__3_0_个__双__键__”__即__可__,_但__答__“__因__C_6_0_含__有__双__键__”__不__行__)____.
(3)通过计算,确定C60分子所含单键数.C60分子所含单键数为___________. 可由欧拉定理计算键数(即棱边数):60+(12+20)-2=90 C60分子中单键为:90-30=60
例4:
金刚石晶体中 含有共价键形成的 C原子环,其中最
小的C环上有__6___
个C原子。
巩固练习一:
石墨晶体的层状结构,层内 为平面正六边形结构(如图), 试回答下列问题: (1)图中平均每个正六边形占
有C原子数为__2__个、占有的碳 碳键数为__3__个。
(2)层内7个六元环完全占有
的C原子数为1_4____个,碳原子
2、当题给信息为晶体中微粒 的排列方式时,可在晶体结构中 确定一个具有代表性的最小重复 单元——晶胞为研究对象,运用 点、线、面的量进行解答。
例2:
右图是石英晶 体平面示意图(它实 际上是立体的网状结 构),其中硅、氧原 子数之比为____.
1:2
例3:Байду номын сангаас
如图直线交点处 的圆圈为NaCl晶体中 Na+或Cl-所处位置, 晶体中,每个Na+周 围与它最接近的且距 离相等的Na+个数为: ____ 12
常见晶体模型及晶胞计算

常见晶体模型及晶胞计算晶体是由晶体胞重复堆积而成的,晶体胞是晶体的最小构造单元。
晶体的结构可以用晶胞参数表示,晶胞参数包括晶格常数、晶胞的角度、晶胞的体积等。
根据晶体的晶胞参数,可以推导出晶胞的几何形状和晶体的晶体类别。
根据晶体的晶胞形状,晶体可以分为立方晶系、四方晶系、六方晶系、正交晶系、单斜晶系和三斜晶系。
每个晶系又可以进一步分为各种晶体类别,如立方晶系下又有体心立方晶体和面心立方晶体等。
晶体模型描述了晶体的结构和排列方式。
常见的晶体模型有球模型、格点模型和球与棍模型。
1.球模型:球模型是一种简化的晶体表示方法,将晶体中的原子用球体表示,球的大小和颜色常用来表示原子的种类和其它信息。
2.格点模型:格点模型是用晶体胞中的原子位置来表示晶体结构的一种方法,晶体胞中的每个原子位置称为格点。
在格点模型中,晶体中的每个原子都用一个点来表示,这样形成了一个点阵,点阵反映了原子的排列方式。
常见的格点模型有立方格点模型、面心立方格点模型和体心立方格点模型。
3.球与棍模型:球与棍模型是一种结合了球模型和格点模型的晶体表示方法。
在球与棍模型中,每个原子用一个球来表示,不同原子之间用直线连接表示键的形成。
在进行晶胞计算时,需要确定晶体的晶胞参数。
晶胞参数可以通过实验测量得到,也可以通过计算方法获得。
晶胞计算主要包括以下几个步骤:1.实验测量:通过实验手段,如X射线衍射、电子衍射等,测量晶体的晶胞参数。
2.计算方法:根据晶体的晶胞参数和晶体的晶格类型,可以使用计算方法来预测和计算晶体的晶胞参数。
常见的计算方法有密度泛函理论(DFT)和分子力场(MM)等。
3.晶胞优化:通过晶胞优化算法,寻找晶体的最稳定结构。
晶胞优化算法可以通过改变晶胞参数、原子位置或局部结构等来寻找最低能量的晶体结构。
4.校正和验证:使用计算得到的晶胞参数进行校正和验证,与实验结果进行比较,确保计算结果的准确性和可靠性。
总之,晶体模型和晶胞计算是研究和描述晶体结构的重要工具。
晶胞计算技巧

晶胞计算技巧一、引言晶体结构的计算是固体物理和化学研究中的重要环节之一。
为了研究晶体的性质和行为,研究者经常需要进行晶胞计算。
晶胞计算是指通过计算机模拟和计算,研究晶体的结构和性质。
在晶胞计算中,有一些技巧和方法可以帮助我们更好地进行计算和分析。
本文将介绍一些常用的晶胞计算技巧。
二、晶胞的生成与优化在晶体结构计算中,首先要生成晶胞。
晶胞的生成可以通过实验测量得到,也可以通过计算方法来得到。
一种常用的计算方法是通过密度泛函理论(DFT)来计算晶胞的结构。
在生成晶胞后,还需要对晶胞进行优化。
晶胞的优化可以通过分子动力学模拟来实现,通过调整晶格参数和原子位置,使得晶胞能量达到最低。
三、晶胞的对称性分析晶胞的对称性分析可以帮助我们更好地理解和描述晶体的结构。
在晶胞计算中,可以通过对晶胞的对称性进行分析,得到晶体的空间群和点群。
晶体的空间群和点群描述了晶体中原子的排列方式和对称性。
通过对晶胞的对称性分析,我们可以得到关于晶体结构的更多信息。
四、电子结构计算在晶胞计算中,电子结构计算是一个重要的步骤。
电子结构计算可以通过密度泛函理论(DFT)来实现。
通过DFT计算,可以得到晶体的能带结构、态密度和电子密度等信息。
这些信息可以帮助我们研究晶体的导电性、磁性和光学性质等。
五、声子计算声子计算是晶胞计算中的另一个重要内容。
声子计算可以用来研究晶体的振动性质。
在声子计算中,可以计算晶体的声子能谱、声子态密度和声子热容等。
这些信息对于研究晶体的热传导和热膨胀等性质非常重要。
六、缺陷和表面计算在晶体中,常常存在各种缺陷和表面。
研究晶体的缺陷和表面性质对于理解晶体的性质和行为非常重要。
在晶胞计算中,可以通过引入缺陷和表面来研究晶体的性质。
通过计算和模拟,可以研究缺陷的形成和扩散机制,以及表面的催化性能和吸附性能等。
七、后处理和可视化在晶胞计算中,后处理和可视化是一个重要的环节。
通过后处理和可视化,可以对计算得到的数据进行分析和展示。
材料成分的计算公式

材料成分的计算公式在化学和工程领域,材料成分的计算是非常重要的。
通过计算材料的成分,我们可以了解材料的性质和用途,以及进行材料的设计和生产。
在本文中,我们将介绍一些常见的材料成分的计算公式,并探讨它们在实际应用中的意义和作用。
一、化学成分的计算公式。
化学成分是指材料中各种化学元素的含量。
在化学成分的计算中,我们通常使用质量分数或摩尔分数来表示各种化学元素的含量。
质量分数是指某种化学元素的质量与材料总质量的比值,通常用百分数表示;摩尔分数是指某种化学元素的摩尔数与所有化学元素摩尔数之和的比值。
化学成分的计算公式如下:质量分数 = (某种化学元素的质量 / 材料总质量) × 100%。
摩尔分数 = (某种化学元素的摩尔数 / 所有化学元素摩尔数之和)。
通过化学成分的计算,我们可以了解材料中各种化学元素的含量,从而确定材料的性质和用途。
例如,在合金材料的设计和生产中,我们可以通过计算各种化学元素的含量,调整合金的成分,以获得特定的性能和用途。
二、晶体结构的计算公式。
晶体结构是指材料中原子或离子的排列方式。
在晶体结构的计算中,我们通常使用晶胞参数和晶体结构参数来描述晶体的结构。
晶胞参数是指晶体中最小重复单元的几何参数,包括晶胞的长度、角度和对称性;晶体结构参数是指晶体中原子或离子的位置和排列方式。
晶体结构的计算公式如下:晶胞参数 = (晶胞的长度、角度和对称性)。
晶体结构参数 = (原子或离子的位置和排列方式)。
通过晶体结构的计算,我们可以了解材料的晶体结构和性质,从而确定材料的用途和加工方法。
例如,在金属材料的设计和生产中,我们可以通过计算晶体结构的参数,控制晶体的生长和形貌,以获得特定的性能和用途。
三、物理性质的计算公式。
物理性质是指材料的各种物理特性,包括密度、热导率、电导率等。
在物理性质的计算中,我们通常使用实验数据和理论模型来描述材料的物理性质。
例如,密度可以通过质量和体积的测量来计算,热导率可以通过热传导实验和热传导模型来计算,电导率可以通过电导实验和电导模型来计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
晶体结构是近几年来高考考查的重点和热点,特别是晶体结构的计算更是其中的重中之重,它体现了高考考试说明中提出的“将化学问题抽象为数学问题,利用数学工具,通过计算推理解决化学问题的能力”的要求。化学教学中,让学生学习和探究原子、离子、晶体结构等微观结构内容,可以促进学生形成比较丰满的三维空间概念,有效地带动学生进行丰富多样的三维空间想像。通过氯化钠、氯化铯、金刚石、石墨、干冰、二氧化硅等曲型晶体结构模型为落点来设计问题考查学生的三维空间思维能力。
从以上的分析可以看出,要正确确定晶体中距离最近的微粒的数目,首先要对晶体结构熟悉,其次要有良好的空间想象能力,要有以晶胞为核心向空间扩展的意识。
例6、二氧化硅晶体的结构计算:书本上介绍了二氧化硅晶体平面示意图(图8),图9表示空间网状示意图,图10表示二氧化硅的晶胞。试回答:
(1)30g二氧化硅中含有molSi-O键。
(2)最小的环上共有个原子,其中个氧原子,硅原子。
解析:(1)从图8,可以清楚地看到一个硅原子与周围的四个氧原子成键,故30g二氧化硅中含有的Si-O键为 。
一、离子晶体:
例1、图中NaCl晶体结构向三维空间延伸得到完美晶体。最近的Na+与Cl-核间距离为a×10-8cm,求晶体密度?
解析:截取一个1/8大的小立方体如图,因各顶点上的Na+或Cl-为8个小立方体共用,故小立方体占1/2个Na+,1/2个Cl-,即占1/2Na+—Cl-离子对。
立方体体积为:V=(a×10-8)3cm3
(2)FeS2中包含有“非极性共价键(S—S)、离子键”。晶体的密度为 。
二、原子晶体及石墨晶体
例5、金刚石结构中,一个碳原子与个碳原子成键,则每个碳原子实际形成的化学键为根;a mol金刚石中,碳碳键数为mol。
解析:从金刚石结构可以看出,一个碳原子与4个碳原子成键,但一根碳碳键是由两个碳原子形成,即每根碳碳键中,一个碳的原子的贡献为 ,故金刚石中,一个碳原子的实际成键数= ×4=2。故a mol金刚石中,碳碳键数为2a mol。
例3.有下列离子晶体结构示意图:●阳离子○阴离子
以M代表阳离子、N代表阴离子。
(1)请写出各离子晶体组成的表达式:
A_______,B________,C____________,D_________。
(2)已知黄铁矿的主要成份FeS2晶体具有A的空间结构。晶体中具有化学键类型是______________,若晶体结构A中相邻的阴阳离子间距离为acm,N2代表阿伏加德罗常数,则FeS2晶体的密度是___________g/cm2。
我们也可以选取一层原子(设有n个),若不计重复则可形成3n根碳碳键,实际形成的碳碳键数为 n根,同样可以计算出碳原子数与碳碳键数目比为2:3。
例7:C60分子是形如球状的多面体,如图6,该结构的建立是基于如下考虑:①C60分子中每个碳原子只跟相邻的3个碳原子形成化学键②C60分子只含有五边形和六边形。C70分子也可制得,它的分子模型可以与C60同样考虑而推知。通过计算确定C70分子中五边形和六边形数。
故密度:ρ=((1/2)个×58.5g·mol-1÷6.02×1023个·mol-1)/(a3×10-24cm3)=(48.6/a3)g·cm-3
例1:在氯化钠晶体中,与氯离子距离最近的钠离子有个;与氯离子距离最近的氯离子有个。
解析:我们可以选定中心的氯离子作为基准,设立方体的边长为a,则氯离子与钠离子之间的最近距离为 ,此钠离子位于立方体六个面的面心上,即有六个钠离子;氯离子间的最近距离为 ,共有12个。
解析:设五边形和六边形数分别为x和y,若形成独立的五边形和六边形所需碳原子数为5x+6y,由于每个碳原子与相邻的3个碳原子成键,故C70分子中的碳原子数可用 表示。故有如下关系:
=70①
再根据欧拉公式,多面体的顶点数、面数、棱边数之间的关系:
顶点数+面数-棱边数=2。对C70分子而言顶点即为碳原子数,面数为五边形和六边形数之和,棱边数为碳碳键数,碳碳键数目共有 ,故可得出如下式子:70+(x+y)- ×3×70=2②
例6:分选取一个正六边形(如图4),此结构中的碳原子数为6,而一个碳原子被三个六元碳环共用,故此正六边形中的碳原子数为6× =2。六边形中的任一条边(即碳碳键)均被2个正六边形共用,故正六边形中的碳碳键数为6× =3,所以碳原子数与碳碳键数目比为2:3。
(2)从图8看到最小的环上有8个原子(4个硅原子与4个氧子),但图8仅是平面示意图,它只表示了二氧化硅晶体中硅、氧原子的成键情况,而不能表示其立体结构。此时应观察图9,该结构可理解为:金刚石结构中的碳原子换成硅原子然后在两个硅原子之间嵌入一个氧原子。可看到形成的最小环上共有12个原子,其中6个为氧原子,6个为硅原子;Si-O键的夹角为为109°28′。
分析:(1)分析图10,离子都在立方体的顶点上,每个顶点都被8个类似的立方体共用,所以图10所表示的立方体中共有阳离子 个、阴离子 个,A的化学式为MN。观察图11,每个立方体单元中有阳离子“ ”个,阴离子共有“ ”个,所以B的化学式为 。观察图12,每个立方体单元中,共有阳离子“ ”个,阴离子1个,所以C的化学式为 。观察图13,每个立方体单元中共有阳离子“ ”,阴离子1个,所以,D的化学式为MN。
①②联立方程组可解得:x=12 y=25
三、分子晶体
例2:二氧化碳晶体中,与二氧化碳分子距离最近的二氧化碳分子有个。
解析:在图2的二氧化碳分子晶体结构中,8个二氧化碳分子处于正方体的8个顶点上,还有6个处于正方体的六个面的面心上。此时可选定面心的二氧化碳分子为基准,设正方体的边长为a,则二氧化碳分子间的最近距离为 ,从图中看有8个,它们分别位于该侧面的四个顶点及与之相连的四个面的面心上。此时应注意,图中所给出的结构仅是晶胞。所谓晶胞,是晶体中最小的重复结构单元,它能全面正确地表示晶体中各微粒的空间关系。也就是说晶体是以晶胞为核心向空间延伸而得到的,单个的晶胞不能表示整个晶体的结构。所以在我们观察晶体结构时应充分发挥空间想象的能力,要将晶胞向各个方向(上,下,左,右,前,后)扩展。图2向右扩展得图3(为容易观察,用 表示二氧化碳分子),从中可以看出与二氧化碳分子距离最近的二氧化碳分子有12个。
