2018届高考数学(文)大一轮复习:选修4-4 第2节 参数方程
2018年高考一轮人教版A数学理科 选修4-4 第2节参数方程
第二节 参数方程[考纲传真] 1.了解参数方程,了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程.1.曲线的参数方程一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x ,y 都是某个变数t 的函数⎩⎨⎧x =f (t ),y =g (t )并且对于t 的每一个允许值,由这个方程组所确定的点M (x ,y )都在这条曲线上,那么这个方程组就叫做这条曲线的参数方程,联系变数x ,y 的变数t 叫做参变数,简称参数.2.参数方程与普通方程的互化通过消去参数从参数方程得到普通方程,如果知道变数x ,y 中的一个与参数t 的关系,例如x =f (t ),把它代入普通方程,求出另一个变数与参数的关系y =g (t ),那么⎩⎨⎧x =f (t ),y =g (t )就是曲线的参数方程.在参数方程与普通方程的互化中,必须使x ,y 的取值范围保持一致.3.常见曲线的参数方程和普通方程何意义且几何意义为:|t |是直线上任一点M (x ,y )到M 0(x 0,y 0)的距离.1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)参数方程⎩⎨⎧x =f (t ),y =g (t )中的x ,y 都是参数t 的函数.( )(2)过M 0(x 0,y 0),倾斜角为α的直线l 的参数方程为⎩⎨⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数).参数t 的几何意义表示:直线l 上以定点M 0为起点,任一点M (x ,y )为终点的有向线段M 0M →的数量.( )(3)方程⎩⎨⎧x =2cos θ,y =1+2sin θ表示以点(0,1)为圆心,以2为半径的圆.( )(4)已知椭圆的参数方程⎩⎨⎧x =2cos t ,y =4sin t (t 为参数),点M 在椭圆上,对应参数t =π3,点O 为原点,则直线OM 的斜率为 3.( )[答案] (1)√ (2)√ (3)√ (4)×2.(教材改编)曲线⎩⎨⎧x =-1+cos θ,y =2+sin θ(θ为参数)的对称中心( )A .在直线y =2x 上 B.在直线y =-2x 上 C .在直线y =x -1上D.在直线y =x +1上B [由⎩⎨⎧ x =-1+cos θ,y =2+sin θ,得⎩⎨⎧cos θ=x +1,sin θ=y -2,所以(x +1)2+(y -2)2=1.曲线是以(-1,2)为圆心,1为半径的圆, 所以对称中心为(-1,2),在直线y =-2x 上.]3.(教材改编)在平面直角坐标系中,曲线C :⎩⎪⎨⎪⎧x =2+22t ,y =1+22t(t 为参数)的普通方程为________.x -y -1=0 [由x =2+22t ,且y =1+22t , 消去t ,得x -y =1,即x -y -1=0.]4.在平面直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.曲线C 1的极坐标方程为ρ(cos θ+sin θ)=-2,曲线C 2的参数方程为⎩⎨⎧x =t 2,y =22t (t 为参数),则C 1与C 2交点的直角坐标为________. (2,-4) [由ρ(cos θ+sin θ)=-2,得x +y =-2.①由⎩⎨⎧x =t 2,y =22t ,消去t 得y 2=8x .② 联立①②得⎩⎨⎧x =2,y =-4,即交点坐标为(2,-4).]5.(2016·江苏高考)在平面直角坐标系xOy 中,已知直线l 的参数方程为⎩⎪⎨⎪⎧x =1+12t ,y =32t(t 为参数),椭圆C 的参数方程为⎩⎨⎧x =cos θ,y =2sin θ(θ为参数).设直线l 与椭圆C 相交于A ,B 两点,求线段AB 的长.[解] 椭圆C 的普通方程为x 2+y 24=1.2分将直线l 的参数方程⎩⎪⎨⎪⎧x =1+12t ,y =32t 代入x 2+y 24=1,得⎝ ⎛⎭⎪⎫1+12t 2+⎝ ⎛⎭⎪⎫32t 24=1,即7t 2+16t =0,8分解得t 1=0,t 2=-167,所以AB =|t 1-t 2|=167.10分已知直线l 的参数方程为⎩⎨⎧x =a -2t ,y =-4t(t 为参数),圆C 的参数方程为⎩⎨⎧x =4cos θ,y =4sin θ(θ为参数). (1)求直线l 和圆C 的普通方程;(2)若直线l 与圆C 有公共点,求实数a 的取值范围. [解] (1)直线l 的普通方程为2x -y -2a =0,2分 圆C 的普通方程为x 2+y 2=16.4分 (2)因为直线l 与圆C 有公共点,故圆C 的圆心到直线l 的距离d =|-2a |5≤4,8分解得-25≤a ≤2 5.10分[规律方法] 1.将参数方程化为普通方程,消参数常用代入法、加减消元法、三角恒等变换消去参数.2.把参数方程化为普通方程时,要注意哪一个量是参数,并且要注意参数的取值对普通方程中x 及y 的取值范围的影响,要保持同解变形.[变式训练1] 在平面直角坐标系xOy 中,若直线l :⎩⎨⎧x =t ,y =t -a (t 为参数)过椭圆C :⎩⎨⎧x =3cos φ,y =2sin φ(φ为参数)的右顶点,求常数a 的值.【导学号:01772440】[解] 直线l 的普通方程为x -y -a =0, 椭圆C 的普通方程为x 29+y 24=1,4分 所以椭圆C 的右顶点坐标为(3,0), 若直线l 过椭圆的右顶点(3,0), 则3-0-a =0,所以a =3.10分已知曲线C :x 24+y 29=1,直线l :⎩⎨⎧x =2+t ,y =2-2t(t 为参数).【导学号:01772441】(1)写出曲线C 的参数方程,直线l 的普通方程;(2)过曲线C 上任意一点P 作与l 夹角为30°的直线,交l 于点A ,求|P A |的最大值与最小值.[解] (1)曲线C 的参数方程为⎩⎨⎧x =2cos θ,y =3sin θ(θ为参数).直线l 的普通方程为2x +y -6=0.4分(2)曲线C 上任意一点P (2cos θ,3sin θ)到l 的距离为d =55|4cos θ+3sin θ-6|,则|P A |=d sin 30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43.8分 当sin(θ+α)=-1时,|P A |取得最大值,最大值为2255. 当sin(θ+α)=1时,|P A |取得最小值,最小值为255.10分 [规律方法] 1.解决直线与圆的参数方程的应用问题时,一般是先化为普通方程,再根据直线与圆的位置关系来解决问题.2.对于形如⎩⎨⎧x =x 0+at ,y =y 0+bt (t 为参数),当a 2+b 2≠1时,应先化为标准形式后才能利用t 的几何意义解题.[变式训练2] (2017·石家庄质检)在平面直角坐标系xOy 中,圆C 的参数方程为⎩⎨⎧x =4cos θ,y =4sin θ(θ为参数),直线l 经过点P (1,2),倾斜角α=π6. (1)写出圆C 的普通方程和直线l 的参数方程;(2)设直线l 与圆C 相交于A ,B 两点,求|P A |·|PB |的值. [解] (1)由⎩⎨⎧x =4cos θ,y =4sin θ,消去θ,得圆C 的普通方程为x 2+y 2=16.2分又直线l 过点P (1,2)且倾斜角α=π6, 所以l 的参数方程为⎩⎪⎨⎪⎧ x =1+t cos π6,y =2+t sin π6,即⎩⎪⎨⎪⎧x =1+32t ,y =2+12t(t 为参数).4分(2)把直线l 的参数方程⎩⎪⎨⎪⎧x =1+32t ,y =2+12t代入x 2+y 2=16,得⎝ ⎛⎭⎪⎫1+32t 2+⎝ ⎛⎭⎪⎫2+12t 2=16,t 2+(3+2)t -11=0,所以t 1t 2=-11,8分由参数方程的几何意义,|P A |·|PB |=|t 1t 2|=11.10分1⎩⎨⎧x =3cos α,y =sin α(α为参数).以坐标原点为极点,以x 轴的正半轴为极轴,建立极坐标系,曲线C 2的极坐标方程为ρsin ⎝ ⎛⎭⎪⎫θ+π4=2 2.(1)写出C 1的普通方程和C 2的直角坐标方程;(2)设点P 在C 1上,点Q 在C 2上,求|PQ |的最小值及此时P 的直角坐标. [解] (1)C 1的普通方程为x 23+y 2=1,2分 由于曲线C 2的方程为ρsin ⎝ ⎛⎭⎪⎫θ+π4=22,所以ρsin θ+ρcos θ=4,因此曲线C 2的直角坐标方程为x +y -4=0.4分 (2)由题意,可设点P 的直角坐标为(3cos α,sin α).因为C 2是直线,所以|PQ |的最小值即为P 到C 2的距离d (α)的最小值,8分 又d (α)=|3cos α+sin α-4|2=2⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫α+π3-2,当且仅当α=2k π+π6(k ∈Z )时,d (α)取得最小值,最小值为2,此时P 的直角坐标为⎝ ⎛⎭⎪⎫32,12.10分[规律方法] 1.参数方程和极坐标方程的综合题,求解的一般方法是分别化为普通方程和直角坐标方程后求解.当然,还要结合题目本身特点,确定选择何种方程.2.数形结合的应用,即充分利用参数方程中参数的几何意义,或者利用ρ和θ的几何意义,直接求解,可化繁为简.[变式训练3] (2017·石家庄市质检)在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =22t ,y =3+22t(t 为参数),在以O 为极点,x 轴正半轴为极轴的极坐标系中,曲线C 的极坐标方程为ρ=4sin θ-2cos θ.(1)求直线l 的普通方程与曲线C 的直角坐标方程;(2)若直线l 与y 轴的交点为P ,直线l 与曲线C 的交点为A ,B ,求|P A ||PB |的值.[解] (1)直线l 的普通方程为x -y +3=0, ∵ρ2=4ρsin θ-2ρcos θ,∴曲线C 的直角坐标方程为(x +1)2+(y -2)2=5.4分 (2)将直线l 的参数方程⎩⎪⎨⎪⎧x =22t ,y =3+22t (t 为参数)代入曲线C :(x +1)2+(y -2)2=5,得到t 2+22t -3=0,8分∴t 1t 2=-3,∴|P A ||PB |=|t 1t 2|=3.10分[思想与方法]1.参数方程化普通方程常用的消参技巧:代入消元、加减消元、平方后加减消元等,经常用到公式:cos 2θ+sin 2θ=1,1+tan 2θ=1cos 2θ.2.利用曲线的参数方程求解两曲线间的最值问题是行之有效的好方法. 3.将参数方程化为普通方程,将极坐标方程化为直角坐标方程,然后在直角坐标系下对问题求解,化生为熟,充分体现了转化与化归思想的应用.[易错与防范]1.将参数方程化为普通方程时,要注意两种方程的等价性.在消去参数的过程中,要注意x ,y 的取值范围.2.确定曲线的参数方程时,一定要根据实际问题的要求确定参数的取值范围,必要时通过限制参数的范围去掉多余的解.3.设过点M (x 0,y 0)的直线l 交曲线C 于A ,B 两点,若直线的参数方程为⎩⎨⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数)注意以下两个结论的应用: (1)|AB |=|t 1-t 2|; (2)|MA |·|MB |=|t 1·t 2|.。
2018年高考数学人教A版一轮复习课时分层提升练 六十一 选修4-4 2参数方程 含解析 精品

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时分层提升练六十一参数方程(45分钟60分)1.(10分)(2016·全国卷Ⅰ)在直角坐标系xOy中,曲线C1的参数方程为错误!未找到引用源。
(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cosθ.(1)说明C1是哪一种曲线,并将C1的方程化为极坐标方程.(2)直线C3的极坐标方程为θ=α0,其中α0满足tanα0=2,若曲线C1与C2的公共点都在C3上,求a.【解析】(1)错误!未找到引用源。
(t为参数,a>0),所以x2+(y-1)2=a2. ①所以C1为以(0,1)为圆心,a为半径的圆,方程为x2+y2-2y+1-a2=0.因为x2+y2=ρ2,y=ρsinθ,所以ρ2-2ρsinθ+1-a2=0,即为C1的极坐标方程.(2)C2:ρ=4cosθ,两边同乘ρ,得ρ2=4ρcosθ,因为ρ2=x2+y2,ρcosθ=x,所以x2+y2=4x.即(x-2)2+y2=4. ②C3:化为普通方程为y=2x,由题意:C1和C2的公共弦所在直线即为C3.①-②得:4x-2y+1-a2=0,即为C3,所以1-a2=0,所以a=1.2.(10分)(2016·全国卷Ⅱ)在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程.(2)直线l的参数方程是错误!未找到引用源。
(t为参数),l与C交于A,B两点,|AB|=错误!未找到引用源。
,求l的斜率.【解题提示】(1)给出的圆的方程为普通方程,要求其极坐标方程,直接套用公式转化即可.(2)由直线l的参数方程可知,直线过原点,可写出其普通方程,利用几何法建立斜率的方程,解方程即可.【解析】(1)整理圆的方程得x2+y2+12x+11=0,由错误!未找到引用源。
高考数学总复习 第2节 参数方程课件 新人教A版选修44

数的关系 y=g(t)
x=ft ,那么 y=gt 就是曲线的参数方程.
第五页,共70页。
在参数方程与普通(pǔtōng)方程的互化中,x,y的取值范围必 须保持一致.
第六页,共70页。
三、常见曲线的参数方程的一般形式
1.直线的参数方程
经过点 P0(x0,y0),倾斜角为 α 的直线的参数方程为
x= x0+tcos α y= y0+tsin α
第十四页,共70页。
2.若 P(2,-1)为圆xy==15+sin5θcos θ, (θ 为参数且 0≤θ
<2π)的弦的中点,则该弦所在的直线方程为( )
A.x-y-3=0
B.x+2y=0
C.x+y-1=0
D.2x-y-5=0
第十五页,共70页。
解析:由xy= =15+sin5θc,os θ 消去参数 θ,得(x-1)2+y2=25, ∴圆心 C(1,0),∴kCP=-1. ∴弦所在的直线的斜率为 1. ∴弦所在的直线方程为 y-(-1)=1·(x-2), 即 x-y-3=0,故选 A.
第二十页,共70页。
解析:曲线
C1:xy==34++csions
θ θ
(θ 为参数)的直角坐标方
程为(x-3)2+(y-4)2=1,可知曲线 C1 是以(3,4)为圆心,1 为半径的圆;曲线 C2:ρ=1 的直角坐标方程是 x2+y2=1, 故 C2 是以原点为圆心,1 为半径的圆.由题意知|AB|的最小 值即为分别在两个圆上的两点 A,B 间的最短距离.由条件
① ②
①2+②2 得 x2+(y-1)2=1,
即所求普通方程为 x2+(y-1)2=1,
答案(dáàn):x2+(y-1)2=1
第二十六页,共70页。
2018高考数学(理)一轮复习课件 选修4-4 坐标系与参数方程 第2讲分层演练直击高考

故当 t=0 时,|PC|取得最小值, 此时,点 P 的直角坐标为(3,0).
4 . (2017· 合肥市第一次教学质量检测)已知直线 l: 1 x=1+2t (t 为参数),以坐标原点为极点,x 轴的非负半轴 y= 3+ 3t 2 为极轴建立极坐标系, 曲线 C 的极坐标方程为 ρ2-2 3ρsin θ =a(a>-3). (1)将曲线 C 的极坐标方程化为直角坐标方程; (2)若曲线 C 与直线 l 有唯一公共点,求 a 的值.
[解 ]
(1)因为 ρ2=4ρ(cos θ+sin θ)-6,
所以 x2+y2=4x+4y-6, 所以 x2+y2-4x-4y+6=0, 即(x-2)2+(y-2)2=2 为圆 C 的直角坐标方程. 所以所求的圆 C
x=2+ 的参数方程为 y=2+
2cos θ, (θ 为参数). 2sin θ
(2)由(1)可得 x+y=4+ 2(sin θ+cos θ)
=4+2sinθ
π + . 4
π 当 θ= , 4 即点 P 的直角坐标为(3,3)时, x+y 取得最大值,为 6.
3.(2015· 高考陕西卷)在直角坐标系 xOy 中,直线 l 的参数方 1 x=3+2t, 程为 (t 为参数).以原点为极点,x 轴正半轴为极 y= 3t 2 轴建立极坐标系,⊙C 的极坐标方程为 ρ=2 3sin θ. (1)写出⊙C 的直角坐标方程; (2)P 为直线 l 上一动点,当 P 到圆心 C 的距离最小时,求 P 的直角坐标.
化简得 t2+t-a-2=0. 因为曲线 C 与直线 l 仅有唯一公共点, 所以 Δ=1-4(-a-2)=0, 9 解得 a=- . 4
5 . (2017· 广西第一次质量检测 ) 已知直线 l 的参数方程为
高考数学一轮复习选修44坐标系与参数方程课件新人教A版理

3
cos +sin
(2)C3 是一条过原点且斜率为正值的直线,
C3 的极坐标方程为 θ=α,α∈ 0,
π
2
,
= 2cos,
联立 C1 与 C3 的极坐标方程
= ,
得 ρ=2cos α,即|OA|=2cos α.
3
= cos +sin ,
联立 C1 与 C2 的极坐标方程
= ,
-11知识梳理
1
双基自测
2
3
4
5
2.若原点与极点重合,x 轴正半轴与极轴重合,则点(-5,-5√3)的极
坐标是(
)
π
A. 10, 3
2π
C. -10,- 3
4π
B. 10, 3
2π
D. 10, 3
关闭
设点(-5,-5√3)的极坐标为(ρ,θ),
-5 √3
则 tan θ=
-5
= √3.
4π
因为 x<0,所以最小正角 θ= ,
由圆 C1 与圆 C2 的方程相减可得公共弦所在的直线方程为
4x-2y+1=0.
圆心(1,1)到直线 4x-2y+1=0 的距离 d=
故弦长|AB|=2 1-
3 2
√20
=
√55
5
.
|4-2+1|
42 +(-2)2
=
3
,
√20
-24考点1
考点2
考点3
考点4
考点5
(2)解 ①圆 O:ρ=cos θ+sin θ,即 ρ2=ρcos θ+ρsin θ,
3
3
得 ρ=cos +sin ,即|OB|=cos +sin ,
选修4-4 第二讲 参数方程 复习课

反思与感悟 (1)关于折线段的长度和或长度差的最大值或最小值的求 法,常常利用对称性以及两点之间线段最短解决. (2)有关点与圆、直线与圆的最大值或最小值问题,常常转化为经过圆 心的直线、圆心到直线的距离等.
跟踪训练 3 已知曲线 C:x42+y92=1,直线 l:yx==22-+2t,t (t 为参数). (1)写出曲线C的参数方程,直线l的普通方程;
解答
(2)直线
l
的参数方程是xy= =ttcsions
α, α
(t 为参数),l 与圆 C 交于 A,B 两点,
|AB|= 10,求 l 的斜率.
解答
解 方法一 在(1)中建立的极坐标系中,直线l的极坐标方程为θ=
α(ρ∈R).
设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方 程,得ρ2+12ρcos α+11=0.
(3)椭圆 中心在原点,对称轴为坐标轴的椭圆b2x2+a2y2=a2b2(a>b>0)的参数方程 为(4)_双__曲__xy线_= =__ab_csio_ns_φ_φ_,___(_φ__为__参_.数) 中心在原点,对称轴为坐标轴的双曲线b2x2-a2y2=a2b2(a>0,b>0)的参 数方程为____xy_= =__ab_st_aen_c_φφ_,____(φ__为__参__数. )
解
曲线
C
的参数方程为xy==23csions
θ, θ
(θ 为参数).
直线l的普通方程为2x+y-6=0.
解答
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最
大值与最小值.
解 曲线 C 上任意一点 P(2cos θ,3sin θ)到 l 的距离为 d= 55|4cos θ+3sin θ-6|,
2018高考数学真题 理科 选修4-4 2考点1 参数方程与普通方程的互化
选修4-4 坐标系与参数方程第二节 参数方程考点1 参数方程与普通方程的互化(2018·全国卷Ⅲ(理))选修4-4:坐标系与参数方程在平面直角坐标系xOy 中,⊙O 的参数方程为{x =cos θ,y =sin θ(θ为参数),过点(0,-√2)且倾斜角为α的直线l 与⊙O 交于A ,B 两点.(1)求α的取值范围;(2)求AB 中点P 的轨迹的参数方程.【解析】(1)⊙O 的直角坐标方程为x 2+y 2=1.当α=π2时,l 与⊙O 交于两点.当α≠π2时,记tan α=k ,则l 的方程为y =kx -√2.l 与⊙O 交于两点当且仅当√2|√1+k 2<1,解得k <-1或k >1,即α∈(π2,3π4)或α∈(π4,π2). 综上,α的取值范围是(π4,3π4).(2)l 的参数方程为 {x =t cos α,y =−√2+t sin α(t 为参数,π4<α<3π4). 设A ,B ,P 对应的参数分别为t A ,t B ,t P ,则t P =t A +t B2,且t A ,t B 满足t 2-2√2t sin α+1=0.于是t A +t B =2√2sin α,t P =√2sin α.又点P 的坐标(x ,y )满足{x =t p cos α,y =−√2+t p sin α,所以点P 的轨迹的参数方程是{x =√22sin 2α,y =−√22−√22cos 2α(α为参数,π4<α<3π4).【答案】见解析(2018·全国Ⅱ卷(理))选修4-4:坐标系与参数方程在直角坐标系xOy 中,曲线C 的参数方程为{x =2cos θ,y =4sin θ(θ为参数),直线l 的参数方程为{x =1+tcos α,y =2+tsin α(t 为参数).(1)求C 和l 的直角坐标方程;(2)若曲线C 截直线l 所得线段的中点坐标为(1,2),求l 的斜率.【解析】(1)曲线C 的直角坐标方程为x 24+y 216=1.当cos α≠0时,l 的直角坐标方程为y =tan α·x +2-tan α,当cos α=0时,l 的直角坐标方程为x =1.(2)将l 的参数方程代入C 的直角坐标方程,整理得关于t 的方程(1+3cos 2α)t 2+4(2cos α+sin α)t -8=0.①因为曲线C 截直线l 所得线段的中点(1,2)在C 内,所以①有两个解,设为t 1,t 2,则t 1+t 2=0.又由①得t 1+t 2=-4(2cosα+sinα)1+3cos 2α,故2cos α+sin α=0,于是直线l 的斜率k =tan α=-2. 【答案】见解析。
2018年高考数学(文)一轮复习文档选修4-4 坐标系与参数方程 第1讲坐标系 Word版含答案
第讲 坐标系 , )
.坐标系
()伸缩变换
设点(,)是平面直角坐标系中的任意一点,在变换φ:的作用下,
点(,)对应到点(λ,μ),称φ为平面直角坐标系中的伸缩变换.
()极坐标系
在平面内取一个定点,叫做极点;自极点引一条射线,叫做极轴;再选一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.
设是平面内一点,极点与点的距离叫做点的极径,记为ρ;以极轴为始边,射线为终边的角叫做点的极角,记为θ,有序数对(ρ,θ)叫做点的极坐标,记为(ρ,θ)..直角坐标与极坐标的互化
把直角坐标系的原点作为极点,轴的正半轴作为极轴,且在两坐标系中取相同的长度单位.设是平面内任意一点,它的直角坐标、极坐标分别为(,)和(ρ,θ),则θ,=ρθ,))θ=()(≠)W.))
.直线的极坐标方程
若直线过点(ρ,θ),且极轴到此直线的角为α,则它的方程为:ρ(θ-α)=ρ(θ-α).
几个特殊位置的直线的极坐标方程:
()直线过极点:θ=θ和θ=π+θ;
()直线过点(,)且垂直于极轴:ρθ=;
()直线过且平行于极轴:ρθ=.
.圆的极坐标方程
若圆心为(ρ,θ),半径为,则该圆的方程为:
ρ-ρρ(θ-θ)+ρ-=.
几个特殊位置的圆的极坐标方程:
()当圆心位于极点,半径为:ρ=;。
高考数学(人教A版)一轮复习课件:选修4-4-2参数方程
2
4
解得t1=0,t2=
16 7
,
由直线参数方程的意义,得|AB|=|t1-t2|=
16 . 7
【规律方法】
直线的参数方程在交点问题中的应用
已知直线l经过点M0(x0,y0),倾斜角为α,点M(x,y)为l上
任意一点,则直线l的参数方程为
x y
x0 y0
tcos, tsin
(t为参
数).
(1)若M1,M2是直线l上的两个点,对应的参数分别为t1,
此时P点的坐标为(3,0).
【加固训练】
1.(2014·江苏高考)在平面直角坐标系xOy中,已知直
线l的参数方程
x 1
2 t, 2
(t是参数),
y 2
2t 2
直线l与抛物线y2=4x相交于A,B两点,求线段AB的长.
【解析】把直线l:x+y=3代入抛物线y2=4x 并整理得x2-10x+9=0, 所以交点A(1,2),B(9,-6), 故|AB|= 82 (8)2 8 2.
6
(1)写出直线l的参数方程.
(2)设直线l与圆x2+y2=4相交于A,B两点,求点P到A,B两
点的距离之积.
【解析】(1)直线l的参数方程为
x y
1 1
tcos π ,
ts即in π6,
6
x 1
3 t, 2
y
1
1 2
t.
(2)把直线
x
1
代23入t, x2+y2=4,
y
1
1 2
t
得 (1 3 t)2 (=141, t)2
x a rcos,
__y___b__r_s_in____ (θ为参数)
高考复习配套讲义:选修4-4 第2讲 参数方程
第2讲 参数方程[最新考纲]1.了解参数方程,了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆的参数方程.3.掌握直线的参数方程及参数的几何意义,能用直线的参数方程解决简单的相关问题.知 识 梳 理1.曲线的参数方程在平面直角坐标系xOy 中,如果曲线上任意一点的坐标x ,y 都是某个变量t 的函数⎩⎨⎧x =f (t ),y =g (t ).并且对于t 的每一个允许值上式所确定的点M (x ,y )都在这条曲线上,则称上式为该曲线的参数方程,其中变量t 称为参数. 2.一些常见曲线的参数方程(1)过点P 0(x 0,y 0),且倾斜角为α的直线的参数方程为⎩⎨⎧x =x 0+t cos αy =y 0+t sin α(t 为参数).(2)圆的方程(x -a )2+(y -b )2=r 2的参数方程为⎩⎨⎧x =a +r cos θy =b +r sin θ(θ为参数).(3)椭圆方程x 2a 2+y 2b 2=1(a >b >0)的参数方程为⎩⎨⎧x =a cos θy =b sin θ(θ为参数).(4)抛物线方程y 2=2px (p >0)的参数方程为⎩⎨⎧x =2pt 2y =2pt (t 为参数).诊 断 自 测1.极坐标方程ρ=cos θ和参数方程⎩⎨⎧x =-1-t ,y =2+t (t 为参数)所表示的图形分别是________.①直线、直线;②直线、圆;③圆、圆;④圆、直线.解析 ∵ρcos θ=x ,∴cos θ=x ρ代入到ρ=cos θ,得ρ=xρ,∴ρ2=x ,∴x 2+y 2=x 表示圆.又∵⎩⎪⎨⎪⎧x =-1-t ,y =2+t ,相加得x +y =1,表示直线.答案 ④2.若直线⎩⎨⎧x =1-2t ,y =2+3t (t 为实数)与直线4x +ky =1垂直,则常数k =________.解析 参数方程⎩⎪⎨⎪⎧x =1-2t ,y =2+3t ,所表示的直线方程为3x +2y =7,由此直线与直线4x +ky =1垂直可得-32×⎝ ⎛⎭⎪⎫-4k =-1,解得k =-6.答案 -63.(2012·北京卷)直线⎩⎨⎧ x =2+t ,y =-1-t (t 为参数)与曲线⎩⎨⎧x =3cos α,y =3sin α(α为参数)的交点个数为________.解析 直线方程可化为x +y -1=0,曲线方程可化为x 2+y 2=9,圆心(0,0)到直线x +y -1=0的距离d =12=22<3.∴直线与圆相交有两个交点. 答案 24.已知直线l :⎩⎨⎧x =1-2t ,y =2+2t (t 为参数)上到点A (1,2)的距离为42的点的坐标为________.解析 设点Q (x ,y )为直线上的点, 则|QA |=(1-1+2t )2+(2-2-2t )2=(2t )2+(-2t )2=42,解之得,t =±22,所以Q (-3,6)或Q (5,-2). 答案 (-3,6)和(5,-2)5.(2013·广东卷)已知曲线C 的极坐标方程为ρ=2cos θ,以极点为原点,极轴为x 轴的正半轴建立直角坐标系,则曲线C 的参数方程为________.解析 由ρ=2cos θ知,ρ2=2ρcos θ 所以x 2+y 2=2x ,即(x -1)2+y 2=1, 故其参数方程为⎩⎪⎨⎪⎧x =1+cos θ,y =sin θ(θ为参数).答案 ⎩⎨⎧x =1+cos θ,y =sin θ(θ为参数)考点一 参数方程与普通方程的互化【例1】 把下列参数方程化为普通方程,并说明它们各表示什么曲线;(1)⎩⎪⎨⎪⎧x =1+12t ,y =2+32t(t 为参数);(2)⎩⎨⎧x =1+t 2,y =2+t(t 为参数); (3)⎩⎪⎨⎪⎧x =t +1t ,y =1t -t(t 为参数).解 (1)由x =1+12t 得t =2x -2. ∴y =2+32(2x -2).∴3x -y +2-3=0,此方程表示直线. (2)由y =2+t 得t =y -2,∴x =1+(y -2)2. 即(y -2)2=x -1,此方程表示抛物线. (3)⎩⎪⎨⎪⎧x =t +1t y =1t -t①②∴①2-②2得x 2-y 2=4,此方程表示双曲线.规律方法 参数方程化为普通方程:化参数方程为普通方程的基本思路是消去参数,常用的消参方法有代入消去法、加减消去法、恒等式(三角的或代数的)消去法,不要忘了参数的范围.【训练1】 将下列参数方程化为普通方程. (1)⎩⎨⎧x =1-sin 2θ,y =sin θ+cos θ(θ为参数); (2)⎩⎪⎨⎪⎧x =12(e t +e -t),y =12(e t-e-t)(t 为参数).解 (1)由(sin θ+cos θ)2=1+sin 2θ=2-(1-sin 2θ), 得y 2=2-x .又x =1-sin 2θ∈[0,2], 得所求的普通方程为y 2=2-x ,x ∈[0,2]. (2)由参数方程得e t =x +y ,e -t =x -y , ∴(x +y )(x -y )=1,即x 2-y 2=1.考点二 直线与圆参数方程的应用【例2】 在直角坐标系xOy 中,直线l 的参数方程为⎩⎪⎨⎪⎧x =3-22t ,y =5+22t(t 为参数).在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为ρ=25sin θ. (1)求圆C 的直角坐标方程;(2)设圆C 与直线l 交于点A ,B ,若点P 的坐标为(3,5),求|P A |+|PB |. 解 (1)由ρ=25sin θ,得ρ2=25ρsin θ. ∴x 2+y 2=25y ,即x 2+(y -5)2=5. (2)将l 的参数方程代入圆C 的直角坐标方程. 得⎝⎛⎭⎪⎫3-22t 2+⎝ ⎛⎭⎪⎫22t 2=5,即t 2-32t +4=0.由于Δ=(32)2-4×4=2>0,故可设t 1,t 2是上述方程的两实根,所以⎩⎨⎧t 1+t 2=32,t 1·t 2=4.又直线l 过点P (3,5),故由上式及t 的几何意义得|P A |+|PB |=|t 1|+|t 2|=t 1+t 2=3 2.规律方法 (1)过定点P 0(x 0,y 0),倾斜角为α的直线参数方程的标准形式为⎩⎪⎨⎪⎧x =x 0+t cos α,y =y 0+t sin α(t 为参数),t 的几何意义是直线上的点P 到点P 0(x 0,y 0)的数量,即t =|PP 0|时为距离.使用该式时直线上任意两点P 1、P 2对应的参数分别为t 1、t 2,则|P 1P 2|=|t 1-t 2|,P 1P 2的中点对应的参数为12(t 1+t 2).(2)对于形如⎩⎪⎨⎪⎧x =x 0+at ,y =y 0+bt (t 为参数),当a 2+b 2≠1时,应先化为标准形式后才能利用t 的几何意义解题.【训练2】 已知直线l 的参数方程为⎩⎨⎧x =1+t ,y =4-2t (参数t ∈R ),圆C 的参数方程为⎩⎨⎧x =2cos θ+2,y =2sin θ(参数θ∈[0,2π]),求直线l 被圆C 所截得的弦长.解 由⎩⎨⎧ x =1+t ,y =4-2t消参数后得普通方程为2x +y -6=0,由⎩⎨⎧x =2cos θ+2,y =2sin θ消参数后得普通方程为(x -2)2+y 2=4,显然圆心坐标为(2,0),半径为2.由于圆心到直线2x +y -6=0的距离为d =|2×2+0-6|22+1=255,所以所求弦长为222-⎝⎛⎭⎪⎫2552=855. 考点三 极坐标、参数方程的综合应用【例3】 已知P 为半圆C :⎩⎨⎧x =cos θ,y =sin θ(θ为参数,0≤θ≤π)上的点,点A 的坐标为(1,0),O 为坐标原点,点M 在射线OP 上,线段OM 与C 的弧AP 的长度均为π3.(1)以O 为极点,x 轴的正半轴为极轴建立极坐标系,求点M 的极坐标; (2)求直线AM 的参数方程.解 (1)由已知,点M 的极角为π3,且点M 的极径等于π3,故点M 的极坐标为⎝ ⎛⎭⎪⎫π3,π3.(2)点M 的直角坐标为⎝ ⎛⎭⎪⎫π6,3π6,A (1,0). 故直线AM 的参数方程为⎩⎪⎨⎪⎧x =1+⎝ ⎛⎭⎪⎫π6-1t ,y =3π6t(t 为参数).规律方法 涉及参数方程和极坐标方程的综合题,求解的一般方法是分别化为普通方程和直角坐标方程后求解.当然,还要结合题目本身特点,确定选择何种方程.【训练3】 (2013·福建卷)在平面直角坐标系中,以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知点A 的极坐标为(2,π4),直线l 的极坐标方程为ρcos(θ-π4)=a ,且点A 在直线l 上. (1)求a 的值及直线l 的直角坐标方程;(2)圆C 的参数方程为⎩⎨⎧x =1+cos α,y =sin α(α为参数),试判断直线l 与圆C 的位置关系.解 (1)由点A (2,π4)在直线ρcos(θ-π4)=a 上,可得a = 2. 所以直线l 的方程可化为ρcos θ+ρsin θ=2, 从而直线l 的直角坐标方程为x +y -2=0.(2)由已知得圆C 的直角坐标方程为(x -1)2+y 2=1,所以圆C 的圆心为(1,0),半径r =1, 因为圆心C 到直线l 的距离d =12=22<1, 所以直线l 与圆C 相交.转化思想在解题中的应用【典例】 已知圆锥曲线⎩⎨⎧x =2cos θy =3sin θ(θ是参数)和定点A (0, 3),F 1、F 2是圆锥曲线的左、右焦点.(1)求经过点F 1且垂直于直线AF 2的直线l 的参数方程;(2)以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,求直线AF 2的极坐标方程.[审题视点] (1)先将圆锥曲线参数方程化为普通方程,求出F 1的坐标,然后求出直线的倾斜角度数,再利用公式就能写出直线l 的参数方程.(2)直线AF 2是已知确定的直线,利用求极坐标方程的一般方法求解.解 (1)圆锥曲线⎩⎪⎨⎪⎧x =2cos θy =3sin θ化为普通方程x 24+y 23=1,所以F 1(-1,0),F 2(1,0),则直线AF 2的斜率k =-3,于是经过点F 1且垂直于直线AF 2的直线l 的斜率k ′=33,直线l 的倾斜角是30°,所以直线l 的参数方程是⎩⎪⎨⎪⎧x =-1+t cos 30°y =t sin 30°(t 为参数),即⎩⎪⎨⎪⎧x =32t -1,y =12t(t 为参数).(2)直线AF 2的斜率k =-3,倾斜角是120°,设P (ρ,θ)是直线AF 2上任一点,则ρsin 60°=1sin (120°-θ),ρsin(120°-θ)=sin 60°,则ρsin θ+3ρcos θ= 3.[反思感悟] (1)本题考查了极坐标方程和参数方程的求法及应用.重点考查了转化与化归能力.(2)当用极坐标或参数方程研究问题不很熟练时,可以转化成我们比较熟悉的普通方程求解.(3)本题易错点是计算不准确,极坐标方程求解错误.【自主体验】已知直线l 的参数方程为⎩⎨⎧ x =4-2t y =t -2(t 为参数),P 是椭圆x 24+y 2=1上任意一点,求点P 到直线l 的距离的最大值.解 将直线l 的参数方程⎩⎨⎧x =4-2ty =t -2(t 为参数)转化为普通方程为x +2y =0,因为P 为椭圆x 24+y 2=1上任意一点, 故可设P (2cos θ,sin θ),其中θ∈R . 因此点P 到直线l 的距离d =|2cos θ+2sin θ|12+22=22⎪⎪⎪⎪⎪⎪sin ⎝ ⎛⎭⎪⎫θ+π45. 所以当θ=k π+π4,k ∈Z 时, d 取得最大值2105.一、填空题1.(2014·芜湖模拟)直线⎩⎨⎧x =-2-2t ,y =3+2t(t 为参数)上与点A (-2,3)的距离等于2的点的坐标是________.解析 由题意知(-2t )2+(2t )2=(2)2,所以t 2=12,t =±22,代入⎩⎪⎨⎪⎧x =-2-2t ,y =3+2t(t 为参数),得所求点的坐标为(-3,4)或(-1,2). 答案 (-3,4)或(-1,2)2.(2014·海淀模拟)若直线l :y =kx 与曲线C :⎩⎨⎧x =2+cos θ,y =sin θ(参数θ∈R )有唯一的公共点,则实数k =________.解析 曲线C 化为普通方程为(x -2)2+y 2=1,圆心坐标为(2,0),半径r =1.由已知l 与圆相切,则r =|2k |1+k 2=1⇒k =±33.答案 ±333.已知椭圆的参数方程⎩⎨⎧x =2cos t y =4sin t (t 为参数),点M 在椭圆上,对应参数t =π3,点O 为原点,则直线OM 的斜率为________.解析 当t =π3时,x =1,y =23,则M (1,23),∴直线OM 的斜率k =2 3. 答案 2 34.(2013·湖南卷)在平面直角坐标系xOy 中,若l :⎩⎨⎧x =t ,y =t -a (t 为参数)过椭圆C :⎩⎨⎧x =3cos φ,y =2sin φ(φ为参数)的右顶点,则常数a 的值为________. 解析 ∵x =t ,且y =t -a , 消去t ,得直线l 的方程y =x -a , 又x =3cos φ且y =2sin φ,消去φ, 得椭圆方程x 29+y 24=1,右顶点为(3,0),依题意0=3-a , ∴a =3. 答案 35.直线3x +4y -7=0截曲线⎩⎨⎧x =cos α,y =1+sin α(α为参数)的弦长为________.解析 曲线可化为x 2+(y -1)2=1,圆心(0,1)到直线的距离d =|0+4-7|9+16=35,则弦长l =2r 2-d 2=85.答案 856.已知直线l 1:⎩⎨⎧ x =1-2t ,y =2+kt (t 为参数),l 2:⎩⎨⎧x =s ,y =1-2s (s 为参数),若l 1∥l 2,则k =________;若l 1⊥l 2,则k =________.解析 将l 1、l 2的方程化为直角坐标方程得l 1:kx +2y -4-k =0,l 2:2x +y -1=0,由l 1∥l 2,得k 2=21≠4+k1⇒k =4,由l 1⊥l 2,得2k +2=0⇒k =-1. 答案 4 -17.(2012·广东卷)在平面直角坐标系xOy 中,曲线C 1和C 2的参数方程分别为⎩⎨⎧ x =t ,y =t (t 为参数)和⎩⎨⎧x =2cos θ,y =2sin θ(θ为参数),则曲线C 1与C 2的交点坐标为________.解析 曲线C 1的普通方程为y 2=x (y ≥0), 曲线C 2的普通方程为x 2+y 2=2.由⎩⎪⎨⎪⎧y 2=x (y ≥0),x 2+y 2=2,解得⎩⎪⎨⎪⎧ x =1,y =1,即交点坐标为(1,1). 答案 (1,1)8.直角坐标系xOy 中,以原点为极点,x 轴的正半轴为极轴建立极坐标系,设点A ,B 分别在曲线C 1:⎩⎨⎧ x =3+cos θ,y =sin θ(θ为参数)和曲线C 2:ρ=1上,则|AB |的最小值为________.解析 消掉参数θ,得到关于x 、y 的一般方程C 1:(x -3)2+y 2=1,表示以(3,0)为圆心,以1为半径的圆;C 2:x 2+y 2=1,表示的是以原点为圆心的单位圆,|AB |的最小值为3-1-1=1.答案 19.(2012·湖南卷)在极坐标系中,曲线C 1:ρ(2cos θ+sin θ)=1与曲线C 2:ρ=a (a >0)的一个交点在极轴上,则a =______.解析 ρ(2cos θ+sin θ)=1,即2ρcos θ+ρsin θ=1对应的普通方程为2x +y -1=0,ρ=a (a >0)对应的普通方程为x 2+y 2=a 2.在2x +y -1=0中,令y =0,得x =22.将⎝ ⎛⎭⎪⎫22,0代入x 2+y 2=a 2得a =22. 答案 22二、解答题10.(2013·新课标全国Ⅰ卷)已知曲线C 1的参数方程为⎩⎨⎧ x =4+5cos t ,y =5+5sin t(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为ρ=2sin θ.(1)把C 1的参数方程化为极坐标方程;(2)求C 1与C 2交点的极坐标(ρ≥0,0≤θ<2π).解 (1)将⎩⎨⎧x =4+5cos t ,y =5+5sin t 消去参数t ,化为普通方程(x -4)2+(y -5)2=25,即C 1:x 2+y 2-8x -10y +16=0.将⎩⎨⎧ x =ρcos θ,y =ρsin θ代入x 2+y 2-8x -10y +16=0得ρ2-8ρcos θ-10ρsin θ+16=0. 所以C 1的极坐标方程为ρ2-8ρcos θ-10ρsin θ+16=0.(2)C 2的普通方程为x 2+y 2-2y =0.由⎩⎨⎧x 2+y 2-8x -10y +16=0,x 2+y 2-2y =0, 解得⎩⎨⎧ x =1,y =1或⎩⎨⎧ x =0,y =2.所以C 1与C 2交点的极坐标分别为⎝ ⎛⎭⎪⎫2,π4,⎝ ⎛⎭⎪⎫2,π2. 11.(2013·新课标全国Ⅱ卷)已知动点P 、Q 都在曲线C :⎩⎨⎧ x =2cos t ,y =2sin t(t 为参数)上,对应参数分别为t =α与t =2α(0<α<2π),M 为PQ 的中点.(1)求M 的轨迹的参数方程;(2)将M 到坐标原点的距离d 表示为α的函数,并判断M 的轨迹是否过坐标原点. 解 (1)依题意有P (2cos α,2sin α),Q (2cos 2α,2sin 2α),因此M (cos α+cos 2α,sin α+sin 2α).M 的轨迹的参数方程为⎩⎨⎧ x =cos α+cos 2α,y =sin α+sin 2α,(α为参数,0<α<2π). (2)M 点到坐标原点的距离d =x 2+y 2=2+2cos α(0<α<2π).当α=π时,d =0,故M 的轨迹通过坐标原点.12.(2012·新课标全国卷)已知曲线C 1的参数方程是⎩⎨⎧x =2cos φ,y =3sin φ(φ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ=2,正方形ABCD 的顶点都在C 2上,且A ,B ,C ,D 依逆时针次序排列,点A 的极坐标为⎝ ⎛⎭⎪⎫2,π3. (1)求点A ,B ,C ,D 的直角坐标;(2)设P 为C 1上任意一点,求|P A |2+|PB |2+|PC |2+|PD |2的取值范围.解 (1)由已知可得A ⎝ ⎛⎭⎪⎫2cos π3,2sin π3, B ⎝ ⎛⎭⎪⎫2cos ⎝ ⎛⎭⎪⎫π3+π2,2sin ⎝ ⎛⎭⎪⎫π3+π2, C ⎝ ⎛⎭⎪⎫2cos ⎝ ⎛⎭⎪⎫π3+π,2sin ⎝ ⎛⎭⎪⎫π3+π, D ⎝ ⎛⎭⎪⎫2cos ⎝ ⎛⎭⎪⎫π3+3π2,2sin ⎝ ⎛⎭⎪⎫π3+3π2, 即A (1,3),B (-3,1),C (-1,-3),D (3,-1).(2)设P (2cos φ,3sin φ),令S =|P A |2+|PB |2+|PC |2+|PD |2,则S =16cos 2φ+36sin 2φ+16=32+20sin 2φ.因为0≤sin 2φ≤1,所以S 的取值范围是[32,52].。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
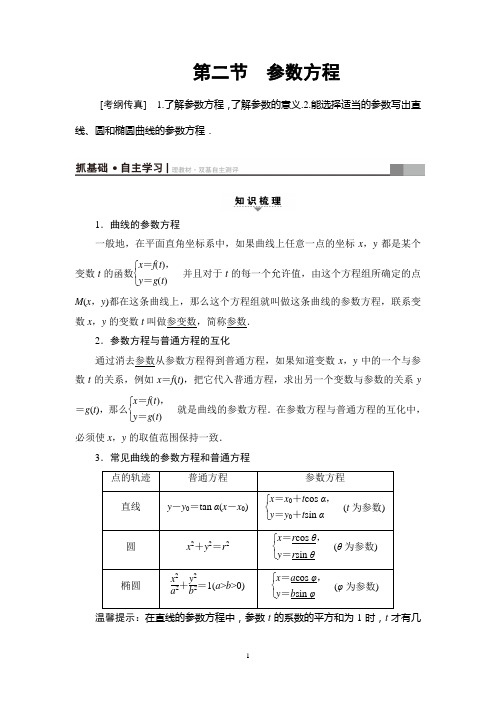
第二节 参数方程 ———————————————————————————————— [考纲传真] 1.了解参数方程,了解参数的意义.2.能选择适当的参数写出直线、圆和椭圆曲线的参数方程.
1.曲线的参数方程 一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x,y都是某个变数t的函数
x=,y=并且对于t的每一个允许值,由这个方程组所确定的点M(x,y)都在这条曲线上,那么
这个方程组就叫做这条曲线的参数方程,联系变数x,y的变数t叫做参变数,简称参数. 2.参数方程与普通方程的互化 通过消去参数从参数方程得到普通方程,如果知道变数x,y中的一个与参数t的关系,例如x=f(t),
把它代入普通方程,求出另一个变数与参数的关系y=g(t),那么 x=,y=就是曲线的参数方程.在参数方程与普通方程的互化中,必须使x,y的取值范围保持一致. 3.常见曲线的参数方程和普通方程 点的轨迹 普通方程 参数方程
直线 y-y0=tan α(x-x0)
x=x0+tcos α,
y=y0+tsin α(t为参数)
圆 x2+y2=r2
x=rcos θ,
y=rsin θ(θ为参数)
椭圆 x2a2+y2b2=1(a>b>0)
x=acos φ,
y=bsin φ(φ为参数)
温馨提示:在直线的参数方程中,参数t的系数的平方和为1时,t才有几何意义且几何意义为:|t|是直线上任一点M(x,y)到M0(x0,y0)的距离.
1.(思考辨析)判断下列结论的正误.(正确的打“√”,错误的打“×”) (1)参数方程 x=,y=中的x,y都是参数t的函数.( )
(2)过M0(x0,y0),倾斜角为α的直线l的参数方程为 x=x0+tcos α,y=y0+tsin α(t为参数).参数t的几何意义表示:直线l上以定点M0为起点,任一点M(x,y)为终点的有向线段M0M→的数量.( ) (3)方程 x=2cos θ,y=1+2sin θ表示以点(0,1)为圆心,以2为半径的圆.( )
(4)已知椭圆的参数方程 x=2cos t,y=4sin t(t为参数),点M在椭圆上,对应参数t=π3,点O为原点,则直线OM的斜率为3.( ) [答案] (1)√ (2)√ (3)√ (4)×
2.(教材改编)曲线 x=-1+cos θ,y=2+sin θ(θ为参数)的对称中心( ) A.在直线y=2x上 B.在直线y=-2x上 C.在直线y=x-1上 D.在直线y=x+1上
B [由 x=-1+cos θ,y=2+sin θ,得 cos θ=x+1,sin θ=y-2, 所以(x+1)2+(y-2)2=1. 曲线是以(-1,2)为圆心,1为半径的圆, 所以对称中心为(-1,2),在直线y=-2x上.]
3.(教材改编)在平面直角坐标系中,曲线C: x=2+22t,y=1+22t(t为参数)的普通方程为________. x-y-1=0 [由x=2+22t,且y=1+22t, 消去t,得x-y=1,即x-y-1=0.] 4.在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1的极坐标
方程为ρ(cos θ+sin θ)=-2,曲线C2的参数方程为 x=t2,y=22t(t为参数),则C1与C2交点的直角坐标为________. (2,-4) [由ρ(cos θ+sin θ)=-2,得x+y=-2.①
由 x=t2,y=22t,消去t得y2=8x.②
联立①②得 x=2,y=-4,即交点坐标为(2,-4).] 5.(2016·江苏高考)在平面直角坐标系xOy中,已知直线l的参数方程为 x=1+12t,y=32t(t为参数),椭圆C的参数方程为 x=cos θ,y=2sin θ(θ为参数).设直线l与椭圆C相交于A,B两点,求线段AB的长. [解] 椭圆C的普通方程为x2+y24=1.2分
将直线l的参数方程 x=1+12t,y=32t代入x2+y24=1,得1+12t2+32t24=1,即7t2+16t=0,8分 解得t1=0,t2=-167,所以AB=|t1-t2|=167.10分
参数方程与普通方程的互化
已知直线l的参数方程为 x=a-2t,y=-4t(t为参数),圆C的参数方程为 x=4cos θ,y=4sin θ(θ为参数). (1)求直线l和圆C的普通方程; (2)若直线l与圆C有公共点,求实数a的取值范围. [解] (1)直线l的普通方程为2x-y-2a=0,2分 圆C的普通方程为x2+y2=16.4分 (2)因为直线l与圆C有公共点,
故圆C的圆心到直线l的距离d=|-2a|5≤4,8分 解得-25≤a≤25.10分 [规律方法] 1.将参数方程化为普通方程,消参数常用代入法、加减消元法、三角恒等变换消去参数. 2.把参数方程化为普通方程时,要注意哪一个量是参数,并且要注意参数的取值对普通方程中x及y的取值范围的影响,要保持同解变形. [变式训练1] 在平面直角坐标系xOy中,若直线l: x=t,y=t-a(t为参数)过椭圆C: x=3cos φ,y=2sin φ(φ为参数)的右顶点,求常数a的值. 【导学号:31222440】
[解] 直线l的普通方程为x-y-a=0, 椭圆C的普通方程为x29+y24=1,4分 所以椭圆C的右顶点坐标为(3,0), 若直线l过椭圆的右顶点(3,0), 则3-0-a=0,所以a=3.10分 参数方程的应用
已知曲线C:x24+y29=1,直线l: x=2+t,y=2-2t(t为参数). 【导学号:31222441】 (1)写出曲线C的参数方程,直线l的普通方程; (2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
[解] (1)曲线C的参数方程为 x=2cos θ,y=3sin θ(θ为参数). 直线l的普通方程为2x+y-6=0.4分 (2)曲线C上任意一点P(2cos θ,3sin θ)到l的距离为d=55|4cos θ+3sin θ-6|,
则|PA|=dsin 30°=255|5sin(θ+α)-6|,其中α为锐角,且tan α=43.8分 当sin(θ+α)=-1时,|PA|取得最大值,最大值为2255. 当sin(θ+α)=1时,|PA|取得最小值,最小值为255.10分 [规律方法] 1.解决直线与圆的参数方程的应用问题时,一般是先化为普通方程,再根据直线与圆的位置关系来解决问题.
2.对于形如 x=x0+at,y=y0+bt(t为参数),当a2+b2≠1时,应先化为标准形式后才能利用t的几何意义解题. [变式训练2] (2017·石家庄质检)在平面直角坐标系xOy中,圆C的参数方程为
x=4cos θ,
y=4sin θ(θ为参数),直线l经过点P(1,2),倾斜角α=π6. (1)写出圆C的普通方程和直线l的参数方程; (2)设直线l与圆C相交于A,B两点,求|PA|·|PB|的值.
[解] (1)由 x=4cos θ,y=4sin θ,消去θ, 得圆C的普通方程为x2+y2=16.2分 又直线l过点P(1,2)且倾斜角α=π6,
所以l的参数方程为 x=1+tcosπ6,y=2+tsinπ6,即 x=1+32t,y=2+12t(t为参数).4分
(2)把直线l的参数方程 x=1+32t,y=2+12t代入x2+y2=16, 得1+32t2+2+12t2=16,t2+(3+2)t-11=0, 所以t1t2=-11,8分 由参数方程的几何意义,|PA|·|PB|=|t1t2|=11.10分 参数方程与极坐标方程的综合应用
(2016·全国卷Ⅲ)在直角坐标系xOy中,曲线C1的参数方程为 x=3cos α,y=sin α(α为参数).以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρsin
θ+π
4
=22. (1)写出C1的普通方程和C2的直角坐标方程; (2)设点P在C1上,点Q在C2上,求|PQ|的最小值及此时P的直角坐标.
[解] (1)C1的普通方程为x23+y2=1,2分
由于曲线C2的方程为ρsinθ+π4=22, 所以ρsin θ+ρcos θ=4, 因此曲线C2的直角坐标方程为x+y-4=0.4分 (2)由题意,可设点P的直角坐标为(3cos α,sin α).
