自动控制理论哈工大课件 (6)
哈工大现代控制理论-CHP1-1-PPT文档资料37页

xnan1x1an2x2annxnbn1u1bn2u2bnurr
16
1-1-7 状态空间表达式(续)
33
1-3-2从系统的机理出发建立状态空间表达式
例5
电网络如下图所示,输入量为电流源,并指定以电容C1 和C2的电压作为输出,求此网络的状态空间表达式
+ C2
-
uc2
l3
a
i1
b
i2
c
i3 L1
u +
L2
c1
i4
i
R1
l1
-
C1
l2
R2
34
例5
uC1` x1,uC2` x2 i1 x3,i2 x4
CT [1 0]
13
1-1-6 状态空间表达式
状态方程和输出合起来,构成对一个系统完整的动态描述, 称为系统的状态空间表达式。
设单输入--单输出定常系统,其状态变量为x1, x2, … , xn, 则状 态方程的一般形式为:
x1 a11x1 a12x2 a1nxn b1u x2 a21x1 a22x2 a2nxn b2u
C1CL,b0L1
xAxbu
12
1-1-5 输出方程
在指定系统输出的情况下,该输出与状态变量之间的函数 关系式,称为系统的输出方程
令 x1 uc 作为输出,则有
R
y uc 或 y x1
+i -
C
uc
L
y [1
0]xx12
或
y CT x
哈工大自动控制原理

哈工大自动控制原理
哈尔滨工业大学自动控制原理(Automatic Control Principles)
是自动控制学科的基础课程之一,旨在介绍自动控制系统的基本原理和方法。
该课程主要内容包括以下几个方面:
1. 控制系统基本概念:介绍控制系统的定义、组成、分类和基本概念,如输入、输出、控制信号和误差等。
2. 控制系统数学模型:介绍控制系统的数学建模方法,包括线性时不变系统和非线性系统的建模方法。
3. 闭环控制原理:介绍闭环控制系统的原理,包括控制器、传感器、执行器和反馈环节的设计与分析。
4. 开环控制原理:介绍开环控制系统的原理,包括传感器、执行器和开环控制器的设计与分析。
5. 稳定性分析与设计:介绍控制系统的稳定性分析方法,包括根轨迹法、频率响应法和Lyapunov稳定性分析法等。
6. 控制系统设计:介绍控制系统的设计方法,包括根轨迹设计、频域设计和状态空间设计等。
7. 多变量控制系统:介绍多变量控制系统的建模、分析和设计方法。
哈尔滨工业大学的自动控制原理课程旨在培养学生对自动控制系统的基本理论和方法的掌握,为进一步学习自动控制专业课程和进行科学研究打下坚实基础。
【精品】自动控制理论20页PPT

36、如果我们国家的法律中只有某种 神灵, 而不是 殚精竭 虑将神 灵揉进 宪法, 总体上 来说, 法律就 会更好பைடு நூலகம்。—— 马克·吐 温 37、纲纪废弃之日,便是暴政兴起之 时。— —威·皮 物特
38、若是没有公众舆论的支持,法律 是丝毫 没有力 量的。 ——菲 力普斯 39、一个判例造出另一个判例,它们 迅速累 聚,进 而变成 法律。 ——朱 尼厄斯
40、人类法律,事物有规律,这是不 容忽视 的。— —爱献 生
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
自动控制原理课件(哈工大)自测题答案
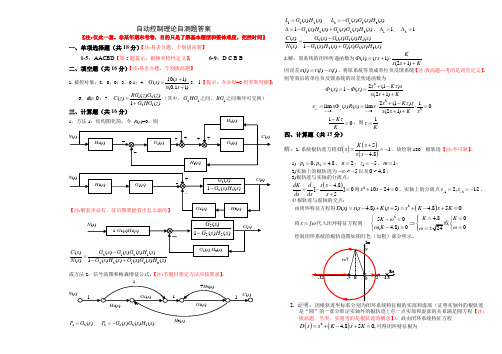
一、单项选择题(共18分)【注:易丢分题,个别拔高题】1-5:AACBD 【第5题提示:据频率特性定义】; 6-9:D C B B 二、填空题(共16分)【注:易丢分题,个别拔高题】1.被控对象;2.0,0;3.0.1;4.10(1)()(0.11)s G s s s +=+5.1【提示:令分母=0用劳斯判据】;6.0=e ;7.1221()()()1()RG z G z C z G HG z =+(其中,21G HG 之间、1RG 之间顺序可交换)三、计算题(共16分)22123()()C s N s122()()L G s H s =, 2123()()()L G s G s H s =-221231()()()()()G s H s G s G s H s ∆=-+,11∆=, 21∆=212122123()()()()()()1()()()()()G s G s G s H s C s N s G s H s G s G s H s -=-+ 2.解:原系统的闭环传递函数为()(1)(21)Ks s s s KΦτ=+⋅++因误差)()()(t c t r t e -=,将原系统等效成单位负反馈系统【注:拔高题---考的是误差定义】,则等效后的单位负反馈系统的误差传递函数为22(1)()1()(21)e s K ss s s s KτΦΦ+-=-=++22002(1)1lim ()()lim 0(21)ss e s s s K s e s s R s s s s K s τ→→+-=Φ=⋅⋅=++10K K τ-=,则1Kτ= 四、计算题(共15分) 解:1.系统根轨迹方程()()()514.8K s G s s s +==--,故绘制180°根轨迹【注:不可缺】。
1) 120, 4.8p p ==,2n =;15z =-,1m =; 2)实轴上的根轨迹为~5-∞-以及0~4.8;3)根轨迹与实轴的分离点:()4.8[]05s s dK dds ds s -=-=+则210240s s +-=,实轴上的分离点122,12x x s s ==-。
第03章1自动控制理论精品PPT课件

典型的试验信号
这一节回答的问题:
1 为什么要使用典型的输入信号? 2 典型的输入信号有哪几种?它们为什么
是典型的? 3 典型的输入信号的数学模型、图象?
4 典型的输入信号相互关系如何?
典型的试验信号
系统的输入信号通常不会都是确定的,更不是典型的, 使用典型的输入 信号只是为了分析和设计的方便。采 用典型的输入信号,可以使问题的数学处理系统化, 另外,它还可以由此去推知更复杂输入下的系统响应。
典型的试验信号
(2.) 斜坡信号
r(t)
0 t 0
r(t)Rt t 0 (3-2)
R
当 R=1 时,称为单位斜坡信号。 斜坡信号又称为等速度输入函数。 斜坡信号拉氏变换式为:
t
斜坡信号
R R(s) S2
典型的试验信号
含义
对于随动系统来说,相当于按照某一恒速 变化的位置信号。
典型的试验信号
(3.) 等加速度信号
典型的试验信号
典型信号之间的关系
S=1
r(t)
r(t)
1 2
0 Rt2
t 0 t 0
(3-3)
R
当 R1时,称为单位等加速度信号。 等加速度信号又称抛物线信号。
t 等加速度信号
等加速度信号拉氏变换式为:
R(s)
R S3
典型的试验信号
含义
对于随动系统来说,相当于按照某一恒定 加速度进行变化的位置信号。
典型的试验信号
(4.) 脉冲信号
r(t) H0
控制系统的时域分析
第一节: 典型的试验信号 第二节: 一阶系统的时域响应 第三节: 二阶系统的时域响应 第四节: 高阶系统的时域响应 第五节: 线性定常系统的稳定性 第六节: 劳斯稳定判行控制系统的时域分析过程 1、先规定典型输入信号 2、求系统在典型信号输入的时域响应 3、根据时域响应分析系统的性能指标
哈工大自动控制1-绪论

自动控制 :
在没有人直接参与的情况下,利用外加的设备或装 控制装置或控制器 置(称 ), 使机器、 被控对象 被控量 设备或生产过程( )的某个工作状态或参 数(即 )自动地按照预定的规律运行。
例2.[程控机床]:自动进刀切削,加工出预期的几何形 状直线、圆弧等各种差补控制,进给量控制,等等。
第一章 自动控制的一般概念
反馈控制系统的工作原理
从人取书的反馈控制系统方块图可见: 给定量位于系统的输入端,称为系统输入量,也称 为参考输入量(信号)。 被控制量位于系统的输出端,称为系统输出量。
输出量通过测量装置返回系统的输入端,使之与输 入量进行比较,产生偏差信号的过程称为反馈。返回 的输出信号称为反馈信号。若反馈信号与输入信号相 减,使产生的偏差越来越小,则称为负反馈;反之, 则称为正反馈。
美国N. Minorsky研制出用于船舶驾驶的伺服结构, 提出PID控制方法(1922)。 美国E. Sperry以及C. Mason研制出火炮控制器 (1925),气压反馈控制器(1929)。
哈尔滨工程大学自动化学院
9
自动控制原理
第一章 自动控制的一般概念
美国H.S. Black提出放大器性能的负反馈方法 (Negative Feedback Amplifier) (1927)
英国E.J. Routh建立 Routh判据(RouthHurwitz Stability Criteria)(1875年) 俄国A.M. Lyapunov博 士论文“论运动稳定性的 一般问题” (1892年)
哈尔滨工程大学自动化学院
8
自动控制原理
第一章 自动控制的一般概念
经典控制(1935-1950)
哈工大自控元件课件
自动控制元件及线路-2 -电气控制常识目录1。
磁场基本理论-磁场基本物理量-电磁基础定律2。
电气控制常识-线路、线缆-低压电器3。
电控线路举例电磁元件是利用磁场做媒介来实现信息(或能量)传递(或转换)的装臵。
磁场产生: 由永久磁铁产生由电流产生磁场分类:按电流性质直流磁场交流磁场磁路:磁通所经过的闭合回路称为磁路。
通过主要路径的磁通称为主磁通,另外还有少量的磁通不在此路径通过,称为漏磁通。
常见的铁心磁路一、磁力线定义:磁力线(或称B 线)是人们用来描述磁场的一种手段,每条磁力线上的任一点的切线方向都和该点磁场的方向一致。
A B C D磁力线的两个基本特征:第一,在任何磁场中每一条磁力线都是环绕电流的无头无尾的闭合曲线,即没有起点也没有终点;第二,在任何磁场中,每一条闭合的磁力线的回转方向和该闭合磁力线所包围的电流方向符合右手螺旋法则。
(a )直线电流磁力线(b )圆电流磁力线I I(c )螺线管电流的磁力线I IN S(d )永久磁铁的磁力线二、磁感应强度B定义:是表示在空间某点磁场强弱和方向的物理量,是一个空间矢量。
通俗的说,磁感应强度为通过某单位面积的磁力线的条数。
所以磁感应强度也称为磁密。
磁感应强度的方向:为该点磁场的方向。
+BFV 磁感应强度的单位为T (特)三、磁通Φ定义:通过磁场中一个给定面A 的磁力线的条数,简称磁通。
通过面积A 的磁通量为:n dAθB Φ=⎰A Bcos θdA=∫A B ·d A在均匀的磁场中磁通量:Φ=B·A磁通单位:Wb(韦伯)四、磁场强度H定义:在任何介质磁场中,某一点的磁感应强度B和同一点上介质磁导率μ的比值,即:H=B/μ单位:H —安每米(A/m)或安每厘米(A/cm)1-1 磁路的基本物理量五、磁导率μ定义:用来表示物质导磁能力大小的物理量称为导磁系数或磁导率。
单位:亨每米(H/m)-7真空的磁导率为:μ0= 4π 10 (H/m)空气的磁导率: 近似等于真空磁导率。
哈工大—现代控制理论课件
则线性化系统方程为:
Δx =结论: i = 1,2, , n ,则非线性 ① 若 Re(λi ) < 0 系统在 xe 处是渐近稳定的,与 g (x) 无关。 ,n ② 若 Re(λi ) > 0 Re(λ j ) < 0 i ≠ j = 1, 则不稳定。 ③ 若 Re(λ ) = 0 ,稳定性与 g (x ) 有关 i
第4章
系统的运动稳定性
例7: 一个弹簧-质量-阻尼器系统,系统的运动方程如下
m x + f x + kx = 0
令 m =1
x + f x + kx = 0
列写系统的状态方程并判定稳定性。
第4章
系统的运动稳定性
实际表明,很多情况下李亚普诺夫函数可取为二次型,因此二次型及其 定号性,是该理论的一个数学基础
要取决于高阶项系统的运动稳定性本章主要知识点42lyapunov意义下的稳定性稳定性定义各种稳定性之间的关系43lyapunov稳定性理论使用李氏第一法判定系统的稳定性二次型正定性李氏第二法的主要定理44线性系统的稳定性分析线性时变系统和线性定常系统的稳定性判定方法利用李雅普诺夫函数求解参数最优化问题45线性系统的有界输入有界输出稳定定义判定方法46非线性系统的稳定性分析克拉索夫斯基法
它是 x 的各元素
x1 , x2 ,
, xn 和时间 t 的函数。
9
第4章
系统的运动稳定性
自治系统 非自治系统
x = f ( x (t ))
基本区别:自治系统的状态轨线不依赖于初始时刻 平衡状态(平衡点): 对于所有t,满足 xe = f ( xe , t ) = 0 的状态 xe 称为平衡 状态. 平衡状态即为系统方程的常数解,或系统的一种静止 的运动。 线性系统,非线性系统的平衡点个数?()①
