2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测文科综合试卷参考答案

合集下载

2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷无答案

2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
20量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷
2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测理科综合试卷

河南省郑州、商丘市名师联盟2021届高三12月教学质量检测试题物理 Word版含答案

高三理科综合物理部分考生注意：1.本试卷分选择题和非选择题两部分。

满分300分，考试时间150分钟。

2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3.考生作答时，请将答案答在答题卡上。

选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．．．．．．．．．．．．．．．．．．．．．．．．．．．。

4.本试卷主要命题范围：高考范围。

二、选择题：本题共8小题，每小题6分，共48分。

在每小题给出的四个选项中，第14～18题只有一项符合题目要求，第19～21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14.如图所示，倾角为θ的斜面a放在水平地面上，小球c置于带有光滑半球形凹槽的物体b 内，b放在a上，整个装置处于静止状态。

则A.b对c的支持力方向竖直向上B.a对b的作用力方向垂直斜面向上C.地面对a的摩擦力方向水平向左D.若减小θ，则c对b的压力增大15.2020年10月12日和26日，我国在西昌卫星发射中心分别将“高分十三号”和“天启星座06”两颗地球卫星成功送入预定轨道。

“高分十三号”是一颗高轨道光学遥感卫星，“天启星座06”是一颗低轨道卫星，若两卫星均绕地球做匀速圆周运动，则由以上信息可知A.“高分十三号”绕地球运动的周期小于“天启星座06”的周期B.“高分十三号”绕地球运动的动能小于“天启星座06”的动能C.“高分十三号”绕地球运动的加速度小于“天启星座06”的加速度D.“高分十三号”绕地球运动的角速度大于“天启星座06”的角速度16.如图甲所示是郑新黄河大桥的照片，乙图中a、b、c、d、e是五个连续等距的桥墩，若一汽车从a点由静止开始做匀加速直线运动，已知通过ab段的时间为t，则通过be段的时间为A.(2＋2)tB.2tC.2tD.t17.图甲为氢原子的能级图，大量处于n ＝4激发态的氢原子向低能级跃迁时能辐射出多种不同频率的光，用辐射出的光照射图乙中光电管的阴极K ，阴极K 的材料为钨，钨的逸出功是4.54eV 。

2021届河南省高三上学期12月教学质量检测(五)文科综合地理试卷及答案

2021届河南省高三上学期12月教学质量检测（五）文科综合地理试卷★祝考试顺利★(含答案)考生注意∶1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分,共300分。

考试时间150分钟。

2.请将各题答案填写在答题卡上。

3.本试卷主要考试内容∶高考全部内容。

第Ⅰ卷（选择题共 140 分）本卷共35小题,每小题4分,共140分。

在每小题给出的四个选项中,只有一项是符合题目要求的。

虚拟水是指在生产商品和服务过程中产业链所需的水资源量。

虚拟水与虚拟水贸易因作为可能解决缺水地区水资源问题的策略,得到了广泛的关注。

下图为青藏高原地区对我国其他区域虚拟水净贸易量地图。

青藏高原地区对其他区域的净虚拟水贸易量是由虚拟水输入量与输出量之间的差值所决定的。

据此完成 1～3 题。

1.青藏高原地区对我国其他区域虚拟水净贸易量A. 西部各区域均为净输入B.净输出仅分布在东部地区C. 经济发达地区贸易量大D. 整体为虚拟水的净输入2.青藏高原地区虚拟水输入和输出的主要行业分别为A.农业工业B. 工业服务业C. 工业农业D. 农业服务业3.青藏高原地区对我国其他地区虚拟水贸易量格局形成的最主要影响因素是A.经济来往强度B. 空间距离远近C. 政策扶持力度D. 民族文化差异津巴布韦是非洲南部的内陆国家,也曾是英属殖民地,为非洲独立最晚的国家之一。

其首都哈拉雷市的人口规模是该国第二位城市的 2 倍,也是该国第三位城市的4倍。

2002 年和 2012年的两次人口普查数据表明,哈拉雷市两次人口普查期间迁入人口占该市常住人口比重超过 30%,而同期其他城市人口都出现了不同程度的下降。

同时,哈拉雷市中心区空心化,居住人口密度也明显偏低,与其高密度的建成区环境非常不符,商业、办公等用途的建筑空置严重。

据此完成4～6题。

4. 哈拉雷市的人口特点会导致津巴布韦。

河南省郑州、商丘市名师联盟2021届高三12月教学质量检测试题化学含答案 (1)

高三理科综合生物部分考生注意：1.本试卷分选择题和非选择题两部分。

满分300分，考试时间150分钟。

2.答题前，考生务必用直径0.5毫米黑色墨水签字笔将密封线内项目填写清楚。

3.考生作答时，请将答案答在答题卡上。

4.本试卷主要命题范围：高考范围。

一、选择题：本题共13小题每小题6分，共78分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.下列有关生物膜结构与功能的叙述，正确的是A.不同物种之间存在生殖隔离可能与细胞膜上的糖蛋白有关B.植物细胞的质壁分离和复原只体现了生物膜的功能特性C.细胞膜上膜蛋白的种类和数量越多，细胞的功能就越复杂D.肺炎双球菌的荚膜结构符合生物膜的流动镶嵌模型2.人体正常细胞内的Rb基因能够编码Rb蛋白，Rb蛋白具有抑制细胞不正常增殖的功能。

当Rb基因发生突变后，会导致细胞发生癌变。

下列有关细胞癌变的叙述，错误．．的是A.癌细胞新陈代谢旺盛，自由水含量较正常细胞高B.Rb基因可能是抑癌基因，能够抑制细胞发生癌变C.Rb基因发生突变一般不会导致DNA中基因排列顺序发生改变D.对癌症患者进行放疗的主要目的是促进癌细胞突变成正常细胞3.某植物的果实颜色受两对独立遗传的等位基因控制，果实细胞内色素的合成过程如图所示，下列有关叙述错误．．的是A.基因b是否表达不受基因A的影响B.该植物果实为白色的基因型种类多于黑色的基因型种类C.图示体现了基因通过控制酶的合成来间接控制该果实的颜色D.基因型为AaBb植株自交，子代表现型及比例为白色：褐色：黑色＝9：4：34.下列关于人类遗传病的叙述，正确的是A.抗维生素D佝偻病女性患者若想生出不患该病的孩子应选择只生男孩B.猫叫综合征属于人类遗传病，但该病与遗传病致病基因及染色体数目无关C.若发现胎儿第21号染色体的DNA序列和母亲不同，则胎儿一定患遗传病D.多基因遗传病属于基因异常疾病，通过遗传基本定律推测出后代的发病率5.如图所示为人体生长激素(GH)分泌调节示意图，其中GHRH为促生长激素释放激素，GHIH为生长激素抑制激素。

河南省郑州、商丘市名师联盟2021届上学期高三年级12月教学质量检测语文试卷

河南省郑州、商丘市名师联盟2021届上学期高三年级12月教学质量检测语文试卷本试卷满分150分，考试时间150分钟。

一、现代文阅读36分一论述类文本阅读本题共3小题，9分阅读下面的文字，完成1～3题。

我国学术界使用“古典学”这个词，是晚近的事，大家对它的理解恐怕并不一致。

我所理解的“古典学”，系指对于蕴含着中华文明源头的先秦典籍的整理和研究。

我们过去虽然没有用“古典学”这个名称，但是实质上，古典学早就存在了。

发源于孔子及其弟子的经学，就属于古典学的范畴。

经学与政治相结合，在古典学中占据统治地位长达两千年。

辛亥革命和五四运动结束了这个局面。

“五四”以后，对包括先秦典籍在内的传统文化，知识界有不少人持简单的否定态度。

几乎与五四运动同时，在西方学术思想的影响下，我国学术界兴起了怀疑古史和古书的思潮。

这种疑古思潮到20世纪二三十年代发展到了顶峰。

疑古派或称“古史辨”派成为商代之前的故事研究和古典学研究的主力。

在将传统的上古史大大缩短的同时，以前代学者的辨伪工作为基础，大大扩展了对古书的怀疑范围。

很多一般认为属于先秦的古书被认为是秦汉以后的伪作。

他们的古典学对传统的古典学的冲击是巨大的。

疑古派有不少值得肯定的地方，但是他们的疑古显然过了头。

新中国成立后，在学术界，疑古派怀疑古书的很多看法，也仍为不少人所信从。

改革开放以后，大家对传统文化才有了比较全面、比较正常的态度。

学术界对传统文化的研究明显加强。

很多有识之士指出，我国人民包括广大知识分子普遍缺乏人文素养，甚至对作为本民族文明源头的先秦典籍中最重要的那些书也被称之为“原典”，也茫然无知，或知之过少，这是关系到国家、民族命运的严重问题。

发展古典学已经成为时代的要求。

我们不能照搬在很多方面都早已过时的传统古典学，也不能接受那种疑古过了头的古典学，必须进行古典学的重建。

出土文献对古典学的发展有举足轻重的作用，古代的“孔壁古文”和“汲家竹书”就是明证。

新中国成立以后，尤其是20世纪70年代以来，在战国至汉代的墓葬里，陆续出土了大量文献资料，其中包含了很多珍贵的先秦典籍有些是已无传本的佚书的抄本，下文把这些抄本简称为“新出文献”。

2021-2022学年河南省高考联盟高三(上)教学检测数学试卷(文科)(12月份)(附详解)

2021-2022学年河南省高考联盟高三（上）教学检测数学试卷（文科）（12月份）一、单选题（本大题共12小题，共60.0分）1. 已知集合U ={1,2,3,4,5}，A ={1,3}，B ={2,3}，则(∁U A)∩B =( )A. {2}B. {2,3}C. {1,2,3}D. {2,3,4,5}2. 等差数列{a n }满足a 3+a 4=4，a 7+a 8=8，则a 11+a 12=( )A. 10B. 12C. 14D. 163. 已知p ：f(x)是幂函数，q ：f(x)图象过点(0,0)，则p 是q 的( )A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4. 已知△ABC 的面积为|AB|2+|AC|2−|BC|24，则( )A. A =π4B. A =π2C. B =π4D. C =π25. 曲线f(x)=ln(x +1)+2sinx 在(0,f(0))处的切线方程为( )A. y =xB. y =2xC. y =3xD. y =4x6. 在一次“剧本杀”游戏中，甲、乙、丙、丁四人各自扮演不同的角色，四人发言如下：甲：我扮演警察；乙：我扮演路人；丙：我扮演嫌疑犯；丁：我扮演路人、嫌疑犯、受害者当中的一个．若其中只有1人说谎，则说谎的人可能是( )A. 甲或丁B. 乙或丙C. 甲或乙D. 丙或丁7. 已知a =√6，b =√6，c =√636√6，则( )A. b >a >cB. a >c >bC. c >a >bD. a >b >c8. 下列函数的图象关于原点对称，又在定义域内单调递增的是( )A. y =x +1x B. y =x 3+x C. y =2x +2−xD. y =lg(10x −10−x )9. 把函数f(x)=sin2x 的图象向左平移π4个单位长度，再将图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，得到g(x)的图象，则g(x)的极大值点为( )A. x =kπ，k ∈ZB. x =kπ+π2，k ∈Z C. x =k4π，k ∈ZD. x =2kπ，k ∈Z10. 某正方体被一平面截去一部分后的空间几何体的三视图如图所示，根据图中数据，可得该几何体的表面积是( )A. 12+12√3B. 24+48√3C. 48+12√3D. 96+24√311. 已知D 是△ABC 内部(不含边界)一点，若S △ABD ：S △BCD ：S △CAD =5：4：3，AD⃗⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗⃗ +y AC⃗⃗⃗⃗⃗ ，则x +y =( ) A. 23B. 34C. 712D. 112. 定义在正整数上的函数满足f(k +2)=√3f(k +1)−f(k)(k ∈N ∗)，则f(65)=( )A. f(1)B. f(3)C. f(5)D. f(7)二、单空题（本大题共4小题，共20.0分）13. 已知向量a ⃗ =(2,3)，b ⃗ =(−1,7)，则|a ⃗ −b ⃗ |=______． 14. 已知函数f(x)=x+a e x，若f′(0)=2，则f(0)=______．15. 中国有悠久的金石文化，印信是金石文化的代表之一，印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美，如图是一个棱数为24的半正多面体，它的所有顶点都在同一个正方体的棱上，且此正方体的棱长为1.该多面体的外接球(即经过多面体所有顶点的球)的半径为______．16.若0<a<b<c<1，则下列结论正确的序号有______．①log a(log a b)<log b(log a b)；②log c(log c a)<log b(log c a)；③log a(log a b)+log b(log b c)+log c(log c a)>0；④log a(log a b)+log b(log b c)+log c(log c a)<0．三、解答题（本大题共6小题，共70.0分）17.在△ABC中，内角A，B，C的对边分别为a，b，c，且a=√b2+c2−bc．(1)求角A的大小；(2)若a=√3，B=π4，求c．18.已知函数f(x)=13x3+12(a−1)x2−ax+1．(1)若a=1，求f(x)的单调递增区间；(2)已知f(x)在区间(1,+∞)上单调递增，求实数a的取值范围．19.记S n为数列{a n}的前n项和，S n=2a n−2(n∈N∗)．(1)求{a n}的通项公式；(2)求T n=log2a1a1+log2a2a2+⋯+log2a na n．20.如图，在四棱锥P−ABCD中，底面ABCD为正方形，E为侧棱PC的中点，PA⊥底面ABCD，且PA=AD=2．(1)在侧棱PD上是否存在点F，使得点A，B，E，F四点共面？若存在，指出F点的位置，并证明；若不存在，说明理由．(2)求几何体BEC−AFD的体积．21.已知向量a⃗=(sinx+cosx+1,sinxcosx)，其中x∈[0,π]．(1)若b⃗ =(2,1)，a⃗//b⃗ ，求a⃗；(2)若c⃗=(−m,1)，函数f(x)=a⃗⋅c⃗的最小值为−2，求实数m的值．22.已知函数f(x)=x⋅e x−e x−x+1，记g(x)=f′(x)．(2)记f(x)的极小值为f(x0)，证明：−12<f(x0)<−16．答案和解析1.【答案】A【解析】解：由U={1,2,3,4,5}，A={1,3}，得∁U A={2,4,5}，又B={2,3}，∴(∁U A)∩B={2}．故选：A．由已知利用补集运算求得∁U A，再由交集运算得答案．本题考查交、并、补集的混合运算，是基础题．2.【答案】B【解析】解：由于等差数列{a n}满足a3+a4=4，a7+a8=8，则a5+a6=6；a9+a10=10；a11+a12=12．故选：B．直接利用等差数列的性质的应用求出结果．本题考查的知识要点：等差数列的性质，主要考查学生的运算能力和数学思维能力，属于基础题．3.【答案】D【解析】解：f(x)=x−2是幂函数，但其图象不过点(0,0)，故不充分；当f(x)图象过点(0,0)时，如f(x)=2x−1不是幂函数，故不必要；故选：D．利用充分条件和必要条件的定义判断．本题考查充分必要条件，属于基础题．4.【答案】A【解析】解：由题意得，2bccosA4=12bcsinA，所以sinA=cosA，即tanA=1，由A为三角形内角得A=π4．故选：A．由已知结合余弦定理及三角形面积公式进行化简可求tanA，进而可求A．本题主要考查了余弦定理及三角形面积公式的应用，属于基础题．5.【答案】C【解析】解：由f(x)=ln(x+1)+2sinx，得f′(x)=1x+1+2cosx，∴f′(0)=1+2=3，又f(0)=0，∴f(x)=ln(x+1)+2sinx在(0,f(0))处的切线方程为y=3x，故选：C．求得f′(x)=1x+1+2cosx，再求得f′(0)与f(0)，利用直线方程的点斜式可得答案．本题考查利用导数研究过曲线上某点处的切线方程，考查直线的点斜式方程的应用，属于中档题．6.【答案】B【解析】解：假设甲说谎，乙、丙、丁没说谎，则乙扮演路人，丙扮演嫌疑犯，丁只能扮演受害者，甲只能扮演警察，矛盾，不符合；假设乙说谎，甲、丙、丁没说谎，则甲扮演警察，丙扮演嫌疑犯，则丁可以扮演受害者或路人，因为乙说谎，乙不扮演路人，只能扮演嫌疑犯，则丁扮演路人，符合；假设丙说谎，甲、乙、丁没说谎，则甲扮演警察，乙扮演路人，则丁可以扮演受害者或嫌疑犯，因为丙说谎，丙不扮演嫌疑犯，只能扮演受害者，则丁扮演嫌疑犯，符合；假设丁说谎，甲、乙、丙没说谎，则丁扮演警察，因为甲没说谎，甲也扮演警察，矛盾，不符合；故选：B．分别假设甲、乙、丙、丁说谎，判断是否符合题意即可．本题主要考查合情推理能力，主要抓住共同点及矛盾点去探索结果，本题属中档题．7.【答案】D【解析】解：根据三角函数线0<α<π2，所以sinα<α<tanα；故√6>√6>0；c=√636√6=26√6<0；故a>b>c；故选：D．直接利用三角函数的线的关系求出数的大小．本题考查的知识要点：三角函数线，数的大小比较，主要考查学生的运算能力和数学思维能力，属于基础题．8.【答案】B【解析】解：对于A，f(x)的定义域为{x|x≠0}，f(−x)=−x+1−x =−(x+1x)=−f(x)，故函数f(x)是奇函数，图象关于原点对称，∵f(12)=f(2)，∴f(x)在定义域内不单调递增，故A错误，对于B，f(x)的定义域为R，f(−x)=−x3−x=−(x3+x)=−f(x)，故函数f(x)是奇函数，∵y=x3，y=x在定义域内都为增函数，∴f(x)在定义域内单调递增，故B正确，对于C，f(x)的定义域为R，f(−x)=2−x+2x=f(x)，故函数f(x)是偶函数，图象不关于原点对称，故C错误，对于D，∵10x−10−x>0，∴10x>10−x，解得x>0，故f(x)定义域为{x|x>0}，不关于原点对称，故D错误．故选：B．根据已知条件，结合函数的奇偶性，以及函数的单调性，即可求解．本题主要考查函数的奇偶性，以及函数的单调性，属于基础题．9.【答案】D【解析】解：函数f(x)=sin2x的图象向左平移π4个单位长度，得到y=sin(2x+π2)=cos2x的图象，再将图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，得到g(x)= cosx的图象，当x=2kπ(k∈Z)时，函数g(x)取得极大值点．故选：D．首先利用函数的图象的平移变换和伸缩变换求出函数g(x)=cosx，进一步求出函数的极值点．本题考查的知识要点：函数的图象的平移变换和伸缩变换，函数的极值，主要考查学生的运算能力和数学思维能力，属于基础题．10.【答案】C【解析】解：由三视图可知，该几何体是将一个棱长为4的正方体沿着如图1所示的截面EFGHMN截去之后剩下的几何体如图2所示，表面积为3[(4+2)×22+2×4]+3×2×22+6×√34×(2√2)2=48+12√3，所以该几何体的表面积为48+12√3．故选：C．由三视图，还原几何体，利用表面积公式求解．本题考查了三视图的理解与应用，空间几何体结构特征以及表面积的求解，解题的关键是由三视图还原几何体，考查了空间想象能力，属于中档题．11.【答案】A【解析】解：根据题意，如图：设AD 与BC 交于点E ，设BE =xBC ，则有BE⃗⃗⃗⃗⃗ =x BC ⃗⃗⃗⃗⃗ ，若S △ABD ：S △BCD ：S △CAD =5：4：3，则有S △BCD ：S △ABC =45+4+3=13，则DE =13AE ，则有AD =23AE ，即AD ⃗⃗⃗⃗⃗⃗ =23AE ⃗⃗⃗⃗⃗ ，故S △ABD =23S △ABE =2x 3S △ABC ，又由S △ABD ：S △BCD ：S △CAD =5：4：3，即S △ABD ：S △ABC =5：(5+4+3)=5：12，则有2x 3=512，解可得x =58，即BE ⃗⃗⃗⃗⃗=58BC ⃗⃗⃗⃗⃗ ，故AD ⃗⃗⃗⃗⃗⃗ =23AE ⃗⃗⃗⃗⃗ =23(AB ⃗⃗⃗⃗⃗ +BE ⃗⃗⃗⃗⃗ )=23AB ⃗⃗⃗⃗⃗ +23×58BC ⃗⃗⃗⃗⃗ =23AB ⃗⃗⃗⃗⃗ +512BC ⃗⃗⃗⃗⃗ =23AB ⃗⃗⃗⃗⃗ +512(AC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=312AB ⃗⃗⃗⃗⃗ +512AC ⃗⃗⃗⃗⃗ ，又由AD ⃗⃗⃗⃗⃗⃗ =x AB ⃗⃗⃗⃗⃗ +y AC ⃗⃗⃗⃗⃗ ，则x =312，y =512，故x +y =312+512=23，故选：A ．根据题意，设AD 与BC 交于点E ，设BE =xBC ，则有BE⃗⃗⃗⃗⃗ =x BC ⃗⃗⃗⃗⃗ ，由三角形面积公式分析可得AD ⃗⃗⃗⃗⃗⃗ =23AE ⃗⃗⃗⃗⃗ ，且x =58，进而由向量的线性运算公式分析，求出x 、y 的值，相加可得答案．本题考查平面基本定理的应用，涉及向量的线性运算，属于基础题，12.【答案】C【解析】解：∵f(k +2)=√3f(k +1)−f(k)(k ∈N ∗)①，∴f(k +3)=√3f(k +2)−f(k +1)=√3[√3f(k +1)−f(k)]−f(k +1)=2f(k +1)−√3f(k)，f(k +4)=√3(k +3)−f(k +2)=√3[2f(k +1)−√3f(k)]−f(k +2)=√3[2f(k +1)−√3f(k)]−[√3f(k +1)−f(k)]=√3f(k +1)−2f(k)②，由①②可得，f(k +4)=f(k +2)−f(k)， ∴f(k +6)=f(k +4)−f(k +2)=−f(k)， ∴f(k +12)=−f(k +6)=f(k)，故函数的周期T =12，f(65)=f(12×5+5)=f(5)．故选：C ．根据已知条件，结合换元法，求出函数的周期T=12，即可求解．本题主要考查求解函数的值，考查计算能力，属于基础题．13.【答案】5【解析】解：向量a⃗=(2,3)，b⃗ =(−1,7)，可得a⃗−b⃗ =(3,−4)则|a⃗−b⃗ |=√32+(−4)2=5．故答案为：5．利用向量的坐标运算以及向量的模的运算法则求解即可．本题考查向量的坐标运算，向量的模的求法，是基础题．14.【答案】−1【解析】解：∵f(x)=x+ae x ，∴f′(x)=ex−(x+a)e x(e x)2=1−x−ae x，∵f′(0)=2，∴1−a=2，∴a=−1，∴f(0)=−1，故答案为：−1．根据导数的运算公式即可得到结论．本题主要考查导数的基本运算，属于基础题．15.【答案】√22【解析】解：由图可知，该多面体由6个正方形与8个正三角形围成，因为正方体的棱长为1，所以正方形与正三角形的边长都为√22，由对称性可知，该几何体的外接球，是正四棱柱ABCD−EFGH的外接球，又因为正四棱柱的底面边长为√22，所以底面对角线的一半为12，因为正四棱柱的高等于正方体的棱长为1，所以外接球的半径R =√(12)2+(12)2=√22，故答案为：√22．由图可知，该多面体由6个正方形与8个正三角形围成，可得正方形与正三角形的边长都为√22，根据该几何体的外接球是正四棱柱ABCD −EFGH 的外接球求解即可．本题主要考查球与多面体的切接问题，空间想象能力的培养等知识，属于中等题．16.【答案】①②④【解析】解：因为0<a <b <c <1，则0<log a b <1，log a (log a b)<log b (log a b)，故①正确； log a a >1，log c (log c a)<log b (log c a)，故②正确；设log a b =m ，log b =n ，则m ，n ∈(0,1)， log c a =log b a log b c=1loga blog bc=1mn ， log a (log a b)+log b (log b c)+log c (log c a)=log a m +log b n +log c 1mm =log a m +log b n −log c m −log c n =1logma−1log mc+1log nb−1log nc=log m c−log m a log m alog m c+log n c−log n b log n blog n c=log mcalog m alog m c+log nc blogn blog n c．由0<a <b <c <1，得ca >1,cb >1,0<m <1,0<n <1，所以log m a >0,log m b >0,log n b >0,log n c >0,log m ca <0,log n cb <0，所以log mc alog ng alog m c+log nc blog n blog n c<0，所以③错误，④正确．故答案为：①②④．根据对数函数的单调性判断．判断③④时，需要设log a b =m ，log b =n ，则m ，n ∈(0,1)，用换底公式变形后再判断．本题考查了命题真假的判断，利用对数单调性比较大小以及换底公式的应用，属于中档题．17.【答案】解：(1)因为a =√b 2+c 2−bc ，由余弦定理得：a 2=b 2+c 2−2bc ⋅cosA ，所以cosA =12，结合A ∈(0,π)，故A =π3．(2)由(1)得：A =π3，于是C =π−A −B =π−π3−π4=5π12，由正弦定理得：asinA =csinC ，于是c =asinC sinA=√3sin(π3+π4)√32=√6+√22，故c =√6+√22．【解析】(1)由已知结合余弦定理可求cosA ，进而可求A ； (2)由已知先求出C ，然后结合正弦定理即可直接求解．本题主要考查了与定理，正弦定理在求解三角形中的应用，属于基础题．18.【答案】解：(1)由题可知：f′(x)=x 2+(a −1)x −a =(x +a)(x −1)，当a =1时，f′(x)=(x +1)(x −1)，由f′(x)≥0，得x ≤−1或x ≥1，故f(x)的单增区间为(−∞,−1]，[1,+∞)． (2)由(1)可知f′(x)=(x +a)(x −1)，若f(x)在区间(1,+∞)上单调递增，则f′(x)≥0对x ∈(1,+∞)恒成立，即(x +a)(x −1)≥0对x ∈(1,+∞)恒成立，结合x −1>0，从而x +a ≥0，即a ≥−x 对∀x ∈(1,+∞)恒成立，于是a ≥−1，即a 的取值范围是[−1,+∞)．【解析】(1)对f(x)求导，令f′(x)≥0，即可求解单调递增区间；(2)由题意可知f′(x)≥0对x ∈(1,+∞)恒成立，从而a ≥−x 对∀x ∈(1,+∞)恒成立，即可求解a 的取值范围．本题主要考查利用导数研究函数的单调性，考查转化思想与运算求解能力，属于中档题．19.【答案】解：(1)当n =1时，S 1=2a 1−2，即a 1=2a 1−2，故a 1=2，当n ≥2时，S n =2a n −2，S n−1=2a n−1−2，两式相减得a n =2a n −2a n−1，即a n =2a n−1，于是数列{a n }是以2为首项，以2为公比的等比数列，故a n =2n ． (2)由(1)可得：a n =2n ，故log 2a n a n =n 2n =n ⋅(12)n ，记T n =log 2a 1a 1+log 2a 2a 2+⋯+log 2a n a n，则T n =1×(12)1+2×(12)2+⋯+n ×(12)n ，故12T n =1×(12)2+2×(12)3+⋯+n ×(12)n+1，两式相减得12T n =1×(12)1+1×(12)2+1×(12)3+⋯+1×(12)n −n ×(12)n+1，故12T n =12×1−(12)n1−12−n ×(12)n+1，即T n =2−(12)n−1−n ×(12)n =2−(n +2)⋅(12)n ．【解析】(1)根据已知条件，分n =1，n ≥2两种情况讨论，即可求解． (2)由(1)可得：a n =2n ，故log 2a n a n=n 2n=n ⋅(12)n ，再结合错位相加减方法，即可求解．本题主要考查数列的求和，掌握错位相加减方法是掌握本题的关键，属于中档题．20.【答案】解：(1)当A ，B ，E ，F 四点共面时，F 为侧棱PD 中点．证明如下：∵E ，F 分别是PC 、PD 中点，∴EF//CD//AB ，故A ，B ，E ，F 四点共面．(2)∵PA ⊥平面ABCD ，CD ⊂平面ABCD ， ∴CD ⊥PA ，又CD ⊥AD ，PA ∩AD =A ， ∴CD ⊥面PAD ，又PD ⊂平面PAD ，∴CD ⊥PD ，又 EF//CD ，∴EF ⊥PD.∵F 是PD 中点，PA =AD ，∴AF ⊥PD ，而AF ∩EF =F ，∴PD ⊥平面AEF ，∴几何体EBC −FAD 的体积V =V P−ABCD −V P−ABEF =13⋅S ABCD ⋅PA −13⋅S ABEF ⋅PF =83−13⋅12(1+2)⋅√2⋅√2=53．【解析】(1)F为侧棱中点，EF//CD//AB可知共面；(2)先证CD⊥面PAD，再证明PD⊥平面AEF，V=V P−ABCD−V P−ABEF计算即可求得．本题考查点面问题与空间几何体的体积的求法，属基础题．21.【答案】解：(1)因为a⃗//b⃗ ，所以2sinxcosx=sinx+cosx+1，于是sinx+cosx+2=2sinxcosx+1=(sinx+cosx)2，因式分解得：(sinx+cosx+1)(sinx+cosx−2)=0，结合sinx+cosx=√2sin(x+π4)∈[−√2,√2]，解得sinx+cosx=−1，sinx+cosx=2(舍)，检验，sinx+cosx=−1，sinxcosx=0在x=π满足，故a⃗=(0,0)．(2)f(x)=a⃗⋅c⃗=−m(sinx+cosx+1)+sinxcosx，x∈[0,π]，设t=sinx+cosx=√2sin(x+π4)∈[−1,√2]，则sinxcosx=t2−12，因为函数f(x)的最小值为−2，所以y=−m(t+1)+t2−12=12t2−mt−m−12，t∈[−1,√2]，y的最小值为−2．根据对称轴所在范围讨论如下：①当对称轴在区间[−1,√2]左侧，即m<−1时，y在t∈[−1,√2]上单调递增，则当t=−1时，y取得最小值，故y min=12+m−m−12=0，不满足y的最小值为−2．②当对称轴在区间[−1,√2]上，即−1≤m≤√2时，当t=m时，y取得最小值，故y min=−12m2−m−12=−2，即m2+2m−3=0，解得m=1或m=−3(舍)．③当对称轴在区间[−1,√2]右侧，即m≥√2时，y在t∈[−1,√2]上单调递减，则当t=√2时，y取得最小值，故y min=1−√2m−m−12=−2，解得m=52(√2−1)，不满足m≥√2，综上，m =1．【解析】(1)由向量共线的坐标表示可求得sinx +cosx =−1，从而可得sinxcosx =0，即可求解a⃗ ； (2)由向量的数量积求出f(x)，利用换元法将函数转化为y =12t 2−mt −m −12，t ∈[−1,√2]，对m 分类讨论，求出y 的最小值，即可求解m 的值．本题主要考查向量平行的坐标运算、数量积的坐标运算，二次函数图象与性质的应用，考查分类讨论思想与转化思想的应用，考查运算求解能力，属于中档题．22.【答案】解：(1)由题可知g(x)=x ⋅e x −1，故g′(x)=(x +1)⋅e x ，由g′(x)≥0得：x ≥−1；由g′(x)≤0得：x ≤−1，故g(x)在x ∈(−∞,−1]上单调递减，在x ∈[−1,+∞)上单调递增，当x <0时，xe x <0，进而x ⋅e x −1<−1；当x →+∞时，g(x)→+∞；结合g(x)在x ∈(−∞,−1]上单调递减，在x ∈[−1,+∞)上单调递增，作出g(x)图象如下：若g(x)=a 恰有两个不同零点，则a ∈(−1−1e ,−1)．(2)证明：设g(x 0)=0，即e x 0=1x 0，由g(x)≥0得：x ≥x 0；由g(x)≤0得：x ≤x 0，故f(x)在x ∈(−∞,x 0]上单调递减，在x ∈[x 0,+∞)上单调递增，于是f(x)的极小值为f(x 0)=x 0⋅e x 0−e x 0−x 0+1，代入e x 0=1x 0得f(x 0)=2−1x 0−x 0，现需估计x 0的范围：对g(x)=x ⋅e x −1，g(x)在x ∈[−1,+∞)上单调递增，g(12)=12⋅e 12−1，g(23)=23⋅e 23−1，由0<e <4得e 12<2，从而g(12)=12⋅e 12−1<0，由(32)3=278<e 2得32<e 23，从而g(23)=23⋅e 23−1>0，故12<x 0<23，于是f(x 0)=2−1x 0−x 0，12<x 0<23，设ℎ(x)=2−1x −x ，12<x <23，ℎ′(x)=1x 2−1=(1−x)(1+x)x 2>0，故ℎ(x)在x ∈(12,23)单调递增，因此ℎ(x)>ℎ(12)=−12，ℎ(x)<ℎ(23)=−16，于是−12<f(x 0)<−16．【解析】(1)由题可知g(x)=x ⋅e x −1，求导分析其单调性，作出图象，数形结合可得实数a 的取值范围；(2)设g(x 0)=0，即e x 0=1x 0，将f(x)的极小值f(x 0)=x 0⋅e x 0−e x 0−x 0+1，代入e x 0=1x 0得f(x 0)=2−1x 0−x 0，经估计x 0的范围为(12,23)，从而可得−12<f(x 0)<−16．本题考查利用导数研究函数的单调性与极值，考查转化化归思想、数形结合思想的综合运用，考查推理论证能力与运算求解能力，属于难题．。

2021届河南省郑州市、商丘市名师联盟高三11月质检数学(文)试题(解析版)

2021届河南省郑州市、商丘市名师联盟高三11月质检数学（文）试题一、单选题1．命题0:0p x ∃>，2001232440x x +-<的否定是（） A ．00x ∃>，2001232440x x +-≥B ．0x ∀>，21232440x x +-≥C ．0x ∀≤，21232440x x +-≥D ．00x ∃≤，2001232440x x +-≥【答案】B【分析】根据特称命题的否定是全称命题即可得出.【详解】命题0:0p x ∃>，2001232440x x +-<是一个特称命题，则其否定是全称命题，即0x ∀>，21232440x x +-≥．故选：B.2．已知集合{}05A x x =<<，{}1216xB x =<<，N 为自然数集，则()N AB ⋂等于（） A ．[)4,5 B ．{}4,5C ．{}4D ．{}5【答案】C【分析】解指数不等式求得集合B ，然后求得()N AB ⋂.【详解】0412*******x x x <<⇔<<⇔<<. ∴{}04B x x =<<，∴{}45AB x x =≤<，(){}4A B N ⋂=．故选：C3．设3log 42a =，则4a -=（） A ．116B ．19C ．18D ．16【答案】B【分析】根据已知等式，利用指数对数运算性质即可得解【详解】由3log 42a =可得3log 42a=，所以49a =，所以有149a-=，故选：B.【点睛】本题考查的是有关指对式的运算的问题，涉及到的知识点有对数的运算法则，指数的运算法则，属于基础题目.4．某几何体的三视图如图所示，其中俯视图中的圆的半径为2，则该几何体的体积为（）A ．51296π-B ．296C ．51224π-D ．512【答案】C【详解】由三视图可知，该几何体是一个正方体挖去一个圆柱所得的组合体，其中正方体的棱长为8，圆柱的底面半径为2，高为6，则该几何体的体积为：3282651224ππ-⨯⨯=-. 本题选择C 选项.点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解． 5．三棱柱111ABC A B C -中，侧面与底面垂直，底面是边长为2的等边三角形，若直线1AB 与平面11ACC A 所成角为45，则棱柱的高为（）A ．22B ．2C ．2D ．1【答案】C【分析】本题首先可绘出三棱柱111ABC A B C -，取11A C 中点D 并连接1B D 、AD 、1AB ，然后通过题意以及线面角的定义得出1B AD 即直线1AB 与平面11ACC A 所成角，145B AD ∠=，最后根据2211A AAD A D 即可得出结果.【详解】如图，绘出三棱柱111ABC A B C -，取11A C 中点D ，连接1B D 、AD 、1AB ，因为三棱柱111ABC A B C -侧面与底面垂直，底面是边长为2的等边三角形，所以111B DA C ，1B D ⊥平面11ACC A ，11AD =，13B D =，由线面角的定义即可得出1B AD 即直线1AB 与平面11ACC A 所成角，则145B AD ∠=，13AD B D ，22112A AAD A D ，故选：C.【点睛】关键点点睛：本题考查线面角的应用，过不平行于平面的直线上一点作平面的垂线，这条直线与平面交点与原直线与平面的交点的连线与原直线构成的角即线面所成角，考查计算能力，考查数形结合思想，是中档题. 6．已知正实数a ，b 满足321a b +=，则61a b+的最小值为（） A ．32 B ．34C ．36D ．38【答案】A【分析】由题中条件，得到()616132a b a b a b ⎛⎫+=++ ⎪⎝⎭，展开后，利用基本不等式，即可求出结果.【详解】由0a >，0b >且321a b +=，得()6161123321823220b a a b a b a b a b ⎛⎫+=++=+++= ⎪⎝⎭≥+，当且仅当123b a a b =，即2a b =时，取等号，此时1,41,8a b ⎧=⎪⎪⎨⎪=⎪⎩，则61a b+的最小值为32．故选：A.【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地. 7．已知函数()x x af x e+=的图像在点(1,(1))f 处的切线与直线20x ey -+=平行，则a =A ．1B ．e -C ．eD ．-1【答案】D【分析】求出曲线()y f x =在点()()1,1f 处切线的斜率k ，求出函数()y f x =的导函数()'f x ，根据两直线平行的条件，令1x =， ()'1f k =，求出a ；【详解】()()()()21'x xxxe x a e x af x e e -+-+==，所以()'1af e-=，又直线20x ey -+=得斜率为1k e =，由两直线平行得：1a e e-=，所以1a =- 故选D【点睛】本题考查了利用导数研究曲线上某点切线方程，考查了运算能力，属于中档题． 8．如图，在三棱柱111ABC A B C -中，M ，N 分别为棱1AA ，1BB 的中点，过MN 作一平面分别交底面三角形ABC 的边BC ，AC 于点E ，F ，则（）A ．//MF NEB ．四边形MNEF 为梯形C ．四边形MNEF 为平行四边形D ．11//A B NE 【答案】B【分析】由已知条件及线面平行的性质可得MN EF ∥且EF MN ≠，可得四边形MNEF 为梯形，可得答案.【详解】解：∵在11AA B B 中，1AM MA =，1BN NB =，AM BN ∴∥，MN AB ∴∥.又MN ⊄平面ABC ，AB平面ABC ，MN ∴平面ABC .又MN ⊂平面MNEF ，平面MNEF平面ABC EF =，MN EF ∴∥，EF AB ∴∥.显然在ABC ∆中，EF AB ≠，EF MN ∴≠， ∴四边形MNEF 为梯形. 故选：B.【点睛】本题主要考查直线与平面平行的性质定理，需注意其灵活运用，属于基础题型. 9．已知函数()2sin()(0,[,])2f x wx w πϕϕπ=+>∈的部分图象如图所示，其中5(0)1,2f MN ==，将()f x 的图象向右平移1个单位，得到函数()g x 的图象，则()g x 的解析式是（）A ．2cos3y x π= B ．22sin()33y x ππ=+C ．22sin()33y x ππ=+ D ．2cos3y x π=-【答案】A 【解析】52MN =，得342T =，所以6T =，3πω=，又()01f =，得1sin 2ϕ=，所以56πϕ=，所以()52sin 36f x x ππ⎛⎫=+⎪⎝⎭，所以()()52sin 12sin 2cos 36323g x x x x πππππ⎡⎤⎛⎫=-+=+= ⎪⎢⎥⎣⎦⎝⎭，故选A ．点睛：三角函数的解析式求解，ω由周期T 决定，ϕ由特殊点确定，结合图象特点，解得()52sin 36f x x ππ⎛⎫=+⎪⎝⎭，左右移动的关键是x 的变化，要提取系数，移动之后得到()2cos3g x x π=．10．已知函数()2ln f x x x =+，则不等式()()211f x f x +>-的解集为（） A ．()()0,11,2 B ．()(),02,-∞+∞C ．()()(),20,11,-∞-⋃⋃+∞D ．()()2,11,-⋃+∞ 【答案】C【分析】先求函数的定义域，再判断函数为偶函数，可得()()f x fx =，再判断当0x >时，()2ln f x x x =+的单调性，即可根据单调性脱掉f ，解不等式即可求解.【详解】函数()2ln f x x x =+的定义域为()(),00,-∞⋃+∞，且()()()22ln ln f x x x x x f x -=-+-=+=，∴()f x 为偶函数，当0x >时，()2ln f x x x =+，由ln y x =和2yx 在()0,∞+上单调递增．所以()2ln f x x x =+在()0,∞+上单调递增．由()()211f x f x +>-可得()()211fx f x +>-，即211x x +>-，所以220x x +>，解得：2x <-或0x >又因为21010x x +≠⎧⎨-≠⎩，解得121x x ⎧≠-⎪⎨⎪≠⎩不等式()()211f x f x +>-的解集为：()()(),20,11,-∞-⋃⋃+∞ 故选：C【点睛】关键点点睛：本题的关键点是判断函数()2ln f x x x =+是偶函数可得()()211f x f x +>-，又由()2ln f x x x =+在()0,∞+上单调递增，即可得211x x +>-，两边平方即可求解.11．如图所示是一个正方体的表面展开图，A ，B ，D 均为棱的中点，C 是顶点，则在正方体中异面直线AB 和CD 所成角的余弦值为（）A 10B 10C 5D 5【答案】B【分析】将正方体的表面展开图还原成正方体，根据异面直线的定义，结合三角形中位线定理、余弦定理进行求解即可.【详解】正方体的表面展开图还原成正方体，如图所示．因为A ，B ，为棱的中点，所以//AB CE ，因此异面直线AB 和CD 所成角为DCE ∠．设正方体棱长为2，在DCE 中，5CD 22CE =3DE =，则222522310cos 2522DCE +-∠==⨯⨯故选：B ．12．已知函数()2ln f x x x =-，()33g x x xm =-+，方程()()f x g x =在区间1,e e⎡⎤⎢⎥⎣⎦内有两个不同的实根，则m 的取值范围是（）A ．2121,333e ⎛⎤+ ⎥⎝⎦B ．22212,333e e ⎡⎤-+⎢⎥⎣⎦ C ．221,133e ⎡⎫+⎪⎢⎣⎭D ．212,33e ⎛⎤- ⎥⎝⎦【答案】A【分析】由题可得232ln m x x =-，构造函数()22ln h x x x =-，讨论其在1,e e⎡⎤⎢⎥⎣⎦的变化情况即可得出答案.【详解】由()()f x g x =，得232ln m x x =-，令()22ln h x x x =-，则()()()211x x h x x-+'=，所以()h x 在1,1e ⎡⎫⎪⎢⎣⎭上单调递减，在(]1,e 上单调递增，所以()()min 11h x h ==，()221122h e e h e e ⎛⎫=->=+ ⎪⎝⎭，则21132m e <≤+，即2121333m e <≤+．故选：A ．【点睛】方法点睛：已知函数有零点(方程有根)求参数值(取值范围)常用的方法：（1）直接法：直接求解方程得到方程的根，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数的值域问题加以解决；（3）数形结合法：先对解析式变形，进而构造两个函数，然后在同一平面直角坐标系中画出函数的图象，利用数形结合的方法求解.二、填空题13．若实数x，y满足约束条件10,220,3230,x yx yx y-+≥⎧⎪-+≤⎨⎪--≤⎩则目标函数45z x y=-的取值范围为______．【答案】5 10,4⎡⎤--⎢⎥⎣⎦【分析】由题意作出可行域，转化目标函数为455zy x=-，数形结合即可得解.【详解】由题意，画出可行域，如图阴影部分，转化目标函数为455zy x=-，上下平移直线455zy x=-，数形结合可得，当直线455zy x=-过点A时，z取最小值；当直线过点B时，z取最大值，由103230x yx y-+=⎧⎨--=⎩可得()5,6A，所以min455610z=⨯-⨯=-；由3230220x yx y--=⎧⎨-+=⎩可得59,24B⎛⎫⎪⎝⎭，所以max59545244z=⨯-⨯=-.所以目标函数45z x y=-的取值范围为510,4⎡⎤--⎢⎥⎣⎦.故答案为：510,4⎡⎤--⎢⎥⎣⎦.14．在ABC ∆中，BA AB CB =-，()2,1BC =-，若BC 边的中点D 的坐标为(3,1)-，点A 的坐标为(2,)t -，则t =________．【答案】3【解析】由BA AB CB =-可得：BA AC =,即△ABC 是等腰三角形，由等腰三角形三线合一可知：AD BC ⊥，且()1,1AD t =--，据此可得：()()1,12,1210,3AD BC t t t ⋅=--⋅-=+-=∴=.15．已知数列{}n a 中，11a =，22a =，对任意正整数n ，22cos n n a a n π+-=+，n S 为{}n a 的前n 项和，则100S =_______. 【答案】5050【分析】分n 为奇数和偶数两种情况讨论，可得知数列{}n a 的奇数项成以1为首项，1为公差的等差数列，偶数项成以2为首项，3为公差的等差数列，然后利用等差数列求和公式可求出100S 的值.【详解】当n 为奇数时，21n n a a +-=，即数列{}n a 的奇数项成以1为首项，1为公差的等差数列；当n 为偶数时，23n n a a +-=，即数列{}n a 的偶数项成以2为首项，3为公差的等差数列，所以()()10013992410050495049350150222S a a a a a a ⨯⨯⨯⎛⎫⎛⎫=+++++++=⨯++⨯+ ⎪ ⎪⎝⎭⎝⎭5050=.故答案为：5050.【点睛】本题考查数列的分组求和法，考查等差数列的定义以及等差数列求和公式的应用，考查计算能力，属于中等题.16．设a ，b R ∈，[)0,2c π∈，若对任意实数x 都有()3sin 2sin 6x a bx c π⎛⎫-=+ ⎪⎝⎭，则满足条件的c 的所有取值的和为______．【答案】4π【分析】结合3,2a b ==进行分类讨论，由此求得c 的所有可能取值，进而求得满足条件的c 的所有取值的和.【详解】因为对任意实数x 都有()3sin 2sin 6x a bx c π⎛⎫-=+ ⎪⎝⎭，所以3a =．当3a =时，方程等价于()sin 2sin 6x bx c π⎛⎫-=+ ⎪⎝⎭，则两函数的周期相同，即2=b ．当2b =时，()sin 2sin 26x x c π⎛⎫-=+ ⎪⎝⎭，此时11266c πππ=-+=；当2b =-时，()7sin 2sin 2sin 2sin 2666x x x x c ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=--=-+=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，此时76c π=．当3a =-时，方程等价于()()sin 2sin sin 6x bx c bx c π⎛⎫-=-+=-- ⎪⎝⎭．当2b =-时，此时6c π=；当2b =时，5sin 2sin 2sin 2666x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=---=-- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()sin 2x c =--，此时56c π=．综上，c 的所有取值为116π，76π，6π，56π，和为4π．故答案为：4π三、解答题17．已知平面直角坐标系内三点A 、B 、C 在一条直线上，满足(3,1)OA m =-+，(,3)OB n =，(7,4)OC =，且OA OB ⊥，其中O 为坐标原点.（1）求实数m ，n 的值；（2）设AOC ∆的重心为G ，且23OG OB =，求cos AOC ∠的值.【答案】（1）8{9m n ==，或12m n =⎧⎨=⎩.（2）5- 【分析】（１）依据题设运用向量的垂直与平行建立方程组求解；（２）借助题设及向量的数量积公式分析求解：【详解】解：（1）因为三点A ，B ，C 在一条直线上，所以ABBC ，又()3,2AB n m =+-，()7,1BC n =-，所以()()372n n m +=--，①因为OA ⊥ OB ，所以()3310n m -++=，即1n m =+，② 由①、②解得8{9m n ==，或1{2m n ==.（2）因为G 为OAC ∆的重心，且23OG OB =，所以点B 为线段AC 的中点，所以1m =，2n =.所以()3,2OA =-，()7,4OC =，因此cos 13OA OC AOC OA OC⋅∠===⋅18．已知正项数列}1是公差为2的等差数列，且24是2a 与3a 的等比中项.（1）求数列的通项公式；（2）若(1)1n n b a -=，求数列{}n b 的前n 项和n S .【答案】(1)24n a n =；(2)21nn +. 【分析】试题分析：(1)2=，则数列的通项公式为24n a n =； (2)结合(1)的结论裂项求和可得数列{}n b 的前n 项和21n nS n =+. 试题解析：(1)∵}1数列是公差为2的等差数列，1 ()121n +-，∴()222n a n =+，∴(222a =+，(234a =+.又24是2a 与3a 的等比中项，∴((222232424a a =++=，∴(2424+=2=8=-不合舍去)，故数列{}n a 的通项公式为24n a n =.(2)∵()11n n b a -=，∴211141n n b a n ===--()()12121n n =-+11122121n n ⎛⎫- ⎪-+⎝⎭，∴1111(12335n S =-+- 11)2121n n ++--+ 11122121n n n ⎛⎫=-= ⎪++⎝⎭. 点睛：使用裂项法求和时，要注意正负项相消时消去了哪些项，保留了哪些项，切不可漏写未被消去的项，未被消去的项有前后对称的特点，实质上造成正负相消是此法的根源与目的．19．在ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，且()222sin 2a b c C ab +-=．（1）求角C 的大小；（2）若4C π>，5c =，ABC 的面积为ABC 的周长．【答案】（1）6C π=或3π；（2）12.【分析】（1）根据()222sin a b c C +-=，结合余弦定理得到sin 2C =求解.（2）由3C π=和ABC 的面积为8ab =，再利用余弦定理求得7a b +=即可.【详解】（1）因为()222sin 2a b c C +-=，且2222cos a b c ab C +-=，所以2cos sin 2ab C C ab =，所以sin 22C =．又0C π<<，所以23C π=或23π，所以6C π=或3π．（2）由（1）及4C π>，得3C π=．因为1sin 2ABCSab C == 所以8ab =．又()22222cos 3c a b ab C a b ab =+-=+-，所以()223252449a b c ab +=+=+=．所以7a b +=，所以12a b c ++=．即ABC 的周长为12．【点睛】方法点睛：有关三角形面积问题的求解方法：(1)灵活运用正、余弦定理实现边角转化；(2)合理运用三角函数公式，如同角三角函数的基本关系、两角和与差的正弦、余弦公式、二倍角公式等．20．如图，在四棱锥P ABCD -中，底面ABCD 为梯形，平面PAD ⊥平面,//,ABCD BC AD ,PA PD ⊥,60,AB AD PDA E ⊥∠=为侧棱PD 的中点，且2AD BC =.（1）证明：//CE 平面PAB ；（2）若点D 到平面PAB 的距离为2，且2=AD AB ，求点A 到平面PBD 的距离. 【答案】（1）见解析；（23.【解析】试题分析：（1）取AD 的中点为O ，连接,OC OE ，可以证明平面//EOC 平面PAB ，故//CE 平面PAB .（2）根据已知条件可以证明：PD ⊥平面PAB 且PAB ∆为直角三角形，注意底面ABCD 是直角梯形，从而可以计算AB ，而PAD ∆是直角三角形且有一个角为60︒，故可以计算AP 的长度，从而可以计算PAB ∆的面积，最后求得体积.解析：（1）证明：取AD 的中点O ，连接OC OE 、.E 为侧棱PD 的中点，OE PA ∴，.OE ⊄ 平面PAB ，PA ⊂平面PAB ，故 //OE 平面PAB .又=2AD BC BC AD ，, ∴四边形ABCO 为平行四边形，则OCAB ，OC ⊄平面PAB ，AB 平面PAB ，故//OC 平面PAB .0OC OE ⋂=,?OCE PAB ∴平面平面，CE OCE ⊂平面，CE PAB ∴平面.（2）PAD ABCD ⊥平面平面,=PAD ABCD AD AB AD ⋂⊥平面平面，，AB 平面ABCD ， AB PAD ∴⊥平面，PD PAD AB PD ⊂∴⊥平面，，,,PA PD PA AB A PD PAB ⊥⋂=∴⊥平面，从而D 到平面PAB 的距离为2PD =，因60PDA ∠=︒，故=4AD .过点A 作AH PB ⊥于H ，则PD AH ⊥.,PB PD P AH PBD ⋂=∴⊥平面，60,2,23PA PD PDAPD PA ⊥∠==∴=，，在Rt PAB ∆中，1,,22AB PA AB AD ⊥== ，由等积法可得3AB PAAH PB⨯==即点A 到平面PBD 的距离为3.21．已知()1221*0,0,n n n n n n u a ab a b ab a b b n ---+>>=++++∈N .（1）当2a =，3b =时，求n u 所表示的和；（2）若a b =，求数列{}n u 的前n 项和n S .【答案】（1）1132n n n u ++=-；（2）()()12(3),1211,0,11(1)n n n n n a S a a a n a a a a a ++⎧=⎪⎪=⎨--+⎪+>≠⎪--⎩. 【分析】（1）变形为213333122222n nn nu -⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，然后利用等比数列的求和公式求出2nn u 的表达式，即可求出n u ；（2）分1a =和0a >且1a ≠两种情况讨论，求出n u 的表达式，分别利用等差数列求和公式以及错位相减法求出n S ，综合可得出答案. 【详解】（1）当2a =，3b =a 时，()1221*22323233n n n n n n u n ---=+⋅+⋅++⋅+∈N ，两边除以2n ，得213333122222n nn n u -⎛⎫⎛⎫⎛⎫=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，所以1111332112322321212n n n n n nn u ++++⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭===---，因此，1132n n n u ++=-；（2）若a b =，则()1nn u n a =+，所以()232341n n S a a a n a =+++++，①当1a =时，()()32312n n n S n +=++++=；当1a ≠时，在①的两边同乘以a ，得()23412341n n aS a a a n a +=+++++，与①式作差，得()()()()2311112111n nn n n a a a S a aa a n aa n aa++--=++++-+=+-+-，所以()()()1211111n n n a a n a aS a aa +-+=+----. 综上，()()()()123,1211,0,111n n n n n a S a a a n a a a a a +⎧+=⎪⎪=⎨--+⎪+>≠⎪--⎩. 【点睛】本题考查数列求和，涉及等差、等比数列求和以及利用错位相减法求和，考查分类讨论思想与计算能力，属于中等题.22．已知函数()()2ln 2f x a x x x a =++-∈R .（1）若()f x 在[)1,+∞上单调递增，求实数a 的取值范围；（2）当2a =时，对于任意[]1,2λ∈，存在正实数12,x x ，使得()()()1212f x f x x x λ+=+，求12x x +的最小值.【答案】（1）[)3,-+∞；（2）3.【分析】（1）采用等价转化的思想，转化为()0f x '≥在[)1,+∞上恒成立，同时结合分离参数()22≥-+a x x ，计算()2max 2⎡⎤-+⎣⎦x x ，可得结果.（2）先化简得()22121212122ln 4x x x x x x x x λ++++-=+，并构造函数()22ln F t t t =-，120x x t =>，计算()min F t ，同时构造函数()λh ，然后计算()()10,20,h h ⎧≥⎪⎨≥⎪⎩，可得结果【详解】（1）()2221a x x af x x x x++'=++=. ∵函数()f x 在[)1,+∞上单调递增， ∴当1≥x 时，()0f x '≥恒成立，即220x x a ++≥，则()2max2a x x ⎡⎤≥-+⎣⎦，又当1≥x 时，()2max23x x ⎡⎤-+=-⎣⎦，∴3a ≥-，即实数a 的取值范围是[)3,-+∞. （2）当2a =时，()22ln 2f x x x x =++-，又∵()()()1212f x f x x x λ+=+，∴()22121212122ln 4x x x x x x x x λ++++-=+，得()()()2121212121422ln x x x x x x x x λ+--+-=-. 设120x x t =>，()22ln F t t t =-，()()'2122-=-=t F t t t， ∴当()0,1t ∈时，()0F t '<，()F t 单调递减；当()1,t ∈+∞时，()0F t '>，()F t 单调递增. ∴函数()F t 的最小值()()min 12F t F ==，可知()()()21212142x x x x λ+--+-≥，即()()()21212160x x x x λ+--+-≥对任意的[]1,2λ∈恒成立.设()()()()212121260h x x x x x x λλ=-+++++-≥，∴()()()()()()()()2121212212121260,10,20,260,x x x x x x h h x x x x x x ⎧-+++++-≥⎧≥⎪⎪⇒⎨⎨≥⎪-+++++-≥⎩⎪⎩解得123x x +≥，∴12x x +的最小值为3.【点睛】本题考查导数的综合应用，灵活应用等价等价转化的思想以及换元法的使用，同时学会构造函数，化繁为简，便于理解，考验分析能力以及逻辑推理能力，属难题.。

河南省商丘市高三上学期文科综合第二次月考(12月)试卷(政治部分)

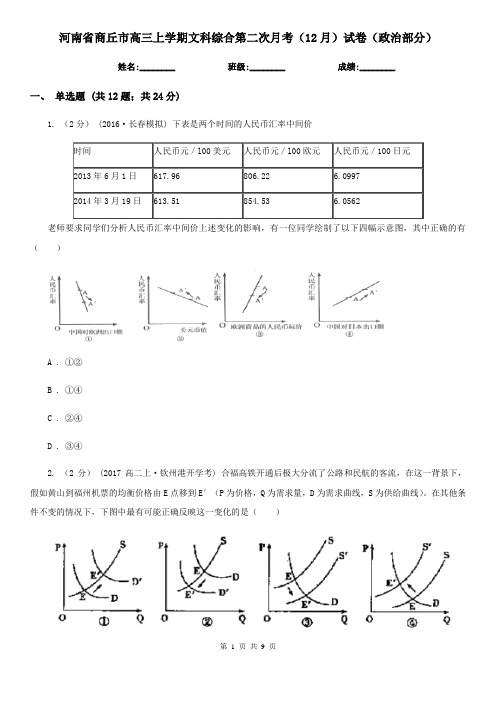
河南省商丘市高三上学期文科综合第二次月考（12月）试卷（政治部分）姓名:________ 班级:________ 成绩:________一、单选题 (共12题；共24分)1. （2分）(2016·长春模拟) 下表是两个时间的人民币汇率中间价时间人民币元／l00美元人民币元／l00欧元人民币元／100日元2013年6月1日617.96806.22 6.09972014年3月19日613.51854.53 6.0562老师要求同学们分析人民币汇率中间价上述变化的影响，有一位同学绘制了以下四幅示意图，其中正确的有（）A . ①②B . ①④C . ②④D . ③④2. （2分） (2017高二上·钦州港开学考) 合福高铁开通后极大分流了公路和民航的客流，在这一背景下，假如黄山到福州机票的均衡价格由E点移到E′（P为价格，Q为需求量，D为需求曲线，S为供给曲线）。

在其他条件不变的情况下，下图中最有可能正确反映这一变化的是（）A . ①B . ②C . ③D . ④3. （2分） (2016高三上·平江期中) 以下是某班学生收集的信息：《全国县域地区网购发展报告》显示，2012年我国县域地区平均每人网购花费5628元，甚至超过一、二线城市的人均花费4700元。

2013年某研究院调查测算的结果显示，中国约61%的网购消费取代了线下零售，约39%的网购消费是如果没有网络零售就不会产生的新增消费。

据此可以推断（）。

①农村消费者比城市消费者更加理性②消费者总是期望尽量减少消费成本③网购消费是从众心理引发的消费④发展电子商务有利于我国转变经济发展方式A . ①②B . ①③C . ②④D . ③④4. （2分） (2017高一上·西城期末) 快递号称是中国的“新四大发明”之一，但堆积如山的快递包装也给人们带来了烦恼。

如何实现包装材料的回收和循环利用，下列建议中可行的是（）①提高快递业的效益②降低包装纸箱的成本③推广可循环使用的共享快递盒④完善立法，对包装回收和循环利用作出规范A . ①②B . ①④C . ②③D . ③④5. （2分） (2017高一上·宜昌期中) 改革开放以来，特别是近年来，中国金融业发生了历史性的变化，中国工商银行、建设银行、农业银行等一批大型国有金融企业完成股份制改造，并在境内外成功上市。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2021届河南省郑州、商丘市名师联盟高三上学期12月教学质量检测
'(!)"*#$%&+,-./01
!$%'()*&+,-./0123456&+,-./0173456&89+:;<=>?@ABC.DE9 F&'GHI+,-J@KL3M,-&+,-J+NO,-'PQ+,-RST<.UVLБайду номын сангаасM,-&KL3 M,-.WRQOCKXYZ[\],^LML.3_`abc(
2021届河!南!省"郑州!"、商#丘"市!名"师联#盟$高%三上&学期$12月!教%学#质&量#检%测文$%科综合试卷
h)tT8K&û¨'={¼JìKé[4wòbx&iò'-.¦b½¾T.Wop&ä¦b¤¼y Z]zN.c§&h¨( ""$(ÿ!1{DÌ®³ÔÎÏër*=Á=x+«&{ÎÏ|X&ÚB%}]bó~L&Pâù°íÐ&¤¼ò úK;,§8N&}~p'1{DÌ®³ÔÎÏër*=Á=x+«& äâù°íÐ&¤¼òÓÔ Y]ªYT6,&}~p'Q-.}c&h¨( "&$'ÐBÕË1¶ËNJ)2lµ&ìì&jP*jçÙ+&iË UÜ.àRUÜ.jR&}~p' ¡¢¤.µéú£¤¼òb¼ËìÜ"ÐafËQ°.c =&}~p'Ë.y¤Ü1;à Ü &1 ; $ ° . ¥ ] ¦ §&q h U ¨ ÿ ; U © ° t )& h ¨' 1-.N¦b¤¼&h¨( "#$*wª«¬.+,(pN«¬tJ&®z=fËü¯*yË.#Y&ü¯*°K.#Y'ü¯*°K.#Y& )ö±ð²+°K._'ü±ð²+°K._&)öQ²+P³J"ò(¤¼ò«¬$ËQ ]´T8 5.ZþQµ¶&û¨ *·(-.!¸UM«¬µ¶Ë)²)+"Rc§&P¹½¾!ºË¢ÕÖúK{Ô.Ø»&û ÀÁ ( ·'-.¼ b*Y+&½.*Y+¾.UË.#Y&«¬¼ñµ*Y¿[+&U-.NP¹¾iÿ!ÀÁÂ. Ã8Ë.¿Y&ûÀÁ %·'pP¹½¾*öñJ#+=!º&ûÀÁ '·( ")$%wªÄç.Åó¥(-.NÅó¥.¨ÆÇ*uÈ+®ÉwÊ&5ËòÌìÍÎ&DïÅóJNÏ]+ .uÈ)ÐÑoÒÓ&ÔùÕ.M,Ö:kl&DÄcìÖá×Ø&û¨ %·&PÀÁ ')*9·(-.N¦b Ù+,1ÅóNW?.\Ú&ûÀÁ ( ·( "+$'wªN°lç.ht¾ÛiZ[(';ÜÛmnR1mn?)ÝwÛ.Þ].[\&TTµh<.ÜÛ tT&pNÞßàáu{i.§çk1â«.¼ãäJ¥¤¤¼&û '·¤î(( ·N*Ùå+.MÒQp NÞßàáu{i.§çk1â«.¼ãh}&ûÀÁ'%·N*¦bÜ+)* ·N*h)\+.MÒC!;æ$ &ûÀÁ( ",$'wªlçN°.è_Á(-.Nçèöé)êìÀJâã.AèÁ{Ê&Dï_ÁL#ërìÀ*x&¸¥ò .QìíÎÏ&î9.ïðRJÏO.5èR&_ÁL#QèÁL#¨=4V?.~&û¨ '·(-.N½¾ .Uçè.è_ÁìÀ&¹½¾ñÁìÀé.¤W¦&ûÀÁ ( ·'-.P¹AèÁìÀ.®xèòï .\Ú&ÀÁ %·'-.Nîb*_Ëªó_õÂìô++.\Ú&õ-.!¸&ûÀÁ *·( "-$(wª¼çO.öÎì|(-.µ¼çOSª+:&1¶ì)ÈÉ)DÞô\Ú.ör]@÷] ú6ø&PübóÚÔ]´B&MiöÎ+:.ùúó¢&û¨ ( ·(¼çOSôØË)ôD)h<. ¶ì¹Xër)h<.ÈÉ®:ûüÞ&öÎì|JÃq89&-.hü=\Ú&ûÀÁ %·'¼çO.ý vSª+:&1ÝþjiT$]ÿ4qRJöÎN.!"&ýv#UOöÎ.=©$&ûÀÁ '·'¼ç ODEo%&l;Pk&h<.DPk)~&¥b&i.\ZY&-.hµ=\Ú&ûÀÁ *·( "/$'wªÌDIa(Ú«p&'E(¸1)7ËñBÍ.*Y&+D°Ë¢,|ò.ø®&°Ëù¤¢b! Ë8*T&*/lø®&*Õ-Ò»&òH¶1&òØ4b.ø®P8élÕ-&û¨ '·(( ·¤ ¼hµ-..!¸&8ÌDIahYÜN°°op]&ûÀÁ'./Ia<eA0.1H2¥cì&./+, !ºmZYH']Þ.Z,°&éHò¹Â°.¶ì3(&ÌDIa6U=4+,þ´Ia&ûÀÁ % ·'~oi*T&'E($N°@c+,hUýù©4&SG *·h}~Ûb&ûÀÁ( &.$*wªÖÝ(-.µJò5.678&97=YÜòU°ñù.¤c)ÝSmk¶1.~Ò :aR);N:+,.y¤b<R(JG&y¼µQy*ÿ+Ä6i=h<.¶ì>â&äQW?] @=AÇiB×;°ñù.¶ì}&û¨ *·(*CU°+UÝji°ñùDEÖIJ/Ö&¥.FÌ&h }~-.!¸&ûÀÁ ( ·'-.hü*G°[+[Ü¾97ùHÏe°&~).\Ú&ûÀÁ %)'9·( &!$(wªÌji.êëñ!¶ìHl(-.\ÚMiÌji1°!ÙÎÏÈÉhI{Ô.êõ&ñIêëñ!¶ ìHl{élÌ.a]J~&JòK¥hL°¹XMNO$¹X$=êõ.PQ&RÐaN°&Àù.*D =Ú#¶ìSñ&öêëù-.HlJêõíéñIêëñ!¶ìHl&û¨ ( ·(S_êë°-.]J~îI ¶ìL|3;íaÌjiñIêëñ!¶ìHl.DT&RÐaN°&Àù.*D=Ú#¶ìSñ&ûÀÁ %)*9·'ý¿°!ÙÎÏÈÉUélñIêëñ!¶ìHl.BU&qhUSñVW&ûÀÁ '·( &"$%wªXYñ!¶ì([*atB\b¥.¼b+*V]+K¥].é=^{Ô+*`_ÃË.`A¶ì¸µ ø+MiZ[±²aWQôjXY.°b¨T~&hð!b%&ö®;c]ÓÔÿ4°&û¨ %·&PÀÁ ( ·( defÈ2øU$-..g]þh&ûÀÁ '·'-.hüZ[±²{Ô b¥.\Ú&ûÀÁ *·( &&$%wªÒiiñÚº]@(!+uj °Ë¶ì+,NHÈÀìò=kl.!ø°#ñÈ°$m](¼çÒ i °Ë.OOiñÚº|a&iy$Eno.¶ìpIø]qr^s.utªøñµòuÝ&<jäiy ¨ñÈ°{Ôå.ÿã]v&û¨ %·(-.NP¹ñ¾A01Hcìwx.\Ú&ûÀÁ ( ·'yeòE no.iñÚºU$-..g]þh&ûÀÁ '·' °zB.OOiñ{°!-ujN|ÆH&ûÀÁ *·(
"$%+,-Jdef.+NO,-&gKh<i&jklEM#EmM$]nKL!,^Lopqr( &$''()*stuvwxdyzw{|+}~&SG}Y~0 &S:;!8O
!&73,V&/&3,VB3_Y& w'/173 w.' :;w¡¢&h zw( #$(stuvwxmyzw~0 £¤!&jGqr&w¥b3_¦B)§¨¦©.ª«( )$*¬"+®U¯°±²³´.µl®&¥b¶·¸¹&8º»¼½¾&¿;ÀÁÂ`&ÃÄÅºµ1GÆ'Ç" +®ÈÉ{Ê&ËÌÍ&ÎÏÐÑ&ÃÄÅÒ1GÓÔÁÕ'Ö×ØÙÚB&ÛaXÜÝ)+ÜÞSßqr&ÃÄÅà á'DâEâãä+®ÓÔ( +$(åæËpçËè&)élêëìÀ&íî?!&=ïYð&ñòìÀóô&ñ!òÀõ.Z')ö÷èÁìÀ øùúû&hüýùþÿ'!"÷òÛaXR#'$ü|%&hb'Bqr( ,$*(+O"-+.)&hbB~*+&c,Yº©''-.)*/012åÏ3;!åÏ&O!&2å{ aåYü¡/&8456#+.)&7/89':;!:;<N&,w=>89&2l?@©&AB®x©&CDïRJº EFåÏ( -$%(+ÈÉãä&åÏGHä)IJKL&{ÔM¢Á&Né$Oow'PQ:RÈ(åÏST¬U&56Q:éV( /$('-.)*&WXÎY¬"¼&+Z:[¸\&¿;]â¬"^_`L&aÀÁÂ`( !.$'blc=dZ&efÀÁg®.ÀÁè)öhJiî'<jñò^_.óô'(+®hk1Hlm+hn.o p'èÁg®]hSJc=dZqÚB( !!$**"m+ÀÁg5rsmÈÉtu³{®ä&c=ò^_`L¶·&¿;{v¶·¸¹( !"$%hwxySß&0zÜÝ¡/&0z{|45&%}~p'()' .U0zÜÝh¦&* .U0zÜÝ