Reliable verification using symbolic simulation with scalar values
基于比特重组快速模约简的高面积效率椭圆曲线标量乘法器设计

基于比特重组快速模约简的高面积效率椭圆曲线标量乘法器设
计
刘志伟;张琦;黄海;杨晓秋;陈冠百;赵石磊;于斌
【期刊名称】《电子与信息学报》
【年(卷),期】2024(46)1
【摘要】针对现有椭圆曲线密码标量乘法器难以兼顾灵活性和面积效率的问题,该文设计了一种基于比特重组快速模约简的高面积效率标量乘法器。
首先,根据椭圆曲线标量乘的运算特点,设计了一种可实现乘法和模逆两种运算的硬件复用运算单元以提高硬件资源使用率,并采用Karatsuba-Ofman算法提高计算性能。
其次,设计了基于比特重组的快速模约简算法,并实现了支持secp256k1, secp256r1和SCA-256(SM2标准推荐曲线)快速模约简计算的硬件架构。
最后,对点加和倍点的模运算操作调度进行了优化,提高乘法与快速模约简的利用率,降低了标量乘计算所需的周期数量。
所设计的标量乘法器在55 nm CMOS工艺下需要275 k个等效门,标量乘运算速度为48 309次/s,面积时间积达到5.7。
【总页数】9页(P344-352)
【作者】刘志伟;张琦;黄海;杨晓秋;陈冠百;赵石磊;于斌
【作者单位】哈尔滨理工大学计算机科学与技术学院
【正文语种】中文
【中图分类】TN918
【相关文献】
1.基于快速标量乘算法的椭圆曲线数字签名方案
2.基于特殊加法链的快速安全椭圆曲线标量乘算法(英文)
3.基于GF(2n)上椭圆曲线标量乘的快速实现
4.面向多椭圆曲线的高速标量乘法器设计与实现
5.基于二进制Edwards曲线的椭圆曲线加密多标量乘结构设计与实现
因版权原因,仅展示原文概要,查看原文内容请购买。
9 Silvaco TCAD器件仿真模块及器件仿真流程

1.1.3 先进的数值方法
• 准确和强大的离散化技术
• Gummel、Newton和Block-Newton非线性迭代策略
• 对线性子问题的有效地求解,直接迭代
• 强大的初步猜测技术
• 小信号计算技术,包括所有的频率 • 稳定和精确的时间集成
Page
7
1.2 ATLAS仿真模块
• • • • • • • • • • • • • •
page112全面的物理模型dcacsmallsignalfulltimedependencydriftdiffusiontransportmodelsenergybalancehydrodynamictransportmodelslatticeheatingabruptheterojunctionsoptoelectronicinteractionsgeneralraytracingpolycrystallinematerialsgeneralcircuitenvironmentsstimulatedemissionboltzmannstatisticsadvancedmobilitymodelspage112全面的物理模型续heavydopingeffectsfullacceptordonortrapdynamicsohmicschottkyinsulatingcontactssrhradiativeaugersurfacerecombinationimpactionizationlocalfloatinggatesfowlernordheimtunnelinghotcarrierinjectionquantumtransportmodelsthermionicemissioncurrentspage113先进的数值方法稳定和精确的时间集成page12atlas仿真模块devedit2d3d二维三维器件编辑器page12atlas仿真模块续page后显示的可用模块12atlas仿真模块续enabledspiscesenabledblazeenabledgigaenabledluminousenabledledenabledtftenabledorganicdisplayenabledorganicsolarenabledmixedmodeenabledlaserenabledvcselenabledferroenabledquantumenablednoise10goatlas13器件仿真的输入和输出page11page器件仿真流程第一部分第二部分器件仿真模块第三部分总结器件仿真流程21器件仿真流程page13meshregionelectrodedopingmaterialmodelscontactinterfacelogsolveloadsavemethodextracttonyplot结果分析211器件
基于元胞自动机微观模拟的随机车流与桥梁耦合振动数值研究

文章编号:1000-4750(2021)02-0187-11基于元胞自动机微观模拟的随机车流与桥梁耦合振动数值研究周军勇,苏建旭,齐 飒(广州大学土木工程学院,广东,广州 510006)摘 要:将经典车桥耦合振动理论与最新提出的多轴单元胞自动机(MSCA)微观车流荷载模拟方法进行融合,形成了一种精细化的随机车流与桥梁耦合振动数值分析方法。
介绍了该研究所采用的车桥耦合振动理论及模型;提出了MSCA 实现车桥动力分析的思路和方法,并进行了程序开发;通过具有实测时程动态挠度的工程算例,验证MSCA 实现车桥耦合动力分析的准确性;将MSCA 用于随机车流激励下某斜拉桥的动力效应分析中,论证基于MSCA 的随机车流与桥梁耦合振动分析程序的可靠性。
研究结果表明:工程算例很好地证明了该文所提方法和模型在进行车桥耦合分析的准确性,最大误差仅为11.6%;斜拉桥在随机车流作用下的静力与动力时程挠度分析显示,两者具有很好的一致性,随着路面粗糙度等级提升两者差异更加显著,说明了该模型和方法在开展随机车流与桥梁耦合振动分析的可靠性。
该研究进一步拓展了MSCA 在随机车流激励下分析桥梁各类动态响应的能力,为该方法程序在实桥监测与评估的应用提供了基础。
关键词:桥梁工程;车桥耦合;随机车流模拟;多轴单元胞自动机;数值分析中图分类号:U441+.2 文献标志码:A doi: 10.6052/j.issn.1000-4750.2020.04.0239NUMERICAL INVESTIGATION ON RANDOM TRAFFIC-BRIDGE COUPLED VIBRATION USING CELLULAR AUTOMATON-BASED MICROSCOPIC SIMULATIONZHOU Jun-yong , SU Jian-xu , QI Sa(College of Civil Engineering, Guangzhou University, Guangdong, Guangzhou 510006, China)Abstract: A numerical delicacy method for random traffic-bridge coupled vibration analysis is proposed.Incorporating the classical vehicle-bridge interaction theory, it is a newly established multi-axle single-cell cellular automaton (MSCA)-based microscopic traffic load simulation approach. The utilized equations and models in the classical vehicle-bridge interaction theory are introduced. The concepts and routes of the realization of MSCA for vehicle-bridge coupled dynamic analysis are proposed, and the relevant code program is developed.An engineering example with measured time-history dynamic deflections is utilized to verify the accuracy of the vehicle-bridge interaction analysis by MSCA. MSCA is used to analyze the dynamic load effects of a cable-stayed bridge under the excitation of random traffic loads, to demonstrate the reliability of the proposed approach. The results indicate that MSCA has good accuracy in vehicle-bridge coupling analysis. The maximum error in the engineering example is 11.6%. The static and dynamic time-history deflections of the cable-stayed bridge under random traffic loads show that they have good consistency, and the difference between them becomes more significant along with the increase in the pavement roughness grade. These prove the reliability of the proposed model and method in the random traffic-bridge coupled vibration analysis. This study forwards MSCA's ability to收稿日期:2020-04-19;修改日期:2020-07-29基金项目:国家自然科学基金项目(51808148);广东省自然科学基金项目(2019A1515010701);广州市科技计划项目(201904010188)通讯作者:周军勇(1990−),男,江西人,讲师,博士,主要从事桥梁工程研究(E-mail: ***************.cn ).作者简介:苏建旭(1994−),男,广东人,硕士生,主要从事桥梁工程研究(E-mail: ****************);齐 飒 (1994−),女,河南人,硕士生,主要从事桥梁工程研究(E-mail: ***************).第 38 卷第 2 期Vol.38 No.2工 程 力 学2021年2 月Feb.2021ENGINEERING MECHANICS187analyze various types of dynamic load effects of bridges under the excitation of random traffic flow, which provides more applications of MSCA in monitoring and evaluation of real bridges.Key words: bridge engineering; vehicle-bridge interaction; random traffic simulation; multi-axle single-cell cellular automaton; numerical investigation车桥耦合振动特性是桥梁在移动车辆荷载作用下结构响应行为的重要表征,不仅可以揭示桥梁结构参数、力学行为和损伤特性[1],还能反演移动车辆荷载特性[2],是桥梁工程领域一直以来的研究热点[3 − 4]。
航空发动机真实机匣的包容性数值仿真

[ 1 ] 吴 继 泽 ,王 统 .齿 根 过 渡 曲 线 和齿 根 应 力 [ M] .北 京 :国 防 工业 出版 社 , 1 9 8 9: 1 — 1 2 8 .
[ 2 ] 杨生华.齿轮接触有限元分析[ J ] .计算力学学报 , 2 0 0 3 , 2 0 ( 2 ) : 1 8 9 — 1 9 4 . Y A NG S h e n g h u a .F i n i t e e l e m e n t a n a l y s i s o f g e a r c o n t a c t [ J ] .C h i n J C o m p u t Me c h , 2 0 0 3, 2 0( 2 ) :1 8 9 — 1 9 4 .
计
算
机
辅
助
工
程
2 0 1 3丘
齿 向分 布 的变 化 为 1 . 1 %, 总 变 形 变 化 为2 . 6 %( 见
齿 变形 , 使 齿轮 动态 设 计 、 优 化设 计 、 可 靠 性设 计 和 C A E分 析 有 新 的基 础. 正确 、 精 确 地心设计 技术 、 制定 标准 和
研究.
研 究提供 方 向.
使 用三 维 2 0节 点等参 单元 模 型计 算 , 为 三维 P
单元 ¨ 4 应 用 在 齿 轮齿 根 应 力 和轮 齿 变 形 计 算 提 供
参考 . 使用 三维 P单元 的并行 计算需 做进一 步研 究.
本文让 A N S Y S的并 行 计 算 能 力得 到 应 用 和 检
e n g i n e , 2 0 0 5, 3 1 ( 4 ) : 3 9 42 .
[ 5 ] 宣海 军 ,洪 伟 荣 ,吴荣 仁 .航 空发 动 机 涡轮 叶 片 包容 试 验 及 数值 模拟 [ J ] .航 空动 力 学报 , 2 0 0 5 , 2 0 ( 5 ) : 7 6 2 - 7 6 7 .
Simulink建模仿真实例详解

=
e −ζω 0t
⎡ ⎢ x0 ⎣
cos(ωd t )
+
x&0
+ ζω0 x0 ωd
sin(ωd
t
⎤ )⎥
⎦
其中:
ω0 =
k m
系统固有频率
ωd = ω0 1− ζ 2
ζ= c
2 km
阻尼固有频率 相对阻尼系数
m&x&+ cx& + kx = 0 &x&+ c x& + k x = 0
mm
1
x(0) = x0 = 1, x&(0) = x&0 = 0 已知参数:m = 1, c = 1, k = 1
Esti m a te d Po si ti o n
Double click here for
SIMULINK Help
运行菜单选项【Simulation>Start】,则屏幕上出现双质量- 弹簧系统运动状态的动画图形。
模型中的Actural Position模块和Estimated Position模块用来 显示在一个周期内的左边质量块的位置轨迹。
模型可以分为实体模型和数学模型。
实体模型又称物理效应模型,是根据系统之间的相似性而建 立起来的物理模型,如建筑模型等。
数学模型包括原始系统数学模型和仿真系统数学模型。原始 系统数学模型是对系统的原始数学描述。仿真系统数学模型 是一种适合于在计算机上演算的模型,主要是指根据计算机 的运算特点、仿真方式、计算方法、精度要求将原始系统数 学模型转换为计算机程序。
1.4 Simulink 的安装
系统要求: 奔腾100以上CPU,16MB以上内存,Windows 9x或Windows NT
DO-254_WP
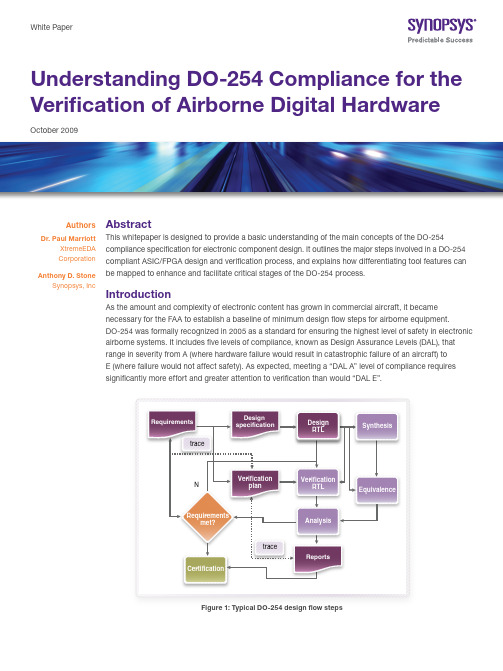
Introduction
As the amount and complexity of electronic content has grown in commercial aircraft, it became necessary for the FAA to establish a baseline of minimum design flow steps for airborne equipment. DO-254 was formally recognized in 2005 as a standard for ensuring the highest level of safety in electronic airborne systems. It includes five levels of compliance, known as Design Assurance Levels (DAL), that range in severity from A (where hardware failure would result in catastrophic failure of an aircraft) to E (where failure would not affect safety). As expected, meeting a “DAL A” level of compliance requires significantly more effort and greater attention to verification than would “DAL E”.
Requirements trace
Design specification
Design RTL
Synthesis
某型雷达系统可靠性分析与仿真
行可靠 性 预计 和 可 靠性 分 配 。下 面根 据本 型雷 达
法, 推导 了可 靠 性计 算 公 式 。其 次 , 根 据 故 障模 式
分析 法对 系统 进行 了分类 分析 , 利 用专 门的故 障树
分 析软 件 , 对 系 统进 行 了故 障树 分 析 , 得 出 了最 小
的工 作流程 状况 建立 一个 可靠 性模 型 , 以方 便 计算
文 根据所 求 出 的 割 集 , 利用 蒙 特 卡 洛 数 字 仿 真 方
法_ 3 建 立 了 系 统 可靠 性 的仿 真 模 型 , 并 利 用 Ma t —
l a b进行 了计 算机仿 真 l 4 ] 。
雷达 的可靠 性是 至关 重要 的 , 它 的好 与坏 决 定着 任
基于Simulink的直接序列扩频通信系统抗干扰的仿真实现
基于Simulink的直接序列扩频通信系统抗干扰的仿真实现王玲【摘要】主要研究了直接序列扩频通信系统( DSSS)的抗干扰能力。
利用Simulink对直接序列扩频通系统的发射机模块和接收机模块进行仿真设计,在高斯信道中加入不同中心频率、幅度的窄带干扰。
通过传输过程中各个波形和频谱变换图,研究直扩系统误码率、信噪比和扩频增益的关系。
当窄带干扰强度超过系统抗干扰容限时,使用自适应滤波器中的LMS(最小均方差)和RLS(最小递推二乘)滤波器来抑制窄带干扰。
仿真结果表明:自适应滤波具有良好放任窄带干扰抑制效果,但RLS算法复杂仿真时间长,LMS收敛速度较慢。
%The visual simulation tool Simulink provided by Matlab is used to build transmitter module and receiver module of DSSS communication system and the narrow-band interference in different carrier fre-quency and amplitude is added to the AWNG channel. The relationship among BER,SNR and spreading gain of DSSS system is researched by means of every waveform and spectrum transformation diagram in the transmission process. When theNarrow -Band Interference overstep the tolerance of the DSSS sys-tem,we can use the adaptive filter such as LMS ( Least Mean Square ) filter and RLS( Recursive Least Square) filter to improve suppressing Narrow-Band Interference. The simulation confirmed that the adap-tive filter has a good effect onNarrow-Band Interference suppression. The RLS filter’ s algorithm is com-plex so its simulation time is long. The LMS filter’ sconvergence speed is slow.【期刊名称】《中国传媒大学学报(自然科学版)》【年(卷),期】2015(000)006【总页数】7页(P21-27)【关键词】直接序列扩频;Simulink;窄带干扰;自适应滤波【作者】王玲【作者单位】中国传媒大学理工学部信息工程学院,北京100024【正文语种】中文【中图分类】TN911.4在众多的通信技术中,扩频通信技术由于具有独特的抗干扰能力以及很宽的使用频带而在军事通信领域中备受青睐。
斜拉桥有限元建模与模型修正
本文研究的斜拉桥是位于新加坡的 7&89: 桥, 如 图 " 所示。该桥于 "44D 年建成, 由世界著名的桥梁 设计师 E F ?:0 设计。该桥由一圆弧形的混凝土桥 面和一独立偏置的斜桥塔组成, 桥面由从桥塔顶端 伸下的一排 4 条斜拉钢索吊住, 斜桥塔又由 3 条钢 索背向拉住。桥面沿中心线的弧长为 "## ’、 曲率 半径为 "6# ’, 双向车道的总宽为 6 ’, 桥面两侧各 高 有一条" ’ 宽的人行道。斜塔高于其基座 <3 ’、 于桥面 3# ’, 由钢筋混凝土浇注而成, 上细下粗, 八 角形横截面。 桥面由钢筋混凝土制成, 横截面为闭室 “翼尖盒 型” 结构, 如图 ! 所示。截面中心高度为 ! ’, 两边 各有一 3 ’ 长的悬臂梁。沿桥面中心线弧长每隔 D 以提高桥面的扭转刚度、 承受横 ’ 有一预应力横梁, 向弯曲并传递桥索与桥面之间的载荷。载荷也通过 两堵 # = 3D ’ 厚的腹墙从桥面传到桥索。为了提高 稳定性, 桥面两端固定在桥台上, 桥台放在一排 " = < ’ 直径的桥桩上。一组地梁结构与背向桥索的锚地 及斜桥塔的基座相连, 斜桥塔、 地梁和背向桥索组成 了一个相对独立的支持结构并通过桥索与桥面相 连。 从结构来看, 该斜拉桥与普通的斜拉桥有明显
。
有限元模型修正技术应用于土木结构有很多优 点: (") 通过模型修正, 可以获得一个接近于真实结 构的分析模型, 从而用来进一步分析结构对异常载 荷的响应, 如对地震或台风的响应; (!) 通过修正实 际结构, 修正结果可以为同类结构的建模提供经验; (3) 可靠的结构模型可以带来更为经济的设计, 为结 构维修提供准确的分析依据; (<) 可用于土木结构的 可用于建立桥梁管理数据 健康检测与损伤评估; (D) 库。 本文研究了一座具有圆弧桥面、 单偏置斜塔的 通过 7&89: 斜拉桥有限元建模技术与模型修正技术, 有限元模型修正, 获得了与测量模态相接近的分析 模态, 并通过建立 “脊骨梁” 有限元模型和 “完整” 有
基于Simulink/Cruise的6AT液力变矩器闭锁性能联合仿真
uig S l k n odrt vry te f s it o ot ls a g , its ua o a oe b s g C i n s i i .I re o ei h e i ly fcn o t ty j n i lin w sdn y ui r s a d n mu n f a bi r r e o m t n u e
Ab t a t Ac o d n t w r i g rn i l s n l c i g c n i o s f h d a l tr u c n e e ,o t l tae f sr c : c r i g o o k n p c p e a d o k n o d t n o y r u i o q e o v r r c n r sr tg o i i c t o y
丁 美 玲 , 福 建 胡
(. 肥 昌河 汽 车 有 限 责任 公 司 , 肥 2 0 0 2合肥 工业 大学 机 械 与 汽 车 学 院 , 肥 2 0 0 1 合 合 30 9;. 合 30 9
摘 要 : 据 液 力 变 矩 器 的 工作 原 理 及 闭锁 条 件 , 根 制定 液 力 变矩 器 控 制 策 略 。 用 Sm l k建 立液 力变 矩 器 控 制模 型 , 利 i ui n 并利 用 Cus 和 Sm l k进 行 联 合 仿 真 , 证 控 制策 略 的可 行 性 。 真 结 果 表 明 , 力 变 矩 器控 制模 型 正 确 , ri e i ui n 验 仿 液 闭锁 离 合器 能够 准 确 按 照 闭锁 条件 闭锁 , 且 可 以显 著 改 善 车 辆 的 燃 油 经 济 性和 排 放 性 能 。本 文 的研 究 可 以为 液 力 变矩 器 并
基 i lk rs的6T 力 矩 锁 能 合 真/ 美 胡 建 于S u /ue A 液 变 器闭 性 联 仿 丁 玲, 福 m i Ci n
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Reliable Verification Using Symbolic Simulation withScalarValuesChris Wilson Computer Systems LaboratoryStanford UniversityStanford,CA,94035 chriswi@David L.Dill Computer Systems Laboratory Stanford UniversityStanford,CA,94035dill@ABSTRACTThis paper presents an algorithm for hardware verification that uses simulation and satisfiability checking techniques to determine the correctness of a symbolic test case on a circuit.The goal is to have coverage greater than that of random testing,but with the ease of use and predictability of directed testing.The user uses symbolic variables in simple directed tests to increase the input space that is explored.The algorithm,which is called quasi-symbolic simu-lation,simulates these tests using only scalar(0,1,X)values inter-nally causing potentially conservative values to be generated at the outputs.Divide and conquer of the symbolic input space is used to resolve this conservativeness.In the best case,this method is as efficient as symbolic simulation using BDDs and,in the worst case,gives coverage and predictability at least as good as directed testing.1.INTRODUCTIONThe ability to verify hardware designs has not scaled with the in-crease in design size over time.Although a lot of new methods have been proposed,they have not replaced directed and random simula-tion in most designs as the primary verification method.One reason for this is that new methods concentrate on improving efficiency with less consideration put on meeting the reliability requirements of mainstream verification.Reliability is the ability to produce at least some results,including predictable coverage and useful feedback,when memory or time limits are exceeded.Efficiency is the number of input patterns that can be verified with a given cost.We define cost to include man-power effort,computer resource usage,and project schedule time allocated.The basic methods used in verification can be characterized by their reliability and efficiency.First,directed tests are reliable becauseScalar simulation is simulation in whichvalues,,range over thedomain .Binary simulation is the subset of scalar simulation which ranges over thedomain,.Verification consists of defining the total input space that needs to be simulated to ensure the design is correct.The input space is defined such that a single binary test covers one point of the input space.The total input space that needs to be verified is usually too large to cover completely,so directed and random testing work by sampling the input space.Symbolic simulation verifies a set of scalar tests in the input space with a single symbolic test.Since each scalar test may require a different value on each input,symbolic functions encoded using BDDs are used to represent all the possible values on each input.This is the method used in Symbolic Trajectory Evaluation (STE)[8].The advantage of STE is that it can cover large input spaces efficiently and completely and that it is design size independent allowing scaling to large designs.However,the use of BDDs means that it is not reliable due to the well known BDD blow up problem [3].When BDD blow up occurs,no coverage is obtained since the simulation does not finish and these cases can be hard to debug.1.2Quasi-Symbolic SimulationIn quasi-symbolic simulation,values are not allowed to take on ar-bitrary functions and,consequently,BDDs are not used.Instead,the scalar domain is extended to include multiple,unique unknowns called symbolic variables .Test cases apply values from this domain to the simulator to produce output values to be checked.The algorithm consists of two parts.First,after input values are ap-plied,a simulation engine quickly computes a potentially conser-vative scalar value at each internal node.Second,a decision pro-cedure looks at the result of each run and divides the input space to resolve any unwanted conservativeness;multiple runs are per-formed to cover the entire input space.The rationale behind this is that,in large circuits,most internal node values do not propagate to outputs that are checked and so it is wasteful to generate exact values for these nodes.When the circuit is re-evaluated,only those nodes that actually propagate to checked outputs need be computed more exactly.The key to making this effective is to search the in-put space efficiently.This paper describes a search method that uses case splitting and depth-first search to get the desired reliability and efficiency.Outline We first describe the lattice that forms the basis of our abstraction method and then the basic simulation algorithm and search procedure.We then describe how this procedure is extended to handle reactivity and report on some experiments done to test our methodology.2.BOOLEAN FORMULASA circuit composed with a simulation relation creates a boolean for-mula that the simulator tries to satisfy.A boolean formula consists of strings over variables and theconnectives,.Formulas are evaluated over thelatticewhereand represent 1a unique symbolic variable and its com-plement having the variable identifier,.The lattice is definedas,,and .For soundness,the boolean connectives are required to be monotonic;that is,the rela-tion must hold.Table 1shows amonotonicXQuasi-symbolic simulation evaluates the simulation relation over the circuit directly rather than by conversion to clausal form.A variant of the Davis-Putnam(DP)[6]procedure is used to search over the symbolic input variables.Forward simulation combined with searching over input variables means that leaf nodes of the search give some amount of input space coverage.DP uses depth-first searching which gets to leaf nodes quickly.If time out occurs, it is likely to have reached at least some number of leaf nodes,and the longer the timeout,the more leaf nodes that have been reached. This gives us the reliability we are looking for.The basic DP algorithm is as follows:1.Determine satisfiability by simulating the circuit.2.If satisfiable,terminate with an error.If unsatisfiable,backtrack to a previous decision.Otherwise3.Perform unit propagation of the symbolic variables if allowed.4.Select a symbolic variable,,from the sub-domain,,tocase split on.5.Recursively do these steps with and.Unit propagation is an implication procedure that reduces the space that must be searched.For example,if a formula has the form, ,where is a variable,then must be set to true to satisfy,eliminating the branch in the search tree.DP allowsunit propagation to occur at any time,however,we will show later that our method must disallow unit propagation at certain times in order for the method to be complete.This is the only difference between our method and classical DP.The simulator uses a non-clausal unit propagation algorithm due to Dalal[5],called PCP(Propositional Constraint Propagation.)In Dalal’s method,each sub-formula is evaluated in a bottom up man-ner and two sets,called the C-set and D-set,are associated with each sub-formula.If a sub-formula can be represented as a con-junction of literals2with some sub-formula,,then it has the C-set,.D-sets are constructedsimilarly from variables that are disjuncted with the sub-formula. Once the formula has been evaluated,if the D-set is non-empty, the formula is known immediately to be satisfiable.If the C-set is non-empty,all literals in the C-set are unit propagated to be true. The value of a sub-formula is denoted as if is the set ofliterals in the D-set or if is the set of literals in the C-set.Aliteral,,in this context has both a C-set and D-set exactly equalto the literal and is equivalent to our notion of symbolic variables since the value of this subformula is exactly or when the literalis or respectively.3.2Variable Selection HeuristicThe algorithm uses a heuristic to select the best variable to split that minimizes the size of the search tree.The heuristic starts by associating a variable with each internal signal in the circuit.This variable is selected from the inputs to the function driving the signal as follows:creating a copy of the thread,called a virtual thread which starts ex-ecuting at the statement after the wait and is guarded with the wait condition being true.The original thread continues to wait,guarded with the wait expression being false.As long as the wait expres-sion evaluatesto ,the simulator forks off new virtual threads and continue to wait in the original thread.The semantics of stopping a test are that if any thread executes a stop statement,the entire test is stopped.Again,to maintain mono-tonicity,if the thread guard valueis when a stop statement is encountered,then the test must both stop and continue executing.For correctness,it is necessary to stop the simulation only when a stop statement is encountered.Since the guard condition for a stop could alsobe ,the decision procedure needs to prove that the test really stops at this point by case splitting on this guard condition before case splitting on any error conditions.Unit propagation cannot be used in this case since this is incom-plete.The problem is that the stop guard condition case splitting is trying to prove that the simulation can stop in this particular cycle ,not whether it may stop in this or some future cycle.Since the test case should stop eventually for all case split values,by not allowing unit propagation,the entire search tree will be enumerated,allow-ing the simulator to reach all cycles in which the test can possibly stop.To illustrate this,consider the following example.A four bit counter is initially loaded with a value and then decremented.The counter outputsa signal when the count reaches zero.For any binary vector loaded into the counter,the output will always eventually be asserted.Thus,if a test consists of loading the counter,waiting for the output to be asserted,and then stopping,the test case will always eventually terminate.Now consider a symbolic vector representing the set of all possible count values being loaded into the counter.The initial state and output after simulating one cycle will be asfollows:Since the stop condition is non-zero,the simulator stops at this point and case splits.If unit propagation was allowed,all vari-ables would be set to 0as indicated by the stop condition C-set.In the nextevaluation in the first cycle which means the test case has been proved to actually stop in the first cycle.The decision procedure now backtracks,but since all variables were unit prop-agated,the search would terminate immediately and would have only tested the case in which the test stops after one cycle.But,clearly,the test can stop at all lengths up to the maximum counter value.CompletenessReactive tests are inherently incomplete,even when limited to the binary domain.For example,a wait statement may wait forever for a signal to be asserted due to a bug in either the circuit or test case.This extends to the symbolic domain since symbolic tests represent sets of binary tests.What we are interested in showing is that if all binary tests repre-sented by a symbolic test are complete,then the symbolic test is complete.By disabling unit propagation in the stop condition casesplitting,we correctly explore all test case lengths.The search will also terminate since in any leaf node,a scalar stop value will be pro-duced,and in any abstract node,an value will be produced for the stop condition at a valid stop point.The search is guaranteed to terminate because there are a finite number of symbolic variables.Therefore,the test will always terminate and be complete.5.EXPERIMENTSWe have implemented a Verilog based quasi-symbolic simulator that supports hierarchical,gate level models,is event-based,and is semantically equivalent to a scalar Verilog simulator.RTL simula-tion is supported by synthesizing hierarchical RTL descriptions into equivalent gate level models.We implemented our own test case language because Verilog does not support the creation of symbolic variables and the RTL subset does not have some of the language constructs needed for test benches.We have performed two experiments,the first measures the effi-ciency of our method in finding a bug and the second demonstrates its reliability.The simulator runs 3at a speed of 85K events/second and four time frames/second for the circuit we used.Test lengths ranged from around 30to 100time frames.The simulator plus de-sign required 36MB of main memory and this value did not grow significantly as a test ran.5.1Test Design DescriptionThe design we are using is an industrial bus bridge chip called the MCU [9].We are modeling the bus interface section of the chip which has approximately 140K gates and 2,402state bits.This chip was taped-out,went through bringup and subsequent follow-on versions were designed.In the process of verifying these follow-on designs,bugs were found in the original design that were not caught in the original verification or in bringup.The bug we are targeting in our first experiment is in this category.5.2Experiment 1:EfficiencyOur method improves efficiency compared to directed and random testing because of its completeness by allowing the user to rule out large parts of the input space quickly when looking for bugs.However,most of the effort in verification is spent in writing and debugging test cases.We expect this to be no different for symbolic simulation and so we need to show that our method does not cause significant bottlenecks when bugs are found.In this experiment,we developed a test case to find a known,but not well characterized bug.We wrote an initial test case and then recorded the number of evaluations (nodes in the search tree)and execution time of each run as we tried to debug it.After performing a number of runs,it became apparent that there were basically four possible results:1.(SAT)A test case protocol violation in driving the requests onto the bus would occur.These typically were found with a few evaluations and required no backtracking.2.(TIMEOUT)The test would timeout waiting for a response from the circuit.These were also typically due to test case protocol violations.case evals rand evalsSAT 3.8 1.12249.0LEAK78 1.07.1UNSAT8k53-886.64UNSAT23111-420.4UNSAT2753-352.0UNSAT3337-143.5random simulator would,in all likelihood,set all variables tobothand at some point during a test.However,this problem is easily overcome by re-running the test with a different variable order if it times out.5.4ConclusionsWe have stated that reliability is an important important factor in mainstream verification.Our goal is to improve mainstream meth-ods and our strategy is to ensure reliabilityfirst,and then work on improving efficiency.Symbolic simulation can efficiently search large input spaces and its completeness allows ruling out large in-put spaces,which is a significant advantage over random simula-tion when looking for bugs.It can also use short tests to give the same coverage as long random tests,making tests easier to debug. However,traditional symbolic simulation based on BDDs does not meet our reliability criteria.Quasi-symbolic simulation uses algo-rithms that use scalar values internally and satisfiability checking methods to search over the set of symbolic test cases allowing it to degrade gracefully in the face of resource limits.The combination of predictability and simple test case debugging make our method comparable to directed testing in its ease of use.In our experiments,we showed that our method had better effi-ciency than random testing in ruling out input spaces to search for bugs and that it does not introduce significant bottlenecks when bugs are encountered.We also showed that our method does de-grade gracefully when resource limits are encountered.In summary,quasi-symbolic simulation has the ease of use and predictability of directed testing and the efficiency of random test-ing while meeting the reliability goals of mainstream verification. Thus,we believe that quasi-symbolic simulation can be used as one of the primary methods offinding the majority of bugs in large de-signs with the advantage that it can perform verification tasks not possible with either random or directed testing.6.REFERENCES[1]A.Biere et al.Verifying safety properties of a powerpcmicroprocessor using symbolic model checking without bdds.In Proceedings,Computer Aided Verification(CAV’99),LNCS 1633,pages60–71,1999.[2]V.Boppana et al.Model checking based on sequential atpg.InProceedings,Computer Aided Verification(CAV’99),LNCS1633,pages418–430,1999.[3]R.E.Bryant.Graph-based algorithms for boolean functionmanipulation.IEEE Transactions on Computers,C-35(8):677–691,August1986.[4]K.-T.Cheng.Gate-level test generation for sequential circuits.ACM Trans.Design Automation of Electronic Systems,1(4):406–442,October1996.[5]M.Dalal.Efficient propositional constraint propagation.InProc.of the Tenth National Conf.on Artificial Intelligence(AAAI-92),pages409–414,1992.[6]M.Davis,G.Logemann,and D.Loveland.Machine programfor munications of the ACM,5(7):394–397,1962.[7]M.Ganai,A.Aziz,and A.Kuehlman.Augmenting simulationwith symbolic algorithms.In Proc.of36th Design Automation Conf.,pages385–390,1999.[8]C.-J.Seger and R.E.Bryant.Formal verification by symbolicevaluation of partially-ordered trajectories.Formal Methods in System Design,6(2):147–189,1995.[9]W.-D.Weber et al.The mercury interconnect architecture:Acost-effective infrastructure for high-performance servers.In Proc.of the24th Annual Intl.Symp.on Computer Architecture (ISCA97),1997.。
