95年天津大学竞赛试题及答案
第二次校内选拔错题比较多的试题答案

2I
2
x sin xdx =2 x sin xdx 2 x cos x
2 0
2 0
2sin x
2 0
2
n x 4 x5 n 1 x f ( x) x 1 o( x n ) , I 1+ 2 3 n2 2 f (0) 2 f ( n ) (0) n n 另一方面, f ( x ) f (0) f (0) x x x o( x ) 。 七、 (8 分) 计算 y x 2 dxdy 2! n! x 1 0 y 2 1 f ( n ) (0) n 1 n 1 n ! (n) 所以有 1 f (0) 1 n2 n! n2 2 1 x2
n
5 设函数 f ( x) 连续,则 答案 xf ( x ) 二、选择题
2
d x tf ( x 2 t 2 )dt ___________ 0 dx
A sin A, A 0
sin xn x2 (2)原式= lim( ) n , 为"1"型 n xn
1
0, 1.设 f ( x ) 2 x ,
e e
e
t 0
lim
t cos t sin t 2t3
e
t2 t3 t 1 0( t 2 ) t 0( t 3 ) 2 6 lim 3 t 0 2t
e
1 6
三、 设数列 xn 满足0 x1 , xn 1 sin xn ( n 1, 2,)
1 Cn ln(1 x)
(2 x) Cn2 ln(1 x)
天津市大学物理竞赛试题答案及评分标准

20XX 年“拓普杯”天津市大学生物理竞赛参考答案及评分标准一、请写出国际单位制中七个基本物理量单位的名称和量纲。
答:长度(m )2分 质量(kg )2分 时间(s )2分 电流(A )1分 热力学温度(K )1分 发光强度(cd )1分 物质的量(mol )1分二、一列静止长度为600米的超快速火车通过一个封闭式的火车站,据站长讲车站全长为450米,火车通过时正好装进车站,即站长观察到火车后端刚好在进口处的同时其前端刚好在出口处。
求: (1)火车的速率是多少? (2) 对火车上的乘务员来说,他观测到的车站长度是多少?解:(1)2021V L L C=- 4分220714L V C L =-=2分(2)221V L L C'=- 2分337.5m = 2分三、航天英雄乘坐的神州六号舱容积为9.0立方米,在标准状态下,求:(1)舱内空气的质量是多少?(2)舱内氮气的分压是多少?(3)在正常照度下,人眼瞳孔直径为 3.0mm ,在可见光中眼最敏感的波长λ=550nm 。
若晴好白天飞船位于长城正上方350公里处,设长城宽度5.0米,航天英雄能直接看清长城吗?(按质量百分比计,氮气76﹪,氧气23﹪,氩气1﹪,其它气体可略,它们的分子量分别为28, 32, 40)解:标准状态,气化P 0=1atm,气温为0 0c ,空气平均mol 质量3109.28-⨯=μ千克/摩尔。
1. 内质量: 330V 910M 28.91011.6V 22.4μ-⨯=∙=⨯⨯=(千克) 3分2. 由气体状态方程可得:RT MV μ=0P 2分RT M V P 222NN N μ=1分0.78442828.90.76MM P P 222N N 0N =⨯=∙=∴μμ()atm 0.78440.7844P P 0N 2==∴ 1分 3. 依瑞利判据知人眼的最小分辨角为51.222.210radDϕλδ-==⨯ 2分可分辨最小间距:77102.23500005y =⨯⨯=∙=-ϕδδL (米) 1分 看不到长城!四、将质量相同、温度分别为T 1、T 2 的两杯水在等压下绝热地混合,试问:(1)此系统达到最后状态,计算此过程的熵变。
天津市大学生物理竞赛(B类)培训习题-力学部分

质量,其质量的增长率正比于它的瞬时质量和瞬
时速度的乘积: dm kmv
dt
式中为常量。试证明雨滴的速率实际上最后成为
常量,并给出终极速率的表达式。忽略空气的阻
力。
解:由变质量的运动方程:
(m dm)(v dv) mv mgdt
dm dv v m mg dt dt dm km v dt dv 2 km v m m g dt dv g kv2 dt
• (4)列方程,求解。
16
• 第三类是功能关系式的应用具体的解题步骤为:
• (1)选择所研究的质点系。 • (2)确定所研究的过程以及过程的始末状态。
• (3) 根据过程中外力的功和非保守内力的功代数和所服从的 条件确定所用的功能关系式。
• (4)列方程,求解。
• 第四类是角动量分量守恒定律的应用具体的求解方法是: (1) 、(2)同上。
6、刚体的转动惯量 7、刚体的角动量
J mk rk2
J r 2 dm
10
L r p r mv Lz J
8、力矩的功 9、功率
dW Md
W Md
1
2
dW d p M M dt dt
11
二、基本规律 basic law
8
9、质心(质量中心):在研究质点系统问题中,与质点系统
质量分布有关的一个代表点,它的位置在平均意义上代表着 质量分布中心。 xC mi xi / M mr M r
dri mi m v drC dt i i vC 质心的速度: dt M M dvi m i mi ai dvC dt 质心的加速度: aC dt M M
2011年天津市大学生物理竞赛真题(含答案)

2011年第二届拓普杯天津市普通高等院校《大学物理》竞赛试题一、如图是长为L 质量为m 的均质细杆处于水平静止状态。
它的一端在光滑的轴上,细杆可绕轴自由转动,另一端用轻绳(不计质量)悬挂于天花板,轻绳垂直于水平面。
问:(1)在剪断轻绳这一瞬间,细杆质心加速度a 、细杆绕其质心转动角加速度β、轴的支撑力N 各是多少?(2)当细杆转动到竖直位置转动角速度ω、质心速度v ? 解法:(1)设轴的支撑力为N ,则: 平动方程:ma N mg =- (1) 1分转动方程:βI Lmg =2(2) 1分由231mL I=, β2La = 代入(2)得 1分 g a43= 1分代入(1)式得: mg ma mg N41=-=细杆绕轴转动的角加速度:L g L a 232==β 1分 刚体的运动可看作:质心的平动和绕质心的转动的复合运动。
如图所示,故绕质心的转动角加速度 L g 23=='ββ1分(2) 竖直位角速度为ω,由机械守恒2223121212ωω⎪⎭⎫ ⎝⎛==mL I L mgL g 3=ω 3分 质心速度: gL L v c3212==ω 1分细杆转动平动解法2L g dt d 23==ωβ θωωθθωωβd d dt d d d dt d L g =⋅===23 2分 ⎰⎰=ωπωωθ02023d d L g L g 3=ω 1分 质心速度: gL L vc3212==ω 1分 二、如图所示,高为a 、底半径为b 的非绝热正圆锥容器,内装一种化学纯气体。
容器置于气压为P 0温度为T 0的大气中。
开始时,锥顶开口与大气相通,内部气体压强为P 0,但温度分布为T = T 0 + x ,此时将开口闭合,最终达到平衡时容器内气压P 是多少? 解:利用初始条件求容器内气体总分子数N 由理想气体压强公式:0P nkT =(2分) (若写成PV C T=或00PV PV T T =也给2分) 分子数密度:000()()P P n x kT k T x ==+ (2分) x —x+dx 内的分子数为:2200()()P b dN n x y dx x dx k T x a ππ⎛⎫== ⎪+⎝⎭(2分)积分求总分子数:2000()aP b N x dx k T x a π⎛⎫= ⎪+⎝⎭⎰22000200aP b T x T dx ka T x π⎛⎫=-+ ⎪+⎝⎭⎰ 222000020ln2P b T a a aT T ka T π⎛⎫+=-+⎪⎝⎭(2分) 将开口闭合,最终达到平衡时,温度与大气相同为T 0,压强为P ,而分子数密度均匀。
天津市历届大学生数学竞赛试题

2001年天津市大学数学竞赛试题参考答案(理工类)一、填空:(本题15分,每空3分。
请将最终结果填在相应的横杠上面。
)1. 函数⎪⎩⎪⎨⎧≥+<-=,,;,0cos 01e )(22x x x a x xx f x 在(-∞,+∞)上连续,则a = 2 。
2. 设函数y = y (x ) 由方程0)cos(e=-+xy yx 所确定,则==0d x y x d - 。
3. 由曲线x x x y 223++-=与x 轴所围成的图形的面积A =1237。
4. 设E 为闭区间[0,4π]上使被积函数有定义的所有点的集合,则⎰=Ex x x d sin cos 38 。
5.设L 是顺时针方向的椭圆1422=+y x ,其周长为l ,则()=++⎰L s y x xy d 422 4l 。
二、选择题:(本题15分,每小题3分。
每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。
选对得分;选错、不选或选出的答案多于一个,不得分。
)1. 若0)(lim 0u x x x =→ϕ且A u f =→)(lim 0u u ,则( D )(A ) )]([lim 0x f x x ϕ→存在; (B ) A x f x x =→)]([lim 0ϕ(C ) )]([lim 0x f x x ϕ→不存在; (D ) A 、B 、C 均不正确。
2. 设⎰=xx x x f sin 02d )sin()(,43)(x x x g +=,则当0→x 时,( A )(A ))(x f 与)(x g 为同阶但非等价无穷小; (B ))(x f 与)(x g 为等价无穷小;(C ))(x f 是比)(x g 更高阶的无穷小; (D ))(x f 是比)(x g 更低阶的无穷小。
3. 设函数)(x f 对任意x 都满足)()1(x af x f =+,且b f =)0(',其中a 、b 均为非零常数,则)(x f 在x = 1处( D )(A )不可导; (B )可导,且a f =')1(; (C )可导,且b f =')1(; (D )可导,且ab f =')1(。
年天津市大学生物理竞赛试题
年天津市大学生物理竞赛试卷注意: 类考生需做至题,类考生做至题及、题。
各题都需写出具体过程和结果。
请将所有答案写在答题纸上,答在此页上无效!交卷时此试卷和答题纸草稿纸一并上交。
注意:以下至题全体考生必答(要求写出具体计算过程与结果)。
.有一质点从开始作半径为的圆周运动,其弧长公式()十一 ()。
求:{)质点从到第秒末的位移?()质点从开始到第秒末的平均速率?()质点运动加速度何时有极值?. 有一长为内壁光滑的水平管道,其一端绕竖直轴以匀角速ω转动,管中有一小球(视为质点)从另一端沿管道以初速度 ω向管道中心滑来。
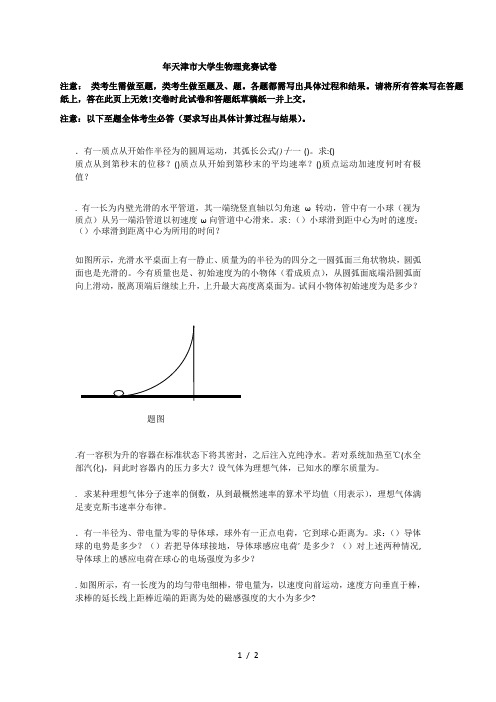
求:()小球滑到距中心为时的速度;()小球滑到距离中心为所用的时间?如图所示,光滑水平桌面上有一静止、质量为的半径为的四分之一圆弧面三角状物块,圆弧面也是光滑的。
今有质量也是、初始速度为的小物体(看成质点),从圆弧面底端沿圆弧面向上滑动,脱离顶端后继续上升,上升最大高度离桌面为。
试问小物体初始速度为是多少?.有一容积为升的容器在标准状态下将其密封,之后注入克纯净水。
若对系统加热至℃(水全部汽化),问此时容器内的压力多大?设气体为理想气体,已知水的摩尔质量为。
. 求某种理想气体分子速率的倒数,从到最概然速率的算术平均值(用表示),理想气体满足麦克斯韦速率分布律。
.有一半径为、带电量为零的导体球,球外有一正点电荷,它到球心距离为。
求:()导体球的电势是多少?()若把导体球接地,导体球感应电荷’ 是多少?()对上述两种情况,导体球上的感应电荷在球心的电场强度为多少?.如图所示,有一长度为的均勻带电细棒,带电量为,以速度向前运动,速度方向垂直于棒,求棒的延长线上距棒近端的距离为处的磁感强度的大小为多少?题图.一平行板电容器,两极板都是半径为厘的圆形导体板,在充电时,其电场强度的变化率为 伏(·秒), 求 ()两极板间位移电流;()求极板板内边缘处的磁感应强度?注意:、题为类考生必答题,类考生作答无分。
天津大学2006~2007学年第一学期期末考试试卷答案
6.(×)由于BF3为非极性分子,所以BF3分子中无极性键。
7.(√)由于Hg2+与S2-之间的相互极化作用比Zn2+比S2-间的极化作用强,所以HgS比ZnS的溶解度小。
8.(√)中心原子的几个原子轨道杂化时,形成数目相同的杂化轨道。
(C)分子间力和氢键能同时存在于分子之间;
(D)大多数分子的分子间力以色散力为主;
三.填空题(本题共22分)
1.50号元素的电子排布式为[Kr]4d105s25p2,该元素属五周期,IVA族,P区元素.
2.在乙醇的水溶液中,分子间存在的分子间力的种类有色散力、诱导力、
取向力和氢键。
3.KCN, NH4F, NH4OAc, NH4NO3, Na2CO3,各溶液浓度均为0.1 mol·L-1,按pH值从小到大顺序排列NH4NO3, NH4F, NH4OAc, KCN, Na2CO3。(已知Kθ(NH3·H2O)=1.8×10-5,Kθ(HF)=6.6×10-4,Kθ(HCN)=6.2×10-10,Kθ(HOAc)=1.8×10-5, (H2CO3)=4.4×10-7, (H2CO3)=4.8×10-11)
15.( )既能衡量元素金属性强弱,又能衡量其非金属性强弱的物理量是________。
(A)电子亲合能(B)电离能(C)电负性(D)原子半径
16.( )下列各组离子化合物的晶格能变化顺序中,正确的是________。
(A) MgO>CaO>Al2O3(B) LiF>NaCl>KI
(C) RbBr<CsI<KCl (D) BaS>BaO>BaCl2
Kө(298.15K)=1.3×1048
(2) (500K)=-248.5kJ·mol-1
1995年天津高考文科数学真题及答案
1995年天津高考文科数学真题及答案本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟.第Ⅰ卷(选择题共65分)一、选择题(本大题共15小题;第1-10题每小题4分,第11-15题每小题5分,共65分,在每小题给出的四个选项中,只有一项有符合题目要求的)1.已知集合I ={0,-1,-2,-3,-4},集合M ={0,-1,-2,},N ={0,-3,-4},则=⋂N M _( )(A) {0} (B) {-3,-4}(C) {-1,-2}(D) φ2.函数y =11+x 的图像是( )3.函数y =4sin(3x +4π)+3cos(3x +4π)的最小正周期是( ) (A) 6π(B) 2π(C) 32π (D)3π 4.正方体的全面积是a 2,它的顶点都在球面上,这个球的表面积是( ) (A)32a π (B)22a π(C) 2πa2(D) 3πa 25.若图中的直线l 1,l 2,l 3的斜率分别为k 1,k 2,k 3,则( )(A) k 1< k 2< k 3 (B) k 3< k 1< k 2 (C) k 3< k 2< k 1(D) k 1< k 3< k 26.双曲线3x 2-y 2=3的渐近线方程是( ) (A) y =±3x(B) 3x ±(C) y =x 3± (D) y =x 33±7.使sin x ≤cos x 成立的x 的一个变化区间是( ) (A) ⎥⎦⎤⎢⎣⎡-443ππ,(B) ⎥⎦⎤⎢⎣⎡-22ππ, (C) ⎥⎦⎤⎢⎣⎡-434ππ, (D) [0,π]8.x 2+y 2-2x =0和x 2+y 2+4y =0的位置关系是( ) (A) 相离(B) 外切(C) 相交 (D) 内切9.已知θ是第三象限角,且sin 4θ+cos 4θ=95,那么sin2θ等于( ) (A)322 (B) -322 (C)32 (D) -32 10.如图ABCD -A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成的角的余弦值是( )(A)1715 (B)21 (C)178 (D)23 11.已知y =log a (2-x )是x 的增函数,则a 的取值范围是( ) (A) (0,2)(B) (0,1)(C) (1,2) (D) (2,+∞)12.在(1-x 3)(1+x )10的展开式中,x 5的系数是( ) (A) -297(B) -252(C) 297(D) 20713.已知直线l ⊥平面α,直线m ⊂平面β,有下面四个命题,①α∥β⇒l ⊥m ②α⊥β⇒l ∥m ③l ∥m ⇒α⊥β ④l ⊥m ⇒α∥β 其中正确的两个命题是( ) (A) ①与②(B) ③与④(C) ②与④(D) ①与③14.等差数列{a n },{b n }的前n 项和分别是S n 与T n ,若132+=n nT S n n ,则nn n b a ∞→lim 等于( )(A) 1(B)36 (C)32 (D)94 15.用1,2,3,4,5这五个数字,组成没有重复数字的三位数,其中偶数共有( ) (A) 24个(B) 30个(C) 40个 (D) 60个第Ⅱ卷(非选择题共85分)二、填空题(本大题共5小题,每小题4分,共20分,把答案填在题中的横线上)16.方程log 2(x +1)2+log 4(x +1)=5的解是_____________17.已知圆台上、下底面圆周都在球面上,且下底面过球心,母线与底面所成角为3π,则圆台的体积与球体积之比为____________18.函数y =cos x +cos(x +3π)的最大值是___________ 19.若直线l 过抛物线y 2=4(x +1)的焦点,并且与x 轴垂直,则l 被抛物线截得的线段长为______________20.四个不同的小球放入编号为1、2、3、4的四个盒子中,则恰有一个空盒的放法共有____________种(用数字作答)三、解答题(本大题共6小题,共65分:解答应写出文字说明、证明过程或推演步骤)21.(本小题满分7分)解方程3x +2-32-x=80.22.(本小题满分12分)设复数z =cos θ+i sin θ,θ∈(π,2π),求复数z 2+z 的模和辐角23.(本小题满分10分)设{a n }是由正数组成的等比数列,S n 是其前n 项和,证明:15.025.05.0log 2log log ++>+n n n S S S .24.(本小题满分12分)如图,ABCD 是圆柱的轴截面,点E 在底面的圆周上,AF ⊥DE ,F 是垂足.(1)求证:AF ⊥DB(2)如果AB =a ,圆柱与三棱锥D -ABE 的体积比等于3π,求点E 到截面ABCD 的距离.25.(本小题满分12分)某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养值提供政府补贴,设淡水鱼的市场价格为千克元x ,政府补贴为千克元t ,根据市场调查,当8≤x ≤14时,淡水鱼的市场日供应量p 千克与市场日需求量Q 近似地满足关系:P =1000(x +t -8) (x ≥8,t ≥0), Q =500()2840--x (8≤x ≤14),当P =Q 时的市场价格为市场平衡价格,(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域: (2)为使市场平衡价格不高于每千克10元,政府补贴至少每千克多少元?26.(本小题满分12分)已知椭圆1162422=+y x ,直线l :x =12,P 是l 上一点,射线OP 交椭圆于点R ,又点Q 在OP上,且满足|OQ |·|OP |=|OR |2,当点P 在l 上移动时,求点Q 的轨迹方程,并说明轨迹是什么曲线.参考答案一、选择题(本题考查基本知识和基本运算)1.B 2.D 3.C 4.B 5.D 6.C 7.A 8.C 9.A 10.A 11.B 12.D 13.D 14.C 15.A二、填空题(本题考查基本知识和基本运算)16.3 17.3237 18.3 19.4 20.144 三、解答题21.本小题主要考查指数方程的解法及运算能力, 解:设y =3x,则原方程可化为9y 2-80y -9=0, 解得:y 1=9,y 2=91- 方程3x=91-无解, 由3x=9得x =2,所以原方程的解为x =2.22.本小题主要考查复数的有关概念,三角公式及运算能力,解:z 2+z =(cos θ+i sin θ)2+(cos θ+i sin θ) =cos2θ+i sin2θ+cos θ+i sin θ=2cos 23θcos 2θ+i (2sin 23θcos 2θ) =2 cos 2θ(cos 23θ+i sin 23θ)=-2 cos 2θ[cos(-π+23θ)+i sin(-π+23θ)]∵ θ∈(π,2π)∴2θ∈(2π,π) ∴ -2cos (2θ)>0所以复数z 2+z 的模为-2cos2θ,辐角(2k -1)π+23θ(k ∈z ).23.本小题主要考查等比数列、对数、不等式等基础知识以及逻辑推理能力, 证法一:设{a n }的公比为q ,由题设知a 1>0,q >0, (1)当q =1时,S n =na 1,从而S n ·S n+2-21+n S =na 1(n +2)a 1-(n +1)221a =-21a <0.(2)当q ≠1时,()qq a S nn --=111,从而S n ·S n+2-21+n S =()()()()()22121222111111q q a q q q a n n n ------++=-21a q n<0.由(1)和(2)得S n ·S n+2<21+n S .根据对数函数的单调性,得log 0.5(S n ·S n+2)>log 0.521+n S ,即15.025.05.0log 2log log ++>+n n n S S S .证法二:设{a n }的公比为q ,由题设知a 1>0,q >0, ∵ S n+1= a 1+qS n ,S n+2=a 1+ qS n +1,∴ S n ·S n+2-21+n S =S n (a 1+ qS n +1)-(a 1+qS n )S n +1= a 1(S n -S n +1)=-a 1 a n+1<0. 即S n ·S n+2<21+n S . (以下同证法一)24.本小题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力. (1)证明:根据圆柱性质,DA ⊥平面ABE , ∵ EB ⊂平面ABE , ∴ DA ⊥EB ,∵ AB 是圆柱底面的直径,点E 在圆周上, ∴ AE ⊥EB ,又AE ∩AD =A ,故得EB ⊥平面DAE , ∵ AF ⊂平面DAE , ∴ EB ⊥AF ,又AF ⊥DE ,且EB ∩DE =E ,故得AF ⊥平面DEB , ∵ DB ⊂平面DEB , ∴ AF ⊥DB .(2)解:设点E 到平面ABCD 的距离为d ,记AD =h ,因圆柱轴截面ABCD 是矩形,所以AD ⊥AB .S △ABD =21AB ·AD =2ah∴ V D -ABE =V E -ABD =3d S △ABD =61dah又V 圆柱=422ππ=⋅⎪⎪⎭⎫ ⎝⎛AD AB a 2h 由题设知dah ha 6142π=3π,即d =2a . 25.本小题主要考查运用所学数学知识和方法解决实际问题的能力,以及函数的概念、方程和不等式的解法等基础知识和方法.解:(1)依题设有1000(x +t -8)=500()2840--x化简得5x 2+(8t -80)x +(4t 2-64t +280)=0, 当判别式△=800-16t 2≥0时,可得:X =8-54t ±52250t -.由△≥0,t ≥0,8≤x ≤14,得不等式组:①⎪⎩⎪⎨⎧≤-+-≤≤≤14505254885002t t t②⎪⎩⎪⎨⎧≤---≤≤≤14505254885002t t t 解不等式组①,得0≤t ≤10,不等式组②无解,故所求的函数关系式为x =8-54t +25052t - 函数的定义域为[0,10] (2)为使x ≤10,应有8-54t +25052t -≤10, 化简得:t 2+4t -5≥0,解得t ≥1或t ≤-5,由于t ≥0知t ≥1,从而政府补贴至少为每千克1元. 26.本小题主要考查直线、椭圆的方程和性质,曲线与方程的关系,轨迹的概念和求法等解析几何的基本思想综合运用知识的能力.解:设点P 、Q 、R 的坐标分别为(12,y p ),(x ,y ),(x R ,y R 由题设知x R >0,x >0,由点R 在椭圆上及点O 、Q 、R 共线,得方程组1162422=+R R y x 解得 22223248yx x x R += ① x y x y R R = 22223248y x y y R += ② 由点O 、Q 、P 共线,得x y y p =12,即y p =xy12. ③ 由题设|OQ |·|OP |=|OR |2得()222222212RR pyx y y x +=+⋅+将①、②、③式代入上式,整理得点Q 的轨迹方程(x -1)2+322y =1 (x >0)所以点Q 的轨迹是以(1,0)为中心,长、短半轴长分别为1和36,且长轴在x 轴上的椭圆、去掉坐标圆点.。
2001-2013天津市大学数学竞赛试题解(经管类)
2001-2013年天津市大学数学竞赛试题参考答案(经济管理类)2001年天津市大学数学竞赛试题参考答案(经济管理类) (1)2002年天津市大学数学竞赛试题参考答案(经济管理类) (7)2003年天津市大学数学竞赛试题参考答案(经济管理类) (13)2004年天津市大学数学竞赛试题参考答案(经济管理类) (20)2005年天津市大学数学竞赛试题参考答案(经济管理类) (28)2006年天津市大学数学竞赛试题参考答案(经济管理类) (33)2007年天津市大学数学竞赛试题参考答案(经济管理类) (42)2008年天津市大学数学竞赛试题参考答案(经济管理类) (48)2009年天津市大学数学竞赛试题参考答案(经济管理类) (55)2010年天津市大学数学竞赛试题参考答案(经济管理类) (61)2011年天津市大学数学竞赛试题参考答案(经济管理类) (66)2001年天津市大学数学竞赛试题参考答案(经济管理类)一、填空:(本题15分,每空3分。
请将最终结果填在相应的横杠上面。
)1. 函数⎪⎩⎪⎨⎧≥+<-=,,;,0cos 01)(22x x x a x xe xf x 在(-∞,+∞)上连续,则a = 2 。
2. 设函数y = y (x ) 由方程0)cos(e =-+xy y x 所确定,则==0d x y x d - 。
3. 由曲线x x x y 223++-=与x 轴所围成的图形的面积A =1237。
4. 设E 为闭区间[0,4π]上使被积函数有定义的所有点的集合,则⎰=Edx x x sin cos 38。
5.已知()yxy z +=1,则=∂∂y z ()()⎥⎦⎤⎢⎣⎡++++xy xy xy xy y 11ln 1 。
二、选择题:(本题15分,每小题3分。
每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。
选对得分;选错、不选或选出的答案多于一个,不得分。
2007年天津大学生数学竞赛(免费)
2007年天津市大学数学竞赛试题(理工类)一、填空:(本题15分,每空3分。
请将最终结果填在相应的横线上面。
) 1. 设函数()()⎰⋅=xt at x f sin 02d sin ,()43x x x g +=,且当x →0时,()x f 与()x g 为等价无穷小,则a = 3 。
2. 设函数x x y 2=在0x x =点处取得极小值,则=0x ln21-。
3.()=+⎰+∞121d x x xln21-。
4. 曲线⎪⎩⎪⎨⎧=+++=+022401223:L 22222z y--z y x z--y x 在点(1,1,2)处的切线方程为524111--=--=-z y x 。
5.=+⎰⎰1132d 1d xy yxy x ()1231-。
二、选择题:(本题15分,每小题3分。
每个小题的四个选项中仅有一个是正确的,把你认为“正确选项”前的字母填在括号内。
选对得分;选错、不选或选出的答案多于一个,不得分。
)1. 设函数()x f 连续,则下列函数中必为偶函数的是( A ) (A )()()[]⎰⋅-+xt t f t f t 0d ; (B )()()[]⎰⋅--xt t f t f t 0d ;(C )()⎰x t tf 02d ; (D )()[]⎰xt t f 02d 。
2. 设函数()x f 具有一阶导数,下述结论中正确的是( D ) (A )若()x f 只有一个零点,则()x f '必至少有两个零点; (B )若()x f '至少有一个零点,则()x f 必至少有两个零点; (C )若()x f 没有零点,则()x f '至少有一个零点; (D )若()x f '没有零点,则()x f 至多有一个零点。
3. 设函数()x f 在区间()+∞,0内具有二阶导数,满足()00=f ,()0<''x f ,又b a <<0,则当b x a <<时恒有( B )(A )()()a xf x af >; (B )()()b xf x bf >;(C )()()b bf x xf >; (D )()()a af x xf >。
