【高考模拟】广东省中山市毕业班2018届高考数学一轮复习模拟试题(7)含答案
2018届广东省中山市高考数学三轮复习冲刺模拟试题(3)含答案

在 x1, x2 0,1 , 使得 f (x1) g(x2) 成立 , 则实数 a 的取值范围是 ____________.
xy
16 . 定 义 在 ( 1,1) 上 的 函 数 f ( x) f ( y) f
, 当 x ( 1,0) 时 f ( x) 0 . 若
1 xy
1 Pf
5
1
1
f
, Q f , R f (0) ,则 P,Q,R 的大小关系为 _____________.
二、填空题
高考数学三轮复习冲刺模拟试题 03 函数 02
1. 定义一种运算
,令
,且
,
则函数
的最大值是 ______.
2. 设函数
______.
3.函数 f(x) 的定义域为 D, 若对于任意的 x 1,x 2∈D, 当 x 1<x2 时都有 f(x 1) ≤f(x 2), 则称函数 f(x) 为 D 上的非减函数 . 设 f(x) 为定义在 [0,1] 上的非减函数 , 且满足一下三个条件 :
f ( x) 是 [ a, b] 上的 “平均值函数 ”, x0 是它的一个
均 值 点 , 如 y x 4 是 [ 1, 1] 上 的 平 均 值 函 数 , 0 就 是 它 的 均 值 点 . 现 有 函 数
f ( x) x 2 mx 1 是 [ 1, 1] 上的平均值函数,则实数 m 的取值范围是
8. 已知函数 f (x ) =
若 f ( x)在( - , + )上单调递增,则实数 a 的
log a x, x 1.
取值范围为 ________。
9. 定义:如果函数 y f ( x) 在定义域内给定区间 [a, b] 上存在 x0 ( a x0 b) ,满足
2018届广东省中山市高考数学三轮复习冲刺模拟试题(2)含答案

D. f( π )<f(-2)<f(-3)
7 . 定义在 R 上的奇函数 f(x), 当 x≥0 时,f(x)=
log (1 x 1), x
2
1 - x - 3x [ 1,
[ 0,1)
, 则关于 x 的函
)
数 F(x)=f(x)-a(0<a<1) 的所有零点之和为
A.
a
2
-1
B. 1-2 a
C.2-a -1
D.1-2 -a
()
8 . 设 f ( x) 是定义在 R 上的周期函数 , 周期为 T 4 , 对 x R 都有 f ( x) f ( x) , 且当
一、选择题
高考数学三轮复习冲刺模拟试题 02 函数 01
1 . 已知函数 f ( x ) x
x 1,g( x )
x
x
2 ,h( x )
x ln x 的零点分别为 x1,x2, x3,则 (
)
A. x1<x2<x3
B. x2<x1<x3
C.x3<x1 <x2
D.x2 <x3<x1
2 . 己 知 函 数 f ( x 1 ) 是 偶 函 数 , 当 x ( ,1 ) 时 , 函 数 f ( x ) 单 调 递 减 , 设
1 a f ( ),b
2
A. c<a<b
f ( 1),c f ( 2 ) ,则 a, b, c 的大小关系为
B. a<b<c
C.a<c<b
D.c<b<a
()
3 .试题)定义在 R 上的函数 则( )
满足
,当
时,
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题: (4) 含答案

个长度单位 12 D.向右平移 个长度单位 6
B.向右平移
8 .在 ABC 中,角 A, B, C 所对边长分别为 a, b, c ,若 a
2
b2 2c 2 ,则 cos C 的最小值为(
D.
)
A.
3 2
B.
2 2
C.
1 2
1 2
9 .在△ABC 中,a,b,c 分别是角 A,B,C 的对边,a=
( A. B. C. D. (
)
3 .在钝角△ABC 中,已知 AB=
3 , AC=1,∠B=30°,则△ABC 的面积是
C.
)
A.
3 2
B.
3 4
3 2
D.
3 4
4 .设函数 f(x)=Asin( x
)(A>0, >0,-
2 < < )的图象关于直线 x= 对称,且周期 2 2 3
高考数学三轮复习冲刺模拟试题 04 三角函数 01
一、选择题 1 .若 f ( x ) a sin x b (a,b 为常数)的最大值是 5,最小值是-1,则
A. 、
2 .边长为
2 3
B. 、
2 2 或 3 3
C. 、
3 2
)
a 的值为 b 3 D. 、 2
(
)
的三角形的最大角与最小角的和是(
值是(
)
A.
2 3
4 B. 3
6 .已知 tan(
4
) 3 5
sin 2 cos 2 1 ,则 的值为( 1 cos 2 2
B.
)
A.
5 6
C. 1
2018届广东省中山市高考数学三轮复习冲刺模拟试题(2)有答案
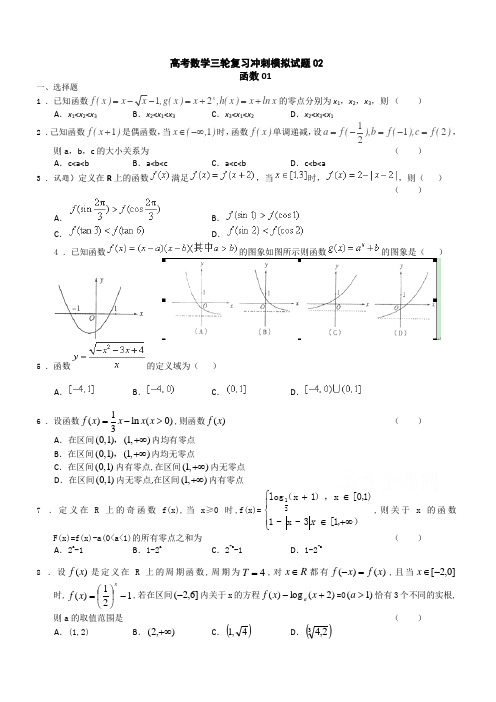
高考数学三轮复习冲刺模拟试题02函数01一、选择题1 .已知函数12x f (x )x x ,g(x )x ,h(x )x ln x =--=+=+的零点分别为x 1,x 2,x 3,则 ( )A .x 1<x 2<x 3B .x 2<x 1<x 3C .x 3<x 1<x 2D .x 2<x 3<x 12 .己知函数1f (x )+是偶函数,当1x (,)∈-∞时,函数f (x )单调递减,设1122a f (),b f (),c f ()=-=-=,则a ,b ,c 的大小关系为 ( )A .c<a<bB .a<b<cC .a<c<bD .c<b<a3 .试题)定义在R 上的函数满足,当时,,则( )( )A .B .C .D .4 .已知函数的图象如图所示则函数的图象是( )5 .函数的定义域为( )A .B .C .D .6 .设函数1()ln (0)3f x x x x =->,则函数()f x( )A .在区间(0,1)(1,)+∞, 内均有零点 B .在区间(0,1)(1,)+∞, 内均无零点C .在区间(0,1)内有零点,在区间(1,)+∞内无零点D .在区间(0,1)内无零点,在区间(1,)+∞内有零点7 .定义在R 上的奇函数f(x),当x≥0时,f(x)=⎪⎩⎪⎨⎧+∞∈∈+),1[3-x -1)1,0[x ),1x (log 21x ,则关于x 的函数F(x)=f(x)-a(0<a<1)的所有零点之和为 ( )A .2a -1B .1-2aC .2-a -1D .1-2-a8 .设)(x f 是定义在R 上的周期函数,周期为4=T ,对R x ∈都有)()(x f x f =-,且当]0,2[-∈x 时,121)(-⎪⎭⎫⎝⎛=xx f ,若在区间]6,2(-内关于x 的方程)2(log )(+-x x f a =0)1(>a 恰有3个不同的实根,则a 的取值范围是 ( )A .(1,2)B .),2(+∞C .()4,1D .()32,49 .已知函数()=ln f x x ,则函数()=()'()g x f x f x -的零点所在的区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4) 10.定义域为R 的函数()f x 满足(+2)=2()f x f x ,当x ∈[0,2)时,2|x-1.5|-,[0,1)()=-(0.5),[1,2)x x x f x x ⎧∈⎨∈⎩若[-4,-2]x ∈时,1()-42t f x t ≥恒成立,则实数t 的取值范围是()A .[-2,0)U (0,l)B .[-2,0) U [l ,+∞)C .[-2,l]D .(-∞,-2]U (0,l]11.在下列区间中,函数()=+43xf x e x -的零点所在的区间为( )A .(1-4,0) B .(0,14) C .(14,12) D .(12,34) 12.定义在R 上的偶函数f(x),当x ∈[0,+∞)时,f(x)是增函数,则f(-2),f(π),f(-3)的大小关系是 ( )A .f(π)>f(-3)>f(-2)B .f(π)>f(-2)>f(-3)C .f(π)<f(-3)<f(-2)D .f(π)<f(-2)<f(-3)13.偶函数f (x )满足(1)(1)f x f x +=-,且在x ∈[0,1]时,f (x )=x 2,则关于x 的方程f (x )=x⎪⎭⎫⎝⎛101在10[0,]3上根的个数是 ( )A .1个B .2个C .3个D .5个14.设5log 4a =, 25(log 3)b =,4log 5c =,则( )A .a<c<bB .b<c<aC .a<b<cD .b a c <<15.设函数1(1)|-1|)=1(=1)x x f x x ⎧≠⎪⎨⎪⎩(,若关于x 的方程2[()]+()+c=0f x bf x 有三个不同的实数根123,,x x x ,则222123++x x x 等于( )A .13B .5C .223c +2cD .222b +2b 16.函数()f x 的定义域为R ,若(1)f x +与(1)f x -都是奇函数,则( )A .()f x 是偶函数B .()f x 是奇函数C .()(2)f x f x =+D .(3)f x +是奇函数17.给定函数①12=y x-,②23+3=2xx y -,③12=log |1-|y x ,④=sin2xy π,其中在(0,1)上单调递减的个数为( ) A .0 B .1 个 C .2个 D .3个18.已知定义在区间[0,2]上的函数=()y f x 的图象如图所示,则=(2-)y f x 的图象为19.已知函数()()2531m f x m m x --=--是幂函数且是()0,+∞上的增函数,则m 的值为( )A .2B .-1C .-1或2D .020.已知函数2342013()12342013x x x x f x x =+-+-++L L ,2342013()12342013x x x x g x x =-+-+--L L ,设函数()(3)(4)F x f x g x =+⋅-,且函数()F x 的零点均在区间),,](,[Z ∈<b a b a b a 内,则-b a 的最小值为( )A .8B .9C .10D .1121.函数21(0)()(1)(0)x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不等的实数根,则实数a 的取值范围为( )A .(-∞,0)B .[0,1)C .(-∞,1)D .[0,+∞)22.函数x x x f 2log 12)(+-=的零点所在的一个区间是( )A .⎪⎭⎫⎝⎛41,81 B .⎪⎭⎫⎝⎛21,41 C .⎪⎭⎫⎝⎛1,21 D .)2,1(23.若直角坐标平面内的两点P 、Q 满足条件:①P 、Q 都在函数)(x f y =的图像上;②P 、Q 关于原点对称,则称点对[P ,Q]是函数)(x f y =的一对“友好点对”(注:点对[P ,Q]与[Q,P]看作同一对“友好点对”).已知函数⎩⎨⎧≤-->=)0(4)0(log )(22x x x x x x f ,则此函数的“友好点对”有 ( )A .0对B .1对C .2对D .3对参考答案一、选择题 1. D 2. A3. 【答案】D【解析】由题意可知,函数的图象关于y 轴对称,且周期为2,故可画出它的大致图象,如图所示:∵且,而函数在是减函数, ∴,选D.4. 【答案】A 【解析】由函数的两个根为.x a x b ==,图象可知01,1a b <<<-。
2018届广东省中山市高考数学三轮复习冲刺专题(1-5)含答案

高考数学三轮复习冲刺模拟试题01集合一、选择题1 .已知集合,,则( ) A .B .C .D .2 .设集合{1}A x x a x R =-<∈,,B={x|1<x<5,x ∈R},若A ⋂B=φ,则实数a 的取值范围是 ( )A .{a|0≤a ≤6}B .{a|a ≤2,或a ≥4}C .{a|a ≤0,或a ≥6}D .{a|2≤a ≤4}3 .已知集合2A={|log <1},B={x|0<<c}x x x ,若=AB B ,则c 的取值范围是( )A .(0,1]B .[1,+)∞C .(0,2]D .[2,+)∞二、填空题4 .若不等式4+-2+1x m x≥对一切非零实数x 均成立,记实数m 的取值范围为M .已知集合{}=A x x M ∈,集合{}2=--6<0B x R x x ∈,则集合=A B ___________.5 .设集合是A={32|()=83+6a f x xax x -是(0,+∞)上的增函数},5={|=,[-1,3]}+2B y y x x ∈,则()R AB ð= ;6 .试题)己知集合222{|28},{|240}xxA xB x x mx -=<=+-<, 若{|11},{|43}A B x x A B x x =-<<=-<<,则实数m 等于__________ .7 .设集合{}1,R A x x a x =-<∈,{}15,R B x x x =<<∈,若∅=B A ,则实数a 取值范围是___________.三、解答题8 .已知={()|1},B={()|3,0x 3}2A x,y y =-x+mx -x,y x+y =≤≤,若A B ⋂是单元素集,求实数m 的取值范围.参考答案一、选择题 1. 【答案】B【解析】{(3)0}{03}P x x x x x =-<=<<,={2}{22}Q x x x x <=-<<,所以{02}(0,2)P Q x x =<<=, 选B.2. 【答案】C【解析】{1}{11}A x x a x R x a x a =-<∈==-<<+,,因为=A B φ,所以有15a -≥或11a +≤,即6a ≥或0a ≤,选C.3. 【答案】D【解析】2{log 1}{01}A x x x x =<=<<.因为AB B =,所以A B ⊆.所以1c ≥,即[1,)+∞,选B.二、填空题4. {}-1<3x x ≤; 5. 【答案】(,1)(4,)-∞+∞【解析】2()=2466f 'x x a x -+,要使函数在(0,)+∞上是增函数,则2()=24660f 'x x ax -+>恒成立,即14a x x <+,因为144x x +≥=,所以4a ≤,即集合{4}A a a =≤.集合5={|=,[-1,3]}+2B y y x x ∈{15}y x =≤≤,所以{14}A B x x ⋂=≤≤,所以()=R A B ð(,1)(4,)-∞+∞.6. 【答案】32222{|28}{|230}{13}x xA x x x x x x -=<=--<=-<<,因为{|11},{|43}AB x x A B x x =-<<=-<<,所以由数轴可知{|41}B x x =-<<,即4,1-是方程2240x mx +-=的两个根,所以4123m -+=-=-,解得32m =。
广东省中山市普通高中2018届高考数学三轮复习冲刺模拟试题: (1) Word版含答案

高考数学三轮复习冲刺模拟试题01集合一、选择题1 .已知集合,,则( ) A .B .C .D . 2 .设集合{1}A x x a x R =-<∈,,B={x|1<x<5,x ∈R},若A ⋂B=φ,则实数a 的取值范围是( ) A .{a|0≤a ≤6}B .{a|a ≤2,或a ≥4}C .{a|a ≤0,或a ≥6}D .{a|2≤a ≤4}3 .已知集合2A={|log <1},B={x|0<<c}x x x ,若=A B B ,则c 的取值范围是( ) A .(0,1]B .[1,+)∞C .(0,2]D .[2,+)∞ 二、填空题 4 .若不等式4+-2+1x m x≥对一切非零实数x 均成立,记实数m 的取值范围为M .已知集合{}=A x x M ∈,集合{}2=--6<0B x R x x ∈,则集合=A B ___________.5 .设集合是A={32|()=83+6a f x x ax x -是(0,+∞)上的增函数},5={|=,[-1,3]}+2B y y x x ∈,则()R A B ð= ;6 .试题)己知集合222{|28},{|240}x x A x B x x mx -=<=+-<, 若{|11},{|43}A B x x A B x x =-<<=-<<,则实数m 等于__________ .7 .设集合{}1,R A x x a x =-<∈,{}15,R B x x x =<<∈,若∅=B A ,则实数a 取值范围是___________.三、解答题8 .已知={()|1},B={()|3,0x 3}2A x,y y =-x +mx -x,y x+y =≤≤,若A B ⋂是单元素集,求实数m 的取值范围.参考答案一、选择题1. 【答案】B【解析】{(3)0}{03}P x x x x x =-<=<<,={2}{22}Q x x x x <=-<<,所以{02}(0,2)P Q x x =<<=, 选B. 2. 【答案】C【解析】{1}{11}A x x a x R x a x a =-<∈==-<<+,,因为=A B φ,所以有15a -≥或11a +≤,即6a ≥或0a ≤,选C.3. 【答案】D 【解析】2{log 1}{01}A x x x x =<=<<.因为A B B =,所以A B ⊆.所以1c ≥,即[1,)+∞,选B.二、填空题4. {}-1<3x x ≤;5. 【答案】(,1)(4,)-∞+∞【解析】2()=2466f 'x x a x -+,要使函数在(0,)+∞上是增函数,则2()=24660f 'x x ax -+>恒成立,即14a x x <+,因为144x x +≥=,所以4a ≤,即集合{4}A a a =≤.集合5={|=,[-1,3]}+2B y y x x ∈{15}y x =≤≤,所以{14}A B x x ⋂=≤≤,所以()=R A B ð(,1)(4,)-∞+∞.6. 【答案】32222{|28}{|230}{13}x x A x x x x x x -=<=--<=-<<,因为{|11},{|4A B x x A B x x =-<<=-<<,所以由数轴可知{|41}B x x =-<<,即4,1-是方程2240x mx +-=的两个根,所以4123m -+=-=-,解得32m =。
推荐-中山市2018年高考模拟试题数学(桂山中学命题)(附
2018年中山市高三数学模拟测试题(5)桂山中学高三数学备课组 执笔人:饶乘风一、选择题:本大题共10小题,每小题5分,共50分.1.已知集合A ⊂{2,3,7},且A 中元素至少有一个为奇数,则这样的集合共有 A .2个 B .4个 C .5个 D .6个 ( ) 2.复数Z 1=-3+i ,Z 2=1+ i ,则Z =Z 1·Z 2在复平面内对应点位于 ( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限 3.“a =1”是“函数y =cos ax ·sin ax 的最小正周期为π”的 ( ) A .充分非必要条件 B .必要非充分条件 C .充要条件 D .既非充分也非必要条件4.曲线23-+=x x y 在点P 0处的切线平行于直线14-=x y ,则点P 0的坐标为 ( )A .(1,0)或(0,2-)B .(0,2-)或(2,8)C .(2,8)或(1-,4-)D .(1,0)或(1-,4-) 5.若函数b a x f x +=)(的图象过点(1,7),且0)4(1=-f ,则)(x f 的表达式是( )A .43)(+=x x fB .34)(+=x x fC .52)(+=x x fD .25)(+=x x f6.椭圆短轴长为52,离心率32=e ,两焦点为F 1、F 2,过F 1作直线交椭圆于A 、B 两点, 则△ABF 2的周长为A .6B .12C .24D .48 ( )7.将一个函数的图象按)2,4(π=平移后得到的图象的函数解析式2)4sin(++=πx y ,那么原来的函数解析式是 A .x y sin =B .x y cos =C .x y sin =+2D .x y cos =+4 ( )8. 某校高二年级共有六个班级,现从外地转入4名学生,要安排到该年级的两个班级且每班安排2名,则不同的安排方案种数为 A. 72 B .90 C .180 D .288 ( )9.数列}{n a 满足121,12210,2{1<≤-<≤=+n n n n n a a a a a ,若761=a ,则2004a 的值为( ) A.76 B. 75 C. 73 D. 71 10.地球北纬45°圈上有两点A 、B ,点A 在东经130°处,点B 在西经140°处,若地球半径为R ,则A 、B 两点在纬度圈上的劣弧长与A 、B 两点的球面距离之比是A .24B .34CD( )二、填空题:本大题共4小题,每小题5分,共20分,把答案填在题中横线上. 11.设随机变量ξ分布列为P (===k k k ,10)ξ1、2、3、4,则=≤≤)2521(ξP .12.定义运算b a *为:()(),⎩⎨⎧>≤=*b a b b a a b a 则函数f (x )=x x cos sin *的值域为 .13.圆1)1(22=++y x 在不等式组⎩⎨⎧≤+≤-0y x y x 所表示的平面区域中所围成的图形的面积为.14.在△ABC 中,有命题:(1)BC AC AB =- (2)0=++CA BC AB (3)若0)()(=-⋅+,则△ABC 为等腰三角形, (4)若0>⋅,则△ABC 为锐角三角形.其中真命题的编号为 (写出所有真命题的编号) 三、解答题:(共6小题,共80分)*15.(本小题满分12分)A 、B 各持有红、蓝两粒质地均匀的正方体形状骰子,红色骰子有两个面是1,四个面是2,蓝色骰子有n (06)n ≤≤个面是1,其余面是2,两人分别随机投掷一次,约定:所得点数和为奇数时,A 获胜,所得点数和为偶数时,B 获胜,(1)若n =4,求A 获胜的概率; (2)若n =4,求投掷两只骰子所得点数和的期望. (3)是否存在自然数n (06)n ≤≤,使得A 、B 获胜的概率相等?若存在,求出n 的值,若不存在,说明理由。
2018届广东省中山市高考数学三轮复习冲刺模拟试题(8)包含答案
高考数学三轮复习冲刺模拟试题08数列02三、解答题1.已知A(,),B(,)是函数的图象上的任意两点(可以重合),点M在 直线上,且. (1)求+的值及+的值(2)已知,当时,+++,求; (3)在(2)的条件下,设=,为数列{}的前项和,若存在正整数、,使得不等式成立,求和的值.2.设等差数列的首项及公差d 都为整数,前n 项和为S n .(1)若,求数列的通项公式;(2)若 求所有可能的数列的通项公式.3.设等比数列{}n a 的前n 项和为n S ,已知122()n n a S n N *+=+∈.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)在n a 与1n a +之间插入n 个数,使这2n +个数组成公差为n d 的等差数列, 设数列1n d ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T ,证明:1516n T <.4.已知数列{a n }中,a 1=1,若2a n+1-a n =)2n )(1n (n 2-n ++,b n =a n -)1n (n 1+(1)求证:{ b n }为等比数列,并求出{a n }的通项公式; (2)若C n =nb n +)1n (n 1+,且其前n 项和为T n ,求证:T n <3.5.已知数列{}n a 的前n 项和11()22n n n S a -=--+(n 为正整数)(Ⅰ)令2n n n b a =,求证:数列{}n b 是等差数列,并求数列{}n a 的通项公式; (Ⅱ)令121,n n n n n C a T C C C n+==+++,试比较n T 与521nn +的大小,并予以证明6.已知数列}{n a 满足()2,34,3,1*1121≥∈-===-+n N n a a a a a n n n ,(1)证明:数列}{1n n a a -+是等比数列,并求出}{n a 的通项公式(2)设数列}{n b 的前n 项和为n S ,且对任意*N n ∈,有1222211+=+++n na b a b a b nn 成立,求n S7.设数列{}n a 的前n 项和为n S .已知11a =,131n n a S +=+,n *∈N .(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)记n T 为数列{}n na 的前n 项和,求n T .8.设数列{a n }的前n 项和为S n ,且满足S n =2-a n ,n=1,2,3,…(1)求数列{a n }的通项公式;(4分)(2)若数列{b n }满足b 1=1,且b 1+n =b n +a n ,求数列{b n }的通项公式;(6分) (3)设C n =n (3- b n ),求数列{ C n }的前n 项和T n 。
2018届广东省中山市高考数学三轮复习冲刺模拟试题(6)有答案
高考数学三轮复习冲刺模拟试题06平面向量一、选择题1 .△ABC 的外接圆的圆心为O,半径为1,2→AO =→AB +→AC 且→AO =→AB ,则向量→AB 在→BC 方向上的投影为 ( )A .21B .23 C .-23D .-212 .平面向量a 与b 的夹角为)0,3(,32=a π,2||=b ,则b a 2+= ( )A .13B .37C .7D .33 .如图,边长为1的正方形ABCD 的顶点A ,D 分别在x 轴、y 轴正半轴上移动,则OC OB ⋅的最大值是( )A .2B .12+C .πD .44 .已知向量,,a b c 中任意两个都不共线,且a b +与c 共线, b c +与a 共线,则向量a b c ++( )A .aB .bC .cD .05 .已知a =(-3,2),b =(-1,0),向量a λ+b 与a -2b 垂直,则实数λ的值为( )A .-71B .71 C .-61 D .616 .在平行四边形ABCD 中,2,AE EB CF FB ==,连接CE 、DF 相交于点M ,若AM AB AD λμ=+,则实数λ与μ的乘积为 ( )A .14B .38C .34D .437 .在平面内,已知1,3OA OB ==,0=⋅, 30=∠AOC ,设n m +=,(,R m n ∈),则nm 等于 ( )A .3±B .3±C .13±D .33±二、填空题8 .已知点M 为等边三角形ABC 的中心,=2AB ,直线L 过点M 交线段AB 于点P ,交线段AC 于点Q ,则BQ CP ⋅的最大值为______________.9 .OA =1OB =3,OA ·OB =0,点C 在∠AOB 内,且∠AOC=30°,设OC =m OA +n OB (m ,n ∈R),则nm=________。
10.若向量a ,b 满足|a |=1,|b |=2且a 与b 的夹角为3π,则|a +b |=________。
2018届广东省中山市高考数学三轮复习冲刺模拟试题(3)有答案
高考数学三轮复习冲刺模拟试题03函数02二、填空题1.定义一种运算,令,且,则函数的最大值是______.2.设函数______.3.函数f(x)的定义域为D,若对于任意的x 1,x 2∈D,当x 1<x 2时都有f(x 1)≤f(x 2),则称函数f(x)为D 上的非减函数.设f(x)为定义在[0,1]上的非减函数,且满足一下三个条件: (1)f(0)=0; (2)f(1-x)+f(x)=1 x ∈[0,1]; (3)当x ∈[0,31]时,f(x)≥23x 恒成立,则f(73)+f(95)= . 4.设f (x )=⎩⎪⎨⎪⎧lg x ,x >0,10x,x ≤0,则f (f (-2))=________.5.已知函数y mx =的图像与函数11x y x -=-的图像没有公共点,则实数m 的取值范围是 6.已知a>0,且a ≠1,若函数2(-2+3)()=lg xx f x a 有最大值,则不筹式2(-5+7)>0a log x x 的解集为 ;7.函数f(x)=a x+2+x a 的值域为_________.8.已知函数f (x )=⎩⎨⎧>≤--.1,log 1,1)2(x x ,x x a a若f (x )在(-∞,+∞)上单调递增,则实数a 的取值范围为________。
9.定义:如果函数)(x f y =在定义域内给定区间b][,a 上存在)(00b x a x <<,满足ab a f b f x f --=)()()(0,则称函数)(x f y =是b][,a 上的“平均值函数”,0x 是它的一个均值点,如4x y =是]1,1[-上的平均值函数,0就是它的均值点.现有函数1)(2++-=mx x x f 是]1,1[-上的平均值函数,则实数m 的取值范围是 .10.已知x R ∀∈,(1+)=(1-)f x f x ,当1x ≥时,()=(1)f x ln x+,则当<1x 时,()=f x .11.已知函数2=+-1+2y x ax a [0,+)∞,则a 的取值范围是 .12.函数212()=log (-2-3)f x x x 的单调递减区间为 .13.已知1f x -,则()=f x (x ∈ ). 14.若(f x ,则()f x 的定义域为 .15.已知函数3111,0,362()21,,112x x f x x x x ⎧⎡⎤-+∈⎪⎢⎥⎣⎦⎪=⎨⎛⎤⎪∈ ⎥⎪+⎝⎦⎩ ,函数π()sin()22,(0)6=-+>g x a x a a ,若存在[]12,0,1x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是____________.16.定义在)1,1(-上的函数⎪⎪⎭⎫⎝⎛--=-xy y x f y f x f 1)()(,当)0,1(-∈x 时0)(>x f .若)0(,21,11151f R f Q f f P =⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=,则P ,Q,R 的大小关系为_____________.三、解答题17.对于函数()f x 若存在0x R ∈,00()=f x x 成立,则称0x 为()f x 的不动点.已知2()=(1)-1(0)f x ax b x b a +++≠ (1)当=1,=-2a b 时,求函数(f x )的不动点;(2)若对任意实数b ,函数()f x 恒有两个相异的不动点,求a 的取值范围;(3)在(2)的条件下,若=()y f x 图象上A 、B 两点的横坐标是函数()f x 的不动点,且A 、B 两点关于直线2121y kx a =++对称,求b 的最小值.18.已知函数()f x 对任意实数,x y 恒有()()()f x y f x f y +=+,且当x >0时,()0f x <又(1)2f =-.(1)判断()f x 的奇偶性;(2)求证:()f x 是R 上的减函数; (3)求()f x 在区间[-3,3]上的值域;(4)若x R ∀∈,不等式2()2()()4f ax f x f x -<+恒成立,求a 的取值范围.参考答案二、填空题 1. 【答案】54【解析】令,则∴由运算定义可知,∴当1sin 2x =,即6x π=时,该函数取得最大值54. 由图象变换可知,所求函数的最大值与函数在区间上的最大值相同.2. 【答案】52【解析】令1x =-得(1)(1)(2)f f f =-+,即1(2)(1)(1)2(1)212f f f f =--==⨯=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一轮复习数学模拟试题07一选择题(每个5分共12题60分)1、函数1()ln(1)f x x =++ ( ) A .[2,0)(0,2]- B . (1,0)(0,2]- C .[2,2]- D .(1,2]-2、,a b 为非零向量,“函数2()()f x ax b =+ 为偶函数”是“a b ⊥ ”的( )A. 充分但不必要条件B. 必要但不充分条件C. 充要条件D. 既不充分也不必要条件3、双曲线222298x y -=-则其焦点坐标为( ) A . ()5,0± B. ()3,0± C. ()0,3± D. ()0,5±4、6名选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( ) A .480种 B .360种 C .240种 D .720种5、已知各项均为均为正数的等比数列中,13213,,22a a a 成等差数列,则1113810a a a a +=+( ) A . -1或3 B. 3 C. 27 D. 1或276、设ABC ∆的三个内角A,B,C 向量s i n ,s i n ),o s ,3c o s )m A B n A ==若1cos()m n A B ⋅=++则C=( )A .6πB 。
3π C 。
23π D 。
56π7、已知某个三棱锥的三视图如图所示,其中正视图是等边三角形,侧视图是直角三角形,俯视图是等腰直角三角形, 则此三棱锥的体积等于ABD8、1,,0,1,ax y a x y x y>+=+设且的最小值为4则a=( ) A .1 B.2 C.3 D.49、设m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:(1)//////αββγαγ⎫⇒⎬⎭(2)//m m αββα⊥⎫⇒⊥⎬⎭(3)//m m ααββ⊥⎫⇒⊥⎬⎭(4)////m n m n αα⎫⇒⎬⊂⎭,其中,假命题是A.(1)(2)B.(2)(3) C 。
(1)(3) D 。
(2)(4)正视图俯视图10、在ABC ∆中,AD 为BC 边上的中线,4====( ) A .6 B .3 C .2 D .3 11.设奇函数()f x 的定义域为R,最小正周期3T =,若23(1)1,(2)1a f f a -≥=+,则a 的取值范围是A .213a a <-≥或 B .213a -<≤ C . 1a <- D .23a ≤ 12、对于四面体ABCD ,有如下命题 ①棱AB 与CD 所在的直线异面;②过点A 作四面体ABCD 的高,其垂足是BCD ∆的三条高线的交点; ③若分别作ABC ∆和ABD ∆的边AB 上的高,则这两条高所在直线异面;④分别作三组相对棱的中点连线,所得的三条线段相交于一点, 其中正确的是 A. ① B. ②③ C. ①④D. ①③二、填空题(本题共4小题每题5分共20分)13、在61(xx -的二项展开式中,常数项等于 _________ 14、执行如图所示的程序框图,若输出的b 的值 为16,图中判断框内?处应填的数为15、过直线0x y +-=,上点P 作圆224x y +=的两条切线,若两条切线的夹角是60︒,则点P 的坐否16、设2[0,1]()1(1,]x x f x x e x ⎧∈⎪=⎨∈⎪⎩,则0()e f x dx =⎰_____.三、解答题(本题要求再解答时写出必要地文字说明) 17、(本小题满分12分已知{}n a 是一个公差大于0的等差数列,且满足3655a a =,2716a a +=.(1)求数列{}n a 的通项公式; (2)若数列{}n a 和数列{}n b 满足等式:*31223()2222n n nb b b b a n N =++++∈ ,求数列{}n b 的前n 项和n S .18、 (本小题满分12分)某单位实行休年假制度三年以来,50名职工休年假的次数进行的调(Ⅰ)从该单位任选两名职工,用h 表示这两人休年假次数之和,记“函数2()1f x x x =--h在区间(4,6)上有且只有一个零点”为事件A ,求事件A 发生的概率P ;(Ⅱ)从该单位任选两名职工,用x 表示这两人休年假次数之差的绝对值,求随机变量x 的分布列及数学期望E x .19、(本小题满分12分如图,PDCE 为矩形,ABCD 为梯形,平面PDCE ^平面ABCD ,90BADADC???,12AB AD CD a ===,PD =. (Ⅰ)若M 为PA 中点,求证://AC 平面MDE ; (Ⅱ) 求平面PAD 与PBC 所成锐二面角的余弦值.20、(本小题满分12分P 是圆221x y +=上的一个动点,过点P 作PQ x ⊥轴于点Q ,设OM OP OQ =+(1)求点M 的轨迹方程(2)求向量OP 和OM夹角最大时的余弦值和P21.(本小题满分12分) 已知函数211()ln ,()22f x ax x x f x '=+-是)(x f (1) 21=a 时,求)(x f 的最小值; (2) 若)(x f 存在单调递增区间,求a 的取值范围;(3) 若关于x 的不等式2231311()2x f x x x x'+-≥≥-在()+∞,0恒成立,求a 的取值范围.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-1:几何证明选讲如图,直线AB 经过⊙O 上的点C ,并且,,CB CA OB OA ==⊙O 交直线OB 于E ,D ,连接CD EC ,.(Ⅰ)求证:直线AB 是⊙O 的切线;(Ⅱ)若,21tan =∠CED ⊙O 的半径为3,求OA 的长.A B CEPDM23.(本小题满分10分)选修4-4:坐标系与参数方程已知在直角坐标系xOy 中,圆锥曲线C 的参数方程为⎩⎨⎧==θθsin 3cos 2y x (θ为参数),定点)3,0(-A ,21,F F 是圆锥曲线C 的左,右焦点.(Ⅰ)以原点为极点、x 轴正半轴为极轴建立极坐标系,求经过点1F 且平行于直线 2AF 的直线l 的极坐标方程;(Ⅱ)在(I )的条件下,设直线l 与圆锥曲线C 交于F E ,两点,求弦EF 的长.24.(本小题满分10分)选修4-5:不等式选讲设函数212)(--+=x x x f . (Ⅰ)求不等式2)(>x f 的解集; (Ⅱ)R x ∈∀,使t t x f 211)(2-≥,求实数t 的取值范围.答案一、选择题1——5 BCDAC 6——10 CBADA 11——12 BC 二、填空题13、-20 14、3 15、( 16、4317、(本小题满分12分)解:(1)设等差数列{}n a 的公差为(0)d >,由2716a a +=,得12716a d += ①----------------2分 由3655,a a ⋅=得11(2)(5)55a d a d ++= ②----------------4 分 易得11,2a d ==,所以*21()n a n n N =-∈ ----------------5 分 备注:也可以由2736a a a a +=+得3627361655a a a a a a +=+=⎧⎨=⎩,由36511a a =⎧⎨=⎩,得到112a d =⎧⎨=⎩(2)令2nn n b c =,则有12n n a c c c =++ ,*1121(,2)n n a c c c n N n --=++∈≥ 1n n n a a c -∴-=,由(1)得12n n a a -∴-=,故*2(,2)n c n N n =∈≥,即22n nb=, 而11a =,所以可得12,12,2n n n b n +=⎧=⎨≥⎩ . ------------------------ 8分 于是3411232222n n n S b b b b +=+++=++++------------------------10 分=234122222n ++++++ 4-=1222(21)426,2621n n n n S +++--=-=--即.-----12分18.(本小题满分12分)解:(Ⅰ) 函数()21f x x x η=--过(0,1)-点,在区间(4,6)上有且只有一个零点,则必有(4)0(6)0f f <⎧⎨>⎩即:1641036610ηη--<⎧⎨-->⎩,解得:153546η<< 所以,4η=或5η=…………3分当4η=时,211201015125068245C C C P C +==,当5η=时,11201522501249C C P C ==…………5分 4η=与5η=为互斥事件,由互斥事件有一个发生的概率公式所以12681212824549245P P P =+=+=…………6分 (Ⅱ) 从该单位任选两名职工,用ξ表示这两人休年假次数之差的绝对值,则ξ的可能取值分别是0,1,2,3,…………7分于是()22225102015250207C C C C P C ξ+++===,1111115101020152025022(1)49C C C C C C P C ξ++===,1111520101525010(2)49C C C C P C ξ+===,115152503(3)49C C P C ξ===…………10分 从而ξ的分布列:ξ的数学期望:0123749494949E ξ=⨯+⨯+⨯+⨯=. …………12分19、(本小题满分12分)(Ⅰ) 证明:连结PC ,交DE 与N ,连结MN ,PAC ∆中,,M N分别为两腰,PA PC 的中 点 ∴//MN AC …………2分因为MN ⊂面MDE ,又AC ⊄面MDE ,所以//AC 平面MDE …………4分(Ⅱ) 设平面PAD 与PBC 所成锐二面角的大小为θ,以D 为空间坐标系的原点,分别以,,DA DC DP 所在直线为,,x y z 轴建立空间直角坐标系,则),(,,0),(0,2,0)P B a a C a(,,),(,,0)PB a a BC a a ==-…………6分设平面PAD 的单位法向量为1n,则可设1(0,1,0)n =…………7分设面PBC 的法向量2(,,1)n x y =,应有x22(,,1)(,,)0(,,1)(,,0)0n PB x y a a n BC x y a a ⎧==⎪⎨=-=⎪⎩即:00ax ay ax ay ⎧+=⎪⎨-+=⎪⎩,解得:2x y ⎧=⎪⎪⎨⎪=⎪⎩,所以2n = …………10分∴12121cos 2||||n n n n θ⋅===…………11分 所以平面PAD 与PBC 所成锐二面角的余弦值为12…………12分 20、(本小题满分12分)解:(1)设(,)Px y ,(,)M x y ,则(,)O P x y = ,(,0)OQ x = ,(2,)OM OP OQ x y =+=222212,1,124x x x x x x y y y y y y ⎧==⎧⎪∴⇒+=∴+=⎨⎨=⎩⎪=⎩…………………………………5分(2)设向量OP 与OM 的夹角为α,则22cos ||||OP OMOP OM α⋅===⋅令231t x =+,则cos 3α== ……………………8分 当且仅当2t =时,即P点坐标为(时,等号成立。
