九年级数学上册3.5《弧长及扇形的面积》教案(1)浙教版
【精选】九年级数学上册3.8弧长及扇形的面积1课件新版浙教版351

360
180
l
nR
180
=
n 360 C圆
1、在公式中变量有哪些?常量是哪些?
2、在变量l、R、n中,只要已知其中两个量
就可以求第三个量,那么请将公式变形求出
R和n。
R 180l
n
n 180l
R
做一做:
1、已知圆的半径为4cm,则300的圆周角所对的弧长
为____4___
3
2、已知弧的长为 3 cm,弧的半径为6cm,则该弧所对
知识回顾
o rp
圆的周长公式
C=2πr
圆的面积公式
S=πr2
已知圆的半径为10cm,求 (1)半圆的弧长 (2)90度圆心角所对的弧长 (3)1度的圆心角所对的弧长
B
弧
n°
O A
在(4半)n径度的为圆心R角的所对圆的中弧长,n°的圆心角
所对的弧长的计算公式为:
l n 2 R n R
优等生经验谈:听课时应注意学习老师解决问题的思考方法。同学们如果理解了老师的思路和过程,那么后面的结论自然就出现了,学习起来才能够举 一反三,事半功倍。2 Nhomakorabea19/8/4
最新中小学教学课件
14
谢谢欣赏!
2019/8/4
最新中小学教学课件
15
听课对同学们的学习有着非常重要的作用。课听得好好,直接关系到大家最终的学习成绩。如何听好课,同学们可以参考如下建议:
一、听要点。
一般来说,一节课的要点就是老师们在备课中准备的讲课大纲。许多老师在讲课正式开始之前会告诉大家,同学们对此要格外注意。例如在学习物理 课“力的三要素”这一节时,老师会先列出力的三要素——大小、方向、作用点。这就是一堂课的要点。把这三点认真听好了,这节课就基本掌握了。
3.8.1 弧长公式 课件(共20张PPT)2023-2024学年浙教版九年级上册数学

运动到A′位置时,点A经过的路线长为
.
1.若扇形的圆心角为40°,半径为18,则它的弧
长为( B )
A.3π
B.4π
C.5π
D.6π
2. 如图,用一个半径为10 cm的定滑轮带动重物上升,滑轮上
一点P旋转了72°,假设绳索(粗细不计)与滑轮之间没有滑
4π
动,则重物上升了________cm.
l=
R=
n=
.
当这条弧所对的圆心角增加1°后,弧长l′=
所以它的弧长增加l′-l=
+ πR πR πR
= .
+ πR
.
例4 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向转动一
次,使它转到三角形A′BC′的位置.若BC=1,∠A=30°.求点A
运动到A′位置时,点A经过的路线长为
N
例2 一段圆弧形的公路弯道,圆弧的半径是2km.一辆汽车以每
小时60km的速度通过弯道,需时20s.求弯道所对圆心角的度
数(精确到0.1°).
解题秘方:如果能求出弯道的弧长,那么由于半径已知,根据
弧长公式就可以求出弯道所对圆心角的度数.
解:汽车在20s内通过的路程为l=
由弧长公式l=
n=
_______.
知识点 2 弧长公式的应用
例1
如图,BM是⊙O的直径,四边形ABMN是矩形,D是⊙O上
一点,DC⊥AN,与AN交于点C.已知AC=15mm,⊙O的半径
Ⴃ
R=30mm,求的长.
B
A
E
C
D
O
M
【精选】九年级数学上册3.8弧长及扇形的面积课件1新版浙教版353

180
9
R
O
弧长公式
l 若设⊙O半径为R, n°的圆心角所对的弧长为 ,
则
l
n R
180
A
B
n°
O
例1:
已知圆弧的半径为50厘米,圆心角为60°,
求此圆弧的长度。
解:
l n R 60 50
180 180
=
50
3
(cm)
答:此圆弧的长度为 50 cm
3
例2制造弯形管道时,要先按中心线计算“展直长
二、听思路。
思路就是我们思考问题的步骤。例如老师在讲解一道数学题时,首先思考应该从什么地方下手,然后在思考用什么方法,通过什么样的过程来进行解 答。听课时关键应该弄清楚老师讲解问题的思路。
三、听问题。
对于自己预习中不懂的内容,上课时要重点把握。在听讲中要特别注意老师和课本中是怎么解释的。如果老师在讲课中一带而过,并没有详细解答, 大家要及时地把它们记下来,下课再向老师请教。
2、已知扇形的圆心角为120°,半径为2,
则这个扇形的面积,S扇=____.
3、已知扇形的圆心角为1500,弧长为 20 cm ,
则扇形的面积为_2_4__0___c_m__2.
颗粒归仓
1.弧长公式:
l nR 180
2.扇形面积公式:S 扇 形
nR 2 360
1 lR 2
注意: (1)两个公式的联系和区别;
度”,再下料,试计算图所示管道的展直长度L(单
位:mm结果取整数)
解:由弧长公式,可得弧AB 的长
L 100 900 500 1570(mm)
180
因此所要求的展直长度 L 27001570 2970 (mm) 答:管道的展直长度为2970mm.
浙教版九年级数学上册课件:3.8 弧长及扇形的面积(第1课时)
5 正解:3
3πcm
错因:没有弄清楚点 A 的运动轨迹,它走的线
路应该是以 B 为圆心的圆弧而不是线段 AA′.
P 是边 CA 的延长线上的点,在 AP 之间拉一条细绳,
绳长 AP=15cm,握住点 P,拉直细绳,
把它全部紧紧绕在△ABC 木块上(缠绕
时木块不动),若圆周率π取 3.14,
则点 P 运动的路线长为多少?(精确
到 0.1cm)
答案:点 P 运动的路线是以 A 为圆心,AP 为半径的 圆弧加上以 B 为圆心,BD 为半径的圆弧再加上以 C 为圆心,CE 为半径的弧,这三条弧的圆心角都为
120°,半径分别为 15cm,9cm,3cm.所以得路线长 为 56.5cm.
例 如图,在 Rt△ABC 中,∠C=90°,∠A=60°,
AC= 3c的
位置,且使 A,B(B)′,C′三点
在同一直线上,则点 A 经过的最
短路线长是________.
错解:2 6+3 3cm
3.8 弧长及扇形的面积(第 1 课时)
计算弧长
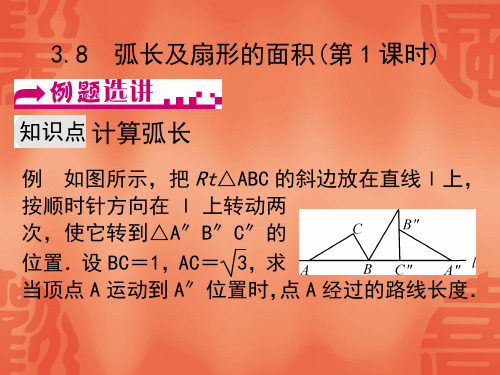
例 如图所示,把 Rt△ABC 的斜边放在直线 l 上,
按顺时针方向在 l 上转动两 次,使它转到△A″B″C″的 位置.设 BC=1,AC= 3,求 当顶点 A 运动到 A″位置时,点 A 经过的路线长度.
解析:要求点 A 经过的路线长度,我们必须先弄清楚点 A 所走的是直线还是弧线,由题意可得是旋转而成的,那么 我们只要求得点 A 旋转的角度以及点 A 经过的路线是由哪 两条弧线所组成的即可.由题意可得点 A 经过的路线是由 以点 B 为圆心,AB 长为半径的弧线和以点 C″为圆心, A″C″为半径的弧线组成的.
∵在 Rt△ABC 中,BC=1,AC= 3,∴AB=2,∠A=30°,
浙教版数学九上3.8《弧长及扇形的面积》word学案

A清流县城关中学师生共用导学案 课题: 3.8弧长和扇形的面积 主备人: 温富友 审核人: 时间:一、学习目标:1、利用圆的周长与面积公式探索弧长和扇形面积的计算公式的过程.2、掌握弧长和扇形面积公式并解决实际问题.二、教学重点:利用圆的周长与面积公式探索弧长和扇形面积的计算公式 教学难点:探索弧长和扇形面积的计算公式 三、知识链接 :1、弧长的概念:弧的长度; 弧长的表示方法:弧AB 的长记作2、扇形的概念:由组成圆心角的两条半径和圆心角所对的弧所围成的图形叫做扇形; 扇形表示方法:阴影部分扇形可记作 ;空白部分扇形可记作3、半径为2的圆的周长是 ,面积为 。
4、⊙0中设半径为R ,则360°的圆心角所对的弧长是 ,面积为 。
四、自学探究:自学教材P139页到P141页完成下列问题: 活动1、探索弧长的计算公式如右图,某传送带的一个转动轮的半径为lO cm .(1)转动轮转一周,传送带上的物品A 被传送 厘米 (2)转动轮转1°,传送带上的物品A 被传送 厘米 (3)转动轮转n °,传送带上的物品A 被传送 厘米探究:在半径为R 的圆中,n °的圆心角所对的弧长的计算公式为: .例1、制作弯形管道时,需要先按中心线计算“展直长度”再下料。
试计算下图中管道的展直长度,即弧AB 的长.(精确到0.1mm )公式应用:1.已知圆的半径为8cm ,则 45︒的圆心角所对的弧长= __ 2.已知弧长为2π,半径为4,则该弧所对圆心角= __° 活动2、探索扇形面积的计算公式在一块空旷的草地上有一根柱子,柱子上拴着一条长3m 的绳子,绳子的另一端拴着一头牛。
(1)这头牛吃草的最大活动区域有多大?(2)如果这头牛只能绕柱子转过n°角,那∠它的最大活动区域有多大?分析: 1.设圆的半径为r ,1°的圆心角所对的扇形面积S 扇形=____________; 2.设圆的半径为r ,2°的圆心角所对的扇形面积S 扇形=____________; 3.设圆的半径为r ,n°的圆心角所对的扇形面积S 扇形=____________;探究:在这两个公式中,弧长和扇形面积都和圆心角n .半径R 有关系,因此L 和S 之间也有一定的关系,你能猜得出吗? S 扇形=______L例2:扇形AOB 的半径为l2cm ,∠AOB=120°,求弧AB 的长和扇形A0B 的面积。
九年级数学下册《弧长和扇形的面积》教案、教学设计

1.引入环节:
利用生活中的实例,如圆蛋糕、时钟等,引导学生观察并思考其中所包含的扇形元素,从而自然引入本章节的学习内容。
2.新课导入:
(1)通过复习圆的相关知识,如周长、面积等,为新课的学习做好铺垫。
(2)以问题驱动的形式,让学生自主探究扇形的定义、性质,培养学生的探究意识。
3.知识讲解:
鼓励学生发挥想象,设计一道具有创意的扇形相关问题,并尝试运用所学知识进行解答。
作业要求:
1.认真完成作业,注意书写规范,保持卷面整洁。
2.对于实践应用题和拓展提高题,要求学生详细阐述解题思路,展示解题过程。
3.小组合作题需充分发挥团队协作精神,共同完成任务。
4.作业完成后,及时进行自我检查,发现问题并及时改正。
3.拓展提高题:
(1)探究扇形的对称性质,并运用对称性质解决相关问题。
(2)研究扇形与三角形、矩形等图形的面积关系,推导相关公式。
4.小组合作题:
以小组为单位,共同探讨以下问题:
(1)扇形在生活中的应用,以及如何利用扇形优化设计。
(2)比较不同扇形面积与半径、圆心角的关系,总结规律。
5.创新思维题:
3.教师指导:
教师巡回指导,关注各小组的讨论进度,给予适当的提示和指导,引导学生深入思考。
(四)课堂练习
1.教学活动设计:
设计具有层次性和挑战性的练习题,让学生独立完成,巩固所学知识。
2.练习题类型:
(1)基础题:计算给定圆心角和半径的扇形的弧长和面积。
(2)提高题:解决实际问题,如计算河流的弯曲长度、不规则图形的面积等。
4.引导学生认识到数学在生活中的广泛应用,体会数学的价值,培养学生的数学素养。
二、学情分析
浙教版数学九年级上册《3.8 弧长及扇形的面积》教案2
浙教版数学九年级上册《3.8 弧长及扇形的面积》教案2一. 教材分析《3.8 弧长及扇形的面积》是浙教版数学九年级上册的一个重要内容。
本节课主要介绍了弧长和扇形面积的计算方法,以及它们在实际问题中的应用。
通过本节课的学习,学生能够掌握弧长和扇形面积的计算公式,提高解决实际问题的能力。
二. 学情分析九年级的学生已经具备了一定的几何基础知识,对图形的认识和理解有一定的基础。
但是,对于弧长和扇形面积的计算方法,以及它们在实际问题中的应用,可能还比较陌生。
因此,在教学过程中,需要注重引导学生理解和掌握计算方法,并通过实例让学生感受其在实际问题中的应用。
三. 教学目标1.知识与技能:学生能够掌握弧长和扇形面积的计算公式,并能应用于实际问题中。
2.过程与方法:通过实例分析,培养学生解决实际问题的能力。
3.情感态度与价值观:激发学生学习数学的兴趣,培养学生的抽象思维能力。
四. 教学重难点1.重点:弧长和扇形面积的计算方法。
2.难点:弧长和扇形面积计算公式的推导过程,以及如何在实际问题中应用。
五. 教学方法采用问题驱动法、案例教学法和小组合作学习法。
通过设置问题,引导学生主动探究;通过案例分析,让学生理解弧长和扇形面积的计算方法;通过小组合作,培养学生解决问题的能力。
六. 教学准备1.准备相关的案例和实际问题,用于课堂分析和讨论。
2.准备弧长和扇形面积的计算公式,以便在课堂上进行讲解和演示。
七. 教学过程1.导入(5分钟)通过提问方式复习之前学习过的几何知识,如圆的周长和面积。
引导学生思考:如何计算弧长和扇形面积?2.呈现(10分钟)展示弧长和扇形面积的计算公式,并进行讲解。
通过示例,让学生了解弧长和扇形面积的计算方法。
3.操练(10分钟)让学生独立完成一些相关的计算题,巩固对弧长和扇形面积计算方法的理解。
教师巡回指导,解答学生的疑问。
4.巩固(10分钟)针对学生完成的情况,进行讲解和分析。
通过实际问题,让学生应用弧长和扇形面积的计算方法,解决实际问题。
浙江省温州市瓯海区实验中学九年级数学上册 3.5《弧长及扇形的面积》教案(2) 浙教版
3.5 弧长及扇形的面积(2)
【教学目标】
1.经历扇形面积计算公式的过程;
2.会应用公式解决问题.
3.训练学生的数学运用能力.
【教学重点】
扇形面积计算公式
【教学难点】
例4较复杂
【教学过程】
一.创设问题情境,引入新课
1、弧长的计算公式l =
180
n πR 如果圆的半径为R ,则圆的面积为 ------ ,
l °的圆心角对应的扇形面积为 ----- ,
n °的圆心角对应的扇形面积为 -------
结论:扇形面积计算公式为
2、P84 做一做(1)--(4) P85 T 1--2
二、新课讲解1、例3教学
如图,有一把折扇和一把团扇。
已知折扇的骨柄与团扇的直径一样长,折扇扇面的宽度是骨柄长的一半,折扇张开的角度为120 °,问哪一把扇子扇面的面积大?
2、练一练 P85 作业题2
3、例4教学
我国著名的引水工程的主干线输水管的直径为2.5m,设计流量为12.73m3 /s.如果水管截面中水面面积如图所示,其中∠AOB=45°,那么水的流速因达到多少m/s.
4、练一练 P85 作业题4
三.课时小结
本节课学习了如下内容:
扇形面积计算公式,并运用公式进行计算;
板书设计
§3.5弧长及扇形的面积(2)
扇形的面积计算公式; 例3 例4
练习 练习
板书设计。
浙江省苍南县灵溪镇第十中学九年级数学上册 3.52 弧长及扇形的面积课件 浙教版
空白部分的面积
O
应如何求呢?
A
B
6cm
如图,在矩形ABCD中,AD=2AB=2, 以B为圆心,BA为半径作圆弧,交CB的延长 线于点E,连结DE,求黄色区域的面积
A
D
E
B
C
如图,三角形ABC是Rt△,∠C=900, AC=6,BC=8,分别是AB,AC,BC为直径, 向外作半径,求图中黄色区域的面积。
如果圆的半径为R,则圆的面积为R 2 ,
Hale Waihona Puke l°的圆心角对应的扇形面积为 R 2
,
360
n°的圆心角对应的扇形面积为 n R2 nR2 360 360
那么: 在半径为R 的圆中,n°的圆心角
所对的扇形面积的计算公式为
S扇 形
nR 2
360
l
弧
=
n 180
πR
S扇形
=
n 360
πR2
S扇形 1 lR
C
A
B
如图,扇形AOB的圆心角为直角,边长为1的 正方形OCDE的顶点C,E,D分别在OA,OB,A⌒B上, 过点A作AF⊥ED,交ED的延长线于点F,求图中阴 影部分的面积.
2
在这两个公式中,弧长和扇形面积都和圆心角n°、 半径R有关系,因此l 和S之间也有一定的关系,你
能猜得出吗?
做一做: 1、已知扇形的圆心角为120°,半径为2,则
这个扇形的面积为___4____.
3
6cm
3cm2
2、已 知扇
3、已知扇形的圆心角为1500,弧长为形的20 cm ,
则扇形的面积为_2_4__0___c_m__2. 圆心
角为
想一想,以下图形中,黄色区域的面积该如何求?
3.8 弧长及扇形的面积九年级上册数学浙教版
3.8 弧长及扇形的面积
学习目标
1.通过复习圆的周长、面积公式,探索 的圆心角所对的弧长 和扇形面积 的计算公式.
2.能应用弧长及扇形的面积公式解决问题.
3.能计算不规则图形的面积.
知识点1 弧长公式 重点
半径为 的圆中, 的圆心角所对的弧长 的计算公式为 . 表示 圆心角的倍数 和180都不带单位 , 为弧所在圆的半径说明 在弧长公式中, , , 三个量,可以知二求一: , , .
示例1
弧长公式的推导过程
辨析“两条弧相等”“两条弧的度数相等”以及“两条弧的长度相等”之间的区别与联系
两条弧相等
两条弧的度数相等
两条弧的长度相等
区别
两条弧能够完全重合,只在同圆或等圆中出现.
两条弧对应的圆心角的度数相等,与圆弧所在圆的半径无关.
与圆弧的形状无关.
联系
(1)如果两条弧相等,那么两条弧的度数和长度都相等;(2)若两条弧的度数相等,或者两条弧的长度相等,则这两条弧不一定相等;(3)只有在同圆或等圆中,“两条弧的度数相等”或“两条弧的长度相等”与“两条弧相等”才是等价的.
链接教材 本题取材于教材第113页第21题,问题的背景一致,条件稍做了变动,教材习题是利用等积变换法求阴影部分的面积,而中考真题则是利用面积的差求阴影部分的面积.两题都考查了扇形的面积公式.
, , , .易知 为 的中位线, . .
中考常考考点
难度
常考题型
考点1:弧长公式的应用.
★★★
选择题、填空题
考点2:求阴影部分的面积.主要考查利用扇形面积公式求不规则图形的面积,这也是中考的热点问题,有一定的综合性.
★★★
选择题、填空题、解答题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
3.5 弧长及扇形的面积(1)
【教学目标】
(一)知识与技能目标
1.经历探索弧长计算公式及扇形面积计算公式的过程;
2.了解弧长计算公式及扇形面积计算公式,并会应用公式解决问题.
(二)过程与方法目标
1.经历探索弧长计算公式及扇形面积计算公式的过程,培养学生的探索能力.
2.了解弧长及扇形面积公式后,能用公式解决问题,训练学生的数学运用能力.
(三)情感与价值观目标
1.经历探索弧长及扇形面积计算公式.让学生体验教学活动充满着探索与创造,感受
数学的严谨性以及数学结论的确定性.
2.通过用弧长及扇形面积公式解决实际问题.让学生体验数学与人类生活的密切联系,
激发学生学习数学的兴趣,提高他们的学习积极性,同时提高大家的运用能力.
【教学重点】
1.经历探索弧长及扇形面积计算公式的过程.
2.了解弧长及扇形面积计算公式.
3.会用公式解决问题.
【教学难点】
1.探索弧长及扇形面积计算公式.
2.用公式解决实际问题.
【教学过程】
Ⅰ.创设问题情境,引入新课
[师]在小学我们已经学习过有关圆的周长和面积公式,弧是圆周的一部分,扇形是圆的
—部分,那么弧长与扇形面积应怎样计算?它们与圆的周长、圆的面积之间有怎样的关系呢?
本节课我们将进行探索.
Ⅱ.新课讲解
一、复习
1.圆的周长如何汁算?
2,圆的面积如何计算?
3.圆的圆心角是多少度?
[生]若圆的半径为r,则周长l=2πr,面积S=πr2,圆的圆心角是360°.
二、探索弧长的计算公式
360°的圆心角对应圆周长2πR,那么1°的圆心角对应的弧长为1803602RR,n°的
圆心角对应的弧长应为1°的圆心角对应的弧长的n倍,即n×180180RnR.
在半径为R的圆中,n°的圆心角所对的弧长(arclength)的计算公式为:
l=180Rn.
下面我们看弧长公式的运用.
三、例题讲解
例1、制作弯形管道时,需要先按中心线计算“展直长度”再下料,试计算下图中管道
相关以往知识:
_______________________
_______________________
____________________
______________________
教学内容和方法:
_______________________
_______________________
_______________________
_______________________
_______________________
_________________
个性化教学思路及改进
建议:
_______________________
_______________________
_______________________
_______________________
_______________________
_________________
______________________
_______________________
_______________________
_______________________
___________________
______________________
2
的展直长度,即弧AB的长(结果精确到0.1 mm).
分析:要求管道的展直长度.即求弧AB的长,根据弧长公式l=180Rn可求得弧AB的
长,其中n为圆心角,R为半径.
解:R=40mm,n=110.
∴弧AB的长= 180nπR=弧180110×40π≈76.8 mm.
因此.管道的展直长度约为76.8 mm.
变形题 课本P82 例2
例1 (P82)
课内练习 P82 1--4
四.课时小结
本节课学习了如下内容:
探索弧长的计算公式l=180nπR,并运用公式进行计算;
板书设计
§3.5 弧长及扇形的面积
1. 复习圆的周长和面积计算公式;
2.探索弧长的计算公式;
3.例题讲解;
