北师大版八年级思品下册第一单元测试卷

合集下载

2020年北师大版八年级数学下册第一章三角形的证明单元测试题及答案

北师大版八年级数学下册第一章三角形的证明单元测试题一．选择题（共10小题，每小题3分，共30分）1．等腰三角形的对称轴是（）A．底边上的高所在的直线B．底边上的高C．底边上的中线D．顶角平分线2．如图在3×3的网格中，点A、B在格点处：以AB为一边，点P在格点处，则使△ABP为等腰三角形的点P有（）个．A．2个B．3个C．4个D．5个3．如图，在△ABC中，∠B与∠C的角平分线相交于点I，过点I作BC的平行线，分别交AB、AC于点D、E．若AB＝9，AC＝6，BC＝8，则△ADE的周长是（）A．14 B．15 C．174．如图所示，在等边三角形ABC中，AD⊥BC，E为AD上一点，∠CED＝50°，则∠ABE等于（）A．10°B．15°C．20°D．25°5．在△ABC中，AB＝AC，∠A＝60°，BC＝6，则AB的值是（）A．12 B．8 C．6 D．36．用反证法证明“a≥b”，对于第一步的假设，下列正确的是（）A．a≤b B．a≠b C．a＜b D．a＝b7．下列说法：①一个底角和一条边分别相等的两个等腰三角形全等；②底边及底边上的高分别相等的两个等腰三角形全等；③两边分别相等的两个直角三角形全等；④一个锐角和一条边分别相等的两个直角三角形全等，其中正确的个数是（）A．1 B．2 C．3 D．48．如图，在△ABC中，∠C＝90°，∠A＝30°，AB的垂直平分线分别交AB，AC于点D，E，则下列结论正确的是（）A．AE＝3CE B．AE＝2CE C．AE＝BD D．BC＝2CE9．如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，点E是边AB的中点，AB＝10，DE ＝4，则S△AEC＝（）A．8 B．7.5 C．7 D．610．如图，在△ABC中，CD⊥AB于点D，BE平分∠ABC，交CD于点E，若S△BCE＝10，BC＝5，则DE等于（）A．10 B．7 C．5 D．4二．填空题（共8小题，每小题3分，共24分）11．等腰三角形的周长为12cm，其中一边长为3cm，则该等腰三角形的腰长为．12．如图：已知∠B＝20°，AB＝A1B，A1B1＝A1A2，A2B2＝A2A3，A3B3＝A3A4，以此类推∠A的度数是．13．如图，在△ABC中，AB＝AC＝10，AD平分∠BAC，点E为AC中点，则DE＝．14．在Rt△ABC中，∠B＝90°，∠A＝30°，DE垂直平分AC，交AC于点E，交AB于点D，连接CD，若BD＝2，则AD的长是．15．如图，DE是△ABC的边AC上的垂直平分线，AB＝5cm，BC＝8cm，则△ABD的周长为cm．16．如图，点D，P在△ABC的边BC上，DE，PF分别垂直平分AB，AC，连接AD、AP，若∠DAP＝20°，则∠BAC＝．17．如图，AB∥CD，∠BAC与∠ACD的平分线交于点P，过P作PE⊥AB于E，交CD于F，EF＝10，则点P到AC的距离为．18．如图，AD是△ABC的角平分线，DE⊥AB于点E，S△ABC＝40，DE＝4，AC＝12，则AB长是．三．解答题（共7小题，共66分）19．如图，在△ABC中，AB＝BC，∠ABC＝110°，AB的垂直平分线DE交AC于点D，连接BD，求∠DBA的度数．20．如图，已知AB∥CD，∠BCF＝180°，BD平分∠ABC，CE平分∠DCF，∠ACE＝90°．求证：AC⊥BD．21．已知：如图，在△ABC中，∠ACB＝90°，CD是高，AE是△ABC内部的一条线段，AE交CD于点F，交CB于点E，且∠CFE＝∠CEF．求证：AE平分∠CAB．22．如图，在Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD于点F，交CB于点E，且∠EAB＝∠DCB．（1）求∠B的度数：（2）求证：BC＝3CE．23．如图，直线l与m分别是△ABC边AC和BC的垂直平分线，l与m分别交边AB，BC于点D 和点E．（1）若AB＝10，则△CDE的周长是多少？为什么？（2）若∠ACB＝125°，求∠DCE的度数．24．如图，已知AB＝AC，∠A＝40°，AB的垂直平分线MN交AC于点D．（1）求∠DBC的度数；（2）若△DBC的周长为14cm，BC＝5cm，求AB的长．25．如图，已知AC∥BD，AE，BE分别平分∠CAB和∠DBA，点E在线段CD上．（1）求∠AEB的度数；（2）求证：CE＝DE．参考答案一．选择题1．解：等腰三角形的对称轴是底边的垂直平分线，故选：A．2．解：如图所示，以AB为腰的等腰三角形的点P有2个，以AB为底边的等腰三角形的点P有3个，∴△ABP为等腰三角形的点P有5个；故选：D．3．解：∵BI平分∠DBC，∴∠DBI＝∠CBI，又∵DE∥BC，∴∠DIB＝∠IBC，∴∠DIB＝∠DBI，∴BD＝DI．同理CE＝EI．∴△ADE的周长＝AD+DI+IE+EA＝AB+AC＝15，故选：B．4．解：∵在等边三角形ABC中，AD⊥BC，∴AD是BC的线段垂直平分线，∵E是AD上一点，∴EB＝EC，∴∠EBD＝∠ECD，∵∠CED＝50°，∴∠ECD＝40°，又∵∠ABC＝60°，∠ECD＝40°，∴∠ABE＝60°﹣40°＝20°，故选：C．5．解：∵AB＝AC，∠A＝60°，∴△ABC是等边三角形，∴AB＝BC＝6，故选：C．6．解：反证法证明“a≥b”，第一步是假设，a＜b，故选：C．7．解：①一个底角和一条边分别相等的两个等腰三角形不一定全等；②底边及底边上的高分别相等的两个等腰三角形全等，正确；③两边分别相等的两个直角三角形不一定全等；④如果在两个直角三角形中，例如：两个30°角的直角三角形，一个三角形的直角边与另一个三角形的斜边相等，这两个直角三角形肯定不全等，错误；故选：A．8．解：连接BE，∵DE是AB的垂直平分线，∴AE＝BE，∴∠ABE＝∠A＝30°，∴∠CBE＝∠ABC﹣∠ABE＝30°，在Rt△BCE中，BE＝2CE，∴AE＝2CE，故选：B．9．解：∵在△ABC中，∠ACB＝90°，C点E是边AB的中点，∴AE＝BE＝CE＝AB＝5，∵CD⊥AB，DE＝4，∴CD＝＝3，∴S△AEC＝S△BEC＝BE•CD＝3＝7.5，故选：B．10．解：作EF⊥BC于F，∵S△BCE＝10，∴×BC×EF＝10，即×5×EF＝10，解得，EF＝4，∵BE平分∠ABC，CD⊥AB，EF⊥BC，∴DE＝EF＝4，故选：D．二．填空题11．解：由题意知，应分两种情况：（1）当腰长为3cm时，则另一腰也为3cm，底边为12﹣2×3＝7cm，∵3+3＜7，∴边长分别为3，3，7不能构成三角形；（2）当底边长为3cm时，腰的长＝（12﹣3）÷2＝4.5cm，∵0＜3＜4.5+4.5＝9，∴边长为3，4.5，4.5，能构成三角形，则该等腰三角形的一腰长是4.5cm．故答案为：4.5cm．12．解：∵∠B＝20°，AB＝A1B，∴∠A＝（180°﹣∠B）＝80°，故答案为：80°．13．解：∵AB＝AC，AD平分∠BAC，∴AD⊥BC，∴∠ADC＝90°，又点E为AC中点，∴DE＝AC＝5，故答案为：5．14．解：∵DE垂直平分AC，∴CD＝AD，∴∠ACD＝∠A＝30°，∵在Rt△ABC中，∠B＝90°，∠A＝30°，∴∠ACB＝90°﹣∠A＝60°，∴∠BCD＝∠ACB﹣∠ACD＝30°，∴CD＝2BD＝2×2＝4，∴AD＝CD＝4．故答案为：4．15．解：∵DE是△ABC中的边AC上的垂直平分线，∴AD＝CD，∵AB＝5cm，BC＝8cm，∴△ABD的周长为：AB+BD+AD＝AB+BD+CD＝AB+BC＝13（cm）．故答案是：13．16．解：∵DE，PF分别垂直平分AB，AC，∴∠B＝∠BAD，∠C＝∠CAP，又∵∠DAP＝20°，∴∠B+∠C＝（180°﹣20°）＝80°，∴∠BAC＝180°﹣80°＝100°，故答案为：100°．17．解：作PH⊥AC于H，∵AP平分∠BAC，PE⊥AB，PH⊥AC，∴PE＝PH，∵AB∥CD，PE⊥AB，∴PF⊥CD，∵CP平分∠ACD，PF⊥CD，PH⊥AC，∴PF＝PH，∴PH＝PE＝PF＝EF＝5，即点P到AC的距离为5，故答案为：5．18．解：作DF⊥AC于F，如图，∵AD是△ABC的角平分线，DE⊥AB，DF⊥AC，∴DF＝DE＝4，∵S△ABD+S△ADC＝S△ABC，∴•4•AB+•12•4＝40，∴AB＝8．故答案为8．三．解答题19．解：∵在△ABC中，AB＝BC，∠ABC＝110°，∴∠A＝∠C＝35°，∵AB的垂直平分线DE交AC于点D，∴AD＝BD，∴∠DBA＝∠A＝35°20．证明：∵AB∥CD，∴∠ABC＝∠DCF．（两直线平行，同位角相等）∵BD平分∠ABC，CE平分∠DCF，∴∠2＝∠ABC，∠4＝∠DCF．（角平分线的定义）∴∠2＝∠4．∴BD∥CE．（同位角相等，两直线平行）∴∠BGC＝∠ACE．（两直线平行，内错角相等）∵∠ACE＝90°，∴∠BGC＝90°，即AC⊥BD．（垂直的定义）21．证明：∵CD⊥AB，∴在△ADF中，∠DAF＝90°﹣∠AFD＝90°﹣∠CFE．∵∠ACE＝90°，∴在△AEC中，∠CAE＝90°﹣∠CEF．∵∠CFE＝∠CEF，∴∠DAF＝∠CAE，即AE平分∠CAB．22．解：（1）∵AE⊥CD，∴∠AFC＝∠ACB＝90°，∴∠CAF+∠ACF＝∠ACF+∠ECF＝90°，∴∠ECF＝∠CAF，∵∠EAD＝∠DCB，∴∠CAD＝2∠DCB，∵CD是斜边AB上的中线，∴CD＝BD，∴∠B＝∠DCB，∴∠CAB＝2∠B，∵∠B+∠CAB＝90°，∴∠B＝30°；（2）∵∠B＝∠BAE＝∠CAE＝30°，∴AE＝BE，CE＝AE，∴BC＝3CE．23．解：（1）△CDE的周长为10．∵直线l与m分别是△ABC边AC和BC的垂直平分线，∴AD＝CD，BE＝CE，∴△CDE的周长＝CD+DE+CE＝AD+DE+BE＝AB＝10；（2）∵直线l与m分别是△ABC边AC和BC的垂直平分线，∴AD＝CD，BE＝CE，∴∠A＝∠ACD，∠B＝∠BCE，又∵∠ACB＝125°，∴∠A+∠B＝180°﹣125°＝55°，∴∠ACD+∠BCE＝55°，∴∠DCE＝∠ACB﹣（∠ACD+∠BCE）＝125°﹣55°＝70°．24．解：（1）∵AB＝AC，∴∠ABC＝∠ACB，∵∠A＝40°，∴∠ABC＝∠ACB＝70°，∵MN是AB的垂直平分线，∴DA＝DB，∴∠A＝∠ABD＝40°，∴∠DBC＝∠ABC﹣∠ABD＝70﹣40°＝30°；（2）∵MN是AB的垂直平分线，∴BD＝AD，∵△DBC的周长为14cm，∴BD+BC+CD＝14cm，∵BC＝5cm，∴BD+CD＝AD+CD＝AC＝9cm，∵AB＝AC，∴AB＝9cm．25．解：（1）∵AC∥BD，∴∠CAB+∠ABD＝180°．∵AE平分∠CAB，∴∠EAB＝∠CAB．同理可得∠EBA＝∠ABD．∴∠EAB+∠EBA＝90°，∴∠AEB＝90°；（2）如图，在AB上截取AF＝AC，连接EF，在△ACE和△AFE中，∴△ACE≌△AFE（SAS）．∴CE＝FE，∠CEA＝∠FEA．∵∠CEA+∠DEB＝90°，∠FEA+∠FEB＝90°，∴∠DEB＝∠FEB．在△DEB和△FEB中∴△DEB≌△FEB（ASA）．∴ED＝EF．∴ED＝CE．。

(常考题)北师大版初中数学八年级数学下册第一单元《三角形的证明》测试(答案解析)(4)

一、选择题1．如图的网格中，每个小正方形的边长为1，A ，B ，C 三点均在格点上，结论错误的是（）A ．AB=25B ．∠BAC=90°C ．ABC S 10=D ．点A 到直线BC 的距离是22．如图，等腰直角ABC 中，90BAC ∠=︒，AD BC ⊥于点D ，ABC ∠的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，延长AM 交BC 于点N ，连接NE ．下列结论：①AE AF =；②AM EF ⊥；③DF DN =；④//AD NE ．正确的有（）A ．①②B ．①②③C ．①②④D ．①②③④ 3．如图，在△ABC 中，AB =AC ，∠BAC =64°，∠BAC 的平分线与AB 的垂直平分线交于点O ，点E 、F 分别在BC 、AC 上，点C 沿EF 折叠后与点O 重合，则∠BEO 的度数是（）A ．26°B ．32°C ．52°D ．58°4．下列几组数能作为直角三角形三边长的是（）A ．3，4，6B ．1，1，3C ．5，12，14D ．5，25，5 5．下面说法中正确的是（）A ．ABC ∆中BC 边上的高线，是过顶点A 向对边所引的垂线B ．ABC ∆中BC 边上的高线，是过顶点A 向对边所引的垂线段C ．三角形的角平分线不是射线D ．等腰三角形的对称轴和底边上的高线、中线以及顶角的平分线，互相重合6．如图，ABC 中，D 、E 为线段BE 上两点，且AC DC =，BA BE =，若52DAE BAC ∠=∠，则DAE ∠的度数为（）A ．40︒B ．45︒C ．50︒D ．60︒7．如图，D 在BC 边上，ABC ADE △△≌，50EAC ∠=︒，则ADE ∠的度数为（）A ．50°B ．55°C ．60°D ．65°8．如图，在四边形ABCD 中，90A BDC ∠=∠=︒，C ADB ∠=∠，点P 是BC 边上的一动点，连接DP ，若3AD =，则DP 的长不可能是（）A ．2B ．3C ．4D ．59．如图，在ABC 中，∠C ＝90°，∠B ＝30°，以点A 为圆心，任意长为半径画弧分别交AB ，AC 于点M 和N ，再分别以M ，N 为圆心，大于12MN 的长为半径画弧，两弧交于点P ，连接AP 并延长交BC 于点D ，则下列结论不正确的是（）A ．AD 平分∠BACB ．∠ADC =60° C ．点D 在AB 的垂直平分线上D ．:DAC ABC S S ＝1：2 10．等腰三角形一腰的垂直平分线与另一腰所在直线的夹角是40°，则这一等腰三角形的底角为（）A ．65°B ．25°C ．50°D ．65°或25° 11．如图，ABC 是等边三角形，BD 是中线，延长BC 至E ，使CE CD =，则下列结论错误．．的是（）A ．30CED ∠=︒B ．120∠=︒BDEC ．DE BD = D ．DE AB = 12．如图，每个小正方形的边长都相等，A ，B ，C 是小正方形的顶点，则ABC ∠的度数为（）A ．45︒B ．50︒C ．55︒D ．60︒二、填空题13．如图，在ABC 中，线段AB 的垂直平分线交AC 于点D ，连接BD ，若80C ∠=︒，40CBD ∠=︒，则A ∠的度数为_____°．14．如图，等边三角形ABC 中，在AB 边上任意取一点D ，作DE BC ⊥于点E ，再作//EF AB 交AC 于点F ．当DEF 是等腰三角形时，EDF ∠的度数是_____________．15．如图，AD 是△ABC 的平分线，DF ⊥AB 于点F ，DE ＝DG ，AG ＝16，AE ＝8，若S △ADG ＝64，则△DEF 的面积为 ________．16．如图，线段AB ，BC 的垂直平分线l 1，l 2相交于点O ，若∠B ＝50°，则∠AOC ＝_____．17．已知：在ABC 中，90ACB ∠=︒，42AC BC ==，点D 在AB 上，连接CD ，若5CD =，则AD 的长为________．18．在锐角ABC 中，AB AC =，CE 是高，且36ECA ∠=︒，平面内有一异于点A ，B ，C ，E 的点D ，若ABC CDA △△≌，则DAE ∠的度数为______．19．如图，在ABC 中，,AB AC AD =是BC 边上的中线，50B ∠=︒，则DAC ∠=___________20．如图，在ABC 中，AB BC =，30C ∠=︒，过点B 作BD BC ⊥，交AC 于点D ，若2CD =，则AD 的长为__________．三、解答题21．已知：如图，ABC ∆中，,,AB AC BD CE =分别是,AC AB 上的中线，,BD CE 相交于点O ，联结OA DE ,．求证：（1）OB OC =；（2）OA 垂直平分DE ．22．如图，在等边△ABC的AC，BC上各取一点D，E，使AD=CE，AE，BD相交于点M，过点B作直线AE的垂线BH，垂足为H．（1）求证：△ACE≌△BAD；（2）若BE=2EC=4．①求△ABC的面积；②求MH的长．23．已知等边ABC，点D为BC上一点，连接AD．=，连接BE，BE与AD的交点为点P，在图（1）若点E是AC上一点，且CE BD∠的大小；（1）中根据题意补全图形，求出APE（2）将AD绕点A逆时针旋转120︒，得到AF，连接BF交AC于点Q，在图（2）中根据题意补全图形，用等式表示线段AQ和CD的数量关系，并证明．（记得充分利用（1）的解题思路和结论）24．如图，在ABC 中，5AB AC ==，3BC =，点D 在AC 边上且点D 到点A 的距离与到点B 的距离相等．（1）尺规作图：作出点D ，不写作法，保留作图痕迹；（2）求BDC 的周长．25．如图，已知AB ＝AC ，E 为AB 上一点，ED ∥AC ，BD ＝CD ，求证：ED ＝AE ．26．已知：任意一个三角形的三条角平分线都交于一点．如图，在ABC 中，BD 、CD 分别平分ABC ∠、ACB ∠，过点D 作直线分别交AB 、AC 于点E 、F ，若AE AF =，解答下列问题：（1）证明：DE DF =；（2）若60A ∠=︒，8AB =，7BC =，5AC =，求EF 的长．【参考答案】***试卷处理标记，请不要删除一、选择题1．C解析：C【分析】根据勾股定理以及其逆定理和三角形的面积公式逐项分析即可得到问题答案．【详解】解：=A 正确，不符合题意；∵AC=BC 5===，∴22252025AC AB BC +=+==，∴△ACB 是直角三角形，∴∠CAB=90°，故选项B 正确，不符合题意；S △ABC 111442421345222=⨯-⨯⨯-⨯⨯-⨯⨯=，故选项C 错误，符合题意；点A 到直线BC 的距离2552AC AB BC ===，故选项D 正确，不符合题意；故选：C ．【点睛】本题考查了勾股定理以及逆定理的运用，在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方．如果直角三角形的两条直角边长分别是a ，b ，斜边长为c ，那么 222+=a b c ．熟记勾股定理的内容是解题得关键．2．D解析：D【分析】根据等腰直角三角形的性质及角平分线的定义求得∠ABE=∠CBE=12∠ABC=22.5°，继而可得∠BFD=∠AEB=90°-22.5°=67.5°，即可判断①；由M 为EF 的中点且AE=AF 可判断②；作FH ⊥AB ，证△FBD ≌△NAD 可判断③，证明△EBA ≌△EBN （SAS ），推出∠BNE=∠BAM=90°，即可判断④．【详解】解：∵∠BAC=90°，AC=AB ，AD ⊥BC ，∴∠ABC=∠C=45°，AD=BD=CD ，∠ADN=∠ADB=90°，∴∠BAD=45°=∠CAD ，∵BE 平分∠ABC ，∴∠ABE=∠CBE=12∠ABC=22.5°， ∴∠BFD=∠AEB=90°-22.5°=67.5° ∴∠AFE=∠BFD=∠AEB=67.5°，∴AF=AE ，故①正确；∵M 为EF 的中点，∴AM ⊥EF ，故②正确；∵AM ⊥EF ，∴∠AMF=∠AME=90°，∴∠DAN=90°-67.5°=22.5°=∠MBN ，在△FBD 和△NAD 中，FBD DAN BD ADBDF ADN ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△FBD ≌△NAD （ASA ），∴DF=DN ，故③正确；∵∠BAM=∠BNM=67.5°，∴BA=BN ，∵∠EBA=∠EBN ，BE=BE ，∴△EBA ≌△EBN （SAS ），∴∠BNE=∠BAE=90°，∴∠ENC=∠ADC=90°，∴AD ∥EN ．故④正确，综上，正确的结论有：①②③④故选：D ．【点睛】本题考查了全等三角形的判定与性质，等腰三角形的性质，三角形内角和定理的应用，能正确证明推出两个三角形全等是解此题的关键．3．C解析：C【分析】连结OB ，根据角平分线定义得到∠OAB=32°，再根据等腰三角形的性质得到∠ABC=∠ACB ，再根据线段垂直平分线的性质得到OA=OB ，则∠OBA=∠OAB ，所以得出∠1，由于AB=AC ，OA 平分∠BAC ，根据等腰三角形的性质得OA 垂直平分BC ，则BO=OC ，所以得出∠1=∠2，然后根据折叠的性质得到EO=EC ，于是∠2=∠3，再根据三角形内角和定理计算∠OEC ，解答即可．【详解】解：连结OB 、OC ，∵∠BAC=64°，∠BAC 的平分线与AB 的中垂线交于点O ，∴∠OAB=32°，∵AB=AC，∠BAC=64°，∴∠ABC=∠ACB=58°，∵OD垂直平分AB，∴OA=OB，∴∠OBA=∠OAB=32°，∴∠1=58°-32°=26°，∵AB=AC，OA平分∠BAC，∴OA垂直平分BC，∴BO=OC，∴∠1=∠2=26°，∵点C沿EF折叠后与点O重合，∴EO=EC，∴∠2=∠3=26°，∴∠BEO=∠2+∠3=52°，故选择:C．【点睛】本题考查了线段的垂直平分线的性质和等腰三角形的性质,折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．4．D解析：D【分析】要能作为直角三角形三边长，需验证两小边的平方和等于最长边的平方．【详解】解：A、32+42≠62，不符合勾股定理的逆定理，不是直角三角形，不符合题意；B、12+12≠32，不符合勾股定理的逆定理，不是直角三角形，不符合题意；C、52+122≠142，不符合勾股定理的逆定理，不是直角三角形，不符合题意；D52+（52＝52，符合勾股定理的逆定理，是直角三角形，符合题意；故选：D．【点睛】本题考查了勾股定理的逆定理：已知△ABC的三边满足a2+b2=c2，则△ABC是直角三角形．5．C解析：C【分析】从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高．三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点间的线段叫做三角形的角平分线．三角形一边的中点与此边所对顶点的连线叫做三角形的中线．据此分析判断即可．【详解】中BC边上的高线，是过顶点A向对边所引的垂线段，原说法错误，故本选解：A．ABC项不符合题意；B．当∠B或∠C是钝角时，过A不存在到线段BC的垂线，故本选项说法错误，不符合题意；C．三角形的角平分线就是三角形的内角平分线与这个内角的对边的交点与这个内角的顶点之间的线段，故本选项正确，符合题意；D．对称轴是直线，不能与线段重合，本故选项说法错误，不符合题意；故选：C．【点睛】本题主要考查了三角形的角平分线、中线以及高线，三角形有三条中线，有三条高线，有三条角平分线，它们都是线段．6．A解析：A【分析】根据等腰三角形的性质可得出∠BAE＝∠BEA，∠ADC＝∠DAC，然后分别用外角的知识表示出这个关系，进而结合5∠DAE＝2∠BAC可得出∠DAE的值．【详解】解：∵AC＝DC，BA＝BE，∴∠DAE+∠EAC＝∠ADE＝∠B+∠BAD①，∠EAD+∠BAD＝∠AED＝∠C+∠EAC②，①+②可得：∠DAE+∠EAC+∠EAD+∠BAD＝∠B+∠BAD+∠C+∠EAC，整理，得∠DAE+∠BAC＝180°﹣∠DAE，又5∠DAE＝2∠BAC，设∠DAE=2x，则∠BAC=5x，上式即为2x+5x=180°－2x，解得：x=20°，即∠DAE＝40°．故选：A．【点睛】本题考查等腰三角形的性质及三角形的内角和定理，有一定的难度，解答本题需用到等腰三角形的两底角相等、三角形的内角和等于180°．7．D解析：D【分析】由全等可得，AB=AD ，∠BAC=∠DAE ，可得∠BAD=EAC=50°，再根据等腰三角形性质求∠B 即可．【详解】解：∵ABC ADE △△≌，∴AB=AD ，∠BAC=∠DAE ，∠B=∠ADE ，∠BAD=∠BAC-∠DAC ，∠EAC=∠DAE-∠DAC ，∠BAD=∠EAC=50°，∵AB=AD ，∴∠B=180652BAD ︒-∠=︒， ∴∠ADE=∠B=65º，故选：D ．【点睛】本题考查了全等三角形的性质和等腰三角形的性质，解题关键是根据全等三角形得出等腰三角形和角的度数，依据等腰三角形的性质进行计算．8．A解析：A【分析】由三角形的内角和定理和角的和差求出∠ABD ＝∠CBD ，角平分线的性质定理得AD ＝DH ，垂线段定义证明DH 最短，求出DP 长的最小值为3，即可得到正确答案．【详解】过点D 作DH ⊥BC 交BC 于点H ，如图所示：∵∠A=∠BDC=90° ，又∵∠C ＋∠BDC ＋∠DBC ＝180°，∠ADB ＋∠A ＋∠ABD ＝180°，∴∠ABD ＝∠CBD ，∴BD 是∠ABC 的角平分线，又∵AD ⊥AB ，DH ⊥BC ，∴AD ＝DH ，又∵AD ＝3，∴DH ＝3，∴当点P 在BC 上运动时，点P 运动到与点H 重合时DP 最短，其长度为DH 长等于3，即DP 长的最小值为3，故DP 的长不可能是2，故选：A ．【点睛】本题综合考查了三角形的内角和定理，角的和差，角平分线的性质定理，垂线段的定义等知识点，重点掌握角平分线的性质定理，难点是作垂线段找线段的最小值．9．D解析：D【分析】由作图可得：AD 平分,BAC ∠ 可判断A ，再求解1302DACDAB BAC ∠=∠=∠=︒，可得60,ADC ∠=︒ 可判断B ，再证明,DA DB = 可判断C ，过D 作DF AB ⊥于,F 再证明,DC DF = 再利用ACD ACD ABC ACD ABD S S S S S =+ ，可判断,D 从而可得答案．【详解】解：90,30,C B ∠=︒∠=︒903060,BAC ∴∠=︒-︒=︒由作图可得：AD 平分,BAC ∠ 故A 不符合题意；1302DAC DAB BAC ∴∠=∠=∠=︒， 903060,ADC ∴∠=︒-︒=︒ 故B 不符合题意；30,DAB B ∠=∠=︒,DA DB ∴=D ∴在AB 的垂直平分线上，故C 不符合题意；过D 作DF AB ⊥于,F90,C AD ∠=︒平分,BAC ∠,DC DF ∴=30B ∠=︒，2,AB AC ∴=11,,22ACD ABDS AC CD SAB DF∴==121122ACD ACDABC ACD ABDAC CDS SS S S AC CD AB DF∴==++1.233AC AC ACAC AB AC AC AC====++故D符合题意；故选：.D【点睛】本题考查的是三角形的内角和定理，角平分线的作图，角平分线的性质，线段垂直平分线的判定，等腰三角形的判定，掌握以上知识是解题的关键．10．D解析：D【分析】由题意可知其为锐角等腰三角形或钝角等腰三角形，不可能是等腰直角三角形，所以应分开来讨论．【详解】解：①当为锐角等腰三角形时，如图：∵∠ADE＝40°，∠AED＝90°，∴∠A＝50°，∴∠B=∠C=180502︒-︒=65°；②当为钝角等腰三角形时，如图：∵∠ADE＝40°，∠AED＝90°，∴∠BAC＝∠ADE+∠AED＝40°+90°＝130°，∴∠B=∠C=1801302︒-︒=25°．故选：D．【点睛】本题考查了等腰三角形的性质、三角形内角和定理以及三角形外角性质，分类讨论是正确解答本题的关键．11．D解析：D【分析】因为△ABC是等边三角形，又BD是AC上的中线，所以有∠ADB＝∠CDB＝90°，且∠ABD ＝∠CBD＝30°，∠ACB＝∠CDE＋∠DEC＝60°，又CD＝CE，可得∠CDE＝∠CED＝30°，所以就有∠CBD＝∠DEC，即DE＝BD，∠BDE＝∠CDB＋∠CDE＝120°.由此得出答案解决问题．【详解】解：∵△ABC是等边三角形，∴∠ABC=∠ACB＝60°，∵BD是AC上的中线，∴∠ADB＝∠CDB＝90°，∠ABD＝∠CBD＝30°，∵∠ACB＝∠CDE＋∠DEC＝60°，又CD＝CE，∴∠CDE＝∠CED＝30°，∴∠CBD＝∠DEC，∴DE=BD，∠BDE＝∠CDB＋∠CDE＝120°，故ABC均正确．故选：D．【点睛】此题考查等边三角形的性质，等腰三角形的性质等知识，注意三线合一这一性质的理解与运用．12．A解析：A【分析】由勾股定理及其逆定理可得三角形ABC是等腰直角三角形，从而得到∠ABC 的度数．【详解】解：如图，连结AC，由题意可得：222222+==+==+=AB AC BC1310,125,125,∴AC=BC，222=+，AB AC BC∴△ABC是等腰直角三角形，∴∠ABC=∠BAC=45°，故选A ．【点睛】本题考查勾股定理的应用，熟练掌握勾股定理及其逆定理、等腰直角三角形的性质是解题关键．二、填空题13．30【分析】根据三角形的外角性质求出∠CDB根据线段垂直平分线的性质得到DA=DB根据等腰三角形的性质得到∠A=∠B根据三角形的外角性质计算得到答案【详解】解：∵∠C=80°∠CBD=40°∴∠CD解析：30【分析】根据三角形的外角性质求出∠CDB，根据线段垂直平分线的性质得到DA=DB，根据等腰三角形的性质得到∠A=∠B，根据三角形的外角性质计算，得到答案．【详解】解：∵∠C=80°，∠CBD=40°，∴∠CDB=180°-∠C-∠CBD=60°，∵线段AB的垂直平分线交AC于点D，∴DA=DB，∴∠A=∠DBA=1∠CDB=30°，2故答案为：30．【点睛】本题考查的是线段的垂直平分线的性质、三角形的外角性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．14．75°或120°【分析】分当△EDF是以E为顶角的等腰三角形当△EDF是以D 为顶角的等腰三角形当△EDF是以F为顶角的等腰三角形三种情况分别求解【详解】解：∵EF∥AB∴∠FEC=∠B=60°∴∠D解析：75°或120°【分析】分当△EDF是以E为顶角的等腰三角形，当△EDF是以D为顶角的等腰三角形，当△EDF 是以F为顶角的等腰三角形三种情况，分别求解．【详解】解：∵EF∥AB，∴∠FEC=∠B=60°，∴∠DEF=90°-60°=30°，当△EDF是以E为顶角的等腰三角形时，∠EDF=280013︒-︒=75°；当△EDF 是以D 为顶角的等腰三角形时，∠EDF=180°-2×30°=120°，当△EDF 是以F 为顶角的等腰三角形时，∠EDF=∠DEF=30°，当∠EDF=30°时，∠BDF=60°，∴DF ∥AC ，即F 不在AC 上，故不符合题意，故答案为：75°或120°．【点睛】本题考查了等腰三角形的性质，当等腰三角形中已知条件中没有明确哪两边相等时，要注意讨论，一些学生往往忽略这一点，造成丢解．15．16【分析】过点D 作于H 先利用三角形的面积公式计算出DH=8再利用角平分线的性质得到DF=DH=8接着证明得到证明得到利用等线段代换得到于是求出EF 的长然后根据三角形的面积公式计算即可【详解】过点D解析：16【分析】过点D 作DH AC ⊥于H ，先利用三角形的面积公式计算出DH=8，再利用角平分线的性质得到DF=DH=8，接着证明Rt DEF DGH △≌Rt △得到EF HG =，证明Rt ADF △≌Rt △ADH 得到AF AH =，利用等线段代换得到EF AG HG AE =--，于是求出EF 的长，然后根据三角形的面积公式计算即可【详解】过点D 作DH AC ⊥于H ，64S =△ADG ，16AG =1642AG DH ∴⨯⨯= 8DH ∴=AD 是ABC 的平分线，,DF AB DH AC ⊥⊥8DF DH ==∴在Rt DEF △和Rt DGH △中DE DG DF DH =⎧⎨=⎩\ ∴Rt DEF △≌Rt DGH △EF HG ∴=同理可得Rt ADF △≌Rt △ADHAF AH ∴=168EF AF AE AH AE AG HG AE EF =-=-=--=--4EF ∴= 11481622DEF S EF DF ∴=⨯⨯=⨯⨯=△ 【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，熟练掌握角平分线的性质，全等三角形的判定定理是解题关键．16．100°【分析】根据线段垂直平分线的性质和等边对等角可得∠OBA=∠A ∠OBC=∠C 根据三角形外角的性质可得∠AOP=∠A+∠ABO=2∠ABO ∠COP=∠C+∠CBO=2∠CBO 再利用角的和差即可解析：100°【分析】根据线段垂直平分线的性质和等边对等角可得∠OBA=∠A ，∠OBC=∠C ，根据三角形外角的性质可得∠AOP=∠A+∠ABO=2∠ABO ，∠COP=∠C+∠CBO=2∠CBO ，再利用角的和差即可得出∠AOC ．【详解】解：如图，连接BO 并延长至P ，∵线段AB 、BC 的垂直平分线l 1、l 2相交于点O ，∴OA=OB ，OB=OC ，∴∠OBA=∠A ，∠OBC=∠C ，∵∠AOP=∠A+∠ABO=2∠ABO ，∠COP=∠C+∠CBO=2∠CBO ，∴∠AOC=∠AOP+∠COP =2(∠ABO+∠CBO)=2∠ABC=100°，故答案为：100°．【点睛】本题考查了线段垂直平分线的性质：垂直平分线垂直且平分其所在线段；垂直平分线上任意一点，到线段两端点的距离相等．也考查了等腰三角形的性质．17．1或7【分析】证明△ACD≌△BCE（SAS）推出∠DBE＝90°根据勾股定理即可解决问题【详解】解：在△ABC中∠ACB＝90°AC＝BC＝4∴AB8①如图1中当点D在线段AB上时绕点C逆时针旋转解析：1或7【分析】证明△ACD≌△BCE（SAS），推出∠DBE＝90°，根据勾股定理即可解决问题．【详解】解：在△ABC中，∠ACB＝90°，AC＝BC＝42，∴AB22AC BC=+=8，①如图1中，当点D在线段AB上时，绕点C逆时针旋转90°到CE，连接BE，DE，则∠DCE＝90°，∴∠ACD＝∠BCE，∵CA＝CB，CD＝CE，∴△ACD≌△BCE（SAS），∴AD＝BE，∠CAD＝∠CBE，∵CA＝CB，∠ACB＝90°，∴∠A＝∠CBA＝45°，∴∠CBE＝∠A＝45°，∴∠ABE＝90°，∵CD＝5，∴DE＝2∵BE2+BD2＝DE2，∴AD2+（8﹣AD）2＝（2）2，解得：AD＝1或7；②如图2，当点D在线段AB的延长线上时，∵5CD =，42AC BC ==∴CD ＜BC图2这种情况不符合条件③如图3，当点D 在线段AB 的延长线上时，∵5CD =，42AC BC ==∴CD ＜BC图3这种情况不符合条件综上所述，AD 的长为1或7；故答案为：1或7．【点睛】本题属于几何变换综合题，考查了等腰直角三角形的性质和判定，勾股定理等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．18．117°或9°【分析】根据等腰三角形的性质和全等三角形的性质解答即可【详解】如图所示∵在△ABC 中AB ＝ACCE 是高且∠ECA ＝36°∴∠BAC ＝90°-36°=54°∠ACB ＝∠ABC ＝63°∵△解析：117°或9°【分析】根据等腰三角形的性质和全等三角形的性质解答即可．【详解】如图所示，∵在△ABC 中，AB ＝AC ，CE 是高，且∠ECA ＝36°，∴∠BAC ＝90°-36°=54°，∠ACB ＝∠ABC ＝63°，∵△ABC ≌△CDA ，∴∠CAD＝∠ACB＝63°，∴∠DAE＝∠CAD+∠BAC＝63°+54°＝117°，同理，∠D1AE＝∠CAD1-∠BAC=63°-54°=9°，故答案为：117°或9°【点睛】本题考查了全等三角形的性质及等腰三角形的性质，熟练掌握等腰三角形的性质，正确找出对应角是解题关键．19．40【分析】首先根据等腰三角形的三线合一的性质得到AD⊥BC然后根据直角三角形的两锐角互余得到答案即可【详解】解：∵AB＝ACAD是BC边上的中线∴AD⊥BC∠BAD＝∠CAD∴∠B＋∠BAD＝90解析：40【分析】首先根据等腰三角形的三线合一的性质得到AD⊥BC，然后根据直角三角形的两锐角互余得到答案即可．【详解】解：∵AB＝AC，AD是BC边上的中线，∴AD⊥BC，∠BAD＝∠CAD，∴∠B＋∠BAD＝90°，∵∠B＝50°，∴∠BAD＝40°，∴∠CAD＝40°，故答案为：40．【点睛】考查了等腰三角形的性质，理解等腰三角形底边的高、底边的中线及顶角的平分线互相重合是解答本题的关键，难度不大．20．【分析】利用等腰三角形的性质判定证明BD=AD利用直角三角形中30°角的性质计算BD即可得解【详解】∵∴∠A=30°∠ABC=120°∵∴∠CBD=90°BD=1∴∠DBA=30°∴∠DBA=∠A∴解析：1.【分析】利用等腰三角形的性质，判定，证明BD=AD，利用直角三角形中30°角的性质计算BD即可得解.【详解】∵AB BC =，30C ∠=︒，∴∠A=30°，∠ABC=120°，∵BD BC ⊥，2CD =，∴∠CBD=90°，BD=1，∴∠DBA=30°，∴∠DBA=∠A ，∴BD=AD ，∴AD=1.【点睛】本题考查了等腰三角形的判定和性质，直角三角形的性质，熟练掌握性质，并灵活运用性质是解题的关键.三、解答题21．（1）见解析；（2）见解析．【分析】（1）利用三角形的全等，得到一对对应角，后利用等角对等边证明即可；（2）逆用线段垂直平分线的判定证明即可．【详解】（1）∵,,AB AC BD CE =分别是,AC AB 上的中线，∴BE=CD ，∠EBC=∠DCB ，∵BC=CB ，∴△EBC ≌△DCB ，∴∠ECB=∠DBC ，∴OB=OC ；（2）设AO 与DE 的交点为F ，∵△EBC ≌△DCB ，∴EC=DB ，∵OB=OC ；∴OD=OE ，∴点O 在线段DE 的垂直平分线上，∵AE=AD ，∴点A 在线段DE 的垂直平分线上，∴直线AO 是线段DE 的垂直平分线，∴OA 垂直平分DE ．【点睛】本题考查了等腰三角形的性质，三角形的全等，中线的定义，垂直平分线的判定和性质，同一个三角形中，等角对等边，熟练掌握线段垂直平分线的逆定理是解题的关键． 22．（1）见解析；（2）①367 【分析】（1）根据等边三角形的性质，直接运用SAS 证明即可；（2）①作AF ⊥BC 于F 点，利用“三线合一”的性质结合已知条件先求出AF 的长度，从而根据12·ABC S BC AF =即可求解； ②先在Rt △AFE 中求解出AE 的长度，再求出△ABE 的面积，结合等面积法即可求出BH 的长度，然后根据（1）的结论进一步证明∠BMH=60°，则在Rt △BMH 中即可求解MH 的长度．【详解】（1）∵△ABC 为等边三角形，∴AB=CA ，∠BAD=∠ACE=60°，在△BAD 和△ACE 中，AD CE BAD ACE AB CA =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△BAD （SAS ）；（2）如图所示，作AF ⊥BC 于F 点，①由“三线合一”知，∠BAF=30°，∵BC=BE+EC=4+2=6，∴AB=6，BF=3，由勾股定理可得：33AF =， ∴116339322ABC S BC AF ==⨯⨯=△ ②由①可知，33AF =，FE=1，∴根据勾股定理可得，2227AE AF FE =+=， ∵114336322ABE S BE AF ==⨯⨯=△， ∴2263621727ABE S BH AE ⨯===△，由（1）可得，∠ABD=∠CAE ，∴∠ABD+∠BAM=∠CAE+∠BAM=60°，即：∠BMH=∠ABD+∠BAM=60°，则在Rt △BHM 中，∠MBH=30°，∴3BH MH =， ∴673MH ==．【点睛】本题主要考查等边三角形的性质以及全等三角形的判定与性质综合运用，灵活运用全等三角形的性质以及等面积法求高是解题关键．23．（1）图见解析，60°；（2）图见解析，12AQ CD =，理由见解析【分析】（1）根据题意补充图形，通过证明ABD BCE △≌△得到BAD CBE ∠=∠，利用三角形外角的性质可得APE BAD ABP ∠=∠+∠CBE ABP ABC =∠+∠=∠即可求解；（2）根据题意补全图形，通过证明BEQ FAQ ≌得到1122AQ QE AE CD ===，即可得证．【详解】解：（1）补全图形证明：在ABD △和BCE 中，60AB BC ABD C BC CE =⎧⎪∠=∠=︒⎨⎪=⎩()ABD BCE SAS ∴≌BAD CBE ∴∠=∠．APE ∠是ABP △的一个外角，APE BAD ABP ∠=∠+∠∴60CBE ABP ABC =∠+∠=∠=︒；（2）补全图形图2，12AQ CD =，证明：根据（1）ABD BCE △≌△可知BD EC =，即DC AE =．再证明BEQ FAQ ≌．得到1122AQ QE AE CD ===．【点睛】本题考查全等三角形的判定与性质、等边三角形的性质，掌握上述性质定理是解题的关键．24．（1）见解析；（2）8【分析】（1）作AB 的垂直平分线即可；（2）根据作图得到AD=BD ，把周长转化为AC+BC 即可．【详解】（1）用尺规作出线段AB 的垂直平分线，交AC 于点D ．（2）由作图可知，AD=BD ，△BDC 的周长=BD+CD+BC=AD+CD+BC=5+3=8．【点睛】本题考查了垂直平分线的作法与性质，解题关键是熟练的进行尺规作图，根据垂直平分线的性质准确计算．25．见解析【分析】利用SSS 证△A DB ≌△ADC 可得∠D AB =∠DAC ，根据平行线性质得∠EDA =∠DAC ，再根据等量代换得到∠EAD=∠EDA ，从而得到ED=AE ．【详解】证明：在△ADB 和△ADC 中，,,,AB AC DB DC AD AD =⎧⎪=⎨⎪=⎩∴△ADB ≌△ADC （SSS ）．∴∠D AB =∠DAC ．∵ED ∥AC ，∴∠EDA =∠DAC ，∴∠EAD=∠EDA∴E D=AE ．【点睛】考核知识点：全等三角形判定，等边对等角的性质．判定三角形全等是关键．26．（1）见解析；（2）4【分析】（1）连接AD 由AE AF =可得AEF 是等腰三角形，由三条角平分线交于一点可证AD 平分BAC ∠即可；（2）在BC 上取点M N 、，使得BE BM CF CN ==，，设2EF x =，则DE DF x ==，易证AEF 为等边三角形，可得2AE AF EF x ===，60AEF ∠=︒，可证BED ≌BMD （SAS ）可得DM DE =，82BM BE x ==-，BED BMD ∠=∠60DMN AEF ∠=∠=︒，再证NCD ≌FCD （SAS ）可得,52DN DF CN CF x ===-，可证DMN 为等边三角形，由BC BM MN NC =++构造方程解之即可．【详解】（1）证明：连接AD ，AE AF =，∴AEF 是等腰三角形，BD 、CD 分别平分ABC ∠、ACB ∠，∴AD 平分BAC ∠，∴DE DF =；（2）解：在BC 上取点M N 、，使得BE BM CF CN ==，，设2EF x =，则DE DF x ==，60A AE AF ∠=︒=，，∴AEF 为等边三角形，∴2AE AF EF x ===，60AEF ∠=︒，在BED 和BMD 中，BE BM EBD MBD BD BD =⎧⎪∠=∠⎨⎪=⎩，∴BED ≌BMD （SAS ），∴DM DE =，82BM BE x ==-，BED BMD ∠=∠，60DMN AEF ∴∠=∠=︒，在CND △和CFD △中，CN CFBM NCD FCD CD CD =⎧⎪∠=∠⎨⎪=⎩，∴NCD ≌FCD （SAS ），∴ ,52DN DF CN CF x ===-，又DE DF =，∴DM DN DE x ===，又60DMN ∠=︒，∴DMN 为等边三角形，∴MN DM x ==，∴(82)(52)7BC BM MN NC x x x =++=-++-=，即2x =，∴24EF x ==．【点睛】本题考查等腰三角形性质，角平分线性质，等边三角形判定与性质，三角形全等判定与性质，利用BC BM MN NC =++构造方程是解题关键．。

281北师大版思品八年级下册板块型能力综合测试卷(含答案)ppt课件33页PPT

4.【健康之行】漫画一：《欢迎进来》
漫画二：《无处可逃》
（1）漫画一中那些青少年经常进手机色情网站的行为健康吗？会造成什么后果？（2 分）．
答（1）不健康，手机“黄祸”败坏社会风气，会荒废学业，腐蚀了青少年的思想，甚至致使青少年走上违法犯罪额道路，不利于青少年的健康成长，不利于建设社会主义和谐文
281北师大版思品八年级下册板块型能力综合测试卷(含
答案)ppt课件
人的差异在于业余时间
思
品
八
年
级
下
册
综
合
测
试卷
执教老师：
一
★塑造健康人格
1.（3分）2010年4月14日晨，青海玉树发生7.1级地震，给玉树人民带来了巨大的灾难，但坚强的玉树人一直都坚信着：“只要格萨尔王的铜像不倒，只要加呐玛尼（地名）还在，只要朋措达杰山不移，玉树就还
在！”。从这些铿锵话语中我们可以感受到玉树人（ 1．B ）
①坚强的意志 ②乐观向上的心态
③盲目崇拜 ④勇于面对挫折
A．①②③ B．①②④ C．②③④ D．①③④
2. 漫画《如此追星》中“追星女”的行为 ( )
A．有利于高雅情趣的培养 B．有利于良好个性的发展 C．有利于实现自己的理想和
目标 D．是盲目从众心理的表现
身，并没收个人全部财产。
【知识链接】（1）文强一案的依法审理体现了所学
的哪些知识？（4分）．答（1）法律面前人人平等；适用法律一视同仁，平等地适用法律，就要反对特权；法律的尊严和法律的权威不容侵犯，任何践踏法律的行为都必定受到制裁和惩罚；党和国家依法维护社会的公
平正义等。（每点2分，共4分）
3. 2009年9月10日是“世界预防自杀日”， 2009年国际预防自杀日的主题是“不同文化的自杀预防”。据统计，我国每两分钟就有一

2020-2021学年北师大版八年级下册数学第一章三角形的证明单元测试(含解析)

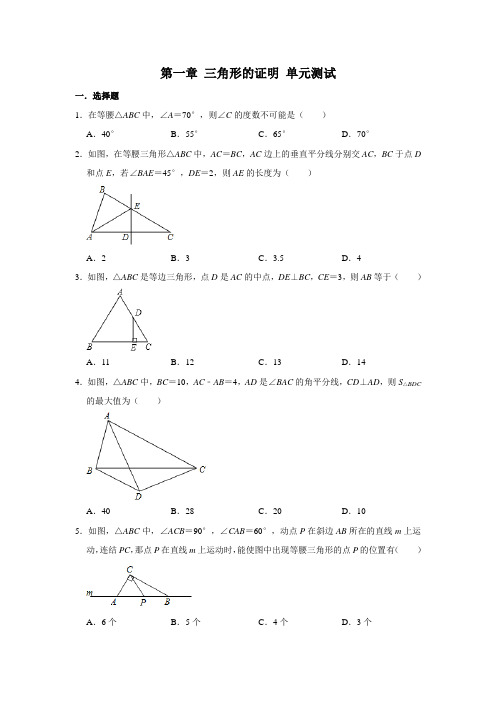
第一章三角形的证明单元测试一．选择题1．在等腰△ABC中，∠A＝70°，则∠C的度数不可能是（）A．40°B．55°C．65°D．70°2．如图，在等腰三角形△ABC中，AC＝BC，AC边上的垂直平分线分别交AC，BC于点D 和点E，若∠BAE＝45°，DE＝2，则AE的长度为（）A．2B．3C．3.5D．43．如图，△ABC是等边三角形，点D是AC的中点，DE⊥BC，CE＝3，则AB等于（）A．11B．12C．13D．144．如图，△ABC中，BC＝10，AC﹣AB＝4，AD是∠BAC的角平分线，CD⊥AD，则S△BDC 的最大值为（）A．40B．28C．20D．105．如图，△ABC中，∠ACB＝90°，∠CAB＝60°，动点P在斜边AB所在的直线m上运动，连结PC，那点P在直线m上运动时，能使图中出现等腰三角形的点P的位置有（）A．6个B．5个C．4个D．3个6．如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，BC＝2，则AB等于（）A．2B．3C．4D．67．如图，在Rt△ABC中，∠BAC＝90°，点D在BC上，过D作DF⊥BC交BA的延长线于F，连接AD，CF，若∠CFE＝32°，∠ADB＝45°，则∠B的大小是（）A．32°B．64°C．77°D．87°8．如图，DE是△ABC中AC边的垂直平分线，若BC＝4cm，AB＝5cm，则△EBC的周长为（）A．8cm B．9cm C．10cm D．11cm9．如图，在△ABC中，∠B＝15o，∠C＝30o，MN是AB的中垂线，PQ是AC的中垂线，已知BC的长为，则阴影部分的面积为（）A．B．C．3D．10．如图，在△ABC中，∠BAC＝90°，AD是BC边上的高，BE是AC边的中线，CF是∠ACB的角平分线，CF交AD于点G，交BE于点H，下面说法正确的是（）①△ABE的面积＝△BCE的面积；②∠F AG＝∠FCB；③AF＝AG；④BH＝CH．A．①②③④B．①②③C．②④D．①③二．填空题11．如图，已知△ABC中，AB＝AC，BD⊥AC于D，∠A＝50°，则∠DBC的度数是．12．等腰三角形ABC中，∠A＝4∠B．若∠A为底角，则∠C＝°．13．如图，在△ABC中，AB＝AC．AD是BC边上的中线，点E在边AB上，且BD＝BE．若∠BAC＝100°，则∠ADE的大小为度．14．如图，在Rt△ABC中，∠ABC＝90°，CD⊥AB，垂足为点D，∠DCB＝30°，BD＝1，则AB的长为．15．如图，在Rt△ABC中，∠A＝90°，∠B＝30°，CM平分∠ACB交AB于点M，过点M作MN∥BC交AC于点N，且MN平分∠AMC，若AN＝1，则BC的长为．16．如图，AD⊥BC，BD＝DC，点C在AE的垂直平分线上．若AB＝5cm，BC＝6cm，则AC＝，DE＝．17．如图所示，在△ABC中，DE、MN是边AB、AC的垂直平分线，其垂足分别为D、M，分别交BC于E、N，且DE和MN交于点F．（1）若∠B＝20°，则∠BAE＝；（2）若∠EAN＝40°，则∠F＝；（3）若AB＝8，AC＝9，设△AEN周长为m，则m的取值范围为．18．如图，在△ABC中AB的垂直平分线交AB于点D，交线段BC于点E．BC＝6，AC＝5，则△ACE的周长是．19．如图，AD垂直平分BC于点D，EF垂直平分AB于点F，点E在AC上，BE+CE＝20cm，则AB＝．20．如图，Rt△ABC中，∠C＝90°，∠BAC的角平分线AE与AC的中线BD交于点F，P 为CE中点，连结PF，若CP＝2，S△BFP＝15，则AB的长度为．三．解答题21．如图，在△ABC中，AB＝AC，D是BC边上的中点，∠B＝40°．求：（1）∠ADC的大小；（2）∠BAD的大小．22．如图，△ABC中，∠ABC＝∠ACB，点D、E分别在AB、AC上，DE∥BC，BE，CD 交于点F．（1）求证：DC＝EB；（2）在不添加任何辅助线的情况下，请直接写出图中所有的等腰三角形．23．如图，已知Rt△ABC中，∠ACB＝90°，∠A＝30°，AC边上的垂直平分线DE交AB 于点D，交AC于E．求：（1）∠BCD的度数；（2）若DE＝3，求AB的长．24．如图，在Rt△ABC中，∠ACB＝90°，∠CAB＝2∠B，AD平分∠CAB．（1）求∠CAD的度数；（2）延长AC至E，使CE＝AC，求证：DB＝DE．25．如图，在△ABC中，∠ACB为直角，AB上的高CD及中线CE恰好把∠ACB三等分，若AC＝20，求△ABC的两锐角及AD、DE、EB各为多少？26．（1）如图1，求证：三角形的三条角平分线相交于一点，并且这一点到三边的距离相等；（2）如图2，若∠ABC的平分线与∠ACB外角∠ACD的平分线相交于点P，连接AP，若∠BAC＝62°，则∠P AC是度．27．如图，已知四边形ABCD中，∠ABC与∠BCD的平分线交于点O，作OE⊥AB于点E，OF⊥CD于点F．求证：OE＝OF．28．如图（1）将三角板ABC与∠DAE摆放在一起，射线AE与AC重合，射线AD在三角形ABC外部，其中∠ACB＝30°，∠B＝60°，∠BAC＝90°，∠DAE＝45°．固定三角板ABC，将∠DAE绕点A按顺时针方向旋转，如图（2），记旋转角∠CAE＝α．（1）当α为60°时，在备用图（1）中画出图形，并判断AE与BC的位置关系，并说明理由；（2）在旋转过程中，当0°＜α＜180°，∠DAE的一边与BC平行时，求旋转角α的值；（3）在旋转过程中，当0°＜α≤90°时，探究∠CAD与∠BAE之间的关系．（温馨提示：对于任意△ABC，都有∠A+∠B+∠C＝180°）参考答案一．选择题1．解：当∠A＝∠C时，∠C＝70°；当∠A＝∠B＝70°时，∠C＝180°﹣∠A﹣∠B＝40°；当∠B＝∠C时，∠C＝∠B＝（180°﹣∠A）＝55°；即∠C的度数可以是70°或40°或55°，故选：C．2．解：设∠C＝x．∵DE垂直平分线段AC，∴EA＝EC，∴∠EAC＝∠C＝x，∴∠AEB＝∠EAC+∠C＝2x，∵CA＝CB，∴∠B＝∠CAB＝45°+x，在△ABE中，∵∠BAE+∠B+∠AEB＝180°，∴45°+45°+x+2x＝180°，∴x＝30°，∵∠EDC＝90°，DE＝2，∴AE＝EC＝2DE＝4，故选：D．3．解：∵△ABC是等边三角形，∴AB＝AC，∠C＝60°，∵DE⊥BC，∴∠DEC＝90°，∴CD＝2CE＝6，∵点D是AC的中点，∴AC＝2CD＝12，∴AB＝AC＝12，故选：B．4．解：如图：延长AB，CD交于点E，∵AD平分∠BAC，∴∠CAD＝∠EAD，∵CD⊥AD，∴∠ADC＝∠ADE＝90°，在△ADE和△ADC中，，∴△ADE≌△ADC（ASA），∴AC＝AE，DE＝CD；∵AC﹣AB＝4，∴AE﹣AB＝4，即BE＝4；∵DE＝DC，∴S△BDC＝S△BEC，∴当BE⊥BC时，S△BDC最大，即S△BDC最大＝××10×4＝10．故选：D．5．解：如图所示：以B为圆心，BC长为半径画弧，交直线m于点P4，P2，以A为圆心，AC长为半径画弧，交直线m于点P1，P3，边AC和BC的垂直平分线都交于点P3位置，因此出现等腰三角形的点P的位置有4个，故选：C．6．解：∵在Rt△ABC中，∠A＝30°，BC＝2，∴AB＝2CB＝4，故选：C．7．解：如图，取CF的中点T，连接DT，AT．∵∠BAC＝90°，FD⊥BC，∴∠CAF＝∠CDF＝90°，∴AT＝DT＝CF，∴TD＝TC＝TA，∴∠TDA＝∠TAD，∠TDC＝∠TCD，∵∠ADB＝45°，∴∠ADT+∠TDC＝135°，∴∠ATC＝360°﹣2×135°＝90°，∴AT⊥CF，∵CT＝TF，∴AC＝AF，∴∠AFC＝45°，∴∠BFD＝45°﹣32°＝13°，∵∠BDF＝90°，∴∠B＝90°﹣∠BFD＝77°，故选：C．8．解：∵DE是△ABC中AC边的垂直平分线，∴AE＝CE，∴AE+BE＝CE+BE＝AB＝5cm，∴△EBC的周长＝BC+BE+CE＝5+4＝9（cm）．故选：B．9．解：∵MN是AB的中垂线，PQ是AC的中垂线，AN＝BN，AQ＝CQ，∴∠BAN＝∠B＝15°，∠CAQ＝∠C＝30°，∴∠ANQ＝∠B+∠BAN＝30°，∠AQN＝∠C+∠CAQ＝60°，∴∠NAQ＝90°，∴BN＝AN＝NQ，AQ＝CQ＝NQ，∵BC＝，∴NQ+NQ+NQ＝3+，∴NQ＝2，∴AN＝，AQ＝1，∴阴影部分的面积＝AN•AQ＝＝，故选：B．10．解：∵BE是AC边的中线，∴AE＝CE，∵△ABE的面积＝，△BCE的面积＝AB，∴△ABE的面积＝△BCE的面积，故①正确；∵AD是BC边上的高，∴∠ADC＝90°，∵∠BAC＝90°，∴∠DAC+∠ACB＝90°，∠F AG+∠DAC＝90°，∴∠F AG＝∠ACB，∵CF是∠ACB的角平分线，∴∠ACF＝∠FCB，∠ACB＝2∠FCB，∴∠F AG＝2∠FCB，故②错误；∵在△ACF和△DGC中，∠BAC＝∠ADC＝90°，∠ACF＝∠FCB，∴∠AFG＝180°﹣∠BAC﹣∠ACF，∠AGF＝∠DGC＝180°﹣∠ADC﹣∠FCB，∴∠AFG＝∠AGF，∴AF＝AG，故③正确；根据已知不能推出∠HBC＝∠HCB，即不能推出HB＝HC，故④错误；即正确的为①③，故选：D．二．填空题11．解：∵AB＝AC，∴∠C＝∠ABC，∵∠A＝50°．∴∠C＝∠ABC＝＝＝65°，∵BD⊥AC，∴∠BDC＝90°，∴∠DBC＝90°﹣∠C＝90°﹣65°＝25°．故答案为：25°．12．解：设∠B＝x°，当∠A是底角时，∠A＝∠C＝4∠B＝4x°，∵∠A+∠B+∠C＝180°，∴4x+x+4x＝180，解得x＝20，∴∠C＝80°故答案为：80．13．解：∵AB＝AC，∠BAC＝100°，∴∠B＝∠C＝（180°﹣∠BAC）＝40°，∵BD＝BE，∴∠BDE＝∠BED＝（180°﹣∠B）＝70°，∵AB＝AC，AD⊥BC，∴∠ADB＝90°，∴∠ADE＝∠ADB﹣∠BDE＝90°﹣70°＝20°，故答案为：20．14．解：在Rt△ABC中，∠ABC＝90°，∠DCB＝30°，∴2BD＝BC，∵CD⊥AB，∴∠A＝∠DCB＝30°，∴2BC＝AB，∴AB＝4BD，∵BD＝1，∴AB＝4．故答案为：4．15．解：在Rt△ABC中，∠A＝90°，∠B＝30°，∴∠ACB＝60°，∵MN∥BC，∴∠AMN＝∠B＝30°，∵∠A＝90°，AN＝1，∴MN＝2AN＝2，∵MN平分∠AMC，∠AMN＝30°，∴∠AMC＝∠NMC＝60°，∵CM平分∠ACB，∠ACB＝60°，∴∠ACM＝ACB＝30°，∴∠ACM＝∠NMC，∴MNCN＝2，∴AC＝AN+CN＝1+2＝3，∵在Rt△ABC中，∠A＝90°，∠B＝30°，∴BC＝2AC＝2×3＝6，16．解：∵BC＝6cm，∴BD＝DC＝3（cm），∵AD⊥BC，BD＝DC，AB＝5cm，∴AC＝AB＝5（cm），∵点C在AE的垂直平分线上，∴EC＝AC＝5（cm），∴DE＝DC+EC＝8（cm），故答案为：5cm；8cm．17．解：（1）∵DE是线段AB的垂直平分线，∴EA＝EB，∴∠BAE＝∠B＝20°；（2））∵DE、MN是边AB、AC的垂直平分线，∴AE＝BE，AN＝CN，∴∠BAE＝∠B，∠CAN＝∠C，∵∠EAN＝40°，∠B+∠BAE+∠EAN+∠CAN+∠C＝180°，∴∠BAE+∠CAN＝70°，∴∠BAC＝∠BAE+∠CAN+∠EAN＝110°，∵∠ADF＝∠AMF＝90°，∴∠F＝360°﹣∠ADF﹣∠AMF﹣∠BAC＝360°﹣90°﹣90°﹣110°＝70°；（3）∵DE、MN是边AB、AC的垂直平分线，∴AE＝BE，AN＝CN，∴△AEN的周长＝AE+EN+AN＝BE+EN+CN＝BC，在△ABC中，AB＝8，AC＝9，∴9﹣8＜BC＜9+8，∴1＜m＜17．故答案为：（1）20°；（2）70°；（3）1＜m＜17．18．解：∵DE是AB的垂直平分线，∴EA＝EB，∴△ACE的周长＝AC+CE+EA＝AC+CE+EB＝AC+CB＝11，19．解：∵EF垂直平分AB于点F，∴AE＝BE，∵BE+CE＝20cm，∴AE+CE＝20cm，即AC＝20cm，∵AD垂直平分BC于点D，∴AB＝AC＝20cm，故答案为：20cm．20．解：过E作EG⊥AB于G，连接CF，∵P为CE中点，∵S△EFP＝S△CFP，设S△EFP＝S△CFP＝y，∵BD是AC边上的中线，∴设S△CDF＝S△AFD＝z，∵S△BFP＝15，∴S△BCD＝15+y+z，∴S△ABC＝2S△BCD＝30+2y+2z，∵S△ACE＝S△ACF+S△CEF＝2y+2z，∴S△ABE＝S△ABC﹣S△ACE＝30+2y+2z﹣（2y+2z）＝30，∵AE是∠CAB的角平分线，∴EG＝CE＝2CP＝4，∴S△ABE＝AB•EG＝30，∴AB＝15，故答案为：15．三．解答题21．解：（1）∵AB＝AC，D是BC边上的中点，∴AD⊥BC，即∠ADC＝90°；（2）∵∠B＝40°，∴∠BAD＝50°．22．（1）证明：∵∠ABC＝∠ACB，∴AB＝AC，∵DE∥BC，∴∠ADE＝∠ABC，∠AED＝∠ACB，∴∠ADE＝∠AED，∴AD＝AE，∴AB＝AD＝AC＝AE，即BD＝CE，在△DBC和△ECB中，，∴△DBC≌△ECB（SAS），∴DC＝EB；（2）解：图中所有的等腰三角形为△ABC、△ADE、△DEF、△BCF，理由如下：由（1）得：AB＝AC，AD＝AE，△DBC≌△ECB，∴△ABC、△ADE是等腰三角形，∠BCD＝∠CBE，∴△BCF是等腰三角形，BF＝CF，∵DE∥BC，∴∠FDE＝∠BCD，∠FED＝∠CBE，∴∠FDE＝∠FED，∴△DEF是等腰三角形，FE＝FD．23．解：（1）∵AC边上的垂直平分线是DE，∴CD＝AD，DE⊥AC，∴∠A＝∠DCA＝30°，∵∠ACB＝90°，∴∠BCD＝∠ACB﹣∠DCA＝90°﹣30°＝60°，（2）∵∠B＝60°∴∠BCD＝∠B＝60°∴BD＝CD，∴BD＝CD＝AD＝AB，∵DE＝3，DE⊥AC，∠A＝30°，∴AD＝2DE＝6，∴AB＝2AD＝12．24．证明：（1）∵∠ACB＝90°，∴∠CAB+∠B＝90°，又∵∠CAB＝2∠B，∴∠B＝30°，∠CAB＝60°，∵AD平分∠CAB，∴∠CAD＝∠DAB＝30°；（2）∵∠DAB＝30°＝∠B，∴AD＝DB，∵AC＝EC，∠ACB＝90°，∴AD＝DE，∴DE＝DB．25．解：∵△ABC中，∠C为直角，AB上的高CD及中线CE恰好把∠ACB三等分，∴∠ACD＝∠DCE＝∠ECB＝30°，又∵CD⊥AB，AC＝20，∴∠A＝60°，AD＝10，∵∠ACB为直角，∴∠B＝30°∵AC＝20，∴AB＝40，∵CE是△ABC中线，∴AE＝BE＝20，∴DE＝10．26．解：（1）已知：△ABC．求证：∠ABC、∠BCA、∠ACB三个角的平分线相交于点F，且点F到三边的距离相等．证明：如图，作∠ABC的角平分线FB，作∠BCA的角平分线FC，两条线相交于点F，作FG⊥AB于点G，FD⊥BC边于点D，FE⊥AC于点E，∵点F是∠ABC平分线上的一点，∴FG＝FD，同理可得，FD＝FE，∴FG＝FD＝FE（等量代换），∴点F在∠BAC的平分线上，∴三角形的三条角平分线相交于一点，并且这一点到三边的距离相等；（2）解：延长BA，作PN⊥BD于N，PF⊥BA于F，PM⊥AC于M，∵CP平分∠ACD，∴∠ACP＝∠PCD，PM＝PN，∵BP平分∠ABC，∴∠ABP＝∠PBC，PF＝PN，∴PF＝PM，∴∠F AP＝∠P AC，∴∠F AC＝2∠P AC，∵∠F AC+∠BAC＝180°，∴2∠P AC+∠BAC＝180°，∴∠P AC＝（180°﹣∠BAC）＝（180°﹣62°）＝59°．故答案为：59．27．证明：作OG⊥BC，∵∠ABC的平分线，OE⊥AB，OG⊥BC，∴OE＝OG，∵∠BCD的平分线，OF⊥CD，OG⊥BC，∴OF＝OG，∴OE＝OF．28．解：（1）当α为60°时，AE⊥BC，如图（1），设AE与BC交于点F，∵∠CAE＝α＝60°，∠ACB＝30°，∴∠AFC＝90°，∴AE⊥BC；（2）当AD∥BC时，如图（2），∠DAC＝∠C＝30°，∵∠DAE＝45°，∴∠CAE＝α＝15°；当AE∥BC时，如图（3），∠B＝∠EAB＝60°，∴∠CAE＝α＝∠BAC+∠EAB＝150°，故旋转角α的值为15°或150°；（3）①如（2），当α≤45°时，α+∠BAE＝90°，α+∠CAD＝45°，∴∠BAE﹣∠CAD＝45°；②如图（1），当45°＜α＜90°时，∵∠DAE+∠CAD+∠BAE＝90°，∠DAE＝45°，∴∠CAD+∠BAE＝45°．。

(北师大版)深圳市八年级数学下册第一单元《三角形的证明》测试(有答案解析)

一、选择题1．在ABC 中，已知::5:12:13AC BC AB =，AD 是ABC 的角平分线，DE AB ⊥于点E ．若ABC 的面积为S ，则ACD △的面积为（）A ．14SB ．518SC ．625SD ．725S 2．如图，在等腰△ABC 中，5AB AC ==，6BC =，O 是△ABC 外一点，O 到三边的垂线段分别为OD ，OE ，OF ，且::1:4:4OD OE OF =，则AO 的长度为（）A ．5B ．6C ．407D ．80173．如图，在Rt △ABC 中，∠BAC=90°，∠C=45°，AD ⊥BC 于点D ，∠ABC 的平分线分别交 AC 、AD 于E 、F 两点，M 为EF 的中点，AM 的延长线交 BC 于点N ，连接EN ，下列结论：①△AFE 为等腰三角形；②DF= DN ；③AN = BF ；④EN ⊥NC ．其中正确的结论有（）A ．1个B ．2个C ．3个D ．4个4．如图，等腰直角ABC 中，90BAC ∠=︒，AD BC ⊥于点D ，ABC ∠的平分线分别交AC 、AD 于E 、F 两点，M 为EF 的中点，延长AM 交BC 于点N ，连接NE ．下列结论：①AE AF =；②AM EF ⊥；③DF DN =；④//AD NE ．正确的有（）A ．①②B ．①②③C ．①②④D ．①②③④5．下列说法中，不正确的有（）①不在角的平分线上的点到这个角的两边的距离不相等；②三角形两内角的平分线的交点到各边的距离相等；③到三角形三边距离相等的点有1个④线段中垂线上的点到线段两端点的距离相等，⑤到三角形三个顶点距离相等的点有1个A ．0个B ．1个C ．2个D ．3个6．如图，平面直角坐标系中，O 是坐标原点，点A （3，2），点P （m ，0），若△POA 是等腰三角形，则m 可取的值最多有（）A ．2个B ．3个C ．4个D ．5个7．如图，已知△ABC 中，AB ＝AC ，∠BAC ＝90°，直角∠EPF 的顶点P 是BC 中点，当∠EPF 在△ABC 内绕顶点P 旋转时（点E 不与A 、B 重合）两边PE 、PF 分别交AB 、AC 于点E 、F ，给出以下四个结论：①AE ＝CF ；②△EPF 是等腰直角三角形；③S 四边形AEPF ＝12S △ABC ；④BE +CF ＝EF ．上述结论始终正确的个数是（）A ．1个B ．2个C ．3个D ．4个8．如图，点123,,,A A A A ，…在同一直线上，111122223,,AB A B A B A A A B A A ===，3334A B A A =，……，若B 的度数为x ，则1n n n A B A +∠的度数为（）A ．()111802n x -︒-B ．()11802nx ︒-C ．()111802n x +︒-D ．()211802n x +︒-9．如图，D 在BC 边上，ABC ADE △△≌，50EAC ∠=︒，则ADE ∠的度数为（）A ．50°B ．55°C ．60°D ．65°10．下列四组线段中，不能组成直角三角形的是（）A ．5a =，12b =，13c =B ．6a =，8b =，10c =C ．7a =，24b =，25c =D ．8a =，12b =，15c =11．如图，直线a ，b 相交形成的夹角中，锐角为52°，交点为O ，点A 在直线a 上，直线b 上存在点B ，使以点O ，A ，B 为顶点的三角形是等腰三角形，这样的点B 有（）A ．1个B ．2个C ．3个D ．4个 12．如图，每个小正方形的边长都相等，A ，B ，C 是小正方形的顶点，则ABC ∠的度数为（）A ．45︒B ．50︒C ．55︒D ．60︒二、填空题13．如图，一副含30和45︒角的三角板ABC 和EDF 拼合在个平面上，边AC 与EF 重合，6cm AC =．当点E 从点A 出发沿AC 方向滑动时，点F 同时从点C 出发沿射线BC 方向滑动．当点E 从点A 滑动到点C 时，连接BD ．则ABD △的面积最大值为_________2cm ．14．如图，在△ABC中，∠ABC的平分线与AC的垂直平分线相交于点D，过点D作DF⊥BC，DG⊥AB，垂足分别为 F、G．若BG＝5，AC＝6，则△ABC 的周长是_____．15．如图，在ABC中，线段AB的垂直平分线交AC于点D，连接BD，若∠=︒，则ACBD∠=︒，40C80∠的度数为_____°．16．如图在第一个△A1BC中，∠B＝40°，A1B＝BC，在边A1B上任取一点D，延长CA1到A2，使A1A2＝A1D，得到第二个△A1A2D，再在边A2D上任取一点E，延长A1A2到A3，使A2A3＝A2E，得到第3个△A2A3E……如此类推，可得到第n个等腰三角形．则第n个等腰三角形中，以An为顶点的内角的度数为_____________．⊥于点E，再作17．如图，等边三角形ABC中，在AB边上任意取一点D，作DE BCEF AB交AC于点F．当DEF是等腰三角形时，EDF//∠的度数是_____________．18．如图，DE ∥BC ，AE ＝DE ＝1，BC ＝3，则线段CE 的长为_____．19．如图，AD 是△ABC 的平分线，DF ⊥AB 于点F ，DE ＝DG ，AG ＝16，AE ＝8，若S △ADG ＝64，则△DEF 的面积为 ________．20．如图，80AOB ∠=︒，OC 平分AOB ∠，如果射线OA 上的点E 满足OCE △是等腰三角形，那么OEC ∠的度数为________．三、解答题21．已知：如图，ABC ∆中，,,AB AC BD CE =分别是,AC AB 上的中线，,BD CE 相交于点O ，联结OA DE ,．求证：（1）OB OC =；（2）OA 垂直平分DE ．22．如图，ABC ，其中AC BC >．（1）尺规作图：作AB 的垂直平分线交AC 于点P （要求：不写作法，保留作图痕迹）；（2）若8,AB PBC =的周长为13，求ABC 的周长；（3）在（2）的条件下，若ABC 是等腰三角形，直接写出ABC 的三条边的长度． 23．已知，如图，线段BC ．（1）作线段BC 的垂直平分线l ，交BC 于点D ．（用不带刻度的直尺和圆规作图，不写作法，保留作图痕迹）（2）在（1）的条件下，在l 上取点A （点D 除外），连接AC ，AB ，过点D 分别作DM ⊥AC 于点M ，DN ⊥AB 于点N ．求证:DM=DN ．24．如图，在△ABC 中，AC=BC ，∠ACB=90°，延长CA 至点D ，延长CB 至点E ，使AD=BE ，连接AE ，BD ，交点为O ．（1）求证：OB=OA ；（2）连接OC ，若AC=OC ，则∠D 的度数是度．25．如图，等边△ABC ，边长为4，动点D 从点B 出发，沿射线BC 方向移动，以AD 为边在右侧作等边△ADE ，取AC 中点F ，连接EF ，当EF 的值最小时，BD ＝_____．26．如图，在Rt ABC中，∠A＝90°，AB＝AC，BC＝10，点D是直线AC上一动点，∠BDE＝90°，DB＝DE（DE在BD的左侧）．（1）直接写出AB长为；（2）若点D在线段AC上，AD＝2，求EC长；（3）当BE＝229时，直接写出CD长为．【参考答案】***试卷处理标记，请不要删除一、选择题1．B解析：B【分析】≅，从根据勾股定理的逆定理可得ABC为直角三角形，再根据AAS得出ACD AED △的面积=AED的面积和BE的长，继而得出AED的面积和BED的面而得出ACD积比，即可得出答案【详解】AC BC AB=，解：∵::5:12:13设AC=5k，BC=12k，AB=13k，∴AC2+BC2=AB2∴ABC为直角三角形，∠C=90°，∵AD是ABC的角平分线，DE AB⊥，∴∠CAD=∠BAD，∠C=∠AED =90°，∵AD=AD，≅，∴ACD AED∴△△S S =ACD AED ，AE=AC=5k ，∴BE=13k-5k=8k ，∵AED 和BED 同高， ∴8:5△BE △S :S =D AED ，∵ABC 的面积为S ， ∴518△S =ACD S ．故选：B【点睛】本题考查了勾股定理的逆定理、全等三角形的性质与判定，根据同高得出8:5△BE △S :S =D AED 是解题的关键．2．D解析：D【分析】连接OA,OB,OC ，由OD:OE:OF=1:4:4，设OD=x ，OE=4x ，OF=4x ，根据OE=OF ，得到AO 为∠BAC 的角平分线，再根据AB=AC ，得到AO ⊥BC ，根据三线合一及勾股定理求出AD=4，再根据ABC ABO ACO BCO S S S S =+-△△△△，得到方程求解即可．【详解】解：连接OA,OB,OC, 由OD:OE:OF=1:4:4，设OD=x,OE=4x,OF=4x ，∵OE=OF ，∴AO 为∠BAC 的角平分线，又∵AB=AC ，∴AO ⊥BC ，∴AD 为△ABC 的中线，∴A 、D 、O 三点共线，∴BD=3，在Rt △ABD 中，222253AB BD -=-=4，∴ABC ABO ACO BCO S S S S =+-△△△△∴12=10x+10x−3x ，∴x=1217∴AO=4+1217=80 17.故选：D．【点睛】本题考查了角平分线的判定及性质，熟知等腰三角形的三线合一、角平分线的判定及三角形的面积公式是解题的关键．3．D解析：D【分析】利用等腰三角形的性质，直角三角形的性质，线段垂直平分线的性质，三角形的全等，角平分线的定义，逐一判断即可．【详解】∵∠BAC=90°，AD⊥BC，BE平分∠ABC ，∴∠DBF+∠DFB=90°，∠ABE+∠AEF=90°，∠ABE=∠DBF，∴∠AEF=∠DFB=∠AFE，∴△AFE为等腰三角形，∴结论①正确；∵△AFE为等腰三角形，M为EF 的中点，∴∠AMF=90°，∴∠DBF=∠DAN，∵∠BAC=90°，∠C=45°，AD⊥BC于点D，∴AD=BD，∴△DBF≌△DAN，∴DF= DN，AN=BF，∴结论②③正确；∵∠ABM=∠NBM，∴∠BMA=∠BMN= 90°，BM=BM，∴△BMA≌△BMN，∴AM=MN，∴BE是线段AN的垂直平分线，∴EA=EN，∴∠EAN=∠ENA=∠DAN，∴AD∥EN，∵AD⊥BC∴EN⊥NC，∴结论④正确；故选D．【点睛】本题考查了等腰三角形的判定和性质，三角形的全等，线段的垂直平分线的定义和性质，平行线的判定和性质，直角三角形的性质，角平分线的定义，熟练掌握知识，灵活运用知识是解题的关键．4．D解析：D【分析】根据等腰直角三角形的性质及角平分线的定义求得∠ABE=∠CBE=12∠ABC=22.5°，继而可得∠BFD=∠AEB=90°-22.5°=67.5°，即可判断①；由M为EF的中点且AE=AF可判断②；作FH⊥AB，证△FBD≌△NAD可判断③，证明△EBA≌△EBN（SAS），推出∠BNE=∠BAM=90°，即可判断④．【详解】解：∵∠BAC=90°，AC=AB，AD⊥BC，∴∠ABC=∠C=45°，AD=BD=CD，∠ADN=∠ADB=90°，∴∠BAD=45°=∠CAD，∵BE平分∠ABC，∴∠ABE=∠CBE=12∠ABC=22.5°，∴∠BFD=∠AEB=90°-22.5°=67.5°∴∠AFE=∠BFD=∠AEB=67.5°，∴AF=AE ，故①正确；∵M 为EF 的中点，∴AM ⊥EF ，故②正确；∵AM ⊥EF ，∴∠AMF=∠AME=90°，∴∠DAN=90°-67.5°=22.5°=∠MBN ，在△FBD 和△NAD 中，FBD DAN BD ADBDF ADN ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝， ∴△FBD ≌△NAD （ASA ），∴DF=DN ，故③正确；∵∠BAM=∠BNM=67.5°，∴BA=BN ，∵∠EBA=∠EBN ，BE=BE ，∴△EBA ≌△EBN （SAS ），∴∠BNE=∠BAE=90°，∴∠ENC=∠ADC=90°，∴AD ∥EN ．故④正确，综上，正确的结论有：①②③④故选：D ．【点睛】本题考查了全等三角形的判定与性质，等腰三角形的性质，三角形内角和定理的应用，能正确证明推出两个三角形全等是解此题的关键．5．C解析：C【分析】根据角平分线的性质和线段垂直平分线的性质逐一进行判断即可．【详解】①根据角平分线的判定可知①正确；②根据角平分线的性质可知②正确；③缺乏前提条件：在三角形内部，若不限制条件，到三角形三边距离相等的点有4个，故③错误；④根据垂直平分线的性质可知④正确；⑤缺乏前提条件：在平面内，若不在平面内到三角形三个顶点距离相等的点有无数个，故⑤错误，∴错误的有2个，故选：C ．【点睛】本题主要考查角平分线的性质和判定及垂直平分线的性质，掌握角平分线的性质和垂直平分线的性质是解题的关键．6．C解析：C【分析】分两种情况分析：①以点OP 为底，②OP 为腰，讨论点P 的个数，再求出m 的值即可.【详解】解：由点P （m ，0）知点P 在x 轴上，分两种情况：当OP 为底时，以A 点为圆心OA 为半径画圆，交x 轴于点P ，以OA=AP 为腰，点P 的坐标为m=2×3=6，当OP 为腰时，以O 为圆心，OA 长为半径，画圆交x 轴于两点P ，点P 在y 轴左侧或右侧，OP=OA=222313+=，∴m=13±，点P 在y 轴右侧，以OA 为底，作AO 的垂直平分线交x 轴与P ，过A 作AB ⊥x 轴，OP=AP=()2223m +-，则m=()2223m +-，解得m=136，综上，共有4个点P ，即m 有4个值，故选择：C.【点睛】本题考察等腰三角形的性质，解题时分两种情况进行讨论，注意以点A 、O 为顶角顶点时应以点为圆心画弧线，避免有遗漏．7．C解析：C【分析】连接AP 根据等腰直角三角形的性质得出∠B ＝∠C ＝∠BAP ＝∠CAP ＝45°，AP ＝PC ＝PB ，∠APC ＝∠EPF ＝90°，求出∠APE ＝∠CPF ，证△APE ≌△CPF ，推出AE ＝CF ，EP ＝PF ，推出S APE ＝S △CPF ，求出S 四边形AEPF ＝S △APC＝12S △ABC ，求出BE +CF ＝AE +AF ＞EF ，即可得出答案．【详解】解：连接AP ，∵△ABC 中，AB ＝AC ，∠BAC ＝90°，P 是BC 中点，∴∠B ＝∠C ＝∠BAP ＝∠CAP ＝45°，AP ＝PC ＝PB ，∠APC ＝∠EPF ＝90°，∴∠EPF ﹣∠APF ＝∠APC ﹣∠APF ，∴∠APE ＝∠CPF ，在△APE 和△CPF 中45EAP C AP CP APE CPF ︒⎧∠=∠=⎪=⎨⎪∠=∠⎩， ∴△APE ≌△CPF （ASA ），∴AE ＝CF ，EP ＝PF ，∴△EPF 是等腰直角三角形，∴①正确；②正确；∵△APE ≌△CPF∴S △APE ＝S △CPF ，∴S 四边形AEPF ＝S △AEP +S △APF ＝S △CPF +S △APF ＝S △APC ＝12S △ABC ，∴③正确； ∵AB ＝AC ，AE ＝CF ，∴AF ＝BE ，∴BE +CF ＝AE +AF ＞EF ，∴④错误；即正确的有3个，故选：C ．【点睛】本题考查了等腰直角三角形的判定与性质，全等三角形的判定与性质，三角形三条边的关系，掌握全等三角形的判定方法（即SSS 、SAS 、ASA 、AAS 和HL ）和全等三角形的性质（即全等三角形的对应边相等、对应角相等）是解题的关键． 8．C解析：C【分析】根据等腰三角形的性质和三角形外角的性质进行求解计算【详解】解：∵在△ABA 1中，∠B=x ，AB=A 1B ，∴∠BA 1A=1802x ︒-， ∵A 1A 2=A 1B 1，∠BA 1A 是△A 1A 2B 1的外角，∴∠A 1B 1A 2=∠A 1A 2B 1=12∠BA 1A=21180180222x x ︒-︒-⨯=；同理可得，∠A 2B 2A 3=∠A 2A 3B 2=12∠A 1B 1A 2=231180180222x x ︒-︒-⨯=； ∴∠A n B n A n +1=()111802n x +︒- 故选：C ．【点睛】本题考查的是等腰三角形的性质及三角形外角的性质，准确识图，找出规律是解答此题的关键．9．D解析：D【分析】由全等可得，AB=AD ，∠BAC=∠DAE ，可得∠BAD=EAC=50°，再根据等腰三角形性质求∠B 即可．【详解】解：∵ABC ADE △△≌，∴AB=AD ，∠BAC=∠DAE ，∠B=∠ADE ，∠BAD=∠BAC-∠DAC ，∠EAC=∠DAE-∠DAC ，∠BAD=∠EAC=50°，∵AB=AD ，∴∠B=180652BAD ︒-∠=︒， ∴∠ADE=∠B=65º，故选：D ．【点睛】本题考查了全等三角形的性质和等腰三角形的性质，解题关键是根据全等三角形得出等腰三角形和角的度数，依据等腰三角形的性质进行计算．10．D解析：D【分析】根据勾股定理的逆定理，只要判断两个较小的数的平方和是否等于最长边的平方即可．【详解】A.∵52+122=132，∴此三角形是直角三角形，不符合题意；B.∵62+82=100=102，∴此三角形是直角三角形，不符合题意；C.∵72+242=625=252，∴此三角形是直角三角形，不符合题意；D.∵82+122=208≠152，∴此三角形不是直角三角形，符合题意；故选：D ．【点睛】本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．11．D解析：D【分析】以点O 、A 、B 为顶点的等腰三角形有3种情况，分别为OA OB =，OA AB =，OB AB =，从这三方面考虑点B 的位置即可．【详解】解：如图所示，①当OA OB =时，以点O 为圆心，OA 为半径作圆，与直线b 在O 点两侧各有一个交点，此时B 点有2个；②当OA AB =时，以点A 为圆心，OA 为半径作圆，与直线b 有另外一个交点，此时B 点有1个；③当OB AB =时，作OA 的垂直平分线，与直线b 有一个交点，此时B 点有1个，综上，B 点总共有4个，故选：D ．【点睛】本题考查了等腰三角形的判定，两条边相等的三角形为等腰三角形，因此要注意分类讨论，由每种情况的特点选择合适的方法确定点B 是解题的关键．12．A解析：A【分析】由勾股定理及其逆定理可得三角形ABC 是等腰直角三角形，从而得到∠ABC 的度数．【详解】解：如图，连结AC ，由题意可得：2222221310,125,125,AB AC BC +==+==+=∴AC=BC ，222AB AC BC =+，∴△ABC 是等腰直角三角形，∴∠ABC=∠BAC=45°，故选A ．【点睛】本题考查勾股定理的应用，熟练掌握勾股定理及其逆定理、等腰直角三角形的性质是解题关键．二、填空题13．cm2【分析】过点作于点作于点连接由直角三角形的性质可得cmcmcm 由可证△△可得由三角形面积公式可求则时有最大值【详解】解：cmcmcmcm 当点从点滑动到点时得△过点作于点作于点连接且且△△当时有解析：(123236)cm 2【分析】过点D 作D N AC '⊥于点N ，作D M BC '⊥于点M ，连接BD '，AD '，由直角三角形的性质可得23BC =，43AB =，32ED DF ==cm ，由“AAS ”可证△D NE ''≅△D MF ''，可得D N D M ''=，由三角形面积公式可求111222AD B S BC AC AC D N BC D M '''=⨯+⨯⨯-⨯⨯△，则E D AC ''⊥时，AD B S '△有最大值．【详解】解：6AC =cm ，30A ∠=︒，45DEF ∠=︒， 233BC ∴==cm ，3AB =，32ED DF ==cm ，当点E 从点A 滑动到点C 时，得△E D F '''，过点D 作D N AC '⊥于点N ，作D M BC '⊥于点M ，连接BD '，AD '，90MD N '∴∠=︒，且90E D F '''∠=︒，E D NF D M ''''∴∠=∠，且90D NE D MF ''''∠=∠=︒，E D D F ''''=，∴△D NE ''≅△()D MF AAS ''，D N D M ''∴=，AD B ABC AD C BD C S S S S '''=+-△△△△当E D AC ''⊥时，AD B S '△有最大值， 1111123(623)2222AD B S BC AC AC D N BC D M D N ''''∴=⨯+⨯⨯-⨯⨯=+-⨯△ AD B S '∴△最大值1123(623)32(1239236)2=+-⨯=+-cm 2．故答案为：(1239236)+-cm 2．【点睛】本题考查了全等三角形的判定和性质，等腰直角三角形的性质，角平分线的性质，三角形面积公式等知识，确定AD B S '△有最大值时的图形位置是本题的关键．14．16【分析】连接ADDC 证明Rt △DGA ≌Rt △DFC （HL ）可得出AG ＝CF 再证明Rt △BDG ≌Rt △BDF （HL ）得出BG ＝BF 则可求出答案【详解】解：连接ADDC ∵BD 平分∠ABCDG ⊥ABD解析：16【分析】连接AD 、DC ．证明Rt △DGA ≌Rt △DFC （HL ）可得出AG ＝CF ，再证明Rt △BDG ≌Rt △BDF （HL ），得出BG ＝BF ，则可求出答案【详解】解：连接AD 、DC ．∵BD 平分∠ABC ，DG ⊥AB ，DF ⊥BC ，∴DG ＝DF ．∵D 在AC 的中垂线上，∴DA ＝DC ．在Rt △DGA 与Rt △DFC 中，∵DG ＝DF ，DA ＝DC ，∴Rt △DGA ≌Rt △DFC （HL ）．∴AG ＝CF ．又∵BD ＝BD ，DG ＝DF ．∴Rt △BDG ≌Rt △BDF （HL ）．∴BG ＝BF ．又∵AG ＝CF ，∴△ABC 的周长＝AB +BC +AC ＝BG ﹣AG +BF +FC +AC ＝2BG +AC ＝2×5+6＝16．故答案为：16．【点睛】此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质，属于中考常考题型．15．30【分析】根据三角形的外角性质求出∠CDB 根据线段垂直平分线的性质得到DA=DB 根据等腰三角形的性质得到∠A=∠B 根据三角形的外角性质计算得到答案【详解】解：∵∠C=80°∠CBD=40°∴∠CD解析：30【分析】根据三角形的外角性质求出∠CDB ，根据线段垂直平分线的性质得到DA=DB ，根据等腰三角形的性质得到∠A=∠B ，根据三角形的外角性质计算，得到答案．【详解】解：∵∠C=80°，∠CBD=40°，∴∠CDB=180°-∠C-∠CBD=60°，∵线段AB 的垂直平分线交AC 于点D ，∴DA=DB ，∴∠A=∠DBA=12∠CDB=30°，故答案为：30．【点睛】本题考查的是线段的垂直平分线的性质、三角形的外角性质，掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键．16．【分析】根据等腰三角形的性质可求出△CBA1的底角的度数再根据三角形外角的性质及等腰三角形的性质可求出△DA1A2的底角的度数同理可求出△EA2A3△FA3A4…底角的度数再找出其规律即可得出第n 个解析：11702n -︒⨯【分析】根据等腰三角形的性质，可求出 △CBA 1 的底角的度数，再根据三角形外角的性质及等腰三角形的性质，可求出 △DA 1A 2 的底角的度数．同理可求出 △EA 2A 3 、 △FA 3A 4 …底角的度数．再找出其规律即可得出第n 个三角形中以 An 为顶点的底角度数．【详解】在 △CBA 1 中， ∠B=40° ， A 1B=CB ，∴ ∠BA 1C=∠BCA 1=（180°−40°)÷2=70° ，又∵ A 1A 2=A 1D ， ∠BA 1C 是 △A 1A 2D 的外角．∴ ∠DA 2A 1=∠A 2DA 1=12∠BA 1C=12×70° ．同理可得：∠EA 3A 2=∠A 3EA 2=12∠DA 2A 1=12×12×70°=(12)2×70° ， ∠FA 4A 3=∠A 4FA 3=12∠EA 3A 2=(12)3×70°，综上可知规律：第n 个三角形中以 An 为顶点的底角度数是：112n -×70° ，故答案为 70° ×112n -．【点睛】本题考查等腰三角形和三角形外角的性质，求出 ∠DA 2A 1 、 ∠EA 3A 2 、 ∠FA 4A 3 的度数，找出其规律是解答本题的关键． 17．75°或120°【分析】分当△EDF 是以E 为顶角的等腰三角形当△EDF 是以D 为顶角的等腰三角形当△EDF 是以F 为顶角的等腰三角形三种情况分别求解【详解】解：∵EF ∥AB ∴∠FEC=∠B=60°∴∠D解析：75°或120°【分析】分当△EDF 是以E 为顶角的等腰三角形，当△EDF 是以D 为顶角的等腰三角形，当△EDF 是以F 为顶角的等腰三角形三种情况，分别求解．【详解】解：∵EF ∥AB ，∴∠FEC=∠B=60°，∴∠DEF=90°-60°=30°，当△EDF 是以E 为顶角的等腰三角形时，∠EDF=280013︒-︒=75°；当△EDF 是以D 为顶角的等腰三角形时，∠EDF=180°-2×30°=120°，当△EDF 是以F 为顶角的等腰三角形时，∠EDF=∠DEF=30°，当∠EDF=30°时，∠BDF=60°，∴DF ∥AC ，即F 不在AC 上，故不符合题意，故答案为：75°或120°．【点睛】本题考查了等腰三角形的性质，当等腰三角形中已知条件中没有明确哪两边相等时，要注意讨论，一些学生往往忽略这一点，造成丢解．18．【分析】由平行线的性质可得∠ADE=∠B 由AE=DE=1可得∠ADE=∠DAE 易得∠DAE=∠B 可得AC=BC 易得结果【详解】解：∵DE ∥BC ∴∠ADE ＝∠B ∵AE ＝DE ＝1∴∠ADE ＝∠DAE ∴∠解析：【分析】由平行线的性质可得∠ADE=∠B ，由AE=DE=1，可得∠ADE=∠DAE ，易得∠DAE=∠B ，可得AC=BC ，易得结果．【详解】解：∵DE ∥BC ，∴∠ADE ＝∠B ，∵AE ＝DE ＝1，∴∠ADE ＝∠DAE ，∴∠DAE ＝∠B ，BC ＝3，∴AC ＝BC ＝3，∴CE ＝AC ﹣AE ＝3﹣1＝2，故答案为：2．【点睛】本题主要考查了平行线的性质和等腰三角形的性质等，关键是运用性质定理得出AC=BC=3．19．16【分析】过点D 作于H 先利用三角形的面积公式计算出DH=8再利用角平分线的性质得到DF=DH=8接着证明得到证明得到利用等线段代换得到于是求出EF 的长然后根据三角形的面积公式计算即可【详解】过点D解析：16【分析】过点D 作DH AC ⊥于H ，先利用三角形的面积公式计算出DH=8，再利用角平分线的性质得到DF=DH=8，接着证明Rt DEF DGH △≌Rt △得到EF HG =，证明Rt ADF △≌Rt △ADH 得到AF AH =，利用等线段代换得到EF AG HG AE =--，于是求出EF 的长，然后根据三角形的面积公式计算即可【详解】过点D 作DH AC ⊥于H ，64S =△ADG ，16AG =1642AG DH ∴⨯⨯= 8DH ∴= AD 是ABC 的平分线，,DF AB DH AC ⊥⊥8DF DH ==∴在Rt DEF △和Rt DGH △中DE DG DF DH =⎧⎨=⎩\ ∴Rt DEF △≌Rt DGH △EF HG ∴=同理可得Rt ADF △≌Rt △ADHAF AH ∴=168EF AF AE AH AE AG HG AE EF =-=-=--=--4EF ∴=11481622DEF S EF DF ∴=⨯⨯=⨯⨯=△ 【点睛】本题考查了角平分线的性质，全等三角形的判定和性质，熟练掌握角平分线的性质，全等三角形的判定定理是解题关键．20．40°或70°或100°【分析】求出∠AOC 根据等腰得出三种情况OE ＝CEOC ＝OEOC ＝CE 根据等腰三角形性质和三角形内角和定理求出即可【详解】解：∵∠AOB ＝80°OC 平分∠AOB ∴∠AOC ＝4解析：40°或70°或100°【分析】求出∠AOC ，根据等腰得出三种情况，OE ＝CE ，OC ＝OE ，OC ＝CE ，根据等腰三角形性质和三角形内角和定理求出即可．【详解】解：∵∠AOB ＝80°，OC 平分∠AOB ，∴∠AOC ＝40°，①当E 在E 1时，OE ＝CE ，∵∠AOC ＝∠OCE ＝40°，∴∠OEC ＝180°﹣40°﹣40°＝100°；②当E 在E 2点时，OC ＝OE ，则∠OCE ＝∠OEC ＝12（180°﹣40°）＝70°； ③当E 在E 3时，OC ＝CE ，则∠OEC ＝∠AOC ＝40°；故答案为：100°或70°或40°．【点睛】本题考查了角平分线定义，等腰三角形性质，三角形的内角和定理的应用，用了分类讨论思想．三、解答题21．（1）见解析；（2）见解析．【分析】（1）利用三角形的全等，得到一对对应角，后利用等角对等边证明即可；（2）逆用线段垂直平分线的判定证明即可．【详解】（1）∵,,AB AC BD CE 分别是,AC AB 上的中线，∴BE=CD ，∠EBC=∠DCB ，∵BC=CB ，∴△EBC ≌△DCB ，∴∠ECB=∠DBC ，∴OB=OC ；（2）设AO 与DE 的交点为F ，∵△EBC ≌△DCB ，∴EC=DB ，∵OB=OC ；∴OD=OE ，∴点O 在线段DE 的垂直平分线上，∵AE=AD，∴点A在线段DE的垂直平分线上，∴直线AO是线段DE的垂直平分线，∴OA垂直平分DE．【点睛】本题考查了等腰三角形的性质，三角形的全等，中线的定义，垂直平分线的判定和性质，同一个三角形中，等角对等边，熟练掌握线段垂直平分线的逆定理是解题的关键．22．（1）画图见解析；（2）△ABC的周长=21；（3）AB=8，AC=8，BC=5．【分析】（1）根据垂直平分线的作法作出图形即可；（2）根据垂直平分线的性质可得AP=BP，从而得出AC+BC的值，再根据AB=8，即可求得△ABC的周长；（3）分两种情况进行讨论即可．【详解】解：（1）如图所示：即PQ为所求；；（2）如图所示：∵AB的垂直平分线交AC于点P，∴PA=PB，∵△PBC的周长为13，∴PB+PC+BC=13，∴PA+PC+BC=13，即AC+BC=13，∴△ABC的周长=AB+AC+BC=8+13=21；（3）∵AC＞BC，∴分两种情况，①AC=AB=8时，BC=21-AC-BC=21-8-8=5；②BC=AB=8时，AC=21-AB-BC=21-8-8=5，∵AC＞BC，∴不合题意舍去；综上所述，若△ABC是等腰三角形，△ABC的三条边的长度为AB=8，AC=8，BC=5．【点睛】本题是三角形综合题目，考查了线段垂直平分线的性质、等腰三角形的性质、尺规作图、三角形周长等知识．本题综合性强，熟练掌握等腰三角形的性质和线段垂直平分线的性质是解题的关键．23．（1）见解析；（2）见解析【分析】（1）根据垂直平分线的尺规作图方法即可作出直线l；（2）根据垂直平分线的性质可AB=AC，BD=DC，再根据等腰三角形的三线合一得到∠DAB=∠DAC，然后根据角平分线的性质即可证得DM=DN．【详解】解：（1）如图直线l即为所求；（2）证明：∵ 直线l 是线段BC 的垂直平分线，点A 是直线l 上一点，∴AB=AC ，BD=DC ，∴ ∠DAB=∠DAC∵ DM ⊥AC ，DN ⊥AB∴ DM=DN【点睛】本题考查了基本尺规作图-线段垂直平分线、线段垂直平分线的性质、等腰三角形的三线合一性质、角平分线的性质，熟练掌握这些知识的灵活运用是解答的关键．24．（1）见解析；（2）22.5【分析】（1）根据全等三角形的判定和性质得出△ABD ≌△BAE ，进而得出OB=OA ；（2）根据全等三角形的判定和性质以及三角形内角和解答．【详解】证明：（1）∵AC=BC ，∠ACB=90°，∴∠ABC=∠BAC=45°．∴∠EBA=∠DAB=135°．在△ABD 与△BAE 中，135BE AD EBA DAB AB AB =⎧⎪∠=∠=︒⎨⎪=⎩，∴△ABD ≌△BAE （SAS ），∴∠DBA=∠EAB ，∴OB=OA ；（2）由（1）得：OB=OA ，在△OBC 与△OAC 中，OB OA OC OC BC AC =⎧⎪=⎨⎪=⎩，∴△OBC ≌△OAC （SSS ），∴∠OCB=∠OCA=12∠ACB=12×90°=45°， ∵AC=BC ，AC=OC ，∴OC=BC ， ∴∠CBO=∠COB 1801804567.522OCB ︒︒︒︒-∠-===，在Rt △BCD 中，∠D=180°-90°-∠CBO=22.5°．故答案为：22.5．【点睛】本题考查了全等三角形的判定和性质，等腰三角形的判定和性质，关键是根据全等三角形的判定和性质解答．25．1【分析】根据题意可证BAD CAE ∠=∠，再证明()ABD ACE SAS ≅，由全等三角形的性质得到,60CE BD ABD ACE =∠=∠=︒，继而证明E 在ACB ∠的外角平分线上，最后根据垂线段最短及含30°角的直角三角形性质解题即可．【详解】解：如图，连接CE ，F 是AC 的中点，4AC =2AF CF ∴== ABC 、ADE 是等边三角形，,,60AB AC AD AE BAC DAE ∴==∠=∠=︒BAC DAC DAE DAE ∴∠-∠=∠-∠BAD CAE ∴∠=∠在ABD △与ACE △中，AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()ABD ACE SAS ∴≅,60CE BD ABD ACE ∴=∠=∠=︒180606060ECG ∴∠=︒-︒-︒=︒E ∴在ACB ∠的外角平分线上，当EF CE ⊥时EF 有最小值，30CFE ∴∠=︒112CE CF ∴== 1BD ∴=故答案为：1．【点睛】本题考查等边三角形的性质、全等三角形的判定与性质、垂线段最短、含30°角的直角三角形等知识，是重要考点，难度较易，掌握相关知识是解题关键．26．（1）；（2）2；（3）；【分析】（1）直接根据等腰直角三角形的性质进行求解即可；（2）过E 作EF ⊥AC ，交AC 的延长线于F ，利用AAS 证明△DEF ≌△BDA ，再根据全等三角形的性质及线段的和差关系即可求解；（3）由题可知BE=，则=，根据勾股定理可以求出 AD 的长，即可求解．【详解】解：（1）∵△ABC 为直角三角形，且AB=AC ，∴△ABC 为等腰直角三角形，∴ AB ：AC ：BC=1：1，∵ BC=10，∴AB=；（2）如图：过E 作EF ⊥AC ，交AC 的延长线于F ，∴∠F=∠A=90°，∠DEF+∠EDF=90°，∵∠BDE=90°，∴∠EDF+∠BDA=90°，∴∠DEF=∠BDA，∵BD=DE，∴△DEF≌△BDA（AAS），∴2，DF=AB=52，∵AB=AC=52CD=2，∴2=EF，∴222EC CF EF+=（3）由题可知 BE=29，则229582=，∴225850822BD AB--=，∴CD=AC-AD=522232=522232=．【点睛】本题考查了全等三角形的判定及性质、勾股定理、以及等腰直角三角形的性质，熟练掌握知识点是解题的关键．。

(北师大版)初中英语八年级下册 Unit 1单元测试(一)附答案

Unit 1 Technology and the Future 单元测试听力部分（共20分）一、听长对话及后面的问题，根据对话内容选择每个问题的最佳答案，对话和问题读两遍。

（共5分，每小题1分）1. A. He has a cold. B. He has a fever. C. He has a headache.2. A. Playing computer games. B. Sleeping all day. C. Dreaming all night.3. A. Keeping warm. B. Having a warm bath. C. Drinking more water.4. A. Half an hour a day. B. Three times a day. C. Once a day.5. A. Relax a little. B. Take more pills once. C. Go to bed early.二、听短对话和问题，选择符合每个问题的正确答案，每段对话和问题读两遍。

（共5分，每小题1分）6. A. Football. B. Table tennis. C. Basketball.7. A. Cakes. B. Fish. C. Vegetables.8. A. Cook. B. Teacher. C. Doctor.9. A. Goldfish. B. Elephant. C. Tortoise.10. A. No photos. B. No smoking. C. No parking.三、听下面的短文，短文后有5个小题，从题中所给的A、B、C三个选项中选出最佳选项，短文读两遍。

（共5分，每小题1分）11. The speaker first came to ________ in the story.A. EnglandB. the U.S.A.C. Australia12. How many days did the speaker go to the language school per week？A. Five.B. Six.C. Seven.13. When did the speaker ask Kate a question？A. After school.B. In an English class.C. During the break.14. What did the speaker think after Kate said those words？A. Kate was really helpful.B. Kate wanted to eat a cake.C. America was really a country where you had to pay for everything.15. Why did Kate look at the speaker with a big smile？A. Because the speaker was funny.B. Because the speaker mistook her.C. Because Kate was very friendly to her.四、听一段电话留言，根据其内容完成下面的信息卡，每空一词，电话留言读两遍。

北师大版八年级数学下册第一章三角形的证明单元测试卷

2020-2021学年北师大版八年级数学下册第一章三角形的证明单元测试卷（时间120分钟满分150分）A 卷(共100分)一、选择题(本大题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案填在下面的答题框内)1.如图，在Rt △ABC 中，∠ACB ＝90°，AD 平分∠CAB.若CD ＝4，则点D 到AB 的距离是( )A ．4B ．3C ．2D ．52．如图，BE ＝CF ，AE ⊥BC ，DF ⊥BC ，要根据“HL ”证明Rt △ABE ≌Rt △DCF ，还需要添加一个条件是( )A ．AE ＝CFB ．AB ＝DCC ．∠B ＝∠CD ．∠A ＝∠D3．在△ABC 中，其两个内角如下，则能判定△ABC 为等腰三角形的是( ) A ．∠A ＝40°，∠B ＝50° B ．∠A ＝40°，∠B ＝60° C ．∠A ＝40°，∠B ＝80° D ．∠A ＝20°，∠B ＝80°4．在线段AB 上，分别以点A ，B 为圆心，大于12AB 的长为半径画弧，两弧分别交于点E ，F ，作直线EF 与AB 交于点C ，连接AE ，BE ，则以下结论不一定成立的是( )A ．AC ＝BCB ．AE ＝BEC ．△ABE 是等边三角形D ．∠AEC ＝∠BEC5．如图，在Rt△ABC中，∠A＝90°，∠C＝30°，BC的垂直平分线交AC于点D，并交BC于点E.若ED＝3，则AC的长为( )A．3 3 B．3 C．6 D．96．等边三角形的边长为6，则它的面积为（）9 B．18 C．36 D．183A．37．观察下列命题的逆命题：①有两边相等的三角形是等腰三角形；②到角的两边的距离相等的点在这个角的平分线上；③直角三角形的两个锐角互余；④全等三角形的面积相等．其中逆命题为假命题的个数是( )A．1 B．2 C．3 D．48．将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD，转动这个四边形，使它形状改变，当∠B＝90°时，如图1，测得AC＝2，当∠B＝60°时，如图2，AC＝( )A. 2 B．2 C. 6 D．2 29．如图，AB∥CD，BE和CE分别平分∠ABC和∠BCD，AD过点E，且与AB互相垂直，点P为线段BC上一动点，连接PE.若AD＝8，则PE的最小值为( )A．8 B．6 C．5 D．410．如图，在四边形ABCD 中，AD ∥BC ，∠D ＝90°，AD ＝4，BC ＝3.分别以点A ，C 为圆心，大于12AC 的长为半径作弧，两弧交于点E ，作射线BE 交AD 于点F ，交AC 于点O.若点O是AC 的中点，则CD 的长为( )A ．4B ．2 2C ．3D.10二、填空题(本大题共4个小题，每小题4分，共16分，答案写在题中的横线上) 11．如图，某失联客机从A 地起飞，飞行1 000 km 到达B 地，再折返飞行1 000 km 到达C 地后在雷达上消失，已知∠ABC ＝60°，则失联客机消失时离起飞地A 地的距离为_________km.12．已知Rt △ABC 的两条边长分别为3和5，则它的另一条边长为_______． 13．如图，长为8 cm 的橡皮筋放置在x 轴上，固定两端A 和B ，然后把中点C 向上拉升3 cm 到D ，则橡皮筋被拉长了_______cm.14．如图，在等腰△ABC 中，AB ＝AC ，∠BAC ＝54°.∠BAC 的平分线与AB 的垂直平分线交于点O ，点C 沿EF 折叠后与点O 重合，则∠OEC 的度数是_______．三、解答题(本大题共6个小题，共54分，解答题应写出必要的文字说明、证明过程或演算步骤)15．(8分)如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，求证：△ADE≌△CFE.16．(8分)如图，∠AOB＝60°，OC平分∠AOB，C为角平分线上一点，过点C作CD⊥OC，垂足为C，交OB于点D，CE∥OA交OB于点E.判断△CED的形状，并说明理由．17．(9分)如图，在四边形ABCD中，∠B＝∠D＝90°，点E，F分别在AB，AD上，AE ＝AF，CE＝CF，求证：CB＝CD.18．(9分)如图，在△ABC中，AC＜AB＜BC.(1)已知线段AB的垂直平分线与BC边交于点P，连接AP，求证：∠APC＝2∠B；(2)以点B为圆心，线段AB的长为半径画弧，与BC边交于点Q，连接AQ.若∠AQC＝3∠B，求∠B的度数．19．(10分)如图，△ACB和△ECD都是等腰直角三角形，∠ACB＝∠ECD＝90°，D为AB 边上一点．求证：(1)△ACE≌△BCD；(2)2CD2＝AD2＋BD2.20．(10分)小明在学习了“等边三角形”后，激发了他的学习和探究的兴趣，就想考考他的朋友小崔，小明作了一个等边△ABC，如图，并在边AC上任意取了一点F(点F不与点A，C重合)，过点F作FH⊥AB交AB于点H，延长CB到G，使得BG＝AF，连接FG交AB 于点I.(1)若AC＝10，则HI的长度为__________；(2)延长BC到D，再延长BA到E，使得AE＝BD，连接ED，EC.求证：∠ECD＝∠EDC.B 卷(共50分)一、填空题(本大题共5个小题，每小题4分，共20分，答案写在题中的横线上) 21．如图，已知△ABC 是等边三角形，点B ，C ，D ，E 在同一直线上，且CG ＝CD ，DF ＝DE ，则∠E ＝________．22．如图，等边三角形ABC 中，D ，E 分别为AB ，BC 边上的两动点，且总使AD ＝BE ，AE 与CD 交于点F ，AG ⊥CD 于点G ，则FGAF＝________．23．如图，∠B ＝∠C ＝90°，AE 平分∠BAD ，DE 平分∠ADC.若S △CDE ＝23S △ABE ，则S △DEC ∶S△ADE＝________．24．如图，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC＋PQ的最小值是________．25．如图，在△ABC中，BF平分∠ABC，AG⊥BF，垂足为点D，交BC于点G，E为AC的中点，连接DE，DE＝2.5 cm，AB＝4 cm，则BC的长为________cm.二、解答题(本大题共3个小题，共30分)26．(8分)如图，在△ABC中，AB＝AC，D为BC边的中点，F为CA的延长线上一点，过点F作FG⊥BC于点G，并交AB于点E，求证：(1)AD∥FG；(2)△AEF是等腰三角形．27．(10分)在四边形ABCD中，AB＝BC＝CD＝DA，∠B＝∠D＝60°，连接AC.(1)如图1，点E，F分别在边BC，CD上，且BE＝CF.求证：①△ABE ≌△ACF ； ②△AEF 是等边三角形；(2)若点E 在BC 的延长线上，则在直线CD 上是否存在点F ，使△AEF 是等边三角形？请证明你的结论(图2备用)．28．(12分)如图，在△ABC 中，AB ＝AC ，∠EAF ＝12∠BAC ，BF ⊥AE 于点E ，交AF 于点F ，连接CF.(1)如图1所示，当∠EAF 在∠BAC 内部时，求证：EF ＝BE ＋CF ；(2)如图2所示，当∠EAF 的边AE ，AF 分别在∠BAC 外部、内部时，求证：CF ＝BF ＋2BE.参考答案A卷(共100分)一、选择题(本大题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案填在下面的答题框内)1.如图，在Rt△ABC中，∠ACB＝90°，AD平分∠CAB.若CD＝4，则点D到AB的距离是(A)A．4 B．3 C．2 D．52．如图，BE ＝CF ，AE ⊥BC ，DF ⊥BC ，要根据“HL ”证明Rt △ABE ≌Rt △DCF ，还需要添加一个条件是(B)A ．AE ＝CFB ．AB ＝DCC ．∠B ＝∠CD ．∠A ＝∠D3．在△ABC 中，其两个内角如下，则能判定△ABC 为等腰三角形的是(D) A ．∠A ＝40°，∠B ＝50° B ．∠A ＝40°，∠B ＝60° C ．∠A ＝40°，∠B ＝80° D ．∠A ＝20°，∠B ＝80°4．在线段AB 上，分别以点A ，B 为圆心，大于12AB 的长为半径画弧，两弧分别交于点E ，F ，作直线EF 与AB 交于点C ，连接AE ，BE ，则以下结论不一定成立的是(C)A ．AC ＝BCB ．AE ＝BEC ．△ABE 是等边三角形D ．∠AEC ＝∠BEC 5．如图，在Rt △ABC 中，∠A ＝90°，∠C ＝30°，BC 的垂直平分线交AC 于点D ，并交BC 于点E.若ED ＝3，则AC 的长为(D)A ．3 3B ．3C ．6D ．96．等边三角形的边长为6，则它的面积为（） A ．39 B ．18C ．36D ．1837．观察下列命题的逆命题：①有两边相等的三角形是等腰三角形；②到角的两边的距离相等的点在这个角的平分线上；③直角三角形的两个锐角互余；④全等三角形的面积相等．其中逆命题为假命题的个数是(A)A ．1B ．2C ．3D ．48．将四根长度相等的细木条首尾相接，用钉子钉成四边形ABCD ，转动这个四边形，使它形状改变，当∠B ＝90°时，如图1，测得AC ＝2，当∠B ＝60°时，如图2，AC ＝(A)A. 2B ．2C. 6D ．2 29．如图，AB ∥CD ，BE 和CE 分别平分∠ABC 和∠BCD ，AD 过点E ，且与AB 互相垂直，点P 为线段BC 上一动点，连接PE.若AD ＝8，则PE 的最小值为(D)A ．8B ．6C ．5D ．410．如图，在四边形ABCD 中，AD ∥BC ，∠D ＝90°，AD ＝4，BC ＝3.分别以点A ，C 为圆心，大于12AC 的长为半径作弧，两弧交于点E ，作射线BE 交AD 于点F ，交AC 于点O.若点O是AC 的中点，则CD 的长为(B)A ．4B ．2 2C ．3D.10二、填空题(本大题共4个小题，每小题4分，共16分，答案写在题中的横线上) 11．如图，某失联客机从A 地起飞，飞行1 000 km 到达B 地，再折返飞行1 000 km 到达C 地后在雷达上消失，已知∠ABC ＝60°，则失联客机消失时离起飞地A 地的距离为1_000km.12．已知Rt△ABC的两条边长分别为3和5，则它的另一条边长为13．如图，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm到D，则橡皮筋被拉长了2cm.14．如图，在等腰△ABC中，AB＝AC，∠BAC＝54°.∠BAC的平分线与AB的垂直平分线交于点O，点C沿EF折叠后与点O重合，则∠OEC的度数是108°．三、解答题(本大题共6个小题，共54分，解答题应写出必要的文字说明、证明过程或演算步骤)15．(8分)如图，D是AB上一点，DF交AC于点E，DE＝FE，FC∥AB，求证：△ADE≌△CFE.证明：∵FC∥AB，∴∠A＝∠FCE，∠ADE＝∠F.在△ADE和△CFE中，⎩⎪⎨⎪⎧∠A ＝∠FCE ，∠ADE ＝∠F ，DE ＝FE ，∴△ADE ≌△CFE(AAS)．16．(8分)如图，∠AOB ＝60°，OC 平分∠AOB ，C 为角平分线上一点，过点C 作CD ⊥OC ，垂足为C ，交OB 于点D ，CE ∥OA 交OB 于点E.判断△CED 的形状，并说明理由．解：△CED 是等边三角形，理由如下： ∵OC 平分∠AOB ，∠AOB ＝60°， ∴∠AOC ＝∠COE ＝30°. ∵CE ∥OA ，∴∠AOB ＝∠CED ＝60°. ∵CD ⊥OC ，∴∠OCD ＝90°. ∴∠EDC ＝60°. ∴△CED 是等边三角形．17．(9分)如图，在四边形ABCD 中，∠B ＝∠D ＝90°，点E ，F 分别在AB ，AD 上，AE ＝AF ，CE ＝CF ，求证：CB ＝CD.证明：连接AC ，在△AEC 和△AFC 中，⎩⎪⎨⎪⎧AC ＝AC ，CE ＝CF ，AE ＝AF ，∴△AEC ≌△AFC(SSS)． ∴∠CAE ＝∠CAF. ∵∠B ＝∠D ＝90°， ∴CB ＝CD.18．(9分)如图，在△ABC 中，AC ＜AB ＜BC.(1)已知线段AB 的垂直平分线与BC 边交于点P ，连接AP ，求证：∠APC ＝2∠B ； (2)以点B 为圆心，线段AB 的长为半径画弧，与BC 边交于点Q ，连接AQ.若∠AQC ＝3∠B ，求∠B 的度数．解：(1)证明：∵线段AB 的垂直平分线与BC 边交于点P ， ∴PA ＝PB. ∴∠B ＝∠BAP. ∵∠APC ＝∠B ＋∠BAP ， ∴∠APC ＝2∠B.(2)根据题意可知BA ＝BQ ， ∴∠BAQ ＝∠BQA.∵∠AQC ＝3∠B ，∠AQC ＝∠B ＋∠BAQ ， ∴∠BAQ ＝∠BQA ＝2∠B. ∵∠BAQ ＋∠BQA ＋∠B ＝180°， ∴5∠B ＝180°. ∴∠B ＝36°.19．(10分)如图，△ACB 和△ECD 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，D 为AB 边上一点．求证：(1)△ACE ≌△BCD ； (2)2CD 2＝AD 2＋BD 2.证明：(1)∵△ABC 和△ECD 都是等腰直角三角形， ∴AC ＝BC ，CD ＝CE. ∵∠ACB ＝∠DCE ＝90°， ∴∠ACE ＋∠ACD ＝∠BCD ＋∠ACD. ∴∠ACE ＝∠BCD.在△ACE 和△BCD 中，⎩⎪⎨⎪⎧AC ＝BC ，∠ACE ＝∠BCD CE ＝CD ，，∴△ACE ≌△BCD(SAS)． (2)∵△ACB 是等腰直角三角形， ∴∠B ＝∠BAC ＝45°. ∵△ACE ≌△BCD ，∴∠B ＝∠CAE ＝45°，AE ＝BD.∴∠DAE ＝∠CAE ＋∠BAC ＝45°＋45°＝90°. ∴AD 2＋AE 2＝DE 2，即AD 2＋BD 2＝DE 2. 又∵在Rt △DEC 中，DE 2＝CE 2＋CD 2＝2CD 2， ∴2CD 2＝AD 2＋BD 2.20．(10分)小明在学习了“等边三角形”后，激发了他的学习和探究的兴趣，就想考考他的朋友小崔，小明作了一个等边△ABC ，如图，并在边AC 上任意取了一点F(点F 不与点A ，C 重合)，过点F 作FH ⊥AB 交AB 于点H ，延长CB 到G ，使得BG ＝AF ，连接FG 交AB 于点I.(1)若AC ＝10，则HI 的长度为5；(2)延长BC 到D ，再延长BA 到E ，使得AE ＝BD ，连接ED ，EC.求证：∠ECD ＝∠EDC.证明：延长CD 至P ，使BC ＝DP ，连接AP ，EP ， ∴BD ＝CP. ∵AE ＝BD ， ∴AE ＝CP.在△ACP 和△CAE 中， ⎩⎪⎨⎪⎧CP ＝AE ，∠ACP ＝∠CAE ＝120°，AC ＝CA ，∴△ACP ≌△CAE(SAS)．∴AP ＝CE. ∵BE ＝AB ＋AE ，BP ＝BC ＋CP ， ∴BE ＝BP. ∵∠ABC ＝60°，∴△EBP 是等边三角形．∴BP ＝EP ，∠EPD ＝60°. ∴∠EPD ＝∠ABC.在△ABP 和△DPE 中，⎩⎪⎨⎪⎧AB ＝DP ，∠ABP ＝∠EPD ，BP ＝EP ，∴△ABP ≌△DPE(SAS)．∴AP ＝ED ＝EC. ∴∠ECD ＝∠EDC.B 卷(共50分)一、填空题(本大题共5个小题，每小题4分，共20分，答案写在题中的横线上) 21．如图，已知△ABC 是等边三角形，点B ，C ，D ，E 在同一直线上，且CG ＝CD ，DF ＝DE ，则∠E ＝15°．22．如图，等边三角形ABC 中，D ，E 分别为AB ，BC 边上的两动点，且总使AD ＝BE ，AE 与CD 交于点F ，AG ⊥CD 于点G ，则FG AF ＝12．23．如图，∠B ＝∠C ＝90°，AE 平分∠BAD ，DE 平分∠ADC.若S △CDE ＝23S △ABE ，则S △DEC ∶S△ADE＝2∶5．24．如图，在Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8，AD 是∠BAC 的平分线．若P ，Q 分别是AD 和AC 上的动点，则PC ＋PQ 的最小值是245．25．如图，在△ABC 中，BF 平分∠ABC ，AG ⊥BF ，垂足为点D ，交BC 于点G ，E 为AC 的中点，连接DE ，DE ＝2.5 cm ，AB ＝4 cm ，则BC 的长为9cm.二、解答题(本大题共3个小题，共30分)26．(8分)如图，在△ABC中，AB＝AC，D为BC边的中点，F为CA的延长线上一点，过点F作FG⊥BC于点G，并交AB于点E，求证：(1)AD∥FG；(2)△AEF是等腰三角形．证明：(1)∵AB＝AC，D是BC的中点，∴AD⊥BC.∴∠ADC＝90°.∵FG⊥BC，∴∠FGC＝90°.∴∠ADC＝∠FGC.∴AD∥FG.(2)∵AB＝AC，D是BC的中点，∴∠BAD＝∠CAD.∵AD∥FG，∴∠F＝∠CAD，∠AEF＝∠BAD.∴∠F＝∠AEF.∴AF＝AE.∴△AEF是等腰三角形．27．(10分)在四边形ABCD中，AB＝BC＝CD＝DA，∠B＝∠D＝60°，连接AC.(1)如图1，点E，F分别在边BC，CD上，且BE＝CF.求证：①△ABE≌△ACF；②△AEF是等边三角形；(2)若点E在BC的延长线上，则在直线CD上是否存在点F，使△AEF是等边三角形？请证明你的结论(图2备用)．解：(1)证明：①∵AB＝BC，∠B＝60°，∴△ABC是等边三角形．∴AB＝AC.同理，△ADC也是等边三角形，∴∠B＝∠ACF＝60°.又∵BE＝CF，∴△ABE≌△ACF(SAS)．②∵△ABE≌△ACF，∴AE＝AF，∠BAE＝∠CAF.∵∠BAE＋∠CAE＝60°，∴∠CAF＋∠CAE＝60°，即∠EAF＝60°.∴△AEF是等边三角形．(2)存在．证明：在CD的延长线上取点F，在BC的延长线上取点E，使CF＝BE，连接AE，EF，AF.与(1)①同理，可证△ABE≌△ACF，∴AE＝AF，∠BAE＝∠CAF.∴∠BAE－∠CAE＝∠CAF－∠CAE.∴∠BAC＝∠EAF＝60°.∴△AEF 是等边三角形．(注：若在CD 的延长线上取点F ，使CE ＝DF 也可)28．(12分)如图，在△ABC 中，AB ＝AC ，∠EAF ＝12∠BAC ，BF ⊥AE 于点E ，交AF 于点F ，连接CF.(1)如图1所示，当∠EAF 在∠BAC 内部时，求证：EF ＝BE ＋CF ；(2)如图2所示，当∠EAF 的边AE ，AF 分别在∠BAC 外部、内部时，求证：CF ＝BF ＋2BE.证明：(1)在EF 上截取EH ＝BE ，连接AH ， ∵EB ＝EH ，AE ⊥BF ， ∴AB ＝AH.∵AB ＝AH ，AE ⊥BH ， ∴∠BAE ＝∠EAH. ∵AB ＝AC. ∴AC ＝AH. ∵∠EAF ＝12∠BAC ，∴∠BAE ＋∠CAF ＝∠EAF. ∴∠BAE ＋∠CAF ＝∠EAH ＋∠FAH. ∴∠CAF ＝∠HAF. 在△ACF 和△AHF 中， ⎩⎪⎨⎪⎧AC ＝AH ，∠CAF ＝∠HAF ，AF ＝AF ，∴△ACF ≌△AHF(SAS)．∴CF ＝HF.∴EF ＝EH ＋HF ＝BE ＋CF.(2)在BE 的延长线上截取EN ＝BE ，连接AN ， ∵AE ⊥BF ，BE ＝EN ，AB ＝AC ，∴AN ＝AB ＝AC.∵AN ＝AB ，AE ⊥BN ，∴∠BAE ＝∠NAE.∵∠EAF ＝12∠BAC ， ∴∠EAF ＋∠NAE ＝12(∠BAC ＋2∠NAE)． ∴∠FAN ＝12∠CAN. ∴∠FAN ＝∠CAF.在△ACF 和△ANF 中，⎩⎪⎨⎪⎧AC ＝AN ，∠CAF ＝∠NAF ，AF ＝AF ，∴△ACF ≌△ANF(SAS)．∴CF ＝NF.∴CF ＝BF ＋2BE.。

北师大版数学八年级下册各单元测试题-含答案(共六套)

7.已知长方形的面积是（），若一边长为，则另一边长为________________.
8.如果a2＋ma＋121是一个完全平方式，那么m＝________或_______.
三、用心算一算（共36分）
1.（20分）因式分解：
(1)4x2－16y2；（2）
（3）x2－10x＋25；（4）
2.（5分）利用因式分解进行计算：
解得．
8．A
提示：不等式组的解集为．
由题意，得解得．
则．
9．B
10．C
三、解答题
1．解：（1）去分母，得．
去括号，得
移项，合并同类项，得．
两边都除以-1，得．
（2）
解不等式①，得．
解不等式②，得．
所以，原不等式组的解集是．
2．解：解方程组得．
由题意，得解得．
因为m为整数，所以m只能为7，8，9，10．
9．7
10．22
提示：设得5分的有x人，若最低得3分的有1人，得4分的有3人，则，且，解得．应取最小整数解，得x=22．
二、选择题
1．C
2．B
3．B
提示：设三个连续奇数中间的一个为x，则．
解得．所以．所以只能取1，3，5，7．
4．C
5．B
6．C
7．B
提示：不等式组的解集为．
因为不等式组有四个整数解，所以．
4．如果，那么[ ]．
A． B． C． D．
5．某数的2倍加上5不大于这个数的3倍减去4，那么该数的范围是[ ]．
A． B． C． D．
6．不等式组的正整数解的个数是[ ]．
A．1B．2 C．3D．4
7．关于x的不等式组有四个整数解，则a的取值范围是[ ]．

北师大版八年级数学下册《第1章三角形的证明》单元培优测试卷【附答案】

北师大版八年级数学下册《第1章三角形的证明》单元培优测试卷一、选择题1．下列命题中，是假命题的是（）A．等腰三角形三个内角的和等于180°B．等腰三角形两边的平方和等于第三边的平方C．角平分线上的点到这个角两边的距离相等D．线段垂直平分线上的点到这条线段两个端点的距离相等2．下列几组数中，能作为直角三角形三边长的是（）A．2，4，5B．3，4，5C．4，4，5D．5，4，53．在等腰三角形中，有一个角是50°，它的一条腰上的高与底边的夹角是（）A．25°B．25°或40°C．25°或35°D．40°4．如图，在△ABC中，AI平分∠BAC，BI平分∠ABC，点O是AC、BC的垂直平分线的交点，连接AO、BO，若∠AIB＝α，则∠AOB的大小为（）A．αB．4α﹣360°C．α+90°D．180°﹣α5．如图，在△ABC中，AC＝6，BC＝8，∠C＝90°，∠ABC与∠BAC的平分线交于点D，过点D作DE∥AC交AB于点E，则DE＝（）A．B．2C．D．36．如图，在△ABC中，∠B＝74°，边AC的垂直平分线交BC于点D，交AC于点E，若AB+BD＝BC，则∠BAC的度数为（）A．74°B．69°C．65°D．60°7．下列命题正确的是（）A．三角形的一个外角大于任何一个内角B．三角形的三条高都在三角形内部C．三角形的一条中线将三角形分成两个三角形面积相等D．两边和其中一边的对角相等的三角形全等8．等腰三角形一边的长为4cm，周长是18cm，则底边的长是（）A．4cm B．10cm C．7或10cm D．4或10cm二、填空题9．如图，BD、CE是等边三角形ABC的中线，则∠EFD＝．10．如图，在△ABC中，AB＝BC，BE平分∠ABC，AD为BC边上的高，且AD＝BD．则∠3＝°．11．平面直角坐标系中，已知A（8，0），△AOP为等腰三角形，且△AOP的面积为16，则满足条件的P点个数是．12．如果等腰三角形的一个内角是80°，那么它的顶角的度数是°．13．如图，BD是△ABC的角平分线，DE⊥AB，垂足为E，△ABC的面积为60，AB＝16，BC＝14，则DE的长等于．14．如图，在△ABC中，线段AB的垂直平分线交AC于点D，连接BD，若∠C＝80°，∠CBD＝40°，则∠A的度数为°．15．如图，在△ABC中，AB＝AC，D为BC的中点，∠BAD＝20°，且AE＝AD，则∠CDE的度数是．16．如图，Rt△ABC中，∠ABC＝90°，DE是边AB的垂直平分线，D为垂足，DE交AC 于点，且AB＝8，BC＝6，则△BEC的周长是．17．如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于E点，∠B＝50°，∠FAE＝20°，则∠C＝度．18．已知C，D两点在线段AB的垂直平分线上，且∠ACB＝50°，∠ADB＝86°，则∠CAD的度数是．三、解答题19．如图，△ABC中，∠ABC＝25°，∠ACB＝55°，DE，FG分别为AB，AC的垂直平分线，E，G分别为垂足．（1）直接写出∠BAC的度数；（2）求∠DAF的度数；（3）若BC的长为30，求△DAF的周长．20．如图，在△ABC中，AB＝AC，DE垂直平分AC，CE⊥AB，AF⊥BC．（1）求证：CF＝EF；（2）求∠EFB的度数．21．如图，在等边三角形ABC中，D是AB上的一点，E是CB延长线上一点，连接CD、DE，已知∠EDB＝∠ACD，BC＝6，（1）求证：△DEC是等腰三角形．（2）当∠BDC＝5∠EDB，EC＝8时，求△EDC的面积．22．如图，在Rt△ABC中，∠ACB＝90°，△CAP和△CBQ都是等边三角形，BQ和CP 交于点H，求证：BQ⊥CP．23．△ABC中，AB＝AC，∠B＝30°，点P在BC边上运动（P不与B、C重合），连接AP，作∠APQ＝∠B，PQ交AB于点Q．（1）如图1，当PQ∥CA时，判断△APB的形状并说明理由；（2）在点P的运动过程中，△APQ的形状可以是等腰三角形吗？若可以，请直接写出∠BQP的度数；若不可以，请说明理由．24．如图，在△ABC中，∠BAC＝90°，BE平分∠ABC，AM⊥BC于点M交BE于点G，AD平分∠MAC，交BC于点D，交BE于点F．求证：线段BF垂直平分线段AD．25．如图，在△ABC中，AB的垂直平分线EF交BC于点E，交AB于点F，D为线段CE 的中点，BE＝AC．（1）求证：AD⊥BC．（2）若∠BAC＝75°，求∠B的度数．26．已知△ABC中，D为边BC上一点，AB＝AD＝CD．（1）试说明∠ABC＝2∠C；（2）过点B作AD的平行线交CA的延长线于点E，若AD平分∠BAC，求证：AE＝AB．参考答案1．解：A、等腰三角形三个内角的和等于180°，正确，是真命题，不符合题意；B、直角三角形两边的平方和等于第三边的平方，故原命题错误，是假命题，符合题意；C、角平分线上的点到这个角两边的距离相等，正确，是真命题，不符合题意；D、线段垂直平分线上的点到这条线段两个端点的距离相等，正确，是真命题，不符合题意，故选：B．2．解：A、22+42≠52，根据勾股定理的逆定理可知三角形不是直角三角形，故不合题意；B、32+42＝52，根据勾股定理的逆定理可知三角形是直角三角形，故符合题意；C、42+42≠52，根据勾股定理的逆定理可知三角形不是直角三角形，故不合题意；D、42+52≠52，根据勾股定理的逆定理可知三角形不是直角三角形，故不合题意；故选：B．3．解：当50°为底角时，∵∠B＝∠ACB＝50°，∴∠BCD＝90°﹣50°＝40°；当50°为顶角时，∵∠A＝50°，∴∠B＝∠ACB＝65°，∴∠BCD＝90°﹣65°＝25°．故选：B．4．解：连接CO并延长至D，∵∠AIB＝α，∴∠IAB+∠IBA＝180°﹣α，∵AI平分∠BAC，BI平分∠ABC，∴∠IAB＝∠CAB，∠IBA＝∠CBA，∴∠CAB+∠CBA＝2（∠IAB+∠IBA）＝360°﹣2α，∴∠ACB＝180°﹣（∠CAB+∠CBA）＝2α﹣180°，∵点O是AC、BC的垂直平分线的交点，∴OA＝OC，OB＝OC，∴∠OCA＝∠OAC，∠OCB＝∠OBC，∵∠AOD是△AOC的一个外角，∴∠AOD＝∠OCA+∠OAC＝2∠OCA，同理，∠BOD＝∠OCB，∴∠AOB＝∠AOD+∠BOD＝2∠OCA+2∠OCB＝4α﹣360°，故选：B．5．解：延长ED交BC于点G，作DF⊥AB于点F，作DH⊥AC于点H，∵DE∥AC，∠C＝90°，∴∠BGE＝∠C＝90°，∴EG⊥BC，∴∠DGC＝∠DHC＝∠C＝90°，∴四边形DGCH为矩形，∵AD平分∠BAC，BD平分∠ABC，DF⊥AB，DH⊥AC，DG⊥BC，∴DF＝DM，DG＝DF，∴DH＝DG，∴四边形DGCH为正方形，在Rt△BDG和Rt△BDF中，，∴Rt△BDG≌Rt△BDF（HL），∴BF＝BG，同理可得：Rt△AHD≌Rt△AFD，由勾股定理可得：AB2＝AC2+BC2＝100，∴AB＝10，设CH＝CG＝x，则AH＝6﹣x，BG＝8﹣x，∴AF＝6﹣x，BF＝8﹣x，∴AB＝10＝AF+BF＝6﹣x+8﹣x＝14﹣2x，即14﹣2x＝10，解得：x＝2，∴CH＝CG＝2，BG＝6，∵DE∥AC，∴△BEG∽△BAC，∴，即，∴EG＝4.5，∴DE＝EG﹣DG＝4.5﹣2＝2.5，故选：A．6．解：如图，连接AD，∵边AC的垂直平分线交BC于点D，∴AD＝CD，∴∠DAC＝∠C，∵AB+BD＝BC，BD+CD＝BC，∴CD＝AB，∴AD＝AB，∴∠ABD＝∠ADB＝74°，∴∠C＝37°，∴∠BAC＝180°﹣74°﹣37°＝69°，故选：B．7．解：A、三角形的一个外角大于与它不相邻的任何一个内角，原命题是假命题；B、钝角三角形的三条高不在三角形内部，原命题是假命题；C、三角形的一条中线将三角形分成两个三角形面积相等，是真命题；D、两边和其夹角相等的三角形全等，原命题是假命题；故选：C．8．解：分情况考虑：①当4cm是腰时，则底边长是18﹣8＝10（cm），此时4，4，10不能组成三角形，应舍去；②当4cm是底边时，腰长是（18﹣4）×＝7（cm），4，7，7能够组成三角形．此时底边的长是4cm．故选：A．9．解：∵BD、CE是等边三角形ABC的中线，∴BD⊥AC，CE⊥AB，∠A＝60°，∴∠AEF＝∠ADF＝90°，∵∠EFD＝360°﹣90°﹣90°﹣∠A＝180°﹣60°＝120°．故答案为120°．10．解：∵AD为BC边上的高，∴∠ADB＝90°，∵AD＝BD，∴∠ABD＝∠BAD＝（180°﹣∠ADB）＝45°，∵BE平分∠ABC，∴∠1＝∠2＝∠ABD＝22.5°，BE⊥AC，∴∠BEA＝90°＝∠ADB，∵∠3+∠BEA+∠AHE＝180°，∠2+∠ADB+∠BHD＝180°，∠AHE＝∠BHD，∴∠3＝∠2＝22.5°．故答案为：22.5°．11．解：∵A（8，0），∴OA＝8，设△AOP的边OA上的高是h，则×8×h＝16，解得：h＝4，在x轴的两侧作直线a和直线b都和x轴平行，且到x轴的距离都等于4，如图：①以A为圆心，以8为半径画弧，交直线a和直线b分别有两个点，即共4个点符合，②以O为圆心，以8为半径画弧，交直线a和直线b分别有两个点，即共4个点符合，③作AO的垂直平分线分别交直线a、b于一点，即共2个点符合，4+4+1+1＝10．故答案为：10．12．解：当80°是等腰三角形的顶角时，则顶角就是80°；当80°是等腰三角形的底角时，则顶角是180°﹣80°×2＝20°．故答案为：80°或20．13．解：作DF⊥BC于F，∵BD是△ABC的角平分线，DE⊥AB，DF⊥BC，∴DF＝DE，∴S△ABC＝S△ABD+S△DBC＝×AB×DE+×BC×DF＝＝60，∴DF＝DE＝4．故答案为：4．14．解：∵∠C＝80°，∠CBD＝40°，∴∠CDB＝180°﹣∠C﹣∠CBD＝60°，∵线段AB的垂直平分线交AC于点D，∴DA＝DB，∴∠A＝∠DBA＝∠CDB＝30°，故答案为：30．15．解：∵AB＝AC，D为BC的中点，∴∠CAD＝∠BAD＝20°，AD⊥BC，∴∠ADC＝90°，∵AD＝AE，∴∠ADE＝∠AED＝＝80°，∴∠CDE＝∠ADC﹣∠ADE＝90°﹣80°＝10°．故答案为：10°．16．解：在Rt△ABC中，∠ABC＝90°，AB＝8，BC＝6，∴AC＝＝＝10，∵DE是边AB的垂直平分线，∴EA＝EB，∴△BEC的周长＝BC+EC+BE＝BC+EC+EA＝BC+AC＝16，故答案为：16．17．解：∵DE是线段AC的垂直平分线，∴EA＝EC，∴∠EAC＝∠C，∵AF平分∠BAC，∴∠BAF＝∠CAF＝∠FAE+∠CAE＝20°+∠C，由三角形内角和定理得，∠B+∠BAC+∠C＝180°，即50°+20°+∠C+20°+∠C+∠C＝180°，解得，∠C＝30°，故答案为：30．18．解：∵C、D两点在线段AB的中垂线上，∴CA＝CB，DA＝DB，∵CD⊥AB，∴∠ACD＝∠ACB＝×50°＝25°，∠ADC＝∠ADB＝×86°＝43°，当点C与点D在线段AB两侧时，∠CAD＝180°﹣∠ACD﹣∠ADC＝180°﹣25°﹣43°＝112°，当点C与点D′在线段AB同侧时，∠CAD′＝∠AD′C﹣∠ACD′＝43°﹣25°＝18°，故答案为：18°或112°．19．解：（1）∵∠ABC＝25°，∠ACB＝55°，∴∠BAC＝180°﹣∠ABC﹣∠ACB＝100°；（2）∵DE，FG分别为AB，AC的垂直平分线，∴DA＝DB，FA＝FC，∴∠DAB＝∠ABC＝25°，∠FAC＝∠ACB＝55°，∴∠DAF＝∠BAC﹣∠DAB﹣∠FAC＝20°；（3）△DAF的周长＝DA+DF+FA＝DB+DF+FC＝BC＝30．20．证明：（1）∵AB＝AC，AF⊥BC，∴BF＝CF，又∵CE⊥AB，∴CF＝EF；（2）∵DE垂直平分AC，∴AE＝EC，又∵∠AEC＝90°，∴∠ACE＝∠EAC＝45°，∴∠B＝∠ACB＝67.5°，∵EF＝CF＝BF，∴∠BEF＝∠FBE＝67.5°，∴∠EFB＝45°．21．（1）证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝60°，∵∠E+∠EDB＝∠ABC＝60°，∠ACD+∠DCB＝60°，∠EDB＝∠ACD，∴∠E＝∠DCE，∴DE＝DC，∴△DEC是等腰三角形；（2）解：设∠EDB＝α，则∠BDC＝5α，∴∠E＝∠DCE＝60°﹣α，∴6α+60°﹣α+60°﹣α＝180°，∴α＝15°，∴∠E＝∠DCE＝45°，∴∠EDC＝90°，如图，过D作DH⊥CE于H，∵△DEC是等腰直角三角形，∴∠EDH＝∠E＝45°，∴EH＝HC＝DH＝EC＝8＝4，∴△EDC的面积＝EC•DH＝8×4＝16．22．证明：∵△CAP和△CBQ都是等边三角形，∴∠CAP＝∠CBQ＝60°，∵∠ACB＝90°，∴∠BCP＝∠ACB﹣∠ACP＝30°，在△BCH中，∠BHC＝180°﹣∠BCH﹣∠CBH＝180°﹣30°﹣60°＝90°，∴BQ⊥CP．23．解：（1）△APB是直角三角形，理由如下：∵AB＝AC，∠B＝30°，∴∠C＝30°＝∠B＝∠APQ，∵PQ∥AC，∴∠BPQ＝∠C，∴∠APB＝60°，∴∠BAP＝90°，∴△APB是直角三角形；（2）当AQ＝QP时，∴∠QAP＝∠APQ＝30°，∴∠BQP＝∠QAP+∠APQ＝60°，当AP＝PQ时，则∠AQP＝∠PAQ＝75°，∴∠BQP＝105°，当AQ＝AP时，则∠AQP＝∠APQ＝30°，∵P不与B、C重合，∴不存在，综上所述：∠BQP＝105°或60°．24．证明：∵∠BAC＝90°，∴∠ABC+∠C＝90°，∵AM⊥BC，∴∠AMB＝90°，∴∠ABC+∠BAM＝90°，∴∠C＝∠BAM，∵AD平分∠MAC，∴∠MAD＝∠CAD，∴∠BAM+∠MAD＝∠C+∠CAD，∵∠ADB＝∠C+∠CAD，∴∠BAD＝∠ADB，∴AB＝BD，∵BE平分∠ABC，∴BF⊥AD，AF＝FD，即线段BF垂直平分线段AD．25．解：（1）连接AE，∵EF垂直平分AB∴AE＝BE∵BE＝AC∴AE＝AC∵D是EC的中点∴AD⊥BC（2）设∠B＝x°∵AE＝BE∴∠BAE＝∠B＝x°∴由三角形的外角的性质，∠AEC＝2x°∵AE＝AC∴∠C＝∠AEC＝2x°在三角形ABC中，3x°+75°＝180°x°＝35°∴∠B＝35°26．证明：（1）∵AB＝AD，∴∠ABC＝∠ADB，∵AD＝CD，∴∠DAC＝∠C，∵∠ADB＝∠DAC+∠C＝2∠C，∴∠ABC＝2∠C；（2）∵AD平分∠BAC，∴∠DAB＝∠CAD，∵BE∥AD，∴∠DAB＝∠ABE，∠E＝∠CAD，∴∠ABE＝∠E，∴AE＝AB．。

北师大版八年级思品下册第一单元测试卷

2020年北师大版八年级数学下册第一章 三角形的证明单元测试题及答案

(常考题)北师大版初中数学八年级数学下册第一单元《三角形的证明》测试(答案解析)(4)

281北师大版思品八年级下册板块型能力综合测试卷(含答案)ppt课件33页PPT

2020-2021学年北师大版八年级下册数学 第一章 三角形的证明 单元测试(含解析)