经典迟滞非线性Preisach模型matlab代码

【国家自然科学基金】_非线性误差_基金支持热词逐年推荐_【万方软件创新助手】_20140730

2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
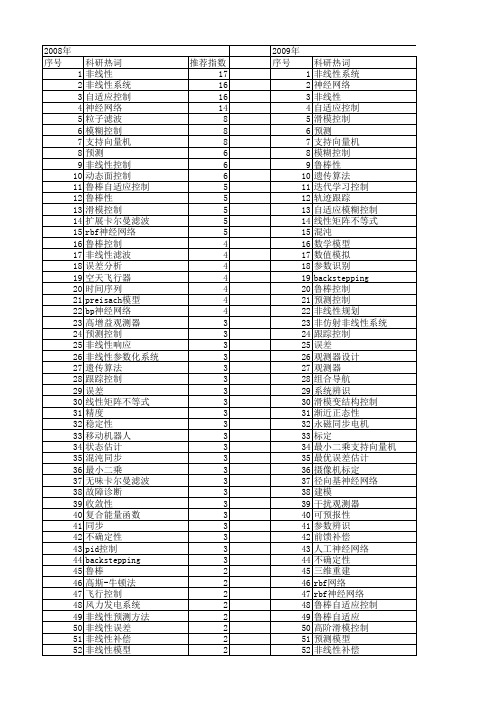
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
推荐指数 17 16 16 14 8 8 8 6 6 6 5 5 5 5 5 4 4 4 4 4 4 4 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2
2009年序号 1 2 3 4 5 பைடு நூலகம் 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52

【系统仿真学报】_非线性函数_期刊发文热词逐年推荐_20140724

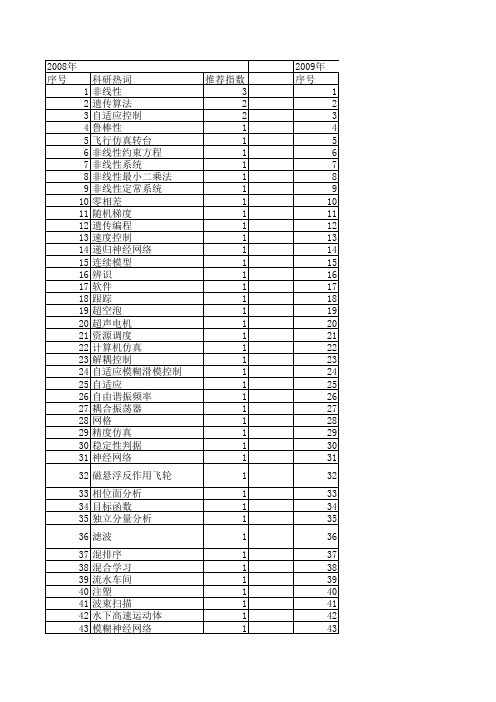
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
modelica mcma lyapunov函数 hopfield神经网络 gpu drivelib模型库
1 1 1 1 1 1
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
科研热词非线性遗传算法自适应控制鲁棒性飞行仿真转台非线性约束方程非线性系统非线递归神经网络连续模型辨识软件跟踪超空泡超声电机资源调度计算机仿真解耦控制自适应模糊滑模控制自适应自由谐振频率耦合振荡器网格精度仿真稳定性判据神经网络磁悬浮反作用飞轮相位面分析目标函数独立分量分析滤波混排序混合学习流水车间注塑波束扫描水下高速运动体模糊神经网络模糊控制模糊前馈控制器
推荐指数 3 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
科研热词非线性时滞大系统闭环迭代学习控制遗传算法近似动态规划自适应算子理论电动汽车模糊逻辑系统极大似然估计有限元分析时变非线性系统开关磁阻电机对数线性加速模型回转窑动态面控制动态仿真加速寿命试验初始状态优化控制 weibull分布 srm elman网 dhp

【系统仿真学报】_非线性系统辨识_期刊发文热词逐年推荐_20140723

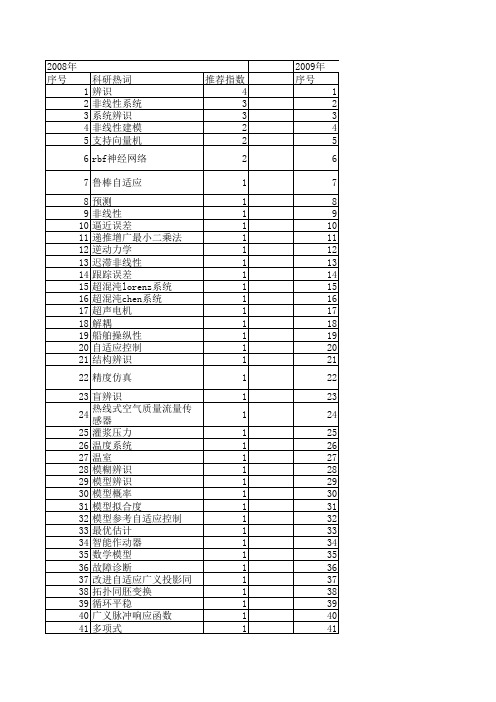
backstepping
1
推荐指数 3 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13
科研热词推荐指数非线性hammerstein模型 1 线性方程 1 滑模控制器 1 气动参数 1 无人水下机器人 1 故障辨识 1 快速建模 1 参数估计 1 低阶等效系统 1 优化 1 主动容错控制 1 rcmac 1 ipso算法 1
2013年序号 1 2 3 4 5 6 7 8
科研热词推荐指数自适应变异 1 混杂系统 1 差分进化算法 1 多参数规划 1 参数辨识 1 分段仿射模型(pwa)hysdel 1 分段仿射含输入自回归模型(pwarx) 1 wiener模型 1
Байду номын сангаас
2009年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
46 47 48 49 50 51 52 53 54 55 56 57
2008年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
科研热词推荐指数辨识 4 非线性系统 3 系统辨识 3 非线性建模 2 支持向量机 2 rbf神经网络 2 鲁棒自适应 1 预测 1 非线性 1 逼近误差 1 递推增广最小二乘法 1 逆动力学 1 迟滞非线性 1 跟踪误差 1 超混沌lorenz系统 1 超混沌chen系统 1 超声电机 1 解耦 1 船舶操纵性 1 自适应控制 1 结构辨识 1 精度仿真 1 盲辨识 1 热线式空气质量流量传感器 1 灌浆压力 1 温度系统 1 温室 1 模糊辨识 1 模型辨识 1 模型概率 1 模型拟合度 1 模型参考自适应控制 1 最优估计 1 智能作动器 1 数学模型 1 故障诊断 1 改进自适应广义投影同步 1 拓扑同胚变换 1 循环平稳 1 广义脉冲响应函数 1 多项式 1 多模型融合 1 多变量系统 1 基因表达式编程 1 可变参数 1

【国家自然科学基金】_迟滞补偿_基金支持热词逐年推荐_【万方软件创新助手】_20140803

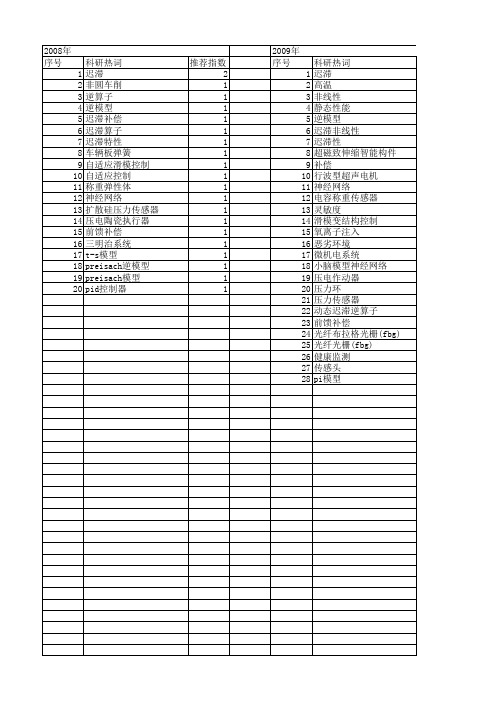
推荐指数 4 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 12 13 14 15 16 17 18
2012年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
2014年序号 1 2 3 4 5 6 7 8 9 10 11 12 13
2014年科研热词迟滞区间自适应滑模控制温度补偿液压源流量控制欠压锁定模型控制条件补偿带隙比较器前馈补偿伺服驱动 priesach逆模型推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
科研热词迟滞神经网络鲁棒控制静态补偿逆模型迟滞误差超磁致补偿自适应脉冲反馈纯水液压滞环温度补偿比例溢流阀恒弹性合金建模定位精度反馈误差学习控制压电陶瓷定位器分类排序光纤光栅光纤光学仿真 preisach迟滞模型
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2011年序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

混合Preisach迟滞模型及其性质研究

维普资讯
第１６卷
第２期
光学精密工程
ＯｐｔｃｎｄＰｒｃｓｏｎＥｎｇｎｅｉｉｓａｅｉｉｉｅｒｎｇ
Ｖｏｌ６ＮＯ＿１．２
Ｆｅ．２８ｂ００源自２００８年２月文章编号
１０ —２Ｘ２０）２０７ —６０４９４（０８０ — ２９０
混合Ｐｅｓｃｒｉｈ迟滞模型及其性质研究ａ
李黎，刘向东，侯朝桢，伟王
（北京理工大学信息科学技术学院自动控制系，北京１０８）００１
摘要：电陶瓷执行器物理结构复杂，过参数化方法辨识经典Ｐｅａｈ模型（Ｐ描述其迟滞特性时，以找到合适压通ｒｉｃｓＣＭ）难
ＡｂｔａｔｔｉｉｆｃｌｏｆｎｕｉａｅＰｒｉａｈｆｎｃｉｎｉｈｌｓｉａｅｓｃｏｌＳＣＰＭ）ｉｓｒｃ：ＩＳｄｆｉｕｔｔｉｄａｓｔｂｌｅｓｃｕｔｏｎｔｅＣａｓｃｌＰｒｉａｈＭｄｅ ’ （－ｄｅｔｆｃｔｏｈｅｐａｅｒｃｓｒｔｇｃｕｅｔｅｐｅｏｅａｉｓａｔａｏｓｃｍｐｅｏｎｓｒｃｉ．ｎｉｉａｉｎｂｙｔａｒｍｔｉｔａｅｙｂｅａｓｈｉｚｃｒｍｃｃｕｔｒｈａｏｌｘｃｔｕｔｏｎＴｏｉｐｒｖｈｅｍｏｄｌｎｃｕｒｃｍｏｅｔｅｉｇａｃａｙ，ｔｉｐｒｐｒｓｎｅｎａｅａｅｈｔｒｓｓｍｏｅｓｃｍｐｅａｉｈｓｐａｅｅｅｔｄａｖｒｇｙｓｅｅｉｄｌａｏｎｓｔｏｎ

转移熵matlab代码精选全文完整版

可编辑修改精选全文完整版以下是一个简单的示例，展示了如何在MATLAB中计算两个向量之间的转移熵：% 计算转移熵function transferEntropy = calculateTransferEntropy(X, Y, delay)% X: 源向量% Y: 目标向量% delay: 延迟步数% 转移熵初始化为0transferEntropy = 0;% 计算源向量和目标向量的长度len = length(X);% 计算延迟后的源向量X_delayed = X(1:len-delay);% 计算延迟后的目标向量Y_delayed = Y(delay+1:len);% 构建延迟后的源向量和目标向量的联合概率分布jointDistribution = zeros(2, 2);for i = 1:len-delayif X_delayed(i) == 0if Y_delayed(i) == 0jointDistribution(1, 1) = jointDistribution(1, 1) + 1;elsejointDistribution(1, 2) = jointDistribution(1, 2) + 1;endelseif Y_delayed(i) == 0jointDistribution(2, 1) = jointDistribution(2, 1) + 1;elsejointDistribution(2, 2) = jointDistribution(2, 2) + 1;endendend% 计算转移熵for i = 1:2for j = 1:2p_xy = jointDistribution(i, j) / (len-delay);p_x = sum(X_delayed == (i-1)) / (len-delay);p_y = sum(Y_delayed == (j-1)) / (len-delay);if p_x ~= 0 && p_y ~= 0 && p_xy ~= 0transferEntropy = transferEntropy + p_xy * log2(p_xy / (p_x * p_y));endendendend请注意，这只是一个基本的示例，用于说明如何在MATLAB中计算转移熵。

Bouc-Wen模型和反演装置应用在压电传动装置上来补偿非线性磁滞现象

Bouc-Wen模型和反演装置应用在压电传动装置上来补偿非线性磁滞现象摘要——现在提出一个新的方法用来补偿压电陶瓷材料的非线性磁滞现象。

基于反演预算的方法,该方法避免了反演模型用于现有的问题。

因此,补偿易于实施,只要直接模式是可用，就不需要额外的计算。

该补偿技术,对于Bouc-Wen方程组模拟的磁滞现象很有价值实验人员注意——这些来,许多研究人员正在研究微米/ 纳米级压电晶体的非线性迟滞现象。

尽管高分辨率和高速度的材料的磁滞现象受限于准确性，但是如果反馈控制律可以很轻松地提高性能,它们将应用于微米/纳米级和微小型系统方便传感器。

一方面,准确、高带宽传感器不仅昂贵,而且庞大(仪、光学传感器)。

另一方面,可积传感器对噪音高度敏感,并且易碎(应变片)。

传感器、前馈控制技术已被使用。

这些技术代表了包含在一个整合的观点,但现有的方法很难实现复杂的计算和运行。

在本文中有三个明确的目标：（1）在微米/纳米级实现高性能的需要（2）避免使用庞大的传感器,（3）需要的是易于计算和控制的技术因此本文的内容关键在于设计一种前馈补偿控制器，并且它方便计算和操作。

当然，即使我们提出一个应用对应到具体的压电驱动器，提出的方法同样适用于其他的Bouc-Wen的表达建模系统。

关键词——磁滞现象补偿、Bouc-Wen模型、反演的方案、压电传动装置一介绍压电材料，尤其是PZT材料，在微米/纳米级的发展研究很有价值。

这是由于压电陶瓷提供高分辨率，高带宽，低成本，处理简单所致。

不幸的是，压电陶瓷表现出强烈的非线性磁滞现象，最后不得不妥协制动器的精度并且产生不需要的谐波。

反馈控制技术似乎是最好的方式,它能够触及到整体的实质性东西（准确性、重复性、干扰和不确定性影响振动排斥、拒绝,等等)。

（1）（2）然而,反馈给微小系统,如微米/纳米执行机构受限于传感器难以整合，而高带宽和足够精确的传感器过于庞大,并且很难制作和非常昂贵(干涉仪,三角光传感器、cameramicroscopes测量系统,等等)。

压电陶瓷2

压电陶瓷基本特性：1.位移特性KS EEQL r2 2εεε+=∆式中，Q r为极化后的剩余电荷，ε为压电介质的介电常数，E为压电陶瓷内部电场强度，S为压电陶瓷的横截面积，K为压电陶瓷碟片的弹性模量，ε0 为真空的介电常数式中的ε不是常量，而是和所加电压和加压史有关，因而压电陶瓷位移和电场强度（电压）的关系存在迟滞特性。

下图为这一陶瓷在正负电压下的位移-电压特性曲线：2.出力位移特性在空载的情况下压电陶瓷的输出位移为最大输出位移，在最大输出力的作用下，压电陶瓷的输出位移将为零，压电陶瓷的输出力和位移的关系曲线如下图：3.温度特性①压电陶瓷随着温度的变化而伸长。

②压电/电致伸缩陶瓷的输出位移随着温度的增加而减少，压电陶瓷的减少幅度较小，电致伸缩陶瓷减少幅度较大。

4.迟滞特性压电陶瓷的迟滞一般在14%左右，目前提出的减少迟滞的方法主要有：①采用电荷控制方法；②采用压电陶瓷两端串联小电容的方法；③运用模型；④采用电阻和电容组成桥路；⑤压电陶瓷元件位移闭环压电陶瓷作动器是高精度定位中的关键部件，它能满足纳米级定位精度，具有体积小、刚度高、响应快等优点。

然而它的相应位移和驱动电压之间存在着非对称迟滞特性，同时自身的蠕变和环境温度的变化也会造成其定位精度的漂移。

而且压电陶瓷作动器的非对称迟滞特性对控制精度的影响十分显著。

为减少和消除该不利影响，目前主要有两种解决途径：①电荷控制：它需要特别设计的电荷驱动放大器，但该放大器价格昂贵，且存在漂移和过饱和等问题，因而极大的限制了其应用；②电压控制：需要建立非线性迟滞的数学模型，并通过逆模型前馈补偿来控制精度。

电压控制逐渐成为压电陶瓷作动器精密控制的首选方案，其关键是非线性迟滞的精确建模。

对于迟滞特性建模存在两个困难：1)非局部存储现象．2)上升曲线和下降曲线是不对称曲线迟滞模型的研究主要分为两个方向：一种是基于机理的物理模型，从基本物理原理出发描述物理特性；如Maxwell模型，Jiles-Atherton模型，Duherm模型。

【国家自然科学基金】_经典模型_基金支持热词逐年推荐_【万方软件创新助手】_20140731

53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
科研热词遗传算法粗糙集数值模拟破产概率数学模型 preisach模型模型预测解析解粒子群算法神经网络支持向量机扩展模型参数估计项目管理非线性扩散隐马尔可夫模型近似算法边缘停止评价计划与调度衍射效率网格纳什均衡级联约简粒子群优化积分方程目标跟踪电磁散射理论浮动电荷气泡概率密度函数核函数有限元方法有限元最小二乘法曲率驱动收敛性排队论损伤异向介质小波变换小世界网络实证研究多肽构象复杂网络基追踪图像复原各相异性极化参数辨识
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
压电陶瓷执行器动物实验创业模型分子动力学共形阵列天线传输矩阵法优化模型伏安特性仿真交流电弧主成分分析不完备信息系统黏性耗散黏弹流体黄金分割反馈控制律鲁棒控制鲁棒性分析鲁棒性高频电磁场高维索引高电荷态离子高斯波束高斯扰动高斯光束高压co2 高分辨雷达骨髓移植驰振马氏链马尔可夫族模型饱和渗流应力耦合饱和度模型飞行力学风险规避风险模型风险厌恶风险分析风险函数风致振动风生涡旋风洞试验风沙运动颜色直方图颗粒动力学颗粒介质频率-波数域频率预紧式传感器面板数据面接触面向对象设计非负约束最小二乘算法非绝热动力学非线性系统

Lyapunov指数的计算方法

【总结】Lyapunov指数的计算方法非线性理论近期为了把计算LE的一些问题弄清楚，看了有7～9本书！下面以吕金虎《混沌时间序列分析及其应用》、马军海《复杂非线性系统的重构技术》为主线，把目前已有的LE计算方法做一个汇总！1. 关于连续系统Lyapunov指数的计算方法? ? 连续系统LE的计算方法主要有定义方法、Jacobian方法、QR分解方法、奇异值分解方法，或者通过求解系统的微分方程，得到微分方程解的时间序列，然后利用时间序列（即离散系统）的LE求解方法来计算得到。

关于连续系统LE的计算，主要以定义方法、Jacobian方法做主要介绍内容。

（1）定义法定义法求解Lyapunov指数.JPG关于定义法求解的程序，和matlab板块的“连续系统LE求解程序”差不多。

以Rossler系统为例Rossler系统微分方程定义程序function dX = Rossler_ly(t,X)%??Rossler吸引子，用来计算Lyapunov指数%? ?? ???a=0.15,b=0.20,c=10.0%? ?? ???dx/dt = -y-z,%? ?? ???dy/dt = x+ay,%? ?? ???dz/dt = b+z(x-c),a = 0.15;b = 0.20;c = 10.0;x=X(1); y=X(2); z=X(3);% Y的三个列向量为相互正交的单位向量Y = [X(4), X(7), X(10);? ? X(5), X(8), X(11);? ? X(6), X(9), X(12)];% 输出向量的初始化，必不可少dX = zeros(12,1);% Rossler吸引子dX(1) = -y-z;dX(2) = x+a*y;dX(3) = b+z*(x-c);% Rossler吸引子的Jacobi矩阵Jaco = [0 -1 -1;? ?? ??? 1 a?? 0;? ?? ??? z 0??x-c];dX(4:12) = Jaco*Y;求解LE代码：% 计算Rossler吸引子的Lyapunov指数clear;yinit = [1,1,1];orthmatrix = [1 0 0;? ?? ?? ?? ???0 1 0;? ?? ?? ?? ???0 0 1];a = 0.15;b = 0.20;c = 10.0;y = zeros(12,1);% 初始化输入y(1:3) = yinit;y(4:12) = orthmatrix;tstart = 0; % 时间初始值tstep = 1e-3; % 时间步长wholetimes = 1e5; % 总的循环次数steps = 10; % 每次演化的步数iteratetimes = wholetimes/steps; % 演化的次数mod = zeros(3,1);lp = zeros(3,1);% 初始化三个Lyapunov指数Lyapunov1 = zeros(iteratetimes,1); Lyapunov2 = zeros(iteratetimes,1); Lyapunov3 = zeros(iteratetimes,1);for i=1:iteratetimes? ? tspan = tstart:tstep:(tstart + tstep*steps);? ? ? ? [T,Y] = ode45('Rossler_ly', tspan, y);? ? % 取积分得到的最后一个时刻的值? ? y = Y(size(Y,1),:);? ? % 重新定义起始时刻? ? tstart = tstart + tstep*steps;? ? y0 = [y(4) y(7) y(10);? ?? ?? ? y(5) y(8) y(11);? ?? ?? ? y(6) y(9) y(12)];? ? %正交化? ? y0 = ThreeGS(y0);? ? % 取三个向量的模? ? mod(1) = sqrt(y0(:,1)'*y0(:,1));? ? mod(2) = sqrt(y0(:,2)'*y0(:,2));? ? mod(3) = sqrt(y0(:,3)'*y0(:,3));? ? y0(:,1) = y0(:,1)/mod(1);? ? y0(:,2) = y0(:,2)/mod(2);? ? y0(:,3) = y0(:,3)/mod(3);? ? lp = lp+log(abs(mod));? ? %三个Lyapunov指数? ? Lyapunov1(i) = lp(1)/(tstart);? ? Lyapunov2(i) = lp(2)/(tstart);? ? Lyapunov3(i) = lp(3)/(tstart);? ?? ???y(4:12) = y0';end% 作Lyapunov指数谱图i = 1:iteratetimes;plot(i,Lyapunov1,i,Lyapunov2,i,Lyapunov3) 程序中用到的ThreeGS程序如下：%G-S正交化function A = ThreeGS(V)??% V 为3*3向量v1 = V(:,1);v2 = V(:,2);v3 = V(:,3);a1 = zeros(3,1);a2 = zeros(3,1);a3 = zeros(3,1);a1 = v1;a2 = v2-((a1'*v2)/(a1'*a1))*a1;a3 = v3-((a1'*v3)/(a1'*a1))*a1-((a2'*v3)/(a2'*a2))*a2;A = [a1,a2,a3];计算得到的Rossler系统的LE为————??0.063231??0.092635??-9.8924Wolf文章中计算得到的Rossler系统的LE为————0.09? ?0? ?-9.77需要注意的是——定义法求解的精度有限，对有些系统的计算往往出现计果和理论值有偏差的现象。