2014年北京市中考试题及答案
2014年北京市中考语文卷

2014年北京市中考语文卷适用年级:九年级建议时长:0分钟试卷总分:120.0分一、选择。
下面各题均有四个选项,其中只有一个符合题意。
1. 阅读下面的文字,完成(1)—(2)题。
(共4分)周口店北京人遗址的发掘,可以追溯到上世纪20年代。
为了更好地保护这一举世闻名的古人类遗址,2011年7月,周口店北京人遗址博物馆开始迁建。
建成后的新馆,面积是旧馆的8倍。
走进博物馆大厅,首先映入眼帘的是一座巨大的雕塑,“北京人”右手持木棍,肩上扛着猎物,身体直立着行走,______(1)____地还原了“北京人”狩猎归来的场景。
作为国家一级博物馆,周口店北京人遗址博物馆用来收藏,保护和研究_____(2)______。
(1).对文中划线字的注音和对画线字笔顺的判断,全部正确的一项是(2分)( ) (2.0分)(单选)A. 追溯(shuò) “为”字的笔顺是:丶ノフ丶B. 追溯(sù) “为”字的笔顺是:丶フノ丶C. 追溯(sù) “为”字的笔顺是:丶ノフ丶D. 追溯(shuò) “为”字的笔顺是:丶フノ丶(2).根据语意,分别在横线(1)(2)处填入语句,最恰当的一项是(2分) ()(2.0分)(单选)A. (1)栩栩如生 (2)周口店遗址历年来的考古发掘物B. (1)巧妙绝伦 (2)周口店历年来的考古遗址发掘物C. (1)巧妙绝伦 (2)周口店遗址历年来的考古发掘物D. (1)栩栩如生 (2)周口店历年来的考古遗址发掘物2.汉字是音形义的结合体。
字谜,就常常借助汉字的间架结构和偏旁来设计。
下列字谜,不属于按照汉字的间架结构和偏旁来设计的一项是(2分)()(2.0分)(单选)A. 上下平行,左右勾连。
(打一字) 谜底:互B. 看时圆,写时方,寒时短,热时长。
(打一字) 谜底:日C. 一点一横长,口字在中央,大口张着嘴,小口里面藏。
(打一字) 谜底:高D. 有女全姓姚,有手能肩挑,有足蹦蹦跳,有木桃花俏。
2014北京中考数学22题和答案
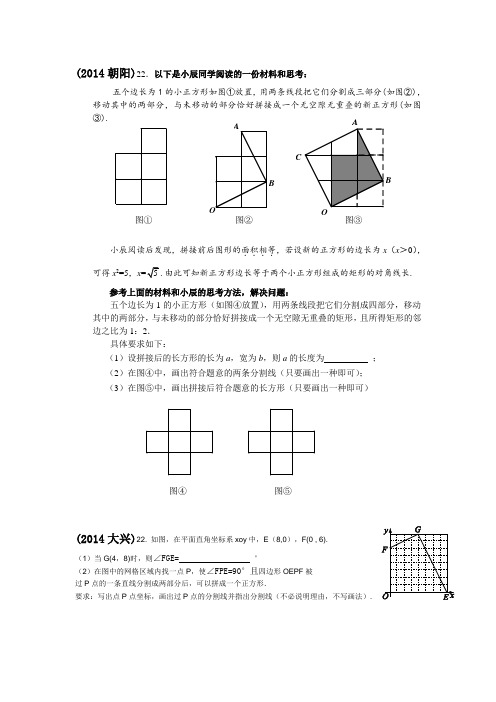
(2014朝阳)22.以下是小辰同学阅读的一份材料和思考:五个边长为1的小正方形如图①放置,用两条线段把它们分割成三部分(如图②),移动其中的两部分,与未移动的部分恰好拼接成一个无空隙无重叠的新正方形(如图③).小辰阅读后发现,拼接前后图形的面积相等....,若设新的正方形的边长为x (x >0),可得x 2=5,x =5.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长. 参考上面的材料和小辰的思考方法,解决问题:五个边长为1的小正方形(如图④放置),用两条线段把它们分割成四部分,移动其中的两部分,与未移动的部分恰好拼接成一个无空隙无重叠的矩形,且所得矩形的邻边之比为1:2.具体要求如下: (1)设拼接后的长方形的长为a ,宽为b ,则a 的长度为 ; (2)在图④中,画出符合题意的两条分割线(只要画出一种即可); (3)在图⑤中,画出拼接后符合题意的长方形(只要画出一种即可)(2014大兴)22. 如图,在平面直角坐标系xoy 中,E (8,0),F(0 , 6).(1)当G(4,8)时,则∠FGE= °(2)在图中的网格区域内找一点P ,使∠FPE=90°且四边形OEPF 被 过P 点的一条直线分割成两部分后,可以拼成一个正方形.要求:写出点P 点坐标,画出过P 点的分割线并指出分割线(不必说明理由,不写画法).图④ 图⑤O BACOBA 图① 图② 图③FE DCB A EDCB A(2014东城)22. 阅读下面材料:小炎遇到这样一个问题:如图1,点E 、F 分别在正方形ABCD 的边BC ,CD 上,∠EAF =45°,连结EF ,则EF =BE +DF ,试说明理由.F E DCBAGF EDCBA图1 图2小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB ,AD 是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE 绕着点A 逆时针旋转90°得到△ADG ,再利用全等的知识解决了这个问题(如图2).参考小炎同学思考问题的方法,解决下列问题:(1)如图3,四边形ABCD 中,AB =AD ,∠BAD =90°点E ,F 分别在边BC ,CD 上,∠EAF =45°.若∠B ,∠D 都不是直角,则当∠B 与∠D 满足_ 关系时,仍有EF =BE +DF ; (2)如图4,在△ABC 中,∠BAC =90°,AB =AC ,点D 、E 均在边BC 上,且∠DAE =45°,若BD =1, EC =2,求DE 的长.图3 图4(2014房山)22.阅读下列材料:小明遇到这样一个问题:已知:在△ABC 中,AB ,BC ,AC 三边的长分别为5、10、13 ,求△ABC 的面积.小明是这样解决问题的:如图1所示,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),从而借助网格就能计算出△ABC的面积. 他把这种解决问题的方法称为构图法.请回答:(1)图1中△ABC的面积为;参考小明解决问题的方法,完成下列问题:(2)图2是一个6×6的正方形网格(每个小正方形的边长为1) .①利用构图法在答题卡的图2中画出三边长分别为13、25、29的格点△DEF;②计算△DEF的面积为.(3)如图3,已知△PQR,以PQ,PR为边向外作正方形PQAF,PRDE,连接EF .若22,13,17PQ PR QR=== ,则六边形AQRDEF的面积为__________.FAQDEPR(2014丰台)22. 在学习三角形中线的知识时,小明了解到:三角形的任意一条中线所在的直线可以把该三角形分为面积相等的两部分。
2014北京中考英语真题

2014北京中考英语真题2014北京中考英语真题试题答案:四、单项选择ACDCB DADAD CBB五、完形填空BCDAB DBACD BC六、阅读理解A篇:ADC B篇:BCA C篇:ABD D篇:BDCB七、五选四ABCE八、任务型阅读64. Milton Hershey. 65. He grew up in Pennsylvania.66. Because he wanted to learn how to make caramels.67. Because his chocolate-flavored caramels were the best selling.68. His courage, new skills, determination and the large and easy supply of milk and sugar.九、完成句子69. Let’s 70. It’s time for 71. good for 72. too glad to73. not onlyhonest but can also keep his word.2013北京中考英语试题答案解析(仅供参考)单项选择22. A 23. B 24. C 25. B 26. A 27. D 28. B 29. C 30. D 31. B 32.C33. D 34. A 完形填空:答案:35- 39 ACCDD 40 -44 BADBC 45-46 BD 阅读理解:A篇:CAB B篇:DDA C篇:ABC D篇:56. B 57. C 58. D 59.A AEDB阅读与表达:64,Yes. 65, Put something soft to lie on on the floor. 66, A simple choice is to lay out a blanket in the sun. 67, By taking photos of us, our family members and friends. 68, What fun of camping is and how we have a great camping.完成句子:69, You’d better 70, used to 71, are looking forward to 72, as soon as I finish reading 73, won’t close until2014 年普通高等学校招生全国统一考试英语(北京卷) 答案第一节单项填空21-25:ACBAD 26-30: BADCB 31-35: CDADB第二节完形填空36-40: ABCCD 41-45: CBDDC 46-50: BDAAB 51-55:DABCA第三节56-60: ADBCB 61-65: ACBDZ 66-70: CBACD 第二节71-75: GDFBA第四部分第一节One possible version Dear Chris,How is everything going? I remember we planned to visit Yunnan in July but now because my left foot was injured, I cannot go with you as planned.I’m sorry about it. Can I suggest that we put it off until early august? I wish you could understand. I’m looking forward to hearing from you soon.Yours, Joe 第二节One possible versionThere was a problem with the parking place for bikes in our school, I noticed the entrance was small and almost blocked. So my classmates and I had a discussion and wrote a report. Then we went to meet the schoolmaster in his office and gave the report to him. He accepted our suggfestions. Soon afterwards, a second entrance was opened to the parking place. Now it is easy to park our bikes there.。
2014年北京中考数学真题

2014年北京市高级中等学校招生考试数学试卷学校___________________ 姓名___________________ 准考证号___________________ 考 生 须 知1.本试卷共6页,共五道大题、25道小题,满分120分。
考试时间120分钟。
2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上、选择题、作图题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个是符合题意的。
1.2的相反数是A.2B.2−C.12−D .122.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨,将300 000用科学记数法表示应为 A.60.310×B .5310×C .6310×D .43010×3.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是4.右图是某几何体的三视图,该几何体是A.圆锥B.圆柱 C.正三棱柱D.正三棱锥5.某篮球队12名队员的年龄如下表所示:则这12名队员年龄的众数和平均数分别是 A .18,19B .19,19C .18,19.5D .19,19.56.园林队在某公园进行绿化,中间休息了一段时间,已知绿化面积S (单位:平方米)与工作时间t (单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为 A .40平方米B .50平方米 年龄(岁)18 19 20 21 人数5 412C .80平方米D .100平方米7.如图,e O 的直径AB 垂直于弦CD ,垂足是E ,22.5A ∠=°,4OC =,CD 的长为A .B .4C .D .88.已知点A 为某封闭图形边界上一定点,动点P 从点A 出发,沿其边界顺时针匀速运动一周,设点P 运动的时间为x ,线段AP 的长为y ,表示y 与x 的函数关系的图象大致如右图所示,则该封闭图形可能是二、填空题(本题共16分,每小题4分)9.分解因式:429ax ay −=________.10.在某一时刻,测得一根高为1.8m 的竹竿的影长为3m ,同时测得一根旗杆的影长为25m ,那么这根旗杆的高度为________m.11.如图,在平面直角坐标系xOy 中,正方形OABC 的边长为2.写出一个函数(0)ky k x=≠,使它的图象与正方形OABC 有公共点,这个函数的表达式为________ 12. 在平面直角坐标系xOy 中,对于点(,)P x y ,我们把'(1,1)P y x −++叫做点P 的伴随点。
2014北京中考数学试题及答案

2014年北京中考题数学题一、 选择题(本题共32分,每题4分)1.2的相反数是( ).A .2 B .2- C .12- D .122.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300000吨,将300000用科学计数法表示应为( ).A .60.310⨯ B .5310⨯ C .6310⨯ D .43010⨯3.如图,有6张扑克牌,从中随机抽取1张,点数为偶数的概率( ).A .16 B .14 C .13D .12 4.右图是某几何体的三视图,该几何体是( ).A .圆锥B .圆柱C .正三棱柱D .正三棱锥5.某篮球队12名队员的年龄如下表所示:则这12名队员年龄的众数和平均数分别是( ). A .18,19 B .19,19 C .18,19.5 D .19,19.56.园林队公园进行绿化,中间休息了一段时间.已知绿化面积S (单位:平方米)与工作时间t (单位:小时)的函数关系的图像如图所示,则休息后园林队每小时绿化面积为( ).A .40平方米B .50平方米C .80平方米D .100平方米 7.如图,⊙O 的直径AB 垂直于弦CD ,垂足是E ,22.5A ∠=︒,4OC =,CD 的长为( ).A. B .4 C. D .8 8.已知点A 为某封闭图形边界的一定点,动点P 从点A 出发,沿其边界顺时针匀速运动一周,设点P 的时间为x ,线段AP 的长为y ,表示y 与x 的函数关系的图象大致如图所示,则该封闭图形可能是( ).二.填空题(本体共16分,每题4分)9.分解因式:24ay 9x a -=___________________.10.在某一时刻,测得一根高为1.8m 的竹竿的影长为3m ,同时测得一根旗杆的影长为25m ,那么这根旗杆的高度为_________________m .11.如图,在平面直角坐标系xOy 中,正方形O ABC 的边长为2.写出一个函数(0)ky k x=≠使它的图象与正方形O ABC 有公共点,这个函数的表达式为______________. 12.在平面直角坐标系xOy 中,对于点(,)P x y ,我们把点(1,1)P y x '-++叫做点P 伴随点,一直点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,这样依次得到点1A ,2A ,3A …,n A …,若点1A 的坐标为(3,1),则点3A 的坐标为__________,点2014A 的坐标为__________;若点1A 的坐标为(,)a b ,对于任意正整数n ,点n A 均在x 轴上方,则a ,b 应满足的条件为_____________. 三.解答题(本题共30分,每小题5分)202113.如图,点B 在线段AD 上,BC DE ∥,AB ED =,BC DB =. 求证:A E ∠=∠.14.计算:()3-3tan30----+⎪⎭⎫ ⎝⎛+15160π.15.解不等式2132121-≤-x x ,并把它的解集在数轴上表示出来.(添加图)16. 已知x-y=3,求代数式(x+1 )2 - 2x + y(y-2x) 的值.17.已知关于x 的方程mx 2-(m+2)x+2=0(m≠0).(1) 求证:方程总有两个实数根;(2) 若方程的两个实数根都是整数,求正整数m 的值.18.列方程或方程组解应用题 小马自驾私家车从A 地到B 地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动汽车所需电费27.已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.19. 如图,在 ABCD 中,AE 平分∠BAD ,交BC 于点E ,BF 平分∠ABC ,交AD 于点F ,AE 与BF 交于点P ,连接EF .PD . (1)求证:四边形ABEF 是菱形;(2)若AB=4,AD=6,∠ABC=60°,求tan ∠ADP 的值.20.根据某研究院公布的2009-2013年我国成年国民阅读调查报告的部分数据,绘制的统计图表如下:根据以上信息解答下列问题:(1)直接写出扇形统计图中m的值;(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为_______本;(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为_____本.21.如图,AB是⊙O的直径,C是弧AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE 的延长线交切线DB于点F,AF交⊙O于点H,连结BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.22.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.E图1 图2过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(图2).请回答:∠ACE的度数为___________,AC的长为_____________.参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC 与BD交于点E,AE=2,BE=2ED,求BC的长.五.解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,-2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.24.在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.(1)依题意补全图1;(2)若∠PAB=20°,求∠ADF的度数;(3)如图2,若45°<∠PAB < 90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.25. 对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y ,都满足-M≤y≤M ,则称这个函数是有界函数.在所有满足条件的M 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(1)分别判断函数y=x1(x > 0)和y= x + 1(-4 < x ≤ 2)是不是有界函数?若是有界函数,求边界值;(2)若函数y=-x+1(a ≤ x ≤ b ,b > a )的边界值是2,且这个函数的最大值也是2,求b 的取值范围;(3)将函数2(1,0)y x x m m =-≤≤≥的图象向下平移m 个单位,得到的函数的边界值是t ,当m 在什么范围时,满足143≤≤t ?2014年北京高级中等学校招生考试数学答案一.二.三. 解答题(本题共30分,每小题5分):13.(本小题满分5分)证明:∵ BC ∥DE ∴∠ABC = ∠EDB;在△ABC 和△EDB中:AB = ED ;∠ABC = ∠ EDB ; BC = DB ;∴△ABC≌ △EDB ;∴ ∠A = ∠E14.(本小题满分5分)解:原式 ===15.(本小题满分5分) 解: 移项得:;合并同类项得:系数化为1: x ≥16.(本小题满分5分)解:化简代数可得: 原式 = ==原式 = = 417.(本小题满分5分)(1)证明:可知 △ = == = = ≥0∴ 方程总有两个实数根。
(高清版)2014年北京市中考数学试卷

2011
4.35
2012
4.56
此
2013
4.78
根据以上信息解答下列问题:
(1)直接写出扇形统计图中 m 的值;
(2)从 2009 到 2013 年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估
卷
算 2014 年成年国民年人均阅读图书的数量约为
本;
(3)2013 年某小区倾向图书阅读的成年国民有 990 人,若该小区 2014 年与 2013 年成
数学试卷 第 6页(共 20页)
24.(本小题满分 7 分) 在正方形 ABCD 外侧作直线 AP ,点 B 关于直线 AP 的对称点为 E ,连接 BE, DE ,其 中 DE 交直线 AP 于点 F .
25.(本小题满分 8 分) 对某一个函数给出 如下定义:若存在实数 M>0 ,对于任意的函数值 y ,都满足 M≤y≤M ,则称这个函数是有界函数.在所有满足条件的 M 中,其最小值称为这
题
无
22.(本小题满分 5 分) 阅读下面材料:
效
数学试卷 第 5页(共 20页)
23.(本小题满分 7 分)
在平面直角坐标系 xOy 中,抛物线 y 2x2 mx n 经过点 A(0,2) , B(3, 4) .
(1)求抛物线的表达式及对称轴; (2)设点 B 关于原点的对称点为 C ,点 D 是抛物线对称轴上一动点,记抛物线在 A , B 之间的部分为图象 G (包含 A , B 两点).若直线 CD 与图象 G 有公共点,结合函 数图象,求点 D 纵坐标 t 的取值范围.
25 m ,那么这根旗杆的高度为
m.
11. 如 图 , 在 平 面 直 角 坐 标 系 xOy 中 , 正 方 形 OABC 的 边 长 为 2 . 写 出 一 个 函 数
2014年北京市高级中等学校招生考试
2014年北京市高级中等学校招生考试数学试题(含答案全解全析)第Ⅰ卷(选择题,共32分)一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个..是符合题意的.1.2的相反数是( )A.2B.-2C.-12D.122.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为( )A.0.3×106B.3×105C.3×106D.30×1043.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是( )A.16B.14C.13D.124.如图是某几何体的三视图,该几何体是( )A.圆锥B.圆柱C.正三棱柱D.正三棱锥5.某篮球队12名队员的年龄如下表所示:年龄(岁)18192021人数5412则这12名队员年龄的众数和平均数分别是( )A.18,19B.19,19C.18,19.5D.19,19.56.园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为( )A.40平方米B.50平方米C.80平方米D.100平方米7.如图,☉O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为( )A.2√2B.4C.4√2D.88.已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y,表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是( )第Ⅱ卷(非选择题,共88分)二、填空题(本题共16分,每小题4分)9.分解因式:ax4-9ay2= .10.在某一时刻,测得一根高为1.8 m的竹竿的影长为3 m,同时测得一根旗杆的影长为25 m,那么这根旗杆的高度为m.(k≠0),使它11.如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数y=kk的图象与正方形OABC有公共点,这个函数的表达式为.12.在平面直角坐标系xOy中,对于点P(x,y),我们把点P'(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,A n,….若点A1的坐标为(3,1),则点A3的坐标为,点A2 014的坐标为;若点A1的坐标为(a,b),对于任意的正整数n,点A n均在x轴上方,则a,b应满足的条件为.三、解答题(本题共30分,每小题5分)13.如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E.)-1-3tan 30°+|-√3|.14.计算:(6-π)0+(-1515.解不等式12x-1≤23x-12,并把它的解集在数轴上表示出来.16.已知x-y=√3,求代数式(x+1)2-2x+y(y-2x)的值.17.已知关于x的方程mx2-(m+2)x+2=0(m≠0).(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数m的值.18.列方程或方程组解应用题:小马自驾私家车从A地到B地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动汽车所需电费27元.已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.四、解答题(本题共20分,每小题5分)19.如图,在▱ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连结EF,PD.(1)求证:四边形ABEF是菱形;(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.20.根据某研究院公布的2009—2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:2013年成年国民倾向的阅读方式人数分布统计图2009—2013年成年国民年人均阅读图书数量统计表年份年人均阅读图书数量(本)2009 3.882010 4.122011 4.352012 4.562013 4.78根据以上信息解答下列问题:(1)直接写出扇形统计图中m的值;(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为本;(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为本.⏜的中点,☉O的切线BD交AC的延长线于点D,E是OB的中21.如图,AB是☉O的直径,C是kk点,CE的延长线交切线DB于点F,AF交☉O于点H,连结BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.22.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC 上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2) .请回答:∠ACE的度数为,AC的长为.参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.图3五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,-2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图象,求点D纵坐标t的取值范围.24.在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连结BE,DE,其中DE交直线AP于点F.(1)依题意补全图1;(2)若∠PAB=20°,求∠ADF的度数;(3)如图2,若45°<∠PAB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.25.对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数.在所有满足条件的M 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(1)分别判断函数y=1k (x>0)和y=x+1(-4<x≤2)是不是有界函数?若是有界函数,求其边界值;(2)若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b 的取值范围;(3)将函数y=x 2(-1≤x≤m,m≥0)的图象向下平移m 个单位,得到的函数的边界值是t,当m 在什么范围时,满足34≤t≤1?答案全解全析:一、选择题1.B ∵2+(-2)=0,∴2的相反数为-2.故选B.2.B 300 000=3×105.故选B.3.D 6张扑克牌中,点数为偶数的有3张,所以抽到点数为偶数的概率是36=12.故选D.4.C 选项A 、B 中的几何体,三视图中一定有一个圆,与所给的三视图不符,排除A,B;选项D 中的几何体的三视图是三个三角形,与所给的三视图也不相符,排除D.只有选项C 中的几何体与所给的三视图相符,故选C.5.A 年龄为18岁的队员最多,故众数为18;12名队员年龄的平均数为18×5+19×4+20×1+21×212=19.故选A.6.B 休息的过程中是不进行绿化工作的,即绿化面积S 不变化,由图象可知第1~2小时为园林队休息时间,则休息后园林队的绿化面积为160-60=100(平方米),所用的时间为4-2=2(小时),所以休息后园林队每小时绿化面积为100÷2=50(平方米).故选B. 7.C∵CO=AO,∴∠COE=2∠A=45°.∵OC=4,∴CE=OC·sin∠COE=4×√22=2√2.∵AB⊥CD,∴CD=2CE=4√2.故选C.8.A 由图象可知,AP 先由短变长,然后略微变短再变长,最后AP 由长变短.选项A 与题目要求相符;选项B 是先由短变长,然后略微变短再变长,接着再略微变短再变长,最后由长变短,与题目要求不符;选项C 是先由短变长,到达第一个顶点后继续变长,到达第二个顶点后开始变短,到达第三个顶点后继续变短,与题目要求不符;选项D 是先由短变长,在经过点A 的直径与圆的另一个交点处时最长,然后开始变短,与题目要求不符.故选A.评析 解决本题的关键是根据图形特征分析函数图象随自变量变化的趋势,结合图形性质通过定性分析来确定选项.属中档题. 二、填空题9.答案 a(x 2+3y)(x 2-3y)解析 ax 4-9ay 2=a(x 4-9y 2)=a(x 2+3y)(x 2-3y).10.答案 15解析 设旗杆的高度为x m,则1.83=k25,解得x=15.即旗杆的高度为15 m.11.答案 y=4k (答案不唯一,满足0<k≤4即可)解析 要使反比例函数的图象与正方形有交点,则至少要经过点B,且k>0,而点B 的坐标为(2,2),所以k 的最大值为4,即0<k≤4. 12.答案 (-3,1);(0,4);-1<a<1,0<b<2解析 由题意可知,点A 2的坐标为(0,4),点A 3的坐标为(-3,1),点A 4的坐标为(0,-2),点A 5的坐标为(3,1),…,所以每四个点坐标为一个循环.∵2 014÷4=503……2,∴点A 2 014的坐标与点A 2的坐标一致,为(0,4).因为每四个点坐标为一个循环,所以要求a,b 应满足的条件,只需要知道前4个点的坐标即可.∵点A 1的坐标为(a,b),∴点A 2、A 3、A 4的坐标依次为(-b+1,a+1)、(-a,-b+2)、(b-1,-a+1).∵点A n 均在x 轴上方,∴{k >0,k +1>0,-k +2>0,-k +1>0,∴-1<a<1,0<b<2.评析 解决本题的关键是读懂题目要求,并按照题目要求正确操作.尤其是“在x 轴上方”即为“纵坐标>0”.属中档题. 三、解答题13.证明 ∵BC∥DE, ∴∠ABC=∠D.在△ABC 和△EDB 中,{kk =kk ,∠kkk =∠k ,kk =kk ,∴△ABC≌△EDB. ∴∠A=∠E.14.解析 原式=1-5-3×√33+√3=-4.15.解析 去分母,得3x-6≤4x -3, 移项,得3x-4x≤6-3. 合并同类项,得-x≤3, 系数化为1,得x≥-3.不等式的解集在数轴上表示如下:16.解析 (x+1)2-2x+y(y-2x) =x 2+2x+1-2x+y 2-2xy =x 2-2xy+y 2+1. ∵x -y=√3,∴原式=(x-y)2+1=4.17.解析 (1)证明:∵m≠0,∴mx 2-(m+2)x+2=0是关于x 的一元二次方程.∴Δ=[-(m+2)]2-4×2m=(m-2)2.∵(m -2)2≥0,∴方程总有两个实数根. (2)由求根公式,得x=(k +2)±(k -2)2k.∴x 1=1,x 2=2k.∵方程的两个实数根都是整数,且m 为正整数, ∴m=1或2.18.解析 设新购买的纯电动汽车每行驶1千米所需的电费为x 元. 由题意,得27k =108k +0.54.解得x=0.18.经检验,x=0.18是原方程的解,且符合题意.答:新购买的纯电动汽车每行驶1千米所需的电费为0.18元. 四、解答题19.解析 (1)证明:∵BF 是∠ABC 的平分线, ∴∠ABF=∠EBF. ∵AD∥BC,∴∠AFB=∠EBF. ∴∠AFB=∠ABF. ∴AB=AF. 同理,AB=BE.∴AF=BE.又∵AF∥BE,∴四边形ABEF 是平行四边形. ∵AB=AF,∴四边形ABEF 是菱形.(2)过点P 作PG⊥AD 于点G,如图. ∵四边形ABEF 是菱形,∠ABC=60°, ∴△ABE 是等边三角形. ∵AB=4, ∴AE=AB=4, ∴AP=12AE=2.在Rt△AGP 中,可求得∠PAG=60°. ∴AG=AP·cos 60°=1, GP=AP·sin 60°=√3. ∵AD=6, ∴DG=5, ∴tan∠ADP=kk kk =√35. 20.解析 (1)66.0. (2)5.00±0.02.(3)7 500±30.(990÷66.0%×5=7 500) 21.解析 (1)证明:连结BC. ∵AB 是☉O 的直径, ∴∠ACB=90°.∵C 是kk⏜的中点, ∴kk ⏜=kk ⏜. ∴AC=BC.∴∠CAB=∠CBA=45°. ∵BD 是☉O 的切线, ∴∠ABD=90°.可得∠CBD=∠D=45°. ∴BC=CD. ∴AC=CD. (2)连结OC. ∵OA=OC,∴∠OCA=∠CAB=45°. ∴∠COE=90°. ∵E 是OB 的中点, ∴OE=BE.∵∠CEO=∠FEB,∴Rt△COE≌Rt△FBE.∴BF=OC. ∵OB=2,∴BF=2.由勾股定理,得AF=2√5. ∵∠ABF=∠AHB=90°, ∴BH=kk ·kk kk=45√5. 22.解析 ∠ACE 的度数为75°,AC 的长为3.解决问题:过点D 作DF∥AB 交AC 于点F,如图.∴∠DFE=∠BAC=90°,又∠AEB=∠FED,∴△ABE∽△FDE. ∴kk kk =kk kk =kkkk .∵BE=2ED,AE=2,∴FE=1,∴AF=3. ∵∠CAD=30°,∴FD=√3,AD=2√3. ∵kkkk =2,∴AB=2√3.∵∠ADC=75°,∠CAD=30°,∴∠ACD=75°, ∴AC=AD=2√3.在Rt△ABC 中,由勾股定理可得BC=2√6.评析 本题考查了相似三角形的判定与性质、三角函数等知识.解决本题的关键是读懂题目中给出的操作方法,由平行想到相似三角形.属中档题.五、解答题23.解析 (1)∵点A,B 在抛物线y=2x 2+mx+n 上,∴{-2=k ,4=2×32+3m +n.解得{k =-4,k =-2.∴抛物线的表达式为y=2x 2-4x-2.∴抛物线的对称轴为x=1.(2)由题意可知,点C 的坐标为(-3,-4).设直线BC 的表达式为y=kx+b(k≠0).∴{4=3k +k ,-4=-3k +k ,解得{k =43,k =0.∴直线BC 的表达式为y=43x.∴当x=1时,y=43.结合图象可知,点A 在直线BC 的下方,且抛物线的顶点坐标为(1,-4),∴-4≤t≤43.24.解析 (1)补全图形,如图所示.(2)连结AE,如图.∵点E 与点B 关于直线AP 对称,∴AE=AB,∠EAP=∠BAP=20°.∵AB=AD,∴AE=AD,∴∠AED=∠ADF.又∠BAD=90°,∴2∠ADF+40°+90°=180°.∴∠ADF=25°.(3)AB,FE,FD 满足的数量关系为FE 2+FD 2=2AB 2.证明:连结AE,BF,BD,设BF 交AD 于点G,如图.∵点E 与点B 关于直线AP 对称,∴AE=AB,FE=FB.可证得∠FEA=∠FBA.∵AB=AD,∴AE=AD.∴∠ADE=∠AED.∴∠ADE=∠ABF.又∵∠DGF=∠AGB,∴∠DFB=∠BAD=90°.∴FB 2+FD 2=BD 2.∵BD 2=2AB 2,∴FE 2+FD 2=2AB 2.25.解析 (1)y=1k (x>0)不是有界函数;y=x+1(-4<x≤2)是有界函数,边界值是3.(2)对于函数y=-x+1(a≤x≤b,b>a),∵y 随x 的增大而减小,∴y 的最大值是-a+1,y 的最小值是-b+1.∵函数的最大值是2,∴a=-1.又∵函数的边界值是2,∴-b+1≥-2,∴b≤3.∴-1<b≤3.(3)由题意,函数平移后的表达式为y=x 2-m(-1≤x≤m,m≥0).当x=-1时,y=1-m;当x=0时,y=-m;当x=m 时,y=m 2-m. 根据二次函数的对称性,当0≤m≤1时,1-m≥m 2-m;当m>1时,1-m<m 2-m.①当0≤m≤12时,1-m≥m,由题意,边界值t=1-m.当34≤t≤1时,0≤m≤14.∴0≤m≤14.②当12<m≤1时,1-m<m.由题意,边界值t=m.当34≤t≤1时,34≤m≤1. ∴34≤m≤1. ③当m>1时,由题意,边界值t≥m. ∴不存在满足34≤t≤1的m 值.综上所述,当0≤m≤14或34≤m≤1时,满足34≤t≤1.。
(试题)北京市2014年中考数学试题含答案(word版)范文
2014年北京市高级中等学校招生考试数学试卷学校姓名准考证号1.本试卷共6页,共五道大题,25道小题,满分120分.考试时间120分钟..在试卷和答题卡上准确填写学校名称、姓名和准考证号..试题答案一律填涂或书写在答题卡上,在试卷上作答无效..在答题卡上,选择题、作图题用铅笔作答,其他试题用黑色字迹签字笔作答..考试结束,将本试卷、答题卡和草稿纸一并交回.下面各题均有四个选项,其中只有一个..是符合题意的. 1.2的相反数是A .2B .2-C .12-D .122.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为A .60.310⨯B .5310⨯C .6310⨯D .43010⨯3.如图,有6张扑克处于,从中随机抽取一张,点数为偶数的概率是A .16B .14C .13D .124.右图是几何体的三视图,该几何体是A.圆锥B .圆柱C .正三棱柱D .正三棱锥5.某篮球队12名队员的年龄如下表所示:名队员年龄的众数和平均数分别是A .18,19B .19,19C .18,19.5D .19,19.56.园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(单位:平方米)与工作时间t (单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为 A .40平方米 B .50平方米 C .80平方米D .100平方米OE DCBA7.如图.O e 的直径AB 垂直于弦CD ,垂足是E ,22.5A ∠=︒,4OC =,CD 的长为A .B .4C .D .88.已知点A 为某封闭图形边界上一定点,动点P 从点A 出发,沿其边界顺时针匀速运动一周.设点P 运动的时间为x ,线段AP的长为y .表示y 与x 的函数关系的图象大致如右图所示,则该封闭图形可能是AADCBAA二、填空题(本题共16分,每小题4分) 9.分解因式:429______________ax ay -=.10.在某一时刻,测得一根高为1.8m 的竹竿的影长为3m ,同时测得一根旗杆的影长为25m ,那么这根旗杆的高度为 m .11.如图,在平面直角坐标系xOy 中,正方形OABC 的边长为2.写出一个函数(0)ky k x=≠,使它的图象与正方形OABC 有公共点,这个函数的表达式为 .12.在平面直角坐标系xOy 中,对于点()P x y ,,我们把点(11)P y x '-++,叫做点P 的伴随点,已知点1A 的伴随点为2A ,点2A 的伴随点为3A ,点3A 的伴随点为4A ,…,这样依次得到点1A ,2A ,3A ,…,n A ,….若点1A 的坐标为(3,1),则点3A 的坐标为 ,点2014A 的坐标为 ;若点1A 的坐标为(a ,b ),对于任意的正整数n ,点n A 均在x 轴上方,则a ,b 应满足的条件为 .三、解答题(本题共30分,每小题5分)13.如图,点B 在线段AD 上,BC DE ∥,AB ED =,BC DB =. 求证:A E ∠=∠.ECBAD生物达人1214.计算:11(6π)()3tan30|5--︒+--︒+.15.解不等式1211232x x --≤,并把它的解集在数轴上表示出来.16.已知x y -2(1)2(2)x x y y x +-+-的值. 17.已知关于x 的方程2(2)20(0)mx m x m -++=≠.(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数m 的值.18.列方程或方程组解应用题:小马自驾私家车从A 地到B 地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元,已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.四、解答题(本题共20分,每小题5分)19.如图,在ABCD Y 中,AE 平分BAD ∠,交BC 于点E ,BF 平分ABC ∠,交AD 于点F ,AE 与BF 交于点P ,连接EF ,PD . (1)求证:四边形ABEF 是菱形;(2)若4AB =,6AD =,60ABC ∠=︒,求tan ADP ∠的值.20.根据某研究院公布的2009~2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:下载并打印阅读1.0%手机阅读15.6%电子阅读器阅读2.4%网络在线阅读15.0%图书阅读m %根据以上信息解答下列问题: (1)直接写出扇形统计图中m 的值;(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为 本;(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为 本.2011 2013 FPECBAD图3ABCDE21.如图,AB 是O e 的直径,C 是»AB 的中点,O e 的切线BD 交AC 的延长线于点D ,E是OB 的中点,CE 的延长线交切线BD 于点F ,AF 交O e 于点H ,连接BH . (1)求证:AC CD =; (2)若2OB =,求BH 的长.22.阅读下面材料:小腾遇到这样一个问题:如图1,在ABC △中,点D 在线段BC 上,75BAD ∠=︒,30CAD ∠=︒,2AD =,2BD DC =,求AC 的长.E图2图1AB CD D CB A小腾发现,过点C 作CE AB ∥,交AD 的延长线于点E ,通过构造ACE △,经过推理和计算能够使问题得到解决(如图2).请回答:ACE ∠的度数为 ,AC 的长为 . 参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD 中,90BAC ∠=︒,30CAD ∠=︒,75ADC ∠=︒,AC 与BD 交于点E ,2AE =,2BE ED =,求BC 的长.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)生物达人1223.在平面直角坐标系xOy 中,抛物线22y x mx n =++经过点A (0,2-),B (3,4).(1)求抛物线的表达式及对称轴;(2)设点B 关于原点的对称点为C ,点D 是抛物线对称轴上一动点,记抛物线在A ,B 之间的部分为图象G (包含A ,B 两点).若直线CD 与图象G 有公共点,结合函数图像,求点D 纵坐标t 的取值范围.24.在正方形ABCD 外侧作直线AP ,点B 关于直线AP 的对称点为E ,连接BE DE ,,其中DE 交直线AP 于点F . (1)依题意补全图1;(2)若20PAB ∠=︒,求ADF ∠的度数;(3)如图2,若4590PAB ︒<∠<︒,用等式表示线段AB FE FD ,,之间的数量关系,并证明.图 1PD CBA A BCDP图 225.对某一个函数给出如下定义:若存在实数0M >,对于任意的函数值y ,都满足M y M -≤≤,则称这个函数是有界函数,在所有满足条件的M 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(1)分别判断函数1y x=()0x >和()142y x x =+-<≤是不是有界函数?若是有界函数,求其边界值;(2)若函数1y x =-+()a x b b a ≤≤>,的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数()210y x x m m =-≤≤≥,的图象向下平移m 个单位,得到的函数的边界值是t ,当m 在什么范围时,满足314t ≤≤?生物达人12生物达人12生物达人12。
2014年北京中考数学真题卷
14年北京中考数学真题卷一、选择题(本大题共8小题,每小题4分,满分32分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.2的相反数是A.2 B.-2 C.12D.122.据报道,某小区居民李先生改进用水设备,在十年内帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为A.0.3×106B.3×105C.3×106D.30×1043.如图,有6张扑克牌,从中随机抽取一张,点数为偶数的概率是A.16B.14C.13D.124.下图是某几何体的三视图,该几何体是A.圆锥B.圆柱C.正三棱柱D.正三棱锥B A第4题第6题第7题5.某篮球队12则这12A.18,19 B.19,19 C.18,19.5 D.19,19.56.园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(单位:平方米)与工作时间t(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为A.40平方米B.50平方米C.80平方米D.100平方米7.如图,⊙O的直径AB垂直于弦CD,垂足是E,∠A=22.5°,OC=4,CD的长为A.B.4C.D.88.已知点A为某封闭图形边界上一定点,动点P从点A出发,沿其边界顺时针匀速运动一周.设点P运动的时间为x,线段AP的长为y.表示y与x的函数关系的图象大致如图所示,则该封闭图形可能是A AAAA.B.C.D.二、填空题(本大题共4小题,每小题4分,满分16分.)9.分解因式:ax4-9ay2=__________.10.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一根旗杆的影长为25m,那么这根旗杆的高度为__________m.11.如图,在平面直角坐标系xOy中,正方形OABC的边长为2.写出一个函数kyx=(k≠0),使它的图象与正方形OABC有公共点,这个函数的表达式为__________.12.在平面直角坐标系xOy中,对于点P(x,y),我们把点P′(-y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,A n,….若点A1的坐标为(3,1),则点A3的坐标为__________,点A2014的坐标为__________;若点A1的坐标为(a,b),对于任意的正整数n,点A n均在x轴上方,则a,b 应满足的条件为__________.三、解答题(本大题共6小题,每小题5分,满分30分,解答应写出文字说明、证明过程或演算步骤)13.如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.求证:∠A=∠E.EB14.计算:(6-π)0+115-⎛⎫- ⎪⎝⎭-3tan30°+.15.解不等式1211232≤--x x,并把它的解集在数轴上表示出来.16.已知x-y(x+1)2-2x+y(y-2x)的值.17.已知关于x的方程mx2-(m+2)x+2=0(m≠0).(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数m的值.18.列方程或方程组解应用题:小马自驾私家车从A地到B地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元.已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.四、解答题(本题共20分,每小题5分)19.如图,在□ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.(1)求证:四边形ABEF是菱形;(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值.D AB20.根据某研究院公布的2009-2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:根据以上信息解答下列问题:(1)直接写出扇形统计图中m的值;(2)从2009 到2013 年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014 年成年国民年人均阅读图书的数量约为__________本;(3)2013 年某小区倾向图书阅读的成年国民有990 人,若该小区2014 年与2013 年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为__________本.21.如图,AB是⊙O的直径,C是AB的中点,⊙O的切线BD交AC的延长线于点D,E是OB的中点,CE的延长线交切线DB于点F,AF交⊙O于点H,连接BH.(1)求证:AC=CD;(2)若OB=2,求BH的长.D A B22.阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.BADBEA图1 图2小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图2).请回答:∠ACE的度数为__________,AC的长为__________.参考小腾思考问题的方法,解决问题:如图3,在四边形ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.BDA图3五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系xOy中,抛物线y=2x2+mx+n经过点A(0,-2),B(3,4).(1)求抛物线的表达式及对称轴;(2)设点B关于原点的对称点为C,点D是抛物线对称轴上一动点,记抛物线在A,B之间的部分为图象G(包含A,B两点).若直线CD与图象G有公共点,结合函数图像,求点D纵坐标t的取值范围.24.在正方形ABCD外侧作直线AP,点B关于直线交直线AP于点F.(1)依题意补全图1;(2)若∠P AB=20°,求∠ADF的度数;(3)如图2,若45°<∠P AB<90°,用等式表示线段AB,FE,FD之间的数量关系,并证明.P图1 图225.对某一个函数给出如下定义:若存在实数M>0,对于任意的函数值y,都满足-M≤y≤M,则称这个函数是有界函数.在所有满足条件的M中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.(1)分别判断函数1yx(x>0)和y=x+1(-4<x≤2)是不是有界函数?若是有界函数,求其边界值;(2)若函数y=-x+1(a≤x≤b,b>a)的边界值是2,且这个函数的最大值也是2,求b的取值范围;(3)将函数y=x2(-1≤x≤m,m≥0)的图象向下平移m个单位,得到的函数的边界值是t,当m在什么范围时,满足34≤t≤1?。
2014年北京市中考数学试卷
2014年市中考数学试卷一、选择题(本题共32分,每小题4分)下面各题均有四个选项,其中只有一个.是符合题意的.1.2的相反数是()A.2B.−2C.−12D.122.据报道,某小区居民先生改进用水设备,在十年帮助他居住小区的居民累计节水300 000吨.将300 000用科学记数法表示应为()A.0.3×106B.3×105C.3×106D.30×1043.如图,有6扑克牌,从中随机抽取一,点数为偶数的概率是()A.16B.14C.13D.124.如图是几何体的三视图,该几何体是()A.圆锥B.圆柱C.正三棱柱D.正三棱锥5.某篮球队12名队员的年龄如表:A.18,19B.19,19C.18,19.5D.19,19.56.园林队在某公园进行绿化,中间休息了一段时间.已知绿化面积S(单位:平方米)与工作时间S(单位:小时)的函数关系的图象如图,则休息后园林队每小时绿化面积为()A.40平方米B.50平方米C.80平方米D.100平方米7.如图,⊙S 的直径SS 垂直于弦SS ,垂足为S ,∠S =22.5∘,SS =4,SS 的长为( )A.2√2B.4C.4√2D.88.已知点S 为某封闭图形边界上一定点,动点S 从点S 出发,沿其边界顺时针匀速运动一周.设点S 运动的时间为S ,线段SS 的长为S .表示S 与S 的函数关系的图象大致如图,则该封闭图形可能是( )A.B. C.D.二、填空题(本题共16分,每小题4分)9.分解因式:SS 4−9SS 2=________.10.在某一时刻,测得一根高为1.8S 的竹竿的影长为3S ,同时测得一根旗杆的影长为25S ,那么这根旗杆的高度为________S .11.如图,在平面直角坐标系SSS 中,正方形SSSS 的边长为2.写出一个函数S =S S (S ≠0),使它的图象与正方形SSSS 有公共点,这个函数的表达式为________.12.在平面直角坐标系SSS 中,对于点S (S , S ),我们把点S′(−S +1, S +1)叫做点S 伴随点.已知点S 1的伴随点为S 2,点S 2的伴随点为S 3,点S 3的伴随点为S 4,…,这样依次得到点S 1,S 2,S 3,…,S S ,….若点S 1的坐标为(3, 1),则点S 3的坐标为________,点S2014的坐标为________;若点S1的坐标为(S, S),对于任意的正整数S,点S S均在S轴上方,则S,S应满足的条件为________.三、解答题(本题共30分,每小题5分)13.如图,点S在线段SS上,SS // SS,SS=SS,SS=SS.求证:∠S=∠S.14.计算:(6−S)0+(−15)−1−3tan30∘+|−√3|15.解不等式12S−1≤23S−12,并把它的解集在数轴上表示出来.16.已知S−S=√3,求代数式(S+1)2−2S+S(S−2S)的值.17.已知关于S的方程SS2−(S+2)S+2=0(S≠0).(1)求证:方程总有两个实数根;(2)若方程的两个实数根都是整数,求正整数S的值.18.列方程或方程组解应用题:小马自驾私家车从S地到S地,驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元,已知每行驶1千米,原来的燃油汽车所需的油费比新购买的纯电动汽车所需的电费多0.54元,求新购买的纯电动汽车每行驶1千米所需的电费.四、解答题(本题共20分,每小题5分)19.如图,在SSSS中,SS平分∠SSS,交SS于点S,SS平分∠SSS,交SS 于点S,SS与SS交于点S,连接SS,SS.(1)求证:四边形SSSS是菱形;(2)若SS=4,SS=6,∠SSS=60∘,求tan∠SSS的值.20.根据某研究院公布的2009∼2013年我国成年国民阅读调查报告的部分相关数据,绘制的统计图表如下:(1)直接写出扇形统计图中S的值;(2)从2009到2013年,成年国民年人均阅读图书的数量每年增长的幅度近似相等,估算2014年成年国民年人均阅读图书的数量约为________本;(3)2013年某小区倾向图书阅读的成年国民有990人,若该小区2014年与2013年成年国民的人数基本持平,估算2014年该小区成年国民阅读图书的总数量约为________本.^的中点,⊙S的切线SS交SS的延长线于点S,21.如图,SS是⊙S的直径,S是SSS是SS的中点,SS的延长线交切线SS于点S,SS交⊙S于点S,连接SS.(1)求证:SS=SS;(2)若SS=2,求SS的长.22.阅读下面材料:小腾遇到这样一个问题:如图1,在△SSS中,点S在线段SS上,∠SSS=75∘,∠SSS=30∘,SS=2,SS=2SS,求SS的长.小腾发现,过点S作SS // SS,交SS的延长线于点S,通过构造△SSS,经过推理和计算能够使问题得到解决(如图2).请回答:∠SSS的度数为________,SS的长为________.参考小腾思考问题的方法,解决问题:如图3,在四边形SSSS中,∠SSS=90∘,∠SSS=30∘,∠SSS=75∘,SS与SS交于点S,SS=2,SS=2SS,求SS的长.五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.在平面直角坐标系SSS中,抛物线S=2S2+SS+S经过点S(0, −2),S(3, 4).(1)求抛物线的表达式及对称轴;(2)设点S关于原点的对称点为S,点S是抛物线对称轴上一动点,且点S纵坐标为S,记抛物线在S,S之间的部分为图象S(包含S,S两点).若直线SS与图象S有公共点,结合函数图象,求点S纵坐标S的取值围.24.在正方形SSSS外侧作直线SS,点S关于直线SS的对称点为S,连接SS,SS,其中SS交直线SS于点S.(1)依题意补全图1;(2)若∠SSS=20∘,求∠SSS的度数;(3)如图2,若45∘<∠SSS<90∘,用等式表示线段SS,SS,SS之间的数量关系,并证明.25.对某一个函数给出如下定义:若存在实数S>0,对于任意的函数值S,都满足−S≤S≤S,则称这个函数是有界函数,在所有满足条件的S中,其最小值称为这个函数的边界值.例如,如图中的函数是有界函数,其边界值是1.(1)分别判断函数S=1S(S>0)和S=S+1(−4≤S≤2)是不是有界函数?若是有界函数,求其边界值;(2)若函数S=−S+1(S≤S≤S, S>S)的边界值是2,且这个函数的最大值也是2,求S的取值围;(3)将函数S=S2(−1≤S≤S, S≥0)的图象向下平移S个单位,得到的函数的边界值是S,当S在什么围时,满足34≤S≤1?答案1. 【答案】B【解析】根据相反数的概念作答即可.【解答】解:根据相反数的定义可知:2的相反数是−2.故选:S.2. 【答案】B【解析】科学记数法的表示形式为S×10S的形式,其中1≤|S|<10,S为整数.确定S的值时,要看把原数变成S时,小数点移动了多少位,S的绝对值与小数点移动的位数相同.当原数绝对值>1时,S是正数;当原数的绝对值<1时,S是负数.【解答】解:300 000=3×105,故选:S.3. 【答案】D【解析】由有6扑克牌,从中随机抽取一,点数为偶数的有3种情况,直接利用概率公式求解即可求得答案.【解答】解:∵有6扑克牌,从中随机抽取一,点数为偶数的有3种情况,∴从中随机抽取一,点数为偶数的概率是:36=12.故选:S.4. 【答案】C【解析】如图:该几何体的俯视图与左视图均为矩形,主视图为三角形,易得出该几何体的形状.【解答】解:该几何体的左视图为矩形,俯视图亦为矩形,主视图是一个三角形,则可得出该几何体为三棱柱.故选:S.5. 【答案】A【解析】根据众数及平均数的概念求解.【解答】解:年龄为18岁的队员人数最多,众数是18;平均数=18×5+19×4+20×1+21×212=19.故选:S.6. 【答案】B【解析】根据图象可得,休息后园林队2小时绿化面积为160−60=100平方米,然后可得绿化速度.【解答】解:根据图象可得,休息后园林队2小时绿化面积为160−60=100平方米,每小时绿化面积为100÷2=50(平方米).故选:S.7. 【答案】C【解析】根据圆周角定理得∠SSS=2∠S=45∘,由于⊙S的直径SS垂直于弦SS,根据垂径定理得SS=SS,且可判断△SSS为等腰直角三角形,所以SS=√22SS=2√2,然后利用SS=2SS进行计算.【解答】解:∵∠S=22.5∘,∴∠SSS=2∠S=45∘,∵⊙S的直径SS垂直于弦SS,∴SS=SS,△SSS为等腰直角三角形,∴SS=√22SS=2√2,∴SS=2SS=4√2.故选:S.8. 【答案】A【解析】根据等边三角形,菱形,正方形,圆的性质,分析得到S随S的增大的变化关系,然后选择答案即可.【解答】解:S、等边三角形,点S在开始与结束的两边上直线变化,在点S的对边上时,设等边三角形的边长为S,则S=(√32S)(32S−S)S<S<2S),符合题干图象;S、菱形,点S在开始与结束的两边上直线变化,在另两边上时,都是先变速减小,再变速增加,题干图象不符合;S、正方形,点S在开始与结束的两边上直线变化,在另两边上,先变速增加至∠S的对角顶点,再变速减小至另一顶点,题干图象不符合;S、圆,SS的长度,先变速增加至SS为直径,然后再变速减小至点S回到点S,题干图象不符合.故选:S.9. 【答案】S(S2−3S)(S2+3S)【解析】首先提取公因式S,进而利用平方差公式进行分解即可.【解答】解:SS4−9SS2=S(S4−9S2)=S(S2−3S)(S2+3S).故答案为:S(S2−3S)(S2+3S).10. 【答案】15【解析】根据同时同地物高与影长成正比列式计算即可得解.【解答】解:设旗杆高度为S米,由题意得,1.83=S25,解得S=15.故答案为:15.11. 【答案】S=1S ,S=SS(0<S≤4)(答案不唯一)【解析】先根据正方形的性质得到S点坐标为(2, 2),然后根据反比例函数图象上点的坐标特征求出过S点的反比例函数解析式即可.【解答】解:∵正方形SSSS的边长为2,∴S点坐标为(2, 2),当函数S=SS (S≠0)过S点时,S=2×2=4,∴满足条件的一个反比例函数解析式为S=1S.故答案为:S=1S ,S=SS(0<S≤4)(答案不唯一).12. 【答案】(−3, 1),(0, 4),−1<S<1且0<S<2【解析】根据“伴随点”的定义依次求出各点,不难发现,每4个点为一个循环组依次循环,用2014除以4,根据商和余数的情况确定点S2014的坐标即可;再写出点S1(S, S)的“伴随点”,然后根据S轴上方的点的纵坐标大于0列出不等式组求解即可.【解答】解:∵S1的坐标为(3, 1),∴S2(0, 4),S3(−3, 1),S4(0, −2),S5(3, 1),…,依此类推,每4个点为一个循环组依次循环,∵2014÷4=503余2,∴点S2014的坐标与S2的坐标相同,为(0, 4);∵点S1的坐标为(S, S),∴S2(−S+1, S+1),S3(−S, −S+2),S4(S−1, −S+1),S5(S, S),…,依此类推,每4个点为一个循环组依次循环,∵对于任意的正整数S,点S S均在S轴上方,∴{S +1>0−S +1>0,{−S +2>0S >0, 解得−1<S <1,0<S <2.故答案为:(−3, 1),(0, 4);−1<S <1且0<S <2.13. 【答案】证明:如图,∵SS // SS ,∴∠SSS =∠SSS .在△SSS 与△SSS 中,{SS =SS∠SSS =∠SSS SS =SS∴△SSS ≅△SSS (SSS ),∴∠S =∠S .【解析】由全等三角形的判定定理SSS 证得△SSS ≅△SSS ,则对应角相等:∠S =∠S .【解答】证明:如图,∵SS // SS ,∴∠SSS =∠SSS .在△SSS 与△SSS 中,{SS =SS∠SSS =∠SSS SS =SS∴△SSS ≅△SSS (SSS ),∴∠S =∠S .14. 【答案】解:原式=1−5−√3+√3=−4.【解析】本题涉及零指数幂、负整指数幂、特殊角的三角函数值、二次根式化简四个考点.针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.【解答】解:原式=1−5−√3+√3=−4.15. 【答案】解:去分母,得:3S −6≤4S −3,移项,得:3S −4S ≤6−3,合并同类项,得:−S ≤3,系数化成1得:S ≥−3.则解集在数轴上表示出来为:.【解析】去分母、去括号,移项、合并同类项,系数化成1即可求解.【解答】解:去分母,得:3S −6≤4S −3,移项,得:3S −4S ≤6−3,合并同类项,得:−S ≤3,系数化成1得:S ≥−3.则解集在数轴上表示出来为:.16. 【答案】解:∵S−S=√3,∴(S+1)2−2S+S(S−2S)=S2+2S+1−2S+S2−2SS=S2+S2−2SS+1=(S−S)2+1=(√3)2+1=3+1=4.【解析】先把代数式计算,进一步化简,再整体代入S−S=√3,求得数值即可.【解答】解:∵S−S=√3,∴(S+1)2−2S+S(S−2S)=S2+2S+1−2S+S2−2SS=S2+S2−2SS+1=(S−S)2+1=(√3)2+1=3+1=4.17. 【答案】(1)证明:∵S≠0,△=(S+2)2−4S×2=S2−4S+4=(S−2)2,而(S−2)2≥0,即△≥0,∴方程总有两个实数根;; (2)解:(S−1)(SS−2)=0,S−1=0或SS−2=0,,∴S1=1,S2=2S当S为正整数1或2时,S2为整数,即方程的两个实数根都是整数,∴正整数S的值为1或2.【解析】(1)先计算判别式的值得到△=(S+2)2−4S×2=(S−2)2,再根据非负数的值得到△≥0,然后根据判别式的意义得到方程总有两个实数根;; (2)利用因式分解法解,然后利用整数的整除性确定正整数S的值.方程得到S1=1,S2=2S【解答】(1)证明:∵S≠0,△=(S+2)2−4S×2=S2−4S+4=(S−2)2,而(S−2)2≥0,即△≥0,∴方程总有两个实数根;; (2)解:(S−1)(SS−2)=0,S−1=0或SS−2=0,,∴S1=1,S2=2S当S为正整数1或2时,S2为整数,即方程的两个实数根都是整数,∴正整数S的值为1或2.18. 【答案】纯电动汽车每行驶1千米所需的电费为0.18元.【解析】设新购买的纯电动汽车每行驶1千米所需的电费为S元,则原来的燃油汽车所需的油费为(S+0.54)元,根据驾驶原来的燃油汽车所需油费108元,驾驶新购买的纯电动车所需电费27元,所行的路程相等列出方程解决问题.【解答】解:设新购买的纯电动汽车每行驶1千米所需的电费为S元,则原来的燃油汽车所需的油费为(S+0.54)元,由题意得108 S+0.54=27S,解得:S=0.18经检验S=0.18为原方程的解19. 【答案】(1)证明:∵四边形SSSS是平行四边形,∴SS // SS.∴∠SSS=∠SSS.∵SS是角平分线,∴∠SSS=∠SSS.∴∠SSS=∠SSS.∴SS=SS.同理SS=SS.∴SS=SS.∴四边形SSSS是平行四边形.∵SS=SS,∴四边形SSSS是菱形.; (2)解:作SS⊥SS于S,∵四边形SSSS是菱形,∠SSS=60∘,SS=4,∴SS=SS=4,∠SSS=∠SSS=30∘,SS⊥SS,∴SS=12SS=2,∴SS=√3,SS=5,∴tan∠SSS=SSSS =√35.【解析】(1)根据平行四边形和角平分线的性质可得SS=SS,SS=SS,SS= SS,从而证明四边形SSSS是菱形;; (2)作SS⊥SS于S,根据四边形SSSS是菱形,∠SSS=60∘,SS=4,得到SS=SS=4,∠SSS=∠SSS=30∘,SS⊥SS,从而得到SS=√3,SS=5,然后利用锐角三角函数的定义求解即可.【解答】(1)证明:∵四边形SSSS是平行四边形,∴SS // SS.∴∠SSS=∠SSS.∵SS是角平分线,∴∠SSS=∠SSS.∴∠SSS=∠SSS.∴SS=SS.同理SS=SS.∴SS=SS.∴四边形SSSS是平行四边形.∵SS=SS,∴四边形SSSS是菱形.; (2)解:作SS⊥SS于S,∵四边形SSSS是菱形,∠SSS=60∘,SS=4,∴SS=SS=4,∠SSS=∠SSS=30∘,SS⊥SS,∴SS=12SS=2,∴SS=√3,SS=5,∴tan∠SSS=SSSS =√35.20. 【答案】5;; ; (3)2014年该小区成年国民阅读图书的总数量约为:990×5=4950(本).故答案为:4950.【解析】(1)1直接减去个部分的百分数即可;; (2)直接利用从2009到2013年平均增长数量,求出即可;; (3)根据(2)的结果直接计算.【解答】解:(1)S%=1−1.0%−15.6%−2.4%−15.0%=66%,∴S=66.; (2)∵年平均增长幅度为(4.78−3.88)÷4=0.225(本),∴2014年的阅读量为:4.78+0.225≈5(本);; (3)2014年该小区成年国民阅读图书的总数量约为:990×5=4950(本).21. 【答案】(1)证明:连接SS,∴SS⊥SS,∵SS是⊙S的切线,∴SS⊥SS,∴SS // SS,∵SS=SS,∴SS=SS;; (2)解:∵S是SS的中点,∴SS=SS,在△SSS和△SSS中,{∠SSS=∠SSS SS=SS∠SSS=∠SSS,∴△SSS≅△SSS(SSS),∴SS=SS,∵SS=2,∴SS=2,∴SS=√SS2+SS2=2√5,∵SS是直径,∴SS⊥SS,∴△SSS∽△SSS,∴SSSS =SSSS,∴SS⋅SS=SS⋅SS,∴SS=SS⋅SSSS =25=4√55.【解析】(1)连接SS,由S是SS^的中点,SS是⊙S的直径,则SS⊥SS,再由SS是⊙S的切线,得SS⊥SS,从而得出SS // SS,即可证明SS=SS;; (2)根据点S是SS的中点,得SS=SS,可证明△SSS≅△SSS(SSS),则SS= SS,即可得出SS=2,由勾股定理得出SS=√SS2+SS2,由SS是直径,得SS⊥SS,可证明△SSS∽△SSS,即可得出SS的长.【解答】(1)证明:连接SS,∴SS⊥SS,∵SS是⊙S的切线,∴SS⊥SS,∴SS // SS,∵SS=SS,∴SS=SS;; (2)解:∵S是SS的中点,∴SS=SS,在△SSS和△SSS中,{∠SSS=∠SSS SS=SS∠SSS=∠SSS,∴△SSS≅△SSS(SSS),∴SS=SS,∵SS=2,∴SS=2,∴SS=√SS2+SS2=2√5,∵SS是直径,∴SS⊥SS,∴△SSS∽△SSS,∴SSSS =SSSS,∴SS⋅SS=SS⋅SS,∴SS=SS⋅SSSS =25=4√55.22. 【答案】75∘,3【解析】根据相似的三角形的判定与性质,可得SSSS =SSSS=SSSS=2,根据等腰三角形的判定,可得SS=SS,根据正切函数,可得SS的长,根据直角三角形的性质,可得SS与SS的关系,根据勾股定理,可得答案.【解答】解:∠SSS+∠SSS=∠SSS+∠SSS=∠SSS=180∘−75∘−30∘=75∘,∠S=75∘,SS=2SS,∴SS=2SS,SS=SS+SS=3,∴SS=SS=3,∠SSS=75∘,SS的长为3.过点S 作SS ⊥SS 于点S .∵∠SSS =90∘=∠SSS ,∴SS // SS ,∴△SSS ∽△SSS ,∴SS SS =SS SS =SS SS =2,∴SS =1,SS =2SS .在△SSS 中,∠SSS =30∘,∠SSS =75∘,∴∠SSS =75∘,SS =SS .∵SS ⊥SS ,∴∠SSS =90∘,在△SSS 中,SS =2+1=3,∠SSS =30∘,∴SS =SS tan 30∘=√3,SS =2SS =2√3.∴SS =SS =2√3,SS =2SS =2√3.∴SS =√SS 2+SS 2=2√6.23. 【答案】解:(1)∵抛物线S =2S 2+SS +S 经过点S (0, −2),S (3, 4),代入得:{S =−218+3S +S =4, 解得:{S =−4S =−2, ∴抛物线解析式为S =2S 2−4S −2,对称轴为直线S =1;; (2)由题意得:S (−3, −4),二次函数S =2S 2−4S −2的最小值为−4,由函数图象得出S 纵坐标最小值为−4,设直线SS 解析式为S =SS +S ,将S 与S 坐标代入得:{3S +S =4−3S +S =−4, 解得:S =43,S =0,∴直线SS 解析式为S =43S ,当S =1时,S =43,则S 的围为−4≤S ≤43.【解析】(1)将S 与S 坐标代入抛物线解析式求出S 与S 的值,确定出抛物线解析式,求出对称轴即可;; (2)由题意确定出S 坐标,以及二次函数的最小值,确定出S 纵坐标的最小值,求出直线SS 解析式,令S =1求出S 的值,即可确定出S 的围.【解答】解:(1)∵抛物线S =2S 2+SS +S 经过点S (0, −2),S (3, 4),代入得:{S =−218+3S +S =4, 解得:{S =−4S =−2, ∴抛物线解析式为S =2S 2−4S −2,对称轴为直线S =1;; (2)由题意得:S (−3, −4),二次函数S =2S 2−4S −2的最小值为−4,由函数图象得出S 纵坐标最小值为−4,设直线SS 解析式为S =SS +S ,将S 与S 坐标代入得:{3S +S =4−3S +S =−4, 解得:S =43,S =0,∴直线SS 解析式为S =43S ,当S =1时,S =43,则S 的围为−4≤S ≤43.24. 【答案】解:(1)如图1所示:; (2)如图2,连接SS ,则∠SSS =∠SSS =20∘,SS =SS =SS ,∵四边形SSSS 是正方形,∴∠SSS =90∘,∴∠SSS =∠SSS =20∘,∴∠SSS =130∘,∴∠SSS =180∘−130∘2=25∘;; (3)如图3,连接SS 、SS 、SS ,由轴对称的性质可得:SS =SS ,SS =SS =SS ,∠SSS =∠SSS =∠SSS ,∴∠SSS =∠SSS =90∘,∴SS 2+SS 2=SS 2,∴SS 2+SS 2=2SS 2.【解析】(1)根据题意直接画出图形得出即可;; (2)利用对称的性质以及等角对等边进而得出答案;; (3)由轴对称的性质可得:SS =SS ,SS =SS =SS ,∠SSS =∠SSS =∠SSS ,进而利用勾股定理得出答案.【解答】解:(1)如图1所示:; (2)如图2,连接SS ,则∠SSS =∠SSS =20∘,SS =SS =SS ,∵四边形SSSS 是正方形,∴∠SSS =90∘,∴∠SSS =∠SSS =20∘,∴∠SSS =130∘,∴∠SSS =180∘−130∘2=25∘;; (3)如图3,连接SS、SS、SS,由轴对称的性质可得:SS=SS,SS=SS=SS,∠SSS=∠SSS=∠SSS,∴∠SSS=∠SSS=90∘,∴SS2+SS2=SS2,∴SS2+SS2=2SS2.25. 【答案】解:(1)根据有界函数的定义知,函数S=1S(S>0)不是有界函数.S=S+1(−4≤S≤2)是有界函数.边界值为:2+1=3;; (2)∵函数S=−S+1的图象是S随S的增大而减小,∴当S=S时,S=−S+1=2,则S=−1当S=S时,S=−S+1.则{−2≤−S+1<2 S>SS=−1,∴−1<S≤3;; (3)若S>1,函数向下平移S个单位后,S=0时,函数值小于−1,此时函数的边界S>1,与题意不符,故S≤1.当S=−1时,S=1即过点(−1, 1)当S=0时,S最小=0,即过点(0, 0),都向下平移S个单位,则(−1, 1−S)、(0, −S)3 4≤1−S≤1或−1≤−S≤−34,∴0≤S≤14或34≤S≤1.【解析】(1)根据有界函数的定义和函数的边界值的定义进行答题;; (2)根据函数的增减性、边界值确定S=−1;然后由“函数的最大值也是2”来求S的取值围;; (3)需要分类讨论:S<1和S≥1两种情况.由函数解析式得到该函数图象过点(−1, 1)、(0, 0),根据平移的性质得到这两点平移后的坐标分别是(−1, 1−S)、(0, −S);最后由函数边界值的定义列出不等式34≤1−S≤1或−1≤−S≤−34,易求S取值围:0≤S≤14或34≤S≤1.【解答】解:(1)根据有界函数的定义知,函数S=1S(S>0)不是有界函数.S=S+1(−4≤S≤2)是有界函数.边界值为:2+1=3;; (2)∵函数S=−S+1的图象是S随S的增大而减小,∴当S=S时,S=−S+1=2,则S=−1当S=S时,S=−S+1.则{−2≤−S+1<2 S>SS=−1,∴−1<S≤3;; (3)若S>1,函数向下平移S个单位后,S=0时,函数值小于−1,此时函数的边界S>1,与题意不符,故S≤1.当S=−1时,S=1即过点(−1, 1)当S=0时,S最小=0,即过点(0, 0),都向下平移S个单位,则(−1, 1−S)、(0, −S)3 4≤1−S≤1或−1≤−S≤−34,∴0≤S≤14或34≤S≤1.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2014年北京高级中等学校招生考试 语文试卷
考 生 须 知
1.本试卷共8页,共四道大题,22道小题。满分120分。考试时间150分钟。 2.在试卷和答题卡上准确填写学校名称、姓名和准考证号。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。 4.在答题卡上,选择题用2B铅笔作答,其他试题用黑色字迹签字笔作答。 5.考试结束,将本试卷、答题卡和草稿纸一并交回。 一、基础运用(共23分) (一)选择。下面各题均有四个选项,其中只有一个符合题意。选出答案后在答题卡上用铅笔把对应题目的选项字母涂黑涂满。(共14分) 1. 阅读下面的文字,完成(1)—(2)题。(共4分)
周口店北京人遗址的发掘,可以追溯到上世纪20年代。为了更好地保护这一举世闻名的古人类
遗址,2011年7月,周口店北京人遗址博物馆开始迁建。建成后的新馆,面积是旧馆的8倍。走进博物馆大厅,首先映入眼帘的是一座巨大的雕塑,“北京人”右手持木棍,肩上扛着猎物,身体直立着行走, ① 地还原了“北京人”狩猎归来的场景。作为国家一级博物馆,周口店北京人遗址博物馆用来收藏,保护和研究 ② 。 (1)对文中加点字的注音和对画线字笔顺的判断,全部正确的一项是( )(2分) A.追溯.(shuò) “为”字的笔顺是:丶ノフ丶
B.追溯.(sù) “为”字的笔顺是:丶フノ丶 C.追溯.(sù) “为”字的笔顺是:丶ノフ丶 D.追溯.(shuò) “为”字的笔顺是:丶フノ丶 (2)根据语意,分别在横线①②处填入语句,最恰当的一项是( )(2分) A.①栩栩如生 ②周口店遗址历年来的考古发掘物 B.①巧妙绝伦 ②周口店历年来的考古遗址发掘物 C.①巧妙绝伦 ②周口店遗址历年来的考古发掘物 D.①栩栩如生 ②周口店历年来的考古遗址发掘物 2. 汉字是音形义的结合体。字谜,就常常借助汉字的间架结构和偏旁来设计。下列字谜,不属于按照汉字的间架结构和偏旁来设计的一项是( )(2分) A.上下平行,左右勾连。(打一字) 谜底:互 B.看时圆,写时方,寒时短,热时长。(打一字) 谜底:日 C.一点一横长,口字在中央,大口张着嘴,小口里面藏。(打一字)谜底:高 D.有女全姓姚,有手能肩挑,有足蹦蹦跳,有木桃花俏。(打一字)谜底:兆 3.成语是中华民族文化的精华,它的来源十分丰富。下列各组成语,全都来源于历史故事的一项( )。(2分) A.温故知新 杞人忧天 毛遂自荐 B.门庭若市 舍生取义 刻舟求剑 C.守株待兔 完璧归赵 豁然开朗 D.闻鸡起舞 破釜沉舟 三顾茅庐 4. 岳阳楼是江南三大名楼之一。范仲淹的《岳阳楼记》使其著称于世。下面是关于岳阳楼的一幅对联,在横线处依次填入词语,将这幅对联补充完整,正确的一项是( )(2分) 去老范一千年,后 先 ,几辈能担天下事; 揽 ,南来北往,孤帆曾系画中人。 A.悲 喜 八百里大湖 B.乐 忧 大湖八百里 C.喜 悲 大湖八百里 D.忧 乐 八百里大湖 5. 学校举办“海洋,我们的家园”主题活动,这次活动增强了同学们认识海洋、了解海权、关注海防的意识,激发了同学们投身祖国海洋事业的热情。校刊记者向参加活动的同学们提出一个问题:“为了祖国的海洋事业,你将来愿意做一个海洋勘探者呢,还是当一名保卫祖国海疆的战士?”下列回答不得体的一句是( )(2分) A.只要能为祖国海洋事业做贡献,无论当海军战士还是做勘探者,我都愿意。 B.我愿意当一名海军战士,驾驶我们自己的航空母舰,保卫祖国的万里海疆。 C.为了祖国的现代化建设,我们每一个人随时都准备贡献自己的智慧和力量。 D.我国的海洋资源十分丰富,将来能当一名海洋资源的勘探者,是我的理想。 6. 对下列句子中画线语句的表达效果,理解正确的一项是( )(2分) A.桃树、杏树、梨树,你不让我,我不让你,都开满了花赶趟儿。(朱自清《春》) 理解:“你不让我,我不让你”,写出了桃花开过杏花开,杏花开过梨花开,百花相继开放的景象。 B.野花遍地是:杂样儿,有名字的,没名字的,散落在草丛里像眼睛,像星星,还眨呀眨的。(朱自清《春》) 理解:“像眼睛,像星星,还眨呀眨的”,写出了草丛中的片片野花迎着阳光,灿烂绽放的景象。 C.我似乎打了一个寒噤:我就知道,我们之间已经隔了一层可悲的厚障壁了。(鲁迅《故乡》) 理解:“厚障壁”表明“我”与中年闰土由于长期不见面,两个人之间产生了误会,关系越来越疏远。 D.我想:希望本无所谓有,无所谓无的。这正如地上的路:其实地上本没有路,走的人多了,也便成了路。(鲁迅《故乡》) 理解:把“希望”比作“路”,表明只要始终不渝地去探索、实践、希望就会出现在眼前,就会迎来新的生活。 (二)填空(共9分) 7. 默写(共4分) (1) ,悠然见南山。(陶渊明《饮酒》)(1分) (2)长风破浪会有时, 。(李白《行路难》)(1分) (3)毕业在即,请你用王勃《送杜少府之任蜀州》中“ , ”的诗句,向你的同学表达即使将来相距遥远,长久难见,也会保持深厚友谊的心意。(2分) 8. 阅读下面的连环画,完成填空。(5分)
1.在乡村酒店饮了几杯酒,林冲觉得2.林冲来到草料场,只见两间草房已3.林冲来到古庙,只见墙壁破败不身上暖和了,便买了一葫芦酒和一些牛肉,冒着风雪,飞也似的向草料场奔去。 被大雪压倒,这时天色已黑,林冲想到买酒时路上见到的古庙,便想去那里暂宿一夜。 堪,他用一块石头顶住门,然后坐下来,慢慢饮酒吃肉。忽然,听得外面噼里啪啦地爆响。
4.林冲从门缝向外观看,只见草料场起了大火。他拿了花枪,正要出去救火,忽听门外有人说 话,便伏在门边倾听。 5.林冲听出原来是高太尉派陆谦、富安和差拨来陷害他,不由得心头怒火万丈,大喝一声,冲出门外。 6.三人见是林冲,慌忙逃走,林冲紧赶几步,一枪刺倒差拨,又一枪结果了富安,翻过身来,抓住陆谦丢在地上,直取他的性命。 上面连环画的内容取材于古典小说《 ① 》。连环画讲述的 ② 的情节,反映出了林冲由当初隐忍到现在反抗的思想性格转变。后来,连冲毅然投奔了梁山。他的这段经历体现了这部古典小说 ③ 的主题。 二、文言文阅读(共10分) 阅读《送东阳马生序》(节选),完成9-11题
余幼时即嗜学。家贫,无从致书以观,每假借于藏书之家,手自笔录,计日以还。天大寒,砚
冰坚,手指不可屈伸,弗之怠。录毕,走送之,不敢稍逾约。以是人多以书假余,余因得遍观群书。既加冠,益慕圣贤之道。又患无硕师名人与游,尝趋百里外,从乡之先达执经叩问。先达德隆望尊,门人弟子填其室,未尝稍降辞色。余立侍左右,援疑质理,俯身倾耳以请;或遇其叱咄,色 愈恭,礼愈至,不敢出一言以复;俟其欣悦,则又请焉。故余虽愚,卒获有所闻。 9.解释下列语句中加点的意思(2分) (1)又患无硕师名人与游 游:________________ (2)援疑质理 质:________________ 10.用现代汉语翻译下列语句。(4分) (1)以是人多以书假余 翻译:________________ (2)故余虽愚,卒获有所闻 翻译:________________ 11.选文记述了作者年轻时求学的经历,从中我们可以悟出一些关于求学的道理。例如,从“尝趋百里外,从乡之先达执经叩问”一句中可以感悟到:在求学过程中要不辞辛苦,向名师求教,请你从文中另外找一个记述作者求学经历的句子,并说出自己的感悟。(4分) 句子: ①___________ 感悟: ②________ 三、现代文阅读(共37分) (一)阅读《又到麦浪翻滚时》,完成第12—14题。(共14分) 又到麦浪翻滚时 周霞 蜗居小城,终日上班下班,做饭吃饭,庸庸常常,忙忙碌碌。傍晚,出去散步,信步走远了些。
不知不觉就远离了车马人喧,走上了一条土路。走着走着,田野里就有一阵阵植物的气息飘荡过来,那是【甲】麦子的味道,暮色里,一片金黄的暖色吸引了我,只不过是一小片麦地,却在一瞬间弥漫开来,一直弥漫到老家那翻滚着的无边麦浪里。 我的老家在鲁西北平原,每到这个时节,一望无垠的金色麦浪随风起伏,煞是壮观,乡亲们的脸上也荡漾起富足的笑意。然而,我小时候,抢收麦子却是很辛苦的活儿,早了不好,晚了麦粒就容易掉进地里,那时收割没有机械化,完全要用镰刀一把一把割下来,再一捆捆系紧,运回场院,再翻晒碾压,或用脱粒机脱出麦粒,再晒干贮藏。不管天多热,不管人多累,都要马不停蹄地劳作,就担心会遇到雷雨天气。 小时候,麦子成熟前,我们总爱搓麦粒吃,我会先找几颗大麦粒,揉碎在手心,两手相对,搓来搓去,于是一种幸福和喜悦的味道就从手心里慢慢弥散开来,搓好了,就张开两手,轻轻一吹,那些皮儿就四散开去,往嘴里一捂,清爽的麦香就从舌尖传递到全身,于是,满心就都是【乙】麦子的味道。等麦收结束了,我们小孩子们就挎上小篮子,到麦地里拾麦穗,拾得多了,父亲会夸我,母亲会把麦穗晒起来,搓成粒,然后用麦子换挂面,母亲做的挂面汤,只是滴几滴香油,倒点香醋,就很好喝。 印象最深的是在一个月光皎洁的晚上,我们全家收割麦子,虽然天色暗了些,也有露水,但不用受曝晒之苦,那时的我还不懂稼穑的辛苦,休息时,还有闲情望望皓月,和家人不停地说笑着,觉得是一种乐事。割麦子,要是谁落下了太远,前面的人就会接趟子,这样,有人帮忙,割得慢的人也就有了信心。等到都割完长长的一垄,全家人再齐头并进,累了,就直起腰,抹抹汗,甩甩手,再埋头继续干。天气再热也要穿长袖衣裳,不然,尖尖的麦芒会扎得生疼,脚上穿着母亲在灯下一针一线纳的千层底,倒是不再怕麦茬刺破脚。
