因式分解:完全平方公式_课件
合集下载
运用完全平方公式因式分解(课件)数学八年级上册同步备课系列(人教版)

=3a(x+y)2
=(a+b-6)2
分解因式:
(1) ax2+2a2x+a3
(2) -3x2+6xy-3y2
(3) (x+y)2-12x-12y+36
解:(1)原式= a(x2+2ax+a2)
(2)原式= -3(x2-2xy+y2)
=a(x+a)2
=-3(x-y)2
(3)原式=(x+y)2-12(x+y)+36
A. x2-y2= (x+y) (x-y)
B. x2+6x+9= (x+3)2
C. x2+xy=x (x+y)
D. x2+y2= (x+y)2
5.若x2- 2(k+1)x+4是完全平方式,则k的值为( A )
A.1或-3
B. -1或3
C.±1
D.±3
6.已知 = + 2,则代数式32 − 6 + 3 2 + 2022的值为( D )
±
10.若x2﹣8x+m2=(x﹣4)2,那么m=_____.
11.若 2 + (3 − ) + 9可以用完全平方式来分解因式,则m的值为
−或9
__________.
12.分解因式:
(1) − 22 + 3 ;
(2)3 − 102 + 25;
(3) 2 − 5
(4)(2 + 2 − 2 )2 −42 2 .
例3.分解因式:
(1) 3ax2+6axy+3ay2
初中数学《完全平方公式》优秀课件北师大版2
a2 2• a •bb2
(1)、解:16x2 24x 9
方法:当一个式子满足完全
(4x)2 2 4x 3 32
平方式的所有特征时,可直 接分解因式。结果为这两平
4x 32
方项底数和或差的平方,是
和是差看中间项的符号
分析:- x2 4xy 4 y2 - x2 2 • x • 2 y 2 y2
• 学习重点:
运用完全平方公式分解因式.
学习难点:综合运用提公因式和公式法分解
因式
复习引入
问题一:大家还记得什么是因式分解吗?
因式分解就是将一个多项式化成几个整式的 积的形式
即: 和
积
问题二:我们已经学习了分解因式的哪
些方法?
1、提公因式法 2、公式法
平方差公式 a2 b2 a ba b
即:两个数的平方差等于 这两个数的和与差的积
方法:若式子有整体满足完全平方 式可直接进行因式分解,需注意中 间项的符号
练习2 将下列多项式分解因式:
1 25a3 ax2 10a2x
2 12x3 12x2 2 y 1- 3x2y -12
答案:
1 a5a x2
a b2 b a2
2 - 3x2 y 1 2x2
或 - 32x 2 y 12
你对因式分解的方法有什么新的发现?请尝试概括 你的发现.
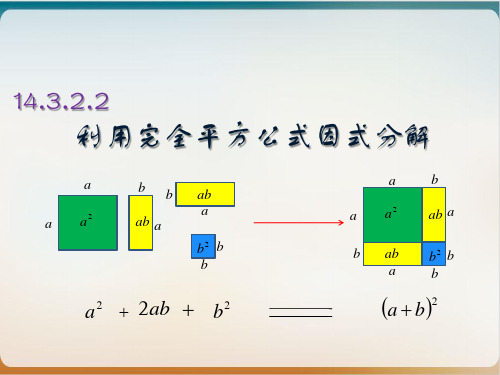
把整式的乘法公式——完全平方公式 倒过来 就得到因式分解的完全平 方公式:
a2 2ab+b2 =(a b)2
首2 2 首 尾 尾2 首 尾2
即两个数的平方和加上(或减去)这两个 数的积的2倍,等于这两个数的和(或差) 的平方
1、在下面括号ቤተ መጻሕፍቲ ባይዱ填空
14.3.2.2 利用完全平方公式因式分解
14.3.2公式法-完全平方公式法 课件人教版数学八年级上册

5.如果x2+mxy+9y2是一个完全平方式,那么m的值为( B ) A.6 B.±6 C.3 D.±3
6.已知a、b、c是三角形的三边,请你判断a2-b2-c2-2bc的值的正负.
7.说明无论a、b为何值,代数(a+b)²+2(a+b)+5 的值均为正值.
8.若a+b=1,a+c=2,b+c=3,利用因式分解求值: a2+b2+c2+ab+ac+bc.
自 学 检 查
1.下列各式是不是完全平方式?
(1)a2-ab+b2 × (2)a2-4a+4 =a2 -4a +22 √ (3)x2+4xy+4y2=x2+4xy + (2y)2√ (4)x2-6x-9 =x2-6x-32 ×
2.按照完全平方公式填空:
(1)a2-10a+( 25 )=( a-5 )2
(4)原式=(2x +y-3) 2
总结:①因式分解的一般思路: 一提(提公因式法) 二套(套用公式法)
②整体思想,例如:把 2x+y 看做一个整体。
巩固练习
1.(1)若x2+2kx+9是一个完全平方式,则k= ___±___3__ (2)若x2+8x+k2是一个完全平方式,则k= __±___4___.
( (23))1(a2-y2()+r2s)a+yr+21s2==((
ay+1)2
½ - rs)2
4
自 3.把下列各式因式分解 1 x2 12x 36 2 2xy x2 y2
学 (3) 3ax2﹢6axy﹢3ay2
检 查
14.3.2.2 公式法——完全平方公式

(1)a2-4a+4; (3)4b2+4b-1; 是 不是 (2)1+4a² ; 不是 (4)a2+ab+b2; 不是
分析: (2)因为它只有两项;
( 3) 4b² 与-1的符号不统一;
(4)因为ab不是a与b的积的2倍.
P118 例2 分解因式:
(1)16x2+24x+9; (2)-x2+4xy-4y2.
2
P118 例6 分解因式:
(1)3ax2+6axy+3ay2 ; (2)(a+b)2-12(a+b)+36.
分析:(1)中有公因式3a,应先提出公因式,再进一步分解因式; (2)中将a+b看成一个整体,设a+b=m,则原式化为m2-12m+36.
解: (1)原式=3a(x2+2xy+y2) =3a(x+y)2 (2)原式=(a+b)2-2· (a+b) · 6+62
=(x2-6-3)2 =(x2-9)2 =[(x+3)(x-3)]2 =(x+3)2(x-3)2
1. 把下列各式分解因式.
2. 因式分解:x4-8x2y2+16y4.
解:原式=(x2)2-2· x2· 4y2 +(4y2)2
=(x2-4y2)2
=[(x+2y)(x-2y)]2
=(x+2y)2(x-2y)2
(2)每个多项式的第一项和第三项有什么特征?
这两项都是数或式的平方,并且符号相同
(3)中间项和第一项,第三项有什么关系?
是第一项和第三项底数的积的±2倍
a 2 2ab b 2
完全平方式的特点: 1.必须是三项式(或可以看成三项的); 2.有两个同号的数或式的平方; 3.中间有两底数之积的±2倍.
分析: (2)因为它只有两项;
( 3) 4b² 与-1的符号不统一;
(4)因为ab不是a与b的积的2倍.
P118 例2 分解因式:
(1)16x2+24x+9; (2)-x2+4xy-4y2.
2
P118 例6 分解因式:
(1)3ax2+6axy+3ay2 ; (2)(a+b)2-12(a+b)+36.
分析:(1)中有公因式3a,应先提出公因式,再进一步分解因式; (2)中将a+b看成一个整体,设a+b=m,则原式化为m2-12m+36.
解: (1)原式=3a(x2+2xy+y2) =3a(x+y)2 (2)原式=(a+b)2-2· (a+b) · 6+62
=(x2-6-3)2 =(x2-9)2 =[(x+3)(x-3)]2 =(x+3)2(x-3)2
1. 把下列各式分解因式.
2. 因式分解:x4-8x2y2+16y4.
解:原式=(x2)2-2· x2· 4y2 +(4y2)2
=(x2-4y2)2
=[(x+2y)(x-2y)]2
=(x+2y)2(x-2y)2
(2)每个多项式的第一项和第三项有什么特征?
这两项都是数或式的平方,并且符号相同
(3)中间项和第一项,第三项有什么关系?
是第一项和第三项底数的积的±2倍
a 2 2ab b 2
完全平方式的特点: 1.必须是三项式(或可以看成三项的); 2.有两个同号的数或式的平方; 3.中间有两底数之积的±2倍.
因式分解ppt课件

方式.
完全平方式的条件:(1)多项式是二次三项式;(2)首末
两项是两个数(或式子)的平方且符号相同,中间项是这
两个数(或式子)的积的2 倍,符号可以是“+”,也可以
是“-”.
感悟新知
知5-讲
2. 完全平方公式
两个数的平方和加上(或减去)这两个数
的积的2 倍,等于这两个数的和(或差)的平方.
即:a2±2ab+b2=(a±b)2 .
知4-讲
3. 运用平方差公式分解因式的步骤
一判:根据平方差公式的特点,判断是否为平方差,若负
平方项在前面,则利用加法的交换律把负平方项放在后面;
二定:确定公式中的a和b,除a和b是单独一个数或字母外,
其余不管是单项式还是多项式都必须用括号括起来,表示
一个整体;三套:套用平方差公式进行分解;四整理:将
(2)确定另一个因式,另一个因式即多项式除以公因式所
得的商;
(3)写成积的形式.
感悟新知
知3-讲
特别解读
1. 提公因式法实质上是逆用乘法的分配律.
2. 提公因式法就是把一个多项式分解成两个因式的积的形
式,其中的一个因式是各项的公因式,另一个因式是多
项式除以这个公因式所得的商.
感悟新知
知3-练
例 5 把下列多项式分解因式:
感悟新知
例 3 仔细阅读下面例题,解答问题:
知1-练
例题:已知把x2-4x+m分解因式后有一个因式是x
+3,求其另一个因式及m的值.
解:设另一个因式为x+n,则x2-4x+m=(x+3)(x
+n),即x2-4x+m=x2+(n+3)x+3n.
=-,
+=-,
所以
解得
=-.
七年级数学下册 第8章 整式乘法和因式分解 8.3 完全平方公式与平方差公式教学课件 (新版)沪科版

做一做
用两数和的完全平方公式计算(填空):
(1)(a + 1)2=(a )2+2(a )(1 )+ ( 1)2
(a + b)2 = a2 + 2 a b + b2
(2)(2a+3b)2= ( 2a)2 + 2(2a )( 3b ) + ( 3b )2
自主探索
你能用两数和的完全平方公式 来计算(a−b)2吗?
完全平方公式
(a+b)2=a2+2ab+b2 (a−b)2=a2−2ab+b2
两个数的和(或差)的平方,等 于它们的平方和,加上(或减去)它 们的积的2倍。
请先计算下列各题:
(1) (a 2)(a 2) _____a_2__4______; (2) (3 x)(3 x) _____9___x_2_____;
我来做一做
一块方巾铺在正方形 的茶几上,四周刚好都垂 下15cm,如果设方巾的 边长为a,怎样求茶几的 面积?结果怎样用关于a 的多项式表示?如果 a=100cm,茶几的面积是 多少cm2?
想一想
(1)用简便的方法计算: 1.23452+0.76552+2.469×0.7655 (2)已知(a+b)2=11,ab=1,求(a-b)2的 值.
(3) (4k 3)(4k 3) (4) (1 x)( x 1)
(5)
1 2
x
y
1 4
x
y
快速计算:例2 用平方差公式计算
(1) 103×97 (2) 59.8×60.2 5678×5680-56792
(2+1)(22+1)(24+1)(28+1)+1
完全平方公式PPT精品课件1

1、想要体面生活,又觉得打拼辛苦;想要健康身体,又无法坚持运动。人最失败的,莫过于对自己不负责任,连答应自己的事都办不到,又何必抱怨这个世界都和你作对?人生的道理很简单,你想要什么,就去付出足够的努力。 2、时间是最公平的,活一天就拥有24小时,差别只是珍惜。你若不相信努力和时光,时光一定第一个辜负你。有梦想就立刻行动,因为现在过的每一天,都是余生中最年轻的一天。 3、无论正在经历什么,都请不要轻言放弃,因为从来没有一种坚持会被辜负。谁的人生不是荆棘前行,生活从来不会一蹴而就,也不会永远安稳,只要努力,就能做独一无二平凡可贵的自己。 4、努力本就是年轻人应有的状态,是件充实且美好的事,可一旦有了表演的成分,就会显得廉价,努力,不该是为了朋友圈多获得几个赞,不该是每次长篇赘述后的自我感动,它是一件平凡而自然而然的事,最佳的努力不过是:但行好事,莫问前程。愿努力,成就更好的你! 5、付出努力却没能实现的梦想,爱了很久却没能在一起的人,活得用力却平淡寂寞的青春,遗憾是每一次小的挫折,它磨去最初柔软的心智、让我们懂得累积时间的力量;那些孤独沉寂的时光,让我们学会守候内心的平和与坚定。那些脆弱的不完美,都会在努力和坚持下,改变模样。 6、人生中总会有一段艰难的路,需要自己独自走完,没人帮助,没人陪伴,不必畏惧,昂头走过去就是了,经历所有的挫折与磨难,你会发现,自己远比想象中要强大得多。多走弯路,才会找到捷径,经历也是人生,修炼一颗强大的内心,做更好的自己! 7、“一定要成功”这种内在的推动力是我们生命中最神奇最有趣的东西。一个人要做成大事,绝不能缺少这种力量,因为这种力量能够驱动人不停地提高自己的能力。一个人只有先在心里肯定自己,相信自己,才能成就自己! 8、人生的旅途中,最清晰的脚印,往往印在最泥泞的路上,所以,别畏惧暂时的困顿,即使无人鼓掌,也要全情投入,优雅坚持。真正改变命运的,并不是等来的机遇,而是我们的态度。 9、这世上没有所谓的天才,也没有不劳而获的回报,你所看到的每个光鲜人物,其背后都付出了令人震惊的努力。请相信,你的潜力还远远没有爆发出来,不要给自己的人生设限,你自以为的极限,只是别人的起点。写给渴望突破瓶颈、实现快速跨越的你。 10、生活中,有人给予帮助,那是幸运,没人给予帮助,那是命运。我们要学会在幸运青睐自己的时候学会感恩,在命运磨练自己的时候学会坚韧。这既是对自己的尊重,也是对自己的负责。 11、失败不可怕,可怕的是从来没有努力过,还怡然自得地安慰自己,连一点点的懊悔都被麻木所掩盖下去。不能怕,没什么比自己背叛自己更可怕。 12、跌倒了,一定要爬起来。不爬起来,别人会看不起你,你自己也会失去机会。在人前微笑,在人后落泪,可这是每个人都要学会的成长。 13、要相信,这个世界上永远能够依靠的只有你自己。所以,管别人怎么看,坚持自己的坚持,直到坚持不下去为止。 14、也许你想要的未来在别人眼里不值一提,也许你已经很努力了可还是有人不满意,也许你的理想离你的距离从来没有拉近过......但请你继续向前走,因为别人看不到你的努力,你却始终看得见自己。 15、所有的辉煌和伟大,一定伴随着挫折和跌倒;所有的风光背后,一定都是一串串揉和着泪水和汗水的脚印。 16、成功的反义词不是失败,而是从未行动。有一天你总会明白,遗憾比失败更让你难以面对。 17、没有一件事情可以一下子把你打垮,也不会有一件事情可以让你一步登天,慢慢走,慢慢看,生命是一个慢慢累积的过程。 18、努力也许不等于成功,可是那段追逐梦想的努力,会让你找到一个更好的自己,一个沉默努力充实安静的自己。 19、你相信梦想,梦想才会相信你。有一种落差是,你配不上自己的野心,也辜负了所受的苦难。 20、生活不会按你想要的方式进行,它会给你一段时间,让你孤独、迷茫又沉默忧郁。但如果靠这段时间跟自己独处,多看一本书,去做可以做的事,放下过去的人,等你度过低潮,那些独处的时光必定能照亮你的路,也是这些不堪陪你成熟。所以,现在没那么糟,看似生活对你的亏欠, 其实都是祝愿。
人教版八年级上册数学同步课件-第14章-14.2.2 完全平方公式

什么关系? 3.两个完全平方式的积中不同的是哪一项?与 a,
b有什么关系?它的符号与什么有关?
数学课堂教学课件设计
新课讲解
想一想:下面各式的计算是否正确?如果不正确,
应当怎样改正?
(1)(x+y)2=x2 +y2
×
(2)(x -y)2 =x2 -y2
×
(x +y)2 =x2+2xy +y2 (x -y)2 =x2 -2xy +y2
a
b
ab
(a−b)2 = a2 −ab −b(a−b) = a2−2ab+b2 .
a
差的完全平方公式: (a-b)2= a2-2ab+b2 .
数学课堂教学课件设计
新课讲解
问题4:观察下面两个完全平方式,比一比,回答下
列问题: (a+b)2= a2+2ab+b2,
(a-b)2=a2-2ab+b2.
1.说一说积的次数和项数. 2.两个完全平方式的积有相同的项吗?与a,b有
新课讲解
【练习】计算:(1)(a-b+c)2; (2)(1-2x+y)(1+2x-y).
解:(1)原式=[(a-b)+c]2 =(a-b)2+2(a-b)c+c2 =a2-2ab+b2+c2+2ac-2bc.
(2)原式=[1-(2x-y)][1+(2x-y)] =12-(2x-y)2 =1-4x2+4xy-y2.
(a+b)2= a2+2ab+b2 ;(a-b)2= a2-2ab+b2 .
数学课堂教学课件设计
新课讲解
(a+b)2= a2+2ab+b2 , (a-b)2= a2-2ab+b2 . 也就是说,两个数的和(或差)的平方,等于 它们的平方和,加上(或减去)它们的积的2倍.这 两个公式叫做(乘法的)完全平方公式. 简记为: “首平方,尾平方,积的2倍放中间”.
b有什么关系?它的符号与什么有关?
数学课堂教学课件设计
新课讲解
想一想:下面各式的计算是否正确?如果不正确,
应当怎样改正?
(1)(x+y)2=x2 +y2
×
(2)(x -y)2 =x2 -y2
×
(x +y)2 =x2+2xy +y2 (x -y)2 =x2 -2xy +y2
a
b
ab
(a−b)2 = a2 −ab −b(a−b) = a2−2ab+b2 .
a
差的完全平方公式: (a-b)2= a2-2ab+b2 .
数学课堂教学课件设计
新课讲解
问题4:观察下面两个完全平方式,比一比,回答下
列问题: (a+b)2= a2+2ab+b2,
(a-b)2=a2-2ab+b2.
1.说一说积的次数和项数. 2.两个完全平方式的积有相同的项吗?与a,b有
新课讲解
【练习】计算:(1)(a-b+c)2; (2)(1-2x+y)(1+2x-y).
解:(1)原式=[(a-b)+c]2 =(a-b)2+2(a-b)c+c2 =a2-2ab+b2+c2+2ac-2bc.
(2)原式=[1-(2x-y)][1+(2x-y)] =12-(2x-y)2 =1-4x2+4xy-y2.
(a+b)2= a2+2ab+b2 ;(a-b)2= a2-2ab+b2 .
数学课堂教学课件设计
新课讲解
(a+b)2= a2+2ab+b2 , (a-b)2= a2-2ab+b2 . 也就是说,两个数的和(或差)的平方,等于 它们的平方和,加上(或减去)它们的积的2倍.这 两个公式叫做(乘法的)完全平方公式. 简记为: “首平方,尾平方,积的2倍放中间”.
