基于自然边界归化的椭圆外区域各向异性问题的重叠型区域分解算法
圆外Stokes问题的边界积分公式

图 3 水平方向速度与半径 r 的关系
图 6 竖直方向速度与半径 r 的关系
由图 5 及图 6 可知 , 水平方向及竖直方向的速 度大小与变化趋势均与边界积分公式计算结果吻 合 , 这验证了边界积分公式的正确性 . 由于 Sto kes 流动中扰动衰减很慢 , 这种纯数值解法应用于无界 流动时往往需取很大的计算区域 , 工作量太大 . 本文 在半径 100 m 处将流场截断成有限区域 , 划分的网
η ( z) p ( x , y) = - 4 Reφ ′ 其中φ( z ) ,ψ( z ) 为Ω上的两个解析函数 , z = x + i y , 珔 z = x - i y. 当单位圆内边界的合速度为零时 , 设 φ( z ) = ψ( z ) =
解并进行比较 ,表明了此方法的正确性与有效性 . 1 Stokes 问题的微分方程及其边界条件 Sto kes 方程组为 Δu + grad p = 0 -η
摘
要 针对圆外区域的 Sto kes 问题 ,利用 Fourier 展开法 ,通过自然边界归化得到了一个只与边界速度有
关的 Stokes 问题的边界积分公式 . 根据此公式及边界速度值 ,求得区域内速度及压力分布的解析表达式 ,并通过数 值积分的方法进行求解 ,计算量小 ,所得速度及压力分布图曲线光滑 . 最后借助流体软件进行数值计算 , 结果验证 了边界积分公式的正确性 、 可行性 . 关键词 圆外区域 ,Stokes 问题 ,Fourier 展开法 ,边界积分公式
・196 ・
固体力学学报 2006 年第 27 卷 学 , 1986 , 8 ( 3) : 281~289
4 余德浩 . 自然边界元方法的数学理论 . 北京 : 科学出版
满足的 ,所得结果与一般 CFD 方法计算结果相比具 有更高的精度 ; 对于边界合速度不为零的问题 ,我们 将另文讨论 . 本文的研究除了为解决 Sto kes 问题本 身所反映的小 Reynolds 数情况下不可压缩粘性流 体的定常问题外 ,还为处理更复杂的 Navier2Sto kes 问题奠定了基础 . 参 考 文 献
图像分割方法概述

(1) 灰度阈值分割法
是一种最常用的并行区域技术, 它是图像分割中应用数量最多的一类。 阈值分割方法实 [6] 际上是输入图像f到输出图像g的如下变换 : g i, j = 1 ������(������, ������) ≥ ������ 0 ������(������, ������) < ������
(2)区域分裂合并 区域生长是从某个或者某些像素点出发,最后得到整个区域,进而实现目标提取。分裂 合并差不多是区域生长的逆过程:从整个图像出发,不断分裂得到各个子区域,然后再把前 景区域合并,实现目标提取。分裂合并的假设是对于一幅图像,前景区域由一些相互连通的 像素组成的, 因此, 如果把一幅图像分裂到像素级, 那么就可以判定该像素是否为前景像素。 当所有像素点或者子区域完成判断以后, 把前景区域或者像素合并就可得到前景目标。 在这 类方法中, 最常用的方法是四叉树分解法。 设R代表整个正方形图像区域, P代表逻辑谓词。 基本分裂合并算法步骤如下: ① 对任一个区域,如果H(Ri)=FALSE就将其分裂成不重叠的四等份; ② 对相邻的两个区域Ri和Rj,它们也可以大小不同(即不在同一层),如果条件H(Ri∪ Rj)=TRUE满足,就将它们合并起来。 ③ 如果进一步的分裂或合并都不可能,则结束。 分裂合并法的关键是分裂合并准则的设计。这种方法对复杂图像的分割效果较好,但算 法较复杂,计算量大,分裂还可能破坏区域的边界。 基于形变模型的方法 基于形变模型的方法是目前应用较多的分割方法。 从物理学角度, 可将形变模型看成是 一个在施加外力和内部约束条件下自然反应的弹性物体。 在血液图像分割中, 主要应用活动 轮廓模型,又称 Snake 模型,是轮廓曲线在外能和内能的作用下向物体边缘靠近,外力推动 轮廓运动,而内力保持轮廓的光滑性。[7]
3自然区划等级系统-图文

3自然区划等级系统-图文自然区划的等级系统一、区域单位等级系统类型自然区划方法:自上而下:依据自然条件的差异性划分自然区域。
自下而上:依据自然条件的相似性使若干小区合并为一个范围较大的自然区。
无论是合并还是划分都必然形成一个区域等级系统。
区划方案正确与否取决于其能否客观地反映自然界的地域分异规律,而制定区划的等级系统正是体现地域分异规律的重要手段。
因此,等级系统的研究是自然区划方法论的重要内容和不可或缺的工作步骤。
而确定分级单位并给予明确定义,则是进行等级系统研究的基础。
1.双列系统:两类区域单位的存在决定有两种等级单位系统地域分异的结果使地表自然界分化为一系列不同等级的区域。
任何一级区域都是同时在地带性和非地带性因素的影响下形成的。
然而,一部分区域单位的分化主要取决于地带性因素,另一部分则主要取决于非地带性因素。
因此,地表自然界存在着两类区域单位,区划也有两种等级单位系统,即地带性等级单位系统和非地带性等级单位系统,区划专家称之为“双列系统”。
2.单列系统:地域分异的实际表现由于地带性因素和非地带性因素同时作用于地表自然界,而上述两类区域单位各自反映其中一种地域分异因素,因此它们是不完全的综合性单位,其等级系统也是不完全综合性的区划等级系统。
地表自然界还存在着同时反映这两种分异因素的完全综合性单位,其等级系统就是一般所说的单列系统。
二、地带性区划单位:成因:地带性因素决定地表的地带性地域分异,形成了地带性区域单位。
地带性单位主要根据区域的地带性属性划分。
区域的地带性属性不仅表现在气候、土壤和植被上,在其他组成成分乃至整个区域综合特征上都有一定程度的表现。
因此,地带性区划单位是综合单位,只是由于其内部在地质基础和地貌方面往往存在着很大的差别,即缺乏这些方面的发生统一性和相对一致性,因此这些单位的综合性不完全或不充分。
纬度辐射因素仍然是决定地带性单位的分化及其界线的主要原因,因此,这些单位的空间变化具有非可逆性和南北半球大致对称分布的特点,彼此逐渐更替,没有鲜明的界线。
【江苏省自然科学基金】_分解算法_期刊发文热词逐年推荐_20140815
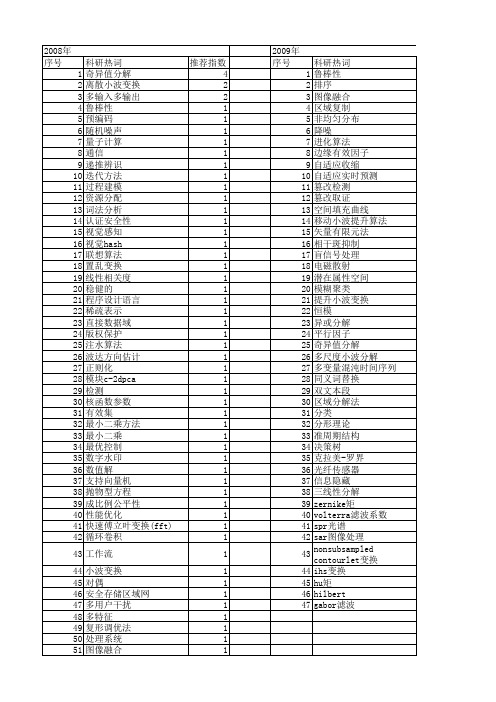
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 4 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82
数值型数据 扩频 强素数 希尔伯特-黄变换 小样本问题 对称线性鉴别分析 对支持向量机(twsvm) 大整数因数分解问题(ifp) 多输入多输出 多类问题 多用户干扰 多敏感属性 多尺度小波分解 多元分析 增量学习 地表温度 在线算法 土地覆盖 图像恢复 图像修复 四量子电路综合 四量子 可逆逻辑 双边判别框架 半脆弱水印 动静碰磨 任意结构阵列 主成分分析 v-i-s模型 rsa
多子空间投影分解法及收敛特性分析

第 1 期
孙 连友等 : 多子 空 问投 影 分 解 法 及 收 敛 特 性 分 析
17 0
A =
“
0 0
0
“
0
0
0
0 0
0
0
0
其 中 A ( =1 … , m 一1 是 稀 疏 的 带 状 矩 阵 , 对 应 干 区 域 , ( =2 … , 对 应 连 接 波 导 和 腔 体 的 颈 i , 2 ) A A i , m)
部 区域 , ( =m+1 … , m一1 对应腔 体 区域 ; , ( A i , 2 ) A A =1 … , , … +( , m) A , =1 … , , m一1 中只 有很 )
[ 者 简 介 ]孙 连 友 (9 5 , , 徽 天 长 , 教授 , 士 , 作 16 一)男 安 副 博 主要 从 事 计 算 电 磁学 研 究 与 应 用 , 京 东 南 大 学 信 息 科 学 与 工 程 学 院 ,106 南 209
维普资讯
形成 一 类特殊 的系数矩 阵 , 即
[ 稿 日期 ]20 0 2 ;[ 回 日期 ] 07— 4—2 收 06— 9— 0 修 20 0 5 [ 金 项 目]国家 自然 科 学 基 金 委 创新 群 体基 金 (02 02 资 助 项 目 基 66 10 )
图 1 腔 体 滤 波 器
Fi 1 A a i be g. c vt f r yi
[ 摘 要 ] 提 出一 种求 解 大 型 区 域 上 电磁 场边 值 问题 的 多子 空 间 投影 分 解 法 ,证 明其 具 有 几 何 的收 敛 速 度 ,并 且 从 理 论 上 分 析 影 响 收 敛 速 度 的 主 要 因 素 及 收 敛 特 性 .该 方 法 非 常 适 合 求 解 多 枝 区域 上 的 问题 ,实 际 算 例 和 理 论 分 析 完 全 一 致 .结 果 表 明子 区域 间 的 连 接 边 界 越 短 ,其 收敛 速 度 越 快 ,且 收 敛 速 度 主 要 取 决 于子 区 域 间 的 关
【国家自然科学基金】_边界元法_基金支持热词逐年推荐_【万方软件创新助手】_20140731

科研热词 边界元法 边界元 气泡 多极边界元法 弹塑性 射流 完全非线性 声辐射 势流理论 三维 高阶边界元 镜像格林函数 边界积分 边界 轧制压力 解析积分 裂纹 自然边界元法 网格 注塑模 水下爆炸 椭圆外区域 数值波浪水槽 数值模拟 快速多极边界元法 快速多极算法 弹性问题 弹塑性摩擦接触 对偶边界积分方程 多物体接触 声学灵敏度 helmholtz方程 高阶边界元法 高压互连线 频率扫描 镁合金 道路工程 远场 近奇异积分 边界识别 边界层效应 边界元偏移 轴对称壳 超轻多孔材料 误差分析 误差估计 识别方法 装配过程 裂纹问题 表面声场 舰船 自由面
107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106
一种基于局部金字塔分解的图像拼接
叠的边界相似区域 。根据被拼接 图像的在色彩 、 结 构意义上的相似性 , 确定重 叠范 围。必要 时重新调
整维数和作几何校正 。然后 , 在拼接过 渡区域范 围 内对被拼接图像进行多分 辨率分解 、 拟合过渡和重 构, 从而以较小 的计算代价得到拼接图像。
拼接算法的效率 。本文在经典的拉普拉斯金字塔分
解算法 的基础上 , 出了一种拼接计算局部化的方 提 法, 以期在保证拼接效果 的前提下实现更高 的拼接 效率。
2 基于 多分辨率图像 融合的 图像拼接
对被融合 ( 拼接) 图像 的内容误差和灰度误差
1 算 法原理
图像拼接可以看作是一种不重叠或部分重叠的 图像融合的特例 , 因此图像融合的方法完全可 以用 于图像拼接 , 实际上许 多图像拼接就是应 用图像融
基金项 目: 国家 自然科学基金资助项 目(0711 33 17 )
作者简 介 : 王长缨 (9 3 )男 , 16 一 , 山东诸城人 , 西北 大学博士生 , 福建农林大学副教授 , 事遥感 与图像 处理 研究。 从
8 - — —
维普资讯
西北大学学报 ( 自然科学版 ) 20 年 6月 , 3 06 第 6卷第 3 ,u .20 ,0 3 ,o3 期 Jn , 6V 1 6 N . 0 . Jun l fN r w s U ie i N t a cec dt n ora o ot et nvr t a rl ineE io ) h sy( u S i
量的前提 下明显提 高了基于金字塔分解的图像拼接算法效率。 关 键 词: 图像拼接 ; 字塔分解;多分辨率 金 中图分 类 号 :P 5 文献 标识 码 : 文章 编号 :0024 20 )30 8 - T71 A 10 -7 X(06 0 -350 4 图像拼接的解决涉及两个方面 : 一是拼接的准 确性问题 , 二是算法 的效率问题 。拼接的主要工作
【国家自然科学基金】_schwarz算法_基金支持热词逐年推荐_【万方软件创新助手】_20140802
科研热词 线性方程组求解 并行算法 块三对角矩阵 加性schwarz 不完全分解
推荐指数 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9
科研热词 线性方程组求解 并行算法 块三对角矩阵 双调和方程 区域分解算法 加性schwarz 不完全分解 schwarz方法 fourier变换
推荐指数 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2013年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
科研热词 并行计算 多址干扰 预条件 粗网格校正 稀疏线性方程组 码间干扰 极小-极大问题 数值离散 并行干扰消除 多址通信系统 区域分解 串行干扰消除 schwarz波形松弛 schwarz robin边界条件 ds-cdma
推荐指数 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5
科研热词 推荐指数 并行算法 1 半光滑函数 1 互补问题 1 schwarz预处理 1 newton-krylov-schwarz 1
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 推荐指数 并行计算 2 预条件 1 间断系数 1 间断有限元 1 脉冲噪声 1 聚集度(cm) 1 稀疏线性方程组 1 混凝土细观数值模拟 1 波形松驰 1 最小均方误差(mse) 1 抛物型方程 1 悬点 1 局部时间步长 1 局部多项式傅里叶变换(lpft) 1 局部多水平算法 1 区域分解 1 中值滤波器 1 不完全lu分解 1 clipping方法 1
热传导方程有限差分法的MATLAB实现
万方数据万方数据万方数据万方数据热传导方程有限差分法的MATLAB实现作者:史策作者单位:西安建筑科技大学,理学院,陕西,西安,710055刊名:咸阳师范学院学报英文刊名:JOURNAL OF XIANYANG NORMAL UNIVERSITY年,卷(期):2009,24(4)被引用次数:0次1.曹钢,王桂珍,任晓荣.一维热传导方程的基本解[J].山东轻工业学院学报,2005,19(4):76-80.2.万正苏,方春华,张再云.关于热传导方程有限差分区域分解并行算法精度的注记[J].湖南理工学院学报(自然科学版),2007,20(3):12-14.3.StephenJ.Chapman.MATLAB编程[M].邢树军,郑碧波,译.北京:科学出版社,2008.4.田兵.用MATLAB解偏微分方程[J].阴山学刊,2006,20(4):12-13.5.王飞,裴永祥.有限差分方法的MATLAB编程[J].新疆师范大学学报(自然科学版),2003,22(4):21-27.6.王宝红.热传导方程的可视化探讨[J].忻州师范学院学报,2008,24(2):31-36.7.李先枝.热传导方程差分解法的最佳网格[J].河南大学学报(自然科学版),2004,34(3):16-18.8.赵德奎,刘勇.MATLAB在有限差分数值计算中的应用[J].四川理工学院学报,2005,18(4):61-64.9.谢焕田,吴艳.拉普拉斯有限差分法的MATLAB实现[J].四川理工学院学报,2008,21(3):1-2.10.南京大学数学系计算数学专业.偏微分方程数值解法[M].北京:科学出版社,1979.1.学位论文申卫东热传导方程有限差分区域分解算法研究2003区域分解算法是在并行机上求解偏微分方程数值解的一种较自然的方法.该方法先将偏微分方程求解区域划分为若干个子区域,然后在各个子区域并行求解.全文共五章.第一章为引言,简要介绍了热传导方程并行算法的概况及该文所讨论的基本内容.在第二章,我们在内边界点为等距分划的多子区域条件下,得到Dawson等人关于求解热传导方程区域分解算法差分解的误差估计.在第三章,我们以Saul'yev非对称格式作内边界处理,发展了新的区域分解算法,得到了差分解的先验误差估计,并与Dawson等人的算法作了比较.给出了关于算法计算精度的数值结果.在第四章,我们发展了一些新技术,在子区域的边界处采用小时间步长古典显式格式求解,构造了新的区域分解算法,得到了差分解的先验误差估计.给出了关于算法计算精度的数值结果.在第五章,我们在二维热传导方程求解上扩充了Dawson等人的区域分解算法.给出了关于算法计算精度的数值结果.第六章为该研究工作的主要结论.2.期刊论文张守慧.王文洽.ZHANG Shou-hui.WANG Wen-qia热传导方程有限差分逼近的数学Stencil及其新型迭代格式-山东大学学报(理学版)2006,41(6)将Stencil应用于偏微分方程有限元差分逼近过程,以两类差分格式为基础建立了求解热传导方程的两种新型迭代算法.此两种算法与经典的Jacobi方法同样具有并行的性质,但比Jacobi方法收敛快.给出的算例说明方法的适用性.3.期刊论文吕桂霞.马富明.Lü Guixia.Ma Fuming二维热传导方程有限差分区域分解算法-数值计算与计算机应用2006,27(2)本文讨论了一类数值求解二维热传导方程的并行差分格式.在这个算法中,通过引进内界点将求解区域分裂成若干子区域.在子区域间内界点上采用非对称格式计算,一旦这些点的值被计算出来,各子区域间的计算可完全并行.本文得到了稳定性条件和最大模误差估计.它表明我们的格式有令人满意的稳定性,并且有着较高的收敛阶.4.学位论文田源地下煤火三维数理模型正演数值模拟2006本文首先给出了几个地下煤火随空间、温度变化的动态和稳态热数学物理模型及其简化模型。
一类优化问题的区域分解法
lm n e l p iaie d man d c mp st n me o s a e p o s .F n l e a d t n mu t l t o i e o o ii t d l mp e h i c v o h d ia y,te c n eg n e o e l h o vre c t f h meh d i e n tae . to s d mo srt d Ke r s:o t z t n;d man d o o sto y wo d pi a i mi o o i e mp i n;c n e e c c i ovr ne g
维普资讯
第2 2卷 第 2期
Vo . 2 No. 12 2
重 庆 工 学 院 学 报( 自然科 学 )
Junl f hnqn s t eo eh o g ( au l c ne ora o ogi I tu f cnl y N t a Si c ) C g n it T o r e
*
收 稿 日期 :0 7 2—1 20 —1 5
基金项 目: 郑州航空工业管理学院青年科研基金资助项 目( O C ̄ ) Q 6, . t 作者简介 : 朱军辉 (9O , , 18一)男 硕士 , 主要从事偏微分方程数值解方面的研究
维普资讯
朱 军辉 , : 类优化 问题 的 区域 分 解法 等 一
Z u —u . HE h nr i HU J n h i C NG C u — u
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
+ , 则存在正 常数 c 使 0
+
“ = O,
l 『 ≤C(I v l + I l ) V 关 lI o I ll ; l , v∈ P P ;
(O 1)
= 1nl 1 + . 2
,
:
// n 2  ̄ 2+ /
_
一
2 棚
u
D r÷ r (一 )
(F 42页 ) ]转 5
42 5
佳 木 斯 大 学 学 年 0 2.
界条件 , 它们是被极值解 自动满足的 , 无须作为定 解 条件 列 出. 因此 , 这 类 边 界 条件 为 自然 边 界条 称
’
柯朗 ・ 希尔伯 特. 学物理 方法 [ . 数 M] 北京 : 高等教 育 出版
Rih r b r n E e nay Ap l d P rilDi ee t c ad Ha e ma . lme tr pi at f rni E- e a l a
q aos( i or rSr sad B u dr a ePolm ) ut n wt Fui ei n on ayV u r e s i h e e l b
=
2 +2 n
内
:
内
:
{ 【
,
,
内
, u
‘
【 ” , 内 ’
, 臾u
,
z
∈
旷 (。且Y = , 厂) o 这里 3 是迹算子 , 3 = / o 即 J o
u ¨ 应 用 Fui l o r r级数 展 开 函数 u r0 , 到 e ( ,) 得
以转化为 +
d"
方程为例研究了一类椭圆边界各 向异性外问题 的 自 然边界元方法. 文献 [ ] 出了基于 自然边界归 6提 化原理的一种重叠型区域分解算法. 本文基于文献 [ ][] 5 ,6 在坐标变换及 圆外区域上 H lhl 边值 e oz m t 问题的 自 然边界归化的基础上 , 提出了一种求解椭 圆外 区域 上一类 各 向异性 常 系数 H l oz e mhl 边值 问 t 题的区域分解算法.
( )中 , 分 方 程 含 有 二 阶导 数 , 变 分 问题 ( ) 1 微 而 4 只含有 一 阶导数. 阶导数 的处 理 总是要 比高 阶导 低 数方便 些. 参考 文献 :
[ ] 艾利斯哥尔兹. 1 变分法 [ . M]北京 : 高等教育 出版社 , 8. 13 9
[ ] 老大中. 2 变分法基础 [ . M] 北京 : 国防工业出版社 , 0 . 2 3 0
+z :0相应地 区域 和边界 ,
J 可以转化为圆外 区域 和圆 r 1
t为 上任 一点 的单 位外 法 向量. , 于是 ( ) ( )可 1 、2 以转 化 为 :
a 毫 +z:, 。 ( 竹 后 o 内 、 … 在 5 )
+
1 问题 的描 述
2
【 ( 一 ,1 :0 Vv 口“ 秒) , 1∈
及
(1 1 )
对 1 r )=P 。0 式中的 r ,, ( u() 求导 , 并令 卜斗 +
0, 到 自然 积分方 程 : 得 ( 0 =一K 00 R ,) u( ) () 8
j E + , 求珏 u 使得
; ≠0 选取 的符 . i } ,
号使 得 I 居 m( )≥ 0 若 I k . m( )=0, 取 =0 是 则 ;
边界,的单位外法线方 向, 指向由,包围的区域内
部, 经计算可得 :
n一 +)詈 ) ( =( 吾} , 手 一詈 4 ( )
引入坐标变换 = ,= , Y 而 则方程() 1可
∈日 ( ) I =0 , 且 在无穷远处满 足辐射条
件 }则 , 可 视 为 俨 的子 空 间. 延拓 , 作
,
周 厂 将 分成两部分 : 1 一个是有界 区域 和一个
是 无界 区域 . 在极 坐标 系里 , ( ,)E ( ) ( 设 r , )∈
厂 ———
收 敛的. 取 可 = / 一 C同 1 嘉, 引理中 . o 所述 关于
0
利 用 Pi o 积 分 公 式 得 到,孙 = o sn s I 尸 ( ) , 中 y 是 上的迹算子. I 其
引理的证 明可以参考文献[ ] 6. 根据上述引理 和定理 , 迭代是几何收敛的, 而 且当区域重叠程度越大时迭代收敛越快.
第3 O卷 第 3期
21 年 0 月 02 5
佳 木 斯 大 学 学 报 (自 然 科 学 版 )
Ju a o a s U ie i N trl c neE io ) or l f i n J mui nvr t a a Si c dt n s y( u e i
Vo . O No. 13 3
”
=
P e P 2 川
+
h
=
,
2 l=O 蜴 + ,
【 e
= PyP i i e“
F
() 9
【
△
?
若 e 收敛 , 则必收敛 到 n 中. 似于文献 类 [ ]中引理 1的证 明, 7 可得到 : = + , + V。
=
{} 0. 引理 : V。 若 =
u 0
=
g 在 / 上 , - 任
,
L) ( O 6 J
-
设r 平 上 一 圆即 = () 詈 其 吾 g + J 面 的 椭 ,, { , ‘ + 中 =√ 1 是 , )
=
y
6
l, }不妨设 口> , 0 b>O力是 以为f内边界的 ,
于是边值问题 ( ) ( ) 5 ,6 又可以转化为变分问题 :
[ ] P n c — a tn l a I . 18 . M . r te H lI e a n . c , 7 ei l n r o1 n 9 Bu e a rn h a u s f a a os M] p ne — r i But eC c l r tn [ .Sr g c Vl .T l u o V ii i r
V = { EH ( , 。 l 1 ) 且 在无穷远处满足辐射条
件}
①
收稿 日期 :02—0 2 21 3- 3 作者简介 : 左文齐 (9 8一 ) 男 , 18 , 安徽安庆人 。 合肥工业大学硕士研究生.
第 3期
左 文 齐 , : 于 自然边界 归化 的椭 圆外 区域各 向异性 问题 的 重 叠型 域 分解 算 法 等 基
.
摘
要 : 以 Henot lhl r z方程 为例 , 于 坐标 变换及 自然边 界 归化 理 论 , 出 了一 种 带 圆型人 工 基 提
边界 的重 叠型 区域 分 解算 法. 造其 算 法并讨论 其相应 的收敛 性 , 明 了算 法是 几何 收 敛的. 构 证
关键词 : 自然边界归化; 重叠型区域分解算法; 收敛性 中 图分类号 : 0 4 . 2 2 18 文献标 识码 : A
【 ( 2一n ) =0 V ∈ a 2 ,2 ,
() 1 2
、
由双线 性形 口 ,) 义 内积 (, ) 和 上 的范数 ( 定 1 : 1 ,
3 算法的构造
以原点为 中心 , 。R ( R ,:0<R <R ) 2 1 为半径的
同心 圆周 , . ,
记
=
l 1, P 1・l 用 表示 到 y 按内积 ( , ) 的投影 : l ・ ・: 算子. 1 ) (2 等价于 : 则( 1 ,1 ) M” =J [ Ⅱ一In P ( Z )一( 2 一un ] 2 )
Pio os n积分 公式 : s 1r 1 , , )= P o ) r>R1 ( u( , () 7
并 且 “ 一 “
∈ ,
一
E .
于 是 ( ) (0 9 , 1 )等价 于 变分 问题 :
I ” ∈ +. 求 1 , 1 使得 , 2 ”
外部区域.
考虑二维 H lhl 方程 N u a n e oz m t e m n 外问题 : 口 ‘ Ⅱ=o 在 内 升‘ +b + , 。 一 () 1
』 EV , 求 使得 0
【( 口 ,)=<g >, tE V 一 , V, 0
r
,
∞
d r
第 四步 : n 置 :=n+l 转到第二步. 这里 u 。E 旷 ( )可 以任意给定 , 这里取为 零. 在第三步中的问题 实际上并不需要 直接求解 , 因为只需要知道 厂 上的函数值 ” , , 。 而 ” 可以
于引理的证明可以参考文献[ ] 8. 定理 : 对于本文所给的算法及区域划分有如下 的 误 差 估 计 ,即 存 在 常 数 ∈ [ ,) 0 1 ,使 得 l vP  ̄l ,I“ I I I迭代是几何 l  ̄ v I≤ P f I≤ I I e e ,
Ma y 2 2 01
文章编号 :0 8—10 2 1 0 o 4 10 4 2(02)3一 4 8—0 2
基 于 自然 边界 归化 的椭 圆外 区域 各 向异 性 问题 的重 叠 型 区域 分 解 算 法①
左 文 齐 , 寿城 王
( 合肥 工业大学 数学学院 , 安徽 合肥 2 0 0 ) 3 0 9
L =P ( —1” ) . t . 2 (3 1)
=
=蜴 I " , :=蜴 n 1 力 ,
构造如下的 S h a 交替算法 : cw r z
第一步 : 初始 o ( )=0, / =0 给定 E ,。 令 Z - , .
f △
“
其中: 是 在 中的正交补空间. 记 误差 为 e 一 , =0,, , (3 = 后 1 … 则 1 )式 表示误差传播关系 :
