八年级下册第四章综合测试卷
人教版初中地理八年级下册第四章单元测试题

八年级地舆(四·西北区域)※考试时刻:50分钟试卷满分:100分※1.单项选择题(下列每小题的4个备选答案中,只要1个是最契合题意的,请选出并将其代号填在下表所对应的方框内。
每小题2分,共50分)题号12345678910111213答案题号141516171819202122232425答案1.对我国四大地舆区域叙说不正确的是A.依据地舆方位、天然环境和人文地舆特征的不同,我国划分为四大地舆区域B.北方区域和西北区域的界限确认,主导要素是降水的影响C.“玉米黄,红高粱,大地笼罩青纱帐”是西北区域风景风光D.青藏区域“高寒”,冰川广布,雪山绵绵,热量缺乏2.我国四大地舆区域中大部分坐落我国地势第二级阶梯上的地舆区域是A.北方区域B.南边区域C.西北区域D.青藏区域3.以下所述不归于西北区域方位或规模的是A.大兴安岭以西B.昆仑山—阿尔金山以北C.祁连山以北D.黄土高原以东读图,答复4—6题4.图中甲地点的地势区是A.塔里木盆地B.四川盆地C.华北平原D.云贵高原5.图中A、B、C三地的植被依次为A.荒漠—荒漠草原—草原B.荒漠—草原—荒漠C.草原—荒漠—草原D.草原—荒漠草原—荒漠6.构成这种差异的首要要素是A.地势要素B.纬度方位C.海陆方位D.人类活动7.雅丹地貌是我国西北沙漠区域常见的一种地貌,构成该地貌的首要外力要素是A.流水B.冰川C.风力 D.生物8.下列不归于西北区域干旱原因的是A.纬度方位B.来自海洋的湿润气流难以抵达C.山脉对湿润气流的隔绝D.深居内陆,距海较远9.如图为一条旅行线路,下列描绘最能出现该线路特征词句的是A.黄河源头冰雪天,绵羊慢走在山间B.重走丝绸古路途,干旱困扰使人愁C.阴山脚下神威鼓,黄土高原信天游D.葡萄瓜果齿留香,青藏高原雪飘荡10.下列四个选项中,描绘西北区域的是A.土地使用类型以水田为主B.重要的草原和天山山地牧场C.从西往东由草原过渡到荒漠D.一起的高原气候,以“高寒”著称11.如图中,归于我国西北区域传统民居景象的是A.高脚屋B.蒙古包C.土楼D.四合院12.西北区域农业开展的限制性条件首要是A.水源条件B.光照条件C.地势条件D.科技条件13西北区域是我国重要的A.林业基地B.渔业基地C.畜牧业基地D.商品粮基地14.下列不归于我国西北区域重要农业区的是A.河套平原B.成都平原C.河西走廊D.宁夏平原15.下列描绘与图示内容不相关的是A.该区域是我国重要的牧区B.①山脉是第二、第三级阶梯的分界限C.三河马、藏绵羊、藏山羊散布本区D.图中从A→B→C降水量逐步削减16.被誉为“沙漠之舟”的畜牧种类是A.藏羚羊B.牦牛C.骆驼D.三河马17.下列家畜种类不归于西北区域优秀家畜的是A.牦牛B.三河马C.三河牛D.细毛羊18.河西走廊、宁夏平原、河套区域的农业首要是A.平原农业B.灌溉农业C.河谷农业D.立体农业读图,完结19—20题。
湘教版八年级数学下册《第四章一次函数》单元测试卷及答案

湘教版八年级数学下册《第四章一次函数》单元测试卷及答案[测试范围4.1~4.3时量:40分钟分值:100分]学校:___________班级:___________姓名:___________考号:___________一、选择题(每小题4分,共24分)1.下列选项中,y是x的函数的是()A.B.C.D.2.下列函数中,y与x成正比例函数关系的是()A.y=−12x−1B.y=−x C.y=5(x+1)D.y=−8x3.函数y=√x−1的自变量x的取值范围是()A.x<1B.x>1C.x≤1D.x≥14.甲、乙两车沿同一路线从A城出发前往B城,在整个行程中,汽车离开A城的距离y(km)与时刻t的对应关系如图所示,有下列结论:①A,B两城相距300km;②甲车的平均速度是60km/h,乙车的平均速度是100km/h;③乙车先出发,先到达B城;④甲车在9:30追上乙车.其中正确的结论有()A.①②B.①③C.②④D.①④5.正比例函数y=kx(k≠0)的图象经过第二、四象限,则一次函数y=x+k的图象大致是()A.B.C.D.6.下列有关一次函数y=−6x−5的说法中,正确的是()A.y随x的增大而增大B.函数图象与y轴的交点坐标为(0,5)C.当x>0时D.函数图象经过第二、三、四象限二、填空题(每小题4分,共20分)7.某水库的水位在5h内持续上涨,初始的水位高度为6m,水位以每小时0.3m的速度匀速上升,则水库的水位高度y(m)关于时间x(h)(0≤x≤5)的函数表达式为________________________.的值为0.8.当x=____时,函数y=3x−12−29.已知正比例函数y=(2−3a)x的图象经过第一、三象限,则a的取值范围是__________.10.在一次函数y=kx+3中,y随x的增大而增大,请你写出一个符合条件的k值:________________. 11.放学后,小明骑车回家,他经过的路程s(km)与所用时间t(min)之间的函数关系如图所示,则小明的骑车速度是____km/min.三、解答题(共56分)12.(8分)写出下列各题中y关于x的函数表达式,并判断y是否为x的一次函数?是否为正比例函数?(1)刚上市时西瓜每千克3.6元,买西瓜的总价y(元)与所买西瓜的质量x(kg)之间的关系;(2)仓库内有粉笔400盒,如果每个星期领出36盒,仓库内余下的粉笔盒数y与星期数x之间的关系;(3)小林的爸爸为小林存了一份教育储蓄,首次存入10 000元,以后每个月存入500元,存入总数y(元)与月数x之间的关系.13.(8分)已知函数y=(m−1)x m2+3是关于x的一次函数.(1)求m的值,并写出函数表达式;(2)判断点(1,2)是否在此函数图象上,并说明理由.14.(10分)已知一次函数y=(2−k)x−2k+6.(1)当k满足什么条件时,它的图象经过原点?(2)当k满足什么条件时,y随x的增大而增大?(3)当k满足什么条件时,图象经过第一、二、四象限?15.(14分)已知把直线y=kx+b向下平移4个单位后,得到直线y=x−1.(1)求直线y=kx+b的函数表达式.(2)求当x=1时y=kx+b中y的值;求当y=2时y=kx+b中x的值.(3)画出直线y=kx+b的图象.(4)直线y=kx+b图象上的两点C(x1,y1),D(x2,y2),如果x1>x2,试比较y1,y2的大小.x+8与x轴和y轴分别交于B,A两点,点C在y轴正半轴上,且OC=3,16.(16分)如图,已知直线y=45点P从点B出发沿x轴正方向以每秒1个单位长度的速度运动.设点P的运动时间为ts,连接AP.(1)写出点A,B的坐标:A(____,____),B(________,____);(2)当△APC为等腰三角形时,求t的值.参考答案一、选择题(每小题4分,共24分)1.D 2.B 3.B 4.D 5.B 6.D二、填空题(每小题4分,共20分)7.y=6+0.3x(0≤x≤5)8.49.a<2310.2(答案不唯一)11.0.2三、解答题(共56分)12.(1) 解:由题意,得y =3.6x ,y 是x 的一次函数,也是正比例函数.(2) 由题意,得y =400−36x ,y 是x 的一次函数,但不是正比例函数.(3) 由题意,得y =10000+500x ,y 是x 的一次函数,但不是正比例函数.13.(1) 解:由y =(m −1)xm 2+3是关于x 的一次函数,得{m 2=1,m −1≠0,解得m =−1. 故函数表达式为y =−2x +3.(2) 不在.理由如下:将x =1代入表达式,得y =1≠2.∴ 点(1,2)不在此函数图象上.14.(1) 解:∵ 一次函数y =(2−k )x −2k +6的图象经过原点∴−2k +6=0解得k =3.(2) ∵ 一次函数y =(2−k )x −2k +6中,y 随x 的增大而增大∴2−k >0解得k <2.(3) ∵ 该函数的图象经过第一、二、四象限∴{2−k <0,−2k +6>0,解得2<k <3. 15.(1) 解:∵ 把直线y =kx +b 向下平移4个单位后,得到直线y =x −1 ∴ 直线y =kx +b 的函数表达式为y =x +3.(2) 由(1)得一次函数的表达式为y =x +3.当x =1时y =4;当y =2时x =−1.(3) 如答图.第15题答图(4) ∵k =1>0∴y 随x 的增大而增大∴ 当x 1>x 2时y 1>y 2.16.(1) 0; 8; -10; 0(2)解:由题意,可得AP≠AC,AP≠PC∴AC=PC.∵AO=8,OC=3∴AC=5,PC=5在Rt△POC中PC2=OC2+OP2∴OP=√52−32=4.①当点P在x轴负半轴上时BP=10−4=6,∴t=6;②当点P在x轴正半轴上时BP=10+4=14,∴t=14.综上所述,t的值为6或14.。
人教版初中地理八年级下册第四章单元测试题
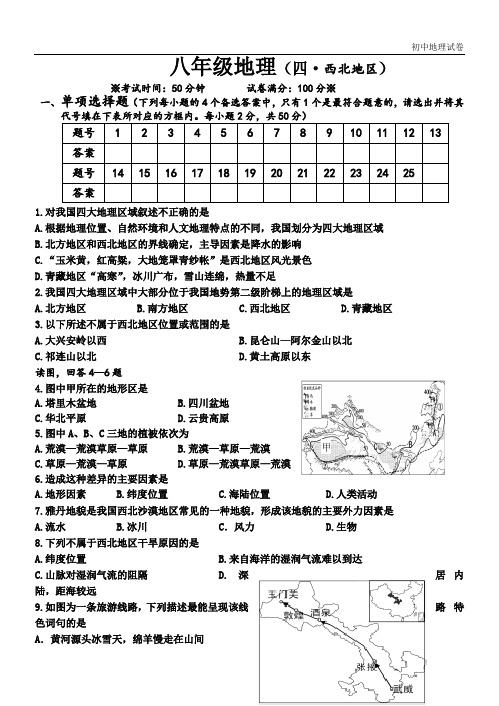
甲八年级地理(四·西北地区)※考试时间:50分钟 试卷满分:100分※一、 单项选择题(下列每小题的4个备选答案中,只有1个是最符合题意的,请选出并将其1.对我国四大地理区域叙述不正确的是A.根据地理位置、自然环境和人文地理特点的不同,我国划分为四大地理区域B.北方地区和西北地区的界线确定,主导因素是降水的影响C.“玉米黄,红高粱,大地笼罩青纱帐”是西北地区风光景色D.青藏地区“高寒”,冰川广布,雪山连绵,热量不足2.我国四大地理区域中大部分位于我国地势第二级阶梯上的地理区域是 A.北方地区B.南方地区C.西北地区D.青藏地区3.以下所述不属于西北地区位置或范围的是 A.大兴安岭以西 B.昆仑山—阿尔金山以北 C.祁连山以北D.黄土高原以东读图,回答4—6题4.图中甲所在的地形区是A.塔里木盆地B.四川盆地C.华北平原D.云贵高原 5.图中A 、B 、C 三地的植被依次为A.荒漠—荒漠草原—草原B.荒漠—草原—荒漠C.草原—荒漠—草原D.草原—荒漠草原—荒漠 6.造成这种差异的主要因素是A.地形因素B.纬度位置C.海陆位置D.人类活动 7.雅丹地貌是我国西北沙漠地区常见的一种地貌,形成该地貌的主要外力因素是 A.流水B.冰川 C .风力D.生物8.下列不属于西北地区干旱原因的是 A.纬度位置B.来自海洋的湿润气流难以到达C.山脉对湿润气流的阻隔D.深居内陆,距海较远9.如图为一条旅游线路,下列描述最能呈现该线路特色词句的是A .黄河源头冰雪天,绵羊慢走在山间C.阴山脚下威风鼓,黄土高原信天游D.葡萄瓜果齿留香,青藏高原雪飘扬10.下列四个选项中,描述西北地区的是A.土地利用类型以水田为主B.重要的草原和天山山地牧场C.从西往东由草原过渡到荒漠D.独特的高原气候,以“高寒”著称11.如图中,属于我国西北地区传统民居景观的是A.高脚屋B.蒙古包C.土楼D.四合院12.西北地区农业发展的限制性条件主要是A.水源条件B.光照条件C.地形条件D.科技条件13西北地区是我国重要的A.林业基地B.渔业基地C.畜牧业基地D.商品粮基地14.下列不属于我国西北地区重要农业区的是A.河套平原B.成都平原C.河西走廊D.宁夏平原15.下列描述与图示内容不相关的是A.该区域是我国重要的牧区B.①山脉是第二、第三级阶梯的分界线C.三河马、藏绵羊、藏山羊分布本区D.图中从A→B→C降水量逐渐减少16.被誉为“沙漠之舟”的畜牧品种是A.藏羚羊B.牦牛C.骆驼D.三河马17.下列牲畜品种不属于西北地区优良牲畜的是A.牦牛B.三河马C.三河牛D.细毛羊18.河西走廊、宁夏平原、河套地区的农业主要是A.平原农业B.灌溉农业C.河谷农业D.立体农业读图,完成19—20题。
2022年最新强化训练北师大版八年级数学下册第四章因式分解综合测试试题(含答案解析)

北师大版八年级数学下册第四章因式分解综合测试考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、下列从左边到右边的变形,是因式分解的是()A.(3﹣x)(3+x)=9﹣x2B.x2+y2=(x+y)(x﹣y)C.x2﹣x=x(x﹣1)D.2yz﹣y2z+z=y(2z﹣yz)+z2、下列等式中,从左往右的变形为因式分解的是()A.a2﹣a﹣1=a(a﹣1﹣1)aB.(a﹣b)(a+b)=a2﹣b2C.m2﹣m﹣1=m(m﹣1)﹣1D.m(a﹣b)+n(b﹣a)=(m﹣n)(a﹣b)3、下列各组多项式中,没有公因式的是()A.ax﹣by和by2﹣axy B.3x﹣9xy和6y2﹣2yC.x2﹣y2和x﹣y D.a+b和a2﹣2ab+b24、下列各式中,能用完全平方公式分解因式的是()A .2161x +B .221x x +-C .2224a ab b ++D .214x x -+5、下列因式分解正确的是( )A .2244(2)a a a ++=+B .24(4)a a a a -+=-+C .22(3)69a a a -=-+D .221(2)1a a a a -+=-+6、多项式22ax ay -分解因式的结果是( )A .()22a x y +B .()()a x y x y +-C .()()a x y x y ++D .()()ax y ax y +-7、已知c <a <b <0,若M =|a (a ﹣c )|,N =|b (a ﹣c )|,则M 与N 的大小关系是()A .M <NB .M =NC .M >ND .不能确定8、下列各式的因式分解中正确的是( )A .2()a ab ac a a b c -+-=-+-B .22963(32)xyz x y xyz xy -=-C .()2236332a x bx x x a b -+=-D .22111()222xy x y xy x y +=+9、若a 、b 、c 为一个三角形的三边,则代数式(a -c )2-b 2的值( )A .一定为正数B .一定为负数C .为非负数D .可能为正数,也可能为负数10、下列变形,属因式分解的是( )A .262(3)x x +=+B .29(9)(9)x x x -=-+C .221(2)1x x x x ++=++D .242(4)mx my m x y -=-第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、分解因式:25105a a ++=___.2、在实数范围内因式分解:y 2﹣2y ﹣1=__________________.3、若2230x y xy +=,6xy =,则x y -的值为______.4、因式分解:(1)22x y -=______; (2)222x xy y ++=______;(3)25a a -=______; (4)276m m -+=______.5、因式分解:2363x x -+=______.三、解答题(5小题,每小题10分,共计50分)1、因式分解:22496m n mn ---.2、分解因式(1)32484xy xy xy ++(2)22-5105a ab b +-3、分解因式:(1)316m m -;(2)()228a b ab -+. 4、因式分解:3269xy xy xy -+5、分解因式:(1)3a 2﹣6a +3(2)(x 2+y 2)2﹣4x 2y 2-参考答案-一、单选题1、C【分析】根据因式分解的定义:把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个因式分解(也叫作分解因式),进行判断即可.【详解】解:A 、(3﹣x )(3+x )=9﹣x 2属于整式的乘法运算,不是因式分解,不符合题意;B 、22()()x y x y x y -=+-,原式错误,不符合题意;C 、x 2﹣x =x (x ﹣1),属于因式分解,符合题意;D 、2yz ﹣y 2z +z =2(21)z y y -+,原式分解错误,不符合题意;故选:C .【点睛】本题考查了因式分解的定义,熟记因式分解的定义即把一个多项式化为几个最简整式的乘积的形式,这种变形叫做把这个因式分解(也叫作分解因式)是解本题的关键.2、D【分析】把一个多项式化为几个整式的乘积的形式叫因式分解,根据定义对各选项进行一一分析判断即可.【详解】A. a 2﹣a ﹣1=a (a ﹣1﹣1a )∵从左往右的变形是乘积形式,但(a ﹣1﹣1a)不是整式,故选项A 不是因式分解;B. (a﹣b)(a+b)=a2﹣b2,从左往右的变形是多项式的乘法,故选项B不是因式分解;C. m2﹣m﹣1=m(m﹣1)﹣1,从左往右的变形不是整体的积的形式,故选项C不是因式分解;D.根据因式分解的定义可知m(a﹣b)+n(b﹣a)=(m﹣n)(a﹣b)是因式分解,故选项D从左往右的变形是因式分解.故选D.【点睛】本题考查因式分解,掌握因式分解的特征从左往右的变形后各因式乘积,各因式必须为整式,各因式之间不有加减号是解题关键.3、D【分析】直接利用公因式的确定方法:①定系数,即确定各项系数的最大公约数;②定字母,即确定各项的相同字母因式(或相同多项式因式);③定指数,即各项相同字母因式(或相同多项式因式)的指数的最低次幂,进而得出答案.【详解】解:A、by2−axy=−y(ax−by),故两多项式的公因式为:ax−by,故此选项不合题意;B、3x−9xy=3x(1−3y)和6y2−2y=−2y(1−3y),故两多项式的公因式为:1−3y,故此选项不合题意;C、x2−y2=(x−y)(x+y)和x−y,故两多项式的公因式为:x−y,故此选项不合题意;D、a+b和a2−2ab+b2=(a−b)2,故两多项式没有公因式,故此选项符合题意;故选:D.【点睛】此题主要考查了公因式,掌握确定公因式的方法是解题关键.4、D【分析】根据完全平方公式法分解因式,即可求解.【详解】解:A 、不能用完全平方公式因式分解,故本选项不符合题意;B 、不能用完全平方公式因式分解,故本选项不符合题意;C 、不能用完全平方公式因式分解,故本选项不符合题意;D 、221142x x x ⎛⎫-+=- ⎪⎝⎭能用完全平方公式因式分解,故本选项符合题意; 故选:D【点睛】本题主要考查了完全平方公式法分解因式,熟练掌握()2222a ab b a b ±+=± 是解题的关键.5、A【分析】根据因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做因式分解,进行判断即可.【详解】解:A 、2244(2)a a a ++=+,选项说法正确,符合题意; B 、24(4)a a a a -+=--,选项说法错误,不符合题意;C 、22(3)69a a a -=-+是整式乘法运算,不是因式分解,选项说法错误,不符合题意;D 、2221(1)a a a -+=-,选项说法错误,不符合题意;故选A .【点睛】本题考查了因式分解,解题的关键是掌握因式分解的定义以及分解的正确性.【分析】先提取公因式a,再根据平方差公式进行二次分解.平方差公式:a2-b2=(a+b)(a-b).【详解】解:ax2-ay2=a(x2-y2)=a(x+y)(x-y).故选:B.【点睛】本题考查了提公因式法,公式法分解因式,提取公因式后利用平方差公式进行二次分解,注意分解要彻底.7、C【分析】方法一:根据整式的乘法与绝对值化简,得到M-N=(a﹣c)(b﹣a)>0,故可求解;方法二:根据题意可设c=-3,a=-2,b=-1,再求出M,N,故可比较求解.【详解】方法一:∵c<a<b<0,∴a-c>0,∴M=|a(a﹣c)|=- a(a﹣c)N=|b(a﹣c)|=- b(a﹣c)∴M-N=- a(a﹣c)-[- b(a﹣c)]= - a(a﹣c)+ b(a﹣c)=(a﹣c)(b﹣a)∵b-a>0,∴(a﹣c)(b﹣a)>0方法二: ∵c <a <b <0,∴可设c =-3,a =-2,b =-1,∴M =|-2×(-2+3)|=2,N =|-1×(-2+3)|=1∴M >N故选C .【点睛】此题主要考查有理数的大小比较与因式分解得应用,解题的关键求出M -N =(a ﹣c )(b ﹣a )>0,再进行判断.8、D【分析】根据提公因式法,先提取各个多项式中的公因式,再对余下的多项式进行观察,能分解的继续分解.【详解】A -a 2+ab -ac =-a (a -b +c ) ,故本选项错误;B 9xyz -6x 2y 2=3xy (3z -2xy ),故本选项错误;C 3a 2x -6bx +3x =3x (a 2-2b +1),故本选项错误;D 22111()222xy x y xy x y +=+,故本选项正确.故选:D .【点睛】本题考查提公因式法分解因式,准确确定公因式是求解的关键.9、B【分析】根据在三角形中任意两边之和大于第三边,任意两边之差小于第三边.即可求解.【详解】解:∵a 、b 、c 为一个三角形的三边,∴a -c +b >0,a -c -b <0,∴(a -c )2-b 2=(a -c +b )(a -c -b )<0.∴代数式(a -c )2-b 2的值一定为负数.故选:B .【点睛】本题考查了运用平方差公式因式分解,利用了三角形中三边的关系:在三角形中,任意两边之和大于第三边,任意两边之差小于第三边.10、A【分析】依据因式分解的定义:把一个多项式化为几个整式的积的形式,这种变形叫做把这个多项式因式分解,也叫做分解因式判断即可.【详解】解:A 、262(3)x x +=+是因式分解,故此选项符合题意;B 、29(3)(3)x x x -=-+分解错误,故此选项不符合题意;C 、221(2)1x x x x ++=++右边不是几个整式的积的形式,故此选项不符合题意;D 、242(2)mx my m x y -=-分解错误,故此选项不符合题意;故选:A .【点睛】本题主要考查的是因式分解的意义,掌握因式分解的定义是解题的关键.二、填空题1、25(1)a +##【分析】先提取公因式5,后用和的完全平方公式即可.【详解】∵25105a a ++=25(1)a +,故答案为25(1)a +.【点睛】本题考查了因式分解,熟练掌握先提取公因式,后用公式的解题策略是解题的关键.2、(y ﹣1)(y ﹣1)【分析】变形整式为y 2﹣2y +1﹣2,前三项利用完全平方公式,再利用平方差公式因式分解.【详解】解:y 2﹣2y ﹣1=y 2﹣2y +1﹣2=(y ﹣1)22=(y ﹣1)(y ﹣1).故答案为:(y ﹣1(y ﹣1.【点睛】本题主要考查了多项式的因式分解,熟练掌握多项式因式分解的方法是解题的关键.3、±1【分析】先把提取公因式xy ,根据6xy =,求出x y +的值,再根据22()()4x y x y xy -=+-,求出2()x y -的值,即可得出x y -的值.【详解】解:2230x y xy +=,()30xy x y ∴+=,6xy =,5x y ∴+=,222()()45461x y x y xy -=+-=-⨯=,1x y ∴-=±;故答案为:±1.【点睛】此题考查了因式分解的应用,解决此类问题要整体观察,根据具体情况综合应用相关公式进行整体代入是解决这类问题的基本思想.4、()()x y x y +- 2()x y + (5)a a - (6)(1)m m --【分析】把一个多项式化成几个整式积的形式叫做这个多项式的因式分解,由此定义因式分解即可.【详解】(1)由平方差公式有22()()x y x y x y -=+-(2)由完全平方公式有222)2(x xy y x y =+++(3)提取公因式a 有25(5)a a a a -=-(4)由十字相乘法分解因式有276(6)(1)m m m m -+=--故答案为:()()x y x y +-;2()x y +;(5)a a -;(6)(1)m m --.【点睛】本题考查了因式分解,常见因式分解的方式有运用平方差公式、运用完全平方公式、提取公因式、十字相乘法,灵活选择因式分解的方式是解题的关键.5、23(1)x -【分析】先提取公因式,再用完全平方公式分解即可.【详解】解:2363x x -+,=23(21)x x -+,=23(1)x -故答案为:23(1)x -.【点睛】本题考查了因式分解,解题关键是熟练运用提取公因式和公式法进行因式分解.三、解答题1、(23)(23)m n m n ++--【分析】首先对后面三项利用完全平方公式进行因式分解,然后利用平方差公式因式分解即可.【详解】解:原式224(96)m n mn =-++222(3)m n =-+(23)(23)m n m n =++--.【点睛】此题考查了因式分解的方法,解题的关键是熟练掌握因式分解的方法.因式分解的方法有:提公因式法,平方差公式法,完全平方公式法,十字相乘法等.2、(1)4xy (y +1)2;(2)-5(a -b )2【分析】(1)提公因式后利用完全平方公式分解即可;(2)提公因式后利用完全平方公式分解即可.【详解】(1)32484xy xy xy ++,()2421xy y y =++ ,=4xy (y +1)2;(2)22-5105a ab b +-,()2252a ab b =--+ ,=-5(a -b )2.【点睛】本题考查了提公因式法与公式法的综合运用,一定要注意有公因式先提公因式,然后再继续分解.3、(1)()()44m m m +-;(2)()22a b + 【分析】(1)先提取公因式,然后再根据平方差公式进行因式分解即可;(2)先利用完全平方公式展开,然后合并同类项,进而再因式分解即可.【详解】解:(1)原式=()()()21644m m m m m -=+-;(2)原式=()22222448442a ab b ab a ab b a b -++=++=+.【点睛】本题主要考查因式分解,熟练掌握因式分解的方法是解题的关键.4、()23xy y -【分析】直接提取公因式xy ,再利用完全平方公式分解因式得出答案【详解】解:3269xy xy xy -+()269xy y y =-+()23xy y =- 【点睛】此题主要考查了提取公因式法以及公式法分解因式,正确运用乘法公式分解因式是解题关键.5、(1)23(1)a -;(2)22()()x y x y +-【分析】(1)先提公因式3,再由完全平方公式进行因式分解;(2)先由完全平方公式去括号,化简再由完全平方公式以及平方差公式进行因式分解即可.【详解】(1)2363a a -+,23(21)a a =-+,23(1)a =-;(2)2222()4x y x y +-,42242224x x y y x y =++-,42242x x y y =-+,222()x y =-,22()()x y x y =+-.【点睛】此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.。
北师大八年级数学下册第四章综合检测题.docx

鑫达捷 初中数学试卷 桑水出品第四章综合检测题一、选择题:1.下列各多项式中,不能用平方差公式分解的是( )A .a 2b 2-1B .4-0.25a 2C .-a 2-b 2D .-x 2+12.如果多项式x 2-mx+9是一个完全平方式,那么m 的值为( )A .-3B .-6C .±3D .±63.下列变形是分解因式的是( )A .6x 2y 2=3xy ·2xyB .a 2-4ab+4b 2=(a -2b)2C .(x+2)(x+1)=x 2+3x+2D .x 2-9-6x=(x+3)(x -3)-6x4.下列多项式的分解因式,正确的是( )A .)34(391222xyz xyz y x xyz -=-B .)2(363322+-=+-a a y y ay y aC .)(22z y x x xz xy x -+-=-+-D .)5(522a a b b ab b a +=-+5.若a -b=6,ab=7,则ab 2-a 2b 的值为( )A .42B .-42C .13D .-136.把多项式)2()2(2a m a m -+-分解因式等于( )A .))(2(2m m a +-B .))(2(2m m a --C .m(a-2)(m-1)D .m(a-2)(m+1)7.下列多项式中,含有因式)1(+y 的多项式是() A .2232x xy y -- B .22)1()1(--+y yC .)1()1(22--+y yD .1)1(2)1(2++++y y8.已知多项式c bx x ++22分解因式为)1)(3(2+-x x ,则c b ,的值为( )A .1,3-==c bB .2,6=-=c bC .4,6-=-=c bD .6,4-=-=c b9.c b a 、、是△ABC 的三边,且bc ac ab c b a ++=++222,那么△ABC 的形状是( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等边三角形鑫达捷 10.若等式x 2-x+k=(x-12)2成立,则k 的值是( ) A .12 B .-14 C .14 D .±14 二、填空题:11.多项式-2x 2-12xy 2+8xy 3的公因式是_____________.12.利用分解因式计算:32003+6×32002-32004=_____________. 13._______+49x 2+y 2=(_______-y)2.14.请将分解因式的过程补充完整: a 3-2a 2b+ab 2=a (________)=a (___________)215.已知a 2-6a+9与|b -1|互为相反数,计算a 3b 3+2a 2b 2+ab 的结果是_________.16.+162x ( )2) (1=+, 2y]) [()] (21[) (4122-+=-x x 17.若)4)(2(2-+=++x x q px x ,则p = ,q = 。
浙教版八年级数学下册第四章测试题(附答案)

浙教版八年级数学下册第四章测试题(附答案)一、单选题1.如图,平行四边形ABCD的对角线AC,BD相交于点O,下列结论错误..的是()A. OA=OCB. AB=CDC. AD=BCD. ∠ABD=∠CBD2.平行四边形不一定具有的性质是()A. 对角线互相平分B. 对边平行C. 对角线互相垂直D. 对边相等3.在平行四边形ABCD中,若∠B=135°,则∠D=()A. 45°B. 55°C. 135°D. 145°4.如图,点E是▱ABCD中边BC延长线上一点,下列结论不一定成立的是()A. AB=CDB. ∠ABD+∠ADB=∠DCEC. ∠BAD=∠BCDD. ∠ABD=∠CBD5.下列手机APP图标中,不是中心对称图形的是()A. B. C. D.6.如图,对四边形ABCD 增加条件,使之成为平行四边形,下面添加不正确的是()A. B.C. D. 与相互平分7.一个多边形的内角和是外角和的倍,则这个多边形是()A. 六边形B. 五边形C. 四边形D. 七边形8.如果一个多边形的每一个内角都是,那么这个多边形是()A. 四边形B. 五边形C. 六边形D. 七边形9.如图,在平行四边形ABCD中,∠A=40°,则∠C大小为( )A. 40°B. 80°C. 140°D. 180°10.在中,,则的度数是()A. B. C. D.11.在下列条件中,不能确定四边形ABCD为平行四边形的是().A. ∠A=∠C,∠B=∠DB. ∠A+∠B=180°,∠C+∠D=180°C. ∠A+∠B=180°,∠B+∠C=180°D. ∠A=∠B=∠C=90°12.在□ABCD中,如果,那么的度数是()A. 115ºB. 65ºC. 25ºD. 35º二、填空题13.一个n边形的内角和与外角和相等,则n=________.14.如图,在▱ABCD中,对角线AC,BD相交于点O,若AC=10,则AO=________.15.已知三角形的周长为20cm,连接各边中点所得的三角形的周长为________cm.16.如图,在▱ABCD中,∠BCD的平分线交AD于点E,AB=3,AE=1,则BC=________.17.若n边形的每一个外角都是72°,则边数n为________.18.已知一个多边形的外角和等于其内角和的,则这个多边形的边数为________.19.平行四边形ABCD中,∠A+∠C=120°,则∠B=________度.20.如图,在四边形中,,要使四边形成为平行四边形,则应增加的条件是________(写一个即可).21.已知一个多边形的每一个外角都等于,则这个多边形的边数是________.22.正十边形的每个外角都等于________度.三、解答题23.如图是一个凹多边形,,,,;求的值.24.多边形的内角和与某一外角的度数总和为1 350°,那么这个多边形的边数是多少?25.一个正多边形的内角和为1800°,求这个多边形的边数.四、综合题26.如图,平行四边形ABCD 的对角线AC、BD 交于O 点,AE∥BD,∠AED=∠AOD,连接OE.(1)求证:AE=OB;(2)求证:四边形CDEO 是平行四边形.27.如图,平行四边形ABCD中,AE、DE分别平分∠BAD、∠ADC,E点在BC上.(1)求证:BC=2AB;(2)若AB=3cm,∠B=60°,一动点F以1cm/s的速度从A点出发,沿线段AD运动,CF交DE于G,当CF∥AE时:①求点F的运动时间t的值;②求线段AG的长度.答案一、单选题1. D2. C3. C4. D5. B6. B7. A8. B9. A 10. C 11. B 12. B二、填空题13. 4.14. 5 15. 10 16. 4 17. 5 18. 5 19. 120 20. AD∥DC 21. 5 22. 36°三、解答题23. 证明:连接∵,∴,∵,,,,∴.24. 解:设边数为n,外角为x°,则x+(n-2)×180=1 350.∴x=1 350-180(n-2).∵0<x<180,∴0<1 350-(n-2)×180<180.解得<n< .∵n为整数,∴n=9.25. 解:设这个多边形的边数是,则,解得:.故这个多边形的边数为12.四、综合题26. (1)∵AE∥BD,∴∠AED+∠EDO=180°,∵∠AED=∠AOD,∴∠AOD +∠EDO =180°,∴AO∥DE,∴四边形DEAO是平行四边形,∴AE=OD,∵四边形ABCD是平行四边形,∴OB=OD,∴AE=OB;(2)∵AE=OB,且AE∥OB,∴四边形AEOB是平行四边形,∴AB=OE,AB∥OE,∵AB=CD,AB∥CD,∴OE = CD,OE∥CD,∴四边形CDEO是平行四边形.27. (1)证明:∵四边形ABCD是平行四边形,∴AB=CD,AD∥BC,∴∠DAE=∠AEB,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∴AB=BE,同理:CE=CD,∴BE=CE=AB,∴BC=BE+CD=2AB;(2)①由(1)知,CE=CD=AB,∵AB=3cm,∴CE=3cm,∵四边形ABCD是平行四边形,∴AD∥BC∵AE∥CF,∴四边形AECF是平行四边形,∴AF=CE=3cm,∴点F的运动时间t=3÷1=3(秒);②由(1)知AB=BE,∵∠B=60°,∴△ABE是等边三角形,∴∠AEB=60°,AE=AB=3cm,∵四边形ABCD是平行四边形,∴∠B+∠BCD=180°,∵∠B=60°,∴∠BCD=120°,∵AE∥CF,∴∠ECF=∠AEB=60°,∴∠DCF=∠BCD﹣∠ECF=60°=∠ECF,由(1)知,CE=CD=AB=3cm,∴CF⊥DE,∴∠CGE=90°,在Rt△CGE中,∠CEG=90°﹣∠ECF=30°,CG=CE=,∴EG=CG=,∵∠AEB=60°,∠CEG=30°,∴∠AEG=90°,在Rt△AEG中,AE=3,根据勾股定理得,AG=.。
初中数学 八年级数学下册 第四章 相似图形单元综合测试考试卷及答案 北师大版
xx 学校xx 学年xx 学期xx 试卷姓名:_____________ 年级:____________ 学号:______________题型选择题 填空题 简答题 xx 题 xx 题 xx 题 总分 得分一、xx 题 (每空xx 分,共xx 分)试题1:已知点C 是直线AB 上的一点,且AB ∶BC =1∶2,那么AC ∶BC 等于( ).A .3∶2B .2∶3或1∶2C .1∶2D .3∶2或1∶2试题2:若两个相似三角形周长的比为9∶25,则它们的面积比为( ).A .3∶5B .9∶25C .81∶625D .以上都不对试题3:“标准对数视力表”对我们来说并不陌生,下图是视力表的一部分,其中最上面较大的“E ”与下面四个较小“E ”中的哪一个是位似图形( ).A .左上B .左下C .右上D .右下试题4:如图,已知DE ∥BC ,EF ∥AB ,下列结论正确的是( ).评卷人得分A. B.C. D.试题5:下列条件中不能判定△ABC和△A′B′C′相似的是( ).A.∠B=25°,∠C=50°,∠B′=105°,∠C′=25°B.AB=9,AC=6,A′B′=4.5,A′C′=3,∠A=50°,∠B′=60°,∠C′=70°C.AB=,AC=,B′C′=2BCD.AB=5,BC=3,A′B′=15,B′C′=9,∠A=∠A′=31°试题6:如图,一个高为1 m的油桶内有油,一根木棒长1.2 m,从桶盖小口斜插入桶内,一端到桶底,另一端正好到小口,抽出棒,量得棒上浸油部分长0.45 m,则桶内油的高度是( ).A.0.375 m B.0.385 mC.0.395 m D.0.42 m试题7:如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是( ).A.2 cm2 B.4 cm2C.8 cm2 D.16 cm2试题8:某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),则小鱼上的点(a,b)对应大鱼上的点( ).A.(-2a,-2b) B.(-a,-2b)C.(-2b,-2a) D.(-2a,-b)试题9:若,则=__________.试题10:如图,△ABC中,DE∥BC,DE分别交边AB,AC于D,E两点,若AD∶AB=1∶3,则△ADE与△ABC的面积比为__________.试题11:晚上,小亮走在大街上.他发现:当他站在大街两边的两盏路灯之间,并且自己被两边路灯照在地上的两个影子成一直线时,自己右边的影子长为3 m,左边的影子长为1.5 m.又知自己身高1.80 m,两盏路灯的高度相同,两盏路灯之间的距离为12 m,则路灯的高为__________m.试题12:要拼出和图①中的菱形相似的较长对角线为88 cm的大菱形(如图②所示),需要图①中的菱形的个数为__________.试题13:陈明同学想知道一根电线杆的高度,他拿着一把刻有厘米的小尺,站在距电线杆约30 m的地方,把手臂向前伸直,小尺竖直,看到刻度尺上有12个厘米刻度恰好遮住电线杆(如图所示),已知臂长约60 cm,请你根据以上数据,帮助陈明同学算出电线杆的高度是__________.试题14:如图,△ABC三个顶点坐标分别为A(1,2),B(3,1),C(2,3),以原点O为位似中心,将△ABC放大为原来的2倍得到△A′B′C′.(1)在图中第一象限内画出符合要求的△A′B′C′;(不要求写画法)(2)△A′B′C′的面积是__________.试题15:小颖用下面的方法来测量学校教学大楼AB的高度:如图所示,在水平地面上放一面平面镜,镜子与教学大楼的距离EA=21 m,当她与镜子的距离CE=2.5 m时,她刚好能从镜子中看到教学大楼的顶端B.已知她的眼睛距地面高度DC=1.6 m,请你帮助小颖计算出教学大楼的高度AB是多少米?(注:根据光的反射定律,有反射角等于入射角.)试题16:如图,在Rt△ABC中,∠B=90°,AB=1,BC=,以点C为圆心,CB为半径的弧交CA于点D;以点A为圆心,AD为半径的弧交AB于点E.(1)求AE的长度;(2)分别以点A,E为圆心,AB长为半径画弧,两弧交于点F(F与C在AB两侧),连接AF,EF,设EF交弧DE所在的圆于点G,连接AG,试猜想∠EAG的大小,并说明理由.试题17:如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC,DE与AB相交于点E,EC与AD相交于点F.(1)△ABC与△FCD相似吗?请说明理由.(2)点F是线段AD的中点吗?为什么?(3)若S△ABC=20,BC=10,求DE的长.试题1答案:D试题2答案:C试题3答案:B试题4答案:B试题5答案:D根据相似三角形的三种判定方法判断即可.试题6答案:A试题7答案:C试题8答案:A试题9答案:试题10答案:1∶9试题11答案:6.6试题12答案:121试题13答案:6 m解析:由实际问题画出数学示意图,借助相似三角形对应高的比等于相似比的性质即可获解.如图所示,作AM⊥BC于M,交DE于N,DE=12 cm,AN=60 cm,AM=30 m.由题意知DE∥BC,所以∠ADE=∠B,∠AED=∠C.所以△ADE∽△ABC.所以AN∶AM=DE∶BC,即0.6∶30=0.12∶BC,解得BC=6 m.试题14答案:解:(1)画图如下图所示:(2)6试题15答案:解:根据光的反射定律,有∠1=∠2,所以∠BEA=∠DEC.又知∠A=∠C=90°,所以△BAE∽△DCE.所以,AB=·DC=×1.6=13.44(m).答:教学大楼的高约为13.44 m.试题16答案:解:(1)在Rt△ABC中,由AB=1,BC=,得AC=. ∵BC=CD,AE=AD,∴AE=AC-CD=.(2)∠EAG=36°,理由如下:∵FA=FE=AB=1,AE=,∴.∴△FAE是黄金三角形.∴∠F=36°,∠AEF=72°.∵AE=AG,FA=FE,∴∠FAE=∠FEA=∠AGE.∴△AEG∽△FEA.∴∠EAG=∠F=36°.试题17答案:解:(1)相似.∵AD=AC,∴∠CDF=∠BCA.∵DE垂直平分线段BC,∴EB=EC,∴∠FCD=∠B.∴△ABC∽△FCD.(2)是.由△ABC∽△FCD,得,∴DF=.∴点F是AD的中点.(3)方法一:作AM⊥BC于M,FN⊥BC于N,由问题(1),(2)的结论可得SΔFCD=5,FN=2,且N为DM的中点,M为CD的中点,又易知△FNC∽△EDC,∴,解得DE=.方法二:作AM⊥BC于M,由·AM=10,解得AM=4.易知△B DE∽△BMA,∴,∴DE=.方法三:作AM⊥BC于M,则有,∴S△BCE=S△ABC=,于是由·DE=,解得DE=.。
第四章 因式分解 综合素质评价(含答案)北师大版数学八年级下册
第四章因式分解综合素质评价一、选择题(每题3分,共30分)1.下列各式从左到右的变形中,是因式分解的为()A.ab+ac+d=a(b+c)+dB.(x+2)(x-2)=x2-4C.6ab=2a·3bD.x2-8x+16=(x-4)22.课堂上老师在黑板上布置了下框所示的题目,小聪马上发现了其中有一道题目错了,错误的题目是()用平方差公式解下列各式:(1)a2-b2;(2)49x2-y2z2;(3)-x2-y2;(4)16m2n2-25p2.A.(1) B.(2) C.(3) D.(4)3.【2022·金华二模】下列多项式中,在实数范围内不能进行因式分解的是() A.a2-4 B.a2+6a+9 C.a2+16 D.9a2-6a+14.下列各组代数式中,没有公因式的是()A.ax+y和x+yB.2x和4yC.a-b和b-aD.-x2+xy和y-x5.下列因式分解正确的是()A.a(a-b)-b(a-b)=(a-b)(a+b)B.a2-9b2=(a-3b)2C.a2+4ab+4b2=(a+2b)2D.a2-ab+a=a(a-b)6.【教材P105复习题T6变式】已知a+b=2,则a2-b2+4b的值是() A.2 B.3 C.4 D.67.【2022·石家庄二模】计算:1252-50×125+252=()A.100 B.150 C.10 000 D.22 5008.【教材P94习题T4变式】从边长为a的大正方形纸板中挖去一个边长为b的小正方形纸板后,将其裁成四个相同的等腰梯形(如图①),然后拼成一个平行四边形(如图②).那么通过计算两个图形阴影部分的面积,可以验证成立的公式为()A.a2-b2=(a-b)2B.(a+b)2=a2+2ab+b2C.a2-b2=(a+b)(a-b) D.(a-b)2=a2-2ab+b29.不论x,y为什么实数,代数式x2+y2+2x-4y+7的值()A.总不小于2 B.总不小于7 C.可为任何实数D.可能为负数10.已知a=2b-2,则代数式a2-4ab+5b2的最小值为()A.0 B.2 C.4 D.无法确定二、填空题(每题3分,共24分)11.18x3y2与12x6y的公因式为________.12.【2022·长春】分解因式:m2+3m=________.13.若整式x2+ky2(k为不等于零的常数)能在有理数范围内因式分解,则k的值可以是________.(写出一个即可)14.【2022·重庆渝北期末】利用1个a×a的正方形,1个b×b的正方形和2个a×b 的矩形可拼成一个正方形(如图所示),从而可得到因式分解的公式:____________.15.【教材P105复习题T13改编】如果x2+kx+64是一个完全平方式,那么k的值是________.16.关于x的二次三项式2x2+bx+c分解因式后为2(x-3)(x+1),则b=________,c=________.17.已知x ,y 是二元一次方程组⎩⎨⎧x -2y =3,2x +4y =5的解,则代数式x 2-4y 2的值为________.18.一个两邻边长分别为a ,b 的长方形,它的周长为14,面积为10,则a 2b +ab 2的值为________.三、解答题(19题12分,20题6分, 21题8分,其余每题10分,共66分)19.把下列各式因式分解:(1)-5x 2y 2+10xy 3-15x 2y ; (2)2x 2-4x +2;(3)(x 2+1)2-4x 2; (4)a 4-8a 2b 2+16b 4.20.【教材P 97习题T 2(3)变式】已知a +b =72,ab =2,求12a 3b +a 2b 2+12ab 3的值.21.【教材P105复习题T14改编】232-1可以被10和20之间某两个整数整除,求这两个数.22.【教材P105复习题T12改编】已知a,b,c分别是△ABC的三边长.(1)分别将多项式ac-bc,-a2+2ab-b2进行因式分解;(2)若ac-bc=-a2+2ab-b2,试判断△ABC的形状,并说明理由.23.【教材P100随堂练习T3变式】如图,在一个边长为a m的正方形广场的四个角上分别留出一个边长为b m的正方形花坛(a>2b),其余的地方种草坪.(1)求种草坪的面积是多少平方米;(2)当a=84,b=8,且种每平方米草坪的成本为5元时,种这块草坪共需投资多少元?24.【教材P105复习题T10拓展】上数学课时,王老师在讲完乘法公式(a±b)2=a2±2ab +b2的多种运用后,要求同学们运用所学知识解答:求代数式x2+4x+5的最小值.同学们经过交流、讨论,最后总结出如下解答方法:解:x2+4x+5=x2+4x+4+1=(x+2)2+1.∵(x+2)2≥0,∴(x+2)2+1≥1.∴x2+4x+5的最小值是1.请你根据上述方法,解答下列各题:(1)知识再现:当x=________时,代数式x2-6x+12有最小值是________;(2)知识运用:若y=-x2+2x-3,当x=________时,y有最________值(填“大”或“小”),这个值是________.写出求解过程.25.【探究题】在乘法公式的学习中,我们采用了构造几何图形的方法研究问题,通过用不同的方法求同一个平面图形的面积验证了平方差公式和完全平方公式,我们把这种方法称为等面积法.类似地,通过不同的方法求同一个立体图形的体积,我们称为等体积法.根据课堂学习的经验,解决下列问题:在一个棱长为a的正方体中挖出一个棱长为b的正方体(如图①),然后利用切割的方法把剩余的立体图形(如图②)分成三部分(如图③),这三个长方体的体积依次为b2(a-b),ab(a-b),a2(a-b).(1)分解因式:a2(a-b)+ab(a-b)+b2(a-b)=______________.(2)请用两种不同的方法求图①中的立体图形的体积(用含有a,b的代数式表示):①____________;②______________________.思考:类比平方差公式,你能得到的等式为______________________________.(3)应用:利用在(2)中所得到的等式进行因式分解:x3-125=______________.(4)拓展:已知a-2b=6,ab=-2,求代数式a4b-8ab4的值.答案一、1.D 2.C 3.C 4.A 5.C 6.C7.C 8.C 9.A 10.C二、11.6x 3y 12.m (m +3) 13.-1(答案不唯一)14.a 2+2ab +b 2=(a +b )2 15.±1616.-4;-6 17.152 18.70三、19.解:(1)原式=-5xy (xy -2y 2+3x );(2)原式=2(x 2-2x +1)=2(x -1)2;(3)原式=[(x 2+1)+2x ][(x 2+1)-2x ]=(x 2+2x +1)(x 2-2x +1)=(x +1)2(x -1)2;(4)原式=(a 2-4b 2)2=(a -2b )2(a +2b )2.20.解:12a 3b +a 2b 2+12ab 3=12ab (a 2+2ab +b 2)=12ab (a +b )2.∵a +b =72,ab =2,∴原式=12×2×⎝ ⎛⎭⎪⎫722=494. 21.解:232-1=(216)2-1=(216+1)(216-1)=(216+1)(28+1)(28-1)=(216+1)·(28+1)(24+1)(24-1).∵24=16,∴24+1=17,24-1=15.∴232-1能被15和17整除.∴所求的两个数为15和17.22.解:(1)ac -bc =c (a -b );-a 2+2ab -b 2=-(a 2-2ab +b 2)=-(a -b )2.(2)△ABC 是等腰三角形.理由:∵ac -bc =-a 2+2ab -b 2,∴c (a -b )=-(a -b )2,c (a -b )+(a -b )2=0,(a-b)(c+a-b)=0.∵a,b,c分别是△ABC的三边长,∴c+a-b>0.∴a-b=0,即a=b.∴△ABC是等腰三角形.23.解:(1)种草坪的面积是(a2-4b2) m2.(2)当a=84,b=8时,种草坪的面积是a2-4b2=(a+2b)(a-2b)=(84+2×8)×(84-2×8)=100×68=6 800(m2).所以种这块草坪共需投资5×6 800=34 000(元).24.解:(1)3;3(2)1;大;-2y=-x2+2x-3=-(x-1)2-2.∵-(x-1)2≤0,∴-(x-1)2-2≤-2.∴当x=1时,y有最大值,最大值是-2.25.解:(1)(a-b)(a2+ab+b2)(2)①a3-b3②b2(a-b)+ab(a-b)+a2(a-b)思考:a3-b3=(a-b)(a2+ab+b2)(3)(x-5)(x2+5x+25)(4)a4b-8ab4=ab(a3-8b3)=ab(a-2b)(a2+2ab+4b2)=ab(a-2b)[(a-2b)2+6ab].当a-2b=6,ab=-2时,原式=-2×6×(36-12)=-288.。
北师版八年级数学下册第四章测试卷
北师版八年级数学下册第四章综合测试总分:120分一、选择题(每题3分,共30分)1.下列式子从左到右的变形是因式分解的是() A.(a-2)(a+3)=a2+a-6B.x2-1+y2=(x-1)(x+1)+y2C.4x2y=2x·2xyD.a2+4a=a(a+4)2.将多项式-6a3b2-3a2b2+12a2b3因式分解时,应提取的公因式是()A.-3a2b2B.-3ab C.-3a2b D.-3a3b3 3.下列各式中能用完全平方公式进行因式分解的是() A.x2+x+1 B.x2+2x-1C.x2-1 D.x2-6x+94.因式分解x3-2x2+x正确的是()A.(x-1)2B.x(x-1)2C.x(x2-2x+1) D.x(x+1)25.若多项式x2+mx-28可因式分解为(x-4)(x+7),则m的值为()A.-3 B.11 C.-11 D.36.已知a+b=2,则a2-b2+4b的值是()A.2 B.3 C.4 D.67.已知△ABC 的三边长分别为a ,b ,c ,且满足a 2+b 2+c 2=ab +ac +bc ,则△ABC 的形状是( )A .直角三角形B .等腰三角形C .等腰直角三角形D .等边三角形8.利用因式分解可以知道,174-154能够被( )整除.A .18B .28C .36D .649.不论x ,y 为什么实数,代数式x 2+y 2+2x -4y +7的值( )A .总不小于2B .总不小于7C .可为任何实数D .可能为负数10.已知a ,b ,c 为△ABC 的三边长,且满足a 2c 2-b 2c 2=a 4-b 4,则△ABC 的形状为( )A .等腰三角形B .直角三角形C .等腰直角三角形D .等腰三角形或直角三角形二、填空题(每题3分,共30分)11.分解因式:3m 3+6m 2+9m =____________.12.把多项式()1+x ()1-x -()x -1提取公因式x -1后,余下的部分是__________.13.分解因式:(2a +1)2-a 2=__________________.14.若关于x 的二次三项式x 2+ax +14是完全平方式,则a 的值是________.15.已知二元一次方程组⎩⎪⎨⎪⎧x +2y =-12 019,2y -x =2 0197,不解方程组直接求出代数式x 2-4y 2的值为________.16.已知a ,b 满足|a +2|+b -4=0,分解因式:(x 2+y 2)-(axy +b )=________________.17.在对多项式x 2+ax +b 进行因式分解时,小明看错了b ,分解的结果是(x -10)(x +2);小亮看错了a ,分解的结果是(x -8)(x -2),则多项式x 2+ax +b 进行因式分解的正确结果为__________.18.计算:123 456 7892-123 456 788×123 456 790=________.19.下面是莉莉对多项式3(x -2)2-(2-x )3进行因式分解的过程:解:原式=3(x -2)2-(x -2)3①=(x -2)2[3-(x -2)]②=(x -2)2(5-x ).③开始出现错误的一步是________.20.观察下列各式:x 2-1=(x -1)(x +1),x 3-1=(x -1)(x 2+x +1),x 4-1=(x -1)(x 3+x 2+x +1),根据前面各式的规律可猜想:x n +1-1=____________________________________.三、解答题(21题16分,26题12分,其余每题8分,共60分)21.把下列各式因式分解:(1)4x2-64;(2)a3b+2a2b2+ab3;(3)(a-b)2-2(b-a)+1; (4)x2-2xy+y2-16z2.22.先因式分解,再求值:(1)4a2(x+7)-3(x+7),其中a=-5,x=3;(2)(2x-3y)2-(2x+3y)2,其中x=16,y=18.23.已知x+y=4,x2+y2=14,求x3y-2x2y2+xy3的值.24.已知a,b是一个等腰三角形的两边长,且满足a2+b2-4a-6b+13=0,求这个等腰三角形的周长.25.先阅读下列材料,再解答问题:材料:因式分解:(x+y)2+2(x+y)+1.解:将“x+y”看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2.再将“A”还原,得原式=(x+y+1)2.上述解题用到的是“整体思想”,“整体思想”是数学解题中常用的一种思想方法,请你解答下列问题:(1)分解因式:1+2(x-y)+(x-y)2=____________;(2)分解因式:(a+b)(a+b-4)+4;(3)求证:若n为正整数,则式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.26.观察猜想如图,大长方形是由四个小长方形拼成的,请根据此图填空:x2+(p+q)x+pq=x2+px+qx+pq=(______)(______).说理验证事实上,我们也可以用如下方法进行变形:x2+(p+q)x+pq=x2+px+qx+pq=(x2+px)+(qx+pq)=________________=(______)(______).于是,我们可以利用上面的方法进行多项式的因式分解.尝试运用例题:把x2+3x+2因式分解.解:x2+3x+2=x2+(2+1)x+2×1=(x+2)(x+1).请利用上述方法将下列多项式因式分解:(1)x2-7x+12;(2)(y2+y)2+7(y2+y)-18.参考答案一、1.D 2.A 3.D 4.B 5.D6.C点拨:a2-b2+4b=(a+b)(a-b)+4b=2(a-b)+4b=2a+2b=2(a+b)=4.7.D8.D点拨:174-154=(172-152)(172+152)=(17-15)(17+15)(172+152)=64×(172+152),故174-154能够被64整除.故选D.9.A10.D二、11.3m(m2+2m+3)12.-x-213.(3a+1)(a+1)14.±115.1 716.(x+y+2)(x+y-2)17.(x-4)218.1 19.①20.(x-1)(x n+x n-1+…+x+1)三、21.解:(1)原式=4(x2-16)=4(x+4)(x-4);(2)原式=ab(a2+2ab+b2)=ab(a+b)2;(3)原式=(a-b)2+2(a-b)+1=(a-b+1)2;(4)原式=(x-y)2-(4z)2=(x-y+4z)(x-y-4z).22.解:(1)原式=(x+7)(4a2-3).当a=-5,x=3时,(x+7)(4a2-3)=(3+7)×[4×(-5)2-3]=970.(2)原式=[(2x-3y)+(2x+3y)]·[(2x-3y)-(2x+3y)]=-24xy.当x=16,y=18时,-24xy=-24×16×18=-12.23.解:∵x+y=4,∴(x+y)2=16.∴x2+y2+2xy=16.而x2+y2=14,∴xy=1.∴x3y-2x2y2+xy3=xy(x2-2xy+y2)=14-2=12.24.解:a2+b2-4a-6b+13=(a-2)2+(b-3)2=0,故a=2,b=3.由题意可知第三边长为2或3,所以所求三角形的周长为7或8.25.(1)(x-y+1)2(2)解:令a+b=A,则原式变为A(A-4)+4=A2-4A+4=(A-2)2.故(a+b)(a+b-4)+4=(a+b-2)2.(3)证明:(n+1)(n+2)(n2+3n)+1=(n2+3n)[(n+1)(n+2)]+1=(n2+3n)(n2+3n+2)+1=(n2+3n)2+2(n2+3n)+1=(n2+3n+1)2.∵n为正整数,∴n2+3n+1也为正整数.∴式子(n+1)(n+2)(n2+3n)+1的值一定是某一个整数的平方.26.解:x+p;x+q;x(x+p)+q(x+p);x+p;x+q(1)原式=(x-3)(x-4);(2)原式=(y2+y+9)(y2+y-2)=(y2+y+9)(y+2)(y-1).。
北师大版八年级数学(下册)第四章测试卷(附答案)
第四章测试卷本试卷共3大题,计20小题,满分100分,考试时间100分钟。
题号 一二三四五总分得分一、选择题(本大题共10小题,每小题3分,满分30分)每小题都给出代号为A 、B 、C 、D 的四个选项,其中只有一个是正确的,请把正确选项的代号写在题后的括号内,每一小题选对得4分,不选、选错或选出的代号超过一个的(不论是否写在括号内)一律得0分 1.若0=+b a ,11=ab ,则的值是( )A .B .33C .D .2.计算22)3()3(b a b a +-+的结果是( )A .2)(8b a - B .2)(8b a + C .2288a b - D .2288b a - 3.对于任何整数m ,多项式( 4m+5)2−9都能( ) A .被8整除 B .被m 整除 C .被(m−1)整除 D .被(2n−1)整除4.将−3x 2n −6x n 分解因式,结果是(n 为正整数)( ) A .−3x n (x n +2) B .−3(x2n +2x n ) C .−3x n (x 2+2) D .3(−x 2n −2x n )5.如果305)(22--=+++⋅x x b x b a x ,则b 为 ( )A .5B .-6C .-5D .66.多项式a x x +-32可分解为(x -5)(x -b ),则a ,b 的值分别为 ( )A .10和-2B .-10和2C .10和2D .-10和-2 7.分解因式2422+-x x 的最终结果是( )A.)2(2-x xB. )12(22+-x x C. 2)1(2-x D. 2)22(-x 8.下列等式不成立的是( )A.)4)(4(162+-=-m m m B. )4(42+=+m m m mC. 22)4(168-=+-m m mD. 22)3(93+=++m m m 9.若代数式1322=+y y ,那么代数式9642-+y y 的值是( )A.2B.10C.-7D.710. 分解结果等于(x +y -4)(2x +2y -5)的多项式是 ( )A .20)(13)(22++-+y x y xB .20)(13)22(2++-+y x y x C .20)(13)(22++++y x y x D .20)(9)(22++-+y x y x二、填空题(本大题共4小题,每小题3分,满分12分) 11. -12c b a 52=-6ab ·( ). 12. 221.229 1.334⨯-⨯=__________;13. 若5,6x y xy -==则22x y xy -=_________,2222x y +=__________。
