(完整版)高考文科数学集合习题精选
高考文科数学专题一:集合题型总结含解析

第一章 集合第一节 集合的含义、表示及基本关系练习一组1.已知A ={1, 2}, B ={}|x x A Î, 则集合A 与B 的关系为________. 解析:由集合B ={}|x x A Î知, B ={1, 2}.答案:A =B2.若{}2,|a a R x x NÆØ, 则实数a 的取值范围是________.解析:由题意知, 2x a £有解, 故0a ³.答案:0a ³3.已知集合A ={}2|21,y y x x x R =--?, 集合B ={}|28x x-#, 则集合A 与B 的关系是________.解析:y =x 2-2x -1=(x -1)2-2≥-2, ∴A ={y|y ≥-2}, ∴BA . 答案:BA4.已知全集U =R , 则正确表示集合M ={-1, 0, 1}和N ={}2|0x x x +=关系的韦恩(Venn)图是________.解析:由N={}2|0x x x +=, 得N ={-1, 0}, 则N M .答案:②5知集合A ={}|5x x >, 集合B ={}|x x a >, 若命题“x ∈A ”是命题“x ∈B ”的充分不必要条件, 则实数a 的取值范围是________.解析:命题“x ∈A ”是命题“x ∈B ” 的充分不必要条件, ∴A B , ∴a <5. 答案:a <56.已知m ∈A , n ∈B , 且集合A ={x |x =2a , a ∈Z }, B ={x |x =2a +1, a ∈Z }, 又C ={x |x =4a +1, a ∈Z }, 判断m +n 属于哪一个集合?解:∵m ∈A , ∴设m =2a 1, a 1∈Z , 又∵n ∈B , ∴设n =2a 2+1, a 2∈Z , ∴m +n =2(a 1+a 2)+1, 而a 1+a 2∈Z , ∴m +n ∈B .练习二组1.设a , b 都是非零实数, y =a |a |+b |b |+ab |ab |可能取的值组成的集合是________. 解析:分四种情况:(1)a >0且b >0;(2)a >0且b <0;(3)a <0且b >0;(4)a <0且b <0, 讨论得y =3或y =-1.答案:{3, -1}2.已知集合A ={-1, 3, 2m -1}, 集合B ={3, m 2}.若B ⊆A , 则实数m =________. 解析:∵B ⊆A , 显然m 2≠-1且m 2≠3, 故m 2=2m -1, 即(m -1)2=0, ∴m =1.答案:1 3.设P , Q 为两个非空实数集合, 定义集合P +Q ={a +b |a ∈P , b ∈Q }, 若P ={0, 2, 5}, Q ={1, 2, 6}, 则P +Q 中元素的个数是________个.解析:依次分别取a =0, 2, 5;b =1, 2, 6, 并分别求和, 注意到集合元素的互异性, ∴P +Q ={1, 2, 6, 3, 4, 8, 7, 11}.答案:84.已知集合M ={x |x 2=1}, 集合N ={x |ax =1}, 若N M , 那么a 的值是________.解析:M ={x |x =1或x =-1}, N M , 所以N =∅时, a =0;当a ≠0时, x =1a=1或-1, ∴a =1或-1.答案:0, 1, -15.满足{1}A ⊆{1, 2, 3}的集合A 的个数是________个.解析:A 中一定有元素1, 所以A 有{1, 2}, {1, 3}, {1, 2, 3}.答案:36.已知集合A ={x |x =a +16, a ∈Z }, B ={x |x =b 2-13, b ∈Z }, C ={x |x =c 2+16, c ∈Z }, 则A 、B 、C 之间的关系是________.解析:用列举法寻找规律.答案:A B =C7.集合A ={x ||x |≤4, x ∈R }, B ={x |x <a }, 则“A ⊆B ”是“a >5”的________.解析:结合数轴若A ⊆B ⇔a ≥4, 故“A ⊆B ”是“a >5”的必要但不充分条件.答案:必要不充分条件8.设集合M ={m |m =2n , n ∈N , 且m <500}, 则M 中所有元素的和为________.解析:∵2n <500, ∴n =0, 1, 2, 3, 4, 5, 6, 7, 8.∴M 中所有元素的和S =1+2+22+…+28=511.答案:5119.设A 是整数集的一个非空子集, 对于k ∈A , 如果k -1∉A , 且k +1∉A , 那么称k 是A 的一个“孤立元”.给定S ={1, 2, 3, 4, 5, 6, 7, 8}, 由S 的3个元素构成的所有集合中, 不含“孤立元”的集合共有________个.解析:依题可知, 由S 的3个元素构成的所有集合中, 不含“孤立元”, 这三个元素一定是相连的三个数.故这样的集合共有6个.答案:610.已知A ={x , xy , lg(xy )}, B ={0, |x |, y }, 且A =B , 试求x , y 的值.解:由lg(xy )知, xy >0, 故x ≠0, xy ≠0, 于是由A =B 得lg(xy )=0, xy =1.∴A ={x , 1, 0}, B ={0, |x |, 1x}. 于是必有|x |=1, 1x=x ≠1, 故x =-1, 从而y =-1.11.已知集合A ={x |x 2-3x -10≤0},(1)若B ⊆A , B ={x |m +1≤x ≤2m -1}, 求实数m 的取值范围;(2)若A ⊆B , B ={x |m -6≤x ≤2m -1}, 求实数m 的取值范围;(3)若A =B , B ={x |m -6≤x ≤2m -1}, 求实数m 的取值范围.解:由A ={x |x 2-3x -10≤0}, 得A ={x |-2≤x ≤5},(1)∵B ⊆A , ∴①若B =∅, 则m +1>2m -1, 即m <2, 此时满足B ⊆A .②若B ≠∅, 则⎩⎪⎨⎪⎧ m +1≤2m -1,-2≤m +1,2m -1≤5.解得2≤m ≤3.由①②得, m 的取值范围是(-∞, 3].(2)若A ⊆B , 则依题意应有⎩⎪⎨⎪⎧ 2m -1>m -6,m -6≤-2,2m -1≥5.解得⎩⎪⎨⎪⎧ m >-5,m ≤4,m ≥3.故3≤m ≤4,∴m 的取值范围是[3, 4].(3)若A =B , 则必有⎩⎪⎨⎪⎧m -6=-2,2m -1=5,解得m ∈∅., 即不存在m 值使得A =B .12.已知集合A ={x |x 2-3x +2≤0}, B ={x |x 2-(a +1)x +a ≤0}.(1)若A 是B 的真子集, 求a 的取值范围;(2)若B 是A 的子集, 求a 的取值范围;(3)若A =B , 求a 的取值范围.解:由x 2-3x +2≤0, 即(x -1)(x -2)≤0, 得1≤x ≤2, 故A ={x |1≤x ≤2}, 而集合B ={x |(x -1)(x -a )≤0},(1)若A 是B 的真子集, 即A B , 则此时B ={x |1≤x ≤ a }, 故a >2.(2)若B 是A 的子集, 即B ⊆A , 由数轴可知1≤a ≤2.(3)若A =B , 则必有a =2第二节 集合的基本运算练习一组1.设U =R , A ={}|0x x >, B ={}|1x x >, 则A ∩∁U B =____.解析:∁U B ={x |x ≤1}, ∴A ∩∁U B ={x |0<x ≤1}.答案:{x |0<x ≤1}2.设集合A ={4, 5, 7, 9}, B ={3, 4, 7, 8, 9}, 全集U =A ∪B , 则集合∁U (A ∩B )中的元素共有________个.解析:A ∩B ={4, 7, 9}, A ∪B ={3, 4, 5, 7, 8, 9}, ∁U (A ∩B )={3, 5, 8}.答案:33.已知集合M ={0, 1, 2}, N ={}|2,x x a a M =?, 则集合M ∩N =________.解析:由题意知, N ={0, 2, 4}, 故M ∩N ={0, 2}.答案:{0, 2}4.设A , B 是非空集合, 定义A ⓐB ={x |x ∈A ∪B 且x ∉A ∩B }, 已知A ={x |0≤x ≤2}, B ={y |y ≥0}, 则A ⓐB =________.解析:A ∪B =[0, +∞), A ∩B =[0, 2], 所以A ⓐB =(2, +∞).答案:(2, +∞)5.某班共30人, 其中15人喜爱篮球运动, 10人喜爱乒乓球运动, 8人对这两项运动都不喜爱, 则喜爱篮球运动但不喜爱乒乓球运动的人数为________.解析:设两项运动都喜欢的人数为x , 画出韦恩图得到方程15-x +x +10-x +8=30x =3, ∴喜爱篮球运动但不喜爱乒乓球运动的人数为15-3=12(人).答案:126.已知集合A ={x |x >1}, 集合B ={x |m ≤x ≤m +3}.(1)当m =-1时, 求A ∩B , A ∪B ;(2)若B ⊆A , 求m 的取值范围.解:(1)当1m =-时, B ={x |-1≤x ≤2}, ∴A ∩B ={x |1<x ≤2}, A ∪B ={x |x ≥-1}.(2)若B ⊆A , 则1m >, 即m 的取值范围为(1, +∞)练习二1.若集合M ={x ∈R |-3<x <1}, N ={x ∈Z |-1≤x ≤2}, 则M ∩N =________.解析:因为集合N ={-1, 0, 1, 2}, 所以M ∩N ={-1, 0}.答案:{-1, 0}2.已知全集U ={-1, 0, 1, 2}, 集合A ={-1, 2}, B ={0, 2}, 则(∁U A )∩B =________.解析:∁U A ={0, 1}, 故(∁U A )∩B ={0}.答案:{0}3.若全集U =R , 集合M ={x |-2≤x ≤2}, N ={x |x 2-3x ≤0}, 则M ∩(∁U N )=________.解析:根据已知得M ∩(∁U N )={x |-2≤x ≤2}∩{x |x <0或x >3}={x |-2≤x <0}.答案:{x |-2≤x <0}4.集合A ={3, log 2a }, B ={a , b }, 若A ∩B ={2}, 则A ∪B =________.解析:由A ∩B ={2}得log 2a =2, ∴a =4, 从而b =2, ∴A ∪B ={2, 3, 4}. 答案:{2, 3, 4}5.已知全集U =A ∪B 中有m 个元素, (∁U A )∪(∁U B )中有n 个元素.若A ∩B 非空, 则A ∩B 的元素个数为________.解析:U =A ∪B 中有m 个元素,∵(∁U A )∪(∁U B )=∁U (A ∩B )中有n 个元素, ∴A ∩B 中有m -n 个元素.答案:m -n6.设U ={n |n 是小于9的正整数}, A ={n ∈U |n 是奇数}, B ={n ∈U |n是3的倍数}, 则∁U (A ∪B )=________.解析:U ={1, 2, 3, 4, 5, 6, 7, 8}, A ={1, 3, 5, 7}, B ={3, 6}, ∴A ∪B ={1, 3, 5, 6, 7},得∁U (A ∪B )={2, 4, 8}.答案:{2, 4, 8}7.定义A ⊗B ={z |z =xy +x y, x ∈A , y ∈B }.设集合A ={0, 2}, B ={1, 2}, C ={1}, 则集合(A ⊗B )⊗C 的所有元素之和为________.解析:由题意可求(A ⊗B )中所含的元素有0, 4, 5, 则(A ⊗B )⊗C 中所含的元素有0, 8, 10, 故所有元素之和为18.答案:188.若集合{(x , y )|x +y -2=0且x -2y +4=0}{(x , y )|y =3x +b }, 则b =________.解析:由⎩⎪⎨⎪⎧ x +y -2=0,x -2y +4=0.⇒⎩⎪⎨⎪⎧x =0,y =2.点(0, 2)在y =3x +b 上, ∴b =2.9.设全集I ={2, 3, a 2+2a -3}, A ={2, |a +1|}, ∁I A ={5}, M ={x |x =log 2|a |}, 则集合M 的所有子集是________.解析:∵A ∪(∁I A )=I , ∴{2, 3, a 2+2a -3}={2, 5, |a +1|}, ∴|a +1|=3, 且a 2+2a -3=5, 解得a =-4或a =2, ∴M ={log 22, log 2|-4|}={1, 2}.答案:∅, {1}, {2}, {1, 2}10.设集合A ={x |x 2-3x +2=0}, B ={x |x 2+2(a +1)x +(a 2-5)=0}.(1)若A∩B={2},求实数a的值;(1)若A=∅,求实数a的取值范围;(2)若A是单元素集,求a的值及集合A;11.已知函数f(x)=6x+1-1的定义域为集合A,函数g(x)=lg(-x2+2x+m)的定义域为集合B.(1)当m=3时,求A∩(∁R B);(2)若A∩B={x|-1<x<4},求实数m的值.解:A={x|-1<x≤5}.(1)当m=3时,B={x|-1<x<3},则∁R B={x|x≤-1或x≥3},∴A∩(∁R B)={x|3≤x≤5}.(2)∵A={x|-1<x≤5},A∩B={x|-1<x<4},∴有-42+2×4+m=0,解得m=8,此时B={x|-2<x<4},符合题意.。
高考数学真题集合专项练习含答案

1.了解集合的含义,元素与集合的属于关系;能用列举法或描述法表示集合. 2.理解集合之间包含与相等的含义,能识别给定集合的子集;了解全集与空集的含义. 3.理解并会求并集、交集、补集;能用Venn(韦恩)图表达集合的关系与运算.集合的概念及运算一直是高考热点,同时近两年新课标高考试题加强了对以集合为工具与其他知识的结合的考查,一般为基础题,解题时要充分利用韦恩图、数轴等直观性迅速得解,预计今后这种考查方式不会变.热点题型一 集合的基本概念例1.【2017课表1,文1】已知集合A ={}|2x x <,B ={}|320x x ->,则A .AB =3|2x x ⎧⎫<⎨⎬⎩⎭B .A B =∅C .AB 3|2x x ⎧⎫=<⎨⎬⎩⎭D .AB=R【答案】A【解析】由320x ->得32x <,所以33{|2}{|}{|}22A B x x x x x x ⋂=<⋂<=<,选A . 【提分秘籍】与集合中的元素有关问题的求解策略 (1)确定集合的元素是什么,即集合是数集还是点集。
(2)看这些元素满足什么限制条件。
(3)根据限制条件列式求参数的值或确定集合中元素的个数,但要注意检验集合是否满足元素的互异性。
【举一反三】已知集合A ={a +2,(a +1)2,a 2+3a +3},若1∈A ,则2015a的值为________。
【答案】1热点题型二 集合间的基本关系例2.【2017课标II ,文1】设集合{1,2,3},{2,3,4}A B ==则AB =A. {}123,4,, B. {}123,, C. {}234,, D. {}134,, 【答案】A 【解析】由题意{1,2,3,4}A B =,故选A.【提分秘籍】1.根据集合的关系求参数的关键点及注意点(1)根据两集合的关系求参数,其关键是将两集合的关系转化为元素间的关系,进而转化为参数满足的关系,解决这类问题常常要合理利用数轴、Venn 图帮助分析,而且常要对参数进行讨论。
高三文科数学复习题(集合)word版本

高三文科数学(集合)A 组1.( 2007 年高考广东文科卷)已知集合 M= { x1x 0} , N= x10 ,则 MN1 x()A . { x 1 x 1}B . { x x 1}C . { x 1 x 1}D . { x x 1}2.( 2008 年高考广东文科卷)第二十九届夏季奥林匹克运动会将于2008 年 8 月 8 日在北京举行,若集合 A { 参加北京奥运会比赛的运动员},集合 B{ 加北京奥运会比赛的男运动员},集合 C { 加北京奥运会比赛的女运动员} ,则下列关系正确的是()A.A BB. B CC. B C AD.ABC3A { 1,1} ,B { x | mx1} ,且 A B A,则 m 的值为 ().已知集合A . 1B .— 1C .1 或— 1D .1或—1或 04.( 2009 年高考广东文科卷)已知全集 U=R ,则正确表示集合M= {— 1, 0, 1}和 N={ x x 21 0 }关系的韦恩( Venn )图是()5.如图, U 是全集, M 、P 、S 是 U 的 3 个子集, 则阴影部分所表示的集合是 ( )A 、 M P SB 、M P SC 、M PC u SD 、 MPC u S6.已知集合 A={1 , 2,3, 4} ,那么 A 的真子集的个数是7.已知集合A( x , y)| y 3x2 ,B( x , y)| y x 2那么集合 A B=8.已知全集 U=2 ,3 , a 22a3,若A= b , 2 , CA 5 ,求实数的 a ,b 值U9.已知集合A=x 3 x 7 ,B={x|2<x<10},C={x | x< a},全集为实数集R.(1)求 A ∪ B, (C R A) ∩ B ;(2) 如果 A ∩ C≠ φ,求 a 的取值范围。
B 组10.设A x 2x2px q 0 , B x 6x 2( p 2)x 5 q0,若A B1,2则 A B()A.1,1, 4B.1,4C.1,1D.1 23223211. 50 名学生做的物理、化学两种实验,已知物理实验做的正确得有40 人,化学实验做的正确的有31 人,两种实验都做错的有 4 人,则这两种实验都做对的有人 .12.已知集合Aa, a d, a2d ,B a,aq,aq 2,其中 a, d,qR ,若 A=B ,求 q 的值。
高中集合练习题及答案

高中集合练习题及答案一、选择题1. 集合A={1,2,3},集合B={2,3,4},求A∪B。
A. {1,2,3}B. {1,2,3,4}C. {2,3}D. {4}2. 集合A={x|x<5},集合B={x|x>3},求A∩B。
A. {x|x<3}B. {x|3<x<5}C. {x|x>5}D. 空集3. 集合M={x|x^2-4=0},求M的元素个数。
A. 0B. 1C. 2D. 34. 对于集合N={1,2,3,...,10},如果a∈N且a为奇数,求a的个数。
A. 5B. 6C. 8D. 105. 集合P={x|x是偶数},集合Q={x|x是质数},判断P和Q的关系。
A. P⊆QB. Q⊆PC. P∩Q=空集D. P∩Q≠空集二、填空题6. 集合S={x|x是小于10的正整数},S的补集是_________。
7. 如果集合A={1,2,3},B={3,4,5},那么A∩B=_________。
8. 集合W={x|x是自然数,且x能被3整除},W的元素个数是_________。
9. 集合X={x|x^2-4=0},X的元素是_________。
10. 如果集合Y={x|x^2+x+1=0},求Y的元素个数是_________。
三、解答题11. 已知集合A={1,2,3},B={3,4,5},求A∪B∩C,其中C是A和B 的交集的补集。
12. 集合D={x|x是小于20的正整数},E={x|x是大于10的正整数},求D∪E,并判断D∪E是否为全集。
13. 集合F={x|x是偶数},G={x|x是大于10的整数},求F∩G,并说明其元素个数。
14. 集合H={x|x^2-3x+2=0},求H的元素,并判断H是否为有限集。
15. 集合I={x|x是小于100的质数},求I的元素个数,并列出前5个元素。
四、证明题16. 证明:对于任意集合A,A的补集的补集等于A本身。
2024年高考文科数学全国甲卷+答案详解

2024年高考文科数学全国甲卷+答案详解(试题部分)一、单选题1.集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B =( ) A .{}1,2,3,4B .{}1,2,3C .{}3,4D .{}1,2,92.设z =,则z z ⋅=( ) A .-iB .1C .-1D .23.若实数,x y 满足约束条件43302202690x y x y x y −−≥⎧⎪−−≤⎨⎪+−≤⎩,则5z x y =−的最小值为( )A .5B .12C .2−D .72−4.等差数列{}n a 的前n 项和为n S ,若91S =,37a a +=( ) A .2−B .73C .1D .295.甲、乙、丙、丁四人排成一列,丙不在排头,且甲或乙在排尾的概率是( ) A .14 B .13C .12D .236.已知双曲线2222:1(0,0)y x C a b a b−=>>的上、下焦点分别为()()120,4,0,4F F −,点()6,4P −在该双曲线上,则该双曲线的离心率为( ) A .4B .3C .2D7.曲线()631f x x x =+−在()0,1−处的切线与坐标轴围成的面积为( )A .16BC .12D. 8.函数()()2e e sin x xf x x x −=−+−在区间[ 2.8,2.8]−的大致图像为( )A .B .C .D .9.已知cos cos sin ααα=−πtan 4α⎛⎫+= ⎪⎝⎭( )A.1 B.1 CD.110.设αβ、是两个平面,m n 、是两条直线,且m αβ=.下列四个命题:①若//m n ,则//n α或//n β ②若m n ⊥,则,n n αβ⊥⊥③若//n α,且//n β,则//m n ④若n 与α和β所成的角相等,则m n ⊥ 其中所有真命题的编号是( )A .①③B .②④C .①②③D .①③④11.在ABC 中内角,,A B C 所对边分别为,,a b c ,若π3B =,294b ac =,则sin sin A C +=( ) A .32BCD二、填空题12.函数()sin f x x x =在[]0,π上的最大值是 . 13.已知1a >,8115log log 42a a −=−,则=a . 14.曲线33y x x =−与()21y x a =−−+在()0,∞+上有两个不同的交点,则a 的取值范围为 . 三、解答题15.已知等比数列{}n a 的前n 项和为n S ,且1233n n S a +=−. (1)求{}n a 的通项公式; (2)求数列{}n S 的通项公式.16.如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形ADEF 均为等腰梯形,//,//BC AD EF AD ,4,2AD AB BC EF ====,ED FB =M 为AD 的中点.(1)证明://BM 平面CDE ; (2)求点M 到ABF 的距离.17.已知函数()()1ln 1f x a x x =−−+. (1)求()f x 的单调区间;(2)若2a ≤时,证明:当1x >时,()1e xf x −<恒成立.18.设椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2M ⎛⎫ ⎪⎝⎭在C 上,且MF x ⊥轴.(1)求C 的方程;(2)过点()4,0P 的直线与C 交于,A B 两点,N 为线段FP 的中点,直线NB 交直线MF 于点Q ,证明:AQ y ⊥轴. 19.在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos 1ρρθ=+.(1)写出C 的直角坐标方程;(2)设直线l :x ty t a =⎧⎨=+⎩(t 为参数),若C 与l 相交于AB 、两点,若2AB =,求a 的值. 20.实数,a b 满足3a b +≥. (1)证明:2222a b a b +>+;(2)证明:22226a b b a −+−≥.2024年高考文科数学全国甲卷+答案详解(答案详解)一、单选题1.集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B =( ) A .{}1,2,3,4 B .{}1,2,3C .{}3,4D .{}1,2,9【答案】A【解析】根据题意得,对于集合B 中的元素x ,满足11,2,3,4,5,9x +=, 则x 可能的取值为0,1,2,3,4,8,即{0,1,2,3,4,8}B =,于是{1,2,3,4}A B ⋂=. 故选A2.设z =,则z z ⋅=( ) A .-i B .1C .-1D .2【答案】D【解析】根据题意得,z =,故22i 2zz =−=. 故选D3.若实数,x y 满足约束条件43302202690x y x y x y −−≥⎧⎪−−≤⎨⎪+−≤⎩,则5z x y =−的最小值为( )A .5B .12C .2−D .72−【答案】D【解析】实数,x y 满足43302202690x y x y x y −−≥⎧⎪−−≤⎨⎪+−≤⎩,作出可行域如图:由5z x y =−可得1155y x z =−,即z 的几何意义为1155y x z =−的截距的15−, 则该直线截距取最大值时,z 有最小值,此时直线1155y x z =−过点A , 联立43302690x y x y −−=⎧⎨+−=⎩,解得321x y ⎧=⎪⎨⎪=⎩,即3,12A ⎛⎫⎪⎝⎭,则min 375122z =−⨯=−. 故选D.4.等差数列{}n a 的前n 项和为n S ,若91S =,37a a +=( ) A .2− B .73C .1D .29【答案】D【分析】可以根据等差数列的基本量,即将题目条件全转化成1a 和d 来处理,亦可用等差数列的性质进行处理,或者特殊值法处理.【解析】方法1:利用等差数列的基本量 由91S =,根据等差数列的求和公式,911989193612S a d a d ⨯=+=⇔+=, 又371111222628(936)99a a a d a d a d a d +=+++=+=+=.故选D方法2:利用等差数列的性质根据等差数列的性质,1937a a a a +=+,由91S =,根据等差数列的求和公式, 193799()9()122a a a a S ++===,故3729a a +=. 故选D方法3:特殊值法不妨取等差数列公差0d =,则9111199S a a ==⇒=,则371229a a a +==. 故选D5.甲、乙、丙、丁四人排成一列,丙不在排头,且甲或乙在排尾的概率是( ) A .14 B .13C .12D .23【答案】B【分析】分类讨论甲乙的位置,得到符合条件的情况,然后根据古典概型计算公式进行求解. 【解析】当甲排在排尾,乙排第一位,丙有2种排法,丁就1种,共2种; 当甲排在排尾,乙排第二位或第三位,丙有1种排法,丁就1种,共2种;于是甲排在排尾共4种方法,同理乙排在排尾共4种方法,于是共8种排法符合题意;基本事件总数显然是44A 24=,根据古典概型的计算公式,丙不在排头,甲或乙在排尾的概率为81243=. 故选B6.已知双曲线2222:1(0,0)y x C a b a b−=>>的上、下焦点分别为()()120,4,0,4F F −,点()6,4P −在该双曲线上,则该双曲线的离心率为( )A.4 B .3 C .2 D 【答案】C【分析】由焦点坐标可得焦距2c ,结合双曲线定义计算可得2a ,即可得离心率. 【解析】根据题意,()10,4F −、()20,4F 、()6,4P −,则1228F F c ==,110PF =,26PF ,则1221064a PF PF =−=−=,则28224c e a ===. 故选C.7.曲线()631f x x x =+−在()0,1−处的切线与坐标轴围成的面积为( )A .16B C .12D . 【答案】A【分析】先求出切线方程,再求出切线的截距,从而可求面积.【解析】()563f x x ='+,所以()03f '=,故切线方程为3(0)131y x x =−−=−,故切线的横截距为13,纵截距为1−,故切线与坐标轴围成的面积为1111236⨯⨯=故选A.8.函数()()2e e sin x xf x x x −=−+−在区间[ 2.8,2.8]−的大致图像为( )A .B .C .D .【答案】B【分析】利用函数的奇偶性可排除A 、C ,代入1x =可得()10f >,可排除D.【解析】()()()()()22e e sin e e sin x x x xf x x x x x f x −−−=−+−−=−+−=,又函数定义域为[]2.8,2.8−,故该函数为偶函数,AC 错误, 又()11πe 11111e sin11e sin 10e e 622e 42e f ⎛⎫⎛⎫=−+−>−+−=−−>−> ⎪ ⎪⎝⎭⎝⎭, D 错误.故选B.9.已知cos cos sin ααα=−πtan 4α⎛⎫+= ⎪⎝⎭( )A .1B .1CD .1【答案】B 【分析】先将cos cos sin αα−α弦化切求得tan α,再根据两角和的正切公式即可求解.【解析】因为cos cos sin ααα=−11tan =−α,tan 1⇒α=,所以tan 1tan 11tan 4α+π⎛⎫==α+ ⎪−α⎝⎭, 故选B.10.设αβ、是两个平面,m n 、是两条直线,且m αβ=.下列四个命题:①若//m n ,则//n α或//n β ②若m n ⊥,则,n n αβ⊥⊥③若//n α,且//n β,则//m n ④若n 与α和β所成的角相等,则m n ⊥ 其中所有真命题的编号是( )A .①③B .②④C .①②③D .①③④【答案】A【分析】根据线面平行的判定定理即可判断①;举反例即可判断②④;根据线面平行的性质即可判断③. 【解析】①,当n ⊂α,因为//m n ,m β⊂,则//n β,当n β⊂,因为//m n ,m α⊂,则//n α, 当n 既不在α也不在β内,因为//m n ,,m m αβ⊂⊂,则//n α且//n β,①正确; ②,若m n ⊥,则n 与,αβ不一定垂直,②错误;③,过直线n 分别作两平面与,αβ分别相交于直线s 和直线t ,因为//n α,过直线n 的平面与平面α的交线为直线s ,则根据线面平行的性质定理知//n s ,同理可得//n t ,则//s t ,因为s ⊄平面β,t ⊂平面β,则//s 平面β,因为s ⊂平面α,m αβ=,则//s m ,又因为//n s ,则//m n ,③正确;④,若,m n αβ⋂=与α和β所成的角相等,如果//,//αβn n ,则//m n ,④错误; ①③正确, 故选A.11.在ABC 中内角,,A B C 所对边分别为,,a b c ,若π3B =,294b ac =,则sin sin A C +=( )A .32BC.2D【答案】C【分析】利用正弦定理得1sin sin 3A C =,再利用余弦定理有22134a c ac +=,再利用正弦定理得到22sin sin A C +的值,最后代入计算即可. 【解析】因为29,34B b ac π==,则由正弦定理得241sin sin sin 93A CB ==. 根据余弦定理可得:22294b a c ac ac =+−=,即:22134a c ac +=,根据正弦定理得221313sin sin sin sin 412A C A C +==,所以2227(sin sin )sin sin 2sin sin 4A C A C A C +=++=, 因为,A C 为三角形内角,则sin sin 0A C +>,则sin sin A C +. 故选C. 二、填空题12.函数()sin f x x x =在[]0,π上的最大值是 . 【答案】2【分析】结合辅助角公式化简成正弦型函数,再求给定区间最值即可.【解析】()πsin 2sin 3f x x x x ⎛⎫==− ⎪⎝⎭,当[]0,πx ∈时,ππ2π,333x ⎡⎤−∈−⎢⎥⎣⎦,当ππ32x −=时,即5π6x =时,()max 2f x =.答案为:2 13.已知1a >,8115log log 42a a −=−,则=a . 【答案】64【分析】将8log ,log 4a a 利用换底公式转化成2log a 来表示即可求解. 【解析】由题28211315log log log 4log 22a a a a −=−=−,整理得()2225log 60log a a −−=, 2log 1a ⇒=−或2log 6a =,又1a >,所以622log 6log 2a ==,故6264a ==答案为:64.14.曲线33y x x =−与()21y x a =−−+在()0,∞+上有两个不同的交点,则a 的取值范围为 .【答案】()2,1−【分析】将函数转化为方程,令()2331x x x a −=−−+,分离参数a ,构造新函数()3251,g x x x x =+−+结合导数求得()g x 单调区间,画出大致图形数形结合即可求解.【解析】令()2331x x x a −=−−+,即3251a x x x =+−+,令()()32510,g x x x x x =+−+>则()()()2325351g x x x x x =+−=+−',令()()00g x x '=>得1x =,当()0,1x ∈时,()0g x '<,()g x 单调递减,当()1,x ∞∈+时,()0g x '>,()g x 单调递增,()()01,12g g ==−,因为曲线33y x x =−与()21y x a =−−+在()0,∞+上有两个不同的交点,所以等价于y a =与()g x 有两个交点,所以()2,1a ∈−.答案为:()2,1− 三、解答题15.已知等比数列{}n a 的前n 项和为n S ,且1233n n S a +=−. (1)求{}n a 的通项公式; (2)求数列{}n S 的通项公式.【答案】(1)153n n a −⎛⎫= ⎪⎝⎭(2)353232n⎛⎫− ⎪⎝⎭ 【分析】(1)利用退位法可求公比,再求出首项后可求通项; (2)利用等比数列的求和公式可求n S .【解析】(1)因为1233n n S a +=−,故1233n n S a −=−,所以()12332n n n a a a n +=−≥即153n n a a +=故等比数列的公比为53q =,故1211523333533a a a a =−=⨯−=−,故11a =,故153n n a −⎛⎫= ⎪⎝⎭.(2)根据等比数列求和公式得5113353523213n nnS ⎡⎤⎛⎫⨯−⎢⎥ ⎪⎝⎭⎢⎥⎛⎫⎣⎦==− ⎪⎝⎭−. 16.如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,四边形ABCD 与四边形ADEF 均为等腰梯形,//,//BC AD EF AD ,4,2AD AB BC EF ====,ED FB =M 为AD 的中点.(1)证明://BM 平面CDE ; (2)求点M 到ABF 的距离. 【答案】(1)见详解;【分析】(1)结合已知易证四边形BCDM 为平行四边形,可证//BM CD ,进而得证;(2)作FO AD ⊥,连接OB ,易证,,OB OD OF 三垂直,结合等体积法M ABF F ABM V V −−=即可求解. 【解析】(1)因为//,2,4,BC AD BC AD M ==为AD 的中点,所以//,BC MD BC MD =,四边形BCDM 为平行四边形,所以//BM CD ,又因为BM ⊄平面CDE ,CD ⊂平面CDE ,所以//BM 平面CDE ; (2)如图所示,作BO AD ⊥交AD 于O ,连接OF ,因为四边形ABCD 为等腰梯形,//,4,BC AD AD =2AB BC ==,所以2CD =,结合(1)BCDM 为平行四边形,可得2BM CD ==,又2AM =,所以ABM 为等边三角形,O 为AM 中点,所以OB =ADEF 为等腰梯形,M 为AD 中点,所以,//EF MD EF MD =,四边形EFMD 为平行四边形,FM ED AF ==,所以AFM △为等腰三角形,ABM 与AFM △底边上中点O 重合,OF AM ⊥,3OF ==,因为222OB OF BF +=,所以OB OF ⊥,所以,,OB OD OF 互相垂直,等体积法可得M ABF F ABM V V −−=,2112333F ABM ABM V S FO −=⋅=⋅=△,2222222cos2FA AB FBFAB FAB FA AB+−+−∠===∠=⋅11sin 222FAB S FA AB FAB =⋅⋅∠==△,设点M 到FAB 的距离为d ,则1133M FAB F ABM FAB V V S d d −−==⋅⋅==△解得d =M 到ABF17.已知函数()()1ln 1f x a x x =−−+.(1)求()f x 的单调区间;(2)若2a ≤时,证明:当1x >时,()1e x f x −<恒成立.【答案】(1)见解析(2)见解析【分析】(1)求导,含参分类讨论得出导函数的符号,从而得出原函数的单调性; (2)先根据题设条件将问题可转化成证明当1x >时,1e 21ln 0x x x −−++>即可.【解析】(1)()f x 定义域为(0,)+∞,11()ax f x a x x'−=−= 当0a ≤时,1()0ax f x x −'=<,故()f x 在(0,)+∞上单调递减;当0a >时,1,x a ∞⎛⎫∈+ ⎪⎝⎭时,()0f x '>,()f x 单调递增,当10,x a ⎛⎫∈ ⎪⎝⎭时,()0f x '<,()f x 单调递减. 综上所述,当0a ≤时,()f x 在(0,)+∞上单调递减;0a >时,()f x 在1,a ∞⎛⎫+ ⎪⎝⎭上单调递增,在10,a ⎛⎫ ⎪⎝⎭上单调递减. (2)2a ≤,且1x >时,111e ()e (1)ln 1e 21ln x x x f x a x x x x −−−−=−−+−≥−++,令1()e 21ln (1)x g x x x x −=−++>,下证()0g x >即可.11()e 2x g x x −'=−+,再令()()h x g x '=,则121()e x h x x−'=−,显然()h x '在(1,)+∞上递增,则0()(1)e 10h x h ''>=−=,即()()g x h x ='在(1,)+∞上递增,故0()(1)e 210g x g ''>=−+=,即()g x 在(1,)+∞上单调递增, 故0()(1)e 21ln10g x g >=−++=,问题得证18.设椭圆2222:1(0)x y C a b a b+=>>的右焦点为F ,点31,2M ⎛⎫ ⎪⎝⎭在C 上,且MF x ⊥轴. (1)求C 的方程;(2)过点()4,0P 的直线与C 交于,A B 两点,N 为线段FP 的中点,直线NB 交直线MF 于点Q ,证明:AQ y ⊥轴.【答案】(1)22143x y += (2)见解析【分析】(1)设(),0F c ,根据M 的坐标及MF ⊥x 轴可求基本量,故可求椭圆方程. (2)设:(4)AB y k x =−,()11,A x y ,()22,B x y ,联立直线方程和椭圆方程,用,A B 的坐标表示1Q y y −,结合韦达定理化简前者可得10Q y y −=,故可证AQ y ⊥轴.【解析】(1)设(),0F c ,由题设有1c =且232b a =,故2132a a −=,故2a =,故b = 所以椭圆方程为22143x y +=. (2)直线AB 的斜率必定存在,设:(4)AB y k x =−,()11,A x y ,()22,B x y ,由223412(4)x y y k x ⎧+=⎨=−⎩可得()2222343264120k x k x k +−+−=, 故()()422Δ102443464120k k k =−+−>,故1122k −<<,又22121222326412,3434k k x x x x k k −+==++, 而5,02N ⎛⎫ ⎪⎝⎭,故直线225:522y BN y x x ⎛⎫=− ⎪⎝⎭−,故22223325252Q y y y x x −−==−−, 所以()1222112225332525Q y x y y y y y x x ⨯−+−=+=−− ()()()12224253425k x x k x x −⨯−+−=−()222212122264123225825834342525k k x x x x k k k k x x −⨯−⨯+−++++==−− 2222212824160243234025k k k k k x −−+++==−,故1Q y y =,即AQ y ⊥轴.19.在平面直角坐标系xOy 中,以坐标原点O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 的极坐标方程为cos 1ρρθ=+.(1)写出C 的直角坐标方程;(2)设直线l :x t y t a=⎧⎨=+⎩(t 为参数),若C 与l 相交于A B 、两点,若2AB =,求a 的值. 【答案】(1)221y x =+ (2)34a =【分析】(1)根据cos xρρθ⎧⎪=⎨=⎪⎩C 的直角方程. (2)将直线的新的参数方程代入C 的直角方程,法1:结合参数s 的几何意义可得关于a 的方程,从而可求参数a 的值; 法2:将直线的直角方程与曲线的直角方程联立,结合弦长公式可求a 的值.【解析】(1)由cos 1ρρθ=+,将cos x ρρθ⎧⎪=⎨=⎪⎩cos 1ρρθ=+,1x =+,两边平方后可得曲线的直角坐标方程为221y x =+. (2)对于直线l 的参数方程消去参数t ,得直线的普通方程为y x a =+. 法1:直线l 的斜率为1,故倾斜角为π4,故直线的参数方程可设为x y a ⎧=⎪⎪⎨⎪=+⎪⎩,s ∈R . 将其代入221y x =+中得()221)210s a s a +−+−=设,A B 两点对应的参数分别为12,s s,则)()212121,21s s a s s a +=−−=−,且()()22Δ818116160a a a =−−−=−>,故1a <,12AB s s ∴=−2=,解得34a =. 法2:联立221y x a y x =+⎧⎨=+⎩,得22(22)10x a x a +−+−=,()22Δ(22)41880a a a =−−−=−+>,解得1a <,设()()1122,,,A x y B x y ,2121222,1x x a x x a ∴+=−=−,则AB =2=, 解得34a = 20.实数,a b 满足3a b +≥.(1)证明:2222a b a b +>+;(2)证明:22226a b b a −+−≥.【答案】(1)见解析(2)见解析【分析】(1)直接利用22222()a b a b +≥+即可证明.(2)根据绝对值不等式并结合(1)中结论即可证明.【解析】(1)因为()()2222222022a b a ab b a b b a −+=−−++=≥, 当a b =时等号成立,则22222()a b a b +≥+,因为3a b +≥,所以22222()a b a b a b +≥+>+;(2)222222222222()a b b a a b b a a b a b −+−≥−+−=+−+ 22222()()()()(1)326a b a b a b a b a b a b =+−+≥+−+=++−≥⨯=。
高考文科数学集合习题优选精选

会合部分一、基础练习1.设会合 A x | x 1 ,B x | 2x 2 ,则 A U B()A. x | x2B. x| x 1 C. x | 2 x1D. x | 1 x 22.已知会合 M ={ x|(x + 2)(x-1) < 0 } , N ={ x| x + 1 < 0 },则 M∩N =()A. ( -1,1)B. ( - 2, 1)C. ( -2,- 1)D. (1 ,2)3.已知会合 A1,3,5,7,9 , B0,3,6,9,12,则 A I B()A.{3 , 5}B.{3 ,6}C.{3 , 7} D . {3 ,9}4.已知会合,则 A I B ()( A)(0,2)(B) [0 ,2]( C) {0 ,2}( D) {0 ,1,2}5.已知会合则的子集共有()( A) 2 个(B)4 个(C)6 个(D)8 个二、基础练习1.设 S { x | 2x 1 0} , T{ x |3x 5 0} ,则S I T()A.B .{ x | x1} C .{ x | x5}D.{ x |1x5}23232.设会合 A={ 4, 5, 7, 9},B={3,4,7,8, 9},全集 U =AUB,则会合 Cu( AI B)中的元素共有(A) 3 个(B) 4个( C)5 个(D)6 个3. 设全集 U1,2,3,4,5,会合 M1,4 , N1,3,5,则 N ∩(C u M )A. 1,3B.1,5C.3,5D.4,5三、基础练习题1. 设会合U{1,2,3,4}, A{ 1,2}, B{ 2,4}, C U(A B ) =( A) {2}( B) {3}(C){1,2,4}(D){1,4}2. 设会合M{ m Z |3m 2} , N { n Z |1≤ n ≤ 3},则 M I N ()A. 01,B.101,, C . 01,,2D.101,,,23.已知全集 U={1 ,2,3,4,5,6,7,8} ,M ={1 ,3,5,7} ,N ={5 , 6, 7} ,则 C u( M∪N)=(A) {5,7}( B) {2,4}( C) {2,4,8}( D) {1,3,5,6,7}4.设全集{x| 会合 A={1,3} ,B={3,5} ,则 C(AB)=uA. {1 , 4}B. {1,5}C.{}D.{2,5}5.设会合 U= 1,2,3,4 , M1,2,3, N2,3,4, 则C U ( M N )(A) 1,2(B) 2,3(C) 2,4(D) 1, 4四、提升题1、设全集U A B x N * | lg x 1 ,若 A C U B m | m2n1,n0,1,2,3,4 ,则会合B=__________、设会合A={-1,1,3}, B={a+2,a2+4},A∩B={3},则实数a2= ___________3、已知全集 U=R,则正确表示会合 M={ - 1, 0, 1} 和 N= { x |x2 +x=0} 关系的韦恩( Venn)图是4、设 P={x|x<4},Q={x|x2<4}, 则 ()5、已知 A,B 均为会合 U={1,3,5,7,9}的子集,且 A∩B={3}, ( C U B)∩A={9},则A= ()A.{1,3}B.{3,7,9}C.{3,5,9}D.{3,9}6、已知全集 U=A∪ B 中有 m个元素,( C U A)∪(C U B)中有n个元素.若A∩B非空,则A∩B的元素个数为 ( )A. mnB. m+n(2015 年高考题)已知会合 A={x|x=3n+2,n N},B={6,8,12,14},则会合 A B 中元素的个数为(A)5(B)4(C)3(D)2(2014 年高考题)已知会合M{ x |1x3} , N { x |2 x1} ,则M I NA. (2,1)B.(1,1)C.(1,3)D.( 2,3)(2013 高考题 ) 已知会合 A= {1,2,3,4}, B= {x|x = n2,n∈A},则 A∩B= () .A. {1,4}B. {2,3}C.{9,16}D.{1,2}(2012 年高考题)已知会合A={x|x2 -x-2<0} ,B={x| -1<x<1} ,则(A)A B ( B) B A(C)A=B(D) A∩ B=( 2011 年高考题)设会合U=,则( A)(B)(C)(D)( 2010 年高考题)已知会合Ax x2, x R, B x | x4, xZ |,则 A I B( A)(0,2)(B) [0 ,2]( C) |0 ,2|( D) |0 ,1,2|。
高考文科数学集合专题讲解及高考真题精选(含答案)
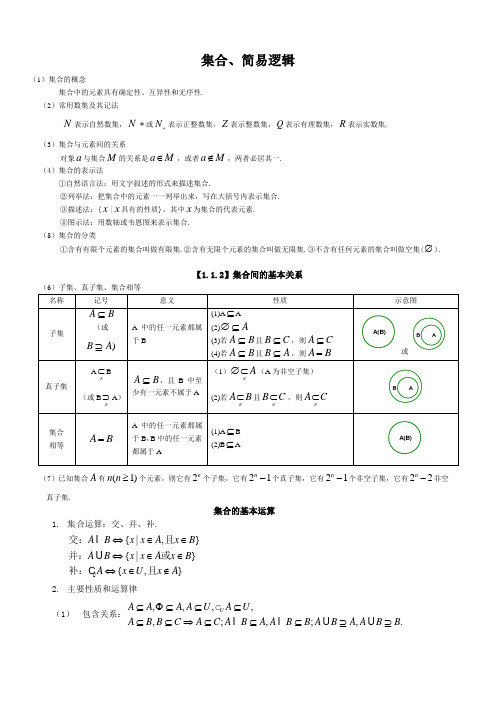
集合、简易逻辑(1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N*或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系(6)子集、真子集、集合相等 名称记号意义性质示意图子集B A ⊆(或)A B ⊇A 中的任一元素都属于B(1)A ⊆A(2)A ∅⊆(3)若B A ⊆且B C ⊆,则A C ⊆ (4)若B A ⊆且B A ⊆,则A B =A(B)或B A真子集A ≠⊂B(或B ≠⊃A )B A ⊆,且B 中至少有一元素不属于A(1)A ≠∅⊂(A 为非空子集)(2)若A B ≠⊂且B C ≠⊂,则A C ≠⊂B A集合 相等A B =A 中的任一元素都属于B ,B 中的任一元素都属于A(1)A ⊆B (2)B ⊆AA(B)(7)已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n -非空真子集.集合的基本运算1. 集合运算:交、并、补.{|,}{|}{,}A B x x A x B A B x x A x B A x U x A ⇔∈∈⇔∈∈⇔∈∉U 交:且并:或补:且C 2. 主要性质和运算律 (1) 包含关系:,,,,,;,;,.U A A A A U A U A B B C A C A B A A B B A B A A B B ⊆Φ⊆⊆⊆⊆⊆⇒⊆⊆⊆⊇⊇C原命题若p 则q 否命题若┐p 则┐q 逆命题若q 则p 逆否命题若┐q 则┐p 互为逆否互逆否互为逆否互互逆否互(2) 等价关系:U A B A B A A B B AB U ⊆⇔=⇔=⇔=C (3) 集合的运算律:交换律:.;A B B A A B B A ==结合律:)()();()(C B A C B A C B A C B A == 分配律:.)()()();()()(C A B A C B A C A B A C B A == 0-1律:,,,A A A U A A U A U Φ=ΦΦ===等幂律:.,A A A A A A ==求补律:A ∩C U A =φ A ∪C U A =U C U U =φ C U φ=U反演律:C U (A ∩B)= (C U A )∪(C U B ) C U (A ∪B)= (C U A )∩(C U B )简易逻辑1、命题的定义:可以判断真假的语句叫做命题。
高考数学专题《集合》习题含答案解析

分析:由题意首先求得 CR B ,然后进行交集运算即可求得最终结果.
详解:由题意可得: CR B x | x 1 ,
结合交集的定义可得: A CR B 0 x 1 .
本题选择 B 选项.
8.(2017·全国高考真题(理))已知集合 A={x|x<1},B={x| 3x 1 },则(
故选:C
8.(2019·北京临川学校高二期末(文))已知集合 = { ―1,3}, = {2,2},若 ∪ = { ―1,3,2,9},则实数
)
的值为(
A. ± 1
B. ± 3
C. ― 1
D.3
【答案】B
【解析】
∵ 集合 = { ―1,3}, = {2,2},且 ∪ = { ―1,3,2,9}, ∴ 2 = 9,因此, =± 3,
对③: {0,1, 2} 是集合, {1, 2, 0} 也是集合,由于一个集合的本身也是该集合的子集,故③正确.
对④: 0 是元素, 是不含任何元素的空集,所以 0 ,故④错误.
对⑤: 0 是元素, 是不含任何元素的空集,所以两者不能进行取交集运算,故⑤错误.
故选:C.
3.(2021·浙江高一期末)已知集合 M 0,1, 2,3, 4 , N 2, 4, 6 , P M N ,则满足条件的 P 的非
则集合 A B 的所有元素之和为(
A.16
B.18
)
C.14
D.8
【答案】A
【解析】
由题设,列举法写出集合 A B ,根据所得集合,加总所有元素即可.
【详解】
由题设知: A B {1, 2,3, 4, 6} ,
∴所有元素之和 1 2 3 4 6 16 .
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集合部分
一、基础练习
1. 设集合{}{}|1|22A x x B x x =>-=-<<,,则A B =( )
A.{}|2x x >- B.{}1x x >-| C.{}|21x x -<<- D.{}|12x x -<<
2. 已知集合M ={ x|(x + 2)(x -1) < 0 },N ={ x| x + 1 < 0 },则M ∩N =( )
A. (-1,1)
B. (-2,1)
C. (-2,-1)
D. (1,2)
3. 已知集合}{{}1,3,5,7,9,0,3,6,9,12A B ==,则A B =( )
A .{3,5}
B .{3,6}
C .{3,7}
D .{3,9}
4. 已知集合{}|2,{|4,|A x x B x x Z =≤=≤∈,则A B =( )
(A )(0,2) (B )[0,2] (C ){0,2} (D ){0,1,2}
5. 已知集合{}{}0,1,2,3,4,1,3,5,,M N P M N ===则P 的子集共有( )
(A )2个 (B )4个 (C )6个 (D )8个
二、基础练习
1. 设{|210}S x x =+>,{|350}T x x =-<,则S T =( )
A .∅
B .1{|}2x x <-
C .5{|}3x x >
D .15{|}23
x x -<<
2. 设集合A={4,5,7,9},B={3,4,7,8,9},全集=A B ,则集合C u (A B )中
的元素共有
(A) 3个 (B ) 4个 (C )5个 (D )6个 3. 设全集{}1,2,3,4,5U =,集合{}1,4M =,{}1,3,5N =,则 N ∩(C u M )
A.{}1,3
B. {}1,5
C. {}3,5
D. {}4,5
三、基础练习题
1. 设集合},4,2{},2,1{},4,3,2,1{===B A U C U (A B )=
(A ){2} (B ){3} (C ){1,2,4} (D ){1,4}
2. 设集合{|32}M m m =∈-<<Z ,{|13}N n n M
N =∈-=Z 则,≤≤( ) A .{}01, B .{}101-,, C .{}012,, D .{}1012-,,,
3. 已知全集U ={1,2,3,4,5,6,7,8},M ={1,3,5,7},N ={5,6,7},则C u ( M ∪N )=
(A) {5,7} (B ) {2,4} (C ){2,4,8} (D ){1,3,5,6,7}
4. 设全集U ={x *N ∈|6}x <集合A={1,3},B={3,5},则C u (A B )=
A. {1,4}
B. {1,5}
C.{2.4}
D.{2,5}
5. 设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则=)(N M C U
(A ){}12, (B ){}23, (C ){}2,4 (D ){}1,4
四、提高题
1、设全集{}1lg |*<∈=⋃=x N x B A U ,
若{}4,3,2,1,0,12|=+==⋂n n m m B C A U ,则集合B=__________
2、设集合A={-1,1,3},B={a+2,a 2+4},A∩B={3},则实数a = ___________
3、已知全集U=R ,则正确表示集合M= {-1,0,1} 和N= { x |x 2+x=0} 关系的韦恩(Venn )图是
4、设P={x|x<4},Q={x|x 2<4},则 ( )
A.P Q
B.Q P
C.P C R Q
D.Q C R P
5、已知A,B 均为集合U={1,3,5,7,9}的子集,且A ∩B={3}, ( C U B)∩A={9},则A= ( )
A.{1,3}
B.{3,7,9}
C.{3,5,9}
D.{3,9}
6、已知全集U=A ∪B 中有m 个元素,( C U A)∪ (C U B)中有n 个元素.若A ∩B 非空,则A ∩B 的元素个数为( )
A. mn
B. m+n
C.n-m
D.m-n
(2015年高考题)已知集合A={x|x=3n+2,n ∈N },B={6,8,12,14},则集合A ⋂B 中元素的个数为
(A )5 (B )4 (C )3 (D )2
(2014年高考题)已知集合{|13}M x x =-<<,{|21}N x x =-<<,则M N =
A. )1,2(-
B. )1,1(-
C. )3,1(
D. )3,2(-
(2013高考题)已知集合A ={1,2,3,4},B ={x|x =n2,n ∈A},则A∩B =( ).
A .{1,4}
B .{2,3}
C .{9,16}
D .{1,2}
(2012年高考题)已知集合A={x|x2-x -2<0},B={x|-1<x<1},则
(A )A ⊂≠B (B )B ⊂≠A (C )A=B (D )A ∩B=∅
(2011年高考题)设集合U={}1,2,3,4,{}1,2,3,M ={}2,3,4,N =则075,2,A b a c ==求与=⋂(M N )
(A ){}12, (B ){}23, (C ){}2,4 (D ){}1,4
(2010年高考题)已知集合2,,4,|A x x x R B x x x Z =≤∈=≤∈,则A B =
(A )(0,2) (B )[0,2] (C )|0,2| (D )|0,1,2|
⊆⊆⊆⊆。
