网络计划优化案例费用优化
网络计划优化案例费用优化

网络计划优化案例费用优化在一个建设项目中,有多个任务需要按照一定的顺序执行,而每个任务的执行需要一些资源投入,比如人力、材料、设备等,同时每个任务的执行时间也是不同的。
为了充分利用资源、缩短项目总工期,并降低项目成本,需要对网络计划进行优化。
首先,我们需要绘制网络计划图,将各个任务按照任务执行的前后关系连接起来,形成一个网络计划。
网络计划图可以清晰地显示每个任务的持续时间、紧前任务和紧后任务等信息。
然后,我们可以利用关键路径法来确定项目的关键路径。
关键路径是指影响整个项目工期的一条路径,即在该路径上的任务不能延迟,否则将导致整个项目工期延长。
确定了关键路径后,我们可以对这条路径上的任务进行优化,以缩短项目总工期。
接下来,我们可以利用资源平衡法来对项目的资源分配进行优化。
资源平衡法是指在满足任务时间要求的前提下,合理调整任务执行时间,以实现资源的合理利用和最小化费用的目标。
具体操作可以参考以下步骤:1.根据任务执行所需的资源量和资源使用限制,计算每个任务执行所需的资源量。
2.制定资源分配策略,即确定每个任务每个时间段所需的资源量。
3.按照资源分配策略,结合网络计划图,制定资源分配计划。
4.对资源分配计划进行优化,调整任务执行时间,以实现资源的合理利用和最小化费用的目标。
在进行资源分配优化时,需要注意以下几点:1.合理利用资源:根据资源的供需情况,尽量避免资源的浪费或过度使用。
2.优化资源分配计划:根据项目实际情况,灵活调整资源分配计划,以达到最小化费用的目标。
3.控制项目总工期:通过调整任务执行顺序和时间,缩短项目总工期,降低项目成本。
4.风险评估与控制:在优化资源分配计划的过程中,要充分考虑项目风险,制定相应的风险评估与控制措施。
通过以上的优化措施,我们可以最大限度地缩短项目总工期,并降低项目成本。
但是需要注意的是,在进行优化时,需要充分考虑项目实际情况,并量化和评估各个因素的影响,以确保优化方案的可行性和有效性。
基于改进粒子群算法的网络计划工期——费用优化

A s at bt c r
A m df dprcesal ot i tn( S o ie atl w r p mz i MP O)aglh a r oe osl epolm o m —ot pi zt no e— i i n i ao lo t w spo sdt ov t rbe f iecs o t ao f t 'm i p eh t mi i n
0 引 言
粒子群优化算法( S 是 K ney和 E ehr受 鸟群觅食 P O) end brat
: = +0 . () 2 其 中 , 是 惯 性权 重 因 子 , 习 因子 c 和 c 是 非 负 常 数 , 和 / 学 。 : ' 2
是两个独立的介 于[ 1 之 间的随机数 ;表示进化代数 。 O,] t
的学习规律 , 更有利于粒子发现 问题 的全局最优解。最后将该方法用于 P R E T网络工期一 费用模 型求解 , 字仿 真表 明 了算 法的有 数
关键词
粒子群算 法 改进 粒子群算 法 工期一 费用优化
APPLYI NG M PROVED I PARTI CLE W ARM PrI I S O I T ZATI ' ON
l mso E T n t o k pa s n me c lsmu ai n r s l h w t e e e t e e sa d ef in y o e p o o e t o . e fP R ew r l n , u r a i lt e u t s o h f c i n s n f ce c ft r p s d me h d i o s v i h Ke wo d y rs P ril w r o t z t n ag r h at es a m pi ai l o t m I r v d p r ce S a] p i z t n ag r h T me c s o t z t n c mi o i mp o e a t l W 1Io t i I miai lo t m o i i o t pi ai mi o
费用优化.ppt

3
280 18(15)
(②,16)
5
(③,34)
200
11
6
(⑤,45)
压缩时间: △t1=15天-11天=4天 增加费用: △s1=200元/天×4天=800元 (3) 此时关键线路有两条:
1-2-3-5-6和1-2-4-6
例题
(①,16)
350 16(14)
2
250 16(13)
1
(②,32)
(①,16)
350 16(14)
2
250 16(13)
(②,32)
4
100 13(12)
1
150 14(13)
3
280 18(15)
(②,16)
5
(③,34)
200 15(11)
6
(⑤,49)
费用优化的方法和步骤
• 步骤
按正常持续时间计算工程总直接费 计算各项工作的直接费率
找出网络计划中的关键线路并求出计算工期
费用优化的定义
• 1、费用优化的定义
费用优化又称时间成本优化,是寻 求最低成本时的最优工期安排,或按要 求工期寻求最低成本的计划安排过程。
工期与费用的关系
• 2、工期与费用的关系
费用的 组成
直接费
间接费
工期与费用的关系
• 2、工期与费用的关系
直接工程费 直接费
费用的
措施费
组成
间接费
工期与费用的关系
找出网络计划中的关键线路并求出计算工期
在网络计划中找出费率(或组合费率)最低的一项 (或一组)关键工作作为缩短持续时间的对象
确定可缩短的持续时间 否
计算相应增加的直接费用
计算间接费用及其他损益,并求总费用增加额
造价案例分析讲义专题四:基于双代号(时标)网络图的方案优化
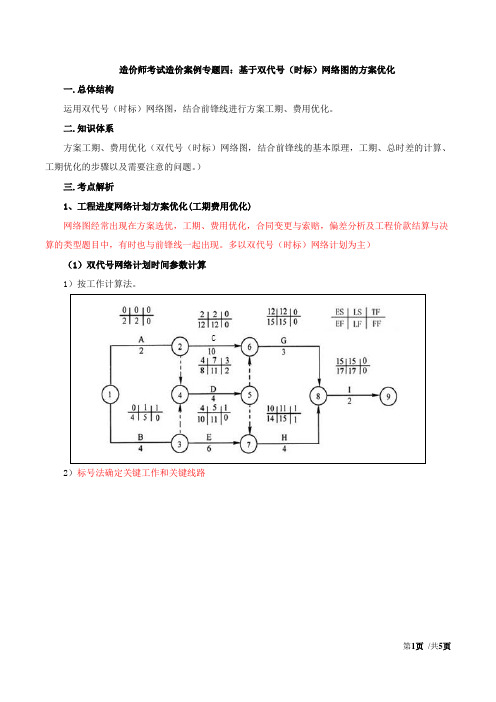
造价师考试造价案例专题四:基于双代号(时标)网络图的方案优化一.总体结构运用双代号(时标)网络图,结合前锋线进行方案工期、费用优化。
二.知识体系方案工期、费用优化(双代号(时标)网络图,结合前锋线的基本原理,工期、总时差的计算、工期优化的步骤以及需要注意的问题。
)三.考点解析1、工程进度网络计划方案优化(工期费用优化)网络图经常出现在方案选优,工期、费用优化,合同变更与索赔,偏差分析及工程价款结算与决算的类型题目中,有时也与前锋线一起出现。
多以双代号(时标)网络计划为主)(1)双代号网络计划时间参数计算1)按工作计算法。
2)标号法确定关键工作和关键线路3)平行线路法——利用封闭线路找关键线路,计算平行工作总时差。
记住三个“一定”:1、封闭圆圈两条线路的交叉节点一定是关键节点;2、找与之平行的线路一定是关键线路;3、封闭圆圈一定是最小封闭圆圈。
(2)双代号时标网络计划(经常与前锋线一起考察)进度对比反映的信息如下。
①工作实际达到的位置在检查日期线的左侧,表示该工作实际进度拖后,拖后的时间为二者之差。
②工作实际达到的位置与检查日期线重合,表明该工作实际进度与计划进度一致。
③工作实际达到的位置在检查日期线的右侧,表示该工作实际进度超前,超前的时间为二者之差。
(3)网络计划的优化包括工期优化,费用优化,资源优化,重点是工期优化。
工期优化一般通过压缩关键工作的持续时间来满足工期要求,但应注意:1)不能改变网络图中各项工作之间的逻辑关系;2)被压缩的关键工作在压缩完成后仍应为关键工作;3)若优化过程中出现多条关键线路时,为使工期缩短,应将各关键线路持续时间压缩同一数值。
化步骤如下:①按标号法确定关键工作和关键线路,并求出计算工期。
②按要求工期计算应缩短的时间ΔT:③选择应优先缩短持续时间的关键工作,主要考虑所需增加的赶工费最少的工作。
④将优先缩短的关键工作(或几个关键工作的组合)压缩到最短持续时间,然后找出关键线路,若被压缩的工作变成非关键工作,应将持续时间延长以保持其仍为关键工作。
运筹与决策PPT:网络优化问题
若向量1的第i个分量=v,则 SUMIF = SUMIF +向量2的第i个分量值
该函数可用于计算流出或流入节点v的流量
5.2 最大流问题
最大流问题,是要在网络中找出一个可 行流方案,使得通过网络的流量最大。
案例2: BMZ公司的配送中心问题
▪ BMZ是欧洲的一家豪华汽车制造商,其对美国的出口 至关重要;
5.1 最小费用流问题
最小费用流问题,也即网络配送问题, 解决如何以最小成本在一个配送网络中运输 货物。
案例1: Distribution Unlimited公司问题
▪ 该公司有两个工厂,生产一种产品,运往两个仓库;
– 工厂 1 生产 80 单位 – 工厂 2 生产 70 单位 – 仓库 1 需要 60 单位 – 仓库 2 需要 90 单位
C
To Rotterdam Bordeaux
Lisbon New York New York New Orleans New Orleans Los Angeles Los Angeles
▪工厂 1 与仓库 1 之间、工厂 2 与仓库 2 之间分别有铁 路相连;
▪ 也可通过卡车先将产品运至配送中心(DC),再从 配送中心运至仓库(每车至多装50单位)
问题:如何运输才能使费用最小?
配送网络图
80 units produced
F1
$700/unit
W1
60 units needed
$300/unit
Bordeaux
[40 units max.]
[50 units max.]
LI Lisbon [30 units max.]
BMZ问题的网络模型
《运筹学》胡运权清华版-9-03网络计划的优化

44
20
18 19 2
15
0
10
9 5
5
1
0
(人数)
按时差将工作排序
(天数)
0 1 2 3 4 5 6 7 8 9 10 11
9
6
7
5
1
1
2
3
5
6
3
44
20
18
15
10
5 0
(人数)
19 工作2 (1,2) , 总时差0,编为1#
工作0 (1,49) , 总时差1,编为2# 工作(1,6) , 总时5 差7,编为1 3#
24
18 6 T=64(天)
18
③ 总直接费用 478+10×1=488(百元)
间接费用 180 -33=147(百元)
总费用
488 +147=635(百元)
第二次调整
①,
1246 1346
同时缩短
(1,3), (1,2) 同时缩小 2.5+1=3.5 可选方案: (1,3), (2,4) 同时缩小 1+2=3
按时差将工作排序
(天数)
0 1 2 3 4 5 6 7 8 9 10 119 Nhomakorabea6
7
5
1
1
2
3假设:已进行5中非关键工作 6
3
4 不4允许中断
工作(1,4) , 总时差1,编为1#
20
19 20
18
工作(2,3) , 总时差0,编为2#
15
10
9
工作(1,6) ,5总时差5,编为3#
5
1
0
第二次调整结果
总费用
634.4(百元)
网络计划优化案例试题及答案

网络计划优化案例试题及答案一、试题。
某工程的网络计划如下图所示,箭线上方括号外为工作名称,括号内为正常持续时间(天),箭线下方括号外为直接费用率(千元/天),括号内为最短持续时间(天)。
工程间接费用率为0.8千元/天,正常工期时的间接费用为16千元。
试进行工期优化,求出最低工程费用及其相应的工期。
[此处应插入网络计划图,图中节点用数字表示,例如1 2之间有工作A,正常持续时间为6天,直接费用率为0.5千元/天,最短持续时间为4天等类似表示]二、答案及解析。
1. 计算各工作的直接费用率和可压缩时间。
对于工作A,正常持续时间D_A=6天,最短持续时间d_A=4天,直接费用率C_A=0.5千元/天,可压缩时间Δ t_A=6 4=2天。
按照同样的方法计算其他工作的相关参数。
2. 找出关键线路并计算总工期和总费用。
通过计算(可采用标号法等计算关键线路的方法),找出关键线路,假设关键线路为1 2 3 4,总工期T = 18天。
总直接费用C_d(假设所有工作按正常持续时间计算直接费用之和),总间接费用C_i=0.8×18 + 16 = 30.4千元,总费用C = C_d+C_i。
3. 进行工期优化。
选择直接费用率最小的关键工作进行压缩。
假设在关键线路上工作A的直接费用率最小。
每次压缩Δ t = min{Δ t_A,Δ t_B,·s}(其中A,B,·s为关键工作),并且要考虑压缩后是否会改变关键线路。
压缩工作A一天,此时总工期变为T'=17天。
重新计算总费用:总直接费用增加0.5×1 = 0.5千元。
总间接费用减少0.8×1 = 0.8千元。
总费用C'=C 0.8+0.5。
继续按照上述方法进行压缩,直到不能再压缩为止(即再压缩会使直接费用增加超过间接费用减少量)。
4. 确定最低工程费用及其相应工期。
通过不断的计算和优化,最终得到最低工程费用及其对应的工期。
网络计划技术-费用优化例题(施工组织设计课件)

第四章 网络计划技术-费用优化
例 某工程任务的网络计划如图4.72所示。箭线上方括号外 为正常时间直接费,括号内为最短时间直接费,箭线下方括 号外为正常持续时间,括号内为最短持续时间。假定平均每 天的间接费(综合管理费)为100元,试对其进行费用优化。
第四章 网络计划技术-费用优化
第一步,列出原始数据表,并计算各工作的费用率(见表)。
工作 正常工期ຫໍສະໝຸດ 最短工期相差费用率△Ci- 费用与时间
代号 时 间 直接费 时 间 直接费 时 间 费用 j(元/天) 变化情况
1-2 16 900 12 1220 4
320
80
1-3 18 1500 10 2500 8 1000
125
2-4 12 1000 6 2200 6 1200
T2 = 66 - 9 = 57(天) C2 = 11840 + 9×100 = 12740(元) 这时关键线路已变成2条(见图4.76)。
第四章 网络计划技术-费用优化
第四章 网络计划技术-费用优化
循环三: 从图4.76可以看得到,关键线路已变为2条:①→②→⑤→⑥→⑦; ①→③→⑤→⑥→⑦ 关键工作为:①-②,②-⑤,⑤-⑥,①-③,③-⑤,⑥-⑦。 其压缩方案为: 方案一:缩短⑤-⑥工作,每天增加费用240元,可缩短10天。 方案二:缩短①-②、①-③工作,每天平均增加费用205元,可缩 短4天。 方案三:缩短①-②、③-⑤工作,只能缩短1天,每天平均增加费 用180天。 方案四:缩短②-⑤、①-③工作,必须缩短4天,每天平均增加费 用200元。
在本例中,循环一:在正常持续时间原始网络计划图(图4.73)中,
关键工作为①-③、③-⑤、⑤-⑥、⑥-⑦,在表4.8中可以看到:⑥
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、费用优化示例
已知某工程双代号网络计划如图7所示,图中箭线下方括号外数字为工作的正常时间,括号内数字为最短持续时间;箭线上方括号外数字为工作按正常持续时间完成时所需的直接费,括号内数字为工作按最短持续时间完成时所需的直接费.该工程的间接费用率为万元/天,试对其进行费用优化.
图7 初始网络计划
1根据各项工作的正常持续时间,用标号法确定网络计划的计算工期和关键线路,如图8所示.计算工期为19天,关键线路有两条,即:①—③—④—⑥和①—③—④—⑤—⑥.
(①,4)
(①,8)(④,15)
(③,13)
图8 初始网络计划中的关键线路2计算各项工作的直接费用率:
△C
1-2
=∕4-2=万元∕天
△C
1-3
=∕8-6=万元∕天
△C
1-2
=∕4-2=万元∕天
△C
2-3
=万元∕天
△C
2-4
=万元∕天
△C
3-4
=万元∕天
△C
3-5
=万元∕天
△C
4-5
=万元∕天
△C
4-6
=万元∕天
△C
5-6
=万元∕天
3计算工程总费用:
①直接费总和:C
d
=++++++++=万元;
②间接费总和:C
i
=×19=万元;
③工程总费用:C
t = C
d
+C
i
=+=万元.
4通过压缩关键工作的持续时间进行费用优化优化过程见表1:
1第一次压缩
从图8可知,该网络计划中有两条关键线路,为了同时缩短两条关键线路的总持续,有以下四个压缩方案:
①压缩工作B,直接费用率为万元/天;
②压缩工作E,直接费用率为万元/天;
③同时压缩工作H和工作I,组合直接费用率为:+=万元/天;
④同时压缩工作I和工作J,组合直接费用率为:+=万元/天.
在上述压缩方案中,由于工作E的直接费用率最小,故应选择工作E为压缩对象.工作E的直接费用率万元/天,小于间接费用率0,8万元/天,说明压缩工作E可使工程总费用降低.将工作E的持续时间压缩至最短持续时间3天,利用标号法重新确定计算工期和关键线路,如图9所示.此时,关键工作E被压缩成非关键工作,故将其持续时间延长为4天,使成为关键工作.第一次压缩后的网络计划如图10所示.图中箭线上方括号内数字为工作的直接费用率.
(①,8)(④,14)
图9 工作E压缩至最短时的关键线路
(③,12)
(①,4)
图10 第一次压缩后的网络计划
2第二次压缩
从图3-44可知,该网络计划中有三条关键线路,即:①—③—④—⑥、①—③—④—⑤—⑥和①—③—⑤—⑥.为了同时缩短三条关键线路的总持续时间,有以下五个压缩方案:
①压缩工作B,直接费用率为万元/天;
②同时压缩工作E和工作G,组合直接费用率为+=万元/天;
③同时压缩工作E和工作J,组合直接费用率为:+=万元/天;
④同时压缩工作G、工作H和工作J,组合直接费用率为:++=万元/天;
⑤同时压缩工作I和工作J,组合直接费用率为:+=万元/天.
在上述压缩方案中,由于工作E和工作J的组合直接费用率最小,故应选择工作E和工作J作为压缩对象.工作E和工作J的组合直接费用率万元/天,小于间接费用率万元/天,说明同时压缩工作E和工作J可使工程总费用降低.由于工作E的持续时间只能压缩1天,工作J的持续时间也只能随之压缩1天.工作E和工作J的持续时间同时压缩1天后,利用标号法
重新确定计算工期和关键线路.此时,关键线路由压缩前的三条变为两条,即:①—③—④—⑥和①—③—⑤—⑥.原来的关键工作H未经压缩而被动地变成了非关键工作.第二次压缩后的网络计划如图11所示.此时,关键工作E的持续时间已达最短,不能再压缩,故其直接费用率变为无穷大.
(①,8)(③,14)
图11 第二次压缩后的网络计划
3第三次压缩
从图11可知,由于工作E不能再压缩,而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间,只有以下三个压缩方案:
①压缩工作B,直接费用率为万元/天;
②同时压缩工作G和工作I,组合直接费用率为+ =万元/天;
③同时压缩工作I和工作J,组合直接费用率为:+=万元/天.
在上述压缩方案中,由于工作I和工作J的组合直接费用率最小,故应选择工作I和工作J作为压缩对象.工作I和工作J的组合直接费用率万元∕天,小于间接费用率万元∕天,说明同时压缩工作I和工作J可使工程总费用降低.由于工作J的持续时间只能压缩1天,工作I的持续时间也只能随之压缩1天.工作I和工作J的持续时间同时压缩l天后,利用标号法
重新确定计算工期和关键线路.此时,关键线路仍然为两条,即:①—③—④—⑥和①—③—⑤—⑥.第三次压缩后的网络计划如图12所示.此时,关键工作/的持续时间也已达最短,不能再压缩,故其直接费用率变为无穷大.
(①,4)
(③,11) Array (①,8)(③,14)
图12 第三次压缩后的网络计划
4第四次压缩:
从图3-46可知,由于工作E和工作/不能再压缩,而为了同时缩短两条关键线路①—③—④—⑥和①—③—⑤—⑥的总持续时间,只有以下两个压缩方案:
①压缩工作B,直接费用率为万元/天;
②同时压缩工作G和工作I,组合直接费用率为+=万元∕天.
在上述压缩方案中,由于工作B的直接费用率最小,故应选择工作B作为压缩对象.但是,由于工作B的直接费用率万元∕天,大于间接费用率万元/天,说明压缩工作B会使工程总费用增加.因此,不需要压缩工作B,优化方案已得到,优化后的网络计划如图13所示.图中箭线上方括号内数字
为工作的直接费.
(①,4)
(①,8)(③,14)
(③,11)
图13 费用优化后的网络计划5计算优化后的工程总费用
①直接费总和:C
d0
=++++++++= 万元;
②间接费总和:C
i0
=×16=万元;
③工程总费用:C
t0 = C
d0
+ C
iO
= +=万元.
优化表
表1。
