成都高新区初三14-15第一次诊断试题
2014-2015成都市高新区九年级上期末物理试题
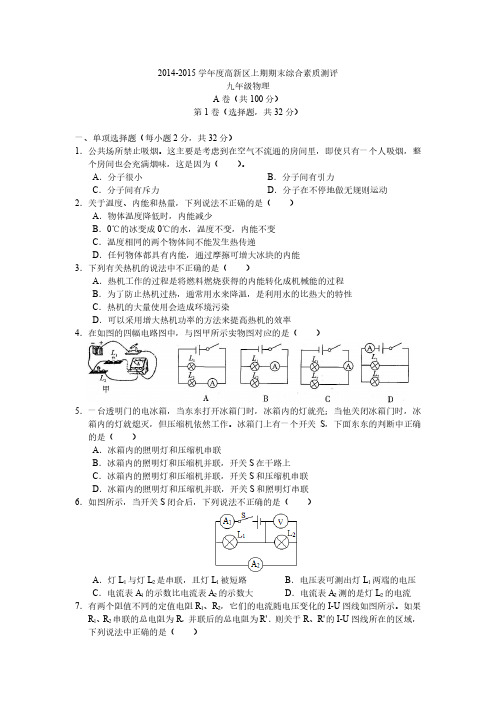
A.8W B.4W C.2W D.1W 14.关于磁体、磁场和磁感线,以下说法中正确的是( ) A.铁和铝都能够被磁体所吸引 B.磁体之间的相互作用是通过磁场发生的 C.小磁针的北极在任何情况下都指向地球的北极 D.磁感线是磁场中真实存在的曲线 15.关于电磁铁,下列说法中正确的是( ) A.电磁铁是利用通电导体在磁场中受到力的作用制作的 B.电磁铁中的铁芯,可以用钢棒代替 C.电磁继电器中的磁体,可以用永磁体,也可以用电磁铁 D.电磁继电器中的磁体,必须用电磁铁 16.POS 刷卡机的广泛应用给人们的生活带来了便利。POS 机的刷卡位置有一个绕有线圈 的小铁环制成的检测头如图所示。在使用时,将带有磁条的信用卡在 POS 机指定位置 刷一下,检测头的线圈中就会产生变化的电流,POS 机便可读出磁条上的信息。图中 能反映 POS 刷卡机读出信息原理的是( )
三、作图与计算题(25 题 4 分,26、27 各 6 分,共 16 分) 25. (1) (2 分)请在图中的圆圈中填上合适的电流表或电压表,使之成为正确的电路图。
(2) (2 分)如图所示,请根据通电螺线管的磁感线方向,在图上标出小磁针静止时的 N 极,并标出电源的正负极。
26. (6 分) 小明家的太阳能集热器中装有 40kg、 20℃的水, 经太阳光照射温度升高到 45℃, 求: (1)水吸收的热量是多少? (2)用电热水器对相同的水也加热到 45℃,标有“900r/kW·h”字样的电能表铝盘转 过了 1200r(电路中只有热水器工作) ,热水器消耗的电能是多少? (3)如果用电来加热,此热水器的效率?
27. (6 分)如图甲所示的电压力锅,集压力锅、电饭锅的优点于一体,省时节电,热效率 高。电压力锅工作原理如图乙,R1、R2 均为发热电阻,已知 R1=484 ,R2=48.4 。 (1)单独闭合开关 S1 时,电压力锅处于 状态(选填“保温”或“加热” ) 。 (2)电压力锅的加热功率是多少? (3),则它一共消耗电能是多少?
2014年成都市高新区中考一模数学试卷

2014年四川成都高新区初三一模数学试卷一、选择题(共10小题;共50分)1. 的绝对值为A. B. C. D.2. 如图所示的几何体的俯视图是A. B.C. D.3. 在一个不透明的盒子里,装有个黑球和若干个白球,它们除颜色外没有任何其他区别,摇匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复,共摸球次,其中次摸到黑球,则估计盒子中大约有白球A. 个B. 个C. 个D. 个4. 数据,,,,,,的众数和中位数分别是A. ,B. ,C. ,D. ,5. 下列命题:(1)有一个角是直角的四边形是矩形;(2)一组邻边相等的平行四边形是菱形;(3)一组邻边相等的矩形是正方形;(4)一组对边平行且相等的四边形是平行四边形.其中真命题的个数是A. 个B. 个C. 个D. 个6. 若关于的一元二次方程有两个不相等的实数根,则的取值范围是A. B. C. D.7. 如图,在平行四边形中,是边上的中点,连接,并延长交延长线于点,则与的周长之比是A. B. C. D.8. 如图,中,,于点,若,则A. B. C. D.9. 已知点,,都在反比例函数的图象上,则,,的大小关系是A. B. C. D.10. 已知二次函数的图象如图所示,对称轴是直线.下列结论:①;②;③;④,其中正确的是A. ①③B. 只有②C. ②④D. ③④二、填空题(共4小题;共20分)11. 抛物线的顶点坐标是.12. 如图,边长为的小正方形网格中,的圆心及,,,均在格点上,交于,则的余弦值是.13. 如图,某山坡的坡角,则该山坡的坡度为.14. 如图,菱形的两条对角线相交于,若,,则菱形的周长是.三、解答题(共6小题;共78分)15. 解答下列各题:(1)计算:;(2)解方程:.16. 已知:抛物线与直线分别交于轴和轴上同一点,交点分别是点和点,且抛物线的对称轴为直线.(1)求出抛物线与轴的两个交点,的坐标;(2)试确定抛物线的解析式.17. 如图,小明周末到郊外放风筝,风筝飞到处时的线长为米,此时小方正好站在处,过作垂直于,并测得,牵引底端离地面米,求此时风筝离地面的高度(结果保留根号).18. 6 月 5 日是“世界环境日”,广安市某校举行了“洁美家园”的演讲比赛,赛后整理参赛同学的成绩,将学生的成绩分成,,,四个等级,并制成了如下的条形统计图和扇形图(如图1、图2).(1)补全条形统计图.(2)学校决定从本次比赛中获得和的学生中各选出一名去参加市中学生环保演讲比赛.已知等中男生有名,等中女生有名,请你用“列表法”或“树形图法”的方法求出所选两位同学恰好是一名男生和一名女生的概率.19. 如图,在平面直角坐标系中,双曲线和直线交于,两点,点的坐标为,轴于点,且.(1)求双曲线和直线的解析式;(2)求的面积.20. 已知在中,,,点是边上一点,点在线段的延长线上,,点在线段上,.(1)如图,当时,求证:.(2)如图,当时,延长到点,使,与交于点,若,.①求证:;②求的长.四、填空题(共5小题;共25分)21. 设,是一元二次方程的两个实数根,则的值为.22. 有四张正面分别标有数字,,,的不透明卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中任取一张,将该卡片上的数学记为,则使关于的分式方程有正整数解的概率为.23. 记,令,称为,,,这列数的“幸运数”.已知,,,这列数的“幸运数”是,那么:,,,,,这列数的“幸运数”为.24. 如图,在中,,,,且,,则的面积为.25. 如图,在形状和大小不确定的中,,,分别是,的中点,在或的延长线上,交于,在上且平分,设,.当(为不小于的常数)时,与之间的函数关系式为(不用写自变量的取值范围).五、解答题(共3小题;共39分)26. 某科技开发公司研制出一种新型的产品,每件产品的成本为元,销售单价定为元,在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过件时,每件按元销售;若一次购买这种产品超过件时,每多购买一件,所购买的全部产品的销售单价均降低元,但销售单价均不低于元.(1)商家一次购买这种产品多少件时,销售单价恰好为元?(2)设商家一次购买这种产品件,开发公司所获得的利润为元,求(元)与(件)之间的函数关系式,并写出自变量的取值范围.(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获得的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)27. 如图,已知为的直径,过上的点的切线交的延长线于点,于点且交于点,连接,,.(1)求证:;(2)若,,求的长;(3)求证:.28. 如图,已知二次函数图象的顶点坐标为,直线的图象与该二次函数的图象交于,两点,且,直线与轴的交点为,满足,点是线段上一动点,且不与,两点重合,轴交抛物线于点.(1)求,和这个二次函数的解析式;(2)点是直线与抛物线对称轴的交点,当时,求点的坐标;(3)若时,另外一点在抛物线上,当时,求点的坐标.答案第一部分1. A2. B 【解析】俯视图是从上往下看到的视图,该几何体的俯视图是画出圆心的圆.3. A4. D5. D6. C7. A8. D9. D 10. C第二部分11. (,)12.13.14.第三部分原式15. (1)(2)方程分解因式得:可得或解得:16. (1)直线方程是,当时,,.又抛物线与直线交于点,且抛物线的对称轴为直线,.综上所述,抛物线与轴的两个交点,的坐标分别是:,.(2)由(1)知,,.直线方程是,当时,,.依题意得解得故该抛物线的解析式是:.17. 依题意得,,四边形是矩形,米,在中,,又米,,(米),(米).答:此时风筝离地面的高度为米.18. (1)补全统计图,如图所示:(2)列表如下:所有等可能的结果有.恰好是一名男生和一名女生19. (1)在反比例图象上,,反比例函数解析式为;轴于点,且,设点坐标为,把代入得,(舍去),点坐标为,把,代入得解得一次函数解析式为.(2)直线交轴于点,如图,把代入得,解得,则点坐标为,的面积20. (1),且,,故在中,,即,又,,,,,,,,,;(2)如图:①连接,,,是等边三角形,又为的中点,,,,,,,,,,又,,,为等边三角形,,即,,,是中位线,,,即;②,,,,,,,在中,,,则,在中,,,而,.第四部分21.22.23.24.【解析】如图,把绕点逆时针旋转得到,连接,,,,由旋转的性质得,,,,,,,,在和中,,,,是直角三角形,,,,,点到的距离为,的面积.25.【解析】如图,延长交于,,,又为的平分线,,,,,,为,的中点,,,,,即,解得.第五部分26. (1)设件数为,依题意,得解得答:商家一次购买这种产品件时,销售单价恰好为元.(2)当时,,当时,,即,当时,.且为整数且为整数.且为整数(3)由可知抛物线开口向下,当时,利润有最大值,此时,销售单价为(元),答:公司应将最低销售单价调整为元.27. (1)连接.切于点,.,,.,,,.(2)在中,,,根据勾股定理得,,,.设的半径为,,,,.(3)过点作于点.,,,,,.,,.,,.28. (1)二次函数图象的顶点坐标为,设,,,解得,,二次函数的解析式为:,,,,,,代入得解得(2)由(1)知,点是直线与抛物线对称轴的交点,抛物线对称轴是,,点,,,设,,,,,,,解得:,或(舍去),.(3)设,当在直线的下方时,,所以,解得,,把,,代入,解得,,所以或;当在直线的上方时,,所以,解得:,,把,代入,解得:,;所以或.。
2024年四川省成都市高新区中考数学一诊试题(原卷版)

2024年四川省成都市高新区中考数学一诊试卷一、选择题(本大题共8小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1. 在数轴上,点A 与点B 位于原点的两侧,且到原点的距离相等.若点A 表示的数为5,则点B 表示的数是( )A B. C. 5 D. 2. 空气,无色无味,无形无质,却承载着生命的呼吸,它的密度约为,将用科学记数法表示应为( )A. B. C. D. 3. 用一个平面去截下列几何体,截面可能是矩形的几何体是( )A. B. C. D.4. 下列计算正确的是( )A. B. C. D. 5. 已知一个多边形的内角和等于900º,则这个多边形是( )A. 五边形B. 六边形C. 七边形D. 八边形6. 若关于的一元二次方程有两个相等的实数根,则的值是( )A. B. C. D. 7. 《九章算术》是中国传统数学的重要著作,其中《盈不足》卷记载了这样一个问题:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?”其大意是:几个人一起去购买某物品,每人出钱,则多钱;每人出钱,则差钱,问人数和物品价格各是多少?设有人.根据题意,下面所列方程正确的是( )A. B. C. D. 8. 如图,,在射线上取一点C ,使,以点O 为圆心,的长为半径作,.1515-5-30.00129g/cm 0.00129412.910⨯﹣31.2910⨯﹣41.2910⨯﹣20.12910⨯﹣222a a -=236a a a ⋅=222632m n m n n ÷=()()22444m n m n m n+-=-x 220x x m -+=m 18-188-88374x 8374x x -=+8374x x +=-3487x x -+=3487x x +-=60AOB ∠=︒OA 6OC =OC MN交射线于点D ,连接,以点D 为圆心,的长为半径作弧,交于点E (不与点C 重合),连接.以下结论错误的是( )A. B.C. 的长为πD. 扇形的面积为12π二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)9. 因式分解=______.10. 如图,一边为平面镜,点在射线上,从点射出的一束光线经上一点反射后,反射光线恰好与平行.现测得入射光线与反射光线的夹角,则的度数为____.11. 某公司要招聘一名职员,根据实际需要,从学历、能力和态度三个方面进行测试,将学历、能力和态度三项成绩按的比例确定最终成绩.某面试者学历、能力和态度三项测试成绩分别为80分,85分,90分,则该面试者的最终成绩为____分.12. 若点,都在二次函数的图象上,则____.(填“>”,“=”或“<”)13. 如图,在中,,点为上一点,过、两点分别作射线的垂线,垂足分别为点,点.若点为中点,,则的长为____.的OB CD CD MN CE OE ,30DCE ∠=︒OD CE ⊥ DECOE 2242x x -+AOB ∠OB C OA C OB D DE OA CD DE 110CDE ∠=︒AOB ∠︒2:4:4()11A y ,()24B y ,()2221y x =--1y 2y Rt ABC △AB AC =D BC B C AD E F F AE 2BE =BC三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)14. (1)计算:;(2)解不等式组:.15. 为学习新时代榜样,某校准备组织师生开展“点亮人生灯塔”的社会实践活动,活动项目有“环境保护”“敬老服务”“文明宣传”“义卖捐赠”四项,每名参加活动的师生只参加其中一项.为了解各项活动参与情况,该校随机调查了部分师生的参与意愿,并根据调查结果绘制成不完整的统计图表. 项目人数环境保护6敬老服务a 文明宣传8义卖捐赠b(1)分别计算出表中a ,b 的值;(2)该校共有1200名师生参加活动,请估计选择参加“环境保护”项目的师生人数;(3)现拟从甲、乙、丙、丁四人中任选两人担任联络员,请利用画树状图或列表的方法,求出恰好选中甲、乙两人的概率.16. 近几年,中国新能源汽车凭借其创新技术、智能化特性和独特设计赢得了全球的关注.某品牌新能源汽21(2cos 45|1|3--︒+-3262723x x x x -<+⎧⎪--⎨≥⎪⎩车的侧面示意图如图所示,当汽车后背箱门关闭时,后备厢门与水平面的夹角,顶端A 和底端B 与水平地面的距离分别为和.现将后背箱门绕顶端A 逆时针旋转至,若,求此时的后备厢门底端到地面的距离.(参考数据:)17. 如图,是外接圆,,直线,的延长线交于点,交直线于点.(1)求证:直线是的切线;(2)若,,求的半径及的长.18. 如图,在平面直角坐标系中,一次函数的图象与反比例函数的图象交于,点.(1)求反比例函数的表达式及点的坐标;(2)过点的直线与轴交于点,与轴负半轴交于点.若,求的面积;AB 72ABH ∠=︒MN 152cm 70.3cm AB AB '102BAB '∠=︒B 'MN sin 720.95cos720.31tan 72 3.08︒≈︒=︒≈,,O ABC AC BC=CD AB ∥AO BC E DC F CF O 6AB =tan 3B ∠=O CF xOy 5y x =-+k y x=(1,)A a B B B x M y N 13BM MN =AMN(3)点在第三象限内反比例函数图象上,横坐标和纵坐标相等.点关于原点的对称点为点.平面内是否存在点,使得?若存在,求点的坐标;若不存在,请说明理由.一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)19. 已知,则代数式的值为____.20. 待定系数法是确定函数表达式的常用方法,也可用于化学方程式配平.石青[]加热分解的化学方程式为:,其中x ,y 为正整数,则____.21. 如图,飞镖游戏板中每一块小正方形除颜色外都相同,任意投掷飞镖次(假设每次飞镖均落在游戏板上),击中阴影部分的概率是_____.22. 如图,中,,,点E ,F 分别在,上,将沿所在直线翻折,点C 的对应点D 恰好在边上,过点D 作的垂线,交的延长线于点G ,设,则的值为____.(用含x 的代数式表示)23. 对于平面直角坐标系中图形M 和图形N ,给出如下定义:P 为图形M 上任意一点,Q 为图形N 上任意一点,如果P ,Q 两点间的距离有最小值,则称这个最小值为图形M ,N 间的“捷径距离”,记为d (图形M ,图形N ).已知三个顶点的坐标分别为,,,将三角形绕点逆时针旋转得到,若上任意点都在半径为4的内部或圆上,则与的“捷径距离”的最小值是____,最大值是_____.的的C C O D E ABD ACE ∽E 2225m m =+211()m m m m+-÷()32CuCO Cu OH x y ⋅()32CuCO Cu OH x y ⋅223CuO H O CO x ++↑y x -=1ABC 90ACB ∠=︒24AC BC ==AC BC CEF EF AB AB BC CG x =tan EFC ∠xOy ABC ()21A -,()32B -,()12C -,ABC ()D a a ,90︒A B C ''' A B C ''' O ABC A B C ''' ()d ABC A B C ''' ,二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)24. 年月日是联合国教科文组织确定的第个“世界读书日”.在世界读书日来临之际,某书店准备购进甲、乙两种图书进行销售,已知每本甲种图书的进价比每本乙种图书的进价多元,用元购买甲种图书的数量与用元购买乙种图书的数量相同.(1)求每本甲种图书与乙种图书的进价;(2)如果该书店决定用不超过元购买本甲种图书和若干本乙种图书,则乙种图书最多能购买多少本?25. 在平面直角坐标系中,抛物线与x 轴交于,B 两点,与y 轴交于点C ,对称轴为.(1)求抛物线的函数表达式;(2)如图1,连接,点D 在直线上方的抛物线上,过点D 作的垂线交于点E ,作y 轴的平行线交于点F .若,求线段的长;(3)直线与抛物线交于P ,Q 两点(点P 在点Q 左侧),直线与直线交点为S ,的面积是否为定值?若是,请求出此定值;若不是,请说明理由.26. 已知,在菱形中,,分别是,边上的点,线段,交于点.的2024423292526001600200020xOy 24y ax bx =++()20A -,1x =BC BC BC BC BC 3CE EF =DF (4)y x m m =-+<PC BQ OCS ABCD E F BC CD AE BF G(1)如图1,,点与点重合,连接;(i )求证:;(ⅱ)若为直角三角形,求的值;(2)如图2,,.当时,求线段的长.BGE ABC ∠=∠F D CG BE AD AE AG ⋅=⋅CDG EG CGAB ==45ABC ∠︒3cos 5AE BGE BF ∠==BE。
四川省成都市高新技术产业开发区2024年中考语文一模试卷

四川省成都市高新技术产业开发区2024年中考语文一模试卷一、基础知识(每小题3分,共12分)1.下列加点字注音有误的一项是()A.隧道(suì)笔砚(yàn)蹑手蹑脚(niè)B.熏陶(xūn)狡黠(xié)吹毛求疵(cī)C.盘桓(huán)契合(qì)两肋插刀(lèi)D.掂量(diān)渲染(xuàn)铢两悉称(zhū)2.下列语句书写完全正确的一项是()A.它们在大海上飞蹿,想把自己对暴风雨的恐惧,掩藏到大海深处。
B.那鹰斜移着,忽然一栽身,射到壁上,倾刻又飞起来,翅膀一鼓一鼓地扇动。
C.两个礼拜画一百多张,这当然只能浮光略影,不能深刻认识对象,更不能创造意境。
D.孔乙己用指甲蘸了酒,想在柜上写字,见我毫不热心,便又叹口气,显出惋惜的样子。
3.下列语段中加点成语使用有误的一项是()有些人一进书房便如坐针毡....的大话。
而真正做学问的人,会安于书斋....,说些哗众取宠....,一上讲台便高谈阔论寻章摘句....,潜心做出有价值的学术成果。
A.如坐针毡B.高谈阔论C.哗众取宠D.寻章摘句4.下列选项中没有语病的一项是()①2024年,成都高新区将进一步提升服务质量、提高服务能力、增强服务意识。
②一是提高营商环境,持续提升区域招商引资的吸引力;③二是新建人才公寓,为“筑梦高新”的各类人才营建“温暖的家”。
④各部门各司其职,携手前行,为奋力谱写高新发展新篇章中作出更大贡献。
A.①B.②C.③D.④二、文言文阅读(每小题3分,共12分)阅读下面文言文,完成各题。
甲若夫淫雨霏霏,连月不开,阴风怒号,浊浪排空,日星隐曜,山岳潜形,商旅不行,樯倾样摧,薄暮冥冥,虎啸猿啼。
登斯楼也,则有去国怀乡,忧谗畏讥,满目萧然,感极而悲者矣。
至若春和景明,波澜不惊,上下天光,一碧万顷,沙鸥翔集,锦鳞游泳,岸芷汀兰,郁郁青青。
而或长烟一空,皓月千里,浮光跃金,静影沉壁,渔歌互答,此乐何极!登斯楼也,则有心旷神怡,宠辱偕忘,把酒临风,其喜洋洋者矣。
成都高新区2020年初三数学第一次诊断题

A BCD O 成都高新区2020年初三数学第一次诊断性试题说明:本试题分A 、B 卷,共150分,120分钟完卷。
题号 A 卷A 卷总分B 卷 B 卷总分 总分总分人一 二 三 四 五 一 二 三 四 得分A 卷(100分)一、 一、选择题。
(每题3分,共24分)1下列运算正确的是 ( )A .532)(a a =B .1)14.3(0=-π C .532=+ D .632-=-2.“红军不怕远征难,万水千山只等闲”。
中国工农红军的二万五千里长征(1里=500米)是中国历史上的伟大壮举,请你用科学记数法将二万五千里表示为 ( ) A .5105.2⨯米 B .71025.1⨯米 C .7105.2⨯米 D .510125⨯米 3.下列图形中,既是轴对称图形,又是中心对称图形是 ( ) A .等腰三角形 B .平行四边形 C .梯形 D .圆4.如图: ABCD 中,对角线AC 和BD 相交于点O ,如果AC =12,BD =10,AB =m ,那么m 的取值范围是 ( ) A .111<<m B .222<<mC .1210<<mD .65<<m 5.如图,是由几个小立方块所搭的几何体的俯视图,小正方形中的数学表示在该位置 的小立方块的个数,这个几何体的主视图是 ( )6.某商品按进价的100%加价后出售,经过一段时间,商家为了减少库存,决定5折销售,这时每件商品 ( )A .赚50%B .赔50%C .赔25%D .不赔不赚7.制作一个底面直径为30cm ,高为40cm 的圆柱形无盖铁桶,所需铁皮至少( ) A .1425π2cm B .1650π2cm C .2100π2cm D .2625π2cm 8.有一大捆粗细均匀的钢筋,现要确定其长度,先称出这捆钢筋的总质量为m 千克,成都高新区20初三数学一诊A 卷 第1 页( 共 4 页)学校: 班级: 姓名: 学号:密 封 线答 题 不 要 超 过 此 线得 分 阅卷人再从中截取5米长的钢筋,称出它的质量为n 千克,那么这捆钢筋的总长度为 ( )A .n m 米 B .5mn 米 C .n m 5米 D .)55(-n m 米二、填空。
2015成都市高新区初三物理一诊试题及答案.

图12015级成都市高新区初三物理一诊试题物 理注意事项:1.全卷分A 卷和B 卷,A 卷满分100分,B 卷满分20分;全卷共120分;考试时间90分钟。
2.考生必须在答题卡上作答,答在试题卷、草稿纸上均无效。
3.在答题卡上作答时,考生需首先准确填写自己的姓名、准考证号,并用2B 铅笔准确填涂好自己的准考证号。
A 卷的第Ⅰ卷和B 卷第一大题为选择题,用2B 铅笔准确填涂作答;A 卷的第Ⅱ卷和B 卷用0.5毫米黑色墨水签字笔书写,字体工整、笔迹清楚。
请按照题号在相应各题目对应的答题区域内作答,超出答题区域书写的答案无效。
4.保持答题卡面清洁,不得折叠、污染、破损等。
A 卷(共100分) 第Ⅰ卷(选择题,共32分)一、单项选择题(每小题2分,共30分)1.小梦从第23届省运动会筹委会获悉,帆船比赛项目将在美丽的微山湖举行。
图1为本届省运会吉祥物宁宁参加帆船比赛项目的宣传画。
下列说法中正确的是 A .风吹帆船前进说明运动需要力来维持 B .比赛中的帆船速度有变化但惯性不变 C .帆船的重力与受到的浮力是一对相互作用力 D .比赛中的两艘帆船始终是相对静止的 2.关于粒子和宇宙,下列认识正确的是A .地球是宇宙的中心B .电子的发现说明原子是可分的C .质子带正电荷,中子带负电荷D .在电子、质子和原子中,尺度最小的是质子 3.下列有关物理量的估计,符合实际是A .一只成熟苹果的质量约150gB .人正常步行的速度约5m/sC .普通家用照明灯的工作电流约2AD .物理课本重约20N4.关于声现象,下列说法正确的是A .声音在不同介质中的传播速度相同B .在真空中也可以传播声音C .有物体振动我们一定会听到声音D .一切发声物体都在振动 5.下列有关力学知识的说法中正确的是A .用桨向后划水,船就会向前运动,利用了力的作用是相互的B .做匀速直线运动的物体,速度越大,受到的力也就越大C .电梯匀速上升的过程中,电梯对人的支持力不做功D .踢出去的足球,能继续向前滚动,是因为足球受到的惯性的作用图2山东煎.饼藜蒿炒.腊肉图3 榆钱蒸.饭香葱拌.豆腐6.下列关于光现象的说法正确的是A.月食是由于光的折射形成的B.光从空气射入水中,传播速度变小C.物体通过平面镜能成正立、等大的实像D.光发生漫反射时,不遵循光的反射定律7.随着数字时代的到来,3G与4G的相继出现,现在我们已经可以很方便的使用3G或4G手机进行无线网络登陆.下列对手机上网的说法中,正确的是A.使用电磁波传输数字信号B.使用超声波传输数字信号C.使用红外线传输数字信号D.使用次声波传输数字信号8.匀速地向某容器内注满水,容器底所受水的压强与注水时间的关系如图2,这个容器可能是9.人直接用F1的力匀速提升重物,所做的功是W1,若人使用某机械匀速提升该重物到同一高度则人的拉力为F2,所做的功是W2A.F1一定大于F2B.F1一定小于F2C.W2一定大于W1D.只有F2大于F1,W2才大于W110.《舌尖上的中国2》聚焦于普通人的家常菜,让海内外观众领略了中华饮食之美.如图3所示,通过煎、炒、蒸、拌烹调的四种美食中所包含的物理知识,认识正确的是A.煎:煎锅一般用铁制造,主要是利用了铁的比热容大B.炒:主要是通过做功的方式使藜蒿和腊肉的内能增加C.蒸:是通过热传递和高温水蒸气液化放热,使榆钱饭蒸熟D.拌:香葱和豆腐要拌才能入味,说明分子没有做无规则运动11.在第十七届“渝洽会”上,重庆造恩斯特龙408型直升机(如图4所示)签下了20架大订单。
成都市高新区2021年中考数学一诊试卷含答案
【考点】根的判别式.
【分析】分别计算出每个方程的判别式即可判断.
【解答】解:A、∵△=25﹣4×2×4=﹣7<0,∴方程没有实数根,故本选项正确;
B、∵△=36﹣4×1×4=0,∴方程有两个相等的实数根,故本选项错误;
23.如图,在五边形ABCDE中,已知∠BAE=120°,∠B=∠E=90°,AB=BC=2,AE=DE=4,在BC、DE上分别找一点M、N,若要使△AMN的周长最小时,则△AMN的最小周长为.
24.如图,已知矩形ABCD的四个顶点位于双曲线y= 上,且点A的横坐标为 ,S矩形ABCD=2 ,则k=.
(3)△<0⇔方程没有实数根.
7.如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A. B. C. D.
【考点】相似三角形的判定与性质.
【分析】易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得 = , = ,从而可得 + = + =1.然后把AB=1,CD=3代入即可求出EF的值.
C.1.5(1+x)2=4.5D.1.5(1+x)+1.4(1+x)2=4.5
10.在反比例函数y= 图象上有两点A(x1,y1),B(x2,y2),x1<0<x2,y1<y2,则m的取值范围是( )
A.m> B.m< C.m≥ D.m≤
二、填空题
11.方程组 的解是.
12.如图,⊙O的内接四边形ABCD中,∠A=115°,则∠BOD等于.
居民(户)
1
2
2015年成都高新区一诊试题.doc
2014-2015 (下期)九年级化学一诊试题答题可能用到的相对原子质量:H-l C-12 0-16 S—32 C1-35.5 A1—27注意:1、木试卷分第I卷和第n卷。
第I卷为选择题,第II卷为.並选姪题I、II卷都请答在答题卡上,答在试卷上不能得分,只交答题卡,不交试题卷。
2、本试卷共五个大题,21个小题,总分100分,答题时间60分钟。
第I卷(选择题,共42分)一、选择题(本题包括14个小题,每小题3分,共42分。
每小题只有一个选项符合题意。
)1.下列各选项中的变化能用化学变化解释的是()A.石汕分离出汽汕、煤汕和柴汕等B.煤隔绝空气加强热,产生焦炭、煤焦油、焦炉气等C.工业上分离空气制取氧气、鉍气;膜法和热法淡化海水D.二氧化碳气体经加压、降溫得到干冰,石墨在一定条件下转化为金刚石2.在盛有水的烧杯中加入以K某种物质,形成溶液的过程中,温度上升。
这种物质是()①鉍氧化钠②氯化钠③浓硫酸④硝酸铵⑤生石灰⑥氯化铵⑦蔗糖A.④⑥B.②④⑥C.②D.①③⑤3.以下生产、生活中的做法不符合环保理念的是()A.开发使用新能源,如太阳能、核能B.生活用水、工业污水无耑净化直接排放或灌溉C.秸秆回收利用,不辦天焚烧D.外出时少开私家车,处地铁或公交车4.下列洗涤方法屮涉及到乳化作川的足()A.用氢氧化钠溶液清洗盛装过植物油的瓶子B.用酒精或汽油清洗掉衣服上的油污C.用稀盐酸清洗盛装过石灰水的试剂瓶D.加了餐具洗洁精的热水洗涤碗碟上的汕污5.下列处理方法不正确的是• • •A.炒菜吋汕锅屮的汕不慎着火,可川锅盖盂灭B.不慎碰倒泗精灯,泗精在桌面上燃烧起来,应立即用水浇灭C.遇到火灾时,可用湿毛巾捂住口箅,蹲下靠近地側或沿墙壁跑离着火区域D.扑火森林火灾的有效方法之一是将人火蔓延路线前的一片树木砍掉,形成隔离带6.掌握化学川语足学好化学的关键。
不列化学川语与所表述的意义相符合的足① FeCl 2—z M 化亚铁②2Ca 2+—2个钙离子③02—2个氣原子®N ! 一钠离子⑤H 20 — 1个水分子⑥2H —2个氢元素®N 2 一組气屮鉍元素的化合价为0A •①④⑤⑦ B.②③④⑥ C.①②⑤⑦D.②⑤⑥⑦7. 去年5月,南京某公司丢失一枚探伤用放射源铱一 192,经过多方寻找终于放回安全箱。
2022-2023学年四川省成都市高新区九年级(上)期末数学试卷(一诊)
2022-2023学年成都市高新区九年级(上)期末(一诊)数学试卷一、选择题(本大题共8小题,每小题4分,共32分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)1.如图所示的几何体的左视图是()A.B.C.D.2.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加下列一个条件,不正确的是()A.∠ABP=∠C B.∠APB=∠ABC C.D.3.已知反比例函数y=的图象经过点(1,6),那么下列四个点中,也在这个函数图象上的是()A.(﹣2,3)B.(﹣3,2)C.(﹣3,﹣2)D.(6,﹣1)4.一个不透明的袋子中装有2个红球和若干个黄球,这些球除颜色外都相同.经过多次试验发现,摸出红球的频率稳定在左右,则袋子中的黄球个数最有可能是()A.1B.2C.4D.65.如图,矩形ABCD∽矩形EFGH,已知AB=3cm,BC=5cm,EF=6cm,则FG的长为()A.8cm B.10cm C.12cm D.15cm6.如图,在Rt△ABC中,∠ACB=90°,点D为边AB的中点,CD=3,AC=2,则BC 的长为()A.3B.4C.6D.7.两个相似三角形一组对应中线的长分别是2cm和5cm,其中较小三角形的周长是10cm,则较大三角形的周长为()A.15cm B.18cm C.20cm D.25cm8.某公司前年缴税40万元,今年缴税48.4万元.该公司这两年缴税的年均增长率为多少?设该公司这两年缴税的年均增长率为x,根据题意,下列所列的方程正确的是()A.40+x2=48.4B.40(1+x2)=48.4C.40(1﹣x)2=48.4D.40(1+x)2=48.4二、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)9.已知=,则的值=.10.如图,在矩形ABCD中,对角线AC,BD相交于点O,若OA=2,则BD的长为.11.已知点A(x1,y1)与点B(x2,y2)都在反比例函数y=﹣的图象上,且x1<0<x2,那么y1y2(填“>”,“=”或“<”).12.已知两条直线被三条平行线所截,截得线段的长度如图所示,则x=.13.如图,平面直角坐标系中,一点光源位于A(﹣3,4),线段BC的两个端点坐标分别为B(﹣2,2)与C(0,2),则线段BC在x轴上的影子B′C′的长度为.三、解答题(本大题共5个小题,共48分,解答过程写在答题卡上)14.解方程:2x2﹣x﹣3=0.15.关于x的一元二次方程x2﹣3x+m=0有两个相等的实数根,求m的值.16.某校同学参与“项目式学习”综合实践活动,小明所在的数学活动小组利用所学知识测量旗杆EF的高度,他在距离旗杆40米的D处立下一根3米高的竖直标杆CD,然后调整自己的位置,当他与标杆的距离BD为4米时,他的眼睛、标杆顶端和旗杆顶位于同一直线上,若小明的眼睛离地面高度AB为1.6米,求旗杆EF的高度.17.为深入推进“双减”,促进优质教育资源共享,更好地满足学生学习发展的需求,成都市教育局推出了“名师导学+在线答疑”服务,为有需求的学生答疑解惑.某学校为了解学生对该服务的了解情况,随机抽取若干名九年级学生进行调查,调查选项分为“A:非常了解;B:比较了解;C:了解较少;D:不了解.”四种,并将调查结果绘制成以下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:(1)m=,并补全条形统计图;(2)若该校九年级学生人数为500名,根据调查结果,估计该校对“名师导学+在线答疑”服务“比较了解”的学生共有名;(3)已知对“名师导学+在线答疑”服务“非常了解”的是1名男生和3名女生,从中随机抽取2名向其他同学做介绍,请用画树状图或列表的方法,求恰好抽到1男1女的概率.18.矩形ABCD中,连接AC,∠CAD的平分线交CD于点E,交BC的延长线于点F.在线段EF上取点G,使∠ECG=∠CAE.(1)判断三角形ACF的形状,并证明;(2)若AD=6,AB=8,求CE及CG的长.19.如图,平面直角坐标系中,过点P(﹣1,﹣3)的直线y=kx+b与反比例函数y=的图象交于点A.(1)若点A的横坐标1,求直线AP的函数表达式;(2)在(1)的条件下,点B为第一象限的反比例函数图象上一点,且在直线P A上方,若S△P AB=2,求点B的坐标;(3)过点P的另一条直线与反比例函数y=的图象交于M,N两点,点M在第一象限,若=,求点N的坐标.一、填空题(太大题共5个小题,每小题4分,共20分,答案写在答题卡上)20.若m,n是一元二次方程x2﹣4x+2=0的两实根,则m﹣mn+n的值为.21.用如图所示的两个转盘进行“配紫色”游戏,配得紫色的概率是.(红色和蓝色配成紫色)22.黄金分割总能给人以美的享受,从人体审美学的角度看,若一个人上半身长与下半身长之比满足黄金比的话,则此人符合和谐完美的身体比例.一芭蕾舞演员的身高为160cm,但其上半身长与下半身长之比大于黄金比,当其表演时掂起脚尖,身高就可以增加10cm,这时上半身长与下半身长之比就恰好满足黄金比,那么该演员的上半身长为cm.(结果保留根号)23.如图,在平面直角坐标中,平行四边形ABCD顶点A的坐标为(1,0),点D在反比例函数y=﹣的图象上,点B,C在反比例函数y=(x>0)的图象上,CD与y轴交于点E,若DE=CE,∠DAO=45°,则k的值为.24.如图,Rt△ABC中,∠ACB=90°,AB=12,点E为AC中点.点D在AC右侧,DE ⊥AC,且∠DAE=∠BAC,射线BE交AD于点F,若△DEF为等腰三角形,则线段EF 的长为.二、解答题(本大题共3个小题,共30分,解答过程写在答题卡上)25.如图,某校准备用54米的围栏修建一边靠墙的矩形花园ABCD(AB<BC),已知墙体的最大可用长度为28米,设AB的长为x米,矩形花园的面积为y平方米.(1)请用含有x的代数式表示y,并写出自变量x的取值范围;(2)如果该矩形花园的面积为360平方米,求AB的长.26.已知直线l1:y=kx﹣4(k>0)分别与x轴,y轴交于A,B两点,直线l2:y=﹣x+4与y轴交于点C,与直线l1交于点D.点P是线段OA上一动点(不与O,A重合),连接CP.(1)如图1,点D的横坐标为5.ⅰ.求直线l的函数表达式;ⅱ.连接DP,若∠CPD=90°,求线段OP的长;(2)如图2,若OP=2,在线段CP上取点M,将线段MP绕点P顺时针旋转90°得到PN,点N恰好在直线l1上,且AP=AN,求线段PM的长.27.如图1,在▱ABCD中,对角线AC,BD交于点O,AC平分∠BAD.(1)求证:四边形ABCD为菱形;(2)如图2,已知四边形ABCD的面积为20,BD=2,点E在BC的延长线上,点F 在AD的延长线上,连接EF.ⅰ.若DF=CE=,连接OE,OF,求线段OF的长及△OEF的面积;ⅱ.过点C作AC的垂线交EF的延长线于点M,连接AM,点P为AM的中点,若四边形CFMP为菱形,求线段CE的长.。
2023年四川省成都市高新区中考数学一诊试卷(含解析)
2023年四川省成都市高新区中考数学一诊试卷学校:___________姓名:___________班级:___________考号:___________ 1. −5的倒数是( )A. 15B. −15C. −5D. 52. 2023年春节期间,我省文化和旅游经济呈现“总体回暖,强势复苏”的可喜局面,其中体现巴蜀文化风韵的2023川渝春晚网络话题反响热烈,累计阅读量超4亿人次.将数据4亿用科学记数法表示为( )A. 40×107B. 4×108C. 0.4×109D. 4×1093. 下列计算正确的是( )A. 3ab−3a=bB. a2⋅a3=a6C. 2a2b÷a=2bD. (a+2)(a−2)=a2−44. 已知直线m//n,将含有30°的直角三角尺ABC按如图方式放置(∠CAB=30°),其中A,C两点分别落在直线m,n上,若∠1=35°.则∠2的度数为( )A. 25°B. 30°C. 35°D. 40°5. 若△ABC∽△DEF,且ABDE =13,若△ABC的周长为2,则△DEF的周长为( )A. 29B. 23C. 6D. 186. 校运会100米项目预赛,15名运动员的成绩各不相同,取前8名参加决赛,其中运动员小明已经知道自己的成绩,他想确定自己是否进入决赛,只需要知道这15名运动员成绩的( )A. 平均数B. 中位数C. 极差D. 方差7. 《九章算术》是我国古代重要的数学专著之一,其中记录的一道题译为白话文是:把一份文件慢马送到900里外的城市,需要的时间比规定时间多1天;如果用快马送,所需的时间比规定时间少3天.已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )A. 900x +1=900x +3×2B. 900x +1×2=900x +3C. 900x +1×2=900x−3 D. 900x +1=900x−3×28. 关于二次函数y =x 2+4x +5,下列说法正确的是( )A. 图象的对称轴在y 轴右侧B. y 的最小值为5C. 图象与x 轴有两个交点D. 当x >2时,y 的值随x 的值的增大而增大9. 计算:x 2x−2−4x−2=______.10. 已知直线y =−2x +1过点(1,a )和(2,b ),则a ______ b (填“>”“<“或“=”).11.如图,小正方形的边长为1,则△ABC 的面积为______ .12. 已知关于x 的一元二次方程x 2−2x +k =0有两个不等实数根,则k 的取值范围为______ .13. 如图,▱ABCD 的周长为16,连接AC ,分别以点A 和点C 为圆心,大于12AC 的长为半径作弧,两弧相交于点M ,N ,作直线MN ,交边AD 于点E ,连接CE ,则△CDE 的周长为______ .14. (1)计算:(12)−2−2cos 30°+ 27+(3−π)0;(2)解不等式组:{4(x +1)≤7x +10①x −5<x−83②.15. 幸福成都,美在文明!为助力成都争创全国文明典范城市,某校采用四种宣传形式:A .宣传单宣传、B .电子屏宣传、C .黑板报宣传、D .志愿者宣传.每名学生从中选择一种最喜欢的宣传形式,学校就最喜欢的宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.请结合图中所给信息,解答下列问题:(1)本次调查的学生共有______ 人,请补全条形统计图;(2)扇形统计图中,“D.志愿者宣传”对应的扇形圆心角度数为______ ;(3)本次调查中,在最喜欢“志愿者宣传”的学生中,有甲、乙、丙、丁四位同学表现优秀,若从这四位同学中随机选出两名同学参加学校的志愿者活动,请用列表或画树状图的方法,求选出两人恰好是甲和乙的概率.16. 成都新世纪环球中心被誉为亚洲第一大单体建筑,可容纳20个悉尼歌剧院,3个五角大楼.某校开展综合实践活动,测量环球中心主体顶端A离地面的高度AB的长,如图,在观测点C 处测得建筑物顶端A的仰角为30°,在观测点C测得建筑物底部B的俯角为14°,观测点C与建筑物的水平距离CD为120米,且AB垂直于CD(点A,B,C,D在同一平面内).求环球中心主体顶端A离地面的高度AB的长.(结果精确到1米;参考数据sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,3≈1.73)17. 如图,在△ABC中,AB=AC,以AB为直径的⊙O与BC交于点D,与边AC交于点E,过点D作AC的垂线,垂足为F.(1)求证:DF为⊙O的切线;(2)若AE=3,EF=1,求⊙O的半径及sin∠ABC的值.18. 在平面直角坐标系xOy中,直线y=−x+6与反比例函数y=kx的图象交于点A(1,a)和点B.(1)求反比例函数的表达式;(2)如图1,若点C为线段AB上一点,过点C作CD//x轴交双曲线于点D,连接OC,OD,若△OCD的面积为32,求点C的坐标;(3)如图2,连接AO,并延长AO至点E,使EO=AO,作∠OAB的平分线AF交x轴于点F,过点E作EH⊥AF于点H,求点H的坐标.19. 已知a+b=3,则a2−b2+6b的值为______.20. 若关于x的分式方程xx−1=ax−1−2的解为非负数,则a的取值范围是______ .21.如图,AB是⊙O的直径,AC为弦,∠BAC=30°,D为直径AB上一点,且AD=AC,连接CD并延长交⊙O于点E,现假设可以随意在圆中取点,则这个点取在阴影部分的概率是______ .22. 如图,抛物线y =12x 2−32x−2与x 轴交于A ,B 两点,抛物线上点C 的横坐标为5,D 点坐标为(3,0),连接AC ,CD ,点M 为平面内任意一点,将△ACD 绕点M 旋转180°得到对应的△A′C′D′(点A ,C ,D 的对应点分别为点A′,C′,D′),若△A′C′D′中恰有两个点落在抛物线上,则此时点C′的坐标为______ (点C′不与点A 重合).23. 如图,在矩形ABCD 中,AB =3,BC =4,点P 为边CD 上一动点,连接AP 交对角线BD 于点E ,过点E 作EF ⊥AP ,EF 交BC 于点F ,连接AF 交BD 于点G ,在点P 的运动过程中,△AEG 面积的最小值为______ .24. 某文具店经销甲、乙两种笔记本,每次购买同一种笔记本的单价相同,购进笔记本的具体信息如表: 进货批次甲种笔记本数量(单位:本)乙种笔记本数量(单位:本)购买总费用(单位:元)第一次1520640第二次3025980(1)求甲、乙两种笔记本的购买单价;(2)若第三次计划用不超过920元购买甲、乙两种笔记本共50本,求至少购买甲种笔记本多少本?25. 在平面直角坐标系xOy 中,抛物线L :y =ax 2−2ax−3a (a >0)与x 轴交于A ,B 两点(点A 在点B 的左侧),直线y =ax +1与抛物线交于C ,D 两点(点D 在第一象限).(1)如图,当点C 与点A 重合时,求抛物线的函数表达式;(2)在(1)的条件下,连接BD ,点E 在抛物线上,若∠DAE =∠ADB ,求出点E 的坐标;(3)将抛物线L 向上平移1个单位得到抛物线L 1,抛物线L 1的顶点为P ,直线y =ax +1与抛物线L1交于M,N两点,连接MP,NP,若∠MPN=90°,求a的值.26. 在矩形ABCD中,AB=4,BC=6,点M为边AD上一点,连接CM.(1)将△CDM沿直线CM翻折,得到对应的△CD′M.(i)如图1,延长CD′交边AD于点E,若点E恰为边AD中点,求线段MD的长;(ii)如图2,连接BD′,若BD′=BC,求线段MD的长;(2)如图3,若DM=DC,点P为边BC上一动点(点P不与B,C两点重合),过点P作PF⊥PA交线段CM于点F,在点P的运动过程中,线段CF的长是否存在最大值,若存在,求出这个最大值,若不存在,请说明理由.答案和解析1.【答案】B)=1,【解析】解:∵(−5)×(−15∴−5的倒数是−1.5故选:B.根据倒数的定义进行解答即可.本题考查的是倒数,熟知乘积是1的两数互为倒数是解答此题的关键.2.【答案】B【解析】解:4亿=400000000=4×108,故选:B.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a的值以及n的值.3.【答案】D【解析】解:A、原式=3ab−3a,不符合题意;B、原式=a5,不符合题意;C、原式=2ab,不符合题意;D、原式=a2−4,符合题意;故选:D.A、根据合并同类项法则判断;B、根据同底数的幂相乘法则计算;C、根据单项式相除法则计算;D、根据平方差公式计算.本题主要考查了整式的混合运算,掌握整式运算法则是解题关键.4.【答案】A【解析】解:如图,由题意得:∠ACB=90°,∠CAB=30°,∵∠1=35°,∴∠ACD=∠ACB+∠1=125°,∵m//n,∴∠CAE+∠ACD=180°,∴∠CAE=180°−∠ACD=55°,∴∠2=∠CAE−∠CAB=25°.故选:A.由题意可得∠ACB=90°,则可求得∠ACD=125°,再由平行线的性质可求得∠CAE=55°,即可求∠2的度数.本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,同旁内角互补.5.【答案】C【解析】解:∵△ABC∽△DEF,且ABDE =13,∴△DEF与△ABC的相似比为:3:1,∵△ABC的周长为2,∴△DEF的周长为:2×3=6.故选:C.直接利用相似三角形的性质,结合相似三角形的周长比等于相比,进而得出答案.此题主要考查了相似三角形的性质,正确掌握相似三角形的周长比等于相比是解题关键.6.【答案】B【解析】解:15个不同的成绩按从小到大排序后,中位数及中位数之后的共有8个数,故只要知道自己的成绩和中位数就可以知道是否进入决赛了.故选:B.由于比赛取前8名参加决赛,共有15名选手参加,根据中位数的意义分析即可.本题考查了统计量的选择,以及中位数意义,解题的关键是正确的求出这组数据的中位数.7.【答案】C【解析】解:设规定时间为x天,则快马所需的时间为(x−3)天,慢马所需的时间为(x+1)天,由题意得:900x+1×2=900x−3.故选:C.首先设规定时间为x天,则快马所需的时间为(x−3)天,慢马所需的时间为(x+1)天,由题意得等量关系:慢马速度×2=快马速度,根据等量关系,可得方程.此题主要考查了由实际问题抽象出分式方程,关键是正确理解题意,找出题目中的等量关系.8.【答案】C【解析】解:∵二次函数y=x2+4x+5=(x+2)2+1,∴抛物线开口向上,对称轴x=−2,顶点为(−2,1),∴函数有最小值1,当x>−2时,y的值随x的值的增大而增大,故A、B、D不正确,不符合题意;∵y=x2+4x+5=(x+5)(x+1),∴图象与x轴的交点坐标为(−5,0)和(−1,0),故C正确,符合题意;故选:C.将二次函数表达式化为顶点式或交点式,即可进行解答.本题主要考查了二次函数y=ax2+bx+c的图象和性质,解题的关键是掌握将二次函数表达式化为顶点式的方法.y=(x−ℎ)2+k的对称轴为x=ℎ,顶点坐标为(ℎ,k);a>0时,函数开口向上,在对称轴左边,y 随x 的增大而减小,在对称轴右边,y 随x 的增大而增大,a <0时,函数开口向下,在对称轴左边,y 随x 的增大而增大,在对称轴右边,y 随x 的增大而减小.9.【答案】x +2【解析】解:x 2x−2−4x−2=x 2−4x−2=x +2.故答案为x +2.根据同分母分式的加减法法则计算,注意结果要化简.本题主要考查了同分母分式的加减法法则:同分母分式相加减,分母不变,把分子相加减.10.【答案】>【解析】解:∵k =−2<0,∴y 随x 的增大而减小,又∵直线y =−2x +1过点(1,a )和(2,b ),且1<2,∴a >b .故答案为:>.由k =−2<0,利用一次函数的性质,可得出y 随x 的增大而减小,结合1<2,即可得出a >b .本题考查了一次函数的性质,牢记“k >0,y 随x 的增大而增大;k <0,y 随x 的增大而减小”是解题的关键.11.【答案】5【解析】解:△ABC 的面积为3×4−12×2×4−12×3×1−12×3×1=5,故答案为:5.用长方形面积减去三个直角三角形面积即可.本题考查三角形面积,解题的关键是掌握三角形面积公式.12.【答案】k <1【解析】解:∵关于x 的一元二次方程x 2−2x +k =0有两个不等实数根,∴Δ=(−2)2−4×1×k >0,解得:k <1,∴k 的取值范围为k <1.故答案为:k<1.根据方程的系数,结合根的判别式Δ=b2−4ac>0,可得出关于k的一元一次不等式,解之即可得出k的取值范围.本题考查了根的判别式,牢记“当Δ>0时,方程有两个不相等的实数根”是解题的关键.13.【答案】8【解析】解:∵平行四边形ABCD的周长为16,∴AD+DC=8,由作图可知MN垂直平分线段AC,∴EA=EC,∴△CDE的周长=CE+ED+CD=EA+ED+CD=AD+DC=8.故答案为:8.求出AD+DC=8,再利用线段的垂直平分线的性质解决问题.本题考查作图−基本作图,线段的垂直平分线的性质,平行四边形的性质等知识,解题关键是理解题意,灵活运用所学知识解决问题.14.【答案】解:(1)原式=4−2×3+33+12=5−23;(2){4(x+1)≤7x+10①②,x−5<x−83解不等式①,得x≥−2,,解不等式②,得x<72.故不等式组的解集为−2≤x<72【解析】(1)根据负整数指数幂的定义,特殊角的三角函数值,二次根式的性质以及零指数幂的定义计算即可;(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集.本题考查了实数的运算以及解不等式组,掌握相关定义与运算法则是解答本题的关键.15.【答案】50108°【解析】解:(1)本次调查的学生共有:10÷20%=50(人),∴B组的人数为:50−20−10−15=5(人),补全统计图如图:故答案为:50;(2)“D.志愿者宣传”对应的扇形圆心角度数为:360°×1550=108°,故答案为:108°;(3)根据题意画树形图:共有12种情况,被选取的两人恰好是甲和乙有2种情况,则被选取的两人恰好是甲和乙的概率是212=16.(1)根据C的人数和所占的百分比求出总人数即可,用总人数减去其它组的人数即可求出B的人数,进而补全统计图;(2)求出D所占是百分比,然后乘以360°即可;(3)根据题意先画出树状图,得出所有等情况数和选取的两人恰好是甲和乙的情况数,然后根据概率公式即可得出答案.本题考查了列表法与树状图法以及统计图,利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.16.【答案】解:∵AB垂直于CD,∴∠ADC=∠BDC=90°,在Rt△ADC中,CD=120米,∠ACD=30°,tan∠ACD=AD,CD=403(米),∴AD=CD⋅tan∠ACD=120×33在Rt△BDC中,CD=120米,∠BCD=14°,tan∠BCD=BD,CD∴DB=CD⋅tan∠BCD≈120×0.25=30(米),∴AB=AD+DB=30+403≈99(米),答:环球中心主体顶端A离地面的高度AB的长约为99米.【解析】根据正切的定义求出AD、BD,进而即可求得AB.本题考查的是解直角三角形的应用−仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.17.【答案】(1)证明:∵AB=AC,∴∠B=∠C,∵OB=OD,∴∠B=∠ODB,∴∠C=∠ODB,∴OD//AC,∵DF⊥AC,∴DF⊥OD,∵OD是⊙O的半径,∴DF为⊙O的切线;(2)解:连接DE,AD,∵四边形ABDE是圆内接四边形,∴∠ABC+AED=180°,∵∠DEF+∠AED=180°,∴∠DEF=∠ABC,∵∠ABC=∠C,∴∠DEC=∠C,∴DE=DC,∴△DEC是等腰三角形,又∵DF⊥EF,∴DF是△DEC的中线,∴EF=FC=1,AF=4,∴AC=AF+CF=5,∴AB=5,∴⊙O的半径为2.5;∵AB为⊙O的直径,∴∠ADB=90°=∠ADC,∴∠DAF=90°−∠ADF=∠FDC,∴△ADF∽△DCF,∴AF DF =DFCF,∴DF2=AF⋅CF=4×1=4,∴DF=2,在Rt△ADF中,,∴sinC=ADAC =255,∴sin∠ABC=255.答:⊙O的半径为2.5,sin∠ABC的值是255.【解析】(1)由AB=AC,得∠B=∠C,即可得∠C=∠ODB,故OD//AC,而DF⊥AC,有DF⊥OD,即知DF为⊙O的切线;(2)连接DE,AD,由∠DEF=∠ABC,可得∠DEC=∠C,DE=DC,而DF⊥EF,故DF是△DEC的中线,可得EF=FC=1,AF=4,AC=AF+CF=5,即得AB=5,⊙O的半径为2.5;证明△ADF∽△DCF,可得DF2=AF⋅CF=4,DF=2,在Rt△ADF中,AD=AF2+DF2=25,得sinC=ADAC =255,从而sin∠ABC=255.本题考查圆的综合应用,涉及圆内接四边形的性质、等腰三角形的性质、三角形的相似和判定,切线的判定,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.18.【答案】解:(1)将点A的坐标代入一次函数表达式得:a=−1+6=5,即点A(1,5),将点A的坐标代入反比例函数表达式得:k=1×5=5,即反比例函数的表达式为:y=5x;(2)设点C(6−t,t),则点D(5t,t),则△OCD的面积=12×CD×y C=12×(6−t−5t)×t=32,解得:t=2或4,即点C的坐标为:(4,2)或(2,4);(3)延长EH交AB于点G,∵AF是∠EAG的角平分线且AH⊥EH,∴△AEG为等腰三角形,则点H是EG的中点,∵EO=AO,即点O是AE的中点,则OH是△EAG的中位线,则OH//AG,则∠OHA=∠HAG,又∵AF是∠EAG的角平分线,则∠EAH=∠GAH,∴∠EAH=∠OFH,即OA=OH,∵OH//AB,故直线OH的表达式为:y=−x,设点H(m,−m),∵OA=OH,即12+52=m2+m2,解得:m=13(负值已舍去),即点H(13,−13).【解析】(1)用待定系数法即可求解;(2)由△OCD的面积=12×CD×y C=12×(6−t−5t)×t=32,即可求解;(3)证明OH是△EAG的中位线,得到OA=OH,进而求解.本题为反比例函数综合题,涉及到图形面积的计算、平行线的性质、等腰三角形的性质、一次函数的性质等,综合性强,难度适中.19.【答案】9【解析】解:a2−b2+6b=(a+b)(a−b)+6b=3(a−b)+6b=3a+3b=3(a+b)=9.故答案是:9.把前两项分解因式,然后把a+b=3代入,化简,然后再利用a+b表示,代入求值即可.本题考查了平方差公式,正确对所求的式子进行变形是关键.20.【答案】a≥−2且a≠1【解析】解:xx−1=ax−1−2,去分母,得x=a−2(x−1).去括号,得x=a−2x+2.移项,得x+2x=a+2.合并同类项,得3x=a+2.x的系数化为1,得x=a+23.∵关于x的分式方程xx−1=ax−1−2的解为非负数,∴a+23≥0且a+23≠1.∴a≥−2且a≠1.故答案为:a≥−2且a≠1.通过去分母、去括号、移项、合并同类项、x的系数化为1解这个分式方程得x=a+23,再根据分式方程的解的定义得a+23≥0且a+23≠1,从而解决此题.本题主要考查分式方程的解,熟练掌握分式方程的解的定义是解决本题的关键.21.【答案】π−24π【解析】解:如图,连接OE ,∵∠BAC =30°,OA =OC ,∴∠ACO =30°,∵AD =AC ,∴∠ADC =∠ACD =75°,∴∠OCE =45°,∵OE =OC ,∴∠OEC =∠OCE =45°,设圆的半径为r ,∴圆的面积为πr 2,阴影的面积为90πr 2360−12×r 2=πr 2−2r 24,∴点取在阴影部分的概率是:πr 2−2r 24÷πr 2=π−24π.故答案为:π−24π.连接OE ,设圆的半径为r ,用r 表示出阴影的面积和圆的面积,用概率公式计算即可.本题考查几何概率,解题的关键是用含r 的代数式表示阴影部分的面积.22.【答案】(2,3)或(−52,−338)【解析】解:令y =12x 2−32x−2=0,解得:x =−1或4,则函数的对称轴为x =32,当x =5时,则y =12x 2−32x−2=3,即点C (5,3);(1)当点A′、D′在抛物线上时,如图,由A′D′=AD =4,抛物线的对称轴为x =32,则点D′的横坐标为32−2=−12,当x =−12时,y =12x 2−32x−2=−98,则点D′(−12,−98),设点C′为(x ,y ),由中点坐标公式得:−12+3=5+x 且−98=3+y ,解得:x =−52,y =−338,即点C′的坐标为:(−52,−338);(2)当C′D′在抛物线上时,设点C′的坐标为:(m ,12m 2−32m−2),由点D 向右平移2个单位向上平移3个单位得到点C ,则点D′(m +2,12m 2−32m−2+3),将点D′的坐标代入抛物线的表达式得:12m 2−32m−2+3=,12(m +2)2−32(m +2)−2,解得:m =2,则点C′的坐标为:(2,3);(3)当A′、C′在抛物线上时,设点C′的坐标为:(m ,12m 2−32m−2),由点D 向右平移6个单位向上平移3个单位得到点C ,则点D′(m +6,12m 2−32m−2+3),将点D′的坐标代入抛物线的表达式得:12m 2−32m−2+3=12(m +6)2−32(m +6)−2,解得:m =−1,则点C′的坐标为:(−1,0),该点和点A 重合,故舍去;综上,点C′的坐标为:(2,3)或(−52,−338),故答案为:(2,3)或(−52,−338).(1)当点A′、D′在抛物线上时,求出点D′的坐标(−12,−98),再由中点坐标公式得到C′的坐标为:(−52,−338);(2)当C′D′在抛物线上时,设点C′的坐标为:(m ,12m 2−32m−2),得到点D′(m +2,12m 2−32m−2+3),进而求解;(3)当A′、C′在抛物线上时,同理可解.本题考查二次函数的综合应用,熟练掌握二次函数的图形及性质,中点坐标公式的运用,图象旋转的性质,其中,分类求解是本题解题的关键.23.【答案】4825【解析】解:设BF =x .∵四边形ABCD 是矩形,∴∠ABF =∠BAD =90°,AD =BC =4,AD //CB ,∵AB =3,∴AF = BF 2+AB 2= x 2+9,BD = AB 2+AD 2= 32+42=5,∵AD //BF ,∴AG GF =DG GB =AD BF =4x,∴AG =4x +4⋅ x 2+9,DG =4x +4×5=20x +4,∵AE ⊥EF ,∴∠AEF =∠ABF =90°,∴A ,B ,F ,E 四点共圆,∴∠FAE =∠FBE ,∵∠ADB =∠FBD ,∴∠GAE =∠ADG ,∵∠AGE =∠AGD ,∴△AGE∽△DGA ,∴AG DG =GE AG ,∴AG 2=GE ⋅GD ,∴EG =AG 2DG =4(x 2+9)5(x +4),令EG =y ,则有5yx +20y =4x 2+36,∴4x 2−5yx +36−20y =0,由题意(5y )2−4×4×(36−20y )≥0,∴25y 2+320y−16×36≥0,∴(5y−8)(5y +72)≥0,解得y ≥85或y ≤−725,∴EG 的最小值为85,过点A 作AH ⊥BD 于点H .∵12⋅BD ⋅AH =12⋅AB ⋅AD ,∴AH =3×45=125,∴△AEG的面积的最小值为12×85×125=4825.故答案为:4825.设BF=x.想办法用x表示出EG,根据一元二次方程,利用根的判别式,求出EG的最小值,可得结论.本题考查相似三角形的判定和性质,一元二次方程的根的判别式等知识,解题的关键是学会利用参数解决问题,属于中考填空题中的压轴题.24.【答案】解:(1)设甲种笔记本的购买单价为x元/本,乙种笔记本的购买单价为y元/本,根据题意得:{15x+20y=64030x+25y=980,解得:{x=16y=20.答:甲种笔记本的购买单价为16元/本,乙种笔记本的购买单价为20元/本;(2)设购买甲种笔记本m本,则购买乙种笔记本(50−m)本,根据题意得:16m+20(50−m)≤920,解得:m≥20,∴m的最小值为20.答:至少购买甲种笔记本20本.【解析】(1)设甲种笔记本的购买单价为x元/本,乙种笔记本的购买单价为y元/本,利用购买总费用=购买单价×购买数量,结合第一次及第二次购买数量及购买总费用,可得出关于x,y的二元一次方程组,解之即可得出结论;(2)设购买甲种笔记本m本,则购买乙种笔记本(50−m)本,利用总价=单价×数量,结合总价不超过920元,可得出关于m的一元一次不等式,解之取其中的最小值,即可得出结论.本题考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式.25.【答案】解:(1)当y=0时,ax2−2ax−3a=a(x2−2x−3)=0,∴(x−3)(x+1)=0,∴x1=3,x2=−1,∴A(−1,0),B(3,0),当C 与A 重合时,C (−1,0),代入直线y =ax +1得,−a +1=0,∴a =1,∴抛物线的函数表达式为:y =x 2−2x−3.(2)在(1)的条件下,y =x +1,①如图1,当点E 在AD 下方时,联立{y =x +1y =x 2−2x −3解得,{x 1=−1y 1=0,{x 2=4y 2=5,∴D (4,5),∵∠DAE =∠ADB ,∴AE =AD ,∴点E 在AD 的中垂线上,设AD 的中点为F ,则F (32,52),设直线EF :y =−x +b ,代入得,b =4,∴EF :y =−x +4,联立{y =−x +4y =x 2−2x −3解得,x =1± 292,∴E (1+ 292,7− 292).②如图2,当点E 在AD 上方时,∵∠DAE =∠ADB ,∴AE //BD ,∵(3,0),D (4,5),∴BD :y =5x−15,设直线AE :y =5x +m ,代入A (−1,0),解得,m =5,∴AE :y =5x +5.联立{y =5x +5y =x 2−2x −3解得,x 1=−1,x 2=8,∵x E >0,∴E (8,45),总上,E (1+ 292,7− 292)或E (8,45).(3)如图3,抛物线L 1:y =a (x−1)2−4a +1,∴P (1,1−4a ),联立{y =a (x −1)2−4a +1y =a x +1得,x =3± 212,∴M (3− 212,3− 212a +1),N (3+ 212,3+ 212a +1),∵∠MPN =90°,∴由勾股定理得,MP 2+NP 2=MN 2,MP 2=(3− 212−1)2+(3− 212a +1−1+4a )2=11− 212+71−11 212a 2,NP 2=(3+ 212−1)2+(3+ 212a +1−1+4a )2=11+ 212+71+11 212a 2,MN 2=(3+ 212−3− 212)2+(3+ 212a +1−3− 212a−1)2=21+21a 2,化简得,a 2=15,∵a >0,∴a = 55. 【解析】(1)将抛物线化为交点式,即得A ,B 的坐标,点C 的坐标,代入直线解析式求出a ,得到结果.(2)分类讨论:①当点E 在AD 下方时,E 在AD 的中垂线上,求出AD 解析式,得到中垂线解析式与抛物线解析式联立即可求出结果.②当点E在AD上方时,AE//BD,由BD解析式得到AE解析式联立方程即可求出结果.(3)由抛物线解析式求出L1得解析式,求得点PD的坐标,再联立方程求出M,N的坐标,由勾股定理MP2+NP2=MN2代入计算即可.本题考查了二次函数与一次函数的解析式的求法,交点坐标的求法,勾股定理等知识点,是一道综合性较强的题目,注重数形结合,正确分类讨论,具有较强的数学运算能力是解决问题的关键.26.【答案】解:(1)(i)∵四边形ABCD是矩形,∴∠D=90°,AD=BC=6,AB=CD=4,∵AE=ED=3,∴EC=DE2+CD2=32+42=5,由翻折变换的性质可知CD=CD′=4,∴ED′=CE−CD′=5−4=1,设DM=MD′=x,则有(3−x)2=x2+12,∴x=4,3∴DM=4;3(ii)如图2中,过点B作BJ⊥CD′于点J,作∠CBJ的角平分线BH交CJ于点H,过点H作HK⊥BC于点K.∵BC=BD′,BJ⊥CD′,∴CJ=JD′=2,∴BJ=BC2−CJ2=62−22=42,∵∠HBJ=∠HBK,∠BJH=∠BKH=90°,BH=BH,∴△BHJ≌△BHK(AAS),∴BK=BJ=42,JH=HK,设HJ=HK=y,则有(2−y)2=y2+(6−42)2,∴y=92−252,∴HK=92−252,∵∠JBC+∠JCB=90°,∠DCD′+∠JCB=90°,∴∠DCD′=∠CBJ,∵∠DCM=∠D′CM,∠CBH=∠HBJ,∴∠CBH=∠DCM,∵∠BKH=∠D=90°,∴△CDM∽△BKH,∴DM HK =CDBK,∴DM92−252=442,∴DM=9−2542;(2)过点F作FT⊥BC于点T.∵DM=DC,∠D=90°,∴∠DCM=∠DMC=45°,∵∠DCB=90°,∴∠FCT=45°,∵FT⊥CB,∴∠CFT=∠FCT=45°,∴TF=TC,设TF=TC=m,则CF=2m,设PB=n.∵AP⊥PF,∴∠APF=90°,∵∠B=∠PTF=90°,∴∠APB+∠FPT=90°,∠FPT+∠PFT=90°,∴∠APB=∠PFT,∴△ABP∽△PTF,∴AB PT =PBFT,∴46−m−n =nm,整理得n2+(m−6)n+4m=0,∵Δ≥0,∴(m−6)2−16m≥0,∴m2−28m+36≥0,解得m≤14−410或m≥14+410(不符合题意舍去),∴y的最大值为14−410,∴CF的最大值为142−85.【解析】(1)(i)设DM=MD′=x,利用勾股定理构建方程解决问题;(ii)如图2中,过点B作BJ⊥CD′于点J,作∠CBJ的角平分线BH交CJ于点H,过点H作HK⊥BC于点K .解直角三角形求出BK,HK,再利用相似三角形的性质求出DM;(2)过点F作FT⊥BC于点T.设TF=TC=m,则CF=2m,设PB=n.利用相似三角形的性质构建一元二次方程,利用根的判别式转化为二次不等式解决问题.本题属于四边形综合题,考查了矩形的性质,翻折变换,解直角三角形,相似三角形的判定和性质,一元二次方程的根的判别式等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,学会利用参数构建方程解决问题.。
