立方根第二课时课件2
合集下载
人教版七年级数学下册6.2立方根(2)优质课件.ppt

教师数学课件PPT模板
CONTENTS
目录
01 教学目标 03 教学准备 02 教学内容 04 教学过程
第一节
教学目标
输入你的文本 根据你所需的内容输入你想要的文本 点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解,
请根据您的具体内容酌情修改。
MORE THAN TEMPLATE
Step
03
Lorem ipsum dolor sit amet, consectetur adipiscing elit.
第四节
教学过程
输入你的文本 根据你所需的内容输入你想要的文本 点击输入本栏的具体文字,简明扼要的说明分项内容,此为概念图解,
请根据您的具体内容酌情修改。
MARK 03 PRESENTATION
四、归纳小结
1、估算一个数的立方根采用逼近法。
2、当被开方数的小数点向右移动3位时, 立方根的小数点只向__右__移动 1__ 位;当 被开方数的小数点向左移动3位时,立方 根的小数点只向__左_ 移动 _1__ 位。
我相信,只要大家勤 于思考,勇于探索,一定 会获得很多的发现,增长 更多的见识,谢谢大家, 再见!
立方根(2)
一、学习目标
1、进一步理解立方根的概念,并能熟练 地求一个数的立方根.
2、能用有理数估计一个无理数的大致范 围,形成估算的意识,培养估算能力.
二、新课引入
1、求下列各式的值:
(1)
3
2 10 27
(2) 3 0.13
(3) 52
二、新课引入
解:
(1)3 2 10 - 4
27
解:
3 100 4.642
3 0.1 0.464
(人教版)七年级下册数学:6.2《立方根》(第2课时)ppt课件

所以 ±3 2197 =‗‗‗±‗‗1‗3‗‗‗‗‗‗.
四、归纳小结
1、估算一个数的立方根采用逼近法;
2、当被开方数的小数点向右移动3位时,
立方根的小数点只向_____移右 动_____位;
当被1 开方数的小数点向左移动3位时,立
方根的小数点只向_____移动_____位。
左
1
五、强化训练
1、利用计算器来求下列各式的值:(精确到0.001)
(1)3 868 ≈‗‗‗9‗.‗5‗3‗‗9‗,(2) 3 0.426254 ≈‗‗0‗.‗7‗5‗‗3
(3) 3 8 ≈‗‗-‗‗0‗‗.6‗‗8‗4,(4) 3 2402≈‗‗±‗‗‗1‗3‗.‗3‗92
25
x 2、求下列各式中的
(1) x3 0.008
(3)x 13 64
(2)x 3
点 事实上,3 50 =3.68403149……,它是一个无限不循环 小数.
一 实际上,很多有理数的立方根都是无限不
循环小数,如 3 3,3 2 等都是
___无__限__不__循__环________小数,我们可以 用‗‗‗有‗‗理‗‗‗‗‗‗‗数近似地表示它们.
三、研读课文
知 识 点ห้องสมุดไป่ตู้一
比较3, 4,3 50 的大小.
解:⑴依次按键 3 1728=,显示:‗‗1‗2‗‗,
所以 3 1728 =‗‗‗1‗2‗‗‗ ;
⑵依次按键‗3‗‗‗1‗5‗6‗‗2‗5‗‗=‗ ,显示:
‗‗‗‗‗‗‗‗2‗‗5‗‗‗,所以 3 15625 =‗‗‗‗‗2‗‗5‗‗‗ ;
⑶依次按键‗3‗‗‗2‗1‗‗9‗7‗=‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗ , 显示:‗‗‗‗‗‗‗1‗3‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗
四、归纳小结
1、估算一个数的立方根采用逼近法;
2、当被开方数的小数点向右移动3位时,
立方根的小数点只向_____移右 动_____位;
当被1 开方数的小数点向左移动3位时,立
方根的小数点只向_____移动_____位。
左
1
五、强化训练
1、利用计算器来求下列各式的值:(精确到0.001)
(1)3 868 ≈‗‗‗9‗.‗5‗3‗‗9‗,(2) 3 0.426254 ≈‗‗0‗.‗7‗5‗‗3
(3) 3 8 ≈‗‗-‗‗0‗‗.6‗‗8‗4,(4) 3 2402≈‗‗±‗‗‗1‗3‗.‗3‗92
25
x 2、求下列各式中的
(1) x3 0.008
(3)x 13 64
(2)x 3
点 事实上,3 50 =3.68403149……,它是一个无限不循环 小数.
一 实际上,很多有理数的立方根都是无限不
循环小数,如 3 3,3 2 等都是
___无__限__不__循__环________小数,我们可以 用‗‗‗有‗‗理‗‗‗‗‗‗‗数近似地表示它们.
三、研读课文
知 识 点ห้องสมุดไป่ตู้一
比较3, 4,3 50 的大小.
解:⑴依次按键 3 1728=,显示:‗‗1‗2‗‗,
所以 3 1728 =‗‗‗1‗2‗‗‗ ;
⑵依次按键‗3‗‗‗1‗5‗6‗‗2‗5‗‗=‗ ,显示:
‗‗‗‗‗‗‗‗2‗‗5‗‗‗,所以 3 15625 =‗‗‗‗‗2‗‗5‗‗‗ ;
⑶依次按键‗3‗‗‗2‗1‗‗9‗7‗=‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗ , 显示:‗‗‗‗‗‗‗1‗3‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗‗
人教版七年级数学下册6.2_立方根(2)第二课时ppt精品课件

(3) 3 0.003 42
= -0.150 7 ——————.
要细心观察哦!
当堂检测
4.已 知 332.83.201, 33.281.486, 30.3280.6896,3 x14.86,3 y68.96,
则 x 3 280; y 328 00 .0
归纳总结
这节课你学到了哪些知识?
,a其中a 是被开方数, 实际上省略了 中的 根2 a指数2
求一个数的立方根的运算叫开 立方;开立方与立方是互逆运算
a
3 ,a其中a 是被开方数,
3是根指数(不能省略)
复习旧知
1.-8的立方要根先是计算512的立方-2根 ,2的立方根是
2.(-3)的3 立方根是
. -3
3. 3 512 的立方根是
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。 • 二、补笔记 • 上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一
解: (1) x3+27=0.
x3=-27.
x 3 27.
∴x=-3.
(2) 125x3-64=0.
x3 64 . 125
x 3 64 . 125
∴x=
4. 5
例3 你能求出下列各式中的未知数x吗? (1)x3+27=0; (2)125x3-64=0; (3)2(x+1)3-16=0.
2019/7/7
最新中小学教学课件
课件《立方根》精品PPT课件_人教版2

当鸟笼的体积变为原来的8倍时,体积为216×8=1 728(dm3).
开方得,x-1=±2,解得x=3或x=-1. 将体积分别为600 cm3和129 cm3的长方体铁块,熔成一个正方体铁块,那么这个正方体的棱长是多少?
求下列各式中x的值: (2)方程整理得,(x-1)2=4,
6 cm~7 cm之间
将体积分别为600 cm3和129 cm3的长方体铁块,熔成一个正方体铁块,那么这个正方体的棱长是多少?
一个数的立方根与被开方数同号
将体积分别为600 cm3和129 cm3的长方体铁块,熔成一个正方体铁块,那么这个正方体的棱长是多少?
4 cm~5 cm之间
如果一个正方体的体积为a,那么它的表面积可表示为
为12 dm.
一个正方体的水晶砖,体积为100 cm3,它的棱长在( )
7 cm~8 cm之间
∴7x+3y=7+42=49.
B
组
C
6. 一个正方体的水晶砖,体积为100 cm3,它的棱长 在( A )
A. 4 cm~5 cm之间 B. 5 cm~6 cm之间 C. 6 cm~7 cm之间 D. 7 cm~8 cm之间
8. 若x-1是125的立方根,则x -7的立方根是 -1 .
9. 已知x+2是27的立方根,3x+y-1的算术平方根是4, 求7x+3y平方根.
解:由x+2是27的立方根,3x+y-1的算术平方根为4,
7x+3y的平方根为±7.
10.将体积分别为600 cm3和129 cm3的长方体铁块,熔成
如果一个正方体的体积为a,那么它的表面积可表示为
.
将体积分别为600 cm3和129 cm3的长方体铁块,熔成一个正方体铁块,那么这个正方体的棱长是多少?
湘教版八年级数学上册《立方根》课件(共14张PPT)

(1)1
13=1
解 由于 1 3= 1 ,
因此3 11
8
(2)27
解:
因为
2
3
2 3
3 8
8 27
3 27
所以3 8 2 27 3
(3)0
03=0
解 由于 0 3= 0 ,
因此 3 0 = 0 .
(4)-0.064 (-0.4)3= -0.064
解 由于 (-0.4 )3= - 0.064 ,
•不习惯读书进修的人,常会自满于现状,觉得再没有什么事情需要学习,于是他们不进则退。经验丰富的人读书用两只眼睛,一只眼睛看到纸面上的话,另 一眼睛看到纸的背面。2022年4月13日星期三2022/4/132022/4/132022/4/13 •书籍是屹立在时间的汪洋大海中的灯塔。2022年4月2022/4/132022/4/132022/4/134/13/2022 •正确的略读可使人用很少的时间接触大量的文献,并挑选出有意义的部分。2022/4/132022/4/13April 13, 2022 •书籍是屹立在时间的汪洋大海中的灯塔。
.
(1)3 1 2 5
解 由于 53=125 ,
因此 31255 . (2)3 2 7
解 由于 33=27,
因此 327 3 .
(3)3 2 7
解
125
由于
3
3 5
3
=
27 125
,
因此
27 125
3 5
.
中考 试题
例1 一个数的平方等于64,则这个数的立方根是 ±2 .
解 因为(±8)2=64,所以这个数为±8. 所以这个数的立方根为 3 ± 8=.±2 故,应填写±2.
14.2 立方根课件(共24张PPT)

随堂练习
1.8的立方根为( )A.2 B.±2C.2 D.±2
2.有下列四个说法:①1的算术平方根是1;②的立方根是±;③-27没有立方根;④互为相反数的两数的立方根互为相反数.其中正确的是( )A.①② B.①③ C.①④ D.②④
C
3.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是( )A.-2 B.2C.3 D.4
D
拓展提升
归纳小结
立方根
立方根!
授课老师:
时间:2024年9月15日
他是这样做的:因为33=27,所以,这个大正方体的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么做的?
做一做
求满足下列各式的x的值:(1)x3=-1;(2)x3=64;(3)x3=0.008;(4)x3=-.
定义:
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.
定义性质表示方法开平方
平方根
一个正数有两个平方根,它们互为相反数.0只有一个平方根,是0本身.负数没有平方根.
开平方与平方互为逆运算.
新知引入
思考
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
小亮是这样想的:由已知小正方体的棱长为2,可以求出它的体积为23=8;同样,根据正方体的体积公式以及立方运算,由大正方体的体积,也可以求出它的棱长.
14.2 立方根
第十四章 实数
学习目标
1.了解立方根的概念,会求一个数的立方根.2.了解开立方与立方互为逆运算.3.探究立方根的性质,并能灵活运用.
学习重难点
理解并掌握立方根的性质.
1.8的立方根为( )A.2 B.±2C.2 D.±2
2.有下列四个说法:①1的算术平方根是1;②的立方根是±;③-27没有立方根;④互为相反数的两数的立方根互为相反数.其中正确的是( )A.①② B.①③ C.①④ D.②④
C
3.已知一个正数的两个平方根分别为3a-1和-5-a,则这个正数的立方根是( )A.-2 B.2C.3 D.4
D
拓展提升
归纳小结
立方根
立方根!
授课老师:
时间:2024年9月15日
他是这样做的:因为33=27,所以,这个大正方体的棱长为3.
你认为小亮的想法和做法有没有道理?你是怎么做的?
做一做
求满足下列各式的x的值:(1)x3=-1;(2)x3=64;(3)x3=0.008;(4)x3=-.
定义:
一般地,如果一个数x的立方等于a,即x3=a,那么这个数x就叫做a的立方根,也叫做a的三次方根.
定义性质表示方法开平方
平方根
一个正数有两个平方根,它们互为相反数.0只有一个平方根,是0本身.负数没有平方根.
开平方与平方互为逆运算.
新知引入
思考
如图,已知小正方体的棱长为2,那么它的体积是多少?反过来,如果大正方体的体积V=27,你能不能求出它的棱长x呢?
小亮是这样想的:由已知小正方体的棱长为2,可以求出它的体积为23=8;同样,根据正方体的体积公式以及立方运算,由大正方体的体积,也可以求出它的棱长.
14.2 立方根
第十四章 实数
学习目标
1.了解立方根的概念,会求一个数的立方根.2.了解开立方与立方互为逆运算.3.探究立方根的性质,并能灵活运用.
学习重难点
理解并掌握立方根的性质.
立方根第二课时2精品PPT课件

),小数部分是( ) ),小数部分是( )
7、比较大小
3 4 3 50
(1)
16 81 (2)
(3) 3 2 3
(4)
64
4、求下列各式中x的值
31 4 16
38 3 1 64
(1) 27(x 1)3 1 (2) 2(x 1)2 32 (3) (2 x)3 27 0 (4) (x 15)2 169
4 a :表示a的四次算术根.
例1:计算:
3
(1) 7 1 2 1.75 8
3
3
3
(2) 216 81 1 64
若3 38 3.362,3 x 33.62, 则x ______;3 0.038 _____
1.已知3 0.342 0.6993,3 3.42 1.507, 3 34.2 3.246,求下列各式的值。 (1)3 0.000342 = 0—.—0—6—9—9—3。 (2)3 34200000 = -—3—2—4—.6——。 (3) 3 0.00342 = -—0—.1—5—0—7—。
2.若已知 7.45 2.729,y 272.9;
那么y 74 50 0 。
3. 已知
3 3.78
=1.558,则
3
3.78
3780000的
值为 155.8 .
4. 891的算术平方根是 3 ;
5. 31525 的平方根是
;
6. 6 5 的小数部分是3 5 ;
探究
3 23 2 , 3 (2)3ቤተ መጻሕፍቲ ባይዱ 2
2.已知3 32.8 3.201,3 2.28 1.486, 3 0.328 0.6896,3 x 14.86,3 y 68.96, 则x 2 28 0; y 3 28 00。 0
北京课改版数学八年级上册 11.2《立方根》 课件(共44张PPT)
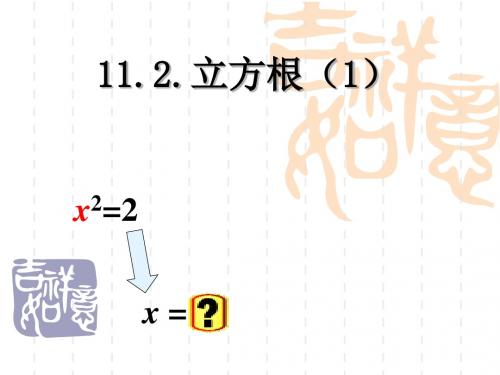
±1 ;立方根为____ (1)1的平方根是____ 1 ;算术 平方根为__ 1. 0 . (2)平方根是它本身的数是____ 0,±1. (3)立方根是其本身的数是____ (4)算术平方根是其本身的数是____ 0, 1 .
(5) 64 的立方根为 -2 . (6) ( 8) 的平方根为
练习
1.-8的立方根是
3
-2
2.(-3)的立方根是
3.
3
,2的立方根是 -3
3
2
8 的立方根是 8 512 4.一个数的立方根是 2 ,则这个数是 27 3 1 5. 3 125的倒数是; 5 相反数是 5
3 m 3 6. 2 -6 ,a-2的立方根为 -2 7.已知 3 4 则 a= a3 3
3 3 3 60 , 0.6 ①已知, 216 6 ,则 216000 ____ 0.216 ____ 3 3 3 1.1 , 110 ②已知, 1331 11 ,则 1.331 ____ 1331000 ____ ③正方体的体积扩大为原 来的 8 倍,
2 倍。 则它的边长变为原来的 ____
如果一个数 x 的立方等于 a, 那么这个数 x 叫做 a 的立方根.
即: 当 x3 =a 时, 称 x 是 a 的立方根.
记作:√a
3
, 读作:3次根号a
注:1. 这里的3表示开根的次数(根指数). 2. 平方根是可以省写根次数2的, 但2次以上的 根次数不能省写.
例练1
求下列各数的立方根: ⑴ 64
例练2
求下列各式的值:
⑴√27 - √8
3
3
⑵ √ -8 + √ 9
⑷
3
3
⑶
⑸√
3
(5) 64 的立方根为 -2 . (6) ( 8) 的平方根为
练习
1.-8的立方根是
3
-2
2.(-3)的立方根是
3.
3
,2的立方根是 -3
3
2
8 的立方根是 8 512 4.一个数的立方根是 2 ,则这个数是 27 3 1 5. 3 125的倒数是; 5 相反数是 5
3 m 3 6. 2 -6 ,a-2的立方根为 -2 7.已知 3 4 则 a= a3 3
3 3 3 60 , 0.6 ①已知, 216 6 ,则 216000 ____ 0.216 ____ 3 3 3 1.1 , 110 ②已知, 1331 11 ,则 1.331 ____ 1331000 ____ ③正方体的体积扩大为原 来的 8 倍,
2 倍。 则它的边长变为原来的 ____
如果一个数 x 的立方等于 a, 那么这个数 x 叫做 a 的立方根.
即: 当 x3 =a 时, 称 x 是 a 的立方根.
记作:√a
3
, 读作:3次根号a
注:1. 这里的3表示开根的次数(根指数). 2. 平方根是可以省写根次数2的, 但2次以上的 根次数不能省写.
例练1
求下列各数的立方根: ⑴ 64
例练2
求下列各式的值:
⑴√27 - √8
3
3
⑵ √ -8 + √ 9
⑷
3
3
⑶
⑸√
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 a :表示a的四次算术根.
例1:计算:
3
7 (1) 1 2 1.75
8
3
3
3
(2) 216 81 1 64
若3 38 3.362,3 x 33.62, 则x ______;3 0.038 _____
1.已 知3 0.342 0.6993,3 3.42 1.507, 3 34.2 3.246, 求 下 列 各 式 的 值 。 (1)3 0.000342 = 0—.—0—6—9—9—3。 (2)3 34200000 = -—3—2—4—.6——。 (3) 3 0.00342 = -—0—.—1—50—7—。
那么 125 1 1.1 8; 0.125 0.3 53 5 。
2.若已知 7.45 2.729,y 272.9;
那么y 745 00 。
3. 已知
3 3.78
=1.558,则
3
3.78
3780000的
值为 155.8 .
4. 891的算术平方根是 3 ;
5. 31525的平方根是 5 ;
求一个负数的立方根的一般方法:
3 a 3 a
也就是说,求一个负数的立方根,可以先 求出这个负数的绝对值的立方根,然后再取它的相 反数.
1、估计68的立方根的大小在( C )
A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间
2、一个正方体的水晶砖,体积为100cm³, 它的棱长大约在 ( A)
2.已知3 32.8 3.201,3 2.28 1.486, 3 0.328 0.6896,3 x 14.86,3 y 68.96, 则x 2 28 0 ; y 3 28 00。 0
SUCCESS
THANK YOU
2019/8/25
1.若 12.5 3.535,1.25 1.118
负数没有平方根 负数的立方根是负数;
开方 求一个数的平方根的 求一个数的立方根的 运算叫开平方;开平 运算叫开立方;开立 方与平方是互逆运算。方与立方是互逆运算。
你会区别下列的数吗?
a, a, 3 a, 4 a.
a :表示a的算术平方根; 3 a :表示a的立方根或a的三次方根; a :表示a的平方根或a的二次方根;
A、4㎝~5㎝之间 B、5cm~6cm之间 C、6㎝~7㎝之间 D、7㎝~8㎝之间
6. 3 5 的整数部分是(
3 12的整数部分是(
7、比较大小
3 4 3 50
),小数部分是( ),小数部分是(
(1)
16 81 (2)
3
(3) 3 2
(4)
64
4、求下列各式中x的值
31 4 16
6. 6 5 的小数部分是3 5 ;
探究
3 23 2 , 3 (2)3 2
(3 2)3 2 , (3 2)3 2
立方根的性质: 3 a3 a
(3 a )3 a
立方根的性质:
3
(1) (a)3 a
3
(2) a 3 a
3
(3)(
a)3 a
。
什么叫立方根?
如果一个数的立方等于a,那么这个数就
叫做a的立方根,也叫做a的三次方根.
一个数a的立方根可以表示为:
根指数
3
a
读作:三次根号 a
被开方数
3是根指数,不能省略。
平方根
立方根
表示方法 a3aa的Fra bibliotek值a≥ 0
a 是任何数
性质
正数有两个平方根,它 们是互为相反数;
0的平方根是0;
正数的立方根是正数 0的立方根是0.
10.2 立方根(二)
回顾 & 思考☞
1、什么是算术平方根 一个正数x的平方等于a,即 x2=a,这个 正数x叫做a的算术平方根
a的算术平方根记为 a
x2 = a (x为正数)
x a
被开方数a≥0 算术平方根 a ≥0
什么叫平方根?
如果一个数的平方等于a,那么这个数叫
做a的平方根或二次方根。
a的平方根可表示为 a
38 3 1 64
(1) 27(x 1)3 1 (2) 2(x 1)2 32 (3) (2 x)3 27 0 (4) (x 15)2 169
SUCCESS
THANK YOU
2019/8/25
例1:计算:
3
7 (1) 1 2 1.75
8
3
3
3
(2) 216 81 1 64
若3 38 3.362,3 x 33.62, 则x ______;3 0.038 _____
1.已 知3 0.342 0.6993,3 3.42 1.507, 3 34.2 3.246, 求 下 列 各 式 的 值 。 (1)3 0.000342 = 0—.—0—6—9—9—3。 (2)3 34200000 = -—3—2—4—.6——。 (3) 3 0.00342 = -—0—.—1—50—7—。
那么 125 1 1.1 8; 0.125 0.3 53 5 。
2.若已知 7.45 2.729,y 272.9;
那么y 745 00 。
3. 已知
3 3.78
=1.558,则
3
3.78
3780000的
值为 155.8 .
4. 891的算术平方根是 3 ;
5. 31525的平方根是 5 ;
求一个负数的立方根的一般方法:
3 a 3 a
也就是说,求一个负数的立方根,可以先 求出这个负数的绝对值的立方根,然后再取它的相 反数.
1、估计68的立方根的大小在( C )
A、2与3之间 B、3与4之间 C、4与5之间 D、5与6之间
2、一个正方体的水晶砖,体积为100cm³, 它的棱长大约在 ( A)
2.已知3 32.8 3.201,3 2.28 1.486, 3 0.328 0.6896,3 x 14.86,3 y 68.96, 则x 2 28 0 ; y 3 28 00。 0
SUCCESS
THANK YOU
2019/8/25
1.若 12.5 3.535,1.25 1.118
负数没有平方根 负数的立方根是负数;
开方 求一个数的平方根的 求一个数的立方根的 运算叫开平方;开平 运算叫开立方;开立 方与平方是互逆运算。方与立方是互逆运算。
你会区别下列的数吗?
a, a, 3 a, 4 a.
a :表示a的算术平方根; 3 a :表示a的立方根或a的三次方根; a :表示a的平方根或a的二次方根;
A、4㎝~5㎝之间 B、5cm~6cm之间 C、6㎝~7㎝之间 D、7㎝~8㎝之间
6. 3 5 的整数部分是(
3 12的整数部分是(
7、比较大小
3 4 3 50
),小数部分是( ),小数部分是(
(1)
16 81 (2)
3
(3) 3 2
(4)
64
4、求下列各式中x的值
31 4 16
6. 6 5 的小数部分是3 5 ;
探究
3 23 2 , 3 (2)3 2
(3 2)3 2 , (3 2)3 2
立方根的性质: 3 a3 a
(3 a )3 a
立方根的性质:
3
(1) (a)3 a
3
(2) a 3 a
3
(3)(
a)3 a
。
什么叫立方根?
如果一个数的立方等于a,那么这个数就
叫做a的立方根,也叫做a的三次方根.
一个数a的立方根可以表示为:
根指数
3
a
读作:三次根号 a
被开方数
3是根指数,不能省略。
平方根
立方根
表示方法 a3aa的Fra bibliotek值a≥ 0
a 是任何数
性质
正数有两个平方根,它 们是互为相反数;
0的平方根是0;
正数的立方根是正数 0的立方根是0.
10.2 立方根(二)
回顾 & 思考☞
1、什么是算术平方根 一个正数x的平方等于a,即 x2=a,这个 正数x叫做a的算术平方根
a的算术平方根记为 a
x2 = a (x为正数)
x a
被开方数a≥0 算术平方根 a ≥0
什么叫平方根?
如果一个数的平方等于a,那么这个数叫
做a的平方根或二次方根。
a的平方根可表示为 a
38 3 1 64
(1) 27(x 1)3 1 (2) 2(x 1)2 32 (3) (2 x)3 27 0 (4) (x 15)2 169
SUCCESS
THANK YOU
2019/8/25
