河南省郑州市2011届高中毕业年级第二次质量预测(数学文)word版
河南省郑州市高中毕业班第二次质量预测(数学文)

河南省郑州市2009年高中毕业班第二次质量预测文科数学(必修+选修I )本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至二页,第Ⅱ卷3至4页。
满分150分。
考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(共60分钟)注意事项:1. 答第Ⅰ卷前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号填写在答题卡和试卷规定的位置,并认真核准条形码上的姓名、座号和准考证号。
2. 第Ⅰ卷共2页。
答题时,考生须用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案。
在试卷上作答无效。
3. 本卷共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A B 、互斥,那么 球的表面积公式24S R π= ()()()P A B P A P B +=+ 其中R 表示球的半径 如果事件A B 、相互独立,那么 球的体积公式343V R π= ()()()P A B P A P B ⋅=⋅ 其中R 表示球的半径如果事件A 在一次实验中发生的概率是P , 那么n 次独立重复实验中恰好发生k 次的概率:()()(1)0.1.2.k k n kn n P k C P P k n -=⋅⋅-=⋅⋅⋅ 一、 选择题:1. 如果集合{}3P x x =≤,那么A . 1p -⊆B . {}1p -∈C . p ∅∈D . {}1p -⊆ 2.若110a b,则下列结论不正确的是 A . 22a b B . 2ab b C .2b aa b+≥ D . a b a b ++ 3.已知函数()()()2log 02 0x x x f x x ⎧⎪=⎨≥⎪⎩,则()()1f f -的值为 A . -1 B . 1 C . 2 D . 44.若直线:1l ax by +=与圆C :221x y +=有两个不同交点,则点P (),a b 与圆C 的位置关系是A . 点在圆上B . 点在园内C . 点在圆外D . 不能确定 5.已知非负实数5,,26,x y x y x y +≤⎧⎨+≤⎩,满足条件,则68z x y =+的最大值是A . 50B .40C . 38D . 186.设,a b 是两条直线,,αβ是两个平面,则a b ⊥的一个充分条件是A . ,//,a b αβαβ⊥⊥B . ,,//a b αβαβ⊥⊥C . ,,//a b αβαβ⊂⊥D . ,//,a b αβαβ⊂⊥ 7.将2cos 36y ππ⎛⎫=+⎪⎝⎭的图像按向量,24a π⎛⎫=- ⎪⎝⎭平移,则平移后所得图像的解析式为 A . 2cos 234y ππ⎛⎫=++ ⎪⎝⎭ B . 2cos 234y ππ⎛⎫=-+ ⎪⎝⎭C . 2cos 2312y ππ⎛⎫=--⎪⎝⎭ D . 2cos 2312y ππ⎛⎫=++ ⎪⎝⎭8.已知函数()()21x f x x R =-∈,则其反函数()1f x -的图像大致是9.已知命题P:不等式()lg 110x x -+⎡⎤⎣⎦ 的解集为{}01x x ;命题Q :在三角形ABC 中,22cos cos 2424A B A B ππ⎛⎫⎛⎫∠∠++ ⎪ ⎪⎝⎭⎝⎭是成立的必要而非充分条件,则A . P 真Q 假B .P 且Q 为真C .P 且Q 为假D . P 假Q 真10.设向量,i j 为直角坐标系的x 轴、y 轴正方向上的单位向量,若向量()1,a x i yj =++,()1b x i yj =-+且1a b -=,则满足上述条件的点(),P x y 的轨迹方程是A . ()22101344x y y +=≥B . ()22101344x y x -=≥C . ()22101344y x y -=≥D . ()22101344y x x -=≥ 11.等比数列{}n a 中,若123423159,88a a a a a a +++==-,则12341111a a a a +++= A . 53 B . 35 C .-53 D .-3512.已知A ,B ,C 是平面上不共线的三点,O 为平面ABC 内任一点,动点P 满足等式()()()()1111,03OP OA OB OC R λλλλλ⎡⎤=-+-+-∈≠⎣⎦ 且,则点P 的轨迹一定通过ABC ∆的 A . 内心 B . 垂心 C . 外心 D . 重心第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共2分13.某校有教师200人,男学生1200人,女学生1000人,先用分层抽样的方法从所有师生中抽取一个容量为n 的样本,已知从女学生中抽取的人数为80人,则n 的值为14.621x x ⎛⎫- ⎪⎝⎭的展开式,常数项等于15.过球一半径的中点作垂直于这条半径的球的截面,则此截面面积与球表面积之比为16.对于函数()11ax f x x +=-(其中a 为实数,1x ≠),给出下列命题:①当1a =时,()f x 在定义域上为单调增函数;②()f x 的图像关于点()1,a 对称;③对任意(),a R f x ∈都不是奇函数;④当1a =-时,()f x 为偶函数;⑤当2a =时,对于满足条件122x x 的所有12,x x 总有()()()12213fx f x x x-- ,其中正确的序号是三、 解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
河南省郑州市2021年高中毕业年级第二次质量预测---文科数学

12.已知 ,若 与 平行,则 __________.
13.三棱锥 的所有顶点都在球 的表面上, 平面 ,则球 的表面积为__________.
三、解答题
14.各项均为正数的等比数列 中, ,且 成等差数列.
(Ⅰ)求数列 的通项公式;
(Ⅱ)数列 ,已知 ,求 的前 项和 .
10.C
【详解】
函数 是连续函数,x=0时,y=0.x>0时,函数的导数为f′(x) ,
当0<x<1时,f′(x)>0,f(x)递增;
当x>1时,f′(x)<0,f(x)递减,
可得f(x)在x=1处取得极大值 ,f(x)∈(0, ]
x<0时,f′(x) 0,函数是减函数,
作出y=f(x)的图象,
设t=f(x),
故答案为D.
9.A
【详解】
分析:由题意,根据 ,求得 ,再由正弦定理可得 ,且 ,所以 ,利用余弦定理即可求解 的长.
详解:由题意, 满足 ,
则 ,即 ,
即 ,解得 或 (舍去),
又因为 ,所以 ,
又由 ,根据正弦定理可得 ,又 ,所以 ,
又由余弦定理得 ,故选A.
点睛:本题主要考查了正弦定理和余弦定理求解三角形问题,对于解三角形问题,通常利用正弦定理进行“边转角”寻求角的关系,利用“角转边”寻求边的关系,利用余弦定理借助三边关系求角,利用两角和差公式及二倍角公式求三角函数值.利用正、余弦定理解三角形问题是高考高频考点,经常利用三角形内角和定理,三角形面积公式,结合正、余弦定理解题.
(Ⅱ)字在选取的样本中,从成绩在80分以上(含80分)的学生中随机抽取2名学生,求所抽取的2名学生中恰有一人得分在 内的概率.
2020年郑州市高中毕业年级第二次质量预测文科数学试卷(含答案)
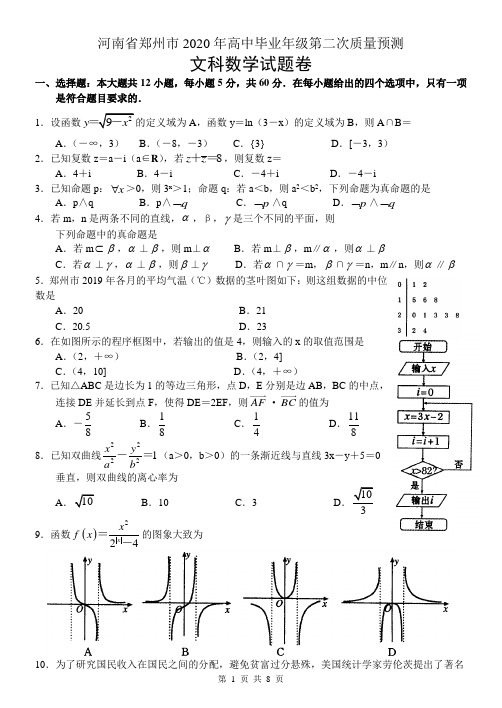
河南省郑州市2020年高中毕业年级第二次质量预测文科数学试题卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设函数29y x =-的定义域为A ,函数y =ln (3-x )的定义域为B ,则A ∩B = A .(-∞,3) B .(-8,-3) C .{3} D .[-3,3) 2.已知复数z =a -i (a ∈R ),若8z z +=,则复数z =A .4+iB .4-iC .-4+iD .-4-i3.已知命题p :x ∀>0,则3x >1;命题q :若a <b ,则a 2<b 2,下列命题为真命题的是 A .p ∧q B .p ∧q ⌝ C .p ⌝∧q D .p ⌝∧q ⌝ 4.若m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是A .若m ⊂β,α⊥β,则m ⊥αB .若m ⊥β,m ∥α,则α⊥βC .若α⊥γ,α⊥β,则β⊥γD .若α∩γ=m ,β∩γ=n ,m ∥n ,则α∥β 5.郑州市2019年各月的平均气温(℃)数据的茎叶图如下:则这组数据的中位数是A .20B .21C .20.5D .236.在如图所示的程序框图中,若输出的值是4,则输入的x 的取值范围是A .(2,+∞)B .(2,4]C .(4,10]D .(4,+∞)7.已知△ABC 是边长为1的等边三角形,点D ,E 分别是边AB ,BC 的中点,连接DE 并延长到点F ,使得DE =2EF ,则AF ·BC 的值为A .-58 B .18 C .14D .118 8.已知双曲线22221x y a b-=(a >0,b >0)的一条渐近线与直线3x -y +5=0垂直,则双曲线的离心率为A .10B .10C .3D .1039.函数()224x x f x =-的图象大致为的劳伦茨曲线,如图所示.劳伦茨曲线为直线OL 时,表示收入完全平等.劳伦茨曲线为折线OKL 时,表示收入完全不平等.记区域A 为不平等区域,a 表示其面积;S 为△OKL 的面积.将aGini S=,称为基尼系数.对于下列说法: ①Gini 越小,则国民分配越公平;②设劳伦茨曲线对应的函数为y =f (x ),则对x ∀∈(0,1),均有()f x x>1; ③若某国家某年的劳伦茨曲线近似为211y x =--(x ∈[0,1]),则12Gini π=-; 其中正确的是:A .①②B .①③C .②③D .①②③11.在正方体ABCD —A 1B 1C 1D 1中,三棱锥A 1—BC 1D 内切球的表面积为4π,则正方体外接球的体积为 A .86π B .36π C .323π D .646π 12.已知函数()2f x xπ=-,g (x )=x ·cosx -sinx ,当x ∈[-4π,4π]且x ≠0时,方程f (x )=g (x )根的个数是A .5B .6C .7D .8 二、填空题:本大题共4小题,每小题5分,共20分.13.幂函数f (x )=(m 2-3m +3)x m 的图象关于y 轴对称,则实数m =_________. 14.将一颗骰子先后投掷两次分别得到点数a ,b ,则直线ax +by =0与圆(x -2)2+y 2=2有公共点的概率为___________.15.在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且b =3,()3sin 3cos c A A b =+, 则△ABC 的面积的最大值为_________.16.据国家统计局发布的数据,2019年11月全国CPI (居民消费价格指数),同比上涨4.5%,CPI 上涨的主要因素是猪肉价格的上涨,猪肉加上其他畜肉影响CPI 上涨3.27个百分点.下图是2019年11月CPI 一篮子商品权重,根据该图,下列四个结论正确的有________.①CPI 一篮子商品中权重最大的是居住②CPI 一篮子商品中吃穿住所占权重超过50% ③猪肉在CPI 一篮子商品中权重为2.5%三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分 17.(12分)已知数列{n a }的前n 项和为n S ,且n S =2n +2n -1. (Ⅰ)求数列{n a }的通项公式; (Ⅱ)若11n n n b a a +=,求数列{n b }的前n 项和为n T .18.(12分)在改革开放40年成就展上有某地区某农产品近几年的产量统计如表:(Ⅰ)根据表中数据,建立y 关于x 的线性回归方程ˆˆˆybx a =+; (Ⅱ)根据线性回归方程预测2020年该地区该农产品的年产量.19.(12分)如图,三棱柱ABC —A 1B 1C 1中,平面AA 1B 1B ⊥平面ABC ,D 是AC 的中点. (Ⅰ)求证:B 1C ∥平面A 1BD;(Ⅱ)若∠A 1AB =∠ACB =60°,AB =BB 1,AC =2,BC =1,求三棱锥C —AA 1B 的体积.20.(12分)已知椭圆C :22221x y a b+=(a >b >0)的短轴长为,离心率为2.(Ⅰ)求椭圆C 的标准方程; (Ⅱ)直线l 平行于直线by x a=,且与椭圆C 交于A ,B 两个不同的点,若∠AOB 为钝 角,求直线l 在x 轴上的截距m 的取值范围. 21.(12分)已知函数()ln x f x x a =+(a ∈R ),曲线y =f (x )在点(e ,f (e ))处的切线方程为1y e=. (Ⅰ)求实数a 的值,并求f (x )的单调区间;(Ⅱ)求证:当x >0时,f (x )≤x -1.(二)选考题:共10分.请考生在第22、23题中任选一题做答,如果多做,则按所做的第一题记分.22.[选修4—4:坐标系与参数方程](10分)在极坐标系中,圆C 的方程为2sin a ρθ=(a >0).以极点为坐标原点,极轴为x 轴的正半轴建立平面直角坐标系,设直线l 的参数方程为3143x t y t ⎧⎨⎩=+,=+(t 为参数).(Ⅰ)求圆C 的标准方程和直线l 的普通方程;(Ⅱ)若直线l 与圆C 交于A ,B 两点,且|AB.求实数a 的取值范围.23.[选修4—5:不等式选讲](10分)已知函数f (x )=|x +1|-a |x -1|. (Ⅰ)当a =-2时,解不等式f (x )>5; (Ⅱ)若f (x )≤a |x +3|,求a 的最小值.2020年高中毕业年级第二次质量预测文科数学 评分参考一、选择题:1.D;2.B;3.B;4.B;5.C;6.B;7.B;8.D;9.D; 10.B; 11.B; 12.D. 二、填空题: 13.2; 14.;12716.1,2.3. 三、解答题:17.解:(1)当1=n 时,.211==S a ………………………1分 当2≥n 时,()()()[].12112112221+=--+---+=-=-n n n n n S S a n n n…3分而11221+⨯≠=a , 所以数列{}n a 的通项公式为⎩⎨⎧≥+==.2,12,1,2n n n a n…………………………5分(2)当1=n 时,101521a a 1b 211=⨯==, …………………………6分 当2≥n 时,()()⎪⎭⎫ ⎝⎛+-+=++=3211212132121n n n n b n ,所以⎪⎪⎩⎪⎪⎨⎧≥⎪⎭⎫ ⎝⎛+-+==.232112121,1,101n n n n b n ,…………………………8分当1=n 时,10111==b T , …………………………9分 当2≥n 时,n n b b b b T +⋅⋅⋅+++=321⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-++⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+=3211219171715121101n n .3020143215121101++=⎪⎭⎫ ⎝⎛+-+=n n n……………………………10分 又301201141011+⨯+⨯==T 适合,所以.302014++=n n T n……………………………12分 18.解:(1)由题意可知:,5.36654321=+++++=x………………………………1分764.72.71.777.66.6=+++++=y , ………………………………2分()()()(),5.175.25.15.05.05.15.2222222612=+++-+-+-=-∑=i ix x…………4分所以()()(),16.05.178.2ˆ121==---=∑∑==ni ini iix x yyx x b…………………………6分又,44.65.316.07ˆˆ=⨯-=-=x b y a…………………………8分故y 关于x 的线性回归方程为.44.616.0ˆ+=x y…………………………9分 (2)由(1)可得,当年份为2020年时,年份代码,7=x ,此时.56.744.6716.0yˆ=+⨯=, …………………………11分 所以可预测2020年该地区该农产品的年产量约为7.56万吨. ………………12分 19.解:(1)连结1AB 交B A 1于点O ,则O 为1AB 的中点, 因为D 是AC 的中点,所以C B OD 1//,…………………2分 又⊂OD 平面BD A 1,C B 1⊄平面BD A 1,所以//1C B 平面BD A 1. ………………………………5分 (2),60ACB ,1BC ,2AC=∠==,3ACB COS BC AC 2BC AC AB 222=∠⋅⋅-+=∴.3AB =∴, ……………6分 .,222BC AB BC AB AC ⊥∴+=∴又 平面B B AA 11⊥平面ABC ,平面 B B AA 11平面AB ABC =,∴⊥BC 平面B B AA 11. ………………………………8分 601=∠AB A ,.3AA ,AA BB AB 111=∴==.433AB A sin AA AB 21S 11AB A 1=∠⋅⋅⋅=∴∆……………………………10分 .4343331BC S 31V AB A AB A C 11=⨯=⋅=∴∆- ………………………12分20.解:(1)由题意可得222=b ,所以2=b , ………………1分32b c ,解得22=a , ……………………………3分所以椭圆C 的标准方程为.12822=+y x……………………………5分 (2)由于直线l 平行于直线x a b y =,即x y 21=,设直线l 在y 轴上的截距为n , 所以l 的方程为()021≠+=n n x y . ……………………………6分 由⎪⎪⎩⎪⎪⎨⎧=++=1282122y x n,x y 得042222=-++n nx x , 因为直线l 与椭圆C 交于A ,B 两个不同的点,所以()()0424222>--=∆n n ,解得2n 2<<-. ……………………………8分设()()2211,,,y x B y x A ,则,221n x x -=+.42221-=n x xAOB ∠为钝角等价于0<⋅OB OA ,且0≠n , ……………………………9分由⎪⎭⎫⎝⎛+⎪⎭⎫⎝⎛++=+=⋅n x n x x x y y x x OB OA 212121212121 ()()()02242452452222121<+-+-=+++=n n nn n x x n x x ,即22<n ,且0≠n , 直线l 在y 轴上的截距n 的取值范围()().2,00,2 - 所以直线l 在x 轴上的截距m 的取值范围()().22,00,22-………………12分21. 解:(1)()()()2ln ln a x xx ax x f a x x x f +-+='∴+=, , ()()2a e e ae f +='∴, ………………………3分 又曲线()x f y =在点()()e f e ,处的切线方程为ey 1=,()0='e f ,即.0=a ()()()2ln 10ln xxx f x a x x x f -='∴>+=, , 令()0>'x f ,得0ln 1>-x ,即;0e x << 令()0<'x f ,得0ln 1<-x ,即e x >,所以()x f 的单调增区间是()e ,0,单调减区间是().,+∞e …………………5分(2)当0>x 时,要证(),1-≤x x f 即证0ln 2≤+-x x x , 令()(),0ln 2>+-=x x x x x g则()()(),121211212xx x x x x x x x g +--=-+=+-='………………………9分 当10<<x 时,(),0>'x g ()x g 单调递增; 当1>x 时,(),0<'x g ()x g 单调递减,所以()(),01=≤g x g 即当0>x 时,().1-≤x x f …………………………12分22. 解:(Ⅰ)C 的直角坐标方程为222()y a x a +=-, ………………………2分消t 得到4350x y -+=………………………………………4分(Ⅱ)要满足弦AB ≥及圆的半径为a 可知只需圆心(0,a )到直线l 的距离12d a ≤即可。
河南省郑州市2011年高中数学 第一次质量预测

河南省郑州市2011年高中毕业年级第一次质量预测数学试题(文科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
考试时间120分钟,满分150分。
考生应首先阅读答题卷上的文字信息,然后在答题卷上作答,在试题卷上作答无效。
参考公式:样本数据n x x x ,,,21 的标准差;x x x x x x x ns n 其中],)()()[(122221-+-+-=为样本平均数; 柱体体积公式:为底面面积其中S Sh V ,=、h 为高;锥体体积公式:h S Sh V ,,31为底面面积其中=为高; 球的表面积、体积公式:,34,432R V R S ππ==其中R 为球的半径。
第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.下列四个命题中的真命题为 ( ) A .00,143x Z x ∃∈<< B .00,510x Z x ∃∈+=C .2,10x R x ∀∈-=D .2,20x R x x ∀∈++>2.若向量a 、b 满足3||||1,(),2a b a b b ==+⋅=且向量a 、b 的夹角为 ( )A .30°B .45°C .60°D .90°3.若复数3(,12a ia i i+∈-R 为虚数单位)是纯虚数,则实数a 的值为 ( )A .—2B .4C .—6D .64.已知集合{2,3},{|60},,A B x mx B A ==-=⊆若则实数m= ( )A .3B .2C .2或3D .0或2或3 5.设a 、b 是实数,且3,22aba b +=+则的最小值是( )A .6B.C.D .86.直线1y kx =+与曲线2y x ax b =++相切于点A (1,3),则a b -= ( )A .—4B .—1C .3D .—27.设α、β是两个不同的平面,a 、b 是两条不同的直线,给出下列四个命题,其中真命题是( )A .若//,//,//a b a b αα则B .若//,//,//,//a b a b αβαβ则C .若,,,a b a b αβαβ⊥⊥⊥⊥则D .若a 、b α在平面内的射影互相垂直,则a b ⊥8.已知等差数列{}n a 的前n 项和为481,3n S S S =且,则816S S = ( )A .18B .13 C .19D .3109.右图是一个空间几何体的三视图,如果直角三角形的直角边长均为1,那么这个几何体的体积为 ( ) A .1 B .12 C .13D .1610.将函数sin(6)4y x π=+图象上各点的横坐标伸长到原来的3倍,再向右平移8π个单位,得到的函数的一个对称中心是( )A .(,0)2πB .(,0)4πC .(,0)9πD .(,0)16π 11.已知双曲线的方程为22221(0,0)x y a b a b-=>>,双曲线的一个焦点到一条渐近线的距离为3(c 为双曲线的半焦距长),则双曲线的离心率为 ( )AB .32CD .23淋浴房 / 整体淋浴房 吘莒咝12.设,,a b c 分别是函数2112211()()log ,()2log ,()()log 22x xxf x xg x xh x x =-=-=-的零点,则,,a b c 的大小关系是( )A .b c a <<B .a b c <<C .b a c <<D .c b a <<第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分。
河南省郑州市高中毕业班第二次质量预测(文)

2008年河南省郑州市高中毕业班第二次质量预测数学试题(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷答在答题卡上,第Ⅱ卷答在答卷上。
答在试题卷上无效。
考试结束后,将本试卷、答题卡和答卷一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如须改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
参考公式:如果时间A 、B 互,那么 球的表面积公式P (A +B )=P (A )+P (B )24S R π=如果事件A 、B 相互独立,那么 其中R 表示球的半径 P (A ·B )=P (A ) ·P (B )球的体积公式如果事件A 在一次试验中发生的概率是P ,那 343V R π=么n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径()(1)k kn k n n P k C P P -=-一、选择题1.a 是第一象限角,则2a所在的象限是( )A .第一象限B .第一、二象限C .第一、三象限D .第一、四象限 2.已知等差数列{a n }中,a 5+a 7+a 9=21,则a 7的值是( )A .7B .9C .11D .133.若直线a ⊥b ,且直线a //平面α,则直线b 与平面α的位置关系是( ) A .α⊂bB .α//bC .α⊂b 或α//bD .b 与α相交或α//b 或α⊂b4.直线x +7y =10把圆a 2+y 2=4分成两段弧,其中劣弧的长为( )A .πB .23πC .2πD .2π 5.某种测试可以随时在网络上报名参加,某人通过这种测验的概率是12,若他连续两次参加,则其中恰有一次通过的概率为 ( )A .14B .13 C .12D .346.二项式81()x x+的展开式中的常数项等于( )A .-38B .-32C .38D .707.在正方体1111ABCD A B C D -中,M 、N 分别为棱11A B 和1BB 的中点,那么异面直线AM和CN 所成角的余弦值是( )A .2B .2C .25D .-258.函数()log (1)(01)xa f x a x a =++<<在[0,1]上的最大值和最小值的和为a ,则a 的值是 ( )A .12B .14C .16D .189.已知椭圆22:132x y C +=,过点(1,0)做直线l ,使l 被C 所截得的弦长为3,则满足条件的直线l 共有 ( )A .1条B .2条C .3条D .4条10.把一个函数的图像按向量(,2)3a π=--平移后得到函数cos y x =的图像,则原图像的函数解析式是( )A . cos()23y x π=+- B . cos()23y x π=-- C . cos()23y x π=++D . cos()23y x π=-+11.设1()fx -是函数3()log (6)f x x =+的反函数,若()[]()[]276611=+⋅+--b f a f,则()f a b +的值为( )A .1B .2C .3D . 3log 612.对于函数2()2f x x x =+,在使()f x M ≥所成立的所有常数M 中,我们把M 的最大值M =-1叫做2()2f x x x =+的下确界.对于,a b R ∈,且a ,b 不全为0,则222()a b a b ++的下确界为 ( )A .14 B .4C .12D .2第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,共20分,将答案填在题中横线上) 13.抛物线的顶点在原点,对称轴为x 轴,焦点在直线34120x y --=上,此抛物线的方程是____________________.14.已知数列{a n }满足111,32n n a a a +==+,则数列{a n }的一个通项公式为_________.15.已知203501x y x y y -≤⎧⎪-+≥⎨⎪≥⎩,则12x y +-的最小值是_________________________.16.已知函数2,(0)()21,(0)x e x f x ax x -⎧-≤=⎨->⎩(a 是常数且a >0).对于下列命题:①函数f (x )的最小值是-1; ②函数f (x )在R 上存在反函数;③对任意120,0x x <<且12x x ≠,恒有1212()()()22x x f x f x f ++<. 其中正确命题的序号是_____________________.三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)已知向量(cos ,sin ),a x x b ==,若85a b =,且42x ππ<<. 求sin 2(1tan )1tan x x x+-的值.18.(本小题满分12分)一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体底面上的数字分别为x 1、x 2,记2212(3)(3)t x x =-+-.(1)分别求出t 取得最大值和最小值时的概率; (2)求t ≥3的概率. 19.(本小题满分12分)如图,梯形ABCD 中,CD //AB ,12AD DC CB AB a ====,E 是AB 的中点,将△ADE 沿DE 折起,使点A 折到点P 的位置,切二面角P —DE —C 的大小为120°.(1)求证DE ⊥PC ;(2)求直线PD 与平面BCDE 所成角的正弦值. 20.(本小题满分12分)若函数3()4f x ax bx =-+,当x =2时,函数f (x )有极值43-. (1)求函数f (x )的解析式;(2)若函数f (x )=k 有3个解,求实数k 的取值范围. 21.(本小题满分12分)过椭圆22221x y a b+=(a >b >0)外一点A (-4,0)作倾斜角为30°的直线与椭圆有且只有一个交点.(1)求ab 最大时椭圆的方程;(2)对应(1)中求出的椭圆,若其左焦点为F ,Q 是椭圆上任一点,是否存在过点F ,Q 的直线l 与y 轴交于M 点,且满足2MQ QF =-,若存在,求出直线l 的方程;否则,说明理由.22.(本小题满分12分)已知函数f (x )对任意x R ∈都有1()(1)2f x f x +-=. (1)求1()2f 的值;(2)若函数{a n }满足*121(0)()()()()()n n na f f f f f n N n n n n-=+++++∈…,数列{a n }是等差数列吗?试证明之;(3)设14(*),41n n n n n b n N c b b a +=∈=-,求数列{c n }的前n 项和T n .。
届河南省郑州市高中毕业班第二次质量预测(文)

2009届河南省郑州市高中毕业班第二次质量预测数学试卷(文科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,考试结束后,将答题卡和答卷(II 卷)一并交回。
第Ⅰ卷考生注意:1.答题前,考生在答题卡上务必用0.5毫米黑色墨水签字笔将自己的姓名、准考评出号填写清楚。
2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,在试题卷上作答无效。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率),,2,1,0()1()(n k P P C k P kn k k n n =-=- 其中R 表示球的半径正棱锥、圆锥的侧面积公式cl S 21=锥侧 其中c 表示底面周长,l 表示斜高或母线长球的体积公式334R V π=球 其中R 表示球的半径一、选择题1.如果集合}3|{≤=x x P ,那么( )A .P ⊆-1B .P ∈-}1{C .P ∈φD .P ⊆-}1{ 2.若011<<ba ,则下列结论不正确的是( ) A .22b a < B .2b ab <C .2≥+baa bD .||||||b a b a +>+3.已知函数))1((,)0(2,)0(||log )(2-⎩⎨⎧≥<=f f x x x x f x则的值为( )A .—1B .1C .2D .44.若直线1:=+by ax l 与圆1:22=+y x C 有两个不同交点,则点P (a ,b )与C 的位置关系是( )A .点在圆上B .点在圆内C .点在圆外D .不能确定5.已知非负实数x ,y 满足条件y x z y x y x 86,62,5+=⎩⎨⎧≤+≤+则的最大值是( )A .50B .40C .38D .186.设a 、b 是两条直线,βα,是两平面,则b a ⊥的一个充分条件是 ( )A .βαβα⊥⊥,//,b aB .βαβα//,,⊥⊥b aC .βαβα//,,⊥⊂b aD .βαβα⊥⊂,//,b a7.将)63c o s (2π+=x y 的图象按向量)2,4(π-=平移,则平移后所得图象的解析式( ) A .2)43cos(2++=πx y B .2)43cos(2+-=πx yC .2)123cos(2--=πx yD .2)123cos(2++=πx y8.已知函数)(12)(R x x f x∈-=,则其反函数)(1x f -的图象大致是( )9.已知命题P :不等式}10|{0]1)1(lg[<<>+-x x x x 的解集为;命题Q :在三角形ABC中,)42(cos )42(cos 22ππ+<+∠>∠B A B A 是成立的必要而非充分条件,则( )A .P 真Q 假B .P 且Q 为真C .P 且Q 为假D .P 假Q 真10.设向量i ,j 为直角坐标系的x 轴、y 轴正方向上的单位向量,若向量,1||||,)1(,)1(=-+-=++=b a i y i x b j y i x a 且且满足上述条件的点P (x ,y )的轨迹方程是 ( )A .)0(1434122≥=-y y x B .)0(1434122≥=-x y xC .)0(1434122≥=-y x y D .)0(1434122≥=-x x y 11.等比数列=+++-==+++43213243211111,89,815,}{a a a a a a a a a a a n 则若中 ( ) A .35B .53 C .35 D .-53 12.已知A ,B ,C 是平面上不共线的三点,O 为平面ABC 内任一点,动点P 满足等式)0]()21()1()1[(31≠∈++-+-=λλλλλ且R ,则点P 的轨迹一定通过△ABC 的 ( )A .内心B .垂心C .外心D .重心第Ⅱ卷注意事项:1.答题前,考生先在答卷(II 卷)上用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚。
河南省郑州市2011年高中毕业年级第三次质量预测文数
河南省郑州市2011年高中毕业年级第三次质量预测数 学 试 题(文)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
考试时间120分钟,满分150分。
考生应首先阅读答题卡上的文字信息,然后在答题卡上作答,在试题卷上作答无效。
第Ⅰ卷参考公式:样本数据n x x x ,,21的标准差锥体体积公式])()()[(122221x x x x x x nS n -++-+-=Sh V 31=其中x 为样本平均数 其中S 为底面面积,h 为高 柱体体积公式球的表面积、体积公式Sh V =3234,4R V R S ππ== 其中S 为底面面积,h 为高其中R 为球的半径一、选择题1.已知集合2{|1},{|20}A x x B x x x =≤=-<,则A B =( )A .(0,1)B .[-1,1]C .(]0,1D .[)1,1- 2.若(1,1),(1,1),(2,4)a b c ==-=-,则c 等于 ( )A .-a+3bB .a-3bC .3a-bD .-3a+b3.已知四棱锥P —ABCD 的三视图如右图所示,则四棱锥P —ABCD的体积为 ( )A .13 B .23C .34D .384.已知函数()sin()(0,0,||)2f x A x A πωϕωϕ=+>><的部分图象如图所示,则()f x 的解析式是 ( )A .()sin(3)()3f x x x R π=+∈B .()sin(2)()6f x x x R π=+∈C .()sin()()3f x x x R π=+∈D .()sin(2)()3f x x x R π=+∈5.阅读下列程序,输出结果为2的是( )6.在ABC ∆中,1tan ,cos 2A B ==,则tan C 的值是 ( )A .-1B .1C D .-27.设m ,n 是两条不同的直线,,,αβγ是三个不同的平面,有下列四个命题: ①若,,;m m βαβα⊂⊥⊥则 ②若//,,//;m m αβαβ⊂则 ③若,,,;n n m m αβαβ⊥⊥⊥⊥则 ④若,,,.m m αγβγαβ⊥⊥⊥⊥则 其中正确命题的序号是 ( )A .①③B .①②C .③④D .②③8.两个正数a 、b 的等差中项是5,2,a b >且则双曲线22221x y a b-=的离心率e 等于( )A B C D 9.已知定义域为R 的函数()f x 在区间(4,)+∞上为减函数,且函数(4)y f x =+为偶函数,则( )A .(2)(3)f f >B .(2)(5)f f >C .(3)(5)f f >D .(3)(6)f f >10.数列{}n a 中,372,1a a ==,且数列1{}1n a +是等差数列,则11a 等于 ( )A .25-B .12 C .23D .511.已知函数0,()ln(1),0.x x f x x x ≤⎧=⎨+>⎩若2(2)()f x f x ->,则实数x 的取值范围是( )A .(,1)(2,)-∞-+∞B .(,2)(1,)-∞-+∞C .(1,2)-D .(2,1)-12.若函数1()axf x e b=的图象在x=0处的切线l 与圆22:1C x y +=相离,则(,)P a b 与圆C 的位置关系是( )A .在圆外B .在圆内C .在圆上D .不能确定第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分。
郑州市高中毕业年级第二次质量预测文数
2015 年高中毕业年级第二次质量预测文科数学参考答案一、选择题题号123456789101112答案C A B C B B A D C C D A二、填空题13. 28; 14.0 ;15. 10 ;16. ①②④ .三、解答题17. 解: (1)由S n2a n 2 可得 a1 2 ,因为 S n2a n 2,所以,当 n2时,a n S n S n 12a n 2a na n2 . 1,即:a n 1数列 {a n} 是以a12为首项,公比为2的等比数列,n2n(n N.6分所以, a)( 2)b n log 2 a1log 2 a2log 2 a n 1 23n n(n 1).2由 (n8)b n nk 对任意 n N *恒成立,即实数( n8)(n 1)k 对 n N*恒成立;1 (n 2设 c n8)( n1) ,则当n3或 4 时,c n取得最小值为10,2所以 k10.12分18.解解:( Ⅰ) 由题意x0.3, x 150 ,所以 y z60 ,500因为 z2y ,所以 y20, z40,则应抽取教师人数50205040 4. 5 分2,应抽取学生人数500500(Ⅱ)所抽取的“不赞成改革”的 2 名教师记为a, b ,4名学生记为1,2,3,4,随机选出三人的不同选法有 (a,b,1), (a,b,2), (a,b,3), (a,b,4), (a,1,2), (a,1,3), (a,1,4), (a,2,3), (a,2,4), ( a,3,4) ,(b,1,2)(b,1,3), (b,1,4), (b,2,3), (b,2,4), (b,3,4) , (1,2,3), (1,2,4), (1,3,4), ( 2,3,4), 共20种,9 分至少有一名教师的选法有(a,b,1), (a,b,2), (a, b,3), (a, b,4), (a,1,2), (a,1,3), (a,1,4), (a,2,3), (a,2,4), (a,3,4) ,(b,1,2)(b,1,3), (b,1,4), (b,2,3), (b,2,4), (b,3,4) 共16种,至少有一名教师被选出的概率 p16 4 .12 分20519.证明( I)取AB得中点E, 连接ME, NE ,因为 M,N 分别为AB和 BC 的中点,所以 NE//AC,ME//AA又因为 AC平面AACC,AA平面AACC,所以 ME//平面AACC,NE//平面AACC,5分所以平面 MNE //平面AA CC ,因为 MN平面A MN,所以MN//平面AACC; 6 分( II )连接BN , 设AA a ,则 AB AA a ,由题意知 BC 2 a, NC BN a212 a2, 2因为三棱柱ABC A B C 侧棱垂直于底面,所以平面ABC平面BBCC,因为 AB AC,点N是BC的中点,所以AN平面BBCC,CN AN,9分要使 CN平面 A MN ,只需CN BN 即可,所以CN2BN 2BC 2,即(2 a 21 2a2)22a2, 2 ,2则2时,CN平面AMN .12 分x2y220.解 : (1)因为椭圆C : a2b21(a b0) ,由题意得SBF1F212c b 4 ,e c2, a 2 b 2c2,2a2a28,所以椭圆 C 的方程为 C :x2y21. 4 分解得4,84b2( 2)假设存在圆心在原点的圆x2y 2r 2,使得该圆的任意一条切线与椭圆 C 恒有两个交点M,N,因为 OM ON OM ON ,所以有OM ON 0,设 M (x1 , y1 ), N ( x2 , y2 ) ,y kx m 当切线斜率存在时,设该圆的切线方程为y kx m 。
河南省郑州市高三数学高中毕业班第二次质量预测(文)
河南省郑州市2009年高中毕业班第二次质量预测文科数学(必修+选修I )本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至二页,第Ⅱ卷3至4页。
满分150分。
考试用时120分钟。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(共60分钟)注意事项:1. 答第Ⅰ卷前,考生务必用0.5毫米黑色签字笔将姓名、座号、准考证号填写在答题卡和试卷规定的位置,并认真核准条形码上的姓名、座号和准考证号。
2. 第Ⅰ卷共2页。
答题时,考生须用2B 铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案。
在试卷上作答无效。
3. 本卷共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A B 、互斥,那么 球的表面积公式24S R π= ()()()P A B P A P B +=+ 其中R 表示球的半径 如果事件A B 、相互独立,那么 球的体积公式343V R π=()()()P A B P A P B ⋅=⋅ 其中R 表示球的半径 如果事件A 在一次实验中发生的概率是P , 那么n 次独立重复实验中恰好发生k 次的概率:()()(1)0.1.2.k k n kn nP k C P P k n -=⋅⋅-=⋅⋅⋅ 一、 选择题:1. 如果集合{}3P x x =≤,那么A . 1p -⊆B . {}1p -∈C . p ∅∈D . {}1p -⊆ 2.若110a b,则下列结论不正确的是A . 22ab B . 2ab b C .2b aa b+≥ D . a b a b ++3.已知函数()()()2log 02 0x x x f x x ⎧⎪=⎨≥⎪⎩,则()()1f f -的值为 A . -1 B . 1 C . 2 D . 44.若直线:1l ax by +=与圆C :221x y +=有两个不同交点,则点P (),a b 与圆C 的位置关系是A . 点在圆上B . 点在园内C . 点在圆外D . 不能确定5.已知非负实数5,,26,x y x y x y +≤⎧⎨+≤⎩,满足条件,则68z x y =+的最大值是A . 50B .40C . 38D . 18 6.设,a b 是两条直线,,αβ是两个平面,则a b ⊥的一个充分条件是A . ,//,a b αβαβ⊥⊥B . ,,//a b αβαβ⊥⊥C . ,,//a b αβαβ⊂⊥D . ,//,a b αβαβ⊂⊥ 7.将2cos 36y ππ⎛⎫=+⎪⎝⎭的图像按向量,24a π⎛⎫=- ⎪⎝⎭平移,则平移后所得图像的解析式为 A . 2cos 234y ππ⎛⎫=++⎪⎝⎭ B . 2cos 234y ππ⎛⎫=-+ ⎪⎝⎭C . 2cos 2312y ππ⎛⎫=--⎪⎝⎭ D . 2cos 2312y ππ⎛⎫=++ ⎪⎝⎭8.已知函数()()21xf x x R =-∈,则其反函数()1f x -的图像大致是9.已知命题P:不等式()lg 110x x -+⎡⎤⎣⎦的解集为{}01x x ;命题Q :在三角形ABC中,22cos cos 2424A B AB ππ⎛⎫⎛⎫∠∠++ ⎪⎪⎝⎭⎝⎭是成立的必要而非充分条件,则A . P 真Q 假B .P 且Q 为真C .P 且Q 为假D . P 假Q 真 10.设向量,i j 为直角坐标系的x 轴、y 轴正方向上的单位向量,若向量()1,a x i yj =++,()1b x i yj =-+且1a b -=,则满足上述条件的点(),P x y 的轨迹方程是A . ()22101344x y y +=≥B . ()22101344x y x -=≥ C . ()22101344y x y -=≥ D . ()22101344y x x -=≥11.等比数列{}n a 中,若123423159,88a a a a a a +++==-,则12341111a a a a +++= A .53 B . 35 C .-53 D .-3512.已知A ,B ,C 是平面上不共线的三点,O 为平面ABC 内任一点,动点P 满足等式()()()()1111,03OP OA OB OC R λλλλλ⎡⎤=-+-+-∈≠⎣⎦且,则点P 的轨迹一定通过ABC ∆的A . 内心B . 垂心C . 外心D . 重心第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共2分13.某校有教师200人,男学生1200人,女学生1000人,先用分层抽样的方法从所有师生中抽取一个容量为n 的样本,已知从女学生中抽取的人数为80人,则n 的值为14.621x x ⎛⎫- ⎪⎝⎭的展开式,常数项等于15.过球一半径的中点作垂直于这条半径的球的截面,则此截面面积与球表面积之比为 16.对于函数()11ax f x x +=-(其中a 为实数,1x ≠),给出下列命题:①当1a =时,()f x 在定义域上为单调增函数;②()f x 的图像关于点()1,a 对称;③对任意(),a R f x ∈都不是奇函数;④当1a =-时,()f x 为偶函数;⑤当2a =时,对于满足条件122x x 的所有12,x x 总有()()()12213f x f x x x --,其中正确的序号是三、 解答题:本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤。
河南省郑州市2020年高中毕业年级第二次质量预测(文科)数学试卷(含答案)
A.5
B.6
C.7
D.8
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分.
13.幂函数 f (x) = (m2 − 3m + 3)xm 的图象关于 y 轴对称,则实数 m=____
14.将一颗骰子先后投掷两次分别得到点数 a, b ,则直线 ax+by=0 与圆 (x − 2)2 + y2 =2 有公共点的概率
4.若 m,n 是两条不同的直线,a,β,γ 是三个不同的平面,则下列命题中的真命题是
A.若 m⊂β,α⊥β,则 m⊥α
B.若 m⊥β,m//α,则 α⊥β
C.若 α⊥γ,α⊥β,则 β⊥γ
D.若 α∩γ=m,β∩γ=n,m//n,则 α//β
5.郑州市 2019 年各月的平均气温(°C)数据的茎叶图如下:则这组数据的中位数是
河南省郑州市 2020 年高中毕业年级第二次质量预测
(文科)数学试卷
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要 求的.
1.设函数 y = 9 − x2 的定义域为 A,函数 y=ln(3-x)的定义域为 B,则 A∩B=
A.(-∞,3)
年份代码 x
1
2
3
4
年产量(万吨) 6.6
6.7
7
7.1
2018 5 7.2
2019 6 7.4
(I)根据表中数据,建立 y 关于 x 的线性回归方程 yˆ = bˆx + aˆ ;
(II)根据线性回归方程预测 2020 年该地区该农产品的年产量.
附:对于一组数据( x1, y1),(x2, y2 ), ,(xn, yn ) ),其回归直线 yˆ = bˆx + aˆ 的斜率和截距的最小二乘估计分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年高中毕业年级第二次质量预测 文科数学试题卷 本试卷分第I卷(选择题)和第II卷(非选择题)两部分.考试时间120分钟,满分150分.考生应首先阅读答题卡上的文宇信息,然后在答题卡上作答,在试题卷上作答无效. 第I卷 参考公式: 样本数据的标准差 锥体体积公式
其中为样本平均数 其中S为底面面积,h为高 柱体体积公式 球的表面积、体积公式
其中S为底面面积,h为髙 其中R为球的半径 —、选择题 (毎小题5分,共60分) 1. 设函数的定义域为M,集合,则
=
A. B. N C. D.M 2. 计箅的结果等于
A. B. C. D. 3. 三边长分别为1,1,的三角形的最大内角的度数是
A.600 B 900 C 120° D 1350 已知向量,若,则向量m与向量n夹角的余弦值为 A. B. C. D. 5.下列命题说法的是 A. 命题“若a>b,则”的否命题为:“若,则” B. “a>b”是“”的充要条件 C. 对于命题P,Q,若PQ为假命题,则命题P、q至少有一个为假命题 D. 对于命题,使得”,则,均有” 6. 已知正方体的外接球的体积是,则这个正方体的棱长是 A. B. C. D. 7. 设a、b是两条不同的直线,是两个不同的平面,则下列四个命题: ①若,则 ②若,则I ③若,则或< ④若,,则. 其中正确命题的个数为 A. 1 B. 2 C. 3 D.4 8. 要得到函数的图象,只需将函数的图象沿x轴 A.向右平移个单位 B.向左平移个单位 C.向右平移个单位 D.向左平移个单位 9. 设函数则的值为 A. 15 B. 16 C. -5 D. -15 10. 右面的程序框图给出了计算数列的前8项和S的箅法,算法
执行完毕后,输出的S为. A. 8 B. 63 C. 92 D. 129 11.把一段长16米的铁丝截成两段,分别围成正方形,则两个正方形面积之和的最小值为 A.4 B.8 C.16 D. 32 12.设双曲线的两条渐近线与直线围成的三角形区
域(包含边界)为P(x,y)为D内的一个动点,则目标函数的最小值为 A. —2 B. C.O D. 第II卷 二、填空埋(毎小埋5分,共20分) 13. 若复数(i为虚数单位)为实数,则实数
___________.
14. 设抛物线的焦点为F,则点F的坐标为
______.
15. 甲、乙两名同学学业水平考试的9科成绩如茎叶图所示,
请你根据茎业图判断谁的平均分高______(填“甲”或“乙”) 16. 设是R上的奇函数,且,当x>0时,
,则不等式的解集为______. 三、解答翅(共70分) 17. (本小题满分12分) 已知数列满足,且. (I)求数列{an}的通项公式 (I)若,求数列的前n项和. 18. (本小题满分12分) 某中学对高二甲、乙两个同类班级进行“加强‘语文阅读理解,训练对提髙‘数学应用题得分率作用”的试验,其中甲班为试验班(加强语文阅读理解训练),乙班为对比班(常规教学,无额外训练),在试验前的测试中,甲、乙两班学生在数学应用题上的得分率基本一致,试验结束后,统计几次数学应用题测试的平均成绩(均取整数)如下表所示:
现规定平均成绩在80分以上(不含80分)的为优秀. (I )试分别估计两个班级的优秀率; (II)由以上统计数据填写下面2 X 2列联表,并问是否有"5匁的把握认为“加强‘语文阅读理解’训练对
提商‘数学应用题’得分率”有帮助.
60分以下 61—70 分 71—80 分 81-90 分 91-100分 甲班(人数) 3 6 11 18 12 乙班(人数) 8 13 15 10 19. (本小题满分12分) 一个几何体的三视图如右图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形. (I)求该几何体的体积V; (II)求该
几何体的表面积s. 20. (本小题满分12分)
已知曲线〉在点(t,>处的切线Z交X轴于点A,交:y轴于点(O为坐标原点)的面积为S. (I)试写出S关于r的函数关系式, (II)求面积s的最小值; (III)若对于•恒成立,求实数a的取值范围. 21. (本小题满分12分〉 在平面直角坐标系xOy中,点P(x,y)为动点,已知点I,直线PA与PB的斜率之积为定值. (I) 求动点P的轨迹E的方程;
(II)若F(1,0),过点F的直线l交轨迹E于M、N两点,以MN为对角线的正方形的第三个顶点恰在y轴上,
求直线l的方程. 22. 选修4_1:(本小题满分10分)几何证明选讲 如图,在厶ABC
中,为钝角,点是边AB上
优秀人数 非优秀人数 合计 甲班 乙班 合计
参考公式及数据:, 0.50 0.40 0.25 0.15 0.10 0. 05 0.025 0.010 0.005 0.001 K0 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.82 的点,点K和M分别是边AC和BC上的点,且AH =AC,EB=BC,AE=AK,BH=BM. (I )求证:E、H、M、K四点共圆; (II)若KE=EH,CE=3求线段 KM 的长.
2011年高中毕业年级第二次质量预测 文科数学 参考答案 一、选择题 BACDB DDBAC BB 二、填空题
13.1; 14.1(0,)16; 15.乙; 16.(,1)(0,1). 三、解答题 17.解:⑴由112(2)nnnaaan知,数列{}na是等差数列, 设其公差为d,------------------- 2分 则5371()92aaa,
所以5124aad,----------- 4分 1(1)21naandn,
即数列{}na的通项公式为21nan.------------------- 6分 ⑵1(21)2nncn, 1230121 =123252(21)2.nnnTccccn
1212 1232(23)2(21)2nnnTnn,
相减得 123112(2222)(21)2nnnTn,------------ 9分
整理得 2212(21)2(23)2312nnnnTnn, 所以(23)23nnTn.------------------- 12分 18.解:⑴由题意,甲、乙两班均有学生50人,------------------- 1分 甲班优秀人数为30人,优秀率为3060%50,----------- 2分 乙班优秀人数为25人,优秀率为2550%50,----------- 4分 所以甲、乙两班的优秀率分别为60%和50%.------------------- 5分 ⑵ 优秀人数 非优秀人数 合计 甲班 30 20 50 乙班 25 25 50 合计 55 45 100 ---------- 7分
注意到22100(30252025)1001.0105050554599K,---------------- 11分 所以由参考数据知,没有75%的把握认为“加强‘语文阅读理解’训练对提高‘数学应用题’得分率”有帮助. ------------------- 12分 19.解:⑴由三视图可知,该几何体是一个平行六面体(如右图),
其底面是边长为1的正方形,高为3 ,------- 3分
所以1133V.-------------------6分 ⑵由三视图可知,该平行六面体中,
111,ADABCDCDBCCB面面,
所以12AA,----------- 9分 侧面1111,ABBACDDC均为矩形, 2(111312)623S.------------------- 12分
(学生只要结果正确,并有适当的语言表述即可得满分) 20.解:⑴曲线1ln()yxxxe在点(,ln)ttt处的切线斜率为1lnyt,--------1分
设(,0),(0,)AmBn,
则0ln(1ln)(),ln(1ln)(0),tttmtntttt----------- 2分
解得,1ln,tmtnt
