土坡稳定分析
第八章 土坡稳定性分析与计算

O
R
Vi+1
MR
(c l N tan ) T R R
i i i i i
H
i
Wi
Ti
Fs
Ms MR
(c l N tan ) R W sin R
i i i i i i
O i 2 1 -1 -2 0
R b B 3 4 5 6
C
7
计 算 程 序 流 程
计算 mi
Fs Fs
计算
Fs
No
Fs Fs Fs
A
变化圆心 O 和半径 R
Fs 最小
END
3.简化毕肖普法的特点
★假设滑裂面为圆弧; ★假设条块间作用力只有法向力没有切向力 (Vi=0); ★满足整体力矩平衡条件; ★满足各条块力的多边形闭合条件,但不满足条块的 力矩平衡条件; ★满足滑动面上的极限平衡条件。
i
f 土坡稳定 安全系数
(一) 瑞典条分法的基本原理
1、假设圆弧滑动面 确定圆心和半径
2、把滑动土体分成若干条(条分法) 3、取第i条土条进行受力分析
O
R
Vi+1 Hi hi Vi Wi Hi+1 hi+1
i
Ti Ni
瑞典条分法
静定化条件:假设条块两侧的作用 力合力Si,Si+1 大小相等、方向相 反且作用于同一直线上——不考虑 条块间的作用力。 1)根据径向力的静力平衡条件 得
表层滑动
砂土
概述 表层滑动的边 坡稳定分析
天然休止角
无粘性土
第八章+土坡稳定性分析

土力学与地基基础
• 由于计算上述安全系数时,滑动面为任意 假定,并不是最危险的滑动面,因此所求 结果并非最小的安全系数。通常在计算时 需要假定一系列滑动面,进行多次试算, 计算工作量很大。 • W.费伦纽斯(Fellenius,1927)通过大量计 算分析,提出了以下所介绍的确定最危险 滑动面圆心的经验方法。
土力学与地基基础
瑞典条分法和毕肖普法的比较
• 瑞典条分法忽略各条间力对Ni的影响,i土 条上只有Gi,Ni,Ti三种力作用,低估安全系 数5~20%。 • 毕肖普法忽略土条竖向剪切力的作用,考 虑了土条两侧的作用力,比瑞典条分法更 合理,低估安全系数约为2~7%。
土力学与地基基础
li
K
1 m cb Gi ui b X i tan i
G sin
i
i
土力学与地基基础
• 毕肖普条分法考虑了土条两侧的作用力, 计算结果比较合理。 • 分析时先后利用每一土条竖向力的平衡及 整个滑动土体的力矩平衡条件,避开了Ei 及其作用点的位置,并假定所有的 X i 均等 于零,使分析过程得到了简化。 • 但该方法同样不能满足所有的平衡条件, 还不是一个严格的方法,由此产生的误差 约为2%~7%。另外,毕肖普条分法也可以 用于总应力分析,即在上述公式中采用总 应力强度指标c、φ计算即可。
土力学与地基基础
土坡形态及各部分名称
坡肩 坡顶
坡高 坡脚
坡面
坡角
土力学与地基基础
土力学与地基基础
土力学与地基基础
土力学与地基基础
4.土坡由于其表面倾斜,在自重或外部荷 载的作用下,存在着向下移动的趋势, 一旦潜在滑动面上的剪应力超过了该面 上的抗剪强度,稳定平衡遭到破坏, 就可 能造成土坡中一部分土体相对于另一部 分的向下滑动,该滑动现象称为滑坡。 5.天然的斜坡、填筑的堤坝以及基坑放坡 开挖等问题,都要演算土坡的稳定性。 亦即比较可能滑动面上的剪应力与抗剪 强度,这种工作称为稳定性分析。
瑞典圆弧法的土坡稳定性分析

东北农业大学
水利与建筑学院
土木工程1001 班
作业组成员: 段晶晶A07110442
徐欣欣
赵越
题兴博
任曼妮
王潇涵
王畑月
王梦莹
1、瑞典圆弧法
这个方法首先是由瑞典的彼得森所提出,故称瑞典圆弧法。
(1)基本假设:均质粘性土坡滑动时,其滑动面常近似为圆弧形状,假定滑动面以上的土体为刚性体,即设计中不考虑滑动土体内部的相互作用力,假定土坡稳定属于平面应变问题。
2、瑞典圆弧法基本原理和公式
(1) 基本原理
瑞典圆弧滑动面条分法,是将假定滑动面以上的土体分成n个垂直土条,对作用于各土条上的力进行力和力矩平衡分析,求出在极限平衡状态下土体稳定的安全系数。
该法由于忽略土条之间的相互作用力的影响,因此是条分法中最简单的一种方法。
(2)基本公式:取圆弧滑动面以上滑动体为脱离体,土体绕圆心O下滑的滑动力矩为Ms=Wa,阻止土体滑动的力是滑弧AED 上的抗滑力,其值等于土的抗剪强度τf与滑弧AED长度L的乘积,故其抗滑力矩为
Mr=
安全系数K=抗滑力矩/滑动力矩=
Mr/Ms>1
式中:L——滑弧弧长;
R——滑弧半径;
α——滑动土体重心离滑弧圆心的水平距
离。
该法适应于粘性土坡。
后经费伦纽斯改进,提出φ=θ的简单土坡最危险的滑弧是通过坡角的圆弧,其圆心O是为位于图9-3中AO与BO两线的交点,可查表确定。
土质边坡稳定分析
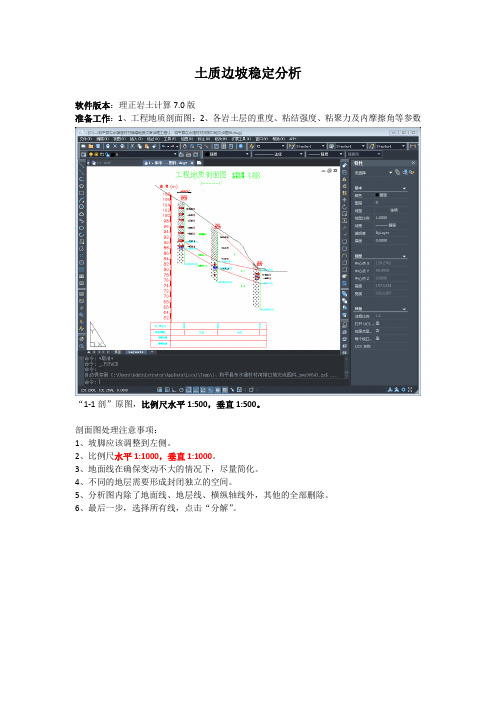
土质边坡稳定分析软件版本:理正岩土计算7.0版准备工作:1、工程地质剖面图;2、各岩土层的重度、粘结强度、粘聚力及内摩擦角等参数“1-1剖”原图,比例尺水平1:500,垂直1:500。
剖面图处理注意事项:1、坡脚应该调整到左侧。
2、比例尺水平1:1000,垂直1:1000。
3、地面线在确保变动不大的情况下,尽量简化。
4、不同的地层需要形成封闭独立的空间。
5、分析图内除了地面线、地层线、横纵轴线外,其他的全部删除。
6、最后一步,选择所有线,点击“分解”。
处理后的“1-1剖”分析图,比例尺水平1:1000,垂直1:1000。
操作步骤:1、打开“理正岩土计算7.0版”软件,选择“边坡稳定分析”。
2、选择“复杂土层土坡稳定计算”。
3、点击“增”,选择“系统默认例题”。
4、打开“辅助功能”菜单,选择“读入DXF文件自动形成坡面、节点、土层数据”,挑出的对话框选“是”,然后选择准备好的“1-1剖”分析图。
5、输入剖面线起始点号及剖面线段数,前面注意事项中提到“简化地面线”在这一步骤起到作用。
“确定”6、修改“基本”页面,注1:采用规范一般选“通用方法”就行,有特殊要求的自行选择。
注2:“滑裂面形状”土质边坡选“圆弧滑动法”,岩质边坡选“折线滑动法”,外倾层状或断层构造选“直线滑动法”,本文以土状边坡为例。
起始点号7、修改“坡面”,坡面或坡顶是否有堆载,如果有,则在相应的线段上加入“超载个数”,以及超载物的局部数据等。
本文以边坡治理为例,默认坡面及坡顶无堆载,则要将“超载个数”全部改为0。
8、完善“土层”参数。
正常情况下,对应左侧图中的区域序号,填写右侧表格中的“重度”、“粘结强度”、“粘聚力”、“内摩擦角”。
如果有需要,可以横拉表格下的滚动条,在表格最后面有一列“本区域边界节点编号”,调整位置可以改变区域序号。
9、“水面”一般默认“否”,如地下水对边坡有较大影响,可以加入测量的地下水位。
“水面线段数”为水位控制点;“水面线起始点X0”为第一个水位控制点在水平方向上距离坡脚的距离;“水面线起始点Y0”为第一个水位控制点在垂直方向上距离坡脚的高差;“水平投影长”为当前水位控制点与前一个水位控制点的水平间距,“竖向投影长”为当前水位控制点与前一个水位控制点的垂直高差。
土质边坡稳定性分析

(4)
将(4)代入(3)式得 1 sec2θi [c l cosθi + (Wi + H i )tgθi ] (Wi + H i )tgθi Pi = tgθi tg i i i Fsi 1 + Fs 第七章 第22页/共26页
又有
Pn = ∑ Pi = 0
i =1
n
土 力 学
并有∑ M oi = 0 可得:
) 抗滑力矩:M R = c AC R + N tgφ L ) 当φ = 0时,M R = c AC R
C
Tf
W
整体圆弧滑动受力示意图
) 抗滑力矩 M R c AC R 稳定安全系数:FS = = = W d 滑动力矩 M s 适用于φ = 0的情况.
第七章 第9页/共26页
二,条分法的基本概念
把(2)式代入 sin 2 θ i (Wi + H i )tgθ i Pi = Ti cos θ i + cosθ i (3)
Pi=Pi+1-Pi
将(2)代入(1)并整理得 1 Fs
Ti =
1 (Wi + H i )tgi ci li + cosθ i tgθi tg i 1+ Fs
第七章
第20页/共26页
五,普遍条分法(Janbu法)
土 力 学
1. 求解前提: 假定条块间水平作用力的位置. 2.求解方法:
如图所示,取条块 i进行分析:
i Hi+1 Pi+1 hi+1 Oi θi Wi Ti Ni Xi
根据滑弧面上极限平衡 条件有 抗剪强度 T fi = Ti = 安全系数 Fs ci li + N i tg i = Fs
粘性土土坡的稳定分析-PPT

大家有疑问的,可以询问和交流
可以互相讨论下,但要小声点
太沙基公式
• 基本假定: 1)土条两侧得推力Pi、Pi+1和摩擦力Hi、Hi+1得合
力大小相等、方向相反; 2)且她们得作用线重合。
• 受力分析: 1)土条得重力Wi 2)土条得径向反力Ni 3)侧向反力Ti
太沙基公式
• 抗转动稳定安全系数: 滑动力矩:
影响土坡稳定得因素
• 地震作用:
影响土坡稳定得因素
• 地震惯性力: 水平向地震惯性力为:
Qi K H CziWi
1)KH就是水平向地震系数,为地面水平最大加速 度得统计平均值与重力加速度之比;
2)Cz就是综合影响系数,一般取0、25; 3)Wi就是土条得自重; 4)i就是地震加速度分布系数。 • 一般只考虑水平向地震作用,但设计烈度9度以 上,应同时考虑水平向和垂直向地震作用。
抗剪强度只发挥了一部分,与侧向力相平衡;
Ti
cili Fs
Nitgi
Fs
3)当整个滑动土体处于平衡状态时,各土条对园 心得力矩之和为0,条间推力为内力,将相互抵消。
• 计算简图:
毕肖普公式
毕肖普公式
• 抗转动稳定安全系数:
Fs
cili [(Wi Hi Hi1) cosi (Pi1 Pi ) sini ]tgi
所有土条自重引起得切向力对园心得力矩。
抗滑力矩:
所有土条底部得抗剪强度对园心得力矩。
则抗转动稳定安全系数为抗滑力矩与滑动力矩之
比:
Fs
MR Ms
(cili Wi cositgi ) Wi sin i
毕肖普公式
• 基本假定: 1)考虑土条两侧得推力; 2)当土坡处于稳定状态时,任一土条内滑弧面上得
土石坝边坡稳定分析与计算方法

土石坝边坡稳定分析与计算方法土石坝作为常见的水利工程构筑物,在防洪、供水、发电等方面发挥着重要的作用。
土石坝边坡稳定性是影响其安全运行的关键因素之一,因此边坡稳定性分析与计算方法十分重要。
本文将介绍土石坝边坡稳定性分析与计算方法的基本理论和应用技术。
一、土石坝边坡稳定性基本理论土石坝边坡稳定性分析的基本理论包括弹性地基理论、破坏力学理论、岩土力学和数值计算方法等。
1.弹性地基理论弹性地基理论是建立在弹性力学基础上的一种土体稳定性分析方法。
其核心思想是将土体与石坝看成一体,在一定的约束条件下,求解土坝体系和地基的弹性应力和应变分布,评估土石坝边坡的稳定性。
这种方法适用于土石坝边坡倾角较小、地基水平变形和竖向应力分布较均匀的情况。
2.破坏力学理论破坏力学理论是通过破裂力学和变形理论相结合的方法,对土石坝边坡的稳定性进行分析。
其核心思想是土体在受力作用下,随着剪切应力和水平应力的增加,会发生变形和破裂,并使边坡处于不稳定状态。
通过破坏力学理论,可以预测土石坝边坡的破坏形式,如滑坡、倾斜、涌浅等。
3.岩土力学岩土力学是土石坝边坡稳定性分析的重要理论基础,它研究土、岩体在地下工程中受力、应力、变形、破坏和稳定性等问题。
其核心思想是通过分析土石坝边坡的岩土力学性质,如强度、压缩模量、剪切模量、抗裂性、渗透性等,预测边坡在不同条件下的稳定性。
4.数值计算方法数值计算方法是通过数学和计算机技术,对复杂的土石坝边坡稳定性问题进行求解的方法。
其核心思想是将边坡分割成若干个小单元,通过模拟不同荷载条件下的应力和变形情况,预测边坡在不同条件下的稳定性。
常用的数值计算方法包括有限元法、有限差分法和边界元法等。
二、土石坝边坡稳定性计算方法1.经验法经验法是一种基于工程经验、检验和修改的方法。
这种方法一般适用于经验较丰富、边坡较小且地质条件比较安全的情况。
其中常用的经验法有刘安钦法、耐均匀法等。
2.解析方法解析方法是通过对已知物理或参考问题进行分析,求解所需要的未知物理的方法。
第三章--边坡稳定性分析

验算方法
⑴ 将土体按地面变
T1
坡点垂直分块后自 α1 W 1 N1
上而下分别计算各 E1
τ1
土块的剩余下滑力.
α1 α2
E2
T2
W2 N2
τ2
E1 α1
⑵自第二块开始, 均需计入上一条块剩余下滑力对本条块的作用 把其当作作用于本块的外力,方向平行于上一块土体滑动面。
⑶Ei计算的结果若出现负值,计算Ei+1时,公式中Ei以零值代入。
cL
N
A ω θ Ntgφ W
H
K f G cos cL G sin
10
二、解析法
D B
θ
K f G cos cL G sin
H
1:m T
cL
N
A ω θ Ntgφ W
因G HL sin( )则
K
f
2
ctg
sin
2c
H
sin(
sin ) sin
令 0
2c
H
K ( f 0 )ctg
②土的极限平衡状态只在破裂面上达到,破裂面的位置要 通过计算才能确定。
力学分析法主要包括:圆弧滑动面法、平面滑动面法、 传递系数法等。
8
§ 3.2 直线滑动面的边坡稳定性计算
K min K
一、试算法
T
KR T
θ ω
N W
K W cos tan cL W sin
纯净砂类土 c = 0,则
15
◆ 计算稳定系数
①切向力
o
Ti x Qi sin i
R
'
i
i'
10 1:m2
E
98
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O
R
瑞典条分法的讨论
C
假设圆弧滑裂面, 与实际滑裂面有差别
i
bB 67
A
-2 -1 0 1 2 3 4 5
• 忽略条间力,使得计算安全系数 K偏小 • 假设圆弧滑裂面,使 K偏大
最终结果是 K偏小,
越大 K 越偏小
工程应用中偏于安全
一般情况下,K偏
小 10% 左右
86.3.粘2粘性性土土坡坡的的稳稳定定分分析析
逸出段
水位骤降的土坝上游
86..32.2 无粘性土坡的稳定分析
讨论:
Fs
sat
tg tg
A
l
J h W’
N
T’
•
sat
0.5与无渗流比较Fs减小近一倍
意味着原来稳定的坡,有沿坡渗流时可能破坏
• 与重度有关
• 与所选V大小无关,亦即在这种坡中各点安全系数相同
6.3.2粘性土坡的稳定分析
破坏特点
n 是 l(x,y) 的函数
思路 离散化
分条
条分法
A
O
R
O
C
i
RBb
B
C
6
7
-2 -1A0
d
12
3W4
5
6.3.2粘性土坡的稳定分析
3 瑞典条分法(简单条分法)
O
R
C
i
bB 67
A
-2 -1 0 1 2 3 4 5
Hi+1 Pi+1
Pi hi Hi
Wi
i
Ti
hi+1
Ni
假定:圆弧滑裂面;不考虑条间力
M s Wi sini R
Wi sini
K
1 mi
[cili
cosi
Witgi
]
A
Wi sini
C
i
bB 67
-2 -1 0 1 2 3 4 5
mi
cosi
sin itgi
K
或查P177图8-15
Pi+1
Pi hi
Wi
i
hi+1
Ti
Ni
圆心 O,半径 R
设 K=1.0
O
R
C
计
计算 mi
i
bB 67
6.3.2无粘性土坡的稳定分析
破坏形式:表面浅层滑动
A
坡与水平夹角为 砂土内摩擦角为
1)微单元A自重: W=V
2)沿坡滑动力:T W sin
3)对坡面压力:N W cos
(由于无限土坡两侧作用力抵消)
4)抗滑力: R Ntg W costg
N W
T
R W
N
5)抗滑安全系数:
Fs
抗滑力 滑动力
L
L
L
M R 0 f dl R 0 (c ntg )dl R cAc R 0 ntgdl R
注:(其中 n n l 是未知函数)
当=0(粘土不排水强度)时, c cu MR cAcR
(3)
安全系数:
Fs
抗滑力矩 滑动力矩
MR Ms
c Ac R Wd
6.3.2粘性土坡的稳定分析
讨论:
O
R B
C
1 当 0 时,n 是 l(x,y) 的函数, 无法得到 Fs 的理论解
A
dW
2 其中圆心 O 及半径 R 是任意假设的,还必须计算若 干组(O, R)找到最小安全系数
——最可能滑动面
3 适用于饱和软粘土,即 =0 情况
6.3.2粘性土坡的稳定分析
2 条分法的基本原理及分析
源起
L
整体圆弧法 : 0 ntg dl
Ti
Ni
补充题:某简单粘性土坡高25m ,坡比1:2,碾压土的重度γ=20KN/m3,内 摩擦角Φ=26.6°,粘聚力C=10kPa,试分别用瑞典条分法和简化毕肖普条分
法计算该滑动圆弧安全系数,并对结果进行比较。
本章结束
感谢下 载
第6.3节
土坡稳定分析
本章目录
6.3.1 概述 6.3.2无粘性土坡的稳定分析 6.3. 3粘性土坡的稳定分析
6.3.1概述
边坡稳定分析对象: 土石坝、库区边坡,堤坝填筑 土质、岩质边坡
土坡:具有倾斜面的土体
坡肩
坡顶
坡度:1:m 坡底
坡 高
坡趾
坡角
天然土坡
• 江、河、湖、海岸坡 • 山、岭、丘、岗、天然坡
6.3.2粘性土坡的稳定分析
1 整体圆弧滑动法(瑞典圆弧法)
假设条件
O R
• 均质土 • 二维 • 圆弧滑动面 • 滑动土体呈刚性转动 • 在滑动面上处于极限平衡条件
6.3.2粘性土坡的稳定分析
平衡条件(各力对圆心O的力矩平衡)
O
(1) 滑动力矩:
R B
C
M s Wd (2) 抗滑力矩:
dW
A
人工土坡
• 挖方:沟、渠、坑、池 • 填方:堤、坝、路基、堆料
滑坡:
一部分土体在外因作用下,相对于另一 部分土体滑动
滑坡堆积区
易贡巨型高速滑坡及堰塞湖平面示意图
滑坡原因
1)振动:地震、爆破 2)土中水位升、降 3)降雨引起渗流、软化
土坡稳定性分析的目的: 检验所设计的土坡断面 是否安全合理。
4)水流冲刷:使坡脚变陡 5)冻融:冻胀力及融化含水量升高 6)人工开挖:基坑、船闸、坝肩、隧洞出入口
O
R
分条:
C
b=R/10 编号:过圆心垂
i
bB 67
计 算 步
线为 0# 条中线
列表计算 li Wi i A
in
-2 -1 0 1 2 3 4 5
骤
tan
Wi cos i cL
K
i 1 in
Wi sin i
i 1
变化圆心 O 和半径 R k 最小 END
Wi
i
Ti
Ni
8.3 粘性土坡的稳定分析
M r fili R (Wi cosi tani cili )R
Wi
i
Ti
Ni
K M r (Gi cos i tani cili )
MS
Gi sin i
对于均质土坡 i , ci c
in
tan Wi cosi cL
K
i 1 in
Wi sin i
i 1
圆心 O,半径 R(如图)
6.3.2粘性土坡的稳定分析
Ni Wi cosi
Ti Wi sin i
fi
i
tan i
ci
1 li
(
N
/ i
tan i
cili )
1 li
(Wi
c os i
tan i
cili
)
A
O
R
C
i
bB 67
-2 -1 0 1 2 3 4 5
滑动力矩
稳定力矩 M s Ti R Wi R sin
由于存在粘聚力C,与无粘性土坡不同; 其危险滑裂面位置在土坡深处; 对于均匀土坡,在平面应变条件下,其滑动面可用一圆 弧(圆柱面)近似。
O R
6.3.2粘性土坡的稳定分析
计算方法:
1 整体圆弧滑动法(瑞典Petterson) 2 瑞典条分法(瑞典Fellenius) 3 毕肖普法( Bishop) 4 Janbu法 5 Spencer(斯宾塞法)方法 6 Morgenstern-Price(摩根斯坦—普赖斯法)方法 7 陈祖煜 的通用条分法 8 不平衡推力传递法 9 Sarma(沙尔玛法)方法
4 毕肖甫(Bishop)法
Hi+1 Pi+1
Pi hi Hi
Wi
i
Ti
hi+1
Ni
假定:圆弧滑裂面;条间切向力=0
6.3.2粘性土坡的稳定分析
∑Fz=0 Wi Ni cosi Ti sini
土坡尚未破坏时(K>1),土条滑动面上的抗 剪强度只发挥了一部分,满足平衡条件:
Ti
cili
Nitgi
R T
W W
cos sin
tg
tg tg
6.3.2 无粘性土坡的稳定分析
Fs
tg tg
当=时,Fs=1.0,天然休止角
•安全系数与土容重无关
•与所选的微单元大小无关 •坡内任一点或平行于坡的任一滑裂面 上安全系数Fs都相等
86..32.2 无粘性土坡的稳定分析 有沿坡渗流情况
降雨
正常蓄水土坝下游
K
方程组求解,得到:
A
(Wi
cili K
sin i )
Ni
mi
O
R
C
bB 67
-2 -1 0 1 2 3 4 5
Pi+1
Ti
1 K
Witgi
cili mi
cosi
mi
cosi
sin itgi
K
Pi hi
Wi
i
hi+1
Ti
Ni
6.3.2粘性土坡的稳定分析
O
R
K Mr fili R (Ni/tgi cili )
算
步
K/= K
骤
No
计算 K/
A
-2 -1 0 1 2 3 4 5
△K=K/ -K <δ
变化圆心 O 和半径 R
K最小
END
6.3.2粘性土坡的稳定分析
毕肖甫法的讨论
(1) 假设圆弧滑裂面
(2) 大多数情况下是精确的
A
O
R
C
i
bB 67
