《平行四边形》同步练习1
平行四边形的判定定理1,2 同步练习
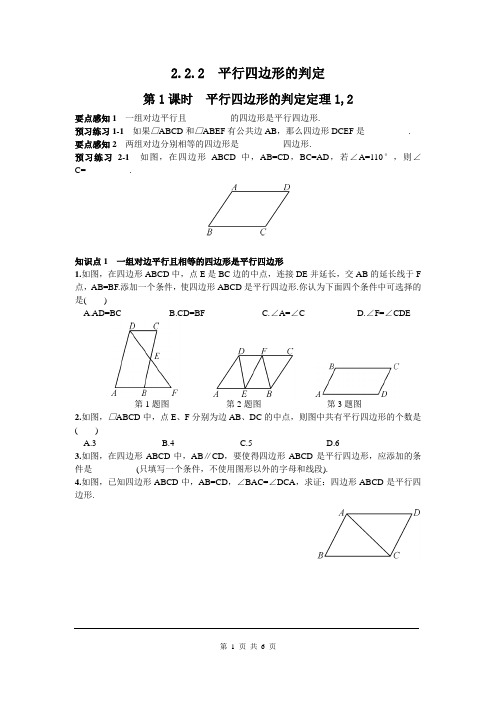
2.2.2 平行四边形的判定第1课时平行四边形的判定定理1,2要点感知1一组对边平行且__________的四边形是平行四边形.预习练习1-1如果□ABCD和□ABEF有公共边AB,那么四边形DCEF是__________. 要点感知2两组对边分别相等的四边形是__________四边形.预习练习2-1如图,在四边形ABCD中,AB=CD,BC=AD,若∠A=110°,则∠C=__________.知识点1 一组对边平行且相等的四边形是平行四边形1.如图,在四边形ABCD中,点E是BC边的中点,连接DE并延长,交AB的延长线于F 点,AB=BF.添加一个条件,使四边形ABCD是平行四边形.你认为下面四个条件中可选择的是( )A.AD=BCB.CD=BFC.∠A=∠CD.∠F=∠CDE第1题图第2题图第3题图2.如图,□ABCD中,点E、F分别为边AB、DC的中点,则图中共有平行四边形的个数是( )A.3B.4C.5D.63.如图,在四边形ABCD中,AB∥CD,要使得四边形ABCD是平行四边形,应添加的条件是__________(只填写一个条件,不使用图形以外的字母和线段).4.如图,已知四边形ABCD中,AB=CD,∠BAC=∠DCA,求证:四边形ABCD是平行四边形.5.已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD相交于点O,BO=DO.求证:四边形ABCD是平行四边形.知识点2 两组对边分别相等的四边形是平行四边形6.四边形ABCD中,AB=CD,AD=BC,∠B=50°,则∠A=__________.7.如图,以△ABC的顶点A为圆心,以BC长为半径作弧,再以顶点C为圆心,以AB长为半径作弧,两弧交于点D,连接AD、CD.若∠B=65°,则∠ADC的大小为__________.8.已知四边形ABCD的四条边长满足(AB-CD)2+(AD-BC)2=0,求证:AB∥CD.9.点A、B、C、D在同一平面内,从①AB∥CD;②AB=CD;③BC∥AD;④BC=AD这四个条件中任意选两个,能使四边形ABCD是平行四边形的有( )A.3种B.4种C.5种D.6种10.如图,□ABCD中,∠ABC=60°,点E、F分别在CD和BC的延长线上,AE∥BD,EF⊥BC,EF=3,则AB的长是__________.11.如图,已知BE∥DF,∠ADF=∠CBE,AF=CE.求证:四边形DEBF是平行四边形.12.如图,在□ABCD中,分别以AD、BC为边向内作等边△ADE和等边△BCF,连接BE、DF.求证:四边形BEDF是平行四边形.13.如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.(1)求证:四边形MNCD是平行四边形;(2)求证:BD=3MN.14.如图,在梯形ABCD中,AD∥BC,AD=6,BC=16,点E是BC的中点.点P以每秒1个单位长度的速度从点A出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动.点P停止运动时,点Q也随之停止运动.求当运动时间t为多少秒时,以点P、Q、E、D为顶点的四边形是平行四边形?参考答案要点感知1相等预习练习1-1平行四边形要点感知2平行预习练习2-1110°1.D2.B3.答案不唯一,如AB=CD或BC∥AD4.证明:∵∠BAC=∠DCA,∴AB∥CD.又∵AB=CD,∴四边形ABCD是平行四边形.5.证明:∵AB∥CD,∴∠ABO=∠CDO,∠BAO=∠DCO.又∵BO=DO,∴△AOB≌△COD(AAS).∴AB=CD.∴四边形ABCD是平行四边形.6.130°7.65°8.证明:∵(AB-CD)2+(AD-BC)2=0,∴AB-CD=0,AD-BC=0.∴AB=CD,AD=BC.∴四边形ABCD是平行四边形.∴AB∥CD.9.B 10.111.证明:∵BE∥DF,∴∠AFD=∠CEB.又∵∠ADF=∠CBE,AF=CE,∴△ADF≌△CBE(AAS).∴DF=BE.又∵BE∥DF,∴四边形DEBF是平行四边形.12.证明:∵四边形ABCD是平行四边形,∴CD=AB,AD=CB,∠DAB=∠BCD.又∵△ADE和△CBF都是等边三角形,∴DE=BF,AE=CF,∠DAE=∠BCF=60°.∴∠BCD-∠BCF=∠DAB-∠DAE,即∠DCF=∠BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.13.证明:(1)∵ABCD是平行四边形,∴AD=BC,AD∥BC.∵M、N分别是AD、BC的中点,∴MD=NC,MD∥NC.∴MNCD是平行四边形;(2)连接ND,∵MNCD是平行四边形,∴MN=DC.∵N是BC的中点,∴BN=CN.∵BC=2CD,∠C=60°,∴△NCD是等边三角形.∴ND=NC,∠DNC=60°.∵∠DNC是△BND的外角,∴∠NBD+∠NDB=∠DNC.∵DN=NC=NB,∴∠DBN=∠BDN=12∠DNC=30°.∴∠BDC=90°.∴BC=2DC,DC.又DC=MN,∴MN.14.由题意可知,AP=t,CQ=2t,CE=12BC=8.∵AD∥BC,∴当PD=EQ时,以点P、Q、E、D为顶点的四边形是平行四边形.当2t<8即t<4时,点Q在C、E之间,如图甲.此时,PD=AD-AP=6-t,EQ=CE-CQ=8-2t,由6-t=8-2t得t=2.当8<2t<16即4<t<8时,点Q在B、E之间,如图乙.此时,PD=AD-AP=6-t,EQ=CQ-CE=2t-8,由6-t=2t-8得t=143.∴当运动时间为2或143时,以点P、Q、E、D为顶点的四边形是平行四边形.。
人教版 四年级数学上册 平行四边形和梯形 同步练习1(含答案)

人教版小学四年级数学上册同步练习5.2平行四边形和梯形(含答案)一、填空题1.等腰梯形周长35cm ,上底5cm ,一条腰长7cm ,它的下底长是( )厘米。
2.一个平行四边形的周长是32cm ,其中一条边长是10cm 。
把它拉成一个长方形(如图)这个长方形的宽是( )cm ,这个长方形的面积是( )cm 2。
(第2题) (第3题) 3.下图四边形ABCD 是一个梯形,它的高是( )cm ;如果把点D 向( )平移( )格,这个梯形就变成一个平行四边形。
4.从平行四边形一条边上的一点向对边引一条( ),这点和( )之间的线段叫做平行四边形的高,( )所在的边叫做平行四边形的底。
5.通过动手拉平行四边形框架的活动,我们知道,平行四边形有( )的特性,生活中( )运用了这一特性。
6.在等腰梯形中画一条高,可以将它分割成两个完全一样的( )形;也可以将它分割成一个( )形和一个( )形。
7.已知四边形ABCD 是等腰梯形,用量角器量一量,你发现了什么? A ∠=( )° B ∠=( )° C ∠=( )° D ∠=( )° 我发现:______________________________________________________。
(第7题) (第8题) 8.如图,在给定的正方形点子图上,找一点D (D 在格点上),使ABCD 成为梯形。
那么符合条件的D点的位置有( )个。
二、选择题9.平行四边形的两组对边()。
A.分别平行B.分别垂直C.相交D.以上答案都不对10.一个等腰梯形上底3米,下底5米,腰4米,这个等腰梯形的周长是()米。
A.12B.15C.1611.把一个平行四边形任意分割成两个梯形,这两个梯形中()总是相等的。
A.高B.面积C.上下两底的和12.平行四边形的高有()条。
A.无数B.2C.413.把一个平行四边形框架拉成长方形,这个长方形和原来的平行四边形比,面积()。
平行四边形单元同步练习

平行四边形单元同步练习一、解答题1.如图,在四边形ABCD 中,AB ∥DC ,AB AD =,对角线AC ,BD 交于点O ,AC 平分BAD ∠,过点C 作CE AB ⊥交AB 的延长线于点E ,连接OE .(1)求证:四边形ABCD 是菱形;(2)若5AE =,3OE =,求线段CE 的长.2.综合与探究(1)如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF BE =.CE 和CF 之间有怎样的关系.请说明理由.(2)如图2,在正方形ABCD 中,E 是AB 上一点,G 是AD 上一点,如果45GCE ∠=︒,请你利用(1)的结论证明:GE BE CD =+.(3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图3在直角梯形ABCD 中,//()AD BC BC AD >,90B ∠=︒,12AB BC ==,E 是AB 上一点,且45DCE ∠=︒,4BE =,求DE 的长.3.已知正方形ABCD .(1)点P 为正方形ABCD 外一点,且点P 在AB 的左侧,45APB ∠=︒.①如图(1),若点P 在DA 的延长线上时,求证:四边形APBC 为平行四边形.②如图(2),若点P 在直线AD 和BC 之间,以AP ,AD 为邻边作APQD □,连结AQ .求∠PAQ 的度数.(2)如图(3),点F 在正方形ABCD 内且满足BC=CF ,连接BF 并延长交AD 边于点E ,过点E 作EH ⊥AD 交CF 于点H ,若EH=3,FH=1,当13AE CF =时.请直接写出HC 的长________.4.如图,点P 是正方形ABCD 内的一点,连接,CP 将线段CP 绕点C 顺时针旋转90,︒得到线段,CQ 连接,BP DQ . ()1如图甲,求证:CBP CDQ ∠=∠;()2如图乙,延长BP 交直线DQ 于点E .求证:BE DQ ⊥;()3如图丙,若BCP 为等边三角形,探索线段,PD PE 之间的数量关系,并说明理由.5.已知正方形,ABCD 点F 是射线DC 上一动点(不与,C D 重合).连接AF 并延长交直线BC 于点E ,交BD 于,H 连接CH .在EF 上取一点,G 使ECG DAH ∠=∠. (1)若点F 在边CD 上,如图1,①求证:CH CG ⊥.②求证:GFC 是等腰三角形.(2)取DF 中点,M 连接MG .若3MG =,正方形边长为4,则BE = .6.共顶点的正方形ABCD 与正方形AEFG 中,AB =13,AE =52.(1)如图1,求证:DG =BE ;(2)如图2,连结BF ,以BF 、BC 为一组邻边作平行四边形BCHF .①连结BH ,BG ,求BH BG的值; ②当四边形BCHF 为菱形时,直接写出BH 的长.7.已知:如下图,ABC 和BCD 中,90BAC BDC ∠=∠=,E 为BC 的中点,连接DE AE 、.若DC AE ,在DC 上取一点F ,使得DF DE =,连接EF 交AD 于O . (1)求证:EF DA ⊥.(2)若4,23BC AD ==,求EF 的长.8.如图,在矩形 ABCD 中, AB =16 , BC =18 ,点 E 在边 AB 上,点 F 是边 BC 上不与点 B 、C 重合的一个动点,把△EBF 沿 EF 折叠,点B 落在点 B' 处.(I)若 AE =0 时,且点 B' 恰好落在 AD 边上,请直接写出 DB' 的长;(II)若 AE =3 时, 且△CDB' 是以 DB' 为腰的等腰三角形,试求 DB' 的长;(III)若AE =8时,且点 B' 落在矩形内部(不含边长),试直接写出 DB' 的取值范围.9.如图,ABCD 中,60ABC ∠=︒,连结BD ,E 是BC 边上一点,连结AE 交BD 于点F .(1)如图1,连结AC ,若6AB AE ==,:5:2BC CE =,求ACE △的面积; (2)如图2,延长AE 至点G ,连结AG 、DG ,点H 在BD 上,且BF DH =,AF AH =,过A 作AM DG ⊥于点M .若180ABG ADG ∠+∠=︒,求证:3BG GD +=.10.已知:正方形ABCD 和等腰直角三角形AEF ,AE=AF (AE <AD ),连接DE 、BF ,P 是DE 的中点,连接AP .将△AEF 绕点A 逆时针旋转.(1)如图①,当△AEF 的顶点E 、F 恰好分别落在边AB 、AD 时,则线段AP 与线段BF 的位置关系为 ,数量关系为 .(2)当△AEF 绕点A 逆时针旋转到如图②所示位置时,证明:第(1)问中的结论仍然成立.(3)若AB=3,AE=1,则线段AP 的取值范围为 .【参考答案】***试卷处理标记,请不要删除一、解答题1.(1)见解析;(2)11【分析】(1)根据题意先证明四边形ABCD是平行四边形,再由AB=AD可得平行四边形ABCD是菱形;(2)根据菱形的性质得出OA的长,根据直角三角形斜边中线定理得出OE=12AC,在Rt ACE∆应用勾股定理即可解答.【详解】(1)证明:∵AB CD∥,∴OAB DCA∠=∠,∵AC为DAB∠的平分线,∴OAB DAC∠=∠,∴DCA DAC∠=∠,∴CD AD AB==,∵AB CD∥,∴四边形ABCD是平行四边形,∵AD AB=,∴ABCD是菱形;(2)∵四边形ABCD是菱形∴AO CO =∵CE AB ⊥∴90AEC ∠=︒∴26AC OE ==在Rt ACE ∆中,2211CE AC AE =-=故答案为(2)11.【点睛】本题主要考查了菱形的判定和性质,平行四边形的判定和性质,角平分线的定义,勾股定理,熟练掌握菱形的判定与性质是解题的关键.2.(1)CE=CF 且CE ⊥CF ,理由见解析;(2)见解析;(3)10【分析】(1)根据正方形的性质,可证明△CBE ≌△CDF (SAS ),从而得出CE=CF ,∠BCE=∠DCF ,再利用余角的性质得到CE ⊥CF ;(2)延长AD 至M ,使DM=BE ,连接CM ,由△BEC ≌△DFC ,可得∠BCE=∠DCF ,即可求∠GCF=∠GCE=45°,且GC=GC ,EC=CF 可证△ECG ≌△GCF (SAS ),则结论可求. (3)过点C 作CF ⊥AD 于F ,可证四边形ABCF 是正方形,根据(2)的结论可得DE=DF+BE=4+DF ,根据勾股定理列方程可求DF 的长,即可得出DE .【详解】解:(1)CE=CF 且CE ⊥CF ,证明:如图1,∵四边形ABCD 是正方形,∴BC=CD ,∠B=∠CDF=90°,又∵BE=DF ,∴△CBE ≌△CDF (SAS ),∴CE=CF ,∠BCE=∠DCF ,∵∠BCD=∠BCE+∠ECD=90°,∴∠ECD+∠DCF=90°,即CE ⊥CF ;(2)延长AD 至M ,使DM=BE ,连接CM ,∵∠GCE=45°,∴∠BCE+∠GCD=45°,∵△BEC ≌△DFC ,∴∠BCE=∠DCF ,∴∠DCF+∠GCD=45°,即∠GCF=45°,∴∠GCE=∠GCF ,且GC=GC ,CE=CF ,∴△GCE ≌△GCF (SAS ),∴GE=GF ,∴GE=GD+DF=BE+GD ;(3)如图:过点C 作CF ⊥AD 于F ,∵AD ∥BC ,∠B=90°,∴∠A=90°,∵∠A=∠B=90°,FC ⊥AD ,∴四边形ABCF 是矩形,且AB=BC=12,∴四边形ABCF 是正方形,∴AF=12,由(2)可得DE=DF+BE ,∴DE=4+DF ,在△ADE 中,AE 2+DA 2=DE 2.∴(12-4)2+(12-DF )2=(4+DF )2.∴DF=6,∴DE=4+6=10.【点睛】本题是四边形综合题,考查了正方形的性质,勾股定理,全等三角形的判定与性质,四边形的面积,熟练掌握正方形的性质是解题的关键.3.(1)①证明见详解;②45PAQ ∠=︒,见解析;(2)5.【分析】(1)①只要证明//PB AC 即可解决问题;②如图2中,连接QC ,作DT DQ ⊥交QC 的延长线于T ,利用全等三角形的性质解决问题即可;(2)如图3中,延长EH 交BC 于点G ,设AE=x ,由题意易得AB=BC=CF=EG=3x ,然后可得CG=2x ,HG=3x-3,CH=3x-1,利用勾股定理求解即可.【详解】(1)①证明:四边形ABCD 是正方形,∴//B DP C ,45DAC ∠=︒,∴135PAC ∠=︒45APB ∠=︒,∴+180APB PAC ∠∠=︒,∴//PB AC∴四边形APBC 是平行四边形; ②四边形PADQ 是平行四边形,∴DQ//,//,AP AD PQ AD PQ BC ==,AD//B C ,∴,//PQ BC PQ BC =,∴四边形PQCB 是平行四边形,∴QC//BP ,∴45APQ DQC ∠=∠=︒,90ADC QDT ∠=∠=︒,∴DQ=DT ,45,T DQT ADQ CDT ∠=∠=︒∠=∠,AD=DC ,∴ADQ CDT ≌,∴45AQD T ∠=∠=︒,AP//DQ ,∴45PAQ DQA ∠=∠=︒;(3)CH=5,理由如下:如图3所示:延长EH 交BC 于点G ;四边形ABCD 是正方形,∴AB=BC ,90D ∠=︒, 又EH=3,FH=1,EH ⊥AD ,∴EH//CD ,∴90HGC ∠=︒设AE=x ,1,3AE CF BC CF ==,∴AB=BC=CF=EG=3x , ∴CG=2x ,HG=3x-3,CH=3x-1 在Rt HGC △中,()()22222243331CG HG CH x x x +=+-=-即,解得121,2x x ==当x=1时,AB=3(不符合题意,舍去);当x=2时,AB=6,∴CH=5.故答案为5.【点睛】本题主要考查正方形的综合问题、三角形全等及勾股定理,关键是利用已知条件及四边形的性质得到它们之间的联系,然后利用勾股定理求解线段的长即可.4.(1)证明见试题解析;(2)证明见试题解析;(3)△DEP为等腰直角三角形,理由见试题解析.【分析】(1)根据正方形性质得出BC=DC,根据旋转图形的性质得出CP=CQ以及∠PCB=∠QCD,从而得出三角形全等来得出结论;(2)由(1)知∠PBC=∠QBC,BE和CD交点为F,根据对顶角得出∠DFE=∠BFC,从而说明BE⊥QD;(3)根据等边三角形的性质得出PB=PC=BC,∠PBC=∠BPC=∠PCB=60°,则∠PCD=30°,根据BC=DC,CP=CQ得出△PCD为等腰三角形,然后根据△DCQ为等边三角形,从而得出∠DEP=90°,从而得出答案.【详解】(1)证明∵四边形ABCD是正方形,∴BC=DC,又∵将线段CP绕点C顺时针旋90°得到线段CQ,∴CP=CQ,∠PCQ=90°,∴∠PCD+∠QCD=90°,又∵∠PCB+∠PCD=90°,∴∠PCB=∠QCD在△BCP和△DCQ中,BC=DC,CP=CQ,∠PCB=∠QCD,∴△BCP≌△DCQ,∴∠CBP=∠CDQ;(2)证明:∵△BCP≌△DCQ,∴∠PBC=∠QDC,∴∠DFE=∠BFC,∠FED=∠FCB=90°,∴BE⊥QD;(3)△DEP为等腰直角三角形,理由如下:∵△BPC为等边三角形,∴PB=PC=BC,∠PBC=∠BPC=∠PCB=60°,∴∠PCD=90°-60°=30°,∴∠DCQ=90°-30°=60°,又∵BC=DC,CP=CQ,∴PC=DC,DC=CQ,∴△PCD是等腰三角形,△DCQ是等边三角形,∴∠CPD=∠CDP=75°,∠CDQ=60°,∴∠EPD=180°-75°-60°=45°,∠EDP =180°-75°-60°=45°,∴∠EPD =∠EDP ,PE =DE ,∴∠DEP =180°-45°-45°=90°,∴△DEP 是等腰直角三形.【点睛】本题考查了正方形的性质、三角形全等的判定和性质以及旋转的性质,掌握正方形的四条边相等、四个角都是直角,旋转的性质证明三角形全等是解题的关键.5.(1)①见解析;②GFC 是等腰三角形,证明见解析;(2)4+25或4﹣25.【分析】(1)①只要证明△DAH ≌△DCH ,即可解决问题;②只要证明∠CFG=∠FCG ,即可解决问题;(2)分两种情形解决问题:①当点F 在线段CD 上时,连接DE .②当点F 在线段DC 的延长线上时,连接DE .分别求出EC 即可解决问题.【详解】(1)①证明:∵四边形ABCD 是正方形,∴∠ADB =∠CDB =45°,DA =DC ,在△DAH 和△DCH 中,DA DC ADH CDH DH DH =⎧⎪∠=∠⎨⎪=⎩,∴△DAH ≌△DCH ,∴∠DAH =∠DCH ;∵∠ECG=∠DAH ,∴∠ECG=∠DCH ,∵∠ECG+∠FCG=∠FCE=90°,∴∠DCH+∠FCG=90°,∴CH ⊥CG.②∵在Rt △ADF 中,∠DFA+∠DAF =90°,由①得∠DCH+∠FCG=90°,∠DAH =∠DCH ;∴∠DFA =∠FCG ,又∵∠DFA =∠CFG ,∴∠CFG =∠FCG ,∴GF=GC,∴△GFC是等腰三角形-.(2)BE的长为 4+25或425①如图①当点F在线段CD上时,连接DE.∵∠GFC=∠GCF,又∵在Rt△FCG中,∠GEC+∠GFC=90°,∠GCF+∠GCE=90°,∴∠GCE=∠GEC,∴EG=GC=FG,∴G是EF的中点,∴GM是△DEF的中位线∴DE=2MG=6,在Rt△DCE中,CE=22-=25,64DE DC-=22∴BE=BC+CE=4+25.②当点F在线段DC的延长线上时,连接DE.同法可知GM是△DEC的中位线,∴DE=2GM=5,在Rt△DCE中,CE22-5DE DC64-22∴BE=BC﹣CE=4﹣5综上所述,BE的长为4+54﹣25【点睛】本题考查正方形的性质、全等三角形的判定和性质、三角形的中位线定理、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.6.(1)证明见解析;(2)①2BH BG =;②BH 的长为172或72. 【分析】(1)证()DAG BAE SAS △≌△,即可得出结论;(2)①连接GH ,延长HF 交AB 于N ,设AB 与EF 的交点为M ,证()GAB GFH SAS △≌△,得GH GB =,GHF GBA ∠=∠,证GHB ∆为等腰直角三角形,即得结论;②分两种情况,证出点B 、E 、G 在一条直线上,求出210AF EG AE ===,则5OA OG OE ===,由勾股定理求出12OB =,求出BG ,即可得出答案.【详解】(1)∵四边形ABCD 和四边形AEFG 是正方形,∴AD =AB =CB ,AG =AE ,∠DAB =∠GCE =90°,∴∠DAB ﹣∠GAF =∠GCE ﹣∠GAF ,即∠DAG =∠BAE ,在△DAG 和△BAE 中,AD AE DAG BAE AG AE =⎧⎪∠=∠⎨⎪=⎩,∴△DAG ≌△BAE (SAS),∴DG =BE ;(2)①连接GH ,延长HF 交AB 于N ,设AB 与EF 的交点为M ,如图2所示:∵四边形BCHF 是平行四边形,∴HF //BC ,HF =BC =AB .∵BC ⊥AB ,∴HF ⊥AB ,∴∠HFG =∠FMB ,又AG //EF ,∴∠GAB =∠FMB ,∴∠HFG =∠GAB ,在△GAB 和△GFH 中,AG FG GAB HFG AB FH =⎧⎪∠=∠⎨⎪=⎩,∴△GAB ≌△GFH (SAS),∴GH =GB ,∠GHF =∠GBA ,∴∠HGB =∠HNB =90°,∴△GHB 为等腰直角三角形,∴BH 2=BG, ∴2BH BG=; ②分两种情况:a 、如图3所示:连接AF 、EG 交于点O ,连接BE .∵四边形BCHF 为菱形,∴CB =FB .∵AB =CB ,∴AB =FB =13,∴点B 在AF 的垂直平分线上.∵四边形AEFG 是正方形,∴AF =EG ,OA =OF =OG =OE ,AF ⊥EG ,AE =FE =AG =FG ,∴点G 、点E 都在AF 的垂直平分线上,∴点B 、E 、G 在一条直线上,∴BG ⊥AF .∵AE 2,∴AF =EG 2==10,∴OA =OG =OE =5,∴OB 2222135AB OA =-=-=12,∴BG =OB +OG =12+5=17, 由①得:BH 2=BG =172; b 、如图4所示:连接AF 、EG 交于点O ,连接BE , 同上得:点B 、E 、G 在一条直线上,OB =12,BG =OG +OB ﹣OG =12﹣5=7,由①得:BH 2=2; 综上所述:BH 的长为2或2. 【点睛】本题是四边形综合题目,考查了正方形的性质、菱形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、线段垂直平分线的判定等知识;本题综合性强,熟练掌握正方形的性质和菱形的性质,证明三角形全等是解题的关键.7.(1)见解析;(2)2【分析】(1)由ABC 和BCD 中,90BAC BDC ∠=∠=︒,E 为BC 的中点,得到12DE AE BC ==,从而EDA EAD ∠=∠,根据//DC AE 得到ADC EDA ∠=∠,再根据等腰三角形的性质得到EF DA ⊥; (2)由4BC =求出DE=AE=2,根据EF DA ⊥,得到132DO AD ==理求出EO ,由此得到22EF EO ==.【详解】(1)∵ABC 和BCD 中,90BAC BDC ∠=∠=︒,E 为BC 的中点∴12DE AE BC == ∴EDA EAD ∠=∠∵//DC AE∴ADC EAD ∠=∠∴ADC EDA ∠=∠∵DF DE =∴EF DA ⊥.(2)∵4BC =, ∴122DE BC == ∵DE AE =, ,23EF DA AD ⊥= ∴132DO AD == Rt DEO 中,221EO DE DO =-=∵DF DE =∴22EF EO ==【点睛】此题考查直角三角形的性质,等腰三角形的性质,勾股定理的运用.(1)中点的运用很关键,确定边相等,利用等边对等角求得角的相等关系;(2)在证明中利用(1)的结论求得132DO AD ==是解题的关键. 8.(I);(II) 16或10;(III) . 【解析】【分析】(I)根据已知条件直接写出答案即可.(II)分两种情况:或讨论即可. (III)根据已知条件直接写出答案即可. 【详解】(I) ;(II)∵四边形是矩形,∴,. 分两种情况讨论:(i )如图1,当时,即是以为腰的等腰三角形. (ii )如图2,当时,过点作∥,分别交与于点、.∵四边形是矩形,∴∥,.又∥,∴四边形是平行四边形,又,'⊥,∴□是矩形,∴,,即B H CD又,∴,,∵,∴,∴,在RtΔEGB'中,由勾股定理得:,∴,在中,由勾股定理得:,综上,的长为16或10.(III) . (或).【点睛】本题主要考查了四边形的动点问题.9.(1)32)见详解.【分析】(1)根据所给的60°,判断出等边三角形,得出BE=6,根据所给比例关系,求出CE,然后求出三角形面积;(2)利用已知条件能够求出ABF≌ADH,之后需要构造全等图形,使所求的BG+GD 转化在同一直线上,然后根据含有30°的特殊直角三角形的关系,即可证明出结果.【详解】解:(1) 如图:过A 点作AN ⊥BE ,交BE 于N .∵60ABC ∠=︒,6AB AE ==∴△ABE 为等边三角形,∴AB=BE=AE=6即:AN=33∵:5:2BC CE =∴:5:3BC BE =∵BE=6∴BC=10∴EC=4 ∴113346322ACE S AN EC ==⨯=即:ACE △的面积为3.(2)如图:延长GD 至P 使DP=BG ,连接AP ,∵AH=AF ,∴∠AFH=∠AHF即:∠AFB=∠AHD ,又∵AF=AH ,BF=DH ,∴ABF ≌ADH∴AB=AD又∵180ABG ADG ∠+∠=︒,180ADP ADG ∠+∠=︒,∴∠ABG=∠ADP∵BG=DP ,∴ABG ≌ADP △∴AG=AP ,∠BAG=∠DAP∵∠ABC=60°∴∠BAD=120°即:∠GAP=120°∴∠AGP=∠APG=60°,又∵AM ⊥GD∴3,∵BG=GP∴BG+GD=GD+DP=GP即:3.【点睛】本题重点考察在平行四边形中利用平行四边形的性质证明图形面积,以及构造全等图形求多边之间的关系,构造全等三角形是本题的解题关键.10.(1)AP⊥BF,12AP BF=(2)见解析;(3)1≤AP≤2【分析】(1)根据直角三角形斜边中线定理可得12AP ED PD==,即△APD为等腰三角形推出∠DAP=∠EDA,可证△AED≌△ABF可得∠ABF=∠EDA=∠DAP 且 BF=ED由三角形内角和可得∠AOF=90°即AP⊥BF由全等可得1122AP ED BF==即12AP BF=(2)延长AP至Q点使得DQ∥AE,PA延长线交于G点,利用P是DE中点,构造△AEP≌△PDQ可得∠EAP=∠PQD,DQ=AE=FA可得∠QDA=∠FAB可证△FAB≌△QDA 得到∠AFB=∠PQD=∠EAP,AQ=FB由三角形内角和可得∠FAG=90°得出AG⊥FB即AP⊥BF由全等可得1122 AP AQ FB ==(3)由于12AP BF=即求BF的取值范围,当BF最小时,即F在AB上,此时BF=2,AP=1当BF最大时,即F在BA延长线上,此时BF=4,AP=2可得1≤AP≤2【详解】(1)根据直角三角形斜边中线定理有AP是△AED中线可得12AP ED PD==,即△APD为等腰三角形.∴∠DAP=∠EDA又AE=AF,∠BAF=∠DAE=90°,AB=AD ∴△AED≌△ABF∴∠ABF=∠EDA=∠DAP 且 BF=ED设AP与BF相交于点O∴∠ABF+∠AFB=90°=∠DAP+∠AFB∴∠AOF=90°即AP⊥BF∴1122AP ED BF==即12AP BF=故答案为AP⊥BF,12 AP BF=(2)延长AP至Q点使得DQ∥AE,PA延长线交于G点∴∠EAP=∠PQD,∠AEP=∠QDP∵P是DE中点,∴EP=DP∴△AEP≌△PDQ则∠EAP=∠PQD,DQ=AE=FA∠QDA=180°-(∠PAD+∠PQD)=180°-∠EAD而∠FAB=180°-∠EAD,则∠QDA=∠FAB∵AF=DQ,∠QDA=∠FAB ,AB=AD∴△FAB≌△QDA∴∠AFB=∠PQD=∠EAP,AQ=FB而∠EAP+∠FAG=90°∴∠AFB+∠FAG=90°∴∠FAG=90°∴AG⊥FB即AP⊥BF又1122 AP AQ FB ==∴1 AP2BF=(3)∵12 AP BF∴即求BF的取值范围BF最小时,即F在AB上,此时BF=2,AP=1BF最大时,即F在BA延长线上,此时BF=4,AP=2∴ 1≤AP≤2【点睛】掌握三角形全等以及直角三角形斜边上的中线,灵活运用各种角关系是解题的关键.。
人教版八年级下册 18.1 平行四边形 同步练习试题

人教版八年级下册 18.1 平行四边形 同步练习试题1 / 5人教八下数学18.1平行四边形练习题一、选择题1. 如图,▱ABCD 的对角线AC ,BD 交于点O ,下列结论不一定成立的是 A.B. C.D. 2. 如图,点D 、E 、F 分别为△ABC 三边的中点,若△ABC 的周长为18,则△DEF 的周长为( )A. 8B. 9C. 10D. 113. 如图,▱ABCD 的对角线AC 、BD 相交于点O ,且AC +BD =16,CD =6,则△ABO 的周长是( ) A. 10 B. 14 C. 20 D. 224. 如图所示,▱ABCD 的对角线AC ,BD 相交于点O , , , ,▱ABCD 的周长A. 11B. 13C. 16D. 225. 如图,在▱ABCD 中,AB =3,AD =5,∠BCD 的平分线交BA 的延长线于点E ,则AE 的长为( ) A. 3B.C. 2D.6.已知四边形ABCD,有以下四个条件:(1)AB=AD,AB=BC;(2)∠A=∠B,∠C=∠D;(3)AB∥CD,AB=CD;(4)AB∥CD,AD∥BC.其中能判定四边形ABCD是平行四边形的个数为().A. 1B. 2C. 3D. 47.如图,在□ABCD中,,,∠ 的平分线交AD于点E,则DE的长为A. 5B. 4C. 3D. 28.平行四边形一边的长是10cm,那么这个平行四边形的两条对角线长可以是()A. 4cm,6cmB. 6cm,8cmC. 8cm,12cmD. 20cm,30cm二、填空题9.▱ABCD中,AB:BC=1:2,周长为24cm,则AB= ______ cm,AD= ______ cm.10.如图,在△ABC中,∠ACB=90°,点D,E,F分别是AB,BC,CA的中点,若CD=2,则线段EF的长是______ .11.已知:在▱ABCD中,对角线AC、BD相交于点O,过点O的直线EF分别交AD于E、BC于F,S△AOE=3,S△BOF=5,则ABCD的面积是______ .人教版八年级下册 18.1 平行四边形 同步练习试题 3 / 5 12.如图,在▱ABCD 中,对角线AC 平分∠BAD ,MN 与AC 交于点O ,M ,N 分别在AB ,CD 上,且AM =CN ,连接BO .若∠DAC =28°,则∠OBC 的度数为______ °.三、计算题13.如图,▱ABCD ,AE 平分∠BAD ,交DC 的延长线于点E ,求证:DA =DE .14.如图,△ABC 中,AD 是高,E 、F 分别是AB 、AC 的中点.(1)若AB =10,AC =8,求四边形AEDF 的周长;(2)EF 与AD 有怎样的位置关系?请证明你的结论.四、解答题15.已知:如图,在▱BEDF中,点A、C在对角线EF所在的直线上,且求证:四边形ABCD是平行四边形.人教版八年级下册 18.1 平行四边形 同步练习试题5 / 5 答案1.D2.B3.B4.D5.C6.B7.D8.D9.4;810.211.3212.6213.证明:∵四边形ABCD 是平行四边形, ∴AB ∥CD ,∴∠E =∠BAE ,∵AE 平分∠BAD ,∴∠BAE =∠DAE ,∴∠E =∠DAE ,∴DA =DE .14.解:(1)∵E 、F 分别是AB 、AC 的中点, ∴AE = AB =5,AF = AC =4,∵AD 是高,E 、F 分别是AB 、AC 的中点, ∴DE = AB =5,DF = AC =4,∴四边形AEDF 的周长=AE +ED +DF +FA =18; (2)EF 垂直平分AD .证明:∵AD 是ABC 的高,∴∠ADB =∠ADC =90°,∵E 是AB 的中点,∴DE =AE ,同理:DF =AF ,∴E 、F 在线段AD 的垂直平分线上,∴EF 垂直平分AD .15.证明:如图,连接BD ,交AC 于点O . ∵四边形BEDF 是平行四边形,∴OD =OB ,OE =OF .又∵AE =CF ,∴AE +OE =CF +OF ,即OA =OC ,∴四边形ABCD 是平行四边形.。
人教版数学四年级上册 第五单元《平行四边形和梯形》同步练习(含答案)

《平行四边形和梯形》(同步练习)四年级上册数学人教版一.填空题(共4小题)1.平行四边形的一个内角是直角,并且相邻的边不相等,这个平行四边形就是,若相邻的边相等,这个平行四边形就是.2.a、b、c、d四条线段围绕了一个平行四边形(如图).其中和互相平行,还有和互相平行.3.从平行四边形的一个顶点出发作一条高,可以把平行四边形分成一个三角形和一个形.4.黑板上下两条边是互相的,三角尺中的两条直角边是互相的。
梯形中最多有个直角。
二.选择题(共5小题)5.平行四边形的()一定相等.A.四个角B.对边C.四条边6.从平行四边形一条边上的一点到对边可以画()条高。
A.1B.2C.4D.无数7.平行四边形的一个角是钝角,与这个角相邻的角一定是()A.直角B.锐角C.钝角D.平角8.一个平行四边形框架沿对角线拉成一个长方形后,周长()A.变大B.不变C.变小9.()只有一组对边平行.A.平行四边形B.梯形C.长方形三.判断题(共4小题)10.学校门口的伸缩门是利用平行四边形的稳定性原理制作的。
11.平行四边形同一条底上的高有无数条,它们的长度都相等。
12.因为梯形有一组对边平行,所以梯形是特殊的平行四边形。
13.梯形有无数条高,且长度都相等。
四.计算题(共2小题)14.一个平行四边形的周长是160分米,其中一条边长26分米,另外三条的长度分别是多少分米?15.计算下面图形的周长.五.操作题(共2小题)16.(1)以O为顶点画一个45°的角。
(2)根据给定的底和高,画一个平行四边形。
17.画出下面平行四边形中底a和b分别对应的两条高。
六.应用题(共4小题)18.用一根217厘米长的铁丝正好围成一个等腰梯形。
梯形的上底是31厘米,下底是66厘米,它的一条腰长多少厘米?19.一根60厘米长的铁丝刚好围成一个平行四边形,其中一条边长12厘米,其他三条边的长度各是多少厘米?请说明理由。
20.王师傅用一根70厘米长的木条做了一个平行四边形框架,其中一条边的长是20厘米,另一条边长是多少厘米?21.一个直角梯形的下底是上底的4倍,如果把梯形的上底延长12厘米,就成为一个正方形,这个梯形的上底和高各是多少厘米?《5.2平行四边形和梯形》(同步练习)四年级上册数学人教版参考答案与试题解析一.填空题(共4小题)1.平行四边形的一个内角是直角,并且相邻的边不相等,这个平行四边形就是长方形,若相邻的边相等,这个平行四边形就是正方形.【解答】解:平行四边形的一个内角是直角,并且相邻的边不相等,这个平行四边形就是长方形,若相邻的边相等,这个平行四边形就是正方形.故答案为:长方形,正方形.2.a、b、c、d四条线段围绕了一个平行四边形(如图).其中a和c互相平行,还有b和d互相平行.【解答】解:这个平行四边形中a和c是一组对边,它们互相平行;b和d是一组对边,它们互相平行.故答案为:a、c;b、d.3.从平行四边形的一个顶点出发作一条高,可以把平行四边形分成一个三角形和一个梯形.【解答】解:由分析可知,从平行四边形的一个顶点出发做一条高,可以把平行四边形分成一个三角形和一个梯形.故答案为:梯.4.黑板上下两条边是互相平行的,三角尺中的两条直角边是互相垂直的。
平行四边形(基础练)(同步练习附答案)(人教版)(2022年最新)

【解答】解:∵点D、E、F分别是三边的中点,
∴DE、EF、DF为△ABC的中位线,
∴DE AB 7 ,DF AC 5 ,EF BC 6=3,
∴△DEF的周长 3=9,
故选:B.
7.(2020秋•苏州期末)如图,四边形ABCD中,以对角线AC为斜边作Rt△ACE,连接BE、DE,BE⊥DE,AC,BD互相平分.若2AB=BC=4,则BD的值为( )
∵∠ABC、∠BCD的平分线BE、CF分别与AD相交于点E、F,
∴∠EBC+∠FCB ∠ABC ∠DCB=90°,
∴EB⊥FC,
∴∠FGB=90°.
过A作AM∥FC,交BC于M,交BE于O,如图所示:
∵AM∥FC,
∴∠AOB=∠FGB=90°,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∵AD∥BC,
∴3x=108°,
∴x=36°,
∴∠AED=∠AEC+∠CED=2x+90°﹣x=90°+x=90°+36°=126°,
故答案为:126°.
19.(2020春•辉县市期末)如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s)当t=2或6s时,以A、C、E、F为顶点四边形是平行四边形.
故选:A.
二.填空题
9.(2020秋•普宁市期末)如图,在△ABC中,D是AB中点,DE∥BC,若DE=6,则BC=12.
【解答】解:∵DE∥BC,D是AB中点,
∴ 1,
∴AE=EC,
∵AD=DB,
人教版八年级数学下册同步练习 18.1《平行四边形》
人教版八年级数学下册同步练习18.1《平行四边形》1. 能判定四边形ABCD为平行四边形的条件是( )A.AB // CD,AD=BCB.∠A=∠B,∠C=∠DC.AB=CD,AD=BCD.AB=AD,CB=CD2. 如图,▱ABCD中,过对角线BD上一点P作EF//BC,GH//AB,图中面积相等的平行四边形有()A.2对B.3对C.4对D.5对3. 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB的长为半径作弧,两弧交于点D,分别连接AB,AD,CD.若∠ABC+∠ADC=120∘,则∠A的度数是()A.100∘B.110∘C.120∘D.125∘4. 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90∘,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为()A.6B.12C.20D.245. 如图,在▱ABCD中,E,F分别在BC,AD上,若想要使四边形AFCE为平行四边形,需添加一个条件,这个条件不可以是()A.AF=CEB.AE=CFC.∠BAE=∠FCDD.∠BEA=∠FCE6. 如果一个四边形的三个内角度数依次如下,那么其中是平行四边形的是()A.88∘,108∘,88∘B.88∘,104∘,88∘C.88∘,92∘,92∘D.88∘,92∘,88∘7. 如图,在△ABC中,AB=5,BC=3,AC=4,E,F分别是AB,BC的中点.以下结论错误的是()A.△ABC是直角三角形B.AF是△ABC的中位线C.EF是△ABC的中位线D.△BEF的周长为68. 如图,在△ABC中,D,E分别是AB,AC的中点,点F在BC上,ED是∠AEF的角平分线.若∠C=80∘,则∠EFB的度数是()A.100∘B.110∘C.115∘D.120∘9. 已知三角形的3条中位线分别为3cm,4cm,6cm,则这个三角形的周长是()A.3cmB.26cmC.24cmD.65cm10. 下列叙述不正确的是()A.一个三角形必有三条中位线B.一个三角形必有三条中线C.三角形的一条中线分成的两个三角形的面积相等D.三角形的一条中位线分成的两部分面积相等11. 如图,在△ABC中,∠A=38∘,AB=AC,点D在AB边上,以BC,BD 为边作▱BCED,则∠E的度数为________.12. 如图,Rt△ABC中,∠ACB=90∘,AB=6,点D是AB的中点,E为AC的中点,F为AD的中点,则EF=________.13. 已知长方形ABCD,AB=3cm,AD=4cm,过对角线BD的中点O作BD 的垂直平分线EF,分别交AD,BC于点E,F,则AE的长为________.14. 如图,在▱ABCD中,过对角线BD上一点P作EF//BC,GH//AB,且CG= 2BG,S△BPG=1,则S▱AEP=________.15. 如图,在▱ABCD中,O是对角线AC的中点,过点O的直线交AD的延长线于点E,交CB的延长线于点F,求证:BF=DE.16. 如图,在△ABC中,D,E,F分别是边AB,BC,AC的中点,以这些点为顶点,在图中,你能画出多少个平行四边形?为什么?17. 如图,已知△ABF,△ACD,△BCE都是等边三角形,求证:四边形ADEF是平行四边形.18. 如图,在四边形ABCD中,AB=CD,M,N分别为AD,BC的中点,BA,CD的延长线分别交MN的延长线于点P,Q.求证:∠APM=∠DQM.参考答案人教版八年级数学下册同步练习 18.1《平行四边形》一、选择题(本题共计 10 小题,每题 3 分,共计30分)1.【答案】C2.【答案】B3.【答案】C4.【答案】D5.【答案】B6.【答案】D7.【答案】B8.【答案】9.【答案】B10.【答案】D二、填空题(本题共计 4 小题,每题 3 分,共计12分)11.【答案】71∘12.【答案】1.513.【答案】7814.【答案】4三、解答题(本题共计 4 小题,每题 10 分,共计40分)15.【答案】证明:∵四边形ABCD为平行四边形,∴AE//CF且AD=BC,∴∠E=∠F.又∵O为对角线AC的中点,∴AO=CO,在△AEO与△CFO中,{∠E=∠F,∠AOE=∠COF, AO=CO,∴△AEO≅△CFO,∴AE=CF.又∵AD=BC,∴AE−AD=CF−BC,∴DE=BF.16.【答案】解:画出3个平行四边形,有平行四边形ADEF,平行四边形CFDE,平行四边形BEFD.理由如下:▱ D,E,F分别是△ABC的边AB,BC,AC的中点,▱ EF//AB,DF//BC,▱ 四边形BEFD是平行四边形,同理四边形ADEF是平行四边形,四边形CFDE是平行四边形;综上所述,能画出3个平行四边形.17.【答案】证明:▱ △ABF,△BCE都是等边△▱ ∠FBA=∠EBC=60∘,AB=BF=AF,BC=BE=EC▱ ∠FBA−∠EBA=∠EBC−∠EBA即∠FBE=∠CBA又∵AB=BF,BC=BE▱ △FBE≅△ABC(SAS)▱ AC=EF.▱ △ACD得等边△▱ AC=AD▱ EF=AD同理:AF=DE▱ 四边形ADEF是平行四边形.18.【答案】证明:连结AC,取AC的中点H,连结NH,MH.▱ N ,H 分别为BC ,AC 的中点, ▱ NH =//12AB ,▱ ∠APM =∠HNM , 同理:MH =//12CD ,▱ ∠DQM =∠HMN .▱ AB =CD ,▱ MH =NH ,▱ ∠HMN =∠HNM , ▱ ∠APM =∠DQM .。
人教版平行四边形单元同步练习
人教版平行四边形单元同步练习一、选择题1.已知点A(4,0),B(0,﹣4),C(a,2a)及点D是一个平行四边形的四个顶点,则线段CD的长的最小值为()A.655B.1255C.32D.422.将个边长都为1cm的正方形按如图所示的方法摆放,点分别是正方形对角线的交点,则2019个正方形重叠形成的重叠部分的面积和为( )A.B.C.D.3.如图,在矩形ABCD中,AB=2,BC=4,P为边AD上一动点,连接BP,把△ABP沿BP折叠,使A落在A′处,当△A′DC为等腰三角形时,AP的长为()A.2 B.23C.2或23D.2或434.正方形ABCD,正方形CEFG如图放置,点B、C、E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M.有下列结论:①EC=BP;②AP=AM:③∠BAP=∠GFP;④AB2+CE2=12AF2;⑤S正方形ABCD+S正方形CGFE=2S△APF,其中正确的是()A.①②③B.①③④C.①②④⑤D.①③④⑤5.如图,正方形ABCD 中,AB=4,E为CD上一动点,连接AE交BD于F,过F作FH⊥AE于F,过H 作HG⊥BD 于 G.则下列结论:①AF=FH;②∠HAE=45°;③BD=2FG;④△CEH 的周长为 8.其中正确的个数是()A .1个B .2个C .3个D .4个6.如图,在矩形ABCD 中,把矩形ABCD 绕点C 旋转,得到矩形FECG ,且点E 落在AD 上,连接BE ,BG ,BG 交CE 于点H ,连接FH ,若FH 平分EFG ,则下列结论:①AE CH EH +=;②2DEC ABE ∠=∠; ③BH HG =;④2CH AB =,其中正确的个数是( )A .1个B .2个C .3个D .4个7.如图,四边形ABCD 是正方形,直线L 1、L 2、L 3,若L 1与L 2的距离为5,L 2与L 3的距离7,则正方形ABCD 的面积等于( )A .70B .74C .144D .1488.如图,直角梯形ABCD 中AD ∥BC ,∠D =90°.∠A 的平分线交DC 于E ,EF ⊥AB 于F .已知AD =3.5cm ,DC =4cm ,BC =6.5cm .那么四边形BCEF 的周长是( )A .10cmB .11cmC .11.5cmD .12cm9.在ABCF 中,2BC AB =,CD AB ⊥于点D ,点E 为AF 的中点,若50ADE ∠=︒,则B 的度数是( )A .50︒B .60︒C .70︒D .80︒10.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB =3 ,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处.则BC 的长为( )A .3B .3C .2D .23二、填空题11.如图,在平面直角坐标系中,矩形ABCO 的边CO 、OA 分别在x 轴、y 轴上,点E 在边BC 上,将该矩形沿AE 折叠,点B 恰好落在边OC 上的F 处.若OA =8,CF =4,则点E 的坐标是_____.12.如图,在平行四边形ABCD 中,对角线AC ,BD 相交于点O ,AB =OB ,点E ,F 分别是OA ,OD 的中点,连接EF ,EM ⊥BC 于点M ,EM 交BD 于点N ,若∠CEF =45°,FN =5,则线段BC 的长为_____.13.如图正方形 ABCD 中,E 是 BC 边的中点,将△ABE 沿 AE 对折至△AFE ,延长 EF 交 CD 于 G ,接 CF ,AG .下列结论:① AE ∥FC ; ②∠EAG = 45°,且BE + DG = EG ;③ABCD 19CEF S S ∆=正方形;④ AD = 3DG ,正确是_______ (填序号).14.如图,在平行四边形ABCD 中,AD=2AB .F 是AD 的中点,作CE ⊥AB, 垂足E 在线段AB 上,连接EF 、CF ,则下列结论:(1)∠DCF+12∠D =90°;(2)∠AEF+∠ECF =90°;(3)BEC S=2CEFS; (4)若∠B=80 ,则∠AEF=50°.其中一定成立的是______ (把所有正确结论的字号都填在横线上).15.如图,正方形ABCD 的边长为6,点E 、F 分别在边AD 、BC 上.将该纸片沿EF 折叠,使点A 的对应点G 落在边DC 上,折痕EF 与AG 交于点Q ,点K 为GH 的中点,则随着折痕EF 位置的变化,△GQK 周长的最小值为____.16.在锐角三角形ABC 中,AH 是边BC 的高,分别以AB ,AC 为边向外作正方形ABDE 和正方形ACFG ,连接CE ,BG 和EG ,EG 与HA 的延长线交于点M ,下列结论:①BG=CE ;②BG ⊥CE ;③AM 是△AEG 的中线;④∠EAM=∠ABC .其中正确的是_________.17.如图,在Rt △ABC 中,∠BAC =90°,AB =8,AC =6,以BC 为一边作正方形BDEC 设正方形的对称中心为O ,连接AO ,则AO =_____.18.如图,在平行四边形ABCD 中,AC ⊥AB ,AC 与BD 相交于点O ,在同一平面内将△ABC 沿AC 翻折,得到△AB’C ,若四边形ABCD 的面积为24cm 2,则翻折后重叠部分(即S △ACE ) 的面积为________cm 2.19.如图,在正方形ABCD 中,点F 为CD 上一点,BF 与AC 交于点E ,若∠CBF=20°,则∠AED 等于__度.20.如图,矩形纸片ABCD ,AB =5,BC =3,点P 在BC 边上,将△CDP 沿DP 折叠,点C 落在点E 处,PE ,DE 分别交AB 于点O ,F ,且OP =OF ,则AF 的值为______.三、解答题21.在四边形ABCD 中,90A B C D ∠∠∠∠====,10AB CD ==,8BC AD ==.()1P为边BC上一点,将ABP沿直线AP翻折至AEP的位置(点B落在点E处)①如图1,当点E落在CD边上时,利用尺规作图,在图1中作出满足条件的图形(不写作法,保留作图痕迹,用2B铅笔加粗加黑).并直接写出此时DE=______;②如图2,若点P为BC边的中点,连接CE,则CE与AP有何位置关系?请说明理由;()2点Q为射线DC上的一个动点,将ADQ沿AQ翻折,点D恰好落在直线BQ上的点'D处,则DQ=______;22.在一次数学探究活动中,小明对对角线互相垂直的四边形进行了探究,得出了如下结⊥,则论:如图1,四边形ABCD的对角线AC与BD相交于点O,AC BD 2222+=+.AB CD AD BC(1)请帮助小明证明这一结论;(2)根据小明的探究,老师又给出了如下的问题:如图2,分别以Rt ACB的直角边AC和斜边AB为边向外作正ACFG和正方形ABDE,连结CE、BG、GE.已知AB=,求GE的长,请你帮助小明解决这一问题.AC=,5423.如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.(1)求证:四边形BCEF是平行四边形;(2)若∠DEF=90°,DE=8,EF=6,当AF为时,四边形BCEF是菱形.24.如图①,已知正方形ABCD中,E,F分别是边AD,CD上的点(点E,F不与端点重合),且AE=DF,BE,AF交于点P,过点C作CH⊥BE交BE于点H.(1)求证:AF ∥CH ;(2)若AB=23 ,AE=2,试求线段PH 的长;(3)如图②,连结CP 并延长交AD 于点Q ,若点H 是BP 的中点,试求 CPPQ的值. 25.已知在平行四边形ABCD 中,AB BC ≠,将ABC 沿直线AC 翻折,点B 落在点尽处,AD 与CE 相交于点O ,联结DE . (1)如图1,求证://AC DE ;(2)如图2,如果90B ∠=︒,3AB =,6=BC ,求OAC 的面积;(3)如果30B ∠=︒,23AB =,当AED 是直角三角形时,求BC 的长.26.如图1,在矩形纸片ABCD 中,AB =3cm ,AD =5cm ,折叠纸片使B 点落在边AD 上的E 处,折痕为PQ ,过点E 作EF ∥AB 交PQ 于F ,连接BF .(1)求证:四边形BFEP 为菱形;(2)当E 在AD 边上移动时,折痕的端点P 、Q 也随着移动. ①当点Q 与点C 重合时, (如图2),求菱形BFEP 的边长;②如果限定P 、Q 分别在线段BA 、BC 上移动,直接写出菱形BFEP 面积的变化范围.27.探究:如图①,△ABC是等边三角形,在边AB、BC的延长线上截取BM=CN,连结MC、AN,延长MC交AN于点P.(1)求证:△ACN≌△CBM;(2)∠CPN= °;(给出求解过程)(3)应用:将图①的△ABC分别改为正方形ABCD和正五边形ABCDE,如图②、③,在边AB、BC的延长线上截取BM=CN,连结MC、DN,延长MC交DN于点P,则图②中∠CPN= °;(直接写出答案)(4)图③中∠CPN= °;(直接写出答案)(5)拓展:若将图①的△ABC改为正n边形,其它条件不变,则∠CPN= °(用含n 的代数式表示,直接写出答案).28.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.(1)如图1,①∠BEC=_________°;②在图1已有的三角形中,找到一对全等的三角形,并证明你的结论;(2)如图2,FH∥CD交AD于点H,交BE于点M.NH∥BE,NB∥HE,连接NE.若AB=4,AH=2,求NE的长.29.在直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 / 4
《平行四边形》同步练习1
一、填空题
1.平行四边形的对边_________,对角_________,对角线_________.
2.已知□ABCD中,AB=5,BC=3,则□ABCD的周长等于_________.
3.平行四边形的一条边长为6,一条对角线为8,则另一边长的范围为
_________;另一条对角线的范围是_________.
4.如果平行四边形的一内角为50°,那么其余三角分别为_________.
5.如果一平行四边形相邻两内角之比为4∶5,那么四内角分别为_________.
6.已知□ABCD的周长为20 cm,短边AB比长边BC短4 cm,则CD=_________,
AD
=_________.
7.等腰梯形的一个底角是65°,则它的其余三个角是_________.
8.梯形ABCD中,AB∥CD,周长为25 cm,CD=4 cm,DE∥BC交AB于E,则△
ADE
的周长为_________.
9.等腰梯形的两底之差为8 cm,高是4 cm,则它的钝角是_________.
10.等腰梯形的一个底角为60°,且对角线与腰垂直,腰长20 cm,则梯形的
周长_____.
二、选择题
11.如图1,□ABCD不具有的性质是( )
图1
A.ABCD B.AO=OC C.AC=BD D.∠BAD=∠BCD
12.平行四边形的一组对角的平分线一定( )
A.垂直 B.重合 C.平行 D.平行或重合
13.下列四边形中,对角互补的是( )
A.平行四边形 B.梯形 C.等腰梯形 D.四边形
14.以不在同一直线上的三个点为顶点作平行四边形,最多能作( )
2 / 4
A.4个 B.3个 C.2个 D.1个
15.平行四边形的对角线和各边可组成全等三角形的对数是( )
A.3 B.2 C.4 D.6
16.如图2所示,□ABCD中,GH过对角线的交点O,AB=5,AD=4,OH=2,则四
边形BCGH的周长为( )
图2
A.11 B.13 C.16 D.17
17.如图3所示,若□ABCD的一内角∠BCD的平分线交AD于F,且CF=FD,则∠
B
的度数为( )
图3
A.120° B.30° C.60°或120° D.60°
18.如图4所示,等腰梯形ABCD中,AD∥BC,AD=2,BC=6,E为CD的中点,四
边形ABED的周长与△BCE的周长之差为1,则AB长为( )
图4
A.3 B.4 C.5 D.4或5
19.下列命题中真命题的个数是( )
①等腰梯形的对角线和各边组成的三角形中,面积相等的有三对.②等腰梯形的
对角线相等.③相邻两角相等的梯形是等腰梯形.④等腰梯形中有可能有直角.
A.4 B.3 C.2 D.1
3 / 4
20.平行四边形具有而一般四边形不具有的性质是( )
A.内角和等于360° B.外角和等于360°
C.不稳定性 D.对角相等
三、解答题
21.已知:如图4所示,在□ABCD中,M、N分别是DC、AB的中点.
求证:△AMD≌△CNB.
图4
22.如图5所示,梯形ABCD中,AB∥CD,E、F分别为CD、AB中点,且EF⊥CD.
求证:梯形 ABCD为等腰梯形.
图5
23.解决梯形的问题往往要转化为什么问题,常见的方法有哪些?你能总结出来
吗?
4 / 4
参考答案
一、1.平行且相等 相等 互相平分 2.16 3.大于2小于14 大于4小
于20 4.130° 130° 50° 5.80° 80° 100° 100°6.3 cm 7cm
7.115° 65° 115° 8.17 cm 9.135° 10.100 cm
二、11.C 12.D 13.C 14.B 15.C 16.B 17.D 18.C 19.C 20.D
三、21.略 22.略 23.略
