高中数学 第1章 算法初步 1.2 流程图 1.2.1 顺序结构教案 苏教版必修3
2019-2020年高中数学第1章算法初步1.2流程图1.2.3循环结构教学案苏教版必修3

2019-2020年高中数学第1章算法初步1.2流程图123循环结构教学案苏教版必修31 •什么叫循环结构?2 •循环结构有哪两种基本模式,它们各自有什么特点?[新知初探]1 •循环结构的定义需要重复执行同一操作的结构称为循环结构.2 •循环结构的结构形式(1) 当型循环:先判断所给条件p是否成立,若p成立,则执行A 再判断条件p是否成立;若p仍成立,则又执行A,如此反复,直到某一次条件p不成立时为止(如右图).(2) 直到型循环:先执行A,再判断所给条件p是否成立,若p不成立,则再执行A,如此反复,直到p成立,该循环过程结束(如右图).[点睛](1)构成循环结构的三要素:循环变量、循环体、循环终止条件.(2)当型循环的顺序是:先判断再执行再循环.直到型循环的顺序是:先执行再判断再循环.[小试身手]1. ①任何一种算法都离不开顺序结构,顺序结构是算法的最基本形式;②循环结构一定包含选择结构;③循环结构只有一个入口和一个出口;④循环结构的形式有且只有一种;以上四种说法中正确个数有_________ .答案:32. _________________________________________ 解决下列冋题可能需用循环结构的是①求函数y =|x—1|的函数值;②求函数y = 2x在x= 1,2,3,…,10时的函数值;③求1 + 2+ 3+-+ 10的值. 答案:②③E3嘉课堂讲练设ii •堆一能通类题[典例]图1、图2是两个循环结构的流程图,分别指出它们是哪种类型的循环结构、循环变量、循环次数、循环终止条件、循环体及输出的结果.图1 图2[解]图1表示的循环结构是直到型循环结构,循环变量是S及i,循环次数9次,循环终止条件是i >10,循环体是S—S+ i和i J i + 1,输出结果为55.图2表示的循环结构是当型循环结构,循环变量是S及i,循环次数10次,循环终止条件是i>10,循环体是S—S+ i和i J i + 1,输出结果为55.(1) 构成循环结构的三个要素是循环变量、循环体及循环终止条件,确定一个循环结构的功能要注意循环变量的初始值、取值范围及变化规律,需特别注意判断框中计数变量的取值限制用等号还是用不等号,用““>”还是用“”它们的含义是不同的.(2) 要注意流程线的箭头及与判断框相连的流程线上的Y及N.(3) 判断是当型循环结构还是直到型循环结构关键要看是先判断再执行,还是先执行再判断.""[活学活用]某流程图如图,则此循环结构是 ________ 循环结构,循环变量是__________ ,若输入的i为2,则输出的S值是_________/输y/「I : 璋iQ1答案:当型S和n 3循环结构的设计[典例]设计一种流程图计算1X2X3X4X-X n(n》2).[解]法一:当型流程图如图所示:(W法二:直到型流程图如图所示:如果算法问题里涉及的运算进行多次重复操作,且先后参与运算的各数之间有相同的变化规律,就可以引入循环变量参与运算,构成循环结构•在循环结构中,要注意根据条件设置合理的计数变量,累计(加、乘)变量,其中计数变量的功能是控制循环的次数并为每次运算提供数据,累计(加、乘)变量的功能是提供每次运算的初始值和最终运算结果•累加变量的初值一般为0,而累乘变量的初值一般为 1.[活学活用]写出求1X 3X 5X 7X 9X 11的值的一个算法,并画出流程图. 解:法一:算法如下:51 A1;52 I —3;53 T—T X I ;54 I —I + 2;S5如果I > 11,那么转S6,否则转S3;S6输出T.上述算法用流程图表示为如图所示.法二1:算法如下:S 1T—1;S 2I —3;S3如果1 < 11, 那么转S4,否则转S6;S 4T—T X I ;S 5I —I + 2,转S3;S 6输出T.上述算法用流程图表示为如图所示.〔结束〕循环结构的实际应用■ --- -------------------------------------------------------------------[典例]某专家称,中国的通货膨胀率保持在3尬右对中国经济的稳定有利无害•所谓通货膨胀率为3%指的是每年消费品的价格增长率为3%.在这种情形下,某种品牌的钢琴xx年的价格是10 000元,请用流程图描述这种钢琴今后4年的价格变化情况,并输出4年后钢琴的价格.[解]由题意知n年后钢琴价格为P= 10 000(1 + F)n (R= 0.03,1 w n w4)故流程图为在解决与累加、累乘等有关的实际应用问题时,往往可以利用循环结构来实现算法. 解决此类问题首先要读懂题目,建立合适的数学模型•然后确定循环变量、循环体、循环终止条件,最后根据算法画出流程图.[活学活用]某班共有学生50人,在一次数学测试中,要搜索出测试中及格(60分及以上)的成绩,试设计一个算法,并画出流程图.解:算法如下:S1 i = 1.谍石层级训练.步步提升隧力[层级一学业水平达标]1 •已知下列说法:①虽然算法叙述的形式有很多类型,但算法表示为流程图按其逻辑 结构分类仅有三种;②循环结构中,循环体根据条件是否成立会被反复无休止的执行; 函数f (x ) = a (1 + r )x (r >— 1且r 丰0),当x = 0,1,2,3 ,…,100时的函数值时可用循环结构; ④选择结构中根据条件是否成立有不同的流向. 其中正确说法的序号为答案:①③④解析:S = 1 + 3+ 5 +…+ 19= 100;S2 输入x ,S3 若x >60,则输出, S4 i = i + 1.S5 判断i >50,是结束; 否则执行 S2. 流程图如下:③求2•如图流程图中,输出的结果为答案:1003•按如图所示的流程图运算,若输出k= 2,则输入x的取值范围是 ___________解析:第一次运行x = 2x+ 1, k= 1,第二次运行x= 2(2 x + 1) + 1, k= 2, 此时输出x的值,则2x+ K 115 且2(2 x + 1) + 1>115,解得28<x W 57. 答案:(28,57]4 •某程序框图如图所示,若该程序运行后输出的值是5,则a= ---------------解析:由程序框图及最后输出的值为当k = 1 时,S= 1, k>a不成立,k= 2>a不成立, k= 3>a不成立, k= 4>a不成立,32,315S+22X33,517S+ —33X44'719S_44X59可知,[WZLZ"/输入工/故故故/输出此时k= 5>a成立,a = 4.答案:4解:如图所示:[层级二应试能力达标]1 •如图所示的流程图的算法功能是 _____________________ 输出的结果i =答案:求积为624的相邻的两个偶数 24 2•执行如图所示的流程图,输入l = 2, m = 3, n =5,则输出的y 值是 ____________丽/输入非负椿數!叔"/-JL-<^y-^105y 105N解析:I = 2, m= 3, n = 5, l 2+ n i + n 2工0,y = 70X 2+ 21 X 3+ 15X 5= 278>105, y = 278 - 105 = 173>105,5 •用循环结构写出计算1 [ 1 1X3 +2X41 3X51100X 102 的流程图.26y = 173- 105 = 68,此时输出的 y 值为68. 答案:683•如图是为求1〜1 000的所有偶数的和而设计的一个流程图,则①处应填②处应填解析:因为当i < 1 000时开始执行①②两部分结合循环结构的形式可知,该程序为当 型循环结构,又i = 2, sum = 0,且计算=sum + i , i = i + 2.答案:sum^sum+ i i J i + 24.(浙江高考)若某流程图如图所示,1 . 1 . 1 . 1 .T = 2,i = 3; T = 6 i = 4; T = 24,i = 5; T = 120,i1=6>5,循环结束•则输出的值为 莎1答案:1205•执行如图所示的流程图,则共经过 __________ 次判断,经过 _________次循环体.2 + 4 + 6+-+ 1 000的值,故①②两处分别填 sum则该程序运行后输出的值是 解析:运行程序后,T = 1, i = 2;&如图所示的流程图表示的算法功能是 答案:35 34 6•如图所示的流程图,则该流程图表示的算法的功能是 ____________7•依不同条件写出下列流程图的运行结果. ⑴图⑴中箭头a 指向①时,输出sum= _____________ ,指向②时,输出 ⑵图⑵中箭头b 指向①时,输出sum= ____________ ,指向②时,输出 簡束〕 答案:计算连续正奇数相乘,所得积不小于 10 000时的最后一个奇数 sum=________ sum=________ 图(1) 图⑵答案:(1)5 15 (2)6 20&如图所示的流程图表示的算法功能是/WW答案:计算函数f (x ) = In x ,当自变量x = 1,2,…,100时的函数值9.以下是某次考试中某班 15名同学的数学成绩:72,91,58,63,84,88,90,55,61,73,64,77,82,94,60.要求将80分以上的同学的平均分求出来.画出流程图.解:流程图如下所示:10.下列三图是为计算22+ 42+ 62+…+ 1002而绘制的算法流程图,根据流程图回答后面的问题:•1恒-0~T~ —1~ ―护 i*4 | i^2pr 卜F<:inZSW /输申歹 (O(1)(1) 其中正确的流程图有哪几个?错误的流程图有哪几个?错误的要指出错在哪里?(2) 错误的流程图中,按该流程图所蕴含的算法,能执行到底吗?若能执行到底,最后输出的结果是什么?解:(1)正确的流程图只有图③,图①有三处错误:2第一处错误,第二个图框中 i -4 ,应该是i -4,因为本流程图中的计数变量是 i ,不 是i 2,在22'42,…,1002中,指数都是2,而底数2,4,6,8,…,100是变化的,但前后两数前后两项相差2.图②所示的流程图中有一处错误, 即判断框中的内容错误, 应将框内的内容“ i V 100” 改为“ i < 100”或改为“ i > 100”且判断框下面的流程线上标注的 Y 和N 互换.(2)图①虽然能进行到底,但执行的结果不是所期望的结果,按照这个流程图最终输出2 2 2 2 2的结果是 p = 2 + 4 + (4 + 1) + (4 + 2) +…+ (4 + 84).图②虽然能进行到底, 但最终输出的结果不是预期的结果而是22 + 42 + 62+…+ 982,少2 了 100 .2019-2020年高中数学第1章算法初步1.2流程图1.2.3循环结构自我检自我检测项的底数相差2,因此计数变量是顺加 2.第二处错误,第三个图框中的内容错误,累加的是第三处错误,第四个图框中的内容,其中的指令 i 2而不是i ,故应改为 P - P + ii — i + 1,应改为i — i + 2,原因是底基础达标1. 指出下列流程图所表示的算法(用算式表示)(1)/输出卩//输出卩/答案:(1)其算法为:1+3+5+ (99)(2)其算法为:1 X2X 3X 4X-X 20.2. 指出下面流程图的运行结果.答案:其运行结果为20.3. 下面是求12+22+32+…+ 1002的值的流程图,请将流程图补充完整:(1) ____________________ 处应填;(2) ____________________ 处应填.〔开始〕If〔结朿】答案:SIHH-SUTT. i4•设计一个算法,求前n个自然数的和大于2 004的最小正整数n,并用流程图表示出来. 解:算法:(1 )取n=1;⑵计算;(3)如果的值大于2 004,那么n即为所求;否则让n的值增加1后转到(2)重复操作;(4)输出n的值.流程图(1)流程图(2)(结束) (1)5.将全班64个学生期中考试成绩不及格者的分数打印出来. 解:更上一层1 .某高中男子体育小组的50米跑成绩(单位:s )为:6.4,6 . 5,7.0,6.8,7.1,7.3,6.9,7.4,7.5 .设计一个算法,从这些成绩中搜索出小于 6.8 s的成绩,并画出流程图.解:算法步骤:第一步:把计数变量n的初值设为1 .第二步:输入一个成绩r,判断r与6. 8的大小.若r >6. 8,则执行下一步;若r<6 . 8,则输出r,并执行下一步;第三步:使计数变量n的值增加1;第四步:判断计数变量n与成绩个数9的大小.若n w 9,则返回第二步;若n>9.则结束.否/输出F /是否结2 (开始〕/输入工/呈jr>SO 否杏束以下是某次考试中某班川n+i/输入r /15 名同学的数学成绩 •要求将80分以上的同学的平均分求出 (开始)72,91,58,63,84,88,90,55,61,73,64,77,82,94,60来.写出流程图.解:流程图如下图:/+1s-s^x3 .有120名学生.(1)要求将他们之中成绩不低于60分者的学号打印出来,画出流程图.(2)要求将他们之中成绩不低于60分者的学号和成绩都打印出来,画出流程图. 解:(1)用n和g i分别表示第i个学生的学号和成绩,流程如图所示:(2)流程图如图所示:叫禺分别表示第i个学生的学号和战绩。
高中苏教版数学必修3 第1章 1.2 流程图课件PPT

构与循环结构的定义 可知,A、B、C 不正 确.D 正确.特别提醒:
B.选择结构的流程图有一个入口和两个 本题易错选 B,判断框
出口 C.选择结构中的两条路径可以同时执行 D.循环结构中存在选择结构
是一个入口和两个出 口,但是选择结构中的 两条路径,只能执行其 一,不能同时执行,故
B 不正确.]
栏目导航
②
也可以用来执行计算语句;
③输入框只能紧接在起始框之后;
④用流程图表示算法,其优点是将算法的基本逻辑结构展现得非
常直接.
栏目导航
④ [①中框图中的图形符号有严格标准,不能由个人确定;②中 只能执行判断语句,不能执行计算语句;③中输入框不一定只
能紧接在起始框之后.故①②③不正确,④正确.]
栏Байду номын сангаас导航
1.理解流程图中各框图的功能是解此类题的关键,用流程图表 示算法更直观、清晰、易懂.
4.如图是求实数 x 的绝对值的算法流程图,则判断框①中可填 ________.
x>0 或 x≥0
[根据绝对值定义解答,|x|=x-,x,
x≥0, x<0. ]
栏目导航
合作探究 提素养
栏目导航
流程图的认识和理解 【例 1】 下列说法正确的是________. ①流程图中的图形符号可以由个人来确定;
栏目导航
3.顺序结构 依次进行_多__个__处__理__的结构称为顺序结构.顺序结构的形式如图 所示,其中 A 和 B 两个框是依次执行的.顺序结构是任何一个算法 都离不开的最简单、最基本的结构.
栏目导航
4.选择结构 先根据条件_作__出__判__断__,再决定执行_哪__一__种__操__作__的结构称为选择 结构,也称为_分__支___结构. 如图所示,虚线框内是一个选择结构,它包含一个判断框,当条
高中数学苏教版必修3《第1章1.2流程图》课件

________.(填序号)
①输入框、输出框有严格的位置限定;
②任何一个流程图都必须有起止框;
③对于一个流程图而言,判断框中的条件是唯一确定的;
④判断框是唯一具有超过一个退出点的图框符号.
②④ [任何一个流程图都必须有开始和结束,因此必须有起止 框;输入框和输出框可以用在算法中的任意需要输入和输出的位置; 判断框中的条件不是唯一的.]
【例 1】 下列说法正确的是________. ①流程图中的图形符号可以由个人来确定;
②
也可以用来执行计算语句;
③输入框只能紧接在起始框之后;
④用流程图表示算法,其优点是将算法的基本逻辑结构展现得非
常直接.
④ [①中框图中的图形符号有严格标准,不能由个人确定;②中
只能执行判断语句,不能执行计算语句;③中输入框不一定只 能紧接在起始框之后.故①②③不正确,④正确.]
公式等可以分别写在不同的用以处理数据的处理框内,另外,对变量
进行赋值时,也用到处理框.
5.判断框是唯一具有超过一个退出点的图框符号.
1.流程图中,符号“
”可用于________.(填序号)
①输入;②输出;③赋值;④判断.
③ [流程图中矩形方框的功能是赋值和计算.]
2.对于流程图的图框符号的理解,下列说法中正确的是
2.通过分析具体问题, 抽象出算法的过程,锻炼
4.在学习用流程图描述算法的过程中, 抽象概括能力,培养数学
发展有条理地思考与表达的能力,提高逻
辑思维能力.(难点)
抽象素养.
1.流程图的概念 流 程 图 是 由 一 些 _图__框__ 和 _流__程__线__ 组 成 的 , 其 中 图 框 表 示 _各__种__操__作__的__类__型__,图框中的文字和符号表示_操__作__的__内__容__,流程线表 示_操__作__的__先__后__次__序___.
高中数学第1章算法初步1.2流程图1.2.1顺序结构练习无答案苏教版必修3word版本
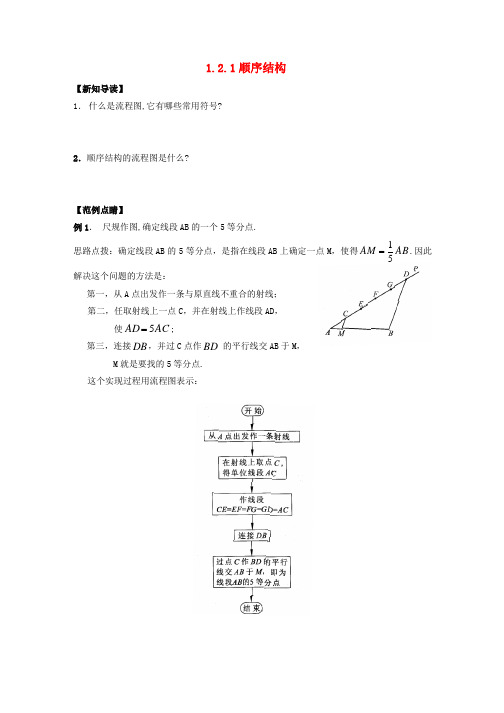
1.2.1顺序结构 【新知导读】 1. 什么是流程图,它有哪些常用符号?
2.顺序结构的流程图是什么? 【范例点睛】 例1. 尺规作图,确定线段AB的一个5等分点.
思路点拨:确定线段AB的5等分点,是指在线段AB上确定一点M,使得ABAM51.因此解决这个问题的方法是: 第一,从A点出发作一条与原直线不重合的射线; 第二,任取射线上一点C,并在射线上作线段AD, 使ACAD5; 第三,连接DB,并过C点作BD 的平行线交AB于M, M就是要找的5等分点. 这个实现过程用流程图表示: 易错辨析:有些同学想直接从已知线段AB下手取5等分点,实际上用尺规是作不出来的。 方法点评:这个算法具有一般性,对于任意自然数n,都可以按照这个算法的思想,设计出确定线段n等分点的步骤,得到解决这个一般问题的算法. 【课外链接】 1.经过市场调查分析得知,2006年第一季度内,某地区对某件商品的需求量为12000件.为保证商品不脱销,商家在月初时将商品按相同数量投放市场.已知年初商品的库存量为50000件,用S表示商品的库存量,请设计一个算法,求出第一季度结束时商品的库存量,并画出流程图.
思路点拨:因为第一季度商品的需求量为12000件,而且每个月以相同数量投放市场,因此每个月向市场投放4000件商品.可以用下表表示库存量随着月份的变化情况
【随堂演练】 1.算法的三种基本结构是 ( ) A. 顺序结构、模块结构、条件结构 B. 顺序结构、循环结构、模块结构 C. 顺序结构、条件结构、循环结构 D. 模块结构、条件结构、循环结构 2.下列图形符号中,表示输入输出框的是( )
3.以下关于流程图(符号)的几种说法: ①任何一个流程图都必须有起止框; ②输入框只能放在开始框后,输出框只能放在结束框前; ③判断框是唯一具有超过一个退出点的符号. 其中正确说法的个数是 ( ) A.1个 B.2个 C.3个 D.0个 4.流程图中的判断框,有m个入口和n个出口,则m,n的值分别为( ) A.1,1 B.1,2 C.2,1 D.2,2 5.将两个数a=8,b=17交换,使a=17,b=8,下面语句正确一组是 ( )
高中数学 第一章 第2课时 流程图与顺序结构教案 苏教版必修3

高中数学教学案第一章算法初步第2课时流程图与顺序结构教学目标:1.了解流程图的概念,了解常用流程图符号(输入输出框、处理框、判断框、起止框、流程线等)的意义;2.能用程序图表示顺序结构的算法;3.发展学生有条理的思考与表达能力,培养学生的逻辑思维能力.教学重点:运用流程图表示顺序结构的算法教学过程:Ⅰ.问题情境Ⅱ.建构数学1.流程图的概念:2.构成流程图的图形符号及其作用:3.流程图的结构包括:4.顺序结构的概念:Ⅲ.数学应用的外接圆的一个算法.例1:写出作ABC练习:已知两个单元分别存放了变量x和y的值,试交换这两个变量值,画出流程图.例2:半径为r 的圆的面积计算公式为2S r π=,当10r =时,写出计算圆面积的算法,画出流程图.练习:半径为r 的球的体积计算公式为334R V π=,当R=3时,写出计算球体积的算法,画出流程图.思考.如图的流程图,其运行结果为 .Ⅳ.课时小结Ⅴ.课堂检测Ⅵ.课后作业 书本P 8 1,2 中国书法艺术说课教案今天我要说课的题目是中国书法艺术,下面我将从教材分析、教学方法、教学过程、课堂评价四个方面对这堂课进行设计。
一、教材分析:本节课讲的是中国书法艺术主要是为了提高学生对书法基础知识的掌握,让学生开始对书法的入门学习有一定了解。
书法作为中国特有的一门线条艺术,在书写中与笔、墨、纸、砚相得益彰,是中国人民勤劳智慧的结晶,是举世公认的艺术奇葩。
早在5000年以前的甲骨文就初露端倪,书法从文字产生到形成文字的书写体系,几经变革创造了多种体式的书写艺术。
1、教学目标:使学生了解书法的发展史概况和特点及书法的总体情况,通过分析代表作品,获得如何欣赏书法作品的知识,并能作简单的书法练习。
2、教学重点与难点:(一)教学重点了解中国书法的基础知识,掌握其基本特点,进行大量的书法练习。
(二)教学难点:如何感受、认识书法作品中的线条美、结构美、气韵美。
3、教具准备:粉笔,钢笔,书写纸等。
高中数学 1.2 流程图与顺序结构教案 苏教版必修3

流程图与顺序结构
教学目标:了解流程图的概念,了解常用流程图符号(输入输出框、处理框、判断框、起止框、流程线等)的意义;能用程序图表示顺序结构的算法;发展学生有条
理的思考与表达能力,培养学生的逻辑思维能力. 教学重点:运用流程图表示顺序结构的算法.
教学难点:规范流程图的表示. 教学过程:
一.问题情境
1.情境:回答下面的问题:
(1)123100++++= ;
(2)123n ++++= ;
2.问题:已知1232006n ++++>,求n 的最小值,试设计算法.
二.学生活动
探究:
上述算法可以用框图直观地描述出来:
三.建构数学
1.流程图的概念:
2.构成流程图的图形符号及其作用:
3.规范流程图的表示:
①使用标准的框图符号;
②框图一般按从上到下、从左到右的方向画,流程线要规范; ③除判断框外,大多数框图符号只有一个进入点和一个退出点. ④在图形符号内描述的语言要非常简练、清楚.
4.顺序结构的概念:
四.数学运用
例1.写出作ABC ∆的外接圆的一个算法.
小结:
例2.已知两个单元分别存放了变量x 和y 的值,试交换这两个变量值.
小结: 例3.半径为r 的圆的面积计算公式为2S r π=,当10r =时,写出计算圆面积的算
法,画出流程图.
小结:
练习:书P9 1、2
1、确定已知线段AB 的三等分点,试设计一个算法,用流程图表示。
高中数学第1章算法初步1.2流程图1.2.3循环结构教案苏教版必修3
1.2.3 循环结构整体设计教材分析在现实生活中,除了用到选择结构进行问题的分支处理外,还会遇到“重复处理”的问题,循环结构(cycle structure)正是可以用来处理需要重复执行的某一组操作.循环结构也称为“重复结构”,即反复执行某一部分的操作.循环结构是程序设计中不可缺少的又富有变化的一种基本结构,是我们学习的第三种程序结构.在某一算法中,如果出现从某处开始,按照一定的条件反复执行同一操作,那么这种结构就称为循环结构,反复执行的处理步骤称为循环体.在循环体中一定有一个选择结构,否则将无法从循环结构中脱离出来,从而形成死循环.此外,循环结构中通常都有一个起到循环计数的变量,这个变量一直都含在执行或终止循环体的条件中.循环结构分为当型循环和直到型循环,它们之间是可以相互转化的.教材考虑到学生的接受能力,对直到型循环和当型循环没有加以定义和区分,仅仅是在《探究·拓展》中以阅读题的形式作了介绍,这样处理是有用意的,教师没有必要在这里提出这两种概念,可待学生有了感性认识和一定的算法基础后,再做适当的回顾与补充.如果某一操作需要重复一定的次数,那么我们可以设置一个统计循环次数的变量,当这个变量的值没有超过我们给定的数值时,就一直重复执行需要的操作,当这个变量的数值超过给定的数值时就脱离循环结构.三维目标通过实例的训练,使学生理解循环结构的意义,并能够用循环结构的流程图表示简单问题的算法,养成良好的逻辑思维习惯,发展有条理的思考与表达能力,达到提升学生逻辑思维能力的目标.重点难点教学重点:用循环结构的流程图表示算法.教学难点:多种结构的嵌套使用.课时安排1课时教学过程导入新课设计思路一:(情境导入)同学们小时候一定都有过缠着父母听故事的经历,有时候爸爸妈妈实在想不出故事了,就会用一个“故事”来哄骗孩子:从前有座山,山里有个庙,庙里有个老和尚.有天老和尚对小和尚说,我给你讲个故事说啊:从前有座山,山里有个庙,庙里有个老和尚.有天老和尚对小和尚说,我给你讲个故事说啊:从前有座山,山里有个庙,庙里有个老和尚.有天老和尚对小和尚说,我给你讲个故事说啊:……现在考虑,为什么说这个“故事”是哄骗小朋友的?因为这个“故事”一直在重复着同样的环节:“从前有座山,山里有个庙,庙里有个老和尚,有天老和尚对小和尚说,我给你讲个故事说啊:……”所以这个“故事”可以无限次循环.我们可以把这个环节写成一个算法,这个算法是一直重复同样的操作,多次循环,直到孩子打断父母的“故事”为止.在现实生活中,还有好多这样的例子,在整个问题的执行过程中,一直循环执行相同的一部分步骤,直到符合或者不符合某个条件时才终止.请同学们举出这样的一些例子.例如:1.同学们从小学开始,每年9月初开学,到学校里上课,一个学期后放寒假,过了寒假再开学,又一个学期后放暑假,然后下一年9月初再开学回到学校上课→寒假→上课→暑假……,直到不再上学为止.2.今天是星期三,过了一天是星期四,过了两天是星期五……过了七天又是星期三,这样周而复始循环出现.3.计算1+2+3+4+ (100)第一步计算1+2;第二步将上一步中的运算结果与第三个数相加;第三步将上一步中的运算结果与第四个数相加;第四步将上一步中的运算结果与第五个数相加;……第i步将上一步中的运算结果与第i-1个数相加;……直到执行完第99步后才得到结果.上述例子都是在运行过程中循环执行相同的步骤,这样的算法结构就是循环结构.(引入新课,板书课题——循环结构)设计思路二:(问题导入)观察下面的流程图(图1),回答这个流程图的功能是什么?其中最主要的操作步骤是什么?图1这个流程图从学号为1的学生开始,输出他的成绩,然后判断学号是否为尾号,如果不是,让学号增加1,继续输出2号学生,再判断学号是否为尾号,如果不是,学号再增加1,输出下一位学生的成绩,直到学号为尾号,即最后一名学生才结束程序,因此这个流程图的功能是输出所有学生的成绩.其中最主要的就是多次重复执行的判断学号、改变学号、输出成绩的过程.要输出所有学生的成绩,应该有很多个输出框,为什么流程图中只有一个输出框?因为每次输出学生的成绩都是一种重复的操作:先确定要输出哪一位学生的成绩,然后再输出.这个过程将重复出现,进行循环操作,直到所有学生全部输出(即学号为尾号)才结束,这样的结构最主要的部分就是有循环形式的结构出现,我们把这样的结构称为循环结构.(引入新课,板书课题——循环结构)推进新课新知探究北京获得了2008年第29届奥林匹克运动会的主办权.你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?对遴选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市将获得主办权;如果所有申办城市得票数都不超过总票数的一半,则将得票数最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.这个表决过程可以用算法写出,请同学们写出这个算法.算法:S1 投票;S2 统计票数,如果有一个城市得票数超过总票数的一半,那么该城市获得主办权,转S3,否则淘汰得票最少的城市,转S1;S3 宣布主办城市.在这个过程中,如果统计票数后任意一个城市得票数都没有超过总票数的一半,那么将重复执行投票→统计票数这一过程,直到有一个城市得票数超过总票数的一半为止.这里出现了一个循环操作的内容,而最终应该循环多少次,在整个表决结果出来以前是无法知道的,也许第一次表决后就结束,也许要表决3次、4次,所以如果用流程图来表示,我们会发现仅仅利用前面学过的顺序结构和选择结构将无法实现,那么将怎样来画出这个问题的流程图呢?根据算法,是否要返回S1,即继续投票,就看是否有一个城市得票数超过总票数的一半,如果没有,将返回S1执行循环,如果有一个城市得票数超过总票数的一半,就立即结束表决,因此我们可以把流程图画成图2的形式:图2像上面的算法中的这种需要重复执行同一种操作的结构称为循环结构.重复执行的那些步骤就称为循环体.如图3,虚线框中的流程结构就是一种常见的循环结构,其功能是先执行框A,然后判断给定的条件P是否成立,若条件P不成立,则再执行框A,执行完框A后继续判断条件P是否成立,如果不成立,再执行框A,再判断条件P……,如此反复执行框A,直到判断条件P时发现成立为止,此时不再执行框A,而是脱离这个循环结构.图3 图4上面的这个循环结构实际上就是最常用的直到型(Until型)循环.在循环结构中还经常出现当型(While型)循环,其结构如图4中虚线框内的形式,它的功能是当给定条件P 成立时,先执行框A,然后判断给定的条件P是否成立,若条件P成立,则再执行框A,执行完框A后继续判断条件P是否成立,如果成立,再执行框A,再判断条件P……,如此反复执行框A,直到判断条件P时发现不成立为止,此时不再执行框A,而是脱离这个循环结构.比较上面的循环结构和上一节课学习的选择结构,它们都有一个判断框,选择结构中从判断框出来的两条分支都不再返回而是直接结束(当然也可以再执行其他步骤),这个判断框只会判断一次,而循环结构中从判断框出来的两条分支一条直接流向结束,另一条会返回上面的某一处继续执行相同的操作,这个判断框会判断多次.因此如果出现判断,就看判断后是不是返回执行相同的操作,如果不再返回,那就是选择结构,如果要返回重复执行某一些操作,那就是循环结构.应用示例思路1例1 用连加的方法写出求2102...222个++++的算法和流程图.分析:本题指明了用连加的方法,所以先进行2+2的运算,然后把结果再加2,然后把结果再加2,……然后把结果再加2,这样一共需要进行9次加法运算就可以输出运算结果了.因此我们在流程图中应该有一个统计进行了多少次加法运算的计数器,这个计数器的功能是每进行一次加法运算就“加1”,直到计数器内的统计数据达到9时就结束加法,输出运算结果.解:算法如下:S1 加法计数器I设置初值0;S2 和存储器S设置初值2;S3 计算S+2,结果放入和存储器S;S4 加法计数器I加1;S5 如果I≥9,则输出S,否则转S3.这个算法也可以用简洁的符号表示:S1 I←0;S2 S←2;S3 S←S+2;S4 I←I+1;S5 如果I≥9,则输出S,否则转S3.流程图如图5所示:图5思考1.这个循环结构中的循环体由哪几个步骤组成?由流程图很清晰地看出,重复执行的循环体由处理框“S←S+2”、“I←I+1”和判断框“I≥9”组成.2.本题中,变量I和S分别起什么作用?为什么两个变量的初值一个为0,一个为2?变量I实际上就是一个统计进行了多少次加法运算的计数器.根据流程图,开始时I←0,说明还没有进行运算,经过一次“S←S+2”后,再执行“I←I+1”,这时I=1,说明进行了一次加法运算,然后判断“I≥9”,结果为“N”,判断后返回执行“S←S+2”(注意:现在进行的是第二次加法运算),再下一步就又是执行“I←I+1”,这时I=2,说明进行了二次加法运算,然后继续判断“I≥9”.我们发现这样的规律:进行了多少次加法(S←S+2),I就等于这个次数.而题目一共要进行9次加法运算,所以如果“I≥9”不成立(判断结果为“N”),则继续累加,直到“I≥9”成立(判断结果为“Y”),才脱离循环结构,输出S,结束程序.当然,变量I只可能出现I=9,不可能出现I>9的情况,因为I=9时就跳出循环体,不再继续返回执行“S←S+2”和“I←I+1”了.图6变量S实际上就是一个存储加法运算的结果的存储单元.每次都是把上一次的运算结果加上2以后作为下一次的一个加数,所以我们把这个加法的结果一直存储在存储器S中.3.如果我们把判断框中的条件“I≥9”改为“I=9”是否可以?根据“思考2”的分析,变量I只可能出现I=9,不可能出现I>9的情况,所以这样修改也是可以的.4.如果我们把选择结构改变为如图6的形式,即把判断框中的条件“I≥9”改为“I<9”,再把“Y”和“N”交换是否也符合要求?根据图6,当加法的次数I满足“I<9”(判断结果为“Y”)时,说明加法的次数还不满9次,所以再返回执行加法运算“S←S+2”,再执行“I←I+1”(计数器增加1),然后继续判断“I<9”是否成立,直到判断结果为“N”(加法次数“不是小于9次”),说明已经加了9次了,这时脱离循环体,输出S,结束程序,所以这样的修改也是可以的.但是一般情况下,在这种循环结构中,我们总是习惯于“满足条件就脱离循环结构,否则返回继续执行”这种格式,这样统一以后便于他人阅读、理解和修改,也便于计算机专业人员把流程图翻译成计算机语言编成计算机程序.点评:特意设置一个难度较低的题目,是为了让学生容易着手,便于理解和掌握这种新型的程序结构.因此写出算法和流程图不难,老师不要急于做下一个例题,要把“思考”中的内容详细讲解,重点讲清变量I和S的意义,直到学生弄清楚循环结构的原理为止.例2 写出求1+2+3+4+5值的一个算法,并画出流程图.分析:本题前面课时已讲过,一共也只有4次加法运算,所以可以直接连加五个数.但是这个方法只能适用于运算次数比较少的形式,对连加次数较多时就显得比较烦琐.当然本题也可以使用等差数列求和公式,直接求前五项的和,这样可以求任意多次连加运算,但是对于没有学习过这个公式的人就不适用了.其实本题实质是连加,每次都是把上一次加法的结果再继续加上下一个数,直到这个加数是5为止.但是与例1相比,这个加数不断在变化,而加法的次数是固定的5次,所以我们可以在判断框中设置条件“I>5”(I就是这个不断变化的加数),当条件成立时就脱离循环体,输出和“S”,否则还将继续进行加法运算.解:算法如下:S1 S←0;S2 I←1;S3 S←S+I;S4 I←I+1;S5 如果I>5,则输出S,否则转S3.流程图如图7所示:图7点评:循环结构的判断框中的条件可以直接是循环的次数,也可以是脱离循环体的条件,应根据不同的情况选择不同的条件.例3 写出求1×2×3×4×5的值的一个算法,并画出流程图.分析:这个变式和例2相比,仅仅是把连加换成连乘,其他没有改变,所以判断框中的条件应该不变,“和存储器”S应该变成“积存储器”T,同时存储器的初值不能是0了,否则每次相乘后的积永远只能是0.同学们思考,这个“积存储器”T的初值应该是多少?应该是1!原理和初值S←0类似.解:算法如下:S1 T←1;S2 I←1;S3 T←T×I;S4 I←I+1;S5 如果I>5,则输出T,否则转S3.流程图如图8所示:图8变式训练1.写出求1×3×5×7×9×11值的一个算法,并画出流程图.分析:与例题相比,最主要的变化是循环变量I增加的幅度(以后称为步长)由1变为2,另外乘积式中因式的个数也由5个变成了6个,所以脱离循环体的条件也应该发生相应的变化,因此算法和流程图中改变的应该就是这两个地方.解:算法如下:S1 T←1;S2 I←1;S3 T←T×I;S4 I←I+2;S5 如果I>11,则输出T,否则转S3.流程图如图9所示:图92.对于输入的不同的正整数n,写出求1×2×4×8×…×2n值的一个算法,并画出流程图.分析:本题中最主要的变化是乘积式中因式的个数由输入的正整数n确定,且每次参与乘积的数都是上一次乘数的2倍,因此算法和流程图中改变的主要就是这两个地方.算法如下:S1 输入n;S2 T←1;S3 I←1;S4 T←T×I; S5 I←I×2;S6 如果I>2n,则输出T,否则转S4.流程图如图10所示:图10点评:从以上例题和变式可以看出,循环结构中必须嵌套一个选择结构,即有一个判断框,这个判断框的用途是用来控制什么时候脱离循环体的.如果没有判断框,或者判断框中的条件永远不可能成立,那么这样的循环就只能永远循环下去,从而形成“死循环”,所以在编写循环结构的算法的时候,要注意不能形成“死循环”.例4 设计计算10个数的平均数的一个算法,并画出流程图.分析:我们用一个循环依次输入10个数,再用一个变量存放数的累加和,在求出10个数的累加和后,除以10,就得到10个数的平均数.解:算法如下:S1 S←0;{使S=0}S2 I←1;{使I=1}S3 如果I≤10,那么转S4,否则转S7;{当I≤10时循环}S4 输入G;{输入一个数}S5 S←S+G;{求S+G,其和仍存放在S中}S6 I←I+1,转S3;{使I的值增加1,并转到S3}S7 A←S/10;{将平均数S/10存放在A中}S8 输出A.{输出平均数}流程图如图11所示:图11点评:如果流程图太长,我们可以把它分割成几块,每块根据连接点可以重新连接(如图11可以分割成图12的形式).图12图13思路2例1 运行图13的流程图后,输出的值是________________.分析:变量I和T的初值为I=0和T=10,然后开始执行循环体.先判断T<22是否成立,如果成立,就让变量I增加1,累加存储器T加4,继续循环,再判断条件T<22是否成立,当条件T<22不成立才脱离循环结构,输出当时计数器I中的值,否则一直进行循环.实际上这个流程图就是统计10加上多少个4才能使得和不大于22的最大次数,容易知道,使10+4n≤22的最大的正整数n为3,所以输出的值为3.答案:3变式训练流程图13表示了一个什么算法?试把“当条件不成立时脱离循环体,并且先判断,再执行”改成“直到条件成立时才脱离循环体,并且先执行,再判断”的形式.分析:变量I和T的初值为I=0和T=10,然后开始执行循环体.先让变量I增加1,累加存储器T加4,然后判断T≥22是否成立,如果不成立,就继续循环,再让变量I增加1,累加存储器T加4,然后判断T≥22是否成立,直到条件T≥22成立才脱离循环结构,输出当时计数器I中的值,否则一直进行循环.解:这个流程图表示的是求使10+4n≤22的最大的正整数n的一个算法.改成“直到条件成立时才脱离循环体,并且先执行,再判断”的形式的算法流程图如图14所示.图14点评:实际上,图13是一个当型循环,图14是直到型循环,这两种循环是有区别的.直到型循环是“直到条件成立时才脱离循环体”,并且是先执行,再判断;当型循环是“当条件不成立时脱离循环体”,并且是先判断,再执行.它们的这个区别目前先不必和学生讲清,通过本题可以让学生先有一个感性认识,知道两种循环可以相互转化,它们的实质性区别可以等学生有了一定的算法基础后,再做适当的回顾与补充.例2 写出求100991...651431211⨯++⨯+⨯+⨯的一个算法,并画出流程图 分析:本例属连加问题,只是每次的加数复杂一些,因此和存储器S 置初值0,循环变量I 与加数的关系为)1(1+⨯I I ,每次循环时增长的步长为2,直到满足条件I>99时脱离循环体,输出结果,结束程序.解:算法如下:S1 S←0;S2 I←1;S3 S←S+)1(1+⨯I I ; S4 I←I+2;S5 如果I>99,则输出S ,否则转S3.流程图如图15所示:图15点评:本题继续巩固和深化循环结构的概念及算法,通过改变步长和加数的复杂化,达到灵活应用的目的.知能训练一、课本本节练习1、2.二、补充练习1.写出计算12+22+32+…+1002的算法的流程图.2.一个两位数,个位数字与十位数字之和为9,写出一个把所有这样的两位数都输出的算法,并画出流程图.解答:一、课本练习1.算法如下:S1 S←0;S2 I←2;S3 S←S+I;S4 I←I+2;S5 如果I>100,则输出S,否则转S3.流程图如图16所示:图162.本题表示的算法是将学号从1号到50号中成绩达到或超过80分的学生的学号和成绩找出来.二、补充练习1.流程图如图17所示.图172.算法如下:S1 a←0;S2 a←a+1;S3 b←9-a;S4 m←10a+b;S5 输出m;S6 如果a>9,则结束程序,否则转S2.流程图如图18所示.图18点评:对于循环结构,要弄清楚循环体是什么,即哪些步骤执行循环操作,另外何时执行循环,何时脱离循环.掌握了上面两个问题,就不难写出算法及流程图.同时算法及流程图还要符合规范.课堂小结在某一算法中,如果出现从某处开始,按照一定的条件反复执行同一操作,那么这种结构就称为循环结构,反复执行的处理步骤称为循环体.在循环体中一定有一个选择结构,否则将无法从循环结构中脱离出来,从而形成死循环.此外,循环结构中通常都有一个起到循环计数的变量,这个变量一直都含在执行或终止循环体的条件中.循环结构的关键在于搞清楚循环体是什么,何时执行循环,脱离循环体的条件是什么.作业课本习题1.1 6、7、8、9.设计感想循环结构是三种算法结构中最复杂的一种,如果在一开始学习时不搞清楚,那么学生就很容易陷入循环中无法解脱出来,把自己给绕进去.所以这节课的关键是讲清概念,弄明白循环结构中各步骤之间的关系,尤其是明确循环体由哪些步骤组成,判断是继续执行循环还是脱离循环的条件是什么.所以在讲解应用示例设计思路1的例1时,速度不宜快,应该把循环变量I和累加器S的作用讲清讲透,因此我们在设计这个课题的时候有意比教材降低了起点,设置了一个更加简单的问题,并且还增加了一些思考的问题,这些问题教师不要轻易放过,一定要让所有的学生都明白了循环变量I和累加器S的作用后才可以继续进行下面的教学.还有变式的设置也都是为了让学生理解循环结构中两个变量的作用.在例题和课堂练习中,可以让学生先写出算法,再用流程图表示出来.如果学生对脱离循环的条件不甚明白,老师可以把流程图实际操作一遍,用表格的形式列出各个变量(尤其是循环变量)的数值变化过程,便于学生找出判断框中的条件.对于溢出循环体的条件,有时候学生会比正确结果相差1,这个问题是由于学生对溢出的边界有些模糊导致的,教师可以引导学生观察循环变量的值和运算(或执行)的次数以及题目要求运算的总次数的关系,从中得到正确的判断条件.习题详解习题1.11.算法如下:S1 输入a,h 的值;S2 S←21ah.流程图如下(左)图所示.2.算法如下:S1 输入x ;S2 判断是否x<2,若是,则输出“不退票”;否则,进入S3;S3 输出“y=x-(10x+1)×2”.流程图如下(右)图所示.第1题图 第2题图3.令⎩⎨⎧=+=-)2(,734)1(,12y x y x 流程图如下(左)图所示. 4.b a的整数部分用[b a]表示,则流程图如下(右)图所示.第3题图 第4题图5.算法如下:S1 输入a,b,c ;S2 如果a<b 且a<c ,则输出a ,否则,进入S3;S3 如果b<c ,则输出b ,否则,输出c.流程图如下(左)图所示.6.算法如下:S1 输入a,b ;S2 如果a>0,则输出x>-b a ,否则,输出x<-b a.流程图如下(右)图所示.第5题图 第6题图7.算法如下:S1 取序列的第一个数;S2 将所取出的数与18比较;S3 如果相等,则输出该数,结束算法;S4 如果不相等,则取下一个数,再执行第二步.流程图:用S i 代表数列中的第i 个数.第7题图第8题图8.算法分析:判断分别以这3个数为三边长的三角形是否存在,只需要验证这三个数当中任意两个数的和是否大于第三个数.这就需要用到条件结构.算法如下:S1 计算a+b,b+c,a+c;S2 判断a+b >c,b+c >a,c+a >b是否同时成立,如成立,则S △ABC =4/])2/)(([222222b a c a c -+-如不成立,则输出不存在这样的三角形.流程图如图所示:9.算法如下:S1 x←2+21; S2 i←1; S3 x←2+x 1; S4 i←i+1;S5 判断是否i≤n,若是,返回S3,否则,进入S6;S6 输出x.流程图如右图所示.第9题图。
2019-2020年高中数学 第1章 算法初步 1.2 流程图 1.2.3 循环结构教案 苏教版必修3
2019-2020年高中数学第1章算法初步 1.2 流程图 1.2.3 循环结构教案苏教版必修3教材分析在现实生活中,除了用到选择结构进行问题的分支处理外,还会遇到“重复处理”的问题,循环结构(cycle structure)正是可以用来处理需要重复执行的某一组操作.循环结构也称为“重复结构”,即反复执行某一部分的操作.循环结构是程序设计中不可缺少的又富有变化的一种基本结构,是我们学习的第三种程序结构.在某一算法中,如果出现从某处开始,按照一定的条件反复执行同一操作,那么这种结构就称为循环结构,反复执行的处理步骤称为循环体.在循环体中一定有一个选择结构,否则将无法从循环结构中脱离出来,从而形成死循环.此外,循环结构中通常都有一个起到循环计数的变量,这个变量一直都含在执行或终止循环体的条件中.循环结构分为当型循环和直到型循环,它们之间是可以相互转化的.教材考虑到学生的接受能力,对直到型循环和当型循环没有加以定义和区分,仅仅是在《探究·拓展》中以阅读题的形式作了介绍,这样处理是有用意的,教师没有必要在这里提出这两种概念,可待学生有了感性认识和一定的算法基础后,再做适当的回顾与补充.如果某一操作需要重复一定的次数,那么我们可以设置一个统计循环次数的变量,当这个变量的值没有超过我们给定的数值时,就一直重复执行需要的操作,当这个变量的数值超过给定的数值时就脱离循环结构.三维目标通过实例的训练,使学生理解循环结构的意义,并能够用循环结构的流程图表示简单问题的算法,养成良好的逻辑思维习惯,发展有条理的思考与表达能力,达到提升学生逻辑思维能力的目标.重点难点教学重点:用循环结构的流程图表示算法.教学难点:多种结构的嵌套使用.课时安排1课时教学过程导入新课设计思路一:(情境导入)同学们小时候一定都有过缠着父母听故事的经历,有时候爸爸妈妈实在想不出故事了,就会用一个“故事”来哄骗孩子:从前有座山,山里有个庙,庙里有个老和尚.有天老和尚对小和尚说,我给你讲个故事说啊:从前有座山,山里有个庙,庙里有个老和尚.有天老和尚对小和尚说,我给你讲个故事说啊:从前有座山,山里有个庙,庙里有个老和尚.有天老和尚对小和尚说,我给你讲个故事说啊:……现在考虑,为什么说这个“故事”是哄骗小朋友的?因为这个“故事”一直在重复着同样的环节:“从前有座山,山里有个庙,庙里有个老和尚,有天老和尚对小和尚说,我给你讲个故事说啊:……”所以这个“故事”可以无限次循环.我们可以把这个环节写成一个算法,这个算法是一直重复同样的操作,多次循环,直到孩子打断父母的“故事”为止.在现实生活中,还有好多这样的例子,在整个问题的执行过程中,一直循环执行相同的一部分步骤,直到符合或者不符合某个条件时才终止.请同学们举出这样的一些例子.例如:1.同学们从小学开始,每年9月初开学,到学校里上课,一个学期后放寒假,过了寒假再开学,又一个学期后放暑假,然后下一年9月初再开学回到学校上课→寒假→上课→暑假……,直到不再上学为止.2.今天是星期三,过了一天是星期四,过了两天是星期五……过了七天又是星期三,这样周而复始循环出现.3.计算1+2+3+4+ (100)第一步计算1+2;第二步将上一步中的运算结果与第三个数相加;第三步将上一步中的运算结果与第四个数相加;第四步将上一步中的运算结果与第五个数相加;……第i步将上一步中的运算结果与第i-1个数相加;……直到执行完第99步后才得到结果.上述例子都是在运行过程中循环执行相同的步骤,这样的算法结构就是循环结构.(引入新课,板书课题——循环结构)设计思路二:(问题导入)观察下面的流程图(图1),回答这个流程图的功能是什么?其中最主要的操作步骤是什么?图1这个流程图从学号为1的学生开始,输出他的成绩,然后判断学号是否为尾号,如果不是,让学号增加1,继续输出2号学生,再判断学号是否为尾号,如果不是,学号再增加1,输出下一位学生的成绩,直到学号为尾号,即最后一名学生才结束程序,因此这个流程图的功能是输出所有学生的成绩.其中最主要的就是多次重复执行的判断学号、改变学号、输出成绩的过程.要输出所有学生的成绩,应该有很多个输出框,为什么流程图中只有一个输出框?因为每次输出学生的成绩都是一种重复的操作:先确定要输出哪一位学生的成绩,然后再输出.这个过程将重复出现,进行循环操作,直到所有学生全部输出(即学号为尾号)才结束,这样的结构最主要的部分就是有循环形式的结构出现,我们把这样的结构称为循环结构.(引入新课,板书课题——循环结构)推进新课新知探究北京获得了xx年第29届奥林匹克运动会的主办权.你知道在申办奥运会的最后阶段,国际奥委会是如何通过投票决定主办权归属的吗?对遴选出的5个申办城市进行表决的操作程序是:首先进行第一轮投票,如果有一个城市得票超过总票数的一半,那么该城市将获得主办权;如果所有申办城市得票数都不超过总票数的一半,则将得票数最少的城市淘汰,然后重复上述过程,直到选出一个申办城市为止.这个表决过程可以用算法写出,请同学们写出这个算法算法:S1 投票;S2 统计票数,如果有一个城市得票数超过总票数的一半,那么该城市获得主办权,转S3,否则淘汰得票最少的城市,转S1;S3 宣布主办城市.在这个过程中,如果统计票数后任意一个城市得票数都没有超过总票数的一半,那么将重复执行投票→统计票数这一过程,直到有一个城市得票数超过总票数的一半为止.这里出现了一个循环操作的内容,而最终应该循环多少次,在整个表决结果出来以前是无法知道的,也许第一次表决后就结束,也许要表决3次、4次,所以如果用流程图来表示,我们会发现仅仅利用前面学过的顺序结构和选择结构将无法实现,那么将怎样来画出这个问题的流程图呢?根据算法,是否要返回S1,即继续投票,就看是否有一个城市得票数超过总票数的一半,如果没有,将返回S1执行循环,如果有一个城市得票数超过总票数的一半,就立即结束表决,因此我们可以把流程图画成图2的形式:图2像上面的算法中的这种需要重复执行同一种操作的结构称为循环结构.重复执行的那些步骤就称为循环体.如图3,虚线框中的流程结构就是一种常见的循环结构,其功能是先执行框A,然后判断给定的条件P是否成立,若条件P不成立,则再执行框A,执行完框A后继续判断条件P是否成立,如果不成立,再执行框A,再判断条件P……,如此反复执行框A,直到判断条件P时发现成立为止,此时不再执行框A,而是脱离这个循环结构.图3 图4上面的这个循环结构实际上就是最常用的直到型(Until 型)循环.在循环结构中还经常出现当型(While 型)循环,其结构如图4中虚线框内的形式,它的功能是当给定条件P 成立时,先执行框A ,然后判断给定的条件P 是否成立,若条件P 成立,则再执行框A ,执行完框A 后继续判断条件P 是否成立,如果成立,再执行框A ,再判断条件P……,如此反复执行框A ,直到判断条件P 时发现不成立为止,此时不再执行框A ,而是脱离这个循环结构.比较上面的循环结构和上一节课学习的选择结构,它们都有一个判断框,选择结构中从判断框出来的两条分支都不再返回而是直接结束(当然也可以再执行其他步骤),这个判断框只会判断一次,而循环结构中从判断框出来的两条分支一条直接流向结束,另一条会返回上面的某一处继续执行相同的操作,这个判断框会判断多次.因此如果出现判断,就看判断后是不是返回执行相同的操作,如果不再返回,那就是选择结构,如果要返回重复执行某一些操作,那就是循环结构.应用示例思路1例1 用连加的方法写出求的算法和流程图.分析:本题指明了用连加的方法,所以先进行2+2的运算,然后把结果再加2,然后把结果再加2,……然后把结果再加2,这样一共需要进行9次加法运算就可以输出运算结果了.因此我们在流程图中应该有一个统计进行了多少次加法运算的计数器,这个计数器的功能是每进行一次加法运算就“加1”,直到计数器内的统计数据达到9时就结束加法,输出运算结果.解:算法如下:S1 加法计数器I 设置初值0;S2 和存储器S 设置初值2;S3 计算S+2,结果放入和存储器S ;S4 加法计数器I 加1;S5 如果I≥9,则输出S ,否则转S3.这个算法也可以用简洁的符号表示:S1 I←0;S2 S←2;S3 S←S+2;S4 I←I+1;S5 如果I≥9,则输出S ,否则转S3.流程图如图5所示:图5思考1.这个循环结构中的循环体由哪几个步骤组成?由流程图很清晰地看出,重复执行的循环体由处理框“S←S+2”、“I←I+1”和判断框“I≥9”组成.2.本题中,变量I和S分别起什么作用?为什么两个变量的初值一个为0,一个为2?变量I实际上就是一个统计进行了多少次加法运算的计数器.根据流程图,开始时I←0,说明还没有进行运算,经过一次“S←S+2”后,再执行“I←I+1”,这时I=1,说明进行了一次加法运算,然后判断“I≥9”,结果为“N”,判断后返回执行“S←S+2”(注意:现在进行的是第二次加法运算),再下一步就又是执行“I←I+1”,这时I=2,说明进行了二次加法运算,然后继续判断“I≥9”.我们发现这样的规律:进行了多少次加法(S←S+2),I就等于这个次数.而题目一共要进行9次加法运算,所以如果“I≥9”不成立(判断结果为“N”),则继续累加,直到“I≥9”成立(判断结果为“Y”),才脱离循环结构,输出S,结束程序.当然,变量I只可能出现I=9,不可能出现I>9的情况,因为I=9时就跳出循环体,不再继续返回执行“S←S+2”和“I←I+1”了.图6变量S实际上就是一个存储加法运算的结果的存储单元.每次都是把上一次的运算结果加上2以后作为下一次的一个加数,所以我们把这个加法的结果一直存储在存储器S中.3.如果我们把判断框中的条件“I≥9”改为“I=9”是否可以?根据“思考2”的分析,变量I只可能出现I=9,不可能出现I>9的情况,所以这样修改也是可以的.4.如果我们把选择结构改变为如图6的形式,即把判断框中的条件“I≥9”改为“I<9”,再把“Y”和“N”交换是否也符合要求?根据图6,当加法的次数I满足“I<9”(判断结果为“Y”)时,说明加法的次数还不满9次,所以再返回执行加法运算“S←S+2”,再执行“I←I+1”(计数器增加1),然后继续判断“I<9”是否成立,直到判断结果为“N”(加法次数“不是小于9次”),说明已经加了9次了,这时脱离循环体,输出S,结束程序,所以这样的修改也是可以的.但是一般情况下,在这种循环结构中,我们总是习惯于“满足条件就脱离循环结构,否则返回继续执行”这种格式,这样统一以后便于他人阅读、理解和修改,也便于计算机专业人员把流程图翻译成计算机语言编成计算机程序.点评:特意设置一个难度较低的题目,是为了让学生容易着手,便于理解和掌握这种新型的程序结构.因此写出算法和流程图不难,老师不要急于做下一个例题,要把“思考”中的内容详细讲解,重点讲清变量I和S的意义,直到学生弄清楚循环结构的原理为止例2 写出求1+2+3+4+5值的一个算法,并画出流程图.分析:本题前面课时已讲过,一共也只有4次加法运算,所以可以直接连加五个数.但是这个方法只能适用于运算次数比较少的形式,对连加次数较多时就显得比较烦琐.当然本题也可以使用等差数列求和公式,直接求前五项的和,这样可以求任意多次连加运算,但是对于没有学习过这个公式的人就不适用了.其实本题实质是连加,每次都是把上一次加法的结果再继续加上下一个数,直到这个加数是5为止.但是与例1相比,这个加数不断在变化,而加法的次数是固定的5次,所以我们可以在判断框中设置条件“I>5”(I就是这个不断变化的加数),当条件成立时就脱离循环体,输出和“S”,否则还将继续进行加法运算.解:算法如下:S1 S←0;S2 I←1;S3 S←S+I;S4 I←I+1;S5 如果I>5,则输出S,否则转S3.流程图如图7所示:图7点评:循环结构的判断框中的条件可以直接是循环的次数,也可以是脱离循环体的条件,应根据不同的情况选择不同的条件.例3 写出求1×2×3×4×5的值的一个算法,并画出流程图.分析:这个变式和例2相比,仅仅是把连加换成连乘,其他没有改变,所以判断框中的条件应该不变,“和存储器”S应该变成“积存储器”T,同时存储器的初值不能是0了,否则每次相乘后的积永远只能是0.同学们思考,这个“积存储器”T的初值应该是多少?应该是1!原理和初值S←0类似.解:算法如下:S1 T←1;S2 I←1;S3 T←T×I;S4 I←I+1;S5 如果I>5,则输出T,否则转S3.流程图如图8所示:图8变式训练1.写出求1×3×5×7×9×11值的一个算法,并画出流程图.分析:与例题相比,最主要的变化是循环变量I增加的幅度(以后称为步长)由1变为2,另外乘积式中因式的个数也由5个变成了6个,所以脱离循环体的条件也应该发生相应的变化,因此算法和流程图中改变的应该就是这两个地方解:算法如下:S1 T←1;S2 I←1;S3 T←T×I;S4 I←I+2;S5 如果I>11,则输出T,否则转S3.流程图如图9所示:图92.对于输入的不同的正整数n,写出求1×2×4×8×…×2n值的一个算法,并画出流程图.分析:本题中最主要的变化是乘积式中因式的个数由输入的正整数n确定,且每次参与乘积的数都是上一次乘数的2倍,因此算法和流程图中改变的主要就是这两个地方.算法如下:S1 输入n;S2 T←1;S3 I←1;S4 T←T×I;I←I×2;S6 如果I>2n,则输出T,否则转S4.流程图如图10所示:图10点评:从以上例题和变式可以看出,循环结构中必须嵌套一个选择结构,即有一个判断框,这个判断框的用途是用来控制什么时候脱离循环体的.如果没有判断框,或者判断框中的条件永远不可能成立,那么这样的循环就只能永远循环下去,从而形成“死循环”,所以在编写循环结构的算法的时候,要注意不能形成“死循环”.例4 设计计算10个数的平均数的一个算法,并画出流程图.分析:我们用一个循环依次输入10个数,再用一个变量存放数的累加和,在求出10个数的累加和后,除以10,就得到10个数的平均数.解:算法如下:S1 S←0;{使S=0}S2 I←1;{使I=1}S3 如果I≤10,那么转S4,否则转S7;{当I≤10时循环}S4 输入G;{输入一个数}S5 S←S+G;{求S+G,其和仍存放在S中}S6 I←I+1,转S3;{使I的值增加1,并转到S3}S7 A←S/10;{将平均数S/10存放在A中}S8 输出A.{输出平均数}流程图如图11所示:图11点评:如果流程图太长,我们可以把它分割成几块,每块根据连接点可以重新连接(如图11可以分割成图12的形式).图12图13思路2例1 运行图13的流程图后,输出的值是________________.分析:变量I和T的初值为I=0和T=10,然后开始执行循环体.先判断T<22是否成立,如果成立,就让变量I增加1,累加存储器T加4,继续循环,再判断条件T<22是否成立,当条件T<22不成立才脱离循环结构,输出当时计数器I中的值,否则一直进行循环.实际上这个流程图就是统计10加上多少个4才能使得和不大于22的最大次数,容易知道,使10+4n≤22的最大的正整数n为3,所以输出的值为3.答案:3变式训练流程图13表示了一个什么算法?试把“当条件不成立时脱离循环体,并且先判断,再执行”改成“直到条件成立时才脱离循环体,并且先执行,再判断”的形式.分析:变量I和T的初值为I=0和T=10,然后开始执行循环体.先让变量I增加1,累加存储器T加4,然后判断T≥22是否成立,如果不成立,就继续循环,再让变量I增加1,累加存储器T加4,然后判断T≥22是否成立,直到条件T≥22成立才脱离循环结构,输出当时计数器I中的值,否则一直进行循环.解:这个流程图表示的是求使10+4n≤22的最大的正整数n的一个算法.改成“直到条件成立时才脱离循环体,并且先执行,再判断”的形式的算法流程图如图14所示.图14点评:实际上,图13是一个当型循环,图14是直到型循环,这两种循环是有区别的.直到型循环是“直到条件成立时才脱离循环体”,并且是先执行,再判断;当型循环是“当条件不成立时脱离循环体”,并且是先判断,再执行.它们的这个区别目前先不必和学生讲清,通过本题可以让学生先有一个感性认识,知道两种循环可以相互转化,它们的实质性区别可以等学生有了一定的算法基础后,再做适当的回顾与补充.例2 写出求100991...651431211⨯++⨯+⨯+⨯的一个算法,并画出流程图 分析:本例属连加问题,只是每次的加数复杂一些,因此和存储器S 置初值0,循环变量I 与加数的关系为,每次循环时增长的步长为2,直到满足条件I>99时脱离循环体,输出结果,结束程序.解:算法如下:S1 S←0;S2 I←1;S3 S←S+;S4 I←I+2;S5 如果I>99,则输出S ,否则转S3.流程图如图15所示:图15点评:本题继续巩固和深化循环结构的概念及算法,通过改变步长和加数的复杂化,达到灵活应用的目的.知能训练一、课本本节练习1、2.二、补充练习1.写出计算12+22+32+…+1002的算法的流程图.2.一个两位数,个位数字与十位数字之和为9,写出一个把所有这样的两位数都输出的算法,并画出流程图.解答:一、课本练习1.算法如下:S1 S←0;S2 I←2;S3 S←S+I;S4 I←I+2;S5 如果I>100,则输出S,否则转S3.流程图如图16所示:图162.本题表示的算法是将学号从1号到50号中成绩达到或超过80分的学生的学号和成绩找出来.二、补充练习1.流程图如图17所示.图172.算法如下:S1 a←0;S2 a←a+1;S3 b←9-a;S4 m←10a+b;S5 输出m;S6 如果a>9,则结束程序,否则转S2.流程图如图18所示.图18点评:对于循环结构,要弄清楚循环体是什么,即哪些步骤执行循环操作,另外何时执行循环,何时脱离循环.掌握了上面两个问题,就不难写出算法及流程图.同时算法及流程图还要符合规范.课堂小结在某一算法中,如果出现从某处开始,按照一定的条件反复执行同一操作,那么这种结构就称为循环结构,反复执行的处理步骤称为循环体.在循环体中一定有一个选择结构,否则将无法从循环结构中脱离出来,从而形成死循环.此外,循环结构中通常都有一个起到循环计数的变量,这个变量一直都含在执行或终止循环体的条件中.循环结构的关键在于搞清楚循环体是什么,何时执行循环,脱离循环体的条件是什么.作业课本习题1.1 6、7、8、9.设计感想循环结构是三种算法结构中最复杂的一种,如果在一开始学习时不搞清楚,那么学生就很容易陷入循环中无法解脱出来,把自己给绕进去.所以这节课的关键是讲清概念,弄明白循环结构中各步骤之间的关系,尤其是明确循环体由哪些步骤组成,判断是继续执行循环还是脱离循环的条件是什么.所以在讲解应用示例设计思路1的例1时,速度不宜快,应该把循环变量I和累加器S的作用讲清讲透,因此我们在设计这个课题的时候有意比教材降低了起点,设置了一个更加简单的问题,并且还增加了一些思考的问题,这些问题教师不要轻易放过,一定要让所有的学生都明白了循环变量I和累加器S的作用后才可以继续进行下面的教学.还有变式的设置也都是为了让学生理解循环结构中两个变量的作用.在例题和课堂练习中,可以让学生先写出算法,再用流程图表示出来.如果学生对脱离循环的条件不甚明白,老师可以把流程图实际操作一遍,用表格的形式列出各个变量(尤其是循环变量)的数值变化过程,便于学生找出判断框中的条件.对于溢出循环体的条件,有时候学生会比正确结果相差1,这个问题是由于学生对溢出的边界有些模糊导致的,教师可以引导学生观察循环变量的值和运算(或执行)的次数以及题目要求运算的总次数的关系,从中得到正确的判断条件.习题详解习题1.11.算法如下:S1 输入a,h的值;S2 S←ah.流程图如下(左)图所示.2.算法如下:S1 输入x;S2 判断是否x<2,若是,则输出“不退票”;否则,进入S3;S3 输出“y=x-(+1)×2”.流程图如下(右)图所示.第1题图第2题图3.令流程图如下(左)图所示.4.的整数部分用[]表示,则流程图如下(右)图所示.第3题图第4题图5.算法如下:S1 输入a,b,c;S2 如果a<b且a<c,则输出a,否则,进入S3;S3 如果b<c,则输出b,否则,输出c.流程图如下(左)图所示.6.算法如下:S1 输入a,b;S2 如果a>0,则输出x>-,否则,输出x<-.流程图如下(右)图所示.第5题图第6题图7.算法如下:S1 取序列的第一个数;S2 将所取出的数与18比较;S3 如果相等,则输出该数,结束算法;S4 如果不相等,则取下一个数,再执行第二步.流程图:用S i代表数列中的第i个数.第7题图第8题图8.算法分析:判断分别以这3个数为三边长的三角形是否存在,只需要验证这三个数当中任意两个数的和是否大于第三个数.这就需要用到条件结构.算法如下:S1 计算a+b,b+c,a+c;S2 判断a+b >c,b+c >a,c+a >b是否同时成立,如成立,则S △ABC =4/])2/)(([222222b a c a c -+-如不成立,则输出不存在这样的三角形.流程图如图所示:9.算法如下:S1 x←2+;S2 i←1;S3 x←2+;S4 i←i+1;S5 判断是否i≤n,若是,返回S3,否则,进入S6; S6 输出x.流程图如右图所示.第9题图。
苏教版高中数学必修三-第一章-算法初步1.2.1ppt课件
SJ ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修3
易 错 易 误 辨 析 当 堂 双 基 达 标
课 时 作 业
课 堂 互 动 探 究
菜 单
教 师 备 课 资 源
SJ ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修3
易 错 易 误 辨 析 当 堂 双 基 达 标
SJ ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修3
易 错 易 误 辨 析 当 堂 双 基 达 标
§ 1.2
流程图
1.2.1 顺序结构
教师用书独具演示
●三维目标 1.知识与技能:掌握顺序结构的特点,设计方法. 2.过程与方法:学会用算法分析问题;能够使用顺序结
课 时 作 业
课 时 作 业
课 堂 互 动 探 究
教 师 备 课 资 源
菜
单
SJ ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
必修3
易 错 易 误 辨 析 当 堂 双 基 达 标
在老师的引导下,充分发挥学生的主观能动性,从问题 入手,通过分析问题、交流方案、解决问题、运用问题的探 索过程,让学生全程参与到问题的探索中而突破难点. 通过学生对常见的图框及功能的理解和认识,结合典型 例题及变式训练,使学生初步掌握顺序结构的流程图的设计 而强化了重点.
必修3
易 错 易 误 辨 析 当 堂 双 基 达 标
课 时 作 业
课 堂 互 动 探 究
菜 单
教 师 备 课 资 源
SJ ·数学
教 学 教 法 分 析 教 学 方 案 设 计 课 前 自 主 导 学
高中数学第1章算法初步1.2流程图1.2.2选择结构教案苏教版必修3
1.2.2 选择结构 整体设计 教材分析 在一个算法中经常会遇到对一个条件进行判断,如果条件成立则执行某个操作,如果条件不成立则执行另一个操作.因此在算法的流程图中,根据条件是否成立有着不同的流向.像这种根据条件作出判断,再决定执行哪一种操作的结构称为选择结构(selection structure)(或称“分支结构”). 一个选择结构都包含一个判断框,当条件成立时执行标有“Y”或者“是”的分支,当条件不成立时执行标有“N”或者“否”的分支. 图1的虚线框内就是常见的几种选择结构,在(1)中,当条件“n>3”成立时执行A,否则执行B;在(2)中,当条件“n>3”成立时执行A,否则直接脱离选择结构;在(3)中,当条件“n>3”成立时直接脱离选择结构,否则执行B.
图1 对于选择结构要注意以下几点: (1)在选择结构中不论条件是否成立,只能执行A框或者B框之一,不能既执行A框,又执行B框,即“Y”和“N”两者之中只能选择一个,不能两者都选择; (2)在选择结构中不论条件是否成立,必须执行A框或者B框之一,不能既不执行A框,又不执行B框,即“Y”和“N”两者之中必须选择一个,不能两者都不选择; (3)A框和B框中可以有一个是空的,即可以不执行任何操作直接脱离选择结构,但是不能两个框都是空的; (4)无论走哪条路径,执行完A或者B之后都经过P,然后才脱离选择结构; (5)选择结构可以是嵌套的,即在选择结构之中还可以出现选择结构,这种结构主要是出现在有多个条件判断的算法中; (6)选择结构可以和其他结构嵌套,形成比较复杂的结构; (7)A框或者B框可以不止一个操作,A框本身就可以是一个独立的算法结构. 三维目标 1.通过实例的训练,使学生理解选择结构的意义. 2.能用流程图表示选择结构以及能用选择结构的流程图表示简单问题的算法,养成良好的逻辑思维习惯,发展有条理的思考与表达能力,达到提升学生逻辑思维能力的目标. 重点难点教学重点: 用选择结构的流程图表示算法. 教学难点:多个选择结构的嵌套. 课时安排 1课时 教学过程 导入新课 设计思路一:(情境导入) 如果坐火车从上海到南京,可以坐普通特快列车,费时3小时左右,最低票价为硬座52元;也可以坐新型的动车组列车,费时2小时左右,最低票价为二等座93元.如果你有急事要从上海赶往南京,打算坐什么车?如果你周末到南京度假,晚上出发,到了南京后就可以休息了,那从经济角度出发,打算坐什么车?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.2.1 顺序结构 整体设计 教材分析
图1 顺序结构是一种最简单、最常用、最重要的程序结构,它不存在条件判断、控制转移和重复执行的操作.顺序结构指的是依次进行多个处理的结构,它是由若干个依次执行的处理步骤组成的,是任何一个算法都离不开的最基本、最简单的结构,因此也是最重要的程序结构,其特点是各个部分按照出现的先后顺序执行. 一个顺序结构可以由一个或多个语句块组成,且仅有一个入口和一个出口.最简单的一种顺序结构是每一个语句块中只含有一条不产生控制转移的执行语句.每个语句块本身也可以是一个顺序结构,因此一个顺序结构可以由许多顺序执行的语句组成. 在顺序结构程序中,各语句是按照位置的先后次序,顺序执行的,且每个语句都会被执行到.在日常生活中有很多这样的例子.例如在淘米煮饭的时候,总是先淘米,然后才煮饭,不可能是先煮饭后淘米.所以在编写顺序结构的应用程序的时候,也存在着明显的先后次序,应注意这种先后顺序关系.当然,为了让计算机处理各种数据,首先就应该把源数据输入到计算机中;计算机处理结束后,再将目标数据以人能够识别的方式输出. 对于顺序结构,学生容易理解,教学时让学生自己举一些只包含顺序结构算法的实例. 三维目标 通过实际生活中的实例和典型的顺序结构案例,使学生理解顺序结构的意义,并能够用流程图表示顺序结构以及能用顺序结构的流程图表示简单问题的算法,养成良好的逻辑思维习惯,达到提升学生逻辑思维能力的目标. 重点难点 教学重点:用顺序结构的流程图表示简单问题的算法. 教学难点:用流程图表示算法. 课时安排 1课时 教学过程 导入新课 设计思路一:(情境导入) 有一个笑话,是赵本山和宋丹丹的小品中演的,宋丹丹问:“要把大象装冰箱,总共分几步?”赵本山答不上来,宋丹丹给出答案:“三步!第一步,把冰箱门打开;第二步,把大象装进去;第三步,把冰箱门带上.” 尽管这是一个笑话,但是宋丹丹的答案中把大象放进冰箱分了明确的三步:第一步,把冰箱门打开;第二步,把大象装进去;第三步,把冰箱门带上.这三步缺一不可,每步都必须执行,且先后顺序不可调换. 我们不知道宋丹丹是不是学习过算法,但是她的回答恰恰体现了算法中最基本、最简单的一种结构,即顺序结构的思想. (引入新课,板书课题——顺序结构) 设计思路二:(问题导入) 我们做任何一件事,都要按照一定的顺序来按部就班地做.例如做饭就是这样,我们必须先淘米,再把米和水按一定比例一起放在电饭锅里,再插上电源打开开关,这三个步骤缺一不可,每步都必须执行,且顺序不能调换. 解决数学问题更是如此,例如我们要确定已知线段AB的三等分点,那么应该怎样来完成呢? S1 过线段AB的一个端点(不妨设A)作射线AP; S2 在AP上依次截取AC=CD=DE; S3 连结BE; S4 分别过C、D作BE的平行线,交AB于点M、N,则M、N就是线段AB的三等分点. 上述四个步骤也是缺一不可,每步都必须执行,且顺序不能调换. 像这样的按一定先后顺序依次执行的一种结构,就是算法中最基本、最简单的一种结构,即顺序结构. (引入新课,板书课题——顺序结构) 推进新课 新知探究 有红和蓝两个墨水瓶,但现在却把红墨水错装在了蓝墨水瓶中,蓝墨水错装在了红墨水瓶中,要求将其互换,应该怎么解决这个问题? 由于两个墨水瓶中的墨水不能直接交换,所以应该通过引进第三个空墨水瓶的办法进行交换.其算法如下: S1 取一只空墨水瓶(设其为白色),将红墨水瓶中的蓝墨水装入白墨水瓶中; S2 将蓝墨水瓶中的红墨水装入红墨水瓶中; S3 将白墨水瓶中的蓝墨水装入蓝墨水瓶中. 在计算机程序中,与这个例子类似,每个变量都有自己的存放空间,即每个变量都有自己的存储单元,每个存储单元都有各自的“门牌号码”(地址),要交换两个变量的值,需要借助一个新的存储单元来完成.例如若x、y的初值为x=1、y=2,现在要交换两个变量x、y的值,使得x=2、y=1,那么我们应该进行如下的操作: S1 p←x; S2 x←y; S3 y←p. S1的意思是先将x的值赋给变量p,这时存储变量x的单元可以做他用,但是这时x的值并没有发生改变,仍然等于1,当然p的值为1; S2的意思是再将y的值赋给变量x,这时存储变量y的单元可以做他用,但是这时y的值并没有发生改变,仍然等于2,而原来变量单元x中的值已经发生变化,不再是1,而变成了y的值2; S3的意思是最后将p的值赋给变量y,这时y的值发生改变,不再是原来的2,而等于p的值1,而变量单元x没有涉及,其中的值没有发生变化,仍然是2,p的值也还是1. 经过上面S1、S2、S3三个步骤,我们发现两个变量x、y的值进行了交换,变成了x=2、y=1. 这个算法可以用如图2所示的流程图来清晰地表示: 图2 图3 在图2的流程图中,虚线框内三个处理框中的步骤依次执行,像这种依次进行多个处理的结构称为顺序结构(sequence structure).顺序结构就是如图3的虚线框内的结构,其中A、B两个框是依次执行的.顺序结构是一种最简单、最基本的结构. 应用示例 思路1 例1 半径为r的圆的面积计算公式为 S=πr2 当r=10时,写出计算圆面积的算法,画出流程图. 分析:本题只需要计算当半径r=10时的圆面积,所以直接取r=10代入圆的面积计算公式S=πr2即可. 解:算法如下: S1 r←10;{把10赋给变量r} S2 S←πr2;{用公式S=πr2计算圆的面积} S3 输出S.{输出圆的面积} 上述算法的流程图可以表示成图4.
图4 图5 点评:已知半径求圆的面积,只需要直接代入公式就行了.由于本题只计算半径r=10时的圆面积,所以直接把10赋给变量r即可.如果是求一组或几个半径不同的圆的面积,可以用输入语句代替赋值语句“r←10”,流程图如图5所示. 输入语句和赋值语句是两种不同的语句,它们是有区别的.输入语句在每次执行的时候要先输入变量的值,然后才执行下一个语句,每次执行都可以输入不同的变量值,而不需要重新修改计算机程序;赋值语句不需要先输入变量的值,运行时直接就可以往下执行了,每一次执行的时候都只能对当前所赋给的值进行运算,变量的值不能修改,要计算新的数据就必须修改计算机程序.所以输入语句适用于计算几个或一组变量,运行程序后不能自动执行,要等待用户输入变量的值;赋值语句只适用于计算固定的一个数值,运行程序后会自动执行直到输出结果.有条件的学校可以在计算机上执行这两种不同的语句,让学生在实践中对比它们的区别. 例2 写出作△ABC的外接圆的一个算法. 分析:作圆其实就是确定圆心位置和半径大小,△ABC的外接圆的圆心就是△ABC中两条边的垂直平分线的交点,半径就是这个圆心到任意一个顶点的距离.因此要作△ABC的外接圆,只需要依次作两条边AB和BC的垂直平分线,得到交点,即外接圆的圆心M,然后再以M为圆心,MA为半径作圆即可.
图6 解: 算法如下: S1 作AB的垂直平分线l1; S2 作BC的垂直平分线l2; S3 以l1与l2的交点M为圆心,以MA为半径作圆,圆M即为△ABC的外接圆. 流程图如图6. 点评:以上过程通过依次执行S1到S3这三个步骤,完成了作外接圆这一问题,这种依次进行多个处理的结构就是顺序结构. 例3 已知一个三角形的三边长分别为2,3,4.利用海伦—秦九韶公式设计一个算法,求出它的面积,画出算法的流程图. 分析:如果一个三角形的三边为a,b,c,根据海伦—秦九韶公式可以直接计算这个三
角形的面积.令p=2cba,则三角形面积为S=))()((cpbpapp.因此这是一个简单的问题,只需先由a=2、b=3、c=4算出p的值,再将它代入公式,最后输出结果S,用顺序结构就能够表达算法. 解:流程图如图7:
图7 点评:本题只需要先求出p,然后再求S,依次代入公式即可,用顺序结构容易完成. 例4 已知一个数的13%为a,写出求这个数的算法,并画出程序框图. 分析:设这个数为b,则b×13%=a,得到b=a÷10013.算法就按照这个计算方法,先输入a,再计算b.
图8 解:算法如下: S1 输入a;
S2 计算b=a÷10013; S3 输出b. 程序框图如图8所示: 点评:设计算法时,一般先用自然语言表述,再根据自然语言所描述的算法画程序框图.在逐步熟练后也可以直接画程序框图.对于较复杂的问题,我们建议还是先用自然语言表述算法过程,后画出程序框图. 思路2 例1 画出用现代汉语词典查阅“仕”字的程序框图. 分析:利用现代汉语词典查字有多种方法,如部首查字法、拼音查字法等,现以部首查字法为例加以说明.先在“部首目录”中查“二画”中“亻”的页码(x),再从x页开始的“亻”部中的“三画”中查找“仕”的页码(y),然后翻到y页,查阅“仕”. 解:流程图如图9所示:
图9 点评:查阅词典的过程是一个按部就班的固定流程,所以可以用顺序结构的流程图来清晰地显示操作流程.
例2 已知函数f(x)=xx1,实数a1=f(1),an+1=f(an)(n∈N*),试写出一个求a4的算法,并画出程序框图. 分析:由f(x)= xx1及a1=f(1),可得到a1=111=21,再由递推公式
