作业题参考答案(1)
数控编程技术作业综合题目及答案(1)
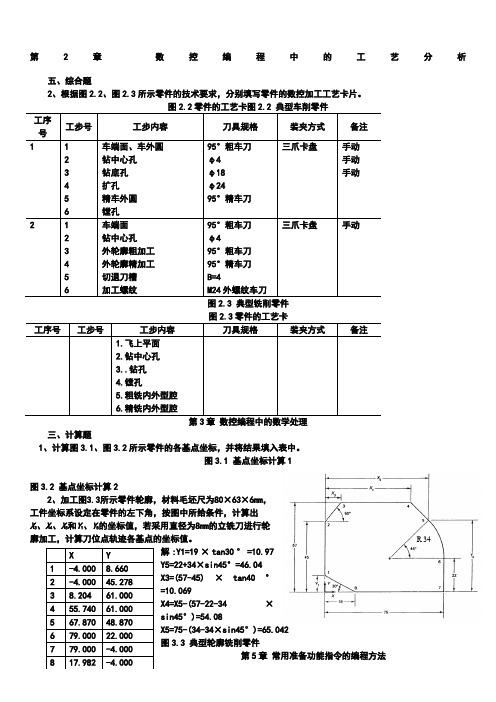
第2章数控编程中的工艺分析五、综合题2、根据图2.2、图2.3所示零件的技术要求,分别填写零件的数控加工工艺卡片。
图2.3 典型铣削零件第3章数控编程中的数学处理三、计算题1、计算图3.1、图3.2所示零件的各基点坐标,并将结果填入表中。
图3.1 基点坐标计算1图3.2 基点坐标计算22、加工图3.3所示零件轮廓,材料毛坯尺为80×63×6mm,工件坐标系设定在零件的左下角,按图中所给条件,计算出X3、X4、X5和Y1、Y5的坐标值,若采用直径为8mm的立铣刀进行轮廓加工,计算刀位点轨迹各基点的坐标值。
R 34解:Y1=19×tan30°=10.97X3=(57-45)×tan40°=10.069X4=X5-(57-22-34×sin45°)=54.08X5=75-(34-34×sin45°)=65.042图3.3 典型轮廓铣削零件第5章常用准备功能指令的编程方法SS五、编程题1、根据图5.1所示零件的轮廓尺寸,分别在G90、G91方式,用G00、G01指令按刀具轨迹(虚线为快速移动轨迹)写出加工程序,并填入程序单中。
2、仔细阅读下列程序,根据程序单,在图5.2的坐标网格中画出刀具运行的轨迹和零件轮廓。
图5.2 坐标网格3、根据图5.3所示零件的轮廓尺寸,在G90方式,用G00、G01、G02/G03指令按刀具轨迹(虚线为快速移动轨迹)写出加工程序,并填入程序单中。
若用91方式编程,程序需做那些改动。
图5.3 试题3的零件轮廓4指令写出刀具运行轨迹的NC 程序,填入程序清单。
图5.4 题4的零件轮廓第6章 刀具补偿指令及其编程方法五、编程题1、刀具起点在(-40,0),法向切入(-20,0)点,切一个40 mm 的整圆工件,并法向切出返回点(-40,0),刀具轨迹如图1所示。
利用刀具半径补偿指令,编写零件的轮廓加工程序。
高等数学第一章课后习题答案(带解析)

第一章函数与极限第一节映射与函数一、填空题1.函数ln(2)y x =+的定义域为[1,)(2,1]+∞-- .2.设函数2(1)f x x x +=+,则=)(x f x x -2.3.设函数()f x 的定义域为[0,1],则(e )xf 的定义域为(,0]-∞.4.已知()sin f x x =,[]2()1f x x ϕ=-,则()x ϕ=2arcsin(1)x -,其定义域为5.设2,0,()e ,0,x x x f x x ⎧-≥=⎨<⎩()ln x x ϕ=,则复合函数[]()f x ϕ=2ln ,1,01x x x x ⎧-≥⎨<<⎩.6.设函数1,1,()0,1,x f x x ⎧≤⎪=⎨>⎪⎩则[]()f f x =1.7.函数(10)y x =-≤<二、单项选择题1.函数lnarcsin 23x xy x =+-的定义域为C .A.(,3)(3,2)-∞-- B.(0,3)C.[3,0)(2,3]- D.(,)-∞+∞2.设(1)f x -的定义域为[0,](0)a a >,则()f x 的定义域为B.A.[1,1]a +B.[1,1]a -- C.[1,1]a a -+ D.[1,1]a a -+3.函数11x y x -=+的反函数是D .A.11x y x -=+ B.11xy x-=+ C.11x y x +=- D.11x y x+=-4.设()f x 为奇函数,()x ϕ为偶函数,且[()]f x ϕ有意义,则[()]f x ϕ为B.A.奇函数B.偶函数C.非奇非偶函数D.以上均不正确三、解答题1.判断函数(ln y x =+的奇偶性,并求其反函数.解:因为()ln(ln(()f x x x f x -=-==-=-,所以()f x 是奇函数.由e yx =,e yx --=,得e e 2y y x --=,所以反函数为e e 2x xy --=2.设)(x f 满足c b a xcx bf x af ,,()1()(=-+均为常数,且)b a ≠,求)(x f .解:x cx bf x af =-+)1()()1(令t x =-1,则t x -=1,故t c t bf t af -=+-1)()1(.xcx bf x af -=+-∴1)()1(.(2)联立(1),(2)得到1(1)(22xbcx ac b a x f ---=.四、证明2()1xf x x =+在其定义域内有界.证明:,x R ∀∈取12M =,使得21()122x x f x M x x =≤==+,所以()f x 在其定义域R 内有界.第二节数列的极限一、单项选择题1.数列极限lim n n y A →∞=的几何意义是D .A.在点A 的某一邻域内部含有{}n y 中的无穷多个点B.在点A 的某一邻域外部含有{}n y 中的无穷多个点C.在点A 的任何一个邻域外部含有{}n y 中的无穷多个点D.在点A 的任何一个邻域外部至多含有{}n y 中的有限多个点nn n 632-∞→A.65-B.31 C.35 D.13.数列有界是数列收敛的C条件.A.充分B.充要C.必要D.两者没有关系二、利用数列极限的定义证明:1cos lim0n nn→∞+=.证明:对0ε∀>,要使1cos 1cos 20n n n n nε++-=≤<,只需2n ε>.0ε∀>,取2N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,就有1cos 0n n ε+-<成立,所以1cos lim0n nn→∞+=.第三节函数的极限一、单项选择题1.=+→x x x 1lim2A.A.32 B.1C.21 D.2.若函数()f x 在某点0x 极限存在,则C.A.()f x 在点0x 的函数值必存在且等于该点极限值B.()f x 在点0x 的函数值必存在,但不一定等于该点极限值C.()f x 在点0x 的函数值可以不存在D.若()f x 在点0x 的函数值存在,必等于该点极限值∞→32x x A.1B.21 C.0D.不存在4.极限0limx x x→=D .A.1B.1- C.0D.不存在二、利用函数极限的定义证明:236lim 53x x x x →--=-.证明:0ε∀>,要使26533x x x x ε---=-<-,只需取δε=,则当03x δ<-<时,就有26533x x x x ε---=-<-成立,所以236lim 53x x x x →--=-.第四节无穷小与无穷大一、单项选择题1.下列命题正确的是C.A.无穷小量的倒数是无穷大量B.无穷小量是绝对值很小很小的数C.无穷小量是以零为极限的变量D.无界变量一定是无穷大量2.下列变量在给定的变化过程中为无穷小量的是C.A.1sin(0)x x→ B.1e (0)xx →C.2ln(1)(0)x x +→ D.21(1)1x x x -→-3.下列命题正确的是D.A.两个无穷小的商仍然是无穷小B.两个无穷大的商仍然是无穷大C.112--x x 是1→x 时的无穷小D.1-x 是1→x 时的无穷小4.(附加题)设数列{}n x 与{}n y 满足lim 0n n n x y →∞=,则下列命题正确的是B.A.若{}n x 发散,则{}n y 发散B.若1n x ⎧⎫⎨⎩⎭为无穷小,则{}n y 必为无穷小C.若{}n x 无界,则{}n y 必有界 D.若{}n x 有界,则{}n y 必为无穷小提示:已知n n x y 为无穷小,当1n x 为无穷小时,必有1()n n n ny x y x =⋅为无穷小;否A,例n x n =发散,21n y n=收敛;否C,例1(1),1(1)n n n n x n y n ⎡⎤⎡⎤=+-⋅=--⋅⎣⎦⎣⎦均无界;否D,例21n x n=有界,n y n =非无穷小.第五节极限运算法则一、填空题1.21lim2x x x x →+=++12. 2.121lim1x x x →+=-∞.3.22121lim1x x x x →-+=-0.4.212lim3n n n →∞+++=+ 12.5.若232lim43x x x kx →-+=-,则常数k =3-.提示:由已知,得23lim(2)0x x x k →-+=,3k ∴=-.6.设213lim 112x a x x x →⎛⎫-=⎪--⎝⎭,则常数a =2.提示:由已知,222113lim ,lim()012x x a x x a x x x →→--=∴--=-,从而2a =.7.e 1lim e 1n nn →∞-=+1.提示:11e 1e lim lim 11e 11en n n n n n→∞→∞--==++8.=-+++∞→)2324(lim 2x x x x 21.9.11021lim 21xx x-→-=+-1,1121lim 21xx x+→-=+1,所以11021lim21xx x →-+不存在.提示:11lim 20,lim 2x xx x -+→→==+∞10.已知21sin ,0()1,0x x x f x x x ⎧<⎪⎪=>⎪⎩,则0lim ()x f x →=0.二、计算题1.220()lim h x h x h→+-解:1.2222220000()22limlim lim lim(2)2h h h h x h x x xh h x xh h x h x h h h →→→→+-++-+===+=.2.231lim (2sin )x x x x x→∞-++解:因为2332111lim lim 011x x x x x x x x→∞→∞--==++,而2sin x +为有界函数,所以根据无穷小量与有界函数的乘积仍为无穷小量,知231lim (2sin )0x x x x x→∞-+=+.3.322232lim 6x x x x x x →-++--解:32222232(1)(2)(1)2lim lim lim 6(3)(2)35x x x x x x x x x x x x x x x x →-→-→-+++++===----+-.4.21lim1x x →-解:211lim1x x x →→=-1x →=14x →=.5.lim x →+∞解:lim x →+∞=limxlimlimx x ==1=-.6.求)1111(lim 31xx x ---→.解:原式32112lim x x x x --+=→)1)(1()2)(1(lim21x x x x x x ++-+-=→112lim21-=+++-=→x x x x .第六节极限存在准则两个重要极限一、填空题1.0sin lim x x x →=1;sin lim x xx→∞=0.提示:0sin lim1x x x →=;sin 1lim lim sin 0x x x x x x →∞→∞=⋅=.2.0sin limsin x x x x x →-=+0;sin lim sin x x xx x→∞-=+1.提示:00sin 1sin lim lim 0sin sin 1x x x x x x x x x x →→--==++;11sin sin lim lim 11sin 1sin x x xx x x x x xx→∞→∞-⋅-==++⋅.3.1lim 1kxx x →∞⎛⎫-= ⎪⎝⎭e k-(k 为正整数).提示:.()11lim 1lim 1e kxx k k x x x x ---→∞→∞⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭.4.10lim 12xx x →⎛⎫-= ⎪⎝⎭12e-.提示:11221200lim 1lim 1e22xxx x x x ---→→⎡⎤⎛⎫⎛⎫⎢⎥-=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦.二、计算题1.30tan sin limx x xx →-解:3200tan sin sin 1cos lim lim cos x x x x x x x x x x →→--=⋅2220002sin sinsin 1122lim lim lim 222x x x x x x x x x →→→⎛⎫ ⎪=⋅== ⎪ ⎪⎝⎭. 2.011limsin x x→解:000011limlim lim lim sin sin sin 2x x x x x x x x x →→→→-=⋅.3.0x →解:原式2220002sin 1sin cos 1cos 2lim 6lim 6lim 311cos sin 32x x x x x x x x x x x x x →→→---====-⋅.4.lim n →∞⎛⎫+解:<++<,又1,1n n n n ====,所以根据夹逼准则知,lim 1n →∞⎛⎫+++=⎪⎭.第七节无穷小的比较一、填空题1.当0x →时,sin 3x 是2x 的低阶无穷小;2sin x x +是x 的等价(或同阶)无穷小;1cos sin x x -+是2x 的低阶无穷小;cos 1x -是2arcsin x 的同阶无穷小;1(1)1nx +-是x n的等价(或同阶)无穷小;32x x -是22x x -的高阶无穷小.提示:222000sin 32sin 1cos sin lim,lim 2,lim,x x x xx x x xx xx →→→+-+=∞==∞13222000cos 11(1)1lim ,lim 1,lim 0arcsin 22nx x x x x x x x x x x n→→→-+--=-==-.2.已知0x →时,()12311ax+-与cos 1x -为等价无穷小,则常数a =32-.提示:12230021(1)1233lim lim 1,1cos 1322x x axax a a x x →→+-==-==---.二、计算题1.21tan 1limx x x →-解:2000tan 1tan 1122lim lim lim 2x x x x xx x x x →→→--===--.2.2220(sec 1)lim3sin x x x x →-解:22222222240002(sec 1)(1cos )1lim lim lim3sin 3cos 312x x x x x x x x x x x x →→→⎛⎫ ⎪--⎝⎭===⋅⋅.3.0tan 2tan lim3sin sin 2x x x x x→--解:000sin 2sin sin tan 2tan cos 2cos cos 2cos lim lim lim 13sin sin 23sin sin 2sin (32cos )x x x x x xx xx x x x x x x x x x →→→--⋅===---.4.20sin cos 1limsin 3x x x x x →+--解:200sin cos 11limlim sin 333x x x x x x x x →→+-==-.第八节函数的连续性与间断点一、填空题1.设2,0()sin ,0a bx x f x bx x x⎧+≤⎪=⎨>⎪⎩在0x =处连续,则常数,a b 应满足的关系为a b =.提示:()2(0)lim (0)x f a bxa f --→=+==,0sin (0)lim x bxf b x-+→==.2.设0()1,0ln(1),0x f x x bx x x <=-=⎨⎪+⎪->⎪⎩在0x =处连续,则常数a =22,b =1.提示:0(0)lim lim lim x x x axf x ----→→→===,(0)1f =-,00ln(1)(0)lim lim x x bx bxf b x x--+→→+=-=-=-.3.()sin xf x x=的可去间断点为0x =;221()32x f x x x -=-+的无穷间断点为2x =.4.若函数e ()(1)x af x x x -=-有无穷间断点0x =及可去间断点1x =,则常数a =e .提示:由已知,1e lim (1)x x a x x →--存在,所以1lim(e )0xx a →-=,从而e a =.二、单项选择题1.0x =是1()sin f x x x=的A .A.可去间断点B.跳跃间断点C.无穷间断点D.振荡间断点提示:01lim ()lim sin0x x f x x x→→==2.函数21,0(),012,12x x f x x x x x ⎧-<⎪=≤≤⎨⎪-<≤⎩D.A.在0,1x x ==处都间断B.在0,1x x ==处都连续C.在0x =处连续,1x =处间断D.在0x =处间断,1x =处连续提示:(0)1,(0)0(0)f f f -+=-==;(1)(1)1,(1)1f f f -+===.3.设函数42,0(),0x f x xk x ≠=⎨⎪=⎩在0x =处连续,则k =B .A.4B.14C.2D.12提示:021lim ()limlim ,(0)4x x x f x f k x →→→===.4.函数111122,0()221,0x x x x x f x x --⎧-⎪≠⎪=⎨+⎪=⎪⎩在0x =处B .A.左连续B.右连续C.左右均不连续D.连续提示:110lim 20,lim 2xxx x -+→→==+∞,从而(0)1(0),(0)1(0)f f f f -+=-≠==.三、讨论函数11e ,0()ln(1),10x x f x x x -⎧⎪>=⎨⎪+-<≤⎩在0x =处的连续性.解:111(0)lim ln(1)0(0),(0)lim ee x x xf x f f -+-+--→→=+====,所以()f x 在0x =处不连续,且0x =是第一类跳跃型间断点.四、若2,0()0e (sin cos ),x x a xf x x x x +≤⎧=⎨>+⎩在-∞(,)∞+内连续,求a .解:由于)(x f 在0=x 处连续,所以)0()0()0(f f f ==-+.(0)lim ()lim e (sin cos )1x x x f f x x x +++→→==+=,a a x x f f x x =+==--→→-)2(lim )(lim )0(0,a f =)0(.故1=a .五、设()f x 在(,)-∞+∞内有定义,且lim ()x f x a →∞=,1,0()0,0f x g x x x ⎧⎛⎫≠⎪ ⎪=⎝⎭⎨⎪=⎩.试讨论()g x 在0x =处的连续性.解:()0011lim ()lim lim 令x x t t x g x f f t a x →→→∞=⎛⎫== ⎪⎝⎭,(0)0g =,所以当0a =时,()g x 在0x =处连续,当0a ≠时,()g x 在0x =处间断.第九节连续函数的运算与初等函数的连续性一、填空题1.设,0()1,0a x x f x x x +≤⎧=>⎩在(,)-∞+∞内连续,则常数a =12.2.设22,1()1,1x bx x f x x a x ⎧++≠⎪=-⎨⎪=⎩在(,)-∞+∞处连续,则常数a =1,b =-3.提示:由题意知,1lim ()(1)x f x f a →==,则212lim1x x bx a x→++=-21lim(2)0x x bx →∴++=,则3b =-,进而1a =.3.211lim cos1x x x →-=-cos 2. 4.()2cot 2lim 1tan xx x→+=e .5.21lim 1xx x x →∞-⎛⎫= ⎪+⎝⎭4e-.提示:41122412lim lim 1e 11xx x xx x x x x -++--→∞→∞⎡⎤-⎛⎫⎛⎫⎢⎥=-= ⎪ ⎪⎢⎥++⎝⎭⎝⎭⎣⎦.6.已知lim 82xx x a x a →∞+⎛⎫= ⎪-⎝⎭,则常数a =ln 2.提示:332233lim lim 1e 822x a x x axx a x aax a a x a x a →∞→∞--⎡⎤+⎛⎫⎛⎫⎢⎥=+== ⎪ ⎪⎢⎥--⎝⎭⎝⎭⎣⎦,所以3ln 8,ln 2a a ==.7.203sin (1)cos lim (1cos )x x x x x →++=+12.8.0x →=12.提示:原式limx→=0x →=22012limsin 222x x x x x →⋅==⋅.9.函数21()23f x x x =--的连续区间是(,1),(1,3),(3,)-∞--+∞.二、单项选择题1.当1→x 时,函数1211e 1x x x ---的极限等于D .A.2B.0C.∞D.不存在但不为∞2.设()f x 在2x =连续,(2)3f =,则2214lim ()24x f x x x →⎛⎫-=⎪--⎝⎭D .A.0B.2C.3D.34提示:22222142113lim ()lim ()lim ()(2)244244x x x x f x f x f x f x x x x →→→-⎛⎫-====⎪---+⎝⎭.三、讨论11()1exxf x -=-的连续性,若有间断点,指出其类型.解:()f x 为初等函数,故在其定义区间(,0),(0,1),(1,)-∞+∞内均连续,在其无定义点0,1x x ==间断.据011lim ()lim1ex x x xf x →→-==∞-,知0x =为第二类无穷间断点;据11111111lim ()lim 0,lim ()lim 11e1exx x x x x xxf x f x --++→→→→--====--,知1x =为第一类跳跃间断点.第十节闭区间上连续函数的性质一、单项选择题1.方程sin 2x x +=有实根的区间为A.A.π,32⎛⎫⎪⎝⎭B.π0,6⎛⎫ ⎪⎝⎭C.ππ,64⎛⎫⎪⎝⎭D.ππ,42⎛⎫⎪⎝⎭提示:令()sin 2f x x x =+-,分别在各个对应的闭区间上验证零点定理是否成立即可.2.方程(1)(2)(3)(1)(2)(4)(1)(3)(4)x x x x x x x x x ---+---+---(2)(3)(4)0x x x +---=有D 个实根.A.0B.1C.2D.3提示:令()(1)(2)(3)(1)(2)(4)(1)(3)(4)f x x x x x x x x x x =---+---+---(2)(3)(4)x x x +---,又(1)0,(2)0,(3)0,(4)0f f f f <><>,则由零点定理知,方程在(1,2),(2,3),(3,4)分别至少存在一个根;又()f x 是三次多项式,则方程至多有三个根,综上可知方程恰好有三个根.二、证明题1.证明方程e 2xx -=在区间(0,2)内至少有一实根.证明:令()e 2xf x x =--,则()f x 在[0,2]上连续,且2(0)10,(2)e 40f f =-<=->,根据零点定理,至少存在一点(0,2)ξ∈,使()0f ξ=,所以方程()0f x =,即e 2xx -=在区间(0,2)内至少有一实根.2.设()f x 在[,]a b 上连续,且(),()f a a f b b <>.证明至少存在一点(,)a b ξ∈,使()f ξξ=.证明:令()()F x f x x =-,则()F x 在[,]a b 上连续,且()()0F a f a a =-<,()()0F b f b b =->,根据零点定理,至少存在一点(,)a b ξ∈,使()0F ξ=,即()f ξξ=.3.附加题设()f x 在[,)a +∞上连续,lim ()0x f x →+∞=.证明()f x 在[,)a +∞上有界.证明:由lim ()0x f x →+∞=,对10,X a ε=>∃>,当x X >时,有()()01f x f x ε=-<=,即()f x 在(,)X +∞上有界;又()f x 在[,]a X 上连续,故()f x 在[,]a X 上有界,所以存在10,M >使[]1(),,f x M x a X ≤∀∈,取{}1max 1,M M =,则对[],x a ∀∈+∞()f x M <,即()f x 在[,)a +∞上有界.第一章自测题一、填空题(每小题3分,共18分)1.()03limsin tan ln 12x x x x →=-+14-.提示:()20003331lim lim lim 4sin tan tan (cos 1)222ln 12x x x xx x x x x x x x →→→-⋅===---+.2.2131lim2x x x →-=+-26-.提示:21lim26x x x x →→==-+-.3.已知212lim31x x ax bx →-++=+,其中b a ,为常数,则a =7,b =5.4.若()2sin 2e 1,0,0ax x x f x xa x ⎧+-≠⎪=⎨⎪=⎩在()+∞∞-,上连续,则a =-2.提示:由题意知,20sin 2e 1lim ax x x x →+-20sin 2e 1lim 22ax x x a a x x →⎛⎫-=+=+= ⎪⎝⎭,从而2a =-.5.曲线21()43x f x x x -=-+的水平渐近线是0y =,铅直渐近线是3x =.二、单项选择题(每小题3分,共18分)1.“对任意给定的()1,0∈ε,总存在整数N ,当N n ≥时,恒有ε2≤-a x n ”是数列{}n x 收敛于a 的C.A.充分条件但非必要条件B.必要条件但非充分条件C.充分必要条件D.既非充分也非必要条件2.设()2,02,0x x g x x x -≤⎧=⎨+>⎩,()2,0,0x x f x x x ⎧<=⎨-≥⎩则()g f x =⎡⎤⎣⎦D .A.22,02,0x x x x ⎧+<⎨-≥⎩ B.22,02,0x x x x ⎧-<⎨+≥⎩ C.22,02,0x x x x ⎧-<⎨-≥⎩ D.22,02,0x x x x ⎧+<⎨+≥⎩3.下列各式中正确的是D.A.01lim 1exx x +→⎛⎫-= ⎪⎝⎭B.01lim 1e xx x +→⎛⎫+= ⎪⎝⎭C.1lim 1e xx x →∞⎛⎫-=- ⎪⎝⎭D.11lim 1e xx x --→∞⎛⎫+= ⎪⎝⎭4.设0→x 时,tan e 1x-与n x 是等价无穷小,则正整数n =A.A.1B.2C.3D.4提示:由题意知,当0→x 时,tan e 1tan xx x - 从而n 取1.5.曲线221e 1ex x y --+=-D .A.没有渐近线B.仅有水平渐近线C.仅有铅直渐近线D.既有水平渐近线又有铅直渐近线6.下列函数在给定区间上无界的是C.A.1sin ,(0,1]x x x ∈ B.1sin ,(0,)x x x∈+∞C.11sin ,(0,1]x x x∈ D.1sin ,(0,)x x x∈+∞三、计算题(每小题7分,共49分)1.2x →解:2222(1)(2)(413)(1)(413)9limlim 4(2)42x x x x x x x →→→+-+===-.2.()21ln(1)lim cos x x x +→解:()()2211ln(1)ln(1)0limcos lim 1cos 1x x x x x x ++→→=+-222001cos 112limlim ln(1)2eeex x x x x x →→---+===.3.()1lim123nnnn →∞++解:()1312333,31233n n n nnnn<++<⋅∴<++<⋅Q1n =,()1lim 1233nnnn →∞∴++=.4.21sinlimx x x解:2111sinsin sinlim lim limlim 112x x x x x x x x x x→+∞→+∞→+∞→+∞=⋅⋅.5.设函数()()1,0≠>=a a a x f x ,求()()()21lim ln 12n f f f n n →∞⎡⎤⎣⎦ .解:()()()()()()22ln 1ln 2ln 1limln 12lim n n f f f n f f f n n n →∞→∞+++=⎡⎤⎣⎦L L ()()222ln 12ln ln limlim22n n n n a n aan n →∞→∞++++===L .6.1402e sin lim 1e xx x x x →⎛⎫+ ⎪+ ⎪ ⎪+⎝⎭解:1144002e sin 2e sin 2lim lim 1111e 1e x x x x x x x x x x --→→⎛⎫⎛⎫++ ⎪ +=-=-= ⎪ ⎪ ⎪++⎝⎭⎝⎭,11114444000e 2e 12e sin 2e sin sin lim lim lim 1e 1e e e 1x x x xx x x x x x x x x x x x x +++-→→→-⎛⎫⎛⎫+ ⎪⎛⎫⎛⎫ ⎪++⎝⎭ ⎪ ⎪ ⎪+=+=+ ⎪ ⎪ ⎪⎛⎫ ⎪ ⎪++ ⎪+⎝⎭⎝⎭ ⎪⎪⎝⎭⎝⎭301lim 1e xx +-→=+=,所以,原式1=.7.已知(lim 1x x →-∞=,求,.a b解:左边22(1)lim limlim x x x x a x b x →-∞→-∞⎡⎤--+⎢==,右边1=,故[]lim (1)1x a x b →-∞--=+,则1,2a b ==-.四、讨论函数,0()(0,0,1,1)0,0x xa b x f x a b a b x x ⎧-≠⎪=>>≠≠⎨⎪=⎩在0x =处的连续性,若不连续,指出该间断点的类型.(本题8分)解:当a b =时,()0f x ≡,此时()f x 在0x =处连续;当a b ≠时,000011lim ()lim lim lim ln (0)0x x x x x x x x a b a b af x f x x x b→→→→---==-=≠=,故()f x 在0x =处不连续,所以0x =为()f x 得第一类(可去)间断点.五、附加题设()f x 在[0,1]上连续,且(0)(1)f f =.证明:一定存在一点10,2ξ⎡⎤∈⎢⎣⎦,使得1()2f f ξξ⎛⎫=+ ⎪⎝⎭.(本题7分)证明:设1()()2F x f x f x ⎛⎫=-+⎪⎝⎭,显然()F x 在10,2⎡⎤⎢⎥⎣⎦上连续,而1(0)(0)2F f f ⎛⎫=-⎪⎝⎭,()()11110222F f f f f ⎛⎫⎛⎫⎛⎫=-=- ⎪ ⎪ ⎝⎭⎝⎭⎝⎭,211(0)(0)022F F f f ⎡⎤⎛⎫⎛⎫=--≤ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,若1(0)02F F ⎛⎫= ⎪⎝⎭,即(0)0F =或102F ⎛⎫= ⎪⎝⎭时,此时取0ξ=或12ξ=即可;若1(0)02F F ⎛⎫< ⎪⎝⎭时,由零点定理知:一定存在一点10,2ξ⎡⎤∈⎢⎣⎦,使()0Fξ=,即1()2f fξξ⎛⎫=+⎪⎝⎭.。
田间试验与统计方法答案

东北农业大学网络教育学院 田间试验与统计方法作业题参考答案作业题(一)参考答案一、名词解释(10分)1 边际效应2 唯一差异性原则3 小概率实际不可能性原理4 统计假设5 连续性矫正1 边际效应:指种植在小区或试验地边上的植株因其光照、通风和根系吸收范围等生长条件与中间的植株不同而产生的差异。
2 唯一差异性原则:指在试验中进行比较的各个处理,其间的差别仅在于不同的试验因素或不同的水平,其余所有的条件都应完全一致。
3 小概率实际不可能性原理:概率很小的事件,在一次试验中几乎不可能发生或可以认为不可能发生。
4 统计假设:就是试验工作者提出有关某一总体参数的假设。
5 连续性矫正:连续性矫正:2χ分布是连续性变数的分布,而次数资料属间断性变数资料。
研究表明,当测验资料的自由度等于1时,算得的2χ值将有所偏大,因此应予以矫正,统计上称为连续性矫正。
二、填空(22分)1、试验观察值与理论真值的接近程度称为(准确度)。
2、试验方案中的各处理间应遵循(唯一差异原则)原则才能正确地进行处理效应的比较。
3、统计假设测验中是根据(小概率实际不可能)原理来确定无效假设能否成立。
4、A 、B 二因素试验结果分析中处理平方和可以分解为(A 因素的平方和)、(B 因素的平方和)和(A ×B 互作的平方和)3部分。
5、用一定的概率保证来给出总体参数所在区间的分析方法称为(区间估计),保证概率称为(置信度)。
6、试验设计中遵循(重复)和(随机排列)原则可以无偏地估计试验误差。
7、样本标准差s =(1)(2--=∑n x x s ),样本均数标准差s x =(5453.0107244.1===n ss x )。
8、次数资料的χ2测验中,χ2=(∑-=k E E O 122)(χ),当自由度为(1),χ2c =( ∑=--=k i ii i CE E O 122)21(χ)。
9、在A 、B 二因素随机区组试验的结果分析中已知总自由度为26,区组自由度为2,处理自由度为8,A 因素自由度为2,则B 因素的自由度为(2),A 、B 二因素互作的自由度为(4),误差的自由度为(16)。
专科电路作业题及参考答案070423

东北农业大学网络教育学院电路专科作业题(一)一、简答题(共8题)1.电压2.欧姆定律3.支路4.树支5.除源的含义6.零状态响应7.三相制8.连通图二、填空(共10题)1.电路的组成包括、和。
2.对直流来说,电容相当于,电感相当于。
3.在一段电路中,当电压、电流为关联参考方向时,p>0表示,p<0表示。
4.凡是具有个引出端的电路或网络,称为一端口网络。
5.图1所示电路的等效电阻R ab=▁▁▁▁。
6.图2中元件u与i的约束方程是。
7.图3电路的电压U= ,电流I= 。
8. 图4电路中2A电流源发出的功率P= 。
9. 图5所示电路中,已知u=100cos1000t V,i=10cos(1000t+90º) A,则Z= ,Y= ,P= ,Q= 。
图1图2图3 图5图4三、选择题(共10题)1.图6所示电路中, R=▁▁▁▁ 。
A .3Ω B.-3Ω C. 4Ω2.理想电流源两端的电压受▁▁▁▁的影响。
A. 其自身电流 B. 其自身电压 C. 外电路3.在电路中,激励指的是▁▁▁▁ 。
A. 独立电源 B. 受控源 C. 负荷4.R 、L 、C 串联电路谐振时,电阻两端的电压▁▁▁▁电源电压。
A .必大于 B.必小于 C.一定等于 D.可能超过5.图7所示电路中,减小G 1将导致▁▁▁▁ 。
A .V A 、VB 均增大 B. V A 、V B 均减小C. V A 不变,V B 减小D. V A 不变,V B 增大6. 图8所示的正弦交流电路中电压有效值分别为:U 14=5V ,U 12=3V ,U 34=6V 。
则U 24=▁▁▁。
A .1V B.4V C.3V D.2V7.图9所示电路的相量图为▁▁▁▁ 。
A . B.C.D. ϕcos 3I U P =图6图7 图9 图8 图10A.线电压与线电流的相位差角 B. 相电压与线电流的相位差角C. 线电压与相电流的相位差角D. 相电压与相电流的相位差角9. 图10所示电路中,电压u等于▁▁▁▁。
01第一部分作业题带答案

第一部分作业题一、单项选择题(题中只有一个答案最符合题意)1、施工定额属于()性质。
A.计价性定额B. 生产性定额C. 通用性定额D. 计划性定额2、规费不包括()。
A. 工伤保险费B. 养老保险费 C .劳动保险费 D .住房公积金3、下列费用不属于措施费的有()A. 安全文明施工费B.医疗保险费 C. 临时保护设施费 D.垂直运输费4、下列不属于建筑安装施工机械使用费的是()A. 大型机械设备进出场及安拆费B.机上司机人工费C. 燃料动力费D. 大修理费5、下列不属于人工费的是()A. 管理人员工资B.生产工人高温津贴C. 生产工人产假工资D. 生产工人加班工资6、()是编制和确定项目建议书和可行性研究报告投资估算的基础和依据。
A、投资估算指标 B 、概算定额 C 、概算指标 D 、预算定额7、下列不属于企业管理费的是()A. 财产保险费B.职工教育经费 C. 失业保险费 D. 劳动保险费8、下列不属于材料费的是()A. 材料原价B.材料检验试验费 C. 材料采购保管费 D. 材料运杂费9、根据我国现行建筑安装工程费用项目组成的规定,下列人工费中不能构成分部分项工程费的有()。
A. 保管建筑材料人员的工资B.绑扎钢筋人员的工资C. 操作施工机械人员的工资D. 现场临时设施搭设人员的工资10、下列不属于措施项目费的是()A. 安全文明施工费B. 水泥材料费C. 脚手架工程费D. 二次搬运费11、下列不属于分部分项材料费的是()A. 水泥原价B. 粘土砖运杂费C. 模板费D. 钢筋采购保管费12、不应计入其他项目费的是()A. 总承包服务费B. 计日工C. 暂列金额D. 临时设施费13、下列不属于规费中的社会保险费的是()A. 劳动保险费B. 医疗保险费C. 生育保险费D. 养老保险费14、下列哪一项不是工程建设定额的特点()。
A、科学性 B 、先进性 C 、系统性 D 、统一性15、机械台班时间定额和产量定额之间的关系是()。
建筑工程概论作业题参考答案

建筑工程概论作业题参考答案东北农业大学网络教育学院建筑工程概论作业题(一)一、判断1、土木工程的内容非常广泛,它和广大人民群众的日常生活密切相关,在国民经济中起着非常重要的作用。
()2、砂是一种常用的砌筑材料。
广泛地用于墙体、基础、柱等砌筑工程中。
()3、工程地质勘察的目的主要是查明工程地质条件,分析存在的地质问题,对建筑地区作出工程地质评价。
()4、单向板指板上的荷载沿两个方向传递到支承构件上的板。
()5、快速道是连接城市主要分区的干道,以交通功能为主,一般为三幅或四幅路。
()6、支道是与主干道组成道路网,起集散交通之用,兼有服务功能。
()7、发展交通运输事业,建立四通八达的现代交通网,则离不开桥梁建设。
()8、辅助跑道指只供起飞用的跑道。
()9、支线运输机是指载客量>100人,航程>3000km的大型运输机。
()10、机场仓库供货运办理手续、装上飞机以及飞机卸货、临时储存、交货等用。
()二、名词解释1、土木工程;2、土木工程材料;3、基础;4、混合结构;5、高速公路三、单项选择题1、()是建造各类工程设施的科学技术的总称。
A、土木工程B、基本建设C、信息化施工D、可持续发展2、()是关于事物的基本原理和事实的有组织、有系统的知识。
A、教学B、科学C、技术D、工程3、水泥浆体在常温下会逐渐变稠直到开始失去塑性,这一现象称为水泥的()。
A、初凝B、终凝C、凝结D、硬化4、按表观密度为()时称为重混凝土。
A、>2900kg/m3B、<1950kg/m3C、1950-2600kg/m3D、>2600kg/m35、通常把位于天然地基上、埋置深度小于()m的一般基础(柱基或墙基)称为天然地基上的浅基础。
A、4B、5C、6D、86、()是指天然地基很软弱,不能满足地基承载力和变形的设计要求,地基需经过人工处理的过程。
A、地基处理B、工程地质C、基础工程D、地基加固7、()指平面尺寸较大而厚度较小的受弯构件,通常水平放置,但有时也斜向设置或竖向设置。
(完整版)电路作业题答案..
第1章电路模型和电路定律一、填空:1、—1.5A2、电路中某支路电流为1A-,表示该支路电流的真实方向与参考方向相反。
若电路电流I的参考方向由a→b,若电压与电流为非关联参考方向,则电压参考方向为 b→a 。
已知I=3A,U= -5V,则功率P= -15W ,是吸收功率(吸收或发出)。
3、电路中A、B两点的电位分别为U A=20V,U B=-20V,则两点间电压U AB= 40V 。
4、一个理想电流源串联5Ω电阻时,流过电阻电流为2A,当改变电阻阻值为10Ω时,流过电阻电流为 2A 。
5、电压源不允许短路,电流源不允许开路。
6、电路中电压U= 115 V。
7、6Ω; 8、U =16 V、R = 2Ω;9、2Ω;10、20V;11、理想电压源,串联,理想电流源,并联 .12、-6Ω二、选择1-5、D、B、B、A、A、6-11、A、C、C、A、B、A三、计算1.在指定的电压u和电流i参考方向下,写出下列元件u和i的约束方程(VCR)。
解:(a)u = -10i(b)u = —10V2、如图所示电路,已知15i A=-,21i A =,62i A=,求4i.解:i3 = i1+i2 = -5+1 = 4A ; i4 = i6-i3= 2-4 = —2A3、求电路中电流I、电压U及电阻的功率P。
解:(a)I = 2—4 = —2A U = 3I = —6V P = UI = 12W(b) I= 6-2 = 4A U = 2I= 8V P= UI= 32W4、图示电路中,分别计算两个电流源的功率,并判断是吸收还是发出功率。
图7解:3A 电流源吸收9w ;6A 电流源发出18w5、U ab=16V6、如图11所示,试计算UAC , UAD 。
解:闭合回路中电流为1A ,UAC =UBC = —1×(20+10)+ 2 = -28 V UAD =UBD =UBC + 2 = -26 V7、图示电路中,求: (1)当开关K合上及断开后,UAB =? (2)当开关K断开后,UCD =?解:(1)当开关合上时,UAB = 0 V当开关断开时,沿最大回顺时针绕行,其电流I = -20/7 A UAB =12-6I —9 UAB = -99 / 7 V(2) 当开关K断开后,UCD = 9 – I ×1 = 43 / 7 V 8、试求图示电路的入端电阻R ab ,图中电阻的单位为欧。
《国际结算》作业题参考答案 一名词解释
《国际结算》作业题参考答案一、名词解释:1、国际结算:即International Settlement,是指国际间由于经济、政治等各方面交往而引起的、以货币所表现的债券债务结算。
2、代理行:即Correspondent Banks,是指两家银行通过签订协议,建立委托代理关系,互相委办诸如国际结算、出口信贷、银团贷款等业务或提供服务。
这样的两家银行互称代理行。
3、控制文件:即control Documents,两家建立代理行关系在银行在互相委办业务或提供服务时所相互交换的用以明确关系和方便业务的文件,包括密押、印鉴、和费率表等。
4、CHIPS:即美国纽约票据交换所银行同业支付系统,有纽约清算协会于1971年成立,专门用于全球美元清算,是一个实时的、银行对银行交易的终局性付款系统。
目前全球大约95%的美元支付都是通过这一系统处理完成的。
5、SWIFT:即环球银行间金融电讯协会,成立于1973年,总部设在比利时的布鲁塞尔,其创建之目的在于创造一个全球共享的使用统一语言的数据处理和通讯网络体系,一边于所有的国际金融交易。
现有设在荷兰、香港、英国和美国的四个基地,主要向全球7000多家会员提供资金划拨、国际贸易支付、国债、证券、外汇交易等服务。
6、CHAPS:即英国伦敦票据交换所银行同业支付系统,成立于1984年,是银行间即日电子支付系统,与英格兰银行合作提供收付和清算服务,它同时是世界上最大的全国性清算系统之一,1999年1月起在运行原有英镑清算系统的同时开始运行欧元清算系统。
7、TARGET:即欧元自动拨付与清算系统,位于德国法兰克福欧洲中央银行总部,与1999年1月4里开始运行。
由15个欧盟成员国的全国实时清算系统和欧洲中央银行的支付系统组成,以提供公共平台便利各成员国之间的跨境支付。
8、存放国外同业:即NOSTRO,代理行之间建立的账户关系之一,属资产类科目,即借方记录资产的增加、负债的减少,贷方记录资产的减少、负债的增加。
电力系统分析作业题参考答案
东北农业大学网络教育学院电力系统分析作业题参考答案作业题一参考答案一、填空题1.降压变压器高压侧的主分接头电压为220kv ,若选择+2×2.5%的分接头,则该分接头电压为 231KV 。
2.电力系统中性点有效接地方式指的是 中性点直接接地 。
3.输电线路的电气参数包括电抗、电导、电纳和 电阻 。
4.输电线路的电压偏移是指线路始端或末端母线的实际运行电压与线路 额定电压 的数值差。
5.电力系统的潮流分布一般是用各节点的电压和 功率 表示。
6.调整发电机组输出的有功功率用来调整电力系统运行的 频率 。
7.复合故障一般是指某一时刻在电力系统 二个及以上地方 发生故障。
8.用对称分量法计算不对称故障,当三相阻抗完全对称时,则其序阻抗矩阵Zsc 的非对角元素为 零 。
9.系统中发生单相接地短路时故障点短路电流的大小是零序电流的 3 倍。
10.减小输出电元件的电抗将 提高(改善) 系统的静态稳定性。
二、单项选择题11.同步发电机的转速和系统频率之间是否有严格的关系( ② )①否 ②是 ③不一定 ④根据发电机的形式定12.三绕组变压器的结构、通常将高压绕组放在( ③ )①内层 ②中间层 ③外层 ④独立设置13.中性点以消弧线圈接地的电力系统,通常采用的补偿方式是( ③ )①全补偿 ②欠补偿 ③过补偿 ④有时全补偿,有时欠补偿14.三相导线的几何均距越大,则导线的电抗( ② )①越大 ②越小 ③不变 ④无法确定15.变压器的电导参数G T ,主要决定于哪一个实验数据( ① )①△P O ②△P K ③U K % ④I O %16.当功率的有名值为s =P +jQ 时(功率因数角为ϕ)取基准功率为S n ,则有功功率的标么值为( ③ ) ①ϕcos S P n ⋅ ②ϕsin S P n ⋅ ③n S P ④nS cos P ϕ⋅17.环网中功率的自然分布是( ④ )①与电阻成正比分布 ②与电抗成正比分布③与阻抗成正比分布 ④与阻抗成反比分布18.电力系统中PQ 节点的数量( ② )①全都是 ②大量的 ③少量的 ④必有且一般只设一个19.潮流计算中,要求某些节点之间电压的相位差应满足的约束条件是(④ )①|-j i δδ|>|-j i δδ|min ②|-j i δδ|<|-j i δδ|min③|-j i δδ|>|-j i δδ|max ④|-j i δδ|<|-j i δδ|max20.在同一时间内,电力网的电能损耗与供电量之比的百分值称为( ② )①负载率 ②网损率 ③供电率 ④厂用电率21.电力系统的频率主要决定于( ① )①有功功率的平衡 ②无功功率的平衡③电压质量 ④电流的大小22.关于顺调压电压调整方式的描述,错误的是( ② )①高峰负荷时允许中枢点电压略低②低谷负荷时允许中枢点电压略低③适用于用户对电压要求不高的场合④适用于供电线路不长的场合23.通过改变变压器变比,实质上( ③ )①改变了电压损耗的数值 ②改变了负荷变化时次级电压的变化幅度③改变了电力网的无功功率分布 ④增加了整个电力系统的无功功率容量24.三相短路时,非周期分量极小值,只能是在某种情况(① )①一相中出现 ②同时在两相中出现③三相均不出现 ④只有故障相出现其它相不出现25.同步机的各种电抗间关系为(③ )①'x "x x x d d q d >>> ②"x 'x x x d d d q >>>③ "x 'x x x d d q d >>> ④"x x 'x x d q d d >>>26.若ac 两相发生短路,则基准相选择为( ② )①a 相 ②b 相 ③c 相 ④a 相和c27.下网K 点发生两相短路接地,其复合序网为图所示( ③ )(其中,1,2,0分别为正序、负序、零序阻抗)28.越靠近电源点负序电压越( ① )①低 ②高 ③不变 ④无法确定29.作为判据0d dP E >δ主要应用于分析简单系统的( ③ ) ①暂态稳定 ②故障计算 ③静态稳定 ④调压计算30.分析简单系统的暂态稳定性可以应用( ② )①等耗量微增率准则 ②等面积定则 ③小干扰法 ④对称分量法三、简答题31.电力变压器的主要作用是什么?答:电力变压器的主要作用是升高或降低电压,另外还起到将不同电压等级电网相联系的作用。
生产与作业管理作业题参考答案081113
东北农业大学网络教育学院生产运作管理作业题参考答案作业题(一)参考答案一判断题(20分,每题1分)1√2×3√4×5√6√7√8√9√10×11√12√13×14√15√16×17×18×19√20×二概念理解:(15分,每题3分)1工时定额:是产品生产过程中劳动消耗的一种数量标准,是在一定的生产技术组织条件下,生产单位产品所需要的时间消耗,或者是在一定的时间内规定生产合格产品的数量。
2工时消耗:是对工人在整个轮班的工作过程中全部时间的分类.3 工艺专业化形式:这种组织方式是以工艺为中心,组织设备、人员等生产运作资源,为每一工序提供一个工作场地4 生产设施单元化:是指企业通过小生产设施的规模及范围,在保持其柔性的同时,集中精力于优势产品或项目,以提高生产经营绩效。
5 生产运作计划: 是指在企业生产策略的指导下,根据需求预测和优化决策对其生产系统产出的品种、数量、速度、时间和劳动力的配置及库存水平等问题预先进行的考虑和安排。
三填空题(30分,每空1分)1生产运作系统的三种基本职能是﹝生产﹞,﹝销售﹞和﹝理财﹞。
2按顾客的需求特征分类,可将服务业分为﹝通用性生产﹞和﹝专用型生产﹞。
按运作系统的特征分类,可分为﹝技术密集型﹞和﹝人员密集型﹞。
3市场竞争的重点要素分为﹝成本﹞,﹝质量﹞,﹝时间﹞和﹝柔性﹞。
4制造业生产运作系统的竞争能力的种类可分为﹝缺乏竞争力﹞,﹝竞争对峙势﹞,﹝有竞争优﹞和﹝世界及制造系统﹞。
5顾客满意度可用顾客让渡价值来衡量,它是指顾客获得的﹝总价值﹞和顾客为之付出的﹝总成本﹞之间的差距。
6生产运作策略是用以支持企业总体经营战略的﹝长远规划﹞,使生产运作系统成为立足于市场并获得长期竞争优势的基础。
7 CIMS 有两个基本观点,一是在(功能设计)方面,一个制造企业的全部生产和经营活动,从市场预测、产品设计,经营管理到(售后服务)是一个整体,要全面考虑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业题:(冷冲压部分)
第三章:
1、 如下图所示零件,材料为45钢,板厚3mm。试确定冲裁凸、凹模刃口尺寸。(分别加工法)
解:该零件外面的矩形由落料制成、内孔由冲孔制成,而中心距尺寸是不变的量,需按三种方法
分别计算。查表3-4得初始单面间隙:mmZmmZ70.064.0maxmin
1) 落料尺寸:062.048
由表3-5查出凸、凹模制造公差:mmmmAT030.002.0
校核:minmax05.003.002.0ZZAT
由表3-6查出:x=0.5
因此得:
)(69.47)62.05.048()(03.0003.000maxmmxDDAA
)(05.47)64.069.47()(0.02.0002.00minmmZDDTAT
2) 冲孔尺寸:058.008
由表3-5查出凸、凹模制造公差:mmmmAT020.002.0
校核:minmax04.002.002.0ZZAT
由表3-6查出:x=0.75
因此得:
)(0435.8)058.075.08()(0020.0002.00minmmxddTT
)(6835.8)64.00435.8()(02.0002.000minmmZddTTA
3) 中心距:13.024
0325.024826.024L
(mm)
2、 如下图所示零件,材料为Q235,板厚1mm。试落料凸、凹模刃口尺寸。(配合加工法)
解:这是一个落料件,选凹模为基准件。
1) 增大的A类尺寸:
0
2.015
:查表3-6得:x=0.75,代入公式得:
05.0020.04100185.14)20.075.015()(1
AxAA
A
(mm)
0
2.030
:查表3-6得:x=0.75,代入公式得:
05.0020.04100285.29)20.075.030()(2
AxAA
A
(mm)
0
2.010
:查表3-6得:x=0.75,代入公式得:
05.0020.04100385.9)20.075.010()(3
AxAA
A
(mm)
2) 变小的尺寸:
1.008
:查表3-6得:x=1,代入公式得:
0025.0010.0410
11.8)10.018()(1BxBBB
(mm)
3) 不变尺寸:12.005
015.0015.0812.0812.0min06.5)12.05.05()21(
CC
(mm)
该零件凸模刃口尺寸按凹模刃口的相应部分尺寸配制,保证双面间隙0.12mm。
第四章:
计算图示弯曲件的毛坯长度。
解:(1)左图
垂直方向的直边长L1=20-3-2.5=15.5(mm)
水平方向的直边长L2=32-4-2.5×2=23(mm)
由r/t=2.5/2=1.25 查表4-2得:x=0.34 得到弯曲部分的展开长度为:
99.418090)234.05.2(14.3180)(xtrA
(mm)
弯曲件的毛坯长度为:
L=2 L1+2A+ L2=2×15.5+2×4.99+23=63.98(mm) 取64mm
(2)右图
由R/t=5/2=2.5 查表(PPT上附表3)得:x1=0.485
代入txR10=5-0.485×2=4.03(mm)
卷圆部分的展开长度为:98.2625203.414.35.125.101tRL(mm)
弯曲件的毛坯长度为:L= L1+ L2=26.98+15=41.98(mm)
第五章:
图示零件的材料为08钢,厚度1mm,试确定各工序的半成品尺寸。
解:(1) 计算毛坯尺寸
查表5-2取3.3h(mm)
中径245.0225cpd(mm) 131252250d(mm)
3.473.3)1550(hh
5.525tr
cp
毛坯直径:
)(49.7382.540024202.4498.45401695.58135.514.323.472441382)(4222020mmrdrhhddDcpcpcp
(2) 拉深次数和半成品尺寸的计算
由 3605.11005.731100Dt查表5-3得各次拉深拉深系数为:
84.081.079.076.053.054321mmmmm
总的拉深系数13265.05.7324mDdmcp总 需要多次拉深
得:955.385.7353.011Dmd
6058.29955.3876.0122dmd
389.236058.2979.0233dmd
<24
∴需拉深3次,调整各次半成品尺寸得:
第1次 531.05.73393911mmmd
第2次 769.039303022mmmd
第3次 80.030242433mmmd
