圆周角PPT课件
合集下载
数学九年级上第三篇第四节《圆周角》课件
数学九年级上第三篇第四节《圆周 角》课件
目录
• 圆周角基本概念与性质 • 圆周角定理及其推论 • 弧长与扇形面积计算 • 圆锥曲线中圆周角应用 • 拓展延伸：其他几何图形中圆周角应用 • 总结回顾与课堂练习
01 圆周角基本概念与性质
圆周角定义及特点
圆周角定义
顶点在圆上，并且两边都和圆相 交的角叫做圆周角。
圆周角性质总结
01
02
03
性质1
在同圆或等圆中，如果两 个圆周角相等，那么它们 所对的弧也相等。
性质2
在同圆或等圆中，如果两 条弧相等，那么它们所对 的圆周角也相等。
性质3
在同圆或等圆中，同弧或 等弧所对的圆周角相等， 都等于这条弧所对的圆心 角的一半。
02 圆周角定理及其推论
圆周角定理内容
ห้องสมุดไป่ตู้圆周角定义
圆柱、圆锥等立体图形中圆周角应用
圆柱中的圆周角
圆柱侧面展开图是一个矩形，其相邻两边夹角即为圆周角。利用圆周角定理可解决圆柱中 的相关问题。
圆锥中的圆周角
圆锥侧面展开图是一个扇形，其圆心角即为圆锥的顶角，而圆周角则为顶角的一半。利用 这些性质可解决圆锥中的相关问题。
圆周角定理在立体图形中的应用
在解决立体图形的问题时，可利用圆周角定理将问题转化为平面问题，从而简化计算过程 。
设扇形半径为r cm，则根据扇 形面积计算公式有 (45° × π × r²) / 360 = 24cm²，解得 r≈4.37cm（保留两位小数）。 再根据弧长计算公式，弧长 = 45° × 4.37cm × π / 180 ≈ 3.43cm（保留两位小数）。
04 圆锥曲线中圆周角应用
圆锥曲线基本概念回顾
典型例题解析
目录
• 圆周角基本概念与性质 • 圆周角定理及其推论 • 弧长与扇形面积计算 • 圆锥曲线中圆周角应用 • 拓展延伸：其他几何图形中圆周角应用 • 总结回顾与课堂练习
01 圆周角基本概念与性质
圆周角定义及特点
圆周角定义
顶点在圆上，并且两边都和圆相 交的角叫做圆周角。
圆周角性质总结
01
02
03
性质1
在同圆或等圆中，如果两 个圆周角相等，那么它们 所对的弧也相等。
性质2
在同圆或等圆中，如果两 条弧相等，那么它们所对 的圆周角也相等。
性质3
在同圆或等圆中，同弧或 等弧所对的圆周角相等， 都等于这条弧所对的圆心 角的一半。
02 圆周角定理及其推论
圆周角定理内容
ห้องสมุดไป่ตู้圆周角定义
圆柱、圆锥等立体图形中圆周角应用
圆柱中的圆周角
圆柱侧面展开图是一个矩形，其相邻两边夹角即为圆周角。利用圆周角定理可解决圆柱中 的相关问题。
圆锥中的圆周角
圆锥侧面展开图是一个扇形，其圆心角即为圆锥的顶角，而圆周角则为顶角的一半。利用 这些性质可解决圆锥中的相关问题。
圆周角定理在立体图形中的应用
在解决立体图形的问题时，可利用圆周角定理将问题转化为平面问题，从而简化计算过程 。
设扇形半径为r cm，则根据扇 形面积计算公式有 (45° × π × r²) / 360 = 24cm²，解得 r≈4.37cm（保留两位小数）。 再根据弧长计算公式，弧长 = 45° × 4.37cm × π / 180 ≈ 3.43cm（保留两位小数）。
04 圆锥曲线中圆周角应用
圆锥曲线基本概念回顾
典型例题解析
课件233圆周角和圆心角的关系.ppt
径。求证：AB ·AC = AE ·AD
分析：要证AB ·AC = AE ·AD
A
AC AD AE AB
O
△ADC∽ △ABE B
DC
或△ACE∽ △ADB E
题后思：1、证明题的思路寻找方法； 2、等积式的证明方法； 3、辅助线的思考方法。
讨论与思考 C
如图，CD是⊙O的直径，
弦AB⊥CD于E，那么你
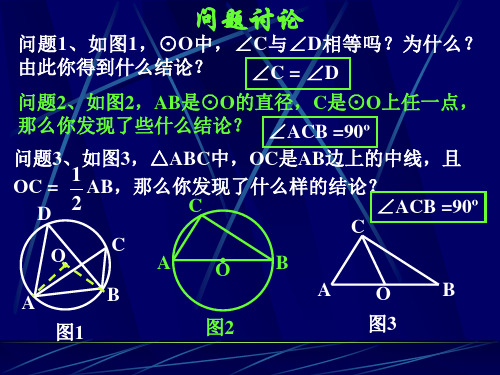
问题讨论
问题1、如图1，⊙O中，∠C与∠D相等吗？为什么？ 由此你得到什么结论？ ∠C = ∠D
问题2、如图2，AB是⊙O的直径，C是⊙O上任一点， 那么你发现了些什么结论？ ∠ACB =90º
问题3、如图3，△ABC中，OC是AB边上的中线，且
OC = 1 AB，那么你发现了什么样的结论？
D2
C
∠ACB =90º C
O
能得到什么结论？
结论：Βιβλιοθήκη AEB（1）AE = BE，AC = BC，AD = BD D
（2）AC = BC，∠CAB = ∠ABC = ∠D，
∠ACE =∠BCE =∠DAB
（3）BC2 = AC2 = CE ·CD，AD2 = DE ·DC
BE2 = AE2 = DE ·CE
小结与作业
1、本节课我们学习了哪些知识？ 2、圆周角定理及其推论的用途你都知道了吗？ 3、证明题思路的寻找方法如何？ 4、证明等积式的一般思路你掌握了吗？
O
C A
O
B
A
B
AO
B
图1
图2
图3
自学与思考
1、圆周角定理的推论1、2、3的内容分别是什么？ 你是怎样理解这些推论的？
2、从课本例2的学习中你认为证明等积式的一般思 路是怎样的？
圆周角-PPT课件
E
20°
30°
∴∠ABF=∠D=20°，∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
A F
C
下列说法是否正确，为什么？
拓展巩固
“在同圆或等圆中，同弦或等弦所对的圆周角相等”.
一条弦所对应的圆周角有两类.
D
如图所示，连接BO、EO. 显然，∠C与∠D所对应的圆心角和为 ，
O.
所以36根0°据圆周角定理可知∠C+∠D = . 180°
通过积极引导，帮助学生有意识地积累活动经验，获得成功的 体验.
知识回顾
O
1.圆心角的定义?
顶点在圆心的角叫圆心角.
A
B
2.图中∠ACB 的顶点和边有哪些特点？
C
考考你：你能仿照圆心角的定义，给下
图中象∠ACB 这样的角下个定义吗？
O
A
B
探索新知
顶点在圆上，并且两边都和圆相交 的角叫圆周角．（两个条件必须同时具备，缺一不可）
24.1 圆的有关性质
24.1.4 圆周角
教学目标
【知识目标】 理解圆周角的概念。探索圆周角与同弧所对的圆心角之间的关
系，并会用圆周角定理及推论进行有关计算和证明. 【能力目标】
经历探索圆周角定理的过程，初步体会分类讨论的数学思想， 渗透解决不确定的探索型问题的思想和方法，提高学生的发散思维能 力. 【情感目标】
意两点，连接AB，AC，BD，CD.∠A与∠D相等吗？ 请说明理由.
D
同弧所对的圆周角相等.
问题2 如图，若
,那么 ∠A与∠B相等吗？
想一想： 反过来，若∠A=∠B，那么
成立吗？
AB E
O
C
圆周角定理 课件
(2)因为△ABE∽△ADC， 所以AABE＝AADC，即 AB·AC＝AD·AE. 又 S＝12AB·AC·sin ∠BAC，且 S＝12AD·AE， 所以 AB·AC·sin ∠BAC＝AD·AE. 则 sin ∠BAC＝1. 又∠BAC 为三角形内角， 所以∠BAC＝90°.
2．已知 AD 是△ABC 的高，AE 是△ABC 的外接圆的直径． 求证：∠BAE＝∠DAC. 证明：连接 BE，因为 AE 为直径， 所以∠ABE＝90°. 因为 AD 是△ABC 的高，所以∠ADC＝90°. 所以∠ADC＝∠ABE. 因为∠E＝∠C，所以∠BAE＝90°－∠E， ∠DAC＝90°－∠C. 所以∠BAE＝∠DAC.
5．如图，△ABC 的角平分线 AD 的延长线交 它的外接圆于点 E. (1)证明：△ABE∽△ADC； (2)若△ABC 的面积 S＝12AD·AE， 求∠BAC 的大小． 解：(1)证明：由已知条件可得∠BAE＝∠CAD. 因为∠AEB 与∠ACB 是同弧上的圆周角， 所以∠AEB＝∠ACD. 故△ABE∽△ADC.
利用圆周角进行计算
[例 2] 如图，已知 BC 为半⊙O 的直径， AD⊥BC，垂足为 D，BF 交 AD 于 E，且 AE ＝BE.
(1)求证： AB＝ AF ； (2)如果 sin ∠FBC＝35，AB＝4 5，求 AD 的长． [思路点拨] BC 为半⊙O 的直径，连接 AC，构造 Rt△ABC.
4．如图，△ABC ຫໍສະໝຸດ 接于⊙O，OD⊥BC 于 D，∠A＝50°，则
∠OCD 的度数是
()
A．40° C．50°
B．25° D．60°
解析：连接 OB.因为∠A＝50°，所以弦 BC 所 对的圆心角∠BOC＝100°，∠COD＝12∠BOC ＝50°，∠OCD＝90°－∠COD＝40°. 答案：A
圆周角定理课件(PPT 17页)
1 = 2 ∠AOD,∠CBD 1 = 2 ∠COD,
●
C O B
1 ∠ABC = ∠AOC. 2
一条弧所对的圆周角等于它所 一条弧所对的圆周角等于它所 圆周角 对的圆心角的一半. 圆心角的一半 对的圆心角的一半.
议一议
圆周角定理 圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 的大小关系是 一条弧所对的圆周角等于它所对的圆心角 圆周角等于它所对的圆心角的一 圆周角定理 : 一条弧所对的圆周角等于它所对的圆心角的一 1 半.
A E
●
驶向胜利 的彼岸
A E B D
C
O
C
B D
在同圆内,同弧或等弧所对的 在同圆内 同弧或等弧所对的 圆周角相等. 圆周角相等
圆周角定理: 在同一圆内,同弧或等弧所对的圆周角相等 同弧或等弧所对的圆周角相等, 在同一圆内 同弧或等弧所对的圆周角相等 都等于该弧所对的圆心角的一半;相等的圆周 都等于该弧所对的圆心角的一半 相等的圆周 角所对的弧相等． 角所对的弧相等．
●
O D C A
●
O C B
O C
D
70o
B
４．如图：四边形ＡＢＣＤ内接于⊙Ｏ，则 ∠BAD = 如图：四边形ＡＢＣＤ内接于⊙Ｏ，则 ＡＢＣＤ内接于
∠BOD =
例２．ＡＢ是⊙Ｏ的直径，ＢＤ是⊙Ｏ的弦，延 长ＢＤ到点Ｃ，使ＣＤ＝ＢＤ，连接ＡＣ． 判断ＡＢ与ＡＣ的大小有什么关系？为什么？
Ａ
Ｂ
Ｄ
Ｃ
如图：已知ＢＣ为 如图：已知ＢＣ为⊙Ｏ的直径，ＡＤ⊥ＢＣ， ＢＣ 的直径，ＡＤ⊥ ，ＡＤ 垂足为Ｄ，ＢＦ ＡＤ于Ｅ，且 Ｄ，ＢＦ交 垂足为Ｄ，ＢＦ交ＡＤ于Ｅ，且ＡＥ＝ＢＥ． ︵ ︵ 求证：ＡＢ＝ＡＦ （１）求证：ＡＢ＝ＡＦ 3 （２）若sin∠ＦＢＣ＝ , AB = 4 5 , 求AD的长。 ∠
●
C O B
1 ∠ABC = ∠AOC. 2
一条弧所对的圆周角等于它所 一条弧所对的圆周角等于它所 圆周角 对的圆心角的一半. 圆心角的一半 对的圆心角的一半.
议一议
圆周角定理 圆周角定理
综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 综上所述,圆周角∠ABC与圆心角∠AOC的大小关系是: 的大小关系是 一条弧所对的圆周角等于它所对的圆心角 圆周角等于它所对的圆心角的一 圆周角定理 : 一条弧所对的圆周角等于它所对的圆心角的一 1 半.
A E
●
驶向胜利 的彼岸
A E B D
C
O
C
B D
在同圆内,同弧或等弧所对的 在同圆内 同弧或等弧所对的 圆周角相等. 圆周角相等
圆周角定理: 在同一圆内,同弧或等弧所对的圆周角相等 同弧或等弧所对的圆周角相等, 在同一圆内 同弧或等弧所对的圆周角相等 都等于该弧所对的圆心角的一半;相等的圆周 都等于该弧所对的圆心角的一半 相等的圆周 角所对的弧相等． 角所对的弧相等．
●
O D C A
●
O C B
O C
D
70o
B
４．如图：四边形ＡＢＣＤ内接于⊙Ｏ，则 ∠BAD = 如图：四边形ＡＢＣＤ内接于⊙Ｏ，则 ＡＢＣＤ内接于
∠BOD =
例２．ＡＢ是⊙Ｏ的直径，ＢＤ是⊙Ｏ的弦，延 长ＢＤ到点Ｃ，使ＣＤ＝ＢＤ，连接ＡＣ． 判断ＡＢ与ＡＣ的大小有什么关系？为什么？
Ａ
Ｂ
Ｄ
Ｃ
如图：已知ＢＣ为 如图：已知ＢＣ为⊙Ｏ的直径，ＡＤ⊥ＢＣ， ＢＣ 的直径，ＡＤ⊥ ，ＡＤ 垂足为Ｄ，ＢＦ ＡＤ于Ｅ，且 Ｄ，ＢＦ交 垂足为Ｄ，ＢＦ交ＡＤ于Ｅ，且ＡＥ＝ＢＥ． ︵ ︵ 求证：ＡＢ＝ＡＦ （１）求证：ＡＢ＝ＡＦ 3 （２）若sin∠ＦＢＣ＝ , AB = 4 5 , 求AD的长。 ∠
《圆周角》九年级数学初三上册PPT课件
时间：20XX
前言
学习目标
1.理解圆周角的定义，了解与圆心角的关系，会在具体情景中辨别圆周角。
2.掌握圆周角定理及推论，并会运用这些知识进行简单的计算和证明;
3.学习中经理操作、观察、猜想、分析、交流、论证等数学活动，体验圆周角的、定理的探索。
重点难点
重点：理解并掌握圆周角定理及推论。
难点：圆周角定理的证明。
Concise And Concise Do Not Need Too Much Text
时间：20XX
第二十四章 圆
24.1.4 圆周角
人 教 版
数 学 九 年 级 上 册
Please Enter Your Detailed Text Here, The Content Should Be Concise And Clear,
Concise And Concise Do Not Need Too Much Text
圆心角和圆周角之间存在的关系
情景二（证明∠BAC=
1 2
3
5
D
4
6
1
∠BOC）:
2
连接AO，延长AO,与⊙O相交于点D
证明二：
OA=OC=>∠4＝∠2
OA=OB=>∠1＝∠3
∠5＝∠1 ＋∠3
∠6＝∠5 ＋∠4
∠=∠5+∠6
=> ∠ = ∠。
圆心角和圆周角之间存在的关系
情景三（证明∠BAC=
B
A
个圆上，这个多边形叫做圆内接多边形。
O
这个圆叫做这个多边形的外接圆。
例：四边形ABCD是⊙O的内接四边形，
⊙O是四边形ABCD的外接圆。
圆周角定理ppt课件
∴∠A=∠C ．
o
又 ∠AOB=∠A+∠C，
B A
∴∠AOB=2∠C. 即
类比转化 考虑两种一般情况：
2.圆心O在圆周角的内部： C
.O
3.圆心O在圆周角的外部:
.C
O
A
B
D
c o
D AB
B A
圆周角定理
一条弧所对的圆周角等于它 所对的圆心角的一半．
符号表示：
∵ A⌒B 所对的圆周角为∠ACB
A⌒B 所对的圆心角为∠AOB
圆周角和圆心O的位置关系：
①圆心在圆周角 ②圆心在圆周 的一条边上； 角的内部；
C
O·
A
B
C
O·
A
B
③圆心在圆 周角的外部.
C
O·
B A
证 明 1.圆心在圆周角的一条边上：
（
已知：在⊙O中，AB 所对的圆周角是 ∠C，圆心
角是 ∠AOB. 求证： ∠C = 1 ∠AOB. 2
c
证明： ∵OA=OC ，
如图, 足球课上,教练在球门前画了一个圆圈进行无人防 守的射门训练，甲，乙,丙三名同学分别在B,D,E三处，他 们都说在自己所在位置所对球门AC的张角大，你认为他们 谁说的对？
回顾圆心角的定义，给下图中像∠ACB这样的角下定义.
1.顶点在圆心的角叫 圆心角 ;
2.顶点在圆上，并且两边都和 圆相交的角叫做 圆周角 .
辨一辨 下列各图中，哪些是圆周角？
探 究 同弧（弧AB）所对的圆周角∠ACB与圆心角∠AOB的关系
1.画一画，量一量
C
在⊙O上任取一条弧，作
出这条弧所对的圆周角和
圆心角， 测量它们的度数，
24.1.4圆周角 教学课件(共33张PPT)初中数学人教版(2012)九年级上册
B.120
C.130
解析：∵四边形 ABCD内接于 O ， ADC 120
∴ ABC 60
∵ AC AC ∴ AOC 2ABC 120 故选：B.
D.135
130° 5.如图，AB 是 O 的直径，点 C，D，E 在⊙O 上，若 AED 40 ，则 BCD 的度数为______.
解析：连接 BE， AB 是直径，
A
A
A
30°
C
O
60°
B C 60° O
120°
C 75° O 150°
B
B
同弧所对的圆周∠角A度C数B=等1于∠这AO条B弧所对圆心角的一半. 2
探索新知
思考 如何证明刚刚的结论呢？ 分类讨论
1.圆心在圆周角的一边上，如图（1）； 2.圆心在圆周角的内部，如图（2）； 3.圆心在圆周角的外部，如图（3）.
不是，边没有 和圆相交
（3）
不是，顶点 不在圆上
（4）
不是，边没有 和圆相交
（5）
（6）
探索新知
探究1 分别测量下图中AB 所对的圆周角∠BAC 和圆心角∠BOC的度数，它
们之间有什么关系？
BAC 1 BOC 2
探索新知
探究2 在☉O中任取一条弧，分别测量这条弧所对的圆心角和圆周角， 你还能得到前面的结论吗？由此你能发现什么规律？
A. 35
B. 40
C. 45
D. 55
解析：连接 AD ， AB 是 O 的直径，
ADB 90 ， ABD 55 ，
BAD ADB ABD 90 55 35 ， BCD BAD 35 ， 故选 A.
C 3.如图， AB 是半圆 O 的直径，C ，D 是半圆上的两点，若 C 125 ，则 ABD的度数是( )
圆周角和圆心角的关系ppt课件
50°，则∠EBC+∠ADC 的度数为 _______.
-18-
3.4 圆周角和圆心角的关系
解析：如解析图，连接 AB，DE，则∠ABE=∠ADE. ∵ 所对的圆心角的度数为 50°，∴∠ABE= ∠ADE =25°. ∵ 点 A，B，C，D 在 ⊙O 上 ，∴四边形 ABCD 是圆内接四边形， ∴∠ABC+∠ADC=180°， ∴∠ABE+∠EBC+∠ADC=180°， ∴∠EBC+∠ADC=180°-∠ABE=180°-25°=155°． 答案：155° 题型解法：本题考查了圆周角定理和圆内接四边形的 性质，作出辅助线构建圆内接四边形是解题的关键．
-10-
3.4 圆周角和圆心角的关系
■考点四 圆内接四边形
定义
四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个 圆叫做四边形的外接圆
推论 圆内接四边形的对角互补
拓展 圆内接四边形的任何外角等于内对角
注意 并不是所有的四边形都存在外接圆，只有对角互补的四边形才存在外接圆
-11-
3.4 圆周角和圆心角的关系
A． 20° B． 40°
C． 50° D． 70°
-7-
3.4 圆周角和圆心角的关系
3. 如图，已知△ABC 的三个顶点都在同一圆上，且 AC=6，BC=8，AB=10， 则该圆的半径长是 ________.
（第 3 题图）
（第 4 题图）
4. 如图，AB=BC，∠ABC =120°，AD 为 ⊙O 的直径 ，AD=6，那么 AB 的
值为 ______.
-8-
3.4 圆周角和圆心角的关系
5. 如图，AB=AC，AB 是直径，求证：BC=2DE． （第 5 题图）
-18-
3.4 圆周角和圆心角的关系
解析：如解析图，连接 AB，DE，则∠ABE=∠ADE. ∵ 所对的圆心角的度数为 50°，∴∠ABE= ∠ADE =25°. ∵ 点 A，B，C，D 在 ⊙O 上 ，∴四边形 ABCD 是圆内接四边形， ∴∠ABC+∠ADC=180°， ∴∠ABE+∠EBC+∠ADC=180°， ∴∠EBC+∠ADC=180°-∠ABE=180°-25°=155°． 答案：155° 题型解法：本题考查了圆周角定理和圆内接四边形的 性质，作出辅助线构建圆内接四边形是解题的关键．
-10-
3.4 圆周角和圆心角的关系
■考点四 圆内接四边形
定义
四边形的四个顶点都在同一个圆上，这个四边形叫做圆内接四边形，这个 圆叫做四边形的外接圆
推论 圆内接四边形的对角互补
拓展 圆内接四边形的任何外角等于内对角
注意 并不是所有的四边形都存在外接圆，只有对角互补的四边形才存在外接圆
-11-
3.4 圆周角和圆心角的关系
A． 20° B． 40°
C． 50° D． 70°
-7-
3.4 圆周角和圆心角的关系
3. 如图，已知△ABC 的三个顶点都在同一圆上，且 AC=6，BC=8，AB=10， 则该圆的半径长是 ________.
（第 3 题图）
（第 4 题图）
4. 如图，AB=BC，∠ABC =120°，AD 为 ⊙O 的直径 ，AD=6，那么 AB 的
值为 ______.
-8-
3.4 圆周角和圆心角的关系
5. 如图，AB=AC，AB 是直径，求证：BC=2DE． （第 5 题图）
圆周角定理 课件
2 点评：只要是在圆中考查角的关系，那么就要考虑弧的 中介作用．
已知AD是△ABC的高，AE是△ABC的外接 圆的直径，求证：∠BAE＝∠DAC.
分析：题目中出现圆的直径，想到直径所对的圆周角 是直角．因此，连结BE，得到∠ABE＝90°，同时，在 △ABE与△ADC中，又有同弧所对的圆周角∠C与∠E相等， 从而结论得以证明．
圆周角定理
1．圆周角定理：圆上一条弧所对的圆周角等于它所对的圆 心角的________．
应当注意的是，圆周角与圆心角一定是对着__________，它 们才有上面定理中所说的数量关系．
2．圆心角定理：圆心角的度数________它所对弧的度数．
3．圆周角定理的推论：
推论1：同弧或等弧所对的圆周角________；同圆或等圆中， 相等的圆周角所对的弧________．
所以 AD=BD= 5 3 (cm)．在 Rt△AOD 中，OD= OA2 AD2 2
= 5 (cm)，所以∠OAD=30，所以∠AOD=60.所以∠AOB= 2
2∠AOD=120，所以∠ACB= 1 ∠AOB=60.因为∠AOB=120， 2
所以 AEB 的度数为 120， ACB 的度数为 240.所以∠AEB= 1 240=120.所以此弦所对的圆周角为 60或 120. 2
推论2：半圆(或直径)所对的圆周角是________；90°的圆 周角所对的弦是________．
1．一半 同一条弧 2.等于
3.相等 也相等 直角 直径
在半径为5 cm的圆内有长为5 3 cm的弦AB，求 此弦所对的圆周角．
OD 经过圆心，
点评：弦所对的圆周角有两个，易丢掉120°而导致错
误．另外，求圆周角时应用到解三角形的知识．
已知AD是△ABC的高，AE是△ABC的外接 圆的直径，求证：∠BAE＝∠DAC.
分析：题目中出现圆的直径，想到直径所对的圆周角 是直角．因此，连结BE，得到∠ABE＝90°，同时，在 △ABE与△ADC中，又有同弧所对的圆周角∠C与∠E相等， 从而结论得以证明．
圆周角定理
1．圆周角定理：圆上一条弧所对的圆周角等于它所对的圆 心角的________．
应当注意的是，圆周角与圆心角一定是对着__________，它 们才有上面定理中所说的数量关系．
2．圆心角定理：圆心角的度数________它所对弧的度数．
3．圆周角定理的推论：
推论1：同弧或等弧所对的圆周角________；同圆或等圆中， 相等的圆周角所对的弧________．
所以 AD=BD= 5 3 (cm)．在 Rt△AOD 中，OD= OA2 AD2 2
= 5 (cm)，所以∠OAD=30，所以∠AOD=60.所以∠AOB= 2
2∠AOD=120，所以∠ACB= 1 ∠AOB=60.因为∠AOB=120， 2
所以 AEB 的度数为 120， ACB 的度数为 240.所以∠AEB= 1 240=120.所以此弦所对的圆周角为 60或 120. 2
推论2：半圆(或直径)所对的圆周角是________；90°的圆 周角所对的弦是________．
1．一半 同一条弧 2.等于
3.相等 也相等 直角 直径
在半径为5 cm的圆内有长为5 3 cm的弦AB，求 此弦所对的圆周角．
OD 经过圆心，
点评：弦所对的圆周角有两个，易丢掉120°而导致错
误．另外，求圆周角时应用到解三角形的知识．
《圆周角》精品课件
任意一点（除点A、B外），那么，∠ACB就是直径AB
所对的圆周角，想一想，∠ACB会是怎样的角？
解：∵OA=OB=OC，
C
∴△AOC,△BOC都是等腰三角形.
·
B
∴ ∠OAC=∠OCA，∠OBC=∠OCB.
A
O
又∵ ∠OAC+∠OBC+∠ACB=180°，
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
圆周角和直径的关系：
半圆（或直径）所对的圆周角是直角，90°的
圆周角所对的弦是直径.
例 如图，⊙O 的直径 AB 为 10 cm，弦 AC为 6 cm，
∠ACB 的平分线交⊙O于点D，求BC，AD，BD的长．
解：如图，连接OD，
∵AB 是直径，∴ ∠ACB= ∠ADB= 90°.
∵CD平分∠ACB，∴∠ACD=∠BCD.
∵△AOC和△BOC是等腰三角形,
∴∠AOD=2∠ACO,∠BOD=2∠BCO,
D
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
1
∴ ∠ = ∠.
2
D
②如图，当圆心O在∠ACB外时，连接CO，并
延长交圆于点D.
∵△AOC和△BOC是等腰三角形,
C
∴∠AOD=2∠ACO,∠BOD=2∠BCO,
新知探究 跟踪训练
1.如图所示，∠BAC 是圆周角的是( A
)
圆周角:顶点在圆上，并且两边都与圆相交的角.
新知探究 知识点2
如图所示，圆周角∠ACB与圆心角∠AOB所对的弧相等，
那么它们之间是否存在什么关系呢？下面我们就来研究
这个问题.
①如图,当圆心O在∠ACB内时,连接CO,
所对的圆周角，想一想，∠ACB会是怎样的角？
解：∵OA=OB=OC，
C
∴△AOC,△BOC都是等腰三角形.
·
B
∴ ∠OAC=∠OCA，∠OBC=∠OCB.
A
O
又∵ ∠OAC+∠OBC+∠ACB=180°，
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
圆周角和直径的关系：
半圆（或直径）所对的圆周角是直角，90°的
圆周角所对的弦是直径.
例 如图，⊙O 的直径 AB 为 10 cm，弦 AC为 6 cm，
∠ACB 的平分线交⊙O于点D，求BC，AD，BD的长．
解：如图，连接OD，
∵AB 是直径，∴ ∠ACB= ∠ADB= 90°.
∵CD平分∠ACB，∴∠ACD=∠BCD.
∵△AOC和△BOC是等腰三角形,
∴∠AOD=2∠ACO,∠BOD=2∠BCO,
D
∴∠AOB=∠AOD+∠BOD=2∠ACO+2∠BCO=2∠ACB,
1
∴ ∠ = ∠.
2
D
②如图，当圆心O在∠ACB外时，连接CO，并
延长交圆于点D.
∵△AOC和△BOC是等腰三角形,
C
∴∠AOD=2∠ACO,∠BOD=2∠BCO,
新知探究 跟踪训练
1.如图所示，∠BAC 是圆周角的是( A
)
圆周角:顶点在圆上，并且两边都与圆相交的角.
新知探究 知识点2
如图所示，圆周角∠ACB与圆心角∠AOB所对的弧相等，
那么它们之间是否存在什么关系呢？下面我们就来研究
这个问题.
①如图,当圆心O在∠ACB内时,连接CO,
《圆周角》PPT课件
O
1.(2008东莞调研文、理)如图所示,圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则圆O的半径等于 ．ABOD
C
分析：由射影定理得
2.如图, ⊙O的直径 AB 为10cm,弦AC为6cm,∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长.
我能行
3.如图，BC为⊙O的直径，AD⊥BC，垂足为D， ，BF和AD相交于E，求证：AE=BE。
比一比，看谁最快！
2、如上题图，若∠3=∠7，则____=____.
圆周角定理的推论3：
半圆（或直径）所对的圆周角是 ， 90°的圆周角所对的弦是 。
直角
直径
如图，∠AC1B=∠AC2B=∠AC3B=
例1 如图，AD是△ABC的高，AE是△ABC的外接圆直径。求证：
A
B
C
D
E
顶点在圆上，并且两边都与圆相交的角叫做圆周角。
顶点在圆心的角叫做圆心角。
什么叫做圆周角？圆心角呢?
下列各图中的∠CDE哪些是圆周角?
E
⑴
⑵
⑶
⑷
√
×
√
×
看一看,谁理解?
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系?
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理：
1、如图，∠A是⊙O的圆周角，∠BOC=80°，则∠A= ，2、如图，∠E=46°则∠DOC=_____,∠OCD=______.
∴AE=BE
3.3 圆周角定理
- .
本节学习目标：1、理解圆周角定理、圆心角定理以及两个 推论；2、会利用圆周角定理、圆心角定理以及 两个推论进行计算、证明。
右图中 所对的圆周角是 ， 所对的圆心角是 .
1.(2008东莞调研文、理)如图所示,圆O上一点C在直径AB上的射影为D，CD=4，BD=8，则圆O的半径等于 ．ABOD
C
分析：由射影定理得
2.如图, ⊙O的直径 AB 为10cm,弦AC为6cm,∠ACB 的平分线交⊙O于 D, 求BC、AD、BD的长.
我能行
3.如图，BC为⊙O的直径，AD⊥BC，垂足为D， ，BF和AD相交于E，求证：AE=BE。
比一比，看谁最快！
2、如上题图，若∠3=∠7，则____=____.
圆周角定理的推论3：
半圆（或直径）所对的圆周角是 ， 90°的圆周角所对的弦是 。
直角
直径
如图，∠AC1B=∠AC2B=∠AC3B=
例1 如图，AD是△ABC的高，AE是△ABC的外接圆直径。求证：
A
B
C
D
E
顶点在圆上，并且两边都与圆相交的角叫做圆周角。
顶点在圆心的角叫做圆心角。
什么叫做圆周角？圆心角呢?
下列各图中的∠CDE哪些是圆周角?
E
⑴
⑵
⑶
⑷
√
×
√
×
看一看,谁理解?
如图,观察圆周角∠ACB与圆心角∠AOB,它们的大小有什么关系?
一条弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理：
1、如图，∠A是⊙O的圆周角，∠BOC=80°，则∠A= ，2、如图，∠E=46°则∠DOC=_____,∠OCD=______.
∴AE=BE
3.3 圆周角定理
- .
本节学习目标：1、理解圆周角定理、圆心角定理以及两个 推论；2、会利用圆周角定理、圆心角定理以及 两个推论进行计算、证明。
右图中 所对的圆周角是 ， 所对的圆心角是 .
圆周角定理 课件
∴ACDD＝BEDD，即63＝E5D，
∴ED＝2.5 cm. 【名师点评】 和圆周角有关的线段、角的计算，不仅可以 通过计算弧、圆心角、圆周角的度数来求相关的角、线段， 有时，还可以通过比例线段，相似比来计算．
又 OB＝OC，∴∠OCB＝∠OBC＝30°， ∴∠BOD＝60°，∴∠CAB＝∠BOD. (2)在 Rt△ABC 中，∠ABC＝30°，得 AC＝12AB， 又 OB＝12AB，∴AC＝OB. 由 BD 切⊙O 于点 B，得∠OBD＝90°. 在△ABC 和△ODB 中，
∠CAB＝∠BOD ∠ACB＝∠OBD ， AC＝OB
的弦是直__径__．
考点突破
考点一 与圆周角定理相关的证明 例1 (高考课标全国卷)如图，D，E 分别为△ABC 边 AB ，AC 的中点，直线 DE 交△ABC 的外接圆于 F ，G 两点．若 CF ∥ AB ，
证明：(1) CD＝BC；
(2)△BCD∽△GBD. 【证明】 (1)因为 D，E 分别为 AB，AC 的中点，所以 DE ∥BC.又已知 CF∥AB，故四边形 BCFD 是平行四边形，所以 CF＝BD＝AD.而 CF∥AD，连接 AF，所以四边形 ADCF 是 平行四边形，故 CD＝AF.
圆周角定理
1．圆周角定理 圆上一条弧所对的圆周角等于它所对的圆心角的_一__半__． 应当注意的是，圆周角与圆心角一定是对着_同__一__条__弧____，它
们才有上面定理中所说的数量关系．
2．圆心角定理 圆心角的度数_等__于___它所对弧的度数． 3．圆周角定理的推论 推论 1：同弧或等弧所对的圆周角相__等__；同圆或等圆中，相等 的圆周角所对的弧也相__等__． 推论 2：半圆(或直径)所对的圆周角是直__角__；90°的圆周角所对
∴ED＝2.5 cm. 【名师点评】 和圆周角有关的线段、角的计算，不仅可以 通过计算弧、圆心角、圆周角的度数来求相关的角、线段， 有时，还可以通过比例线段，相似比来计算．
又 OB＝OC，∴∠OCB＝∠OBC＝30°， ∴∠BOD＝60°，∴∠CAB＝∠BOD. (2)在 Rt△ABC 中，∠ABC＝30°，得 AC＝12AB， 又 OB＝12AB，∴AC＝OB. 由 BD 切⊙O 于点 B，得∠OBD＝90°. 在△ABC 和△ODB 中，
∠CAB＝∠BOD ∠ACB＝∠OBD ， AC＝OB
的弦是直__径__．
考点突破
考点一 与圆周角定理相关的证明 例1 (高考课标全国卷)如图，D，E 分别为△ABC 边 AB ，AC 的中点，直线 DE 交△ABC 的外接圆于 F ，G 两点．若 CF ∥ AB ，
证明：(1) CD＝BC；
(2)△BCD∽△GBD. 【证明】 (1)因为 D，E 分别为 AB，AC 的中点，所以 DE ∥BC.又已知 CF∥AB，故四边形 BCFD 是平行四边形，所以 CF＝BD＝AD.而 CF∥AD，连接 AF，所以四边形 ADCF 是 平行四边形，故 CD＝AF.
圆周角定理
1．圆周角定理 圆上一条弧所对的圆周角等于它所对的圆心角的_一__半__． 应当注意的是，圆周角与圆心角一定是对着_同__一__条__弧____，它
们才有上面定理中所说的数量关系．
2．圆心角定理 圆心角的度数_等__于___它所对弧的度数． 3．圆周角定理的推论 推论 1：同弧或等弧所对的圆周角相__等__；同圆或等圆中，相等 的圆周角所对的弧也相__等__． 推论 2：半圆(或直径)所对的圆周角是直__角__；90°的圆周角所对
人教版九年级上册 24.1.4 圆周角 课件30张
五、思维拓展
与圆有关的角除了圆心角、圆周角还有其 它的角，比较∠A、∠D、∠E的大小关系，你 有什么发现？能说明你的结论吗？
D’
A
E’ E
D
B
C
练习. 如图，在⊙O中，BC=2DE,∠BOC=84°，求
∠A的度数.
C E
A
O
D
B
活动六：反思提升
目标检测
1.如左图，OA、OB、OC都是⊙O的半径，
24.1.4圆周角
一、温故探新 定义 顶点在圆心的角叫做圆心角.
O
B
C
二、建立概念
圆周角
类 比 思
定义 顶点在圆上， 并且两边都和圆相交 的角叫做圆周角.
想
圆心角
B C
· · B 定义O 顶点A 在圆心 O
A
的角叫做圆心角.
C
（1）√
（2） ×
A O
B
C
A C
·O
B
（3）×
圆周角
定义 顶点在圆上， 并且两边都和圆相交 的角叫做圆周角.
四边形ABCD的对角线.填空：
(1)∠1=∠ 4 ; (2)∠2=∠ 7 ; (3)∠3=∠ 6 ; (4)∠5=∠ 8 .
1.如图，点A、B、C都在⊙O上. （1）若∠AOC=120°，则求∠ABC的度数. （2）写出∠AOC与∠ABC的数量关系.
O
C
A
B
2.如图，点A、B、C都在⊙O上. ∠AOB = 2∠BOC. 请说明∠ACB = 2∠BAC.
O
C
A
B
一、温故探新 定义 顶点在圆心的角叫做圆心角. 性质 弧的度数等于它所对圆心角的度数.
O
B
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
同弧 所对的圆周角相等.
∠ACB= ∠ADB
小试牛刀
试找出下图中所有相等的圆周角。
1 2
D
︵ 3 ︵ 4
A
8 7
.
6
B
5
C
A O B C B
A O C B
A O C D
D
结论：
一条弧所对的圆周角等于这条 弧所对的圆心角的一半.
例：已知⊙O中弦AB的长
等于半径， 求弦AB所对的圆心角 和圆周角的度数。
1.圆心角的定义?
顶点在圆心的角叫圆心角..圆心角、弧、弦之间的关系 在同圆或等圆中，两 个圆心角、两条弧、 两条弦中如果有一组 量相等，则它们所 对应的其余各组量也 分别对应相等.
A＇ B＇ O B A
1、如图，∠AOB是什么角？ 它所对的弧是哪一段弧？ ∠ACB与 ∠AOB 有何异同点？
则∠BPC等于（
A.30° B.60° C.90°
）
D.45°
A P
B
3、如图，∠A是圆O的圆周角， ∠A=40°，求∠OBC的度数。
4、
如图，AB是⊙O的直径，CD是 弦，若∠ACD=40°，则∠BOD 的度数为
C
A O . B
D
5.如图，△ABC的顶点A、B、C都在⊙O上，
∠C＝30°，AB＝2，则⊙O的半径是多少？
C
O
A B
6. 如图，以 ABCD的一边AB为直 径作⊙O， ⊙O过点C，若 ∠AOC=70 °，则∠BAD的度数为
D
A O . C B
谈谈你的收获吧
作业
阅读课本85 至86页内容
C
B O A
圆周角的 概念 ：
顶点在圆上， 两边与圆相交的角, 是圆周角。
特征： ① 角的顶点在圆上. ② 角的两边都与圆相交.
辨别是非
1.判别下列各图形中的角是不是圆周角。
①
②
③
⑤
④
⑥
⑦
如图所示，∠ADB、∠ACB、∠AOB
有何共同点？ 它们 分别是什么角？ ∠ADB与∠ACB有什么关系？
结论：
练习
1、在圆中，一条弧所对的圆心角和
圆周角分别为（2x+100）°和
（5x-30）°，求这条弧所对的 圆心角和圆周角的度数。
1、如图，在⊙O中，∠ABC=50°， 则∠AOC等于（ ）
B O
A
A.50°
B.80°
C.90°
D.100°
C
C
2、如图，△ABC是等边三角形，动点P在 圆周的劣弧AB上，且不与A、B重合，
∠ACB= ∠ADB
小试牛刀
试找出下图中所有相等的圆周角。
1 2
D
︵ 3 ︵ 4
A
8 7
.
6
B
5
C
A O B C B
A O C B
A O C D
D
结论：
一条弧所对的圆周角等于这条 弧所对的圆心角的一半.
例：已知⊙O中弦AB的长
等于半径， 求弦AB所对的圆心角 和圆周角的度数。
1.圆心角的定义?
顶点在圆心的角叫圆心角..圆心角、弧、弦之间的关系 在同圆或等圆中，两 个圆心角、两条弧、 两条弦中如果有一组 量相等，则它们所 对应的其余各组量也 分别对应相等.
A＇ B＇ O B A
1、如图，∠AOB是什么角？ 它所对的弧是哪一段弧？ ∠ACB与 ∠AOB 有何异同点？
则∠BPC等于（
A.30° B.60° C.90°
）
D.45°
A P
B
3、如图，∠A是圆O的圆周角， ∠A=40°，求∠OBC的度数。
4、
如图，AB是⊙O的直径，CD是 弦，若∠ACD=40°，则∠BOD 的度数为
C
A O . B
D
5.如图，△ABC的顶点A、B、C都在⊙O上，
∠C＝30°，AB＝2，则⊙O的半径是多少？
C
O
A B
6. 如图，以 ABCD的一边AB为直 径作⊙O， ⊙O过点C，若 ∠AOC=70 °，则∠BAD的度数为
D
A O . C B
谈谈你的收获吧
作业
阅读课本85 至86页内容
C
B O A
圆周角的 概念 ：
顶点在圆上， 两边与圆相交的角, 是圆周角。
特征： ① 角的顶点在圆上. ② 角的两边都与圆相交.
辨别是非
1.判别下列各图形中的角是不是圆周角。
①
②
③
⑤
④
⑥
⑦
如图所示，∠ADB、∠ACB、∠AOB
有何共同点？ 它们 分别是什么角？ ∠ADB与∠ACB有什么关系？
结论：
练习
1、在圆中，一条弧所对的圆心角和
圆周角分别为（2x+100）°和
（5x-30）°，求这条弧所对的 圆心角和圆周角的度数。
1、如图，在⊙O中，∠ABC=50°， 则∠AOC等于（ ）
B O
A
A.50°
B.80°
C.90°
D.100°
C
C
2、如图，△ABC是等边三角形，动点P在 圆周的劣弧AB上，且不与A、B重合，