3.第三讲直线与平面的投影
第3讲 直线的投影

正垂线
(V )
侧垂线
(W )
投影面垂直线
立体图
投影图
Z
X
o
YW
YH Z
X
o
YW
YH Z
X
o
YW
YH
(3) 一般位置直线
V
Z
b
a
W
a
b
X
O
YW
b
H a
YH
投影特性:三个投影皆为倾斜直线,
均不反映实长、夹角.
归纳 直线相对于投影面的位置
一般位置线
投影面平行线
水平线: ∥H面 正平线: ∥V面 侧平线: ∥W面 投影面垂直线
直线的投影
直线的投影由两端点同名投影的连线确定
Z
b'
b"
a' X
a
o b
YH
a" YW
(1) 投影面的平行直线
Z
a b
a
b
a
b
A
a
B
X
o
YW
b
a
a
b
b
投影特性
1.在平行投影面上的投影反映实长
及与另两投影面的倾角
2.另两投影分别平行相应的投影轴
YH α=AB^H β =AB^V γ =AB^W
Z 连线⊥Z
b′ c″ b″
P11
a″ d″
YW
b
d
YH 交叉 两直线
Z
a′ c′ a″ c″
b′
X
a
d′ d″ d
b″ YW
b
c
YH 交叉 两直线
11-1
点、直线及平面的投影

X
a●
O
a●
H
3、点的两面投影特性
(1)点的投影连线垂直于投影轴。 即a´a⊥OX.
O (2)点的投影与投影轴的距离, 等 于该点与相邻投影面的距离。 即axa′=aA axa=a'A
3.1.2 点在三面投影体系中的投影
1、三投影面体系的组成
投影面
Z V
Hale Waihona Puke ◆正立投影面(简称正投影面或V面)
◆水平投影面(简称水平面或H面) X ◆侧立投影面(简称侧面或W面)
3.1.1 点在两投影面体系中的投影
2、点的两面投影图
V
a
点A的正面投影
a●
A
a
点A的水平投影
X ax
●
O
a● H
注意: 空间点用大写字母 表示,点的投影用 小写字母表示。
立体图
3.1.1 点在两投影面体系中的投影
2、点的两面投影图
投影面展开
V a
●
V a
●
A
X ax
●
不动
向下翻 O
X ax
a● H
A●
B
●
M●
A●
B●
●
a≡b≡m
●b a●
●B
A●
●b a●
直线垂直于投影面 投影重合为一点
积聚性
直线平行于投影面 投影反映线段实长
ab=AB
直线倾斜于投影面 投影比空间线段短
ab=AB.cos
3.2.1 直线及直线上点的投影特性
3、直线上点的投影特性
V
b′
b ′ Z b″
c′
c″
c ′ B b″
b’
工程制图 点、直线及平面的投影

工程制图
B b b
A a
a
a
b
Z
b
a
a
X a
b
O
YW
b
YH
27
工学院 机械系 张文斌
红河学院
从属于V 投影面的铅垂线
工程制图
Z
a
a
b
b
X
O
YW
a(b)
YH
28
工学院 机械系 张文斌
红河学院
从属于OX轴的直线
工程制图
Z
X a
b O
YW
(b)
a
b a(b)
YH
29
工学院 机械系 张文斌
红河学院
二、一般位置直线
(2) 正垂线
(3) 侧垂线
3.从属于投影面的直线
从属于投影面的直线
从属于投影面的铅垂线
从属于投影轴的直线 二、一般位置直线
20
工学院 机械系 张文斌
红河学院 (1) 水平线 — 只平行于水平投影面的直线 工程制图
z
a b
a
b
a
b
A
a
X
O
YW
B
b a
a
b
b YH
投影特性:1.ab OX ; ab OYW
O
YW
b
a(b)
YH
投影特性:1. a b 积聚 成一点
2. a bOX ; a b OYW 3. a b = a b = AB
24
工学院 机械系 张文斌
红河学院 (2)正垂线— 垂直于正面投影面的直线 工程制图
(a)b
(a)b
z a
b
A
工程图学:点、直线和平面的投影

b′ (b′) B A A ba
b″ a″ a″
B (b″) b″ B Ab a(b) a
a″
⊥H 点 积聚性
Y
∥V、W 直线 实形性
a′b′∥OZ a″b″∥OZ
3).侧垂线
X
Z
a′ a′ (b′) a′ b′
b″ b′
a″ a″
a″(b″) b″ O
YW
⊥W ab∥OX
点
积聚性
a
b b a(b)
过空间点A的投射线与投影面P的交点 即为点A在P面上的投影。
●
A
a
●
点在一个投影面上的投影不能 确定点的空间位置。
P
B2
●
B1
●
●
b
B3
●
采用多面投影。
二.点在两个投影面上的投影 1.两投影面体系的建立
V
X
水平投影面 —— H
正面投影面 —— V 投 影 轴 —— OX
O
2 .两投影面体系中点的投影 V
X
o
◆侧面投影面(简称侧面或W面) 投影轴 OX轴 OY轴 OZ轴 V面与H面的交线 H面与W面的交线 V面与W面的交线
H
Y
三个投影面互相垂 直
2.空间点A在三个投影面上的投影
Z a a a 点A的正面投影 点A的水平投影 X V a ● A ● ●a
o
● a H
W
点A的侧面投影
Y
空间点用大写字母表示,点的 投影用小写字母表示。
由此得出求水平迹点的方法:
(1) 延长直线的正面投影a′b′,与OX轴相交得m′; (2)由m′定出m,则m和m′为所求水平迹点M的两投影。
同理可求得正面迹点N。
点、直线、平面的投影

提示:已知两个视图,要补画其他视图 时,首先应根据已知视图中对应线框的投影 想象其立体图,然后再根据立体图,并结合 投影关系补画其他视图。在想象立体图时, 可从反映该特征最明显的视图入手,忽略图 中的虚线和部分线条想象其基础形体,然后 再考虑其他图线产生的原由。
补画某个视图时,为了防止出现错误,一 定要按该物体的形成过程绘制,切记不要看 到棱边就画,想画哪就画哪。
机械制图
1 点的投影
无论点在空间处于什 么位置,其三面投影仍然 遵守“长对正、高平齐、 宽相等”的投影规律。
1
空间点对于由V、H和W平面组成的投影体系有以下三种位置关系:
当点的x、y、z坐标均不为零时,点的三面投影均落在投影面内,如图下中A点的投影。
当点的x、y、z坐标有一个为零时,空间点在投影面上,其两个投影落在投影轴上。
水平线
正平线
侧平线
若将投影面平 行线与V、H、W面 的夹角定义为α、β 和γ,则该直线和与 其平行的投影面的 夹角为0°,和其他两 个投影面的夹角在 其平行的投影面上 反映真实大小。
3.一般位置直线
一般位置直线和三个投影面均处于倾斜位置,其三个投影均与
2 投影轴倾斜,且投影线段的长小于空间线段的实长,从投影图上也
不能直接反映出空间直线和投影平面的夹角,如下图所示。
3 平面的投影
空间平面对投影面有三种位置关系:平行、垂直和倾斜(一般位置)。
3
1.投影面平行面
水平面
正平面
侧平面
若空间平面平行于一个投影面, 则必垂直于其他两个投影面,这样 的平面称为投影面平行面。平行于 V、H、W投影面的平面分别称为 正平面、水平面和侧平面。投影面 平行面在与其平行的投影面上的投 影反映实形,在其他两个投影面上 的投影积聚成一条直线,且平行于 相应的投影轴,如右表所示。
点、直线、平面的投影.
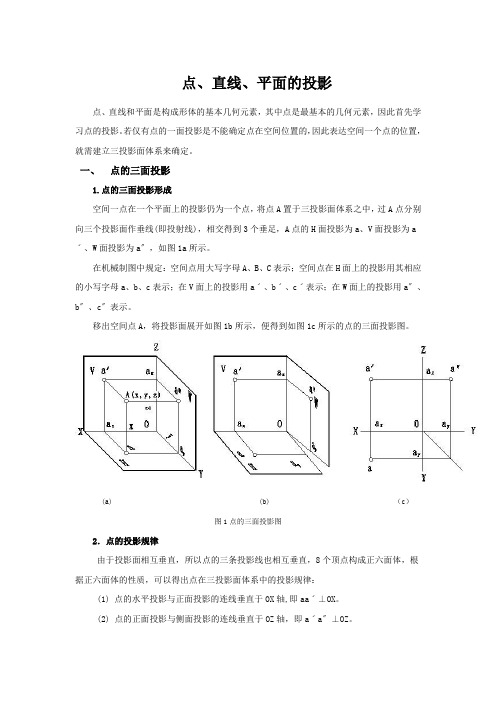
点、直线、平面的投影点、直线和平面是构成形体的基本几何元素,其中点是最基本的几何元素,因此首先学习点的投影。
若仅有点的一面投影是不能确定点在空间位置的,因此表达空间一个点的位置,就需建立三投影面体系来确定。
一、点的三面投影1.点的三面投影形成空间一点在一个平面上的投影仍为一个点,将点A置于三投影面体系之中,过A点分别向三个投影面作垂线(即投射线),相交得到3个垂足,A点的H面投影为a、V面投影为a ˊ、W面投影为a〞,如图1a所示。
在机械制图中规定:空间点用大写字母A、B、C表示;空间点在H面上的投影用其相应的小写字母a、b、c表示;在V面上的投影用aˊ、bˊ、cˊ表示;在W面上的投影用a〞、b〞、c〞表示。
移出空间点A,将投影面展开如图1b所示,便得到如图1c所示的点的三面投影图。
(a) (b) (c)图1点的三面投影图2.点的投影规律由于投影面相互垂直,所以点的三条投影线也相互垂直,8个顶点构成正六面体,根据正六面体的性质,可以得出点在三投影面体系中的投影规律:(1) 点的水平投影与正面投影的连线垂直于OX轴,即aaˊ⊥OX。
(2) 点的正面投影与侧面投影的连线垂直于OZ轴,即aˊa〞⊥OZ。
(3)点的水平投影到OX轴的距离等于侧面投影到OZ轴的距离,即aa x= a〞a z。
3. 点的投影与空间直角坐标的关系点的空间位置也可由直角坐标来确定。
把三投影面体系看成空间直角坐标系,把投影面当做坐标面,投影轴当作坐标轴,O即为坐标原点。
如图2所示,空间点A(x,y,z)到三个投影面的距离可以用直角坐标来表示,即:点A到W面的距离=Oa X=x坐标;点A到V面的距离=aa x=y坐标;点A到H面的距离=a′a x=z坐标。
由此可见,若已知点的直角坐标,可作出点的三面投影。
而点的任何一面投影都反映了点的两个坐标,点的两面投影即可反映点的三个坐标,也就是确定了点的空间位置。
因而,若已知点的任意两个投影,就可作出点的第三面投影。
第三章点、直线、平面的投影
个人收集整理 勿做商业用途 第3章 点、直线、平面的投影
教学大纲规定的知识点 (1) 投影法基本知识 (2) 物体的投影和视图 (3) 物体上的点、直线和平面的投影 (4) 平面内的点和直线 (5) 投影变换
6学时
教学目的和要求 本章通过介绍点、直线和平面的投影特点,使学生熟悉和掌握绘制、阅读工程图样以及图解空间几何问题所需的理论基础。
重点难点 本章的重点就是三视图的形成及其投影规律,点、直线和平面的投影特点,难点是绘制物体的三视图。
学习指导 在学习点、直线和平面的投影时,要和立体的投影结合起来,要用“长对正、高平齐、宽相等"的规律研究几何元素的投影,反过来用几何元素的投影规律研究立体的投影。可结合生产上的管道图研究直线的投影及其应用,生产上的板金图研究平面的投影及其应用.
教学安排 教学内容 习题 第一讲 (1) 投影法基本知识 (2) 物体的投影和视图 习题集3-1
第二讲 (3) 物体上的点、直线和平面的投影 (4) 平面内的点和直线 习题集3—2、3—3
第三讲 (5) 投影变换 习题集3—4 习题集3—5、3-6
【本章的总体教学设计】 首先在第一讲介绍三视图的形成及其投影规律,并介绍三视图的画法,在介绍三视图画法时,紧紧抓住“长对正、高平齐、宽相等”的投影规律和“形体分析法”绘制三视图的步骤,在这儿介绍“形体分析法"目的是从开始就培养学生正确的分析、观察物体的方法,此时的作业模型上不宜出现过多的斜面.然后第二讲介绍点、直线和平面的投影规律,可结合生产上的管道图研究直线的投影及其应用,生产上的板金图研究平面的投影及其应用,一定要将点、线、面的投影和立体的投影结合起来,不宜单纯介绍点、线、面的投影,要用三视图的投影规律分析点、线、面的投影;第三讲介绍绘制三视图综合举例,目的是在研究点、线、面的投影后,利用“线面分析法"研究带斜面的平面立体的投影,可选一些斜面比较多的模型,在绘制三视图时,要将“形体分析法”和“线面分析法”结合起来。第三章重点介绍曲面立体,但在讲曲面立体之前可进一步归纳平面基本体的投影. 个人收集整理 勿做商业用途 第一讲 投影法及三视图的形成 【知识要点】 (1) 中心投影的概念 (2) 斜投影的概念 (3) 正投影的概念 (4) 三视图的形成及其投影规律 (5)画三视图的方法和步骤 【教学方法】用动画和电子挂图介绍三视图的形成及其投影规律,然后介绍三视图的画法,在介绍三视图的画法时,要紧紧抓住形体分析法,从一开始就要同学养成正确观察方法和正确的画图习惯,千万不能看到一条棱就画一条线,不作形体分析。在介绍三视图的画图步骤时,对具体模型可将“形体分析法”和“线面分析法”结合起来,不能等到在组合体中才介绍形体分析法和线面分析法,那样学生如养成了不正确的观察方法和绘图习惯,该就困难了。这样讲为第三章的相贯线和截交线也打下了基础。 【课前准备】准备好上课用的模型和往届学生的作业,教师要画一些示范作业,收集一些生产上用的简单物体的图纸,让同学看一看三视图在生产上的应用。
机械制图机械工业出版社第二版03点、直线、平面的投影
第3章点、直线、平面的投影3.1 点的投影3.2 直线的投影3.3 平面的投影3.4 直线与平面、平面与平面的相对位置3.1 点的投影3.1.1 点在三面体系中的投影3.1.2 特殊位置点的投影3.1.3 两点的相对位置和重影点3.1.1 点在三面体系中的投影1.符号规定空间点:用大写字母投影点:用小写字母a 、b 、c●水平投影a′、b′、c′●正面投影a″、b″、c″等●侧面投影WHV oXa '点A 的正面投影a 点A 的水平投影a "点A 的侧面投影a "●a ●a '●A●ZYWVH三投影面的展开V 面不动,H 面朝下旋转90°,W 面朝右旋转90°。
向右翻向下翻不动a a Za a 'ya ya XY Y O"●●a z●x W(1) 建立三面投影体系V 面:正立投影面H 面:水平投影面W 面:侧立投影面2.点的投影特性a z●a y●a x●WVHa a Za a 'ya ya XY Y O"●●a z●x W(2)点的投影特性①a 'a ⊥OX 轴a 'a "⊥OZ 轴②Aa '=aa x =a "a z =y A (A 到V Aa =a 'a x =a "a y =z A (A 到H 面的距离)Aa "=aa y =a 'a z =x A (A 到W 面的距离)WHV oXa "●a ●a '●A ●ZYa z●a y●a x●x Ay A z A画图注意:投影线为细实线【例3-1 】已知点的两个投影,求第三投影。
a 'aa xa "a 'aa xa za z解法一:通过作45°斜线使a "a z =aa x解法二:用圆规直接量取a "a z =aa xa "a) 解法一b) 解法二XOXO3.点的坐标与投影的关系a) 直观图b) 投影图图3-3 点的坐标与投影关系(1) 空间点可用三个坐标表示,如A点坐标(X A,Y A,Z A)。
