上海市杨浦、静安、宝山、青浦四区2014届下学期高三年级二模考试数学试卷(理科) 有答案

合集下载

上海市杨浦区2014年5月中考二模数学试卷含答案解析(WORD版)

2014年上海市杨浦区中考数学二模试卷参考答案与试题解析一、选择题：（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上】1．（2014•杨浦区二模）点A是数轴上的任意一点，则下列说法正确的是（）A．点A表示的数一定是整数B．点A表示的数一定是分数C．点A表示的数一定是有理数D．点A表示的数可能是无理数考点：实数与数轴．分析：根据数轴上的点与实数一一对应，可得答案．解答：解：数轴上的点与实数一一对性应，故A错误；数轴上的点与实数一一对应，故B错误；根据互为相反数的两个数的绝对值相等，故C错误；数轴上的点与实数一一对应，所以点A有可能是无理数，故D正确；故选：D．点评：本题考查了数轴，注意数轴上的点与实数一一对应．2．（2014•杨浦区二模）下列关于x的方程一定有实数解的是（）+=0 B．=1﹣x C．x2﹣x﹣1=0 D．x2﹣x+1=0A．考点：根的判别式；无理方程；分式方程的解．分析：根据解分式方程、无理方程的步骤和方法以及根的判别式逐一判定即可．解答：解：A、去分母的2﹣1﹣x=0，解得x=1，x﹣1=0，此方程无解，此选项错误；B、两边平方的x﹣2=x2﹣2x+1，x2﹣3x+3=0，△=（﹣3）2﹣4×1×3＜0，此方程无解，此选项错误；C、△=（﹣1）2﹣4×1×（﹣1）＞0，此方程有两个不相等的实数根，此选项正确；D、△=（﹣1）2﹣4×1×1＜0，此方程无解，此选项错误．故选：C．点评：此题考查一元二次方程根的判别式，以及解分式方程和无理方程的步骤．3．某学校为了了解九年级体能情况，随机选取30名学生测试一分钟仰卧起坐次数，并绘制了如图的直方图，学生仰卧起坐次数在25～30之间的频率为（）A．0.1 B．0.17 C．0.33 D．0.4考点：频数（率）分布直方图．专题：应用题；图表型．分析：首先根据频数分布直方图可以知道仰卧起坐次数在25～30之间的频数，然后除以总次数（30）即可得到仰卧起坐次数在25～30之间的频率．解答：解：∵从频数率分布直方图可以知道仰卧起坐次数在25～30之间的频数为12，而仰卧起坐总次数为：3+10+12+5=30，∴学生仰卧起坐次数在25～30之间的频率为12÷30=0.4．故选D．点评：本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题．4．（2014•杨浦区二模）将抛物线y=x2﹣2平移到抛物线y=x2+2x﹣2的位置，以下描述正确的是（）A．向左平移1个单位，向上平移1个单位B．向右平移1个单位，向上平移1个单位C．向左平移1个单位，向下平移1个单位D．向右平移1个单位，向下平移1个单位考点：二次函数图象与几何变换．分析：根据配方法，可化成顶点式，根据两顶点式函数图象的关系，左加右减，上加下减，可得答案．解答：解：y=x2+2x﹣2转化成y=（x+1）2﹣3，将抛物线y=x2﹣2平移到抛物线y=（x+1）2﹣3，图象向左平移了1个单位，向下平移了1个单位，故选：C．点评：本题考查了二次函数图象与几何变换，先化成顶点式，再根据左加右减，上加下减．5．（2014•杨浦区二模）下列图形既是中心对称又是轴对称的是（）A．菱形B．梯形C．正三角形D．正五边形考点：中心对称图形；轴对称图形．分析：根据轴对称图形与中心对称图形的概念求解．解答：解：A、是轴对称图形，也是中心对称图形，故本选项正确；B、不是轴对称图形，也不是中心对称图形，故本选项错误；C、是轴对称图形，不是中心对称图形，故本选项错误；D、是轴对称图形，不是中心对称图形，故本选项错误．故选A．点评：本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后与原图重合．6．（2014•杨浦区二模）下列条件一定能推得△ABC与△DEF全等的是（）A．在△ABC和△DEF中，∠A=∠B，∠D=∠E，AB=DEB．在△ABC和△DEF中，AB=AC，∠A=∠F，FD=FEC．在△ABC和△DEF中，==1，∠B=∠ED．在△ABC和△DEF中，==1，∠B=∠E考点：全等三角形的判定．分析：根据全等三角形的判定定理（SAS，ASA，AAS，SSS）逐个判断即可．解答：解：A、两三角形没有一个相等的条件，不符合全等三角形的判定定理，不能推出两三角形全等，故本选项错误；B、两三角形只有一个相等的条件∠A=∠F，不符合全等三角形的判定定理，不能推出两三角形全等，故本选项错误；C、两三角形只有一个相等的条件∠B=∠E，不符合全等三角形的判定定理，不能推出两三角形全等，故本选项错误；D、能推出AB=DE，BC=EF，∠B=∠E，符合全等三角形的判定定理SAS，能推出两三角形全等，故本选项正确；故选D．点评：本题考查了全等三角形的判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．二、填空题：（本大题共12题，每题4分，满分48分）【请将结果直接填入答题纸的相应位置上】7．（2014•杨浦区二模）计算：+=5．考点：二次根式的加减法．分析：先将二次根式化为最简，然后合并同类二次根式即可．解答：解：原式=2+3=；故答案为：5．点评：本题考查了二次根式的加减，属于基础题，解答本题的关键是掌握二次根式的化简及同类二次根式的合并．8．（2014•杨浦区二模）方程的根是x=2．考点：无理方程．专题：计算题．分析：先把方程两边平方，使原方程化为整式方程x+2=x2，解此一元二次方程得到x1=2，x2=﹣1，把它们分别代入原方程得到x2=﹣1是原方程的增根，由此得到原方程的根为x=2．解答：解：方程两边平方得，x+2=x2，解方程x2﹣x﹣2=0得x1=2，x2=﹣1，经检验x2=﹣1是原方程的增根，所以原方程的根为x=2．故答案为x=2．点评：本题考查了无理方程：根号内含有未知数的方程叫无理方程；解无理方程的基本思想是把无理方程转化为有理方程来解，常常采用平方法去根号．9．（2014•杨浦区二模）如果反比例函数y=的图象在第二、四象限，那么k的取值范围是k＞1．考点：反比例函数的性质．分析：由于反比例函数y=的图象在二、四象限内，则1﹣k＜0，解得k的取值范围即可．解答：解：由题意得，反比例函数y=的图象在二、四象限内，则1﹣k＜0，解得k＞1．故答案为：k＞1．点评：本题考查了反比例函数的性质，重点是注意y=（k≠0）中k的取值，①当k＞0时，反比例函数的图象位于一、三象限；②当k＜0时，反比例函数的图象位于二、四象限．10．（2014•杨浦区二模）函数y=kx+b的大致图象如图所示，则当x＜0时，y的取值范围是y＜1．考点：一次函数与一元一次不等式．分析：观察图象得到直线与y轴的交点坐标为（0，1），且图象从左往右逐渐上升，根据一次函数性质得到y随x的增大而增大，所以当x＜0时，y＜1．解答：解：∵一次函数y=kx+b（k≠0）与y轴的交点坐标为（0，1），且图象从左往右逐渐上升，∴y随x的增大而增大，∴当x＜0时，y＜1．故答案为y＜1．点评：本题考查了一次函数的性质：一次函数y=kx+b（k、b为常数，k≠0）的图象为直线，当k＞0，图象从左往右逐渐上升，y随x的增大而增大；当k＜0，图象从左往右逐渐下降，y随x的增大而减小；直线与y轴的交点坐标为（0，b）．11．（2014•杨浦区二模）黄老师在数学课上给出了6道练习题，要求每位同学独立完成．现将答对的题目数与相应的人数列表如下：答对题目数 2 3 4 5 6相应的人数 1 2 6 8 3则这些同学平均答对 4.5道题．考点：加权平均数．分析：平均数的计算方法是求出所有数据的和，然后除以数据的总个数．解答：解：该组数据的平均数===4.5（道）．故答案为4.5．点评：本题考查的是加权平均数的求法．本题易出现的错误是求2，3，4，5，6这五个数的平均数，对平均数的理解不正确．12．从分别标有1、2、3、4的四张卡片中，一次同时抽2张，其中和为奇数的概率是．考点：列表法与树状图法．分析：依据题意先用列表法或画树状图法分析所有等可能的出现结果，然后根据概率公式求出该事件的概率．解答：解：由树状图可知共有4×3=12种可能，和为奇数的有8种，所以概率是．点评：考查概率的概念和求法，用到的知识点为：概率=所求情况数与总情况数之比．13．（2014•杨浦区二模）在Rt△ABC中，∠C=90°，点D为AB边上的中点，如果=，=，那么=﹣（用，表示）．考点：*平面向量．分析：根据线段中点的定义表示出，再根据向量的三角形法则解答即可．解答：解：∵点D为AB边上的中点，∴==，由三角形法则得，=﹣=﹣．故答案为：﹣．点评：本题考查了平面向量，向量的问题熟练掌握平行四边形法则和三角形法则是解题的关键．14．（2014•杨浦区二模）如果人在一斜坡坡面上前行100米时，恰好在铅垂方向上上升了10米，那么该斜坡的坡度是1：3．考点：解直角三角形的应用-坡度坡角问题．分析：先求出这个人走的水平距离，再根据坡度的定义即可求解．解答：解：由题意得：人在一斜坡坡面上前行100米时，恰好在铅垂方向上上升了10米，则这个人走的水平距离==30，∴坡度i=10：30=1：3．故答案为：1：3．点评：此题主要考查学生对坡度的理解．坡度是坡面的铅直高度h和水平宽度l的比，又叫做坡比，它是一个比值，反映了斜坡的陡峭程度，一般用i表示，常写成i=1：m的形式．15．（2014•杨浦区二模）如图，△ABC中，∠A=80°，∠B=40°，BC的垂直平分线交AB于点D，联结DC．如果AD=2，BD=6，那么△ADC的周长为14．考点：线段垂直平分线的性质；等腰三角形的判定与性质．分析：由BC的垂直平分线交AB于点D，可得CD=BD=6，又由等边对等角，可求得∠BCD的度数，继而求得∠ADC的度数，则可判定△ACD是等腰三角形，继而求得答案．解答：解：∵BC的垂直平分线交AB于点D，∴CD=BD=6，∴∠DCB=∠B=40°，∴∠ADC=∠B+∠BCD=80°，∴∠ADC=∠A=80°，∴AC=CD=6，∴△ADC的周长为：AD+DC+AC=2+6+6=14．故答案为：14．点评：此题考查了线段垂直平分线的性质以及等腰三角形的判定与性质．此题难度适中，注意掌握转化思想与数形结合思想的应用．16．（2014•杨浦区二模）如图，在Rt△ABC中，∠A=90°，∠B=30°，BC=10，以A为圆心画圆，如果⊙A与直线BC相切，那么⊙A的半径长为．考点：切线的性质．分析：此题可以转化为求斜边BC上的高的问题；在Rt△ABC中，∠B=30°，可知∠C=60°；进而在Rt△ADC中，由AC及∠C的正弦值可求得AD的长，即⊙A的半径．解答：解：过点A作AD⊥BC，∵∠A=90°，∠B=30°，∴∠C=60°∵BC=10，∴AC=BC=5，∴AD=AC•sin60°=，故答案为：．点评：此题考查了切线的性质，将由切线求半径的问题转化为解直角三角形的问题是解题的关键．17．（2014•杨浦区二模）如果将点（﹣b，﹣a）称为点（a，b）的“反称点”，那么点（a，b）也是点（﹣b，﹣a）的“反称点”，此时，称点（a，b）和点（﹣b，﹣a）是互为“反称点”．容易发现，互为“反称点”的两点有时是重合的，例如（0，0）的“反称点”还是（0，0）．请再写出一个这样的点：（3，﹣3）．考点：关于原点对称的点的坐标．专题：新定义．分析：首先正确理解题意，然后再找出符合条件的点的坐标即可．解答：解：根据题意可得这样的点是（3，﹣3），故答案为：（3，﹣3）；点评：此题主要考查了点的坐标，关键是正确理解题意．18．（2014•杨浦区二模）如图，在菱形ABCD中，AB=a，∠ABC=α．将菱形ABCD绕点B顺时针旋转（旋转角小于90°），点A、C、D分别落在A′、C′、D′处，当A′C′⊥BC时A′D=2acos﹣a（用含有a和α的代数式表示）．考点：菱形的性质；旋转的性质．分析：当A′C′⊥BC时，D'在BC的延长线上，据此作出图形，利用三角函数求解．解答：解：∵四边形ABCD是菱形，∴对角线AC⊥BD，又∵A'C'⊥BC，∴D'在BC的延长线上．∵∠ABC=α，∴BD=2a•cos，而A'D=BD﹣BA'=2a•cos﹣a．故答案是：2a•cos﹣a．点评：本题考查了菱形的性质，根据菱形的性质，注意到D'和A'的位置，D'在BC的延长线上是关键．三、解答题：（本大题共7题，满分78分）19．（10分）先化简，再求值：，其中．考点：二次根式的化简求值；分式的化简求值．专题：压轴题．分析：把分式化简，然后把x的值代入化简后的式子求值就可以了．解答：解：原式=×+=，当x=+1时，原式==．点评：分式先化简再求值的问题，难度不大．20．（10分）（2014•杨浦区二模）解不等式组：，且写出使不等式组成立的所有整数．考点：解一元一次不等式组；一元一次不等式组的整数解．专题：计算题．分析：分别求出不等式组两不等式的解集，找出解集的公共部分确定出不等式组的解集，找出解集中的所有整数解即可．解答：解：，由①得：x≤3；由②得：x＞﹣2，∴不等式组的解集是﹣2＜x≤3，则使不等式组成立的所有整数是﹣1、0、1、2、3．点评：此题考查了解一元一次不等式组，熟练掌握运算法则是解本题的关键．21．（10分）甲、乙两名运动员进行长跑训练，两人距终点的路程y（米）与跑步时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答问题：（1）他们在进行米的长跑训练，在0＜x＜15的时段内，速度较快的人是；（2）求甲距终点的路程y（米）和跑步时间x（分）之间的函数关系式；（3）当x=15时，两人相距多少米？在15＜x＜20的时段内，求两人速度之差．考点：一次函数的应用．专题：压轴题；图表型．分析：根据图象信息可知，甲运动员图象经过（0，5000）（20，0）所以可用待定系数法求解．距离可根据图象求出，时间可求：20﹣15=5．速度=也就迎刃而解了．解答：解：（1）根据图象信息可知他们在进行5000米的长跑训练，（1分）直线倾斜程度越大表明变化大；甲．（2）设所求直线的解析式为：y=kx+b（0≤x≤20），（1分）由图象可知：b=5000，当x=20时，y=0，∴0=20k+5000，解得k=﹣250．（1分）即y=﹣250x+5000（0≤x≤20）（1分）（3）当x=15时，y=﹣250x+5000=﹣250×15+5000=5000﹣3750=1250．（1分）两人相距：（5000﹣1250）﹣（5000﹣2000）=750（米）．（1分）两人速度之差：=150（米/分）．（1分）点评：找准本题突破点是甲运动员的图象很关键．22．（10分）（2014•杨浦区二模）如图，已知⊙0是△ABC的外接圆，半径长为5，点D、E分别是边AB和边AC是中点，AB=AC，BC=6．求∠OED的正切值．考点：垂径定理；三角形中位线定理；圆周角定理；解直角三角形．分析：连接AO并延长交BC于点H，连接OC，先根据AB=AC得出=，根据垂径定理得出OH及AH的长，由锐角三角函数的定义得出tan∠HAC=tan∠OAE=，再根据D、E分别是边AB和边AC的中点，得出DE∥BC，根据直角三角形的性质得出∠OAE+∠AED=90°，∠AED+∠OED=90°，故可得出∠OAE=∠OED，进而得出结论．解答：解：连接AO并延长交BC于点H，连接OC，∵AB=AC，∴=，∵O为圆心，∴AH⊥BC，BH=HC，∴HC=3，∵半径OC=5，∴OH=4，AH=9，∴在Rt△AHC中，tan∠HAC===，即tan∠OAE=，∵D、E分别是边AB和边AC的中点，∴DE∥BC，∴AH⊥DE，∴∠OAE+∠AED=90°，∵E是边AC的中点，O为圆心，∴OE⊥AC，∴∠AED+∠OED=90°，∴∠OAE=∠OED，∴tan∠OED=tan∠OAE=．点评：本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键．23．（12分）（2014•杨浦区二模）梯形ABCE中，AD∥BC，DC⊥BC，CE⊥AB于点E，点F在边CD 上，且BE•CE=BC•CF．（1）求证：AE•CF=BE•DF；（2）若点E为AB中点，求证：AD•BC=2EC2﹣BC2．考点：相似三角形的判定与性质．专题：证明题．分析：（1）求出∠B=∠DCE，证△BCE∽△CEF，推出∠BCE=∠CEF，推出EF∥BC，根据平行线分线段成比例定理得出即可．（2）求出EF=（AD+BC），根据相似三角形的性质得出CE2=BC•EF，代入求出即可．解答：证明：（1）∵CE⊥AB，∴∠B+∠BCE=90°，∵DC⊥BC，∴∠DCE+∠BCE=90°，∴∠B=∠DCE，∵BE×CE=BC×CF，∴=，∴△BCE∽△CEF，∴∠BCE=∠CEF，∴EF∥BC，∴=，即AE•CF=BE•DF．（2）∵在梯形ABCD中，EF∥BC∥AD，E为AB中点，∴F为DC的中点，∴EF=（AD+BC），∵△BCE∽△CEF，∴，即CE2=BC•EF，∴CE2=（AD+BC）•BC，整理得：AD•BC=2EC2﹣BC2．点评：本题考查了相似三角形的性质和判定，平行线分线段成比例定理，三角形的中位线的应用，主要考查了学生的推理能力，题目比较典型，难度适中．24．（12分）（2014•杨浦区二模）直线y=kx﹣6过点A（1，﹣4），与x轴交于点B，与y轴交于点D，以点A为顶点的抛物线经过点B，且交y轴于点C．（1）求抛物线的表达式；（2）如果点P在x轴上，且△ACD与△PBC相似，求点P的坐标；（3）如果直线l与直线y=kx﹣6关于直线BC对称，求直线l的表达式．考点：二次函数综合题．专题：综合题．分析：（1）将A坐标代入一次函数解析式求出k的值，进而求出B坐标，根据A为抛物线的顶点，设出抛物线顶点形式，将B坐标代入求出a的值，确定出抛物线解析式；（2）由k的值确定出一次函数解析式，求出D的坐标，由抛物线解析式求出C坐标，由A的坐标得到∠DCA=45°，且AC=，CD=3，根据B与C坐标得到∠OCB=45°，可得出∠DCA=∠OCB，由△ACD与△PBC相似，且点P在x轴上，得到点P在B点的左侧，分两种情况考虑：当△BPC∽△ACD时；当△BCP∽△CAD时，分别求出BP的长，即可确定出P的坐标；（3）过点D作DH⊥BC并延长DH到点M，使HM=HD，连接CM、BM，可得直线BM即为直线l，且CM=CD，∠MCH=∠DCH，根据C与D坐标得到CM=CD，根据B与C坐标得到三角形BOC为等腰直角三角形，利用等腰三角形的性质得到∠OCB=45°，进而得到∠MCH=45°，∠MCD=90°，得出MC⊥y轴，确定出M坐标，设直线l的解析式为y=kx+b，将B与M坐标代入求出k与b的值，即可确定出直线l解析式．解答：解：（1）∵y=kx﹣6过点A（1，﹣4），∴﹣4=k﹣6，∴k=2，即y=2x﹣6，令y=0，得到x=3，即B（3，0），∵以点A为顶点的抛物线经过点B，∴设解析式为y=a（x﹣1）2﹣4，将x=3，y=0代入得：0=a（3﹣1）2﹣4，解得：a=1，∴抛物线的表达式为y=x2﹣2x﹣3；（2）∵k=2，∴y=kx﹣6，即y=2x﹣6，∴D（0，﹣6），∵抛物线与y轴交于点C，∴C（0，﹣3），∵A（1，﹣4），∴∠DCA=45°，且AC=，CD=3，∵B（3，0），C（0，﹣3），∴∠OCB=45°，∴∠DCA=∠OCB，∵△ACD与△PBC相似，且点P在x轴上，∴点P在B点的左侧，当△BPC∽△ACD时，=，即=，解得：BP=2；当△BCP∽△CAD时，=，即=，解得：BP=9，∴BP=2或9，∴点P坐标为（1，0）或（﹣6，0）；（3）过点D作DH⊥BC并延长DH到点M，使HM=HD，连接CM、BM，∴直线BM即为直线l，且CM=CD，∠MCH=∠DCH，∵C（0，﹣3），D（0，﹣6），∴CM=CD=3，∵B（3，0），C（0，﹣3），∴∠OCB=45°，∴∠DCH=∠OCB=45°，∴∠MCH=45°，∴∠MCD=90°，即MC⊥y轴，∵MC=CD=3，∴M（﹣3，﹣3），设直线l的解析式为y=kx+b，则，解得：，∴直线l的解析式为y=x﹣．点评：此题属于二次函数综合题，涉及的知识有：待定系数法求函数解析式，坐标与图形性质，相似三角形的判定与性质，等腰直角三角形的判定与性质，熟练掌握待定系数法是解本题的关键．25．（14分）（2014•杨浦区二模）已知梯形ABCD中，AD∥BC，AD=1，BC=2，sinB=，过点C在∠BCD的内部作射线交射线BA于点E，使得∠DCE=∠B．（1）如图1，当ABCD为等腰梯形时，求AB的长；（2）当点E与点A重合时（如图2），求AB的长；（3）当△BCE为直角三角形时，求AB的长．考点：相似形综合题．分析：（1）作AM∥DC交BC于点M，AH⊥BC于点H，AD=1，BC=2，sinB=，得到AM=AB，BH=HM=，结合三角函数的定义可以求得AB的长．（2））由AD∥BC得到∠DAC=∠ACB，又∵∠DCE=∠B，∴△ADC∽△CAB，得到AC2=AD•BC，求得AC 的长度，结合勾股定理，即可构造出关于AB的方程，解方程即可求得相应的AB的长度．（3）分两种情况来讨论：如图3﹣1，当BE⊥CE时，∵∠DCE=∠B，∠B+∠BCE=90°，∴∠DCE+∠BCE=90°，作AH⊥BC，则HC=AD=1，∴BH=BC﹣HC=2﹣1=1，由sinB即可求得cosB的值，继而求得AB的长度；如图3﹣2，当BC⊥CE时，延长DA交CE的延长线于点F，由△FDC∽△CEB，可以得到AE的长度，继而求得AB的长度．解答：解：（1）如图1，作AM∥DC交BC于点M，作AH⊥BC于点H，∵AD∥BC，∴AMCD为平行四边形，∴AM=DC，MC=AD=1，∴BM=BC﹣MC=2﹣1=1，∵四边形ABCD为等腰梯形，∴AB=DC，∴AB=AM，∴BH=HM=在直角三角形ABH中，∵sinB==，∴cosB=，∵，∴．（2）如图2，∵AD∥BC，∴∠DAC=∠ACB，又∵∠DCE=∠B，∴△ADC∽△CAB，∴，∴AC2=AD•BC=2，作AF⊥BC于点F，设AB=x，∵sinB=，∴，在直角三角形AFC中，AF2+CF2=AC2，即：，∴，即当点A与点E重合时，AB=，或者AB=．（3）∵△BCE为直角三角形，∴BE⊥CE或BC⊥CE，情况一，当BE⊥CE时，如图3﹣1，∵∠DCE=∠B，∠B+∠BCE=90°，∴∠DCE+∠BCE=90°，作AH⊥BC，则HC=AD=1，∴BH=BC﹣HC=2﹣1=1，又由sinB=可得，cosB=，解得：．情况二，当BC⊥CE时，如图3﹣2，延长DA交CE的延长线于点F，设AE=a，则，在直角三角形BCE中，∵BC=2，sinB=，∵AD∥BC，BC⊥CE，∴AD⊥EC，又∵∠DCE=∠B，∴△FDC∽△CEB，∴，∴，∴．∴∴当△BCE为直角三角形时，．点评：本题主要考查了相似三角形的判定与性质的综合应用，解答本题的关键在于学会用分类讨论和类比的思想解决问题．。

2014年上海市十三校联考高考数学二模试卷(理科)(2)含详解

2014年上海市十三校联考高考数学二模试卷（理科）（2）一、选择题（12×5分=60分）1．（5分）若复数z=+（a2+2a﹣15）i为实数，则实数a的值是（）A．3B．﹣5C．3或﹣5D．﹣3或5 2．（5分）某西方国家流传这样的一个政治笑话：“鹅吃白菜，参议员先生也吃白菜，所以参议员先生是鹅．”结论显然是错误的，是因为（）A．大前提错误B．小前提错误C．推理形式错误D．非以上错误3．（5分）（+x）dx=（）A．ln2+B．ln2+C．ln2﹣D．ln2+34．（5分）已知a=1+，b=+，c=4，则a，b，c的大小关系为（）A．a＞b＞c B．c＞a＞b C．c＞b＞a D．b＞c＞a 5．（5分）已知f（x）=alnx+x2（a＞0），若对任意两个不等的正实数x1，x2，都有＞2恒成立，则a的取值范围是（）A．（0，1]B．（1，+∞）C．（0，1）D．[1，+∞）6．（5分）已知f（x）=（2x+1）3﹣+3a，若f′（﹣1）=8，则f（﹣1）=（）A．4B．5C．﹣2D．﹣37．（5分）已知正四棱锥S﹣ABCD中，SA=2，那么当该棱锥的体积最大时，它的高为（）A．1B．C．2D．38．（5分）若函数f（x）=e﹣x+ax，x∈R有大于零的极值点，则实数a的取值范围为（）A．a＜1B．0＜a＜1C．﹣1＜a＜0D．a＜﹣19．（5分）设0＜a＜b，且f（x）=，则下列大小关系式成立的是（）A．f （a）＜f （）＜f （）B．f （）＜f （b）＜f （）C．f （）＜f （）＜f （a）D．f （b）＜f （）＜f （）10．（5分）∫01（﹣x）dx=（）A．B．C．D．11．（5分）一个机器人每一秒钟前进或后退一步，程序设计师让机器人以前进3步，然后再后退2步的规律移动．如果将机器人放在数轴的原点，面向正的方向，以1步的距离为1个单位长度．令P（n）表示第n秒时机器人所在位置的坐标，且记P（0）=0，则下列结论中错误的是（）A．P（3）=3B．P（5）=1C．P（2003）＞P（2005）D．P（2003）＜P（2005）12．（5分）对于任意两个正整数m，n，定义某种运算⊗：当m，n都为偶数或奇数时，m⊗n=m+n；当m，n中一个为奇数，另一个为偶数时，m⊗n=m•n．则在上述定义下，集合M={（x，y）|x⊗y=36，x∈N*，y∈N*}中元素的个数为（）A．48B．41C．40D．39二．填空题：（4×5分=20分）13．（5分）由曲线y=x2与x=y2所围成的曲边形的面积为．14．（5分）已知z，ω为复数，i为虚数单位，（1+3i）•z为纯虚数，ω=，且|ω|=5，则复数ω=．15．（5分）已知f（x）为一次函数，且f（x）=x+3f（t）dt，则f（x）=．16．（5分）图1是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律放下去，至第七个叠放的图形中，小正方体木块总数就是．三．解答题（17题10分，其他题每题12分，计70分）17．（10分）已知z为复数，z+2i和均为实数，其中i是虚数单位．（Ⅰ）求复数z；（Ⅱ）若复数（z+ai）2在复平面上对应的点在第一象限，求实数a的取值范围．18．（12分）请观察以下三个式子：①1×3=；②1×3+2×4=；③1×3+2×4+3×5=，归纳出一般的结论，并用数学归纳法证明之．19．（12分）已知：函数f（x）=x3﹣6x+5，x∈R，（1）求：函数f（x）的单调区间和极值；（2）若关于x的方程f（x）=a有3个不同实根，求：实数a的取值范围；（3）当x∈（1，+∞）时，f（x）≥k（x﹣1）恒成立，求：实数k的取值范围．20．（12分）设y=f（x）是二次函数，方程f（x）=0有两个相等的实根，且f′（x）=2x+2．（1）求y=f（x）的表达式；（2）若直线x=﹣t（0＜t＜1）把y=f（x）的图象与两坐标轴所围成图形的面积二等分，求t的值．21．（12分）已知x=1是函数f（x）=（ax﹣2）e x的一个极值点．（a∈R）（Ⅰ）求a的值；（Ⅱ）当x1，x2∈[0，2]时，证明：f（x1）﹣f（x2）≤e．22．（12分）已知函数f（x）=lnax﹣（a≠0）．（Ⅰ）讨论函数f（x）的单调区间；（Ⅱ）当a=1时，是否存在过点（1，﹣1）的直线与函数y=f（x）的图象相切？若存在，有多少条？若不存在，说明理由．2014年上海市十三校联考高考数学二模试卷（理科）（2）参考答案与试题解析一、选择题（12×5分=60分）1．（5分）若复数z=+（a2+2a﹣15）i为实数，则实数a的值是（）A．3B．﹣5C．3或﹣5D．﹣3或5【考点】A1：虚数单位i、复数．【专题】11：计算题．【分析】通过复数的虚部为0，即可求出实数a的值．【解答】解：因为复数为实数，所以a2+2a﹣15=0，解得a=3，或a=﹣5（舍去）．故选：A．【点评】本题考查复数的基本概念，基本知识的考查．2．（5分）某西方国家流传这样的一个政治笑话：“鹅吃白菜，参议员先生也吃白菜，所以参议员先生是鹅．”结论显然是错误的，是因为（）A．大前提错误B．小前提错误C．推理形式错误D．非以上错误【考点】F5：演绎推理．【专题】29：规律型．【分析】本题考查的知识点是演绎推理的基本方法及整数的，在使用三段论推理证明中，如果命题是错误的，则可能是“大前提”错误，也可能是“小前提”错误，也可能是推理形式错误，分析的其大前提，以及小前提，不难得到结论．【解答】解：∵大前提的形式：“鹅吃白菜”，不是全称命题，大前提本身正确，小前提“参议员先生也吃白菜”本身也正确，但是不是大前提下的特殊情况，鹅与人不能类比．∴不符合三段论推理形式，∴推理形式错误，故选：C．【点评】本题考查演绎推理，主要形式就是由大前提、小前提推出结论的三段论推理．三段论推理的依据用集合论的观点来讲就是：若集合M的所有元素都具有性质P，S是M的子集，那么S中所有元素都具有性质P．三段论的公式中包含三个判断：第一个判断称为大前提，它提供了一个一般的原理；第二个判断叫小前提，它指出了一个特殊情况；这两个判断联合起来，揭示了一般原理和特殊情况的内在联系，从而产生了第三个判断结论．演绎推理是一种必然性推理，演绎推理的前提与结论之间有蕴涵关系．因而，只要前提是真实的，推理的形式是正确的，那么结论必定是真实的，但错误的前提可能导致错误的结论．3．（5分）（+x）dx=（）A．ln2+B．ln2+C．ln2﹣D．ln2+3【考点】67：定积分、微积分基本定理．【专题】11：计算题；52：导数的概念及应用．【分析】由定积分运算公式，求出函数的f（x）=+x的一个原函数F（x）=lnx+，利用微积分基本定理即可得到所求积分的值．【解答】解：由积分运算法则，得（+x）dx=（lnx+）=（ln2+）﹣（ln1+）=ln2+故选：A．【点评】本题求一个定积分的值，着重考查了定积分计算公式和微积分基本定理等知识，属于基础题．4．（5分）已知a=1+，b=+，c=4，则a，b，c的大小关系为（）A．a＞b＞c B．c＞a＞b C．c＞b＞a D．b＞c＞a【考点】72：不等式比较大小；7I：不等式的综合．【专题】35：转化思想．【分析】根据，则比较a，b，c的大小关系即可转化为比较2 ，2 ，2×4的大小关系即可．【解答】解：，∵∴∴∴a2＜b2＜c2∴a＜b＜c．故选：C．【点评】此题主要考查了无理数的估算能力，两个正的二次根式比较大小可以通过平方的方法进行，两个式子平方的值大的，对应的式子的值就大．5．（5分）已知f（x）=alnx+x2（a＞0），若对任意两个不等的正实数x1，x2，都有＞2恒成立，则a的取值范围是（）A．（0，1]B．（1，+∞）C．（0，1）D．[1，+∞）【考点】62：导数及其几何意义；6B：利用导数研究函数的单调性．【专题】11：计算题；16：压轴题．【分析】先将条件“对任意两个不等的正实数x1，x2，都有＞2恒成立”转换成当x＞0时，f'（x）≥2恒成立，然后利用参变量分离的方法求出a的范围即可．【解答】解：对任意两个不等的正实数x1，x2，都有＞2恒成立则当x＞0时，f'（x）≥2恒成立f'（x）=+x≥2在（0，+∞）上恒成立则a≥（2x﹣x2）max=1故选：D．【点评】本题主要考查了导数的几何意义，以及函数恒成立问题，同时考查了转化与划归的数学思想，属于基础题．6．（5分）已知f（x）=（2x+1）3﹣+3a，若f′（﹣1）=8，则f（﹣1）=（）A．4B．5C．﹣2D．﹣3【考点】64：导数的加法与减法法则．【专题】11：计算题．【分析】先求出函数的导数，再把x=﹣1代入f′（x）的解析式得到f'（﹣1），再由f'（﹣1）=8，求得a的值，即可得到函数f（x）的解析式，从而求得f （﹣1）的值．【解答】解：已知，∴f′（x）=3（2x+1）2×2+，∵f'（﹣1）=8，∴3×2+2a=8，故有a=1，∴=，∴f（﹣1）=﹣1+2+3=4，故选：A．【点评】本题主要考查函数在某一点的导数的定义，求一个函数的导数的方法，属于基础题．7．（5分）已知正四棱锥S﹣ABCD中，SA=2，那么当该棱锥的体积最大时，它的高为（）A．1B．C．2D．3【考点】LF：棱柱、棱锥、棱台的体积．【专题】11：计算题；16：压轴题．【分析】设出底面边长，求出正四棱锥的高，写出体积表达式，利用求导求得最大值时，高的值．【解答】解：设底面边长为a，则高h==，所以体积V=a2h=，设y=12a4﹣a6，则y′=48a3﹣3a5，当y取最值时，y′=48a3﹣3a5=0，解得a=0或a=4时，当a=4时，体积最大，此时h==2，故选：C．【点评】本试题主要考查椎体的体积，考查高次函数的最值问题的求法．是中档题．8．（5分）若函数f（x）=e﹣x+ax，x∈R有大于零的极值点，则实数a的取值范围为（）A．a＜1B．0＜a＜1C．﹣1＜a＜0D．a＜﹣1【考点】52：函数零点的判定定理．【专题】51：函数的性质及应用．【分析】令函数f（x）的导数为0，求出x=lna﹣1，由x＞0，解出a即可．【解答】解：∵f′（x）=a﹣e﹣x，令f′（x）=0，∴a=e﹣x，∴x=﹣lna=lna﹣1，∵x＞0，∴lna﹣1＞0，∴＞1，∴0＜a＜1，故选：B．【点评】本题考察了函数的零点问题，对数函数的性质，导数的应用，是一道基础题．9．（5分）设0＜a＜b，且f（x）=，则下列大小关系式成立的是（）A．f （a）＜f （）＜f （）B．f （）＜f （b）＜f （）C．f （）＜f （）＜f （a）D．f （b）＜f （）＜f （）【考点】3E：函数单调性的性质与判断；7F：基本不等式及其应用．【专题】11：计算题；51：函数的性质及应用．【分析】明确f（x）=在（0，+∞）上是单调减函数，再由基本不等式明确b＞＞，利用函数的单调性定义来求解．【解答】解：∵0＜a＜b，∴b＞＞又∵f（x）=，∴f′（x）==＜0，∴f（x）=在（0，+∞）上是单调减函数，∴f （b）＜f （）＜f （）故选：D．【点评】本题主要考查指数函数的单调性和基本不等式．解答的关键是在比较大小时体现了函数思想．10．（5分）∫01（﹣x）dx=（）A．B．C．D．【考点】67：定积分、微积分基本定理．【专题】11：计算题．【分析】由积分的形式分析，求解它的值得分为两部分来求，∫01（﹣X）dx=∫01（）dx+∫01（﹣X）dx【解答】解：由题意，∫01（﹣X）dx=∫01（）dx+∫01（﹣X）dx∫01（）dx的大小相当于是以（1，0）为圆心，以1为半径的圆的面积的，故其值为∫01（﹣x）dx=（﹣x2）|01=﹣所以，∫01（﹣X）dx=∫01（）dx+∫01（﹣X）dx=故选：D．【点评】本题考查求定积分，求解本题关键是根据定积分的运算性质将其值分为两部分来求，其中一部分要借用其几何意义求值，在求定积分时要注意灵活选用方法，求定积分的方法主要有两种，一种是几何法，借助相关的几何图形，一种是定义法，求出其原函数，本题两种方法都涉及到了．11．（5分）一个机器人每一秒钟前进或后退一步，程序设计师让机器人以前进3步，然后再后退2步的规律移动．如果将机器人放在数轴的原点，面向正的方向，以1步的距离为1个单位长度．令P（n）表示第n秒时机器人所在位置的坐标，且记P（0）=0，则下列结论中错误的是（）A．P（3）=3B．P（5）=1C．P（2003）＞P（2005）D．P（2003）＜P（2005）【考点】82：数列的函数特性；F4：进行简单的合情推理．【专题】11：计算题．【分析】按“前进3步后退2步”的步骤去算，发现机器人每5秒完成一个循环，解出对应的数值，再根据规律推导，就可得出正确选项【解答】解：根据题中的规律可得：P（0）=0，P（1）=1，P（2）=2，P（3）=3，P（4）=2，P（5）=1，…以此类推得：P（5k）=k （k为正整数）因此P（2003）=403，且P（2005）=401，所以P（2003）＞P（2005）故选：D．【点评】本题主要考查了数列的应用，要注意数轴上点的移动规律是“左减右加”，属于中档题．12．（5分）对于任意两个正整数m，n，定义某种运算⊗：当m，n都为偶数或奇数时，m⊗n=m+n；当m，n中一个为奇数，另一个为偶数时，m⊗n=m•n．则在上述定义下，集合M={（x，y）|x⊗y=36，x∈N*，y∈N*}中元素的个数为（）A．48B．41C．40D．39【考点】12：元素与集合关系的判断．【专题】23：新定义．【分析】根据定义，x⊗y=36分两类进行考虑：x和y一奇一偶，则x•y=36；x 和y同奇偶，则x+y=36．由x、y∈N*列出满足条件的所有可能情况，再考虑点（x，y）的个数即可．【解答】解：x⊗y=36，x、y∈N*，若x和y一奇一偶，则xy=36，满足此条件的有1×36=3×12=4×9，故点（x，y）有6个；若x和y同奇偶，则x+y=36，满足此条件的有1+35=2+34=3+33=4+32=…=35+1，故点（x，y）有35个，∴满足条件的个数为6+35=41个．故选：B．【点评】本题为新定义问题，考查对新定义和集合的理解，正确理解新定义的含义是解决本题的关键．二．填空题：（4×5分=20分）13．（5分）由曲线y=x2与x=y2所围成的曲边形的面积为．【考点】69：定积分的应用．【专题】11：计算题．【分析】由题意，可作出两个曲线y=x2与x=y2的图象，由图象知阴影部分即为所求的面积，本题可用积分求阴影部分的面积，先求出两曲线交点A的坐标，根据曲线确定出被积函数与积分区间[0，1]，计算出定积分的值，即可出面积曲线y2=x，y=x2所围成图形的面积．【解答】解：作出如图的图象…（2分）联立解得，…（5分）即点O（0，0），A（1，1）．故所求面积为：===…（10分）所以所围成图形的面积S=．故答案为：．【点评】本题考查了定积分在求面积中的应用，解题的关键是确定出被积函数与积分区间，熟练掌握积分的运算．14．（5分）已知z，ω为复数，i为虚数单位，（1+3i）•z为纯虚数，ω=，且|ω|=5，则复数ω=±（7﹣i）．【考点】A5：复数的运算；A8：复数的模．【分析】设z=a+bi（a，b∈R），利用复数的运算及（1+3i）•z=（1+3i）（a+bi）=a﹣3b+（3a+b）i为纯虚数，可得．又ω=，|ω|=，可得．即可得出a，b．【解答】解：设z=a+bi（a，b∈R），∵（1+3i）•z=（1+3i）（a+bi）=a﹣3b+（3a+b）i为纯虚数，∴．又ω===，|ω|=，∴．把a=3b代入化为b2=25，解得b=±5，∴a=±15．∴ω=±=±（7﹣i）．故答案为±（7﹣i）．【点评】熟练掌握复数的运算法则、纯虚数的定义及其模的计算公式即可得出．15．（5分）已知f（x）为一次函数，且f（x）=x+3f（t）dt，则f（x）=x ﹣．【考点】3U：一次函数的性质与图象；67：定积分、微积分基本定理．【专题】53：导数的综合应用．【分析】设f（x）=ax+b，根据积分公式，即可求出f（x）的表达式．【解答】解：∵f（x）为一次函数，且f（x）=x+3f（t）dt∴设f（x）=x+b，则f（x）=x+3f（t）dt=x+3（t+b）dt=x+3（）|=x+，∴=b，即b=，∴f（x）=x．故答案为：x【点评】本题主要考查积分的计算，利用待定系数法即可得到结论．比较基础．16．（5分）图1是一个水平摆放的小正方体木块，图2，图3是由这样的小正方体木块叠放而成的，按照这样的规律放下去，至第七个叠放的图形中，小正方体木块总数就是91．【考点】F1：归纳推理．【专题】29：规律型．【分析】先分别观察给出正方体的个数为：1，1+5，1+5+9，…总结一般性的规律，将一般性的数列转化为特殊的数列再求解．【解答】解：分别观察正方体的个数为：1，1+5，1+5+9，…归纳可知，第n个叠放图形中共有n层，构成了以1为首项，以4为公差的等差数列所以∴s7=2×72﹣7=91故答案为：91【点评】本题主要考查归纳推理，其基本思路是先分析具体，观察，总结其内在联系，得到一般性的结论，若求解的项数较少，可一直推理出结果，若项数较多，则要得到一般求解方法，再求具体问题．三．解答题（17题10分，其他题每题12分，计70分）17．（10分）已知z为复数，z+2i和均为实数，其中i是虚数单位．（Ⅰ）求复数z；（Ⅱ）若复数（z+ai）2在复平面上对应的点在第一象限，求实数a的取值范围．【考点】A4：复数的代数表示法及其几何意义；A5：复数的运算．【专题】11：计算题．【分析】（I）设出复数的代数形式，整理出z+2i和，根据两个都是实数虚部都等于0，得到复数的代数形式．（II）根据上一问做出的复数的结果，代入复数（z+ai）2，利用复数的加减和乘方运算，写出代数的标准形式，根据复数对应的点在第一象限，写出关于实部大于0和虚部大于0，解不等式组，得到结果．【解答】解：（Ⅰ）设复数z=a+bi（a，b∈R），由题意，z+2i=a+bi+2i=a+（b+2）i∈R，∴b+2=0，即b=﹣2．又，∴2b+a=0，即a=﹣2b=4．∴z=4﹣2i．（Ⅱ）由（Ⅰ）可知z=4﹣2i，∵（z+ai）2=（4﹣2i+ai）2=[4+（a﹣2）i]2=16﹣（a﹣2）2+8（a﹣2）i对应的点在复平面的第一象限，∴解得a的取值范围为2＜a＜6．【点评】本题考查复数的加减乘除运算，考查复数的代数形式和几何意义，考查复数与复平面上点的对应，考查解决实际问题的能力，是一个综合题．18．（12分）请观察以下三个式子：①1×3=；②1×3+2×4=；③1×3+2×4+3×5=，归纳出一般的结论，并用数学归纳法证明之．【考点】F1：归纳推理；RG：数学归纳法．【专题】55：点列、递归数列与数学归纳法．【分析】观察所给等式，注意等式的左边与右边的特征，得到猜想，然后利用数学归纳法的证明标准，验证n=1时成立，假设n=k是成立，证明n=k+1时等式也成立即可．【解答】解：由于所给的等式的左边，是两两自然数的积再求和的形式，右边是一个分式，分母是6，分子是三个自然数的积，注意自然数与序号之间的关系，所以，猜想：1×3+2×4+3×5+…+n（n+2）=﹣﹣﹣﹣﹣﹣﹣﹣﹣（4分）证明：（1）当n=1时，左边=3，右边=3，等式成立．（2）假设当n=k时，等式成立，即1×3+2×4+3×5+…+k（k+2）=﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（6分）那么，当n=k+1时，1×3+2×4+3×5+…+k（k+2）+（k+1）（k+3）=+（k+1）（k+3）=（2k2+7k+6k+18）=（2k2+13k+18）=，就是说，当n=k+1时等式也成立．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（13分）综上所述，对任何n∈N+都成立．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（14分）【点评】本题考查数学归纳法的应用，归纳推理推出猜想是解题的关键，注意数学归纳法证明时，必须用上假设．属于中档题，19．（12分）已知：函数f（x）=x3﹣6x+5，x∈R，（1）求：函数f（x）的单调区间和极值；（2）若关于x的方程f（x）=a有3个不同实根，求：实数a的取值范围；（3）当x∈（1，+∞）时，f（x）≥k（x﹣1）恒成立，求：实数k的取值范围．【考点】53：函数的零点与方程根的关系；6B：利用导数研究函数的单调性；6D：利用导数研究函数的极值；6E：利用导数研究函数的最值．【专题】11：计算题．【分析】（1）先求函数的导数，令导数等于0，求出极值点，再列表判断极值点左右两侧导数的正负，当左正右负时有极大值，当左负右正时有极小值，且在某区间导数大于0时，此区间为函数的增区间，在某区间导数小于0时，此区间为函数的减区间．（2）由（1）知函数f（x）的大致图象，然后将关于x的方程f（x）=a有3个不同实根，转化为y=f（x）图象与直线y=a有3个不同交点，数形结合解决问题（3）先将f（x）≥k（x﹣1）恒成立，转化为k≤x2+x﹣5在（1，+∞）上恒成立，进而转化为求函数g（x）=x2+x﹣5在（1，+∞）上的值域即可【解答】解：（1）求函数f（x）=x3﹣6x+5的导数，得f'（x）=3（x2﹣2），令f'（x）=0，即3（x2﹣2）=0，解得，列表讨论f′（x）的符号，得xf'（x）+0﹣0+f（x）↗极大值↘极小值↗∴f（x）的单调递增区间是，，单调递减区间是，当x=﹣时，函数有极大值为5+4，当x=时，函数有极小值为5﹣4（2）由（1）的分析可知y=f（x）图象的大致形状及走向如图：若关于x的方程f（x）=a有3个不同实根，即y=f（x）图象与直线y=a有3个不同交点，由图数形结合可得（3）f（x）≥k（x﹣1）即（x﹣1）（x2+x﹣5）≥k（x﹣1）．∵x＞1，∴k≤x2+x﹣5在（1，+∞）上恒成立，令，则g（x）在（1，+∞）上是增函数，∴g（x）＞g（1）=﹣3，∴k≤﹣3．【点评】本题考查了利用导数求函数单调区间和极值的方法，利用导数研究函数图象解决根的个数问题的方法，不等式恒成立问题的解法20．（12分）设y=f（x）是二次函数，方程f（x）=0有两个相等的实根，且f′（x）=2x+2．（1）求y=f（x）的表达式；（2）若直线x=﹣t（0＜t＜1）把y=f（x）的图象与两坐标轴所围成图形的面积二等分，求t的值．【考点】36：函数解析式的求解及常用方法；63：导数的运算；67：定积分、微积分基本定理．【专题】51：函数的性质及应用．【分析】（1）设f（x）=ax2+bx+c，根据f′（x）=2x+2求出a、b的值，再由方程f（x）=0有两个相等的实根，△=0，求得c的值，即可得到函数的解析式．（2）由题意可得（x2+2x+1）dx=（x2+2x+1）dx，即（x3+x2+x）=（x3+x2+x），化简得2（t﹣1）3=﹣1，由此求得t的值．【解答】解：（1）设f（x）=ax2+bx+c，则f′（x）=2ax+b，又因为f′（x）=2x+2，∴a=1，b=2，∴f（x）=x2+2x+c．由于方程f（x）=0有两个相等的实根，∴△=4﹣4c=0，解得c=1，∴f（x）=x2+2x+1．（2）由题意可得（x2+2x+1）dx=（x2+2x+1）dx，即（x3+x2+x）=（x3+x2+x），即﹣t3+t2﹣t+=t3﹣t2+t，∴2t3﹣6t2+6t﹣1=0，即2（t﹣1）3=﹣1，∴t=1﹣．【点评】本题主要考查用待定系数法求函数的解析式，导数的运算，定积分的应用，属于中档题．21．（12分）已知x=1是函数f（x）=（ax﹣2）e x的一个极值点．（a∈R）（Ⅰ）求a的值；（Ⅱ）当x1，x2∈[0，2]时，证明：f（x1）﹣f（x2）≤e．【考点】6D：利用导数研究函数的极值；6E：利用导数研究函数的最值．【专题】15：综合题；53：导数的综合应用．【分析】（I）先求出函数f（x）的导函数，然后根据在极值点处的导数等于0，建立等式关系，求出a即可；（II）确定函数f（x）在区间[0，2]上的最大值与最小值，从而f（x1）﹣f（x2）≤f max（x）﹣f min（x），由此可得到结论．【解答】（Ⅰ）解：已知f′（x）=（ax+a﹣2）e x，f'（1）=0，∴a=1．当a=1时，f′（x）=（x﹣1）e x，在x=1处取得极小值．（Ⅱ）证明：由（Ⅰ）知，f（x）=（x﹣2）e x，f′（x）=（x﹣1）e x．当x∈[0，1]时，f′（x）=（x﹣1）e x≤0，∴f（x）在区间[0，1]单调递减；当x∈（1，2]时，f′（x）=（x﹣1）e x＞0，∴f（x）在区间（1，2]单调递增．所以在区间[0，2]上，f（x）的最小值为f（1）=﹣e，又f（0）=﹣2，f（2）=0，所以在区间[0，2]上，f（x）的最大值为f（2）=0．对于x1，x2∈[0，2]，有f（x1）﹣f（x2）≤f max（x）﹣f min（x）．所以f（x1）﹣f（x2）≤0﹣（﹣e）=e．【点评】本题综合考查函数的极值以及利用导数研究函数的单调性，同时考查函数的最值的求解，是一道综合题．22．（12分）已知函数f（x）=lnax﹣（a≠0）．（Ⅰ）讨论函数f（x）的单调区间；（Ⅱ）当a=1时，是否存在过点（1，﹣1）的直线与函数y=f（x）的图象相切？若存在，有多少条？若不存在，说明理由．【考点】6B：利用导数研究函数的单调性；6H：利用导数研究曲线上某点切线方程．【专题】53：导数的综合应用．【分析】（Ⅰ）求导数，利用导数讨论函数f（x）的单调区间；（Ⅱ）求导数，利用导数的几何意义进行判断．【解答】解析：（1）由题意．…（1分）当a＞0时，函数f（x）的定义域为（0，+∞），f'（x）＞0，则x∈（a，+∞），f'（x）＜0，则x∈（0，a），此时函数在（0，a）上是减函数，在（a，+∞）上是增函数，…（3分）当a＜0时，函数f（x）的定义域为（﹣∞，0），f'（x）＞0，则x∈（a，0），f'（x）＜0，则x∈（﹣∞，a），此时函数在（﹣∞，a）上是减函数，在（a，0）上是增函数．…（5分）（2）假设存在这样的切线，设其中一个切点T，∴切线方程：，将点T坐标代入得：，即，①设，则．令g'（x）=0，则x=1或x=2．…（8分）x（0，1）1（1，2）2（2，+∞）g'（x）+0﹣0+g（x）递增极大值递减极小值递增所以g（x）在区间（0，1），（2，+∞）上是增函数，在区间（1，2）上是减函数，g（x）在x=1处取得极大值g（1）=1，在x=2处取得极小值，所以g（x）＞0在[1，+∞）上恒成立，即g（x）=0在[1，+∞）上无解．因为，g（1）=1＞0，g（x）在区间（0，1）上单调递增，根据零点定理，g（x）在区间（0，1）上有且仅有一个实数根，即方程①有且仅有一解，故符合条件的切线有且仅有一条．…（12分）【点评】本题主要考查利用导数研究函数的性质，要求熟练掌握导数和函数单调性，极值之间的关系，考查学生的运算能力．。

上海市静安、杨浦、青浦、宝山四区2014年高三联合高考模拟考数学试卷(理科)--含答案

上海市静安、杨浦、青浦、宝山 2013—2014学年联合高考模拟考试理科数学试卷（满分150分，完卷时间120分钟） 2014.4一、填空题 (本大题共有14题，满分56分)考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分． 1.二阶行列式ii i ++-1101的值是 . （其中i 为虚数单位）2. 已知j i,是方向分别与x 轴和y 轴正方向相同的两个基本单位向量，则平面向量j i +的模等于 .3．二项式7)1(+x 的展开式中含3x 项的系数值为_______________.4.已知圆锥的母线长为5,侧面积为π15,则此圆锥的体积为__________.(结果中保留π)5.已知集合{}sin ,A y y x x R ==∈，{}21,B x x n n Z ==+∈，则AB = .理6文7.在平面直角坐标系xOy 中，若圆22(1)4x y +-=上存在A ，B 两点，且弦AB 的中点为(1,2)P ，则直线AB 的方程为 .理7文8.已知1log log 22=+y x ，则y x +的最小值为_____________.理8文10. 已知首项31=a 的无穷等比数列{}n a )(*N n ∈的各项和等于4，则这个数列{}n a 的公比是．9．（理）在平面直角坐标系xOy 中，曲线1C 的参数方程为⎩⎨⎧==,sin 2,cos 2ααy x （α为参数），O 为坐标原点，M 为1C 上的动点，P 点满足2OP OM =，点P 的轨迹为曲线2C ．则2C 的参数方程为 .10. 阅读右面的程序框图，运行相应的程序，输出的结果为 .11．（理）从5男和3女8位志愿者中任选3人参加冬奥会火炬接力活动，若随机变量ξ表示所选3人中女志愿者的人数，则ξ的数学期望是．12．（理）设各项均不为零的数列{}n c 中，所有满足01<⋅+i i c c 的正整数i 的个数称为这个数列{}n c 的变号数.第10题图已知数列{}n a 的前n 项和442+-=n n S n ，nn a b 41-=（*N n ∈），则数列{}n b 的变号数为 .13.（理）已知定义在[)+∞,0上的函数)(x f 满足)2(3)(+=x f x f .当[)2,0∈x 时x x x f 2)(2+-=.设)(x f 在[)n n 2,22-上的最大值为n a ，且数列}{n a 的前n 项和为n S ，则=∞→n n S l i m . （其中*N n ∈）14．（理）正方形1S 和2S 内接于同一个直角三角形ABC 中，如图所示，设α=∠A ，若4411=S ，4402=S ，则=α2sin .二、选择题(本大题共有4题，满分20分)每题有且只有一个正确答案，考生应在答题纸相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15. （理）在实数集R 上定义运算*：(1)x y x y *=⋅-．若关于x 的不等式()0x x a *->的解集是集合{|11}x x -≤≤的子集，则实数a 的取值范围是…………………（）.)(A [0,2] )(B [2,1)(1,0]---)(C [0,1)(1,2] )(D [2,0]- 16．“1=ω”是“函数x x x f ωω22cos sin )(-=的最小正周期为π”的…………（）.)(A 充分必要条件 )(B 充分不必要条件 )(C 必要不充分条件 )(D 既不充分又必要条件17. 若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为1S 、2S ,则1S :2S =………………………………………………………………（）. )(A 1:1 )(B 2:1 )(C 3:2 )(D 4:118.（理）函数()f x 的定义域为实数集R ，⎪⎩⎪⎨⎧<≤--≤≤=.01,1)21(,10,)(x x x x f x 对于任意的x R ∈都有(1)(1)f x f x +=-.若在区间[1,3]-上函数()()g x f x mx m =--恰有四个不同的零点，则实数m 的取值范围是…………………………………………（）.ABCDEFS 1αABCPNF S 2αMQ)(A 10,2⎡⎤⎢⎥⎣⎦ )(B 10,4⎡⎫⎪⎢⎣⎭ )(C 10,2⎛⎤ ⎥⎝⎦ )(D 10,4⎛⎤ ⎥⎝⎦三、解答题(本大题共有5题，满分74分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤． 19．（本题满分12分）（理）如图，四棱锥P ABCD -中，底面ABCD 是平行四边形，︒=∠90CAD ，PA ⊥平面ABCD ，1PA BC ==，AB =F 是BC的中点.(1) 求证：DA ⊥平面PAC ；（2）若以A 为坐标原点，射线AC 、AD 、AP 分别是x 轴、y 轴、z 轴的正半轴，建立空间直角坐标系，已经计算得)1,1,1(=是平面PCD 的法向量，求平面PAF 与平面PCD 所成锐二面角的余弦值. 20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分某公司承建扇环面形状的花坛如图所示，该扇环面花坛是由以点O 为圆心的两个同心圆弧AD 、弧BC 以及两条线段AB 和CD 围成的封闭图形．花坛设计周长为30米，其中大圆弧AD 所在圆的半径为10米．设小圆弧BC 所在圆的半径为x 米（100<<x ），圆心角为θ弧度．（1）求θ关于x 的函数关系式；（2）在对花坛的边缘进行装饰时，已知两条线段的装饰费用为4元/米，两条弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为y ，当x 为何值时，y 取得最大值？21．（本题满分14分）本题共有2个小题，第1小题满分5分，第2小题满分9分（理）已知椭圆2222:1x y C a b+=(0)a b >>的右焦点为F (1,0)，短轴的端点分别为12,B B ,且12FB FB a ⋅=-.（1）求椭圆C 的方程；ADC F PB(第20题图)（2）过点F 且斜率为k (0)k ≠的直线l 交椭圆于,M N 两点，弦MN 的垂直平分线与x 轴相交于点D .设弦MN 的中点为P ，试求DPMN的取值范围． 22．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分（理）设函数xx g 3)(=，xx h 9)(=.（1）解方程：)9)((log )8)(2(log 33+=-+x h x g x ；（2）令3)()()(+=x g x g x p ，3)(3)(+=x h x q ，求证：)20142013()20142012()20142()20141()20142013()20142012()20142()20141(q q q q p p p p ++++=++++ （3）若bx g ax g x f +++=)()1()(是实数集R 上的奇函数，且0))(2()1)((>⋅-+-x g k f x h f 对任意实数x恒成立，求实数k 的取值范围. 23．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分（理）设各项都是正整数的无穷数列{}n a 满足：对任意*N n ∈，有1+<n n a a ．记n a n a b =．（1）若数列{}n a 是首项11a =，公比2=q 的等比数列，求数列{}n b 的通项公式；（2）若n b n 3=，证明：21=a ；（3）若数列{}n a 的首项11a =，1+=n a n a c ，{}n c 是公差为1的等差数列．记n nn a d ⋅-=2，n n n d d d d S ++++=-121 ，问：使5021>⋅++n n n S 成立的最小正整数n 是否存在？并说明理由．四区2013学年度高考模拟考试数学试卷文理科解答参考答案及评分标准 2014.04说明1．本解答列出试题一种或几种解法，如果考生的解法与所列解法不同，可参照解答中评分标准的精神进行评分．2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅．当考生的解答在某一步出现错误，影响了后续部分，但该步以后的解答未改变这一题的内容和难度时，可视影响程度决定后面部分的给分，但是原则上不应超出后面部分应给分数之半，如果有较严重的概念性错误，就不给分．3．第19题至第23题中右端所注的分数，表示考生正确做到这一步应得的该题分数． 4．给分或扣分均以1分为单位．一．填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．理1．2； 2．2 3．35； 4．π125．{}1,1-；6． 30x y +-= 7. 22； 8．41 9． ⎩⎨⎧==,sin 4,cos 4ααy x （α为参数）；10. 13811．.895613561525630156100=⨯+⨯+⨯+⨯=ξE 12．3． 13.2314．1012sin =α 3．35； 4．π125．{}1,1-；6．}2,6,2,65{ππππ--7.30x y +-= ； 8．229．37； 10. 41 11. 2213y x -=； 12．1253381556C C C = 13．当1-=ac 时，0lim 622222=⎪⎭⎫⎝⎛++∴⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++∞→nn n n c a c a c a c a ；当1=ac 时，c a =舍去． 14.]41,0(二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答案纸的相应编号上，填上正确的答案，选对得5分，否则一律得零分. 15．D ；16．B ；17．C ；18．理D ；三、解答题（本大题满分74分）本大题共5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤 .19．（理）1(0,0,0),(1,0,0),(1,1,0),(0,1,0),(1,,0),(0,0,1)2A CB D F P --. (1) 证明方法一：Q 四边形是平行四边形，Q PA ⊥平面ABCD ∴PA DA ⊥，又AC DA ⊥，AC PA A =I ，∴DA ⊥平面PAC .方法二：证得DA uu u r是平面PAC 的一个法向量，∴DA ⊥平面PAC .(2)通过平面几何图形性质或者解线性方程组,计算得平面PAF 一个法向量为(1,2,0)m =u r，又平面PCD 法向量为(1,1,1)n =r，所以||cos ,5||||m n m n m n ⋅<>==u r ru r r u r r∴所求二面角的余弦值为5. 20．(1)设扇环的圆心角为θ，则()30102(10)x x θ=++-，所以10210xxθ+=+， (2) 花坛的面积为2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<．装饰总费用为()9108(10)17010x x x θ++-=+，所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++，令17t x =+，则3913243()101010y t t =-+≤，当且仅当t =18时取等号，此时121,11x θ==．答：当1x =时，花坛的面积与装饰总费用的比最大．21．理（1）依题意不妨设1(0,)B b -，2(0,)B b ，则1(1,)FB b =--，2(1,)FB b =-.由12FB FB a ⋅=-，得21b a -=-. 又因为221a b -=，解得2,a b ==.所以椭圆C 的方程为22143x y +=. （2）依题意直线l 的方程为(1)y k x =-.由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(34)84120k x k x k +-+-=.设11(,)M x y ，22(,)N x y ，则2122834k x x k +=+，212241234k x x k -=+. 所以弦MN 的中点为22243(,)3434k kP k k -++.所以MN ===2212(1)43k k +=+.直线PD 的方程为222314()4343k k y x k k k +=--++，由0y =，得2243k x k =+，则22(,0)43k D k +，所以DP =所以224312(1)43DP k k MN k +==++=. 又因为211k +>，所以21011k <<+.所以104<<. 所以DP MN的取值范围是1(0,)4.22．理（1）99)832(3+=-⋅⋅xx x ，93=x ，2=x（2）21323)21()20141007(===p p ，2163)21()20141007(===q q ．因为1333333333333)1()(11=+++=+++=-+--xxx xx xx x p x p ，1393399399399)1()(11=+++=+++=-+--x x x x x x x x q x q所以，211006)20142013()20142()20141(+=+++p p p ， 211006)20142013()20142()20141(+=+++q q q ． )20142013()20142()20141(p p p +++ =)20142013()20142()20141(q q q +++ ．（3）因为bx ax x f +++=)()1()(ϕϕ是实数集上的奇函数，所以1,3=-=b a .)1321(3)(+-=x x f ，)(x f 在实数集上单调递增. 由0))(2()1)((>⋅-+-x g k f x h f 得))(2()1)((x g k f x h f ⋅-->-，又因为)(x f 是实数集上的奇函数，所以，)2)(()1)((-⋅>-x g k f x h f ，又因为)(x f 在实数集上单调递增，所以2)(1)(-⋅>-x g k x h 即23132-⋅>-x x k 对任意的R x ∈都成立，即x x k 313+<对任意的R x ∈都成立，2<k . 23．理（1）1111a b a a ===，242112211--====--n a n n n n a a b ；（2）根据反证法排除11a =和*113()a a N ≥∈证明：假设12a ≠，又*N a n ∈，所以11a =或*113()a a N ≥∈①当11a =时，1111a b a a ===与13b =矛盾，所以11a ≠；②当*113()a a N ≥∈时，即1113a a b a ≥==，即11a a a ≥，又1+<n n a a ，所以11a ≤与*113()a a N ≥∈矛盾；由①②可知21=a ．（3）首先{}n a 是公差为1的等差数列，证明如下：1n n a a +>*2,n n N ⇒≥∈时1n n a a ->，所以11n n a a -≥+()n m a a n m ⇒≥+-，*(,)m n m n N <∈、1111[1(1)]n n a a n n a a a a ++++⇒≥++-+即11n n n n c c a a ++-≥-由题设11n n a a +≥-又11n n a a +-≥11n n a a +⇒-=即{}n a 是等差数列．又{}n a 的首项11a =，所以n a n =，)223222(32nn n S ⋅++⋅+⋅+-= ，对此式两边乘以2，得14322232222+⋅--⋅-⋅--=n n n S两式相减得=⋅-++++=+13222222n n n n S 22211-⋅-++n n n 22211-=⋅+++n n n n S ，5021>⋅++n n n S 即5221≥+n ，当5≥n 时，526421>=+n ，即存在最小正整数5使得5021>⋅++n n n S 成立．注：也可以归纳猜想后用数学归纳法证明n a n =．。

上海市六校2014届高三下学期第二次联考数学(理)试题(解析版)

上海市六校2014届高三下学期第二次联考数学（理）试题（解析版）一、填空题（每题4分，满分56分，将答案填在答题纸上）1.已知,2παπ⎛⎫∈⎪⎝⎭，4sin 5α=，则tan α= ．2.已知集合{}1,A m =-，{}|1B x x =>，若A B ≠∅，则实数m 的取值范围是．3.设等差数列{}n a 的前项和为n S ，若911a =，119a =，则19S 等于．4.若()()2i i a ++是纯虚数（i 是虚数单位），则实数a 的值为．【答案】12【解析】试题分析：()(2)221(21)(2)a i i a ai i a a i ++=++-=-++是纯虚数，则21020a a -=⎧⎨+≠⎩，解得12a =．考点：复数的概念．5.抛物线24y x =的焦点到双曲线2214x y -=的渐近线的距离是．6.执行下图的程序框图，如果输入6i =，则输出的S 值为．7.不等式1011ax x <+对任意R x ∈恒成立，则实数a 的取值范围是．【答案】(]4,0- 【解析】试题分析：原不等式为(1)10ax x +-<，即210ax ax +-<，0a =时，不等式为10-<，符合题意，当0a ≠时，有240a a a <⎧⎨∆=-<⎩40a ⇒-<<，综上所述a 的范围是40a -<≤．考点：行列式的定义，不等式恒成立问题．8.若n a 是()()*2,2,nx n n x +∈≥∈N R 展开式中2x项的系数，则2323222lim n n n a a a →∞⎛⎫++⋅⋅⋅+= ⎪⎝⎭ ．9.已知一个圆锥的侧面展开图是一个半径为3，圆心角为23π的扇形，则此圆锥的体积为．10.若点(,)P x y 在曲线cos ,2sin ,x y θθ=⎧⎨=+⎩（θ为参数，θ∈R ）上，则yx 的取值范围是．【答案】(),3,⎡-∞+∞⎣【解析】试题分析：由cos ,2sin ,x y θθ=⎧⎨=+⎩消去参数θ得22(2)1x y +-=①，设yk x =，则y kx =，代入①式并化简得：22(1)430k x kx +-+=，此方程有实数解，∴221612(1)0k k ∆=-+≥，解得k ≤k ≥考点：参数方程化普通方程，直线和圆有公共点．11.从0,1,2,,9⋅⋅⋅这10个整数中任意取3个不同的数作为二次函数()2f x ax bx c =++的系数，则使得()12f ∈Z 的概率为．12.已知点F 为椭圆:C 2212x y +=的左焦点，点P 为椭圆C 上任意一点，点Q 的坐标为()4,3，则PQ PF +取最大值时，点P 的坐标为．考点：椭圆的定义，三角形的性质．13.已知A、B、C为直线l上不同的三点，点O∉直线l，实数x满足关系式220x OA xOB OC++=，有下列命题：①2OB OC OA-⋅≥；②20OB OC OA-⋅<；③x的值有且只有一个；④x的值有两个；⑤点B是线段AC的中点．则正确的命题是．（写出所有正确命题的编号）14.已知数列{}n a 的通项公式为52n n a -=，数列{}n b 的通项公式为n b n k =+，设,,,,n n n n n n n b a b c a a b ≤⎧=⎨>⎩若在数列{}n c 中，5n c c ≤对任意*n ∈N 恒成立，则实数k 的取值范围是．【答案】[]5,3--二、选择题：本大题共4个小题,每小题5分,共20分.在每小题给出的四个选项中，只有一项是符合题目要求的.（C ）充要条件（D ）既非充分又非必要条件16.下列函数中，既是偶函数，又在区间()1,2内是增函数的为（）（A ）2log y x = （B ）cos 2y x =（C ）222x xy --=（D ）22log 2x y x -=+17.已知m 和n 是两条不同的直线，α和β是两个不重合的平面，下面给出的条件中一定能推出m β⊥的是（）（A ）αβ⊥且m α⊂≠（B ）αβ⊥且mα∥（C ）m n 且n β⊥ （D ）m n ⊥且αβ18.对于函数()f x ，若存在区间[],A m n =，使得(){},y y f x x A A =∈=，则称函数()f x 为“可等域函数”，区间A 为函数()f x 的一个“可等域区间”．给出下列4个函数： ①()sin 2f x x π⎛⎫=⎪⎝⎭；②()221f x x =-； ③()12x f x =-； ④()()2log 22f x x =-．其中存在唯一“可等域区间”的“可等域函数”为（）（A ）①②③ （B ）②③ （C ）①③ （D ）②③④[0,)+∞，所以0m ≥，函数()12x f x =-在[0,)+∞上是增函数，考察方程21x x -=，由于函数2xy =与1y x =+只有两个交点(0,1),(1,2)，即方程21xx -=只有两个解0和1，因此此函数只有一个等可域区间[0,1]，对于④，函数2()log (22)f x x =-在定义域(1,)+∞上是增函数，若上函数有等可域区间[,]m n ，则(),()f m m f n n ==，但方程2log (22)x x -=无解（方程2log x x =无解），故此函数无可等域区间．综上只有②③正确，选B ．考点：函数的定义域与值域，单调性，方程的解等综合问题．三、解答题（本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.）19.（本题满分12分）本题共有2小题，第（1）小题满分6分，第（2）小题满分6分．在△ABC 中，角A 、B 、C 所对的边长分别为a 、b 、c ，且1cos22A C +=．（1）若3a =，b =c 的值；（2）若())sin sin f A AA A =-，求()f A 的取值范围．所以cos cos 22A C B π+-=1sin 22B ==．26B π=，所以3B π=． ………………3分由余弦定理2222cos b a c ac B =+-，由（1）得3B π=，所以23A C π+=，20,3A π⎛⎫∈ ⎪⎝⎭，则32,662A πππ⎛⎫+∈ ⎪⎝⎭. ∴sin 2(1,1]6A π⎛⎫+∈- ⎪⎝⎭. ∴()31,22f A ⎛⎤∈- ⎥⎝⎦.∴()f A 的取值范围是31,22⎛⎤- ⎥⎝⎦. ………………12分考点：（1）余弦定理；（2）二倍角公式与降幂公式，三角函数的取值范围20.（本题满分14分）本题共有2小题，第（1）小题满分7分，第（2）小题满分7分．如图，几何体EF ABCD -中，CDEF 为边长为2的正方形，ABCD 为直角梯形，AB CD ，AD DC ⊥，2AD =，4AB =，90ADF ∠=．（1）求异面直线DF 和BE 所成角的大小；（2）求几何体EF ABCD -的体积．BED CA由题意得，AD DC⊥，AD DF⊥，,DC DF⊂≠平面CDEF，∴AD⊥平面CDEF，∴AD DE⊥，同理可证DE⊥面ABCD.∵//CD EF，CD EF DM==，∴EFDM为平行四边形，∴//ME DF.则MEB∠（或其补角）为异面直线DF和BE所成的角. ………………3分由平面几何知识及勾股定理可以得2226210ME BE BM===，，在MEB△中，由余弦定理得2223cos2ME BE BMMEBME BE+-∠==⋅．∵异面直线的夹角范围为0,2π⎛⎤⎥⎝⎦，∴异面直线DF和BE所成的角为MBEACD………………7分（２）如图，连结EC ，过B 作CD 的垂线，垂足为N ，则BN ⊥平面CDEF ，且2BN =.………………9分∵EF ABCD V -E ABCD B ECF V V --=+ ……………11分1133ABCD EFC S DE S BN =⋅+⋅△△ 1111(42)222223232=⋅⋅+⋅⋅+⋅⋅⋅⋅ 163=. ∴ 几何体EF ABCD -的体积为163.……14分考点：（1）异面直线所成的角；（2）几何体的体积．21.（本题满分14分）本题共有2小题，第（1）小题满分7分，第（2）小题满分7分．NA为了保护环境，某工厂在国家的号召下，把废弃物回收转化为某种产品，经测算，处理成本y （万元）与处理量x （吨）之间的函数关系可近似的表示为：250900y x x =-+，且每处理一吨废弃物可得价值为10万元的某种产品，同时获得国家补贴10万元．（1）当[]10,15x ∈时，判断该项举措能否获利？如果能获利，求出最大利润；如果不能获利，请求出国家最少补贴多少万元，该工厂才不会亏损？（2）当处理量为多少吨时，每吨的平均处理成本最少？∵35[10,15]x =∉，()235325P x =--+在[10,15]上为增函数，可求得[P ∈--. ………………5分 ∴ 国家只需要补贴75万元，该工厂就不会亏损． ………………7分（2）设平均处理成本为90050y Q x x x==+- ………………9分5010≥=， ………………11分当且仅当900x x=时等号成立，由0x > 得30x =．因此，当处理量为30吨时，每吨的处理成本最少为10万元． ………………14分考点：函数应用题，二次函数的值域，基本不等式的应用.22.（本题满分16分）本题共有3小题，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分6分．已知数列{}n a 中，11a =，对任意的*k ∈N ，21k a -、2k a 、21k a +成等比数列，公比为k q ；2k a 、21k a +、22k a +成等差数列，公差为k d ，且12d =．（1）写出数列{}n a 的前四项；（2）设11k k b q =-，求数列{}k b 的通项公式；（3）求数列{}k d 的前k 项和k D ．试题解析：（1）由题意得2213322a a a a a ⎧=⎪⎨=+⎪⎩，2222a a =+，22a =或21a =-. ………………2分故数列{}n a 的前四项为1,2,4,6或1,1,1,3-. ………………4分221211k k a k a k +-+⎛⎫= ⎪⎝⎭，()22222121321121231121111k k k k k a a a k k a a k a a a k k +-+--+⎛⎫⎛⎫⎛⎫=⋅⋅⋅⋅⋅⋅⋅=⋅⋅⋅⋅⋅⋅⋅=+ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭， ()2121k k ka a k k q +==+， ()2121231,2k k k k k k k k a d a a k D q +++=-==+=. ………………13分当112b =-时，同理可得42k d k =-，22k D k =. ………………16分解法二：（2）对1,1,1,3,-这个数列，猜想()*2123N m m q m m -=∈-，下面用数学归纳法证明：ⅰ）当1m =时，12111213q ⋅-==-⋅-，结论成立.ⅱ）假设()*N m k k =∈时，结论成立，即2123k k q k -=-.（3）对1,1,1,3,-这个数列，猜想奇数项通项公式为()22123k a k -=-.显然结论对1k =成立. 设结论对k 成立，考虑1k +的情形. 由（2），()211,23k k q k k k -=≥∈-N 且21221,,k k k a a a -+成等比数列，故()()22222121212123212323k k k k a a k k k k +---⎛⎫⎛⎫=⋅=-⋅=- ⎪ ⎪--⎝⎭⎝⎭，即结论对1k +也成立. 从而由数学归纳法原理知()22123k a k -=-.于是()()22321k a k k =--（易见从第三项起每项均为正数）以及21242k k k d a a k +=-=-，此时()22422k D k k =++-=. ………………13分对于1,2,4,6,这个数列，同样用数学归纳法可证221k a k -=，此时()22121,1k k k k a k k d a a k +=+=-=+.此时()()32312k k k D k +=++++=. ………………16分考点：（1）数列的项；（2）等差数列、等比数列与递推公式；（3）累乘法，构造法求通项公式. 或数学归纳法.23.（本题满分18分）本题共有3小题，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分8分．如图，圆O与直线20x +=相切于点P ，与x 正半轴交于点A，与直线y 在第一象限的交点为B . 点C 为圆O 上任一点，且满足OC xOA yOB =+，动点(),D x y 的轨迹记为曲线Γ．（1）求圆O 的方程及曲线Γ的方程；（2）若两条直线1:l y kx =和21:l y x k=-分别交曲线Γ于点E 、F 和M 、N ，求四边形EMFN 面积的最大值，并求此时的k 的值．（3）证明：曲线Γ为椭圆，并求椭圆Γ的焦点坐标．【答案】（1）圆O 的方程为221xy +=，曲线Γ的方程为221x y xy ++=（,x y ⎡∈⎢⎣⎦）；（2）当1k =±时，四边形EMFN（3）证明见解析，其焦点坐标为1F ⎛⎝⎭， 2F ⎝⎭. 【解析】试题分析：（1）圆的半径等于圆心到切线的距离，曲线Γ的方程可通过已知OC xOA yOB =+变形得到，条件是1OA OB OC ===，3AOB π∠=，把已知式平方可得出,x y 的方程；（2）从12,l l 方程可看出12l l ⊥，即EF MN ⊥，因此12ABCD S EF MN =⋅，我们把1l 方程与曲线Γ方程联立方程组可解得E F 、两点坐标，从而得到EF ，把EF 中的k ，用1k -代可得出MN ，从而求出2EMFNS =，变试题解析：（1）由题意圆O的半径1r ==，故圆O 的方程为221x y +=. ………………2分由OC xOA yOB =+得，()22OC xOA yOB =+，即222222cos60OC x OA y OB xy OA OB =++，得221x y xy ++=（,x y ⎡∈⎢⎣⎦）为曲线Γ的方程.（未写,x y 范围不扣分）…4分（2）由221y kx x y xy =⎧⎨++=⎩得E ⎛⎫，F ⎛⎫ ⎝，所以EF =MN ==. ………………6分由题意知12l l ⊥ ，所以四边形EMFN 的面积12S EF MN =⋅. 221x y xy ++=和直线y x =-的交点坐标为()()121,1,1,1A A --，1OA =1OB ===.在y x =-上取点12,F F ⎛ ⎝⎭⎝⎭.下面证明曲线Γ为椭圆：ⅰ）设(),P x y 为曲线Γ上任一点，则12PF PF +=======（因为43xy ≤）12A A ==..。

江西2015年高考数学二轮复习小题精做系列之行列式与矩阵2

一．基础题组
1. 【上海市长宁、嘉定区2014届高三4月第二次模拟考试数学（理）试题】对于任意),1()1,0(∞+∈ a ，函数)1(log 11
1)(--=x x f a 的反函数)(1x f -的图像经过的定点的坐标是______________．
2. 【上海市奉贤区2014届下学期高三二模数学试卷（理科）】已知函数cos ()sin x f x x
=，则方程()02
1cos =+⋅x x f 的解是________.
3. 【上海市静安、杨浦、青浦、宝山四区2014高考模拟（理科）数学】二阶行列式
i i i ++-1101的值是 . （其中i 为虚数单位）
【答案】2
【解析】试题分析：由i
i i ++-1101可得(1)(1)2i i -+=. 考点：1.行列式的运算.2.复数的运算.
4. 【上海市闵行区2014届高三下学期教育质量调研（二模）数学(理)试题】关于方程
211323x x =-的
解为．
5. 【上海市徐
汇、金山、松江区2014届高三第二学期学习能力诊断数学（理）试题】函数
()()
sin cos cos 2sin cos sin x x x f x x x x π+-=-的最小正周期T =____________．。

2014届上海市十三校高三第二次联考理科数学试题(含答案解析)

2014年上海市高三年级十三校第二次联考数学(理科)试卷考试时间：120分钟满分：150分一、填空题(本大题满分56分)本大题共有14题，每题4分． 1、方程211log 1log 2x x ++=的解是．2、已知函数11()13x f x -=，则1(4)f -= ． 3、若实数,x y 满足1xy =，则224y x +的最小值为． 4、设(12i)34i z +=-（i 为虚数单位），则||z = ． 5、已知,x R ∈的值为．6、123101011111111111392733C C C C -+-+--+ 除以5的余数是．7、在棱长为1的正方体1111ABCD A B C D -中，点M 和N 分别是矩形ABCD 和11BB C C 的中心，则过点A 、M 、N 的平面截正方体的截面面积为______． 9 等差数列{}n a 的前n 项和为n S ，则12lim (32)nn n nS n S →+∞+=+ ．10 某公司推出了下表所示的QQ 在线等级制度，设等级为n 级需要的天数为(*)n a n N ∈，则等级为50级需要的天数50a =__________．10.若关于x 的方程sin 2cos 2x x k +=在区间0,2π⎡⎤⎢⎥⎣⎦上有两个不同的实数解，则k 的取值范围为 .11.已知直线:l ρ=交极轴于A 点，过极点O 作l 的垂线，垂足为C ，现将线段CA 绕极点O 旋转2π，则在旋转过程中线段CA 所扫过的面积为________．12.给定平面上四点,,,O A B C 满足4,3,2,3OA OB OC OB OC ===⋅=，则ABC ∆面积的最大值为．13. 对于非空实数集A ，定义{},A z x A z x *=∈≥对任意．设非空实数集(],1C D ⊂⊆-∞≠．现给出以下命题：（1）对于任意给定符合题设条件的集合,,C D 必有;D C **⊆ （2）对于任意给定符合题设条件的集合,,C D 必有C D *≠∅ ；（3）对于任意给定符合题设条件的集合,,C D 必有C D *=∅ ；（4）对于任意给定符合题设条件的集合,,C D 必存在常数a ，使得对任意的b C *∈，恒有a b D *+∈．以上命题正确的是． 14. 已知当12x <时，有21124(2)12n x x x x=-+-+-++ ，根据以上信息，若对任意12x <,都有20123,(1)(12)n n x a a x a x a x x x =+++++-+ 则10a = ．二、选择题(本大题满分20分)本大题共有4题，每题5分． 15.集合{}20,()()01x A xB x x a x b x ⎧-⎫=<=--<⎨⎬+⎩⎭，若“2a =-”是“A B ≠∅I ”的充分条件，则b 的取值范围是（）（A ）1b <- （B ）1b >- （C ）1b ≥- （D ）12b -<< 16.函数1211111(),(),,(),,()()n n f x f x f x x x f x x f x +===++ 则函数2014()f x 是（）（A ）奇函数但不是偶函数（B ）偶函数但不是奇函数（C ）既是奇函数又是偶函数（D ）既不是奇函数又不是偶函数 17.若,,22ππαβ⎡⎤∈-⎢⎥⎣⎦,且sin sin 0ααββ->．则下列结论正确的是( )（A ）αβ> （B ）0αβ+> （C ）αβ< （D ）22αβ> 18.设B 、C 是定点，且均不在平面α上,动点A 在平面α上,且1sin 2ABC ∠=，则点A 的轨迹为（）（A ）圆或椭圆（B ）抛物线或双曲线（C ）椭圆或双曲线（D ）以上均有可能三、解答题(本大题共5小题，满分74分) 19.(本题满分12分)如图,设S ABCD -是一个高为3的四棱锥,底面ABCD 是边长为2的正方形,顶点S 在底面上的射影是正方形ABCD 的中心．K 是棱SC 的中点．试求直线AK 与平面SBC 所成角的大小．20.（本题满分14分，第一小题满分5分，第二小题满分9分）对于函数()f x ，若在定义域存在实数x ，满足()()f x f x -=-，则称()f x 为“局部奇函数”．（1）已知二次函数2()24(,)f x ax bx a a b R =+-∈，试判断()f x 是否为“局部奇函数”？并说明理由；（2）设()2x f x m =+是定义在[]1,1-上的“局部奇函数”，求实数m 的取值范围．21.（本题满分14分，第一小题满分4分，第二小题满分10分）某超市在节日期间进行有奖促销，凡在该超市购物满400元的顾客，将获得一次摸奖机会，规则如下：奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球．顾客不放回的每次摸出1个球，若摸到黑球则停止摸奖，否则就继续摸球．规定摸到红球奖励20元，摸到白球或黄球奖励10元，摸到黑球不奖励．（1）求1名顾客摸球2次停止摸奖的概率；（2）记X 为1名顾客摸奖获得的奖金数额，求随机变量X 的分布律和数学期望．22.（本题满分16分，第一小题满分4分，第二小题满分5分，第三小题满分7分）已知抛物线24y x =．(1) 若圆心在抛物线24y x =上的动圆，大小随位置而变化，但总是与直线10x +=相切，求所有的圆都经过的定点坐标；(2) 抛物线24y x =的焦点为F ,若过F 点的直线与抛物线相交于,M N 两点,若4FM FN =-,求直线MN 的斜率；(3)若过x 正半轴上(,0)Q t 点的直线与该抛物线交于,M N 两点,P 为抛物线上异于,M N 的任意一点,记,,PM QP PN 连线的斜率为,,,PM QP PN k k k 试求满足,,PM QP PN k k k 成等差数列的充要条件．23. （本题满分18分，第一小题满分4分，第二小题满分7分，第三小题满分7分）设等差数列{}n a 的公差为d ，且1,a d N *∈．若设1M 是从1a 开始的前1t 项数列的和，即1*1111(1,)t M a a t t N =++≤∈ ，112*2122(1)t t t M a a a t N ++=+++<∈ ，如此下去，其中数列{}i M 是从第101(0)i t t -+=开始到第(1i i t t ≤)项为止的数列的和，即1*1(1,)i i i t t i i M a a t t N -+=++≤∈ ．(1)若数列*(113,)n a n n n N =≤≤∈,试找出一组满足条件的123,,M M M ,使得： 2213M M M =；(2) 试证明对于数列()n a n n N *=∈，一定可通过适当的划分，使所得的数列{}n M 中的各数都为平方数；(3)若等差数列{}n a 中11,2a d ==．试探索该数列中是否存在无穷整数数列{}*123,(1),n n t t t t t n N ≤<<<<∈ ,使得{}n M 为等比数列,如存在,就求出数列{}n M ；如不存在，则说明理由．2014年高三年级十三校第二次联考数学试卷答案（理科）考试时间：120分钟满分：150分一、填空题(本大题满分56分)本大题共有14题，每题4分． 1. 方程211log 1log 2x x ++=的解是 {}1 ．2. 已知函数11()13x f x -=，则1(4)f -= 1 ． 3. 若实数,x y 满足1xy =，则224y x +的最小值为 4 ． 4. 设(12i)34i z +=-（i 为虚数单位），则||z5.已知,x R ∈的值为 0 ．6. 123101011111111111392733C C C C -+-+--+ 除以5的余数是 3 ． 7. （理）在棱长为1的正方体1111ABCD A B C D -中，点M 和N 分别是矩形ABCD 和11BB C C 的中心，则过点A 、M 、N 的平面截正方体的截面面积为．8. 某公司推出了下表所示的QQ 在线等级制度，设等级为n 级需要的天数为(*)n a n N ∈，则等级为50级需要的天数50a =____2700______。

上海市静安、杨浦、青浦、宝山四区2014届高三模拟文科数学试卷(带解析)

上海市静安、杨浦、青浦、宝山四区2014届高三模拟文科数学试卷（带解析）1．不等式12x x->的解集为（）. A. }01|{>-<x x x 或 B. }1|{-<x x C. }1|{->x x D. }01|{<<-x x 【答案】D 【解析】试题分析：由12x x ->可得10x x+<，所以解集为10x -<<.故选D. 考点：1.分式不等式的解法.2.转化的思想.2．“1=ω”是“函数x x x f ωω22cos sin )(-=的最小正周期为π”的（）.A.充分必要条件B.充分不必要条件C.必要不充分条件D.既不充分又必要条件【答案】B 【解析】试题分析：因为x x x f ωω22cos sin)(-=可化为()cos 2f x x ω=-.所以可得1=ω是函数()f x 最小正周期为π的充分条件.由于函数的最小正周期为π,则2,12T ππωω==∴=±.所以必要性不成立.故选B.考点：1.三角函数的恒等变形.2.充要条件的知识.3．若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为1S 、2S ,则1S :2S =（）.A. 1:1B.2:1C. 3:2D. 4:1 【答案】C 【解析】试题分析：假设球的半径为r .则圆柱的底面半径为r .高为2r .所以圆柱的表面积为216S r π=.球的表面积为224S r π=.所以12:3:2S S =.故选C.考点：1.圆柱的表面积.2.球的表面积.3.方程的思想.4．已知向量，满足：1||||==，且||3||k k -=+（0>k ）．则向量与向量的夹角的最大值为（）.A.3πB. 32πC. 6πD.65π【答案】A 【解析】试题分析：假设向量a ，b 的夹角为(0)θθπ≤≤，由1||||==，且||3||b k a b a k -=+（0>k ）.可得21111cos ()442k k k k θ+==+≥当且仅当1k =时取等号.所以03πθ≤≤.即选A.考点：1.向量的数量积运算.2.向量的夹角.3.三角函数的最值问题.5．二阶行列式ii i ++-1101的值是 . （其中i 为虚数单位）【答案】2 【解析】试题分析：由ii i ++-1101可得(1)(1)2i i -+=.考点：1.行列式的运算.2.复数的运算.6．已知j i,是方向分别与x 轴和y 轴正方向相同的两个基本单位向量，则平面向量ji +的模等于 .【解析】试题分析：由2i j +=.考点：向量的模的含义.7．二项式7)1(+x 的展开式中含3x 项的系数值为_______________. 【答案】35 【解析】试题分析：717r rr T C x -+=.依题意可得73,4r r -=∴=.所以展开式中含3x 项的系数值为35.考点：1.二项式定理的展开式.2.项的系数的概念.8．已知圆锥的母线长为5,侧面积为π15,则此圆锥的体积为__________.(结果中保留π) 【答案】12π 【解析】试题分析：由圆锥的母线长为5,侧面积为π15.则根据12s lr =.即可求出圆锥的底面周长6π.从而解出底面半径3r =.再求出圆锥的高4h =.根据体积公式213V r h π= 12π=.考点：1.圆锥曲线的侧面积.2.圆锥曲线的体积公式.3.图形的展开前后的变化. 9．若),(ππ-∈x ，则方程12cos 2sin 3=-x x 的解是_____________. 【答案】5,,,6262ππππ-- 【解析】试题分析：由12cos 2sin 3=-x x 即1sin(2)62x π-=.所以2266x k πππ-=+或522 ()66x k k z πππ-=+∈.又因为),(ππ-∈x .所以可得方程12cos 2sin 3=-x x 的解是5,,,6262x ππππ=--. 考点：1.三角方程的解法.2.化一公式的应用.3.三角函数的周期性.10．在平面直角坐标系xOy 中，若圆22(1)4x y +-=上存在A ，B 两点，且弦AB 的中点为(1,2)P ，则直线AB 的方程为 .【答案】30x y +-= 【解析】试题分析：假设1122(,),(,)A x y B x y .AB 的中点坐标为00(,)x y .所以可得22112222(1) 4(1) 4x y x y ⎧+-=⎪⎨+-=⎪⎩①②.由①-②可得001AB x k y =-.即1AB k =-.所以:30AB l x y +-=. 考点：1.点差法的应用.2.直线与圆的位置关系.3.直线方程的表示. 11．已知1log log 22=+y x ，则y x +的最小值为_____________.【答案】【解析】试题分析：由1log log 22=+y x 可得2log ()1,2xy xy =∴=.又y x+≥=.当且仅当x y =时取等号. 考点：1.对数的知识.2.基本不等式.12．已知首项31=a 的无穷等比数列{}n a )(*N n ∈的各项和等于4，则这个数列{}n a 的公比是．【答案】14【解析】试题分析：首项31=a 的无穷等比数列{}n a )(*N n ∈，设公比为q ,由各项和等于4.即341q=-.解得14q =.考点：无穷等比数列的求和公式.13．满足约束条件⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+,0,0,32,42y x y x y x 的目标函数y x f +=的最大值为_______.AO2x+y -3=0x +2y-4=0xy【答案】73【解析】试题分析：由x,y 满足⎪⎪⎩⎪⎪⎨⎧≥≥≥+≥+,0,0,32,42y x y x y x 如图可得可行域.目标函数过点A 时在y 轴上的截距最大，最小值为73.考点：1.线性规划的知识.2.线性的最值问题.14．阅读右面的程序框图，运行相应的程序，输出的结果为 .【答案】138【解析】试题分析：由程序框图可知，x=1,y=1,z=2;当x=2,y=3,z=5;当x=3,y=5,z=8;当x=5,y=8,z=13;当x=8,y=13,z=21.由21>20.所以退出循环.即可得138y x =. 考点：1.程序框图.2.数的交换运算.15．在平面直角坐标系xOy 中，若中心在坐标原点的双曲线过点()2,3，且它的一个顶点与抛物线24y x =的焦点重合，则该双曲线的方程为 .【答案】2213y x -=【解析】试题分析：因为抛物线24y x =的焦点为（1,0）且是双曲线的顶点，假设双曲线的方程为22221(0,0)x y a b a b -=>>.所以1a =.又过点()2,3可得. 23b =.所以双曲线方程为2213y x -=.考点：1.抛物线的性质.2.双曲线的性质.3.待定系数的思想. 16．从5男3女8位志愿者中任选3人参加冬奥会火炬接力活动，所选3人中恰有两位女志愿者的概率是．【答案】1556【解析】试题分析：8人中选3任选人的情况有3856C =种，所选3人中恰有两位女志愿者的情况有15种.所以所选3人中恰有两位女志愿者的概率是1556P =. 考点：1.概率问题.2.组合问题.17．若三个数c a ,1,成等差数列（其中c a ≠），且22,1,c a 成等比数列，则nn c a c a )(lim 22++∞→的值为．【答案】0 【解析】试题分析：依题意可得2221a c a c +=⎧⎨=⎩.所以可得222a c +=(1a c ==舍去)或226a c +=.所以nn ca c a )(lim 22++∞→=0. 考点：1.等差数列的性质.2.等比数列的性质.3.极限的概念.18．()f x 的定义域为实数集R ，⎪⎩⎪⎨⎧<≤--≤≤=.01,1)21(,10,)(x x x x f x 对于任意的x R ∈都有(1)(1)f x f x +=-.若在区间[1,3]-上函数()()g x f x mx m =--恰有四个不同的零点，则实数m 的取值范围是 .Oxy【答案】1(0,]4m ∈ 【解析】试题分析：因为对任意的x R ∈都有(1)(1)f x f x +=-，所以函数()f x 的周期为2. 由在区间[1,3]-上函数()()g x f x mx m =--恰有四个不同的零点，即函数()f x mx m =+在[1,3]-上有四个不同的零点.即函数()y f x =与函数()h x mx m =+在[1,3]-有四个不同的交点.所以0(3)1h <≤.解得1(0,]4m ∈. 考点：1.分段函数的性质.2.函数的周期性.3.函数的等价变换.19．已知几何体由正方体和直三棱柱组成，其三视图和直观图（单位：cm ）如图所示．设两条异面直线1AQ 和PD 所成的角为θ，求cos θ的值．【答案】15【解析】试题分析：几何体由正方体和直三棱柱组成，求两条异面直线1AQ和PD所成的角. 由三视图和直观图可得线段的数量，异面直线1AQ和PD所成的角转化为1AQC∠.在通过解三角形即求得1AQC∠的余弦值，及为所求的结论.试题解析：由//PQ CD，且PQ CD=，可知//PD QC，故1AQC∠为异面直线1AQ、PD所成的角（或其补角）．由题设知2222111126AQ A B B Q=+=+=，12AC=取BC中点E，则QE BC⊥，且3QE=，222223110QC QE EC=+=+=．由余弦定理，得2221111cos cos2AQ QC ACAQCAQ QCθ+-=∠=⋅==考点：异面直线所成的角.2.解三角形的知识.3.空间想象力.20．某公司承建扇环面形状的花坛如图所示，该扇环面花坛是由以点O为圆心的两个同心圆弧AD、弧BC以及两条线段AB和CD围成的封闭图形．花坛设计周长为30米，其中大圆弧AD所在圆的半径为10米．设小圆弧BC所在圆的半径为x米（100<<x），圆心角为θ弧度．A1PA11D1P Q1A正视图侧视图俯视图（1）求θ关于x 的函数关系式；（2）在对花坛的边缘进行装饰时，已知两条线段的装饰费用为4元/米，两条弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为y ，当x 为何值时，y 取得最大值？【答案】（1）10210x x θ+=+；（2）参考解析【解析】试题分析：（1）由于花坛设计周长为30米，其中大圆弧AD 所在圆的半径为10米．设小圆弧BC 所在圆的半径为x 米（100<<x ），圆心角为θ弧度.所以AD 的弧长为10θ，BC 的弧长为x θ.所以可得102(10)30x x θθ++-=.即可得结论.（2）由花坛两条线段的装饰费用为4元/米，两条弧线部分的装饰费用为9元/米．即可得所需费用的关系式. 花坛的面积由大扇形面积减去小的扇形面积即可，再利用基本不等式即可求得结论.试题解析：(1)设扇环的圆心角为θ，则()30102(10)x x θ=++-，所以10210xxθ+=+， (2) 花坛的面积为 2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<．装饰总费用为()9108(10)17010x x x θ++-=+，所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++，令17t x =+，则3913243()101010y t t =-+≤，当且仅当t =18时取等号，此时121,11x θ==．答：当1x =时，花坛的面积与装饰总费用的比最大．考点：1.扇形的面积.2.函数的最值.3.基本不等式的应用.21．已知椭圆2222:1x y C a b +=()0a b >>的右焦点F (1,0)，长轴的左、右端点分别为12,A A ,且121FA FA ⋅=-.（1）求椭圆C 的方程；（2）过焦点F 斜率为k （0>k ）的直线l 交椭圆C 于,A B 两点，弦AB 的垂直平分线与x 轴相交于D 点. 试问椭圆C 上是否存在点E 使得四边形ADBE 为菱形？若存在，求k 的值；若不存在，请说明理由.【答案】（1）2212x y +=；（2）2k =【解析】试题分析：（1）由椭圆2222:1x y C a b +=()0a b >>的右焦点F (1,0)，即1c =.又长轴的左、右端点分别为12,A A ,且121FA FA ⋅=-，即可得a ，即可求出1b =.从而得到椭圆的方程.（2）由（1）可得假设直线AB 的方程联立椭圆方程消去y 即可得到一个关于x 的二次方程，由韦达定理得到根与直线斜率k 的关系式.写出线段AB 的中点坐标以及线段AB 的垂直平分线的方程.即可得到点D 的坐标.假设存在点E 由于对称性本小题的问题等价转化为AD EB =即可.所以表示出点E 的坐标.代入椭圆方程根据的解得情况即可结论.试题解析：（1）依题设1(,0)A a -，2(,0)A a ，则1(1,0)FA a =--，2(1,0)FA a =-. 由121FA FA ⋅=-，解得22a =，所以21b =. 所以椭圆C 的方程为2212x y +=. （2）依题直线l 的方程为(1)y k x =-.由22(1),22y k x x y =-⎧⎨+=⎩得()2222214220k x k x k +-+-=. 设11(,)A x y ,22(,)B x y ,弦AB 的中点为00(,)M x y ，则2122421k x x k +=+，21222(1)21k x x k -=+，202221k x k =+，0221k y k -=+，所以2222(,)2121k kM k k -++.直线MD 的方程为22212()2121kk y x k k k +=--++，令0y =，得2221D k x k =+，则22(,0)21k D k +. 若四边形ADBE 为菱形，则02E D x x x +=，02E D y y y +=.所以22232(,)2121k kE k k -++.若点E 在椭圆C 上，则2222232()2()22121k kk k -+=++.整理得42k =，解得2k =所以椭圆C 上存在点E 使得四边形ADBE 为菱形.考点：1.向量的数量积.2.椭圆的性质.3.等价转化的数学思想.4.运算能力.22．已知数列}{n a 满足⎪⎩⎪⎨⎧≥=+==-+).2(,,8,21121n ca a a a a n n n （c 为常数，*N n ∈）（１）当2=c 时，求n a ；（２）当1=c 时，求2014a 的值；（3）问：使n n a a =+3恒成立的常数c 是否存在？并证明你的结论．【答案】（1）64n a n =-；（2）20142a =-；（3）存在1-=c 【解析】试题分析：（1）由2=c ，所以112n n n a a a +-+=，(2)n ≥.所以数列{}n a 是一个等差数列.首项为2，公差为6，所以可求得通项公式.（2）由1=c ，由于需要求2014a 的值，所以考虑数列{}n a 的周期性，通过列举即可得到数列{}n a 的周期为6.从而可求得2014a 的值.（3）假设存在常数c 使得n n a a =+3恒成立.由11n n n a a ca +-+=，向前递推一个式子，再利用n n a a =+3将得到两个关于11,,n n n a a a +-的等式，从而消去一个即可得到01=-+n n a a ，或01=+c ．由于12a a ≠.所以只有1c =-.再结合已知即可得到结论.试题解析：（1）46)1(62-=-+=n n a n（2） 21=a ，82=a ，63=a ，24-=a ，85-=a ，66-=a ，27=a ，88=a ，69=a ，210-=a ，811-=a ， 612-=a ，我们发现数列为一周期为６的数列．事实上，由n n n a a a =+-+11有n n n n a a a a -=-=+++123，n n n n a a a a =-==++++3336．……8分(理由和结论各2分) 因为 463352014+⨯=，所以242014-==a a ．（3）假设存在常数c ，使n n a a =+3恒成立．由n n n ca a a =+-+11 ①，及n n a a =+3，有1112+-++=+⇒=+n n n n n n ca a a ca a a ②○1式减○2式得0)1)((1=+-+c a a n n ．所以01=-+n n a a ，或01=+c ．当*N n ∈，01=-+n n a a 时，数列｛n a ｝为常数数列，不满足要求．由01=+c 得1-=c ，于是n n n a a a -=+-+11，即对于2≥∈n N n 且，都有11-+--=n n n a a a ，所以 n n n n n n a a a a a a --=--=+++++12123,，从而n n n n n n n a a a a a a a =-+=--=+++++11123, )1(≥n ．所以存在常数1-=c ，使n n a a =+3恒成立．考点：1.等差数列的判断.2.数列的周期性.3.数列恒成立问题.4.递推的思想.23．设函数x x g 3)(=，x x h 9)(=.（1）解方程：0)1()(8)(=--h x g x h ；（2）令3)()()(+=x g x g x p ，求证：22013)20142013()20142012()20142()20141(=++++p p p p ；（3）若b x g a x g x f +++=)()1()(是实数集R 上的奇函数，且 0))(2()1)((>⋅-+-x g k f x h f 对任意实数x 恒成立，求实数k 的取值范围.【答案】（1）2=x ；（2）参考解析；（3）2<k【解析】试题分析：（1）由于函数x x g 3)(=，xx h 9)(=，所以解方程0)1()(8)(=--h x g x h .通过换元即可转化为解二次方程.即可求得结论. （2）由于3)()()(+=x g x g x p 即得到()xP x =.所以()(1)1p x p x +-=.所以两个一组的和为1，还剩中间一个21323)21()20141007(===p p .即可求得结论. （3）由bx g a x g x f +++=)()1()(是实数集R 上的奇函数，可求得1,3=-=b a .又由于0))(2()1)((>⋅-+-x g k f x h f 对任意实数x 恒成立.该式的理解较困难，所以研究函数()f x 的单调性可得.函数()f x 在实数集上是递增.集合奇函数，由函数值大小即可得到变量的大小，再利用基本不等式，从而得到结论.试题解析：（1）0)1()(8)(=--h x g x h 即：09389=-⋅-x x ，解得93=x ，2=x（2）21323)21()20141007(===p p . 因为1333333333333)1()(11=+++=+++=-+--x x x x x x xx p x p ，所以，22013211006)20142013()20142()20141(=+=+++p p p ，（3）因为bx a x x f +++=)()1()(ϕϕ是实数集上的奇函数，所以1,3=-=b a . )1321(3)(+-=x x f ，)(x f 在实数集上单调递增. 由0))(2()1)((>⋅-+-x g k f x h f 得))(2()1)((x g k f x h f ⋅-->-，又因为)(x f 是实数集上的奇函数，所以，)2)(()1)((-⋅>-x g k f x h f ，又因为)(x f 在实数集上单调递增，所以2)(1)(-⋅>-x g k x h即23132-⋅>-x x k 对任意的R x ∈都成立，即x x k 313+<对任意的R x ∈都成立，2<k . 考点：1.解方程的思想.2.函数的单调性.3.归纳推理的思想.4.基本不等式.。

(上海版)2014届高三数学(第04期)名校试题分省分项汇编专题07.行列式与矩阵理(含解析)

（上海版）2014届高三数学（第04期）名校试题分省分项汇编专
题07.行列式与矩阵理（含解析）
一．基础题组
1. 【上海市长宁、嘉定区2014届高三4月第二次模拟考试数学（理）试题】对于任意),1()1,0(∞+∈ a ，函数)1(log 111)(--=
x x f a 的反函数)(1x f -的图像经过的定点的
坐标是______________．
2. 【上海市奉贤区2014届下学期高三二模数学试卷（理科）】已知函数cos ()sin x f x x =，则方程()02
1cos =+⋅x x f 的解是________.
3. 【上海市静安、杨浦、青浦、宝山四区2014高考模拟（理科）数学】二阶行列式
i
i i ++-1101的值是 . （其中i 为虚数单位）【答案】2
【解析】
试题分析：由i i i ++-110
1可得(1)(1)2i i -+=.
考点：1.行列式的运算.2.复数的运算.
4. 【上海市闵行区2014届高三下学期教育质量调研（二模）数学(理)试题】关于方程211323x
x =-的解为．
5. 【上海市徐汇、金山、松江区2014届高三第二学期学习能力诊断数学（理）试题】函数()()
sin cos cos 2sin cos sin x x x f x x x x π+-=-的最小正周期T =____________．。

上海市浦东新区2014届高三数学二模试卷(文理合卷,含答案)

浦东新区2014年高考预测数学（文、理）试卷一、填空题（本大题小水满分56分）本大题共有14题，考生应在答题纸编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分.1. 已知全集{}1,2,3,4,5U =，若集合{}2,3A =，则U A ð=_____2. 双曲线221916x y -=的渐近线方程为 . 3.函数()31cos 4sin xx x f =的最大值为_______4.已知直线1:210l ax y a -++=和()()2:2130l x a y a R --+=∈，若12l l ⊥，则a =___.5.函数()y f x =的反函数为()1y f x -=，如果函数()y f x =的图像过点()2,2-，那么函数()11y fx -=+的图像一定过点______.6. 已知数列{}n a 为等差数列，若134a a +=，2410a a +=，则{}n a 的前n 项的和n S =_____.7.π，则球的体积为 ____ ． 8.(理) 一名工人维护甲、乙两台独立的机床，在一小时内，甲、乙需要维护的概率分别为0.9、0.8，则一小时内有机床需要维护的概率为_____(文) 把3本不同的语文书、7本不同的数学书随机的排在书架上，则语文书排在一起的概率是____小水制作9.设a R ∈，8(1)ax -的二项展开式中含3x 项的系数为7，则2lim()nn a a a →∞+++=L ____．10.(理)在平面直角坐标系xoy 中,若直线:x t l y t a =⎧⎨=-⎩（t 为参数）过椭圆3cos C:2sin x y ϕϕ=⎧⎨=⎩（ϕ为参数）的右顶点,则常数a =___.(文) 一个用若干块大小相同的立方块搭成的立体图形，主视图和俯视图是同一图形(如图)，那么搭成这样一个立体图形最少需要个小立方块． P.F. Productions 后期制作11.(理)已知随机变量ξ的分布列如右表，若3E ξ=，则D ξ=__ ．(文) 已知数据3,4,,,11x y 的均值为6，方差为8，则x y -=____ _.12.在ABC ∆中, 角B 所对的边长6b =,ABC ∆的面积为15,外接圆半径5R =，则ABC ∆的周长为_______第10题13．抛物线24(0)y mx m =>的焦点为F ，点P 为该抛物线上的动点，又点(,0)A m -，则PF PA的最小值为 .14.(理)已知函数()f x 的定义域为{}1,2,3，值域为集合{}1,2,3,4的非空真子集，设点()1,(1)A f ，()2,(2)B f ，()3,(3)C f ，ABC ∆的外接圆圆心为M ，且()MA MC MB R +=∈λλu u u r u u u r u u u r，则满足条件的函数()f x 有＿＿个．(文) 已知函数()f x 的定义域为{}1,2,3，值域为集合{}1,2,3,4的非空真子集，设点()A 1,(1)f ，()B 2,(2)f ，()C 3,(3)f ，且()0B A B C A C +⋅=u u r u u u r u u u r ，则满足条件的函数()f x 有＿＿个．二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答题纸的相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分. 15. “1x >”是“11x<”的( ) （A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件16. （理）已知z x yi =+，,x y R ∈， i 是虚数单位.若复数+1zi i+是实数，则z 的最小值为( ) 小水制作（A ）0（B ）52（C ） 5（D （文）设x 、y 均是实数，i 是虚数单位，复数(2)(52)i x y x y -+--的实部大于0，虚部不小于0，则复数z x yi ＝＋在复平面上的点集用阴影表示为下图中的（）17.能够把椭圆2214x y +=的周长和面积同时分为相等的两部分的函数称为椭圆的“可分函数”，下列函数不是．．椭圆的“可分函数”为（）P.F. Productions 后期制作（A ）3()4f x x x =+（B ）5()ln5x f x x -=+（C ）()arctan 4x f x =（D ）()x xf x e e -=+ 18. （理）方程27lg(100)(||200)(||202)2x x x -=---的解的个数为（）（A ）2（B ）4（C ）6（D ）8（文）方程2lg 4(||200)(||202)x x x =---的解的个数为（）（A ）2 （B ）4 （C ）6 （D ）8三、解答题（本大题满分74分）本大题共有5题，解答下列各题必须在答题纸相应编号规定的区域内写出必要的步骤.19．（本题满分12分）本题共有2个小题，第（1）小题满分6分，第（2）小题满分6分.（理）如图，在直三棱柱111ABC A B C -中，AB AC ⊥，11AA AB AC ===，4ABC π∠=，D 、M 、N 分别是1CC 、11A B 、BC 的中点.（1）求异面直线MN 与AC 所成角的大小；（2）求点M 到平面ADN 之间的距离.（文）如图，在直三棱柱111ABC A B C -中，AB AC ⊥，11AA AB AC ===，4ABC π∠=，D 是1CC 的中点，点M 在P.F. Productions 后期制作线段11A B 上.（1）当M 为11A B 中点时，求异面直线DM 与AB 所成角的大小.（2）指出直线1CC 与平面MAB 的位置关系（不用证明），并求三棱锥D MAB -的体积. 20．（本题满分14分）本题共有2个小题，第（1）小题满分6分，第（2）小题满分8分.如图，ABCD 是边长为10海里的正方形海域.现有一架飞机在该海域失事，两艘海事搜救船在A 处同时出发，沿直线AP 、AQ 向前联合搜索，且4PAQ π∠=（其中点P 、Q 分别在边BC 、CD 上），搜索区域为平面四边形APCQ 围成的海平面.设PAB θ∠=，搜索区域的面积为S . （1）试建立S 与tan θ的关系式，并指出θ的取值范围；（2）求S 的最大值，并求此时θ的值.21. （本题满分14分）本题共有2个小题，第（1）小题满分6分，第（2）小题满分8分. （理）已知定义在小水R 上的函数)(x f ，对任意实数21,x x 都有1212()1()()f x x f x f x +=++，且(1)1f =.（1）若对任意正整数n ，有112n n a f ⎛⎫=+ ⎪⎝⎭，求1a 、2a 的值，并证明{}n a 为等比数列；（2）设对任意正整数n ，有1()n b f n =．若不等式P.F. Productions 后期制作 12226log (1)35n n n b b b x +++++>+ 对任意不小于2的正整数n 都成立，求实数x 的取值范围．（文）已知定义在*N 上的函数)(x f ，对任意正整数1n 、2n ，都有BCAQP1212()1()()f n n f n f n +=++，且(1)1f =.（1）若对任意正整数n ，有(2)1n n a f =+，求1a 、2a 的值，并证明{}n a 为等比数列；（2）若对任意正整数n ，()f n 使得不等式2()3log (1)28n f n x <+恒成立，求实数x 的取值范围．22.（本题满分16分）本题学科网真没用共有3个小题，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分6分.（理）已知中心在原点O ，左焦点为1(1,0)F -的椭圆1C 的左顶点为A ，上顶点为B ，1F 到直线AB的距离为||7OB . (1) 求椭圆1C 的方程；(2) 过点(3,0)P 作直线l ，使其交椭圆1C 于R 、S 两点，交直线1x =于Q 点. 问：是否存在这样的直线l ，使||PQ 是||PR 、||PS 的等比中项？若存在，求出直线l 的方程；若不存在，说明理由.(3) 若椭圆1C 方程为：22221x y m n+=（0m n >>），椭圆2C 方程为：2222x y m n λ+=（0λ>，且1λ≠），则称椭圆2C 是椭圆1C 的λ倍相似椭圆.已知2C 是椭圆1C 的3倍相似椭圆，若直线y kx b =+与两椭圆1C 、2C 交于四点(依次为P 、Q 、R 、S )，且2PS RS QS +=，试研究动点(,)E k b P.F. Productions 后期制作的轨迹方程.（文）定义区间),(d c ，),[d c ，],(d c ，],[d c 的长度均为c d -，其中c d >．（1）已知函数21xy =-的定义域为[],a b ，值域为10,2⎡⎤⎢⎥⎣⎦，写出区间[],a b 长度的最大值与最小值.（2）已知函数()2sin f x x =，将函数()y f x =的图像的每点横坐标缩短到原来的12倍，然后向左平移8π个单位，得到函数()y g x =的图像，区间[,]ab（,a b R ∈且a b <）满足：()y g x =在[,]a b 上至少含有2014个零点，在所有满足上述条件的[,]a b 中，求区间[,]a b 长度的最小值．（3）已知函数()M f x 的定义域为实数集[2,2]D =-,满足(),,M x x Mf x x x M ∈⎧=⎨-∉⎩(M 是D 的非空真子集) . 集合[]1,2A =,[]2,1B =-- ,求()()()()3A B A B f x F x f x f x =++ 的值域所在区间长度的总和．23．（本题满分18分）本题共有3个小题，第（1）小题满分4分，第（2）小题满分6分，第（3）小题满分8分.（理）定义区间),(d c ，),[d c ，],(d c ，],[d c 的长度均为c d -，其中c d >．（1）已知函数21xy =-的定义域为[],a b ，值域为10,2⎡⎤⎢⎥⎣⎦，写出区间[],a b 长度的最大值与最小值.（2）已知小水制作函数()M f x 的定义域为实数集[2,2]D =-,满足(),,M x x Mf x x x M ∈⎧=⎨-∉⎩(M 是D 的非空真子集) . 集合[]1,2A =,[]2,1B =-- ,求()()()()3A B A B f x F x f x f x =++ 的值域所在区间长度的总和．（3）定义函数1234()11234f x x x x x =+++-----，判断函数()f x 在区间(2,3)上是否有零点，并求不等式()0f x >解集区间的长度总和．（文）已知中心在原点O ，左焦点为1(1,0)F -的椭圆C 的左顶点为A ，上顶点为B ，1F 到直线AB的距离为||7OB . (1) 求椭圆C 的方程；(2) 过(3,0)P 的直线l 交椭圆C 于R 、S 两点，交直线1x =于Q 点，若||PQ 是||PR 、||PS 的等比中项，求直线l 的方程；小水 (3) 圆D 以椭圆C 的两焦点为直径，圆D 的任意一条切线m 交椭圆C 于两点M 、N ，试求弦长||MN 的取值范围.参考答案（供参考）一、填空题 1. {}1,4,5 2. 43y x =± 3. 5 4.135. (2,3)-6. 23522n n - 7.323π8. (理) 0.98 (文) 1159. 13- 10. (理) 3 (文) 511. (理) 1 (文) 212. 6+13.14. (理) 12 (文) 20二、选择题 15. A16. (理) D (文) A17. D18. (理) B (文) C三、简答题19. 解：（1）设AB 的中点为E ，连接EN ，则//EN AC ，且12EN AC =，所以MNE ∠或其补角即为异面直线MN 与AC 所成的角。

2014年上海高三数学四区(静安区杨浦区青浦区宝山区)联考二模试卷理科含答案

2013年静安、杨浦、青浦宝山区高三二模卷(理科) 2013.04.（满分150分，答题时间120分钟）一、填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1．已知全集R U =，集合{}0322>--=x x x A ，则=A C U . 2．若复数z 满足)2(z i z -=（i 是虚数单位），则=z . 3．已知直线012=++y x 的倾斜角大小是θ，则=θ2tan . 4．若关于y x 、的二元一次方程组⎩⎨⎧=-+-=+-04)12(03y x m y mx 有唯一一组解，则实数m 的取值范围是 .5．已知函数)(x f y =和函数)1(l o g 2+=x y 的图像关于直线0=-y x 对称，则函数)(x f y =的解析式为 .6．已知双曲线的方程为1322=-y x ，则此双曲线的焦点到渐近线的距离为 . 7．函数xx xx x x x f sin cos sin 2)cos(cos sin )(--+=π的最小正周期=T .8．若nx )21(+展开式中含3x 项的系数等于含x 项系数的8倍，则正整数=n .9．执行如图所示的程序框图，若输入p 的值是7，则输出S 的值是 .10．已知圆锥底面半径与球的半径都是1cm ，如果圆锥的体积恰好也与球的体积相等，那么这个圆锥的母线长为 cm ．11．某中学在高一年级开设了4门选修课，每名学生必须参加这4门选修课中的一门，对于该年级的甲、乙、丙3名学生，这3名学生选择的选修课互不相同的概率是 (结果用最简分数表示)． 12．各项为正数的无穷等比数列{}n a 的前n 项和为n S ，若1lim 1=+∞→n nn S S ，则其公比q 的取值范围是 .13．已知两个不相等的平面向量α，β(≠α)满足|β|＝2，且α与－α的夹角为120°，则|α|的最大值是 .14．给出30行30列的数表A ：⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛10742161831501172163427201318327211591502015105，其特点是每行每列都构成等差数列，记数表主对角线上的数10743421101，，，，，按顺序构成数列{}n b ，存在正整数)1(t s t s <<、使t s b b b ,,1成等差数列，试写出一组),(t s 的值 .二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答案纸的相应编号上，填上正确的答案，选对得5分，否则一律得零分. 15．已知),2(ππα∈，53sin =α，则)4tan(πα-的值等于………………………（）（A ）71．（B ）71- ．（C ） 7．（D ）7-． 16．已知圆C 的极坐标方程为θρsin a =，则“2=a ”是“圆C 与极轴所在直线相切”的 ………………………………………………………………………………（）（A ）充分不必要条件．（B ）必要不充分条件．（C ）充要条件．（D ）既不充分又不必要条件． 17．若直线2=+by ax 经过点)sin ,(cos ααM ，则 …………………………（）（A ） 422≤+b a ．（B ） 422≥+b a ．（C ）41122≤+b a ．（D ）41122≥+ba ． 18．已知集合{})(),(x f y y x M ==，若对于任意M y x ∈),(11，存在M y x ∈),(22，使得02121=+y y x x 成立，则称集合M 是“Ω集合”. 给出下列4个集合： ① ⎭⎬⎫⎩⎨⎧==x y y x M 1),( ②{}2),(-==xe y y x M ③{}x y y x M cos ),(== ④ {}x y y x M ln ),(==其中所有“Ω集合”的序号是……………………………………………………（）（A ）②③ ．（B ）③④ ．（C ）①②④．（D ）①③④．要的步骤.19．（本题满分12分）本题共有2小题，第1小题满分5分，第2小题满分7分．在棱长为2的正方体1111D C B A ABCD -中，F E ,分别为CD B A ,11的中点．（1）求直线EC 与平面11BCC B 所成角的大小；（2）求二面角B AF E --的大小．20．（本题满分14分）本题共有2小题，第1小题满分6分，第2小题满分8分．如图所示，扇形AOB ，圆心角AOB 的大小等于3π，半径为2，在半径OA 上有一动点C ，过点C 作平行于OB 的直线交弧AB 于点P ．（1）若C 是半径OA 的中点，求线段PC 的大小；（2）设θ=∠COP ，求△POC 面积的最大值及此时θ的值．已知函数a x x f +=2)(．（1）若12)()(++=bx x f x F 是偶函数，在定义域上ax x F ≥)(恒成立，求实数a 的取值范围；（2）当1=a 时，令)())(()(x f x f f x λϕ-=，问是否存在实数λ，使)(x ϕ在()1,-∞-上是减函数，在()0,1-上是增函数？如果存在，求出λ的值；如果不存在，请说明理由．22．（本题满分16分）本题共有3小题，第1小题满分4分，第2小题满分6分，第3小题满分6分.已知点)0,1(A ，1P 、2P 、3P 是平面直角坐标系上的三点，且1AP 、2AP 、3AP 成等差数列，公差为d ，0≠d ．（1）若1P 坐标为()1,1-，2d =，点3P 在直线3180x y --=上时，求点3P 的坐标；（2）已知圆C 的方程是222)3()3(r y x =-+-)0(>r ，过点A 的直线交圆于31P P 、两点，2P 是圆C 上另外一点，求实数d 的取值范围；（3）若1P 、2P 、3P 都在抛物线24y x =上，点2P 的横坐标为3，求证：线段13PP 的垂直平分线与x 轴的交点为一定点，并求该定点的坐标．23．（本题满分18分）本题共有3小题，第1小题满分4分，第2小题满分6分，第3小题满分8分.已知数列{}n a 的前n 项和为n S ，且满足a a =1 (3≠a )，nn n S a 31+=+，设n n n S b 3-=，*∈N n ．（1）求证：数列{}n b 是等比数列；（2）若1+n a ≥n a ，*∈N n ，求实数a 的最小值；（3）当4=a 时，给出一个新数列{}n e ，其中⎩⎨⎧≥==2,1,3n b n e nn ，设这个新数列的前n 项和为n C ，若nC 可以写成p t (*∈N p t ,且1,1>>p t )的形式，则称n C 为“指数型和”．问{}n C 中的项是否存在“指数型和”，若存在，求出所有“指数型和”；若不存在，请说明理由．2013年静安、杨浦、青浦宝山区高三二模卷(理科)参考答案及评分标准 2013.04说明1．本解答列出试题一种或几种解法，如果考生的解法与所列解法不同，可参照解答中评分标准的精神进行评分．2．评阅试卷，应坚持每题评阅到底，不要因为考生的解答中出现错误而中断对该题的评阅．当考生的解答在某一步出现错误，影响了后续部分，但该步以后的解答未改变这一题的内容和难度时，可视影响程度决定后面部分的给分，但是原则上不应超出后面部分应给分数之半，如果有较严重的概念性错误，就不给分．3．第19题至第23题中右端所注的分数，表示考生正确做到这一步应得的该题分数． 4．给分或扣分均以1分为单位．一．填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．1．]3,1[-； 2．2； 3．34； 4．31≠m ； 5．12-=xy ； 6．1； 7．（文、理）π；8．（文）4（理）5；9．6463；10．17；11．（文）414214=C （理）834334=P ；12．(]1,0；13．（文）(1,)+∞（理）334；14．（文）②③⑤（理）)25,17(． ②二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答案纸的相应编号上，填上正确的答案，选对得5分，否则一律得零分.15． D ； 16．（文）B （理）A ； 17． B ；18．（文）C （理）A三、解答题（本大题满分74分）本大题共5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤 .19．（本题满分12分）本题共有2小题，第1小题满分5分，第2小题满分7分． (文)解：（1）如图正四棱锥底面的边长是5.1米，高是85.0米 sh V 31=36375.085.05.15.131m =⨯⨯⨯= 所以这个四棱锥冷水塔的容积是36375.0m ．(2)如图，取底面边长的中点E ，连接SE ，222275.085.0+=+=EO SO SESE ⨯⨯⨯=5.1214S 侧22240.375.085.05.1214m ≈+⨯⨯⨯=答：制造这个水塔的侧面需要3.40平方米钢板．（理）19．（1）（理）解法一：建立坐标系如图平面11BCC B 的一个法向量为)0,1,0(1=n可知直线EC 的一个方向向量为)2,1,2(--=∴．设直线EC 与平面1BCC B 成角为θ，d 与1n 所成角为ϕ，则31191cos sin =⨯===ϕθ31arcsin BCC B 11成角大小为与平面故EC19（1）解法二：⊥1EB 平面11BCC B ，即C B 1为EC 在平面11BCC B 内的射影，故1ECB ∠为直线EC 与平面11BCC B 所成角，在C EB Rt 1∆中，22,1EB 11==C B ,42221tan 111===∠C B EB ECB 故42arctanBCC B 11成角大小为与平面故EC 19（2）（理科）解法一：建立坐标系如图．平面ABCD 的一个法向量为)1,0,0(1=n设平面AEF 的一个法向量为),,(2z y x n =，因为)0,1,2(-=，)2,1,0(= 所以⎩⎨⎧=+=+-0202z y y x ，令1=x ，则1,2-==z y )1,2,1(2-=⇒n661411cos =++-==θ由图知二面角B AF E --为锐二面角，故其大小为66arccos．19（2）解法二：过E 作平面ABC 的垂线，垂足为E '，E EG '∠即为所求 AB E ∈'，过E '作AF 的垂线设垂足为G ，ADF ∆∽AGE ∆521='⇒=''E G AF AD E A E G 即52='E G在Q E E Rt '∆中5tan =''='∠E G E E E EG所以二面角B AF E --的大小为5arctan ．20．（本题满分14分）本题共有2小题，第1小题满分6分，第2小题满分8分．解:（1）在△POC 中，32π=∠OCP ，1,2==OC OP 由32cos 2222πPC OC PC OC OP ⋅-+=得032=-+PC PC ，解得2131+-=PC ．（2）∵CP ∥OB ，∴θπ-=∠=∠3POB CPO ，在△POC 中，由正弦定理得θsin sin PCO =∠，即θπsin 32sin = ∴θsin 34=CP ,又32sin )3sin(πθπCP OC =-)3sin(34θπ-=∴OC ．（文）记△POC 的周长为)(θC ，则2)3sin(34sin 342)(+-+=++=θπθθOC CP C1sin 2223πθθθ⎫⎛⎫++=++⎪ ⎪⎪⎝⎭⎭∴6πθ=时，)(θC 取得最大值为23+. （理）解法一：记△POC 的面积为)(θS ，则32sin 21)(πθOC CP S ⋅=， 23)3sin(34sin 3421⨯-⋅⋅=θπθ)3sin(sin 34θπθ-⋅= )sin 21cos 23(sin 34θθθ-=θθθ2sin 32cos sin 2-= 332cos 332sin -+=θθ33)62(sin 332-+=πθ∴6πθ=时，)(θS 取得最大值为33. 解法二：212432cos 22-=⋅-+=PC OC PC OC π即422=⋅++PC OC PC OC ，又PC OC PC OC PC OC ⋅≥⋅++322即43≤⋅PC OC当且仅当PC OC =时等号成立, 所以3323342132sin 21=⨯⨯≤⋅=πOC CP SPC OC = ∴6πθ=时，)(θS 取得最大值为33.（文）解：(1)依题意，32=a ，)0,32(C ，由221124x y y x ⎧+=⎪⎨⎪=⎩，得y = 设),(11y x A ),(22y x B ，32=OC∴63232212121=⨯⨯=-⋅=∆y y OC S ABC ； (2)如图，由2221124y kx x y =+⎧⎪⎨+=⎪⎩得22(31)120k x kx ++=，0)12(2≥=∆k 依题意，0k ≠，设1122()()P x y Q x y ，，，，线段PQ 的中点00()H x y ，，则12026231x x k x k+-==+，0022231y kx k =+=+，D (0 2)-，，由1-=⋅PQ DH k k ，得2222311631k k k k ++⋅=--+，∴3k =±（理）解:（1）12)(2+++=bx a x x F 是偶函数，0=∴b即2)(2++=a x x F ，R x ∈ 又ax x F ≥)(恒成立即2)1(222+≤-⇒≥++x x a ax a x 当1=x 时R a ∈⇒当1>x 时，213)1(122+-+-=-+≤x x x x a ，232+≤a当1<x 时，213)1(122+-+-=-+≥x x x x a ， 232+-≥a综上： 232232+≤≤+-a （2）)())(()(x f x f f x λϕ-=)2()2(24λλ-+-+=x x)(x ϕ∴是偶函数，要使)(x ϕ在()1,-∞-上是减函数在()0,1-上是增函数，即)(x ϕ只要满足在区间()+∞,1上是增函数在()1,0上是减函数．令2x t =，当()1,0∈x 时()1,0∈t ；()+∞∈,1x 时()+∞∈,1t ，由于()+∞∈,0x 时，2x t =是增函数记)2()2()()(2λλϕ-+-+==t t t H x ，故)(x ϕ与)(t H 在区间()+∞,0上有相同的增减性，当二次函数)2()2()(2λλ-+-+=t t t H 在区间()+∞,1上是增函数在()1,0上是减函数，其对称轴方程为1=t 4122=⇒=--⇒λλ． 22．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分.（文）解:（1）a a ax x x f f y +++==2))(( 过原点，0=+a a10-==⇒a a 或得2)(x x f =或1)(2-=x x f(2)(3)同理21（理）解（1）11AP =，所以35AP =，设()3,Px y 则()221253180x y x y ⎧-+=⎪⎨--=⎪⎩，消去y ，得211300x x -+=，…（2分）解得15x =，26x =,所以3P 的坐标为()5,3-或()6,0（2）由题意可知点A 到圆心的距离为13)03()13(22=-+-=t …（6分）（ⅰ）当130<<r 时，点()1,0A 在圆上或圆外，31132P P AP AP d =-=，又已知0≠d ，r P P 2031≤≤，所以 0<≤-d r 或 r d ≤<0 （ⅱ）当13≥r 时，点()1,0A 在圆内，所以13213132max=--+=r r d，又已知0≠d ，13220≤<d ，即013<≤-d 或130≤<d结论：当130<<r 时，0<≤-d r 或 r d ≤<0；当13≥r 时，013<≤-d 或130≤<d （3）因为抛物线方程为x y 42=，所以()1,0A 是它的焦点坐标，点2P 的横坐标为3，即82=AP设()111,P x y ，()333,P x y ，则111+=x AP ，133+=x AP ，1322AP AP AP +=，所以13226x x x +==直线13PP 的斜率3131314y y k x x y y -==-+，则线段13PP 的垂直平分线l 的斜率314ly y k +=- 则线段13PP 的垂直平分线l 的方程为()3131324y y y y y x ++-=-- 直线l 与x 轴的交点为定点()5,023．（本题满分18分）本题共有3小题，第1小题满分4分，第2小题满分6分，第3小题满分8分. （文）解：（1）令1=n 得321112⋅+=⋅a a ，即3212=-a a ；又21=a 382=⇒a （2）由3212=-a a 和⎪⎪⎩⎪⎪⎨⎧-+=-++=-+3)1()1(,3)1(11n n S a n n n S na n n nn32)1(1na a n na n n n +=--⇒+321=-⇒+n n a a ，所以数列}{n a 是以2为首项，32为公差的等差数列，所以)2(32+=n a n ．解法一：数列}{n a 是正项递增等差数列，故数列}{n k a 的公比1>q ，若22=k ，则由382=a 得3412==a a q ，此时9)3(223=⋅=k a ，由)2(39+=n 解得*3N n ∉=，所以22>k ，同理32>k ；若42=k ，则由44=a 得2=q ，此时122-⋅=n k n a 组成等比数列，所以)2(32221+=⋅-m n ，2231+=⋅-m n ，对任何正整数n ，只要取2231-⋅=-n m ，即n k a 是数列}{n a 的第2231-⋅-n 项．最小的公比2=q ．所以2231-⋅=-n n k ．………（10分）解法二: 数列}{n a 是正项递增等差数列，故数列}{n k a 的公比1>q ，设存在,,,,21n k k k a a a )(21 <<<<n k k k 组成的数列}{n k a 是等比数列，则3122k k k a a a ⋅=，即()()232)2(322)2(32322322+=+⇒+⨯=⎥⎦⎤⎢⎣⎡+k k k k 因为1*232>∈k N k k 且、所以22+k 必有因数3，即可设N t t t k ∈≥=+,2,322，当数列}{n k a 的公比q 最小时，即42=k ，2=⇒q 最小的公比2=q ．所以2231-⋅=-n n k ．（3）由（2）可得从}{n a 中抽出部分项 ,,,,21n k k k a a a )(21 <<<<n k k k 组成的数列}{n k a 是等比数列，其中11=k ，那么}{n k a 的公比是322+=k q ，其中由解法二可得N t t t k ∈≥-=,2,232． )2(32)32(312+=+⋅=-n n k k k a n 2)32(312-+⋅=⇒-n n k k 2)3223(31-+-⋅=⇒-n n t k 231-⋅=⇒-n n t k ，N t t ∈≥,2所以3232)1(31221--⋅=-++++=+++-n t n tt t k k k n n n （理）解：（1）⇒+=+n n n S a 31n n n S S 321+=+，n n n S b 3-=，*∈N n ，当3≠a 时，1111323333n n n n n n n nn n n b S S b S S ++++-+-==--=2，所以{}n b 为等比数列． 3311-=-=a S b ，12)3(-⨯-=n n a b ．（2）由（1）可得12)3(3-⨯-=-n n n a S*-∈≥-=N n n S S a n n n ,2,1212)3(3221≥=⎩⎨⎧⨯-+⨯=--n n a a a n n n ； n n a a ≥+1，2112>⎩⎨⎧>>+n a a a a n n ，9-≥a 所以9-≥a ，且3≠a ．所以a 的最小值为（3）由（1）当4=a 时，12-=n n b当2≥n 时，n n C 2423++++= 12+=n ，31=C ，所以对正整数n 都有12+=n n C ．由12+=n p t ，n p t 21=-，(*∈N p t ,且1,1>>p t )，t 只能是不小于3的奇数．①当p 为偶数时，n p t tt 2)1)(1(122=-+=-，因为12+pt 和12-p t 都是大于1的正整数，所以存在正整数h g ,，使得g pt 212=+，h p t 212=-， 222=-h g ,2)12(2=--h g h ，所以22=h 且112=--h g 2,1==⇒g h ，相应的3=n ，即有233=C ，3C 为“指数型和”；②当p 为奇数时，)1)(1(112-++++-=-p p tt t t t ，由于121-++++p t t t 是p 个奇数之和，仍为奇数，又1-t 为正偶数，所以n p tt t t 2)1)(1(12=++++-- 不成立，此时没有“指数型和”．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

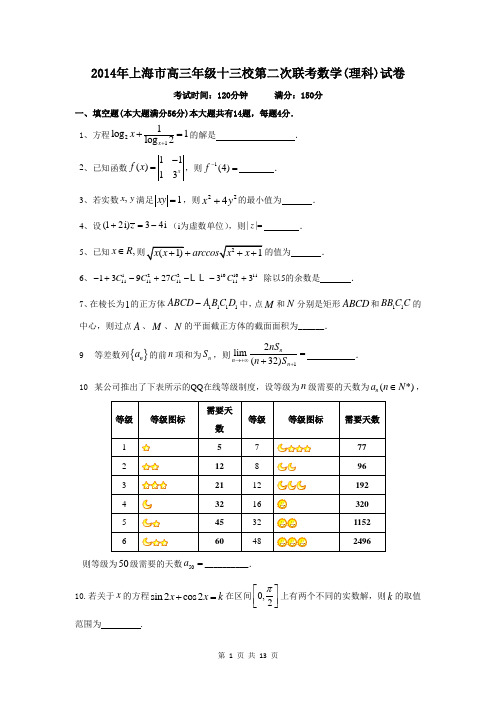
上海市杨浦、静安、宝山、青浦四区2014届下学期高三年级二模考试数学试卷（理科）（满分150分，完卷时间120分钟） 2014.4一、填空题 (本大题共有14题，满分56分)考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分． 1.二阶行列式ii i ++-1101的值是 . （其中i 为虚数单位）2. 已知j i,是方向分别与x 轴和y 轴正方向相同的两个基本单位向量，则平面向量ji +的模等于 .3．二项式7)1(+x 的展开式中含3x 项的系数值为_______________.4.已知圆锥的母线长为5,侧面积为π15,则此圆锥的体积为__________.(结果中保留π)5.已知集合{}sin ,A y y x x R ==∈，{}21,B x x n n Z ==+∈，则AB = .理6文7.在平面直角坐标系xOy 中，若圆22(1)4x y +-=上存在A ，B 两点，且弦AB 的中点为(1,2)P ，则直线AB 的方程为 .理7文8.已知1log log 22=+y x ，则y x +的最小值为_____________.理8文10. 已知首项31=a 的无穷等比数列{}n a )(*N n ∈的各项和等于4，则这个数列{}n a 的公比是．9．（理）在平面直角坐标系xOy 中，曲线1C 的参数方程为⎩⎨⎧==,sin 2,cos 2ααy x （α为参数），O为坐标原点，M 为1C 上的动点，P 点满足2OP OM =，点P 的轨迹为曲线2C ．则2C 的参数方程为 .10. 阅读程序框图，运行相应的程序，输出的结果为 .11．（理）从5男和3女8位志愿者中任选3人参加冬奥会火炬接力活动，若随机变量ξ表示所选3人中女志愿者的人数，则ξ的数学期望是．12．（理）设各项均不为零的数列{}n c 中，所有满足01<⋅+i i c c 的正整数i 的个数称为这个数列{}n c 的变号数.已知数列{}n a 的前n 项和442+-=n n S n ，nn a b 41-=（*N n ∈），则数列{}n b 的变号数为 .13.（理）已知定义在[)+∞,0上的函数)(x f 满足)2(3)(+=x f x f .当[)2,0∈x 时x x x f 2)(2+-=.设)(x f 在[)n n 2,22-上的最大值为n a ，且数列}{n a 的前n 项和为n S ，则=∞→n n S lim . （其中*N n ∈）14．（理）正方形1S 和2S 内接于同一个直角三角形ABC 中，如图所示，设α=∠A ，若4411=S ，4402=S ，则=α2sin.二、选择题(本大题共有4题，满分20分)每题有且只有一个正确答案，考生应在答题纸相应编号上，将代表答案的小方格涂黑，选对得5分，否则一律得零分．15. （理）在实数集R 上定义运算*：(1)x y x y *=⋅-．若关于x 的不等式()0x x a *->第10题图的解集是集合{|11}x x -≤≤的子集，则实数a 的取值范围是…………………（）.)(A [0,2] )(B [2,1)(1,0]---)(C [0,1)(1,2] )(D [2,0]-16．“1=ω”是“函数x x x f ωω22cos sin )(-=的最小正周期为π”的…………（）.)(A 充分必要条件 )(B 充分不必要条件)(C 必要不充分条件 )(D 既不充分又必要条件17. 若圆柱的底面直径和高都与球的直径相等,圆柱、球的表面积分别记为1S 、2S ,则1S :2S =………………………………………………………………（）.)(A 1:1 )(B 2:1 )(C 3:2 )(D 4:118.（理）函数()f x 的定义域为实数集R ，⎪⎩⎪⎨⎧<≤--≤≤=.01,1)21(,10,)(x x x x f x 对于任意的x R ∈都有(1)(1)f x f x +=-.若在区间[1,3]-上函数()()g x f x mx m =--恰有四个不同的零点，则实数m 的取值范围是…………………………………………（）.)(A 10,2⎡⎤⎢⎥⎣⎦)(B 10,4⎡⎫⎪⎢⎣⎭ )(C 10,2⎛⎤ ⎥⎝⎦ )(D 10,4⎛⎤ ⎥⎝⎦三、解答题(本大题共有5题，满分74分)解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤． 19．（本题满分12分）ADCFPB（理）如图，四棱锥P ABCD -中，底面ABCD 是平行四边形，︒=∠90CAD ，PA ⊥平面ABCD ，1PA BC ==，AB =，F 是BC 的中点. (1) 求证：DA ⊥平面PAC ；（2）若以A 为坐标原点，射线AC 、AD 、AP 分别是x 轴、y 轴、z 轴的正半轴，建立空间直角坐标系，已经计算得)1,1,1(=n 是平面PCD 的法向量，求平面PAF 与平面PCD 所成锐二面角的余弦值.20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分某公司承建扇环面形状的花坛如图所示，该扇环面花坛是由以点O 为圆心的两个同心圆弧AD 、弧BC 以及两条线段AB 和CD 围成的封闭图形．花坛设计周长为30米，其中大圆弧AD 所在圆的半径为10米．设小圆弧BC 所在圆的半径为x 米（100<<x ），圆心角为θ弧度．（1）求θ关于x 的函数关系式；（2）在对花坛的边缘进行装饰时，已知两条线段的装饰费用为4元/米，两条弧线部分的装饰费用为9元/米．设花坛的面积与装饰总费用的比为y ，当x 为何值时，y 取得最大值？21．（本题满分14分）本题共有2个小题，第1小题满分5分，第2小题满分9分（理）已知椭圆2222:1x y C a b+=(0)a b >>的右焦点为F (1,0)，短轴的端点分别为12,B B ,且12FB FB a ⋅=-.（1）求椭圆C 的方程；（2）过点F 且斜率为k (0)k ≠的直线l 交椭圆于,M N 两点，弦MN 的垂直平分线与x 轴相交于点D .设弦MN 的中点为P ，试求DP MN的取值范围．22．（本题满分16分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分6分（理）设函数xx g 3)(=，xx h 9)(=.（1）解方程：)9)((log )8)(2(log 33+=-+x h x g x ；（2）令3)()()(+=x g x g x p ，3)(3)(+=x h x q ，求证：)20142013()20142012()20142()20141()20142013()20142012()20142()20141(q q q q p p p p ++++=++++ （3）若bx g ax g x f +++=)()1()(是实数集R 上的奇函数，且0))(2()1)((>⋅-+-x g k f x h f 对任意实数x 恒成立，求实数k 的取值范围.23．（本题满分18分）本题共有3个小题，第1小题满分4分，第2小题满分6分，第3小题满分8分（理）设各项都是正整数的无穷数列{}n a 满足：对任意*N n ∈，有1+<n n a a ．记n a n a b =．（1）若数列{}n a 是首项11a =，公比2=q 的等比数列，求数列{}n b 的通项公式；（2）若n b n 3=，证明：21=a ；（3）若数列{}n a 的首项11a =，1+=n a n a c ，{}n c 是公差为1的等差数列．记n n n a d ⋅-=2，n n n d d d d S ++++=-121 ，问：使5021>⋅++n n n S 成立的最小正整数n 是否存在？并说明理由．四区2013学年度高考模拟考试数学试卷文理科解答参考答案及评分标准 2014.04一．填空题（本大题满分56分）本大题共有14题，考生应在答题纸相应编号的空格内直接填写结果，每个空格填对得4分，否则一律得零分．理1．2； 2．2 3．35； 4．π125．{}1,1-；6． 30x y +-= 7. 22； 8．41 9． ⎩⎨⎧==,sin 4,cos 4ααy x （α为参数）；10. 13811．.895613561525630156100=⨯+⨯+⨯+⨯=ξE 12．3． 13.2314．1012sin =α 3．35； 4．π12 5．{}1,1-；6．}2,6,2,65{ππππ--7.30x y +-= ； 8．22 9．37； 10. 4111. 2213y x -=； 12．1253381556C C C = 13．当1-=ac 时，0lim 622222=⎪⎭⎫⎝⎛++∴⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛++∞→nn n n c a c a c a c a ；当1=ac 时，c a =舍去． 14.]41,0(二、选择题（本大题满分20分）本大题共有4题，每题有且只有一个正确答案，考生应在答案纸的相应编号上，填上正确的答案，选对得5分，否则一律得零分. 15．D ；16．B ；17．C ；18．理D ；三、解答题（本大题满分74分）本大题共5题，解答下列各题必须在答题纸相应编号的规定区域内写出必要的步骤 .19．（理）1(0,0,0),(1,0,0),(1,1,0),(0,1,0),(1,,0),(0,0,1)2A CB D F P --. (1) 证明方法一：Q 四边形是平行四边形，Q PA ⊥平面A B C D ∴P A D A ⊥，又A C D A ⊥，AC PA A =I ，∴DA ⊥平面PAC .方法二：证得DA uu u r是平面PAC 的一个法向量，∴DA ⊥平面PAC .(2)通过平面几何图形性质或者解线性方程组,计算得平面PAF 一个法向量为(1,2,0)m =u r，又平面PCD 法向量为(1,1,1)n =r ，所以||cos ,||||m n m n m n ⋅<>==u r ru r r u r r∴20．(1)设扇环的圆心角为θ，则()30102(10)x x θ=++-，所以10210xxθ+=+， (2) 花坛的面积为2221(10)(5)(10)550,(010)2x x x x x x θ-=+-=-++<<．装饰总费用为()9108(10)17010x x x θ++-=+，所以花坛的面积与装饰总费用的比22550550==1701010(17)x x x x y x x -++---++，令17t x =+，则3913243()101010y t t =-+≤，当且仅当t =18时取等号，此时121,11x θ==．答：当1x =时，花坛的面积与装饰总费用的比最大．21．理（1）依题意不妨设1(0,)B b -，2(0,)B b ，则1(1,)FB b =--，2(1,)FB b =-.由12FB FB a ⋅=-，得21b a -=-. 又因为221a b -=，解得2,a b ==.所以椭圆C 的方程为22143x y +=. （2）依题意直线l 的方程为(1)y k x =-.由22(1),143y k x x y =-⎧⎪⎨+=⎪⎩得2222(34)84120k x k x k +-+-=.设11(,)M x y ，22(,)N x y ，则2122834k x x k +=+，212241234k x x k -=+.所以弦MN 的中点为22243(,)3434k kP k k-++.所以MN === 2212(1)43k k +=+. 直线PD 的方程为222314()4343k k y x k k k +=--++，由0y =，得2243k x k =+，则22(,0)43k D k +，所以DP =.所以224312(1)43DP k k MN k +==++=. 又因为211k +>，所以21011k <<+.所以104<<. 所以DP MN 的取值范围是1(0,)4.22．理（1）99)832(3+=-⋅⋅x x x ，93=x ，2=x （2）21323)21()20141007(===p p ，2163)21()20141007(===q q ．因为1333333333333)1()(11=+++=+++=-+--xxx xx xx x p x p ，1393399399399)1()(11=+++=+++=-+--x x x x x x x x q x q所以，211006)20142013()20142()20141(+=+++p p p ， 211006)20142013()20142()20141(+=+++q q q ． )20142013()20142()20141(p p p +++ =)20142013()20142()20141(q q q +++ ．（3）因为bx ax x f +++=)()1()(ϕϕ是实数集上的奇函数，所以1,3=-=b a .)1321(3)(+-=xx f ，)(x f 在实数集上单调递增. 由0))(2()1)((>⋅-+-x g k f x h f 得))(2()1)((x g k f x h f ⋅-->-，又因为)(x f 是实数集上的奇函数，所以，)2)(()1)((-⋅>-x g k f x h f ，又因为)(x f 在实数集上单调递增，所以2)(1)(-⋅>-x g k x h 即23132-⋅>-x xk 对任意的R x ∈都成立，即x x k 313+<对任意的R x ∈都成立，2<k . 23．理（1）1111a b a a ===，242112211--====--n a n n n n a a b ；（2）根据反证法排除11a =和*113()a a N ≥∈证明：假设12a ≠，又*N a n ∈，所以11a =或*113()a a N ≥∈ ①当11a =时，1111a b a a ===与13b =矛盾，所以11a ≠；②当*113()a a N ≥∈时，即1113a a b a ≥==，即11a a a ≥，又1+<n n a a ，所以11a ≤与*113()a a N ≥∈矛盾；由①②可知21=a ．（3）首先{}n a 是公差为1的等差数列，证明如下：1n n a a +>*2,n n N ⇒≥∈时1n n a a ->，所以11n n a a -≥+()n m a a n m ⇒≥+-，*(,)m n m n N <∈、1111[1(1)]n n a a n n a a a a ++++⇒≥++-+即11n n n n c c a a ++-≥-由题设11n n a a +≥-又11n n a a +-≥11n n a a +⇒-= 即{}n a 是等差数列．又{}n a 的首项11a =，所以n a n =，)223222(32n n n S ⋅++⋅+⋅+-= ，对此式两边乘以2，得14322232222+⋅--⋅-⋅--=n n n S两式相减得=⋅-++++=+13222222n n n n S 22211-⋅-++n n n22211-=⋅+++n n n n S ，5021>⋅++n n n S 即5221≥+n ，当5≥n 时，526421>=+n ，即存在最小正整数5使得5021>⋅++n n n S 成立．注：也可以归纳猜想后用数学归纳法证明n a n =．。