第7-8章-分组码和卷积码
合集下载
移动通信实验线性分组码卷积码实验

3、运行仿真,开启所有模块的电源开关。
4、设置主控菜单,选择【主菜单】→【移动通信】→【卷积码实验】。在“卷积及交织误码设置”界面中,先选择【无误码】。此时系统初始状态为:输入数据为8K,通过模块4进行卷积编码,再经过模块5完成卷积译码。
5、观察并记录原始码元和卷积译码恢复的码元,看是否一致。
由图可知:波形一致
编码信号输入
3、调用示波器观测信号源模块的“PN”和4号模块的编码输出“编码数据TH,即观测原始码元和卷积编码输出信号。
4、运行仿真,开启所有模块的电源开关。
5、设置主控菜单,选择【主菜单】→【移动通信】→【卷积码实验】。在“卷积及交织误码设置”界面中,先选择【无误码】。此时系统初始状态为:编码输入8K数据,进行卷积编码,无差错插入模式。
【突发错】译码结果与输入信号
由图可知:卷积码能纠正随机错,而不能纠正突发错。
五、实验报告
1、观察和记录实验波形,验证卷积码检错及纠错能力。
2、简述卷积码在生活中的应用。
无线通信,移动通信如GSM
六、实验小结
通过本次实验学习了卷积码的编译码原理,观察和记录了实验波形,验证了卷积码的检错及纠错能力。
3、分析汉明码实现检错及纠错的原理。
以接收到的数据为7bit为例,从左到右的位数分别以二进制表示:001,010,011,100,101,110,111。三位二进制以某一位为1可分为三组,第一组为001,011,101,111;第二组为010,011,110,111;第三组为100,101,110,111。将每个小组中二进制所代表的位数(1~7)中的值(0或1)拿出来(每组共4个值),进行奇偶校验,以奇校验为例,1的个数为奇数标0,偶数标1,最后倒叙查看纠错。如:第一组1为奇数标0,第二组为偶数标1,第三组为偶数标1,最后得到110,即第六位数据错误。
4、设置主控菜单,选择【主菜单】→【移动通信】→【卷积码实验】。在“卷积及交织误码设置”界面中,先选择【无误码】。此时系统初始状态为:输入数据为8K,通过模块4进行卷积编码,再经过模块5完成卷积译码。
5、观察并记录原始码元和卷积译码恢复的码元,看是否一致。
由图可知:波形一致
编码信号输入
3、调用示波器观测信号源模块的“PN”和4号模块的编码输出“编码数据TH,即观测原始码元和卷积编码输出信号。
4、运行仿真,开启所有模块的电源开关。
5、设置主控菜单,选择【主菜单】→【移动通信】→【卷积码实验】。在“卷积及交织误码设置”界面中,先选择【无误码】。此时系统初始状态为:编码输入8K数据,进行卷积编码,无差错插入模式。
【突发错】译码结果与输入信号
由图可知:卷积码能纠正随机错,而不能纠正突发错。
五、实验报告
1、观察和记录实验波形,验证卷积码检错及纠错能力。
2、简述卷积码在生活中的应用。
无线通信,移动通信如GSM
六、实验小结
通过本次实验学习了卷积码的编译码原理,观察和记录了实验波形,验证了卷积码的检错及纠错能力。
3、分析汉明码实现检错及纠错的原理。
以接收到的数据为7bit为例,从左到右的位数分别以二进制表示:001,010,011,100,101,110,111。三位二进制以某一位为1可分为三组,第一组为001,011,101,111;第二组为010,011,110,111;第三组为100,101,110,111。将每个小组中二进制所代表的位数(1~7)中的值(0或1)拿出来(每组共4个值),进行奇偶校验,以奇校验为例,1的个数为奇数标0,偶数标1,最后倒叙查看纠错。如:第一组1为奇数标0,第二组为偶数标1,第三组为偶数标1,最后得到110,即第六位数据错误。
第7章差错控制编码

第7章 差错控制编码
7.2.2 行列监督码(二维奇偶校验码)
行列监督码(又称二维奇偶校验码、方阵码),它是垂直奇 偶校验与水平奇偶校验的组合,其发现差错的能力很强。这 种码是将若干码字排列成矩阵,在每行和每列的末尾均加监 督码(奇监督或偶监督)。
例如
1100101100010100110001011000011001110101…… 为用户要发送的信息序列,现将每8个码元分成一 组编成方阵,对方阵的行与列都进行偶数监督,则 在发送端编成如表7-1所示的方阵。
息码为10101,码后的码字为1010110101; 当信息码有偶数个“1”时,则监督码是信息码的反码,如
信息码为11011,则编码后的码字为1101100100。
第7章 差错控制编码
监督码的解码规则如下:
解码时先将接收码组中信息码和监督码对应码位模2相加, 得到一个合成码。 若接收的信息码中有奇数个“1”,则此合成码就是检验 码; 若接收的信息码中有偶数个“1”,则校验码为合成码的 反码。 观察校验码中“1”的个数,就能判决信码是否有错并纠 正错误。
信道中差错的类型:
随机差错:由随机噪声导致,表现为独立的、稀疏 的和互不相关发生的差错。
突发差错:相对集中出现,即在短时段内有很多错 码出现,而在其间有较长的无错码时间段,例如由 脉冲干扰引起的错码或信道特性产生的衰落等。
第7章 差错控制编码
7.1.2 差错控制方式 常用的差错控制方式:
➢ 检错重发(ARQ)
7.1.3 纠错码的分类
1)按差错控制编码的功能分:检错码、纠错码 2)按信息码与监督码间的检验关系分:
线性码、非线性码 3)按信息码与监督码间的约束关系分:分组码、卷积码 4)按信息码的编码前后的形式分:系统码、非系统码 5)按信道差错类型分:随机纠错码、突发纠错码 6)按用于差错编码的数学方法分:
信息论与编码-第7章-第14讲-信道编码-线性分组码2

5
2013/4/5
第六章 信道编码
6.2.6 线性分组码的译码
表 6.2.2 码字 禁 用 码 组
6.2 线 性 分 组 码
C1(=0)
(陪集首)
C2aaaaaaaaaaa …Ciaaaaaaaaa C2+ E2 C2+ E3
…
… … …
…
aaaaaaaaaa
E2 E3
…
…Ci + E2 …Ci + E3
11
第六章 信道编码
6.2.6 线性分组码的译码
对纠两个错误的 (n,k) 线性码,必须能纠 误图样,所以 个错
6.2 线 性 分 组 码
依此类推,一个纠 t 个错误的 (n,k) 线性码必须满足
对于完备码,由码的纠错能力所确定的伴随式数恰好等于可纠 的错误图样数,所以完备码的 (n-k) 个监督码元得到了充分 的利用。
然后在剩下的 (2n-2k) 个 n 重中选取一个重量最轻的 n 重 E2 放 在全0码矢 C1 下面,再将 E2 分别和码矢 相加,放 在对应码矢下面构成阵列第二行; 在第二次剩下的 n 重中,选取重量最轻的 n 重 E3,放在 E2 下面, 并将 E3 分别加到第一行各码矢上,得到第三行; …,继续这样做下去,直到全部 n 重用完为止。得到表6.2.2所示 的给定 (n,k) 线性码的标准阵列。
设 H 为给定 (n,k) 线性码的监督矩阵,在陪集首为 El 的陪集 中的任意矢量 R 为 R=El+Ci, i=1,2,…,2k 其伴随式为 S=RHT=(El+Ci)HT=ElHT+CiHT =ElHT 上式表明:陪集中任意矢量的伴随式等于陪集首的伴随式。 即同一陪集中所有伴随式相同。 不同陪集中,由于陪集首不同所以伴随式不同。
2013/4/5
第六章 信道编码
6.2.6 线性分组码的译码
表 6.2.2 码字 禁 用 码 组
6.2 线 性 分 组 码
C1(=0)
(陪集首)
C2aaaaaaaaaaa …Ciaaaaaaaaa C2+ E2 C2+ E3
…
… … …
…
aaaaaaaaaa
E2 E3
…
…Ci + E2 …Ci + E3
11
第六章 信道编码
6.2.6 线性分组码的译码
对纠两个错误的 (n,k) 线性码,必须能纠 误图样,所以 个错
6.2 线 性 分 组 码
依此类推,一个纠 t 个错误的 (n,k) 线性码必须满足
对于完备码,由码的纠错能力所确定的伴随式数恰好等于可纠 的错误图样数,所以完备码的 (n-k) 个监督码元得到了充分 的利用。
然后在剩下的 (2n-2k) 个 n 重中选取一个重量最轻的 n 重 E2 放 在全0码矢 C1 下面,再将 E2 分别和码矢 相加,放 在对应码矢下面构成阵列第二行; 在第二次剩下的 n 重中,选取重量最轻的 n 重 E3,放在 E2 下面, 并将 E3 分别加到第一行各码矢上,得到第三行; …,继续这样做下去,直到全部 n 重用完为止。得到表6.2.2所示 的给定 (n,k) 线性码的标准阵列。
设 H 为给定 (n,k) 线性码的监督矩阵,在陪集首为 El 的陪集 中的任意矢量 R 为 R=El+Ci, i=1,2,…,2k 其伴随式为 S=RHT=(El+Ci)HT=ElHT+CiHT =ElHT 上式表明:陪集中任意矢量的伴随式等于陪集首的伴随式。 即同一陪集中所有伴随式相同。 不同陪集中,由于陪集首不同所以伴随式不同。
卷积码的图解表示

3
信息论
卷积码的基本概念
卷积码的编码器是由一个有k个输入端、n个输出端,且具有L节移 位寄存器所构成的有限状态的有记忆系统,通常称之为时序网络。 卷积码编码的原理图如图所示,
电子信息工程学院
4
信息论
1 卷积码的解析表示
输入M
m0
t
m0
t 1
m0
t 2
二元(3,1,2) 卷积码编码器原理图
9
信息论
1 卷积码的解析表示
m0
t
0 输入M 1
m0
t 1
m0
t 2
c1
t
c0
t
m1
t
m1
t 1
m1
t 2
c2
t
输出 C t
二元(3,2,2)卷积码并行编码器的原理图
电子信息工程学院
10
信息论
9.5.1 卷积码的解析表示
基本生成矩阵
g
101 011
000 001
S0 S2 S3 S3 S1 S0 S2
由此很快求得输入信息序列为111001…,输出的码字 序列为111,100,101,010,001,111…。
电子信息工程学院
16
1/111
1/100
1/101
0/010
0/001
1/111
001 000
000 000
000 000
电子信息工程学院
11
信息论
1 卷积码的解析表示
生成矩阵
101 011 G
000 001 101 011
第二章 线性分组码(zhb)
1
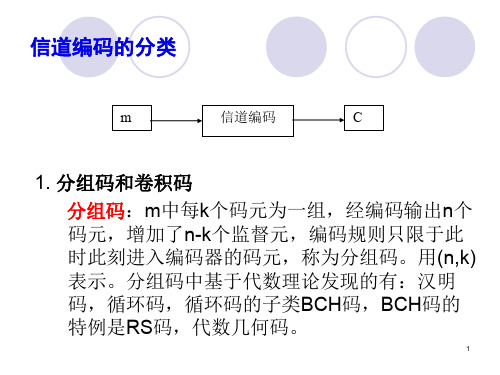
卷积码:m中每k0个码元为一组,经编码输出n0个
码元,增加了n0-k0个监督元,编码规则不仅于此
时此刻进入编码器的码元有关,还与此刻相邻的
m时刻有关,称为卷积码。用(n0,k0,m) 表示。 目前常见的几种码:
级联码:将分组码和卷积码结合起来的码,一般用RS码为外码,卷
积码作为内码。
Turbo码:是并行结构的级联码系统码,将卷积码和随机交织器相结 合。被IS-2000标准作为第三代移动通信手机中的纠错抗干扰方案。 LDPC码:是一种线性分组码,Low-Density-Parity-CheckCodes, 它 能比其它码带来更高的编码增益。被通信公司作为第四代移动通信中
h11Cn 1 h12Cn 2 h1k Cn k Cn k 1 0 h C h C h C C 21 n 1 22 n 2 2k n k n k 2 0 h r1Cn 1 h r2Cn 2 h rk C n k C0 0
Wmin minWV, V C, V 0
线性分组码的最小距离等于它的最小重量
d min Wmin
线性分组码纠t个错误的充要条件是码的最小距离为:
d
2t 1
10
三、(n,k)码的监督矩阵H和生成矩阵G 1. 监督矩阵(也称校验矩阵)
h11 h12 h h 22 21 H h r1 h r2 h1k h 2k h rk 1 0 0 0 0 1
23
伴随式计算电路
R0 R1 R2 R3 R4 R5 R6
输入
输出
+
S0
+
S1
卷积码:m中每k0个码元为一组,经编码输出n0个
码元,增加了n0-k0个监督元,编码规则不仅于此
时此刻进入编码器的码元有关,还与此刻相邻的
m时刻有关,称为卷积码。用(n0,k0,m) 表示。 目前常见的几种码:
级联码:将分组码和卷积码结合起来的码,一般用RS码为外码,卷
积码作为内码。
Turbo码:是并行结构的级联码系统码,将卷积码和随机交织器相结 合。被IS-2000标准作为第三代移动通信手机中的纠错抗干扰方案。 LDPC码:是一种线性分组码,Low-Density-Parity-CheckCodes, 它 能比其它码带来更高的编码增益。被通信公司作为第四代移动通信中
h11Cn 1 h12Cn 2 h1k Cn k Cn k 1 0 h C h C h C C 21 n 1 22 n 2 2k n k n k 2 0 h r1Cn 1 h r2Cn 2 h rk C n k C0 0
Wmin minWV, V C, V 0
线性分组码的最小距离等于它的最小重量
d min Wmin
线性分组码纠t个错误的充要条件是码的最小距离为:
d
2t 1
10
三、(n,k)码的监督矩阵H和生成矩阵G 1. 监督矩阵(也称校验矩阵)
h11 h12 h h 22 21 H h r1 h r2 h1k h 2k h rk 1 0 0 0 0 1
23
伴随式计算电路
R0 R1 R2 R3 R4 R5 R6
输入
输出
+
S0
+
S1
信息论基础第七章信道编码

若将上述监督线性方程组改写为:
线性分组码(续)
C3 u0 u2 C0 C2
CC54
u0 u0
u1 u1
u2 C0
C0 C1
C1
C2
C6 u1 u2 C1 C2
即
C0 C 2 C3 0 C0 C1 C 2 C3 0 C0 C1 C5 0 C1 C 2 C6 0
线性分组码(续)
亦趋于0,仅有少数比如turbo码,两者性能都比较好。
信道编码的基本概念 (续)
目前大多数信道编码性能却不很理想,因此目前信道编码的主要 目标是以可靠性为主,即在寻求抗干扰强的码的基础上,寻求适当的有 效性,寻求和构造最小距离 d m in 比较大的码。
有关线性分组码的n种等效研究方法
所谓有限域,是指有限个元素的集合,可以进行按规定的代数四 则运算,其结果仍属于集合中的有限元素。
采用系统(组织)码来描述生成矩阵G与监督矩阵H,仅是其中的一种。 在很多情况下是采用非系统码的描述方式,那么两者之间有没有什么实 质上的差别?
线性分组码(续)
由线性代数理论,任何一个非系统的生成矩阵G均可以通过矩阵的初等 变换得到相应的系统码的生成矩阵G。因此,我们可以得到如下结论: 任何一个线性分组(n,k)码,均可找到一个等价的系统码,而且还可以 进一步证明只要在码率R和码长n相同的条件下,最优的系统码与最优的 线性分组码具有相同的错误概率。
例:以(7,3)二元线性分组码为例,其中: n7 , k 3 , nk734,k 3
n7
这时输入编码器的信息分成三个一组,即 u(u0u1u2),
它可按下列线性方程组编码:
写成矩阵形式
线性分组码(续)
u(I Q)
称G为生成矩阵,若G (I Q)即能分解出单位方阵为子阵,且I的位
线性分组码(续)
C3 u0 u2 C0 C2
CC54
u0 u0
u1 u1
u2 C0
C0 C1
C1
C2
C6 u1 u2 C1 C2
即
C0 C 2 C3 0 C0 C1 C 2 C3 0 C0 C1 C5 0 C1 C 2 C6 0
线性分组码(续)
亦趋于0,仅有少数比如turbo码,两者性能都比较好。
信道编码的基本概念 (续)
目前大多数信道编码性能却不很理想,因此目前信道编码的主要 目标是以可靠性为主,即在寻求抗干扰强的码的基础上,寻求适当的有 效性,寻求和构造最小距离 d m in 比较大的码。
有关线性分组码的n种等效研究方法
所谓有限域,是指有限个元素的集合,可以进行按规定的代数四 则运算,其结果仍属于集合中的有限元素。
采用系统(组织)码来描述生成矩阵G与监督矩阵H,仅是其中的一种。 在很多情况下是采用非系统码的描述方式,那么两者之间有没有什么实 质上的差别?
线性分组码(续)
由线性代数理论,任何一个非系统的生成矩阵G均可以通过矩阵的初等 变换得到相应的系统码的生成矩阵G。因此,我们可以得到如下结论: 任何一个线性分组(n,k)码,均可找到一个等价的系统码,而且还可以 进一步证明只要在码率R和码长n相同的条件下,最优的系统码与最优的 线性分组码具有相同的错误概率。
例:以(7,3)二元线性分组码为例,其中: n7 , k 3 , nk734,k 3
n7
这时输入编码器的信息分成三个一组,即 u(u0u1u2),
它可按下列线性方程组编码:
写成矩阵形式
线性分组码(续)
u(I Q)
称G为生成矩阵,若G (I Q)即能分解出单位方阵为子阵,且I的位
第07讲-信道编码

译码原理----序列译码(续)
• 优点
–运算量和约束长度无关。
• 缺点
–没有利用卷积码的记忆特性,不是最优算法。
译码原理----维特比译码
• 这是一种基于最大似然算法的译码方法 • 是由A.J.Viterbi首先提出的。 • 可以采用硬判决或软判决。
硬判决:解调器直接判0,1,即1比特量化 软判决:解调器对输出进行多比特量化
B
A A B
线性分组码----举例
• • • • • 奇偶监督码 汉明码 BCH码 RS码 CRC码
奇偶监督码
• 采用奇偶校验原理。 • 只能检错,不能纠错。 • 只能检查出某一分组的单个错误或奇数个错误, 而不能发现偶数个错误。 • 水平奇偶监督码 • 水平垂直奇偶监督码。
奇偶监督码(续)
11100110100011 0 11000101100011 1
译码原理----方法分类
• 代数译码:纠错译码的经典方法。利用 纠错码的代数结构,经过一定的代数运 算,消除误差,恢复正确的信息。常用 的有:大数译码逻辑。特点:电路简单, 编码增益低。 • 概率译码:纠错译码的新方法。考虑到 信道的统计特性。常用的有:序列译码、 维特比译码。特点:电路复杂,编码增 益高。
基本概念
• 信道编码的目的 信道编码是为了保证信息传输的可靠性、提高传输质量而 设计的一种编码。它是在信息码中增加一定数量的多余码 元,使码字具有一定的抗干扰能力。 • 信道编码的实质 信道编码的实质就是在信息码中增加一定数量的多余码元 (称为监督码元),使它们满足一定的约束关系,这样由 信息码元和监督码元共同组成一个由信道传输的码字。 举例而言,欲传输k位信息,经过编码得到长为n(n>k)的 码字,则增加了 n - k = r 位多余码元,我们定义 R = k / n 为编码效率。
第7章 信道编码(1)

r(x) c(x) e(x) a(x) g( x) e(x) • 接收多项式 e(x) d( x) g( x) s( x) • 错误图案多项式
– 其中 d( x) 是一个k-1阶的多项式 – 而 s( x) 阶数小于n-k, 其系数即为校验子 ,的阶数不足 n-k-1时,多项式高次项的系数补“0”。
– 稀疏性意味着校验矩阵H中“1”的个数很“稀少” – 随机性说明H矩阵中“1”出现的位置具有随机性
• 规则码和不规则码:规则码
– 是指其H矩阵中,每行中的“1”的个数(称为行权)相等,且每 列中的“1”的个数也相等,否则称为非规则码
现代数字通信原理、系统及仿真
多项式除法例子
code T ( x) x 6 x5 x 2 1, xi x3 1100101 left shift 3
现代数字通信原理、系统及仿真
卷积码
编码器结构图
1 ck
mk
D1
D2
ck
2
ck
现代数字通信原理、系统及仿真
由图可知,(2,1,2)卷积码的编码规则为
ck mk mk 2 ck mk mk 1 mk 2
输出码字为
1
2
ck ck , ck
1
2
Байду номын сангаас 线性分组码
• 对应上述的错误图案表,建立如下的校验方程
• 用s0为例,从错误图案表中可见s0 1 接收码字 r [r0 r1 r7 ] 中,出现错误位置可能是第位、第4位、第5位或第7位(但不同时 发生错误),因此可以用接收的这些位进行模2相加来表示s0。 • 用系数为“0”补充校验方程组的右边的其他接收位,可得
– 其中 d( x) 是一个k-1阶的多项式 – 而 s( x) 阶数小于n-k, 其系数即为校验子 ,的阶数不足 n-k-1时,多项式高次项的系数补“0”。
– 稀疏性意味着校验矩阵H中“1”的个数很“稀少” – 随机性说明H矩阵中“1”出现的位置具有随机性
• 规则码和不规则码:规则码
– 是指其H矩阵中,每行中的“1”的个数(称为行权)相等,且每 列中的“1”的个数也相等,否则称为非规则码
现代数字通信原理、系统及仿真
多项式除法例子
code T ( x) x 6 x5 x 2 1, xi x3 1100101 left shift 3
现代数字通信原理、系统及仿真
卷积码
编码器结构图
1 ck
mk
D1
D2
ck
2
ck
现代数字通信原理、系统及仿真
由图可知,(2,1,2)卷积码的编码规则为
ck mk mk 2 ck mk mk 1 mk 2
输出码字为
1
2
ck ck , ck
1
2
Байду номын сангаас 线性分组码
• 对应上述的错误图案表,建立如下的校验方程
• 用s0为例,从错误图案表中可见s0 1 接收码字 r [r0 r1 r7 ] 中,出现错误位置可能是第位、第4位、第5位或第7位(但不同时 发生错误),因此可以用接收的这些位进行模2相加来表示s0。 • 用系数为“0”补充校验方程组的右边的其他接收位,可得
