新课标人教版34选修三15.2时间和空间的相对性WORD教案1
数学知识点人教版选修(3-4)15.2《时间和空间的相对性》word教案1-总结

普通高中课程标准实验教科书—物理选修3-4[人教版]
第十五章相对论简介
新课程学习
15.2 时间和空间的相对性
★新课标要求
(一)知识与技能
1.理解“同时”的相对性。
2.通过推理,知道时间间隔的相对性和长度的相对性。
3.通过对两个结论的分析认识时间和空间是不能脱离物质而单独存在的。
(二)过程与方法
1.通过时间间隔相对性和长度相对性的推导,培养逻辑推理能力。
2.通过建立相对论时空观,提高学生认识物质世界的能力。
(三)情感、态度与价值观
培养学生对逻辑推理形成的结论要有一个科学的接受态度。
★教学重点
同时的相对性,长度的相对性,时间间隔的相对性。
★教学难点
相对论的时空观。
★教学方法。
湖北省荆州市沙市第五中学高中物理15.2时间和空间的相对性学案新人教版选修34

15、2 时间和空间的相对性寄语:长度的变短是相对的!学习目标:(1)同时的相对性(2)运动长度的收缩(3)时间间隔的相对学习重点 难点:从“同时”的相对性得出运动长度和时间间隔的相对性导读:在经典物理家的头脑中,如果两个事件在一个参考系中看来是同时的,在另一个参考系中看来也一定是同时的,但是如果接受爱因斯坦的两个假设,我们会得出“同时是相对的”这样一个结论.学习过程:B 一、“同时”的相对性下面我们通过一个实例分析,来看看经典物理和相对论对同时的理解有何不同。
车厢长为L ,正以速度v 匀速向右运动,车厢底面光滑,现有两只完全相同的小球,从车厢中点以相同的速率v 0分别向前后匀速运动,(相对于车厢),问(1)在车厢内的观察者看来,小球是否同时到达两壁?分析:在车上的观察者看来,A 球经时间t A =02v L =02v LB 球经时间t B =02v L =02v L 因此两球 到达前后壁。
在经典物理学家看来,同时发生的两件事在任何参照系中观察,结果都是同时的,两球也应同时到达前后壁.这是我们在日常生活中得到的结论。
如果把上述事件换成两列光的传播,情况如何呢?在车上的观察者看来,闪光同时到达前后壁,在地上的观察者看来,闪光先到达后壁. 这是为什么呢?根据爱因斯坦相对性原理,在不同参考系中一切物理规律都是相同的,这里匀速运动规律也一样,据s =ct 得t =cs ,车上观察者看来s 相同,c 也一样,所以t 相同,而对地面的观察者,光向后位移s 小(参见课本图15.2-1),而光速仍然不变,所以向后运动光需要较短时间到达后壁。
分析得不错,由此看来,根据爱因斯坦相对性原理和光速不变原理,我们自然会得出“同时是 的”这样一个原理,也就是说,在一个参考系中看来“同时”的,在另一个参考系中却可能“不同时”。
那么为什么我们平时不能观察这种现象呢?B2.长度的相对性请大家看课本图15.2-3,地面上的人看到杆的M 、N 两端发出的光同时到达他的眼睛,他读出N 、M 的坐标之差为l ,即地上的观察者测到的杆长。
物理人教版选修3-4课堂探究 第十五章 2时间和空间的相对性 Word版含解析
课堂探究一、怎样理解“动尺变短”和“动钟变慢”1.动尺变短:狭义相对论中的长度公式:l =l 01-(v c)2中,l 0是相对于杆静止的观察者测出的杆的长度,而l 可以认为是杆沿自己的长度方向以速度v 运动时,静止的观察者测量的长度。
还可以认为杆不动,而观察者沿杆的长度方向以速度v 运动时测出的杆的长度。
2.动钟变慢:时间间隔的相对性公式:Δt =Δτ1-(v c )2中,Δτ是相对事件发生地静止的观察者测量同一地点的两个事件发生的时间间隔,而Δt 是相对于事件发生地以速度v 运动的观察者测量同一地点的同样两个事件发生的时间间隔。
也就是说:在相对运动的参考系中观测,事件变化过程的时间间隔变大了,这叫做狭义相对论中的时间膨胀。
二、“动钟变慢”公式的推导两个完全相同的时钟,对好指针,一个放在静止的参考系中,一个放在运动的参考系中,运动的时钟走得比静止的要慢。
一个物理事件发生在运动惯性系中,运动系中的观察者测量的时间是Δt ′,静止的参考系中测量的时间是Δt ,结果是Δt >Δt ′。
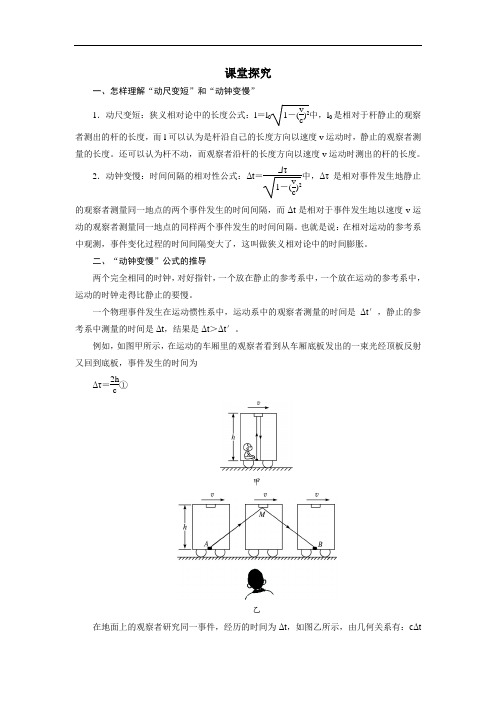
例如,如图甲所示,在运动的车厢里的观察者看到从车厢底板发出的一束光经顶板反射又回到底板,事件发生的时间为Δτ=2h c①甲乙在地面上的观察者研究同一事件,经历的时间为Δt ,如图乙所示,由几何关系有:cΔt=2h 2+(v Δt 2)2,即 Δt =4h 2c 2-v 2② 由①②两式得:Δt =Δτ1-(v c )2。
类型一 长度的相对性【例1】 长度测量与被测物体相对于观察者的运动有关,物体在运动方向上长度缩短了。
一艘宇宙飞船的船身长度为l 0=90 m ,相对地面以v =0.8c 的速度从一观测站的上空飞过。
(1)观测站测得飞船的船身通过观测站的时间间隔是多少?(2)宇航员测得船身通过观测站的时间间隔是多少?解析:(1)观测站测得船身的长度为l =l 01-v 2c2=901-0.82 m =54 m 通过观测站的时间间隔为Δt =l v =54 m 0.8c=2.25×10-7 s (2)宇航员测得飞船船身通过观测站的时间间隔为Δt =l 0v =90 m 0.8c=3.75×10-7 s 答案:(1)2.25×10-7 s (2)3.75×10-7 s 题后反思:在和被测物体有相对运动的观察者看来,物体沿运动方向的长度变短了。
高中物理人教版选修3-4第15章第2节教案设计《时间和空间的相对性》教案设计

时间和空间的相对性【教课目的】知识与技术: 1.理解“同时”的相对性。
2.经过推理,知道时间间隔的相对性和长度的相对性。
3.经过对两个结论的剖析认识时间和空间是不可以离开物质而独自存在的。
过程与方法: 1.经过时间间隔相对性和长度相对性的推导,培育逻辑推理能力。
2.经过成立相对论时空观,提升学生认识物质世界的能力。
感情、态度与价值观:培育学生对逻辑推理形成的结论要有一个科学的接受态度。
【教课重难点】要点:同时的相对性,长度的相对性,时间间隔的相对性。
难点:相对论的时空观。
【教课方法】在教师的指引下,经过对详细实例的剖析,成立模型、形成结论、形成理论,并在应用中加以稳固。
【教课器具】投影仪及投电影。
【教课过程】(一)引入新课教师:上一节课我们学习了狭义相对论的两个假定。
请同学们回想一下这两个假定的内容。
学生:在不一样惯性参照系中,全部物理规律都是同样的;真空中的光速在不一样惯性系中都是同样的。
教师:依据这两个假定,我们能够得出那些推论呢?这节课我们持续来学习狭义相对论的相关知识。
(二)进行新课一 .“同时”的相对性教师:第一我们来认识一下“事件”的看法,在这里我们说的事件能够指一个婴儿的诞生,一个光子与观察仪器的撞击或闪电打击地面等等.请大家再举几个例子。
学生:光从光源发出,宇宙中某个星体的迸发,一个车辆的启动等都是“事件”。
教师:下边我们经过一个实例剖析,来看看经典物理和相对论对同时的理解有何不一样。
[投影问题]车厢长为 L ,正以速度v 匀速向右运动,车厢底面圆滑,现有两只完整同样的小球,从车厢中点以同样的速率v0分别向前后匀速运动,(相关于车厢),问:(1)在车厢内的观察者看来,小球能否同时抵达两壁?(2)在地上的察看者看来两球能否同时抵达两壁?L剖析: 在车上的察看者看来, A 球经时间 t A = 2=Lv 02v 0LL所以两球同时抵达前后壁。
B 球经时间 t B =2=v 0 2v 0在经典物理学家看来,同时发生的两件事在任何参照系中察看,结果都是同时的,两 球也应同时抵达前后壁 .这是我们在平常生活中获得的结论。
人教版高中物理教案-时间和空间的相对性

【教學目標】(一)知識與技能1.理解“同時”的相對性。
2.通過推理,知道時間間隔的相對性和長度的相對性。
3.通過對兩個結論的分析認識時間和空間是不能脫離物質而單獨存在的。
(二)過程與方法1.通過時間間隔相對性和長度相對性的推導,培養邏輯推理能力。
2.通過建立相對論時空觀,提高學生認識物質世界的能力。
(三)情感、態度與價值觀培養學生對邏輯推理形成的結論要有一個科學的接受態度。
【教學重點】同時的相對性,長度的相對性,時間間隔的相對性。
【教學難點】相對論的時空觀。
【教學方法】在教師的引導下,通過對具體實例的分析,建立模型、形成結論、形成理論,並在應用中加以鞏固。
【教學用具】投影儀及投影片。
【教學過程】(一)引入新課師:上一節課我們學習了狹義相對論的兩個假設。
請同學們回憶一下這兩個假設的內容。
生:在不同慣性參照系中,一切物理規律都是相同的;真空中的光速在不同慣性系中都是相同的。
師:根據這兩個假設,我們可以得出那些推論呢?這節課我們繼續來學習狹義相對論的有關知識。
(二)進行新課1.“同時”的相對性師:首先我們來認識一下“事件”的概念,在這裡我們說的事件可以指一個嬰兒的誕生,一個光子與觀測儀器的撞擊或閃電打擊地面等等.請大家再舉幾個例子。
生:光從光源發出,宇宙中某個星體的爆發,一個車輛的啟動等都是“事件”。
師:下面我們通過一個實例分析,來看看經典物理和相對論對同時的理解有何不同。
[投影問題]車廂長為L ,正以速度v 勻速向右運動,車廂底面光滑,現有兩隻完全相同的小球,從車廂中點以相同的速率v 0分別向前後勻速運動,(相對於車廂),問(1)在車廂內的觀察者看來,小球是否同時到達兩壁?(2)在地上的觀察者看來兩球是否同時到達兩壁?分析:在車上的觀察者看來,A 球經時間t A =02v L =02v L B 球經時間t B =02v L =02v L 因此兩球同時到達前後壁。
在經典物理學家看來,同時發生的兩件事在任何參照系中觀察,結果都是同時的,兩球也應同時到達前後壁.這是我們在日常生活中得到的結論。
时间和空间的相对性讲义

1971年铯原子钟实验
将铯原子钟放在飞机上,沿赤道向东和向西绕地球一周,回到原处后,分别比静止在地面上的钟慢59纳秒和快273纳秒。
地球以一定的角速度向东转,地面不是惯性系,而从地心指向太阳的参考系是惯性系(忽略地球公转)。飞机的速度总小于地球自转速度,所以无论飞机向东还是向西,它相对于惯性系都是向东,只是前者速度大,后者小。而地面上的钟的转速度介于二者之间。
一节长为10米的列车,A在车后部,B在车前部。当列车以0.6c的高速度通过一个站台的时候,突然站台上的人看到A先向B开枪,过了12.5毫微秒,B又向A发射。因而站台上的人作证:这场枪战是由A挑起的。但是,车上的乘客却提供相反的情况,他们说,是B先开枪,过了10毫微秒,A才动手。事件是由B发动的。
在日常生活和生产中,用时钟测量时间,用米尺测量长度,也是司空见惯的事情。无论是运动的描述,还是运动规律的说明,都跟时间和长度的测量有关。对于不同的参考系,长度和时间的测量结果是否是一样的?对上述问题的讨论,物理学经历了一场关于时空观的变革,从牛顿时代的经典力学跨越到爱因斯坦的相对论。爱因斯坦的狭义相对论告诉我们:运动的时钟变慢、运动的尺子在运动的方向上缩短。这到底是为什么?
这暗示着,人要活得更长久,应该不断地向东飞去,使得地球的转动速度叠加上飞机的速度。
五、相对论的时空观
绝对时空观认为时间和空间是脱离物质而存在的,是绝对的,时间和空间之间也是没有联系的。 相对论时空观认为有物质才有时间和空间,时间和空间与物质的运动状态有关。
绝对时空观与相对论时空观的区别:
这暗示着,人要活得更长久,应该不断地向东飞去,使得地球的转动速度叠加上飞机的速度。
上述实验表明,相对于惯性系转速越大的钟走得越慢。这和孪生子问题所预期的效应是一致的。所以似也不应再说:“孪生子佯谬”,而应是孪生子效应了。
高中物理 第十五章 1 相对论的诞生 2 时间和空间的相对性教材梳理教案 新人教版选修34
1 相对论的诞生2 时间和空间的相对性疱丁巧解牛知识·巧学一、经典的相对性原理1.惯性系如果牛顿运动定律在某个参考系中成立,这个参考系叫做惯性系,相对一个惯性系做匀速直线运动的另一个参考系也是惯性系.2.伽利略相对性原理力学规律在任何惯性系中都是相同的.二、相对性原理与电磁规律1.经典力学遇到的困难在经典力学中如果某一惯性系相对另一惯性系的速度为v ,在此惯性系中有一物体速度为c ,那么,此物体相对于另一惯性系的速度是c+v 吗?根据经典力学理论是肯定的,但是这种答案被迈克尔逊的实验否定了.迈克尔逊实验证明了光速是不变的.这和传统的速度合成法是矛盾的.2.迈克尔逊—莫雷实验的结论光的传播速度与参考系(地球)运动的方向和大小无关.三、狭义相对论的两个基本假设1.爱因斯坦相对性原理:在不同的惯性参考系中,一切物理规律都是相同的. 辨析比较 两个相对性原理的区别对于伽利略的相对性原理来说,参考系中的坐标单位与参考系的运动无关;参考系中的时间与参考系的运动无关.其速度合成规律应满足v=v′+u.v′是某个惯性系相对另一个惯性系的速度,u 是物体相对某个惯性系的速度,那么,物体相对另一个惯性系的速度为v=v′+u.以此类推,若u 是光速c ,则在某个惯性系的光速相对于另一个惯性系的速度为v=v′+c .那么,光速是可以变大或变小的(在真空中).对于狭义相对论的相对性原理来说,力学规律对惯性系来说都是相同的,但是光速是不变的.由于光速是不变的,造成了与经典理论一些不同的结论.这些结论在低速的世界里不易搞清,但从天体的物理现象中却得到了证实.2.光速不变原理:真空中的光速在不同的惯性参考系中都相同.深化升华 还要大量的实验来证明,还要经过逻辑推理的大量结论来验证才能成为真正的原理.四、“同时”的相对性由于光速不变,即光速在任何惯性系中都是相同的,那么当另一惯性系的速度能够和光速相比时,同时性就是相对的,即在一个惯性系中同时发生的两事件,在另一惯性系中就不一定是同时发生的.深化升华 光速不变原理是判断同时相对性的主要依据.可以通过判断某一事件从发生到接收地点所经过的路程来判断接收时间的先后.五、长度的相对性如果在匀速直线运动的火车上沿着运动的方向放着一根木杆,坐在火车上的人测得的木杆头尾坐标之差是木杆的长,但地面上的人则认为他不是同时测得木杆头尾的坐标,因为由于车在运动、杆在运动,他们的同时有相对性,同样,地面上的人认为是同时测量的,火车上的人认为是不同时的,经过严格的推导可得l=l′2)(1c v ,其中l′为车上人测得的长度,l 为地面上的人测得的长度,由于1-(cv )2<1,所以l <l′.其意义是:相对地面以速度v 运动的物体,从地面上看,沿着运动方向上的长度变短了,速度越大,变短得越多,但是高度却没有什么变化.对于车上的人来说,车上一切和往常一样,只是地面上的物体和距离都变窄了、变短了.学法一得 由于两个参考系相对速度很大,从一个参考系看另一个参考系里的长度,而且是顺着速度方向的长度会变短,这也是严格推算出来的.这可以从两列车高速对开时笛声频率发生变化受到启发,也可以从速度较快的汽车上看到外面的树木感到似乎有某种变化等,可以理解长度变短.误区提示 虽然观测结果不同,物体本身并未收缩,长度收缩效应是一种观测结果.在垂直于速度方向的长度基本不变,这一点在学习时要注意.六、时间间隔的相对性在一匀速前进的车厢顶上有一平面镜,正下方有一光源(闪光源),车顶到光源距离为h ,对火车上的人来说,光从光源经平面镜回到光源所经过的时间为Δt′=ch 2.对于地面上的人看到的光通过的路程为(2v t •∆)2=(2t c ∆•)2-h 2可得Δt=2)(1'cv t -∆,可知Δt>Δt′.上面的式子具有普遍意义,当从地面观察以速度v 前进的火车时,车上的时间进程变慢了,不仅时间变慢了,物理、化学过程和生命的过程都变慢了.但车上的人都没有这种感觉,他们反而认为地面上的时间进程变慢了.深化升华 时间进程对于同一个参考系(惯性系)是没有变化的,而从另一个参考系来看这个参考系才会有变化.时间进程要能感觉出来必须是两个参考系的相对速度很大,大到能和光速相比.这时在光传播的很短的时间内,相对位移就很大.时间进程变慢在低速世界只能从推算中得知,需要从科技实验中找例证.由于运动是相对的,故在某一个参考系中观察另一个不同参考系里发生的物理事件时,总有时间延缓效应.牛顿的绝对时空观是相对论时空观在低速情况下的近似.七、时空相对性的验证μ子的寿命不长,只有3.0 μs,其速度为0.99 c ,在100 km 的高空,其运动距离只有890 m ,要到达地面是不可能的,但实际上从地面是可以测到的.原因是它的速度很大,达到0.99 c ,这时大气层的厚度不再是100 km ,而是很短的,这样在3.0 μs 的时间内可以到达地面,从而证明了相对论时空观的正确性.八、相对论的时空观时间和空间不能脱离物质和物质的运动状态.时间变慢,空间的长度会变短,这都与物质的运动速度有关.深化升华 在速度较低的时候,长度、时间是感觉不出变化的,所以容易理解为长度、时间与物质之间没有什么关系,尤其是时间会认为是流逝的均匀的坐标.当速度很大时,长度和时间都跟着变化了,这时对宇宙的看法也必然要变化,长度和时间与物质是紧密相关的,长度和时间是不能离开物质而独立存在的.典题·热题知识点一 经典力学的相对性原理例1如图15-1-2所示,在列车车厢的光滑水平面上有一个质量为m=5 kg 的小球,正随车厢一起以20 m/s 的速度匀速前进,现在给小球一个水平向前的F=5 N 的拉力作用,求经10 s 时,车厢里的观察者和地面上的观察者看到小球的速度分别是多少?图15-1-2解析:利用经典力学的相对性原理进行计算.答案:对车上的观察者:物体的初速度v 0=0,加速度a=m F =1 m/s 2,10 s 时速度v 1=at=10 m/s. 对地面上的观察者:物体初速度v 0=20 m/s加速度相同a=mF =1 m/s 2 10 s 末速度v 2=v 0 +at=30 m/s.方法归纳 在两个惯性系中,虽然观察到的结果并不相同,一个是10 m/s ,另一个是30 m/s ,但我们却应用了同样的运动定律和速度合成法则,也就是说,力学规律在任何惯性系中都是相同的.知识点二 光速不变原理例2考虑以下几个问题:(1)如图15-1-3所示,参考系O′相对于参考系O 静止时,人看到的光速应是多少?(2)参考系O′相对于参考系O 以速度v 向右运动,人看到的光速应是多少?(3)参考系O 相对于参考系O′以速度v 向左运动,人看到的光速又是多少?图15-1-3解析:根据速度合成法则,第一种情况人看到的光速应是c ,第二种情况应是c+v ,第三种情况应是(c-v ).而根据狭义相对理论,光速是不变的,都应是c.答案:三种情况都是c.知识点三 时间空间的相对性例3地面上A 、B 两个事件同时发生.对于坐在火箭中沿两个事件发生地点连线飞行的人来说(如图15-1-4所示),哪个事件先发生?图15-1-4解析:可以设想,在事件A 发生时A 处发出一个闪光.事件B 发生时B 处发生一个闪光.“两闪光相遇”作为一个事件,发生在线段AB 的中点,这在不同参考系中看都是一样的.“相遇在中点”这个现象在地面系中很容易解释.火箭上的人则有如下推理:地面在向火箭的方向运动,从闪光发生到两闪光相遇,线段中点向火箭的方向运动了一段距离,因此闪光B 传播的距离比闪光A 长些,既然两个闪光的光速相同,一定是闪光B 发出得早一些.答案:B 事件先发生巧解提示 根据运动的相对性,可以认为火箭不动,地面系向火箭运动.设A 、B 发出闪光,由于地面系中的观察者随地面一起运动,在运动的地面系中观察到A 、B 同时发光,说明观察者位置离B 近些.由于光速是不变的,对火箭上飞行的人来说,应当先接收到B 处闪光,即B 事件先发生.例4一支静止时长30 m 的火箭以3 km/s 的速度从观察者的身边掠过.观察者测得火箭的长度应为多少?火箭上的人测得火箭的长度应为多少?如果火箭的速度为光的二分之一呢? 解析:根据长度的相对性,利用公式l=l′2)(1c v -可得.答案:火箭相对于火箭上的人是静止的,所以不管火箭的速度是多少,火箭上测得的火箭与静止时相同,为l′=30 m.如果火箭的速度为v=3×103 m/s ,地面观察者测得的火箭长l 为 l=l′2)(1c v -=30×283)103103(1⨯⨯- m=30×10101-- m. 如果火箭的速度为v=c/2,地面观察者测得的火箭长l 为 l=l′2)(1c v-=30×2)2/(1cc - m≈26 m. 误区警示 当相对运动速度很小时,相对性效应很微弱,因此在低速运动中牛顿运动定律仍然成立,牛顿运动定律仍是解题的主要依据.全盘否定经典力学的做法是错误的.例5π+介子是一不稳定粒子,平均寿命是2.6×10-8 s (在它自己参考系中测得)(1)如果此粒子相对于实验室以0.8 c 的速度运动,那么在实验室坐标系中测量的π+介子寿命多长?(2)π+介子在衰变前运动了多长距离?解析:Δt′是π+介子在自己参考系中的寿命,在实验中的寿命用Δt=2)(1'c v t -∆来求,衰变前运动的距离可用s=v·Δt 来求得.答案:π+在实验室中的寿命为Δt=282)8.0(1106.2)(1'-⨯=-∆-c v t s=4.3×10-8 s. 该粒子在衰变前,运动的距离s=vΔt=0.8×4.3×10-8×3×108 m=10.32 m方法归纳 π+介子的寿命很短,我们可以通过增大其相对速度的方法“延长”其寿命,以便于观测和研究.例6A 、B 、C 是三个完全相同的时钟,A 放在地面上,B 、C 分别放在两个火箭上,以速度v B 和v C 朝同一方向飞行,v B <v C ,地面上的观察者认为哪个时钟走得最慢?哪个走得最快? 解析:地面上的观察者认为C 钟走得最慢,因为它相对于观察者的速度最大.根据公式Δt=2)(1'c v t -∆可知,相对于观察者的速度v 越大,其上的时间进程越慢.地面钟v=0,它记录的两事件的时间间隔最大,即地面钟走得最快.答案:地面上的观察者认为C 钟走得最慢,地面钟走得最快.方法归纳 时间间隔具有相对性,对于不同的参考系,时间间隔是不相同的.例7一飞船以u=9×103 m/s 的速率相对于地面飞行,飞船上的钟走了5 s ,用地面上的钟测量经过了多长时间?解析:利用时间间隔的相对性计算.答案:此问题就是在不同参考系中测量时间的问题.u=9×103 m/sΔt′=5 s由时间膨胀效应Δt=221'c ut -∆≈5.000 000 002 s.方法归纳 由此可见,即使在这么高的速度下,时间膨胀还是非常微弱的,所以在一般的速度下,可完全不考虑相对论效应,使用牛顿力学处理.问题·探究交流讨论探究问题 如何理解钟慢效应和尺缩效应?探究过程:刘小露:有一宇宙火箭相对于地球飞行,在地球上的观察者将看到火箭上的物体长度缩短,时钟变慢.张海:火箭上的观察者看到地球上的物体将比火箭上同类物体更长,时间更短.王小刚:根据相对性原理,运动的描述只有相对意义,因此,长度的缩短,时钟的变慢都是相对的,而不是绝对的.在火箭上观察,地球也以同样大的速率向相反方向运动,因此,观察者看到地球上的物体,同样是长度缩短,时钟变慢.李兵:按这样推理,一对孪生兄弟,一个在地球上,一个在高速运动的火箭上,地球上人看到火箭上的人时钟延缓,新陈代谢变缓,若干年后,应当火箭上的人显得年轻.同样,在火箭上的人看地球上的人,也应当显得年轻.其真实情况应如何?王丹丹:根据l=l 02)(1c v -可以看出:v 越大,l 越短,长度收缩效应越明显;当v<<c ,l≈l 0,这时又回到了经典时空观;空间的量度与参考系无关.这也说明,牛顿的绝对时空观是相对论时空观在低速情形下的近似.探究结论:时钟变慢效应和尺缩效应是相对的,只是观察的结果.实际上,对于观察者本人来说,钟慢效应没有实际意义.相对本人所处的惯性系而言,相对速度始终为零,其新陈代谢快慢和时间的长短是不会变化的.思维发散探究问题 根据本节的学习,认识正确的时空观?探究过程:观点一:什么是时间?什么是空间?时间和空间有什么性质?经典物理学对这些问题并没有正面回答.但是从它对问题的处理上,我们体会到,经典物理学认为空间好像一个大盒子(一个没有边界的盒子),它是物质运动的场所.至于某一时刻在某一空间区域是否有物质存在,物质在做什么样的运动,这些对于空间本身没有影响,就像盒子里是否装了东西对于盒子的性质没有影响一样,时间与此相似,它在一分一秒地流逝,与物质的运动无关.换句话说,经典物理学认为空间和时间是脱离物质而存在的,是绝对的,空间和时间之间也是没有联系的.观点二:相对论则认为有物质才有空间和时间,空间和时间与物质的运动状态有关.在一个确定的参考系中观察,运动物体的长度(空间距离)和它物理过程的快慢(时间进程)都跟物体的运动状态有关.观点三:我们生活在低速运动的世界里,因此自然而然地接受了经典的时空观.使用经典的时空观,处理低速问题是正确的,没有必要有意识地考虑空间和时间的性质.但在处理高速问题时,新的实验事实与传统观念不一致时,我们必须摒弃经典的时空观,应用相对论的时空观来处理和认识我们周围的世界.探究结论:经典的时空观是相对论时空观在低速情况下的近似.。
高中物理 第十五章 相对论简介 2 时间和空间的相对性学案1 新人教版选修34
2 时间和空间的相对性1.“同时”的相对性 (1)经典的时空观在同一个惯性系中不同地点同时发生的两个事件,在另一个惯性系中观察也是同时的。
(2)相对论的时空观 “同时”具有相对性,即在同一个惯性系中不同地点同时发生的两个事件,在另一个惯性系中观察不一定是同时的。
【例1】利用爱因斯坦理想实验说明同时的相对性。
解析:假设一列很长的火车在沿平直轨道飞快地匀速行驶,车厢中央有一个光源发出一个闪光,闪光照到了车厢的前壁和后壁,这是两个事件。
车上的观察者认为两个事件是同时的,在他看来这很好接受,因为车厢是个惯性系,光向前、向后传播的速度相同,光源又在车厢的中央,闪光当然会同时到达前后两壁。
车下的观察者则不以为然,他观测到,闪光先到达后壁,后到达前壁。
他的解释是:地面也是一个惯性系,闪光向前、向后传播的速度对地面也是相同的,但是在闪光飞向两壁的过程中,车厢向前行进了一段距离,所以向前的光传播的路程长些,到达前壁的时刻也就晚些,这两个事件不同时。
答案:见解析2.“长度”的相对性 (1)经典的时空观一条杆的长度不会因为观察者是否与杆做相对运动而不同。
(2)相对论的时空观“长度”也具有相对性,一条沿自身长度方向运动的杆,其长度总比静止时的长度小。
设相对于杆静止的观察者认为杆的长度为l 0,与杆有相对运动的人认为杆的长度为l ,杆相对于观察者的速度为v ,则l 、l 0、v 的关系是:l =l 01-⎝ ⎛⎭⎪⎫v c2。
【例2】假想在2015年,有一太空船以0.8c 的速度飞向“月球太空站”。
一科学家在月球上测量运动中的太空船长度为200 m ,此太空船最后在月球上登陆,此科学家再度测量静止的太空船的长度,测量的结果如何?解析:设在月球上测得运动的太空船的长度为l ,静止的太空船长度为l 0, 依据狭义相对论的长度收缩效应有l =l 01-⎝ ⎛⎭⎪⎫v c2,所以l 0=lc c 2-v 2=200cc 2-0.64c 2≈333 m答案:333 m3.时间间隔的相对性 (1)经典的时空观某两个事件,在不同的惯性系中观察,它们的时间间隔总是相同的。
新课标人教版3-4选修三15.2《时间和空间的相对性》精品
本编为大家提供各种类型的PPT课件,如数学课件、语文课件、英语课件、地理课件、 历史课件、政治课件、化学课件、物理课件等等,想了解不同课件格式和写法,敬请下载!
Moreover, our store provides various types of classic sample essays, such as contract agreements, documentary evidence, planning plans, summary reports, party and youth organization materials, reading notes, post reading reflections, essay encyclopedias, lesson plan materials, other sample essays, etc. If you want to learn about different formats and writing methods of sample essays, please stay tuned!
Download prompt: This PPT courseware has been carefully prepared by our store. We hope that after downloading, it can help everyone solve practical problems. After downloading the PPT courseware, it can be customized and modified. Please adjust and use it according to actual needs. Thank you!
人教版高中物理选修3-415.1相对论的诞生、15.2时间和空间的相对性教学案
1相对论的诞生2时间和空间的相对性能说出狭义相对论)相对论的诞生[先填空]1.经典的相对性原理(1)表述一:力学规律在任何惯性系中都是相同的.(2)表述二:在一个惯性参考系内进行的任何力学实验都不能判断这个惯性参考系是否相对于另一个惯性系做匀速直线运动.(3)表述三:任何惯性参考系都是平权的.2.狭义相对论的两个基本假设(1)狭义相对性原理:在不同的惯性参考系中,一切物理规律都是相同的.(2)光速不变原理:真空中的光速在不同的惯性参考系中都是相同的.[再判断]1.静止或匀速直线运动的参考系是惯性系.(√)2.由于在任何惯性系中力学规律都是相同的,因此,研究力学问题时可以选择任何惯性系.(√)3.在不同的惯性系中,光速是不相同的.(×)[后思考]1.牛顿运动定律的适用条件是什么?【提示】宏观物体、低速运动和惯性参考系.2.伽利略的相对性原理与狭义相对性原理有什么不同?【提示】伽利略的相对性原理认为力学规律在任何惯性系中是相同的;狭义相对性原理认为在不同惯性系中一切物理规律都是相同的.[核心点击]1.惯性系和非惯性系牛顿运动定律能够成立的参考系,相对于这个惯性系做匀速直线运动的另一个参考系也是惯性系.牛顿运动定律不成立的参考系称为非惯性系.2.伽利略相对性原理力学规律在任何惯性系中都是相同的,即任何惯性参考系都是平权的.3.相对性原理与电磁规律根据麦克斯韦的电磁理论,真空中的光速在任何惯性系中都是一个常量,但是按照伽利略的相对性原理,在不同惯性系中的光速应是各不相同的.迈克耳孙—莫雷实验证明:不论光源和观察者做怎样的相对运动,光速都是相同的.4.迈克耳孙—莫雷实验(1)实验背景:根据麦克斯韦的电磁理论可以直接得到真空中电磁波的速度,并不需要初始条件,也就是说,“电磁波的速度是c”,这本身就是电磁规律的一部分,而不是电磁规律应用于某个具体事物的结论.于是,问题出现了:麦克斯韦的电磁理论相对哪个参考系成立?如果它相对参考系S是正确的,另外还有一个参考系S′,S′相对于S以速度v运动,那么光相对于S′的速度应该是(c-v)而不是c,好像电磁规律不是对任何惯性系都一样.(2)实验结论:不论光源与观察者做怎样的相对运动,光速都是一样的.1.假设有一天某人坐在“神舟”号飞船上,以0.5c的速度遨游太空,当他打开一个光源时飞船正前方地面上的观察者看到这一光速为________,飞船正后方地面上的观察者看到这一光速为________,在垂直飞船前进方向地面上的观察者看到这一光速是________.【解析】根据狭义相对论的假设,真空中的光速相对于不同的惯性参考系是相同的,即在地面上任何地方的观察者看到的光速都是c.【答案】c c c2.如图15-1-1所示,思考以下几个问题:(光速用c表示)图15-1-1(1)若参考系O ′相对于参考系O 静止,人看到的光速应是多少?(2)若参考系O ′相对于参考系O 以速度v 向右运动,人看到的光速应是多少?(3)若参考系O 相对于参考系O ′以速度v 向左运动,人看到的光速又是多少?【解析】 根据狭义相对论的光速不变原理:真空中的光速在不同的惯性参考系中都是相同的,光速与光源、观察者间的相对运动没有关系.因此三种情况下,人观察到的光速都是c .【答案】 (1)c (2)c (3)c1.爱因斯坦提出的两条基本假设是相对论的基础,对同时的相对性等经典力学所无法解决的问题,应紧紧抓住两条基本假设这一关键点来解决.2.真空中对不同的惯性参考系来说,光速都是相同的.3.经典力学的结论是有一定局限性的,一般只适用于宏观物体的低速运动.时间和空间的相对性[先填空]1.“同时”的相对性(1)经典时空观:在同一个惯性系中不同地点同时发生的两个事件,在另一个惯性系中观察也是同时的.(2)相对论时空观:“同时”具有相对性,即在同一个惯性系中不同地点同时发生的两个事件,在另一个惯性系中观察可能不是同时的.2.“长度”的相对性(1)经典的时空观:一条杆的长度不会因为观察者是否与杆做相对运动而不同.(2)相对论的时空观:“长度”也具有相对性,一条沿自身长度方向运动的杆,其长度总比静止长度小,但在垂直于杆的运动方向上,杆的长度没有变化.(3)相对长度公式:设相对于杆静止的观察者认为杆的长度为l 0,与杆有相对运动的人认为杆的长度为l ,杆相对于观察者的速度为v ,则l 、l 0、v 的关系是:l =l 01-⎝⎛⎭⎫v c 2. 3.时间间隔的相对性 (1)经典的时空观:某两个事件,在不同的惯性系中观察,它们的时间间隔总是相同的.(2)相对论的时空观:某两个事件,在不同的惯性参考系中观察,它们的时间间隔是不同的,惯性系速度越大,惯性系中的时间进程进行得越慢.非但如此,惯性系中的一切物理、化学过程和生命过程都变慢了.(3)相对时间间隔公式:设Δτ表示静止的惯性系中观测的时间间隔,Δt 表示以v 高速运动的参考系中观察同样两事件的时间间隔,则它们的关系是:Δt =Δ τ1-⎝⎛⎭⎫v c 2.[再判断]1.根据相对论的时空观,“同时”具有相对性.(√)2.相对论时空观认为,运动的杆比静止的杆长度变大.(×)3.高速飞行的火箭中的时钟要变慢.(√)[后思考]1.尺子沿任何方向运动其长度都缩短吗?【提示】 尺子沿其长度方向运动时缩短,在垂直于运动方向长度不变.2.以任何速度运动,时间延缓效应都很显著吗?【提示】 不是.当u →c 时,时间延缓效应显著;当u ≪c 时,时间延缓效应可忽略.[核心点击]1.“动尺缩短”狭义相对论中的长度公式l =l 01-⎝⎛⎭⎫v c 2中,l 0是相对于杆静止的观察者测出的杆的长度,而l 可以认为是杆沿自己的长度方向以速度v 运动时,静止的观察者测量的长度.2.“动钟变慢”时间间隔的相对性公式Δ t =Δτ1-⎝⎛⎭⎫v c 2中,Δτ是相对事件发生地静止的观察者测量同一地点的两个事件发生的时间间隔,而Δt 是相对于事件发生地以速度v 高速运动的观察者测量同一地点的同样两个事件发生的时间间隔.3.分析时间间隔和长度变化时应注意的问题(1)时间间隔、长度的变化,都是由于物质的相对运动引起的一种观测效应,它与所选取的参考系有关,物质本身的结构并没有变化. (2)两个事件的时间间隔和物体的长度,必须与所选取的参考系相联系,如果在没有选取参考系的情况下讨论时间的长短及空间的尺寸,是没有任何意义的.3.某宇航员要到离地球5光年的星球上去旅行,如果希望把这路程缩短为3光年,则他所乘飞船相对地球的速度为________.【解析】 由l =l 01-⎝⎛⎭⎫v c 2得,3=51-⎝⎛⎭⎫v c 2,解得v =0.8c . 【答案】 0.8c 4.用相对论的观点判断,下列说法正确的是( )【导学号:23570153】A .时间是绝对的,空间是相对的B .时间和空间都是绝对的,在任何参考系中一个事件发生的时间和一个物体的长度总不会改变C .在地面上的人看来,高速运动的飞船中的时钟会变慢,但是飞船中的宇航员却看到时钟是准确的D .在地面上的人看来,高速运动的飞船在运动方向上会变窄,而飞船中的宇航员却感觉到地面上的人看起来比飞船中的人扁一些E .当物体运动的速度v ≪c 时,“时间膨胀”和“长度收缩”效应可忽略不计【解析】 时间和空间都是相对的,故选项A 、B 的说法错误;根据“时间膨胀”和“长度收缩”效应,选项C 、D 的说法正确;当速度v ≪c 时,1-⎝⎛⎭⎫v c 2≈1,所以“时间膨胀”和“长度收缩”效应可忽略不计,故选项E 说法正确.【答案】 CDE5.地面上长100 km 的铁路上空有一火箭沿铁路方向以30 km/s 的速度掠过,则火箭上的人看到铁路的长度应该为多少?如果火箭的速度达到0.6c ,则火箭上的人看到的铁路的长度又是多少?【解析】 当火箭速度较低时,长度基本不变,还是100 km.当火箭的速度达到0.6c 时,由相对论长度公式l =l 01-⎝⎛⎭⎫v c 2代入相应的数据解得:l =100×1-0.62 km =80 km. 【答案】 100 km 80 km应用相对论“效应”解题的一般步骤1.应该通过审题确定研究对象及研究对象的运动速度.2.明确求解的问题,即明确求解静止参考系中的观察结果,还是运动参考系中的观察结果.3.应用“尺缩效应公式”或“时间延缓效应公式”进行计算.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§15.2 时间和空间的相对性
学习目标:
(1)知道狭义相对论关于时空相对性的主要结论;
(2)了解经典时空观与相对论时空观的主要区别,体会相对论时空观的建立对人类认识世界的影响。
(3)通过实例,了解时间和空间的相对性,体会相对论时空观与低速世界的差异。
学习过程:、【温故知新】上一节课我们学习了狭义相对论的两个假设。
请同学们回忆一下这两个假设的内容:
一、“同时”的相对性
1.在物理学中,什么叫“事件”?在数学上,一个事件可以如何表示?
2.实例分析:车厢长为L,正以速度v匀速向右运动,车厢底面光滑,
现有两只完全相同的小球,从车厢中点以相同的速率v0分别向前后匀
速运动,(相对于车厢),问(1)在车厢内的观察者看来,小球是否同
时到达两壁?(2)在地上的观察者看来两球是否同时到达两壁?
分析:在车上的观察者看来,A球经时间t A= ;B球经时间t B= ;因此两球同时到达前后壁。
在经典物理学家看来,同时发生的两
件事在任何参照系中观察,结果都是同时
的,两球也应同时到达前后壁.这是我们
在日常生活中得到的结论。
如果把上述事
件换成两列光的传播,情况如何呢?
结论:车厢上的人和地面上的人看到车厢中间灯光到达前后车厢的先后是不一样的.车上的观察者认为光到达车厢的前后两壁;站台上的观察者认为光先到车厢壁后到壁;
思考与讨论:见教材P99,运动的火车L里,观察者认为,沿着运动方向位置靠前一些的事件A先发生,还是靠后一些的事件B先发生?
规律小结:
1、对于运动的火车上同时发生的两个事件,对于地面就不是同时的;(关
键:在各个参考系中光速都为c)
2、地面上同时发生的两个事件,对于运动的火车也不是同时的;
3、观察者站在发生事件的两地之间,迎面而来的事件发生;背离而驰
的事件发生。
针对训练1、地面上的人认为A、B两个事件同时发生。
对于坐在火箭中沿两个事件发生地点连线飞行的人来说(图15.2-5),哪个事件先发生?
二、长度的相对性
下面我们来讨论在不同参考系中测量一个杆的长度结果会如何。
如下图所示:
1、甲图中是一个刻度尺测出的静止的杆的长度,大家看
是多少?怎么求出的呢?
2、乙图中尺仍然静止,杆水平向右匀速运动,我们应该
怎么算杆长?
注意:其实这里你是用某时刻N 、M 坐标差值或另一时
刻N ′、M ′坐标差值得到的。
如果有人用N ′、M 的
坐标差值算出杆长是9.7 m-8 m=1.7 m 显然是没有意义的,它不能代表杆的长度。
因此我们
要测量这一杆长,就必须“同时”读出杆两端坐标才行。
现在的问题是不同参考系中“同时
是相对的”。
思考与讨论:请大家看课本图15.2-3,一个相对于所选参考系静止的物体(如杆或者尺子),
在这个参考系中的长度可以称作它的“正确长度”0l ,地面上的人看到杆的M 、N 两端发出
的光同时到达他的眼睛,他读出N 、M 的坐标之差为l ,即地上的观察者测到的杆长。
1、请大家考虑车上的观察者是同时看到N 、M 两端的闪光吗?
2、观察者B 认为观察者A 读哪端早?读哪端晚?
3、观察者A 认为观察者B 读哪端早?读哪端晚?
4、根据3,火车上的观察者A 认为:地面上观察者B 测得杆长会比自己测得的数值大些还
是小些?
5、结论:①_________________________________________________________公式:
_____________________
②_____________________________________________________________________________
__
三、时间间隔的相对性 根据公式20)(1c v l l -=,两边同时除以光速c ,再通过洛仑兹变换可以得出:Δt =2
)(1c v t -'
∆,式中t '∆是
的时间间隔,习惯上用希腊字母Δτ表示。
于是上式写成Δ
t =
结论:由于Δτ<Δt ,说明运动的时钟所描述的物理过程变 了。
四、时空相对性
的验证:哪些实
验和相对论的理论预言符合得很好?
五、相对论的时空观
1、牛顿物理学的绝对时空观: 。
2、相对论认
为:。
3、新科学和经典物理学的关系是怎样的?
六、本节小结:1、“同时”是相对的:
2、长度的相对性:20)(1c
v
l l -=,即尺缩 3、时间间隔的相对性:Δt =2
)(1c v -∆τ
,即钟慢
七、巩固练习:教材P 104 问题与练习:2、3、4、5。
