完整版)菱形的性质和判定练习题
菱形的性质和判定(人教版)(含答案)

菱形的性质和判定(人教版)一、单选题(共9道,每道10分)1.下列说法错误的是( )A.菱形的对边互相平行B.菱形的对角相等C.菱形的对角线相等D.菱形的每一条对角线平分一组对角答案:C解题思路:试题难度:三颗星知识点:菱形的性质2.菱形具有而平行四边形不具有的性质是( )A.对角线互相平分B.邻角互补C.每条对角线平分一组对角D.对角相等答案:C解题思路:试题难度:三颗星知识点:菱形的性质3.如图,已知菱形ABCD的对角线AC,BD的长分别为6、8,AE⊥BC于点E,则AE的长是( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:菱形的性质4.菱形ABCD的周长为8,高为1,则该菱形两邻角度数比为( )A.3:1B.4:1C.5:1D.6:1答案:C解题思路:试题难度:三颗星知识点:菱形的性质5.如图,已知E是菱形ABCD的边BC上一点,且∠DAE=∠B=80°,则∠CDE的度数为( )A.30°B.25°C.20°D.35°答案:A解题思路:试题难度:三颗星知识点:菱形的性质6.如图,等边△AEF的边长与菱形ABCD的边长相等,且它们有一个公共顶点A,E,F分别在BC,CD边上,则∠BAD等于( )A.90°B.80°C.120°D.100°答案:D解题思路:试题难度:三颗星知识点:菱形的性质7.如图,在菱形ABCD中,∠ADC=50°,AD的垂直平分线交对角线BD于点P,垂足为E,连接CP,则∠CPB的度数为( )A.40°B.50°C.60°D.80°答案:B解题思路:试题难度:三颗星知识点:菱形的性质8.在菱形ABCD中,AE⊥BC于E,AF⊥CD于F,且E,F分别为BC,CD的中点,则∠EAF的度数为( )A.75°B.60°C.45°D.30°答案:B解题思路:试题难度:三颗星知识点:菱形的性质9.如图,四边形ABCD是菱形,过点A作BD的平行线交CD的延长线于点E,则下列结论错误的是( )A.DA=DEB.BD=CEC.∠EAC=90°D.∠ABC=2∠E答案:B解题思路:试题难度:三颗星知识点:菱形的性质二、填空题(共1道,每道10分)10.如图,在菱形ABCD中,AB=BD,E,F分别是边AD,CD上的两个动点,且满足AE+CF=AB,则∠EBF为____度.答案:60解题思路:试题难度:知识点:菱形的性质。
菱形的性质和判定经典试题综合训练(含解析)

菱形的性质和判定经典试题综合训练(含解析)一.选择题(共15小题)1.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是()A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC2.求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.求证:AC⊥BD.以下是排乱的证明过程:①又BO=DO;②∴AO⊥BD,即AC⊥BD;③∵四边形ABCD是菱形;④∴AB=AD.证明步骤正确的顺序是()A.③→②→①→④B.③→④→①→②C.①→②→④→③D.①→④→③→②3.下列性质中菱形不一定具有的性质是()A.对角线互相平分B.对角线互相垂直C.对角线相等D.既是轴对称图形又是中心对称图形4.如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是()A.cm B.cm C.cm D.5cm5.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是()A.AB=AD B.AC=BD C.AD=BC D.AB=CD6.如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于()A.6 B.3 C.1.5 D.0.757.若菱形的周长为52cm,面积为120cm2,则它的对角线之和为()A.14cm B.17cm C.28cm D.34cm8.如图,作菱形ABCD的高AE,E为CD的中点.AE=cm,则菱形ABCD的周长是()A.4cm B.4cm C.4cm D.8cm9.如图,菱形ABCD中,过A作BD的平行线交CD的延长线于点E,下列结论:(1)∠EAC=90°,(2)DA=DE,(3)∠ABC=2∠E,其中正确的有()A.0个B.1个C.2个D.3个10.如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,当△ABC 满足什么条件时,四边形ADEF是菱形?()A.AB=AC B.∠BAC=90°C.∠BAC=120°D.∠BAC=150°11.已知菱形的周长为4,两条对角线的和为6,则菱形的面积为()A.2 B.C.3 D.412.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=BC;⑤AD∥BC,这五个条件中任选三个,能使四边形ABCD是菱形的选法有()A.1种B.2种C.3种D.4种13.已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是()A.DF⊥AB B.CG=2GA C.CG=DF+GE D.S四边形BFGC=﹣114.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称△EOD图形.其中正确的结论有()A.5个B.4个C.3个D.2个15.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,动点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC 翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为()A.B.2 C. D.3二.填空题(共9小题)16.如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为cm.17.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD ∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是(只填写序号)18.如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件.19.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是(只填写序号).20.如图,菱形ABCD的周长为40,面积为25,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于.21.如图,菱形纸片ABCD,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于度.22.如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积.23.如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足条件时,四边形EFGH是菱形.24.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPBP′为正方形,则t的值为.三.解答题(共9小题)25.如图,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于E,交AC于F,求证:四边形AEDF是菱形.26.如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.(1)求证:AD⊥BF;(2)若BF=BC,求∠ADC的度数.27.如图,△ABC中,AB=AC,∠BAC=40°,将△ABC绕点A按逆时针方向旋转100°.得到△ADE,连接BD,CE交于点F.(1)求证:△ABD≌△ACE;(2)求证:四边形ABFE是菱形.28.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(2)若∠ADB=30°,BD=6,求AD的长.29.如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.(1)求证:四边形AEDF是菱形;(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.30.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,若BE⊥CD,试证明∠EFD=∠BCD.31.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.32.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(2)若AF=8,CF=6,求四边形BDFG的面积.33.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.菱形的性质和判定经典试题综合训练参考答案与试题解析一.选择题(共15小题)1.如图,△ABC中,DE∥BC,EF∥AB,要判定四边形DBFE是菱形,还需要添加的条件是()A.AB=AC B.AD=BD C.BE⊥AC D.BE平分∠ABC【分析】当BE平分∠ABC时,四边形DBFE是菱形,可知先证明四边形BDEF是平行四边形,再证明BD=DE 即可解决问题.【解答】解:当BE平分∠ABC时,四边形DBFE是菱形,理由:∵DE∥BC,∴∠DEB=∠EBC,∵∠EBC=∠EBD,∴∠EBD=∠DEB,∴BD=DE,∵DE∥BC,EF∥AB,∴四边形DBEF是平行四边形,∵BD=DE,∴四边形DBEF是菱形.其余选项均无法判断四边形DBEF是菱形,故选D.2.求证:菱形的两条对角线互相垂直.已知:如图,四边形ABCD是菱形,对角线AC,BD交于点O.求证:AC⊥BD.以下是排乱的证明过程:①又BO=DO;②∴AO⊥BD,即AC⊥BD;③∵四边形ABCD是菱形;④∴AB=AD.证明步骤正确的顺序是()A.③→②→①→④B.③→④→①→②C.①→②→④→③D.①→④→③→②【分析】根据菱形是特殊的平行四边形以及等腰三角形的性质证明即可.【解答】证明:∵四边形ABCD是菱形,∴AB=AD,∵对角线AC,BD交于点O,∴BO=DO,∴AO⊥BD,即AC⊥BD,∴证明步骤正确的顺序是③→④→①→②,故选B.3.下列性质中菱形不一定具有的性质是()A.对角线互相平分B.对角线互相垂直C.对角线相等D.既是轴对称图形又是中心对称图形【分析】根据菱形的性质解答即可得.【解答】解:A、菱形的对角线互相平分,此选项正确;B、菱形的对角线互相垂直,此选项正确;C、菱形的对角线不一定相等,此选项错误;D、菱形既是轴对称图形又是中心对称图形,此选项正确;故选:C.4.如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是()A.cm B.cm C.cm D.5cm【分析】根据菱形的性质得出BO、CO的长,在RT△BOC中求出BC,利用菱形面积等于对角线乘积的一半,也等于BC×AE,可得出AE的长度.【解答】解:∵四边形ABCD是菱形,∴CO=AC=3cm,BO=BD=4cm,AO⊥BO,∴BC==5cm,∴S菱形ABCD==×6×8=24cm2,∵S菱形ABCD=BC×AE,∴BC×AE=24,∴AE=cm.故选:B.5.如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是()A.AB=AD B.AC=BD C.AD=BC D.AB=CD【分析】由点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,根据三角形中位线的性质,可得EF=GH=AB,EH=FG=CD,又由当EF=FG=GH=EH时,四边形EFGH是菱形,即可求得答案.【解答】解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,∴EF=GH=AB,EH=FG=CD,∵当EF=FG=GH=EH时,四边形EFGH是菱形,∴当AB=CD时,四边形EFGH是菱形.故选:D.6.如图,菱形ABCD的周长为16,面积为12,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于()A.6 B.3 C.1.5 D.0.75【分析】连AP,由菱形ABCD的周长为16,根据了菱形的性质得AB=AD=4,并且S菱形ABCD=2S△ABD,则S△=×12=6,由于S△ABD=S△APB+S△APD,再根据三角形的面积公式得到•PE•AB+•PF•AD=6,即可得到ABDPE+PF的值.【解答】解:连AP,如图,∵菱形ABCD的周长为16,∴AB=AD=4,∴S菱形ABCD=2S△ABD,∴S△ABD=×12=6,而S△ABD=S△APB+S△APD,PE⊥AB,PF⊥AD,∴•PE•AB+•PF•AD=6,∴2PE+2PF=6,∴PE+PF=3.故选B.7.若菱形的周长为52cm,面积为120cm2,则它的对角线之和为()A.14cm B.17cm C.28cm D.34cm【分析】作出图形,根据菱形的对角线互相垂直平分可得AC⊥BD,AO=CO=AC,BO=DO=BD,然后根据菱形的面积等于对角线乘积的一半列式整理可得AO•BO=60,根据菱形的周长求出AB=13,再利用勾股定理可得AO2+BO2=169,然后利用完全平方公式整理并求出AO+BO,再求解即可.【解答】解:如图,∵四边形ABCD是菱形,∴AC⊥BD,AO=CO=AC,BO=DO=BD,∵菱形的面积为120cm2,∴AC•BD=120,即×2AO•2BO=120,所以,AO•BO=60,∵菱形的周长为52cm,∴AB=13cm,在Rt△AOB中,由勾股定理得,AO2+BO2=AB2=132=169,所以,(AO+BO)2=AO2+2AO•BO+BO2=169+60×2=289,所以,AO+BO=17,所以,AC+BD=2(AO+BO)=2×17=34cm.故选D.8.如图,作菱形ABCD的高AE,E为CD的中点.AE=cm,则菱形ABCD的周长是()A.4cm B.4cm C.4cm D.8cm【分析】通过解直角三角形ADE得到边AD的长度,然后由菱形的周长公式进行解答.【解答】解:在菱形ABCD中,AD=CD.∵E为CD的中点,AE⊥CD,∴ED=CD=AD,∴∠DAE=30°,∵AE=cm,∴AD===2(cm),∴菱形ABCD的周长=4AD=8cm.故选:D.9.如图,菱形ABCD中,过A作BD的平行线交CD的延长线于点E,下列结论:(1)∠EAC=90°,(2)DA=DE,(3)∠ABC=2∠E,其中正确的有()A.0个B.1个C.2个D.3个【分析】根据菱形的性质、平行线的性质、平行四边形的判定和性质等知识一一判断即可.【解答】解:∵四边形ABCD是菱形,∴AC⊥BD,AB∥CD,AB=AD,∠ABC=2∠ABD,∵AE∥BD,∴AE⊥AC,∴∠EAC=90°,故①正确,∵AB∥DE,AE∥BD,∴四边形ABDE是平行四边形,∴AB=DE,∠E=∠ABD,∴AD=DE,故②正确,∴∠ABC=2∠E,故③正确,故选D.10.如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形,即△ABD、△BCE、△ACF,当△ABC 满足什么条件时,四边形ADEF是菱形?()A.AB=AC B.∠BAC=90°C.∠BAC=120°D.∠BAC=150°【分析】根据等边三角形性质得出BD=AB,BE=BC,∠DBA=∠EBC=60°,求出∠DBE,证△DBE≌△ABC,推出DE=AC=AF,同理AD=EF得出平行四边形ADEF,根据菱形的判定判断即可.【解答】解:∵△ABD和△BCE是等边三角形,∴BD=AB,BE=BC,∠DBA=∠EBC=60°,∴∠DBE=∠CBA=60°﹣∠EBA,在△DBE和△ABC中,,∴△DBE≌△ABC(SAS),∴DE=AC,∵△AFC是等边三角形,∴AF=AC,∴AF=DE,同理AD=EF,∴四边形ADEF是平行四边形,当AB=AC时,∵AD=AB,AC=AF,∴AD=AF,∴四边形ADEF是菱形,故选A.11.已知菱形的周长为4,两条对角线的和为6,则菱形的面积为()A.2 B.C.3 D.4【分析】由菱形的性质和勾股定理得出AO+BO=3,AO2+BO2=AB2,(AO+BO)2=9,求出2AO•BO=4,即可得出答案.【解答】解:如图四边形ABCD是菱形,AC+BD=6,∴AB=,AC⊥BD,AO=AC,BO=BD,∴AO+BO=3,∴AO2+BO2=AB2,(AO+BO)2=9,即AO2+BO2=5,AO2+2AO•BO+BO2=9,∴2AO•BO=4,∴菱形的面积=AC•BD=2AO•BO=4;故选:D.12.四个点A,B,C,D在同一平面内,从①AB∥CD;②AB=CD;③AC⊥BD;④AD=BC;⑤AD∥BC,这五个条件中任选三个,能使四边形ABCD是菱形的选法有()A.1种B.2种C.3种D.4种【分析】由平行四边形的判定方法和菱形的判定方法得出能使四边形ABCD是菱形的选法有4种,即可得出结论.【解答】解:∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形;∴①②③能使四边形ABCD是菱形;∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形;∴①③⑤能使四边形ABCD是菱形;∵AD=BC,AD∥BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形;∴③④⑤能使四边形ABCD是菱形;∵AB=CD,AD=BC,∴四边形ABCD是平行四边形,∵AC⊥BD,∴四边形ABCD是菱形;∴②③④能使四边形ABCD是菱形;∴能使四边形ABCD是菱形的选法有4种.故选:D.13.已知:如图,在菱形ABCD中,F为边AB的中点,DF与对角线AC交于点G,过G作GE⊥AD于点E,若AB=2,且∠1=∠2,则下列结论不正确的是()A.DF⊥AB B.CG=2GA C.CG=DF+GE D.S四边形BFGC=﹣1【分析】A、由四边形ABCD是菱形,得出对角线平分对角,求得∠GAD=∠2,得出AG=GD,AE=ED,由SAS证得△AFG≌△AEG,得出∠AFG=∠AEG=90°,即可得出A正确;B、由DF⊥AB,F为边AB的中点,证得AD=BD,证出△ABD为等边三角形,得出∠BAC=∠1=∠2=30°,由AC=2AB•cos∠BAC,AG=,求出AC,AG,即可得出B正确;C、由勾股定理求出DF=,由GE=tan∠2•ED求出GE,即可得出C正确;D、由S四边形BFGC=S△ABC﹣S△AGF求出数值,即可得出D不正确.【解答】解:∵四边形ABCD是菱形,∴∠FAG=∠EAG,∠1=∠GAD,AB=AD,∵∠1=∠2,∴∠GAD=∠2,∴AG=GD,∵GE⊥AD,∴GE垂直平分AD,∴AE=ED,∵F为边AB的中点,∴AF=AE,在△AFG和△AEG中,,∴△AFG≌△AEG(SAS),∴∠AFG=∠AEG=90°,∴DF⊥AB,∴A正确;∵DF⊥AB,F为边AB的中点,∴AF=AB=1,AD=BD,∵AB=AD,∴AD=BD=AB,∴△ABD为等边三角形,∴∠BAD=∠BCD=60°,∴∠BAC=∠1=∠2=30°,∴AC=2AB•cos∠BAC=2×2×=2,AG===,∴CG=AC﹣AG=2﹣=,∴CG=2GA,∴B正确;∵GE垂直平分AD,∴ED=AD=1,由勾股定理得:DF===,GE=tan∠2•ED=tan30°×1=,∴DF+GE=+==CG,∴C正确;∵∠BAC=∠1=30°,∴△ABC的边AC上的高等于AB的一半,即为1,FG=AG=,S四边形BFGC=S△ABC﹣S△AGF=×2×1﹣×1×=﹣=,∴D不正确;故选:D.14.如图,O是菱形ABCD的对角线AC、BD的交点,E、F分别是OA、OC的中点.下列结论:①S△ADE=S;②四边形BFDE也是菱形;③四边形ABCD的面积为EF×BD;④∠ADE=∠EDO;⑤△DEF是轴对称△EOD图形.其中正确的结论有()A.5个B.4个C.3个D.2个【分析】①正确,根据三角形的面积公式可得到结论.②根据已知条件利用菱形的判定定理可证得其正确.③正确,根据菱形的面积等于对角线乘积的一半即可求得.④不正确,根据已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确,由已知可证得△DEO≌△DFO,从而可推出结论正确.【解答】解:①正确∵E、F分别是OA、OC的中点.∴AE=OE.∵S△ADE=×AE×OD=×OE×OD=S△EOD∴S△ADE=S△EOD.②正确∵四边形ABCD是菱形,E,F分别是OA,OC的中点.∴EF⊥OD,OE=OF.∵OD=OD.∴DE=DF.同理:BE=BF∴四边形BFDE是菱形.③正确∵菱形ABCD的面积=AC×BD.E、F分别是OA、OC的中点.∴EF=AC.∴菱形ABCD的面积=EF×BD.④不正确,由已知可求得∠FDO=∠EDO,而无法求得∠ADE=∠EDO.⑤正确∵EF⊥OD,OE=OF,OD=OD.∴△DEO≌△DFO.∴△DEF是轴对称图形.∴正确的结论有四个,分别是①②③⑤,故选B.15.如图,在Rt△ABC中,∠ACB=90°,AC=BC=6cm,动点P从点A出发,沿AB方向以每秒cm的速度向终点B运动;同时,动点Q从点B出发沿BC方向以每秒1cm的速度向终点C运动,将△PQC沿BC 翻折,点P的对应点为点P′.设Q点运动的时间为t秒,若四边形QP′CP为菱形,则t的值为()A.B.2 C. D.3【分析】首先连接PP′交BC于O,根据菱形的性质可得PP′⊥CQ,可证出PO∥AC,根据平行线分线段成比例可得=,再表示出AP、AB、CO的长,代入比例式可以算出t的值.【解答】解:连接PP′交BC于O,∵若四边形QPCP′为菱形,∴PP′⊥QC,∴∠POQ=90°,∵∠ACB=90°,∴PO∥AC,∴=,∵设点Q运动的时间为t秒,∴AP=t,QB=t,∴QC=6﹣t,∴CO=3﹣,∵AC=CB=6,∠ACB=90°,∴AB=6,∴=,解得:t=2,故选:B.二.填空题(共9小题)16.如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2.则OC的长为4cm.【分析】根据作法判定出四边形OACB是菱形,再根据菱形的面积等于对角线乘积的一半列式计算即可得解.【解答】解:根据作图,AC=BC=OA,∵OA=OB,∴OA=OB=BC=AC,∴四边形OACB是菱形,∵AB=2cm,四边形OACB的面积为4cm2,∴AB•OC=×2×OC=4,解得OC=4cm.故答案为:4.17.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD,则下列结论:①AC⊥BD;②AD ∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.其中正确的是①②③④(只填写序号)【分析】根据轴对称图形的性质,结合菱形的判定方法以及全等三角形的判定方法分析得出答案.【解答】解:因为l是四边形ABCD的对称轴,AB∥CD,则AD=AB,∠1=∠2,∠1=∠4,则∠2=∠4,∴AD=DC,同理可得:AB=AD=BC=DC,所以四边形ABCD是菱形.根据菱形的性质,可以得出以下结论:所以①AC⊥BD,正确;②AD∥BC,正确;③四边形ABCD是菱形,正确;④在△ABD和△CDB中∵∴△ABD≌△CDB(SSS),正确.故答案为:①②③④.18.如图,四边形ABCD中,E,F,G,H分别是边AB、BC、CD、DA的中点.若四边形EFGH为菱形,则对角线AC、BD应满足条件AC=BD.【分析】添加的条件应为:AC=BD,把AC=BD作为已知条件,根据三角形的中位线定理可得,HG平行且等于AC的一半,EF平行且等于AC的一半,根据等量代换和平行于同一条直线的两直线平行,得到HG 和EF平行且相等,所以EFGH为平行四边形,又EH等于BD的一半且AC=BD,所以得到所证四边形的邻边EH与HG相等,所以四边形EFGH为菱形.【解答】解:添加的条件应为:AC=BD.证明:∵E,F,G,H分别是边AB、BC、CD、DA的中点,∴在△ADC中,HG为△ADC的中位线,所以HG∥AC且HG=AC;同理EF∥AC且EF=AC,同理可得EH=BD,则HG∥EF且HG=EF,∴四边形EFGH为平行四边形,又AC=BD,所以EF=EH,∴四边形EFGH为菱形.故答案为:AC=BD19.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是③(只填写序号).【分析】首先利用对角线互相平分的四边形是平行四边形判定该四边形为平行四边形,然后结合菱形的判定得到答案即可.【解答】解:由题意得:BD=CD,ED=FD,∴四边形EBFC是平行四边形,①BE⊥EC,根据这个条件只能得出四边形EBFC是矩形,②BF∥CE,根据EBFC是平行四边形已可以得出BF∥CE,因此不能根据此条件得出菱形,③AB=AC,∵,∴△ADB≌△ADC,∴∠BAD=∠CAD∴△AEB≌△AEC(SAS),∴BE=CE,∴四边形BECF是菱形.故答案为:③.20.如图,菱形ABCD的周长为40,面积为25,P是对角线BD上一点,分别作P点到直线AB、AD的垂线段PE、PF,则PE+PF等于 2.5.【分析】直接利用菱形的性质得出AB=AD=10,S△ABD=12.5,进而利用三角形面积求法得出答案.【解答】解:∵菱形ABCD的周长为40,面积为25,∴AB=AD=10,S△ABD=12.5,∵分别作P点到直线AB、AD的垂线段PE、PF,∴×AB×PE+×PF×AD=12.5,∴×10(PE+PF)=12.5,∴PE+PF=2.5.故答案为:2.5.21.如图,菱形纸片ABCD,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于75度.【分析】连接BD,由菱形的性质及∠A=60°,得到三角形ABD为等边三角形,P为AB的中点,利用三线合一得到DP为角平分线,得到∠ADP=30°,∠ADC=120°,∠C=60°,进而求出∠PDC=90°,由折叠的性质得到∠CDE=∠PDE=45°,利用三角形的内角和定理即可求出所求角的度数.【解答】解:连接BD,∵四边形ABCD为菱形,∠A=60°,∴△ABD为等边三角形,∠ADC=120°,∠C=60°,∵P为AB的中点,∴DP为∠ADB的平分线,即∠ADP=∠BDP=30°,∴∠PDC=90°,∴由折叠的性质得到∠CDE=∠PDE=45°,在△DEC中,∠DEC=180°﹣(∠CDE+∠C)=75°.故答案为:75.22.如图,菱形ABCD和菱形ECGF的边长分别为3和4,∠A=120°,则图中阴影部分的面积.【分析】作BM⊥FG于M,交EC于N,如图,根据菱形的性质得BC=CD=3,CG=GF=4,AB∥CE∥GF,∠ABC=∠BCD=∠CGF=120°,则∠BCN=∠BGM=60°,再根据含30度的直角三角形三边的关系,在Rt△BCN中可计算出BN=CN=,在Rt△BMG中可计算出BM=GM=,则MN=BM﹣BN=﹣=2,然后根据三角形面积公式和梯形面积公式,利用S阴影部分=S△BCD+S梯形CDFG﹣S△BGF进行计算即可.另一种解法为把阴影部分的面积转化为△BCD的面积进行计算.【解答】解:连接CF,如图,∵四边形ABCD和四边形CGFE为菱形,∠A=120°,∴∠DBC=∠FCG=30°,∴BD∥CF,∴S△FDB=S△CDB=S菱形ABCD=•2••32=.故答案为.23.如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足AB=CD条件时,四边形EFGH是菱形.【分析】首先利用三角形的中位线定理证出EF∥AB,EF=AB,HG∥AB,HG=AB,可得四边形EFGH是平行四边形,再根据邻边相等的平行四边形是菱形,添加条件AB=CD后,证明EF=EH即可.【解答】解:需添加条件AB=CD.∵E,F是AD,DB中点,∴EF∥AB,EF=AB,∵H,G是AC,BC中点,∴HG∥AB,HG=AB,∴EF∥HG,EF=HG,∴四边形EFGH是平行四边形,∵E,H是AD,AC中点,∴EH=CD,∵AB=CD,∴EF=EH,∴四边形EFGH是菱形.故答案为:AB=CD.24.如图,在Rt△ABC中,∠C=90°,AC=BC=6cm,点P从点B出发,沿BA方向以每秒cm的速度向终点A运动;同时,动点Q从点C出发沿CB方向以每秒1cm的速度向终点B运动,将△BPQ沿BC翻折,点P的对应点为点P′.设Q点运动的时间t秒,若四边形QPBP′为正方形,则t的值为2.【分析】根据正方形的判定定理得到BQ=BP时,四边形QPBP′为正方形进行解答即可.【解答】解:由题意得,当△BPQ为等腰直角三角形时,四边形QPBP′为正方形,则BQ=BP,即6﹣t=×t,解得t=2.故答案为:2.三.解答题(共9小题)25.如图,AD是△ABC的角平分线,过点D分别作AC和AB的平行线,交AB于E,交AC于F,求证:四边形AEDF是菱形.【分析】由已知易得四边形AEDF是平行四边形,由角平分线和平行线的定义可得∠FAD=∠FDA,∴AF=DF,∴四边形AEDF是菱形;【解答】证明:∵AD是△ABC的角平分线,∴∠EAD=∠FAD,∵DE∥AC,DF∥AB,∴四边形AEDF是平行四边形,∠EAD=∠ADF,∴∠FAD=∠FDA∴AF=DF,∴四边形AEDF是菱形.26.如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.(1)求证:AD⊥BF;(2)若BF=BC,求∠ADC的度数.【分析】(1)连结DB 、DF .根据菱形四边相等得出AB=AD=FA ,再利用SAS 证明△BAD ≌△FAD ,得出DB=DF ,那么D 在线段BF 的垂直平分线上,又AB=AF ,即A 在线段BF 的垂直平分线上,进而证明AD ⊥BF ;(2)设AD ⊥BF 于H ,作DG ⊥BC 于G ,证明DG=CD .在直角△CDG 中得出∠C=30°,再根据平行线的性质即可求出∠ADC=180°﹣∠C=150°.【解答】(1)证明:如图,连结DB 、DF .∵四边形ABCD ,ADEF 都是菱形,∴AB=BC=CD=DA ,AD=DE=EF=FA .在△BAD 与△FAD 中,,∴△BAD ≌△FAD ,∴DB=DF ,∴D 在线段BF 的垂直平分线上, ∵AB=AF ,∴A 在线段BF 的垂直平分线上,∴AD 是线段BF 的垂直平分线,∴AD ⊥BF ;(2)如图,设AD ⊥BF 于H ,作DG ⊥BC 于G ,则四边形BGDH 是矩形,∴DG=BH=BF .∵BF=BC ,BC=CD ,∴DG=CD .在直角△CDG 中,∵∠CGD=90°,DG=CD ,∴∠C=30°,∵BC ∥AD ,∴∠ADC=180°﹣∠C=150°.27.如图,△ABC 中,AB=AC ,∠BAC=40°,将△ABC 绕点A 按逆时针方向旋转100°.得到△ADE ,连接BD ,CE 交于点F .(1)求证:△ABD ≌△ACE ;(2)求证:四边形ABFE 是菱形.【分析】(1)根据旋转角求出∠BAD=∠CAE ,然后利用“边角边”证明△ABD 和△ACE 全等.(2)根据对角相等的四边形是平行四边形,可证得四边形ABFE 是平行四边形,然后依据邻边相等的平行四边形是菱形,即可证得.【解答】(1)证明:∵ABC绕点A按逆时针方向旋转100°,∴∠BAC=∠DAE=40°,∴∠BAD=∠CAE=100°,又∵AB=AC,∴AB=AC=AD=AE,在△ABD与△ACE中,,∴△ABD≌△ACE(SAS).(2)证明:∵∠BAD=∠CAE=100°AB=AC=AD=AE,∴∠ABD=∠ADB=∠ACE=∠AEC=40°.∵∠BAE=∠BAD+∠DAE=140°,∴∠BFE=360°﹣∠BAE﹣∠ABD﹣∠AEC=140°,∴∠BAE=∠BFE,∴四边形ABFE是平行四边形,∵AB=AE,∴平行四边形ABFE是菱形.28.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,连接CD.(1)求证:四边形ABCD是菱形;(2)若∠ADB=30°,BD=6,求AD的长.【分析】(1)由平行线的性质和角平分线定义得出∠ABD=∠ADB,证出AB=AD,同理:AB=BC,得出AD=BC,证出四边形ABCD是平行四边形,即可得出结论;(2)由菱形的性质得出AC⊥BD,OD=OB=BD=3,再由三角函数即可得出AD的长.【解答】(1)证明:∵AE∥BF,∴∠ADB=∠CBD,又∵BD平分∠ABF,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AB=AD,同理:AB=BC,∴AD=BC,∴四边形ABCD是平行四边形,又∵AB=AD,∴四边形ABCD是菱形;(2)解:∵四边形ABCD是菱形,BD=6,∴AC⊥BD,OD=OB=BD=3,∵∠ADB=30°,∴cos∠ADB==,∴AD==2.29.如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.(1)求证:四边形AEDF是菱形;(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.【分析】(1)先根据直角三角形斜边上中线的性质,得出DE=AB=AE,DF=AC=AF,再根据AB=AC,点E、F分别是AB、AC的中点,即可得到AE=AF=DE=DF,进而判定四边形AEDF是菱形;(2)设EF=x,AD=y,则x+y=7,进而得到x2+2xy+y2=49,再根据Rt△AOE中,AO2+EO2=AE2,得到x2+y2=36,据此可得xy=,进而得到菱形AEDF的面积S.【解答】解:(1)∵AD⊥BC,点E、F分别是AB、AC的中点,∴Rt△ABD中,DE=AB=AE,Rt△ACD中,DF=AC=AF,又∵AB=AC,点E、F分别是AB、AC的中点,∴AE=AF,∴AE=AF=DE=DF,∴四边形AEDF是菱形;(2)如图,∵菱形AEDF的周长为12,∴AE=3,设EF=x,AD=y,则x+y=7,∴x2+2xy+y2=49,①∵AD⊥EF于O,∴Rt△AOE中,AO2+EO2=AE2,∴(y)2+(x)2=32,即x2+y2=36,②把②代入①,可得2xy=13,∴xy=,∴菱形AEDF的面积S=xy=.30.如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE;(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,若BE⊥CD,试证明∠EFD=∠BCD.【分析】(1)先判断出△ABC≌△ADC得到∠BAC=∠DAC,再判断出△ABF≌△ADF得出∠AFB=∠AFD,最后进行简单的推算即可;(2)先由平行得到角相等,用等量代换得出∠DAC=∠ACD,最后判断出四边相等;(3)由(2)得到判断出△BCF≌△DCF,结合BE⊥CD即可.【解答】证明:(1)在△ABC和△ADC中.∴△ABC≌△ADC,∴∠BAC=∠DAC,在△ABF和△ADF中,∴△ABF≌△ADF,∴∠AFB=∠AFD,∵∠CFE=∠AFB,∴∠AFD=∠CFE,∴∠BAC=∠DAC,∠AFD=∠CFE;(2)∵AB∥CD,∴∠BAC=∠ACD,∵∠BAC=∠DAC,∴∠BAC=∠ACD,∴∠DAC=∠ACD,∴AD=CD,∵AB=AD,CB=CD,∴AB=CB=CD=AD,∴四边形ABCD是菱形;(3)∵四边形ABCD是菱形,∴BC=CD,∠BCF=∠DCF,∵CF=CF,∴△BCF≌△DCF,∴∠CBF=∠CDF,∵BE⊥CD,∴∠BEC=∠DEF=90°,∴∠EFD=∠BCD.31.如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DE,连接CE、AF.(1)证明:AF=CE;(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.【分析】(1)由三角形中位线定理得出DE∥AC,AC=2DE,求出EF∥AC,EF=AC,得出四边形ACEF是平行四边形,即可得出AF=CE;(2)由直角三角形的性质得出∠BAC=60°,AC=AB=AE,证出△AEC是等边三角形,得出AC=CE,即可得出结论.【解答】(1)证明:∵点D,E分别是边BC,AB上的中点,∴DE∥AC,AC=2DE,∵EF=2DE,∴EF∥AC,EF=AC,∴四边形ACEF是平行四边形,∴AF=CE;(2)解:当∠B=30°时,四边形ACEF是菱形;理由如下:∵∠ACB=90°,∠B=30°,∴∠BAC=60°,AC=AB=AE,∴△AEC是等边三角形,∴AC=CE,又∵四边形ACEF是平行四边形,∴四边形ACEF是菱形.32.如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.(1)求证:四边形BDFG是菱形;(2)若AF=8,CF=6,求四边形BDFG的面积.【分析】(1)首先可判断四边形BDFG是平行四边形,再由直角三角形斜边中线等于斜边一半,可得BD=FD,则可证明四边形BDFG是菱形;(2)首先过点B作BH⊥AG于点H,由AF=8,CF=6,可利用勾股定理求得AC的长,即可求得DF的长,然后由菱形的性质求得BG=GF=DF=5,再求出EF的长即可解决问题.【解答】证明:(1)∵AG∥BD,BD=FG,∴四边形BGFD是平行四边形,∵CE⊥BD,∴CE⊥AG,又∵BD为AC的中线,∴BD=DF=AC,∴四边形BDFG是菱形,(2)∵AF=8,CF=6,CF⊥AG,∴AC==10,∴DF=AC=5,∵四边形BDFG是菱形,∴BD=GF=DF=5,∵DE∥AG,CD=AD,∴CE=EF=3∴S菱形BDFG=GF•EF=15.33.如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.(1)证明不论E、F在BC、CD上如何滑动,总有BE=CF;(2)当点E、F在BC、CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.【分析】(1)先求证AB=AC,进而求证△ABC、△ACD为等边三角形,得∠4=60°,AC=AB进而求证△ABE ≌△ACF,即可求得BE=CF;(2)根据△ABE≌△ACF可得S△ABE=S△ACF,故根据S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC即可解题;当正三角形AEF的边AE与BC垂直时,边AE最短.△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又根据S△CEF=S四边形AECF﹣S△AEF,则△CEF的面积就会最大.【解答】(1)证明:连接AC,如下图所示,∵四边形ABCD为菱形,∠BAD=120°,∠1+∠EAC=60°,∠3+∠EAC=60°,∴∠1=∠3,∵∠BAD=120°,∴∠ABC=60°,∴△ABC和△ACD为等边三角形,∴∠4=60°,AC=AB,∴在△ABE和△ACF中,,∴△ABE≌△ACF(ASA).∴BE=CF;(2)解:四边形AECF的面积不变,△CEF的面积发生变化.理由:由(1)得△ABE≌△ACF,则S△ABE=S△ACF,故S四边形AECF=S△AEC+S△ACF=S△AEC+S△ABE=S△ABC,是定值,作AH⊥BC于H点,则BH=2,S四边形AECF=S△ABC=BC•AH=BC•=4,由“垂线段最短”可知:当正三角形AEF的边AE与BC垂直时,边AE最短.故△AEF的面积会随着AE的变化而变化,且当AE最短时,正三角形AEF的面积会最小,又S△CEF=S四边形AECF﹣S△AEF,则此时△CEF的面积就会最大.∴S△CEF=S四边形AECF﹣S△AEF=4﹣×2×=.答:最大值是.。
(初中)数学《菱形的性质与判定》中考专项复习训练典型试题梳理汇总

(初中)数学《菱形的性质与判定》中考专项复习训练典型试题梳理汇总菱形的性质与判定基础同步过关知识点一:菱形的性质定理1.如图,四边形ABCD的对角线互相平分,则添加下列条件之一,不能使它成为菱形的是()A.AB=ADB.AC=BDC.BD平分∠ABCD.AC∠BD2.如图,顺次连接四边形ABCD各边的中点得到四边形EFGH,要使四边形EFGH为菱形,应添加的条件是。
3.如图,下列对菱形ABCD表述正确的有。
∠AC=BD;∠∠OAB=∠OBA;∠AC∠BD;∠有4条对称轴;∠AD=BD;∠∠OAB=∠OAD。
4.如图,四边形ABCD是菱形,AC BD相交于点O,AC=8,BD=6,DH∠AB于点H,则DH的长为。
第1题图第2题图第3题图第4题图5.如图,在菱形ABCD中,AB=2,∠ABC=120°,则菱形ABCD的面积是。
6.如图,在菱形ABCD中,对角线AC与BD交于点O,OE∠AB,垂足为E,若∠ADC=128°,则∠AOE的度数为()A.62°B.52°C.68°D.64°7.如图,在菱形ABCD中,∠B=60°,AB=3,点E是BC边上的一个动点(点E与点C不重合),点F,G分别是AE,CE的中点,则线段FG的长度为()B.3第5第6题图第7题图知识点二:菱形的判定定理8.已知四边形ABCD中,AC∠BD,再补充一个条件使得四边形ABCD为菱形,这个条件可以是()A.AC=BDB.AB=BCC.AC与BD互相平分D.∠ABC=90°9.如图,将∠ABC沿BC方向平移得到∠DCE,连接AD.下列条件中,能够判定四边形ACED为菱形的是()A .AB=BC B. AC=BC C.∠ABC=60° D.∠ACB=60°10.AC,BD相交于点O,点E,F,G,H分别是OA,OB,OC,OD的中点,若要使四边形EFGH成为菱形,(写出一种即可)11.折纸游戏一直很受大家的欢迎,小丽同学要用一张矩形纸片折出一个菱形,她用沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图)。
菱形的性质与判定练习题
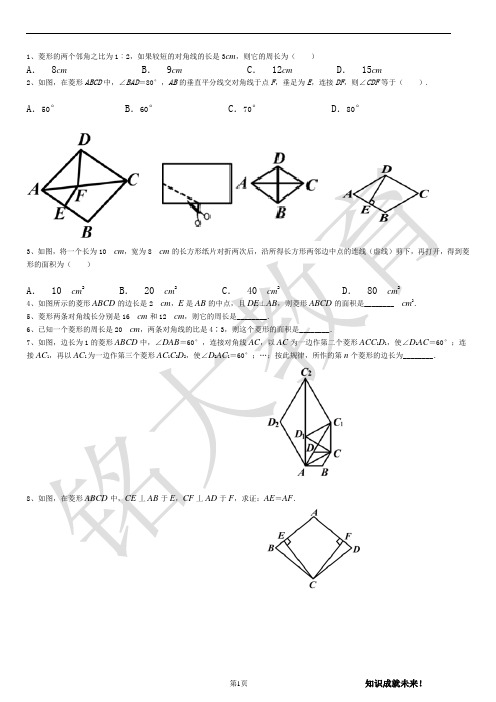
1、菱形的两个邻角之比为1︰2,如果较短的对角线的长是3cm,则它的周长为()A. 8cm B. 9cm C. 12cm D. 15cm2、如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线于点F,垂足为E,连接DF,则∠CDF等于(). A.50° B.60° C.70° D.80°3、如图,将一个长为10 cm,宽为8 cm的长方形纸片对折两次后,沿所得长方形两邻边中点的连线(虚线)剪下,再打开,得到菱形的面积为()A. 10 cm2 B. 20 cm2 C. 40 cm2 D. 80 cm24、如图所示的菱形ABCD的边长是2 cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积是________ cm2.5、菱形两条对角线长分别是16 cm和12 cm,则它的周长是________.6、已知一个菱形的周长是20 cm,两条对角线的比是4∶3,则这个菱形的面积是________.7、如图,边长为1的菱形ABCD中,∠DAB=60°,连接对角线AC,以AC为一边作第二个菱形ACC1D1,使∠D1AC=60°;连接AC1,再以AC1为一边作第三个菱形AC1C2D2,使∠D2AC1=60°;…;按此规律,所作的第n个菱形的边长为________.8、如图,在菱形ABCD中,CE丄AB于E,CF丄AD于F,求证:AE=AF.9、如图,四边形ABCD是菱形,对角线AC、BD相交于点O,DH⊥AB于H,连接OH,求证:∠DHO=∠DCO.10、已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;(2)若∠EOD=30°,求CE的长.11、如图,矩形ABCD的对角线AC、BD相交于点O,CE∥BD,DE∥AC.若AC=4,则四边形CODE的周长是()A.4 B.6 C.8 D.1012、如图,在平行四边形ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE,CF,则四边形AECF是().A.梯形 B.矩形 C.菱形 D.正方形13、如图,平行四边形ABCD的对角线相交于点O,分别添加下列条件:①AC⊥BD;②AB=BC;③AC平分∠BAD;④AO=DO.其中使得平行四边形ABCD是菱形的条件有()A. 1个B. 2个C. 3个D. 4个14、在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,则四边形ABCD的对角线AC,BD满足条件________时,四边形EFGH是菱形.15、如图,已知□ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.求证:四边形AFCE是菱形.16、如图,△ABC中,AB=AC,AD是△ABC一个外角的平分线,且∠BAC=∠ACD.(1)求证:△ABC≌△ACD.(2)若∠ACB=60°,求证:四边形ABCD是菱形.17、如图,□ABCD的边AD=2AB,AE=BF=AB,EC交AD于点M,FD交BC于点N.求证:四边形CDMN是菱形.18、如图所示,在菱形ABCD中,∠A=110°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FEP等于( )A.35° B.45° C.50° D.55°20、如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2 009米停下,则这个微型机器人停在________点.21、已知菱形ABCD的边长为6,∠A=60°,如果点P是菱形内一点,且PB=PD=2,那么AP的长为________.22、如图,点E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.23、如图,已知菱形ABCD的周长为16 cm,∠ABC=60°,对角线AC与BD相交于点O,求AC和BD的长.24、如图,在菱形ABCD中,边长为10,∠A=60°.顺次连结菱形ABCD各边中点,可得四边形A1B1C1D1;顺次连结四边形A1B1C1D1各边中点,可得四边形A2B2C2D2;顺次连结四边形A2B2C2D2各边中点,可得四边形A3B3C3D3;按此规律继续下去….则四边形A2B2C2D2的周长是________;四边形A2013B2013C2013D2013的周长是________25、如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A、B、C的对应点分别是D、E、F,连接AD.求证:四边形ACFD是菱形.26、如图.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,分别于BC、CD交于E、F,EH⊥AB于H.连接FH,求证:四边形CFHE是菱形.27、如图所示,在四边形ABCD中,点E,F是对角线BD上的两点,且BE=DF.(1)若四边形AECF是平行四边形,求证四边形ABCD是平行四边形;(2)若四边形AECF是菱形,则四边形ABCD也是菱形吗?为什么?28、如图,AD是△ABC的角平分线,DE∥AC,DF∥AB.求证:四边形AEDF是菱形。
菱形性质习题

菱形性质:1.对边平行,四边相等;2对角相等,邻角互补。
3对角线互相垂直平分且平分每一组对角,菱形判定:1四条边都相等的四边形是菱形.2一组邻边相等的平行四边形是菱形。
3.对角线相互垂直的平行四边形是菱形。
(2013•滨州)(2013•淄博)(2013•梧州)(2013•随州)(2013•河北)1.(2013•滨州)如图,等边△ABC沿射线BC向右平移到△DCE的位置,连接AD、BD,则下列结论:①AD=BC;②BD、AC互相平分;③四边形ACED是菱形.其中正确的个数是()2.(2013•淄博)如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()3.(2013•梧州)如图,在菱形ABCD中,已知∠A=60°,AB=5,则△ABD的周长是()4.(2013•随州)如图,在菱形ABCD中,∠BAD=120°.已知△ABC的周长是15,则菱形ABCD的周长是()5.(2013•河北)如图,菱形ABCD中,点M,N在AC上,ME⊥AD,NF⊥AB.若NF=NM=2,ME=3,则AN=()(2013•泉州)(2013•南京)(2013•内江)(2013•临沂)(2012•沈阳)6.(2013•泉州)如图,菱形ABCD的周长为8√(5),对角线AC和BD相交于点O,AC:BD=1:2,则AO:BO=,菱形ABCD的面积S=7.(2013•南京)如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF,若菱形ABCD的边长为2cm,∠A=120°,则EF= cm.8. (2013•内江)已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=9.(2013•临沂)如图,菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为E,F,连接EF,则△AEF的面积是 cm2.10.(2012•沈阳)如图,菱形ABCD的边长为8cm,∠A=60°,DE⊥AB于点E,DF⊥BC于点F,则四边形BEDF的面积为11.(2013•雅安)在▱ABCD中,点E、F分别在AB、CD上,且AE=CF.(1)求证:△ADE≌△CBF;(2)若DF=BF,求证:四边形DEBF为菱形.12.(2013•乌鲁木齐)如图.在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,分别于BC、CD交于E、F,EH⊥AB于H.连接FH,求证:四边形CFHE是菱形.13.(2012•柳州)如图,用两张等宽的纸条交叉重叠地放在一起,重合的四边形ABCD是一个特殊的四边形.(1)这个特殊的四边形形状(2)请证明你的结论.14.(2011•湖州)如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.15.(2013•昭通)已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.。
菱形的性质与判定习题

菱形的性质与判定习题课一:知识回顾、课前预习班级姓名1.如图,在菱形ABCD中,∠BAD=60°,BD=4,则菱形ABCD的周长是_________.2、如图,菱形ABCD的边长是2cm,E是AB的中点,且DE丄AB,则菱形ABCD的面积为____________cm2.3.已知菱形两条对角线的长分别为5cm和8cm,则这个菱形的面积是________cm.4、如图,菱形ABCD的对角相交于点O,且AC=8,BD=6,过点O作OH丄AB,垂足为H,则点O到边AB的距离___________5、如图,将两张等宽的长方形纸重叠部分是一个四边形ABCD,若AD=6cm,∠ABC=60°,则四边形ABCD的面积等于__________cm2.二:例题选讲1、如图,在平行四边形ABCD中,∠DAB=60°,AB=2AD,点 E、F分别是CD的中点,过点A作AG∥BD,交CB的延长线于点G。
(1)求证:四边形DEBF是菱形;(2)请判断四边形AGBD是什么特殊四边形?并加以证明。
2、如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF=CE=AE.(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由。
3、如图,在平行四边形ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.(1)求证:△ABE≌△CDF;(2)当四边形AECF为菱形时,求出该菱形的面积.4、如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.5、如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=6,∠BAD=60°,且AB>6.(1)求∠EPF的大小;(2)若AP=10,求AE+AF的值;(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.菱形的性质与判定达标自测班级姓名1a.菱形具有而一般平行四边形不具有的性质是()A.对边相等 B.对角相等 C.对角线互相平分 D.对角线互相垂直2a.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A. B. C.5 D.43a.如图,菱形ABCD的对角线AC、BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为.4b.如图,已知菱形ABCD的边长2,∠A=60°,点E、F分别在边AB、AD上,若将△AEF沿直线EF折叠,使得点A恰好落在CD边的中点G处,则EF= .5b.如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为.6b. 如图,在□ABCD中,E、F分别为边AB、CD的中点,BD是对角线,过A点作AG∥DB交CB的延长线于点G.(1)求证:DE∥BF;(2)若∠G=90°,那么四边形DEBF是菱形吗?请证明你的结论.7b.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AE平分∠BAC,分别与BC、CD交于E、F,EH⊥AB于H,连接FH.求证:四边形CFHE是菱形.8b如图,在△ABC中,∠ACB=90°,D,E分别为AC,AB的中点,BF∥CE交DE的延长线于点F.(1)求证:四边形ECBF是平行四边形;(2)当∠A=30°时,求证:四边形ECBF是菱形.9b.如图:已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
菱形性质及判定测试练习
菱形性质及判定测试练习一.选择题(共12小题)1.(2016•雅安)如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为()A.52cm B.40cm C.39cm D.26cm2.(2016•枣庄)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A.B.C.5 D.43.(2016•咸宁)已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为()A.(0,0)B.(1,)C.(,)D.(,)4.(2016•重庆)如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()A.18﹣9πB.18﹣3πC.9﹣D.18﹣3π5.(2016•黔东南州)如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为()A.2 B.3 C.D.26.(2016•宁夏)菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为()A.2 B.C.6D.87.(2016•鄂州)如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ 的长为()A.5 B.7 C.8 D.8.(2016•龙岩模拟)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1 B.2 C.3 D.49.(2016•新化县三模)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC 的中点,则下列等式中一定成立的是()A.AB=BE B.AC=2AB C.AB=2OE D.AC=2OE10.(2016•槐荫区二模)如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是()A.﹣πB.﹣2πC.2﹣πD.2﹣2π11.(2016•建昌县二模)已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.112°B.114°C.116°D.118°12.(2016•蜀山区二模)如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是()A.AB=AD B.AC=BD C.AD=BC D.AB=CD二.填空题(共6小题)13.(2016•内江)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=.14.(2016•哈尔滨)如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为.15.(2016•丽水)如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则=.16.(2016•石家庄一模)如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE 和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是.17.(2016•江西模拟)如图,在菱形ABCD中,sin∠D=,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为.18.(2016•新乡模拟)如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=.三.解答题(共10小题)19.(2016•苏州)如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.20.(2016•沈阳)如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.21.(2016•聊城)如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC 的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.22.(2016•通州区一模)如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.(1)求证:四边形AECD是菱形;(2)如果点E是AB的中点,AC=4,EC=2.5,求四边形ABCD的面积.23.(2016•哈尔滨模拟)如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.(1)求证:四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.24.(2016•金东区模拟)如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.(1)求证:AC⊥CE;(2)若AB=4,求图中阴影部分的面积.(结果保留根号和π)25.(2016•泰安模拟)如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.(1)求证:∠DCP=∠DAP;(2)如果PE=4,EF=5,求线段PC的长.26.(2016•黄冈模拟)如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.27.(2016•武侯区模拟)如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.(1)求证:△ADE≌△CDF;(2)若∠A=40°,∠DEF=65°,求∠DFC的度数.28.(2016•泰安模拟)在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)如图1,当E是线段AC的中点时,求证:BE=EF.(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论:.(填“成立”或“不成立”)(3)如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.菱形性质及判定测试练习参考答案与试题解析一.选择题(共12小题)1.(2016•雅安)如图,四边形ABCD的四边相等,且面积为120cm2,对角线AC=24cm,则四边形ABCD的周长为()A.52cm B.40cm C.39cm D.26cm【解答】解:如图,连接AC、BD相交于点O,∵四边形ABCD的四边相等,∴四边形ABCD为菱形,∴AC⊥BD,S四边形ABCD=AC•BD,∴×24BD=120,解得BD=10cm,∴OA=12cm,OB=5cm,在Rt△AOB中,由勾股定理可得AB==13(cm),∴四边形ABCD的周长=4×13=52(cm),故选A.2.(2016•枣庄)如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于H,则DH等于()A.B.C.5 D.4【解答】解:∵四边形ABCD是菱形,∴AO=OC,BO=OD,AC⊥BD,∵AC=8,DB=6,∴AO=4,OB=3,∠AOB=90°,由勾股定理得:AB==5,∵S菱形ABCD=,∴,∴DH=,故选A.3.(2016•咸宁)已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为()A.(0,0)B.(1,)C.(,)D.(,)【解答】解:如图连接AC,AD,分别交OB于G、P,作BK⊥OA于K.∵四边形OABC是菱形,∴AC⊥OB,GC=AG,OG=BG=2,A、C关于直线OB对称,∴PC+PD=PA+PD=DA,∴此时PC+PD最短,在RT△AOG中,AG===,∴AC=2,∵OA•BK=•AC•OB,∴BK=4,AK==3,∴点B坐标(8,4),∴直线OB解析式为y=x,直线AD解析式为y=﹣x+1,由解得,∴点P坐标(,).故选D.4.(2016•重庆)如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是()A.18﹣9πB.18﹣3πC.9﹣D.18﹣3π【解答】解:∵四边形ABCD是菱形,∠DAB=60°,∴AD=AB=6,∠ADC=180°﹣60°=120°,∵DF是菱形的高,∴DF⊥AB,∴DF=AD•sin60°=6×=3,∴图中阴影部分的面积=菱形ABCD的面积﹣扇形DEFG的面积=6×3﹣=18﹣9π.故选:A.5.(2016•黔东南州)如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为()A.2 B.3 C.D.2【解答】解:∵四边形ABCD菱形,∴AC⊥BD,BD=2BO,∵∠ABC=60°,∴△ABC是正三角形,∴∠BAO=60°,∴BO=sin60°•AB=2×=,∴BD=2.故选:D.6.(2016•宁夏)菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=,BD=2,则菱形ABCD的面积为()A.2 B.C.6D.8【解答】解:∵E,F分别是AD,CD边上的中点,EF=,∴AC=2EF=2,又∵BD=2,∴菱形ABCD的面积S=×AC×BD=×2×2=2,故选:A.7.(2016•鄂州)如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ 的长为()A.5 B.7 C.8 D.【解答】解:作CH⊥AB于H,如图,∵菱形ABCD的边AB=8,∠B=60°,∴△ABC为等边三角形,∴CH=AB=4,AH=BH=4,∵PB=3,∴HP=1,在Rt△CHP中,CP==7,∵梯形APQD沿直线PQ折叠,A的对应点A′,∴点A′在以P点为圆心,PA为半径的弧上,∴当点A′在PC上时,CA′的值最小,∴∠APQ=∠CPQ,而CD∥AB,∴∠APQ=∠CQP,∴∠CQP=∠CPQ,∴CQ=CP=7.故选B.8.(2016•龙岩模拟)如图,在周长为12的菱形ABCD中,AE=1,AF=2,若P为对角线BD上一动点,则EP+FP的最小值为()A.1 B.2 C.3 D.4【解答】解:作F点关于BD的对称点F′,则PF=PF′,连接EF′交BD于点P.∴EP+FP=EP+F′P.由两点之间线段最短可知:当E、P、F′在一条直线上时,EP+FP的值最小,此时EP+FP=EP+F′P=EF′.∵四边形ABCD为菱形,周长为12,∴AB=BC=CD=DA=3,AB∥CD,∵AF=2,AE=1,∴DF=AE=1,∴四边形AEF′D是平行四边形,∴EF′=AD=3.∴EP+FP的最小值为3.故选:C.9.(2016•新化县三模)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E为BC 的中点,则下列等式中一定成立的是()A.AB=BE B.AC=2AB C.AB=2OE D.AC=2OE【解答】解:∵点E为BC的中点,∴CE=BE=BC,∵AB=BC,∴AB=2BE,故选项A错误;∵在菱形ABCD中,对角线AC,BD相交于点O,∴AO=CO=AC,∴OE是△ABC的中位线,∴OE=AB,故选项C正确;∵AC≠AB≠BC,∴AC≠2AB≠2OE,故选项B,D错误,故选C.10.(2016•槐荫区二模)如图,菱形ABCD的边长为2,且AE⊥BC,E、F、G、H分别为BC、CD、DA、AB的中点,以A、B、C、D四点为圆心,半径为1作圆,则图中阴影部分的面积是()A.﹣πB.﹣2πC.2﹣πD.2﹣2π【解答】解:根据题意得:AB=BC=AC,∴∠B=60°,∵菱形ABCD的边长为2,∴AB=BC=2,∵AE⊥BC,∴BE=CE=BC=1,∴AE==,∴S菱形ABCD=BC•AE=2,S扇形AGH+S扇形BEH+S扇形CEF+S扇形DGF==π,∴S阴影=2﹣π.故选C.11.(2016•建昌县二模)已知:如图,在菱形ABCD中,∠BAD=44°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF等于()A.112°B.114°C.116°D.118°【解答】解:连接BF,∵四边形ABCD是菱形,∴DC=BC,∠1=∠2,∠DAC=∠BAC,在△DCF和△BCF中∵,∴△DCF≌△BCF(SAS),∴∠CDF=∠CBF,∵EF的垂直平分AB,∴AF=BF,∴∠FAB=∠FBA,∵∠BAD=44°,∴∠DAC=∠BAC=22°,∠ABC=136°,∴∠FAB=∠FBA=22°,则∠FBC=136°﹣22°=114°,故∠CDF=114°.故选:B.12.(2016•蜀山区二模)如图,四边形ABCD中,对角线相交于点O,E、F、G、H分别是AD、BD、BC、AC的中点,要使四边形EFGH是菱形,则四边形ABCD需满足的条件是()A.AB=AD B.AC=BD C.AD=BC D.AB=CD【解答】解:∵点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,∴EF=GH=AB,EH=FG=CD,∵当EF=FG=GH=EH时,四边形EFGH是菱形,∴当AB=CD时,四边形EFGH是菱形.故选:D.二.填空题(共6小题)13.(2016•内江)如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥BC,垂足为点E,则OE=.【解答】解:∵四边形ABCD为菱形,∴AC⊥BD,OB=OD=BD=3,OA=OC=AC=4,在Rt△OBC中,∵OB=3,OC=4,∴BC==5,∵OE⊥BC,∴OE•BC=OB•OC,∴OE==.故答案为.14.(2016•哈尔滨)如图,在菱形ABCD中,∠BAD=120°,点E、F分别在边AB、BC上,△BEF与△GEF关于直线EF对称,点B的对称点是点G,且点G在边AD上.若EG⊥AC,AB=6,则FG的长为3.【解答】解:∵四边形ABCD是菱形,∠BAD=120°,∴AB=BC=CD=AD,∠CAB=∠CAD=60°,∴△ABC,△ACD是等边三角形,∵EG⊥AC,∴∠AEG=∠AGE=30°,∵∠B=∠EGF=60°,∴∠AGF=90°,∴FG⊥BC,∴2•S△ABC=BC•FG,∴2××(6)2=6•FG,∴FG=3.故答案为3.15.(2016•丽水)如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则=.【解答】解:如图,连接AC、EF,在菱形ABCD中,AC⊥BD,∵BE⊥AD,AE=DE,∴AB=BD,又∵菱形的边AB=AD,∴△ABD是等边三角形,∴∠ADB=60°,设EF与BD相交于点H,AB=4x,∵AE=DE,∴由菱形的对称性,CF=DF,∴EF是△ACD的中位线,∴DH=DO=BD=x,在Rt△EDH中,EH=DH=x,∵DG=BD,∴GH=BD+DH=4x+x=5x,在Rt△EGH中,由勾股定理得,EG===2x,所以,==.故答案为:.16.(2016•石家庄一模)如图,在线段AB上取一点C,分别以AC、BC为边长作菱形ACDE 和菱形BCFG,使点D在CF上,连接EG,H是EG的中点,EG=4,则CH的长是2.【解答】解:连接AD,CE,CG,∵四边形ACDE与四边形BCFG均是菱形,∴AD⊥CE,∠CAD=∠EAC,∠BCG=∠BCF.∵AE∥CF,∴∠EAC=∠BCF,∴∠CAD=∠BCG,∴AD∥CG,∴CE⊥CG.∵H是EG的中点,EG=4,∴CH=EG=2.故答案为:2.17.(2016•江西模拟)如图,在菱形ABCD中,sin∠D=,E,F分别是AB和CD上的点,BC=5,AE=CF=2,点P是线段EF上一点,则当△BPC是直角三角形时,CP的长为或4或.【解答】解:∵sin∠D=,菱形边AD=BC=5,∴以AD为斜边的直角三角形的两直角边分别为3、4如图,以DC所在的直线为x轴,点F为坐标原点建立平面直角坐标系,∵菱形ABCD的对角线AC⊥BD,∴点P为菱形的对角线的交点时∠BPC=90°,此时,CP=AC=×=,点P与点E重合时∠BPC=90°,此时,CP=4;∠BCP=90°时,由图可知,点B(5,4)、C(2,0),易求直线OE的解析式为y=2x,设直线BC的解析式为y=kx+b,则,解得,所以,直线BC的解析式为y=x﹣,∵CP⊥BC,∴设直线CP的解析式为y=﹣x+c,将点C(2,0)代入得,﹣×2+c=0,解得c=,所以,直线CP的解析式为y=﹣x+,联立,解得,所以,点P的坐标为(,),此时,CP==,综上所述,当△BPC是直角三角形时,CP的长为或4或.故答案为:或4或.18.(2016•新乡模拟)如图,在菱形ABCD中,点M、N在AC上,ME⊥AD,NF⊥AB,若NF=NM=2,ME=3,则AM=6.【解答】解:在菱形ABCD中,∠1=∠2,又∵ME⊥AD,NF⊥AB,∴∠AEM=∠AFN=90°,∴△AFN∽△AEM,∴=,即=,解得AN=4,则AM=AN+MN=6.故答案是:6.三.解答题(共10小题)19.(2016•苏州)如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.(1)证明:四边形ACDE是平行四边形;(2)若AC=8,BD=6,求△ADE的周长.【解答】(1)证明:∵四边形ABCD是菱形,∴AB∥CD,AC⊥BD,∴AE∥CD,∠AOB=90°,∵DE⊥BD,即∠EDB=90°,∴∠AOB=∠EDB,∴DE∥AC,∴四边形ACDE是平行四边形;(2)解:∵四边形ABCD是菱形,AC=8,BD=6,∴AO=4,DO=3,AD=CD=5,∵四边形ACDE是平行四边形,∴AE=CD=5,DE=AC=8,∴△ADE的周长为AD+AE+DE=5+5+8=18.20.(2016•沈阳)如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1)∠CEB=∠CBE;(2)四边形BCED是菱形.【解答】证明;(1)∵△ABC≌△ABD,∴∠ABC=∠ABD,∵CE∥BD,∴∠CEB=∠DBE,∴∠CEB=∠CBE.(2))∵△ABC≌△ABD,∴BC=BD,∵∠CEB=∠CBE,∴CE=CB,∴CE=BD∵CE∥BD,∴四边形CEDB是平行四边形,∵BC=BD,∴四边形CEDB是菱形.21.(2016•聊城)如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC 的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF是菱形.【解答】证明:∵AF∥CD,∴∠AFE=∠CDE,在△AFE和△CDE中,,∴△AEF≌△CED,∴AF=CD,∵AF∥CD,∴四边形ADCF是平行四边形,∵∠B=90°,∠ACB=30°,∴∠CAB=60°,∵AD平分∠CAB,∴∠DAC=∠DAB=30°=∠ACD,∴DA=DC,∴四边形ADCF是菱形.22.(2016•通州区一模)如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.(1)求证:四边形AECD是菱形;(2)如果点E是AB的中点,AC=4,EC=2.5,求四边形ABCD的面积.【解答】(1)证明:∵AB∥CD,CE∥AD,∴四边形AECD是平行四边形,…(1分);∵AC平分∠BAD,∴∠EAC=∠DAC,∵AB∥CD,∴∠EAC=∠ACD,∴∠DAC=∠ACD,∴AD=CD,∴四边形AECD是菱形.(2)解:∵四边形AECD是菱形,∴AE=CE,∴∠EAC=∠ACE,∵点E是AB的中点,∴AE=BE,∴∠B=∠ECB,∴∠ACE+∠ECB=90°,即∠ACB=90°;∵点E是AB的中点,EC=2.5,∴AB=2EC=5,∴BC=3.∴S△ABC=BC•AC=6.∵点E是AB的中点,四边形AECD是菱形,∴S△AEC=S△EBC=S△ACD=3.∴四边形ABCD的面积=S△AEC+S△EBC+S△ACD=9.23.(2016•哈尔滨模拟)如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,并且AF=CE.(1)求证:四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形?请回答并证明你的结论.【解答】解:(1)∵ED是BC的垂直平分线∴EB=EC,ED⊥BC,∴∠3=∠4,∵∠ACB=90°,∴FE∥AC,∴∠1=∠5,∵∠2与∠4互余,∠1与∠3互余∴∠1=∠2,∴AE=CE,又∵AF=CE,∴△ACE和△EFA都是等腰三角形,∴∠5=∠F,∴∠2=∠F,∴在△EFA和△ACE中∵,∴△EFA≌△ACE(AAS),∴∠AEC=∠EAF∴AF∥CE∴四边形ACEF是平行四边形;(2)当∠B=30°时,四边形ACEF是菱形.证明如下:∵∠B=30°,∠ACB=90°∴∠1=∠2=60°∴∠AEC=60°∴AC=EC∴平行四边形ACEF是菱形.24.(2016•金东区模拟)如图:已知菱形ABCD,∠DAB=60°,延长AB到点E,使BE=AB,以CE为直径作⊙O,交BC、BE于点G、F.(1)求证:AC⊥CE;(2)若AB=4,求图中阴影部分的面积.(结果保留根号和π)【解答】(1)证明:∵菱形ABCD,∠DAB=60°,∴∠CAB=DAB=30°,AB=BC,∠ABC=180°﹣∠DAB=120°,∴∠CBE=60°,∵BE=AB,∴BE=BC,∴△BCE是等边三角形,∴∠E=60°,∴∠ACE=180°﹣∠CAB﹣∠E=90°,即AC⊥CE;(2)解:连接OG,OF,过点O作OH⊥BE于点H,∵OF=OE=OG=OC,∠E=∠BCE=60°,∴△OCG与△OEF是等边三角形,∴∠COG=∠EOF=60°,∴∠GOF=60°,∵AB=4,∴CE=BE=4,∴EF=BF=2,∴OH=OE•sin60°=,∴BF=OF=OG=BG,∴四边形BFOG是菱形,∴S阴影=S菱形BFOG﹣S扇形OFG=2×﹣=.25.(2016•泰安模拟)如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.(1)求证:∠DCP=∠DAP;(2)如果PE=4,EF=5,求线段PC的长.【解答】(1)证明:在菱形ABCD中,AD=CD,∠BDC=∠BDA,在△APD和△CPD中,,∴△APD≌△CPD(SAS),∴∠DCP=∠DAP;(2)∵△APD≌△CPD,∴∠DAP=∠DCP,∵CD∥AB,∴∠DCF=∠DAP=∠CFB,又∵∠FPA=∠FPA,∴△APE∽△FPA.∴.∴PA2=PE•PF.∵△APD≌△CPD,∴PA=PC.∴PC2=PE•PF,∵PE=4,EF=5,∴PF=9,∴PC=6.26.(2016•黄冈模拟)如图,在菱形ABCD中,F为对角线BD上一点,点E为AB延长线上一点,DF=BE,CE=CF.求证:(1)△CFD≌△CEB;(2)∠CFE=60°.【解答】(1)证明:∵四边形ABCD是菱形,∴CD=CB.在△CFD和△CEB中,,∴△CFD≌△CEB(SSS);(2)解:∵△CFD≌△CEB,∴∠CDB=∠CBE,∠DCF=∠BCE.∵四边形ABCD是菱形,∴∠CBD=∠ABD.∵CD=CB,∴∠CDB=∠CBD,∴∠ABD=∠CBD=∠CBE=60°.∴∠DCB=60°.∵∠FCE=60°,∵CF=CE,∴∠CFE=∠CEF=60°.27.(2016•武侯区模拟)如图,在菱形ABCD中,E、F分别是AB和BC上的点,且BE=BF.(1)求证:△ADE≌△CDF;(2)若∠A=40°,∠DEF=65°,求∠DFC的度数.【解答】解:(1)∵四边形ABCD是菱形,∴∠A=∠C,AB=CB,AD=DC,∵BE=BF,∴AE=CF,在△ADE和△CDF中,∴△ADE≌△CDF;(2)∵△ADE≌△CDF,∴DE=DF,∵∠DEF=65°,∴∠EDB=∠FDB=25°,∵四边形ABCD是菱形,∴AB=AD,∵∠A=40°,∴∠ADB=70°,∴∠ADE=70°﹣25°=45°,∴∠DFC=180°﹣40°﹣45°=95°.28.(2016•泰安模拟)在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)如图1,当E是线段AC的中点时,求证:BE=EF.(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论:成立.(填“成立”或“不成立”)(3)如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.【解答】(1)证明:∵四边形ABCD是菱形,∴AB=BC,∵∠ABC=60°,∴△ABC是等边三角形,∴∠BCA=60°,∵E是线段AC的中点,∴∠CBE=∠ABE=30°,AE=CE,∵CF=AE,∴CE=CF,∴∠F=∠CEF=∠BCA=30°,∴∠CBE=∠F=30°,∴BE=EF;(2)解:结论成立;理由如下:过点E作EG∥BC交AB于点G,如图2所示:∵四边形ABCD为菱形,∴AB=BC,∠BCD=120°,AB∥CD,∴∠ACD=60°,∠DCF=∠ABC=60°,∴∠ECF=120°,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE,∠AGE=60°,∴BG=CE,∠BGE=120°=∠ECF,又∵CF=AE,∴GE=CF,在△BGE和△CEF中,,∴△BGE≌△ECF(SAS),∴BE=EF.(3)解:结论成立.证明如下:过点E作EG∥BC交AB延长线于点G,如图3所示:∵四边形ABCD为菱形,∴AB=BC,又∵∠ABC=60°,∴△ABC是等边三角形,∴AB=AC,∠ACB=60°,∴∠ECF=60°,又∵EG∥BC,∴∠AGE=∠ABC=60°,又∵∠BAC=60°,∴△AGE是等边三角形,∴AG=AE=GE,∠AGE=60°,∴BG=CE,∠AGE=∠ECF,又∵CF=AE,∴GE=CF,在△BGE和△CEF中,,∴△BGE≌△ECF(SAS),∴BE=EF.。
1.1 菱形的性质与判定 北师大版九年级数学上册同步练习(含解析)
北师大版九上1.1菱形的性质与判定同步练习一、选择题(共10题)1. 菱形不具备的性质是( )A.四条边都相等B.对角线一定相等C.是轴对称图形D.是中心对称图形2. 菱形ABCD中,∠A:∠B=1:5,若其周长为8,则菱形ABCD的高为( )B.4C.1D.2 A.123. 菱形ABCD中,AB=2,∠D=120∘,则对角线AC的长为( )A.1B.3C.2D.234. 菱形ABCD中,AC=10,BD=24,则该菱形的周长等于( )A.13B.52C.120D.2405. 如图,菱形ABCD中,E,F分别是AB,AC的中点,若EF=3,则菱形ABCD的周长是( )A.12B.16C.20D.246. 已知O为平行四边形ABCD对角线的交点,下列条件能使平行四边形ABCD成为菱形的是( )A.AB=BC B.AC=BDC.OA=OC,OB=OD D.∠A=∠B=∠C=90∘7. 如图,B,C分别是锐角∠A两边上的点,AB=AC,分别以点B,C为圆心,以AB的长为半径画弧,两弧相交于点D,连接BD,CD,则根据作图过程判定四边形ABDC 是菱形的依据是( )A.一组邻边相等的四边形是菱形B.四条边都相等的四边形是菱形C.对角线互相垂直的平行四边形是菱形D.对角线平分一组对角的四边形是菱形8. 点E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点,AC,BD交于点O,当四边形ABCD的对角线满足( )条件时,四边形EFGH是菱形.A.AC⊥BD B.AC=BDC.OA=OC,OB=OD D.OA=OB9. 平面直角坐标系中,四边形ABCD的顶点坐标分别是A(―3,0),B(0,2),C(3,0),D(0,―2),则四边形ABCD是( )A.矩形B.菱形C.正方形D.平行四边形10. 如图,四边形ABCD的对角线AC,BD互相垂直,则下列条件能判定四边形ABCD为菱形的是( )A.BA=BC B.AC,BD互相平分C.AC=BD D.AB∥CD二、填空题(共10题)11. 如图,菱形ABCD的周长是8 cm,AB的长是cm.12. 已知菱形两条对角线的长分别为4和6,则菱形的边长为.13. 已知菱形的周长为20 cm,一条对角线长为6 cm,则这个菱形的面积是cm2.14. 如图,若菱形的边长为4,∠BAD=120∘,则较短对角线AC长为.15. 如图,菱形ABCD的对角线AC,BD交于点O,E为DC的中点,若OE=3,则菱形的周长为.16. 如图,在菱形ABCD中,对角线AC与BD相交于点O,AC=8,BD=6,OE⊥AD于点E,反向延长交BC于点F,则EF的长为.17. 如图,菱形ABCD的对角线AC,BD相交于点O,已知OB=4,菱形ABCD的面积为24,则AC的长为.18. 如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②AB=AC;③BF∥CE.从中选择条件可使四边形BECF是菱形.19. 如图,在四边形ABCD中,AB≠CD,E,F,G,H分别是AB,BD,CD,AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是.20. 如图,在△ABC中,AD⊥BC于点D,点E,F分别是AB,AC边的中点,请你在△ABC中添加一个条件:,使得四边形AEDF是菱形.三、解答题(共7题)21. 【测试4】如图,在四边形ABCD中,AD∥BC,对角线BD的垂直平分线与边AD,BC分别相交于点M,N.(1) 求证:四边形BNDM是菱形;(2) 若BD=24,MN=10,求菱形BNDM的周长.22. 已知:如图,在平行四边形ABCD中,E,F分别是边AD,BC上的点,且AE=CF,直线EF分别交BA的延长线、DC的延长线于点G,H,交BD于点O.(1) 求证:△ABE≌△CDF;(2) 连接DG,若DG=BG,则四边形BECF是什么特殊四边形?请说明理由.23. 如图,△ABC≌△ABD,点E在边AB上,CE∥BD,连接DE.求证:(1) ∠CEB=∠CBE;(2) 四边形BCED是菱形.24. 如图,AC是平行四边形ABCD的对角线,∠BAC=∠DAC.(1) 求证AB=BC;(2) 若AB=2,AC=23,求平行四边形ABCD的面积.25. 在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED=∠ABC,∠ABF=∠BPF,求证:(1) △ABF≌△DAE.(2) DE=BF+EF.26. 在正方形ABCD中,对角线BD所在的直线上有两点E,F满足BE=DF,连接AE,AF,CE,CF,如图所示.(1) 求证:△ABE≌△ADF;(2) 试判断四边形AECF的形状,并说明理由.27. 如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD∥BC,AC=8,BD=6.(1) 求证:四边形ABCD是平行四边形;(2) 若AC⊥BD,求平行四边形ABCD的面积.答案一、选择题(共10题)1. 【答案】B2. 【答案】C3. 【答案】D4. 【答案】B5. 【答案】D6. 【答案】A7. 【答案】B8. 【答案】B9. 【答案】B10. 【答案】B二、填空题(共10题)11. 【答案】212. 【答案】1313. 【答案】2414. 【答案】415. 【答案】2416. 【答案】24517. 【答案】618. 【答案】②19. 【答案】AD=BC20. 【答案】如:AB=AC,答案不唯一三、解答题(共7题)21. 【答案】(1) ∵AD∥BC,∴∠DMO=∠BNO,∵MN 是对角线 BD 的垂直平分线,∴OB =OD ,MN ⊥BD ,在 △MOD 和 △NOB 中,∠DMO =∠BNO,∠MOD =∠NOB,OD =OB,∴△MOD ≌△NOB (AAS),∴OM =ON ,∵OB =OD ,∴ 四边形 BNDM 是平行四边形,∵MN ⊥BD ,∴ 四边形 BNDM 是菱形.(2) ∵ 四边形 BNDM 是菱形,BD =24,MN =10,∴BM =BN =DM =DN ,OB =12BD =12,OM =12MN =5,在 Rt △BOM 中,由勾股定理得:BM =OM 2+OB 2=52+122=13, ∴ 菱形 BNDM 的周长 =4BM =4×13=52.22. 【答案】(1) ∵ 四边形 ABCD 是平行四边形,∴AB =CD ,∠BAE =∠DCF ,在 △ABE 和 △CDF 中,AB =CD,∠BAE =∠DCF,AE =CF,∴△ABE ≌△CDF (SAS);(2) 四边形 BEDF 是菱形;理由如下:如图所示:∵ 四边形 ABCD 是平行四边形,∴AD ∥BC ,AD =BC ,∵AE =CF ,∴DE =BF ,∴ 四边形 BEDF 是平行四边形,∴OB =OD ,∵DG =BG ,∴EF ⊥BD ,∴ 四边形 BEDF 是菱形.23. 【答案】(1) ∵ △ABC ≌△ABD ,∴ ∠ABC =∠ABD .∵ CE ∥BD ,∴ ∠CEB =∠DBE ,∴ ∠CEB =∠CBE .(2) ∵ △ABC ≌△ABD ,∴ BC =BD .∵ ∠CEB =∠CBE ,∴ CE =CB ,∴ CE =BD .∵ CE ∥BD ,∴ 四边形 CEDB 是平行四边形.∵ BC =BD ,∴ 四边形 CEDB 是菱形.24. 【答案】(1) 因为四边形 ABCD 是平行四边形,所以 AD ∥BC ,所以 ∠DAC =∠BCA ,因为 ∠BAC =∠DAC ,所以 ∠BAC =∠BCA ,所以 AB =BC .(2) 连接 BD 交 AC 于点 O ,因为四边形 ABCD 是平行四边形,AB =BC ,所以四边形 ABCD 是菱形,所以 AC ⊥BD ,OA =OC =12AC =3,OB =OD =12BD ,所以 OB =AB 2―OA 2=22―(3)2=1,所以 BD =2OB =2,所以 S 平行四边形ABCD =12AC ⋅BD =12×23×2=23.25. 【答案】(1) ∵ 四边形 ABCD 是菱形,∴AB =AD ,AD ∥BC ,∴∠BOA =∠DAE ,∵∠ABC =∠AED ,∴∠BAF =∠ADE ,∵∠ABF =∠BPF ,∠BPA =∠DAE ,∴∠ABF =∠DAE ,∵AB =DA ,∴△ABF ≌△DAE (ASA).(2) ∵△ABF ≌△DAE ,∴AE =BF ,DE =AF ,∵AF =AE +EF =BF +EF ,∴DE =BF +EF .26. 【答案】(1) ∵ 正方形 ABCD ,∴AB =AD ,∠ABE =∠ADF =135∘,在 △ABE 和 △ADF 中,AB =AD,∠ABE =∠ADF,BE =DF,∴△ABE ≌△ADF (SAS).(2) 四边形 AECF 为菱形.证明:连接 AC ,∵△ABE ≌△ADF ,∴AE =AF ,∵正方形ABCD,∴EF垂直平分AC,∴EA=EC,FA=FC,∴EA=EC=FA=FC,∴四边形AECF是菱形.27. 【答案】(1) ∵O是AC的中点,∴OA=OC,∵AD∥BC,∴∠ADO=∠CBO.在△AOD和△COB中,∠ADO=∠CBO,∠AOD=∠COB,OA=OC,∴△AOD≌△COB,∴OD=OB,∴四边形ABCD是平行四边形.(2) ∵四边形ABCD是平行四边形,AC⊥BD,∴四边形ABCD是菱形,∴平行四边形ABCD的面积=1AC⋅BD=24.2。
北师大九上数学菱形的性质和判定课堂讲义及练习(含答案)
1.1菱形的性质和判定【菱形的性质】1.菱形的定义有一组邻边相等的平行四边形叫做菱形.符号语言:∵四边形ABCD是平行四边形,且AB=BC,∴四边形ABCD是菱形 .温馨提示:①菱形必须满足两个条件:一是平行四边形;二是一组邻边相等;②菱形是特殊的平行四边形,即当一个平行四边形满足一组邻边相等时,该平行四边形是菱形,不能错误地认为有一组邻边相等的四边形就是菱形;③菱形的定义既提供了菱形的基本性质,也提供了基本判定方法。
2.菱形的性质(1)菱形具有平行四边形的所有性质.(2)菱形的四条边都相等.(3)菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.(4)菱形是轴对称图形,它有两条对称轴,对角线所在直线就是它的对称轴.菱形又是中心对称图形,对角线的交点为对称中心.菱形中相等的线段:AB = CD = AD = BC.OA = OC ,OB = OD.菱形中相等的角:∠AOB = ∠DOC = ∠AOD = ∠BOC = 90°.∠ADC=∠ABC.∠DAB=∠DCB∠1 = ∠2 = ∠3 = ∠4,∠5 = ∠6 = ∠7 = ∠8.菱形中的全等三角形:全等的等腰三角形有:,全等的直角三角形有:点拨:有关菱形问题可转化为直角三角形或等腰三角形的问题来解决(转化思想).温馨提示:①菱形具有平行四边形的一切性质;②“菱形的对角线互相垂直”这一性质可用来证明两条线段互相垂直,“菱形的每一条对角线平分一组对角”这一性质可用来证明角相等;③菱形的两条对角线分菱形为四个全等的直角三角形。
1、下列四边形中不一定为菱形的是()A. 对角线相等的平行四边形B. 对角线平分一组对角的平行四边形C. 对角线互相垂直的平行四边形D. 用两个全等的等边三角形拼成的四边形2.如图,菱形的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是。
3.菱形ABCD的两条对角线长分别为6和8,则它的周长和面积分别为()A. 28、48B.20、24C.28、24D.20、484.如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于()A. 5B. 10C. 15D. 205.如图,已知菱形ABCD的周长为16,面积为,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )A. 2B. 2C. 4D. 4第2题第3题第4题第5题6.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF.7.如图,已知E、F分别是▱ABCD的边BC、AD上的点,且BE=DF .(1)求证:四边形AECF是平行四边形;(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.8.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.(1)求证:AE=CF;(2)若AB=2,点E是AB中点,求EF的长.【菱形的判定】1. 菱形的判定定理(1)定义法:有一组邻边相等的平行四边形是菱形.(2)对角线互相垂直的平行四边形是菱形 .(3)四边相等的四边形是菱形 .①证明一个四边形是菱形,一般情况下,先证明它是一个平行四边形,然后要么证明“一组邻边相等”,要么证明“对角线互相垂直”.若要直接证明一个四边形是菱形,只要证明“四条边相等”即可;②对角线互相垂直平分的四边形是菱形;③对角线平分一个内角的平行四边形是菱形。
菱形的性质和判定典型解答题综合训练(含解析)印刷版
菱形的性质和判定解答题综合训练一.解答题(共20小题)1.如图,AC=8,分别以A、C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D.依次连接A、B、C、D,连接BD交AC于点O.(1)判断四边形ABCD的形状并说明理由;(2)求BD的长.2.(1)将两条宽度一样的矩形纸条如图交叉,请判断重叠部分是一个什么图形?并证明你的结论.(2)若两张矩形纸条的长度均为8,宽度均为2,请求出重叠部分的图形的周长的最大值.3.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.4.在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED =∠ABC,∠ABF=∠BPF.求证:(1)△ABF≌△DAE;(2)DE=BF+EF.5.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.(1)求证:四边形ABCD是菱形;(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.6.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.(1)求证:AE=BF;(2)若点E恰好是AD的中点,AB=2,求BD的值.7.同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).(1)证明:四边形AECF是菱形;(2)求菱形AECF的面积.8.如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.(1)求证:△ABC≌△DEF;(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.9.如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:(1)∠BOD=∠C;(2)四边形OBCD是菱形.10.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.(1)求证:△APD≌△BQC;(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.11.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.(1)求证:四边形EFGH是菱形;(2)若EF=4,∠HEF=60°,求EG的长.12.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.(1)求证:△ADO≌△CBO.(2)求证:四边形ABCD是菱形.(3)若DE=AB=2,求菱形ABCD的面积.13.已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.(1)求证:四边形GEHF是平行四边形;(2)当平行四边形ABCD满足条件时,四边形GEHF是菱形;(3)若BD=2AB,探究四边形GEHF的形状,并说明理由.14.如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.(1)求证:△FCE≌△BOE;(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.15.如图,▱ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.(1)求证:四边形ABCD是菱形;(2)若AD=2,当四边形ABCD是形时,四边形AOBE的面积取得最大值,说明理由,并求出四边形AOBE面积的最大值.16.如图,在四边形ABCD和四边形BFGH都是菱形,且A,B,F三点共线.DE是菱形ABCD的高,连接DG,点K是DG的中点,连接CK,KH.(1)若AE=3,BE=5,求菱形ABCD的面积;(2)求证:CK⊥KH.17.如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.18.如图,在▱ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作▱ECFG.(1)证明▱ECFG是菱形;(2)若∠ABC=120°,连结BD、CG,求∠BDG的度数;(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.19.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.(1)证明平行四边形ECFG是菱形;(2)若∠ABC=120°,连结BG、CG、DG,①求证:△DGC≌△BGE;②求∠BDG的度数;(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,求DM的长.20.【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC 于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是.【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2,则△ABD的面积是.菱形的性质和判定解答题综合训练参考答案与试题解析一.解答题(共20小题)1.如图,AC=8,分别以A、C为圆心,以长度5为半径作弧,两条弧分别相交于点B和D.依次连接A、B、C、D,连接BD交AC于点O.(1)判断四边形ABCD的形状并说明理由;(2)求BD的长.【分析】(1)利用作法得到四边相等,从而可判断四边形ABCD为菱形;(2)根据菱形的性质得OA=OC=4,OB=OD,AC⊥BD,然后利用勾股定理计算出OB,从而得到BD的长.【解答】解:(1)四边形ABCD为菱形;由作法得AB=AD=CB=CD=5,所以四边形ABCD为菱形;(2)∵四边形ABCD为菱形,∴OA=OC=4,OB=OD,AC⊥BD,在Rt△AOB中,OB==3,∴BD=2OB=6.2.(1)将两条宽度一样的矩形纸条如图交叉,请判断重叠部分是一个什么图形?并证明你的结论.(2)若两张矩形纸条的长度均为8,宽度均为2,请求出重叠部分的图形的周长的最大值.【分析】(1)首先可判断重叠部分为平行四边形,且两条纸条宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形;(2)画出图形,设菱形的边长为x,根据勾股定理求出周长即可.【解答】解:(1)过点A作AE⊥BC于E,AF⊥CD于F,∵两条纸条宽度相同(对边平行),∴AB∥CD,AD∥BC,AE=AF,∴四边形ABCD是平行四边形,∵S▱ABCD=BC•AE=CD•AF,AE=AF,∴BC=CD,∴四边形ABCD是菱形.(2)当两张纸条如图所示放置时,菱形周长最大,设这时菱形的边长为xcm,在Rt△ABC中,由勾股定理:x2=(8﹣x)2+22,解得:x=,∴4x=17,即菱形的最大周长为17cm.3.如图,在▱ABCD中,E,F分别是AD,BC上的点,且DE=BF,AC⊥EF.求证:四边形AECF是菱形.【分析】根据对角线互相垂直的平行四边形是菱形即可证明;【解答】证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∵DE=BF,∴AE=CF,∵AE∥CF,∴四边形AECF是平行四边形,∵AC⊥EF,∴四边形AECF是菱形.4.在菱形ABCD中,点P是BC边上一点,连接AP,点E,F是AP上的两点,连接DE,BF,使得∠AED =∠ABC,∠ABF=∠BPF.求证:(1)△ABF≌△DAE;(2)DE=BF+EF.【分析】(1)根据菱形的性质得到AB=AD,AD∥BC,由平行线的性质得到∠BOA=∠DAE,等量代换得到∠BAF=∠ADE,求得∠ABF=∠DAE,根据全等三角形的判定定理即可得到结论;(2)根据全等三角形的性质得到AE=BF,DE=AF,根据线段的和差即可得到结论.【解答】证明:(1)∵四边形ABCD是菱形,∴AB=AD,AD∥BC,∴∠BPA=∠DAE,∵∠ABC=∠AED,∴∠BAF=∠ADE,∵∠ABF=∠BPF,∠BPA=∠DAE,∴∠ABF=∠DAE,∵AB=DA,∴△ABF≌△DAE(ASA);(2)∵△ABF≌△DAE,∴AE=BF,DE=AF,∵AF=AE+EF=BF+EF,∴DE=BF+EF.5.如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.(1)求证:四边形ABCD是菱形;(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.【分析】(1)根据平行线的性质得到∠ADB=∠CBD,根据角平分线定义得到∠ABD=∠CBD,等量代换得到∠ADB=∠ABD,根据等腰三角形的判定定理得到AD=AB,根据菱形的判定即可得到结论;(2)由垂直的定义得到∠BDE=90°,等量代换得到∠CDE=∠E,根据等腰三角形的判定得到CD=CE=BC,根据勾股定理得到DE==6,于是得到结论.【解答】(1)证明:∵AD∥BC,∴∠ADB=∠CBD,∵BD平分∠ABC,∴∠ABD=∠CBD,∴∠ADB=∠ABD,∴AD=AB,∵BA=BC,∴AD=BC,∴四边形ABCD是平行四边形,∵BA=BC,∴四边形ABCD是菱形;(2)解:∵DE⊥BD,∴∠BDE=90°,∴∠DBC+∠E=∠BDC+∠CDE=90°,∵CB=CD,∴∠DBC=∠BDC,∴∠CDE=∠E,∴CD=CE=BC,∴BE=2BC=10,∵BD=8,∴DE==6,∵四边形ABCD是菱形,∴AD=AB=BC=5,∴四边形ABED的周长=AD+AB+BE+DE=26.6.如图,菱形ABCD中,作BE⊥AD、CF⊥AB,分别交AD、AB的延长线于点E、F.(1)求证:AE=BF;(2)若点E恰好是AD的中点,AB=2,求BD的值.【分析】(1)由“AAS”可证△AEB≌△BFC,可得AE=BF;(2)由线段垂直平分线的性质可得BD=AB=2.【解答】(1)证明:四边形ABCD是菱形,∴AB=BC,AD∥BC,∴∠A=∠CBF∵BE⊥AD、CF⊥AB,∴∠AEB=∠BFC=90°,∴△AEB≌△BFC(AAS)∴AE=BF(2)∵E是AD中点,且BE⊥AD,∴直线BE为AD的垂直平分线,∴BD=AB=27.同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).(1)证明:四边形AECF是菱形;(2)求菱形AECF的面积.【分析】(1)先证明四边形AECF是平行四边形,再证明AF=CE即可.=S矩形ABCD﹣S△ABE﹣S△DFC求出面积(2)在RT△ABE中利用勾股定理求出BE、AE,再根据S菱形AECF即可.【解答】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠FAC=∠ACE,∵∠CAE=∠DAC,∠ACF=∠ACB,∴∠EAC=∠ACF,∴AE∥CF,∵AF∥EC,∴四边形AECF是平行四边形,∵∠FAC=∠FCA,∴AF=CF,∴四边形AECF是菱形.(2)解:∵四边形AECF是菱形,∴AE=EC=CF=AF,设菱形的边长为a,在RT△ABE中,∵∠B=90°,AB=12,AE=a,BE=18﹣a,∴a2=122+(18﹣a)2,∴a=13,=S矩形ABCD﹣S△ABE﹣S△DFC=216﹣30﹣30=156cm2.∴BE=DF=5,AF=EC=13,∴S菱形AECF8.如图,已知A、F、C、D四点在同一条直线上,AF=CD,AB∥DE,且AB=DE.(1)求证:△ABC≌△DEF;(2)若EF=3,DE=4,∠DEF=90°,请直接写出使四边形EFBC为菱形时AF的长度.【分析】(1)根据SAS即可证明.(2)解直角三角形求出DF、OE、OF即可解决问题;【解答】(1)证明:∵AB∥DE,∴∠A=∠D,∵AF=CD,∴AF+FC=CD+FC,即AC=DF,∵AB=DE,∴△ABC≌△DEF.(2)如图,连接EB交AD于O.在Rt△EFD中,∵∠DEF=90°,EF=3,DE=4,∴DF==5,∵四边形EFBC是菱形,∴BE⊥CF,∴EO==,∴OF=OC==,∴CF=,∴AF=CD=DF﹣FC=5﹣=.9.如图,在四边形ABCD中,BC=CD,∠C=2∠BAD.O是四边形ABCD内一点,且OA=OB=OD.求证:(1)∠BOD=∠C;(2)四边形OBCD是菱形.【分析】(1)延长AO到E,利用等边对等角和角之间关系解答即可;(2)连接OC,根据全等三角形的判定和性质以及菱形的判定解答即可.【解答】证明:(1)延长OA到E,∵OA=OB,∴∠ABO=∠BAO,又∠BOE=∠ABO+∠BAO,∴∠BOE=2∠BAO,同理∠DOE=2∠DAO,∴∠BOE+∠DOE=2∠BAO+2∠DAO=2(∠BAO+∠DAO)即∠BOD=2∠BAD,又∠C=2∠BAD,∴∠BOD=∠C;(2)连接OC,∵BC=CD,OA=OB=OD,OC是公共边,∵OB=OD,CB=CD,OC=OC,∴△OBC≌△ODC,∴∠BOC=∠DOC,∠BCO=∠DCO,∵∠BOD=∠BOC+∠DOC,∠BCD=∠BCO+∠DCO,∴∠BOC=∠BOD,∠BCO=∠BCD,又∠BOD=∠BCD,∴∠BOC=∠BCO,∴BO=BC,又OB=OD,BC=CD,∴OB=BC=CD=DO,∴四边形OBCD是菱形.10.如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.(1)求证:△APD≌△BQC;(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.【分析】(1)只要证明AD=BC,∠ADP=∠BCQ,DP=CQ即可解决问题;(2)首先证明四边形ABQP是平行四边形,再证明AB=AP即可解决问题;【解答】(1)证明:∵四边形ABCD是平行四边形,∴AD=BC,AD∥BC,∴∠ADB=∠DBC,∵CQ∥DB,∴∠BCQ=∠DBC,∴∠ADB=∠BCQ∵DP=CQ,∴△ADP≌△BCQ.(2)证明:∵CQ∥DB,且CQ=DP,∴四边形CQPD是平行四边形,∴CD=PQ,CD∥PQ,∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴AB=PQ,AB∥PQ,∴四边形ABQP是平行四边形,∵△ADP≌△BCQ,∴∠APD=∠BQC,∵∠APD+∠APB=180°,∠ABP+∠BQC=180°,∴∠ABP=∠APB,∴AB=AP,∴四边形ABQP是菱形.11.如图,在平行四边形ABCD中,点E,F,G,H分别在边AB,BC,CD,DA上,AE=CG,AH=CF,且EG平分∠HEF.(1)求证:四边形EFGH是菱形;(2)若EF=4,∠HEF=60°,求EG的长.【分析】(1)首先证明四边形EFGH是平行四边形,那么EF∥GH,那么∠HGE=∠FEG,而EG是角平分线,易得∠HEG=∠FEG,根据等量代换可得∠HEG=∠HGE,从而有HE=HG,易证四边形EFGH 是菱形;(2)连接FH交EG于O,在Rt△EOF中,解直角三角形即可解决问题;【解答】(1)证明:如图,∵四边形ABCD是平行四边形,∴∠A=∠C,在△AEH与△CGF中,,∴△AEH≌△CGF(SAS);∴EH=FG∵四边形ABCD是平行四边形,∴AB=CD,AD=BC,∠B=∠D.又∵AE=CG,AH=CF,∴BE=DG,BF=DH,在△BEF与△DGH中,,△BEF≌△DGH(SAS),∴EF=GH.∴四边形EFGH是平行四边形,∴HG∥EF,∴∠HGE=∠FEG,∵EG平分∠HEF,∴∠HEG=∠FEG,∴∠HEG=∠HGE,∴HE=HG,∴四边形EFGH是菱形.(2)解:连接HF交EG于O.∵四边形EFGH是菱形,∴EG⊥FH,∠FEO=∠HEF=30°,∵EF=4,∴OE=EF•cos30°=2,∴EG=2EO=4.12.如图,AM∥BN,C是BN上一点,BD平分∠ABN且过AC的中点O,交AM于点D,DE⊥BD,交BN于点E.(1)求证:△ADO≌△CBO.(2)求证:四边形ABCD是菱形.(3)若DE=AB=2,求菱形ABCD的面积.【分析】(1)由ASA即可得出结论;(2)先证明四边形ABCD是平行四边形,再证明AD=AB,即可得出结论;(3)由菱形的性质得出AC⊥BD,证明四边形ACED是平行四边形,得出AC=DE=2,AD=EC,由菱形的性质得出EC=CB=AB=2,得出EB=4,由勾股定理得BD═,即可得出答案.【解答】解:(1)证明:∵点O是AC的中点,∴AO=CO,∵AM∥BN,∴∠DAC=∠ACB,在△AOD和△COB中,,∴△ADO≌△CBO(ASA);(2)证明:由(1)得△ADO≌△CBO,∴AD=CB,又∵AM∥BN,∴四边形ABCD是平行四边形,∵AM∥BN,∴∠ADB=∠CBD,∵BD平分∠ABN,∴∠ABD=∠CBD,∴∠ABD=∠ADB,∴AD=AB,∴平行四边形ABCD是菱形;(3)解:由(2)得四边形ABCD是菱形,∴AC⊥BD,AD=CB,又DE⊥BD,∴AC∥DE,∵AM∥BN,∴四边形ACED是平行四边形,∴AC=DE=2,AD=EC,∴EC=CB,∵四边形ABCD是菱形,∴EC=CB=AB=2,∴EB=4,在Rt△DEB中,由勾股定理得BD==,∴.13.已知:如图,在平行四边形ABCD中,G、H分别是AD、BC的中点,E、O、F分别是对角线BD上的四等分点,顺次连接G、E、H、F.(1)求证:四边形GEHF是平行四边形;(2)当平行四边形ABCD满足AB⊥BD条件时,四边形GEHF是菱形;(3)若BD=2AB,探究四边形GEHF的形状,并说明理由.【分析】(1)连接AC,由平行四边形的性质和已知条件得出E、F分别为OB、OD的中点,证出GF为△AOD的中位线,由三角形中位线定理得出GF∥OA,GF=OA,同理:EH∥OC,EH=OC,得出EH=GF,EH∥GF,即可得出结论;(2)连接GH,证出四边形ABHG是平行四边形,再证明GH⊥EF,即可得出四边形GEHF是菱形;(3)由(2)得:四边形GEHF是平行四边形,得出GH=AB,证出GH=EF,即可得出四边形GEHF 是矩形.【解答】(1)证明:连接AC,如图1所示:∵四边形ABCD是平行四边形,∴OA=OC,OB=OD,∴BD的中点在AC上,∵E、O、F分别是对角线BD上的四等分点,∴E、F分别为OB、OD的中点,∵G是AD的中点,∴GF为△AOD的中位线,∴GF∥OA,GF=OA,同理:EH∥OC,EH=OC,∴EH=GF,EH∥GF,∴四边形GEHF是平行四边形;(2)解:当▱ABCD满足AB⊥BD条件时,四边形GEHF是菱形;理由如下:连接GH,如图2所示:则AG=BH,AG∥BH,∴四边形ABHG是平行四边形,∴AB∥GH,∵AB⊥BD,∴GH⊥BD,∴GH⊥EF,∴四边形GEHF是菱形;故答案为:AB⊥BD;(3)解:四边形GEHF是矩形;理由如下:由(2)得:四边形GEHF是平行四边形,∴GH=AB,∵BD=2AB,∴AB=BD=EF,∴GH=EF,∴四边形GEHF是矩形.14.如图,平行四边形ABCD的对角线AC、BD交于点O,分别过点C、D作CF∥BD,DF∥AC,连接BF交AC于点E.(1)求证:△FCE≌△BOE;(2)当△ADC满足什么条件时,四边形OCFD为菱形?请说明理由.【分析】(1)证明四边形OCFD是平行四边形,得出OD=CF,证出OB=CF,即可得出△FCE≌△BOE (AAS);(2)证出四边形ABCD是矩形,由矩形的性质得出OC=OD,即可得出四边形OCFD为菱形.【解答】(1)证明:∵CF∥BD,DF∥AC,∴四边形OCFD是平行四边形,∠OBE=∠CFE,∴OD=CF,∵四边形ABCD是平行四边形,∴OB=OD,∴OB=CF,在△FCE和△BOE中,,∴△FCE≌△BOE(AAS);(2)解:当△ADC满足∠ADC=90°时,四边形OCFD为菱形;理由如下:∵∠ADC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,∴OA=OC,OB=OD,AC=BD,∴OC=OD,∴四边形OCFD为菱形.15.如图,▱ABCD的对角线AC,BD相交于点O,且AE∥BD,BE∥AC,OE=CD.(1)求证:四边形ABCD是菱形;(2)若AD=2,当四边形ABCD是正方形时,四边形AOBE的面积取得最大值,说明理由,并求出四边形AOBE面积的最大值.【分析】(1)根据平行四边形的性质和菱形的判定证明即可;(2)根据正方形的判定和性质解答即可.【解答】(1)证明:∵AE∥BD,BE∥AC,∴四边形AEBO是平行四边形,∵四边形ABCD是平行四边形,∴DC=AB.∵OE=CD,∴OE=AB.∴平行四边形AEBO是矩形,∴∠BOA=90°.∴AC⊥BD.∴平行四边形ABCD是菱形;(2)当AD=2时,四边形ABCD的形状是正方形,AB=AD=2,OE=AB=2,即四边形AOBE的面积取得最大值是2.故答案为:正方.16.如图,在四边形ABCD和四边形BFGH都是菱形,且A,B,F三点共线.DE是菱形ABCD的高,连接DG,点K是DG的中点,连接CK,KH.(1)若AE=3,BE=5,求菱形ABCD的面积;(2)求证:CK⊥KH.【分析】(1)利用勾股定理求出DE,再根据菱形的面积公式计算即可.(2)延长HK交CD于M.证明△DMK≌△GHK(ASA),推出KM=KH,DM=HG,利用等腰三角形的三线合一的性质解决问题即可.【解答】(1)解:∵四边形ABCD是菱形,∴AB=CD=AE+EB=3+5=8,∵DE⊥AB,∴∠DEA=90°,∴DE===,∴菱形ABCD的面积=AB•DE=8.(2)证明:延长HK交CD于M.∵四边形ABCD和四边形BFGH都是菱形,∴CD∥AB∥GH,CD=CB,BH=GH,∴∠MDK=∠HGK,∵∠MKD=∠HKG,DK=KG,∴△DMK≌△GHK(ASA),∴KM=KH,DM=HG,∴DM=BH,∵CD=CB,∴CM=CH,∵KM=KH,∴CK⊥KH.17.如图,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.(1)求证:△ECG≌△GHD;(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论.(3)若∠B=30°,判定四边形AEGF是否为菱形,并说明理由.【分析】(1)依据条件得出∠C=∠DHG=90°,∠CGE=∠GED,依据F是AD的中点,FG∥AE,即可得到FG是线段ED的垂直平分线,进而得到GE=GD,∠CGE=∠GDE,利用AAS即可判定△ECG ≌△GHD;(注:本小题也可以通过证明四边形ECGH为矩形得出结论)(2)过点G作GP⊥AB于P,判定△CAG≌△PAG,可得AC=AP,由(1)可得EG=DG,即可得到Rt△ECG≌Rt△DPG,依据EC=PD,即可得出AD=AP+PD=AC+EC;(3)依据∠B=30°,可得∠ADE=30°,进而得到AE=AD,故AE=AF=FG,再根据四边形AEGF 是平行四边形,即可得到四边形AEGF是菱形.【解答】解:(1)∵AF=FG,∴∠FAG=∠FGA,∵AG平分∠CAB,∴∠CAG=∠FAG,∴∠CAG=∠FGA,∴AC∥FG,∵DE⊥AC,∴FG⊥DE,∵FG⊥BC,∴DE∥BC,∴AC⊥BC,∴∠C=∠DHG=90°,∠CGE=∠GED,∵F是AD的中点,FG∥AE,∴H是ED的中点,∴FG是线段ED的垂直平分线,∴GE=GD,∠GDE=∠GED,∴∠CGE=∠GDE,∴△ECG≌△GHD;(2)证明:过点G作GP⊥AB于P,∴GC=GP,而AG=AG,∴△CAG≌△PAG,∴AC=AP,由(1)可得EG=DG,∴Rt△ECG≌Rt△DPG,∴EC=PD,∴AD=AP+PD=AC+EC;(3)四边形AEGF是菱形,证明:∵∠B=30°,∴∠ADE=30°,∴AE=AD,∴AE=AF=FG,由(1)得AE∥FG,∴四边形AEGF是平行四边形,∴四边形AEGF是菱形.18.如图,在▱ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作▱ECFG.(1)证明▱ECFG是菱形;(2)若∠ABC=120°,连结BD、CG,求∠BDG的度数;(3)若∠ABC=90°,AB=6,AD=8,M是EF的中点,求DM的长.【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.【解答】解:(1)证明:,∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形;(2)∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,AD∥BC,∵∠ABC=120°,∴∠BCD=60°,∠BCF=120°由(1)知,四边形CEGF是菱形,∴CE=GE,∠BCG=∠BCF=60°,∴CG=GE=CE,∠DCG=120°,∵EG∥DF,∴∠BEG=120°=∠DCG,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD,∴△BEG≌△DCG(SAS),∴BG=DG,∠BGE=∠DGC,∴∠BGD=∠CGE,∵CG=GE=CE,∴△CEG是等边三角形,∴∠CGE=60°,∴∠BGD=60°,∵BG=DG,∴△BDG是等边三角形,∴∠BDG=60°;(3)如图2中,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=6,AD=8,∴BD=10,∴DM=BD=5.19.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于F,以EC、CF为邻边作平行四边形ECFG.(1)证明平行四边形ECFG是菱形;(2)若∠ABC=120°,连结BG、CG、DG,①求证:△DGC≌△BGE;②求∠BDG的度数;(3)若∠ABC=90°,AB=8,AD=14,M是EF的中点,求DM的长.【分析】(1)平行四边形的性质可得AD∥BC,AB∥CD,再根据平行线的性质证明∠CEF=∠CFE,根据等角对等边可得CE=CF,再有条件四边形ECFG是平行四边形,可得四边形ECFG为菱形,即可解决问题;(2)先判断出∠BEG=120°=∠DCG,再判断出AB=BE,进而得出BE=CD,即可判断出△BEG≌△DCG(SAS),再判断出∠CGE=60°,进而得出△BDG是等边三角形,即可得出结论;(3)首先证明四边形ECFG为正方形,再证明△BME≌△DMC可得DM=BM,∠DMC=∠BME,再根据∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°可得到△BDM是等腰直角三角形,由等腰直角三角形的性质即可得到结论.【解答】解:(1)证明:∵AF平分∠BAD,∴∠BAF=∠DAF,∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,∴∠DAF=∠CEF,∠BAF=∠CFE,∴∠CEF=∠CFE,∴CE=CF,又∵四边形ECFG是平行四边形,∴四边形ECFG为菱形;(2)①∵四边形ABCD是平行四边形,∴AB∥DC,AB=DC,AD∥BC,∵∠ABC=120°,∴∠BCD=60°,∠BCF=120°由(1)知,四边形CEGF是菱形,∴CE=GE,∠BCG=∠BCF=60°,∴CG=GE=CE,∠DCG=120°,∵EG∥DF,∴∠BEG=120°=∠DCG,∵AE是∠BAD的平分线,∴∠DAE=∠BAE,∵AD∥BC,∴∠DAE=∠AEB,∴∠BAE=∠AEB,∴AB=BE,∴BE=CD,∴△DGC≌△BGE(SAS);②∵△DGC≌△BGE,∴BG=DG,∠BGE=∠DGC,∴∠BGD=∠CGE,∵CG=GE=CE,∴△CEG是等边三角形,∴∠CGE=60°,∴∠BGD=60°,∵BG=DG,∴△BDG是等边三角形,∴∠BDG=60°;(3)如图2中,连接BM,MC,∵∠ABC=90°,四边形ABCD是平行四边形,∴四边形ABCD是矩形,又由(1)可知四边形ECFG为菱形,∠ECF=90°,∴四边形ECFG为正方形.∵∠BAF=∠DAF,∴BE=AB=DC,∵M为EF中点,∴∠CEM=∠ECM=45°,∴∠BEM=∠DCM=135°,在△BME和△DMC中,∵,∴△BME≌△DMC(SAS),∴MB=MD,∠DMC=∠BME.∴∠BMD=∠BME+∠EMD=∠DMC+∠EMD=90°,∴△BMD是等腰直角三角形.∵AB=8,AD=14,∴BD=2,∴DM=BD=.20.【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC 于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是4.【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2,则△ABD的面积是6.【分析】猜想:首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS定理证明△AEO≌△CFO,再根据全等三角形的性质可得结论;探究:根据菱形的性质得到AD∥BC,AO=CO=AC=2.5,BO=BD=5,根据全等三角形的判定定理得到△AOE≌△COF,由于AC⊥BD,于是得到结果;应用:延长AC到E使CE=AC=3,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到DE=,即可得到结论.【解答】解:猜想:∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO,在△AOE与△COF中,,∴△AEO≌△CFO(AAS),=▱ABCD的面积=4;故答案为:4;∴四边形CDEF的面积=S△ACD探究:∵四边形ABCD是菱形,∴AD∥BC,AO=CO=AC=2.5,BO=BD=5,∠AOD=90°,∴AB=,∠OAE=∠OCF,∠OEA=∠OFC,在△AOE与△COF中,,∴△AOE≌△COF(AAS),=S△ABC=AC•BO=×5×5=.∵AC⊥BD,∴S四边形ABFE应用:延长AC到E使CE=AC=3,在△ABC与△CDE中,,∴△ABC≌△CDE(SAS),∴∠E=∠BAC=90°,∴DE=,=S△ADE=AE•DE=×6×2=6.故答案为:6∴S△ABD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
完整版)菱形的性质和判定练习题1.这个菱形的高为9cm。
2.较短对角线长为10cm。
3.边长为5cm。
4.各角分别为72°和108°。
5.添加的条件可以是AB=AD或BC=CD。
6.错误的说法是A,即两组对边分别平行。
7.对角线互相垂直。
8.菱形。
9.不正确的说法是B,即菱形的对角线平分各内角。
10.周长为40cm。
11.互相垂直且不平分。
12.AB长为8cm。
13.CD的长为4.14.对角线BD的长为2.15.边长为5.16.OH的长为7.17.若菱形的周长为20cm,则它的边长为4cm。
18.在菱形ABCD中,由对角线AC和BD相交于点O可知,菱形的对角线相等,即AC=BD。
又已知BD=6,则AC=6.设菱形ABCD的边长为a,则2a=20,即a=10.由菱形对角线的长度公式可得。
$AC=\sqrt{a^2+a^2}=a\sqrt{2}$,代入AC=6可得a=6/$\sqrt{2}$,因此菱形ABCD的面积为36.19.在菱形ABCD中,由$\angle ADC=120^\circ$可知,$\angle ADB=60^\circ$。
设$\angle ABD=\theta$,则$\angle ADB=120^\circ-\theta$。
由余弦定理可得,$BD^2=15^2+15^2-2\times15\times15\times\cos\theta$,化简可得$\cos\theta=1/2$,因此$\sin\theta=\sqrt{3}/2$。
由正弦定理可得,$BD/\sin\theta=2a$,其中a为菱形的边长。
又已知BD=15,代入可得$a=15\sqrt{3}/4$。
设B、D两点之间的距离为h,则$h=\sqrt{(15\sqrt{3}/4)^2-(15/2)^2}=15\sqrt{3}/4$,因此选项D 正确。
20.设菱形的较长对角线为2x,较短对角线为x,则菱形的面积为$x^2$。
由勾股定理可得,$x^2+(x/2)^2=3^2$,解得$x=2\sqrt{2}$,因此菱形的周长为8,选项A正确。
21.设菱形的邻角分别为$\alpha$和$2\alpha$,则菱形的周长为$4a=8$,菱形的高为$h=1$,由菱形的面积公式可得,$ah=15\sqrt{3}/4$。
由正弦定理可得,$a/\sin\alpha=2h$,代入可得$\sin\alpha=15\sqrt{3}/32$,因此$\sin2\alpha=2\sin\alpha\cos\alpha=15\sqrt{3}/32$,即$\cos\alpha=8/17$,$\sin\alpha=15\sqrt{3}/17$。
因此,$\tan\alpha=\sqrt{3}/2$,$\tan2\alpha=3\sqrt{3}/5$,即邻角之比为3:1,选项A正确。
22.由对角线的性质可知,$\triangle ABD$和$\triangle ABC$共边且共顶点,因此它们的周长和面积相等,选项A和B都正确。
菱形的周长等于4倍的边长,也等于两条对角线的长度之和,因此选项C正确。
菱形的面积等于两条对角线长度之积的一半,因此选项D正确。
23.由对角线的性质可知,$\angle ABC=\angle ABD$,又由菱形的性质可知,$\angle ABD=\angle BDC$。
因此,$\angle ABC=\angle BDC$,且它们之和为180°,因此$\angle ABC=\angle BDC=65$°,选项C正确。
24.设菱形的较长对角线为4x,较短对角线为3x,则菱形的周长为$2(4x+3x)=14x$。
由周长公式可得,$14x=20$,因此$x=10/7$,菱形的面积为$4x\times 3x=12x^2=1200/49$,约等于24,选项B正确。
25.设AE的长度为h,则$\triangle AEC$和$\triangle AEB$都是等腰直角三角形,因此$EC=EB=h/\sqrt{2}$,$BC=h$。
由勾股定理可得,$AC^2=AB^2+BC^2$,代入可得$h=2\sqrt{2}$,因此选项A正确。
26.由菱形的对角线长度公式可得,$AC=BD=4$。
由正弦定理可得,$EF/(\sqrt{3}/2)=4$,因此$EF=2\sqrt{3}$。
$\triangle AEF$的面积为$AE\times EF/2=2\sqrt{3}$,因此选项B正确。
27.由菱形的性质可知,EF是菱形的对角线,因此$EF=\sqrt{2}\times 2=2\sqrt{2}$。
由余弦定理可得,$AD^2=2^2+2^2-2\times 2\times 2\times\cos 120^\circ=12$,因此$OD=\sqrt{3}$。
由勾股定理可得,$OE^2=DE^2-OD^2=2^2-3=1$,因此$OE=1$。
由正弦定理可得,$AE/\sin 120^\circ=2\sqrt{2}$,因此$AE=2\sqrt{6}/3$。
由勾股定理可得,$AF=\sqrt{AD^2-OD^2}=2\sqrt{2}$。
$\triangle AEF$的面积为$AE\times AF/2=4\sqrt{3}/3$,因此选项A正确。
2)求证:四边形ABEF是菱形;3)求证:四边形CEFD是菱形;4)求证:菱形ABCD和三角形CEF的面积比为4:3.28.已知菱形ABCD,AB=5,AO=4,求BD的长度。
解:根据菱形性质,AO和BO分别是BD的中线和高线,因此BO=2AO=8.又因为ABCD是菱形,所以BD=2BO=16.29.已知四边形ABCD是菱形,点E,F分别是边CD,AD的中点,证明AE=CF。
解:连接AE和CF,由于ABCD是菱形,所以AC和BD 相交于O,且AO和BO分别是AE和CF的中线。
因此,AO=BO,即AE=CF。
30.已知菱形ABCD,E是AB的中点,DE⊥AB,AB=4,求(1)∠ABC的度数;(2)AC的长;(3)菱形ABCD的面积。
解:(1)由于DE⊥AB,所以∠BED=90°,又因为BE=ED,所以∠XXX∠EDB=45°,因此∠ABC=2∠EBD=90°。
2)由于AC是菱形的对角线,所以AC=BD=4√2.3)菱形的面积为S=AC×BD/2=16.31.已知四边形ABCD是菱形,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,证明∠DHO=∠DCO。
解:连接AD和BC,由于ABCD是菱形,所以AC和BD相交于O,且AO和BO分别是DH和CO的中线。
因此,AO=BO,即DO=CO。
又因为DH⊥AB,所以∠DHO=90°,因此∠DCO=∠DHO。
32.在三角形ABC中,BD平分∠ABC,BD的中垂线交AB于点E,交BC于点F,证明四边形BEDF是菱形。
解:由于BD平分∠ABC,所以∠ABD=∠CBD,又因为BE=ED,所以∠BED=∠BDE。
又因为BD的中垂线FE垂直于AB,所以∠FEB=90°,又因为BE=ED,所以∠XXX∠EDB。
因此,∠BED=∠BDE=∠XXX∠EDB,即四边形BEDF是菱形。
33.在四边形ABCD中,点E,F分别是AD,BC的中点,G,H分别是BD,AC的中点,求满足四边形EGFH是菱形的条件。
解:由于E和F分别是AD和BC的中点,所以EF∥AB∥CD,又因为G和H分别是BD和AC的中点,所以GH∥AB∥CD。
因此,四边形EGFH是平行四边形。
又因为EG=GF=HF=HE,所以四边形EGFH是菱形。
因此,四边形ABCD必须是平行四边形,即AB∥CD且AD∥BC。
34.在菱形ABCD中,点O是对角线AC和BD的交点,DE∥AC,CE∥BD,连接OE,证明OE=BC。
解:由于DE∥AC,所以∠XXX∠OAC,又因为CE∥BD,所以∠XXX∠XXX。
因此,∠OED+∠XXX∠OAC+∠OBD=180°。
又因为ABCD是菱形,所以AC=BD,即∠XXX∠OBD,因此∠OED=∠OCE。
因此,三角形OED和OCE相似,所以OE/OC=ED/CE=BD/BC,即OE=BC。
35.已知等边三角形CEF的边长与菱形ABCD的边长相等,证明(1)∠AEF=∠AFE;(2)四边形ABEF是菱形;(3)四边形CEFD是菱形;(4)菱形ABCD和三角形CEF的面积比为4:3.解:(1)由于CEF是等边三角形,所以∠XXX∠CFE=60°,又因为ABCD是菱形,所以AC和BD相交于O,且∠AOC=∠BOC=120°。
因此,∠AEF=180°-∠CEF-∠AOC=∠AFE。
2)由于ABCD是菱形,所以AC和BD相交于O,且AO和BO分别是AE和BF的中线。
因此,AO=BO,即AE=BF。
又因为ABCD是菱形,所以AC=BD,即CE=EF=FD。
因此,四边形ABEF是菱形。
3)由于ABCD是菱形,所以AC和BD相交于O,且AO和BO分别是CE和DF的中线。
因此,AO=BO,即CE=DF。
又因为ABCD是菱形,所以AC=BD,即CE=EF=FD。
因此,四边形CEFD是菱形。
4)菱形ABCD的面积为S1=AC×BD/2,等边三角形CEF的面积为S2=CE×EF/2.因为AC=BD,CE=EF=FD,所以S1/S2=AC×BD/CE×EF=4/3.。
