【全国百强校】河北省定州中学2017届高三上学期周练(7.8)数学(原卷版)
【全国百强校】河北省定州中学2017届高三上学期周练(二)物理(原卷版)

河北省定州中学2017届新高三周练(二)物理试题第I 卷(选择题)一、选择题(共44分,本大题共11小题,每小题4分,在每小题给出的四个选项中,第1至7题只有一项符合题目要求,第8至11题有多项符合题目要求. 全部选对的得4分,选对但不全的得2分,有选错的得0分)1.把一个凸透镜的弯曲表面压在另一个玻璃平面上,让单色光从上方射入,这时可以看到亮暗相间的同心圆环,对这些亮暗圆环的相关阐释合理的是A .远离中心点处亮环的分布较疏B .用白光照射时,不会出现干涉形成的圆环C .是透镜曲面上反射光与透镜上方平面上的反射光干涉形成的D .与同一亮环相对应的空气薄膜的厚度是相同的2.如图为安检门原理图,左边门框中有一通电线圈,右边门框中有一接收线圈。
工作过程中某段时间通电线圈中存在顺时针方向均匀减小的电流,则A .无金属片通过时,接收线圈中的感应电流方向为逆时针B .无金属片通过时,接收线圈中的感应电流增大C .有金属片通过时,接收线圈中的感应电流方向为逆时针D .有金属片通过时,接收线圈中的感应电流大小发生变化3.如图所示,A 、B 、C 为匀强电场中的三个点,已知∠CAB=60°,AB=2AC=2cm ,0V,8V A B ϕϕ==-将一带电量为q=3×10-5C 的正电荷从A 点移到C 点,电场力做功6×10-5J ,则下列说法正确的是A .C 点电势为2VB .电场强度E 沿AB 方向由A→B ,大小为400N /CC .该正电荷在B 点具有的电势能为2.4×10-4JD .将该正电荷从C 点移到B 点,电势能增加了1.8×10-4J4.如图所示,金属球壳A 带有正电,其上方有一小孔a ,静电计B 的金属球b 用导线与金属小球c 相连,以下操作所发生的现象正确的是( )A .将c 移近A ,但不与A 接触,B 会张开一定角度B .将c 与A 外表面接触后移开A ,B 不会张开一定角度C .将c 与A 内表面接触时,B 不会张开角度D .将c 从导线上解下,然后用绝缘细绳吊着从A 中小孔置入A 内,并与其内壁接触,再提出空腔,与b 接触,B 会张开一定角度5.下列说法正确的是A .安培发现了电流磁效应;法拉第发现了电磁感应现象B .开普勒首先发现了行星运动规律;哈雷利用万有引力定律推算出彗星的回归周期C .库仑发现了点电荷的相互作用规律并提出了电场线;密立根通过油滴实验测定了元电荷的数值D .富兰克林首先命名了正负电荷;奥斯特通过实验发现在磁场中转动的金属圆盘可以对外输出电流6.用等效思想分析变压器电路。
【全国百强校】河北省衡水中学2017届高三上学期四调考试理数试题解析(解析版)

河北省衡水中学2017届高三上学期四调考试理科数学试题第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}21log A x N x k =∈<<,集合A 中至少有3个元素,则( ) A .8k > B .8k ≥ C .16k > D .16k ≥ 【答案】C考点:1.集合的运算;2.对数函数的性质. 2. 若()1z i i +=,则z 等于( )A .1BC .D .12【答案】C 【解析】试题分析:由()1z i i +=得()()()11111122i i i z i i i i -===+++-,所以2z ==,故选C. 考点:1.复数相关的概念;2.复数的运算.3. 在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”这首古诗描述的这个宝塔其古称浮屠,本题说它一共有7层,每层悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯?( ) A .5 B .6 C .4 D .3 【答案】D 【解析】试题分析:由题意可知,每层悬挂的灯数从上到下依次构成比差数列,公比为2,设顶层的灯数为1a ,则77111(12)(2112738112a a a -==--)=,解之得13a =,故选D.考点:1.数学文化;2.等比数列的性质与求和.4. 已知双曲线()2222:10 0x y C a b a b-=>>,,则C 的渐近线方程为( ) A .14y x =± B .13y x =± C.12y x =± D .y x =±【答案】C考点:双曲线的标准议程与几何性质.5. 执行如图所示的程序框图,则输出的结果为( )A .4B .9 C.7 D .5 【答案】B 【解析】试题分析:模拟算法,开始:输入0,0,1T S n ===;2,9(11)18,123,T S n T S ==+==+=≥不成立; 328,9(31)36,325,T S n T S ===+==+=≥不成立; 5232,9(51)54,527,T S n T S ===+==+=≥不成立; 72128,9(71)63,729,T S n T S ===+==+=≥成立;输出9n =,结束得算法.故选B.考点:程序框图.6. 已知函数()()()cos 0f x A x ωϕω=+>的部分图象如图所示,下面结论错误的是( )A .函数()f x 的最小正周期为23πB .函数()f x 的图象可由()()cos g x A x ω=的图象向右平移12π个单位得到 C.函数()f x 的图象关于直线12x π=对称D .函数()f x 在区间 42ππ⎛⎫ ⎪⎝⎭,上单调递增【答案】D考点:三角函数的图象和性质.7. 德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数() 1 0 x f x x ⎧=⎨⎩,为有理数,为无理数,称为狄利克雷函数,则关于函数()f x 有以下四个命题: ①()()1f f x =;②函数()f x 是偶函数;③任意一个非零有理数T ,()()f x T f x +=对任意x R ∈恒成立;④存在三个点()()()()()()112233 A x f x B x f x C x f x ,,,,,,使得ABC △为等边三角形. 其中真命题的个数是( )A .4B .3 C.2 D .1 【答案】A考点:1.函数的奇偶性;2.函数的周期性;3.分段函数的表示与求值. 8. 某几何体的三视图如图所示,则该几何体的体积为( )A .10B .20 C.40 D .60 【答案】B 【解析】试题分析:由三视图可知该几何体的直观图如下图所示,且三角形ABC 是以角A 为直角的直角三角形,4,3AB AC ==,从而5BC =,又5BD =,且BD ⊥平面ABC ,故四边形BCED 中边长为5的正方形,过A 作AH BC ⊥于H ,由易知AH ⊥平面BCED ,在直角三角形ABC 中可求得125AH =,从而ABCD 11125520335A BCED V V S AH -==⨯⨯=⨯⨯⨯=正方形,故选B.考点:1.三视图;2.多面体和体积.9. 已知A 、B 是椭圆()222210x y a b a b +=>>长轴的两个端点,M 、N 是椭圆上关于x 轴对称的两点,直线AM 、BN 的斜率分别为()1212 0k k k k≠,,则12k k +的最小值为( )A .1 BD【答案】A考点:1.双曲线的标准方程与几何性质;2.基本不等式;3.斜率公式.【名师点睛】本题考查双曲线的标准方程与几何性质、基本不等式、斜率公式,属中档题;双曲线的标准方程与几何性质是高考的热点,特别是双曲线的性质,几乎每年均有涉及,主要以选择题、填空题为主,解题时,应利用图形,挖掘题目中的隐含条件,结合图形求解.10. 在棱长为6的正方体1111ABCD A B C D -中,M 是BC 的中点,点P 是面11DCC D 所在的平面内的动点,且满足APD MPC ∠=∠,则三棱锥P BCD -的体积最大值是( )A .36B .C.24 D . 【答案】A考点:1.线面垂直的判定与性质;2.轨迹方程的求法;3.多面体的体积.11. 已知函数()()()3ln 1 01 1 0x x f x x x -<⎧⎪=⎨-+≥⎪⎩,,,若()f x ax ≥恒成立,则实数a 的取值范围是( ) A .20 3⎡⎤⎢⎥⎣⎦,B .30 4⎡⎤⎢⎥⎣⎦, C.[]0 1, D .30 2⎡⎤⎢⎥⎣⎦, 【答案】B 【解析】试题分析:在同一坐标系内作出函数()()()3ln 1 01 1 0x x f x x x -<⎧⎪=⎨-+≥⎪⎩,,与函数y ax =和图象,通过图象可知,当直线y ax =绕着原点从x 轴旋转到与图中直线l 重合时,符合题意,当0x >时,2()3(1)f x x '=-,设直线l与函数()y f x =的切点为00(,)P x y ,则3200000(1)3(1)y x x x x --==,解之得032x =,所以直线l 的斜率2333(1)24k =⨯-=,所以a 的取值范围为30 4⎡⎤⎢⎥⎣⎦,,故选B.考点:1.函数与不等式;2.导数的几何意义.【名师点睛】本题考查函数与不等式、导数的几何意义,属中档题;导数的几何意义是每年高考的必考内容,利用导数解决不等式恒成立问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的范围;或参变分离,构造函数,直接把问题转化为函数的最值问题;或通过数列结合解题.12. 已知过抛物线()2:20G y px p =>焦点F 的直线l 与抛物线G 交于M 、N 两点(M 在x 轴上方),满足3MF FN =,163MN =,则以M 为圆心且与抛物线准线相切的圆的标准方程为( )A .2211633x y ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭ B .2211633x y ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭C.()(22316x y -+-= D .()(22316x y -+=【答案】C考点:1.抛物线的标准方程与几何性质;2.直线与抛物线的位置关系;2.圆的标准方程.【名师点睛】本题考查抛物线的标准方程与几何性质、直线与抛物线的位置关系、圆的标准方程,属难题;在解抛物线有关问题时,凡涉及抛物线上的点到焦点的距离时,一般要运用定义转化为到准线的距离处理;抛物线的焦点弦一直是高考的热点,对于焦点弦的性质应牢固掌握.第Ⅱ卷(非选择题共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若x、y满足约束条件1040xx yx y-≥⎧⎪-≤⎨⎪+-≤⎩,则1yx-的最大值为.【答案】2考点:线性规划.14. 在ABC △中, 3 5AB AC ==,,若O 为ABC △外接圆的圆心(即满足OA OB OC ==),则AO BC ⋅的值为 . 【答案】8考点:数量积的几何运算.【名师点睛】本题考查数量积的几何运算,属中档题;平面向量的数量积有两种运算,一是依据长度与夹角,即数量积的几何意义运算,一是利用坐标运算,本题充分利用向量线性运算的几何意义与数量积的几何意义进行运算,运算量不大,考查子学生逻辑思维能力,体现了数形结合的数学思想. 15. 已知数列{}n a 的各项均为正数,11142 n n n n a a a a a ++=-=+,,若数列11n n a a -⎧⎫⎨⎬+⎩⎭的前n 项和为5,则n = .【答案】120 【解析】试题分析:数列11n n a a -⎧⎫⎨⎬+⎩⎭的前n 项和为321121211223111154444n n n a a a a a a a a a a a a a a +-----+++=++==+++,所以122n a +=, 又114 n n n na a a a ++-=+,所以221 4n n a a +-=,由此可得22211444,2244,120n a a n n n n +=+=+∴=+=,即应填120.考点:1.数列求和;2.累和法求数列通项.【名师点睛】本题考查数列求和,累和法求数列通项,属中档题;由数列的递推公式求通项公式时,若递推关系为a n +1=a n +f (n )或a n +1=f (n )·a n ,则可以分别通过累加、累乘法求得通项公式,另外,通过迭代法也可以求得上面两类数列的通项公式,数列求和的常用方法有倒序相加法,错位相减法,裂项相消法,分组求和法,并项求和法等,可根据通项特点进行选用.16. 过抛物线()220y px p =>的焦点F 的直线l 与抛物线在第一象限的交点为A ,与抛物线的准线的的交点为B ,点A 在抛物线的准线上的射影为C ,若 48AF FB BA BC =⋅=,,则抛物线的方程为 . 【答案】24y x =考点:1.抛物线的标准方程与几何性质;2.向量数量积的几何意义.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)在ABC △中,内角A 、B 、C 所对的边分别为 a b c ,,,已知 4 6 2b c C B ===,,. (1)求cos B 的值; (2)求ABC △的面积.【答案】(1)34;(2.试题解析:(1)在ABC △中,sin sin b c B C =,因为 4 6 2b c C B ===,,,所以46sin sin 2B B=,即 46sin 2sin cos B B B =,又sin 0B ≠,∴3cos 4B =.(2)由(1)知3cos 4B =,从而sin B =.因此sin sin 22sin cos C B B B ===21cos cos22cos 18C B B ==-=.所以()()13sin sin sin sin cos cos sin 84A B C B C B C B C π=--=+=+=+=所以ABC △的面积为1462⨯⨯. 考点:1.正弦定理;2.三角恒等变换;3.三角形内角和与三角形面积公式.【名师点睛】本题考查正弦定理、三角恒等变换、三角形内角和与三角形面积公式,属中档题. 正、余弦定理是揭示三角形边角关系的重要定理,直接运用正弦定理解决一类已知三角形两边及一角对边求其它元素,或已知两边及一边对角求其它元素的问题,这时要讨论三角形解的个数问题;利用余弦定理可以快捷求第三边直接运用余弦定理解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题;知道两边和其中一边的对角,利用余弦定理可以快捷求第三边. 18. (本小题满分12分)如图所示,在三棱柱111ABC A B C -中,11AA B B 为正方形,11BB C C 为菱形,1160BB C ∠=︒,平面11AA B B ⊥平面11BB C C .(1)求证:11B C AC ⊥;(2)设点E 、F 分别是1B C ,1AA 的中点,试判断直线EF 与平面ABC 的位置关系,并说明理由; (3)求二面角1B AC C --的余弦值.【答案】(1)见解析;(2) EF ∥平面ABC ;.试题解析:(1)连接1BC ,在正方形11ABB A 中,1AB BB ⊥, 因为平面11AA B B ⊥平面11BB C C ,平面11AA B B平面111BB C C BB =,AB ⊂平面11ABB A ,所以AB ⊥平面11BB C C ,因为1B C ⊥平面11BB C C ,所以1AB B C ⊥.在菱形11BB C C 中,11BC B C ⊥,因为1BC ⊥面1ABC ,AB ⊥平面1ABC ,1BC AB B =,所以1B C ⊥平面1ABC ,因为1AC ⊥平面1ABC ,所以11B C AC ⊥.(2)EF ∥平面ABC ,理由如下:取BC 的中点G ,连接GE 、GA ,因为E 是1B C 的中点,所以1GE BB ∥,且112GE BB =,因为F 是 1AA 的中点,所以112AF AA =. 在正方形11ABB A 中,1111 AA BB AA BB =∥,,所以GE AF ∥,且GE AF =. ∴四边形GEFA 为平行四边形,所以EF GA ∥. 因为EF ABC ⊄平面,GA ABC ⊂平面, 所以EF ABC ∥平面.(3)在平面11BB C C 内过点B 作1Bz BB ⊥,由(1)可知:11AB BB C C ⊥平面,以点B 为坐标原点,分别以BA 、1BB 所在的直线为x 、y 轴,建立如图所示的空间直角坐标系B xyz -,设()2 0 0A ,,,则()10 2 0B ,,. 在菱形11BB C C 中,1160BB C ∠=︒,所以(0 1 C -,,(10 1 C ,. 设平面1ACC 的一个法向量为() 1x y =n ,,. 因为100n AC n CC ⎧⋅=⎪⎨⋅=⎪⎩即()(()() 1 2 1 0 10 2 00x y x y ⎧⋅--=⎪⎨⋅=⎪⎩,,,,,,,,所以0x y ⎧=⎪⎨⎪=⎩0 1n ⎫=⎪⎪⎝⎭,,, 由(1)可知:1CB 是平面1ABC 的一个法向量.所以(1110 10 3 cosn CB n CB n CB ⎛⎫⋅ ⎪ ⎪⋅⎝<>===⋅,,,,,,所以二面角1B AC C --. 考点:1.面面垂直的判定与性质;2.线面平行、垂直的判定与性质;3.空间向量的应用.【名师点睛】本题考查.面面垂直的判定与性质、线面平行、垂直的判定与性质及空间向量的应用,属中档题;解答空间几何体中的平行、垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间的平行、垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;求二面角,则通过求两个半平面的法向量的夹角间接求解.此时建立恰当的空间直角坐标系以及正确求出各点的坐标是解题的关键所在.19. (本小题满分12分)如图,在平面直角坐标系xOy 中,已知()00 R x y ,是椭圆22:12412x y C +=上的一点,从原点O 向圆()()2200:8R x x y y -+-=作两条切线,分别交椭圆于P ,Q .(1)若R 点在第一象限,且直线OP ,OQ 互相垂直,求圆R 的方程; (2)若直线OP ,OQ 的斜率存在,并记为12 k k ,,求12k k 的值; (3)试问22OP OQ +是否为定值?若是,求出该值;若不是,说明理由.【答案】(1)((228x y-+-=;(2)12-;(3)36.试题解析:(1)由圆R的方程知圆R的半径r=,因为直线OP,OQ互相垂直,且和圆R相切,所以4OR==,即220016x y+=①又点R在椭圆C上,所以220012412x y+=②联立①②,解得0xy⎧=⎪⎨=⎪⎩R的方程为((228x y-+-=.(2)因为直线1:OP y k x=和2:OQ y k x=都与圆R==212288yk kx-⋅=-,因为点()00R x y,在椭圆C上,所以220012412x y+=,即22001122y x=-,所以2122141228xk kx-==--.(3)方法一(1)当直线OP、OQ不落在坐标轴上时,设()11P x y,,()22Q x y,,由(2)知12210k k+=,所以121221y yx x=,故2222121214y y x x=,因为()11P x y,,()22Q x y,,在椭圆C上,所以221112412x y+=,222212412x y+=,即22111122y x =-,22221122y x =-,所以222212121111212224x x x x ⎛⎫⎛⎫--= ⎪⎪⎝⎭⎝⎭,整理得221224x x +=,所以222212121112121222y y x x ⎛⎫⎛⎫+=-+-= ⎪ ⎪⎝⎭⎝⎭,所以()()22222222221122121236OP OQ x y x y x x y y +=+++=+++=.(2)当直线OP 、OQ 落在坐标轴上时,显然有2236OP OQ +=. 综上:2236OP OQ +=.考点:1.椭圆的标准方程与几何性质;2.圆的标准方程;3.直线与圆的位置关系. 20. (本小题满分12分)设椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为1F 、2F ,上顶点为A ,过A 与2AF 垂直的直线交x 轴负半轴于Q 点,且12220F F F Q +=. (1)求椭圆C 的离心率;(2)若过A 、Q 、2F 三点的圆恰好与直线30x --=相切,求椭圆C 的方程;(3)过2F 的直线l 与(2)中椭圆交于不同的两点M 、N ,则1F MN △的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.【答案】(1)12;(2) 22143x y +=;(3)1F MN △的内切圆的面积的最大值为916π,此时直线l 的方程为1x =.(3)设1F MN △的内切圆的半径为R ,则1F MN △的周长为48a =,由此可得112121212F MN S F F y y y y =⋅-=-△,设直线l 的方程为1x my =+,与椭圆方程联立得()2234690my my ++-=,由根与系数关系代入112F MNS y y =-=△,换元令t =()12121211313F MN t S t t t t==≥-+△,可知当1t =时,14F MN S R =△有最大值3,从而求出内切圆面积的最大值与相应的直线方程即可.试题解析:(1)由题()0 A b ,,1F 为2QF 的中点.设()()12 0 0F c F c -,,,,则()3 0Q c -,, ()3 AQ c b =--,,()2 AF c b =-,,由题2AQ AF ⊥,即22230AQ AF c b ⋅=-+=,∴()22230c a c -+-=即224a c =,∴12c e a ==. (2)由题2Rt QAF △外接圆圆心为斜边2QF 的中点()1 0F c -,,半径2r c =, ∵由题2Rt QAF △外接圆与直线30x -=相切,∴d r =,即322c c --=,即34c c +=,∴1c =,22a c ==,b =C 的方程为22143x y +=.(3)设()11 M x y ,,()22 N x y ,,由题12 y y ,异号,设1F MN △的内切圆的半径为R ,则1F MN △的周长为48a =,()111142F MN S MN F M F N R R =++=△, 因此要使1F MN △内切圆的面积最大,只需R 最大,此时1F MN S △也最大,112121212F MN S F F y y y y =⋅-=-△, 由题知,直线l 的斜率不为零,可设直线l 的方程为1x my =+,由221143x my x y =+⎧⎪⎨+=⎪⎩得()2234690m y my ++-=,由韦达定理得122634m y y m -+=+,122934y y m -=+,(0m R ∆>∈⇒)112F MN S y y =-=△令t =1t ≥,()12121211313F MN t S t t t t==≥-+△, 当1t =时,14F MN S R =△有最大值3,此时,0m =,max 34R =, 故1F MN △的内切圆的面积的最大值为916π,此时直线l 的方程为1x =. 考点:1.椭圆的标准方程与几何性质;2.直线与椭圆的位置关系;3.直线与圆的位置关系. 21. (本小题满分12分) 已知0t >,设函数()()3231312t f x x x tx +=-++.(1)存在()00 2x ∈,,使得()0f x 是()f x 在[]0 2,上的最大值,求t 的取值范围; (2)()2x f x xe m ≤-+对任意[0 )x ∈+∞,恒成立时,m 的最大值为1,求t 的取值范围.【答案】(1)5[ )3+∞,;(2) 1(0 ]3,.(2)()()()323223131313123131222x x x t t t x x tx xe m m xe x x tx x e x x t +++⎛⎫-++≤-+⇔≤-+-+=-+-+ ⎪⎝⎭,构造函数()()23132x t g x e x x t +=-+-,道m 的最大值为1,等价于()()231302x t g x e x x t +=-+-≥在区间[0 )+∞,上恒成立,由于()0130g t =-≥,则103t <≤,此时()0g x '>恒成立,即()g x 在区间[0 )+∞,上单调递增,符合题意.试题解析:(1)()()()()2'331331f x x t x t x x t =-++=--,①当01t <<时,()f x 在()0 t ,上单调递增,在() 1t ,单调递减,在()1 2,单调递增, ∴()()2f t f ≥,由()()2f t f ≥,得3234t t -+≥在01t <<时无解, ②当1t =时,不合题意;③当12t <<时,()f x 在()0 1,单调递增,在()1 t ,递减,在() 2t ,单调递增, ∴()()1212f f t ⎧≥⎪⎨<<⎪⎩即1332212t t ⎧+≥⎪⎨⎪<<⎩,∴523t ≤<,④当2t ≥时,()f x 在()0 1,单调递增,在()1 2,单调递减,满足条件, 综上所述:5[ )3t ∈+∞,时,存在()00 2x ∈,,使得()0f x 是()f x 在[]0 2,上的最大值. ∴()()0130g x g t ≥=-≥,满足条件,∴t 的取值范围是1(0 ]3,.考点:1.导数与函数的单调性、极值,最值;2.函数与不等式.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-4:坐标系与参数方程已知圆锥曲线2cos :x C y αα=⎧⎪⎨=⎪⎩(α为参数)和定点(0 A ,1F 、2F 是此圆锥曲线的左、右焦点,以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系. (1)求直线2AF 的直角坐标方程;(2)经过点1F 且与直线2AF 垂直的直线l 交此圆锥曲线于M 、N 两点,求12MF NF -的值. 【答案】0y +-=;(2. 试题解析:(1)曲线2cos :x C y αα=⎧⎪⎨=⎪⎩可化为22143x y +=,其轨迹为椭圆,焦点为()1 1 0F -,,()21 0F ,.经过(0 A 和()21 0F ,的直线方程为11x =0y +. (2)由(1)知,直线2AF的斜率为2l AF ⊥,所以l,倾斜角为30︒, 所以l的参数方程为112x y t ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数).代入椭圆C的方程中,得213360t --=. 因为 M N ,在点1F的两侧,所以1112MF NF t t -=+=考点:1.参数方程与普通方程的互化;2.直线参数方程的应用. 23. (本小题满分10分)选修4-5:不等式选讲 设()34f x x x =-+-. (1)解不等式()2f x ≤;(2)若存在实数x 满足()1f x ax ≤-,试求实数a 的取值范围. 【答案】(1) 59 22⎡⎤⎢⎥⎣⎦,;(2)()1 2[ )2-∞-+∞,, 【解析】试题分析:(1)由绝对值的意义去掉绝对值符号,将函数()f x 表示成分段函数的形式,作出函数()f x 的图象,数形结合可得到不等式的解集;(2)在同一坐标系内作出函数()y f x =与函数1y ax =-的图象,数形结合可求出a 的范围.(2)函数1y ax =-的图象是过点()0 1-,的直线, 当且仅当函数()y f x =与直线1y ax =-有公共点时,存在题设的x .由图象知,a 的取值范围为()1 2[ )2-∞-+∞,,.考点:1.含绝对值不等式的解法;2.分段函数的表示与作图;3.函数与不等式.。
2017届河北省定州中学高三上学期周练(三)(8.21)数学试题(解析版)

河北定州中学2016-2017学年第一学期高三数学周练试题(三)一、选择题(共12小题,共60分) 1.若函数()xxx f ln =,若)5(),4(),3(f c f b f a ===则( ) A. a< b < c B. c < b < a C. c < a < b D. b < a < c 2.设非空集合P Q 、满足P Q P = ,则( ) A .x Q ∀∈,有x P ∈ B .x Q ∀∉,有x P ∉ C .0x Q ∃∉,使得0x P ∈ D .0x P ∃∈,使得0x Q ∉3.已知集合P ={x|x 2≤1},M ={a},若P ∪M =P ,则a 的取值范围是A .(-∞,-1]B .[1,+∞)C .[-1,1]D .(-∞,-1]∪[1,+∞) 4.已知函数()()s i n c o s ,0,fx a x b x a b x R =-≠∈为常数a 在4x π=处取得最小值,则函数y =34f x π⎛⎫-⎪⎝⎭是( ) A .偶函数且它的图象关于点(),0π对称 B .偶函数且它的图象关于点3,02π⎛⎫⎪⎝⎭对称 C .奇函数且它的图象关于点3,02π⎛⎫⎪⎝⎭对称 D .奇函数且它的图象关于点(),0π对称 5.2002年8月,在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,若直角三角形中较小的锐角为θ,大正方形的面积是1,小正方形的面积是θθ22cos sin ,251-则的值等于( )A .1B .2524-C .-257D .2576.已知0,0a b >>,且24a b +=,则1ab的最小值为( )A .4B .41C .2D .217.已知函数()211x f x x +=-,[)8,4x ∈--,则下列说法正确的是( )A .()f x 有最大值53,无最小值B .()f x 有最大值53,最小值75C .()f x 有最大值75,无最小值D .()f x 有最大值2,最小值758.已知两个单位向量,a b 的夹角为60°,(1)c ta t b =+- ,若0b c =,则t =A .2B .3C .3-D .4 9.已知x 1是方程2010lg =x x 的根,x 2是方程201010=⋅xx 的根,则x 1·x 2=( ) A .2008B .2009C .2010D .201110.平行线3490x y +-=和620x my ++=的距离是( ) A .85 B .2 C .115 D .7511.已知函数2,0()1,0ab x f x x x x x x ⎧+>⎪=+⎨⎪+≤⎩在R 上连续,则a b -=A .2B .1C .0D .1-12.某企业生产甲乙两种产品均需用A ,B 两种原料,已知生产1吨每种产品需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为A .12万元B .16万元C .17万元D .18万元第II 卷(非选择题)二、填空题(4小题,共20分)13.在平面直角坐标系中,O 为坐标原点,设向量(1,2)OA =, (2,1)OB =- ,若OP xOA yOB =+且12x y ≤≤≤,则点P 所有可能的位置所构成的区域面积是 . 14.如图,函数y=2sin (x π+ϕ),x ∈R,(其中0≤φ≤2π)的图象与y 轴交于点(0,1). 设P 是图象上的最高点,M 、N 是图象与x 轴的交点, 则PN PM ⋅=________.15.若函数,则 .16.如图所示,在四面体OABC 中,OA 、OB 、OC 两两垂直,且OB=OC=3,OA=4.给出以下命题:①存在点D(O 点除外),使得四面体DABC 有三个面是直角三角形; ②存在点D,使得点O 在四面体DABC 外接球的球面上; ③存在唯一的点D 使得四面体DABC 是正棱锥; ④存在无数个点D,使得AD 与BC 垂直且相等.其中正确命题的序号是 (把你认为正确命题的序号填上). 三、解答题(8小题,共70分) 17.(本小题满分14分) 若函数321a +1f(x)=x x +bx +a 32- (a ,b ∈R),且其导函数f ′ (x)的图象过原点. (Ⅰ)当a=1时,求函数f(x)的图象在x=3处的切线方程; (Ⅱ)若存在x<0使得f ′ (x)=-9,求实数a 的最大值. 18.已知R a ∈,函数1ln ()ax x f x e x-=-+(e 为自然对数的底数). (Ⅰ)若1a =,求函数()f x 的单调区间;(Ⅱ)若()f x 的最小值为a ,求a 的最小值.19.(本题满分13分)用一枚质地均匀的硬币,甲、乙两人做抛掷硬币游戏,甲抛掷4次,记正面朝上的次为ξ;乙抛掷3次,记正面朝上的次为η.(Ⅰ)分别求ξ和η的期望;(Ⅱ)规定:若ξ>η,则甲获胜;否则,乙获胜.求甲获胜的概率.20.已知向量)cos ,sin 2(x x m -=,)cos 2,cos 3(x x n =,函数n m x f ∙-=1)(, (1)求)(x f 的最小正周期;(2)当[]π,0∈x 时,求)(x f 的单调递增区间;(3)说明)(x f 的图像可以由x x g sin )(=的图像经过怎样的变换而得到。
【全国百强校word】河北省衡水中学2017届高三上学期一调考试理数试题
数学试卷(理科)第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1. 已知集合{}2log 1P x x =<-,{}1Q x x =<,则P Q =I ( ) A .10,2⎛⎫ ⎪⎝⎭B .1,12⎛⎫⎪⎝⎭C .()0,1D .11,2⎛⎫- ⎪⎝⎭2. 已知i 为虚数单位,复数z 满足()2313i1i z +=-,则z 为( )A .12B .22 C .24D .2163. 如图,网格纸上小正方形的边长为1,粗线或虚线画出某几何体的三视图,该几何体的体积为( )A .8B .12C .18D .244. 已知命题p :方程2210x ax --=有两个实数根;命题q :函数()4f x x x=+的最小值为4.给出下列命题:①p q ∧;②p q ∨;③p q ∧⌝;④p q ⌝∨⌝. 则其中真命题的个数为( ) A .1 B .2C .3D .45. 由曲线y x =2y x =-及y 轴所围成的图形的面积为( )A .103 B .4C .163D .66. 函数()21cos 1e xf x x ⎛⎫=-⎪+⎝⎭的图象的大致形状是( )A .B .C .D .7. 阅读下面的程序框图,运行相应的程序,输出的结果为( )A .1321B .2113C .813D .1388. 定义在R 上的函数()f x 满足()()1f x f x '+>,()04f =,则不等式()e e 3x x f x >+(其中e 为自然对数的底数)的解集为( ) A .()0,+∞B .()(),03,-∞+∞UC .()(),00,-∞+∞UD .()3,+∞9. 若实数a ,b ,c ,d 满足()()2223ln 20b a a c d +-+-+=,则()()22a cb d -+-的最小值为( )A 2B .2C .22D .810. 已知()21,01,3log ,1,2x x f x x x +≤<⎧⎪=⎨+≥⎪⎩存在210x x >≥,使得()()12f x f x =,则()12x f x g 的取值范围为( ) A .3,24⎡⎫⎪⎢⎣⎭B .3,22⎡⎫⎪⎢⎣⎭C .34,43⎡⎫⎪⎢⎣⎭D .2,23⎡⎫⎪⎢⎣⎭11. 设函数()32133f x x x x =+-,若方程()()210f x t f x ++=有12个不同的根,则实数t 的取值范围为( ) A .10,23⎛⎫-- ⎪⎝⎭B .(),2-∞-C .34,215⎛⎫-- ⎪⎝⎭D .()1,2-12. 设曲线()e x f x x =--(e 为自然对数的底数)上任意一点处的切线为1l ,总存在曲线()32cos g x ax x =+上某点处的切线2l ,使得12l l ⊥,则实数a 的取值范围为( )A .[]1,2-B .()3,+∞C .21,33⎡⎤-⎢⎥⎣⎦ D .12,33⎡⎤-⎢⎥⎣⎦第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 设1m >,变量x ,y 在约束条件,,1y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z x my =+的最大值为2,则m =_________.14. 函数e xy mx =-在区间(]0,3上有两个零点,则m 的取值范围是_________.15. 已知函数()3223f x x mx nx m =+++在1x =-时有极值0,则m n +=_________. 16. 定义在R 上的函数()f x 满足:()()2f x f x x -+=,当0x <时,()f x x '<,则不等式()()112f x f x x +≥-+的解集为_________. 三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(本小题满分12分)在ABC ∆中,a ,b ,c 分别为角A ,B ,C 所对的边,且cos 2cos 3cos a b cA B C==. (1)求角A 的大小;(2)若ABC ∆的面积为3,求a 的值. 18.(本小题满分12分) 函数21()ln 22f x x ax x =--. (1)当3a =时,求()f x 的单调区间;(2)若()1,a ∀∈-+∞,()1,e x ∃∈,有()0f x b -<,求实数b 的取值范围. 19.(本小题满分12分)在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,且4sin 7b A a =.(1)求sin B 的值;(2)若a ,b ,c 成等差数列,且公差大于0,求cos cos A C -的值. 20.(本小题满分12分)已知函数()242ln f x ax bx a x =-+(,a b ∈R ). (1)若函数()y f x =存在极大值和极小值,求ba的取值范围; (2)设m ,n 分别为()f x 的极大值和极小值,若存在实数2e 1,2e 2eb a a ⎛⎫+∈ ⎪⎝⎭,使得1m n -=,求a 的取值范围.21.(本小题满分12分) 已知函数()ln f x x x =,()e xxg x =. (1)记()()()F x f x g x =-,判断()F x 在区间()1,2内的零点个数并说明理由;(2)记()F x 在()1,2内的零点为0x ,()()(){}min ,m x f x g x =,若()m x n =(n ∈R )在()1,+∞内有两个不等实根1x ,2x (12x x <),判断12x x +与02x 的大小,并给出对应的证明.请考生在22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.22.(本小题满分10分)选修4-1:几何证明选讲如图,AE 是圆O 的切线,A 是切点,AD OE ⊥于D ,割线EC 交圆O 于B ,C 两点.(1)证明:O ,D ,B ,C 四点共圆;(2)设50DBC ∠=︒,30ODC ∠=︒,求OEC ∠的大小. 23.(本小题满分10分)选修4-4:坐标系与参数方程 已知直线l 的参数方程为10,x t y t =-+⎧⎨=⎩(t 为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,圆C 的极坐标方程为24sin 20ρρθ-+=. (1)把圆C 的极坐标方程化为直角坐标方程;(2)将直线l 向右平移h 个单位,所得直线l '与圆C 相切,求h . 24.(本小题满分10分)选修4-5:不等式选讲已知函数()2f x x a a =-+,a ∈R ,()21g x x =-. (1)若当()5g x ≤时,恒有()6f x ≤,求a 的最大值; (2)若当x ∈R 时,恒有()()3f x g x +≥,求a 的取值范围.试卷答案一、选择题1.A2.C3. B4.C5.C6.B7.D8.A9.D 10.A 11.C 12.D11.解析:()32133f x x x x =+-,()2230f x x x '=+-=,3x =-,1x =,函数在(),3-∞-,()1,+∞单调递增,且在()3,1-单调递减,函数的极大值为()39f -=,函数的极小值为()513f =-,根据函数的图象可知,设()f x m =,可知210m tm ++=,原方程有12个不同的根,则210m tm ++=方程应在50,3⎛⎫ ⎪⎝⎭内有两个不同的根,设()21h m m tm =++则250353402231540h t t t ⎧⎛⎫> ⎪⎪⎝⎭⎪⎪<-<⇒-<<-⎨⎪⎪∆=->⎪⎩,所以取值的范围34215t -<<-. 二、填空题13. 1m =3e e,3⎛⎤ ⎥⎝⎦15. 11 16. 12x ≤三、解答题 17.解(1)cos 2cos 3cos a b cA B C==Q, sin sin sin cos 2cos 3cos A B CA B C∴==, 即tan tan tan 23B CA ==,则tan 2tan B A =,tan 3tan C A =. 又在ABC ∆中,()tan tan tan tan 1tan tan B CA B C B C+=-+=--.则22tan 3tan tan 16tan A A A A+=-,解得2tan 1A =, tan 1A ∴=-或tan 1A =,sin 5B =,sin 10C =.在ABC ∆中有sin sin a bA B =, 则sin 105sin 52B b a a A ===,则2112103sin 322510ABCa S ab C a ∆====. 得25a =,所以5a =18.(Ⅰ)增区间10,3⎛⎫⎪⎝⎭是,减区间1,3⎛⎫+∞ ⎪⎝⎭;(Ⅱ)3,2⎛⎫-+∞ ⎪⎝⎭. 试题解析:(Ⅰ)()2321x x f x x +-'=-(0x >),10,3x ⎛⎫∈ ⎪⎝⎭时,()0f x '>,()f x 单增1,3x ⎛⎫∈+∞ ⎪⎝⎭时,()0f x '<,()f x 单减。
【全国百强校】河北省衡水中学2017届高三上学期四调考试理数试题解析(解析版)

河北省衡水中学2017届高三上学期四调考试理科数学试题第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{}21log A x N x k =∈<<,集合A 中至少有3个元素,则( ) A .8k > B .8k ≥ C .16k > D .16k ≥ 【答案】C考点:1.集合的运算;2.对数函数的性质. 2. 若()1z i i +=,则z 等于( )A .1BC .2D .12【答案】C 【解析】试题分析:由()1z i i +=得()()()11111122i i i z i i i i -===+++-,所以2z ==,故选C. 考点:1.复数相关的概念;2.复数的运算.3. 在明朝程大位《算法统宗》中有这样的一首歌谣:“远看巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”这首古诗描述的这个宝塔其古称浮屠,本题说它一共有7层,每层悬挂的红灯数是上一层的2倍,共有381盏灯,问塔顶有几盏灯?( ) A .5 B .6 C .4 D .3 【答案】D 【解析】试题分析:由题意可知,每层悬挂的灯数从上到下依次构成比差数列,公比为2,设顶层的灯数为1a ,则77111(12)(2112738112a a a -==--)=,解之得13a =,故选D.考点:1.数学文化;2.等比数列的性质与求和.4. 已知双曲线()2222:10 0x y C a b a b-=>>,,则C 的渐近线方程为( ) A .14y x =± B .13y x =± C.12y x =± D .y x =±【答案】C考点:双曲线的标准议程与几何性质.5. 执行如图所示的程序框图,则输出的结果为( )A .4B .9 C.7 D .5 【答案】B 【解析】试题分析:模拟算法,开始:输入0,0,1T S n ===;2,9(11)18,123,T S n T S ==+==+=≥不成立; 328,9(31)36,325,T S n T S ===+==+=≥不成立; 5232,9(51)54,527,T S n T S ===+==+=≥不成立; 72128,9(71)63,729,T S n T S ===+==+=≥成立;输出9n =,结束得算法.故选B.考点:程序框图.6. 已知函数()()()cos 0f x A x ωϕω=+>的部分图象如图所示,下面结论错误的是( )A .函数()f x 的最小正周期为23πB .函数()f x 的图象可由()()cos g x A x ω=的图象向右平移12π个单位得到 C.函数()f x 的图象关于直线12x π=对称D .函数()f x 在区间 42ππ⎛⎫ ⎪⎝⎭,上单调递增【答案】D考点:三角函数的图象和性质.7. 德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数() 1 0 x f x x ⎧=⎨⎩,为有理数,为无理数,称为狄利克雷函数,则关于函数()f x 有以下四个命题: ①()()1f f x =; ②函数()f x 是偶函数;③任意一个非零有理数T ,()()f x T f x +=对任意x R ∈恒成立;④存在三个点()()()()()()112233 A x f x B x f x C x f x ,,,,,,使得ABC △为等边三角形.其中真命题的个数是( )A .4B .3 C.2 D .1 【答案】A考点:1.函数的奇偶性;2.函数的周期性;3.分段函数的表示与求值. 8. 某几何体的三视图如图所示,则该几何体的体积为( )A .10B .20 C.40 D .60 【答案】B 【解析】试题分析:由三视图可知该几何体的直观图如下图所示,且三角形ABC 是以角A 为直角的直角三角形,4,3AB AC ==,从而5BC =,又5BD =,且BD ⊥平面ABC ,故四边形BCED 中边长为5的正方形,过A 作AH BC ⊥于H ,由易知AH ⊥平面BCED ,在直角三角形ABC 中可求得125AH =,从而ABCD 11125520335A BCED V V S AH -==⨯⨯=⨯⨯⨯=正方形,故选B.考点:1.三视图;2.多面体和体积.9. 已知A 、B 是椭圆()222210x y a b a b +=>>长轴的两个端点,M 、N 是椭圆上关于x 轴对称的两点,直线AM 、BN 的斜率分别为()1212 0k k k k≠,,则12k k +的最小值为( )A .1 BD【答案】A考点:1.双曲线的标准方程与几何性质;2.基本不等式;3.斜率公式.【名师点睛】本题考查双曲线的标准方程与几何性质、基本不等式、斜率公式,属中档题;双曲线的标准方程与几何性质是高考的热点,特别是双曲线的性质,几乎每年均有涉及,主要以选择题、填空题为主,解题时,应利用图形,挖掘题目中的隐含条件,结合图形求解.10. 在棱长为6的正方体1111ABCD A B C D -中,M 是BC 的中点,点P 是面11DCC D 所在的平面内的动点,且满足APD MPC ∠=∠,则三棱锥P BCD -的体积最大值是( )A .36B .24 D . 【答案】A考点:1.线面垂直的判定与性质;2.轨迹方程的求法;3.多面体的体积.11. 已知函数()()()3ln 1 01 1 0x x f x x x -<⎧⎪=⎨-+≥⎪⎩,,,若()f x ax ≥恒成立,则实数a 的取值范围是( ) A .20 3⎡⎤⎢⎥⎣⎦,B .30 4⎡⎤⎢⎥⎣⎦, C.[]0 1, D .30 2⎡⎤⎢⎥⎣⎦, 【答案】B 【解析】试题分析:在同一坐标系内作出函数()()()3ln 1 01 1 0x x f x x x -<⎧⎪=⎨-+≥⎪⎩,,与函数y ax =和图象,通过图象可知,当直线y ax =绕着原点从x 轴旋转到与图中直线l 重合时,符合题意,当0x >时,2()3(1)f x x '=-,设直线l与函数()y f x =的切点为00(,)P x y ,则3200000(1)3(1)y x x x x --==,解之得032x =,所以直线l 的斜率2333(1)24k =⨯-=,所以a 的取值范围为30 4⎡⎤⎢⎥⎣⎦,,故选B.考点:1.函数与不等式;2.导数的几何意义.【名师点睛】本题考查函数与不等式、导数的几何意义,属中档题;导数的几何意义是每年高考的必考内容,利用导数解决不等式恒成立问题,首先要构造函数,利用导数研究函数的单调性,求出最值,进而得出相应的含参不等式,从而求出参数的范围;或参变分离,构造函数,直接把问题转化为函数的最值问题;或通过数列结合解题.12. 已知过抛物线()2:20G y px p =>焦点F 的直线l 与抛物线G 交于M 、N 两点(M 在x 轴上方),满足3MF FN =,163MN =,则以M 为圆心且与抛物线准线相切的圆的标准方程为( )A .2211633x y ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭ B .2211633x y ⎛⎛⎫-+= ⎪ ⎝⎭⎝⎭C.()(22316x y -+-= D .()(22316x y -+=【答案】C考点:1.抛物线的标准方程与几何性质;2.直线与抛物线的位置关系;2.圆的标准方程.【名师点睛】本题考查抛物线的标准方程与几何性质、直线与抛物线的位置关系、圆的标准方程,属难题;在解抛物线有关问题时,凡涉及抛物线上的点到焦点的距离时,一般要运用定义转化为到准线的距离处理;抛物线的焦点弦一直是高考的热点,对于焦点弦的性质应牢固掌握.第Ⅱ卷(非选择题 共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若x 、y 满足约束条件10040x x y x y -≥⎧⎪-≤⎨⎪+-≤⎩,则1y x -的最大值为 .【答案】2考点:线性规划.14. 在ABC △中, 3 5AB AC ==,,若O 为ABC △外接圆的圆心(即满足OA OB OC ==),则AO BC ⋅的值为 . 【答案】8考点:数量积的几何运算.【名师点睛】本题考查数量积的几何运算,属中档题;平面向量的数量积有两种运算,一是依据长度与夹角,即数量积的几何意义运算,一是利用坐标运算,本题充分利用向量线性运算的几何意义与数量积的几何意义进行运算,运算量不大,考查子学生逻辑思维能力,体现了数形结合的数学思想. 15. 已知数列{}n a 的各项均为正数,11142 n n n n a a a a a ++=-=+,,若数列11n n a a -⎧⎫⎨⎬+⎩⎭的前n 项和为5,则n = .【答案】120 【解析】试题分析:数列11n n a a -⎧⎫⎨⎬+⎩⎭的前n 项和为321121211223111154444n n n a a a a a a a a a a a a a a +-----+++=++==+++,所以122n a +=, 又114 n n n na a a a ++-=+,所以221 4n n a a +-=,由此可得22211444,2244,120n a a n n n n +=+=+∴=+=,即应填120.考点:1.数列求和;2.累和法求数列通项.【名师点睛】本题考查数列求和,累和法求数列通项,属中档题;由数列的递推公式求通项公式时,若递推关系为a n +1=a n +f (n )或a n +1=f (n )·a n ,则可以分别通过累加、累乘法求得通项公式,另外,通过迭代法也可以求得上面两类数列的通项公式,数列求和的常用方法有倒序相加法,错位相减法,裂项相消法,分组求和法,并项求和法等,可根据通项特点进行选用.16. 过抛物线()220y px p =>的焦点F 的直线l 与抛物线在第一象限的交点为A ,与抛物线的准线的的交点为B ,点A 在抛物线的准线上的射影为C ,若 48AF FB BA BC =⋅=,,则抛物线的方程为 . 【答案】24y x =考点:1.抛物线的标准方程与几何性质;2.向量数量积的几何意义.三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. (本小题满分12分)在ABC △中,内角A 、B 、C 所对的边分别为 a b c ,,,已知 4 6 2b c C B ===,,. (1)求cos B 的值; (2)求ABC △的面积.【答案】(1)34;(2.试题解析:(1)在ABC △中,sin sin b c B C =,因为 4 6 2b c C B ===,,,所以46sin sin 2B B=,即46sin 2sin cos B B B =,又sin 0B ≠,∴3cos 4B =.(2)由(1)知3cos 4B =,从而sin B =.因此sin sin 22sin cos C B B B ===21cos cos22cos 18C B B ==-=.所以()()13sin sin sin sin cos cos sin 84A B C B C B C B C π=--=+=+=+=所以ABC △的面积为1462⨯⨯. 考点:1.正弦定理;2.三角恒等变换;3.三角形内角和与三角形面积公式.【名师点睛】本题考查正弦定理、三角恒等变换、三角形内角和与三角形面积公式,属中档题. 正、余弦定理是揭示三角形边角关系的重要定理,直接运用正弦定理解决一类已知三角形两边及一角对边求其它元素,或已知两边及一边对角求其它元素的问题,这时要讨论三角形解的个数问题;利用余弦定理可以快捷求第三边直接运用余弦定理解决一类已知三角形两边及夹角求第三边或者是已知三个边求角的问题;知道两边和其中一边的对角,利用余弦定理可以快捷求第三边. 18. (本小题满分12分)如图所示,在三棱柱111ABC A B C -中,11AA B B 为正方形,11BB C C 为菱形,1160BB C ∠=︒,平面11AA B B ⊥平面11BB C C .(1)求证:11B C AC ⊥;(2)设点E 、F 分别是1B C ,1AA 的中点,试判断直线EF 与平面ABC 的位置关系,并说明理由; (3)求二面角1B AC C --的余弦值.【答案】(1)见解析;(2) EF ∥平面ABC ;.试题解析:(1)连接1BC ,在正方形11ABB A 中,1AB BB ⊥, 因为平面11AA B B ⊥平面11BB C C ,平面11AA B B平面111BB C C BB =,AB ⊂平面11ABB A ,所以AB ⊥平面11BB C C ,因为1B C ⊥平面11BB C C ,所以1AB B C ⊥.在菱形11BB C C 中,11BC B C ⊥,因为1BC ⊥面1ABC ,AB ⊥平面1ABC ,1BC AB B =,所以1B C ⊥平面1ABC ,因为1AC ⊥平面1ABC ,所以11B C AC ⊥.(2)EF ∥平面ABC ,理由如下:取BC 的中点G ,连接GE 、GA ,因为E 是1B C 的中点,所以1GE BB ∥,且112GE BB =,因为F 是 1AA 的中点,所以112AF AA =. 在正方形11ABB A 中,1111 AA BB AA BB =∥,,所以GE AF ∥,且GE AF =. ∴四边形GEFA 为平行四边形,所以EF GA ∥. 因为EF ABC ⊄平面,GA ABC ⊂平面, 所以EF ABC ∥平面.(3)在平面11BB C C 内过点B 作1Bz BB ⊥,由(1)可知:11AB BB C C ⊥平面,以点B 为坐标原点,分别以BA 、1BB 所在的直线为x 、y 轴,建立如图所示的空间直角坐标系B xyz -,设()2 0 0A ,,,则()10 2 0B ,,.在菱形11BB C C 中,1160BB C ∠=︒,所以(0 1 C -,,(10 1 C ,. 设平面1ACC 的一个法向量为() 1x y =n ,,.因为100n AC n CC ⎧⋅=⎪⎨⋅=⎪⎩即()(()() 1 2 1 0 10 2 00x y x y ⎧⋅--=⎪⎨⋅=⎪⎩,,,,,,,,所以0x y ⎧=⎪⎨⎪=⎩0 1n ⎫=⎪⎪⎝⎭,,, 由(1)可知:1CB 是平面1ABC 的一个法向量.所以(1110 10 3 cos nCB n CB n CB ⎛⎫⋅ ⎪ ⎪⋅⎝<>===⋅,,,,,,所以二面角1B AC C --. 考点:1.面面垂直的判定与性质;2.线面平行、垂直的判定与性质;3.空间向量的应用.【名师点睛】本题考查.面面垂直的判定与性质、线面平行、垂直的判定与性质及空间向量的应用,属中档题;解答空间几何体中的平行、垂直关系时,一般要根据已知条件把空间中的线线、线面、面面之间的平行、垂直关系进行转化,转化时要正确运用有关的定理,找出足够的条件进行推理;求二面角,则通过求两个半平面的法向量的夹角间接求解.此时建立恰当的空间直角坐标系以及正确求出各点的坐标是解题的关键所在.19. (本小题满分12分)如图,在平面直角坐标系xOy 中,已知()00 R x y ,是椭圆22:12412x y C +=上的一点,从原点O 向圆()()2200:8R x x y y -+-=作两条切线,分别交椭圆于P ,Q .(1)若R 点在第一象限,且直线OP ,OQ 互相垂直,求圆R 的方程;(2)若直线OP ,OQ 的斜率存在,并记为12 k k ,,求12k k 的值; (3)试问22OP OQ +是否为定值?若是,求出该值;若不是,说明理由. 【答案】(1)((228x y -+-=;(2)12-;(3)36.试题解析:(1)由圆R的方程知圆R的半径r=OP,OQ互相垂直,且和圆R相切,所以4OR==,即220016x y+=①又点R在椭圆C上,所以220012412x y+=②联立①②,解得0xy⎧=⎪⎨=⎪⎩R的方程为((228x y-+-=.(2)因为直线1:OP y k x=和2:OQ y k x=都与圆R==212288yk kx-⋅=-,因为点()00R x y,在椭圆C上,所以220012412x y+=,即22001122y x=-,所以2122141228xk kx-==--.(3)方法一(1)当直线OP、OQ不落在坐标轴上时,设()11P x y,,()22Q x y,,由(2)知12210k k+=,所以121221y yx x=,故2222121214y y x x=,因为()11P x y,,()22Q x y,,在椭圆C上,所以221112412x y+=,222212412x y+=,即22111122y x=-,22221122y x=-,所以222212121111212224x x x x⎛⎫⎛⎫--=⎪⎪⎝⎭⎝⎭,整理得221224x x+=,所以222212121112121222y y x x⎛⎫⎛⎫+=-+-=⎪ ⎪⎝⎭⎝⎭,所以()()22222222221122121236OP OQ x y x y x x y y +=+++=+++=.(2)当直线OP 、OQ 落在坐标轴上时,显然有2236OP OQ +=. 综上:2236OP OQ +=.考点:1.椭圆的标准方程与几何性质;2.圆的标准方程;3.直线与圆的位置关系. 20. (本小题满分12分)设椭圆()2222:10x y C a b a b +=>>的左、右焦点分别为1F 、2F ,上顶点为A ,过A 与2AF 垂直的直线交x 轴负半轴于Q 点,且12220F F F Q +=. (1)求椭圆C 的离心率;(2)若过A 、Q 、2F 三点的圆恰好与直线30x --=相切,求椭圆C 的方程;(3)过2F 的直线l 与(2)中椭圆交于不同的两点M 、N ,则1F MN △的内切圆的面积是否存在最大值?若存在,求出这个最大值及此时的直线方程;若不存在,请说明理由.【答案】(1)12;(2) 22143x y +=;(3)1F MN △的内切圆的面积的最大值为916π,此时直线l 的方程为1x =.(3)设1F MN △的内切圆的半径为R ,则1F MN △的周长为48a =,由此可得112121212F MN S F F y y y y =⋅-=-△,设直线l 的方程为1x my =+,与椭圆方程联立得()2234690my my ++-=,由根与系数关系代入112F MNS y y =-=△,换元令t =()12121211313F MN t S t t t t==≥-+△,可知当1t =时,14F MN S R =△有最大值3,从而求出内切圆面积的最大值与相应的直线方程即可.试题解析:(1)由题()0 A b ,,1F 为2QF 的中点.设()()12 0 0F c F c -,,,,则()3 0Q c -,, ()3 AQ c b =--,,()2 AF c b =-,,由题2AQ AF ⊥,即22230AQ AF c b ⋅=-+=,∴()22230c a c -+-=即224a c =,∴12c e a ==. (2)由题2Rt QAF △外接圆圆心为斜边2QF 的中点()1 0F c -,,半径2r c =, ∵由题2Rt QAF △外接圆与直线30x -=相切,∴d r =,即322c c --=,即34c c +=,∴1c =,22a c ==,b =C 的方程为22143x y +=.(3)设()11 M x y ,,()22 N x y ,,由题12 y y ,异号,设1F MN △的内切圆的半径为R ,则1F MN △的周长为48a =,()111142F MN S MN F M F N R R =++=△, 因此要使1F MN △内切圆的面积最大,只需R 最大,此时1F MN S △也最大,112121212F MN S F F y y y y =⋅-=-△, 由题知,直线l 的斜率不为零,可设直线l 的方程为1x my =+, 由221143x my x y =+⎧⎪⎨+=⎪⎩得()2234690m y my ++-=,由韦达定理得122634m y y m -+=+,122934y y m -=+,(0m R ∆>∈⇒)112F MN S y y =-=△令t =1t ≥,()12121211313F MN t S t t t t==≥-+△, 当1t =时,14F MN S R =△有最大值3,此时,0m =,max 34R =,故1F MN △的内切圆的面积的最大值为916π,此时直线l 的方程为1x =. 考点:1.椭圆的标准方程与几何性质;2.直线与椭圆的位置关系;3.直线与圆的位置关系. 21. (本小题满分12分) 已知0t >,设函数()()3231312t f x x x tx +=-++.(1)存在()00 2x ∈,,使得()0f x 是()f x 在[]0 2,上的最大值,求t 的取值范围; (2)()2x f x xe m ≤-+对任意[0 )x ∈+∞,恒成立时,m 的最大值为1,求t 的取值范围.【答案】(1)5[ )3+∞,;(2) 1(0 ]3,.(2)()()()323223131313123131222x x x t t t x x tx xe m m xe x x tx x e x x t +++⎛⎫-++≤-+⇔≤-+-+=-+-+ ⎪⎝⎭,构造函数()()23132x t g x e x x t +=-+-,道m 的最大值为1,等价于()()231302x t g x e x x t +=-+-≥在区间[0 )+∞,上恒成立,由于()0130g t =-≥,则103t <≤,此时()0g x '>恒成立,即()g x 在区间[0 )+∞,上单调递增,符合题意.试题解析:(1)()()()()2'331331f x x t x t x x t =-++=--,①当01t <<时,()f x 在()0 t ,上单调递增,在() 1t ,单调递减,在()1 2,单调递增, ∴()()2f t f ≥,由()()2f t f ≥,得3234t t -+≥在01t <<时无解, ②当1t =时,不合题意;③当12t <<时,()f x 在()0 1,单调递增,在()1 t ,递减,在() 2t ,单调递增, ∴()()1212f f t ⎧≥⎪⎨<<⎪⎩即1332212t t ⎧+≥⎪⎨⎪<<⎩,∴523t ≤<,④当2t ≥时,()f x 在()0 1,单调递增,在()1 2,单调递减,满足条件, 综上所述:5[ )3t ∈+∞,时,存在()00 2x ∈,,使得()0f x 是()f x 在[]0 2,上的最大值.∴()()0130g x g t ≥=-≥,满足条件,∴t 的取值范围是1(0 ]3,.考点:1.导数与函数的单调性、极值,最值;2.函数与不等式.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22. (本小题满分10分)选修4-4:坐标系与参数方程已知圆锥曲线2cos :x C y αα=⎧⎪⎨=⎪⎩(α为参数)和定点(0 A ,1F 、2F 是此圆锥曲线的左、右焦点,以原点O 为极点,以x 轴的正半轴为极轴建立极坐标系. (1)求直线2AF 的直角坐标方程;(2)经过点1F 且与直线2AF 垂直的直线l 交此圆锥曲线于M 、N 两点,求12MF NF -的值.【答案】0y +-=;(2试题解析:(1)曲线2cos :x C y αα=⎧⎪⎨=⎪⎩可化为22143x y +=,其轨迹为椭圆,焦点为()1 1 0F -,,()21 0F ,.经过(0 A 和()21 0F ,的直线方程为11x =0y +. (2)由(1)知,直线2AF的斜率为2l AF ⊥,所以l,倾斜角为30︒, 所以l的参数方程为112x y t ⎧=-+⎪⎪⎨⎪=⎪⎩(t 为参数). 代入椭圆C的方程中,得213360t --=. 因为 M N ,在点1F的两侧,所以1112MF NF t t -=+=考点:1.参数方程与普通方程的互化;2.直线参数方程的应用. 23. (本小题满分10分)选修4-5:不等式选讲 设()34f x x x =-+-. (1)解不等式()2f x ≤;(2)若存在实数x 满足()1f x ax ≤-,试求实数a 的取值范围. 【答案】(1) 59 22⎡⎤⎢⎥⎣⎦,;(2)()1 2[ )2-∞-+∞,,【解析】试题分析:(1)由绝对值的意义去掉绝对值符号,将函数()f x 表示成分段函数的形式,作出函数()f x 的图象,数形结合可得到不等式的解集;(2)在同一坐标系内作出函数()yf x =与函数1y ax =-的图象,数形结合可求出a 的范围.(2)函数1y ax =-的图象是过点()0 1-,的直线, 当且仅当函数()y f x =与直线1y ax =-有公共点时,存在题设的x .由图象知,a 的取值范围为()12[ )2-∞-+∞,,.考点:1.含绝对值不等式的解法;2.分段函数的表示与作图;3.函数与不等式.。
2017届河北省定州中学高三(高补班)上学期周练(三)(8.21)数学试题(解析版)

河北定州中学2016-2017学年第一学期高四数学周练试题(三)一、选择题(共12小题,共60分)1.已知F 2,F 1是双曲线)0,0(2222>>-b a bx a y 的上,下两个焦点,点F 2关于渐近线的对称点恰好落在以F 1为圆心,| OF 1 |为半径的圆上,则双曲线的离心率为( ) A .2 B .3 C .3 D .22.以椭圆1492422=+y x 的焦点为顶点、顶点为焦点的的双曲线方程是( ) A .1242522=-y x B .1252422=-y x C .1242522=-x y D .1252422=-x y 3.已知函数()222015222015f x x x x x =-+-++++()x R ∈,则使方程2(32)(1)f m m f m -+=-成立的整数..m 的个数是( )A .3个B .4个C .5个D .无穷多个4.已知函数()f x 是定义在(,0)(0,)-∞⋃+∞上的奇函数, 在区间(,0)-∞单调递增且(1)0f -=.若实数a 满足212(log )(log )2(1)f a f a f -≤, 则实数a 的取值范围是( )A .[1,2]B .1(,](1,2]2-∞⋃ C .(0,2] D .1(0,](1,2]2⋃5.若关于x 的方程2(1lg )10x x a m a +++=(0a >且1)a ≠有实数解,则实数m 的取值范围是( ) A .3010m -<≤或10m ≥ B .3010m -<≤C .10m ≥D .1010m <<6.方程32log 0x x ++=的根所在的区间为( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)7.如图,在等腰梯形ABCD 中,AB ∥CD ,且AB=2AD ,设θ=∠DAB ,)2,0(πθ∈,以A 、B 为焦点且过点D的双曲线的离心率为1e ,以C 、D 为焦点且过点A 的椭圆的离心率为2e ,则12e e ⋅( )A .随着θ角的增大而增大B .随着θ角的增大而减小C .为定值1D .为定值28.若所有满足)0,0(1||||>>=+b a y b x a 的实数x, y 均满足12122222+-+++++y y x y y x 22≤,则b a 2+的取值范围为( )A .),2[+∞B .]2,1[C .),1[+∞D .]2,0(9.对实数a 和b 定义运算“⊗”:,1,, 1.a ab a b b a b -≤⎧⊗=⎨->⎩设函数()()22()2,f x x x x x R =-⊗-∈,若函数()y f x c =-恰有两个不同的零点,则实数c 的取值范围是( ) A 、(]3,21,2⎛⎫-∞-- ⎪⎝⎭B 、(]3,21,4⎛⎫-∞--- ⎪⎝⎭C 、111,,44⎛⎫⎛⎫-+∞ ⎪ ⎪⎝⎭⎝⎭D 、311,,44⎛⎫⎛⎫--+∞ ⎪ ⎪⎝⎭⎝⎭10.函数ln cos 22y x x ππ⎛⎫=-<< ⎪⎝⎭的大致图像是( )11.已知函数32()f x x ax bx c =+++,且0(1)(2)(3)3f f f <-=-=-≤,则( ) A .3c ≤ B .36c <≤ C .69c <≤ D .9c > 12.定义在()1,1- 上的函数 ()()⎪⎪⎭⎫⎝⎛--=-xy y x f y f x f 1;当()()1,00.x f x∈->时若()111,,05112P f f Q f R f ⎛⎫⎛⎫⎛⎫=+== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;则,,P Q R 的大小关系为( ). A .R Q P >> B .R P Q >> C .P R Q >> D .Q P R >>第II 卷(非选择题)二、填空题(4小题,共20分)13.设AB 是椭圆22221x y a b+=的不垂直于对称轴的弦,M 为AB 的中点,O 为坐标原点,则AB OM k k ⋅=___________.14.设P 是双曲线116922=-y x 上一点,M ,N 分别是两圆:4)5(22=+-y x 和1)5(22=++y x 上的点,则||||PN PM -的最大值为____________.15.已知抛物线2:2C y x =,过抛物线C 上一点)2,1(P 作倾斜角互补的两条直线PA 、PB ,分别交抛物线C 于A 、B 两点.则直线AB 的斜率为 .16.已知()f x 是定义在R 上且周期为3的函数,当[)0,3x ∈时,21()22f x x x =-+, 若函数()y f x a =-在区间[]3,4-上有10个零点(互不相同),则实数a 的取值范围是 . 三、解答题(8小题,共70分)17.在平面直角坐标系xOy 中,点P (a ,b )(a >b >0)为动点,F 1、F 2分别为椭圆x 2a 2+y 2b 2=1的左、右焦点.已知△F 1PF 2为等腰三角形. (1)求椭圆的离心率e ;(2)设直线PF 2与椭圆相交于A ,B 两点,M 是直线PF 2上的点,满足AM BM=-2,求点M 的轨迹方程.18.已知抛物线C :y 2=2px (p>0)过点A (1,-2). (Ⅰ)求抛物线C 的方程,并求其准线方程;(Ⅱ)是否存在平行于OA (O 为坐标原点)的直线l ,使得直线l 与抛物线C 有公共点,且直线OA 与l 的距离等于55?若存在,求出直线l 的方程;若不存在,说明理由. 19.(本题满分18分,第1小题满分4分,第2小题满分6分,第3小 题满分8分. ) 已知数列{n a }满足:*111,||,nn n a a a p n N +=-=∈,n S 为数列{}n a 的前n 项和。
【全国百强校】河北省衡水中学2017届高三上学期第二次调研考试理数试题解析(原卷版)
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.z 是z 的共轭复数,若()2,2(z z z z i i +=-=为虚数单位),则z =( )A .1i +B .1i --C .1i -+D .1i - 2.已知向量a 与b 的夹角为60,2,5a b ==,则2a b -在a 方向上的投影为( )A .32 B .2 C .52D .3 3.在我国古代著名的数学专著《九章算术》里有—段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,曰增十三里:驽马初日行九十七里,曰减半里,良马先 至齐,复还迎驽马,二马相逢,问:几日相逢?( )A .12日B .16日C . 8日D .9日 4.已知0,0a b >>,若不等式3103m a b a b--≤+恒成立,则m 的最大值为( ) A .4 B .16 C . 9 D .35.动点(),P x y 满足1253y x y x y ≥⎧⎪+≤⎨⎪+≥⎩,点Q 为()1,1,O -为原点,OQ OP OQ λ=,则λ的最大值是( )A .1-B .1C .2 D.2 6.如图为某几何体的三视图,則该几何体的表面积为( )A . 105+B . 102+C .6226++D .626++7.已知函数()()2sin sin 3f x x x ϕ=+是奇函数,其中0,2πϕ⎛⎫∈ ⎪⎝⎭,则函数()()cos 2g x x ϕ=-的 图象( ) A .关于点,012π⎛⎫⎪⎝⎭对称 B .可由函数()f x 的图象向右平移3π个单位得到 C .可由函数()f x 的图象向左平移6π个单位得到 D .可由函数()f x 的图象向左平移3π个单位得到 8.ABC ∆中,若()sin 3cos sin cos C A A B =+,则( )A .3B π=B .2b a c =+C .ABC ∆是直角三角形D .222a b c =+或2B A C =+ 9.已知数列{}n a 满足()111,2n n n a a a n N a *+==∈+,若()()11121,n n b n n N b a λλ*+⎛⎫=-+∈=- ⎪⎝⎭, 且数列{}n b 是单调递增数列,則实数λ的取值范围是( ) A .23λ>B .32λ>C .23λ<D .32λ< 10.如图,正方形ABCD 中,M 是BC 的中点,若AC AM BD λμ=+,则λμ+=( )A .43 B .53 C .158D .2 11.已知函数()3212f x ax x =+,在1x =-处取得极大值,记()()1'g x f x =,程序框图如图所示,若输出的结果20142015S >,则判断框中可以填人的关于n 的判断条件是( )A .2014n ≤?B .2015n ≤?C .2014n >?D .2015n >?12.已知{}n a 满足()211112311,,44...44nn n n n n a a a n N S a a a a *-+⎛⎫=+=∈=++++ ⎪⎝⎭,则54n n n S a -=( )A .1n -B .nC .2nD .2n第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题,每题5分,满分20分.)13.数列{}n a 满足:11a =,且对任意的,m n N *∈都有:n m n m a a a nm +=++,则100a = .14.在ABC ∆中,111,2,4,,,2224A AB AC AF AB CE CA BD BC π∠======,则DE DF 的 值为 .15.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,5cos 23C =,且cos cos 2a B b A +=, 则ABC ∆面积的最大值为 . 16.已知方程23ln 02x ax -+=有4个不同的实数根,則实数a 的取值范围是 . 三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.) 17.(本小题满分12分)在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且()3cos 23cos a C b c A =-.(1)求角A 的大小; (2)求25cos 2sin 22C B π⎛⎫-- ⎪⎝⎭的取值范围.18.(本小题满分12分)设数列{}n a 的前n 和为n S ,()211,22n n a S na n n n N*==-+∈.(1)求证:数列{}n a 为等差数列, 并分别写出n a 和n S 关于n 的表达式; (2)是否存在自然数n ,使得321...2112423n n S S S S n+++++=?若存在,求出n 的值; 若不存在, 请说 明理由; (3)设()()()1232,...7n n n n c n N T c c c c n N n a **=∈=++++∈+,若不等式()32n mT m Z >∈,对 n N *∈恒成立, 求m 的最大值.19.(本小题满分12分)如图, 以坐标原点O 为圆心的单位圆与x 轴正半轴交于点A ,点,B P 在单位圆上, 且525,,55B AOB α⎛⎫-∠= ⎪ ⎪⎝⎭.(1)求4cos 3sin 5cos 3sin αααα-+的值;(2)若四边形OAQP 是平行四边形.①当P 在单位圆上运动时,求点Q 的轨迹方程; ②设()02POA θθπ∠=≤≤,点(),Q m n ,且()3f m n θ=+,求关于θ的函数()f θ的解析式, 并求其单调增区间.20.(本小题满分12分)已知函数()()1ln f x x a x a R x=-+∈. (1)若函数()f x 在[)1,+∞上单调递增,求实数a 的取值范围; (2)已知()()()()()211321,,22g x x m x m h x f x g x x =+-+≤-=+,当1a =时, ()h x 有两个扱值 点12,x x ,且12x x <,求()()12h x h x -的最小值.21.(本小题满分12分)在单调递增数列{}n a 中, 122,4a a ==,且21221,,n n n a a a -+成等差数 列,22122,n n n a a a ++ 成等比数列,1,2,3,...n =.(1)①求证:数列{}2n a 为等差数列;②求数列{}n a 通项公式;(2)设数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,证明:()4,33nn S n N n *>∈+.请考生在第22、23、24三题中任选一题作答,如果多做,则按所做的第一题记分.解答时请写清题号. 22.(本小题满分10分)选修4-1:几何证明选讲如图,,A B 是圆O 上两点, 延长AB 至点C ,满足22AB BC ==,过C 作直线CD 与圆O 相切于点,D ADB ∠的平分线交AB 于点E.(1)证明:CD CE =; (2)求ADBD的值.23.(本小题满分10分)选修4-4:坐标系与参数方程在平面直角坐标系中,曲线1C 的参数方程为cos (0,sin x a a b y b ϕϕϕ=⎧>>⎨=⎩为参数),以O 为极点,x 轴的正 半轴为极轴建立极坐标系,曲线2C 是圆心在极轴上且经过极点的圆,已知曲线1C 上的点()2,3M 对应 的参数,34ππϕθ==与曲线2C 交于点2,4D π⎛⎫⎪⎝⎭. (1)求曲线1C ,2C 的普通方程; (2)()12,,,2A B πρθρθ⎛⎫+ ⎪⎝⎭是曲线1C 上的两点, 求221211ρρ+的值.24.(本小题满分10分)选修4-5:不等式选讲 已知()2122f x x x x =-++++. (1)求证:()5f x ≥;(2)若对任意实数()229,1521x f x a a -<++都成立, 求实数a 的取值范围.。
河北省定州中学2017届高三(高补班)上学期期中考试数学试题doc
河北省定州中学2017届高三(高补班)上学期期中考试数学试题doc定州中学XX年第一学期高四数学期中考试试题时间:120分钟总分:150分I卷一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若集合B?{y|y?2x,x?R},且A?B?A则集合A可能是A. ?1,2? B . xx?1C. ??1,0,1?D . R 2.函数y?x|x|?px , x?RA .是偶函数B.是奇函数 C.不具有奇偶性D .奇偶性与p有关3.复数z???i的共轭复数在复平面上对应的点在1?iA .第一象限B.第二象限C.第三象限D.第四象限4.为了得到y?cos2x,只需将y?sin(2x??3) 作如下变换A .向右平移?3 个单位B.向右平移?6 个单位C .向左平移?? 个单位 D.向右平移个单位12125. 已知平面向量a,b满足a?(a?b)?5,且a?2,b?1,则向量a与b夹角的余弦值为A .1133 B . ? C. D. ?22222??6. 已知函数f(x)?sin(x??) ,且|?|?,又?3f(x)dx?0 ,贝U函数f(x)的图象的一02 条对称轴是A .x??5?7?? B.x? C.x? D.x? 612367.已知??(??,), a?(cos?)cos? , b?(sin?)cos? , c?(cos?)sin?则42A . a?b?cB.a?c?b C. b?a?c D. c?a?b8. 已知函数f(x)的定义域为R 当x?0 时,f(x)?x3?1当?1?x?1 时,f(?x)??f(x) ;当x?111)? 时,f(x?)?f(x?) ,f(2016222A . ?2 B . ?1 C . 0 D .9. 已知定义在R上的奇函数y?f(x)满足f(x)?2 ,不等式f(x?1)?ln(x?2)?2?ex?1?3x 的解集为A . (?2,?1)B . (?1,??) C. (?1,2) D . (2,??)12201612x4?x2sinx?4f()?f()??f()?10. 已知函数f(x?)?,则… 42017201720172x?2A . 2017 B . 2016 C. 4034 D . 4032 11.已知函数f(x)?? 不可能为A . 2个B . 3个C . 4个D . 5个12 .函数f(x)?Asin(2x??)(???log5(1?x)(x?1)??(x?2)?2(x?1)2 ,则关于x的方程f(x)?a(a?R)实根个数?2,A?0) 部分图象如图所示,且f(a)?f(b)?0 ,对不同的x1,x2??a,b?,若f(x1)?f(x2),有f(x1?x2)?3 , 则5??,) 上是减函数A . f(x)在(?1212B . f(x)在(?y 2 5??,) 上是增函数1212a C . f(x)在(?5?3,6)上是减函数O b x D . f(x)在(?5?3,6)上是增函数□卷二、填空题13. 已知tan(???)??12? , tan(??)?,贝U tan(??)的值为544414. 在?ABC 中,?A??2,AB?2,AC?4,AF?111AB,CE?CA,BD?BC 贝U224DE?DF 的值为.15. 在?ABC中,边AB的垂直平分线交边AC于D若C??3,BC?8,BD?7,贝U?ABC的面积为.g(x1)f(x2)x2?1x,g(x)?x ,对任意x1,x2?(0,??),不等式16.设函数f(x)?恒?kk?1xe成立,则正数k的取值范围是.三、解答题17. ( 本小题满分10分)已知平面上三个向量a,b,c的模均为1,他们之间的夹角均为120。
河北省定州中学2017届高三上学期周练(11.11)数学试题 含答案
河北定州中学2016-2017学年第一学期高三数学周练试题(9)一、选择题1.设全集U R =,2{|ln(2)},{|2}A x Z y x B x x x =∈=-=≤,则AB =( ) A .}2|{<∈x Z x B .{}02x Z x ∈≤<C . {}1,2D .{}0,1,2 2.设45log ,45,54212.03.0=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=c b a ,则c b a ,,的大小关系是( )A .c a b >>B .c b a >>C .a b c >>D .a c b <>3.在复平面内与复数21i z i=+所对应的点关于实轴对称的点为A ,则A 对应的复数为( )A .1i +B .1i -+C .1i --D .1i -4.已知命题“()()p q ⌝∨⌝”是假命题,给出下列四个结论:①命题“p q ∧"是真命题;②命题“p q ∧”是假命题;③命题“p q ∨”是假命题;④命题“p q ∨”是真命题.其中正确的结论为( )A 、①③B 、②③C 、①④D 、②④5.已知()522100121031...x x a a x a x a x -+=++++,则12310...a a a a ++++=( )A .1-B .1C .2-D .06.(2014春•凉州区校级期末)设f (x )=,则f (5)的值为( )A .8B .9C .10D .117.N 为圆221xy +=上的一个动点,平面内动点00(,)M x y 满足01y ≥且030OMN ∠= (O 为 坐标原点),则动点M 运动的区域面积为( ) A.8233π- B.433π- C 。
233π+ D 。
433π+ 8.ABC ∆中,5,,BC G O =分别为ABC ∆的重心和外心,且5GO BC ⋅=,则ABC ∆的形状是( )A .锐角三角形B .钝角三角形C .直角三角形D .上述均不是9.以()()1,3,5,1A B -为端点的线段的垂直平分线方程是(A)3x —y-8=0 (B )3x+y+4=0 (C )3x-y+6=0 (D) 3x+y+2=010.已知函数log (2)a y ax =-在区间[]0,1上是x 的减函数,则a 的范围是( )A .()0,1B .()1,2C .()0,2D .()2,+∞11.已知(,5,21)A x x x --(1,2,2)B x x +-,当||AB 取最小值时,x 的值等于( )A .87B .-87C .19D .191412.椭圆的离心率为( ) A .23 B .43 C .22D .32 二、填空题13.已知复数21i z i+=-(i 是虚数单位),则||z = . 14.0x 是x 的方程x a a x log =)10(≠>a a ,且的解,则0,1,x a 这三个数的大小关系是 .15.函数()f x 是R 上的增函数,且(sin )(cos )(sin )(cos )f f f f ωωωω+->-+,其中ω为锐角,并且使得函数()sin()4g x x πω=+在(,)2ππ上单调递减,则ω的取值范围是 .16.已知点A(x ,lgx1),B (x2,lgx2)是函数f (x)=lgx 的图象上任意不同两点,依据图象可知,线段AB 总是位于A ,B 两点之间函数图象的下方,因此有结论122lg lg x x <lg ()成立.运用类比思想方法可知,若点A (x1,2x1),B(x2,2x2) 是函数g (x)=2x 的图象上的不同两点,则类似地有__________成立.三、解答题17.已知数列}{n a 满足11=a ,)(2211*++∈+=N n a a a n n n n n . (1)证明数列}2{nn a 是等差数列;(2)求数列}{na 的通项公式. 18.选修4—1:几何证明选讲如图所示,在ABC ∆中,CD 是ACB ∠的角平分线,ACD ∆的外接圆交BC 于E 点。
【全国百强校】河北省定州中学2017届高三(高补班)上学期周练(8.7)语文(原卷版)
河北省定州中学(高补班)2017届高三上学期周练(8.7)语文试题时间:150分钟分数:150分第I 卷阅读题一、现代文阅读(9 分,毎小题3分)丹尼尔·贝尔认为:“目前居统治地位的是视觉观念。
声音和景象,尤其是后者组织了美学、统率了观众。
在一个大众社会里,这几乎是不可避免的。
”生活在都市中的人们被光怪陆离的形象的海洋淹没了。
不管是电视屏幕,还是公交车体广告,或者商店橱窗,触目全是形象。
语言是思维的工具,我们用语言思考和交流,但得到的信息80%以上却来自形象。
而现代都市正在纵容这种视觉依赖性,只要有形象,作为一个生活在当代文化中的人就会如鱼得水,用语言思考的环节正在被忽略。
这恰好与中国传统文化中关于言、象关系的经典论述相吻合:“言者所以明象,得象而忘言。
”这也许能说明,作为一个发展中国家,当代中国何以能够亦步亦趋地追随“当代文化正在变成一种视觉文化”的潮流:中国历史上本来就不象西方那样确立过高扬理性的“语言的中心地位”,所以即使没有经历西方那祥完备发展的“扫荡文化遗产的传统价值”的“机械复制时代”,中国同样可以沐浴着全球化浪潮中的欧风美雨,欣然接受这个当代文化向视觉文化转变的事实。
广告无疑是一种站在时代的风头浪尖上的文化现象。
它当然不可能逃脱当代文化整体走向的制约。
就大多数电视广告而言,假如你按下遥控器的静音钮,你一样可以看明白它们想要贩卖的是什么。
就平面广告来说,语言也一样受到了形象的巨大的挑战。
视觉文化时代的特点不仅体现在形象的“霸权”,更重要的是形象的大批量复制和无孔不入的渗透性正在导致现实与形象之间的区别的消失。
在这个意义上,形象的生产实际上也是在塑造着现实。
这就导致了现实“虚拟性和可模型化”的审美化倾向。
现实的审美化造就了德国哲学家威尔什所谓的“审美人”。
广告人正是从事“象征符号生产”职业的一类审美人。
广告人一方面具有审美化现实所塑造的审美人的普遍角色特征,另一方面由于职业关系他们也积极向社会提供着用形象说话的“象征商品”,亦即广告作品。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
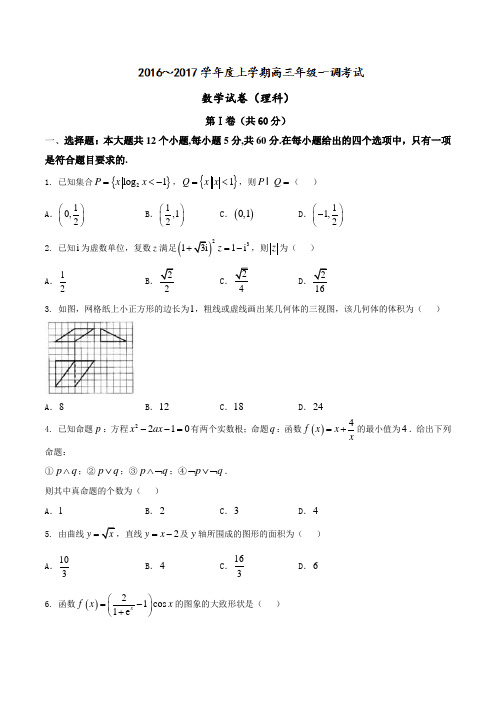
河北省定州中学2017届高三上学期周练(7.8)数学试题
一、选择题(本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有
一项是符合题目要求的.)
1.已知O为坐标原点,双曲线C:22221xyab(0a,0b)的左焦点为F,0c(0c),
以OF为直径的圆交双曲线C的渐近线于A,B,O三点,且FF0.关于x的方程
2
0axbxc
的两个实数根分别为1x和2x,则以1x,2x,2为边长的三角形的形状是( )
A.钝角三角形 B.直角三角形 C. 锐角三角形 D.等腰直角三角形
2.已知2,4a,3,bm,若0abab,则实数m( )
A.32 B.3 C.6 D.8
3.函数fx是定义在R上的奇函数,当0x时,2,0111,12xxfxfxx,则方程1fxx
在3,5上的所有实根之和为( )
A.0 B.2 C.4 D.6
4.已知直线1yx与双曲线221axby(0a,0b)的渐近线交于,两点,且过原
点和线段中点的直线的斜率为32,则ab的值( )
A.2327 B.32 C.932 D.233
5.已知抛物线C:28yx的焦点为F,准线与x轴的交点为,点在C上且2F,
则F的面积为( )
A.4 B.8 C.16 D.32
6.已知xfxxe,又2()()()gxfxtfx()tR若满足()1gx的x有四个,则t的取
值范围为( )
A.21,ee B.21,ee
C.21,2ee D.212,ee
7.设12,FF是双曲线2214yx的左、右两个焦点,若双曲线右支上存在一点,使
220OPOFFP(O为坐标原点)且12
PFPF
则的值为( )
A.2 B.12 C.3 D.13
8.已知函数2()2lnfxxx与()sin()gxx有两个公共点,则在下列函数中满足条件的
周期最大的()gx( )
A.sin(2)2x B.sin()22x
C.sin()2x D.sin()2x
9.已知函数21131xfxeaxa,若存在0,x,使得不等式1fx成立,则
实数a的取值范围为( )
A.20,31ee B.20,1e
C.2,31ee D.1,1e
10.点A是抛物线21:20Cypxp与双曲线22222:10,0xyCabab的一条渐近线的交
点,若点A到抛物线1C的准线的距离为p,则双曲线2C的离心率等于( )
A.2 B.3 C.5 D.6
11.已知函数21,11,11xxfxxxx或,且函数2gxfxkxk有两个不同的零点,则
实数k的取值范围是( )
A.303k B.103k或33k
C.33k或13k D.3133k或0k
12.过双曲线22221(0,0)xyabab左支上一点A作相互垂直的两条直线分别经过两焦点12,FF,
其中一条与双曲线交于点B,若220ABAFBF,则双曲线的离心率为( )
A.522 B.522 C.422 D.422
第Ⅱ卷(非选择题共90分)
二、填空题(本大题共4小题,每题5分,满分20分.)
13.已知抛物线xy42与经过该抛物线焦点的直线l在第一象限的交点为AA,在y轴和准线上的
投影分别为点,BC,2ABBC,则直线l的斜率为 .
14.已知1F、2F是椭圆C:22221(0)xyabab的两个焦点,P为椭圆C上一点,且12PFPF.
若12PFF的面积为9,则b____________.
15.已知)2,1(A,)2,1(B,动点满足BPAP,若双曲线)0,0(12222babyax的渐近线与
动点的轨迹没有公共点,则双曲线离心率的取值范围是 .
16.已知函数224,04log22,46xxxfxxx,若存在1x,2Rx,当12046xx时,
12fxfx,则
12
xfx
的取值范围是 .
三、解答题(本大题共8小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.已知函数ln0xafxaxax.
(Ⅰ)求此函数的单调区间及最值;
(Ⅱ)求证:对于任意正整数n,均有1+12+13…+1n≥ln!nen(e为自然对数的底数).
18.工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派
一次,工作时间不超过10分钟,如果前一个人10分钟内不能完成任务则撤出,再派下一个人。现在一
共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别123,,ppp,假设123,,ppp互不相等,且
假定各人能否完成任务的事件相互独立.
(1)如果按甲最先,乙次之,丙最后的顺序派人,求任务能被完成的概率.若改变三个人被派出的先后
顺序,任务能被完成的概率是否发生变化?
(2)若按某指定顺序派人,这三个人各自能完成任务的概率依次为123,,qqq,其中123,,qqq是123,,ppp的
一个排列,求所需要派出人员数目X的分布列和均值(数字期望);
(3)假定3211ppp,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字
期望)达到最小.
19.已知函数3().fxxx
(1)求曲线()yfx在点(1,0)M处的切线方程;
(2)如果过点(1,)b可作曲线()yfx的三条切线, 求实数b的取值范围.
20.如图,12FF、分别是椭圆2222:1(0)xyCabab 的左、右焦点,A是椭圆C的顶点,B是
直线2AF与椭圆C的另一个交点,1260FAFo.
(1)求椭圆C的离心率;
(2)若1AFB的面积为403, 求椭圆C的方程.
21.已知函数21()ln(1)2fxaxxax(1)a.
(1)讨论()fx的单调性与极值点;
(2)若21()1(1)2gxxxx,证明:当1a时,()gx的图象恒在()fx的图象上方;
(3)证明:2222ln2ln3ln21234(1)nnnnn*(,2)nNn.
22.已知函数),(22)(RaRxaxexfx.
(1)当1a时,求曲线)(xfy在1x处的切线方程;
(2)当0x时,若不等式0)(xf恒成立,求实数a的取值范围.
23.如图,在四棱锥ABCDP中, PD平面ABCD,DCAB//,
60,4,3,5,PADADDCBCADAB
.
(1)若M为PA的中点,求证://DM平面PBC;
(2)求三棱锥PBCD的体积.
24.已知函数)3cos(cos)(xxxf.
(1)求)32(f的值;
(2)求使41)(xf成立的x的取值集合.
:
