三角形经典问题总结
相似三角形 经典模型总结与例题分类

相似三角形经典模型总结与例题分类相似三角形经典模型总结在相似三角形中,有一些经典的模型,包括平移型、平行型、旋转180°型、翻折180°型、一般型、特殊型、斜交型、双垂直型等。
这些模型可以帮助我们更好地理解和解决相似三角形的问题。
其中,平移型、平行型、翻折180°型、斜交型和双垂直型都是比较常见的模型。
在解决相似三角形的问题时,可以根据具体情况选择相应的模型进行分析。
以下是一些例题,可以帮助我们更好地理解相似三角形的模型和应用。
例1:如图,EE1∥FF1∥MM1,若AE=EF=FM=MB,则S△.例2:如图,AD∥EF∥MN∥BC,若AD=9,BC=18,.例3:已知,P为平行四边形ABCD对角线,AC上一点,过点P的直线与AD,BC,CD的延长线,AB的延长线分别相交于点E,F,G,H。
则PEPH=PFPG。
例4:已知:在△ABC中,D为AB中点,E为AC上一点,且AE=2,BE、CD相交于点F。
则ABF=2EFD。
例5:已知:在△ABC中,AD=11AB,延长BC到F,使CF=BC,连接FD交AC于点E。
则①DE=EF②AE=2CE。
例6:已知:D,E为三角形ABC中AB、BC边上的点,连接DE并延长交AC的延长线于点F,例7:如图,已知XXX,若AB=a,CD=b,EF=c,则a/b=c/(a+c)。
例8:如图,S△.例9:如图,四边形ABCD中,∠B=∠D=90°,M是AC上一点,ME⊥AD于点E,MF⊥BC于点F。
则MF/ME+1=BD/AC。
例10:如图,在△ABC中,D是AC边的中点,过D作直线EF交AB于E,交BC的延长线于F。
则AE·BF=BE·CF。
BCF:在线段AB上取一点C,以AC、CB为底在AB同侧作两个顶角相等的等腰三角形ADC和CEB,AE交CD于点P,BD交CE于点Q,证明CP=CQ。
解法:首先,由等腰三角形的性质可知,∠XXX∠CEB,∠ACD=∠BCD,因此△ADC≌△CEB,从而AP=BP,AQ=CQ。
全等三角形经典模型总结

全等三角形相关模型总结一、角平分线模型(一)角平分线的性质模型辅助线:过点G作GE1射线ACA、例题1 如图,在△ ABC中,/ C=90°, AD平分/ CAB BC=6cm BD=4cm 那么点D到直线AB的距离是cm.2、如图,已知,/ 1 = 7 2,/ 3=7 4,求证:AP平分/ BAC.B模型巩固1、如图,在四边形ABCD中, BC> AB, AD= CD BD平分7 ABC 求证:7 A+7 C= 180° .(二)角平分线+垂线,等腰三角形必呈现A、例题辅助线:延长ED交射线0B于F 辅助线:过点E作EF//射线OB例1、如图,在△ ABC中,7 ABC= 37 C, AD是7 BAC的平分线,BE X AD于F .1求证:BE -(AC AB).例2、如图,在△ ABC中,/ BAC的角平分线AD交BC于点D,且AB= AD,作CM L AD交AD 1的延长线于M.求证:AM —(AB AC).2(三)角分线,分两边,对称全等要记全两个图形飞辅助线都是在射线ON上取点B,使0B= OA从而使△ OAQ A OBC .A、例题1、如图,在△ ABC中,/ BAC=60,/ C=40°, AP平分/ BAC交BC于P, BQ平分/ ABC交AC于Q,求证:AB+ BP= BQ+ AQ .2、如图,在△ ABC中,AD是/ BAC的外角平分线,P是AD上异于点A的任意一点,试比较PB+ PC与AB+ AC的大小,并说明理由.B模型巩固1、在厶ABC中,AB> AC, AD是/ BAC的平分线,P是线段AD上任意一点(不与A重合)求证:AB- AO PB- PC .2、如图,△ ABC中,AB= AC, / A= 100°,/ B的平分线交AC于D,求证:AD+ BD= BC .3、如图,△ ABC中,BC= AC, / C= 90°,/ A的平分线交BC于D,求证:AC+ CD= AB .二、等腰直角三角形模型(一)旋转中心为直角顶点,在斜边上任取一点的旋转全等:操作过程:(1 )将厶ABD逆时针旋转90°,得厶ACM也△ ABD从而推出厶ADM为等腰直角三角形(2) 辅助线作法:过点C作MCL BC,使CM= BD连结AM.二)旋转中心为斜边中点动点在两直角边上滚动的旋转全等:操作过程:连结AD.(1 )使BF= AE (或AF= CE,导出△ BDF 也△ ADE.(2)使/ EDF^Z BAC= 180 °,导出△ BDF 也△ ADE.A、例题1、如图,在等腰直角△ ABC中,/ BAC= 90°,点M N在斜边BC上滑动,且/ MAN= 45 试探究BM MN CN之间的数量关系.2、两个全等的含有30°, 60°角的直角三角板ADE和ABC按如图所示放置,E、A C三点在一条直线上,连接BD,取BD的中点M 连接ME MC.试判断△ EMC勺形状,并证明你的结论.B模型巩固1、已知,如图所示,Rt△ ABC中, AB= AC, / BAC= 90° , O为BC中点,若M N分别在线段AC AB上移动,且在移动中保持AN= CM.(1)试判断△ OMN勺形状,并证明你的结论.(2)当M N分别在线段AC AB上移动时,四边形AMON勺面积如何变化2、在正方形ABCD中, BE= 3, EF= 5, DF= 4,求/ BAE+Z DCF为多少度.(三)构造等腰直角三角形( 1 )利用以上(一)和(二)都可以构造等腰直角三角形(略);(2)利用平移、对称和弦图也可以构造等腰直角三角形.(四)将等腰直角三角形补全为正方形,如下图:A、例题应用1、如图,在等腰直角△ ABC中,AC= BC, Z ACB= 90°, P为三角形ABC内部一点, 满足PB= PC AP= AC 求证:Z BCP= 15三、三垂直模型(弦图模型)A、例题已知:如图所示,在△ ABC中,AB= AC, / BAC= 90°, D为AC中点,AF丄BD于点E,交BC 于F,连接DF .求证:/ ADB=Z CDF .变式1、已知:如图所示,在厶ABC中,AB= AC, AM k CN AF丄BM于E,交BC于F,连接NF. 求证:(1)Z AMB=Z CNF; (2) BMI= AF+ FN .变式2、在变式1的基础上,其他条件不变,只是将BM和FN分别延长交于点P,求证:( 1 ) PM= PN;( 2) PB= PF+AF .四、手拉手模型〔、△ ABE和△ ACF均为等边三角形结论:(〔)△ ABF^A AEC .(2)Z BOE=Z BAE= 60°.(3)OA平分/ EOF .(四点共圆证)拓展:△ ABC^n^ CDE均为等边三角形结论:(1) AD= BE;(2)Z ACB=Z AOB(3) A PCQ为等边三角形;(4)PQ// AE;(5)AP= BQ(6)CO平分/ AOE (四点共圆证)(7)OA= OB+ OC(8)OE= OC+ OD .(7),(8)需构造等边三角形证明 )例、如图①,点M为锐角三角形ABC内任意一点,连接AM BM CM以AB为一边向外作等边三角形厶ABE将BM绕点B逆时针旋转60°得到BN连接EN(1) 求证:△ AMB^A ENB(2) 若AM+BM+C的值最小,则称点皿为厶ABC的费尔马点.若点皿为厶ABC的费尔马点,试求此时/ AMB / BMC / CMA的度数;(3) 小翔受以上启发,得到一个作锐角三角形费尔马点的简便方法:如图②,分别以厶ABC的AB AC为一边向外作等边△ ABE和等边△ ACF连接CE BF,设交点为M则点M 即为△ ABC的费尔马点•试说明这种作法的依据.2、\ ABD^D^ ACE均为等腰直角三角形结论:(1) BE= CD (2) BE丄CD .3、四边形ABEF和四边形ACH[均为正方形结论:(1) BD= CF; (2) BD丄CF .变式1、四边形ABEF和四边形ACHD匀为正方形,AS丄BC交FD于T, 求证:(1)T 为FD中点;(2)SV A BC SV A DF .变式2、四边形ABEF和四边形ACHD匀为正方形,T为FD中点,TA交BC于S, 求证:AS丄BC .360 4、如图,以△ ABC 的边AB AC 为边构造正多边形时,总有: 五、半角模型1条件:,且+ =180, 两边相等.2 思路:1、旋转辅助线:①延长 CD 到E ,使ED=BM 连AE 或延长CB 到F ,使FB=DN 连AF②将△ ADN 绕点A 顺时针旋转90°得厶ABF,注意:旋转需证 F 、B结论:(1) MN= BM+ DN ;(2) CV CMN =2 AB ; 1 2 180M 三点共线360 (3) AM AN分别平分/ BMN / MND .2、翻折(对称)辅助线:①作AP丄MN交MN于点P②将△ ADN △ ABM分别沿AN AM翻折,但一定要证明MA、例题例1、在正方形ABCD中,若M N分别在边BC CD上移动,且满足求证:(1)Z MAN= 45°;P、N 三点共线MN= BM+ DN⑵ CV CMN =2 AB ;(3) AM AN分别平分/ DNM .变式:在正方形ABCD中,已知/ MAN= 45°,若M N分别在边CB DC的延长线上移动, AH L MN垂足为H,(1)试探究线段MN BM DN之间的数量关系;(2)求证:AB= AH例2、在四边形ABCD中, Z B+Z D= 180°, AB= AD,若E、F分别为边BC CD上的点,且1满足EF= BE+ DF,求证:EAF BAD .2变式:在四边形ABCD中,/ B= 90°,/ D= 90°, AB= AD,若E、F分别为边BC CD上的 -口1点,且EAF — BAD,求证:EF= BE+ DF .2。
(完整版)相似三角形经典模型总结及例题分类.doc
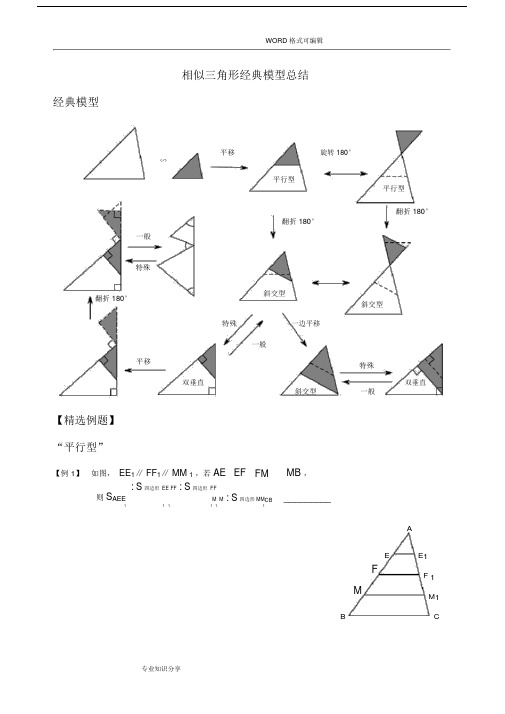
WORD 格式可编辑相似三角形经典模型总结经典模型平移旋转 180°∽平行型平行型翻折 180°翻折 180°一般特殊翻折 180°斜交型斜交型特殊一边平移一般平移特殊双垂直斜交型双垂直一般【精选例题】“平行型”【例 1】如图,EE1∥FF1∥MM1,若AE EF FM MB ,则S AEE : S四边形EE FF : S四边形FFM M : S四边形 MM C B _________1 1 1 1 1 1AE E1FF 1MM1B CWORD 格式可编辑【例 2】如图,AD∥EF∥MN∥BC,若AD 9,BC 18 , AE:EM :MB 2:3:4,则EF _____ , MN _____A DE FMNB C【例 3】已知,P为平行四边形ABCD 对角线, AC 上一点,过点P 的直线与 AD , BC , CD 的延长线, AB 的延长线分别相交于点 E , F , G , H求证: PE PHPF PGG D CE PFA B H【例 4】已知:在ABC 中, D 为 AB 中点, E 为 AC 上一点,且AE2, BE、 CD相交于点 F ,求BF的值ECEF ADF EB C【例 5】已知:在ABC 中, AD 1AB,延长 BC到F ,使CF1BC,连接 FD交 AC于点 E 2 3求证:① DE EF ② AE 2CEADEB专业知识分享【例 6】已知:D,E为三角形ABC 中 AB 、BC 边上的点,连接 DE 并延长交 AC 的延长线于点 F ,BD: DE AB: AC求证:CEF 为等腰三角形ACDEB F【例7】如图,已知 AB / / EF / /CD ,若 AB a , CD b , EF c ,求证:11 1 .c a bACEB F D【例 8】如图,找出S ABD、 S BED、 S BCD之间的关系,并证明你的结论.CAEB F D【例 9】如图,四边形ABCD中,B D90M是AC上一点,ME AD于点EMF BC,,于点 F 求证:MFME 1AB CDDEMA CFB【例 10】如图,在ABC 中, D 是 AC 边的中点,过 D 作直线 EF 交 AB 于 E ,交 BC 的延长线于 F 求证: AE BF BE CFAEDBC F 【例 11】如图,在线段AB 上,取一点 C ,以 AC , CB 为底在 AB 同侧作两个顶角相等的等腰三角形ADC 和CEB, AE交 CD于点 P, BD交 CE于点Q,求证: CP CQDEP QA C B【例 12】阅读并解答问题 .在给定的锐角三角形ABC 中,求作一个正方形DEFG,使 D, E落在 BC边上, F , G分别落在AC , AB 边上,作法如下:ABC 两边上的正方形D'E'F 'G'如图,第一步:画一个有三个顶点落在第二步:连接 BF ' 并延长交 AC 于点 F第三步:过 F 点作 FE BC ,垂足为点 E第四步:过 F 点作 FG∥BC 交 AB 于点 G第五步:过 G 点作 GD BC ,垂足为点 D四边形 DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在 ABC 中,如果BC 6 3,ABC 45 , BAC 75 ,求上述正方形DEFG 的边长AG FG'F'E CWORD 格式可编辑“平行旋转型”图形梳理:E'F'AAAF'E'AEF'EFFFEE'FEF'BCBCBBCAEF 旋转到 AE ‘ F ’CAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’AEF 旋转到AE ‘F ’特殊情况: B 、 E'、 F '共线AAEF' EF'E'FE'FBC B CAEF 旋转到 AE ‘ F ’ AEF 旋转到 AE ‘ F ’C , E', F '共线E'AE'AEFEF'FF'BCBCAEF 旋转到 AE ‘ F ’AEF 旋转到 AE ‘ F ’【例 13】已知梯形 ABCD , AD ∥BC ,对角线AC 、 BD 互相垂直,则①证明: AD 2 BC 2AB 2 CD 2ADOB CWORD 格式可编辑【例 14】当AOD ,以点 O 为旋转中心,逆时针旋转度(090 ),问上面的结论是否成立,请说明理由DAOB C【例 15】(全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和 BEFG 均为正方形,求AG : DF : CE_________.A DGFB CE“斜交型”【例 16】如图,ABC 中, D 在 AB 上,且 DE∥BC 交 AC 于 E , F 在 AD 上,且 AD2AF AB ,求证:AEF :ACDAFD EB C【例 17】如图,等边三角形ABC中,D,E分别在BC,AB上,且CE BE ,AD ,CE 相交于 M ,求证 : EAM : ECAAEMB DC AGF BE【例 18】如图,四边形ABCD 的对角线相交于点O ,BAC CDB ,求证:DAC CBDADOB C【例 19】如图,设ABBCCA,则 1 2 吗?AD DE EAA1 DE2B C【例 20】在锐角三角形ABC 中, AD , CE 分别为 BC , AB 边上的高,ABC 和BDE 的面积分别等于 18和 2 , DE 2,求 AC 边上的高AEB D C【例 21】如图,在等边ABC 的边 BC 上取点 D ,使BD 1,作CH AD,H为垂足,连结BH。
相似三角形-经典模型总结与例题分类

相似三角形经典模型总结经典模型【精选例题】 “平行型”【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,则111111:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形M 1F 1E 1M E F A BC【例2】 如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =,_____MN =M N A BCD E F【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H求证:PE PHPF PG=PHGFEDCBA【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且2AEEC=,BE 、CD 相交于点F ,求BFEF的值【例5】 已知:在ABC ∆中,12AD AB =,延长BC 到F ,使13CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE =ABCDFEFE DCBA【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC =求证:CEF ∆为等腰三角形FEDCBA【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC⊥于点F求证:1MF MEAB CD+= ABCDEF M【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F求证:AE BF BE CF ⋅=⋅FEDC BA【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,求证:CP CQ =QPEDC BA【例12】 阅读并解答问题.在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D 四边形DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在ABC ∆中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长G'F'E'D'ABCDEFG“平行旋转型”图形梳理:AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况:B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEF E'F'AEF 旋转到AE‘F’C ,'E ,'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则①证明:2222AD BC AB CD +=+OAB CD【例14】 当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由DCB AO【例15】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求::AG DF CE =_________.ABEF GGFEDCBA“斜交型”【例16】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2AD AF AB =⋅,求证:AEFACD ∆∆F ED CBA【例17】 如图,等边三角形ABC 中,D ,E 分别在BC ,AB 上,且CE BE =,AD ,CE 相交于M ,求证:EAM ECA ∆∆M E DC B A【例18】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠ODCBA【例19】 如图,设AB BC CAAD DE EA==,则12∠=∠吗? 21ABCDE【例20】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别等于18和2,2DE =,求AC 边上的高ABCDE【例21】 如图,在等边ABC ∆的边BC 上取点D ,使21=CD BD ,作CH AD ⊥,H 为垂足,连结BH 。
解三角形常用知识点归纳与题型总结-解三角形题型归纳总结

解三角形常用知识点归纳与题型总结1、①三角形三角关系:A+B+C=180°;C=180°—(A+B);②.角平分线性质定理:角平分线分对边所得两段线段的比等于角两边之比. ③.锐角三角形性质:若A>B>C 则6090,060A C ︒≤<︒︒<≤︒. 2、三角形三边关系:a+b>c; a-b<c3、三角形中的基本关系:sin()sin ,A B C +=cos()cos ,A B C +=-tan()tan ,A B C +=- sincos ,cos sin ,tan cot 222222A B C A B C A B C+++=== (1)和角与差角公式sin()sin cos cos sin αβαβαβ±=±;cos()cos cos sin sin αβαβαβ±=; tan tan tan()1tan tan αβαβαβ±±=.(2) 二倍角公式 sin2α = 2cosαsinα.2222cos 2cos sin 2cos 112sin ααααα=-=-=-221tan 1tan αα-=+. 221cos 21cos 2sin ,cos 22αααα-+==(3)辅助角公式(化一公式))sin(cos sin 22ϕ±+=±=x b a x b x a y 其中ab =ϕtan 4、正弦定理:在C ∆AB 中,a 、b 、c 分别为角A 、B 、C 的对边,R 为C ∆AB 的外接圆的半径,则有2sin sin sin a b cR C===A B . 5、正弦定理的变形公式:①化角为边:2sin a R =A ,2sin b R =B ,2sin c R C =;②化边为角:sin 2a R A =,sin 2b R B =,sin 2c C R=; ③::sin :sin :sin a b c C =A B ;④sin sin sin sin sin sin a b c a b cC C++===A +B +A B =2R 6、两类正弦定理解三角形的问题:①已知两角和任意一边,求其他的两边及一角. ②已知两角和其中一边的对角,求其他边角.(对于已知两边和其中一边所对的角的题型要注意解的情况(一解、两解、三解)) 7、三角形面积公式:111sin sin sin 222C S bc ab C ac ∆AB =A ==B .=2R 2sinAsinBsinC=R abc 4=2)(c b a r ++=))()((c p b p a p p ---(海伦公式)8、余弦定理:在C ∆AB 中,有2222cos a b c bc =+-A ,2222cos b a c ac =+-B ,2222cos c a b ab C =+-.9、余弦定理的推论:222cos 2b c a bc +-A =,222cos 2a c b ac +-B =,222cos 2a b c C ab+-=.注明:余弦定理的作用是进行三角形中的边角互化,当题中含有二次项时,常使用余弦定理。
初中三角形最值问题归纳总结

初中三角形最值问题归纳总结哎呀,今天咱们聊聊三角形的最值问题,嘿,这可不是简单的几何题哦。
三角形在初中数学里可真是个大明星。
它的形状、大小、角度,简直是个万花筒,千变万化,让人眼花缭乱。
说到三角形,咱们就得先来个引子,想象一下,三角形就像一位热情的朋友,永远带着它的三条边,三角形可是个爱社交的角色。
你看,它跟直线、圆形这些静态的图形可完全不一样,三角形总是让人觉得充满了生机。
什么是最值问题呢?别急,简单来说,就是让你找到在某些条件下三角形能达到的最大或最小值。
比如说,给你三条边的长度,问你能组成的三角形的面积最大是多少。
听起来有点复杂?别担心,咱们一步步来,慢慢讲。
咱们得了解一下三角形的面积公式。
嘿嘿,没错,就是那个大家都很熟悉的公式:面积等于底乘以高除以二。
可问题来了,底和高咋选呢?这可得看你是哪个角度切入这个问题。
比如说,你可以选择把其中一条边当作底边,然后找出对应的高来计算。
可这个高就像抓小鱼一样,费劲。
于是,这里就有了一个小窍门:如果你把三角形变成等边三角形,嘿嘿,往往能得到最大的面积!这就像吃西瓜,切得越均匀,越容易吃得爽。
再说说三角形的周长问题,哎哟,周长就像是三角形的腰围。
想要三角形的周长最大,听起来简单,其实得看你怎么组合这三条边。
三条边之间的关系就像朋友之间的互动,得有个平衡,才能让三角形稳稳当当。
如果你把一条边选得过长,嘿,那另一条边就得跟着变短,结果可能就不成三角形了,这就尴尬了。
讲到这里,很多同学可能会问,嘿,如何才能快速找到这些最值呢?有些基本的几何特性可以帮到你,比如说三角不等式。
这可是个了不得的定理,任何三角形的两边之和必须大于第三边。
就像是你跟朋友出门,俩人得一起吃个饭,不能只一个人吃,另一个人在旁边看,那可太不公平了。
还得提一下三角形的内角和,总是等于180度,别问我为什么,反正就是这样。
利用这个特性,我们可以推导出各种最值,比如说,当三角形的角度是60度时,它的面积就会最大,这就像是黄金比例的存在,简直美妙。
三角形解的个数问题
05
三角形解的个数问题的扩 展和深化
三角形解的个数问题的推广
要点一
推广到多边形
要点二
推广到组合优化
将三角形解的个数问题推广到多边形,研究多边形的可解 性、解的个数和最优解等问题。
将三角形解的个数问题看作是组合优化问题的一种,研究 其他组合优化问题的解法,如旅行商问题、排班问题等。
三角形解的个数问题的变种
详细描述
在几何问题中,三角形解的个数问题通常涉及到三角形边长和角度的条件约束。根据三角形的性质, 任意两边之和大于第三边,任意两边之差小于第三边。同时,角度的条件也会影响三角形解的个数。 通过分析这些条件,可以判断三角形解的个数。
三角函数中的三角形解的个数问题
总结词
三角函数中的三角形解的个数问题主要 涉及到三角函数的性质和图象,通过分 析三角函数的性质和图象,判断三角形 解的个数。
考虑三角形边的长度
在三角形解的个数问题中,可以考虑 三角形的边长限制,研究不同边长条 件下三角形的可解性。
考虑三角形角度
在三角形解的个数问题中,可以考虑 三角形的角度限制,研究不同角度条 件下三角形的可解性。
三角形解的个数问题与其他数学知识的结合
与几何学结合
将三角形解的个数问题与几何学知识相结合,研究几 何图形中的可解性问题,如多边形、曲面等。
与图论结合
将三角形解的个数问题与图论知识相结合,研究图论 中的可解性问题,如子图、路径、连通性等。
感谢您的观看
THANKS
三角形解的个数问题
目 录
• 三角形解的个数问题的定义和分类 • 三角形解的个数问题的基本定理和公式 • 三角形解的个数问题的应用实例 • 三角形解的个数问题的解题技巧和方法 • 三角形解的个数问题的扩展和深化
全等三角形经典模型总结
全等三角形经典模型总结1.S-A-S(边-角-边)全等法则:当一个三角形的两边和夹角分别等于另一个三角形的两边和夹角时,两个三角形全等。
例如,在三角形ABC和DEF中,如果AB=DE,∠ABC=∠DEF,并且BC=EF,那么三角形ABC全等于三角形DEF。
2.A-S-A(角-边-角)全等法则:当一个三角形的两角和夹边分别等于另一个三角形的两角和夹边时,两个三角形全等。
例如,在三角形ABC和DEF中,如果∠ABC=∠DEF,BC=EF,并且∠BCA=∠EFD,那么三角形ABC全等于三角形DEF。
3.S-S-S(边-边-边)全等法则:当两个三角形的三边分别对应相等时,两个三角形全等。
例如,在三角形ABC和DEF中,如果AB=DE,BC=EF,并且AC=DF,那么三角形ABC全等于三角形DEF。
4.H-L(高-底)全等法则:如果两个三角形的高和底分别相等,那么这两个三角形全等。
例如,在三角形ABC和DEF中,如果h1是三角形ABC的高,b1是它的底,h2是三角形DEF的高,b2是它的底,如果h1=h2,b1=b2,则三角形ABC全等于三角形DEF。
5.A-A-S’(角-角-边)全等法则:若三角形的两个角和两个边分别与另一三角形的两个相对角和边对应,则两个三角形全等。
例如,在三角形ABC和DEF中,如果∠ABC=∠DEF,∠BCA=∠EFD,并且AC/DF=BC/EF,那么三角形ABC全等于三角形DEF。
6.1-1-1全等法则:如果两个三角形的边长度分别相等,那么这两个三角形全等。
例如,在三角形ABC和DEF中,如果AB=DE,AC=DF,并且BC=EF,那么三角形ABC全等于三角形DEF。
7.1-1-边(边-边)全等法则:如果两个三角形的两个边和一个夹角分别相等,那么这两个三角形全等。
例如,在三角形ABC和DEF中,如果AB=DE,BC=EF,并且∠ABC=∠DEF,那么三角形ABC全等于三角形DEF。
正弦定理经典题型总结
正弦定理经典题型总结知识总结一、正弦定理在一个三角形中,各边和它所对角的正弦的比相等,即= 丄=—=2/?,实中尺是三角形外按恻半径. sin A別口占SJD L公式适用于任意三角形。
二、正弦定理的变形(】} {tifi/jfB ■ a =2/?sin A.h =2/?^Lnfi,c =22fsinC;sin A= —,sin S =—,sin C =—; 化殆为边:2尺2R 2R................................................. —=-^—sinJ +sin B tsinC sin A sin B sinC三、三角形面积公式111 在任意斜厶ABC 当中S\ AB(=-absi nC -acs in B 一bcsi nA2 2 2四、正弦定理解三角形1)已知两角和任意一边,求其它两边和一角;2)已知两边和其中一边对角,求另一边的对角,进而可求其它的边和角例如:已知a, b和A,用正弦定理求B时的各种情况:(多解情况)①若A为锐角时:a bsi nA 无解a bsinA —解(直角)bsinA a b 二解(一锐,一钝) a b 一解(锐角)已知边a,b和A变形:(2016 年全国】1)少別?的Wflj 的对®cosJ = -t cosC = —5 B题型二:已知两边及一边对角解三角形1.在△ABC 中,角A、B、C 的对边分别为a、b、c, A = 60 ° ,a = 4 J3, b = 4" 2,则角B为()A. 45 ° 或135 °B. 135 °C. 45 ° D .以上答案都不对2 . △ABC的内角A、B、C的对边分别为a、b、c.若c= 2, b = 6, B= 120。
,贝临等于()A/ 6 B. 2 C.“ 3 D.“ 2a<CH=bsinA无解仅有一个解CH=bsinA<a<b有两个解a b仅有一个解a b②若A为直角或钝角时:a b无解一解(锐角)题型一:已知两角及任意一边解三角形1 .在△ABC 中,A.『62 .在△ABC 中,A = 45 °,B= 60 °B"已知a = 8, B = 60,a= 2,则b等于(C.捋,C = 75。
最新相似三角形-经典模型总结与例题分类
相似三角形经典模型总结经典模型【精选例题】 “平行型”【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===,则111111:::_________AEE EE F F FF M M MM CB S S S S ∆=四边形四边形四边形M 1F 1E 1M E F A BC【例2】 如图,AD EF MN BC ∥∥∥,若9AD =,18BC =,::2:3:4AE EM MB =,则_____EF =,_____MN =M N A BCD E F【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H求证:PE PHPF PG=PHGFEDCBA【例4】 已知:在ABC ∆中,D 为AB 中点,E 为AC 上一点,且2AEEC=,BE 、CD 相交于点F ,求BFEF的值【例5】 已知:在ABC ∆中,12AD AB =,延长BC 到F ,使13CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE =ABCDFEFE DCBA【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC =求证:CEF ∆为等腰三角形FEDCBA【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证:111c a b=+.FE DCBA【例8】 如图,找出ABD S ∆、BED S ∆、BCD S ∆之间的关系,并证明你的结论.FE DCBA【例9】 如图,四边形ABCD 中,90B D ∠=∠=︒,M 是AC 上一点,ME AD ⊥于点E ,MF BC⊥于点F求证:1MF MEAB CD+= ABCDEF M【例10】 如图,在ABC ∆中,D 是AC 边的中点,过D 作直线EF 交AB 于E ,交BC 的延长线于F求证:AE BF BE CF ⋅=⋅FEDC BA【例11】 如图,在线段AB 上,取一点C ,以AC ,CB 为底在AB 同侧作两个顶角相等的等腰三角形ADC ∆和CEB ∆,AE 交CD 于点P ,BD 交CE 于点Q ,求证:CP CQ =QPEDC BA【例12】 阅读并解答问题.在给定的锐角三角形ABC 中,求作一个正方形DEFG ,使D ,E 落在BC 边上,F ,G 分别落在AC ,AB 边上,作法如下:第一步:画一个有三个顶点落在ABC ∆两边上的正方形''''D E F G 如图, 第二步:连接'BF 并延长交AC 于点F 第三步:过F 点作FE BC ⊥,垂足为点E 第四步:过F 点作FG BC ∥交AB 于点G 第五步:过G 点作GD BC ⊥,垂足为点D 四边形DEFG 即为所求作的正方形问题:⑴证明上述所作的四边形DEFG 为正方形⑵在ABC ∆中,如果6BC =+45ABC ∠=︒,75BAC ∠=︒,求上述正方形DEFG 的边长G'F'E'D'ABCDEFG“平行旋转型”图形梳理:AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBBCAEF 旋转到AE‘F’ABCAEF 旋转到AE‘F’特殊情况:B 、'E 、'F 共线AEF 旋转到AE‘F’CBAAB CEF E'F'AEF 旋转到AE‘F’C ,'E ,'F 共线AEF 旋转到AE‘F’CBAAEF 旋转到AE‘F’CBA【例13】 已知梯形ABCD ,AD BC ∥,对角线AC 、BD 互相垂直,则①证明:2222AD BC AB CD +=+OAB CD【例14】 当AOD ∆,以点O 为旋转中心,逆时针旋转θ度(090θ<<),问上面的结论是否成立,请说明理由DCB AO【例15】 (全国初中数学联赛武汉选拔赛试题)如图,四边形ABCD 和BEFG 均为正方形,求::AG DF CE =_________.ABEF GGFEDCBA“斜交型”【例16】 如图,ABC ∆中,D 在AB 上,且DE BC ∥交AC 于E ,F 在AD 上,且2AD AF AB =⋅,求证:AEF ACD ∆∆:F ED CBA【例17】 如图,等边三角形ABC 中,D ,E 分别在BC ,AB 上,且CE BE =,AD ,CE 相交于M ,求证:EAM ECA ∆∆:M E D C B A【例18】 如图,四边形ABCD 的对角线相交于点O ,BAC CDB ∠=∠,求证:DAC CBD ∠=∠ODCBA【例19】 如图,设AB BC CAAD DE EA==,则12∠=∠吗? 21ABCDE【例20】 在锐角三角形ABC 中,AD ,CE 分别为BC ,AB 边上的高,ABC ∆和BDE ∆的面积分别等于18和2,2DE =,求AC 边上的高ABCDE【例21】 如图,在等边ABC ∆的边BC 上取点D ,使21=CD BD ,作CH AD ⊥,H 为垂足,连结BH 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形经典问题总结
三角形是几何学中研究的重要图形之一,它具有丰富的性质和问题,并且在数学、物理以及工程等领域中有着广泛的应用。
在这篇文章中,我将总结三角形的经典问题,并探讨它们的解决方法和相关应用。
1. 三角形边长关系问题:
三角形的边长关系问题是三角形的基础问题之一。
根据三角形任意
两边之和大于第三边的条件,可以得出以下结论:任意一边大于另外
两边之差,小于另外两边之和。
这个结论在解决三角形边长关系问题
时起到了重要的作用,可用于判定三角形是否存在,以及确定三角形
的类型,如等边三角形、等腰三角形和一般三角形等。
2. 三角形内角和问题:
三角形的内角和定理是三角形的经典问题之一。
根据三角形的定义,三个内角之和总是等于180度。
由此推论,可得到在已知两个角的情
况下,可以通过计算第三个角的值来解决问题。
此外,我们还可以应
用内角和定理来解决三角形内外角、平行线与三角形内角和的关系等
问题。
3. 三角形的相似性问题:
三角形的相似性问题是三角形研究中的重要内容。
两个三角形相似
的条件是对应角相等,并且对应边的比例相等。
利用相似三角形的性质,我们可以解决三角形的边长比例问题,以及一些几何形状的相似
性问题。
此外,相似性问题还与三角形的投影问题以及三角形的三垂
线等有关联。
4. 三角形的面积问题:
三角形的面积问题是解决实际问题中常见的数学题目。
根据三角形
面积公式,即面积等于底边长度乘以高的一半,我们可以计算任意三
角形的面积。
在实际问题中,例如土地测量、建筑设计等领域,我们
经常需要计算三角形的面积。
此外,通过应用海伦公式或正弦定理,
我们可以计算无法直接通过底边和高计算的三角形的面积。
5. 三角形的角平分线和中位线问题:
三角形的角平分线问题和中位线问题是三角形的特殊性质问题之一。
角平分线将三角形的一个内角分成两个相等的角,而中位线则将三角
形的一边中点连成一条垂直于该边的线段。
这些特殊性质与三角形的
对称性、三角形的重心等有关。
在解决与这些特殊线段相关的问题时,我们可以利用它们的性质快速求解。
总结:
通过对三角形的经典问题进行总结,我们可以看到三角形具有丰富
的性质和应用。
在解决三角形问题时,我们可以运用三角形的边长关系、内角和、相似性、面积、角平分线和中位线等性质,从而得出准
确的结论。
这些问题不仅仅在数学学科中有着重要的地位,同时也在
物理学、工程学和建筑学等领域中发挥着重要的作用。
通过深入研究
和实际应用,我们可以更好地理解和应用三角形的经典问题,促进数学和科学的发展。
