静电驱动的亚微米悬臂梁谐振器非线性特性
基于ANSYS的静电微执行器吸合现象分析

C h i 2 0 1 4 N O . O 8 ( 下) n a N e w T e c h n o l o z i e s a n d P r o d ;
基于 A NS YS的静 电微 执行器吸合现 象分析
●
郑丽云
龚友平
Hale Waihona Puke 刘彦辉 ( 杭 州电子科技 大学机械 工程 学院 ,浙江 杭 州 3 1 0 0 1 8 )
弹性回复力
V
电场 力
为了分析静态吸合 现象 ,我们需要 关 系 曲 线 如 下 图 。 由 图 2可 知 随着 施 加 对 所 提 出 的 电 容模 型做 一 定 的假 设 和 简 在 电 容 器极 板 两端 的 电压 逐 渐 增 大 ,可 化 :即 忽 略惯 性 阻 尼 等 因素 的影 响 ,极 动 极 板 的 位移 逐渐 增 大 ,系 统 此 时 处 于 板 间 施 加 电 压 变 化 缓慢 以 至 于可 动 极 板 稳 定 平 衡 状 态 ,当平 行 板 电容 器 极 板 两 在 电场 力 、上 极板 回复 力 共 同作 用 下 在 端 的 电压 增 大 到 吸合 电压 时 ,即 系 统达 任 意 时 刻 都 能 够 保 持 在 稳定 状 态 ,可 动 到 临 界 平 衡 点 ,也 就 是 图 中的 曲 线 的 最 极板的速度以及加速度 都为零且期 问不 右 侧 位 置 ;此 时 系统 也 处 于 平 衡 状 态 ,
=
亨
( 8 )
( 9 )
连 线 。 同样 处 于 空 间 介 质 中的 两 个 增大 。
点 电荷 同样 适 用 于库 仑 定律 。 1 . 2微 开关 电容器 简 化模 型
・
2 静 态 吸合 分 析 2 . 1 模 型假 设 与简 化
静电排斥驱动六边形MEMS微镜

静电排斥驱动六边形MEMS微镜胡放荣;王爱娜;邱传凯;姚军【期刊名称】《纳米技术与精密工程》【年(卷),期】2010(008)002【摘要】为消除静电吸引型微镜因存在静电吸合效应而导致的短路现象,基于电场的非均匀分布可以产生静电排斥力的原理,设计了一种静电排斥型六边形微机械反射镜.微镜包含7组驱动电极,最大的一组驱动电极由镜面和其正下方的六边形下电极组成,其他6组分别位于微镜的各条边上,其中3组为梳齿结构,另外3组为U形弹簧,镜面由3组U形弹簧支撑.利用有限元软件对微镜频率响应和暂态响应特性进行了仿真,结果表明谐振频率高达7 kHz,暂态响应时间小于0.000 3 s.利用表面硅工艺加工出了样片,并用白光干涉仪对其静态位移特性进行了测试,在50 V直流电压下微镜位移量为0.7 μm.由结果可知该微镜可消除静电吸合效应.故该微镜不仅可用于对反射光进行光程和相位的调制,也可用于自适应光学系统中波前畸变的校正.【总页数】6页(P171-176)【作者】胡放荣;王爱娜;邱传凯;姚军【作者单位】中国科学院光电技术研究所微细加工光学技术国家重点实验室,成都,610209;桂林电子科技大学电子工程学院,桂林,541004;中国科学院光电技术研究所微细加工光学技术国家重点实验室,成都,610209;中国科学院光电技术研究所微细加工光学技术国家重点实验室,成都,610209;中国科学院光电技术研究所微细加工光学技术国家重点实验室,成都,610209【正文语种】中文【中图分类】TN241【相关文献】1.环形静电排斥旋转驱动器微光机电系统微镜 [J], 马文英;魏耀华;汪为民;王强2.静电排斥型微机电系统变形镜驱动器 [J], 胡放荣;姚军3.静电驱动MEMS扭转微镜系统的分岔与吸合 [J], 叶坤涛;罗艳4.三层平板静电驱动MEMS微镜 [J], 冯仁剑;万江文;凌坚5.一维MEMS微镜静电弹性耦合 [J], 凌坚;万江文因版权原因,仅展示原文概要,查看原文内容请购买。
滤波器的非线性特性和非线性失真分析

滤波器的非线性特性和非线性失真分析滤波器是一种常用的信号处理工具,常常用于去除噪声、改善信号质量和实现频率选择等功能。
然而,由于电子元件的非线性特性,滤波器的输出信号往往会产生非线性失真,影响信号的准确传递和处理。
本文将从滤波器的非线性特性以及非线性失真的分析角度,探讨这一问题。
一、滤波器的非线性特性滤波器包含许多电子元件,比如电容、电感和操作放大器等。
尽管这些元件在理想状态下应具有线性特性,但实际上它们往往存在一定的非线性特性。
主要的非线性特性包括饱和、截止、失谐和畸变等。
1.1 饱和当输入信号电压过大时,电子元件可能会进入饱和状态。
在饱和状态下,元件的输出电压将无法继续线性增加,而是保持在一个固定的最大值或最小值。
这种非线性特性会导致滤波器输出信号的失真。
1.2 截止截止是指滤波器在输入信号电压较小时无法正常工作的情况。
这通常是由于元件的启动电压或偏置电压的影响,使得滤波器的输出信号无法完全跟随输入信号的变化,导致滤波器的频率响应出现非线性失真。
1.3 失谐失谐是指滤波器输出信号的频率与输入信号频率不一致的情况。
这可能是由于电子元件的参数固有非线性,或者滤波器结构的设计限制导致的。
失谐将产生频率混叠和互调失真等非线性失真效应。
1.4 畸变畸变是指滤波器输出信号与输入信号之间的形状、幅度或相位等方面的变化。
这种非线性特性可能是由于电子元件的非线性特性,以及滤波器的非理想结构和工作条件引起的。
畸变会使得滤波器无法准确地复制输入信号,并引入额外的失真成分。
二、非线性失真分析非线性失真是指滤波器输出信号与输入信号之间的差异,这些差异主要由滤波器的非线性特性引起。
在实际应用中,我们通常可以通过一些数学方法分析和评估非线性失真的程度。
2.1 傅里叶分析傅里叶分析是一种常用的分析滤波器非线性失真的方法。
通过将滤波器输入信号和输出信号进行傅里叶变换,我们可以得到它们的频谱分布。
如果滤波器存在非线性失真,那么在频谱中会出现额外的周期性分量或非谐波分量,从而可以通过观察频谱来判断滤波器的非线性程度。
非简谐效应

非简谐效应非简谐效应,又称为高次谐波失真,是指在非线性系统中,当外部激励力幅度较大时,系统的响应将产生谐波成分,且谐波的频率与激励频率不成正比的现象。
非简谐效应广泛应用于物理学、工程学和生物学等领域,例如在音响系统中产生音乐的谐音,或者在桥梁等结构中引起震动。
非简谐效应的研究主要基于非线性动力学理论。
线性系统满足叠加原理,即系统的响应与激励成线性比例关系;而非线性系统则不满足该原理,导致系统产生谐波失真。
非简谐效应包括主要谐波失真、次谐波失真和相位失谐。
非简谐效应的表征通常通过功率谱密度来描述,即将系统的响应信号分解成频谱分量。
常用的频谱分析方法有快速傅里叶变换(FFT)等,通过将时域信号转换为频域信号,可以直观地观察到谐波失真的情况。
非简谐效应的研究具有广泛的应用价值。
在物理学中,非简谐效应被广泛应用于微振动、光学等领域的研究中,例如利用非线性光学效应生成高次谐波。
在工程学中,非简谐效应的研究对于设计和控制非线性系统具有重要意义,例如在结构健康监测中,通过分析桥梁等结构的非简谐效应可以判断其结构的健康状况。
在生物学中,非简谐效应的研究可用于了解生物系统的非线性行为,进而揭示生物系统的运行机制。
非简谐效应的发生机制可以归结为两个方面:非线性特性和耦合作用。
非线性特性是指系统响应与激励响应成非线性关系,例如当激励力较大时,系统的响应会出现非线性增长。
耦合作用是指系统中不同模态或分量之间的相互作用,例如在桥梁中,不同结构分量受到不同频率的激励力,导致谐波失真的产生。
非简谐效应的研究方法主要包括实验方法和理论方法。
实验方法是通过搭建实验装置以及采集和分析实验数据来研究非简谐效应的发生机制和特性。
理论方法是通过建立数学模型,运用非线性动力学理论等工具,对非简谐效应进行定量研究。
这两种方法相辅相成,可以相互验证和支持。
总而言之,非简谐效应是非线性系统中的一种重要现象,广泛应用于各个领域。
通过研究非简谐效应,可以揭示非线性系统的运动特性以及响应规律,对于设计和控制非线性系统具有重要意义。
【国家自然科学基金】_非线性隔振_基金支持热词逐年推荐_【万方软件创新助手】_20140802
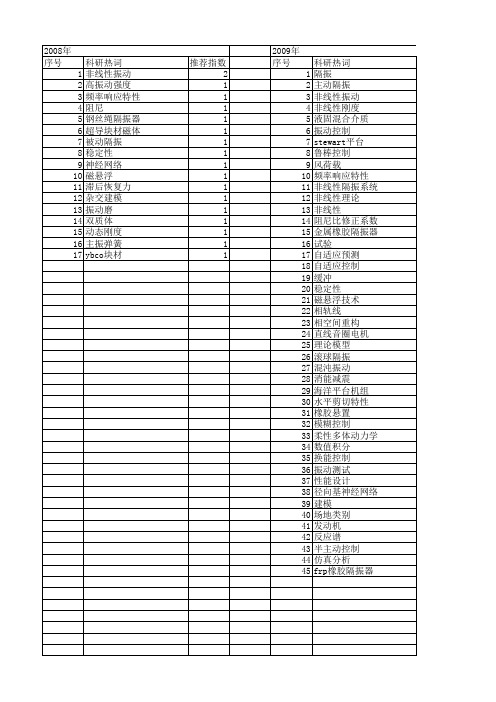
推荐指数 3 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
科研热词 隔振 非线性系统 非线性 参数辨识 非线性隔振器 非线性不确定扰动系统 非对称 零刚度 隔振支座 镇定 车辆 超磁致伸缩作动器模型 超低频隔振器 负刚度 谐波平衡法 谐波平衡 自适应模糊控制 结构参数优化 竖向振动 空气弹簧 磁流变 混合控制 橡胶隔振器 模型 有限元 最优控制 摆机构 振动分析 振动传递率 振动与波 惯容器 悬架 多自由度 地铁 可调式气动弹簧 发动机 动特性 力的控制 刚性漂移 准零刚度 低频隔振 低频 二次开发 乘坐舒适性 主动隔振器 主动减振 backstepping
2011年 科研热词 隔振 非线性 混沌 非线性振动 线谱 气动隔振 准零刚度 非线性隔振 非线性系统 非线性特性 运行机理 输出特性 跟踪控制 负刚度 谐波响应 行波型旋转超声电机 膨胀土 缓冲 激励频率 液固混合介质 波纹管 时延反馈控制 数值解法 振动分析 幅频特性 实验 多频激励 多自由度混沌 多尺度法 双路行波 剪应力松弛 分段刚度 共振响应 低频隔振 仿真分析 k-h模型 推荐指数 5 4 3 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
磁流变减振器的外特性及非线性特性

磁流变减振器的外特性及非线性特性王靖岳;郭胜;王浩天【摘要】In order to study the motion state of the Magnetorheological (MR) damper, the influence of the cur-rent and the piston velocity on the external characteristics of the MR damper is investigated by using the test data of the MTS849 damper test bench .Considering the nonlinear characteristics of magnetorheological damping force , Using LabVIEW software to design the program diagram of the polynomial and the front panel , and the damping force of MR damper polynomial fitting simulation , accurate polynomial mathematical model is established , and in comparison with the use of MATLAB software to establish a polynomial model and the data of test bench test .The results show that when the speed is constant , the damping force increases with the increase of the control current . The damping force increases relatively slowly when the current is small , and the damping force increases rapidly when the current is larger .When the current is constant , the damping force increases with the increase of piston speed .The polynomial model fitted by LabVIEW software is more close to the experimental data curve , which shows that the polynomial mathematical model can well describe the hysteretic and nonlinear characteristics of the damping force of the MR damper .%为了更好地研究控制磁流变减振器的运动状态,运用MTS849减振器试验台测试的试验数据来探究电流和活塞运动速度对磁流变减振器外特性的影响.考虑到磁流变阻尼力非线性的特性,运用LabVIEW软件设计出了多项式的程序框图和前面板,并进行了磁流变减振器阻尼力的多项式拟合仿真,准确地建立了多项式数学模型,并与利用MATLAB软件建立的多项式模型和试验台测试的数据相比较.结果表明:当速度一定时,随着控制电流的增加,减振器阻尼力也随着增加,电流较小时阻尼力增加相对较慢,电流较大时阻尼力增加相对较快;当电流一定时,减振器阻尼力随着活塞速度的增加而增加.运用LabVIEW软件拟合的多项式模型更接近试验数据曲线,说明该多项式数学模型能很好地描述磁流变减振器阻尼力的滞回特性和非线性特性.【期刊名称】《科学技术与工程》【年(卷),期】2017(017)034【总页数】5页(P332-336)【关键词】磁流变阻尼器;LabVIEW;多项式模型;滞回特性;非线性【作者】王靖岳;郭胜;王浩天【作者单位】沈阳理工大学汽车与交通学院,沈阳 110159;沈阳理工大学汽车与交通学院,沈阳 110159;沈阳航空航天大学自动化学院,沈阳110136【正文语种】中文【中图分类】U461.4磁流变液(MRF)是一种低磁滞性、高磁导率的微小软磁性颗粒,与非导磁性液体混合组成的智能材料[1]。
微带线谐振频率
微带线(Microstrip Line)是一种用于传输高频电磁波的平面传输线,它由一个导电带(通常由金属制成)和两侧的绝缘介质(如聚四氟乙烯)组成,导电带通常印制在印刷电路板上。
微带线的谐振频率与线的长度、宽度、介质常数以及工作频率有关。
谐振频率是指传输线上的电磁波振荡的频率,此时传输线的特性阻抗接近于开放电路的阻抗,能量主要在传输线上来回反射,而不是向前传输。
对于微带线来说,谐振通常是不希望发生的,因为它会导致传输线成为天线,从而发射或接收不必要的信号。
微带线的谐振频率可以通过以下公式估算:
\[ f_{resonance} = \frac{1}{2\pi \sqrt{LC}} \]
其中:
- \( f_{resonance} \) 是谐振频率(单位:赫兹Hz)。
- \( L \) 是微带线的电感(单位:亨利H),与线的长度和相对电感率有关。
- \( C \) 是微带线的电容(单位:法拉F),与线的宽度和介质的相对电容率有关。
要精确计算微带线的谐振频率,还需要考虑许多其他因素,如介质的有效介电常数、导体的损耗、绝缘层的厚度等。
实际设计中,工程师会使用专门的软件或在线计算工具来计算微带线的特性,以确保其工作在所需的工作频率范围内,避免谐振现象的发生。
ZnO非线性电阻的特性及ZnO均能
ZnO非线性电阻的特性及ZnO均能/均流技术的机理正广电隔直设备的核心技术——氧化锌阀片,有许多客户还不太了解,今天,小编就来给大家讲一讲,关于ZnO非线性电阻的特性及ZnO均能/均流技术的机理。
氧化锌阀片作为电力系统过电压过电流防治领域的常见元件,其具有良好的非线性伏安特性。
目前市面上有高压片和高能片之分。
高压片主要应用于过电压保护器、避雷器等过电压治理的产品中,高能片一般采用均能技术可以应用于灭磁柜、隔直等过电流治理产品中。
下面小编将为大家系统介绍氧化锌材料特性和均能/均流技术的机理:1、 ZnO非线性电阻的特性通过对三种电阻的伏安特性曲线分析(见图1),可见电阻具有优良的的伏安特性:即在低电压时,泄漏电流极小(μA级)。
当电压升高到其“导通点”(即保护电压)以上时, ZnO非线性立即导通,此时随着通过电流在不断增大其电压反被“钳制”住不上升,伏安特性十分平坦。
ZnO这种优良的非线性伏安特性给过电压保护带来一系列优点.图1、三种电阻的曲线1.线性电阻2.SiC电阻3.ZnO电阻l) 吸能元件可以直接跨接在被保护设备两端, 其泄漏电流很小(微安级)不产生很大功耗;对被保护设备无影响。
2) 消耗(短路、灭磁等)能量速度最快(微秒级);3) 过压保护装置可以自动复位(电压一旦下降到保护定值以下,ZnO立刻恢复高阻状态),而不需要任何附加措施( 如熔丝,逆变甚至停机);ZnO非线性电阻优良的伏安特性在国内得到广泛的应用。
但是目前用于过电压保护的单片ZnO压敏电阻片( 阀片),其单片“标称”吸能容量为15~30 kJ,而过系统电压保护所需要吸能元件的能容量一般均为几百kJ到几个MJ,因此必须多个阀片串并联组合才能达到消耗能量的目的。
图2、两个ZnO电阻阀片并联时电流分配由上述可见,ZnO非线性电阻的伏安特性虽然呈现出一系列优点, 但它却给组合时的均能(特别是均流)配片带来极大困难。
由于其导通区的伏安特性过于“平坦”,极小的电压差距就会带来极大的电流差距。
微机电系统综述
微机电系统综述摘要:微机电系统(MEMS)是在微电子技术的基础上兴起的一个多学科交叉的前沿领域,集中了当今科学技术发展的许多尖端成果,在汽车电子、航空航天、信息通讯、生物医学、自动控制、国防军工等领域应用前景广阔[1]。
本文介绍了微机电系统起源及研究发展的背景,综述了微机电系统所涉及的器件设计、制作材料、制作工艺、封装与测试等关键技术,介绍了微机电系统在微传感器、微执行器、微机器人、微飞行器、微动力能源系统、微型生物芯片等方面的典型应用,大量先进的MEMS器件有望在未来几十年中从实验室推向实用化和产业化。
关键词:MEMS;微机械加工;封装;测试;应用Abstract;Micro-electromechanical system(MEMS),developed on the basis of microelectronics,is a scientific research frontier of multidiscipline and assimilates the most advanced achievements in current research and development.MEMS extends into various fields with wide application prospects,such as automotive electronics, aeronautics and astronautics,information communication, biomedicine,auto-control and defense industry,and so on.This paper introduces the basic theory research of MEMS development and its background.Summarizes the key technologies of MEMS such as device design,fabricating material, machining processes ,micro-packaging and testing.Further more,the typical applications and latest development in fields including micro-sensor,micro-actuator,micro-robot,micro air vehicle,micro-power energy system,micro biological chip are discussed.A plenty of advanced MEMS devices would be put into practicality and industrialization from laboratory in recent decades.Keywords:micro-electromechanical system; micro -machining; package; testing; usage1 引言微机电系统简称为MEMS(Micro-Electro-Mechanical System),是利用微米/纳米技术,以微细加工为基础,将微传感器、微执行器和电子电路、微能源等组合在一起的微机电器件、装置或系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静电驱动的亚微米悬臂梁谐振器非线性特性岳东旭;于虹;袁卫民【摘要】理论分析了亚微米尺寸的悬臂梁结构的非线性力学模型,研究了非线性产生的物理机制.采用外部静电激励机制,使悬臂梁谐振器产生谐振,借助Polytec激光多普勒测振系统检测了悬臂梁的频率响应曲线.测试结果表明,悬臂梁具有显著的非线性效应(即"弹簧变软"效应).实验证实了这种非线性效应几乎和交流电压无关,却随着直流电压的增大而显著增大,最大峰值偏移达到0.5 MHz.提取出3组-阶机械弹性系数分别为79.62,31.75和14.92 N/m,实验结果符合理论规律.对实验中的偏差做了进-步的分析和讨论,利用软件ANSYS对过腐蚀对结构刚度和频率响应的影响做了相应的模拟,结果和实验测量数据相吻合.%A nonlinear mechanical model for sub-micron cantilevers was analyzed in detail and its physical mechanism was researched to provide a theoretical basis for experiments. The electrostatical force was used to achieve the resonance state cantilever beams and a Polytec laser Doppler vibration measurement system was taken to observe the frequency response curve. Experimental results show that the beams have significant nonlinear effects (the spring softening effect) and the nonlinearity is relatively independent on the AC voltage, but it is markedly enhanced with increasing the DC voltage.The obtained maximum peak shift is 0. 5 MHz and extracted first-order mechanical elasticity coefficients are 79.62, 31.75, and 14.92 N/m, respectively. Furthermore,the deviation of the experiment was also disccussed and analyzed. The effects of overetching by wet chemical etching on the stiffness and frequency response were stimulated by ANSYS software. Inconclusion, the corresponding simulation results are well coincident with the experimental data.【期刊名称】《光学精密工程》【年(卷),期】2011(019)004【总页数】6页(P783-788)【关键词】静电驱动;悬臂梁谐振器;非线性;频率响应【作者】岳东旭;于虹;袁卫民【作者单位】东南大学电子科学与工程学院MEMS教育部重点实验室,江苏南京210096;东南大学电子科学与工程学院MEMS教育部重点实验室,江苏南京210096;东南大学电子科学与工程学院MEMS教育部重点实验室,江苏南京210096【正文语种】中文【中图分类】TP212.11 引言纳米线、纳米薄膜、纳米梁等[1-3]微纳结构谐振式传感器因其性能良好一直是微纳领域的研究热点,其中静电驱动的微/纳米梁谐振器因其在质量、生物化学传感,信号滤波和无线传输等领域卓越的性能而受到人们更多的关注[4-7]。
这不仅由于它们结构简单易于设计优化,更重要的是其具有超高的灵敏度、超高的分辨率和较低功耗等良好的特性,在微/纳机械系统(MEMS/NEMS)的研究中始终扮演着重要角色。
目前,人们研究的微纳机械谐振器其频率已达到MHz甚至GHz,并且发现工作在高频段的谐振器,除具有超高的灵敏度和分辨率、低功耗等特性外,其非线性行为也非常明显。
A.Erbe等人研究了电磁激励下的纳米谐振梁的非线性效应,并利用这种效应实现了机械混频[3]。
M.Agarwal利用静电驱动,实验上观察到了双端固定的音叉谐振器的非线性现象[7]。
M.Palaniapan研究了SOI工艺自由-自由微米梁谐振器的非线性行为并观察到了滞回现象[8]。
L.C.Shao也在实验上研究了面内振动的双端固支谐振梁的非线性特性并进一步讨论了如何取消非线性带来的影响等[9]。
本文研究了亚微米尺寸的悬臂梁结构的非线性力学行为,分析了非线性产生的物理机制,解释了实验中观察到的频率偏移现象,得出悬臂梁的非线性由直流电压决定而与交流电压几乎无关的结论,得到的实验结果符合理论规律。
2 工艺制造本文实验设计的悬臂梁谐振器采用SMIOX(深注入氧工艺)工艺制做晶面为(100)方向的SOI硅片,由中芯国际0.18μm工艺线流片完成,实验中用到的悬臂梁的晶向均沿<110>方向。
其上层硅的厚度为200 nm,中间二氧化硅氧化层的厚度为200 nm,底层硅为350μm。
具体工艺步骤如下图:图1 悬臂梁谐振器制作工艺流程Fig.1 Fabrication process of cantilever resonators3 非线性振动的动力学模型3.1 非线性模型的一般形式A.Erbe首次提出了利用达芬方程描述纳机械谐振器的非线性特性,基于宏观连续体理论用质量-弹簧-阻尼系统来表示其力学模型[6]。
一般认为亚微米尺度下的纳米梁振动方程依然遵循此模型,当受迫振动的谐振梁的非线性刚度系数需要考虑时,系统动态特性可以由下面的的动力学方程来表示:其中x为位移;μ为阻尼系数;ω0为角速度分别代表有效线性、二次和三次弹性常数;m是结构的集中质量分别是结构恢复力和外加静电引力的线性系数,则有类似的定义,对于悬臂梁有是外部施加的简谐力。
3.2 悬臂梁结构的非线性模型本论文设计采用静电驱动方法,通过施加在梁与衬底之间的交流电压来驱动梁,其中衬底作为下电极。
文中采用了典型的悬臂梁结构,图2为成功释放的5μm长的悬臂梁SEM照片。
驱动信号一般采用直流加交流的形式,这样可以更为容易地使梁产生谐振。
当输入电压为V(t)=Vdc+Vac cos(2πft)时,结构受到的静电力泰勒展开式有以下形式:图2 5μm×2μm×0.2μm悬臂梁的SEM照片Fig.2 SEM micrograph of5μm×2μm×0.2μm released beam其中A表示悬臂梁正对下极板的面积,w表示梁的宽度,d0表示梁和下极板的间距。
直流Vdc和Vac别是所施加的直流电压和交流电压,且Vac≪Vdc,故公式(3)中的第三项常忽略不计。
由(2)式易得静电力的线性和非线性系数的表达式,从而提取出静电力的各项系数如公式(4)。
这里忽略ke2,ke3的影响(其更详细的分析见文献[10]),只考虑静电力线性弹性常数的作用,因w/d0较小边缘效应不可忽略[11],故此时结构的一阶本征谐振频率为由上式可知,外加电压V(t)起着调控结构机械谐振频率f0 的作用,f0′将随着V (t)增大而减小,ke1表达式的后3项为考虑了电容边缘效应的结果。
4 实验结果与讨论实验中采用Polytec激光多普勒测振仪测量系统检测谐振梁的频率特性。
图3为半个大气压下谐振频率为11.37 MHz悬臂梁的频率响应曲线,其品质因数大约为80。
选择了3组不同尺寸的悬臂梁,用于说明非线性与尺寸以及过腐蚀深度对本征频率的影响。
第一组在常压下测量得到尺寸为3.5μm×1.5μm×0.2μm 的悬臂梁谐振频率为13.69 MHz,接着对其不同偏置条件下的频率响应特性进行了测试,结果表明在恒Vdc下,随着Vac驱动电压的增加,频率响应曲线几乎不变,如图4(b);然而,当保持Vac不变增加直流时其幅频曲线却明显地向左偏移,即出现“弹簧变软”效应[12]如图4(a)。
Vdc从10 V增大到30 V,谐振峰偏移量达0.5 MHz,是先前报道的近50倍[9]。
究其原因后面提到的过腐蚀降低了结构本身的弹性系数,另一方面,d0足够小致使机构受到的静电力增大到和结构恢复力可以比拟的程度。
如此大的频率偏移量对于常见的利用频率偏移原理的传感器来说具有足够大的灵敏度。
图3 谐振频率为11.37 MHz悬臂梁的频率响应曲线Fig.3 Frequency response of cantilever beam with 11.37 MHz of resonant frenquency第二组选择了较长的尺寸5μm×1.5μm×0.2μm的梁做了同样的测试,得到类似的特性曲线如图5(a)和(b)所示,当Vdc在5~20 V区间变化时,偏移量达0.48 MHz。
第三组选了与以上两组等宽、等高、长为9μm的结构,得到了它在Vdc增大时的一组频率曲线如图(6),同样观察到了明显的“弹簧变软”效应,同时也得出在一定尺度范围内,随着梁尺寸的增大偏移量有稍微变大的趋势。
图4 施加电压变化时,3.5μm×1.5μm×0.2μm悬臂梁的频率特性Fig.4 Frequency response curves of 3.5μm×1.5 μm×0.2μm cantilever beam resonator with applying voltages varied对以上三组实验进行了参数分析,图7为Vdc-f0′二次关系曲线,其中图7(b)中小图为9.0 μm×1.5μm×0.2μm 悬臂梁的Vdc-f0′拟合曲线。
把3组相应的结构尺寸代入,根据公式(5)、(6),可以从曲线提取出一阶机械线性弹性系数km1分别为79.62、31.75和14.92 N/m。
图5 施加电压变化时,5.0μm×1.5μm×0.2μm悬臂梁的频率特性Fig.5 Frequency response curves of 5.0μm×1.5 μm×0.2μm cantilever beam resonator with applying voltages varied图6 9.0μm×1.5μm×0.2μm悬臂梁Vdc变化时的频率特性Fig.6 Frequency response curves of 9.0μm×1.5 μm×0.2μm cantilever beam resonator图7 3组不同尺寸的悬臂梁的Vdc~fo′拟合曲线Fig.7 Plot of resonant frequency fo′verse Vdc for cantli lever beam图8 ANSYS模拟无过腐蚀和过腐蚀2μm载荷-挠度关系曲线Fig.8 ANSYA simulation curve of load-flexivity between over-etching and non over-etching由于在湿法释放结构时不可避免地会产生过腐蚀现象,此时原先设计的悬臂梁结构却演变成了T型梁,而这必然会对结构谐振频率和弹性系数产生影响。
