习题一
电工电子技术习题1

习 题 一1-1 在图1.51中,方框代表电源或负载。
已知,100V =U ,2A -=I 。
试问,哪些方框 是电源,哪些是负载?解:〔a 〕电源 〔b 〕电源 〔c 〕负载 〔d 〕负载1-2 已知蓄电池充电电路如图1.52。
电动势20V =E ,设Ω2=R ,当端电压12V =U 时求 电路中的充电电流I 及各元件的功率。
并验证功率平衡的关系。
解:RI U E += 201242I -∴== A 2220480W423212448WE R U P P R I P =-⨯=-==⨯==⨯=W80R U P P +=W电路中电源发出的功率等于负载消耗的功率,功率是平衡的1-3 在图1.53所示电路中,已知,14V 1=U ,2A 1=I ,10V 2=U ,1A 2=I ,4V 3-=U , 1A 4-=I 。
求各元件的功率。
并说明是吸收还是发出。
并验证功率平衡的关系。
解:由上面计算得:元件1发出功率,元件2、3、4吸收功率123428W 28WP P P P =-++=1-4 求图1.54示电路中电流源两端的电压及通过电压源的电流。
解:〔a 〕图1.52 习题1-2的电路=U 1U 2 图1.53 习题1-3的电路+=- =(a) (b)I S 2Ω2Ω5V 2A 图1.54习题1-4的电路(a)(b)(c)(d)图1.51 习题1-1的电路11122233342414228W 10110W 428W (10)(1)10WP U I P U I P U I P U I =-=-⨯=-==⨯==-=⨯==-=-⨯-=(b) 5409V U U ++=∴=-2A I =1-5 一直流电源,其额定功率为200W N =P ,额定电压50V N =U ,内阻为0.5Ω0=R ,负载电阻L R 可调。
试求:〔1〕额定工作状态下的电流及负载电阻;〔2〕开路电压U 0;〔3〕短路电流S I 。
解:〔1〕N N N P U I = 200450N I == A N L N U R I = 12.5L R =Ω 〔2〕05040.552E U IR =+=+⨯=V 〔3〕0104S EI R == A 1-6 图1.55中已知10V 1=U ,4V 1=E ,2V 2=E ,4Ω1=R ,2Ω2=R ,5Ω3=R ,2Ω4=R 。
船舶习题解1-5
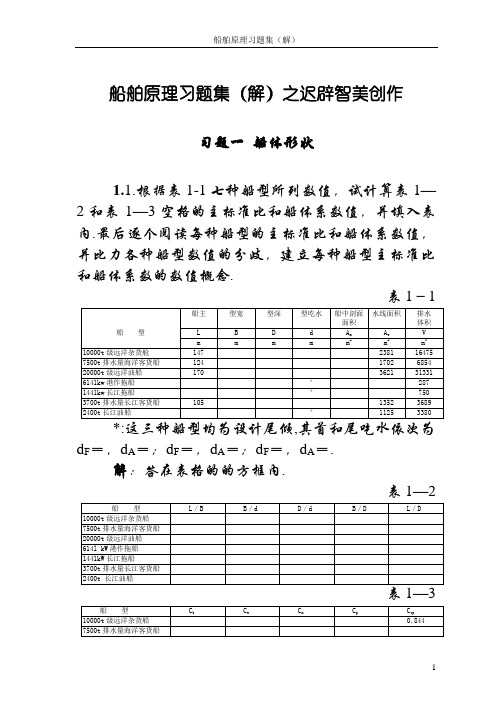
船舶原理习题集(解)之迟辟智美创作习题一船体形状1.1.根据表1-1七种船型所列数值,试计算表1—2和表1—3空格的主标准比和船体系数值,并填入表内.最后逐个阅读每种船型的主标准比和船体系数值,并比力各种船型数值的分歧,建立每种船型主标准比和船体系数的数值概念.表1-1d F=,d A=;d F=,d A=;d F=,d A=.解:答在表格的的方框内.表1—2表1—3b=,C w =;试求其A w解:A W =C W LB C b =LBdV LB =dC V b A W =b WC C dV =8.5*62.07350*75.0=1532.95=1533m 21.3. 名词解释:船中,舷弧,梁拱,型概况,型线图,型线图的三个基准面,平行中体,船主,型宽,型深,型吃水,船体系数答:略.习题二 船体的近似计算2.1.已知某船吃水为的水线分为10个等分,其横向坐标间距l =,自首向尾的横向坐标值(半宽,m)分别为:0,,,,,,,,,,.试分别用梯形法则和辛氏法则求其水线面积.解:梯形法计算:通用公式:A =∑=ni i y l 0(-20ny y +) ∑=ni i y 0=0+3.3+5.3+4*5.90+5.85+5.22+3.66+1.03=47.96ε=20n y y +=203.10+=0.515 因水线面面积是对称的,故A W =2AA W =2 ∑=ni i y l 0(-ε)2●辛氏一法计算:公式A =31l (y 0+4y 1+2y 2+4y 3+……4y n-3+2y n-2+4y n-1+ y n )=31A W =2A =2*168.13=336.26m 22.2.某船中横剖面的半宽坐标,自基线起向上分别为0,,,,,,6.80 m ,两半宽坐标间的垂向间距为1m.试用辛氏法则求船中横剖面的面积.解:● 辛氏一法:A m =2*31(1*0+4*2.43+2*5.23+4*6.28+2*6.6+4*6.75+6.8)=2● 辛氏二法:A m =2*83(1*0+3*2.43+3*5.23+2*6.28+3*6.6+3*6.75+6.8)=2=22.5000t 货船各水线面积如表2—1所示.试用梯形法求水线以下的排水体积. 解::● 梯形法: I ==∑=ni iy 00+980+1123+1165+1200+1225+1240+1258+1268+1280+1293+1305+1320+1335+1350+1360+1380+1400=21482ε=214000+=700排水体积V =l (I-ε)=0.4*(21482-3 ● 辛氏法联合应用:V =31*0.4*(0+4*980+2*1123+4*1165+2*1200+4*1225+2*1240+4*1258+2*1268+4*1268+2*1293+4*1305+2*1320+4*1335+1350)+83*0.4*(1350+3*1360+3*1380+1400)=8363.1m 3习题三 浮性3.1.已知某船重量分布如表3—9所示,试求船舶的重量和重心坐标.表3-9按图表3-9所示数值计算(上表) ,将计算结果∑+i i g Z P Z W 00、W =W0+∑i P =19521.00代入公式,得Z g =m P W Z P Z W iii g 935.71952161.154901000==++∑∑,将计算结果∑+i i g X P X W 00=-34927.24、W =W 0+∑i P =19521.00代入公式,得X g =m P W X P X W iii g 789.100.1952124.34927000-=-=++∑∑.3.2.若题1船在航行中途消耗油和谈水如表3—10,求此时船舶的重心坐标及移动方向.表3-10由上题已知: W 0=19521t, Z g0=7.935m, X g0=- 由题中给的表计算得∑i P t, Z pi =2.836, X p = -12.611W 1=W 0+∑i P =19521-1449.5=18071.5Z g1=∑∑++ipig P W Z P Z W i 000=5.1807116.4110154899-=8.344,上移X g1=∑∑++iii g P W X P X W 000=5.1807178.1828074.34927+-=-0.921,前移.3.3.某船某航次离港时船舶重量为w =19503t ,重心距基线高为z g =,到港时油和海水共消耗,其重心距基线高为,试求到港时船舶重心距基线高.又以上算出的船舶重心偏高,为保证船舶在到港前的平安,在第三和第四压载舱内加装压载水,其重量和重心见表3—11,试求压载到港后船舶重心距基线高.表3-113.13, 求Zg1=?解::列表计算:Z g1=∑∑++PW PZ WZ pg =m 338.86.152********.3*6.152693.7*19503=--Z g2=3233221)()(P P P W Z P Z P Z P W P P g ++-++-=603366.152********.0*6072.0*336338.8*)6.152619503(++-++-=8.174m3.4.已知船舶重量为16700t ,今有船内重量10t 自底舱上移14m 后,又水平右移9m ,试求船舶重心移距及其方向.已知:W 0=16700t P =10t l zp =14m l py =9m 求l gz , l gy解::l zg2=W Pl zp =1670014*10=0.0084m(上移)l yg2=W Pl yp =167009*10m(右移)3.5.已知船舶重量为16700t ,今有船内重量50t自首部水平后移60m ,试求船舶重心移距及其方向.已知W =16700t l x =60m P =50t 求 G’G =?解: G’G =WxPl =17006)60(*50-=0.018m(后移)3.6. 从舷外测得船舶吃水d =,该船的静水力曲线如图3—9所示,试求船在海水中的排水量.解:据dm 查船的静水力曲线如图3—9得:D=12800t.3.7.从舷外测得船舶吃水d =,该船的载重量表尺如图3—10所示,试求船在海水中的载重量.解:据d =查船的载重量表尺图3—10得:D=15100t.3.8.已知船舶重量W =15430t ,试利用图3-9或图3—10,求船在海水中的吃水.若自船上卸去3000t 货物时,则船在海水中的吃水即是几多米?解::据d =查船的载重量表尺图3—10得:d=7.6m, 卸去3000t 货物后.3.9.某船在青岛空载(Do =5176t)装煤运往上海,估计船过南水道铜沙浅滩时水深为8.5m,试利用图3—9或3—10估算该船最年夜允许的载重量(注:设过铜沙浅滩时规定最低富裕水探为,铜沙水的密度lo =/m 3).已知:D 0=5176t, d =8.5-0.5=8.0m, pt/m 2, 求载重量i P ∑解:先求d =8m 时的排水量.查3-11图获得:d =8m 时海水(γ13)中的排水量D 1=400*41.25=16500t d =8m 时海水 (γ23)中的排水量D 2=400*4=16120t用插值法求d =8m 时,γ32t/m 3时的排水量D 3D 3=)()()(21123231γγγγγγ--+-D D =000.1025.116500*)1002.1(16120*)002.1025.1(--+-=16150.4t载重量∑i P =D 3-D 0=16150.4-5176=10974.4t 3.10.根据图3—9,量得各吃水时的水线面积A w 如表3—12所示.算出各吃水时的zA w 值,并据此画出zA w =f(z)曲线 (如图3-11),试利用梯形法则,根据式(3-6d )求出6m 吃水时浮心距基线高.表3-12由上表计算出Z g =3.402m.3.11.已知吃水d =5m ,试利用图3—9求出该船浮心距基线和浮心距船中值.已知:d =5m,解::查表图3-9(21页),得Z b =0.4*6.5=2.6m , X b3.12.已知首吃水d f =8m ,尾吃水d A =,试根据图3—18求该船在海水中的排水量和浮心距船中值.解:根据d f =8m 查35页费尔索夫图谱得V=17100m 3, x b =-2m.3.8m ,试根据图3—9或图3—10,求出其每厘米吃水吨数.今欲卸货150t ,问卸货后船舶的吃水是几多? .已知:d=8m p=150t 图例-9 3-10 解t/cmd 1=d-Δd p3.14.已知吃水分别为3m 、4m 、5m 、6血、m cm TPC p d p 62.017.62403150====∆7m 、8 m 和9m,试根据图3—9,求其漂心距船中值.解:据已给条件查出漂心纵座标分别为x f .3.15.根据图2-4,量得某半宽水线各横坐标值如表3-13所示,横向坐标间距lm,算出各纵坐标的y i x I 值.试利用梯形法则,根据教材式(3-8),求出该水线的漂心纵坐标.表3-133.16.某船某航次自日本装货运往上海,到上海时船舶重量为17400t ,相当于在海水中吃水8.4m ,其每厘米吃水吨数为24.75t /cm ,海水密度为1.025t /m 3.若上海港水的密度为 1.010t /m 3,求船在上海港时的吃水为几多(设船重不变,且平行沉浮)?已知:W=17400t d=8.4ρ13 ρ= 解::mTPC W d p 1044.0)1010.1025.1(75.24*10017400)1(10021=-=-=∆ρρd 2=d 1-Δd p3.17.某船自上海港装货运往斯德哥尔摩,问在上海港(ρ=1.010t /m 3)应装到几多吃水,才华使船出海时(ρ海=1.025t /m 3)到达满载吃水8.23m?解::d 1=122γγd =010.123.8*025.13.18.画简图说明如何利用邦金曲线图计算波形水线下的排水体积和浮心纵向坐标.答:略.3.解释:浮性,正浮,浮体平衡条件,平行力移动原理,平行沉浮条件,静水力曲线图,邦金曲线图,费尔索夫图谱,每厘米吃水吨数,重心,浮心,漂心,储藏浮力.答:略.习题四 稳性4.1.今有断面为正方形的一根木质柱体,其长L =2m ,正方形边长b =0.2m ,密度ρ =0.5t /m 3.说明,当将其放入水中后,它在什么漂浮状态时才处于稳定平衡?(提示:本题为浮性和初稳性的综合题.首先需根据平衡条件选择几种典范的浮态,然后根据稳定平衡条件计算其GM 值是否满GM >0.掌握处置这类问题的思路后,则可预计任一形状的物体投入水中后,其稳定的漂浮状态.)解:⑴如右图a 所示的漂浮状态V =22L b (m 2) I xf =123Lb (m 4)r =V I xf =6b (m ) Z b =4b (m ) Z g =2b (m)GM = r + Z b + Z g =6b +4b -2b =-0.017m <0结论为:不稳定的漂浮状态. ⑵如右图所示的漂浮状态V =22L b (m 2) I xf =12)2(3b L (m 4)r =V I xf =32b (m ) Z b =d 32=32b (m ) Z g =22b (m)GM = r + Z b + Z g =32b +32b -22b =62b =0.047m >0结论为:最稳定的漂浮状态,木柱将以此种状态漂浮.⑶ 其它的漂浮状态也均为不稳定的漂浮状态,因为浮心和稳心不在同一条铅垂线上.4.2.今有断面为圆形的一根均质柱体平浮于海水水面,其长L =2m ,圆的直径D =0.4m ,密度为0.5t /m 3,试求它的稳性高度.若密度为lt /m 3,当吃水d =5m 时,求得其GM =0,试分析其原因.解::圆木与水的密度比为/1=,所以圆木的浸水体积为圆木体积的一半,如图所示.当ρt/m 3时, V =42D π2L=82LD π(m 2) I xf =123LD (m 4)r =VI xf=123LD L D 28π=π32D (m ) Z b =2D -π324D =2D (1-π34)(m ) Z g GM = r + Z b + Z g =π32D +2D (1-π34) -2D=0说明均质圆柱体在水中处于中性平衡.稳心与重心重合.当ρ=1t/m 3时,吃水d=5m , V=πR 2L, 其水线面面积为0,即y=0,所以I xf =⎰-FA l l32y 3dx =0 r =VI xf =0Zb =2D (m ) Z g =2D (m)GM = r + Z b + Z g =0+2D -2D=0重合.结论:均质圆柱体在水中总是处于中性平衡. 问题:非均质的如何?4.3.已知箱形船和横剖面为等腰三角形的纵柱体船,船主L =100m ,水线处船宽B 和b =10m ,吃水d =5m ,试求两船的稳心半径和稳心距基线高,并画出其Z b =f(d),r =f(d)和z m =f(d)曲线.解:箱形船 I xf =3LB V=LBd(2)三棱柱体船3LB I xf= tg γ=15= B ˊ=2d4.—39所示,已知坞长为L ,坞宽为B ,两舷浮箱三棱柱体船船型r、Zb、Zm曲线012345601234567Zb、r、Zm(m)d (m )宽为b ,底部浮箱深为h,吃水为d ,试列出其稳心半径和稳心距基线高的表达式.解:根据书中图所示,=L b Bb bB )322(322+-=)(2)2(222h d b Bh b B h bd -+-+ Zm=Z b +r=)(2)2(222h d b Bh b B h bd -+-++[])(26)463(22h d b Bh b Bb B b -++-4.5.已知某半宽水线各半宽坐标值自首至尾分别为0、1.55、3.60、 5.82、7.79、9.19、 9.89、10.20、10.20、10.20、10.20、10.20、10.20、10.20、10.08、9.79、9.10、7.79、5.69、3.20和0.42,半宽坐标间距l =7.35m ,试利用近似计算法则,求该水线面积对ox 轴(图2—4)的面积惯矩I xf .又已知该水线下船体排水体积V =13800m 3,试求其稳心半径r.解: 梯形法计算:3333333333333333201308.1329842.02.369.579.710.979.908.1020.10*789.919.979.782.56.355.10m yi i=++++++++++++++=∑=修正值:035.0207.0023332030=+=+=y y ε 72.41380042.65160===V I r xf m4.6.某船排水量D =5150t ,稳性高度GM=0.5m ,船舶初始向左横倾3o .为使船舶恢复正浮,需将船内甲板货水平横移.若水平横距为5m ,试求应移货的重量和方向.(提示:货物横移,求P)解: θ2=0o θ1=-3o θ=θ2-θ10o -(-3o )=3o 由GMD Pl tg y =θ 而得θtg l GM D P y**=因为 0>θ ∴货物向右舷移动.4.7.某船建造完成后作倾斜试验.试验时船舶排水量D =6145t ,其稳心距基线高z m = 10.9l m.试验重量P=40t ,水平横移距离l y =16.84m ,悬距b =8m ,测得摆距a =0.32m.试验时,过剩重量为200t(含试验重量),其重心距基线高为3m ;缺乏重量为5t ,其重心距基线高为8m ,求空船重心距基线高.(提示:倾斜试验,求Z g0)解:832.0==b a tg θ mW Z P Z P Z D Z t P P D D W m GM Z Z mtg D Pl GM i i i j gg i j m gy 344.859503*2008*517.8*614559502005614517.874.291.1074.232.08*614584.16*401*000000=-+=-+'==-+=-+===-=-='===∑∑∑∑θ4.8.已知某船初步配载计划做好后,排水量D =17006t ,稳性高度GM =0.76m.若要求GM 到达l m ,需从甲板间舱向底舱移动货物,设垂移距离l z =8m ,问应该移动几多吨货物?(提示:货物垂移,求P)已知:D=17006t GM =0.76m M G '=1m l Z =8m 求P=? 解::4.9.已知某船排水量D =19503t ,稳性高度GM =0.78m.在第三货舱内有年夜件货,货重P =100t ,今有船上重吊将此年夜件货吊离舱底,其初始重心q 至悬挂点m 的距离l z =22m ,问此悬挂年夜件货将使GM 减少几多米?另外,在考虑悬重影响后,若P自q 渐渐上升,在上升过程中GM 是否继续改变,为什么?(提示:悬挂物问题,求∆GM )已知:D =19503t m GM 78.0= P =100t l z =22m 求 ∆GM解::113.01950322*100===∆D Pl GM zm重物在渐渐上升过程中,不改变GM 值.因为悬挂物自己的虚重心就是在M 点.沿着l Z 上升,M 点其实不改变.4.10.已知某船D =19503t ,GM =0.78m ,吃水d =8m ,每厘米吃水吨数TPC =25t /cm.今用船内重吊将第三舱内重量为150t 的年夜件货吊卸至码头,货重初始位于中纵剖面,其重心距基线高为10m ,挂点距基线高为42m.当货重转向码头后,挂点水平横移距为19m ,挂点高度下降2m ,试求货重在卸落码头前船的横倾角.(提示:吊卸货物, 求θ)已知:D=19503t m GM 78.0= P=150t Z P =10m l Z =42-10=32m l y =19m l m =2m 求θ解::()()5514266.01950323215078.01950319*1500'==⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡--=θθD l l P GM D Pl tg m z y说明:垂移30m 、横移19m 后GM 值下降,并发生了横倾角θ.4.,每厘米吃水吨数TPC =23t /cm.今有船舶重吊自码头吊起货重为150t 的年夜件货,其挂点距基线高为40m ,挂点至船舷的水平横距为9m ,船宽为22.1m ,试求吊起货重后船舶的横倾角,试检验上述年夜件货的装卸是否符合要求? 如果不符合要求,则可采用哪些办法?(提示:吊装货物)已知:D =14000t GM =1.2m d=7.02m TPC=23t/cmP=150t l y =9+21.22m m B 1.22= 求θ解:: 40='+'P z Z lD 1=D+P=14000+150=14150t⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛'+'-∆++==+=∆+====∆GM l Z d d D PGM M G m d d d TPC P d z P 2085.70652.002.70652.023*1001501001111838.02.14020652.002.7141501502.1=⎥⎦⎤⎢⎣⎡--++=m 4.12.已知某船排水量D =19004t ,平均吃水d M =9m ,稳性高度GM =0.63m.船内有一双层底舱未装满燃油,舱的首尾向长度L z =14.6m ,左右向宽度L y =9m(设舱的形状为箱形),燃油的密度ρ=0.98t /m 3,问其自由液面使GM 改变了几多?并求自由液面修正后的稳性高度.(提示:本题属自由液面问题)已知:D=19004t d m =9m m GM 63.0= 3/98.0m t =ρ 求GM解::4.13.已知某船排水量D =19503t ,稳性高度GM =0.78m ,若船内有下列液体舱柜未装满:第一压载舱、清水舱、No.1(右)、燃油舱No.1(左)、轻柴油舱(左)和滑油循环柜,各舱柜自由液面对稳心高度的降低值见表4—l.试求该船自由液面修正后的稳性高度.(提示:属于自由液面问题)已知:D=19503t m GM 78.0= 第一压载舱,清水舱№1(右),燃油舱№(左),轻柴油舱(左),滑油循环柜,均有自由液面,求:自由液面修正后的GM 值.解::由书P51表4-1查得D=19000时(为平安起见,如准确应在19000-20000之间插值19503时的)各舱柜的稳心高度降低值,并根据(4-10d )得 ()m M G 6867.00017.00186.00241.00059.0043.078.0=++++-='(准确插值法得6891?0='M G )4.—9.在海水中排水量D =16050t ,稳性高度GM =0.76m.今有500t 货加装在船上,货物重心距基线高z p =8.17m ,试求装货后船舶的稳性高度.(提示:属于少量装货问题)已知:D=16050t, m GM 76.0=, P=500t, Z p =8.17m 求:='M G ?解::根据D=16050t,3-9图 d=7.8m ,TPC=24*1t/cm4.15.某船某航次于上海装货运往日本,在日本门司港中途卸货.卸货前,排水量D =17006t ,重心距基线高z g=7.84m.其静水力曲线图见图3—9,卸货重量及重心见表4—7,试求卸货后的稳性高度.表4-7已知:略解::1g1根据D1=14193t查21页图3-9,得d1 Z m14.16.已知某船排水体积V =15000m 3,重心距基线高z g =7.7m ,稳性交叉曲线见图4—20b .试画出其静稳性图.(提示:属于利用稳性交叉曲线绘制静稳性曲线的问题)已知:V=15000m 3 Z g =7.7m 求静稳性图.解:①用假定重心法.假定重心Z gA =8m 则Z g - Z GA =7.77-8=0.3m根据V=15000m 3 查书中70页的4-20b )图曲线,量得各θ时的A A Z G 值填入下表,并按表中项目计算,如下表:GZ GZ 稳性曲线.②用基点法.V=15000m 3 Z g =7.7m 用70页图4-20a )稳性交叉曲线,量得各θ时的KN 值,填入下表,并按表中项目计算,如下表:4.17.试根据基本装载情况下的静稳性图(表4—3)的已知条件,求平均吃水d M =3.333m ,横倾角θ=30o 时的形状稳性力臂KN(注:静稳性图的数值见书中表4—8).静稳性力臂GZ(m)值表4-8水)下的倾角为30o 时的KN 曲线 ,在曲线上可找到吃水时的KN 值,这其实是上一题逆作:已知静稳性曲线求KN 曲线)解: 1 根据题已给的表4-8,查出各种装载条件下的θ=30o 时的l s ;四-16题曲线00.20.40.60.811.20102030405060708090θ0G Z2 从65页,66页表中查出各种装条件下的Z g ,将上述值列表如下曲线,如下图.在图上求得:d=3.3m 时,KN=4.66m(A 点).4.18.已知某船排水体积V =16000m 3,重心距基线高z g =7.8m ,各倾角时稳性力臂值见表4—4.若横倾力矩M I ×103N ·m),试分别求出其θs ,θd .(提示:利用静稳性曲线求θs ,θd )已知:V=16000m 3,Zg=7.8m,M I =5000tm, M I =10000tm求:θs ,θd解: m Dg M GZ 3125.09810*160009810*500011===m Dg M GZ 625.09810*160009810*1000022==下在71页上的图4-21上用作图法求出:M I=5000tm时, θs1=18.5o,θd1oM I=10000tm,θs2o θd2---倾覆.4.d=7m,船舶重心距基线高z g=7m,排水量D =14200t,船舶在中线面上受风投影面积S x=1600m2,风力作用点距基线高z A=13m.若船舶在10m /s相对横向稳定风速作用下,试求此时的风力横倾力矩.又若船舶在蒲氏6级正横风作用下,试求此时的突风横倾力矩.19(提示:风压动倾力矩的计算)解:稳定风速的横倾力矩:p A根据v A=10m/s查72页图4-24,得P A=75Pa蒲氏6级风的突风力矩:突风风速(10.8~13.8)*1.3=(14.04~17.94)m/s,查图4-24得P a=145~235P a,得横倾力矩M I=(145~235)*1600*(13~7)=(142~230)*9810Nm突风风速(10.8~13.8)*1.5=(1)m/s,查图4-24得P a =191~315P a ,得横倾力矩M I =(191~315)*1600*(13~7)=(187~308)*9810Nm4.20.已知某船排水体积V =19059m 3,重心距基线高z g =7.89m ,进水角θj o ,横摇角θo ,风压倾侧力臂l f =0.046m ,各倾角形状稳性力臂值见表4—9,试检验稳性是否满足基本衡准的要求.()()()[],2l ,30;,:30202010100d300l l l l l l ld l Dl ld D d M W o d d S S +++++∆≅=====⎰⎰⎰θθθθθ则有为例以故有注即[…]为θ=30o 的积分和,故l d =2θ∆[…];Δθ为横倾角间距,以弧度计.(提示:动稳性曲线的应用,求l d 的问题)已知:V=19059m 3 Zg=7.89m θj O θ=o l f ,倾角形状稳性力臂值在书中的表4-9.求:检验稳性是否满足衡准要求.解:计算动稳性力臂l d 填入书中表格,依据表格中的GZ 及l d 绘出GZ 及l d 曲线见下图.用作图法作出最小倾覆力臂l q =0. 22m ,稳性衡准数1046.022.0 ==fq l l K ,满足基本衡准的要求. 4.解释船舶横倾至迎风一侧,开始回摇时受突风作用的情况为风浪联合作用下的最晦气情况?答:船舶横倾至迎风一侧,开始回摇时受突风作用时,船舶所具有稳性力矩与横倾力矩的方向是一致的,稳性力矩做的功与横倾力矩做的功起着同样的作用.这实际上是相当于加年夜了横倾力矩,而招致横倾角的增年夜,这是风浪联合作用下的最晦气情况.4. l q 的年夜小有什么影响?答:进水角的若年夜于极限动平衡角则对最小倾覆力臂l q 无影响,若小于极限动平衡角则则会减小最小倾覆力臂l q 值,这对船舶航行平安是晦气的.习题五 吃水差5.1.已知某万吨级货船:z g =,d =7m ,其静水力曲线图为图3—9.试求其:D ;TPC ;MTC ,x b ;x f ;z b ;z m ;GM ;GM L .解::根据d=7m 查图3-9.答:略.5.2.已知某船:D =8750t ; d F =;d A =; d M =;MTC =·m /cm ;x f =-;L =147m.今自第五压载舱(重心在船中后56.5m)抽50t 水到第一压载舱(重心在船中前55.5m),试求抽水后首尾吃水和吃水差.(提示:属货移,压载水移动)已知:D=8750t ,d F =3.2m ,d A =6.1m , d m =4.65m ,MTC=146.5tm/cm ,X f =-0.25m ,L=147m ,X 1=-56.5m ,X 2=55.5m ,P=50t ,求:首尾吃水d F1, d A1,t.解:m cm MTC Pl t x 382.023.385.146)5.565.55(50==+==∆ m L x t x L L t d f f F 192.014725.05.0*382.05.02=⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛-∆=⎪⎭⎫ ⎝⎛-∆=∆m L x t d f A 190.014725.05.0382.05.0=⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛+∆=∆ 5.3.已知某船:D =17000t ;d F =;d A =;d M=;·m /cm ;x f =-;L =147m.为要调整为平吃水,需从第三压载舱(重心在船中后32.5m)抽几多吨压载水到第一压载舱(重心在船中前53.9m)?(提示:货移,压载水移动)已知:D=17000,d F =7.8m d A =8.6m d m =8.2m MTC=211.2*9.8*103Nm x f =-4.4m L=147m t =0 l x =(53.9+32.5)m 求:P解::原吃水差t=d F -d A需调整的吃水差改变量m t t t 8.0)08.0(0=--=-'=∆由MTC pl t x=∆ 得 t l MTC p x∆= t p 56.195)5.329.53(100*8.0*2.211=+= 向首移动.5.4. 已知某船:D =12200t ;d F =;d A =6m ;d M=;TPC:=/cm ;MTC =·m /cm ;x f ==;L =147m.今在其第四货舱内(重心在船中后35m)加装100t 货,试求装货后的首尾吃水和吃水差.(提示:少量装货,求吃水差)已知:D=12200t d F =6.4m d A =6.0m d m =6.2 TPC=22.7t P=100t MTC=161.5*9.8*103Nm,x f =-1.42L=147m l x=(-35-x f)m 求:d F1,d A1,t1.解::因是少量装货,所以5.5.已知某船年夜量装货前排水量D=7200t,船舶重心距船中x g=,船主L=147m.各舱年夜量装货的要素如表5-2所示,其静水力曲线图见图3—9,试求年夜量装货后首尾吃水和吃水差.表5-2已知:D=7200t x g=-5.1m L=147m 及表5-2求:d F1 d A1 t1解::从表5-2的表格中计算得据D1=18440t查图3-9得d m1=8.7m MTC1=22*10=220tm/cmx f1=-5.5*1=-5.5m x b1=-1*1=-1m5.6.某船满载出港,其海水排水量D=18440t,重心坐标x g=,船主L=147m.该船在中途港年夜量卸货(第——货舱400t,第二货舱1200t,第三货舱1450t,第四货舱l 050t,第五货舱500t,设其重心距船中同表5—2,试求年夜量卸货后的首尾吃和吃水差,(提示:年夜量卸货)已知:D=18440t x g=-m L=147m 卸货列表:F1 A1解::从上述卸货表格中计算得据D1=13840t查图3-9得d m1=6.8m ,MTC1=17.5*10=175tm/cm ,x f1=-2*1=-2m ,b1=*1=m ,Z b15.7.为什么装卸重物的重心位于装卸前船舶重心的垂线上其实不能保证船舶平行沉浮?答:因为装卸的重量与浮力的改变量一样,但新增(减)重力的重心与新增(减)的浮力的浮心纷歧定在同一垂线上,如不在同一垂线上则新增(减)重力与新增(减)的浮力没有到达平衡.则不能满足船舶的平衡条件,所以不能保证船舶平行沉浮.。
09-习题课(一)

计算
f ( x ) ∗ h( x )
y
并作图
y
y
-3
-2
-1
1
2
3
x
-3
-2
-1
0
1
2
3
x
X-3
-3
-2
x X+1
-1 0
1
2
3
x
第一步
翻 转
第二步 平 移
17
第三步 乘 积
习 题 一 解 答
y y
求面积) 第四步 积 分(求面积)
y
?
X-3
f(x)*h(x)
3 2 1
-3
-2
-1
1
2
3
4
5
6
x
19
傅里叶光学
习 题 一 解 答
x x − a / 2 1 x 1.7 求证: rect + rect . 求证: ∗ comb = 1 b a − b a a
分析
0<x<a
y
x a2 − x2 1 1 f ( x ) Λh ( x ) = a − × x × = 2 2 a 2a
a/2
1
-a -3
-2
-1
1
2
3
a
x
25
习 题 一 解 答
• 同理
a2 − x2 2a h ( x ) Λf ( x ) = (a − x) 2 2a
可见, 可见,求相关不满足交换律
点的矩形函数, (1)第一项是宽度为 、中心在 点的矩形函数, )第一项是宽度为b、中心在0点的矩形函数 第二项是宽度为( - )、中心在a/2处的矩形函数 )、中心在 处的矩形函数, 第二项是宽度为(a-b)、中心在 处的矩形函数, 由图可见,两者相加得到一个宽度为a的矩形函数 的矩形函数。 由图可见,两者相加得到一个宽度为 的矩形函数。 (2)Comb函数由间隔为 的一系列δ函数组成 ) 函数由间隔为a的一系列 函数组成 函数由间隔为 的一系列 1 a x b/2 a-b/2 -2a -a 1 0 a x 2a
2023学年统编版高二语文选择性必修下册《大堰河——我的保姆》习题(一) 统编版高二选择性必修下

2023学年统编版高二语文选择性必修下册《大堰河——我的保姆》习题(一)统编版高二选择性必修下部编版高中语文选择性必修下册第二单元第6课大堰河-我的保姆习题一一、选择题1.下列各句中,加线的成语使用正确的一项是( )A.艾青是一个懂得感恩的人,从幼年起便濡染了农民的忧郁,他常常追本溯源,想到贫困的乳母和患难的兄弟们。
B.在《大堰河——我的保姆》一诗中,诗人采用了大量的细节描写,生动地表现了大堰河对诗人无所不至的关怀。
C.大堰河的生活虽然贫困,却不失希望,她希望有朝一日能在乳儿冠冕堂皇的婚礼上,听到娇美的媳妇叫她“婆婆”。
D.朴素、凝练、想象丰富、意象独特是艾青诗歌的一贯特点,这种风格在新中国成立后的诗篇中表现得更是炉火纯青。
2.下列各句中,没有语病的一项是( )A.艾青的诗,总是能把个人的悲欢融合到时代的悲欢里,反映自己民族和人民的苦难和命运,反映现实的生活和斗争,鲜明地抒发时代的呼唤和人民的心声。
B.大堰河被贫苦的生活剥夺了受教育的权利,但却剥夺不了她内心世界的美丽丰富。
虽然她与乳儿之间存在一种金钱关系,但这丝毫没影响她对乳儿的深切关爱。
C.《大堰河——我的保姆》以真挚的感情沟通了诗人与广大人民的联系,为当时的诗坛吹进了一股清新之风,受到茅盾等老一辈作家的推崇。
D.由于《大堰河——我的保姆》这首诗带有自传的性质,所以诗人选取的情景和细节都十分富有人情味,着力塑造了大堰河这个旧中国劳动妇女形象是十分感人的。
3.下列词语中,加线字的注音不正确的一项是( )A.斑斓(lán) 河畔(pàn) 荡漾(yànɡ) 浮藻(zǎo)B.青荇(xìnɡ)长篙(ɡāo)笙箫(xiāo)溯源(sù)C.残羹(ɡēnɡ)发酵(xiào)罗绮(qǐ)细腻(nì)D.榆阴(yīn)霉菌(jūn)粗糙(cāo)沉淀(diàn)4.下列词语中,字形全都正确的一项是( )A.诅咒花瓣叫嚣踟蹰B.倾圯漪伦揉碎沉淀C.开垦枯缟呼啸翡翠D.佝褛凝固寂寞喉咙5.下列各句所运用的修辞手法,与其他三句不相同的一句是( )A.那河畔的金柳,是夕阳中的新娘。
线性代数习题及答案(复旦版)1

线性代数习题及答案习题一1. 求下列各排列的逆序数.(1) 9; (2) 1;(3) n (n 1)…321; (4) 13…(2n 1)(2n )(2n 2)…2. 【解】(1) τ(9)=11; (2) τ(1)=36;(3) τ(n (n 1)…3·2·1)= 0+1+2 +…+(n 1)=(1)2n n -; (4) τ(13…(2n 1)(2n )(2n 2)…2)=0+1+…+(n 1)+(n 1)+(n 2)+…+1+0=n (n 1). 2. 略.见教材习题参考答案. 3. 略.见教材习题参考答案.4. 本行列式4512312123122x x x D x xx=的展开式中包含3x 和4x 的项.解: 设 123412341234()41234(1)i i i i i i i i i i i i D a a a a τ=-∑ ,其中1234,,,i i i i 分别为不同列中对应元素的行下标,则4D 展开式中含3x 项有(2134)(4231)333(1)12(1)32(3)5x x x x x x x x x ττ-⋅⋅⋅⋅+-⋅⋅⋅⋅=-+-=-4D 展开式中含4x 项有(1234)4(1)2210x x x x x τ-⋅⋅⋅⋅=.5. 用定义计算下列各行列式.(1)0200001030000004; (2)1230002030450001.【解】(1) D =(1)τ(2314)4!=24; (2) D =12.6. 计算下列各行列式.(1)214131211232562-----; (2) abac ae bd cd de bfcf ef-------; (3)10011001101a b c d ---; (4) 1234234134124123. 【解】(1) 125062312101232562r r D+---=--;(2) 1114111111D abcdef abcdef --==------;21011111(3)(1)11101100111;b c D a a b cd c c d d d dabcd ab ad cd --⎡--⎤=+-=+++--⎢⎥⎣⎦=++++ 321221133142144121023410234102341034101130113(4)160.10412022200441012301110004r r c c r r c c r r r r c c r r D -+-+-++---====-------7. 证明下列各式.(1) 22222()111a ab b a a b b a b +=-;(2) 2222222222222222(1)(2)(3)(1)(2)(3)0(1)(2)(3)(1)(2)(3)a a a a b b b b c c c c d d d d ++++++=++++++; (3) 232232232111()111a a a a b b ab bc ca b b c c c c =++(4) 20000()000n n a b a b D ad bc c d cd==-ONN O;(5)121111111111111nn i i i i na a a a a ==++⎛⎫=+ ⎪⎝⎭+∑∏L L M M M . 【证明】(1)1323223()()()2()2001()()()()()2()21c c c c a b a b b a b b a b a b ba b a b b a b a b ba b a b a b a b --+--=--+--+==-=-=--左端右端.(2) 32213142412222-2-2232221446921262144692126021446921262144692126c c c c c c c c c c a a a a a a b b b b b b cc c c cc d d d d d d ---++++++++====++++++++左端右端.(3) 首先考虑4阶范德蒙行列式:2323232311()()()()()()()(*)11xx x a a a f x x a x b x c a b a c b c b b b c c c ==------从上面的4阶范德蒙行列式知,多项式f (x )的x 的系数为2221()()()()(),11a a ab bc ac a b a c b c ab bc ac b b cc ++---=++但对(*)式右端行列式按第一行展开知x 的系数为两者应相等,故231123231(1),11a a b b c c +- (4) 对D 2n 按第一行展开,得22(1)2(1)2(1)0000000(),n n n n a b aba b a b D abc dc dc d c d d c ad D bc D ad bc D ---=-=⋅-⋅=-ONONN O NO据此递推下去,可得222(1)2(2)112()()()()()()n n n n n nD ad bc D ad bc D ad bc D ad bc ad bc ad bc ----=-=-==-=--=-L 2().n n D ad bc ∴=-(5) 对行列式的阶数n 用数学归纳法.当n =2时,可直接验算结论成立,假定对这样的n 1阶行列式结论成立,进而证明阶数为n 时结论也成立.按D n 的最后一列,把D n 拆成两个n 阶行列式相加:112211211111011111110111111101111111.n n nn n n a a a a D a a a a a a D ---++++=++=+L L LL L L L L L L L L L LL LLL但由归纳假设11121111,n n n i iD a a a a ---=⎛⎫+= ⎪⎝⎭∑L 从而有11211211121111111111.n n n n n i i n n nn n i i i i i i D a a a a a a a a a a a a a a a ---=-===⎛⎫+=+ ⎪⎝⎭⎛⎫⎛⎫++== ⎪ ⎪⎝⎭⎝⎭∑∑∑∏L L L8. 计算下列n 阶行列式.(1) 111111n x x D x=LL M M ML(2) 122222222232222n D n=L L L LL L L L L; (3)000000000000n x y x y D x y y x=L L LL L L L L L L . (4)n ij D a =其中(,1,2,,)ij a i j i j n =-=L ; (5)2100012100012000002100012n D =LL LM M MM M L L. 【解】(1) 各行都加到第一行,再从第一行提出x +(n 1),得11111[(1)],11n x D x n x=+-L L M M M L 将第一行乘(1)后分别加到其余各行,得1111110[(1)](1)(1).01n n x D x n x n x x --=+-=+---LL M M M L(2) 213111222210000101001002010002n r r n r r r r D n ---=-MLL L L M M M M M L按第二行展开222201002(2)!.00200002n n =---L LL M M M M L(3) 行列式按第一列展开后,得1(1)(1)(1)10000000000000(1)0000000000(1)(1).n n n n n n n n x y y x y x y D x y x y x y y xxyx x y y x y +-+-+=+-=⋅+⋅-⋅=+-L L L L M M M M M M L L M M MM M LL(4)由题意,知1112121222120121101221031230n nn n n nnn a a a n a a a D n a a a n n n --==----L L L LL M M MM M MM LL122111111111111111111111n n ------------LL LM M MM M L L后一行减去前一行自第三行起后一行减去前一行012211221111112000020000200000000022n n n n --------=-L L L LL LM M M M M M MM M L LL按第一列展开1122000201(1)(1)(1)(1)2002n n n n n n -----=---LL M M M L按第列展开. (5) 210002000001000121001210012100012000120001200000210002100021000120001200012n D ==+LL L L L L LLLM M MM M M M M M M M M M M M L L L LLL122n n D D --=-.即有 112211n n n n D D D D D D ----=-==-=L 由 ()()()112211n n n n D D D D D D n ----+-++-=-L 得 11,121n n D D n D n n -=-=-+=+. 9. 计算n 阶行列式.121212111n nn na a a a a a D a a a ++=+LL M M M L【解】各列都加到第一列,再从第一列提出11nii a=+∑,得232323123111111,11n n nn i n i na a a a a a D a a a a a a a =+⎛⎫=++ ⎪⎝⎭+∑L LLM MM M L将第一行乘(1)后加到其余各行,得23111010011.00100001n nnn i i i i a a a D a a ==⎛⎫=+=+ ⎪⎝⎭∑∑L L LM M M M L10. 计算n 阶行列式(其中0,1,2,,i a i n ≠=L ).1111123222211223322221122331111123n n n n n n n n n n nn n n n n n nn n n n na a a a ab a b a b a b D a b a b a b a b b b b b ----------------=L L MM M M L L. 【解】行列式的各列提取因子1(1,2,,)n j a j n -=L ,然后应用范德蒙行列式.3121232222312112123111131212311211111()().n n n n n n n n n n n n n j i n n j i n ij b b b b a a a a b b b b D a a a a a a a b b b b a a a a b b a a a a a ------≤<≤⎛⎫⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫-= ⎪⎝⎭∏L LL L L L L L LL 11. 已知4阶行列式41234334415671122D =;试求4142A A +与4344A A +,其中4j A 为行列式4D 的第4行第j 个元素的代数余子式. 【解】41424142234134(1)(1)3912.344344567167A A +++=-+-=+=同理43441569.A A +=-+=- 12. 用克莱姆法则解方程组.(1) 12312341234234 5,2 1, 2 2, 23 3.x x x x x x x x x x x x x x ++=⎧⎪+-+=⎪⎨+-+=⎪⎪++=⎩ (2) 121232343454556 1,56 0,56 0, 560, 5 1.x x x x x x x x x x x x x +=⎧⎪++=⎪⎪++=⎨⎪++=⎪+=⎪⎩【解】方程组的系数行列式为1110111013113121110131180;121052*********23140123123D -------=====≠-----1234511015101111211118;36;2211121131230323115011152111211136;18.122112120133123D D D D --====---====--故原方程组有惟一解,为312412341,2,2, 1.D D D Dx x x x D D D D========- 12345123452)665,1507,1145,703,395,212.15072293779212,,,,.66513335133665D D D D D D x x x x x ===-==-=∴==-==-=13. λ和μ为何值时,齐次方程组1231231230,0,20x x x x x x x x x λμμ++=⎧⎪++=⎨⎪++=⎩ 有非零解【解】要使该齐次方程组有非零解只需其系数行列式110,11121λμμ= 即(1)0.μλ-=故0μ=或1λ=时,方程组有非零解. 14. 问:齐次线性方程组12341234123412340,20,30,0x x x ax x x x x x x x x x x ax bx +++=⎧⎪+++=⎪⎨+-+=⎪⎪+++=⎩ 有非零解时,a ,b 必须满足什么条件【解】该齐次线性方程组有非零解,a ,b 需满足11112110,113111aa b=-即(a +1)2=4b .15. 求三次多项式230123()f x a a x a x a x =+++,使得(1)0,(1)4,(2)3,(3)16.f f f f -====【解】根据题意,得0123012301230123(1)0;(1)4;(2)2483;(3)392716.f a a a a f a a a a f a a a a f a a a a -=-+-==+++==+++==+++=这是关于四个未知数0123,,,a a a a 的一个线性方程组,由于012348,336,0,240,96.D D D D D ====-=故得01237,0,5,2a a a a ===-= 于是所求的多项式为23()752f x x x =-+16. 求出使一平面上三个点112233(,),(,),(,)x y x y x y 位于同一直线上的充分必要条件. 【解】设平面上的直线方程为ax +by +c =0 (a ,b 不同时为0)按题设有1122330,0,0,ax by c ax by c ax by c ++=⎧⎪++=⎨⎪++=⎩ 则以a ,b ,c 为未知数的三元齐次线性方程组有非零解的充分必要条件为1122331101x y x y x y = 上式即为三点112233(,),(,),(,)x y x y x y 位于同一直线上的充分必要条件.习题 二1. 计算下列矩阵的乘积.(1)[]11321023⎡⎤⎢⎥-⎢⎥-⎢⎥⎢⎥⎣⎦=; (2)500103120213⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦; (3) []32123410⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; (4)()111213112321222323132333a a a x x x x a a a x a a a x ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦; (5) 111213212223313233100011001a a a a a a a a a ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦; (6) 1210131010101210021002300030003⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦. 【解】(1) 32103210;64209630-⎡⎤⎢⎥--⎢⎥⎢⎥-⎢⎥-⎣⎦(2)531⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦; (3) (10);(4) 3322211122233312211213311323322311()()()ij iji j a x a x a x a a x x a a x x a a x x a x x==++++++++=∑∑(5)111212132122222331323233a a a a a a a a a a a a +⎡⎤⎢⎥+⎢⎥⎢⎥+⎣⎦; (6) 1252012400430009⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦.2. 设111111111⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦A ,121131214⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦B , 求(1)2-AB A ;(2) -AB BA ;(3) 22()()-=-A+B A B A B 吗【解】(1) 2422;400024⎡⎤⎢⎥-=⎢⎥⎢⎥⎣⎦AB A (2) 440;531311⎡⎤⎢⎥-=--⎢⎥⎢⎥--⎣⎦AB BA (3) 由于AB ≠BA ,故(A +B )(AB )≠A 2B 2.3. 举例说明下列命题是错误的.(1) 若2=A O , 则=A O ; (2) 若2=A A , 则=A O 或=A E ; (3) 若AX =AY ,≠A O , 则X =Y . 【解】(1) 以三阶矩阵为例,取2001,000000⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦0A A ,但A ≠0(2) 令110000001-⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦A ,则A 2=A ,但A ≠0且A ≠E (3) 令11021,=,0111210110⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=≠=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦A Y X 0 则AX =AY ,但X ≠Y .4. 设101A λ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦, 求A 2,A 3,…,A k .【解】2312131,,,.010101kk λλλ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A A A L 5. 100100λλλ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦A =, 求23A ,A 并证明:121(1)2000kk k k kk k k k k k λλλλλλ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A =.【解】2322233223213302,03.0000λλλλλλλλλλλ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A =A =今归纳假设121(1)2000kk k k kk k k k k k λλλλλλ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A =那么11211111(1)1020100000(1)(1)2,0(1)00k k k k k k k k k kk k kk k k k k k k k k λλλλλλλλλλλλλλλ+---+-++=-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦+⎡⎤+⎢⎥⎢⎥=+⎢⎥⎢⎥⎣⎦A A A= 所以,对于一切自然数k ,都有121(1)2.000kk k k kk k k k k k λλλλλλ----⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A =6. 已知AP =PB ,其中100100000210001211⎡⎤⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦B =,P =求A 及5A .【解】因为|P |= 1≠0,故由AP =PB ,得1100200,611-⎡⎤⎢⎥==⎢⎥⎢⎥--⎣⎦A PBP而51551()()100100100100210000210200.211001411611--==⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=--==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦⎣⎦⎣⎦A PBP PB P A7. 设a bc d ba d c c d ab dcba ⎡⎤⎢⎥--⎢⎥⎢⎥--⎢⎥--⎣⎦A =,求|A |. 解:由已知条件,A 的伴随矩阵为22222222()()a b cd b a d c a b c d a b c d c d a b dcba *⎡⎤⎢⎥--⎢⎥-+++=-+++⎢⎥--⎢⎥--⎣⎦A =A 又因为*A A =A E ,所以有22222()a b c d -+++A =A E ,且0<A ,即 42222222224()()a b c d a b c d -++++++A =A A =A E 于是有22222()a b c d =-+++A . 8. 已知线性变换112112212321331233232,3,232,2,45;3,x y y y z z x y y y y z z x y y y y z z =+=-+⎧⎧⎪⎪=-++=+⎨⎨⎪⎪=++=-+⎩⎩ 利用矩阵乘法求从123,,z z z 到123,,x x x 的线性变换. 【解】已知112233112233210,232415310,201013421124910116x y x y x y y z y z y z ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦-⎡⎤⎢⎥==-⎢⎥⎢⎥--⎣⎦X AY Y Bz X AY ABz z, 从而由123,,z z z 到123,,x x x 的线性变换为11232123312342,1249,1016.x z z z x z z z x z z z =-++⎧⎪=-+⎨⎪=--+⎩ 9. 设A ,B 为n 阶方阵,且A 为对称阵,证明:'B AB 也是对称阵.【证明】因为n 阶方阵A 为对称阵,即A ′=A ,所以 (B ′AB )′=B ′A ′B =B ′AB , 故'B AB 也为对称阵.10. 设A ,B 为n 阶对称方阵,证明:AB 为对称阵的充分必要条件是AB =BA . 【证明】已知A ′=A ,B ′=B ,若AB 是对称阵,即(AB )′=AB .则 AB =(AB )′=B ′A ′=BA , 反之,因AB =BA ,则(AB )′=B ′A ′=BA =AB ,所以,AB 为对称阵.11. A 为n 阶对称矩阵,B 为n 阶反对称矩阵,证明: (1) B 2是对称矩阵.(2) ABBA 是对称矩阵,AB +BA 是反对称矩阵. 【证明】因A ′=A ,B ′= B ,故(B 2)′=B ′·B ′= B ·(B )=B 2;(ABBA )′=(AB )′(BA )′=B ′A ′A ′B ′= BAA ·(B )=ABBA ;(AB +BA )′=(AB )′+(BA )′=B ′A ′+A ′B ′= BA +A ·(B )= (AB +BA ).所以B 2是对称矩阵,ABBA 是对称矩阵,AB+BA 是反对称矩阵. 12. 求与A =1101⎡⎤⎢⎥⎣⎦可交换的全体二阶矩阵. 【解】设与A 可交换的方阵为a b c d ⎡⎤⎢⎥⎣⎦,则由1101⎡⎤⎢⎥⎣⎦a b c d ⎡⎤⎢⎥⎣⎦=a b c d ⎡⎤⎢⎥⎣⎦1101⎡⎤⎢⎥⎣⎦, 得a cb d a a bcd c c d +++⎡⎤⎡⎤=⎢⎥⎢⎥+⎣⎦⎣⎦.由对应元素相等得c =0,d =a ,即与A 可交换的方阵为一切形如0a b a ⎡⎤⎢⎥⎣⎦的方阵,其中a,b 为任意数.13. 求与A =100012012⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦可交换的全体三阶矩阵. 【解】由于A =E +000002013⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦, 而且由111111222222333333000000,002002013013a b c a b c a b c a b c a b c a b c ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦⎣⎦可得11122233333323232302300023222.023333c b c cb c a b c c b c a a b b c c -⎡⎤⎡⎤⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦由此又可得1113232332322333230,230,20,30,2,3,232,233,c b c a a a c b c b b b c c b c c c =-==-===--=-=-所以2311233230,2,3.a a b c c b c b b ======-即与A 可交换的一切方阵为12332300203a b b b b b ⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦其中123,,a b b 为任意数. 14. 求下列矩阵的逆矩阵.(1) 1225⎡⎤⎢⎥⎣⎦; (2) 123012001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; (3)121342541-⎡⎤⎢⎥-⎢⎥⎢⎥--⎣⎦; (4) 1000120021301214⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; (5) 5200210000830052⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; (6) ()1212,,,0nn a a a a a a ⎡⎤⎢⎥⎢⎥≠⎢⎥⎢⎥⎣⎦L O ,未写出的元素都是0(以下均同,不另注). 【解】(1) 5221-⎡⎤⎢⎥-⎣⎦; (2)121012001-⎡⎤⎢⎥-⎢⎥⎢⎥⎣⎦;(3) 12601741632142-⎡⎤⎢⎥--⎢⎥⎢⎥--⎣⎦; (4) 100011002211102631511824124⎡⎤⎢⎥⎢⎥-⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦; (5) 1200250000230058-⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦; (6) 12111n a a a ⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦O. 15. 利用逆矩阵,解线性方程组12323121,221,2.x x x x x x x ++=⎧⎪+=⎨⎪-=⎩ 【解】因123111102211102x x x ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦,而1110022110≠- 故112311101111122.02211130122110221112x x x -⎡⎤⎡⎤-⎢⎥⎢⎥⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎢⎥-⎣⎦⎣⎦16. 证明下列命题:(1) 若A ,B 是同阶可逆矩阵,则(AB )*=B *A *. (2) 若A 可逆,则A *可逆且(A *)1=(A 1)*. (3) 若AA ′=E ,则(A *)′=(A *)1. 【证明】(1) 因对任意方阵c ,均有c *c =cc *=|c |E ,而A ,B 均可逆且同阶,故可得|A |·|B |·B *A *=|AB |E (B *A *)=(AB ) *AB (B *A *)=(AB ) *A (BB *)A * =(AB ) *A |B |EA *=|A |·|B |(AB ) *.∵ |A |≠0,|B |≠0, ∴ (AB ) *=B *A *.(2) 由于AA *=|A |E ,故A *=|A |A 1,从而(A 1) *=|A 1|(A 1)1=|A |1A . 于是A * (A 1) *=|A |A 1·|A |1A =E ,所以(A 1) *=(A *)1. (3) 因AA ′=E ,故A 可逆且A 1=A ′. 由(2)(A *)1=(A 1) *,得(A *)1=(A ′) *=(A *)′.17. 已知线性变换11232123312322,35,323,x y y y x y y y x y y y =++⎧⎪=++⎨⎪=++⎩ 求从变量123,,x x x 到变量123,,y y y 的线性变换. 【解】已知112233221,315323x y x y x y ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦X AY且|A |=1≠0,故A 可逆,因而1749,637324---⎡⎤⎢⎥==-⎢⎥⎢⎥-⎣⎦Y A X X所以从变量123,,x x x 到变量123,,y y y 的线性变换为112321233123749,637,324,y x x x y x x x y x x x =--+⎧⎪=+-⎨⎪=+-⎩ 18. 解下列矩阵方程.(1) 12461321-⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦X =; (2)211211************--⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦X ;(3) 142031121101⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦X =; (4) 010100043100001201001010120-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦X .【解】(1) 令A =1213⎡⎤⎢⎥⎣⎦;B =4621-⎡⎤⎢⎥⎣⎦.由于13211--⎡⎤=⎢⎥-⎣⎦A 故原方程的惟一解为13246820.112127----⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦⎣⎦X A B同理(2) X =100010001⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦; (3) X =11104⎡⎤⎢⎥⎢⎥⎣⎦; (4) X =210.034102-⎡⎤⎢⎥-⎢⎥⎢⎥-⎣⎦19. 若kA =O (k 为正整数),证明:121()k ---L E A =E +A+A ++A .【证明】作乘法212121()()k k k k k ----=-----=-=E A E +A+A ++A E +A+A ++A A A A A E A E,L L L 从而EA 可逆,且121()k ---L E A =E +A+A ++A20.设方阵A 满足A 2-A -2E =O ,证明A 及A +2E 都可逆,并求A 1及(A +2E )1. 【证】因为A 2A 2E =0, 故212().2-=⇒-=A A E A E A E由此可知,A 可逆,且11().2-=-A A E同样地2220,64(3)(2)41(3)(2)4--=--=--+=---+=A A E A A E E,A E A E E,A E A E E. 由此知,A +2E 可逆,且1211(2)(3)().44-+=--=-A E A E A E21. 设423110123⎡⎤⎢⎥⎢⎥⎢⎥-⎣⎦A =,2AB =A+B ,求B . 【解】由AB =A +2B 得(A 2E )B =A .而22310,1102121==-≠---A E即A 2E 可逆,故11223423(2)110110121123143423386.1531102961641232129--⎡⎤⎡⎤⎢⎥⎢⎥=-=-⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦----⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==----⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦B A E A 22. 设1-P AP =Λ. 其中1411--⎡⎤⎢⎥⎣⎦P =,1002-⎡⎤⎢⎥⎣⎦=Λ, 求10A . 【解】因1-P 可逆,且1141,113-⎡⎤=⎢⎥--⎣⎦P 故由1Λ-A =P P 得10110101101012121010()()141410331102113314141033110211331365136412421.34134031242--==⎡⎤⎢⎥---⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥--⎢⎥⎣⎦⎡⎤⎢⎥--⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥--⎢⎥⎣⎦⎡⎤-+-+⎡⎤==⎢⎥⎢⎥----⎣⎦⎣⎦A P P P P ΛΛ 23. 设m 次多项式01()m m f x a a x a x =+++L ,记01()mm f a a a =+++L A E A A ,()f A 称为方阵A 的m 次多项式.(1)12λλ⎡⎤⎢⎥⎣⎦A =, 证明12kk k λλ⎡⎤⎢⎥⎣⎦A =,12()()()f f f λλ⎡⎤=⎢⎥⎣⎦A ; (2) 设1-A =P BP , 证明1k k -B =PA P ,1()()f f -=B P A P . 【证明】(1)232311232200,00λλλλ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦A A 即k =2和k =3时,结论成立. 今假设120,0kkk λλ⎡⎤=⎢⎥⎣⎦A 那么111111222000,000kk k k k k λλλλλλ+++⎡⎤⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦AA A = 所以,对一切自然数k ,都有120,0kkk λλ⎡⎤=⎢⎥⎣⎦A 而011101220111012212()1100().()mm mm m m m m m f a a a a a a a a a a a a f f λλλλλλλλλλ=⎡⎤⎡⎤⎡⎤=+⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎡⎤+=⎢⎥+⎣⎦⎡⎤=⎢⎥⎣⎦L L L L A E +A++A ++++++ (2) 由(1)与A =P 1BP ,得B =PAP 1.且B k =( PAP 1)k = PA k P 1,又0111011011()()().mm m m mm f a a a a a a a a a f ----=+++=+++=++=B E B B E PAP PA P P E A+A P P A P L L L24. a b c d ⎡⎤⎢⎥⎣⎦A =,证明矩阵满足方程2()0x a d x ad bc -++-=.【证明】将A 代入式子2()x a d x ad bc -++-得222222()()10()()010000.00a d ad bc a b a b a d ad bc c d c d ad bca bc ab bd a ad ab bd ad bc ac cd cb d ac cd ad d -++-⎡⎤⎡⎤⎡⎤=-++-⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦-⎡⎤⎡⎤++++⎡⎤=-+⎢⎥⎢⎥⎢⎥-++++⎣⎦⎣⎦⎣⎦⎡⎤==⎢⎥⎣⎦A A E0 故A 满足方程2()0x a d x ad bc -++-=. 25. 设n 阶方阵A 的伴随矩阵为*A ,证明:(1) 若|A |=0,则|*A |=0;(2) 1n *-=A A .【证明】(1) 若|A |=0,则必有|A *|=0,因若| A *|≠0,则有A *( A *)1=E ,由此又得A =AE =AA *( A *)1=|A |( A *)1=0,这与| A *|≠0是矛盾的,故当|A | =0,则必有| A *|=0. (2) 由A A *=|A |E ,两边取行列式,得|A || A *|=|A |n , 若|A |≠0,则| A *|=|A |n 1 若|A |=0,由(1)知也有| A *|=|A |n 1.26. 设52003200210045000073004100520062⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦A =,B . 求(1) AB ; (2)BA ; (3) 1-A ;(4)|A |k (k 为正整数). 【解】(1)2320001090000461300329⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦AB =; (2) 19800301300003314005222⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦BA =;(3) 11200250000230057--⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦A =; (4)(1)k k =-A . 27. 用矩阵分块的方法,证明下列矩阵可逆,并求其逆矩阵.(1)1200025000003000001000001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; (2)00310021********-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦; (3)20102020130010*******0001⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦.【解】(1) 对A 做如下分块 12⎡⎤=⎢⎥⎣⎦A A A 00其中1230012;,01025001⎡⎤⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦A A12,A A 的逆矩阵分别为1112100523;,01021001--⎡⎤⎢⎥-⎡⎤⎢⎥==⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦A A 所以A 可逆,且1111252000210001.000030001000001----⎡⎤⎢⎥-⎢⎥⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎢⎥⎣⎦A A A同理(2)11112121310088110044.110055230055----⎡⎤-⎢⎥⎢⎥⎢⎥⎡⎤⎢⎥⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦A A A A A (3)1110012211300222.001000001001-⎡⎤--⎢⎥⎢⎥⎢⎥--⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦A习题 三1. 略.见教材习题参考答案.2. 略.见教材习题参考答案.3. 略.见教材习题参考答案.4. 略.见教材习题参考答案.5.112223334441,,,=+=+=+=+βααβααβααβαα,证明向量组1234,,,ββββ线性相关.【证明】因为1234123412341312342()2()0+++=+++⇒+++=+⇒-+-=ββββααααββββββββββ 所以向量组1234,,,ββββ线性相关.6. 设向量组12,,,r L ααα线性无关,证明向量组12,,,r L βββ也线性无关,这里12.i i +++L β=ααα【证明】 设向量组12,,,r L βββ线性相关,则存在不全为零的数12,,,,r k k k L 使得1122.r r k k k +++=L 0βββ把12i i +++L β=ααα代入上式,得121232()()r r r r k k k k k k k +++++++++=0L L L ααα.又已知12,,,r L ααα线性无关,故1220,0, 0.r rr k k k k k k +++=⎧⎪++=⎪⎨⎪⎪=⎩L L L L L 该方程组只有惟一零解120r k k k ====L ,这与题设矛盾,故向量组12,,,r L βββ线性无关.7. 略.见教材习题参考答案.8. 12(,,,),1,2,,i i i in i n ααα==L L α.证明:如果0ij a ≠,那么12,,,n L ααα线性无关. 【证明】已知0ij a =≠A ,故R (A )=n ,而A 是由n 个n 维向量12(,,,),i i i in ααα=L α1,2,,i n =L 组成的,所以12,,,n L ααα线性无关.9. 设12,,,,r t t t L 是互不相同的数,r ≤n .证明:1(1,,,),1,2,,n i i i t t i r -==L L α是线性无关的.【证明】任取nr 个数t r +1,…,t n 使t 1,…,t r ,t r +1,…,t n 互不相同,于是n 阶范德蒙行列式21111212111121110,11n n rr r n r r r n nnnt t t t t t t t tt t t ---+++-≠L M M M M LL M M M ML从而其n 个行向量线性无关,由此知其部分行向量12,,,r L ααα也线性无关.10. 设12,,,s L ααα的秩为r 且其中每个向量都可经12,,,r L ααα线性表出.证明:12,,,r L ααα为12,,,s L ααα的一个极大线性无关组.【证明】若 12,,,r L ααα(1)线性相关,且不妨设12,,,t L ααα (t <r ) (2)是(1)的一个极大无关组,则显然(2)是12,,,s L ααα的一个极大无关组,这与12,,,s L ααα的秩为r 矛盾,故12,,,r L ααα必线性无关且为12,,,s L ααα的一个极大无关组. 11. 求向量组1α=(1,1,1,k ),2α=(1,1,k ,1),3α=(1,2,1,1)的秩和一个极大无关组. 【解】把123,,ααα按列排成矩阵A ,并对其施行初等变换.1111111111111120010010101101001000111011001000k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥=→→→⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦⎣⎦A 当k =1时,123,,ααα的秩为132,,αα为其一极大无关组. 当k ≠1时,123,,ααα线性无关,秩为3,极大无关组为其本身.12. 确定向量3(2,,)a b =β,使向量组123(1,1,0),(1,1,1),==βββ与向量组1α=(0,1,1),2α=(1,2,1),3α=(1,0,1)的秩相同,且3β可由123,,ααα线性表出.【解】由于123123011120(,,);120011111000112112(,,),110101002a b b a ⎡⎤⎡⎤⎢⎥⎢⎥==→--⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎡⎤⎢⎥⎢⎥==→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦A B αααβββ而R (A )=2,要使R (A )=R (B )=2,需a 2=0,即a =2,又12330112120(,,,),12001121110002a a b b a ⎡⎤⎡⎤⎢⎥⎢⎥==→⎢⎥⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦c αααβ要使3β可由123,,ααα线性表出,需ba +2=0,故a =2,b =0时满足题设要求,即3β=(2,2,0).13. 设12,,,n L ααα为一组n 维向量.证明:12,,,n L ααα线性无关的充要条件是任一n 维向量都可经它们线性表出.【证明】充分性: 设任意n 维向量都可由12,,,n L ααα线性表示,则单位向量12,,,n L εεε,当然可由它线性表示,从而这两组向量等价,且有相同的秩,所以向量组12,,,n L ααα的秩为n ,因此线性无关.必要性:设12,,,n L ααα线性无关,任取一个n 维向量α,则12,,,n L ααα线性相关,所以α能由12,,,n L ααα线性表示.14. 若向量组(1,0,0),(1,1,0),(1,1,1)可由向量组α1,α2,α3线性表出,也可由向量组β1,β2,β3,β4线性表出,则向量组α1,α2,α3与向量组β1,β2,β3,β4等价.证明:由已知条件,1001103111R ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,且向量组(1,0,0),(1,1,0),(1,1,1)可由向量组α1,α2,α3线性表出,即两向量组等价,且123(,,)3R =ααα,又,向量组(1,0,0),(1,1,0),(1,1,1)可由向量组β1,β2,β3,β4线性表出,即两向量组等价,且1234(,,,)3R =ββββ,所以向量组α1,α2,α3与向量组β1,β2,β3,β4等价.15. 略.见教材习题参考答案.16. 设向量组12,,,m L ααα与12,,,s L βββ秩相同且12,,,m L ααα能经12,,,s L βββ线性表出.证明12,,,m L ααα与12,,,s L βββ等价.【解】设向量组12,,,m L ααα (1)与向量组12,,,s L βββ (2)的极大线性无关组分别为12,,,r L ααα (3)和12,,,r L βββ (4)由于(1)可由(2)线性表出,那么(1)也可由(4)线性表出,从而(3)可以由(4)线性表出,即1(1,2,,).ri ij jj a i r ===∑L αβ因(4)线性无关,故(3)线性无关的充分必要条件是|a ij |≠0,可由(*)解出(1,2,,)j j r =L β,即(4)可由(3)线性表出,从而它们等价,再由它们分别同(1),(2)等价,所以(1)和(2)等价.17. 设A 为m ×n 矩阵,B 为s ×n 矩阵.证明:max{(),()}()()R R R R R ⎡⎤≤≤+⎢⎥⎣⎦A AB A B B .【证明】因A ,B 的列数相同,故A ,B 的行向量有相同的维数,矩阵⎡⎤⎢⎥⎣⎦A B 可视为由矩阵A 扩充行向量而成,故A 中任一行向量均可由⎡⎤⎢⎥⎣⎦A B 中的行向量线性表示,故()R R ⎡⎤≤⎢⎥⎣⎦A A B同理()R R ⎡⎤≤⎢⎥⎣⎦A B B故有max{(),()}R R R ⎡⎤≤⎢⎥⎣⎦A AB B又设R (A )=r ,12,,,i i ir L ααα是A 的行向量组的极大线性无关组,R (B )=k , 12,,,j j jk L βββ是B 的行向量组的极大线性无关组.设α是⎡⎤⎢⎥⎣⎦A B 中的任一行向量,则若α属于A 的行向量组,则α可由12,,,i i ir L ααα表示,若α属于B 的行向量组,则它可由12,,,j j jk L βββ线性表示,故⎡⎤⎢⎥⎣⎦A B 中任一行向量均可由12,,,i i ir L ααα,12,,,j j jk L βββ线性表示,故()(),R r k R R ⎡⎤≤+=+⎢⎥⎣⎦A AB B 所以有max{(),()}()()R R R R R ⎡⎤≤≤+⎢⎥⎣⎦A AB A B B .18. 设A 为s ×n 矩阵且A 的行向量组线性无关,K 为r ×s 矩阵.证明:B =KA 行无关的充分必要条件是R (K )=r .【证明】设A =(A s ,P s ×(ns )),因为A 为行无关的s ×n 矩阵,故s 阶方阵A s 可逆. (⇒)当B =KA 行无关时,B 为r ×n 矩阵.r =R (B )=R (KA )≤R (K ),又K 为r ×s 矩阵R (K )≤r ,∴ R (K )=r . (⇐)当r =R (K )时,即K 行无关,由B =KA =K (A s ,P s ×(ns ))=(KA s ,KP s ×(n s)) 知R (B )=r ,即B 行无关.19. 略.见教材习题参考答案.20. 求下列矩阵的行向量组的一个极大线性无关组.(1)2531174375945313275945413425322048⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦; (2)11221021512031311041⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎣⎦.【解】(1) 矩阵的行向量组1234⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦αααα的一个极大无关组为123,,ααα;(2) 矩阵的行向量组1234⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦αααα的一个极大无关组为124,,ααα.21. 略.见教材习题参考答案.22. 集合V 1={(12,,,n x x x L )|12,,,n x x x L ∈R 且12n +++L x x x =0}是否构成向量空间为什么 【解】由(0,0,…,0)∈V 1知V 1非空,设121122(,,,),(,,,),n n V V k =∈=∈∈x x x y y y L L αβR )则112212(,,,)(,,,).n n n x y x y x y k kx kx kx +=+++=L L αβα因为112212121212()()()()()0,()0,n n n n n n x y x y x y x x x y y y kx kx kx k x x x ++++++=+++++++=+++=+++=L L L L L 所以11,V k V +∈∈αβα,故1V 是向量空间.23. 试证:由123(1,1,0),(1,0,1),(0,1,1)===ααα,生成的向量空间恰为R 3.【证明】把123,,ααα排成矩阵A =(123,,ααα),则11020101011==-≠A ,所以123,,ααα线性无关,故123,,ααα是R 3的一个基,因而123,,ααα生成的向量空间恰为R 3.24. 求由向量1234(1,2,1,0),(1,1,1,2),(3,4,3,4),(1,1,2,1)====αααα所生的向量空间的一组基及其维数. 【解】因为矩阵12345(,,,,)113141131411314214150121301213,113260001200012024140241400000=⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥--------⎢⎥⎢⎥⎢⎥=→→⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦A ααααα∴124,,ααα是一组基,其维数是3维的.25. 设1212(1,1,0,0),(1,0,1,1),(2,1,3,3),(0,1,1,1)===-=--ααββ,证明:1212(,)(,)L L =ααββ.【解】因为矩阵1212(,,,)1120112010110131,0131000001310000=⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥=→⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦⎣⎦A ααββ 由此知向量组12,αα与向量组12,ββ的秩都是2,并且向量组12,ββ可由向量组12,αα线性表出.由习题15知这两向量组等价,从而12,αα也可由12,ββ线性表出.所以1212(,)(,)L L =ααββ.26. 在R 3中求一个向量γ,使它在下面两个基123123(1)(1,0,1),(1,0,0)(0,1,1)(2)(0,1,1),(1,1,0)(1,0,1)==-==-=-=αααβββ下有相同的坐标.【解】设γ在两组基下的坐标均为(123,,x x x ),即111232123233112233(,,)(,,),110011001110101101x x x x x x x x x x x x ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦-⎡⎤⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦γαααβββ即1231210,111000x x x --⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦求该齐次线性方程组得通解123,2,3x k x k x k ===- (k 为任意实数)故112233(,2,3).x x x k k k =++=-γεεε27. 验证123(1,1,0),(2,1,3),(3,1,2)=-==ααα为R 3的一个基,并把1(5,0,7),=β2(9,8,13)=---β用这个基线性表示.【解】设12312(,,),(,),==A B αααββ又设11112123132121222323,x x x x x x =++=++βαααβααα,即11121212321223132(,)(,,),x x x x x x ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ββααα 记作 B =AX .则2321231235912359()111080345170327130327131235910023032713010330022400112r r r r r r -+↔--⎡⎤⎡⎤⎢⎥⎢⎥=−−−→−−−→---⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦-⎡⎤⎡⎤⎢⎥⎢⎥−−−−−→--⎢⎥⎢⎥⎢⎥⎢⎥----⎣⎦⎣⎦M A B 作初等行变换因有↔A E ,故123,,ααα为R 3的一个基,且1212323(,)(,,),3312⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦ββααα即1123212323,332=+-=--βαααβααα.习题四1. 用消元法解下列方程组.(1) 12341241234123442362242322312338;x x x x ,x x x ,x x x x ,x x x x +-+=⎧⎪++=⎪⎨++-=⎪⎪++-=⎩ (2)1231231232222524246;x x x ,x x x ,x x x ++=⎧⎪++=⎨⎪++=⎩ 【解】(1)412213223123(1)14236142362204211021()322313223112338123381423603215012920256214236012920321502562r r r r r r r r r r -⋅---⋅↔--⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=−−→−−−→⎢⎥⎢⎥--⎢⎥⎢⎥--⎣⎦⎣⎦-⎡⎤⎢⎥---⎢⎥−−−−→⎢⎥---⎢⎥--⎣⎦-⎡⎤⎢⎥-⎢⎥⎢⎥---⎢⎥--⎣⎦A b M 32434243324142360129200426100112614236142360129201292,0011260011260042610007425r r r r r r r +↔++-⎡⎤⎢⎥-⎢⎥−−−→−−−→⎢⎥-⎢⎥⎣⎦--⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥−−−→⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦得12342343444236 292 126 7425x x x x x x x x x x +-+=⎧⎪-+=⎪⎨+=⎪⎪=⎩ 所以1234187,74211,74144,7425.74x x x x ⎧=-⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩解②①×2得 x 22x 3=0③① 得2x 3=4 由⑥得 x 3=2,由⑤得 x 2=2x 3=4,由④得 x 1=22x 3 2x 2 = 10, 得 (x 1,x 2,x 3)T =(10,4,2)T . 2. 求下列齐次线性方程组的基础解系.(1) 123123123 320 5 03580;x x x ,x x x ,x x x ++=⎧⎪++=⎨⎪++=⎩ (2)1234123412341234 5 0 2303 8 0 3970;x x x x ,x x x x ,x x x x ,x x x x -+-=⎧⎪+-+=⎪⎨-++=⎪⎪+-+=⎩ (3) 1234512341234 22702345 03568 0;x x x x x ,x x x x ,x x x x ++++=⎧⎪+++=⎨⎪+++=⎩ (4)123451234512345 222 0 2 320247 0.x x x x x ,x x x x x ,x x x x x +-+-=⎧⎪+-+-=⎨⎪+-++=⎩ 【解】(1)。
四年级数学每日一练习题可打印

四年级数学每日一练习题可打印在四年级的数学学习中,每日一练对于提高学生的数学能力非常重要。
为了方便学生更好地进行练习,以下是一份可打印的四年级数学每日一练习题。
【习题一】1. 填入适当的运算符(+、-、×、÷)使等式成立:a) 16 ____ 8 ____ 2 = 10b) 45 ____ 9 ____ 5 = 36c) 24 ____ 6 ____ 4 = 42. 计算下列数学表达式:a) 28 + 14 - 5b) 45 - 23 + 12c) 6 × 7 - 3 × 43. 在横线上填入适当的数字,使等式成立:a) 48 × ____ = 480b) ____ ÷ 5 = 12c) 72 - ____ = 45【习题二】1. 选择合适的运算符(+、-、×、÷)填入空格:a) 28 ____ 4 = 7b) 63 ____ 7 = 9c) 25 ____ 5 = 1252. 计算下列数学运算:a) 57 + 38 - 15b) 96 - 24 + 15c) 8 × 9 + 5 × 43. 在横线上填入适当的数字,使等式成立:a) ____ × 8 = 48b) 100 ÷ ____ = 25c) ____ - 37 = 63【习题三】1. 填入适当的运算符(+、-、×、÷)使等式成立:a) 42 ____ 7 ____ 2 = 20b) 120 ____ 12 ____ 5 = 45c) 9 ____ 3 ____ 2 = 22. 计算下列数学表达式:a) 36 + 18 - 9b) 75 - 32 + 16c) 5 × 6 - 2 × 43. 在横线上填入适当的数字,使等式成立:a) 9 × ____ = 54b) ____ ÷ 3 = 15c) 40 - ____ = 27【习题四】1. 选择合适的运算符(+、-、×、÷)填入空格:a) 56 ____ 7 = 8b) 96 ____ 8 = 12c) 125 ____ 5 = 252. 计算下列数学运算:a) 68 + 37 - 19b) 84 - 29 + 15c) 7 × 5 + 4 × 33. 在横线上填入适当的数字,使等式成立:a) ____ × 7 = 21b) 120 ÷ ____ = 24c) ____ - 13 = 52以上是四年级数学每日一练习题的部分内容,希望能够帮助到四年级的学生们进行日常练习。
金融学-习题1-货币与货币制度
金融学期末考试复习资料习题一第二章货币与货币制度一、单选题1、某公司以延期付款方式销售给某商场一批商品,则该商场到期偿还欠款时,货币执行职能。
A 支付手段B 流通手段 C购买手段 D贮藏手段3、金银复本位制包括三种货币制度,其中金银两种货币均各按其所含金属的实际价值任意流通的货币制度是。
A平行本位制 B 双本位制 C跛行本位制 D汇兑本位制14、金属货币制度的基础是。
A 货币单位B 货币金属C 金准备D 货币发行和流通15、在价值形式发展到一般价值形式时,等价物被称为。
A 个别等价物B 货币C 一般等价物D 特殊等价物16、“金银天然不是货币,但货币天然是金银”是指。
A 货币就是金银 B金银就是货币C金银天然地最适宜于充当货币 D金银不是货币17、货币在发挥职能时,可以用观念上的货币。
A 价值尺度B 流通手段C 贮藏手段D 支付手段18、纸币产生的可能性包含在货币的职能中。
A价值尺度B流通手段 C贮藏手段 D支付手段19、金本位崩溃的根本原因是。
A经济危机 B第一次世界大战C黄金储备不足且分布不平衡 D纸币的产生20、以金币为本位币,但并不铸造和流通金币,银行券只能兑换金块的货币制度是。
A金本位B金块本位 C金汇兑本位 D信用货币制度二、多选题2、货币制度的基本内容包括。
A货币材料 B货币单位 C货币的铸造、发行和管理D货币的支付能力4、现代货币制度的基本特点主要包括。
A通货是中央银行发行的纸币B纸币不与金银保持等价关系C货币是通过信用程序发行的D纸币具有无限法偿能力5、金币本位制的内容有。
A以黄金为币材B金币可以自由铸造与私自熔化C银币可以自由铸造与私自熔化D价值符号可以自由兑现金币6、商品价值形式的演变经历了等几种形式。
A简单价值形式B扩大价值形式C一般价值形式D货币价值形式7、货币的基本职能包括。
A价值尺度B流通手段 C贮藏手段 D支付手段8、代用货币是。
A纸质货币 B不可兑换成金属货币的货币C可随时兑换成金属货币的货币 D只能有国家发行的货币9、信用货币是。
习题1 随机事件及其概率
习题一 随机事件及其概率一、填空题1.设随机试验E 对应的样本空间S ,与其任何事件不相容的事件为φ,而与其任何事件相互独立的事件为φP (A|B )=1, 则A 、B 两事件的关系为 A=B ;设E 为等可能型试验,且S 包含 10 个样本点,则按古典概率的定义其任一基本事件发生的概率为 0.1 。
2.若A 表示某甲得100分的事件,B 表示某乙得100分的事件,则(1)A 表示 甲未得100分的事件;(2)A B ⋃表示 甲乙至少有一人得100分的事件;(3)AB 表示 甲乙都得100的事件;(4)AB 表示 甲得100分,但乙未得100分的事件;(5)AB 表示 甲乙都没得100分的事件;(6)AB 表示 甲乙不都得100分的事件;3.若事件,,A B C 相互独立,则()P A B C ⋃⋃= ()()()()()()()()()()P A P B P C P A P B P A P C P B P C P A PB PC ++---+。
4.若事件,A B 相互独立,且()0.5,()0.25,P A P B ==则 ()P A B ⋃=0.625。
5.设111()()(),()()(),(),4816P A P B P C P AB P AC P BC P ABC =======则 ()P A B C ⋃⋃=167;()P ABC =169;(,,)P A B C =至多发生一个43;(,,P A B C =恰好发生一个)163;(|)P A A B C ⋃⋃=74。
6.袋中有 50 个乒乓球,其中 20 个是黄球,30 个白球,今有两人依次随机地从袋中各取1球,取后不放回,则第二个人取得黄球的概率是 0.4 。
7.将 C ,C ,E ,E ,I,N,S 七个字母随机地排成一行,则恰好排成英文单词 SCIENCE 的概率为11260。
8.10 件产品有 4 件次品,现逐个进行检查,则不连续出现 2 个次品的概率为 。
电路与电子技术基础第一章习题答案
P 1000 = = 4.55A U 220
1-4 某电流表的量程为 10mA.当某电阻两端的电压为 8V 时,通过的电流为 2mA.如 果给这个电阻两端加上 50V 的电压,能否用这个电流表测量通过这个电阻的电流? 解:根据电阻两端压降和流过电阻中的电流,由欧姆定理可以确定电阻的值为: U 8 R= = = 4 ( kΩ ) I 2 × 10 −3 如果给电阻上加 50V 的电压,流过电阻的电流为: 50 U = 12.5 (mA) I= = R 4 × 10 3 电流表的量程为 10mA,也就是允许通过的最大电流为 10mA,显然不能使用该电流表 测量通过流过该电阻的电流。 1-5 在电路中已经定义了电流、电压的实际方向,为什么还要引入参考方向?参考方 向与实际方向有何区别和联系? 答:在求解电路参数时,对于稍微复杂的电路,必须列方程求解,列出方程又必须知 道电流、电压的方向,为此,引入电流、电压参考方向,根据参考方向列出电路方程,利用 方程求出电路参数,若结果为负,表明实际的方向与参考方向相反,若结果为正,表明参考 方向就是实际方向。 1-6 如何计算元件的吸收功率?如何从计算结果判断该元件为有源元件或无源元件? 答:在关联参考方向下: P = UI ;在非关联参考方向下: P = −UI 。在此前提下,当 P>0 时为吸收功率。若 P<0 为有源元件,否则为无源元件。 1-7 标有 10kΩ(称为标称值) 、1/4W(额定功率)的金属膜电阻,若使用在直流电路 中,试问其工作电流和电压不能超过多大数值? 答:因为功率 P =
U2 = I 2R R
工作电流: I < 工作电压: U < 1-8
中药习题续作一
中药习题一一.A型题1.收载药物最多的本草著作是:A 本草纲目 b 新修本草c 证类本草d 中华本草e 本草纲目拾遗2.由苏敬等人编著的药典性的本草是A 《证类本草》b 《新修本草》c 《神农本草经》d 《本草纲目》e 《本草纲目拾遗》3.新增药物最多的本草著作是A 本草纲目 b 新修本草c 中华本草d 本草纲目拾遗e 经史证类备急本草4.《本草纲目拾遗》新增药品的种数是A 921 b 716 c 844 d 365 e 7305 系统总结了汉代以前我国药学发展成就,为本草学发展奠定的基础是A 《伤寒论》b《内经》c 《证类本草》d 《嘉佑本草》e《神农本草经》6 《神农本草经》各论载药A 565种 b 265种 c 365种d 335种e 635种7 现存最早的药学著作是A 《本草经集注》b 《本草纲目》c 《神农本草经》d 《证类本草》e 《新修本草》8 《本草经集注》作者是A 陶弘景b 苏敬c 张元素d 张仲景e 赵学敏9 《本草经集注》是哪个朝代的代表作A 隋朝b 唐朝c 宋元时期d 魏晋南北朝e 汉朝10 我国历史上第一部官修药典性本草是A 《神农本草经》b 《新修本草》c 《本草纲目》d 《经史证类备急本草》 e 《嘉佑本草》11 首创按自然属性进行分类的本草著作是A《神农本草经》b 《本草经集注》c 《本草纲目》d 《新修本草》e 《嘉佑本草》12. 《经史证类备急本草》是那个时期的代表作A 唐朝b 汉朝c 隋朝d 宋金元朝e 魏晋南北朝13. 明代本草代表作A 《图经本草》b 《新修本草》c 《本经》 d 《本草纲目》e 《本草纲目拾遗》14 《本草纲目拾遗》是哪个朝代本草的代表作A 明朝 b 宋代 c 清代 d 元朝 e 唐朝15 首次全面系统整理‘补充《神农本草经》的本草著作是A 《本草纲目》b 《新修本草》c 《本草经集注》d 《本草纲目拾遗》e 《证类本草》16 药性理论种,为药物作用定位的是A 四气b 五味c 归经d 升降沉浮e 有毒无毒17升浮性所示的功效是A 清热 b 息风 c 开窍 d 消积 e 潜阳18 寒凉药对人体的不良作用是A 伤阴 b 耗气 c 伤阳 d 敛邪 e 生热19 关于辛味,指出下面错误的是A 能发散b 能行气c 能活血d 能润燥 e 能收敛20 下列哪种说法有错A 一药中气只能有一,而味可以有一个,也可以有二个或更多 b 气味相同,功能相近 c 任何气与任何味均可以组配 d 味越多,说明其作用越广泛 e 气偏于定能,味偏于定性21 确定升降浮沉的依据A 疾病影响人体的部位b 病症的寒热程度 c 药物的气味厚薄 d 用药的反应情况e药物作用的部位特征22 属对因功效的是A 发散风寒b利胆退黄c 消痈排浓d 涩肠止泻e 降逆止呕23 细辛的主治病症不包括a 风寒表证b 阳虚外感c 风寒湿痹d 头风头痛e 肺热喘咳24 石膏与知母均有的功效是A 清热泻火 b 滋阴生津 c 润燥滑肠d 消肿止痛e 利尿消肿25 生用泻下力较强久煎泻下力减弱的药是A 芒硝 b 大黄 c 芦荟 d 巴豆 e 郁李仁26 酸不收敛湿邪,温不燥烈伤阴的药是A 白芍 b 栀子 c 木瓜 d 五味子 e 夏枯草27 藿香最善治A 胃热呕吐 b 胃虚呕吐 c 食积呕吐d 畏寒呕吐e 湿阻呕吐28 既利水通淋,又清热解暑的药是A 滑石b 木桶c 金钱草d 车前子e 地肤子29 丁香的功效是A 温肾固精 b 温肺化饮 c 暖肝散结d 暖宫止带e 温中降逆30 生用兼发表,醋制嫩增强止痛作用的药是A 青皮b 香附c 川楝子d 青木香e 延胡索31 在含大量的金石类的丸剂中,起赋形与消化作用的药是A 麦芽 b 谷芽 c 荆芥 d 苍耳子 e 牛蒡子33 既清肝明目,又润肠通便的药是A 决明子b 火麻仁c 蔓荆子d 青箱子e 冬葵子34 青蒿与地骨皮均能退虚热外,又均能A 生津b 解暑c 疏肝解郁d 清利湿热e 升举阳气32 发表透疹宜生用,止血须炒碳的药是A 薄荷b 西河柳c 荆芥d 苍耳子e 牛蒡子35 银柴胡的功效是A 退虚热除肝热b 疏散风热c 疏肝解郁d 清利湿热e 升举阳气36 能泻下软坚,善治燥屎坚结难下的药是A 昆布 b 芦荟 c 瓜蒌 d 芒硝 e 胖大海37 既峻下冷积,又逐水腿肿的药是a甘遂b 商陆c 巴豆d 郁李仁e 牵牛子38 既治风寒湿痹,又治寒湿头痛的药是A 草果b 川乌c 香加皮d 伸筋草e 穿山龙39 治水肿伴心悸失眠,宜选的药是A 茯苓 b 朱砂 c 磁石 d 泽泻 e 薏苡仁40 香附配高良姜除温中散寒疏肝理气外,有善A 止泻 b 止咳 c 止血 d 止带 e 止痛41 小儿内服使君子,每日最大量是A 20粒b 25粒c 30粒d 40粒e 5 0粒42 茜草不具有的功效是A 止血 b 凉血 c 通经 d 通乳 e 祛瘀43 既燥湿化痰,有祛风止径的药是A 橘红 b 半夏 c 蝉蜕 d 天南星 e 牛黄44 既息风止径,又通络止痛的药是A 僵蚕 b 熊胆 c 蒺藜 d 羚羊角 e 全蝎45 既开窍,有止痛的药是A 木香b 沉香c 青木香d 苏合香e 小茴香46 性温,既补肾,又祛风湿的药是A 续断b 狗脊c 骨碎补d 桑寄生e 雷公藤47 既补血活血,有调经润肠的药是A 红花b 当归c 熟地黄d 肉苁蓉e 月季花48 能涌吐痰饮的药是A 硼砂 b 铅丹 c 常山 d 香薷 e 儿茶49 入药忌火煅的药是A 礞石b 珍珠母c 雄黄d 炉甘石e 牡蛎50 升药的功效是A 拔毒祛腐 b 软坚散结 c 清热解毒d 开窍醒神e 化痰散结51 生姜和肉豆蔻均有的功效是A 涩肠 b 发表 c 温中 d 止咳 e 止汗52 菊花的主治病症不包括A 燥咳谈黏 b 温病初起 c 毒疮肿 d 眼目昏花e 肝阳头痛53 生用走气分而泻火,炒黑入血分而止血的药是A 蒲黄 b 栀子 c 芦根 d 知母 e 小蓟54 天花粉不具有的功效A 清热b 生津c 凉血利尿d 清肺润燥e 消肿排脓55 阴亏血虚者应慎用的药是A止血药b 消食药c 退虚热药d祛风湿药e 清热凉血药56 砂仁不具有的功效是A 化湿 b 行气 c 解暑 d 温中 e 安胎57 善治沙淋与肝胆结石的药是A茵陈b 篇蓄c 瞿麦d 灯芯草e 金钱草58 纯阳温散,长于引火归元的药是A 仙茅 b 肉桂 c 丁香 d 花椒 e 高良姜59 荔枝核除能行气散结外,又能A 燥湿化痰 b 开郁醒神 c 通阳散结d 祛寒止痛e 解毒消肿60 山楂不具有的药理作用是A 降血脂b 助消化c 扩张血管d 收缩子宫e 镇咳祛痰61 既凉血止血,又祛痰止咳的药是A 大蓟b白及c 地榆d侧柏叶e 棕榈炭62 莪术除破血行气外,又能A 凉血清心 b 化癖止血 c 下乳消肿d 消极止痛e 消肿生机63 白前的功效是A 降气祛痰 b 发散表邪 c 润肺止咳d 清泄肺火e宣肺平喘64 朱砂配磁石的功效是A 滋阴潜阳 b 重镇安神 c 清心泻火d解毒消肿e 纳气平喘65 石决明的功效是A 平肝通络 b 平肝养血 c 平肝安神d 平肝熄风e 平肝潜阳66 成人内服冰片的一日常用量是A 0.15~0.3 b 0.4~0.6 c 0.7~0.9 d 1~1.2 e 1.5~367 核桃仁的功效是A 补肾益精缩尿 b 补肾润肺名目 c 补肾清火滋阴 d 补肾活血续伤e 补肾温肺润肠68 既滋肾补肝,又清虚热的药是A 黄精b 秦艽c 地骨皮d 女贞子e 枸杞子69 既攻毒杀虫,又利水通便的药是A 轻粉 b 硫磺 c 雄黄 d 鸦胆子 e 土荆皮70 既攻毒蚀疮,有破血逐瘀的药是A 砒石 b 斑蝥 c 升药 d 干漆 e 猫爪草71 贯众的主治病症不包括A 痄腮b 钩虫病c 风热感冒d 疟疾寒热e 血热衄血72 蒲黄不具有的药理作用是A 止血b 降血压c 兴奋子宫d 抗心律失常e 抗心肌缺血73 郁金不具有的功效是A 活血止痛 b 行气解郁 c 凉血清心d 利胆退黄e 消肿生肌74 紫菀的功效是A 清肺化痰 b 消痰利水 c 泻肺平喘d 化痰止咳e 纳气平喘75 煅龙骨长于A 平肝潜阳 b 聪耳明目 c 收敛固涩d 镇惊安神e 熄风止痛76 既平肝潜阳,又降胃气的药是A 磁石 b 珍珠c’枇杷叶 d 代赭石e 珍珠母77 既开窍宁神,又化湿和胃的药是A 朱砂b 琥珀c 石菖蒲d 苏合香e 安息香78 既润肺止咳,又清心安神的药是A 百合b 百部c 酸枣仁d 龙眼肉e 天门冬79 既涩肠止泻,又敛肺利咽的药是A 莲子 b 诃子 c 桔梗 d 射干 e 罂粟壳80 内服涌吐痰热,研末吹鼻引去湿热的药是A 常山 b 瓜蒂 c 甘松 d 铅丹 e 砒石81 蛇床子不具有的功效是A 燥湿b 杀虫c 补肝明目d 散寒祛风e 温肾壮阳82 既解毒消肿,又开窍辟pi秽的药是A 硼砂b 蟾chan酥c 白芷d远志e 白僵蚕83 寒凉类药物所不具备的功效是A 凉血b 回阳救逆c 解毒药d 清热e 泻火84 既能祛风解表,又能解痉的药物是A 荆芥 b 白芷 c 羌活 d 防风 e 蒿本85后期阴虚发热,久病伤阴无汗骨蒸宜选用的中药是A 青蒿b 银柴胡c 牡丹皮d 玄参e 地骨皮86 外感伤寒,内伤暑湿,恶寒发热,呕吐腹泻的阴暑证宜选用A 紫苏 b 香茹 c 荆芥 d 生姜 e 白芷87 既可治疗麻疹不透,又可治疗气虚下陷的药物是A 柴胡 b 牛蒡子 c 升麻 d 蝉蜕 e 白芷88 既可以清热解毒,消痈散结,又可以利尿通淋的药物是A 蒲公英b 穿心莲c连翘d 金银花e 板蓝根89 不属于苍术的主治病症是A 表证夹湿 b 痰饮水肿 c 风寒湿痹d 湿阻中焦e 脾虚乏力90 既利尿通淋,又通经下乳的药是A 石伟 b 茵陈 c 篇蓄 d 滑石 e 木通91 附子与干姜均有的功效是A 补火 b 回阳 c 温肺 d 止呕 e 降逆92 既行气止痛,又温肾散寒的药是A 木香 b 甘松 c 佛手 d 青皮 e 乌药93 谷芽的功效是A 消食和中健脾开胃b 消食运脾,固精止遗 c 消食和中 d 消食健脾 e 消食除胀94 既善杀虫消积,又能行气利水的药是A 槟榔b 香加皮c 苦楝皮d 紫珠e 南瓜子95 既收敛止血,又截疟的药是A 地榆 b 藕节 c 棕榈炭 d 紫珠 e 仙鹤草96 川芎不宜治A 风寒头痛 b 淤血头痛 c 风湿头痛d 风热头痛e 肝火头痛97 白前与前胡均有的功效是A 降气祛痰 b 宣散风热 c 清肺化痰d 润肺化痰e 化痰软坚98 内服琥珀的方法是A 捣汁服b 洋化服c 水煎服d 熬膏服 e 研末冲服99 既熄风止痉,又清热平肝的药是A 天麻 b 蜈蚣 c 刺蒺藜 d 钩藤 e 罗布麻100 既开窍醒神,又活血散结的药是A 冰片 b 远志 c 麝香 d 苏合香 e 石菖蒲101 善温脾开胃摄唾的药是A 砂仁b 益智仁c 肉豆蔻d 沙苑子e 菟丝子102 既益气,又除热止汗的药是A 浮小麦b 白芍c 麻黄根d 刺五加e 山茱萸103 明矾不具有的功效是A 解毒杀虫 b 清热解毒 c 利水通便d 燥湿止痒e 止血止泻104 成人内服马钱子的一日用量是A 0.3~0.6 b 1~2 c 2~5 d 5~9 e 9~15105 瓜蒂研末吹鼻,可A 通鼻窍b 开心窍c 去湿热d 止痹痛 e 止牙痛106 臣药的含义是A 治疗主证的药 b 治疗兼证的药 c 治疗次兼证的药 d 引药直达病所的药 e 消除君药毒烈之性的药107 解表宜生用,平喘宜蜜炙用的药是A 桂枝 b 麻黄 c 紫苏 d 橘皮 e 白果108 芦根不具有的功效是A 清热生津 b 除烦止呕 c 凉血解毒d 透疹排脓e 清热利尿109 大黄不能主治的病症是A 肠燥便秘 b 水火烫伤 c 湿热黄疸d 跌打损伤e 湿热泻痢初起110 善治风痹或痹症重的药是A 桑枝 b 络石藤c’丝瓜络 d 徐长卿e 五加皮111 厚朴不具有的功效是A 行气 b 燥湿c 发表d 消积e 平喘112 生用渗利湿热,炒用健脾止泻的药是A 泽泻b 地肤子c 青木香d 薏苡仁e 车前子113 治湿痰雍肺之咳喘,常以橘皮配A 半夏 b 佩兰 c 砂仁 d 枳壳 e 木香114 既助消化,又抑制催乳素分泌的药是A 谷芽 b 麦芽 c 山楂 d 神曲 e 鸡内金115 使君子的功效是A 杀虫疗癣 b 杀虫利水 c 杀虫止血d 杀虫祛痰e 杀虫消积116 既凉血止血,又清肝泻火的药是A 槐花 b 大蓟 c 地榆 d 白茅根 e 侧柏叶117 既活血祛瘀,又止咳平喘的药是A 干漆 b 桃仁 c 牛膝 d 杏仁 e 血竭118 既化痰止咳,又和胃降逆的药是A 紫菀 b 苏子 c 批把叶 d 枳实 e 柿蒂119 成人内服朱砂的一日计量是A 0.1~0.5 b 0.3~1 c 1~3 d 3~6 e 6~10120 既平肝潜阳,又凉血止血的药是A 牡蛎 b 琥珀 c 地龙 d 代赭石 e 磁石121 既补中益气,又生津养血的药是A 黄芪 b 甘草 c 党参 d 大枣 e 当归122 温中止泻宜煨用的药是A 金樱子b 乌贼骨c 罂粟壳d 补骨脂e 肉豆蔻123 既涌吐痰涎,又截疟的药是A 升药 b 常山 c 瓜蒂 d 明矾 e 轻粉124 雄黄不具有的功效是A 解毒b 杀虫c 止血d 燥湿祛痰e 截疟定惊125 能明目去翳,收湿生肌的药是A 炉甘石b 煅石膏c 决明子d 煅龙骨 e 野菊花126 不属于沉降性所示的功效是A 清热泻火 b 利水渗湿 c 平肝潜阳d 涌吐开窍e 收敛固涩127 与草乌不相反的药是A 赤芍b 川贝母c 天花粉d 全瓜蒌e 半夏128 堪称为发表散风通用的药是A 生姜 b 紫苏 c 桂枝 d 荆芥 e 细辛129 泻下药的主要功效不包括A 泻热b 通便c 攻下积滞d 活血化瘀 e 逐水退肿130 威灵仙的主治病症不包括A 风寒湿痹 b 痰饮积聚 c 瘫痪麻木d 诸骨鲠喉e 吐泻转筋131 藿香的主治病症是A 水肿b 痰饮c 热淋d 湿浊困脾e 湿痹肿痈132 既温中止痛又杀虫的药是A 花椒b 安息香c 小茴香d 草豆蔻e 沉香133 生用行气力强,煨用力缓并止泻的药是A 橘皮 b 甘松 c 木香 d 白扁豆 e 川楝子134 莱菔子不具有的药理作用是A 助消化b 缓解心绞痛c 镇咳d 祛痰 e 抗菌135 既杀虫,又疗癣的药是A 苦楝皮b 香加皮c 地骨皮d 桑白皮 e 合欢皮136 酸枣仁的功效A 养心安神通便b 养心安神通络c 养心安神敛汗 d 养心安神调经e养心安神止泻137 成人内服麝香的一日量是A 0.06~0.1 b0.1~0.3 c0.3~0.6 d0.6~1 e1~3138 黄芪的功效A 补脾肺肾,固精止带b 补气养血,清火生津c 补气健脾,止汗安胎d 补气升阳,利水消肿e 健脾化湿消暑解暑139 内服涩肠止泻,外用收湿敛疮的药是A 赤石脂b 石榴皮c 椿皮d 金樱子e 肉豆蔻140 外用杀虫止痒,内服壮阳通便的药是A 雄黄 b 硫磺 c 轻粉 d 明矾 e 蛇床子141 性凉,既收涩敛疮,又升肌止血的药是A 琥珀 b 乳香 c 儿茶 d 血竭 e 自然铜142 辛味对人体的不良作用A 耗气伤津b腻膈碍胃c收敛邪气d 泻下伤阳e 以上皆是143 性味皆属于升浮的是A 辛苦热b 辛甘温c 辛甘寒d 甘酸凉e 以上皆是144 消食健胃药宜在何时服A 饭前 b 睡前 c 饭后 d 空腹 e 不拘时145 既可散风解表,通窍止痛,又可消肿排脓的药物是A 防风 b 白芷 c 荆芥 d 细辛 e 辛夷146 既可解表,又可除烦的药物是A 升麻 b 辛夷 c 柴胡 d 淡豆豉 e 蔓荆子147 既可清热解毒,有可明目止痉的药物是A 大血藤b 土茯苓c 熊胆d 紫花地丁e 半边莲148 甘遂京大戟均有的功效A软坚泻下b 俊下寒积c 润肠通便d 泻下逐水消肿散结e 俊下热结149 既能清肺润燥,又能消肿排脓的药物是A 茯苓 b 薏苡仁 c 泽泻 d 白芷 e 天花粉150 气滞湿阻痰痈之证兼寒者最宜用的中药是A 橘皮 b 木香 c 薤白 d 香附 e 化橘红151 被称为治疗水火烫伤之要药的中药是A 苎麻根b 小蓟c 侧柏叶d 三七e 地榆152 治淤血及食积重症宜用A 乳香配没药 b 川芎配当归 c 丹参配虎杖d 莪术配三棱e 桃仁配红花153 功效止咳平喘,润肠通便的药物是A 百步桔梗 b 瓜蒌半夏 c 海藻昆布 d 川贝母浙贝母e 杏仁苏子154 川贝母与浙贝母都具有的功效是A 润肺止咳开郁b 温肺化痰止咳c 清热化痰散结 d 清热化痰开郁 e 润肺化痰止咳155 为治心火抗盛之心神不安惊悸失眠之要药是A 朱砂 b 龙骨 c 琥珀 d 磁石 e 合欢皮156 可用于治疗惊痫抽搐妊娠子痫的中药是A 天麻 b 珍珠 c 钩藤 d 石决明 e 羚羊角157 为活血通经止痛之佳品治疗血瘀诸证无论新久皆宜的中药是A 冰片b 麝香c 苏合香d 安息香e 石菖蒲158 善补气养阴,为平补气阴之佳品的中药是A 党参b大枣c 白术d 山药e 甘草159 为血肉有情之品,善俊补元阳,大补经血的中药是A 淫羊藿 b 锁阳 c 鹿茸 d 阿胶 e 肉苁蓉160 治疗脾肾阳虚的泄泻及肾虚作喘宜选用的中药是A 巴戟天 b 补骨脂 c 益智仁 d 淫羊藿e 鹿茸161主治回厥腹痛的中药是A 五味子b 芡实c 石榴皮d 山茱萸e 乌梅162 以下可以治疗带状疱疹的中药是A 黄芩 b 黄连 c 黄柏 d 龙胆草 e 苦参二B型题A 《本草纲目》b《本草纲目拾遗》c《新修本草》d《经史证类备急本草》e《本草经集注》1 载药921种的是2 载药1746种的是3 载药730种的是4 载药850种的是A 凉血b利湿c 理气d 温里e 安蛔5 寒凉性表示药物具有的作用是6 温热性表示药物具有的作用A 川乌b 人参c 甘遂d 半夏e 海藻7 不能与藜芦同用的药是8 不能与五灵脂同用的药是A 辛b 苦c 酸d 咸e 甘9 能安蛔生津的味是10 能行气活血的味是A 相恶b 相反c 相杀d 相使e 相畏11 表示增毒的配伍关系12 表示增效的配伍关系A 先煎b 后下c 包煎d 另煎e 烊化13 蒲黄旋复花入煎剂宜14 阿胶鹿角胶入煎剂宜15 薄荷白豆蔻宜16 磁石牡蛎川乌宜A 定时服b睡前服c 饭前服d 饭后服e 空腹服17 俊下逐水药,驱虫药宜18 补药宜19 对胃肠刺激或消食健胃的药宜20 截疟药宜A 柴胡 b 葛根 c 升麻 d 蔓荆子 e 淡豆豉21 除解表外,又能除烦的药是22 除能解表退热外,有能疏肝的药是23 除发表解肌外,又能生津的药是A 宣肺平喘b 透疹止痒c 化湿和中d 燥湿止带e 开窍止痛24 麻黄除发汗利水外又能25 香薷除发汗利水外又能A 凉血养阴 b 凉血清肺 c 凉血通淋 d 凉血利咽e 凉血丁惊26 水牛角的功效27 马齿苋的功效A 息风止径b 活血消肿c 疏散风热d 利尿通淋e 凉血止痢28 牛黄除清热解毒外,又能29 鱼腥草除清热解毒外又能30 白头翁除清热解毒外有能A 芫花 b 牵牛子 c 京大戟 d 郁李仁 e 番泻叶31 性寒,既泻下逐水,又祛积杀虫的药是32性温,既泻下逐水,有杀虫疗癣的药是A 止血b活血c 降血压d 消痰水e 利小便33 青风藤除祛风湿,通经络外,又能34 豨莶草除祛风湿,同经络外,又能35 臭梧桐除祛风湿,同经络外,又能A 滑石b血竭c 硼砂d 车前子e 地肤子36 外用能清热收敛的药是37 内服能清肝明目的药是A 温阳利水b 补火助阳c 疏肝燥湿d 下气降逆e 温肺化饮38 附子的功效是39 干姜的功效是A 枳实b 佛手c 薤白d 青皮e 柿蒂40 既行气导滞,又通阳散结的药是41 既破气消积,有化痰除痞的药是42 既疏肝破气,又消积化滞的药43 既疏肝理气,又和中化痰的药是A 清热安胎b解毒止痢c 散寒止痛d 疏肝止痛e 清肝泻火44 艾叶除温经止血外,有能45 槐花除凉血止血,有能46 苎麻根除凉血止血外,又能A 疏肝解郁b 祛风止痛c 利尿通淋d 止咳平喘e 清心除烦47川芎除活血行气外,又能48 丹参除祛瘀止痛外,又能49 牛膝除活血通经外,又能50 桃仁除活血祛瘀外,又能A 清热化痰b 消痰软坚c 燥湿化痰d 敛肺平喘e 泻肺平喘51 海藻的功效52 竹沥的功效53昆布的功效54 白果的功效A 珍珠 b 蒺藜 c 僵蚕 d 珍珠母 e 罗布麻叶55 既平肝清热,又降压利水的药是56 既平肝潜阳,又清肝明目的药57 既平肝疏肝,又祛风明目的药是A 补气养血b 补气解毒c 补气活血d 补气养阴e补气燥湿58 甘草的功效是59 党参的功效是60 山药的功效是61 白术的功效是A 当归b鹿茸c 黑旱莲d 沙苑子e 熟地黄62 既补血又活血的药是63 既补血,又滋阴的药是64 既益精血,又壮阳的药是A 芡实b椿皮c 赤石脂d 山茱萸e 覆盆子65 外用治外伤出血的药是66 内服治湿热泻痢的药是67 内服治虚汗不止的药是A 麻黄配桂枝 b 肉桂配黄连 c 生姜配半夏d 甘草配甘遂e 乌头配白芨68 属于增效的配伍药组是69 属于减毒的配伍药组是A 柴胡b 淡豆豉c 浮萍d 葛根e 升麻70 既疏散风热,又生津的药是71 既疏散风热,有疏肝的药是72 既疏散风热有清热解毒的是A 赤芍 b 紫草 c 红花 d 牡丹皮 e 马齿苋73 既凉血活血,又解毒透疹的药是74 既凉血活血,有退虚热的药是75 既凉血止血又清肝火的是A 利咽凉血 b 利咽祛痰 c 利咽通便 d 利咽止血e 利咽疏肝76 射干的功效77马勃的功效78 板蓝根的功效79 木蝴蝶的功效A 木瓜 b 秦尻 c 桑枝 d 络石藤 e 臭梧桐80 性平,既祛风湿,又利水的药是81 性微寒,既祛风湿,又利湿退黄的药是A 截疟b行气c 温中d 解暑e 消积82 佩兰的功效83 广藿香的功效A 除湿退黄b祛风止痒c 凉血止血d 清心除烦e 破血通经84石伟除利尿通淋外,又能85 金钱草除利尿通淋外,又能A 香附 b 青皮 c 川楝子 d 荔枝核 e 化橘红86能杀虫疗癣的是87善调经止痛的药是88 能祛寒止痛的药是89 能燥湿化痰的药是A 温经止痛b 滋阴止血c 收敛止血d 凉血止血e 补血止血90 炮姜的功效是91 大蓟的功效是92 白茅根的功效A 苏木 b 虎杖 c 西红花 d 川牛膝 e 鸡血藤93 能泻下通便的药是94 能引血下行的药是95 能活血补血的药是96 能化痰止咳的药是A姜黄b 丹参c 没药d 自然铜e 益母草97 能活血止痛,消肿生机的药是98 能活血祛瘀,利尿消肿的药是a降气止呕b泻肺平喘c 消痰软坚d 祛风止径e 燥湿化痰99 海藻的功效是100 葶苈子的功效是101 旋复花的功效是A 珍珠 b 酸枣仁 c 柏子仁 d 夜交藤 e 合欢皮102 既安神,又祛风的药是103 既安神,有润肠的药是104 既安神,有敛汗的药是A 党参 b 人参 c 西洋参 d 太子参 e 刺五加105 能益肾强腰的药是106 能安神益智的药是107能清火生津的药是108能大补元气的药是A 益气b 清心c 潜阳d 明目e 敛汗109 麦冬的功效110 枸杞的功效111 百合的功效A 清心除烦b 补益肝肾c 养心安神d 补脾祛湿e 益气养阴112 莲子肉的功效是113 芡实的功效是A 黄连b 黄芩c 黄柏d 苦参e 土茯苓114 善治肺热咳喘的药是115 善治胃火牙疼的药是116 善治骨蒸潮热的药物是117 善治梅毒湿疮的药物是A 祛痰利咽b 祛积杀虫c 消肿散结d 祛痰止咳e 活血祛瘀118 京大戟除能逐水外,又能119 牵牛子除泻下逐水外,又能120 红大戟除泻水逐饮外,又能A 人参 b 白术 c 山药 d 西洋参 e 太子参121性味甘,微苦,微温的药是122 性味甘微平的药是123 性味微甘,苦寒的药是124性味甘,苦温的药是A 利水渗湿健脾 b 利水渗湿退黄 c 利水通淋止泻 d 利水通淋清心 e 利水通淋,止痛125 茯苓的功效是126 灯芯草的功效127 海金沙的功效128 薏苡仁的功效A 木香b 佛手c 橘皮d 枳壳e橘红129能行气,燥湿,发表的药是130 能行气,燥湿,消食的药是A 1~3 b 3~6 c 6~15 d15~30 e 60~120131槟榔驱绦虫的成人一日用量是132 苦楝皮驱虫的成人一日用量是A 凉血止血清热利尿b 凉血止血活血化瘀c 收敛止血,清热生津d 化瘀止血,清热利尿e 收敛止血,祛痰止咳133 白茅根的功效134 苎麻根的功效A、川芎b 三棱c 五灵脂d 穿山甲e 土鳖虫135既破血逐瘀,又续筋接骨的药是136 既活血行气,又祛风止痛的药是137 既活血止痛,有解蛇毒的药是A 燥湿化痰,消痞散结b 泻肺平喘,利水消肿 c 温肺祛痰,利气散结 d 消痰行谁,降逆止呕e 清肺化痰,软坚散结138 葶苈子的功效139 旋复花的功效140 桑白皮的功效A 礞石b 天麻c 钩藤d 全蝎e 石决明141 既平肝潜阳,又清肝明目的药是142 既息风平肝,又祛风通络的药是143 既息风止径,又解毒散结的药是A 大枣b 沙苑子c 骨碎补d太子参e 玉竹144 既补肾固精,又养肝明目的药是145 既补中益气,又养血安神的药是146 既滋阴润肺,又养胃生津的药是A 益胃生津b 补肝明目c 补阴益气d 壮阳健骨e软坚散结147 石斛的功效148 麦冬的功效149 黄精的功效150 枸杞子的功效A 涩肠杀虫b敛肺生津c 固精止带d 益肾固精e 敛汗止血151 乌梅的功效152 椿皮的功效A 攻毒蚀疮b 开窍醒神c 通络散结d 收湿生机e 祛痰平喘153 斑蝥除能破血散结外,有能154 马钱子除能消肿定痛外,又能A 能散b 能涩c 能坚d 能软e 能和155 酸味的作用156 辛味的作用157 咸味的作用158 苦味的作用A 息风止径b 平肝明目c 消肿疗疮d 凉血止血e 升阳止泻159 蝉蜕的功效160 牛蒡子的功效A 夏枯草b 淡竹叶c 决明子d 天花粉e 龙胆草161 既清肝或,又润肠燥的药是162既清肝火,有散郁结的药是A 疏散风热b 凉血消斑c 利湿退黄d 祛痰利咽e 活血止痛163 连翘除能清热解毒外又能164 大青叶除能清热解毒外又能165 金银花除能清热解毒外又能A 薏苡仁b 火麻仁c 郁李仁d 番泻叶e 巴豆霜166 既润肠通便,又兼补虚的药是167 既润肠通便,又利水消肿的药是A 祛风通络,利小便b 祛风通络,降血压c 祛风通络,安神智 d 祛风通络,消痰水 e 祛风通络,化淤血168 青风藤的功效是169 威灵仙的功效170臭梧桐的功效是171 桑枝的功效是A 破血通经b 通气下乳c 清肺止咳d 杀虫止痒e 祛风湿172 萆薢除是谁通淋外,又能173 瞿麦除利水通淋外,又能174 通草除清热利水外,又能A 温中降逆b 文通经脉c 温经止血d 温肺化饮e 文中杀虫175 丁香的功效是176 肉桂的功效是A 橘皮b 沉香c 枳实d 薤白e 川楝子177 治脏器小锤宜用178 治头癣、虫积宜用179 治肾不纳气之虚喘宜用A 蝉蜕 b 防风 c 天南星 d 白僵蚕 e 蜈蚣180 既止痉,又明目退翳的药物是181 既止痉,有祛风止痛的药物是182 既止痉,又通络止痛的药物是A 乳香 b 苏木 c 姜黄 d 没药 e 王不留行183 既活血止痛,又消肿生机的药是184 既破血逐瘀,有消积杀虫的药是A 清肠通便b 降气止呕c 收湿止带d 润肺止咳e 选散风热185 白果除敛肺平喘外,又能186 胖大海除清热宣肺气外,又能187 旋复花除消痰行水外,又能A 阳亢眩晕,心悸失眠b 阳亢眩晕,目赤目婚 c 阳亢眩晕,吐血衄血 d 阳亢眩晕,湿疹湿疮e 阳亢眩晕,肝热急惊188 代赭石的主治病症是189 羚羊角的主治病症是190 石决明的主治病症是A 杀虫止血b 杀虫截疟c 杀虫利水d 杀虫止痒e杀虫壮阳191 雄黄的功效是192 轻粉的功效是A 肉苁蓉 b 山药 c 何首乌 d 石斛 e 麦冬193 既润肺养阴,又清心除烦的药是194 既益气养阴,有固精止带的药是195 既养胃生津,又明目强腰的药是196 既补益经血,又解毒截疟的药是A 阴虚消渴b 肺虚久咳c 须发早百d 阴虚动风e 肺热咳嗽197 龟甲主治198 鳖甲主治A 五倍子 b 五味子 c 乌梅 d 诃子 e 罂粟壳199 能敛肺,涩肠,止痛的药是200 能敛肺,涩肠,降火的药是201 能敛肺,涩肠,利咽的药是202 能敛肺,涩肠,安蛔的药是A 硼砂 b 升药 c 炉甘石 d 大蒜 e 猫爪草203 性温,能解毒杀虫的药是204性温,能散结消肿的药是205 性凉,能清热化痰的药是206 性平,能明目去翳的药是A 清热 b 凉血 c 散瘀血 d 退虚热 e 清肝火207 赤芍不具有的功效是208 牡丹皮不具有的功效是A 解暑截疟b 清肺生津c利尿通络d清除湿热e 收敛止血209 白薇的功效210 胡黄连的功效是A 巴豆 b 甘遂 c 芫花 d 红大戟 e 牵牛子211 既泻水逐饮,又祛痰止咳的药是212 既泻水逐饮,有祛积杀虫的药是213 既泻下冷积,又祛痰利咽的药是。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作业基本信息 名称 习题一 所属章节 专题一:教育与教育学/课后作业 分值 0 截止提交时间 2013.01.15 作业类型 必做作业 作业要求 习题
一、名词解释 1.教育:在给“教育”下定义时,应该兼顾社会和个体两个方面,可以将教育定义为:教育是在一定社会背景下发生的促使个体的社会化和社会的个性化的实践活动。 教育学:教育学是以教育现象、教育问题为研究对象,归纳总结人类教育活动的科学理论与实践,探索解决教育活动产生、发展过程中遇到的实际教育问题,从而揭示出一般教育规律的一门社会科学。 3.教育事件:所谓“教育事件”,则是将教育事实进行有效还原后生成的关系性、情境性的实在,表征着教育的极端复杂性,往往不能用既定的教育规律来解释和说明,在教育事件中蕴藏着真实的教育问题。有价值的教育一般问题就是从教育事件蕴藏的真实的教育问题中抽象出来的、相对脱离各种具体教育情形的最一般的教育问题。 二、填空 1.根据教育系统自身形式化的程度,可以将教育划分为(非制度化)的教育与(制度化)的教育。 2.根据教育系统所赖以运行的场所或空间标准,可以将教育划分为(家庭教育)、学校教育与(社会教育)。 3.根据教育系统的层次,可以将教育划分为(学前境遇)、初等教育、(中等教育)和高等教育。 4.美国教育家杜威认为,教育即生活,教育即生长,教育即(生活经验)的不断改造或改组。 5.教育学的科学化就是教育学的(合理性)。 三、简答 1.立足中西文教育的不同词源分析中西方教育思想的差异。 答:中西教育思想差异形成因素及对比 1、中国教育重同一性 西方教育重多样性 中国是一个以群体文化为主要文化特征的国家。 中国人的群体意识来源于以农耕为主的 小农经济生产方式。中国人习惯于集体作业,从而造就了中国人的群体文化心理。在群体文 化中,群体的整体利益是个体利益的唯一参照物,是个体利益的出发点和归宿。中国人关心 的是“别人怎么看”,因而常常会用普遍认可的道德行为规范自觉约束自己的言行,来获得群 体的认同。 这种求同的群体文化意识投射在教育思想上,决定了中国教育天然地排斥“多样”性,注 重“同一”性。即用统一的内容、方法、进度、单一评价机制“生产成品”。教育毫无生气,窒 息着学生个性的发展。在中国,一堂课上得好的标准是:教师讲得条理清楚、重点突出;学 生则认真听讲、细做笔记,回答提问态度谦虚,甚至连学生坐、立、举手的姿势都有统一要 求。这种整齐划一的教学形式貌似规范、紧凑,实则缺乏内在感染力。过于追求同一性和规 范性的中国式教育不利于活跃学生思维和激活学生的活力, 不易使学生感受到自己的主体地 位。 西方文化的基本特征是个体主义。 个体主义强调个人的价值与尊严, 强调个人的特征与 差异,提倡新颖,鼓励独特风格。这种文化心理助长了西方人对多样性的追求,造就了以多 样性为特征、多元化思想共存的西方教育理念。 “多样性”在西方教育制度方面得到了充分体现。西方学校的教学氛围自然灵活,较少形 式主义, 教师的教和学生的学都没有太多必须遵守的强制规范和统一要求, 在教与学的设计、 内容和方式上具有较大的自由度和灵活性。 学生在这种氛围下会感到轻松与自由, 有助于激 发学生的内在活力,发挥其学习的主观能动性。 2、中国教育重持久稳定 西方教育重变革创新 中国几千年的农耕社会生产方式为人们提供的时空关系是固定、 静态的。 在这样的社会 环境中,很容易滋生永恒意识,认为世界是悠久的、静止的。 中国文化“求久”、“拒变”的特性压制了国人的独立性和创造性。反映在教育上,就是经 世济用的教育观和学术价值观。 中西方教育在对待基础知识和教育改革的态度上表现出极大 差异。中国教育特别强调基础知识的重要性。强调基础知识本身并没有错,然而基础知识并 不是僵化的、凝固不变的。与飞速发展变化的世界极不相称的却是我国停滞不前、呆板得令 人窒息的教育现状。 课程设置多年来一成不变, 教材内容十几年大同小异„„这使得使得中 国教育保守有余而创新不足。 西方个体文化鼓励独特、有创见,激励和促进个人创造力和潜能的发挥。西方人看中独 辟蹊径、标新立异,喜欢新奇且富于创新和冒险精神,随时都会弃旧图新。 这种喜变、 求变、 善变的文化心理,使西方人拥有了那种独立创新的科学精神,推动西方教育不断改革、不断 向前。 3、中国教育重权威 西方教育重平等 以儒家思想为核心的中国传统文化,历来主张尊卑有别,长幼有序。儒家伦理对中国人 的社会行为有着相当深远的影响, 并构成人们判断是非的标准。 传统文化中这种较强的等级 观念也充分体现在中国的教育思想上。中国教育传统历来提倡“师道尊严”。教师被认为是传 道、授业、解惑者,被塑造成学生顶礼膜拜、不可平视的对象。中国教育思想中的等级、权 威观念, 使中国教育必然携带着强制和暴力的色彩。 主要是指以一元化的真理观和价值观为 基础的知识专制和文化霸权。说一不二,不容置疑,这对学生来说是一种灵魂上的蹂躏。学 生的批判性和独特性、自尊心和自制力逐渐被销蚀,他们变得卑微、 盲从、 胆怯,缺乏冒险、 开拓和创新意识。 与中国文化相比, 西方文化的一个显著特征是人人平等的价值取向。 平等是西方人权观 念的一个重要组成部分。西方人坚信,每个人都是天生独立、自由和平等的。人生而平等的 观念渗透到西方社会的各个领域,现实生活中的各种关系无不受平等观念的制约。 追求平等的文化心理折射在教育上,西方教育理念认为师生平等,强调建立“平等、民 主、对话”的师生关系,教师在教育过程中扮演学生的向导和平等交往的伙伴的角色。西方 教育观念认为,教育的目标是充分开发学生的潜质,提高其内在素质,培养具有个性和独创 性的人才。西方学生从来不会屈就教师的权威而放弃对真理的追求,他们比较敢想、敢说、 敢问、敢做,敢于向权威发起挑战,具有强烈的创新意识和批判精神。 前文对两种不同教育思想的主要特征进行了比较。 通过比较, 我们不难发现双方教育观 念的巨大差异和中国教育所存在的弊端。然而,中西方教育思想不能简单地说孰是孰非,它 们各有特色、各有短长,在许多方面有着较强的互补性。因此,我们应该站在自我超越的立 场上,反观中国传统 教育的弊端,学习和借鉴西方教育的精华,转变教育思想和教育观念, 深入进行教育改革, 更快地适应世界教育发展的潮流, 培养出更多符合我国现代化建设需要 的栋梁之才。 2.教育学的研究任务是什么? 以往常常将教育学研究任务规定为通过研究教育现象揭示教育规律,这种理解突出了对教育规律的认识和遵循,忽视了对教育目的的认识和追求。因为教育规律不是为人服务而是为人选择,但人们选择什么教育规律和怎样选择教育规律,都与教育目的紧密相关。所以教育学不仅要认识教育规律,更要认识教育目的。对教育目的认识的困难在于,在规律层面认识到教育是培养人的活动并非表明就有了明确的教育目的。教育的根本问题是培养什么人和怎样培养人的问题,人是什么,教育就培养什么样的人,人怎样形成,教育就怎样培养人。建构合理性的教育学理论首先要研究人是什么,教育培养什么样的人,然后是研究教育应该怎样培养人,怎样发展和进行。教育发展本身就是合规律与合目的的统一,教育学研究就是要探求这种合理性的历史轨迹、现实需要和未来追求。这构成了教育学研究任务的合理性 四、论述 1.学习化社会的教育本质观。
答:理解和把握学习化社会的教育本质,首先需要通过更新理解教育本质的思维方式形成对教育本质本身
的新认识,然后在此基础上,以教育和学习的内在关联为出发点,探求教育本质的复杂意蕴。
(一)对教育本质本身的新认识 合理区分教育本质与教育本体并着力研究二者的关系形成了对教育本质本身的新认识。教育本体是教育本质的本质,是古今中外教育的必然、内在、普遍和稳定的联系,是不变、永恒和纯客观的;教育本质是教育现象的本质,其形成是教育主体确认自我价值和选择教育规律的过程和结果,是抽象和设想的过程和结果,是主客观的统一,不存在永恒不变的教育本质。教育本质以教育本体为基础,作为教育实践的教学成人是教育的本体,它作为教育本质生成的终极根据和终极目标是抽象的、不变的、绝对的,教育的本质是在教育本体的基础上变化的,是教育本体的展开、丰富、现实化和具体化。
教育本体与教育本质既一分为二又合二为一的观点,是合理的看待本质主义与反本质主义长期争论并力图打破二者对立怪圈的一种可行的思路,也是马克思主义唯物辩证法思想的必然要求。因为其实,“无论是本质主义还是反本质主义,都没有看到„„绝对本质和相对本质之间的必然、普遍、内在和稳定的联系,„„本质从绝对向相对变化的规律。然而,这恰恰是本质主义与反本质主义形成的根本原因和解决本质主义以一般代替特殊和反本质主义以偏概全矛盾的关键„„”
(二)教育首先是一种学习 教育与学习具有内在联系,学习是教育的基础,教育是学习的规范和效率的提高。学习和教育是人的生产、生活的必要条件和普遍现象。具有教育意义的学习是“凭借经验产生的、按教育目标进行的比较持久的行为变化。”人有学习的巨大潜能和持续不断的需要,通过学习掌握知识和方法、提升能力、形成合理的情感、态度和价值观,从而使自身发展成为真正的人,因而学习是成人之本。教育的根源在于学习,学习未必就是教育,但没有学习就不可能有教育,教育必定是一种学习。学习效率和水平、层次的提高离不开教育,但不论从教育的直接目的还是就教育教学过程说,教育都是为了学习者的学习,教育的目的是学习,指向学习层次的提升。
教育和学习的内在联系在联合国教科文组织的一系列文献中有明确体现,《教育——财富蕴藏其中》一书把学会认知、学会做事、学会共同生活(包括学会做人)、学会生存作为教育的四大支柱,并指出终身学习和教育是迈向21世纪的钥匙。世界全民教育大会把全民教育的目标规定为,“每一个人——儿童、青年和成人——都能获得旨在满足其基本学习需要的受教育机会。”《学会生存》指出:既然教育对社会有如此重要的地位
