中职数学基础模块上册《实数指数幂及其运算法则》课件 (一)
合集下载
实数指数幂及其运算ppt1 人教课标版
3 3
5
③（ 2） 2 8
5 3 5
④
2
⑤ （ 3 ） | 3| 3
4 4
(a ) a a
1 3 3
1 3 3
(a ) a a
2 3
2 3 3
2 3 3
2
a 3 a
1 3
a a
3
分数指数幂
2
分数指数幂
a a(a0 )
n
1 n
a
n
1 n a
a ( a) a
读一本好书，就是和许多高尚的人谈话。 ---歌德 书籍是人类知识的总结。书籍是全世界的营养品。 ---莎士比亚 书籍是巨大的力量。 ---列宁 好的书籍是最贵重的珍宝。 ---别林斯基 任何时候我也不会满足，越是多读书，就越是深刻地感到不满足，越感到自己知识贫乏。 ---马克思 书籍便是这种改造灵魂的工具。人类所需要的，是富有启发性的养料。而阅读，则正是这种养料。 ---雨果 喜欢读书，就等于把生活中寂寞的辰光换成巨大享受的时刻。 ---孟德斯鸠 如果我阅读得和别人一样多，我就知道得和别人一样少。 ---霍伯斯[英国作家] 读书有三种方法：一种是读而不懂，另一种是既读也懂，还有一种是读而懂得书上所没有的东西。 ---克尼雅日宁[俄国剧作家・诗人] 要学会读书，必须首先读的非常慢，直到最后值得你精读的一本书，还是应该很慢地读。 ---法奇(法国科学家) 了解一页书，胜于匆促地阅读一卷书。 ---麦考利[英国作家] 读书而不回想，犹如食物而不消化。 ---伯克[美国想思家] 读书而不能运用，则所读书等于废纸。 ---华盛顿(美国政治家) 书籍使一些人博学多识，但也使一些食而不化的人疯疯颠颠。 ---彼特拉克[意大利诗人] 生活在我们这个世界里，不读书就完全不可能了解人。 ---高尔基 读书越多，越感到腹中空虚。 ---雪莱(英国诗人) 读书是我唯一的娱乐。我不把时间浪费于酒店、赌博或任何一种恶劣的游戏；而我对于事业的勤劳，仍是按照必要，不倦不厌。 ---富兰克林 书读的越多而不加思索，你就会觉得你知道得很多；但当你读书而思考越多的时候，你就会清楚地看到你知道得很少。 ---伏尔泰(法国哲学家、文学家) 读书破万卷，下笔如有神。---杜甫 读万卷书，行万里路。 ---顾炎武 读书之法无他，惟是笃志虚心，反复详玩，为有功耳。 ---朱熹 读书无嗜好，就能尽其多。不先泛览群书，则会无所适从或失之偏好，广然后深，博然后专。 ---鲁迅 读书之法，在循序渐进，熟读而精思。 ---朱煮 读书务在循序渐进；一书已熟，方读一书，勿得卤莽躐等，虽多无益。 ---胡居仁[明] 读书是学习，摘抄是整理，写作是创造。 ---吴晗 看书不能信仰而无思考，要大胆地提出问题，勤于摘录资料，分析资料，找出其中的相互关系，是做学问的一种方法。---顾颉刚 书犹药也，善读之可以医愚。 ---刘向 读书破万卷，胸中无适主，便如暴富儿，颇为用钱苦。 ---郑板桥 知古不知今，谓之落沉。知今不知古，谓之盲瞽。 ---王充 举一纲而万目张，解一卷而众篇明。 ---郑玄
5
③（ 2） 2 8
5 3 5
④
2
⑤ （ 3 ） | 3| 3
4 4
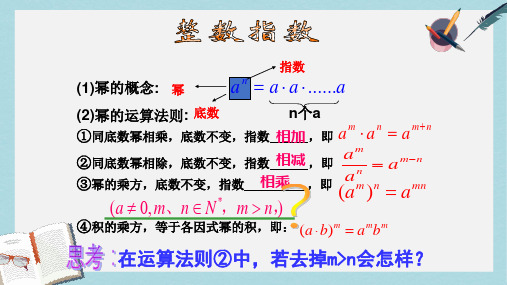
(a ) a a
1 3 3
1 3 3
(a ) a a
2 3
2 3 3
2 3 3
2
a 3 a
1 3
a a
3
分数指数幂
2
分数指数幂
a a(a0 )
n
1 n
a
n
1 n a
a ( a) a
读一本好书，就是和许多高尚的人谈话。 ---歌德 书籍是人类知识的总结。书籍是全世界的营养品。 ---莎士比亚 书籍是巨大的力量。 ---列宁 好的书籍是最贵重的珍宝。 ---别林斯基 任何时候我也不会满足，越是多读书，就越是深刻地感到不满足，越感到自己知识贫乏。 ---马克思 书籍便是这种改造灵魂的工具。人类所需要的，是富有启发性的养料。而阅读，则正是这种养料。 ---雨果 喜欢读书，就等于把生活中寂寞的辰光换成巨大享受的时刻。 ---孟德斯鸠 如果我阅读得和别人一样多，我就知道得和别人一样少。 ---霍伯斯[英国作家] 读书有三种方法：一种是读而不懂，另一种是既读也懂，还有一种是读而懂得书上所没有的东西。 ---克尼雅日宁[俄国剧作家・诗人] 要学会读书，必须首先读的非常慢，直到最后值得你精读的一本书，还是应该很慢地读。 ---法奇(法国科学家) 了解一页书，胜于匆促地阅读一卷书。 ---麦考利[英国作家] 读书而不回想，犹如食物而不消化。 ---伯克[美国想思家] 读书而不能运用，则所读书等于废纸。 ---华盛顿(美国政治家) 书籍使一些人博学多识，但也使一些食而不化的人疯疯颠颠。 ---彼特拉克[意大利诗人] 生活在我们这个世界里，不读书就完全不可能了解人。 ---高尔基 读书越多，越感到腹中空虚。 ---雪莱(英国诗人) 读书是我唯一的娱乐。我不把时间浪费于酒店、赌博或任何一种恶劣的游戏；而我对于事业的勤劳，仍是按照必要，不倦不厌。 ---富兰克林 书读的越多而不加思索，你就会觉得你知道得很多；但当你读书而思考越多的时候，你就会清楚地看到你知道得很少。 ---伏尔泰(法国哲学家、文学家) 读书破万卷，下笔如有神。---杜甫 读万卷书，行万里路。 ---顾炎武 读书之法无他，惟是笃志虚心，反复详玩，为有功耳。 ---朱熹 读书无嗜好，就能尽其多。不先泛览群书，则会无所适从或失之偏好，广然后深，博然后专。 ---鲁迅 读书之法，在循序渐进，熟读而精思。 ---朱煮 读书务在循序渐进；一书已熟，方读一书，勿得卤莽躐等，虽多无益。 ---胡居仁[明] 读书是学习，摘抄是整理，写作是创造。 ---吴晗 看书不能信仰而无思考，要大胆地提出问题，勤于摘录资料，分析资料，找出其中的相互关系，是做学问的一种方法。---顾颉刚 书犹药也，善读之可以医愚。 ---刘向 读书破万卷，胸中无适主，便如暴富儿，颇为用钱苦。 ---郑板桥 知古不知今，谓之落沉。知今不知古，谓之盲瞽。 ---王充 举一纲而万目张，解一卷而众篇明。 ---郑玄
最新中职数学基础模块上册《实数指数幂及其运算法则》ppt课件3精品文档
21
小结：①分数指数幂的意义及运算性质
②指数概念的扩充，引入分数指数幂概念后，
指数概念就实现了由整数指数幂向有理数指数 幂的扩充 ．
而且有理指数幂的运算性质对于无理指数幂也适 用，这样指数概念就扩充到了整个实数范围。
③对于指数幂 a n ,当指数n扩大至有理数时，
要注意底数a的变化范围。如当n=0时底数a≠0； 当n为负整数指数时，底数a≠0；当n为分数时， 底数a>0。
8
有理数指数幂
10
复习：（口算）5 a10 5 (a2)5 a2 a 5
1）5 32 2）4 81 3） 210
12
3 a12 3 (a4)3 a4 a 3
2
2
3 a2 3 (a 3 )3 a 3
4）3 312
1
1
a (a 2 )2 a 2
n
am
m
m
n(an)nan(m ,nN*且 ,n1)
1、计算下列各式：
1 1 3
(1)a2a4a 8
(2)(x
1 2
1
y3
)6
(3)(
8a3
1
)3
27b6
(4)2x13(1x13
2
2x 3)
2
19
3 、下列正确的是（）
1
A 、 x ( x ) 2 ( x 0 )
B、
1
x3
3
x
C
、(
x
)
3 4
4
( y )3(x, y
0)
y
x
1
D 、6 y 2 y 3 ( y 0 )
6
三、负整数指数幂
a－n ＝
1 an
（a ≠ 0，n N＋ )
小结：①分数指数幂的意义及运算性质
②指数概念的扩充，引入分数指数幂概念后，
指数概念就实现了由整数指数幂向有理数指数 幂的扩充 ．
而且有理指数幂的运算性质对于无理指数幂也适 用，这样指数概念就扩充到了整个实数范围。
③对于指数幂 a n ,当指数n扩大至有理数时，
要注意底数a的变化范围。如当n=0时底数a≠0； 当n为负整数指数时，底数a≠0；当n为分数时， 底数a>0。
8
有理数指数幂
10
复习：（口算）5 a10 5 (a2)5 a2 a 5
1）5 32 2）4 81 3） 210
12
3 a12 3 (a4)3 a4 a 3
2
2
3 a2 3 (a 3 )3 a 3
4）3 312
1
1
a (a 2 )2 a 2
n
am
m
m
n(an)nan(m ,nN*且 ,n1)
1、计算下列各式：
1 1 3
(1)a2a4a 8
(2)(x
1 2
1
y3
)6
(3)(
8a3
1
)3
27b6
(4)2x13(1x13
2
2x 3)
2
19
3 、下列正确的是（）
1
A 、 x ( x ) 2 ( x 0 )
B、
1
x3
3
x
C
、(
x
)
3 4
4
( y )3(x, y
0)
y
x
1
D 、6 y 2 y 3 ( y 0 )
6
三、负整数指数幂
a－n ＝
1 an
（a ≠ 0，n N＋ )
高一上学期劳保版(第七版)中职数学(上册)《指数函数》PPT课件
ar as ars (a 0, r, s Q) (ar )s ars (a 0, r, s Q)
(ab)r arbr (a 0, b 0, r Q)
有理数指数幂
例题
例1 用分数指数幂形式表示下列各式(式中 a 0 )：
(1)a2· a；
(2)a3·3 a2；
(3) a a；
解：（1）
例1 指出下列函数哪些是指数函数：
（1）y＝4×3x；
（2） y＝x ；
（3）y＝（－0.3)x； （4） y＝x3.
感谢同学们观看学习， 再见！
任意角的概念 课前导入
思考 当根式的被开方数的指数不能被根指数整 除时，根式是否可以写成分数指数幂的形式？
2
如： 3 a2 a 3 是否可行？
有理数指数幂 定义
一般地，分数指数幂定义：
m
(1)规定正数的正分数指数幂的意义是：a n
＝n am (a>0，m，n∈N*，且n>1)；
1
(2)规定正数的负分数指数幂的意义是：a
问题二 庄子曰：一尺之棰，日取其半，万世不竭。
第1次后
一
第2次后
尺
之
木
第3次后
y (1)x 2
日 取
第4次后
第x次后
其
半
剩余长度y 1 2
(1)2 2
(1)3 2
(1)4 2
…...
(1)x 2
指数函数的概念 课前导入
从前面我们的两个实例抽象得到的两个式子：
y
2x
与y
1 2
x
（1）均为幂的形式 （2）底数是一个正的常数
m n
＝
m
a n (a>0，m，n∈N*，且n>1)；
(ab)r arbr (a 0, b 0, r Q)
有理数指数幂
例题
例1 用分数指数幂形式表示下列各式(式中 a 0 )：
(1)a2· a；
(2)a3·3 a2；
(3) a a；
解：（1）
例1 指出下列函数哪些是指数函数：
（1）y＝4×3x；
（2） y＝x ；
（3）y＝（－0.3)x； （4） y＝x3.
感谢同学们观看学习， 再见！
任意角的概念 课前导入
思考 当根式的被开方数的指数不能被根指数整 除时，根式是否可以写成分数指数幂的形式？
2
如： 3 a2 a 3 是否可行？
有理数指数幂 定义
一般地，分数指数幂定义：
m
(1)规定正数的正分数指数幂的意义是：a n
＝n am (a>0，m，n∈N*，且n>1)；
1
(2)规定正数的负分数指数幂的意义是：a
问题二 庄子曰：一尺之棰，日取其半，万世不竭。
第1次后
一
第2次后
尺
之
木
第3次后
y (1)x 2
日 取
第4次后
第x次后
其
半
剩余长度y 1 2
(1)2 2
(1)3 2
(1)4 2
…...
(1)x 2
指数函数的概念 课前导入
从前面我们的两个实例抽象得到的两个式子：
y
2x
与y
1 2
x
（1）均为幂的形式 （2）底数是一个正的常数
m n
＝
m
a n (a>0，m，n∈N*，且n>1)；
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件3
同时，大家要开动脑筋，思考老师是怎样提出问题、分析问题、解决问题的，要边听边想。为讲明一个定理，推出一个公式，老师讲解顺序是怎样的， 为什么这么安排？两个例题之间又有什么相同点和不同之处？特别要从中学习理科思维的方法，如观察、比较、分析、综合、归纳、演绎等。 • 作为实验科学的物理、化学和生物，就要特别重视实验和观察，并在获得感性知识的基础上，进一步通过思考来掌握科学的概念和规律，等等。 • 二、听文科课要注重在理解中记忆 • 文科多以记忆为主，比如政治，要注意哪些是观点，哪些是事例，哪些是用观点解释社会现象。听历史课时，首先要弄清楚本节教材的主要观点，然 后，弄清教材为了说明这一观点引用了哪些史实，这些史料涉及的时间、地点、人物、事件。最后，也是关键的一环，看你是否真正弄懂观点与史料间 的关系。最好还能进一步思索：这些史料能不能充分说明观点？是否还可以补充新的史料？有无相反的史料证明原观点不正确。 • 三、听英语课要注重实践 • 英语课老师往往讲得不太多，在大部分的时间里，进行的师生之间、学生之间的大量语言实践练习。因此，要上好英语课，就应积极参加语言实践活 动，珍惜课堂上的每一个练习机会。
一般地，当m，n Î
N
且n>1时，规定：
+
m
an
=
n
am ( a
?
0)
-m n
=
1
a >0
a a ( ) n
m
二、实数指数幂及其运算法则
1、求出下列各式的值
18
(1)、 33.33
1
7
(2)、2 2.2 2
(3)、a
1
3.a
8 3
二、实数指数幂及其运算法则
(1) ar.as = a (r+s a > 0, r, s ? Q)
一般地，当m，n Î
N
且n>1时，规定：
+
m
an
=
n
am ( a
?
0)
-m n
=
1
a >0
a a ( ) n
m
二、实数指数幂及其运算法则
1、求出下列各式的值
18
(1)、 33.33
1
7
(2)、2 2.2 2
(3)、a
1
3.a
8 3
二、实数指数幂及其运算法则
(1) ar.as = a (r+s a > 0, r, s ? Q)
实数指数幂及其运算完整版
实数指数幂及其运算
精选ppt
1
复习引入
1 初中学习的正整数指数
2 正整数指数幂的运算法则
（1）amanamn (2) (am)n amn (3) aamn amn(mn,a0) (4) (ab)mambm
精选ppt
2
思考讨论
规定： a0 1(a0)
ana1n(a0,nN)
精选ppt
3
分数指数
❖ 1.回顾初中学习的平方根，立方根的概念
1 1 3
(1)a2a4a 8
1
(2)(x2
1
y3
)6
8a3
(3)( 2
7b6
1
)3
(4)2x13(1x13
2
2x 3)
2
精选ppt
17
3 、下列正确的是（）
1
A 、 x ( x ) 2 ( x 0 )
B、
1
x3
3
x
C
、(
x
)
3
4
4
( y )3(x, y
0)
y
x
1
D 、6 y 2 y 3 ( y 0 )
（ 16） － 3 4＝ （ 2） 4 （ － 3 4） ＝ （ 2） － 3＝ 27。
81
3 精选ppt
38
12
练习:求值：
912，6432
,
(
1
1
)5
32
精选ppt
13
例3：用分数指数幂的形式表示下列各式：
a2 a,a 33a2, aa(式 中 a0 )
分析：此题应结合分数指数幂意义与有理指数幂运算性质。
⑴ ar·as=ar+s (a>0,r,s∈Q)；
精选ppt
1
复习引入
1 初中学习的正整数指数
2 正整数指数幂的运算法则
（1）amanamn (2) (am)n amn (3) aamn amn(mn,a0) (4) (ab)mambm
精选ppt
2
思考讨论
规定： a0 1(a0)
ana1n(a0,nN)
精选ppt
3
分数指数
❖ 1.回顾初中学习的平方根，立方根的概念
1 1 3
(1)a2a4a 8
1
(2)(x2
1
y3
)6
8a3
(3)( 2
7b6
1
)3
(4)2x13(1x13
2
2x 3)
2
精选ppt
17
3 、下列正确的是（）
1
A 、 x ( x ) 2 ( x 0 )
B、
1
x3
3
x
C
、(
x
)
3
4
4
( y )3(x, y
0)
y
x
1
D 、6 y 2 y 3 ( y 0 )
（ 16） － 3 4＝ （ 2） 4 （ － 3 4） ＝ （ 2） － 3＝ 27。
81
3 精选ppt
38
12
练习:求值：
912，6432
,
(
1
1
)5
32
精选ppt
13
例3：用分数指数幂的形式表示下列各式：
a2 a,a 33a2, aa(式 中 a0 )
分析：此题应结合分数指数幂意义与有理指数幂运算性质。
⑴ ar·as=ar+s (a>0,r,s∈Q)；
语文版中职数学基础模块上册4.2《实数指数幂及其运算法则》ppt课件4
【1】下列各式中, 不正确的序号是( ① ④ ).
① 4 16 2 ② ( 5 3)5 3 ③ 5 (3)5 3 ④ 5 (3)10 3 ⑤ 4 (3)4 3
【2】求下列各式的值.
⑴ 5 32;
⑵ （ 3）4 ;
⑶ （ 2 3）2 ; ⑷ 5 2 6 .
分数指数幂在底数小于0时无意义.
⒉负分数指数幂的意义
注回意忆：负整负数分指数数指幂数的幂意在义：有意义的情况下，
总在指表数示上正.数a－，n=而a1不n (是a≠负0,n数∈,N负*)号. 只是出现
正数的负分数指数幂的意义和正数的负整
数指数幂的意义相仿，就是：
m
an
1
m
an
1 (a>0,m,n∈N*,且n>1). n am
64的6次方根是2，-2.
记作： 6 64 2.
1.正数的偶次方根有两个且互为相反数
偶次方根 2.负数的偶次方根没有意义
正数a的n次方根用符号 n a 表示(n为偶数）
(1) 奇次方根有以下性质： 正数的奇次方根是正数. 负数的奇次方根是负数. 零的奇次方根是零.
(2)偶次方根有以下性质：
r4
0.0001 104
a2 b2c
a 2b 2c 1
回顾初中知识,根式是如何定义的？有
那些规定？
①如果一个数的平方等于a,则这个数叫做 a
的平方根.
22=4 (-2)2=4
2,-2叫4的平方根.
②如果一个数的立方等于a,则这个数叫做a
的立方根.
23=8
2叫8的立方根.
(-2)3=-8
-2叫-8的立方根.
例2．如果 2x2 5x 2 0, 化简代
实数指数幂及其运算 PPT课件 1 人教课标版
1 4 6 r x 6 1 x r4
0 .0001 10 4
a 2 2 1 a b c 2 b c
2
2 分数指数
2
若 x a ，则 x叫 a 的平方根（或二次方根 ）
a 0 时，两个平方根： a， a a 0时，有一个平方根： 0 a 0时，无实根
3
若 x a ，则 x叫 a 的立方根（或三次方根 ）
a 根式
n 根指数
n
正 数 a 的 正 n 次 方 根 叫 做 a 的 n 次 算 术 方 根
根式性质
( 1 )( a ) a ( n 1 , n N )
n n
a
(2) a
n n
当n为奇数时
|a |
当n为偶数时
练习1
①( 5)
4 4
5
3
②（ 5 ）
a 只有一个立方根
方根
n 若 存 在 实 数 x ， 使（ x = a aR ? ，， n1 n ? N ） ， +
则 xan 叫 的 次 方 根 。
求a 的 n 次方根，叫做把 a 开 n 次方 ,称作开方运算
偶次方根 奇次方根
n
实 a 0 n a 数 a a 0 不存在
n
a 0 a 0
（ 3 ）（ ab ） a b
转
练习2
① 8 8 ② 8
2 3
3 5
2 5
1 3 2
8
3 2 5 5
8
（ 8） 2 4
2
③ 3 3
2 3
3
3
6
3
2 33
3 3 3 3 3
实数指数幂及其运算课件
实数指数幂的运算示例
示例1
通过实际计算示范，加深对实数 指数幂运算的理解。
示例2
解答含有实数指数幂的方程，锻 炼解题技巧和思维能力。
示例3
利用数据图表展示实数指数幂的 应用场景，如经济增长和人口变 化。
对数的引入与基本性质
1
对数的定义
引入对数的概念和基本定义，与实数指数幂相互对应。
2
对数的性质
讲解对数的一些基本性质，如底数为1和对数为0的特殊情况。
实数指数幂及其运算课件
本课件将详细介绍实数指数幂及其运算的重要性和应用价值，通过生动的示 例和动人的图像，让你轻松理解这一概念。
实数指数幂的基本性质
定义
引入实数指数幂的概念和基 本定义。
性质
讲解实数指数幂的一些基本 性质，如指数为0和1时的特 殊情况。
运算法则
介绍实数指数幂的运算法则， 包括幂的乘法和除法法则。
3
对数的计算法则
介绍对数的运算法则，包括对数的乘法和除法法则。
对数与指数幂的关系
互为反函数
对数函数与指数幂函数之间的反 函数关系，图像形象展示。
换底公式
讲解换底公式的推导和应用，解 决不同底数的对数运算问题。
实际应用
结合实际应用领域，展示对数与 指数幂的关系。
对数函数与指数函数Байду номын сангаас图像与性质
图像特点
讲解对数函数和指数函数的 图像特点和可视化展示。
性质比较
对比对数函数和指数函数的 性质，如增长趋势和极限值。
应用场景
探索对数函数和指数函数在 物理、生物、经济等领域中 的应用。
常用对数与自然对数
常用对数
引入常用对数的定义和基本计算 法则。
实数指数幂及其运算法则
练习３：化简下列各式 (课后练习) 5x y
1 - 1 2 2 3 1 2 1 3 1 6
（1）
1 5 （ - x y ）（ - x y ） 4 6
m + m- 1 + 2 （2） 1 1 m
2
+ m2
总结：
• 1
a a
0
= 1
（a 0）
• 2 • 3
- n
1 （a 0，n N ） = n a
山阳职教中心 陈新芳
实数分类:
有理数 整数 分数
正整数 0 负整数
实 数 无理数
在初中学过整数指数幂概念及运算，这节我们将其推广 到实数指数幂及运算。
1 整数指数幂
正整数指数幂:
a2 a a
指数
n
a3 a a a
规定： a
１
幂
a a a ......a
底数
＝a
n个
1 2
1 2
1 2
1 2
1 2 2
1 2 2
⑥（a b ） a b 2a b
1 2
1 2 2
1 2
1 2
无理数指数幂
例： 3 2 是一个什么样的数？
用 1.4 ， 1.41 ， 1.414 ，（ ..... 2的不足近似值）；
3 ， 3 ， 3
和
1.5 1.42
1.4
1.41
1.414
将正整数指数幂推广到整数指数幂
规定： a 0 1 （a 0） 1 n a n （a 0，n N ） a
• 运算法则(m,n∈z) (1) am·an=am+n (2) (am)n=amn
中职数学4.1.2实数指数幂及其运算法则
（2）有理数、实数指数幂的运算法则
a>0 ,P、q为实数时：
课后反思
4、知识巩固：
例4 计算下列各式：
多媒体放映解题过程
例5 化简下列各式：
师生一起探讨，再多媒体放映解题过程
计算：（学生上台做）
， ， ，
归纳小结：
引导学生回顾本节课所学的知识：
（1）有理数、实数指数幂的概念
（2）有理数、实数指数幂的运算法则
布置作业：73-74页1、2题
板
书
设
计
（1）有理数、实数指数幂的概念
整数指数幂的运算法则有：
新课：
1、有理数指数幂的定义：
分数指数幂的意义
规定：
0的正分数指数幂等于0，0的负分数指数幂没有意义。
规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂
2、有理数指数幂的运算法则
将以上整数指数幂的运算法则运用到有理数指数幂也适用：
课
题
实数指数幂及其运算法则
教
学
目
的
① 理解有理指数幂的含义，能运用有理指数幂的运算性质进行运算和化简，会进行根式与分数指数幂的相互转化；
②了解实数指数幂的意义,体会有理指数幂向无理指数幂逼近的过程.
重
点
难
点
实数指数幂的运算性质，实数指数幂的运算性质综合应用与综合运算
学
时
2
教具Βιβλιοθήκη 多媒体教学
过
程
教
学
过
程
复习：
即当a>0，p、q为有理数时有：
运用法则的条件是，出现的每个有理数指数幂有意义。
实数指数幂及其运算法则：
a>0 ,P、q为实数时：
课后反思
4、知识巩固：
例4 计算下列各式：
多媒体放映解题过程
例5 化简下列各式：
师生一起探讨，再多媒体放映解题过程
计算：（学生上台做）
， ， ，
归纳小结：
引导学生回顾本节课所学的知识：
（1）有理数、实数指数幂的概念
（2）有理数、实数指数幂的运算法则
布置作业：73-74页1、2题
板
书
设
计
（1）有理数、实数指数幂的概念
整数指数幂的运算法则有：
新课：
1、有理数指数幂的定义：
分数指数幂的意义
规定：
0的正分数指数幂等于0，0的负分数指数幂没有意义。
规定了分数指数幂的意义后，指数的概念就从整数指数推广到了有理数指数，那么整数指数幂的运算性质也同样可以推广到有理数指数幂
2、有理数指数幂的运算法则
将以上整数指数幂的运算法则运用到有理数指数幂也适用：
课
题
实数指数幂及其运算法则
教
学
目
的
① 理解有理指数幂的含义，能运用有理指数幂的运算性质进行运算和化简，会进行根式与分数指数幂的相互转化；
②了解实数指数幂的意义,体会有理指数幂向无理指数幂逼近的过程.
重
点
难
点
实数指数幂的运算性质，实数指数幂的运算性质综合应用与综合运算
学
时
2
教具Βιβλιοθήκη 多媒体教学
过
程
教
学
过
程
复习：
即当a>0，p、q为有理数时有：
运用法则的条件是，出现的每个有理数指数幂有意义。
实数指数幂及其运算法则：
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
中职数学基础模块上册《实数指数幂及其运
算法则》课件 (一)
中职数学基础模块上册《实数指数幂及其运算法则》课件是数学学习过程必不可少的教育资源，本文将从以下几个方面对这一课件进行探讨。
一、课件简介
《实数指数幂及其运算法则》是中职数学基础模块上册的一个重要课程，主要介绍了实数指数幂的概念、性质和运算法则等内容。
而课件则是一种多媒体教育资源，通过PPT、图片、视频等形式，生动直观地向学生展示课程内容，帮助学生更好地理解和掌握知识点。
二、课件特点
1.重点突出：课件针对实数指数幂的重要性，将其作为重点内容进行讲解，对于常规知识点和易混淆点也有特别的突出。
2.图文并茂：课件采用大量图片、图表、公式等形式，生动直观地展示知识点，能够帮助学生对内容有更加深入的理解。
3.多元化表现：课件应用了视频、音频等多媒体资料，进行思维导图和演示，有很好的视觉和听觉效果，对于记忆理解和知识拓展有着显著的效果。
三、课件分析
《实数指数幂及其运算法则》课件分为以下几个部分：
1.引言：介绍实数指数幂的概念和特点，为后面的内容做好铺垫。
2.基础知识：讲解实数指数幂的基本定义、性质及其重要的运算法则。
3.练习题：通过练习题来检验学生对课程内容的理解和掌握情况，帮
助学生加深对重要知识点的记忆和理解。
4.案例分析：通过实际案例的分析，向学生演示实数指数幂在实际问
题中的应用场景，拓展学生的思维和知识领域。
四、课件应用
《实数指数幂及其运算法则》课件能够提供丰富多样化的视听体验，
使学生对实数指数幂这一内容更加深入地认识和理解。
同时，教师可
以通过课件中的思维导图和案例分析等内容，培养学生的思维反应能
力和创造性思维能力，提升教学效果和质量。
总之，中职数学基础模块上册《实数指数幂及其运算法则》课件的设
计合理、内容丰富、形式多样，极大地提升了教学效果，为学生打下
更坚实的数学基础。