《5.3应用二元一次方程组----鸡兔同笼》练习题
北师大版八年级上册数学 9.同步练习5.3 应用二元一次方程组——鸡兔同笼

5.3 应用二元一次方程组——鸡兔同笼 一、填空题 1.已知甲库存粮x吨,乙库存粮y吨.若从甲库调出10吨给乙库,乙库的存粮数是甲库存粮数的2倍,则以上用等式表示为_______. 2.兄弟两人,弟弟五年后的年龄与哥哥五年前的年龄相等,3年后兄弟两人的年龄和是他们年龄之差的3倍,则兄弟两人今年的岁数分别是________. 3.两抵相距300千米,一艘船航行与两地之间.若顺流需15时,逆流需用20时,则船在静水中速度和水流速度分别是_______. 4.现有面值总和为570元的人民币50元和20元的共15张,问其中50元人民币和20元人民币分别有_____张.
二、选择题 5.一张试卷有25道题,做对一题得4分,做错一题扣1分,小明做了全部试题得70分,则他做对的题数是( ). (A)16 (B)17 (C)18 (D)19 6.某校150名学生参加数学考试,平均分55分,其中及格学生平均77分,不及格学生平均47分,则不及格的学生人数为( ) . (A)49 (B)101 (C)110 (D)40
三、解答题 7.某校办工厂有工人60名,生产某种由一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?
8.六一儿童节,某动物园的成人门票8元,儿童门票半价(即每张4元),全天共售出门票3000张,共收入15600元,问这天售出成人票和儿童票多少张?
四、 探究升级 9.100元钱买15张邮票,其中有4元、8元、10元的三种,有几种买的方法?
答案:1.).10(210xy 2.17岁和7岁. 3.17.5千米/时, 2.5千米/时. 4.9张和6张. 5.D. 6.C. 7.25个和35个. 8.900张和2100张. 9.有三种:4元、8元、10元的邮票分别为6张、7张、2张,或7张、4张、4张 ,或8张、1张、6张.
北师大版数学八年级上册5.3应用二元一次方程组——鸡兔同笼练习题

5.3 应用二元一次方程组——鸡兔同笼【课堂练习】1.中国古代第一部数学专著《九章算术》中记载了一个问题,大意是:有几个人一起去买一件物品,每人出8元,多3元;每人出7元,少4元,问有多少人?该物品价几何?设有x 人,物品价值y 元,则所列方程组正确的是( )A.⎩⎪⎨⎪⎧8y +3=x ,7y -4=xB.⎩⎪⎨⎪⎧8x +3=y ,7x -4=yC.⎩⎪⎨⎪⎧8x -3=y ,7x +4=yD.⎩⎪⎨⎪⎧8y -3=x ,7y +4=x2.某年级共有学生246人,其中男生人数y 比女生人数x 的2倍多2人,则下面所列的方程组中符合题意的是( )A.⎩⎪⎨⎪⎧x +y =246,2y =x -2B.⎩⎪⎨⎪⎧x +y =246,2x =y +2C.⎩⎪⎨⎪⎧x +y =246,y =2x +2D.⎩⎪⎨⎪⎧x +y =246,2y =x +23.有若干只鸡和兔关在一个笼子里,从上面数,有30个头;从下面数,有84条腿,问笼中鸡和兔各有几只?4.小明同学发现他奶奶今年的年龄是他年龄的5倍,12年后,他奶奶的年龄是他年龄的3倍.问小明和他奶奶今年的年龄各是多少?答案:1.C 2.C3.解:设这个笼中的鸡有x 只,兔有y 只,根据题意得⎩⎪⎨⎪⎧x +y =30,2x +4y =84,解得⎩⎪⎨⎪⎧x =18,y =12. 答:笼子里鸡有18只,兔有12只.4.解:设小明今年的年龄是x 岁,他奶奶今年的年龄是y 岁,根据题意得⎩⎪⎨⎪⎧5x =y ,3(x +12)=y +12,解得⎩⎪⎨⎪⎧x =12,y =60. 答:小明今年的年龄是12岁,他奶奶今年的年龄是60岁.【课后作业】一、填空题1.已知甲库存粮x 吨,乙库存粮y 吨.若从甲库调出10吨给乙库,乙库的存粮数是甲库存粮数的2倍,则以上用等式表示为_______.2.兄弟两人,弟弟五年后的年龄与哥哥五年前的年龄相等,3年后兄弟两人的年龄和是他们年龄之差的3倍,则兄弟两人今年的岁数分别是________.3.两抵相距300千米,一艘船航行与两地之间.若顺流需15时,逆流需用20时,则船在静水中速度和水流速度分别是_______.4.现有面值总和为570元的人民币50元和20元的共15张,问其中50元人民币和20元人民币分别有_____张.二、选择题5.一张试卷有25道题,做对一题得4分,做错一题扣1分,小明做了全部试题得70分,则他做对的题数是( ).(A)16 (B)17 (C)18 (D)196.某校150名学生参加数学考试,平均分55分,其中及格学生平均77分,不及格学生平均47分,则不及格的学生人数为( ) .(A)49 (B)101 (C)110 (D)40三、解答题7.某校办工厂有工人60名,生产某种由一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?8.六一儿童节,某动物园的成人门票8元,儿童门票半价(即每张4元),全天共售出门票3000张,共收入15600元,问这天售出成人票和儿童票多少张?四、探究升级9.100元钱买15张邮票,其中有4元、8元、10元的三种,有几种买的方法?答案:1.).+x=y 2.17岁和7岁.1010-(23.17.5千米/时, 2.5千米/时.4.9张和6张.5.D.6.C.7.25个和35个. 8.900张和2100张.9.有三种:4元、8元、10元的邮票分别为6张、7张、2张,或7张、4张、4张,或8张、1张、6张.【拓展提升】1、21枚1角与5角的硬币,共是5元3角,其中1角与5角的硬币各是多少?设1角硬币x枚,5角硬币y枚,填写下表,并求出x、y的值.2.小兰在玩具厂劳动,做4个小狗、7个小汽车用去3小时42分,做5个小狗、6个小汽车用去3小时37分.平均做一个小狗与1个小汽车各用多少时间?设做1个小狗用x分,做1个小汽车用y分,填写下表,并求出x、y的值.3.某中学某班买了35张电影票,共用250元,其中甲种票每张8元,乙种票每张6元,甲、乙两种票各买多少张?设甲、乙两种票分别买了x张、y张,填写下表,并求出x、y的值.4.有大小两种盛米的桶,已经知道5个大桶加上一个小桶可以盛3斛米,1个大桶加上5个小桶可以盛2斛米,问1个大桶、1个小桶分别可以盛多少斛米?设大桶盛米量为x 斛,小桶盛米量为y 斛,填写下表,并求出x 、y 的值.参考答案1.⎩⎨⎧=+=+53521y x y x ,解得⎩⎨⎧==813y x 填表略2.⎩⎨⎧+⨯=++⨯=+37603654260374y x y x ,解得⎩⎨⎧==2217y x 表略3.⎩⎨⎧=+=+2506835y x y x ,解得⎩⎨⎧==1520y x 表略4.⎩⎨⎧=+=+2535y x y x ,解得⎪⎪⎩⎪⎪⎨⎧==2472413y x 表略。
5.3 应用二元一次方程组——鸡兔同笼2 课时配套练习 专项练习
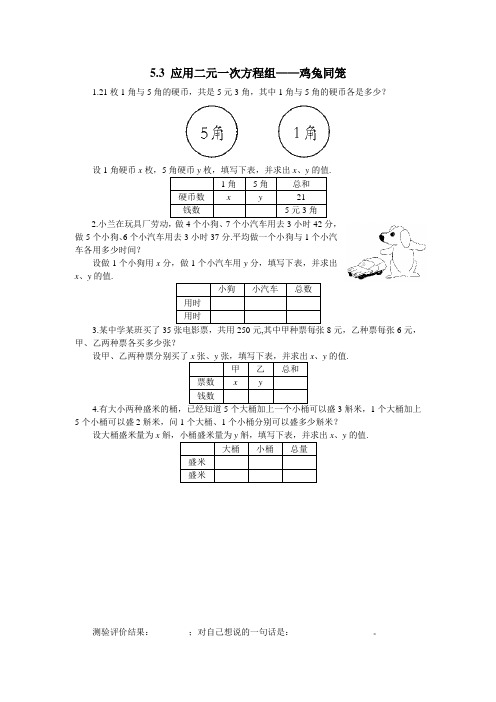
5.3 应用二元一次方程组——鸡兔同笼1.21枚1角与5角的硬币,共是5元3角,其中1角与5角的硬币各是多少?设1角硬币x枚,5角硬币y枚,填写下表,并求出x、y的值.2.小兰在玩具厂劳动,做4个小狗、7个小汽车用去3小时42分,做5个小狗、6个小汽车用去3小时37分.平均做一个小狗与1个小汽车各用多少时间?设做1个小狗用x分,做1个小汽车用y分,填写下表,并求出x、y的值.3.某中学某班买了358元,乙种票每张6元,甲、乙两种票各买多少张?x、y的值.4.有大小两种盛米的桶,已经知道5个大桶加上一个小桶可以盛3斛米,1个大桶加上5个小桶可以盛2斛米,问1个大桶、1个小桶分别可以盛多少斛米?设大桶盛米量为x斛,小桶盛米量为y斛,填写下表,并求出x、y的值.测验评价结果:________;对自己想说的一句话是:__________________。
参考答案1.⎩⎨⎧=+=+53521y x y x ,解得⎩⎨⎧==813y x 填表略2.⎩⎨⎧+⨯=++⨯=+37603654260374y x y x ,解得⎩⎨⎧==2217y x 表略3.⎩⎨⎧=+=+2506835y x y x ,解得⎩⎨⎧==1520y x 表略4.⎩⎨⎧=+=+2535y x y x ,解得⎪⎪⎩⎪⎪⎨⎧==2472413y x 表略7.5 三角形内角和定理 第1课时 三角形内角和定理1.填空:(1)如果三角形的三个内角都相等,那么每一个角的度数等于_______. (2)在△ABC 中,若∠A =65°,∠B =∠C ,则∠B =_______. (3)在△ABC 中,若∠C =90°,∠A =30°,则∠B =_______.(4)在△ABC 中,若∠A ∶∠B ∶∠C =1∶2∶3,则∠A =_______,∠B =_______,∠C =_______.(5)在下两图中,∠1、∠2与∠B 、∠C 的关系是_______(6)如图,在△ABC中,∠C=∠ABC=2∠A,BD⊥AC,垂足为D,则∠DBC的度数为_______.2.在△ABC中,∠A=50°,∠B、∠C的平分线交于O点,则∠BOC等于( ) A.65°B.115°C.80°D.50°3.两条平行线被第三条直线所截,那么一组同旁内角的平分线( )A.相互重合B.互相平行C.相互垂直D.无法确定相互关系4.如图,AB∥CD,∠A=35°,∠C=80°,那么∠E等于( )A.35°B.45°C.55°D.75°5.一块大型模板如图,设计要求BA与CD相交成30°角,DA与CB相交成20°的角,怎样通过测量∠A,∠B,∠C,∠D的度数,来检查模板是否合格?6.小芳和小白在一起温习三角形内角和定理,小芳灵机一动,想考考小白对知识掌握的程度,她给小白出了一道这样的题目:如图,证明五边形的内角和等于540°.即:∠A+∠B+∠C+∠D+∠E=540°.。
八年级数学上册 5.3 应用二元一次方程组—鸡兔同笼练

5.3 应用二元一次方程组——鸡兔同笼基础题知识点1 列二元一次方程组解应用题1.设马四匹,牛六头,共价四十八两;马三匹,牛五头,共价三十八两,则( )A .马价4两,牛价6两B .马价3两,牛价8两C .马价6两,牛价4两D .马价8两,牛价3两2.一群鹅来一群狗,鹅头狗头五十五,一百五十条腿齐步走,多少鹅来多少狗?设鹅与狗分别有x 、y 只,由题意可列方程组为________________.3.(绍兴中考)我国古代数学名著《孙子算经》中有这样一题,今有鸡兔同笼,上有35头,下有94足,问鸡兔各几何?此题的答案是:鸡有23只,兔有12只.现在小敏将此题改编为:今有鸡兔同笼,上有33头,下有88足,问鸡兔各几何?则此时的答案是:鸡有________只,兔有________只.4.在《一千零一夜》中有这样一段文字:有一群鸽子一部分在树上欢歌,一部分在地上觅食,树上一只鸽子对地上觅食的鸽子说:“若从你们中飞上来一只,则地上的鸽子就是整群的13,若从树上飞下来一只到地上,则树上和地上的鸽子就一样多了”.则树上鸽子有________只,地上鸽子有________只.5.《九章算术》方程问题:“五只雀、六只燕,共重1斤(等于16两),雀重燕轻.互换其中一只,恰好一样重.问:每只雀、燕的重量各为多少?”知识点2 列二元一次方程组解和、差、倍、分问题6.(温州中考)20位同学在植树节这天共种了52棵树苗,其中男生每人种3棵,女生每人种2棵.设男生有x 人,女生有y 人.根据题意,列方程组正确的是( )A.⎩⎪⎨⎪⎧x +y =523x +2y =20B.⎩⎪⎨⎪⎧x +y =522x +3y =20 C.⎩⎪⎨⎪⎧x +y =202x +3y =52 D.⎩⎪⎨⎪⎧x +y =203x +2y =52 7.学校的篮球比排球数的2倍少3个,篮球数与排球数的比是3∶2,求两种球各有多少个.若设篮球有x 个,排球有y 个,根据题意列方程组为( )A.⎩⎪⎨⎪⎧x =2y -33x =2yB.⎩⎪⎨⎪⎧x =2y +33x =2y C.⎩⎪⎨⎪⎧x =2y +32x =3y D.⎩⎪⎨⎪⎧x =2y -32x =3y8.小鸣的妈妈叫他到农贸市场买猪肉,到了市场后他发现妈妈给的钱,若买1千克猪肉,则少4元;若买0.5千克猪肉,则余8元.那么猪肉每千克________元,妈妈给他的钱是________元.9.为迎接中考,平时很多同学购买了2B 铅笔和涂卡尺.根据图中信息,求2B 铅笔和涂卡尺的单价.中档题10.(鞍山中考)如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的13,另一根露出水面的长度是它的15.两根铁棒长度之和为220 cm ,此时木桶中水的深度是________cm.11.阅读下面的诗句,求出诗句中的鸦与树的数量:“栖树一群鸦,鸦树不知数,三只栖一树,五只没去处,五只栖一树,闲了一棵树,请你仔细数,鸦树各几何?”12.(铜仁中考)某旅行社组织一批游客外出旅游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.已知45座客车租金为每辆220元,60座客车租金为每辆300元,问:(1)这批游客的人数是多少?原计划租用多少辆45座客车?(2)若租用同一种车,要使每位游客都有座位,应该怎样租用才合算?综合题13.某班将举行“庆祝建党95周年知识竞赛”活动,班长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:请根据上面的信息,解决问题:(1)试计算两种笔记本各买了多少本?(2)请你解释:小明为什么不可能找回68元?参考答案1.C2.⎩⎪⎨⎪⎧x +y =552x +4y =150 3.22 11 4.7 5 5.设每只雀、燕的重量各为x 两,y 两,由题意得⎩⎪⎨⎪⎧5x +6y =16,4x +y =5y +x.解得⎩⎪⎨⎪⎧x =3219,y =2419.答:每只雀、燕的重量各为3219两,2419两.6.D7.D8.24 209.设2B 铅笔和涂卡尺的单价分别为x 元、y 元,根据题意,得⎩⎪⎨⎪⎧5x +y =5.5,3x +2y =5.4.解得⎩⎪⎨⎪⎧x =0.8,y =1.5.答:2B 铅笔和涂卡尺的单价分别为0.8元和1.5元.10.8011.设鸦有x 只,树有y 棵.根据题意,得⎩⎪⎨⎪⎧x -53=y ,x 5=y -1,解得⎩⎪⎨⎪⎧x =20,y =5.答:鸦有20只,树有5棵.12.(1)设这批游客的人数共x 人,原计划租用45座客车y 辆. 根据题意,得⎩⎪⎨⎪⎧45y +15=x ,60(y -1)=x. 解得⎩⎪⎨⎪⎧x =240,y =5.答:这批游客共240人,原计划租45座客车5辆.(2)租45座客车:240÷45≈5.3(辆),所以需租6辆,租金为220×6=1 320(元);租60座客车:240÷60=4(辆),所以需租4辆,租金为300×4=1 200(元).答:租用4辆60座客车更合算.13.(1)设5元、8元的笔记本分别买x 本、y 本,依题意,得⎩⎪⎨⎪⎧x +y =40,5x +8y =300-68+13.解得⎩⎪⎨⎪⎧x =25,y =15.答:5元和8元的笔记本分别买了25本和15本.(2)假设小明找回68元,设5元,8元的笔记本分别买m 本,n 本, 则⎩⎪⎨⎪⎧m +n =40,5m +8n =300-68.解得⎩⎪⎨⎪⎧m =883,n =323.因为m ,n 为正整数,所以不合题意.故不可能找回68元.。
北师大版八年级数学上册《5.3 应用二元一次方程组——鸡兔同笼2》课时作业(含答案)

5.3 应用二元一次方程组——鸡兔同笼
1.21枚1角与5角的硬币,共是5元3角,其中1角与5角的硬币各是多少?
设1角硬币x枚,5角硬币y枚,填写下表,并求出x、y的值.
2.小兰在玩具厂劳动,做4个小狗、7个小汽车用去3小时42分,
做5个小狗、6个小汽车用去3小时37分.平均做一个小狗与1个小汽
车各用多少时间?
设做1个小狗用x分,做1个小汽车用y分,填写下表,并求出
x、y的值.
3.某中学某班买了358元,乙种票每张6元,甲、乙两种票各买多少张?
x、y的值.
4.有大小两种盛米的桶,已经知道5个大桶加上一个小桶可以盛3斛米,1个大桶加上5个小桶可以盛2斛米,问1个大桶、1个小桶分别可以盛多少斛米?
设大桶盛米量为x斛,小桶盛米量为y斛,填写下表,并求出x、y的值.
测验评价结果:________;对自己想说的一句话是:__________________。
参考答案
1.⎩
⎨⎧=+=+53521
y x y x ,解得⎩⎨⎧==813y x 填表略
2.⎩
⎨⎧+⨯=++⨯=+376036542
60374y x y x ,解得⎩⎨⎧==2217y x 表略
3.⎩
⎨⎧=+=+2506835
y x y x ,解得⎩⎨⎧==1520y x 表略
4.⎩⎨⎧=+=+2535y x y x ,解得⎪⎪⎩
⎪⎪⎨⎧==247
2413y x 表略。
5.3应用二元一次方程组---鸡兔同笼课件导学案练习(北师大)全面版

情境导入 你能找出问题中的等量关系吗?
等量关系:
{鸡鸡头脚++兔兔头脚==9354,.
x y 35 2x 4y 94
总数
头 x y 35 足 2x 4x 94
情境导入
解:设有鸡x只,有兔y只.由题意,得
x y 35 ① 2x 4y 94 ②
①×2 得: 2x+2y=70,③ ②-③ 得: 2y=24,
议一议
(1)“将绳三折测之,绳多五尺”,什么意思? (2)“若将绳四折测之,绳多一尺”,又是什么意思?
讲授新课 题目大意
用绳子测量水井的深度.如果将绳子 折成三等份,一份绳长比井深多5尺; 如果将绳子折成四等份,一份绳长比 井深多1尺.绳长、井深各是多少尺?
想一想 题中有哪些等量关系?
讲授新课
等量关系:
y=12. 把 y=12 代入①,得:x=23.
原方程组的解是 x=23, y=12.
答:有鸡23只,兔12只.
练一练今有牛五、羊二,直金十两.牛二、羊五,
直金八两.牛、羊各直金几何?
练一练
5头牛、2只羊共价值10两“金”;2头 牛、5只羊共价值8两“金”.问每头牛、每只羊 各价值多少“金”?
{ 5x+2y=10,
课堂小结 本节课你学习了哪些知识?
我学会了如何利用二元一次方程组解决实际问题
随堂练习
1.设甲数为x,乙数为y,则“甲数的
二倍与乙数的一半的和是15”,列出 方程为___2_x__12__y__1_5_. 2.小刚有5角硬币和1元硬币各若干枚,币值
共有六元五角,设5角有x枚,1元有y枚,
列出方程为 ___0_.5_x__y___6_.5__.
5.3 应用二元一次方程组——鸡兔同笼2 对应配套练习题附答案
5.3 应用二元一次方程组——鸡兔同笼1.21枚1角与5角的硬币,共是5元3角,其中1角与5角的硬币各是多少?设1角硬币x枚,5角硬币y枚,填写下表,并求出x、y的值.2.小兰在玩具厂劳动,做4个小狗、7个小汽车用去3小时42分,做5个小狗、6个小汽车用去3小时37分.平均做一个小狗与1个小汽车各用多少时间?设做1个小狗用x分,做1个小汽车用y分,填写下表,并求出x、y的值.3.某中学某班买了358元,乙种票每张6元,甲、乙两种票各买多少张?x、y的值.4.有大小两种盛米的桶,已经知道5个大桶加上一个小桶可以盛3斛米,1个大桶加上5个小桶可以盛2斛米,问1个大桶、1个小桶分别可以盛多少斛米?设大桶盛米量为x斛,小桶盛米量为y斛,填写下表,并求出x、y的值.测验评价结果:________;对自己想说的一句话是:__________________。
参考答案1.⎩⎨⎧=+=+53521y x y x ,解得⎩⎨⎧==813y x 填表略2.⎩⎨⎧+⨯=++⨯=+37603654260374y x y x ,解得⎩⎨⎧==2217y x 表略3.⎩⎨⎧=+=+2506835y x y x ,解得⎩⎨⎧==1520y x 表略4.⎩⎨⎧=+=+2535y x y x ,解得⎪⎪⎩⎪⎪⎨⎧==2472413y x 表略7.4 平行线的性质1.如图,DE ∥BC ,分别交AB 、AC 于点D 、E ,求证:BCDEAC AE AB AD ==。
2 如图,△ABC 中,E 、G 、D 、F 分别是边AB 、CB 上的点,且GF ∥ED ∥AC ,EF ∥AD 。
求证:BCBDBE BG =。
3 已知:在△ABC 中,AD 为BC 边上的中线,过C 任作一直线交AD 于E ,交AB 于F 。
求证:FBAFED AE 2=。
4 如图,已知:D 为BC 的中点,AG ∥BC 。
求证:FCAFED EG =。
5 已知:在△ABC 中,AD 平分∠BAC 。
北师大版八年级数学上5.3 应用二元一次方程组—鸡兔同笼
初中数学试卷5.3 应用二元一次方程组——鸡兔同笼一、选择题1.一张试卷有25道题,做对一题得4分,做错一题扣1分,小明做了全部试题得70分,则他做对的题数是()A.16 B.17 C.18 D.192.某校150名学生参加数学考试,平均分55分,其中及格学生平均77分,不及格学生平均47分,则不及格的学生人数为()A.49 B.101 C.110 D.40二、填空题3.现有面值总和为570元的人民币50元和20元的共15张,设50元人民币有x张,20元人民币有y张,根据题意,列出方程组:4.六一儿童节,某动物园的成人门票8元,儿童门票半价(即每张4元),全天共售出门票3000张,共收入15600元,设这天售出成人票x张,儿童票y张,根据题意,列出方程组:三、解答题5.21枚1角与5角的硬币,共是5元3角,其中1角与5角的硬币各是多少?6.小兰在玩具厂劳动,做4只小狗、7辆小汽车用去3小时42分,做5只小狗、6辆小汽车用去3小时37分.平均做1只小狗与1辆小汽车各用多少时间?7.某中学某班买了35张电影票,共用250元,其中甲种票每张8元,乙种票每张6元,甲、乙两种票各买多少张?5.3 应用二元一次方程组——鸡兔同笼1.D 2.C3.⎩⎨⎧=+=+570205015y x y x 4.⎩⎨⎧=+=+15600489000y x y x5.解:设1角的硬币有x 枚,5角的硬币有y 枚,依题意得:⎩⎨⎧=+=+53521y x y x 解得:⎩⎨⎧==813y x答:1角的硬币有13枚,5角的硬币有8枚。
6.解:设做一只小狗x 分钟,做一辆小汽车y 分钟,依题意得:⎩⎨⎧=+=+2176522274y x y x解得:⎩⎨⎧==2219y x 答:做一只小狗19分钟,做一辆小汽车22分钟。
7.解:设买甲种票x 张,乙种票y 张,依题意得:⎩⎨⎧=+=+2506835y x y x 解得:⎩⎨⎧==1520y x答:买甲种票20张,乙种票15张。
5.3应用二元一次方程组_---鸡兔同笼
x 2 y3
1 x ,而正确的解是 的方程组是什么吗? y 1
,你知道正确
初中二年级(八年级)(下)
第五章
二元一次方程组
“鸡兔同笼”是我国古代数学名著 《孙子算经》中的31题:今有鸡兔同笼,上有 三十五头,下有九十四足.问鸡兔各几何?
设鸡有x只,兔有y只,可以得到关于x,y的二元一次方程组:
x y 35 2x 4 y 94
5.3 应用二元一次方程组1
自学检测
用代入消元法解下列方程组: x-7y=0, y=x , 2. 1. x–9y+8=0 ; 看看你掌 4x+y=15 ;
握了吗?
3x+2y=1, 2x-3y=1 , 3. 4. -x+2y=4 ; 3x + 4y= -7 .
用代入消元法解二元一次方程组的一般步骤:
1.给两个方程编号①、②; 变形. 通常将系数为1或-1的方程变形,用含有一 个未知数的代数式表示另一个未知数,并 编号为③. 2.将③代入没有变形的方程,从而将二元一次 方程组转化为一元一次方程. 3.解这个一元一次方程. 4.将已求出的未知数的值代入方程③,求 出另一个未知数的值. X= 5.下结论. ∴原方程组的解是 y=
学习目标
会用代入消元法
解二元一次方程ห้องสมุดไป่ตู้.
自学指导
认真看P.108-109的内容: 1.看例1时思考是如何消去x的?可以通过 消去y解这个方程组吗? 2.看例2时思考是如何消去x的?可以通 过消去y解这个方程组吗? 3.结合P.109的“议一议”下面一段文字 思考用代入消元法解二元一次方程组的 一般步骤; 5分钟后,比谁能正确地做出与例题 类似的习题.
5 3 应用二元一次方程组 鸡兔同笼(课后练习) 北师大版数学八年级上册
5.3 应用二元一次方程组--鸡兔同笼(课后练习)北师大版八年级上册一.选择题1.《九章算术》中有这样的问题:质问隔壁人分银,不知多少银和人,每人6两少6两,每人半斤多半斤,试问各位善算者,多少人分多少银?(注:这里的斤是指市斤,1市斤=1﹣两),设共有x人,y两银子,下列方程组中,正确的是()A.B.C.D.2.如图,直线AB与CD相交于点O,且∠AOD=150°.∠EOB比∠COE大90°,设∠COE=x°,∠EOB=y°,则可得到的方程组为()A.B.C.D.3.一道来自课本的习题:从甲地到乙地先有一段上坡路后有一段平路.如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54分钟,从乙地到甲地需42分钟,甲地到乙地全程是多少?小红将这个实际问题转化为二元一次方程组问题,采用间接设法:设坡路有xkm,平路有ykm,则全程为(x+y)km.已经列出一个方程=,则另一个方程正确的是()A.=B.C.D.=4.程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?下列是四位同学的解答:①小明:设大和尚有x人,小和尚有y人,根据题意可列方程组为;②小丽:设大和尚有x人,小和尚有y人,根据题意可列方程组为;③小东:设大和尚有x人,则小和尚有(100﹣x)人,根据题意可列方程为;④小华:设大和尚有x人,则小和尚有(100﹣x)人,根据题意可列方程为100﹣3x=.其中,以上解答一定正确的是()A.①②③B.②③④C.①④D.①③5.《孙子算经》是中国传统数学的重要著作,其中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根木头的长,绳子还剩余4.5尺;将绳子对折再量木头,则木头还剩余1尺,问木头长多少尺?可设木头长为x尺,绳子长为y尺,则所列方程组正确的是()A.B.C.D.6.《孙子算经》中有一道题,原文是:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余4.5尺;将绳子对折再量长木,长木还剩余1尺,问木长多少尺?设木长为x尺,绳子长为y尺,则可列方程组为()A.B.C.D.7.《九章算术》是人类科学史上应用数学的“算经之首”,书中记载:今有二人共车九人步;三人共车,二车空.问:人与车各几何?译文:若每辆车都坐2人,则9需要步行:若每辆车都坐3人,则两辆车是空的,问:车与人各多少?设有x辆车,y个人,根据题意,列方程组是()A.B.C.D.8.《增删算法统宗》提到:“今有布绢三十疋,共卖价钞五百七.四疋绢价九十贯,三疋布价该五十.欲问绢布各几何?……”其大意是:今有绢与布30疋,卖得570贯钱,4疋绢价90贯,3疋布价50贯,问绢与布各有多少.设绢有x疋,布有y疋,依据题意可列方程组为()A.B.C.D.9.某工厂有26名工人,一个工人每天可加工800个螺栓或1000个螺帽,1个螺栓与2个螺帽配套,现要求工人每天加工的螺栓和螺帽完整配套且没有剩余.若设安排x个工人加工螺栓,y个工人加工螺帽,则列出正确的二元一次方程组为()A.B.C.D.10.一条船顺流航行,每小时行25km;逆流航行,每小时行17km.设轮船在静水中的速度为xkm/h,水的流速为ykm/h.根据题意,得到的方程组是()A.B.C.D.二.填空题11.某校准备购买签字笔和笔袋奖励优秀学生,第一次购买签字笔40支,笔袋30个,购买总价为960元.第二次购买签字笔60支,笔袋50个,购买总价为1500元.每次购买签字笔和笔袋的单价都相同,求签字笔和笔袋的单价分别是多少元?若设签字笔x元/支,笔袋y 元/个,则根据题意可列方程组为.12.某校为美化校园,计划对一些区域进行绿化,安排了甲、乙两个工程队完成,两队共完成了面积为400m2区域的绿化.已知甲队每天能完成绿化的面积是10m2,乙队每天能完成绿化的面积是5m2,甲队比乙队晚10天完成任务.设甲队和乙队分别完成的绿化面积为xm2和ym2,根据题意列出方程组:.13.甲乙两人加工一批零件,甲先加工了一半,然后乙加工了剩下部分,前后共用了10天完成,如果甲乙两人一起加工,6天可加工完,如设甲、乙两人单独加工完成这批零件各需x天、y天可列方程组为.14.小明与爸爸的年龄和是52岁,爸爸对小明说:“当我的年龄是你现在的年龄的时候,你还要16年才出生呢.”如果设现在小明的年龄是x岁,爸爸的年龄是y岁,则可列二元一次方程组为:.15.根据图中提供的信息,写出T恤衫的单价x(元/件)与驱虫剂的单价y(元/瓶)满足的二元一次方程组.三.解答题16.《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱.如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的,那么乙也共有钱48文.甲、乙两人原来各有多少钱?17.如图:用8块相同的长方形拼成一个宽为48厘米的大长方形,每块小长方形的长和宽分别是多少?解:设小长方形的长是x厘米,宽是y厘米题中的两个相等关系:(1)小长方形的长+=大长方形的宽可列方程为:;(2)小长方形的长=,可列方程为:.18.根据题意列二元一次方程组:(1)两批货物,第一批360吨,用5节火车皮和12辆汽车正好装完;第二批500吨,用7节火车皮和16辆汽车正好装完.每节火车皮和每辆汽车平均各装货物多少吨?(2)某校课外小组的学生准备外出活动;若每组7人,则余下3人;若每组8人,则有一组只有3人;求这个课外小组分成几组?共有多少人?19.某县在创建省级卫生文明县城中,对县城内的河道进行整治.现有一段长为180米的河道整治任务由甲、乙两个工程队先后接力完成.甲工程队每天整治8米,乙工程队每天整治12米,共用时20天.(1)小明、小华两位同学提出的解题思路如下:小明同学:设整治任务完成后甲工程队整治河道x米,乙工程队整治河道y米.根据题意,得小华同学:设整治任务完成后,m表示,n表示;得请你补全小明、小华两位同学的解题思路.(2)求甲、乙两工程队分别整治河道多少米?请从中任选一个方程组求解.(写出完整的解答过程)20.在当地农业技术部门指导下,小明家种植的菠萝喜获丰收.去年菠萝的收入结余12000元,今年菠萝的收入比去年增加了20%,支出减少10%,结余今年预计比去年多11400元.请计算:(1)今年结余元;(2)若设去年的收入为x元,支出为y元,则今年的收入为元,支出为元.(以上两空用含x、y的代数式表示)(3)列方程组计算小明家今年种植菠萝的收入和支出.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.一张方桌由1张桌面和4条桌腿做成,已知1 m3木料可以做桌面50张或桌腿300条.现有5 m3木料,恰好能做成方桌多少张?【解】:设用x m3木料做桌面,y m3木料做桌腿,由题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩解得__________________________⎧⎨⎩方桌的数量:________________________,答:______________________________________________________________.2.某校办工厂有工人60名,生产某种由一个螺栓套两个螺母的配套产品,每人每天平均生产螺栓14个或螺母20个,应分配多少人生产螺栓,多少人生产螺母,能使生产出的螺栓和螺母刚好配套?【解】:设分配x人生产螺栓,y人生产螺母,由题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩解得__________________________⎧⎨⎩答:______________________________________________________________.3.用白铁皮做罐头盒。
每张铁皮可制盒身16个,或制盒底43个,一个盒身与两个盒底配成一套罐头盒。
现有150张白铁皮,用x张制盒身,y张制盒底,可以刚好配套,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩4.如图,10块相同的长方形墙砖拼成一个矩形,设长方形墙砖的长和宽分别为x厘米和y厘米,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩5.如图,长方形ABCD中放置9个形状大小都相同的小长方形(尺寸如图,单位:cm),求图中阴影部分面积.【解】:设小长方形的长和宽分别为x cm和y cm,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩解得__________________________⎧⎨⎩∴S阴影部分=______________________________________________________________.答:______________________________________________________________.【分配类应用题】1.某校师生到甲、乙两个工厂参加劳动,如果从甲厂抽9人到乙厂,则两厂的人数相同;如果从乙厂抽5人到甲厂,则甲厂的人数是乙厂的2倍,到两个工厂的人数各是多少?【解】:设到甲工厂的人数为x 人,到乙工厂的人数为y 人 ,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩ 解得__________________________⎧⎨⎩答:______________________________________________________________.2.在早餐店里,王伯伯买了5个馒头,3个包子,老板少拿了0.2元,只要5元,李太太买了11个馒头,5个包子,老板以售价的九 折优待,只要9元,若馒头每个x 元,包子每个y 元,试求馒头和包子的单价.【解】:设馒头每个x 元,包子每个y 元,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩ 解得__________________________⎧⎨⎩答:______________________________________________________________.3.某旅游团在旅店住宿,若每个房间住5人,则有4人无住处;若每个房间住6人。
则有一间只住了4人,且空三个房间,求房间数和该旅 游团的人数。
【解】:设旅游团在旅店住宿的房间有x 间,该旅游团有y 人,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩解得__________________________⎧⎨⎩答:______________________________________________________________.4.某蔬菜公司收购到某种蔬菜104吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?【解】:设该公司应安排x 天精加工,y 天粗加工,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩解得__________________________⎧⎨⎩答:______________________________________________________________.【解】:设甜果x 个,苦果y 个,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩ 解得__________________________⎧⎨⎩甜果_______________________________苦果_______________________________.答:______________________________________________________________.6.某地要在规定的时间内安置一批居民,若每个月安置12户居民,则在规定时间内只能安置90%的居民户;若每个月安置16户居民,则可提前一个月完成安置任务,问要安置多少户居民?规定时间为多少个月?(列方程(组)求解)【解】:设安置x 户居民,规定时间为y 个月.依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩ 解得__________________________⎧⎨⎩答:______________________________________________________________.7.学校书法兴趣小组准备到文具店购买A 、B 两种类型的毛笔,文具店的销售方法是:一次性购买A 型毛笔不超过20支时,按零售价销售;超过20支时,超过部分每支比零售价低0.4元,其余部分仍按零售价销售. 一次性购买B 型毛笔不超过15支时,按零售价销售;超过15支时,超过部分每支比零售价低0.6元,其余部分仍按零售价销售. 如果全组共有20名同学,若每人各买1支A 型毛笔和2支B 型毛笔,共支付145元;若每人各买2支A 型毛笔和1支B 型毛笔,共支付129元.这家文具店的A 、B 两种类型毛笔的零售价各是多少?【解】:设该家文具店A 型毛笔的零售价为每支x 元,B 型毛笔的零售价为每支y 元,依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩ 解得__________________________⎧⎨⎩答:______________________________________________________________.【调配运输类应用题】1. 北京、上海两地的两个厂家同时生产同种型号的计算机,除本地使用外,北京可调运给外地10台,上海可调运给外地4台,现协议给武汉6台,重庆8台,每台的运费如下表所示,现有一种调运方案,预计的运费为7600元,这种调运方案中,北京、上海应分别调往武汉、重庆各多少台?【解】:设北京运往武汉x 台计算机,运往重庆y 台,则上海运往武汉( )台,运往重庆( )台。
依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩ 解得__________________________⎧⎨⎩上海运往武汉_______________________________运往重庆_______________________________.答:______________________________________________________________.2.如图,长青化工厂与A ,B 两地有公路、铁路相连.这家工厂从A 地购买一批每吨100元的原料运回工厂, 制成每吨8000元的产品运到B 地.已知公路运价为 1.5元/(吨·千米),铁路运价为 1.2元/(吨·千米),且这两次运输共支出公路运输费15000元,铁路运输费97200元.求:(1)该工厂从A 地购买了多少吨原料?制成运往B 地的产品多少吨?(2)这批产品的销售款比原料费与运输费的和多多少元?解:(1)设工厂从A 地购买了x 吨原料,制成运往B 地的产品y 吨.依题意列方程组____________________________________________________⎧⎪⎪⎨⎪⎪⎩解得__________________________⎧⎨⎩答:______________________________________________________________.(2)原料费:______________________________________________________________.运输费:______________________________________________________________.销售款:______________________________________________________________.销售款比原料费与运输费的和多:___________________________________________________.答:______________________________________________________________.。
