2018武汉元调数学试卷及答案(Word精校版)

合集下载

湖北省武汉市部分学校2018届高三起点调研考试数学(理)试卷(含答案)

2017-2018学年度武汉市部分学校新高三起点调研测试理科数学第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设集合2{20}A x x x =-≥，{12}B x x =<≤，则A B =I （）A ．{2}B ．{12}x x <<C ．{12}x x <≤D ．{01}x x <≤ 2.设(1)1i x yi -=+，其中,x y 是实数，则x yi +在复平面内所对应的点位于（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 3.已知等比数列{}n a 中，23a ，32a ，4a 成等比数列，设n S 为数列{}n a 的前n 项和，则33S a 等于（） A ．139 B ．3或139 C ．3 D ．794.将一枚质地均匀的骰子投两次，得到的点数依次记为a 和b ，则方程210ax bx ++=有实数解的概率是（） A ．736 B ．12 C. 1936D ．5185.函数2()log (45)a f x x x =--（1a >）的单调递增区间是（） A ．(,2)-∞- B ．(,1)-∞- C. (2,)+∞ D ．(5,)+∞ 6.一个几何体的三视图如图，则它的表面积为（）A ．28B ．245+ 2045+．205+7.已知,x y R ∈，且0x y >>，若1a b >>，则一定有（）A ．a bx y> B ．sin sin ax by > C. log log a b x y > D ．x y a b > 8.某公司生产甲、乙两种桶装产品，已知生产甲产品1桶需耗A 原料2千克，B 原料3千克；生产乙产品1桶需耗A 原料2千克，B 原料1千克，每桶甲产品的利润是300元，每桶乙产品的利润是400元，公司在要求每天消耗,A B 原料都不超过12千克的条件下，生产产品A 、产品B 的利润之和的最大值为（）A ．1800元B ．2100元 C. 2400元 D ．2700元9.已知不等式2230x y ->所表示的平面区域内一点(,)P x y 到直线3y x =和直线3y x =的垂线段分别为,PA PB ，若三角形PAB 33，则点P 轨迹的一个焦点坐标可以是（） A ．(2,0) B ．(3,0) C. (0,2) D ．(0,3)10.执行下面的程序框图，如果输入的0x =，1y =，1n =，则输出,x y 的值满足（）A ．2y x =B ．3y x = C. 4y x = D ．5y x =11.已知,A B 分别为椭圆22219x y b +=（03b <<）的左、右顶点，,P Q 是椭圆上的不同两点且关于x 轴对称，设直线,AP BQ 的斜率分别为,m n ，若点A 到直线1y mnx =-的距离为1，则该椭圆的离心率为（） A ．12 B ．24 C. 13D ．2212.设点M 是棱长为2的正方体1111ABCD A B C D -的棱AD 的中点，点P 在面11BCC B 所在的平面内，若平面1D PM 分别与平面ABCD 和平面11BCC B 所成的锐二面角相等，则点P 到点1C 的最短距离是（） A 25 B ．22 C. 1 D 6第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.设向量(,1)a m =r ，(1,)b m =r ，且3a b b +=-r r r，则实数m = ．14. 12展开式中2x 的系数为．（用数学填写答案）15.设等差数列{}n a 满足3736a a +=，46275a a =，且1n n a a +有最小值，则这个最小值为．16.已知函数()sin()f x x πωϕ=+（0a ≠，0ω>，2πϕ≤），直线y a =与()f x 的图象的相邻两个交点的横坐标分别是2和4，现有如下命题：①该函数在[2,4]上的值域是[]a ； ②在[2,4]上，当且仅当3x =时函数取最大值；③该函数的最小正周期可以是83； ④()f x 的图象可能过原点.其中的真命题有（写出所有真命题的序号）三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17. 已知等差数列{}n a 的前n 项和为n S ，等比数列{}n b 的前n 项和为n T ，11a =-，11b =，223a b +=.（1）若337a b +=，求{}n b 的通项公式；（2）若313T =，求n S .18. 在锐角ABC ∆中，内角,,A B C 的对边分别是,,a b c ，满足cos 2cos 22cos()cos()066A B B B ππ-+-+=.（1）求角A 的值；（2）若b =b a ≤，求a 的取值范围.19. 甲、乙两名运动员参加“选拔测试赛”，在相同条件下，两人6次测试的成绩（单位：分）记录如下：甲 86 77 92 72 78 84 乙 78 82 88 82 95 90（1）用茎叶图表示这两组数据，现要从中选派一名运动员参加比赛，你认为选派谁参赛更好？说明理由（不用计算）；（2）若将频率视为概率，对运动员甲在今后三次测试成绩进行预测，记这三次成绩高于85分的次数为X ，求X 的分布列和数学期望()E X 及方差()D X .20. 如图1，在矩形ABCD 中，4AB =，2AD =，E 是CD 的中点，将ADE ∆沿AE 折起，得到如图2所示的四棱锥1D ABCE -，其中平面1D AE ⊥平面ABCE .（1）设F 为1CD 的中点，试在AB 上找一点M ，使得//MF 平面1D AE ；（2）求直线1BD 与平面1CD E 所成的角的正弦值.21. 已知抛物线2:2C x py =（0p >）和定点(0,1)M ，设过点M 的动直线交抛物线C 于,A B 两点，抛物线C 在,A B 处的切线交点为N . （1）若N 在以AB 为直径的圆上，求p 的值；（2）若三角形ABN 的面积最小值为4，求抛物线C 的方程.22.已知函数()1xf x e ax =--（a R ∈）（ 2.71828e =…是自然对数的底数）. （1）求()f x 单调区间；（2）讨论1()()()2g x f x x =•-在区间[]0,1内零点的个数.试卷答案一、选择题1-5:CDBCD 6-10: BDCAD 11、12：BA二、填空题13.2± 14. 552-15. -12 16.③ 三、解答题17.（1）设{}n a 的公差为d ，{}n b 的公比为q ，则1(1)n a n d =-+-，1n n b q -=.由223a b +=，得4d q += ① 由227a b +=，得228d q += ②联立①和②解得0q =（舍去），或2q =，因此{}n b 的通项公式12n n b -=.（2）∵231(1)T b q q =++，∴2113q q ++=，3q =或4q =-，∴41d q =-=或8.∴21113(1)222n S na n n d n n =+-=-或245n n -. 18.（1）由已知cos 2cos 22cos()cos()066A B B B ππ-+-+=得2222312sin 2sin 2(cos sin )044B A B B -+-=化简得sin 2A =，又三角形ABC 为锐角三角形，故3A π=. （2）∵b a =≤，∴c a ≥，∴32C ππ≤<，63B ππ<≤由正弦定理得：sin sin a bA B=sin 2B=，即32sin a B =由13sin (,]2B ∈知[3,3)a ∈. 19.（1）由图可知乙的平均水平比甲高，故选乙（2）甲运动员每次测试高于85分的概率大约是13，成绩高于85分的次数为X 服从二项分布，分布列为X 0 1 2 3P827 49 29 1271()313E X =•=，122()3333D X =••=20.（1）14AM AB =取1D E 中点L ，连接AL ，∵//FL EC ，//EC AB ，∴//FL AB 且14FL AB =，所以,,,M F L A 共面，若//MF 平面1AD E ，则//MF AL ， ∴AMFL 为平行四边形，所以14AM FL AB ==（2）设点B 到1CD E 的距离为d ，由11B BCD D BCE V V --=可得122CED d S ∆•=. 设AE 中点为H ，作HG 垂直直线CE 于G ，连接DG ，∵1D E ⊥平面AECB ∴1D G EC ⊥，则13DG =，123D B =，∴11132CED S EC D G ∆=••=d =，所以直线1BD 与平面1CD E. 21.解：（1）可设:1AB y kx =+，11(,)A x y ，22(,)B x y ，将AB 方程代入抛物线C 方程得2220x pkx p --= 则122x x pk +=，122x x p =- ①又22x py =得'x y p=，则,A B 处的切线斜率乘积为12221x x p p =-=-则有2p =（2）由①可得122N x x x pk +==21AB x =-=点N 到直线AB的距离d ==12ABN S AB d ∆=••=≥∴4=，∴2p =，故抛物线C 的方程为24x y = 22.解：（1）'()xf x e a =-当0a ≤时，'()0f x >，()f x 单调增间为(,)-∞+∞，无减区间；当0a >时，()f x 单调减间为(,ln )a -∞，增区间为(ln ,)a +∞（2）由()0g x =得()0f x =或12x =先考虑()f x 在区间[]0,1的零点个数当1a ≤时，()f x 在(0,)+∞单调增且(0)0f =，()f x 有一个零点；当a e ≥时，()f x 在(,1)-∞单调递减，()f x 有一个零点；当1a e <<时，()f x 在(0,ln )a 单调递减，(ln ,1)a 单调递增.而(1)1f e a =--，所以1a ≤或1a e >-时，()f x 有一个零点，当11a e <≤-时，()f x 有两个零点而12x =时，由1()02f =得1)a =所以1a ≤或1a e >-或1)a =时，()g x 有两个零点；当11a e <≤-且1)a ≠时，()g x 有三个零点。

2018年武汉市九年级数学元调复习(一)

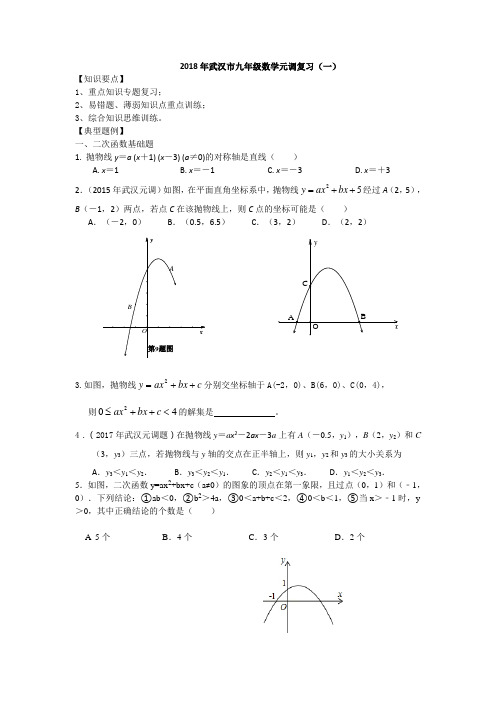
第9题图y x O A B O y xC B A 2018年武汉市九年级数学元调复习（一）【知识要点】1、重点知识专题复习；2、易错题、薄弱知识点重点训练；3、综合知识思维训练。

【典型题例】一、二次函数基础题1. 抛物线y ＝a (x ＋1) (x －3) (a ≠0)的对称轴是直线（）A. x ＝1B. x ＝－1C. x ＝－3D. x ＝＋32．（2015年武汉元调）如图，在平面直角坐标系中，抛物线25y ax bx =++经过A （2，5），B （－1，2）两点，若点C 在该抛物线上，则C 点的坐标可能是（）A ．（－2，0）B ．（0.5，6.5）C ．（3，2）D ．（2，2）3.如图，抛物线c bx ax y ++=2分别交坐标轴于A(-2，0)、B(6，0)、C(0，4)，则402<++≤c bx ax 的解集是。

4．（2017年武汉元调题）在抛物线y ＝a x 2－2ax －3a 上有A （－0.5，y 1），B （2，y 2）和C（3，y 3）三点，若抛物线与y 轴的交点在正半轴上，则y 1，y 2和y 3的大小关系为A ．y 3＜y 1＜y 2．B ．y 3＜y 2＜y 1．C ．y 2＜y 1＜y 3．D ．y 1＜y 2＜y 3．5．如图，二次函数y=ax 2+bx+c （a ≠0）的图象的顶点在第一象限，且过点（0，1）和（﹣1，0）．下列结论：①ab ＜0，②b 2＞4a ，③0＜a+b+c ＜2，④0＜b ＜1，⑤当x ＞﹣1时，y ＞0，其中正确结论的个数是（）A5个 B ． 4个 C ． 3个 D ． 2个．二、旋转6．如图，将△ABC绕顶点C逆时针旋转得到△A′B′C′，且点B刚好落在A′B′上．若∠A＝30°，∠BCA′＝40°，则∠A′BA等于（）A．30°B．35° C．40°D．45°7．如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD=3，BC=5，将腰DC绕点D逆时针方向旋转90°至DE，连接AE，则△ADE的面积是________8．如图，在Rt△ABC中，∠ABC=90°，AB=BC=，将△ABC绕点C逆时针旋转60°，得到△MNC，连接BM，则BM的长是．三、一元二次方程9．关于x的一元二次方程x2＋(2k－1)x＋k2－1＝0有实数根(1) 求k的取值范围(2) 若此方程的两个实数根互为倒数，求出k的值10．已知关于x的方程（x﹣3）（x﹣2）﹣p2=0．（1）求证：方程总有两个不相等的实数根．（2）设方程的两根为x1，x2（x1＜x2），则当0≤p时，请直接写出x1和x2的取值范围．四、圆中计算与动点问题11．如图，点A、B、C、D在O上，⊙O点在∠D内部，四边形OABC为平行四边形，则∠D ＝__________．12．如图，圆内两条弦互相垂直，其中一条被分成长为4和3两段，另一条被分成长为2和6两段，则该圆的直径为（）4B．65C．9 D．10A．613．如图，在平面直角坐标系中，⊙P 的圆心是(2，a )（a ＞2），半径为2，函数y ＝x 的图象被⊙P 截得的弦AB 的长为32，则a 的值是（）A ．22B ．22+C ．32D ．32+14．如图，正方形ABCD 和正△AEF 都内接于⊙O ，EF 与BC 、CD 分别相交于点G 、H ，则的值是（）A ．B ．C ．D ．2五、二次函数的实际应用15．一座拱桥的轮廓是抛物线型（如图1所示），拱高6 m ，跨度20 m ，相邻两支柱间的距离均为5 m(1) 将抛物线放在所给的直角坐标系中（如图2所示），求此抛物线的解析式。

2018~2019学年度武汉市九年级元月调考数学试卷(含实用标准问题详解)

2018~2019学年度市部分学校九年级调研测试数学试卷考试时间：2019年1月17日14:00~16:00 一、选择题（共10小题，每小题3分，共30分）1．将下列一元二次方程化成一般形式后，其中二次项系数是3，一次项系数是－6，常数项是1的方程是（） A ．3x 2＋1＝6xB ．3x 2－1＝6xC ．3x 2＋6x ＝1D ．3x 2－6x ＝12．下列图形中，是中心对称图形的是（）A ．B ．C ．D ．3．若将抛物线y ＝x 2先向右平移1个单位长度，再向上平移2个单位长度，就得到抛物线（）A ．y ＝(x －1)2＋2B ．y ＝(x －1)2－2C ．y ＝(x ＋1)2＋2D ．y ＝(x ＋1)2－24．投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（）A ．两枚骰子向上一面的点数之和大于1B ．两枚骰子向上一面的点数之和等于1C ．两枚骰子向上一面的点数之和大于12D ．两枚骰子向上一面的点数之和等于12 5．已知⊙O 的半径等于8 cm ，圆心O 到直线l 的距离为9 cm ，则直线l 与⊙O 的公共点的个数为（） A ．0B ．1C ．2D ．无法确定6．如图，“圆材埋壁”和我国古代著名数学著作《九章算术》中的问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何”用几何语言可表述为：CD 为 ⊙O 的直径，弦AB 垂直CD 于点E ，CE ＝1寸，AB ＝10寸，则直径CD 的长为（） A ．12.5寸B ．13寸C ．25寸D ．26寸第6题图第8题图第9题图7．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．如果3枚鸟卵全部成功孵化，那么3只雏鸟中恰有2只雄鸟的概率是（） A ．61B ．83 C ．85 D ．32 8．如图，将半径为1，圆心角为120°的扇形OAB 绕点A 逆时针旋转一个角度，使点O 的对应点D 落在弧AB 上，点B 的对应点为C ，连接BC ，则图中CD 、BC 和弧BD 围成的封闭图形面积是（）A ．63π-B ．623π- C ．823π-D ．33π- 9．古希腊数学家欧几里得的《几何原本》记载，形如x 2＋ax ＝b 2的方程的图解法是：如图，画Rt △ABC ，∠ACB ＝90°，BC ＝2a ，AC ＝b ，再在斜边AB 上截取BD ＝2a，则该方程的一个正根是（） A ．AC 的长B ．BC 的长 C ．AD 的长 D ．CD 的长10．已知抛物线y ＝ax 2＋bx ＋c （a ＜0）的对称轴为x ＝－1，与x 轴的一个交点为(2，0)．若关于x 的一元二次方程ax 2＋bx ＋c ＝p （p ＞0）有整数根，则p 的值有（） A ．2个B ．3个C ．4个D ．5个二、填空题（本大题共6个小题，每小题3分，共18分）11．已知3是一元二次方程x 2＝p 的一个根，则另一根是___________12．在平面直角坐标系中，点P 的坐标是(－1，－2)，则点P 关于原点对称的点的坐标是_____ 13．一个口袋中有3个黑球和若干个白球，在不允许将球倒出来数的前提下，小刚为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色……，不断重复上述过程，小刚共摸了100次，其中20次摸到黑球，根据上述数据，小刚可估计口袋中的白球大约有___________个14．第七届世界军人运动会将于2019年10月18日至27日在中国举行，小明幸运获得了一军运会吉祥物“兵兵”的照片．如图，该照片（中间的矩形）长29 cm ，宽为20 cm ，他想为此照片配一个四条边宽度相等的镜框（阴影部分），且镜框所占面积为照片面积的41．为求镜框的宽度，他设镜框的宽度为x cm ，依题意列方程，化成一般式为_____________第14题图第15题图第16题图15．如图是抛物线形拱桥，当拱顶离水面2 m 时，水面宽4 m ．水面下降2.5 m ，水面宽度增加___________m16．如图，形ABCD 的边长为4，点E 是CD 边上一点，连接AE ，过点B 作BG ⊥AE 于点G ，连接CG 并延长交AD 于点F ，则AF 的最大值是___________ 三、解答题（共8题，共72分） 17．（本题8分）解方程：x 2－3x －1＝018．（本题8分）如图，A 、B 、C 、D 是⊙O 上四点，且AD ＝CB ，求证：AB ＝CD第18题图19．（本题8分）的早点种类丰富，品种繁多，某早餐店供应甲类食品有：“热干面”、 “面窝”、“生煎包”、“锅贴饺”（分别记为A ，B ，C ，D ）；乙类食品有：“米粑粑”、“烧梅”、“欢喜坨”、“发糕”（分别记为E、F、G、H），共八种美食．小和小王同时去品尝美食，小准备在“热干面”、“面窝”、“米粑粑”、“烧梅”（即A，B，E，F）这四种美食中选择一种，小王准备在“生煎包”、“锅贴饺”、“欢喜坨”、“发糕”（即C，D，G，H）这四种美食中选择一种，用列举法求小和小王同时选择的美食都会是甲类食品的概率20．（本题8分）如图，在边长为1的形网格中，点A的坐标为(1，7)，点B的坐标为(5，5)，点C的坐标为(7，5)，点D的坐标为(5，1)(1) 将线段AB绕点B逆时针旋转，得到对应线段BE．当BE与CD第一次平行时，画出点A运动的路径，并直接写出点A运动的路径长(2) 小贝同学发现：线段AB与线段CD存在一种特殊关系，即其中一条线段绕着某点旋转一个角度可以得到另一条线段，直接写出这个旋转中心的坐标第20题图21．（本题8分）如图，在四边形ABCD中，AD∥BC，AD⊥CD，AC＝AB，⊙O为△ABC的外接圆(1) 如图1，求证：AD是⊙O的切线(2) 如图2，CD交⊙O于点E，过点A作AG⊥BE，垂足为F，交BC于点G①求证：AG＝BG②若AD＝2，CD＝3，求FG的长22．（本题10分）某商家销售一种成本为20元的商品，销售一段时间后发现，每天的销量y（件）与当天的销售单价x（元/件）满足一次函数关系，并且当x＝25时，y＝550；当x＝30时，y＝500．物价部门规定，该商品的销售单价不能超过48元/件(1) 求出y与x的函数关系式(2) 问销售单价定为多少元时，商家销售该商品每天获得的利润是8000元？(3) 直接写出商家销售该商品每天获得的最大利润23．（本题10分）如图，等边△ABC与等腰三角形△EDC有公共顶点C，其中∠EDC＝120°，2，连接BE，P为BE的中点，连接PD、ADAB＝CE＝6(1) 小亮为了研究线段AD与PD的数量关系，将图1中的△EDC绕点C旋转一个适当的角度，使CE与CA重合，如图2，请直接写出AD与PD的数量关系(2) 如图1，(1)中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由(3) 如图3，若∠ACD＝45°，求△P AD的面积24．（本题12分）如图，在平面直角坐标系中，抛物线y＝x2＋(1－m)x－m交x轴于A，B两点（点A在点B的左边），交y轴负半轴于点C(1) 如图1，m＝3①直接写出A，B，C三点的坐标②若抛物线上有一点D，∠ACD＝45°，求点D的坐标(2) 如图2，过点E(m，2)作一直线交抛物线于P，Q两点，连接AP，AQ，分别交y轴于M，N两点，求证：OM·ON是一个定值。

2018年武汉元月调考卷(三)

2018武汉元月调考冲刺卷·数学体例（卷三）2017武汉元月调考冲刺卷，供武汉市2017年初中毕业生复习时使用.试卷结构以及试题的设置均与2016武汉元月调考试卷一致.试题要求紧贴武汉元月调考考情，如：知识点的分布、分值比例、出题形式.试题编写要求试题要求1、题量为24道,三大题型，详见试卷结构编写部分.2、试题要求原创或教材改编，坚决避免出现最近几年的元调题、中考原题，杜绝从其他教辅书上直接摘题，个别好题必须经过改编后才可使用，所出题型均不能超出元调考试范围.3、试题具有时代性和地域性，能结合教材知识，联系中学生的生活实际.每套试卷选择3道教材改编题编写.4、试题要求具有详细的解析过程，并且解答题解题过程中要求有评分标准.严格按照武汉市元月调考答案评分标准来附分.5、选题要求（1）选题要符合武汉元月调考的考查形式；（2）设题的问数要与武汉元月调考相符合；（3）应用性试题要注意加入题材设置及其考查背景.试卷结构2017—2018学年度武汉市九年级调研测试·数学冲刺卷（元月）（三）题号卷三卷三具体要求1 一元二次方程的概念确定二次项、一次项、常数项的系数2 事件的可能性大小摸球3 中心对称图形不是中心对称的图形4 二次函数对称轴一般式5 频率估计概率/6 一元二次方程根的判别式判断下列四个方程中有两个相等的实数根的是7 直线与圆的位置关系/8 一元二次方程配方/9 二次函数图象上点的特征判断函数图象点坐标是否在函数图象上10 旋转后求路径长/11 几何概型/12 关于原点对称两个含参坐标关于原点对称，求参数的值13 一元二次方程的应用增长率问题14 二次函数平移求平移后函数解析式15 圆的综合题老师认为可能考察的题型16 圆锥的相关计算/17 一元二次方程的解法公式法18 圆内的相关证明与计算2问19 一元二次方程的应用1问，图形面积20 概率计算2问，除纸牌、摸球外的其他游戏21 切线的证明与计算2问22 二次函数的实际应用3问，商品销售求最大利润23 旋转2问，以几何图形为背景24 二次函数的综合应用3问，结合一次函数答案要求1.选择题、填空题【答案】+【解析】（解题过程）+【活动性栏目】（以方法指导、技巧点拨、思维方式、一题多解、易错警示、难点突破等为主）【解析】根据选择题具体题目的出题方式及解答特点，将其解题思路——主要写解题方法和解题的详细过程，可以表格或文字形式呈现.若一题有多解，在活动性栏目中写出【一题多解】。

2018届湖北省武汉市高中毕业生调研测试文科数学试题及答案1

武汉市2018届高中毕业生调研测试文科数学第Ⅰ卷一、选择题（本大题共10个小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的） 1、复数23i z i+=-的实部与虚部之和为A ．0B ．12C ．1D ．2 2、设全集U R=，集合2{|lg (1)},{02}Mx y x N x ==-=<<，则()UCM N =A ．{|21}x x -≤≤ B ．{|01}x x <≤ C ．{|02}x x << D ．{|1}x x <3、函数()s inc o s22x x fx =的最小正周期是A ．4π B ．2π C ．π D ．2π4、已知某赛季甲乙两名篮球运动员每场比赛的得分茎叶图，则甲乙两人得分的中位数之和为 A ．62 B ．63 C ．64 D ．65 5、4、若命题200:,230P x R x x ∃∈++≤，则命题P 的否定P⌝是A ．2,230x R x x ∀∈++> B ．2,230x R x x ∀∈++≥ C ．2,230x R x x ∀∈++< D ．2,230x R xx ∀∈++≤6、已知A B C∆外接圆的半径为1，圆心为O ，且2,A B A C A O A B A+==，则C A C B ⋅的值是A ．3B ．C 2D ．17、先后抛掷两颗质地均匀的骰子，则两次朝上的点数之积为奇数的概率为 A ．112B ．16C ．14D ．138、已知某产品连续4个月的广告费ix （千元）与销售额iy （万元）（1,2,3,4i =）满足4118i i x ==∑，4114i i y ==∑，若广告费x 和销售量y 之间具有线性相关关系，且回归直线方程为ˆ0.8yx a =+，那么广告费用为6千元时，可预测的销售量为A ．3.5万元B ．4.7万元C ．4.9万元D ．6.5万元 9、已知直线1k x y k -=-与2k x y k --的交点在第二象限，则实数k 的取值范围是A ．1(0,)2B ．1(,1)2C ．(0,1)D ．{}1-10、过点(2,3)A -作抛物线24yx=的两条切线12,l l ，设12,l l 与y 轴分别交于点B 、C ，则A B C ∆的外接圆的方程为 A ．22340x y x +--= B ．222310xy x y +--+=C ．22320xy x y ++--= D ．223210xy x y +--+=第Ⅱ卷二、填空题：本大题共7小题，每小题5分，共35分，把答案填在答题卷的横线上。

武汉市元调数学试卷

选择题在平面直角坐标系中，点A(3, -2)关于x轴对称的点的坐标是：A. (-3, -2)B. (-3, 2)（正确答案）C. (3, 2)D. (2, -3)已知等腰三角形的两边长分别为3和5，则这个等腰三角形的周长为：A. 8B. 11C. 13（正确答案）D. 11或13下列计算正确的是：A. 7a - a = 6B. a2 * a3 = a6C. (a + b)2 = a2 + 2ab + b2（正确答案）D. a6 ÷ a2 = a3若关于x的一元一次不等式组{ x - 2 ≤ 0, x + m > 0 } 有解，则m的取值范围是：A. m < -2B. m ≤ -2C. m > -2（正确答案）D. m ≥ -2已知|x| = 5，y = 3，则x - y = _______ 或_______．A. 2或8B. -2或-8（正确答案）C. 2或-8D. -2或8下列函数中，图像经过坐标原点的是：A. y = x2 - 2x + 1B. y = 1/xC. y = x - 5D. y = 2x（正确答案）若关于x的方程(x - 2)/2 = x - 3 的解也是方程ax - 2x = 4 的解，则a 的值为：A. -1B. 1C. 2D. 3（正确答案）下列四个命题中，真命题是：A. 同位角相等B. 垂直于同一直线的两直线垂直C. 相等的角是对顶角D. 平行于同一直线的两直线平行（正确答案）已知数据x₁，x₂，x₃，...，xₙ 的平均数是3，方差是2，则数据5 - x₁，5 - x₂，5 - x₃，...，5 - xₙ 的平均数和方差之和是：A. 11B. 9（正确答案）C. 7D. 5。

2018年武汉市元调模拟题+(答案)

2018年武汉市元调模拟题+(答案)则ma ＞mb13. 取两个相同的验电器A和B，使A带上负电荷，可以看到A的金属箔张开，B的金属箔闭合．用带有绝缘柄的金属棒把A和B连接起来（如图所示），观察到A的金属箔张开的角度减小，B 的金属箔由闭合变为张开．下列描述错误的是A．金属杆是导体B．两金属箔片能够张开是因为带上了同种电荷C．实验中金属杆和金属球接触的一瞬间，B验电器中的金属箔带上了负电荷D．实验中金属杆和金属球接触的一瞬间，金属杆中电流方向是自A流向B14.教室内安装有六盏日光灯，由三个开关控制，每个开关控制其中两个灯同时亮，同时熄灭。

这两盏灯的连接方式是（）A.串联B.并联C.串联或并联D.无法判断15.如图所示为小明连接的电路，他检查导线连接无误后，闭合开关S，发现两灯均不发光，于是他用一根导线分别连接到ab，bc，cd和ac两点，灯L1，L2均不发光，再用导线连接到bd两点时，灯L1发光，L2不发光，由此判定电路的故障是（）A．灯L1与开关S均开路B．灯L2与开关S均开路C．灯L1与开关S均短路D．灯L2与开关S均短路16. 如图所示的电路中，电源电压6V保持不变，定值电阻阻值为10Ω，滑动变阻器的最大阻值为20Ω．当开关闭合，滑片由b端向a端移动的过程中，以下说法正确的是（）A．电压表的示数减小B．当滑片移到a端时，电流表示数为0.2AC．当滑片移到中点时，电压表示数为2V D．电压表示数与电流表的示数之比不变17.小明设计了一种简易烟雾报警控制器如图所示．电路中R0为定值电阻，R为光敏电阻，其阻值随光照强度的增大而减小，烟雾增大到一定程度使电压表V的指针偏转到某区域时出发报警系统．以下做法能使控制器在烟雾较淡时就触发报警的是（）阻值B．增大激光强度A．减少RC．V改接大量程D．减小电源电压18.如图是学校的自动饮水机的简化电路图，电热丝电阻分别为R、R，其加热功率为 4.4kW,保温功率40W，下列说法不正确的是（）与R串联A．开关S断开时，电阻RB．当温度较低时，温控开关S闭合状态进入加热状态C．当水沸腾后，温控开关S断开进入保温状态保温状态D．电阻 R在保温状态下的功率大于R下的功率19.如图是探究电流通过导体时产生热的多少与哪些因素有关的实验装置。

2018-2019学年度武汉市九年级元月调考数学模拟试卷及答案

2018-2019学年度武汉市部分学校元月调考数学模拟试卷一、选择题（共10小题，每小题3分，共30分）1．方程3x2＋1＝6x的二次项系数和一次项系数分别为（）A．3和6 B．3和－6 C．3和－1 D．3和1 2．抛物线y＝(x－5)2＋6的对称轴是（）A．直线x＝－5 B．直线x＝5 C．直线x＝－6 D．直线x＝6 3．下列图形既是轴对称图形又是中心对称图形的是（）A．B．C． D4．下列事件：①在足球赛中，弱队战胜强队；②抛掷一枚硬币，落地后正面朝上；③任取两个正整数，其和大于1；④长分别为3、3、3的三条线段围成一个等腰三角形，其中确定事件的个数是（）A．1 B．2 C．3 D．45．“明天降水概率是30%”，对此消息下列说法中正确的是( ).A．明天降水的可能性较小B．明天将有30%的时间降水C．明天将有30%的地区降水D．明天肯定不降水6．如果关于x的一元二次方程mx2＋4x－1＝0没有实数根，那么m的取值范围是（）A．m＜4且m≠0 B．m＜－4 C．m＞－4且m≠0 D．m＞4 7．在⊙O 中，弦AB 的长为6，圆心O 到AB 的距离为4，OP=6，则点P 与⊙O 的位置关系是（）A．P 在⊙O 上B．P 在⊙O 外C．P 在⊙O 内D．P 与A 或B 重合8．如图所示，ABC△为O⊙的内接三角形，130AB C=∠=，°，则O⊙的内接正方形的面积为（）A．2 B．4 C．89．如图，Rt△ABC中，∠C=90°，内切圆⊙O与其三边的切点分别为D、E、F，若AB、BC、AC的长分别为c、a、b，且AE∙BE =m，a+b+c=n，则⊙O的半径r的值为( )A.n m B ．)(21n m + C ．n m 2 D ．n m -2110．如图，抛物线y ＝ax 2＋bx ＋c （c ≠0）过点(－1，0)和(0，－3)，且顶点在第四象限．设s ＝a ＋b ＋c ，则s 的取值范围是（） A ．－3＜s ＜－1 B ．－6＜s ＜0 C ．－3＜s ＜0 D ．－6＜s ＜－3二、填空题（本大题共6个小题，每小题3分，共18分） 11．点A （－2，5）关于原点的对称点B 的坐标是__________12．将抛物线 y=x2 ﹣2x+3 向左平移 2 个单位，再向上平移 1 个单位，得到的抛物线的解析式为 __________13．已知在一个不透明的口袋中有4个只有颜色不相同的球，其中1个红色球，3个黄色球．从口袋中随机取出一个球(不放回)，接着再取出一个球，则取出的两个都是黄色球的概率为__________________14．某树主干长出若干数目的支干，每个支干又长出同样数目小分支，主干、支干和小分支总数共73．若设主干长出x 个支干，则可列方程是 .15．如图，正方形ABCD 和正△AEF 都内接于⊙O ，EF 与BC 、CD 分别相交于点G 、H ，则的值是 .第15题图第16题图16. 已知⊙O 的半径为 2，A 为圆上一定点，P 为圆上一动点，以 AP 为边作等腰 Rt △APG ，P 点在圆上运动一周的过程中，OG 的最大值为___________三、解答题（共8题，共72分） 17．（本题8分）解方程：x 2－4x ＋1＝018．（本题8分）如图，⊙O中，直径CD⊥弦AB于M，AE⊥BD于E，交CD 于N，连AC（1）求证：AC＝AN；（2）若OM∶OC＝3∶5，AB＝5，求⊙O的半径；19．（本题8分）“红灯停，绿灯行”是我们在日常生活中必须遵守的交通规则，这样才能保障交通顺畅和行人安全，小刚每天从家骑自行车上学都经过三个路口，且每个路口只安装了红灯和绿灯，假如每个路口红灯和绿灯亮的时间相同，那么小刚从家随时出发去学校，回答以下问题：(1)请画树状图，列举所有可能出现的结果；(2)他遇到三次红灯的概率是多大？20．（本题8分）如图，在平面直角坐标系中，点A，B，C的坐标分别为(－1，3)，(－4，1)，(－2，1)，先将△ABC沿一确定方向平移得到△A1B1C1，点B的对应点B1的坐标是(1，2)，再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2，点A1的对应点为点A2.(1)画出△A1B1C1；(2)画出△A2B2C2；(3)求出在这两次变换过程中，点A经过点A1到达A2的路径总长．21．（本题8分）如图，A 是⊙O 上一点，半径OC 的延长线与过点A 的直线交于点B ，OC ＝BC ，AC ＝12OB. (1)求证：AB 是⊙O 的切线；(2)若∠ACD ＝45°，OC ＝2，求弦AD 的长．22．（本题10分）如图所示，为了改造小区环境，某小区决定要在一块一边靠墙（墙的最大可使用长度13 m ）的空地上建造一个矩形绿化带．除靠墙一边（AD ）外，用长为36 m 的栅栏围成矩形ABCD ，中间隔有一道栅栏（EF ）．设绿化带宽AB 为x m ，面积为S m 2（1）求S 与x 的函数关系式，并求出x 的取值范围（2）绿化带的面积能达到108 m 2吗？若能，请求出AB 的长度；若不能，请说明理由（3）当x 为何值时，满足条件的绿化带面积最大?23．（本题10分）23．已知正方形ABCD和正方形CGEF，且D点在CF边上，M为AE中点，连接MD、MF（1）如图1，请直接给出线段MD、MF的数量及位置关系是；（2）如图2，把正方形CGEF绕点C顺时针旋转，则（1）中的结论是否成立？若成立，请证明；若不成立，请给出你的结论并证明；（3）若将正方形CGEF绕点C顺时针旋转30°时，CF边恰好平分线段AE，请直接写出的值．24．（本题12分）已知抛物线y＝ax2－2amx＋am2＋2m＋4的顶点P在一条定直线l上．（1）直接写出直线l的解析式；（2）若存在唯一的实数m，使抛物线经过原点．①求此时的a和m的值；②抛物线的对称轴与x轴交于点A，B为抛物线上一动点，以OA、OB为边作□OACB，若点C在抛物线上，求B的坐标．（3）抛物线与直线l的另一个交点Q，若a＝1，直接写出△OPQ的面积的值或取值范围．参考答案二、填空题（共6小题，每小题3分，共18分） 11．（ 2，－5） 12．y=(x+1)2+313．1214． 1＋x ＋x 2＝7315．16．222+三、解答题（共8题，共72分） 17．解：32±=x18．解：（1）连接AC ，∵∠AED=∠AMO=90°，∴∠BDC=∠EAB=∠BAC ．∵AM ⊥OC ，∴∠AMC=∠AMN ．在△AMN 与△AMC 中，∵∠EAB=∠BAC ，AM=AM ，∠AMN=∠AMC ，∴△AMN ≌△AMC （ASA ），∴AC=AN ；（2）连接OA ，设OM=3x ，OC=5x ，∴OA=5x ，AM=4x ，∵AB=5，∴19．解：(1) 由树状图可以看出，共有8种等可能的结果，即：红红红、红红绿、红绿红、红绿绿、绿红红、绿红绿、绿绿红、绿绿绿、(2) P(三次红灯)＝1 8．20．解：(1)如图，△A1B1C1为所作．(2)如图，△A2B2C2为所作．(3)OA1＝42＋42＝42，点A经过点A1到达A2的路径总长＝52＋12＋90×42π180＝26＋22π.21．（1）证明：连接OA．∵OC=BC，AC=OB，∴OC=BC=AC=OA，∴△ACO是等边三角形，∴∠O=∠OCA=60°，又∵∠B=∠CAB，∴∠B=30°，∴∠OAB=90°．∴AB是⊙O的切线；（2）解：作AE⊥CD于点E．∵∠O=60°，∴∠D=30°．∵∠ACD=45°，AC=OC=2，∴在Rt△ACE中，CE=AE=，∵∠D=30°，∴AD=2．22．解：（1）∵四边形ABCD是矩形，∴AB=CD=EF，AD=BC，∵AB=xm，AB+BC+CD+EF=36m，∴BC=36-3x，∴绿化带的面积为：y=x•（36-3x）=﹣3x2+36x，y与x之间的函数关系式为：y=﹣3x2+36x；（2）由题意得：﹣3x 2+36x=108，解得：x 1=x 2=6，∵6能达到108 m 2．（3）∵y=﹣3x 2+36x =﹣3（x ﹣6）2+108，∵a=﹣3＜0，∴当x ＞6时，y 随x 的增大而减小，∴当y 最大，∴当x23．解：（1）线段MD 、MF 的数量及位置关系是MD=MF ，MD ⊥MF ，理由：如图1，延长DM 交EF 于点P ，∵四边形ABCD 和四边形FCGE 是正方形， ∴AD ∥EF ，∠MAD=∠MEP ．∠CFE=90°． ∴△DFP 是直角三角形． ∵M 为AE 的中点， ∴AM=EM ．在△ADM 和△EPM 中，，∴△ADM ≌△EPM （ASA ）， ∴DM=PM ，AD=PE ， ∴M 是DP 的中点．∴MF=DP=MD ， ∵AD=CD ， ∴CD=PE ， ∵FC=FE ， ∴FD=FP ，∴△DFP是等腰直角三角形，∴FM⊥DP，即FM⊥DM．故答案为：MD=MF，MD⊥MF；（2）MD=MF，MD⊥MF仍成立．证明：如图2，延长DM交CE于点N，连接FN、DF，∵CE是正方形CFEG对角线，∴∠FCN=∠CEF=45°，∵∠DCE=90°，∴∠DCF=45°，∵AD∥BC，∴∠DAM=∠NEM，在△ADM和△ENM中，，∴△ADM≌△ENM（ASA），∴EN=AD，DM=MN，∵AD=CD，∴CD=EN，在△CDF和△ENF中，，∴△CDF≌△ENF，（SAS）∴DF=NF，∴FM=DM ，FM ⊥DM ．（3）如图所示，若CF 边恰好平分线段AE ，则CF 过点M ，由（1）可得FM=DM ，FM ⊥DM ，设FM=DM=1， ∵∠DCF=30°，∴Rt △DCM 中，CM=，CD=2=CB ，∴CF=+1=CG ，∴=．24．解：(1) y=a （x-m ）2+2m+4，P （m ，2m+4），∴y=2x+4；（2）①将x=0，y=0代入，∴am 2+2m+4=0∴△=0，a=14，m=-4；②B 、C 关于对称轴对称，∴B 的横坐标为-2，y=14 （x+4）2-4，∴B （-2，-3）；（3）y=2x+4与x 轴交于点B （-2,0），交y 轴于点A （0,4），作OM ⊥AB 于M 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

018武汉元调数学试卷及答案(Word精校版) 第5页 / 共21页

2017-2018学年度武汉市部分学校九年级元月调考一.选择题(共10小题，每小题3分，共30分)

1.方程x(x-5)=0化成一般形式后，它的常数项是 A．-5 B．5 C．0 D．1 2.二次函数y=2(x-3)2-6 A．最小值为-6 B．最大值为-6 C．最小值为3 D．最大值为3 3.下列交通标志中，是中心对称图形的是

A． B． C． D． 4.事件①：射击运动员射击一次，命中靶心；事件②：购买一张彩票，没中奖，则 A．事件①是必然事件，事件②是随机事件. B．事件①是随机事件，事件②是必然事件. C．事件①和②都是随机事件. D．事件①和②都是必然事件. 5.投掷一枚质地均匀的硬币，正面朝上的概率为0.5，下列说法正确的是 A．连续投掷2次必有1次正面朝上. B．连续投掷10次不可能都正面朝上. C．大量反复投掷每100次出现正面朝上50次. D．通过投掷硬币确定谁先发球的比赛规则是公平的. 6.一元二次方程2230xxm有两个不相等的实数根则 A．3m B．3m C．3m D．3m 第6页 / 共21页

7.圆的直径是13cm，如果圆心与直线上某一点的距离是6.5cm，那么直线和圆的位置关系是 A．相离 B．相切 C．相交 D．相交或相切 8.如图，等边△ABC的边长为4，D，E，F分别为边AB，BC，AC的中点，分别以A，B，C三点为圆心，以AD长为半径作三条圆弧，则图中三条圆弧的弧长之和是 A． B．2 C．4 D．6

9.如图，△ABC的内切圆与三边分别相切于点D，E，F，则下列等式：①∠EDF=∠B，②2∠EDF=∠A+∠C，③2∠A=∠FED+∠EDF，④∠AED+∠BFE+∠CDF=180°，其中成立的个数是 A．1个 B．2个 C．3个 D．4个 10.二次函数y=-x2-2x+c在32x的范围内有最小值-5，则c的值是 A．-6 B．-2 C．2 D．3

二.填空题(共6小题，每小题3分，共18分) 11.一元二次方程20xa的一个根是2，则a的值

EFDC

BDE

FBC

A 第7页 / 共21页

是 . 12.把抛物线22yx先向下平移1个单位，再向左平移2个

单位，得到的抛物线的解析式是 . 13.一个不透明的口袋中有四个完全相同的小球，把它们

分别标记为1，2，3，4.随机摸取一个小球然后放回，再随机摸出一个小球，两次取出的小球标号的和为5的概率是 . 14.设计人体雕像时，使雕像的上部(腰以上)与下部(腰以

下)的高度比，等于下部与全部(全身)的比，可以增加视觉美感，按此比例，如果雕像的高为2m，那么上部应设计为多高？设雕像的上部高为x m，列方程，并化成一般形式为 . 15.如图，正六边形ABCDEF中，P是边ED的中点，连

接AP，则APAB＝ 16.在O中，AB所对的圆心角108AOB，点C为O上的动点，以AO，AC为边构造AODC，当∠A= °时，线段BD最长.

三.解答题(共8小题，共72分) PA

BCD

FED

BOAC 第8页 / 共21页

17. (本题8分)解方程230xx 第9页 / 共21页

18. (本题8分)如图在O中，半径OA与弦BD垂直，点C在O上，∠AOB=80°. (1)若点C在优弧BD上，求∠ACD的大小； (2)若点C在劣弧BD上，直接写出∠ACD的大小.

19.(本题8分)甲，乙，丙三个盒子中分别装有除颜色以BDA

AO 第10页 / 共21页

外都相同的小球，甲盒中装有两个球，分别为一个红球和一个绿球，乙盒中装有三个球，分别为两个绿球和一个红球；丙盒中装有两个球，分别为一个红球和一个绿球，从三个盒子中各随机取出一个小球. (1)请画树状图，列举所有可能的结果； (2)请直接写出事件“取出至少一个红球”的概率. 第11页 / 共21页 20. (本题8分)如图，在平面直角坐标系中有点A(-4，0)，B(0，3)，P(a，-a)三点.线段CD与AB关于点P中心对称，其中A，B的对应点分别为C，D． (1)当a=-4时， ①在图中画出线段CD，保留作图痕迹； ②线段CD向下平移个单位时，四边形ABCD为菱形； (2)当a= 时，四边形ABCD为正方形.

21. (本题8分)如图，点D在⊙O的直径AB的延长线上，CD切⊙O于点C，AE⊥CD于点E. (1)求证：AC平分∠DAE. (2)若AB=6，BD=2，求CE的长.

xyBAO 第12页 / 共21页 BECOAD 第13页 / 共21页 22. (本题10分)投资1万元围一个矩形菜园(如图)，其中一边靠墙，另外三边选用不同材料建造.墙长24m，平行于墙的边的费用为200元/m，垂直于墙的边的费用为150元/m.设平行于墙的边长为xm. (1)设垂直于墙的一边长为y，请直接写出y与x之间的函数关系式. (2)若菜园面积为384m2，求x的值. (3)求菜园的最大面积.

23. (本题10分)如图，点C为线段AB上一点，分别以AB，AC，CB为底作顶角为120°的等腰三角形，顶角顶点分别为D，E，F，(点E，F在AB的同侧，点D在另一侧). (1)如图1，若点C是AB的中点，则∠AED=__________； (2)如图2，若点C不是AB的中点， ①求证：△DEF为等边三角形；

菜园墙（24m2）第14页 / 共21页

②连接CD，若∠ADC=90°，AB=3，请直接写出EF的长.

FEABCD

BAC 第15页 / 共21页 24.(本题12分)已知抛物线22yaxxc与x轴交于A(-1，0)，B(3，0)两点，一次函数y=kx+b的图象l经过抛物线上的点C(m，n). (1)求抛物线的解析式； (2)若m=3，直线l与抛物线只有一个公共点，求k的值； (3)若k=-2m+2，直线l与抛物线的对称轴相交于点D，点P在对称轴上，当PD=PC时，求点P的坐标. 第16页 / 共21页

2017-2018学年度武汉市部分学校九年级元月调考解析一.选择题 1 2 3 4 5 6 7 8 9 10 C A D C D C D B B D

9.如图： ①∵∠EOF=2∠EDF，∠EOF+∠B=180°， ∴2∠EDF+∠B=180°所以①错误 ②∵∠EOF=2∠EDF，∠EOF+∠B=180°， ∠A+∠B+∠C=180°，∴2∠EDF=∠A+∠C

所以②正确

③∵∠EDF+∠DEF=2x+y+z=90°+x， ∵∠A+∠EOD=180°，∴∠A=180°-2(y+z)=2x， ∴2(∠EDF+∠DEF)-180°=∠A

所以③错误

④∠AED+∠BFE+∠CDF=90°-x+90°-y+90°-z =270°-(x+y+z)=270°-90°=180°

所以④正确

二.填空题 11. 4 12. 2287yxx 13. 14

zxyxDE

FBC

A 第17页 / 共21页

14. 2-640xx 15. 132 16.27°

16.延长AO与O交于点P，连接DP，如图，则 OCAODP≌ DPOC，即点D的运动轨迹是以点P为圆心，OC长为半径的圆.如图所示，连接BP，BP与P的交点记作'D

BD最大值为'BD，此时1'272APODAPB

三.解答题 17.11132x，11132x



18. (1)∵OA⊥BD， ∴AB=AD，∴∠ACD=12∠AOB=40° (2)40°或140°

19.(1)由题意可得如下树状图，由图可知共有12种等可能的情况.

PD’BOA

C 第18页 / 共21页 (2)5

20. (1)如图所示 (2)2

(3)7

2

21.(1)证明：连OC ∵CD与⊙O切于点C， ∴OC⊥DE，∠OCD=90° ∵AE⊥DE， ∴∠E=90°，∴∠OCD=∠E=90°，∴OC//AE， ∴∠1=∠2 ∵OC=OA， ∴∠1=∠3， ∴∠2=∠3， ∴AC平分∠DAE (2)解：作CH⊥OD ∵AB=6， ∴AO=OB=OC=3 ∵AC平分∠DAE，CH⊥OD，CE⊥AE， ∴CE=CH ∵∠OCD=90°， ∴CD=22ODOC=4 ∵OCDS=12OC·CD=12OD·CH， ∴CH=125， ∴CE=125

22. (1)由题意可知：

xyD

132HBECOAD