中考几何规律专题
中考数学几何专题——对角互补模型几何压轴

全等型---90 °相似型如图,若将条件"OC 平分/AOB”去掉,条件"N AOB = N DCE = 90°不变CD 和CE 有什么关系?对角互补模型结论:(1) CD = CE(2) OD + OE = V2OC (3)S ODCE = S -OCD + S -OCE =1OC 22条件:(1) Z AOB = Z DCE = 90° (2) OC 平分 N AOB全等型---120条件:(1)Z AOB=2Z DCE=120°(2)OC平分N AOB结论:(1)CD=CE (2)OD+OE=OC(3)S ODCE=S A OCD+S A OCE=亨0c 24(2014山西10,3分)如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的变长为a,则重叠部分四边形EMCN的面积为()(2015湖北黄冈,14 )如图,在正方形ABCD 中,AC 与BD 交于点O ,正方形外有一点E ,使/AED = 90°,且DE=3, OE= 1 6,则AE=如图,正方形ABCD 中,AC 是对角线,今有较大的直角三角板,一边始终经过点B ,直角 顶点P 在射线AC 上移动,另一边交DC 于Q - ⑴如图1,当点Q 在DC 边上时,猜想并写出PB 与PQ 所满足的数量关系;并加以证明;⑵如图2,当点Q 落在DC 的延长线上时,猜想并写出PB 与PQ 满足的数量关系,请证明你 的猜想•A ______________ 5 A B已知/人08=90°,在N AOB 的平分线0乂上有一点C ,将一个三角板的直角顶点与(2 重合,它的两条直角边分别与0人、0B (或它们的反向延长线)相交于点D 、E •(1)当三角板绕点C 旋转到CD 与OA 垂直时(如图1),易证:0D+0E=、=0C;B. 1a 2 4 A. 2a 23 C. 5a 2 D. 4a 2 9 9B C(2 )当三角板绕点C旋转到CD与OA不垂直时,在图2、图3这两种情况下,上述结论是否还成立?若成立,请给予证明;若不成立,线段0D、0E、0C2间又有怎样的数量关系?请写出你的猜想,不需证明•已知/MAN,AC平分N MAN。
中考数学复习专题图形规律

专题:图形找规律一.选择题(共19小题)1.观察下列图形及所对应的算式,根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为()A.(2n+1)2B.1+8n C.1+8(n﹣1)D.4n2+4n2.如图,观察下列图形,第一个图形有3个三角形,第二个图形有7个三角形,第三个图形有11个三角形,依照此规律,第八个图形中共有()个三角形.A.29 B.30 C.31 D.323.下列各图形都是由同样大小的菱形按一定规律组成的,其中第(1)个图形中菱形的个数是1,第(2)个图形中菱形的个数是5,第(3)个图形中菱形的个数是14,第(4)个图形中菱形的个数是30,…,则第(8)个图形中菱形的个数是()A.196 B.204 C.214 D.2284.观察下列图形,第1个图形中有4个三角形,第二个图形中有12个三角形,…,则第10个图形中三角形的个数是()A.4000 B.92 C.76 D.845.如图是经典手机游戏“俄罗斯方块”中的图案,图1中有8个矩形,图2中有11个矩形,图3中有15个矩形,根据此规律,图5中共有()个矩形.A.19 B.25 C.26 D.316.用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第10个图案中,所包含的黑色正三角形的个数是()A.36 B.38 C.40 D.427.下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n (n≥2)个圆点时,图案的圆点数为S n.则S10有()个圆点.A.51 B.36 C.30 D.198.如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成,…那么第n个黑色L 形的正方形个数是()A.n2+1 B.n2+2 C.4n+1 D.4n﹣19.如图案中由“△”按一定的规律组成的,从左到右排成一列(如图所示),第一个图是由3个“△”组成,第二个由6个“△”组成的,第三个是由10个“△”组成的,依此规律,由55个“△”组成的图案是左起第()个图.A.7 B.8 C.9 D.1010.现有3×3的方格,每个小方格内均有数目不同的点图,要求方格内每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图中给出了部分点图,则P处所对应的点图是()A.B.C.D.11.如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有()个黑子.A.37 B.42 C.73 D.12112.将一些半径相同的小圆按如图所示的方式摆放,图①中有8个小圆,图②中有13个小圆,图③中有19个小圆,图④中有26个小圆,照此规律,图⑨中小圆的个数为()A.64 B.76 C.89 D.9313.下列图形都是由同样大小的等边三角形按一定的规律摆成,其中第①个图形有4个等边三角形,第②个图形有8个等边三角形,第③个图形有14个等边三角形,第④个图形有22个等边三角形,……,则第⑨个图形中等边三角形的个数是()A.76 B.84 C.91 D.9214.找出以如图形变化的规律,则第101个图形中黑色正方形的数量是()A.149 B.150 C.151 D.15215.下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第(8)个图形中圆的个数为()A.121 B.113 C.92 D.19116.下列图案均是用长度相同的小木棒按一定的规律拼搭而成;拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,…,依此规律,拼搭第8个图案需小木棒()根.A.144 B.108 C.88 D.8417.同样大小的黑色棋子按如图所示的规律摆放,第()个图形有2013个黑色棋子.A.668 B.669 C.670 D.67118.下列图形都是用同样大小的按一定的规律组成的,其中第①个图形中一共有1个“•”,第②个图形一共有5个“•”,第③个图形一共有11个“•”,…,则第⑧个图形中“•”的个数为()A.55 B.71 C.81 D.9019.观察图中正方形四个顶点所标的数字规律,推测数2019应标在()A.第504个正方形的左下角B.第504个正方形的右下角C.第505个正方形的右下角D.第505个正方形的左上角二.填空题(共18小题)20.现有各边长度均为1cm的小正方体若干个,按下图规律摆放,则第5个图形的表面积是cm2.21.探索规律:右边是用棋子摆成的“H”字,按这样的规律摆下去,摆成第10个“H”字需要个棋子.22.观察下列各图中小圆点的摆放规律,并按这样的规律继续摆放下去,则第5个图形中小圆点的个数为.23.如图,已知△ABC的面积S△ABC=1.在图(1)中,若,则;在图(2)中,若,则;在图(3)中,若,则;按此规律,若,则=.24.如图,由等圆组成的一组图中,第1个图由1个圆组成,第2个图由7个圆组成,…,按照这样的规律排列下去,则第8个图形由个圆组成.25.按照如图所示的方法排列黑色小正方形地砖,则第14个图案中黑色小正方形地砖的块数是.26.观察下列砌钢管的横截面图:则第n个图的钢管数是(用含n的式子表示)27.如图是由火柴棒搭成的几何图案,则第n个图案中有根火柴棒.(用含n的代数式表示)28.如图是一组有规律的图案,图案1是由4个组成的,图案2是由7个组成的,那么图案5是由个组成的,依此,第n个图案是由个组成的.29.观察下图找规律.(1)填出缺少的图形;(2)按照这样的规律,第21个图中,○在最.(填“上”“下”“左”“右).30.如图,下列图形是将正三角形按一定规律排列,则第5个图形中所有正三角形的个数有.31.下面是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:第n个“上”字需用枚棋子.32.用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为(用含n的代数式表示).33.用同样大小的黑色棋子按如图所示的方式摆图案,按照这样的规律下去,第4个图案需要棋子枚,第n个图案需要棋子枚.34.观察如图图形的构成规律,依照此规律,第100个图形中共有个“•”.35.下列图案是晋商大院窗格的一部分,其中“○”代表窗纸上所贴的剪纸,则第5个图中所贴剪纸“○”的个数为;第n个图中所贴剪纸“○”的个数为.36.如图所示,用大小相等的小正方形拼大正方形,拼第一个正方形需要4个小正方形,拼第二个正方形需要9个小正方形…拼一拼,想一想,按照这样的方法拼成的第n个正方形比第(n﹣1)个正方形多个小正方形.37.如图,是用三角形摆成的图案,摆第一层图需要1个三角形,摆第二层图需要3个三角形,摆第三层图需要7个三角形,摆第四层图需要13个三角形,摆第五层图需要21个三角形,…,摆第n层图需要个三角形.三.解答题(共3小题)38.“数缺形时少直观,形少数时难入微”,小明在探究…+结果时,发现可利用图形的知识来解决问题.他是这样规定的:在图1中,若线段AB的长为1,C1为AB的中点,C2为C1B的中点,C3为C2B的中点,…,C n为C n﹣1B的中点.(1)则可以得出线段C1B=,C1C2=,ACn=;(2)从而发现了…+=;(3)小明学习上爱动脑,经过认真思考和分析后,发现在计算时,也可以利用构造一个图形,通过面积来计算.他构造图形是:如图2,正△ABC面积为1,分别取AC、BC两边的中点A1、B1,再分别取A1C、B1C的中点A2、B2,依次取下去…,能直观地计算出结果.请你根据这个图形说明小明的结果:=.请你对小明的发现,试给出必要的说理.39.某餐厅中,一张桌子可坐6人,有以下两种摆放方式:(1)当有4张桌子时,两种摆放方式各能坐多少人?(2)当有n张桌子时,两种摆放方式各能坐多少人?(3)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌,为什么?40.观察下面的点阵图和相应的等式,探究其中的规律:(1)认真观察,并在④后面的横线上写出相应的等式.①1=1 ②1+2==3 ③1+2+3==6 ④…(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.1=12②1+3=22③3+6=32④6+10=42⑤…(3)通过猜想,写出(2)中与第n个点阵相对应的等式.参考答案与试题解析一.选择题(共19小题)1.观察下列图形及所对应的算式,根据你发现的规律计算1+8+16+24+…+8n(n是正整数)的结果为()A.(2n+1)2B.1+8n C.1+8(n﹣1)D.4n2+4n【分析】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.【解答】解:图(1):1+8=9=(2×1+1)2;图(2):1+8+16=25=(2×2+1)2;图(3):1+8+16+24=49=(3×2+1)2;…;那么图(n):1+8+16+24+…+8n=(2n+1)2.故选:A.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.注意此题的规律为:(2n+1)2.2.如图,观察下列图形,第一个图形有3个三角形,第二个图形有7个三角形,第三个图形有11个三角形,依照此规律,第八个图形中共有()个三角形.A.29 B.30 C.31 D.32【分析】易得第1个图形中三角形的个数,进而得到其余图形中三角形的个数在第1个图形中三角形的个数的基础上增加了几个4即可.【解答】解:第1个图形中有3个三角形;第2个图形中有3+4=7个三角形;第3个图形中有3+2×4=11个三角形;…第n个图形中有3+(n﹣1)×4=4n﹣1,当n=8时,4×8﹣1=31,故选:C.【点评】考查图形的规律性问题;得到不变的量及变化的量与n的关系是解决本题的关键.3.下列各图形都是由同样大小的菱形按一定规律组成的,其中第(1)个图形中菱形的个数是1,第(2)个图形中菱形的个数是5,第(3)个图形中菱形的个数是14,第(4)个图形中菱形的个数是30,…,则第(8)个图形中菱形的个数是()A.196 B.204 C.214 D.228【分析】仔细观察图形知道第1个图形有1个菱形,第2个有5=12+22个,第3个图形有14=12+22+32个,…由此得到规律求得第8个图形中菱形的个数即可.【解答】解:第1个图形有1个菱形,第2个有5=12+22个,第3个图形有14=12+22+32个,…第8个图形有1+4+9+16+25+36+49+64=204个菱形.故选:B.【点评】本题考查了规律型问题,解题的关键是仔细观察图形并找到有关图形个数的规律.4.观察下列图形,第1个图形中有4个三角形,第二个图形中有12个三角形,…,则第10个图形中三角形的个数是()A.4000 B.92 C.76 D.84【分析】由已知的三个图可得到一般的规律,即第n个图形中三角形的个数是8n﹣4,根据一般规律解题即可.【解答】解:第一个图形中有4个三角形;第二个图形中有12个三角形;第三个图形中有20个三角形;…第n个图形中三角形的个数为8n﹣4,当n=10时,8n﹣4=76.故选:C.【点评】此题主要考查了数字变化规律,解决此类探究性问题,关键在观察、分析已知数据.5.如图是经典手机游戏“俄罗斯方块”中的图案,图1中有8个矩形,图2中有11个矩形,图3中有15个矩形,根据此规律,图5中共有()个矩形.A.19 B.25 C.26 D.31【分析】通过观察已知图形可得:图1中的矩形个数为8个,图2中的矩形个数为8+3个,图3中的矩形个数为8+3+4,依此类推,即可解答.【解答】解:图1中的矩形个数为8个,图2中的矩形个数为8+3,图3中的矩形个数为8+3+4,图4中的矩形个数为8+3+4+5,图3中的矩形个数为8+3+4+5+6=26(个),故选:C.【点评】本题考查了图形的变化规律,解决本题的关键是观察图形,得出规律.6.用边长相等的黑色正三角形与白色正六边形镶嵌图案,按图①②③所示的规律依次下去,则第10个图案中,所包含的黑色正三角形的个数是()A.36 B.38 C.40 D.42【分析】仔细观察发现第n个图案中,黑色正三角形的个数分别是4n.【解答】解:第1个图案中,黑色正三角形的个数分别是4;第2个图案中,黑色正三角形的个数分别是2×4=8;第3个图案中,黑色正三角形的个数分别是3×4=12;…第n个图案中,黑色正三角形的个数分别是4n.故当n=10时,4n=4×10=40.故选:C.【点评】本题考查了图形的变化类问题,找规律的题,应以第一个图象为基准,细心观察,得到第n个图形与第一个图形之间的关系.7.下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n (n≥2)个圆点时,图案的圆点数为S n.则S10有()个圆点.A.51 B.36 C.30 D.19【分析】此题重点注意各个顶点同时在两条边上,计算点的个数时,不要把顶点重复计算了.【解答】解:此题中药计算点的个数,可以类似周长的计算方法进行,但应注意各个顶点重复了一次.如当n=2时,共有S2=4×2﹣4=4;当n=3时,共有S3=4×3﹣4,…,依此类推,即S n=4n ﹣4,当n=10时,S10=4×10﹣4=36,故选:B.【点评】本题考查了图形的变化类问题,关键是通过归纳与总结,得到其中的规律.8.如图,某广场地面的图案是用大小相同的黑、白正方形地砖镶嵌而成,图中第1个黑色L形由3个正方形组成,第2个黑色L形由7个正方形组成,…那么第n个黑色L 形的正方形个数是()A.n2+1 B.n2+2 C.4n+1 D.4n﹣1【分析】看后面每个图形中正方形的个数是在3的基础上增加几个4即可.【解答】解:第1个黑色“”形由3个正方形组成,第2个黑色“”形由3+4=7个正方形组成,第3个黑色“”形由3+2×4=11个正方形组成,…,那么组成第n个黑色“”形的正方形个数是3+(n﹣1)×4=4n﹣1.故选:D.【点评】考查图形的变化规律;得到第n个图形与第1个图形中正方形个数之间的关系是解决本题的关键.9.如图案中由“△”按一定的规律组成的,从左到右排成一列(如图所示),第一个图是由3个“△”组成,第二个由6个“△”组成的,第三个是由10个“△”组成的,依此规律,由55个“△”组成的图案是左起第()个图.A.7 B.8 C.9 D.10【分析】仔细观察图形会发现第1个图有2+1个三角形,第2个图形有3+2+1个三角形,第3个图形有4+3+2+1个图形,故第n个图形+2+3有1+4+…n+1个图形,从而得到答案即可.【解答】解:观察图形会发现,仔细观察图形会发现第1个图有2+1个三角形,第2个图形有3+2+1个三角形,第3个图形有4+3+2+1个图形,…第n个图形有1+2+3+4+…n+1=个图形,故=55解得:n=9.故选:C.【点评】本题考查了图形的变化类问题,解题的关键是仔细观察并找到通项公式.10.现有3×3的方格,每个小方格内均有数目不同的点图,要求方格内每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.图中给出了部分点图,则P处所对应的点图是()A.B.C.D.【分析】根据图形可得x﹣2+1+x=1+5+x+1,解方程求得x,进一步得到P处所对应的点即可求解.【解答】解:如图,依题意有x﹣2+1+x=1+5+x+1,解得x=8,P=1+5+8+1﹣2﹣8﹣1=4.故选:B.【点评】本题考查了有理数的加法.考查了学生的观察归纳能力.11.如图,小桥用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有()个黑子.A.37 B.42 C.73 D.121【分析】观察图象得到第1、2图案中黑子有1个,第3、4图案中黑子有1+2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,…,据此规律可得.【解答】解:第1、2图案中黑子有1个,第3、4图案中黑子有1+2×6=13个,第5、6图案中黑子有1+2×6+4×6=37个,第7、8图案中黑子有1+2×6+4×6+6×6=73个,故选:C.【点评】本题考查了规律型:图形的变化类:通过从一些特殊的图形变化中发现不变的因素或按规律变化的因素,然后推广到一般情况.12.将一些半径相同的小圆按如图所示的方式摆放,图①中有8个小圆,图②中有13个小圆,图③中有19个小圆,图④中有26个小圆,照此规律,图⑨中小圆的个数为()A.64 B.76 C.89 D.93【分析】图①中有1+2+3+2=8个小圆,图②中有1+2+3+4+3=13个小圆,图③中有1+2+3+4+5+4=19个小圆,按此规律第9个图形中小圆的个数为1+2+3+4+5+6+7+8+9+10+11+10=76个小圆.【解答】解:图①中有1+2+3+2=8个小圆,图②中有1+2+3+4+3=13个小圆,图③中有1+2+3+4+5+4=19个小圆,…第9个图形中小圆的个数为1+2+3+4+5+6+7+8+9+10+11+10=76个.故选:B.【点评】此题考查图形的变化规律,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律,利用穷举法解答此题是一种很好的方法.13.下列图形都是由同样大小的等边三角形按一定的规律摆成,其中第①个图形有4个等边三角形,第②个图形有8个等边三角形,第③个图形有14个等边三角形,第④个图形有22个等边三角形,……,则第⑨个图形中等边三角形的个数是()A.76 B.84 C.91 D.92【分析】先根据题意求找出其中的规律,即可求出第⑨个图形中等边三角形的个数.【解答】解:第①个图形有4个等边三角形,第②个图形有4+2×2=8个等边三角形,第③个图形有4+2×2+2×3=14个等边三角形,第④个图形有4+2×2+2×3+2×4=22个等边三角形,所以第⑨个图形中等边三角形的个数是4+2×2+2×3+2×4+2×5+2×6+2×7+2×8+2×9=92,故选:D.【点评】此题考查图形的变化规律,找出图形之间的数字运算规律,得出规律,解决问题.14.找出以如图形变化的规律,则第101个图形中黑色正方形的数量是()A.149 B.150 C.151 D.152【分析】仔细观察图形并从中找到规律,然后利用找到的规律即可得到答案.【解答】解:∵当n为偶数时第n个图形中黑色正方形的数量为n+个;当n为奇数时第n个图形中黑色正方形的数量为n+个,∴当n=101时,黑色正方形的个数为101+51=152个.故选:D.【点评】本题考查了图形的变化类问题,解题的关键是仔细的观察图形并正确的找到规律.15.下列图形都是由同样大小的圆按一定的规律组成,其中,第(1)个图形中一共有2个圆;第(2)个图形中一共有7个圆;第(3)个图形中一共有16个圆;第(4)个图形中一共有29个圆,…,则第(8)个图形中圆的个数为()A.121 B.113 C.92 D.191【分析】第(1)个图形中最下面有1个圆,上面有一个圆;第(2)个图形中最下面有2个圆,上面有1+3+1个圆;第(3)个图形中最下面有3个圆,上面有1+3+5+3+1个圆,那么可得第(8)个图形最下面有8个圆,上面有1+3+5+7+9+11+13+15+13+11+9+7+5+3+1个圆,相加即可.【解答】解:第(1)个图形中最下面有1个圆,上面有1个圆共有2个;第(2)个图形中最下面有2个圆,上面有1+3+1个圆共有7个;第(3)个图形中最下面有3个圆,上面有1+3+5+3+1个圆共有16个;…第(n)个图形中共有(2n2﹣n+1)个圆;第(8)个图形中共有2×82﹣8+1=121,故选:A.【点评】考查图形的变换规律;根据图形的排列规律得到最下面圆的个数与图形的序号相同,上面圆的个数与n个连续奇数的和相关是解决本题的关键.16.下列图案均是用长度相同的小木棒按一定的规律拼搭而成;拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,…,依此规律,拼搭第8个图案需小木棒()根.A.144 B.108 C.88 D.84【分析】分析题意,找到规律,并进行推导得出答案.【解答】解:分析可得:第1个图形中,有4根火柴;第2个图形中,有4+6=10根火柴;第3个图形中,有10+8=18根火柴;…第8个图形中,共用火柴的根数是4+6+8+10+12+14+16+18=88根.故选:C.【点评】本题考查学生通过观察、归纳、抽象出数列的规律的能力.17.同样大小的黑色棋子按如图所示的规律摆放,第()个图形有2013个黑色棋子.A.668 B.669 C.670 D.671【分析】根据图中所给的黑色棋子的颗数,找出其中的规律,根据规律列出式子,即可求出答案.【解答】解:(1)第一个图需棋子6,第二个图需棋子9,第三个图需棋子12,第四个图需棋子15,第五个图需棋子18,…第n个图需棋子3(n+1)枚.设第n个图形有2013颗黑色棋子,得3(n+1)=2013解得n=670,所以第670个图形有2013颗黑色棋子故选:C.【点评】此题考查了图形的变化类,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律.18.下列图形都是用同样大小的按一定的规律组成的,其中第①个图形中一共有1个“•”,第②个图形一共有5个“•”,第③个图形一共有11个“•”,…,则第⑧个图形中“•”的个数为()A.55 B.71 C.81 D.90【分析】根据图形的变化得出规律进行解答即可.【解答】解:由图形可以得出:第一个图形点的个数为1×2﹣1,第二个图形点的个数为2×3﹣1,第三个图形点的个数为3×4﹣1,第四个图形为4×5﹣1,所以第八个图形为8×9﹣1=71,故选:B.【点评】此题考查图形的变化规律问题,关键是由图形变化探究出其规律解答.19.观察图中正方形四个顶点所标的数字规律,推测数2019应标在()A.第504个正方形的左下角B.第504个正方形的右下角C.第505个正方形的右下角D.第505个正方形的左上角【分析】设第n个正方形中标记的最大的数为a n,观察给定图形,可找出规律“a n=4n”,依此规律即可得出结论.【解答】解:设第n个正方形中标记的最大的数为a n.观察给定正方形,可得出:每个正方形有4个数,即a n=4n.∵2019=504×4+3,∴数2019应标在第505个正方形左上角.故选:D.【点评】本题考查了规律型中的图形的变化类,解题的关键是找出变换规律a n=4n.本题属于基础题,难度不大,需找出2019在第几个正方形上.二.填空题(共18小题)20.现有各边长度均为1cm的小正方体若干个,按下图规律摆放,则第5个图形的表面积是90cm2.【分析】对于找规律的题目首先应找出哪个部分发生了变化,是按照什么规律变化的.【解答】解:根据题意可得:每个图形的表面积为最下层正方体的表面积之和;第5个图形中,共5层;从上到下,每层正方体个数为1,3,6,10,15,共35个正方体;其表面积为15×6=90cm2.【点评】本题是一道找规律的题目,这类题型在中考中经常出现.21.探索规律:右边是用棋子摆成的“H”字,按这样的规律摆下去,摆成第10个“H”字需要52个棋子.【分析】图形①用棋子的个数=2×(2×1+1)+1;图形②用棋子的个数=2×(2×2+1)+2;图形③用棋子的个数=2×(2×3+1)+3;…图形⑩用棋子的个数=2×(2×10+1)+10=52个.故答案为:52.【解答】解:观察图形可知第10个“H”字用棋子的个数=2×(2×10+1)+10=52个.【点评】通过观察,分析、归纳并发现其中的规律,并应用发现的规律解决问题是应该具备的基本能力.本题的关键规律为各个图形中两竖行棋子的个数均为2n+1,横行棋子的个数为n.22.观察下列各图中小圆点的摆放规律,并按这样的规律继续摆放下去,则第5个图形中小圆点的个数为50.【分析】对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.【解答】解:根据题意分析可得:第1个图形中小圆点的个数为10=(1+2)2+1;第2个图形中小圆点的个数为17=(2+2)2+1;第3个图形中小圆点的个数为26=(3+2)2+1;…;第5个图形中小圆点的个数为7×7+1=50.故第5个图形中小圆点的个数为50.【点评】本题是一道找规律的题目,这类题型在中考中经常出现.23.如图,已知△ABC的面积S△ABC=1.在图(1)中,若,则;在图(2)中,若,则;在图(3)中,若,则;按此规律,若,则=(提示:用三点式求出抛物线的解析式,再求函数值).【分析】求得三角形ABC的面积S与对应边的比值之间的函数关系,然后代入比值求函数值即可.【解答】解:设函数关系为S=ax2+bx+c,∵若,则;若,则;若,则;∴解得:a=3,b=﹣3,c=1∴S=3x2﹣3x+1∴若,S=3×()2+(﹣3)×+1=.故答案为.【点评】主要考查了学生通过特例分析从而归纳总结出一般结论的能力.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.24.如图,由等圆组成的一组图中,第1个图由1个圆组成,第2个图由7个圆组成,…,按照这样的规律排列下去,则第8个图形由169个圆组成.【分析】首先分析题意,找到规律,并进行推导得出答案.【解答】解:观察分析可得:第1个图形有1个圆,第2个图由1+6=7个圆组成,第3个图由7+2×6=19即1+6+12个圆组成,…,第8个图形由1+6+12+18+24+30+36+42=169个圆.故答案为:169.【点评】本题考查了规律型中的图形变化问题,同时考查了学生通过观察、归纳、抽象出数列的规律的能力.25.按照如图所示的方法排列黑色小正方形地砖,则第14个图案中黑色小正方形地砖的块数是365.【分析】观察图形可知,黑色与白色的地砖的个数的和是连续奇数的平方,而黑色地砖比白色地砖多1个,求出第n个图案中的黑色与白色地砖的和,然后求出黑色地砖的块数,再把n=14代入进行计算即可.【解答】解:第1个图案只有1块黑色地砖,第2个图案有黑色与白色地砖共32=9,其中黑色的有5块,第3个图案有黑色与白色地砖共52=25,其中黑色的有13块,…第n个图案有黑色与白色地砖共(2n﹣1)2,其中黑色的有[(2n﹣1)2+1],当n=14时,黑色地砖的块数有[(2×14﹣1)2+1]=×730=365.故答案为:365.【点评】本题是对图形变化规律的考查,观察图形找出黑色与白色地砖的总块数与图案序号之间的关系是解题的关键.26.观察下列砌钢管的横截面图:则第n个图的钢管数是n2+n(用含n的式子表示)【分析】本题可依次解出n=1,2,3,…,钢管的个数.再根据规律以此类推,可得出第n堆的钢管个数.【解答】解:第一个图中钢管数为1+2=3;第二个图中钢管数为2+3+4=9;第三个图中钢管数为3+4+5+6=18;第四个图中钢管数为4+5+6+7+8=30,。
中考数学几何专题——手拉手模型一

手拉手模型一、手拉手模型1.手的判别:人站在等腰三角形顶角的位置,张开双臂,左手边的腰为左手,右手边的腰为右手。
2.手拉手模型的定义:两个等顶角的等腰三角形组成的图形,且顶角的顶点为公共顶点。
(顶角相等、等腰三角形、共顶点)条件模型结论特殊结论△ABC与△CDE是等腰三角形,且∠ACB=∠DCE (1)D ACD@D BCE (SSS)(2)AD=BE(左手拉左手,右手拉右手)(3)ÐBHA=ÐBCA(4)HC平分ÐAHE△ABC与△CDE是等腰直角三角形,且∠ACB=∠DCE=90°(5)S D BCD=S D ACE(6)BD2+AE2=AB2+DE2正方形ACBP与正方形CEQD是正方形△ABC 与△CDE是等边三角形(5)D ACM@D BCND DCM@D ECN(6) CM=CN(7)D CMN是等边三角形(8)MN∥AE,CD∥AB, CB∥DE(9) BH+CH=AHDH+CH=EH二、手拉手模型的变形:(两三角形相似,且对应角共顶点)条件模型结论D BAC∽D DAE,且ÐDAE=ÐBAC (1)D BAD∽D CAE(两边对应成比例且夹角相等) (2)BDCE=BACA(3) ÐBHC=ÐBAC【巩固练习】1、如图所示,若△ABC、△ADE都是正三角形,试比较线段BD与线段CE的大小.2、如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是()3、如图,分别以△ABC的三边为边在BC的同侧作三个等边三角形,即△ABD,△BCE,△ACF.请回答下列问题:(1)说明四边形ADEF是什么四边形?(2)当△ABC满足什么条件时,四边形ADEF是矩形?(3)当△ABC满足什么条件时,四边形ADEF是菱形?(4)当△ABC满足什么条件时,四边形ADEF是正方形?(5)当△ABC满足什么条件时,以A,D,E,F为顶点的四边形不存在?4、问题情境:如图1,已知△ABC和△DCE中,∠ACB=∠DCE=90°,AC=BC=2,CD=CE=1,点D在AC 边上,点E 在BC 延长线上。
2023年中考数学 几何培优专题:线段等量关系的证明(含答案)
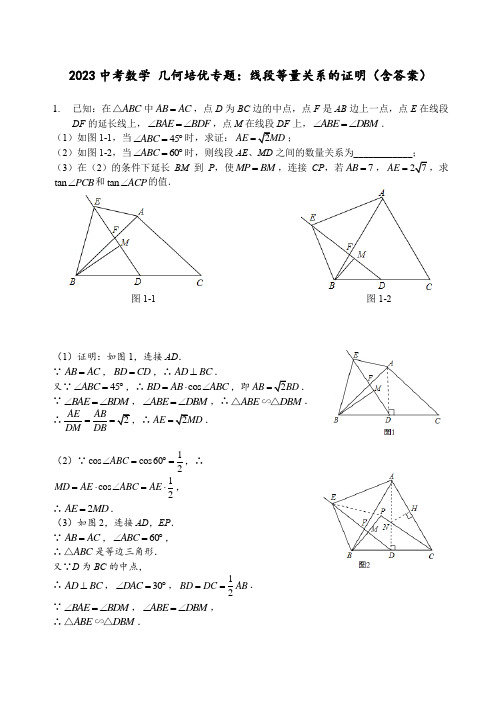
2023中考数学 几何培优专题:线段等量关系的证明(含答案)1. 已知:在ABC △中AB AC =,点D 为BC 边的中点,点F 是AB 边上一点,点E 在线段DF 的延长线上,BAE BDF ∠=∠,点M 在线段DF 上,ABE DBM ∠=∠. (1)如图1-1,当45ABC ∠=︒时,求证:2AE MD =;(2)如图1-2,当60ABC ∠=︒时,则线段AE 、MD 之间的数量关系为____________;(3)在(2)的条件下延长BM 到P ,使MP BM =,连接CP ,若7AB =,27AE =,求tan PCB ∠和tan ACP ∠的值.图1-1 图1-2(1)证明:如图1,连接AD .∵AB AC =,BD CD =,∴AD BC ⊥.又∵45ABC ∠=︒,∴cos BD AB ABC =⋅∠,即2AB BD =. ∵BAE BDM ∠=∠,ABE DBM ∠=∠,∴ABE DBM ∽△△.∴2AE AB DM DB ==,∴2AE MD =.(2)∵1cos cos602ABC ∠=︒=,∴1cos 2MD AE ABC AE =⋅∠=⋅,∴2AE MD =.(3)如图2,连接AD ,EP . ∵AB AC =,60ABC ∠=︒, ∴ABC △是等边三角形. 又∵D 为BC 的中点,∴AD BC ⊥,30DAC ∠=︒,12BD DC AB ==.∵BAE BDM ∠=∠,ABE DBM ∠=∠, ∴ABE DBM ∽△△.∴2BE ABBM DB ==,AEB DMB ∠=∠. ∴2EB BM =. 又∵BM MP =, ∴EB BP =.∵60EBM ABC ∠=∠=︒, ∴BEP △为等边三角形, ∴EM BP ⊥, ∴90BMD ∠=︒, ∴90AEB ∠=︒,在Rt AEB △中,AE =7AB =,∴BE∴tan EAB ∠. ∵D 为BC 中点,M 为BP 中点,∴DM//PC .∴MDB PCB ∠=∠,∴EAB PCB ∠=∠.∴tan PCB ∠=.在Rt ABD △中,sin AD AB ABD =⋅∠在Rt NDC △中,tan ND DC NCD =⋅∠,∴NA AD ND =-.过N 作NH AC ⊥,垂足为H .在Rt ANH △中,12NH AN ==,21cos 8AH AN NAH =⋅∠=,∴358CH AC AH =-=,∴tan ACP ∠=.2.如图,在Rt ABC△中,90ACB∠=︒,1AC=,7BC=,点D是边CA延长线的一点,AE BD⊥,垂足为点E,AE的延长线交CA的平行线BF于点F,连结CE交AB于点G.(1)当点E是BD的中点时,求tan AFB∠的值;(2)CE AF⋅的值是否随线段AD长度的改变而变化?如果不变,求出CE AF⋅的值;如果变化,请说明理由;(3)当BGE△和BAF△相似时,求线段AF的长.(1)过点E作EH CD⊥于H,如图1,则有90EHA EHD∠=∠=︒.∵90BCD∠=︒,BE DE=,∴CE DE=.∴CH DH=,∴1722 EH BC==.设AH x=,则1DH CH x==+.∵AE BD⊥,∴90 AEH DEH AED∠+∠=∠=︒.∵90AEH EAH∠+∠=︒,∴EAH DEH∠=∠,∴AHE EHD∽△△,∴AH EH EH DH=,∴2EH AH DH=⋅,∴27(1)2x x⎛⎫=+⎪⎝⎭,解得5212x-=(舍负),∴75212tan75212EHEAHAH+∠===-.∵BF//CD,∴AFB EAH∠=∠,∴521tan 7AFB +∠=; (2)CE AF ⋅的值不变.取AB 的中点O ,连接OC 、OE ,如图2, ∵90BCA BEA ∠=∠=︒, ∴OC OA OB OE ===, ∴点A 、C 、B 、E 共圆,∴BCE BAF ∠=∠,180CBE CAE ∠+∠=︒. ∵BF//CD ,∴180BFA CAE ∠+∠=︒, ∴CBE BFA ∠=∠,∴BCE FAB ∽△△, ∴BC CE FA AB=,∴CE FA BC AB ⋅=⋅. ∵90BCA ∠=︒,7BC =,1AC =,∴52AB =,∴752=352CE FA ⋅=⨯;(3)过点E 作EH CD ⊥于H ,作EM BC ⊥于M ,如图3, ∴90EMC MCH CHE ∠=∠=∠=︒, ∴四边形EMCH 是矩形.∵BCE FAB ∽△△,BGE △与FAB △相似, ∴BGE △与BCE △相似, ∴EBG ECB ∠=∠.∵点A 、C 、B 、E 共圆, ∴ECA EBG ∠=∠,∴ECB ECA ∠=∠,∴EM EH =, ∴矩形EMCH 是正方形, ∴CM CH =.∵1452ECB ECA BCA ∠=∠=∠=︒,∴45EBA EAB ∠=∠=︒, ∴EB EA =,∴Rt Rt (HL)BME AHE ≌△△,∴BM AH =.设AH x =,则BM x =,7CM x =-,1CH x =+, ∴71x x -=+,∴3x =,∴4CH =.在Rt CHE △中,42cos 2CH ECH CE CE ∠===, ∴42CE =.由(2)可得352CE FA ⋅=,∴35235=442AF =.3. 已知:ACB △与DCE △为两个有公共顶点C 的等腰直角三角形,且90ACB DCE ∠=∠=︒,AC BC =,DC EC =.把DCE △绕点C 旋转,在整个旋转过程中,设BD 的中点为N ,连接CN .(1)如图3-1,当点D 在BA 的延长线上时,连接AE ,求证:2AE CN =;(2)如图3-2,当DE 经过点A 时,过点C 作CH BD ⊥,垂足为H ,设AC 、BD 相交于F ,若4NH =,16BH =,求CF 的长.(1)证明:延长CN 至点K ,使NK CN =,连接DK , ∵90DCA ACE ∠+∠=︒,90BCE ACE ∠+∠=︒, ∴180DCB ACE ∠+∠=︒,∴KDN CBN ∠=∠,∴DK//BC ,∵DN NB =,CN NK =,DNK BNC ∠=∠, ∴DNK BNC ≌△△,∴DK BC AC ==,∴180KDC DCB ∠+∠=︒,∵KDC ACE ∠=∠, 又∵DK AC =,CD CE =,∵KDC ACE ≌△△, ∴AE CK =,∴2AE CN =;(2)延长CN 交DE 于点P ,延长CH 交DE 于点M ,图3-1D A NB EC图① 图② 备用图D A N BE DF A N H C C B ED B EF A N H KP M C备用图BF AN H CE图3-2A F N H DC B E4. 已知:在ABC △中,90ACB ∠=︒,点P 是线段AC 上一点,过点A 作AB 的垂线,交BP的延长线于点M ,MN AC ⊥于点N ,PQ AB ⊥于点Q ,AQ MN =.(1)如图4-1,求证:PC AN =;(2)如图4-2,点E 是MN 上一点,连接EP 并延长交BC 于点K ,点D 是AB 上一点,连接DK ,DKE ABC ∠=∠,EF PM ⊥于点H ,交BC 延长线于点F ,若2NP =,3PC =,:2:3CK CF =,求DQ 的长.图4-1 图4-2AQNPMAMQDNEPHAQ NPM B CAMQDNEPHB KC F GT图①图②5. 在ABC △中,90ACB ∠=︒.经过点B 的直线l (l 不与直线AB 重合)与直线BC 的夹角等于ABC ∠,分别过点C 、点A 作直线l 的垂线,垂足分别为点D 、点E .(1)若45ABC ∠=︒,1CD =(如图),则AE 的长为_______; (2)写出线段AE 、CD 之间的数量关系,并加以证明; (3)若直线CE 、AB 交于点F ,56CF EF =,4CD =,求BD 的长.(1)2AE =.(2)线段AE 、CD 之间的数量关系为2AE CD =. 证明:如图1,延长AC 与直线l 交于点G . 依题意,可得12∠=∠. ∵90ACB ∠=︒,∴34∠=∠. ∴BA BG =,∴CA CG =.∵AE l ⊥,CD l ⊥,∴CD //AE . ∵C 为AG 的中点,∴2AE CD =.(3)解:当点F 在线段AB 上时,如图2, 过点C 作CG //l 交AB 于点H ,交AE 于点G . ∴2HCB ∠=∠.∵12∠=∠,∴1HCB ∠=∠. ∴CH BH =.∵90ACB ∠=︒,∴34901HCB ∠+∠∠+∠=︒=. ∴34∠∠=.∴CH AH BH ==. ∵CG //l ,∴FCH △∽FEB △. ∴56CF CH EF EB ==. 设5CH x =,6BE x =,则10AB x =. ∴在AEB △中,90AEB ∠=︒,8AE x =. 由(2)得,2AE CD =.∵4CD =,∴8AE =.∴1x =. ∴10AB =,6BE =,5CH =. ∵CG //l ,∴AGH AEB △△∽. ∴12HG AH BE AB ==.∴3HG =. ∴8CG CH HG =+=. ∵CG //l ,CD //AE ,A C()D B E l图1A C3124G D B E l图2AC124D B El3GHF∴四边形CDEG 为平行四边形. ∴8DE CG ==.∴2BD DE BE =-=.当点F 在线段BA 的延长线上时,如图3, 同理可得5CH =,3GH =,6BE =. ∴2DE CG CH HG ==-=. ∴8BD DE BE =+=. ∴2BD =或8.6. 如图,在平面直角坐标系中,直线l 平行x 轴,交y 轴于点A ,第一象限内的点B 在l 上,连结OB ,动点P 满足90APQ ∠=︒,PQ 交x 轴于点C .(1)当动点P 与点B 重合时,若点B 的坐标是(2,1),求P A 的长.(2)当动点P 在线段OB 的延长线上时,若点A 的纵坐标与点B 的横坐标相等,求:PA PC 的值.(3)当动点P 在直线OB 上时,点D 是直线OB 与直线CA 的交点,点E 是直线CP 与y 轴的交点,若ACE AEC ∠=∠,2PD OD =,求:PA PC 的值.(1)∵点P 与点B 重合,点B 的坐标是(2,1), ∴点P 的坐标是(2,1).∴P A 的长为2.(2)过点P 作PM x ⊥轴,垂足为M ,过点P 作PN y ⊥轴,垂足为N ,如图1所示.∵点A 的纵坐标与点B 的横坐标相等, ∴OA AB =.∵90OAB ∠=︒,∴45AOB ABO ∠=∠=︒. ∵90AOC ∠=︒,∴45POC ∠=︒. ∵PM x ⊥轴,PN y ⊥轴,∴PM PN =,90ANP CMP ∠=∠=︒. ∴90NPM ∠=︒.∵90APC ∠=︒. ∵APN CPM ∠=∠,PN PM =,ANP CMP ∠=∠, ∴ANP CMP ≌△△.∴PA PC =. ∴:PA PC 的值为1:1.(3)①若点P 在线段OB 的延长线上,过点P 作PM x ⊥轴,垂足为M ,过点P 作PN y ⊥轴,垂足为N ,PM 与直线AC 的交点为F ,如图2所示. ∵APN CPM ∠=∠,ANP CMP ∠=∠,∴ANP CMP ∽△△.∴PA PNPC PM=. ∵ACE AEC ∠=∠,∴AC AE =. ∵AP PC ⊥,∴EP CP =.∵PM//y 轴,∴AF CF =,OM CM =.∴12FM OA =.设OA x =,∵PF//OA ,∴PDF ODA ∽△△.∴PF PDOA OD=∵2PD OD =,∴22PF OA x ==,12FM x =.∴52PM x =.∵90APC ∠=︒,AF CF =, ∴24AC PF x ==. ∵90AOC ∠=︒,∴OC =.∵90PNO NOM OMP ∠=∠=∠=︒, ∴四边形PMON 是矩形.∴PN OM =.∴5:::2PA PC PN PM x ===. ②点P 在BO 延长线上时,同理可得:32PM x =,24CA PF x ==,OC =.∴12PN OM OC ==.∴3:::PA PC PN PM x ===. 综上所述::PA PC.7. 正方形ABCD 和等腰直角DEF △有公共点D ,点E 在AD 边上,点F 在CD 的延长线上,连接CE ,AF .(1)试判断线段CE 和AF 的数量关系和位置关系,并证明你的结论;(2)将DEF △绕点D 按顺时针方向旋转,当点E 落在AC 上时,设EF 与AD 交于点M . ①求证:AEM CDE ∽△△;②当34AE EC =时,求AM MD的值.(1)CE AF ⊥,CE AF =.证明略 (2)①∵AC 为正方形ABCD 的对角线 ∴45DAC ACD ∠=∠=︒,∵45FED ∠=︒,180FED AEM CED ∠+∠+∠=︒,180MAE AME AEM ∠+∠+∠=︒, ∴CED AME ∠=∠,∴AEM CDE ∽△△,②∵AEM CDE ∽△△,∴AE AMDC=, ∴设3AE a =,4EC a =,则DC =,4AMa=,∴AM ,∴MD =, ∴2425AM MD =. A B C E A BF D CEM8. 已知:在菱形ABCD 中,O 是对角线BD 上的一动点.(1)如图2-1,P 为线段BC 上一点,连接PO 并延长交AD 于点Q ,当O 是BD 的中点时,求证:OP OQ =;(2)如图2-2,连接AO 并延长,与DC 交于点R ,与BC 的延长线交于点S .若4AD =,60DCB ∠=︒,10BS =,求AS 和OR 的长.图2-1 图2-2(1)证明:∵ABCD 为菱形,∴AD//BC ,∴OBP ODQ ∠=∠,∵O 是是BD 的中点,∴OB OD =,在BOP △和DOQ △中,∵OBP ODQ ∠=∠,OB OD =,BOP DOQ ∠=∠,∴(ASA)BOP DOQ ≌△△,∴OP OQ =. (2)解:如图,过A 作AT BC ⊥,与CB 的延长线交于T .∵ABCD 是菱形,60DCB ∠=︒,∴4AB AD ==,60ABT ∠=︒,∴sin 60AT AB =︒=,cos602TB AB =︒=, ∵10BS =,∴12TS TB BS =+=,∴AS = ∵AD//BS ,∴AOD SOB △△∽. ∴42105AO AD OS SB ===, 则25AS OS OS -=,∴75AS OS =,∵AS =75OS AS ==. 同理可得ARD SRC △△∽,∴4263AR AD RS SC ===,则23AS SR RS -=,∴5AS =,∴3RS AS ==∴OR OS RS =-=-=.A DB C S O R TA QDOBP CA DB C SOR9. 在矩形ABCD 中,点P 在AD 上,2AB =,1AP =.将直角尺的顶点放在P 处,直角尺的两边分别交AB ,BC 于点E ,F ,连接EF (如图3-1). (1)当点E 与点B 重合时,点F 恰好与点C 重合(如图3-2),求PC 的长; (2)探究:将直尺从图3-2中的位置开始,绕点P 顺时针旋转,当点E 和点A 重合时停止.在这个过程中,请你观察、猜想,并解答:①tan ∠PEF 的值是否发生变化?请说明理由;②直接写出从开始到停止,线段EF 的中点经过的路线长.图3-1 图3-2(1)在矩形ABCD 中,90A D ∠=∠=︒,1AP =,2CD AB ==,则PB =, ∴90ABP APB ∠+∠=︒,又∵90BPC ∠=︒,∴90APB DPC ∠+∠=︒,∴ABP DPC ∠=∠,∴APB DCP ∽△△,∴AP PBCD PC=,即12=PC =故答案为:(2)①PF PE的值不变,理由为:证明:过F 作FG AD ⊥,垂足为G ,则四边形ABFG 是矩形,∴90A PGF ∠=∠=︒,2GF AB ==, ∴90AEP APE ∠+∠=︒,又∵90EPF ∠=︒, ∴90APE GPF ∠+∠=︒,∴AEP GPF ∠=∠,∴APE GFP ∽△△,∴2PF GFPE AP==,∴Rt EPF △中,tan 2PFPEF PE∠==,∴PF PE的值不变. ②线段EF.A P DEB F CGA P DE BF C A P D ()()B E C F10. 已知:ABC △中,2ACB ABC ∠=∠,AD 为BAC ∠的平分线,E 为线段AC 上一点,过E作AD 的垂线交直线AB 于F . (1)当E 点与C 点重合时(如图4-1),求证:BF DE =;(2)连接BE 交AD 于点N ,M 是BF 的中点,连接DM (如图4-2),若DM BF ⊥,4DC =,:3:2ABD ACD S S =△△,求DN 的长.图4-1 图4-2(1)连接DF ,设AD 与EF 交于点K ,∵AD 是BAC ∠的平分线,∴BAD CAD ∠=∠, ∵EF AD ⊥,∴90AKF AKE ∠=∠=︒,∴AFK AEK ∠=∠,∴AF AE =,∴AFD AED ≌△△, ∴DF DE =,AFD AED ∠=∠,又∵2ACB ABC ∠=∠,∴FBD FDB ∠=∠,∴BF DF =,∴DE BF =; (2)过A 作AP ⊥BC 于点P ,过D 作DQ ⊥AC 于点Q .连接DF ,∵:3:2ABD ACD S S =△△,即132122BD APDC AP ⋅=⋅, ∴32BD DC =,∵4DC =,∴6BD =, AF()BD CE BD CFAMEN图1 图2 A F ()B D C E B D C F A M E N K Q P∵AD 是BAC ∠的平分线,DM AB ⊥,DQ AC ⊥,∴DM DQ =,∴132122AB DMAC DQ ⋅=⋅,∴32AB AC =由(1)可得:AQ AM =,DC BM =,∴AB AC DC =+, ∴32AC DC AC +=,∴8AC =,12AB =,设PC x =,则10BP x =-,又勾股定理得:22222AB BP AC PC AP -=-=, 即22122(10)82x x --=-,解得:1x =,∴3DP =, 又22222AD DP AC PC AP -=-=, ∴272AD =,AD =EF AD ⊥, ∴90AKF AKE ∠=∠=︒. ∵DA 平分BAC ∠, ∴FAD EAD ∠=∠,∴AFE AEF ∠=∠,∴AF AE =, ∴AFD AED ≌△△,∴AFD AED ∠=∠,DF DE =, 又∵DB DF =, ∴6DB DE ==,∴BFD DEC DBF ∠=∠=∠,∴180180C DEC C DBF ︒-∠-∠=︒-∠-∠, ∴2EDC BAC DAE ∠=∠=∠, 又∵2EDC NED ∠=∠, ∴DAE NED ∠=∠, ∵ADE EDN ∠=∠, ∴DAE DEN ∽△△, ∴DA DE DE DN=, ∴2DE DN DA =⋅,即36DN =⋅,∴DN =。
2023年九年级数学中考专题:几何探究压轴题

2023年九年级数学中考专题:几何探究压轴题一、解答题1.如图,在ABC 中,4AC =,3BC =,90ACB ∠=︒,D 是边AC 上一动点(不与点A 、C 重合),CE BD ⊥,垂足为E ,交边AB 于点F .(1)当点D 是边AC 中点时,求DE ,EC 的值;(2)设CD x =,AF y =,求y 关于x 的函数关系式,并写出定义域;(3)当EFD △与EFB △相似时,求线段CD 的长.2.【温故知新】黄金分割是一种最能引起美感的分割比例,具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值.我们知道:如图1,点C 把线段AB 分成两部分,如果BC AC AC AB=,那么称点C 为线段AB 的黄金分割点.(1)【问题发现】如图1,点C 为线段AB 的黄金分割点,且AC BC >,若2AB =,请直接写出CB 的值是__________.(2)【问题探究】如图2,在Rt ABC △中,90C ∠=︒,2AC =,1BC =,在BA 上截取BD BC =,再在AC 上截取AE AD =,则AE AC的值为__________. (3)【问题解决】如图3,用边长为6的正方形纸片进行如下操作:对折正方形ABDE 得折痕MN ,连接EN ,将AE 折叠到EN 上,点A 对应点H ,得折痕CE ,试说明:C 是AB 的黄金分割点.3.定义:若连接三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形,我们称这条线段为该三角形的智慧线,这个三角形叫做智慧三角形.(1)如图1,在智慧三角形ABC 中,AD BC ⊥,AD 为该三角形的智慧线,1CD =,则BD 长为_____,B ∠的度数为_____.(2)如图2,ABC 为等腰直角三角形,90BAC ∠︒=,2AB =,F 是斜边BC 延长线上一点,连接AF ,以AF为直角边作等腰直角三角形AFE (点A ,F ,E 按顺时针排列),90EAF ∠=︒, CF =AE 交BC 于点D ,连接EC ,EB .当2BDE BCE ∠=∠时,求线段ED 的长;(3)如图3,ABC 中,5AB AC ==,BC =BCD △是智慧三角形,且AC 为智慧线,求BCD △的面积.4.【问题提出】如图1,在等边三角形ABC 内部有一点P ,3PA=,4PB =,5PC =,求APB ∠的度数.(1)【尝试解决】将APC △绕点A 逆时针旋转60︒,得到AP B '△,连接PP ',则APP '为等边三角形. ∵3P P PA '==,4PB =,5P B PC '==,∴222=P P PB P B ''+∴BPP '为三角形∴APB ∠的度数为.(2)【类比探究】如图2,在等边三角形ABC 外部有一点P ,若∠BP A =30°,求证222PA PB PC +=.(3)【联想拓展】如图3,在ABC 中,90BAC ∠︒=,AB AC =.点P 在直线BC 上方且45APB ∠︒=,PC BC ==求PA 的长.5.已知正方形 ABCD 和正方形 CEFG ,连接 AF 交 BC 于点 O ,点 P 是 AF 的中点,过点 P 作 PH DG ⊥ 于 H ,2CD =,1CG =.(1)如图1,点 D ,C ,G 在同一直线上,点 E 在 BC 边上,求 PH 的长;(2)把正方形 CEFG 绕着点C 逆时针旋转 ()0180αα<<.①如图2,当点E 落在AF 上时,求CO 的长;②如图3,当DG =PH 的长.6.在ABC ∆中,点E 为AC 边上一动点,以CE 为边在CE 上方作等边CEN .(1)如图1,EN 与AB 交于点P ,连接PC ,若tan A =,1AE =,5CN =,求PC 的长: (2)如图2.当N 与B 重合时,在BC 上取一点D ,过点D 作DF AC ∥,连接BF ,EF ,过C 作CH EF ⊥交EF 于点H ,若30FBC DFE ︒∠-∠=,求证:CH BF +=;(3)如图3,若BC AB ⊥,且4AB BC ==,过点B 作BQ AC ∥,I 为射线.BQ 上一动点,取AC 中点M ,连接MI ,过点B 作BK MI ⊥交M 于点K ,连接NK ,直接写出NK 的最小值.7.问题情境:如图1,在Rt △ABC 和Rt △BEF 中,∠ACB =∠EFB =90°,AC =3,BC =4,且M ,N 分别为AE ,CF 的中点.(1)猜想证明:如图2,将Rt △BEF 绕点B 按逆时针方向旋转90°,其他条件不变.试判断54AM CN =是否成立?若成立,请写出证明过程;若不成立,请说明理由.(2)解决问题:如图3,将图2中的Rt △BEF 沿BF 所在直线折叠得到Rt BE F ',连接AE ',CF ,并分别取它们的中点P ,H ,连接CP ,FP ,PH .①试判断CP 与FP 之间的数量关系,并说明理由.②若AB =2BE ',BC =2BF ,请直接写出PH 的长.8.【方法尝试】(1)如图1,矩形ABFC 是矩形ADGE 以点A 为旋转中心,按逆时针方向旋转90︒所得的图形,CB ED 、分别是它们的对角线.则CB 与ED 数量关系________,位置关系________.【类比迁移】(2)如图2,在Rt ABC 和Rt ADE △中,90,9,6,3,2BAC DAE AC AB AE AD ∠=∠=︒====.将DAE 绕点A 在平面内逆时针旋转,设旋转角BAE ∠为()0360αα︒<︒,连接,CE BD .请判断线段CE 和BD 的数量关系和位置关系,并说明理由;【拓展延伸】(3)如图3,在Rt ABC 中,90,6ACB AB ∠=︒=,过点A 作AP BC ∥,在射线AP 上取一点D ,连结CD,使得3tan4ACD∠=,请求写出线段BD的最大值.9.如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连接AM、AN、MN.∠MAN=45°,将△AMD 绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.【实践探究】(1)在图①条件下,若CN=6,CM=8,则正方形ABCD的边长是______.(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.(3)【拓展应用】如图③,在矩形ABCD中,AB=6,AD=8,点M、N分别在边DC、BC上,连接AM,AN,已知∠MAN=45°,BN=2,求DM的长.10.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.(1)猜测探究:在△ABC中,AB=AC,M是平面内任意一点,将线段AM绕点A按顺时针方向旋转与∠BAC 相等的角度,得到线段AN,连接NB.①如图1,若M是线段BC上的任意一点,请直接写出∠NAB与∠MAC的数量关系是,NB与MC的数量关系是;②如图2,点E是AB延长线上点,若M是∠CBE内部射线BD上任意一点,连接MC,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(2)拓展应用:如图3,在△A 1B 1C 1中,A 1B 1=8,∠A 1B 1C 1=60°,∠B 1A 1C 1=75°,P 是B 1C 1上的任意点,连接A 1P ,将A 1P 绕点A 1按顺时针方向旋转75°,得到线段A 1Q ,连接B 1Q .求线段B 1Q 长度的最小值. 11.如图,在Rt ABC △中,90BAC ∠=︒,AB AC =,D 为AC 边上一点,连接BD ,作AP BD ⊥于点P ,过点C 作CE AC ⊥交AP 延长线于点E .(1)如图1,求证:AD CE =;(2)如图2,以AD ,BD 为邻边作ADBF ,连接EF 交BC 于点G ,连接AG ,①求证:AG EF ⊥;②若点D 为AC 中点,EF 、AB 交于点H ,求BH AB的值. 12.如图1,在ABC 中,90ACB ∠=︒,D 为AC 边上的一点,过点D 作DE AB ⊥,垂足为E ,连接BD ,P 为BD 中点,连接PC ,PE .(1)求证:PC PE =;(2)将图1中ADE 绕着点A 顺时针旋转如图2的位置,其他条件不变,(1)中的结论是否成立?若成立,请证明:若不成立,请说明理由;(3)若10AB =,6AD =,30BAC DAE ∠=∠=︒,在平面内,将Rt ADE △绕点A 旋转一周,当A ,C ,E 三点共线时,请直接写出PCE 的面积.13.如图1,在直角坐标系中,点()2,0A ,点()0,2C ,点D ,点E 分别为OA ,OC 的中点,ODE 绕原点O 顺时针旋转α角(090α︒<<︒)得11OD E ,射线1CD ,1AE 相交于点F .(1)求证:11OCD OAE △≌△;(2)如图2,在ODE 旋转过程中,当点1D 恰好落在线段CE 上时,求AF 的长;(3)如图3,在旋转α角从090α︒≤≤︒逐渐增大ODE 旋转过程中,求点F 的运动路线长.14.已知ABC 为等边三角形,边长为4,点D 、E 分别是BC 、AC 边上一点,连接AD 、BE .AE CD =.(1)如图1,若2AE =,求BE 的长度;(2)如图2,点F 为AD 延长线上一点,连接BF 、CF ,AD 、BE 相交于点G ,连接CG ,已知60,∠=︒=EBF CE CG ,求证:2+=BF GE CF ;(3)如图3,点P 是ABC 内部一动点,顺次连接PA PB PC 、、++的最小值.15.【问题提出】(1)如图1,在ABC 中,90C ∠=︒,BD 平分ABC ∠交AC 于点D ,设CD 的长为m ,点D 到边AB 的距离为n ,则m _______n ;(填“>”“<”或“=”)【问题探究】(2)如图2,在梯形ABCD 中,90A ∠=︒,AD BC ∥,(201AB =,BD 为对角线,且45BDC ∠=︒,求BCD △面积的最小值;【问题解决】(3)某景点有一个形状为菱形ABCD 的草坪,如图3,AB ==60B ∠︒,现欲将该草坪扩建为BEF △,使得点E 、F 分别在BA 、BC 的延长线上,且边EF 经过点D ,为了节省成本,要求扩建后的草坪面积(BEF △的面积)尽可能小,问BEF △的面积是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.16.综合与实践:数学课外小组研究了两个问题,请你帮助解答.问题一:如图1,在矩形ABCD 中,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为矩形,连接CG .问题二:数学小组对图形的旋转进行了拓展研究,如图4,在平行四边形ABCD 中,=60B ∠︒,6AB =,8AD =,E ,F 分别为AB ,AD 边的中点,四边形AEGF 为平行四边形,连接CG .数学小组发现DF 与CG 仍然存在着特定的数量关系.(1)请直接写出CG 的长是______.如图2,当矩形AEGF 绕点A 旋转(如顺时针旋转)至点G 落在边AB 上时,DF =______,CG =______,DF 与CG 之间的数量关系是______.(2)当矩形AEGF 绕点A 旋转至如图3的位置时,(1)中DF 与CG 之间的数量关系是否还成立?并说明理由.(3)如图5,当平行四边形ABCD 绕点A 旋转(如顺时针旋转),其它条件不变时,数学小组发现DF 与CG 仍然存在着这一特定的数量关系.请你直接写出这个特定的数量关系是______.17.如图,在四边形ABCD 中,AD ∥BC ,∠ABC =90°,AD =CD ,O 是对角线AC 的中点,连接BO 并延长交边AD 或边CD 于点E .(1)如图1,当点E 在AD 上时,连接CE ,求证:四边形ABCE 是矩形.(2)如图2,当点E 在CD 上时,当AC =4,BC =3时,求DAC S △与OBC S的比值.(3)若DE =2,OE =3,直接写出CD 的长.18.已知在正方形ABCD 中,E 是BC 边上一动点,作点B 关于AE 的对称点F ,BF 交AE 于点G ,连结DF .(1)如图1,求DFB ∠的度数;(2)如图2,过点D 作DM BF ⊥交BF 的延长线于点M ,连结,CM CF .若DF CM =,试探究四边形DFCM 的形状,并说明理由;(3)如图3,连结BD ,在AG 上截取=GT GB ,点P ,Q 分别是,AD BD 上的动点.若正方形ABCD 的面积为32,直接写出PTQ 周长的最小值.。
中考数学压轴题专题十动态几何问题

中考数学压轴题专题十动态几何问题试题特点用运动的观点来探究几何图形变化规律的问题称为动态几何问题,此类问题的显著特点是图形中的某个元素(如点、线段、三角形等)或整个图形按照某种规律运动,图形的各个元素在运动变化过程中互相依存、和谐统一,体现了数学中“变”与“不变”、“一般”与“特殊”的辩证思想.其主要类型有:1.点的运动(单点运动、多点运动);2.线段(直线)的运动;3.图形的运动(三角形运动、四边形运动、圆运动等).方式趋势动态几何题已成为中考试题的一大热点题型.在近几年各地的中考试卷中,以动点问题、平面图形的平移、翻折、旋转、剪拼问题等为代表的动态几何题频频出现在填空、选择、解答等各种题型中,总体呈现源于教材、高于教材,入口宽、难易适度、梯度分明,考查同学们对图形的直觉能力以及从变化中看到不变实质的数学洞察力.热点解析一、点的运动【题1】(2011盐城)如图1,已知一次函数y=-x+7与正比例函数y=43x的图象交于点A,且与x轴交于点B.(1)求点A和点B的坐标;(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴,动点P从点O出发,以每秒1个单位长的速度,沿O-C-A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.①当t为何值时,以A、P、R为顶点的三角形的面积为8?②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.【思路】(1)联立方程y=-x+7和y=43x即可求出点A的坐标,令-x+7=0即可得点B的坐标.(2)①只要把三角形的面积用t表示,求出即可.应注意分P在OC上运动和P在CA上运动两种情况.(D只要把有关线段用t表示,找出满足AP=AQ,AP=PQ,AQ=PQ的条件时t的值即可,应注意分别讨论P在OC上运动(此时直线∠与AB相交)和P在CA上运动(此时直线∠与AO相交)时AP=AQ,AP=PQ,AQ=PQ的条件.【失分点】以A、P、Q为顶点的三角形是等腰三角形有多种可能,容易考虑不周.【反思】涉及的主要知识点有:一次函数的图象和性质,解二元一次方程组,勾股定理,锐角三角函数,解一元二次方程,等腰三角形的判定.【牛刀小试】1.(2010湖北咸宁)如图6,直角梯形ABCD中,AB∥DC,∠DAB=90°,AD=2DC=4,AB=6.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动,当点M到达点B 时,两点同时停止运动.过点M作直线∠∥AD,与线段CD的交点为E,与折线A-C -B的交点为Q.点M运动的时间为t(秒).(1)当t=时,求线段QM的长.(2)当0<t<2时,如果以C,P,Q为顶点的三角形为直角三角形,求t的值.(3)当t>2时,连接PQ交线段AC于点R,请探究CQRQ是否为定值.若是,试求这个定值;若不是,请说明理由.2.(2010湖南娄底)如图7,在梯形ABCD中,AB∥CD,AB=2,DC=10,AD=BC=5,点M,N分别在边AD,BC上运动,并保持MN∥AB,ME⊥DC,NF⊥DC,垂足分别为E,F.(1)求梯形ABCD的面积.(2)探究一:四边形MNFE的面积有无最大值?若有,请求出这个最大值;若无,请说明理由.(3)探究二:四边形MNFF能否为正方形?若能,请求出正方形的面积;若不能,请说明理由.3.(2010广西钦州)如图8,将OA=6,AB=4的矩形OABC放置在平面直角坐标系中,动点M,N以每秒1个单位的速度分别从点A,C同时出发,其中点M沿AO向终点0运动,点N沿CB向终点B运动,当两个动点运动了ts时,过点N作NP⊥BC,交OB 于点P,连接MP.(1)点B的坐标为_______;用含£的式子表示点P的坐标为_______.(2)记△OMP的面积为S,求S与t的函数关系式(0<t<6).并求t为何值时,S有最大值.(3)试探究:当S有最大值时,在y轴上是否存在点T,使直线MT把△ONC分割成三角形和四边形两部分,且三角形的面积是△ONC面积的13?若存在,求出点T的坐标;若不存在,请说明理由.二、线的运动【题2】(2010云南昭通)如图,已知直线l的解析式为y=-x+6,它与x轴,y 轴分别相交于A,B两点.平行于直线l的直线n从原点出发,沿x轴正方向以每秒1个单位长度的速度运动,运动时间为t秒,运动过程中始终保持n∥l.直线n与x轴,y轴分别相交于C,D两点.线段CD的中点为P,以P为圆心,以CD为直径在CD上方作半圆,半圆面积为S.当直线n与直线l重合时,运动结束.(1)求A,B两点的坐标.(2)求S与t的函数关系式及自变量t的取值范围.(3)直线n在运动过程中,①当t为何值时,半圆与直线l相切?②是否存在这样的T值,使得半圆面积S=12S梯形ABCD?若存在,求出t值;若不存在,说明理由。
中考数学必会几何模型(含答案)
MATH微信:beijingdaxue777QQ:1456770148中考必会几何模型目录专题一角平分线相关问题模型 (3)模型1角平分线相关模型 (3)专题二8字模型与飞镖模型 (6)模型1:角的8字模型 (6)模型2:角的飞镖模型 (8)模型3边的“8”字模型 (10)模型4边的飞镖模型 (11)专题三半角模型 (15)专题四将军饮马模型 (23)模型1:直线与两定点 (23)模型2角与定点 (28)模型3两定点一定长 (31)专题五角平分线四大模型 (34)模型1角平分线的点向两边作垂线 (34)模型2截取构造对称全等 (35)模型3角平分线+垂线构造等腰三角形 (37)模型4角平分线+平行线 (39)专题六截长补短辅助线模型 (42)模型1截长补短 (42)专题七蚂蚁行程 (48)模型1立体图形展开的最短路径 (48)专题八三垂直全等模型 (55)模型1三垂直全等模型 (55)专题九手拉手模型 (62)模型1手拉手 (62)专题十相似模型 (68)模型1A、8模型 (68)模型2共边共角型 (72)模型3一线三等角型 (75)模型4倒数型 (79)模型5与圆有关的简单相似 (82)模型6相似和旋转 (85)专题十一圆中的辅助线 (89)模型1连半径构造等腰三角形 (89)模型2构造直角三角形 (90)模型3与圆的切线有关的辅助线 (94)专题十二中点四大模型 (97)模型1倍长中线或类中线(与中点有关的线段)构造全等三角形 (97)模型2已知等腰三角形底边中点,可以考虑与顶点连接用“三线合一”. (99)模型3已知三角形一边的中点,可考虑中位线定理 (102)模型4已知直角三角形斜边中点,可以考虑构造斜边中线 (107)专题一角平分线相关问题模型模型1角平分线相关模型(1)如图1,若点P是∠ABC和∠ACB的角平分线的交点,则∠P=90°+∠A;(2)如图2,若点P是外角∠CBF和∠BCE的角平分线的交点,则∠P=90°﹣∠A;(3)如图3,若点P是∠ABC和外角∠ACE的角平分线的交点,则∠P=∠A.图1图2图3针对训练1.(2016•枣庄)如图,在△ABC中,AB=AC,∠A=30°,E为BC延长线上一点,∠ABC与∠ACE的平分线相交于点D,则∠D的度数为()A.15°B.17.5°C.20°D.22.5°【小结】本题若不套用模型,则需要通过三角形的外角性质证明得到∠A、∠D的数量关系.2.(2018•巴中)如图,在△ABC中,BO、CO分别平分∠ABC、∠ACB.若∠BOC=110°,则∠A=.【分析】由解题模型一中的(1)可知,∠BOC=90°+∠A,把∠BOC=110°代入计算可得到∠A的度数.【详解】∵∠BOC=90°+∠A,∠BOC=110°,∴90°+∠A=110°.∴∠A=40°.【小结】本题若不套用模型,需要利用三角形的内角和定理、角平分线的定义得到∠BO C、∠A的数量关系.3.(2018•济南历城区模拟)如图,BA1和CA1分别是△ABC的内角平分线和外角平分线,BA2是∠A1BD的角平分线,CA2是∠A1CD的角平分线,BA3是∠A2BD的角平分线,CA3是∠A2CD的角平分线,若∠A1=α,则∠A2018=.【详解】∵A1B是∠ABC的平分线,A1C是∠ACD的平分线,∴∠A1BC=∠ABC,∠A1CD=∠ACD,又∵∠ACD=∠A+∠ABC,∠A1CD=∠A1BC+∠A1,【小结】本题主要考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,以及角平分线的定义,熟记性质然后推出后一个角是前一个角的一半是解题的关键。
(全国通用)中考数学复习几何专题:平移与旋转变换(含答案)
中考数学 几何复习:平移与旋转变换(含答案)1.将图1所示的图案通过平移后可以得到的图案是( )2.在如图所示的四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A .B .C .D . 3.如图l ,P 是正△ABC 内的一点,若将△PBC 绕点B 旋转到△PBA ,则∠PBP ’的度数是 ( ) A .45° B .60° C .90° D .120°4.在平面直角坐标系xOy 中,已知点A(2,3),若将OA 绕原点O 逆时针旋转180°得到0A′,则点A ′在平面直角坐标系中的位置是在( )A.第一象限B.第二象限C.第三象限D.第四象限 5.如图,已知中,∠ABC=90°,将绕顶点C 顺时针旋转至的位置,且三点在同一条直线上,则点A 经过的最短路线的长度是( )cm .A .8B .C .D .二、填空题1.如图,四边形EFGH 是由四边形经过旋转得到的.如果用有序数对(2,1)表示方格纸上A 点的位置,用(1,2)表示B 点的位置,那么四边形旋转得到四边形EFGHRt ABC △ABC △A B C '''△A C B '、、4332π38π3ABCD ABCD BC A A 'B '时的旋转中心用有序数对表示是 .2.如图,在中,,,将绕点沿逆时针方向旋转得到.(1)线段的长是,的度数是;(2)连结,求证:四边形是平行四边形; (3)求四边形的面积.3.点A的坐标为(,0),把点A 绕着坐标原点顺时针旋转135º到点B ,那么点B 的坐标是 _________ .4.如图,将△OAB 绕点0按逆时针方面旋转至△0′A ′B ′,使点B 恰好落在边A ′B ′上.已知AB=4cm ,BB′=lcm ,则A ′B 长是cm .5.如图,在平面直角坐标系中,点A 的坐标为(1,4),将线段O A 绕点O 顺时针旋转90°得到线段OA′,则点A′的坐标是.6.如图所示,五角星的顶点是一个正五边形的五个顶点.这个五角星可以由一个基本图形(图中的阴影部分)绕中心O 至少经过____________次旋转而得到, 每一次旋转_______度.Rt OAB ∆90OAB ∠=︒6OA AB ==OAB ∆O 90︒11OA B ∆1OA 1AOB ∠1AA 11OAA B 11OAA B 2三、解答题1.如图,请借助直尺按要求画图:(1)平移方格纸中左下角的图形,使点平移到点处. (2)将点平移到点处,并画出将原图放大为两倍的图形.2.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,的三个顶点都在格点上(每个小方格的顶点叫格点).画出绕点O 逆时针旋转90°后的.3.如图,已知的三个顶点的坐标分别为、、. (1)请直接写出点关于轴对称的点的坐标;(2)将绕坐标原点逆时针旋转90°.画出图形,直接写出点的对应点的坐标;1P 2P 1P 3P ABC △ABC △A B C '''△ABC △(23)A -,(60)B -,(10)C -,A y ABC △OB(3)请直接写出:以为顶点的平行四边形的第四个顶点的坐标.4.如图9所示,每个小方格都是边长为1的正方形,以O 点为坐标原点建立平面直角坐标系. (1)画出四边形OABC 关于y 轴对称的四边形OA 1B 1C 1, 并写出点B 1的坐标是.(2)画出四边形OABC 绕点O 顺时针方向旋转90°后得 到的四边形OA 2B 2C 2,并求出点C 旋转到点C 2经过的路径 的长度.5.如图,已知A 、B 是线段MN 上的两点,,,.以A 为中心顺时针旋转点M ,以B 为中心逆时针旋转点N ,使M 、N 两点重合成一点C ,构成△ABC ,设. (1)求x 的取值范围;(2)若△ABC 为直角三角形,求x 的值; (3)探究:△ABC 的最大面积?【参考答案】A B C 、、D 4=MN 1=MA 1>MB x AB =C一、选择题1.A2.D3.B4.C5.D 二、填空题 1.(5,2)2.(1)6,135°(2) ∴ 又 ∴四边形是平行四边形 3. (1,-1) 4.3 5.(4,-1) 6.4,72 三、解答题1.(1)从平移到处,; (2)放大2倍且正确,.2.3.解:(1)(2,3);11190AOA OA B ∠=∠=︒Q 11//OA A B 11OA AB A B ==11OAA B 1P 2P(2)图形略.(0,);(3)()或或. 4.解:(1)如图:B 1的坐标是(-6,2) (2)如图:L ==5.解:(1)在△ABC 中,∵,,. ∴,解得.(2)①若AC 为斜边,则,即,无解.②若AB 为斜边,则,解得,满足. ③若BC 为斜边,则,解得,满足. ∴或. (3)在△ABC 中,作于D , 设,△ABC 的面积为S ,则.①若点D 在线段AB 上,则.∴,即. ∴,即.6-7-3,(53)--,(33),903180π⨯⨯32π1=AC x AB =x BC -=3⎩⎨⎧>-+->+x x xx 313121<<x 22)3(1x x -+=0432=+-x x 1)3(22+-=x x 35=x 21<<x 221)3(x x +=-34=x 21<<x 35=x 34=x AB CD ⊥h CD =xh S 21=x h x h =--+-222)3(122222112)3(h h x x h x -+--=--4312-=-x h x 16249)1(222+-=-x x h x 16248222-+-=x x h x C(例3-1)D∴(). 当时(满足),取最大值,从而S 取最大值②若点D 在线段MA 上, 则. 同理可得, (),易知此时. 综合①②得,△ABC 的最大面积为462412222-+-==x x h x S 21)23(22+--=x 423x <≤23=x 423x <≤2S 2122x h h x =----2221)3(462412222-+-==x x h x S 21)23(22+--=x 413x <≤22<S 22(例3-2)。
中考压轴题突破:几何最值问题大全(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)
中考压轴题突破:几何最值问题大全(将军饮马、造桥选址、胡不归、阿波罗尼斯圆等)一、基本图形所有问题的老祖宗只有两个:①[定点到定点]:两点之间,线段最短;②[定点到定线]:点线之间,垂线段最短。
由此派生:③[定点到定点]:三角形两边之和大于第三边;④[定线到定线]:平行线之间,垂线段最短;⑤[定点到定圆]:点圆之间,点心线截距最短(长);⑥[定线到定圆]:线圆之间,心垂线截距最短;⑦[定圆到定圆]:圆圆之间,连心线截距最短(长)。
余不赘述,下面仅举一例证明:[定点到定圆]:点圆之间,点心线截距最短(长)。
已知⊙O半径为r,AO=d,P是⊙O上一点,求AP的最大值和最小值。
证明:由“两点之间,线段最短”得AP≤AO+PO,AO≤AP+PO,得d-r≤AP≤d+r,AP最小时点P在B处,最大时点P在C处。
即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。
(可用“三角形两边之和大于第三边”,其实质也是由“两点之间,线段最短”推得)。
上面几种是解决相关问题的基本图形,所有的几何最值问题都是转化成上述基本图形解决的。
二、考试中出现的问题都是在基本图形的基础上进行变式,如圆与线这些图形不是直接给出,而是以符合一定条件的动点的形式确定的;再如过定点的直线与动点所在路径不相交而需要进行变换的。
类型分三种情况:(1)直接包含基本图形;(2)动点路径待确定;(3)动线(定点)位置需变换。
(一)直接包含基本图形例 1.在⊙O中,圆的半径为6,∠B=30°,AC是⊙O的切线,则CD的最小值是。
(二)动点路径待确定例2.,如图,在△ABC中,∠ACB=90°,AB=5,BC=3,P是AB边上的动点(不与点B 重合),将△BCP沿CP所在的直线翻折,得到△B′CP,连接B′A,则B′A长度的最小值是。
(三)动线(定点)位置需变换线段变换的方法:(1)等值变换:翻折、平移;(2)比例变换:三角、相似。
中考数学专题复习:几何综合题
【考点总结】四、全等三角形的性质与判定
1.概念:能够完全重合的两个三角形叫做全等三角形. 2.性质:全等三角形的对应边、对应角分别相等. 3.判定:(1)有三边对应相等的两个三角形全等,简记为(SSS); (2)有两边和它们的夹角对应相等的两个三角形全等,简记为(SAS); (3)有两角和它们的夹边对应相等的两个三角形全等,简记为(ASA); (4)有两角和其中一角的对边对应相等的两个三角形全等,简记为(AAS); (5)有斜边和一条直角边对应相等的两个直角三角形全等,简记为(HL).
三角形专题
1,掌握三角形相关基础知识(2课时)
目标
2,掌握三角形有关模型的全等或相似证明(3课时) 3,完成三角形有关模型的全等或相似证明(3课时)
三角形
模型
手拉手模型
三垂直模型
相似模型
三角形有关的知识
【考点总结】一、三角形中的重要线段 1.三角形的高线:从三角形的一个顶点向它的对边所在的直线作垂线,顶点和垂足之间的线段叫做 三角形的高线,简称高. 特性:三角形的三条高线相交于一点. 2.三角形的中线:在三角形中,连接一个顶点和它对边中点的线段叫做三角形的中线.特性:三角 形的三条中线交于一点. 3.三角形的中位线:连接三角形两边中点的线段叫做三角形的中位线. 定理:三角形的中位线平行于第三边,且等于它的一半 4.三角形的角平分线:三角形一个角的平分线和这个角的对边相交,这个角的顶点和交点之间的线 段叫做三角形的角平分线. 特性:三角形的三条角平分线交于一点,这点叫做三角形的内心. 性质:角平分线上的点到角的两边的距离相等.
小组合作
1.在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题---几何规律
基本步骤
1、先看增幅是否相等,如相等,等差规律解题。
2、如增幅不相等,看增幅的比例是否相等,及是否存在倍数关系。考虑用等
比规律解题。
3、如增幅不相等,看增幅的差是否相等,如相等可考虑等差规律。
4、通过标序综合运用观察法、整体法、等差规律和等比规律解题。
一、选择题
1.图中共有线段的条数是 ( )
A.5条 B.8条 C.10条 D.12条
2.如图,小于平角的角有 ( )
A.8个 B.8个 C. 7个 D.6个
3.平面内三条直线最多可以把平面分成 ( )
A.四部分 B.五部分 C.六部分 D.七部分
4.平面上画出四条直线,交点的个数最多有 ( )
A.5个 B.6个 C 7个 D.8个
5.一条信息可通过如图的格线由上(A点)往下向各站点传送,例如信息到点由b2经
a1的站点送达,也可由经a2的站直送达,共有两条途径传送,则信息由A点到达d3的不
同途径共有 ( )
A.3条 B.4条 C.6条 D.12条
6.如图,图中不同的线段的条数有 ( )
A.52条 B.63条 C.141条 D.154条
7.(2012年重庆)观察下列图形,则第n个图形中三角形的个数是( )
A.22n B.44n C.44n D.4n
……
第1个 第2个 第3个
二、填空题
7.如图,图中共有____条线段,图中直线共有_______条,能用图中字母表示的射线共有
_______条。
8.过一点A可以画____条直线,过两点A、B可以画_______条直线,过A、B、C三点中任
两点可以画_______条直线。
9.如图,在线段AB上依次取A1、A2…A10等10个点,则图中共有线段_________条。
10、(2012丽水市)如图,图①是一块边长为1,周长记为P1的正三角形纸板,沿图①的底
边剪去一块边长为12的正三角形纸板后得到图②,然后沿同一底边依次剪去一块更小的正三
角形纸板(即其边长为前一块被剪掉正三角形纸板边长的21)后,得图③,④,…,记第
n(n≥3) 块纸板的周长为Pn,则Pn-Pn-1= .
11.(2013年益阳市)图8是一组有规律的图案,第1个 图案由4个基础图形组成,第2
个图案由7个基础图形组成,……,第n(n是正整数)个图案中由 个基础图形组
成.
-
12. 观察下表,回答问题:
第 个图形中“△”的个数是“○”的个数的5倍.
序号 1 2 3 …
图形 …
…
① ② ③ ④
(1)
(2)
(3)
……
13.(2013年济宁市)观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角
形中白色三角形有 个 .
14.(2012年铁岭市)如图所示,把同样大小的黑色棋子摆放在正多边形的边上,按照这样
的规律摆下去,则第n个图形需要黑色棋子的个数是 .
15.(2014年抚顺市)观察下列图形(每幅图中最小..的三角形都是全等的),请写出第n个图
中最小..的三角形的个数有 个.
16.下列是由同型号黑白两种颜色的正三角形瓷砖按一定规律铺设的图形.
仔细观察图形可知:
实践与探索:
(1)请在图4的虚线框内画出第4个图形。
(2)第10个图形有______块黑色的瓷砖;
第n个图形有________块黑色的瓷砖.
17.观察下列图形,则第n个图形中三角形的个数是 个.
第1个
第2个第3个
第1个图 第2个图 第3个图 第4个图
……
第1个 第2个 第3个
18.用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板,则第(3)个图形中有
黑色瓷砖 __________块,第n个图形中需要黑色瓷砖__________块(用含n的代数式表
示).
19.(2005年连云港市中考题)右图是一回形图,其回形通道的宽与OB的长均为1,回形线与
射线OA交于点A1,A2,A3,…。若从O点到A1点的回形线为第1圈(长为7),从A1点到
A2点的回形线为第2圈,……,依此类推。则第10圈的长为 。
20.如图,按英语字母表A、B、C、D、E、F、G、H…的顺序有规律排列而成的鱼状图案中,
字母“G”出现的个数为________.
21.一串有趣的图案按一定规律排列,请仔细观察,按此规律画出的第10个图案是
________;在前16个图案中有_______个,第2012个图案是_____.
22.某同学在电脑中打出如下排列的若干个圆(图中●表示实心圆,O表示空心圆)
……
若将上面一组圆依此规律连续复制得到一系列圆,那么前2012个圆中,有___个空心圆.
(1) (2) (3)
23.已知直线l上有若干个互不重合的点,D为l外一点.请把以D点和l上任意两点为顶点
组成的三角形个数填入下表:
24.探索常见图形的规律,用火柴棒按下图的方式搭三角形,照这样的规律搭建下去,搭n
个这样的三角形需要多少根火柴棒?
25.若按图中方式摆放桌子和椅子,8张桌子可坐 人。按照上图方式继续排列
桌子,完成下表:
26.(05山东泉州)下图是某同学在沙滩上用石于摆成的小房子.
观察图形的变化规律,写出第n个小房子用了 块石子.
27.如图,把一个面积为1的正方形分等分成两个面积为21的矩形,接着把面积为21的矩形
等分成两个面积为41的正方形,再把面积为41的矩形等分成两个面积为81的矩形,如此进
行下去,试利用图形提示的规律计算:
2561128164132116181412
1
l
上互不相同的个数
2 3 4 5 … n(n≥2)的自然数
组成三角形的个数 1
32
1
2
1
4
1
8
1
16
1
28.把棱长为a的正方体摆成如图的形状,从上向下数,第一层1个,第二层3个……按这
种规律摆放,第五层的正方体的个数是
29.下列每个图形都是若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都
有)2(nn个棋子,每个图案棋子总数为S,按下图的排列规律推断,S与n之间的关系可
以用式子 来表示。
…
30.如图的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形,根据图中的数构成
的规律填写:
a
所表示的数: 。
b
所表示的数: 。
31.如图,是用棋子摆成的图案,摆第1个图案需要7枚棋子,摆第2个图案需要19枚棋
子,摆第3个图案需要37枚棋子,按照这样的方式摆下去,则摆第6个图案需要 枚
棋子,摆第n个图案需要 枚棋子.
32.(2010盐城)填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m的值
42s
n
83s
n
124s
n
165s
n
155114411331121111bb
a
…
0 2 8 4 2 4 6 24 6 8 4m 6
第32题图
第31题图
是
33.(2014年门汕头)如图,45AOB,过OA上到点O的距离分别为1357911,,,,,, 的
点作OA的垂线与OB相交,得到并标出一组黑色梯形,它们的面积分别为
1234
SSSS,,,,
.
则第一个黑色梯形的面积1S ;观察图中的规律,
第n(n为正整数)个黑色梯形的面积nS .
34.(2013年宁波市)十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、
棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式。请你观察下列几种简单多面体
模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体 顶点数(V) 面数(F) 棱数(E)
四面体 4 7
长方体 8 6 12
正八面体 8 12
正十二面体 20 12 30
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________。
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是____________。
(3)某个玻璃鉓品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接
而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八
边形的个数为y个,求yx的值。
四面体 长方体 正八面体 正十二面体
