2021年中考数学压轴题提升训练图形规律探索题含解析

合集下载

2021中考数学真题分类专题31 规律探究题(共33题含解析)

专题31规律探究题（共33题）一、单选题1．（2021·湖北鄂州市·中考真题）已知1a 为实数﹐规定运算：2111a a =-，3211a a =-，4311a a =-，5411a a =-，……，111n n a a -=-．按上述方法计算：当13a =时，2021a 的值等于（） A ．23-B ．13C ．12-D ．232．（2021·湖北中考真题）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）A ．2025B ．2023C ．2021D ．20193．（2021·山东济宁市·中考真题）按规律排列的一组数据：12，35，□，717，926，1137，…，其中□内应填的数是（） A ．23B ．511C ．59D ．124．（2021·湖北中考真题）根据图中数字的规律，若第n 个图中的143q =，则p 的值为（）A ．100B ．121C ．144D ．1695．（2021·山东临沂市·中考真题）实验证实，放射性物质在放出射线后，质量将减少，减少的速度开始较快，后来较慢，实际上，物质所剩的质量与时间成某种函数关系．下图为表示镭的放射规律的函数图象，据此可计算32mg 镭缩减为1mg 所用的时间大约是（）A ．4860年B ．6480年C ．8100年D ．9720年6．（2021·四川达州市·中考真题）在平面直角坐标系中，等边AOB ∆如图放置，点A 的坐标为()1,0，每一次将AOB ∆绕着点О逆时针方向旋转60︒，同时每边扩大为原来的2倍，第一次旋转后得到11A OB ∆，第二次旋转后得到22A OB ∆，…，依次类推，则点2021A 的坐标为（）A ．()202020202,2-B ．()202120212,2C ．()202020202,2D ．()201120212,2-7．（2021·广西玉林市·中考真题）观察下列树枝分杈的规律图，若第n 个图树枝数用n Y 表示，则94Y Y -=（）A ．4152⨯B ．4312⨯C ．4332⨯D ．4632⨯二、填空题8．（2021·贵州铜仁市·中考真题）观察下列各项：112，124，138，1416，…，则第n 项是______________．9．（2021·陕西）幻方，最早源于我国，古人称之为纵横图．如图所示的幻方中，各行、各列及各条对角线上的三个数字之和均相等，则图中a 的值为______．10．（2021·湖南怀化市·中考真题）观察等式：232222+=-，23422222++=-，2345222222+++=-，……，已知按一定规律排列的一组数：1002，1012，1022，……，1992，若1002=m ，用含m 的代数式表示这组数的和是___________．11．（2021·江苏扬州市·中考真题）将黑色圆点按如图所示的规律进行排列，图中黑色圆点的个数依次为：1，3，6，10，……，将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据，则新数据中的第33个数为___________．12．（2021·甘肃武威市·中考真题）一组按规律排列的代数式：2335472,2,2,2a b a b a b a b +-+-，…，则第n 个式子是___________．13．（2021·江西中考真题）下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，因而人们把这个表叫做杨辉三角，请你根据杨辉三角的规律补全下表第四行空缺的数字是______．14．（2021·浙江嘉兴市·中考真题）观察下列等式：22110=-，22321=-，22532=-，…按此规律，则第n 个等式为21n -=__________________．15．（2021·黑龙江中考真题）如图，3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，则20条直线两两相交最多有______个交点16．（2021·四川中考真题）如图，用火柴棍拼成一个由三角形组成的图形，拼第一个图形共需要3根火柴棍，拼第二个图形共需要5根火柴棍；拼第三个图形共需要7根火柴棍；……照这样拼图，则第n 个图形需要___________根火柴棍．17．（2021·四川中考真题）如图都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第___个图形共有210个小球．18．（2021·湖南常德市·中考真题）如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有11⨯个正方形，所有线段的和为4，第二个图形有22⨯个小正方形，所有线段的和为12，第三个图形有33⨯个小正方形，所有线段的和为24，按此规律，则第n 个网格所有线段的和为____________．(用含n 的代数式表示)19．（2021·贵州毕节市·中考真题）如图，在平面直角坐标系中，点()11,1N 在直线:l y x =上，过点1N 作11N M l ⊥，交x 轴于点1M ；过点1M 作12M N x ⊥轴，交直线l 于点2N ；过点2N 作22N M l ⊥，交x 轴于点2M ；过点2M 作23M N x ⊥轴，交直线l 于点3N ；…；按此作法进行下去，则点2021M 的坐标为_____________．20．（内蒙古呼伦贝尔2021年中考数学试卷）如图，点1B 在直线1:2l y x =上，点1B 的横坐标为2，过点1B 作11B A x ⊥轴，垂足为1A ，以11A B 为边向右作正方形1112A B C A ，延长21A C 交直线l 于点2B ；以22A B 为边向右作正方形2223A B C A ，延长32A C 交直线l 于点3B ；……；按照这个规律进行下去，点2021B 的坐标为___________．21．（2021·湖北中考真题）如图，在平面直角坐标系中，动点P 从原点O 出发，水平向左平移1个单位长度，再竖直向下平移1个单位长度得到点()11,1P --；接着水平向右平移2个单位长度，再竖直向上平移2个单位长度得到点2P ；接着水平向左平移3个单位长度，再竖直向下平移3个单位长度得到点3P ；接着水平向右平移4个单位长度，再竖直向上平移4个单位长度得到点4P ，…，按此作法进行下去，则点2021P 的坐标为___________．22．（2021·内蒙古通辽市·中考真题）如图，11OA B ，122A A B ，233A A B △…，1n n n A A B -都是斜边在x 轴上的等腰直角三角形，点1A ，2A ，3A ，…，n A 都在x 轴上，点1B ，2B ，3B ，…，n B 都在反比例函数()10y x x=>的图象上，则点n B 的坐标为__________．（用含有正整数n 的式子表示）23．（2021·山东菏泽市·中考真题）如图，一次函数y x =与反比例函数1y x=（0x >）的图象交于点A ，过点A 作AB OA ⊥，交x 轴于点B ；作1//BA OA ，交反比例函数图象于点1A ；过点1A 作111A B A B ⊥交x 轴于点B ；再作121//B A BA ，交反比例函数图象于点2A ，依次进行下去，……，则点2021A 的横坐标为_______．24．（2021·山东中考真题）如图，点1B 在直线1:2l y x =上，点1B 的横坐标为2，过点1B 作1B l ⊥，交x 轴于点1A ，以11A B 为边，向右作正方形1121A B B C ，延长21B C 交x 轴于点2A ；以22A B 为边，向右作正方形2232A B B C ，延长32B C 交x 轴于点3A ；以33A B 为边，向右作正方形3343A B B C ，延长的43B C 交x 轴于点4A ；…；按照这个规律进行下去，则第n 个正方形1n n n n A B B C +的边长为________（结果用含正整数n 的代数式表示）．25．（2021·湖北中考真题）如图，过反比例函数()0,0ky k x x=>>图象上的四点1P ，2P ，3P ，4P 分别作x 轴的垂线，垂足分别为1A ，2A ，3A ，4A ，再过1P ，2P ，3P ，4P 分别作y 轴，11P A ，22P A ，33P A 的垂线，构造了四个相邻的矩形．若这四个矩形的面积从左到右依次为1S ，2S ，3S ，4S ，1122334OA A A A A A A ===，则1S 与4S 的数量关系为_____________．26．（2021·四川）如图，在平面直角坐标系中，AB y ⊥轴，垂足为B ，将ABO 绕点A 逆时针旋转到11AB O 的位置，使点B 的对应点1B 落在直线34y x =-上，再将11AB O 绕点1B 逆时针旋转到112A B O 的位置，使点1O 的对应点2O 也落在直线34y x =-上，以此进行下去……若点B 的坐标为()0,3，则点21B 的纵坐．．标．为______．27．（2021·山东东营市·中考真题）如图，正方形1ABCB 中，AB =AB 与直线l 所夹锐角为60︒，延长1CB 交直线l 于点1A ，作正方形1112A B C B ，延长12C B 交直线l 于点2A ，作正方形2223A B C B ，延长23C B 交直线l 于点3A ，作正方形3334A B C B ，…，依此规律，则线段20202021A A =________．28．（2021·黑龙江中考真题）如图，菱形ABCD 中，120ABC ∠=︒，1AB =，延长CD 至1A ，使1DA CD =，以1A C 为一边，在BC 的延长线上作菱形111A CC D ，连接1AA ，得到1ADA ∆；再延长11C D 至2A ，使1211D A C D =，以21A C 为一边，在1CC 的延长线上作菱形2122A C C D ，连接12A A ，得到112A D A ∆……按此规律，得到202020202021A D A ∆，记1ADA ∆的面积为1S ，112A D A ∆的面积为2S ……202020202021A D A ∆的面积为2021S ，则2021S =_____．29．（2021·吉林长春市·中考真题）如图，在平面直角坐标系中，等腰直角三角形AOB 的斜边OA 在y 轴上，2OA ，点B 在第一象限．标记点B 的位置后，将AOB 沿x 轴正方向平移至111AO B 的位置，使11A O 经过点B ，再标记点1B 的位置，继续平移至222A O B △的位置，使22A O 经过点1B ，此时点2B 的坐标为__________．30．（2021·湖北荆门市·中考真题）如图，将正整数按此规律排列成数表，则2021是表中第____行第________列．31．（2021·湖南湘西土家族苗族自治州·中考真题）古希腊数学家把1，3，6，10，15，21，…这样的数叫做三角形数，因为它的规律性可以用如图表示．根据图形，若把第一个图形表示的三角形数记为11a =，第二个图形表示的三角形数记为23a =，…，则第n 个图形表示的三角形数n a ＝___．（用含n 的式子表达）32．（2021·内蒙古鄂尔多斯市·中考真题）将一些相同的“〇”按如图所示的规律依次摆放，观察每个“龟图”的“〇”的个数，则第30个“龟图”中有___________个“〇”．33．（2021·黑龙江绥化市·中考真题）下面各图形是由大小相同的三角形摆放而成的，图①中有1个三角形，图①中有5个三角形，图①中有11个三角形，图①中有19个三角形…，依此规律，则第n 个图形中三角形个数是_______．2021年中考数学真题分项汇编【全国通用】专题31规律探究题试题解析（共33题）一、单选题1．（2021·湖北鄂州市·中考真题）已知1a 为实数﹐规定运算：2111a a =-，3211a a =-，4311a a =-，5411a a =-，……，111n n a a -=-．按上述方法计算：当13a =时，2021a 的值等于（）A ．23-B ．13C ．12-D ．23【答案】D 【分析】当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现呈周期性出现，即可得到2021a 的值．【详解】解：当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现是以：213,,32-，循环出现的规律， 202136732=⨯+，2021223a a ∴==，故选：D ．【点睛】本题考查了实数运算规律的问题，解题的关键是：通过条件，先计算出部分数的值，从中找到相应的规律，利用其规律来解答．2．（2021·湖北中考真题）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）A ．2025B ．2023C ．2021D ．2019【答案】B 【分析】根据数字的变化关系发现规律第n 行，第n 列的数据为：2n (n -1)+1，即可得第32行，第32列的数据为：2×32×(32-1)+1=1985，再依次加2，到第32行，第13列的数据，即可．【详解】解：观察数字的变化，发现规律：第n 行，第n 列的数据为：2n (n -1)+1， ①第32行，第32列的数据为：2×32×(32-1)+1=1985，根据数据的排列规律，第偶数行从右往左的数据一次增加2， ①第32行，第13列的数据为：1985+2×(32-13)=2023，故选：B ．【点睛】本题考查了数字的变化类，解决本题的关键是观察数字的变化寻找探究规律，利用规律解决问题． 3．（2021·山东济宁市·中考真题）按规律排列的一组数据：12，35，□，717，926，1137，…，其中□内应填的数是（） A ．23B ．511C ．59D ．12【答案】D 【分析】分子为连续奇数，分母为序号的平方1+，根据规律即可得到答案．【详解】观察这排数据发现，分子为连续奇数，分母为序号的平方1+，∴第n 个数据为：2211n n -+ 当3n =时的分子为5，分母为23110+=∴这个数为51102= 故选：D ．【点睛】本题考查了数字的探索规律，分子和分母分别寻找规律是解题关键．4．（2021·湖北中考真题）根据图中数字的规律，若第n 个图中的143q =，则p 的值为（）A ．100B ．121C ．144D ．169【答案】B 【分析】分别分析n 的规律、p 的规律、q 的规律，再找n 、p 、q 之间的联系即可．【详解】解：根据图中数据可知：1,2,3,4n =，……22221,2,3,4,p =……222221,31,41,51,q =----……则2p n =，2(1)1q n =+-， ①第n 个图中的143q =， ①2(1)1=143q n =+-，解得：11n =或13n =-(不符合题意，舍去) ①2=121p n =，故选：B ．【点睛】本题主要考查数字之间规律问题，将题中数据分组讨论是解决本题的关键．5．（2021·山东临沂市·中考真题）实验证实，放射性物质在放出射线后，质量将减少，减少的速度开始较快，后来较慢，实际上，物质所剩的质量与时间成某种函数关系．下图为表示镭的放射规律的函数图象，据此可计算32mg 镭缩减为1mg 所用的时间大约是（）A ．4860年B ．6480年C ．8100年D ．9720年【答案】C 【分析】根据物质所剩的质量与时间的规律，可得答案．【详解】解：由图可知：1620年时，镭质量缩减为原来的12，再经过1620年，即当3240年时，镭质量缩减为原来的21142=，再经过1620×2=3240年，即当4860年时，镭质量缩减为原来的31182=， ...，①再经过1620×4=6480年，即当8100年时，镭质量缩减为原来的511232=，此时132132⨯=mg ，故选C ．【点睛】本题考查了函数图象，规律型问题，利用函数图象的意义是解题关键．6．（2021·四川达州市·中考真题）在平面直角坐标系中，等边AOB ∆如图放置，点A 的坐标为()1,0，每一次将AOB ∆绕着点О逆时针方向旋转60︒，同时每边扩大为原来的2倍，第一次旋转后得到11A OB ∆，第二次旋转后得到22A OB ∆，…，依次类推，则点2021A 的坐标为（）A ．()202020202,2-B ．()202120212,2C ．()202020202,2D ．()201120212,2-【答案】C 【分析】由题意，点A 每6次绕原点循环一周，利用每边扩大为原来的2倍即可解决问题．【详解】解：由题意，点A 每6次绕原点循环一周， 20216371......5÷=，2021A ∴点在第四象限，202120212OA =，202160xOA ∠=︒ ，∴点2020A 的横坐标为20212020122=2⨯，纵坐标为20212020=22，()2020202020212,2A ∴，故选：C ．【点睛】本题考查坐标与图形变化-旋转，规律型问题，解题的关键是理解题意，学会探究规律的方法，属于中考常考题型．7．（2021·广西玉林市·中考真题）观察下列树枝分杈的规律图，若第n 个图树枝数用n Y 表示，则94Y Y -=（）A ．4152⨯B ．4312⨯C ．4332⨯D ．4632⨯【答案】B 【分析】根据题目中的图形，可以写出前几幅图中树枝分杈的数量，从而可以发现树枝分杈的变化规律，进而得到规律21nn Y =-，代入规律求解即可．【详解】解：由图可得到：11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则：9921Y =-，①944942121312Y Y -=--+=⨯，故答案选：B ．【点睛】本题考查图形规律，解答本题的关键是明确题意，利用数形结合的思想解答．二、填空题8．（2021·贵州铜仁市·中考真题）观察下列各项：112，124，138，1416，…，则第n 项是______________．【答案】12nn + 【分析】根据已知可得出规律：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+…即可得出结果．【详解】解：根据题意可知：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+，第四项：41144162=+， …则第n 项是12n n +；故答案为：12n n +．【点睛】此题属于数字类规律问题，根据已知各项的规律得出结论是解决此类题目的关键．9．（2021·陕西）幻方，最早源于我国，古人称之为纵横图．如图所示的幻方中，各行、各列及各条对角线上的三个数字之和均相等，则图中a 的值为______．【答案】-2 【分析】先通过计算第一行数字之和得到各行、各列及各条对角线上的三个数字之和，再利用第二列三个数之和得到a 的值．【详解】解：由表第一行可知，各行、各列及各条对角线上的三个数字之和均为1616--+=-，①626a -++=-， ①2a =-，故答案为：2-．【点睛】本题考查了数字之间的关系，解决本题的关键是读懂题意，正确提取表中数据，找到它们之间的关系等，该题对学生的观察分析能力有一定的要求，同时也考查了学生对有理数的和差计算的基本功． 10．（2021·湖南怀化市·中考真题）观察等式：232222+=-，23422222++=-，2345222222+++=-，……，已知按一定规律排列的一组数：1002，1012，1022，……，1992，若1002=m ，用含m 的代数式表示这组数的和是___________．【答案】2m m - 【分析】根据规律将1002，1012，1022，……，1992用含m 的代数式表示，再计算0199222+++的和，即可计算1001011011992222++++的和．【详解】由题意规律可得：2399100222222++++=-．①1002=m ①23991000222222=2m m +++++==，①22991001012222222+++++=-，①10123991002222222=++++++12=2m m m m =+=．102239910010122222222+=++++++224=2m m m m m =++=．1032399100101102222222222=++++++++3248=2m m m m m m =+++=．……①1999922m =．故10010110110199992222222m m m ++++=+++．令012992222S ++++=①12310022222S ++++=②①-①，得10021S -= ①10010110110199992222222m m m ++++=+++=()100221m m m -=-故答案为：2m m -．【点睛】本题考查规律问题，用含有字母的式子表示数、灵活计算数列的和是解题的关键．11．（2021·江苏扬州市·中考真题）将黑色圆点按如图所示的规律进行排列，图中黑色圆点的个数依次为：1，3，6，10，……，将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据，则新数据中的第33个数为___________．【答案】1275 【分析】首先得到前n 个图形中每个图形中的黑色圆点的个数，得到第n 个图形中的黑色圆点的个数为()12n n +，再判断其中能被3整除的数，得到每3个数中，都有2个能被3整除，再计算出第33个能被3整除的数所在组，为原数列中第50个数，代入计算即可．【详解】解：第①个图形中的黑色圆点的个数为：1，第①个图形中的黑色圆点的个数为：()1222+⨯=3，第①个图形中的黑色圆点的个数为：()1332+⨯=6，第①个图形中的黑色圆点的个数为：()1442+⨯=10，...第n 个图形中的黑色圆点的个数为()12n n +，则这列数为1，3，6，10，15，21，28，36，45，55，66，78，91，...，其中每3个数中，都有2个能被3整除， 33÷2=16...1， 16×3+2=50，则第33个被3整除的数为原数列中第50个数，即50512⨯=1275，故答案为：1275．【点睛】此题考查了规律型：图形的变化类，关键是通过归纳与总结，得到其中的规律．12．（2021·甘肃武威市·中考真题）一组按规律排列的代数式：2335472,2,2,2a b a b a b a b +-+-，…，则第n 个式子是___________．【答案】()12112n n n a b +-+-⋅【分析】根据已知的式子可以看出：每个式子的第一项中a 的次数是式子的序号；第二项中b 的次数是序号的2倍减1，而第二项的符号是第奇数项时是正号，第偶数项时是负号．【详解】解：①当n 为奇数时，()111n +-=；当n 为偶数时，()111n +-=-，①第n 个式子是：()1211?2n n n a b +-+-．故答案为：()1211?2n n n a b +-+-【点睛】本题考查了多项式的知识点，认真观察式子的规律是解题的关键．13．（2021·江西中考真题）下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，因而人们把这个表叫做杨辉三角，请你根据杨辉三角的规律补全下表第四行空缺的数字是______．【答案】3【分析】通过观察每一个数字等于它上方相邻两数之和．【详解】解：通过观察杨辉三角发现每一个数字等于它上方相邻两数之和的规律，例如：第3行中的2，等于它上方两个相邻的数1，1相加，即：211=+；第4行中的3，等于它上方两个相邻的数2，1相加，即：321=+；⋅⋅⋅⋅⋅⋅由此规律：故空缺数等于它上方两个相邻的数1，2相加，即空缺数为：3，故答案是：3．【点睛】本题考查了杨辉三角数的规律，解题的关键是：通过观察找到数与数之间的关系，从来解决问题． 14．（2021·浙江嘉兴市·中考真题）观察下列等式：22110=-，22321=-，22532=-，…按此规律，则第n 个等式为21n -=__________________．【答案】()221n n --．【分析】第一个底数是从1开始连续的自然数的平方，减去从0开始连续的自然数的平方，与从1开始连续的奇数相同，由此规律得出答案即可．【详解】解：①22110=-，22321=-，22532=-，…①第n 个等式为：()22211n n n -=-- 故答案是：()221n n --．【点睛】本题考查了数字的变化类，通过观察，分析、归纳并发现其中的规律，并应用发现的规律解决问题的关键． 15．（2021·黑龙江中考真题）如图，3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数，找出n 条直线相交最多有的交点个数公式：1(1)2n n -．【详解】解：2条直线相交有1个交点； 3条直线相交最多有1123322+==⨯⨯个交点； 4条直线相交最多有11236432++==⨯⨯个交点； 5条直线相交最多有1123410542+++==⨯⨯个交点； ⋯20条直线相交最多有120191902⨯⨯=．故答案为：190．【点睛】本题考查的是多条直线相交的交点问题，解答此题的关键是找出规律，即n条直线相交最多有1(1) 2n n ．16．（2021·四川中考真题）如图，用火柴棍拼成一个由三角形组成的图形，拼第一个图形共需要3根火柴棍，拼第二个图形共需要5根火柴棍；拼第三个图形共需要7根火柴棍；……照这样拼图，则第n个图形需要___________根火柴棍．【答案】2n+1【分析】分别得到第一个、第二个、第三个图形需要的火柴棍，找到规律，再总结即可．【详解】解：由图可知：拼成第一个图形共需要3根火柴棍，拼成第二个图形共需要3+2=5根火柴棍，拼成第三个图形共需要3+2×2=7根火柴棍，...拼成第n个图形共需要3+2×（n-1）=2n+1根火柴棍，故答案为：2n+1．【点睛】此题考查图形的变化规律，找出图形之间的联系，得出运算规律解决问题．17．（2021·四川中考真题）如图都是由同样大小的小球按一定规律排列的，依照此规律排列下去，第___个图形共有210个小球．【答案】20【分析】根据已知图形得出第n 个图形中黑色三角形的个数为1+2+3++n =()12n n +，列一元二次方程求解可得．【详解】解：①第1个图形中黑色三角形的个数1，第2个图形中黑色三角形的个数3=1+2，第3个图形中黑色三角形的个数6=1+2+3，第4个图形中黑色三角形的个数10=1+2+3+4，……①第n 个图形中黑色三角形的个数为1+2+3+4+5++n =()12n n +，当共有210个小球时， ()12102n n +=，解得：20n =或21-(不合题意，舍去)，①第20个图形共有210个小球．故答案为：20．【点睛】本题考查了图形的变化规律，解一元二次方程，解题的关键是得出第n 个图形中黑色三角形的个数为1+2+3+……+n ．18．（2021·湖南常德市·中考真题）如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有11⨯个正方形，所有线段的和为4，第二个图形有22⨯个小正方形，所有线段的和为12，第三个图形有33⨯个小正方形，所有线段的和为24，按此规律，则第n 个网格所有线段的和为____________．(用含n 的代数式表示)【答案】2n 2+2n【分析】本题要通过第1、2、3和4个图案找出普遍规律，进而得出第n 个图案的规律为S n =4n +2n ×(n -1)，得出结论即可．【详解】解：观察图形可知：第1个图案由1个小正方形组成，共用的木条根数141221,S =⨯=⨯⨯第2个图案由4个小正方形组成，共用的木条根数262232,S =⨯=⨯⨯第3个图案由9个小正方形组成，共用的木条根数383243,S =⨯=⨯⨯第4个图案由16个小正方形组成，共用的木条根数4104254,S =⨯=⨯⨯…由此发现规律是：第n 个图案由n 2个小正方形组成，共用的木条根数()22122,n S n n n n =+=+ 故答案为：2n 2+2n ．【点睛】本题考查了规律型-图形的变化类，熟练找出前四个图形的规律是解题的关键．19．（2021·贵州毕节市·中考真题）如图，在平面直角坐标系中，点()11,1N 在直线:l y x =上，过点1N 作11N M l ⊥，交x 轴于点1M ；过点1M 作12M N x ⊥轴，交直线l 于点2N ；过点2N 作22N M l ⊥，交x 轴于点2M ；过点2M 作23M N x ⊥轴，交直线l 于点3N ；…；按此作法进行下去，则点2021M 的坐标为_____________．【答案】（20212，0）.【分析】根据题目所给的解析式，求出对应的1M 坐标，然后根据规律求出n M 的坐标，最后根据题目要求求出最后答案即可.【详解】解：如图，过点N 作NM ①x 轴于M将1x =代入直线解析式y x =中得1y =①1OM MN ==，MON ∠=45°①1ONM =∠90°①1ON NM =①1ON NM ⊥①11OM MM ==①1M 的坐标为（2，0）同理可以求出2M 的坐标为（4，0）同理可以求出3M 的坐标为（8，0）同理可以求出n M 的坐标为（2n ，0）①2021M 的坐标为（20212，0）故答案为：（20212，0）.【点睛】本题主要考查了直线与坐标轴之间的关系，解题的关键在于能够发现规律.20．（内蒙古呼伦贝尔2021年中考数学试卷）如图，点1B 在直线1:2l y x =上，点1B 的横坐标为2，过点1B 作11B A x ⊥轴，垂足为1A ，以11A B 为边向右作正方形1112A B C A ，延长21A C 交直线l 于点2B ；以22A B 为边向右作正方形2223A B C A ，延长32A C 交直线l 于点3B ；……；按照这个规律进行下去，点2021B 的坐标为___________．【答案】202020202019202033(,)22【分析】由题意分别求出A 1、A 2、A 3、A 4……A n 、B 1、B 2、B 3、B 4……B n 、的坐标，根据规律进而可求解．【详解】解：①点1B 在直线1:2l y x =上，点1B 的横坐标为2，过点1B 作11B A x ⊥轴，垂足为1A ， ①1(2,0)A ，1(2,1)B ，①A 1B 1=1，根据题意，OA 2=2+1=3，①2(3,0)A ，23(3,)2B ，同理，39(,0)2A ，399(,)24B ， 427(,0)4A ，42727(,)48B …… 由此规律，可得：123(,0)2n n n A --，112133(,)22n n n n n B ----， ①20211202112021202122021133(,)22B ----即2020202020212019202033(,)22B ，故答案为：202020202019202033(,)22．【点睛】本题考查一次函数的应用、正方形的性质、点的坐标规律，理解题意，结合图象和正方形的性质，探索点的坐标规律是解答的关键．21．（2021·湖北中考真题）如图，在平面直角坐标系中，动点P 从原点O 出发，水平向左平移1个单位长度，再竖直向下平移1个单位长度得到点()11,1P --；接着水平向右平移2个单位长度，再竖直向上平移2个单位长度得到点2P ；接着水平向左平移3个单位长度，再竖直向下平移3个单位长度得到点3P ；接着水平向右平移4个单位长度，再竖直向上平移4个单位长度得到点4P ，…，按此作法进行下去，则点2021P 的坐标为___________．【答案】(1011,1011)--【分析】先根据点坐标的平移变换规律求出点2345,,,P P P P 的坐标，再归纳类推出一般规律即可得．【详解】解：由题意得：2(12,12)P -+-+，即2(1,1)P ，3(13,13)P --，即3(2,2)P --，4(24,24)P -+-+，即4(2,2)P ，5(25,25)P --，即5(3,3)P --，观察可知，点1P 的坐标为(1,1)--，其中1211=⨯-，点3P 的坐标为(2,2)--，其中3221=⨯-，点5P 的坐标为(3,3)--，其中5231=⨯-，归纳类推得：点21n P -的坐标为(,)n n --，其中n 为正整数，2021210111=⨯-，∴点2021P 的坐标为(1011,1011)--，故答案为：(1011,1011)--．【点睛】本题考查了点坐标的平移变换规律、点坐标的规律探索，正确归纳类推出一般规律是解题关键． 22．（2021·内蒙古通辽市·中考真题）如图，11OA B ，122A A B ，233A A B △…，1n n n A A B -都是斜边在x 轴上的等腰直角三角形，点1A ，2A ，3A ，…，n A 都在x 轴上，点1B ，2B ，3B ，…，n B 都在反比例函数()10y x x=>的图象上，则点n B 的坐标为__________．（用含有正整数n 的式子表示）【答案】【分析】根据等腰直角三角形的性质，得到1B 的横，纵坐标相等，在结合反比例函数解析式求得该点的坐标，再根据等腰三角形的性质和反比例函数的解析式首先求得各个点的坐标，发现其中的规律，从而得到答案．【详解】11OB A △为等腰三角形∴直线1OB 的解析式为y x = 由题意得：1y x y x =⎧⎪⎨=⎪⎩解得1x =()111B ∴，1OB ∴=112OA ∴==()12,0A ∴122A A B △为等腰三角形∴设直线12A B 的解析式为y x b =+02b ∴=+，解得2b =-∴直线12A B 的解析式为2y x =- ∴21y x y x =-⎧⎪⎨=⎪⎩解得1x =)21B ∴21222B A A y ∴==∴点2A ()233A A B △为等腰三角形∴设直线23A B 的解析式为1y x b =+∴10b =解得1b =-∴直线23A B的解析式为y x =-1y x y x ⎧=-⎪⎨=⎪⎩解得x =∴3B 综上可得：点()111B ，，点)21B，点3B 总结规律可得n B坐标为：故答案为：【点睛】本题综合考查了等腰直角三角形的性质以及结合反比例函数的解析式求得点的坐标，解答本题的关键是找出其中的规律求出坐标．23．（2021·山东菏泽市·中考真题）如图，一次函数y x =与反比例函数1y x=（0x >）的图象交于点A ，过点A 作AB OA ⊥，交x 轴于点B ；作1//BA OA ，交反比例函数图象于点1A ；过点1A 作111A B A B ⊥交x轴于点B ；再作121//B A BA ，交反比例函数图象于点2A ，依次进行下去，……，则点2021A 的横坐标为_______．【分析】由点A 是直线y x =与双曲线1y x=的交点，即可求出点A 的坐标，且可知45AOB ∠=︒，又AB AO ⊥可知AOB ∆是等腰直角三角形，再结合1BA OA //可知11BA B ∆是等腰直角三角形，同理可知图中所有三角形都是等腰直角三角形，由求2021A 的坐标，即n A 的坐标（n =1,2,3……），故想到过点2021A 作20212021A C x ⊥轴，即过n A 作n n A C x ⊥轴．设1A 的纵坐标为()10m m >，则1A 的横坐标为2m +，再利用点1A 在双曲线上即可求解1A 坐标，同理可得2021A 的坐标．【详解】解：过n A 作n n A C x ⊥轴于点n C点A 是直线y x =与双曲线1y x=的交点 1y x y x =⎧⎪∴⎨=⎪⎩解得11x y =⎧⎨=⎩ ()1,1A ∴1,45OC AC AOC ∴==∠=︒AB AO ⊥∴AOB ∆是等腰直角三角形∴22OB AC ==1BA OA //∴11BA B ∆是等腰直角三角形∴111AC BC =设1A 的纵坐标为()10m m >，则1A 的横坐标为12m +点1A 在双曲线上∴()1121m m +=解得11m =设2A 的纵坐标为()20m m >，则2A 的横坐标为12222m m m ++=∴()221m m =解得2m =同理可得3m =由以上规律知：n m =2021m ∴2021A∴2021A =【点睛】本题考察一次函数、反比例函数、交点坐标的求法、等腰直角三角形的性质、一元二次方程的应用和规律探究，属于综合几何题型，难度偏大．解题的关键是结合等腰直角三角形的性质做出辅助线，并在计算过程中找到规律．24．（2021·山东中考真题）如图，点1B 在直线1:2l y x =上，点1B 的横坐标为2，过点1B 作1B l ⊥，交x 轴于点1A ，以11A B 为边，向右作正方形1121A B B C ，延长21B C 交x 轴于点2A ；以22A B 为边，向右作正方形2232A B B C ，延长32B C 交x 轴于点3A ；以33A B 为边，向右作正方形3343A B B C ，延长的43B C 交x 轴于点4A ；…；按照这个规律进行下去，则第n 个正方形1n n n n A B B C +的边长为________（结果用含正整数n 的代数式表示）．【答案】1322n -⎛⎫⨯ ⎪⎝⎭【分析】根据题中条件，证明所有的直角三角形都相似且确定相似比，再具体算出前几个正方形的边长，然后再找规律得出第n 个正方形的边长．【详解】解：点1B 在直线1:2l y x =上，点1B 的横坐标为2，∴点1B 纵坐标为1．1OB ∴==分别过1B ，14,,C C ⋅⋅⋅作x 轴的垂线，分别交于14,,,D D D ⋅⋅⋅，下图只显示一条；。

专练05 三角形中的最值问题-2021年中考数学压轴题专项高分突破训练(全国通用)(解析版)

专练05三角形中的最值问题1.几何探究题（1）发现：在平面内，若AB=a，BC=b，其中b>a．当点A在线段BC上时，线段AC的长取得最小值，最小值为________；当点A在线段CB延长线上时，线段AC的长取得最大值，最大值为________．（2）应用：点A为线段BC外一动点，如图2，分别以AB、AC为边，作等边△ABD和等边△ACE，连接CD、BE．①证明：CD=BE；②若BC=5，AB=2，则线段BE长度的最大值为________．（3）拓展：如图3，在平面直角坐标系中，点A的坐标为(2，0)，点B的坐标为(7，0)，点P为线AB 外一动点，且PA=2，PM=PB，∠BPM＝90°．请直接写出线段AM长的最大值及此时点P的坐标．【答案】（1）∵当点A在线段BC上时，线段AC的长取得最小值，最小值为BC-AB，∵BC=b，AB=a，∴BC-AB=b-a，当点A在线段CB延长线上时，线段AC的长取得最大值，最大值为BC+AB，∵BC=b，AB=a，∴BC+AB=b+a，故答案为：b-a，b+a；（2）解：①CD=BE，理由：∵△ABD与△ACE是等边三角形，∴AD=AB，AC=AE，∠BAD=∠CAE=60°，∴∠BAD+∠BAC=∠CAE+∠BAC，即∠CAD=∠EAB，在△CAD与△EAB中，{AD＝AB∠CAD＝∠EABAC＝AE，∴△CAD≌△EAB（SAS），∴CD=BE；7 ②∵线段BE长的最大值=线段CD的最大值，∴由（1）知，当线段CD的长取得最大值时，点D在CB的延长线上，∴最大值为BE=CD=BD+BC=AB+BC=5+2=7；故答案为：7．（3）解：最大值为5+2 √2；∴P（2- √2，√2）．如图1，连接BM，∵将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，则△APN是等腰直角三角形，∴PN=PA=2，BN=AM，∵A的坐标为（2，0），点B的坐标为（7，0），∴AO=2，OB=7，∴AB=5，∴线段AM长的最大值=线段BN长的最大值，∴当N在线段BA的延长线时，线段BN取得最大值，最大值=AB+AN，∵AN= √2AP=2 √2，∴最大值为 5+2 √2；如图2，过P作PE⊥x轴于E，∵△APN是等腰直角三角形，∴PE=AE= √2，∴OE=OA-AE=2- √2，∴P（2- √2，√2）．2.阅读下列材料，解决提出的问题：【最短路径问题】如图（1），点A，B分别是直线l异侧的两个点，如何在直线l上找到一个点C，使得点C到点A，点B 的距离和最短？我们只需连接AB，与直线l相交于一点，可知这个交点即为所求.如图（2），如果点A，B分别是直线l同侧的两个点，如何在l上找到一个点C，使得这个点到点A、点B 的距离和最短？我们可以利用轴对称的性质，作出点B关于的对称点B’，这时对于直线l上的任一点C，都保持CB＝CB’，从而把问题（2）变为问题（1）.因此，线段AB’与直线l的交点C的位置即为所求.为了说明点C的位置即为所求，我们不妨在直线上另外任取一点C’，连接AC’，BC’，B’C’.因为AB’≤AC’+C’B’，∴AC+CB≤AC’+C’B，即AC+BC最小.（1）【数学思考】材料中划线部分的依据是________.（2）材料中解决图（2）所示问题体现的数学思想是.（填字母代号即可）A.转化思想B.分类讨论思想C.整体思想（3）【迁移应用】如图3，在Rt△ABC中，∠C＝90°，∠BAC＝15°，点P为C边上的动点，点D为AB边上的动点，若AB ＝6cm，求BP+DP的最小值.【答案】（1）两点之间线段最短或者三角形任何两边的和大于第三边（2）A（3）解：如图，作点B关于点C的对称点B′，连接AB′.作BH⊥AB′于H.作点D关于AC的对称点D′，则PD＝PD′，∴PB+PD＝PB+PD′，根据垂线段最短可知，当点D′与H重合，B，P，D′共线时，PB+PD的最小值＝线段BH的长，∵BC＝CB′，AC⊥BB′，∴AB＝AB′，∴∠BAC＝∠CAB′＝15°，∴∠BAH＝30°，在Rt△ABH中，∵AB＝3cm，∠BAH＝30°，∴BH＝12AB＝3cm，∴PB+PD的最小值为3cm3.如图（1）性质：角平分线上的点到角两边的距离相等，如图1：OP平分∠MON，PC⊥OM于C，PB⊥ON于B，则PB________PC（填“ >”“ <”或“=”）；（2）探索：如图2，小明发现，在△ABC中，AD是∠BAC的平分线，则S△ABDS△ADC =ABAC，请帮小明说明原因.（3）应用：如图3，在小区三条交叉的道路AB，BC，CA上各建一个菜鸟驿站D，P，E，工作人员每天来回的路径为P→D→E→P，①问点P应选在BC的何处时，才能使PD+DE+PE最小？②若∠BAC=30°，S△ABC=10，BC=5，则PD+DE+PE的最小值是多少？【答案】（1）∵OP平分∠MON，PC⊥OM于C，PB⊥ON于B，∴PB=PC（2）解：理由：过点D作DE⊥AB于E，DF⊥AC于F∵AD是∠BAC的平分线，∴DE=DF∴S△ABDS△ADC =12DE·AB12DF·AC=ABAC；（3）解：①过点A作AP⊥BC于P，分别作点P关于AB、AC的对称点P1、P2 ，连接P1P2分别交AB、AC于D、E，连接PD、PE、AP1、AP2 ，由对称的性质可得AP1=AP=AP2 ，DP1=DP，EP2=EP，∴PD+DE+PE= DP1+DE+ EP2= P1P2 ，根据两点之间，线段最短和垂线段最短，即可得出此时PD+DE+PE最小，即P1P2的长即当AP⊥BC于P时，PD+DE+PE最小；②∵S△ABC=10，BC=5，∴12BC·AP=10解得：AP=4由对称的性质可得AP1=AP=AP2=4，DP1=DP，EP2=EP，∠DAP1=∠DAP，∠EAP2=∠EAP∴∠DAP1＋∠EAP2=∠DAP＋∠EAP=∠DAE=30°∴∠P1AP2=60°∴△P1AP2是等边三角形∴P1P2= AP1=4即PD+DE+PE的最小值是4.4.如图（1）探索1：如图1，点A 是线段BC 外一动点，若AB＝2，BC＝4，填空：当点A 位于________线段AC 长取得最大值，且最大值为________；（2）探索2：如图2，点A 是线段BC 外一动点，且AB＝1，BC＝3，分别以AB、BC 为直角边作等腰直角三角形ABD 和等腰直角三角形CBE，连接AC、DE.①请找出图中与AC 相等的线段，并说明理由；②直接写出线段DE 长的最大值；（3）如图3，在平面直角坐标系中，已知点A（2，0）、B（5，0），点P、M 是线段AB 外的两个动点，且PA＝2，PM＝PB，∠BPM＝90°，求线段AM 长的最大值及此时点P 的坐标.（提示：在图 4 中作PN⊥PA，PN=PA，连接BN 后，利用探索 1 和探索2中的结论，可以解决这个问题）【答案】（1）∵点A为线段BC外一动点，且AB=2，BC=4，∴当点A位于CB的延长线上时，线段AC的长取最大值，最大值为2+4=6，故答案是：CB的延长线上，6；（2）解：①∵△ABD和△CBE是等腰直角三角形，∴AB=DB，CB=EC，∠ABD=∠CBE=90°，∴∠ABD−∠ABE=∠CBE−∠ABE，即∠DBE=∠ABC，在△BAC和△BDE中，{BA=BD∠ABC=∠DBEBC=BE，∴△BAC≅△BDE(SAS)，∴AC=DE；②由（1）知AC的最大值是AB+BC=4，∵DE=AC，∴DE长的最大值是4；类比应用：（3）解：如图，过点P作PN⊥PA，PN=PA，连接BN，根据（2）中的方法，同理可以证明△AMP≅△NBP，∴AM=BN，当点N在线段BA的延长线上时，线段BN取最大值，也就是线段AM取最大值，最大值是AB+AN，∵A(2,0)，B(5,0)，∴AB=3，∵△APN是等腰直角三角形，∴AN=√2AP=2√2，∴最大值是2√2+3，如图，过点P作PE⊥x轴于点E，∵△APN是等腰直角三角形，∴PE=AE=√2，∴OE=BO−AB−AE=5−3−√2=2−√2，∴P(2−√2,√2)，如图，点P也有可能在x轴下方，与刚刚的点P关于x轴对称，P(2−√2,−√2)，综上：点P的坐标是(2−√2,√2)或(2−√2,−√2).5.在等腰Rt△ABC中，∠BAC=90°，AB=AC=6 √2，D是射线CB上的动点，过点A作AF⊥AD（AF始终在AD上方），且AF=AD，连接BF（1）如图1，当点D在线段BC上时，BF与DC的关系是________.（2）如图2，若D、E为线段BC上的两个动点，且∠DAE=45°，连接EF，DC=3，求ED的长.（3）若在点D的运动过程中，BD=3，则AF=________.（4）如图3，若M为AB中点，连接MF，在点D的运动过程中，当BD=________时，MF的长最小？最小值是________.【答案】（1）当点D在线段BC上时，∵AF=AD，∠BAF=90°−∠BAD=∠DAC，AB=AC∴△FAB≅△DAC(SAS)∴BF=DC（2）解：∵AE=AE，∠EAF=90°−∠DAE=45°=∠EAD，AF=AD，∴△FAE≅△DAE(SAS)∴ED=EF=3（ 3 ）BD=3，设AG为BC边上的高，G为垂足，在等腰Rt△ABC中，G为BC的中点，∴AF=AD=√AG2+DG2=√62+(6−3)2=3√5（ 4 ）点F的轨迹是过点B，且垂直于BC的射线，根据垂线段最短的性质，当MF⊥BF时，线段MF 最短，又因为BC⊥BF，∠ABC=45°，∠FBD=90°∴△BFM为等腰直角三角形，MF=BF=√22BM=√22×AB2=√24×6√2=3BD=BC-DC=12-3=9此时MF=3.6.（1）发现如图①所示，点A为线段BC外的一个动点，且BC＝a，AB＝b.填空：当点A位于________时，线段AC 的长取得最大值，且最大值为________（用含a、b 的式子表示）.（2）应用点A为线段BC外一个动点，且BC=4，AB=1.如图②所示，分别以AB，AC为边，作等边三角形ABD和等边三角形ACE，连接CD，BE.①找出图中与BE相等的线段，并说明理由；②直接写出线段BE长的最大值_▲ .（3）拓展如图③所示，在平面直角坐标系中，点A的坐标为（2，0），点B的坐标为（6，0），点P为线段AB外一个动点，且PA=2，PM=PB，∠BPM=90°.请直接写出线段AM的最大值________及此时点P的坐标________.【答案】（1）∵点A为线段BC外一动点，且BC=a，AB=b，∴当点A位于CB的延长线上时，线段AC的长取得最大值，且最大值为BC+AB=a+b，故答案为：CB的延长线上；a+b；（2）解：①CD=BE；理由：∵△ABD与△ACE是等边三角形，∴AD=AB，AC=AE，∠BAD=∠CAE=60°，∴∠BAD+∠BAC=∠CAE+∠BAC，即∠CAD=∠EAB，在△CAD与△EAB中，{AD＝AB∠CAD＝∠EABAC＝AE，∴△CAD≌△EAB，②∵线段BE长的最大值=线段CD的最大值，由（1）知，当线段CD的长取得最大值时，点D在CB的延长线上，∴最大值为BD+BC=AB+BC=5故答案为：5；（ 3 ）∵将△APM绕着点P顺时针旋转90°得到△PBN，连接AN，则△APN是等腰直角三角形，∴PN=PA=2，BN=AM，∵A的坐标为（2，0），点B的坐标为（6，0），∴OA=2，OB=6，∴AB=4，∴线段AM长的最大值=线段BN长的最大值，∴当N在线段BA的延长线时，线段BN取得最大值，最大值=AB+AN，∵AN= √2AP=2 √2，∴AM长的最大值为2 √2+4；如图2，当点P在第一象限时，过P作PE⊥x轴于E，∵△APN是等腰直角三角形，∴PE=AE= √2，∴OE=OA-AE=2- √2，∴P（2- √2，√2）；如图3，当点P在第四象限时，根据对称性可知，P（2- √2，- √2）也符合题意综上：点P的坐标为（2- √2，√2）或（2- √2，- √2）故答案为：2 √2+4；（2- √2，√2）或（2- √2，- √2）.7.在等腰Rt△ABC中，∠BAC=90°，AB=AC=6√2，D是射线CB上的动点，过点A作AF⊥AD（AF始终在AD上方），且AF=AD，连接BF.（1）如图1，当点D在线段BC上时，BF与DC的关系是________；（2）如图2，若点D，E为线段BC上的两个动点，且∠DAE=45°，连接EF，DC=3，求ED 的长；（3）若在点D的运动过程中，BD=3，则AF=________；（4）如图3，若M为AB中点，连接MF，在点D的运动过程中，当BD=________时，MF的长最小？最小值是________.【答案】（1）长度相等（2）5（3）3√5（4）9；3【解析】（1）∵AF⊥AD∴∠DAF=90°∵∠BAC=90°∴∠CAD=∠BAC-∠BAD=∠DAF-∠BAD=∠BAF 即∠CAD =∠BAF∵AB=AC，AF=AD∴△ADC≌△AFB，∴BF= DC故答案为：长度相等；（2）由（1）可知△ADC≌△AFB，∵∠DAE=45°，∠BAC=90°∴∠CAD+∠BAE=45°∵∠CAD =∠BAF∴∠BAF +∠BAE=45°∴∠FAE=45°= ∠DAE∵AD=AF,AE=AE∴△AED≌△AEF，得到EF=DE，设DE=x，∵∠BAC=90°，AB=AC=6√2，∴BC= √AB2+AC2=12,∠C=∠ABC=45°，∴∠ABF=∠C=45°∴∠FBE=90°∴△BEF是直角三角形，∵EF=DE =x，CD=3∴BE=9-x,BF=CD=3在Rt△BEF中，EF2=BF2+BE2,即x2=32+(9-x)2,解得x=5即DE的长为5；（3）如图，过A点作AH⊥BC于H点，∵△ABC为的等腰直角三角形∴AH是△ABC的中线，BC=6∴AH= 12∵BD=3，∴DH=BH-BD=3∴AD= √AH2+DH2=3√5∴AF= 3√5故答案为：3√5；（4）如图，取AC中点M’，故BM=CM’∵∠FBM=∠C，BF=CD∴△FBM≌△DCM’∴MF=M’D，故当M’D最短时，则MF最短，作M’D⊥BC于D’点，AC=3√2则△CD’M’是等腰直角三角形，M’C= 12设CD’=D’M’=a∴a2+a2=(3√2)2解得a=3（负值舍去）∴CD’=3故此时BD=12-3=9,MF=D’M’=3故答案为：9；3.8.如图1，已知直线l的同侧有两个点A，B，在直线l上找一点P，使P点到A，B两点的距离之和最短的问题，可以通过轴对称来确定，即作出其中一点关于直线l的对称点，对称点与另一点的连线与直线l的交点就是所要找的点，通过这种方法可以求解很多问题（1）如图2，在平面直角坐标系内，点A的坐标为(1，1)，点B的坐标为(5，4)，动点P在x轴上，求PA+PB的最小值；（2）如图3，在锐角三角形ABC中，AB=8，∠BAC=45°，∠BAC的角平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值为________（3）如图4，∠AOB=30°，OC=4，OD=10，点E，F分别是射线OA，OB上的动点，则CF+EF+DE的最小值为________。

2021年中考数学压轴题提升训练正确分析函数图象含解析

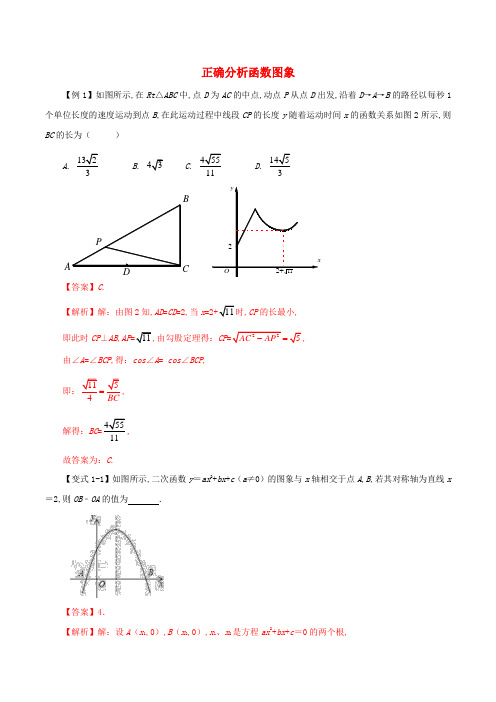
正确分析函数图象【例1】如图所示,在Rt △ABC 中,点D 为AC 的中点,动点P 从点D 出发,沿着D →A →B 的路径以每秒1个单位长度的速度运动到点B ,在此运动过程中线段CP 的长度y 随着运动时间x 的函数关系如图2所示,则BC 的长为（） AB. CD【答案】C .【解析】解：由图2知,AD =CD =2,当x,CP 的长最小, 即此时CP ⊥AB ,AP由勾股定理得：CP=由∠A =∠BCP ,得：cos ∠A = cos ∠BCP ,即：4BC=, 解得：BC故答案为：C .【变式1-1】如图所示,二次函数y ＝ax 2+bx +c （a ≠0）的图象与x 轴相交于点A ,B ,若其对称轴为直线x ＝2,则OB ﹣OA 的值为．【答案】4．【解析】解：设A （x 1,0）,B （x 2,0）,x 1、x 2是方程ax 2+bx +c ＝0的两个根,BC∵抛物线的对称轴是：x ＝2, ∴﹣2ba＝2, ∴ba＝﹣4, 由图可知：x 1＜0,x 2＞0, ∴OB ﹣OA ＝x 2﹣（﹣x 1）＝x 2+x 1 ＝﹣ba＝4, 故答案为：4．【变式1-2】如图1,正方形ABCD 在直角坐标系中,其中AB 边在y 轴上,其余各边均与坐标轴平行,直线l ：y ＝x ﹣5沿y 轴的正方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD 的边所截得的线段长为m ,平移的时间为t （秒）,m 与t 的函数图象如图2所示,则图2中b 的值为（）图1 图2A ．B ．C ．D ．【答案】C .【解析】解：在y ＝x ﹣5中,当y ＝0时, x ＝5；当x ＝0,y ＝﹣5, ∴直线y ＝x ﹣5与坐标轴围成的三角形为等腰直角三角形, ∴直线l 与直线BD 平行,由图2可得,t ＝3时,直线l 经过点A , ∴AO ＝5﹣3×1＝2,即A （﹣2,0）,t ＝15时,直线l 经过点C ,∴当t ＝9时,直线l 经过B ,D 两点, ∴AD ＝6,∴BD ＝,即b ＝,故答案为：C．【例2】如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点(-1,-4),下列结论：①b2＞4ac；②ax2+bx+c≥-6；③若点(-2,m),(-5,n)在抛物线上,则m＞n；④关于x的一元二次方程ax2+bx+c=-4的两根为-5和-1,其中正确的是__________．【解析】解：由图象知,抛物线与x轴有2个公共点,∴b2－4ac＞0,即①正确；抛物线有最低点,当x=－3时,y有最小值－6,即ax2+bx+c≥-6,故②正确；抛物线的对称轴为x=－3,点(-2,m),(-5,n)在抛物线上,∴m<n,故③错误；由图象知,当x=－1时,y=－4,由对称性可知,当x=－5时,y=－4,故④正确；综上,答案为：①②④.【变式2-1】如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是（）A．乙前4秒行驶的路程为48米B．在0到8秒内甲的速度每秒增加4米/秒C．两车到第3秒时行驶的路程相同D．在4到8秒内甲的速度都大于乙的速度【答案】C.【解析】解：根据图象可得：乙前4秒匀速运动,速度为12米/秒,行驶的路程为12×4=48米,故A正确；0~8秒内甲的速度是一条过原点的直线,甲的速度每秒增加4米/秒,故B正确；甲的速度与时间的关系为：v=4t,t=3时,v=12,即在t=3时,甲乙速度相等,在0~3秒时甲的速度小于乙的速度,故两车行驶路程不相等,故C错误；在4至8秒内甲的速度图象一直在乙的上方,所以甲的速度都大于乙的速度,故D正确；故答案为：C．【变式2-2】如图,若二次函数y＝ax2+bx+c（a≠0）图象的对称轴为x＝1,与y轴交于点C,与x轴交于点A、点B（﹣1,0）,则①二次函数的最大值为a+b+c；②a﹣b+c＜0；③b2﹣4ac＜0；④当y＞0时,﹣1＜x ＜3．其中正确的个数是（）A．1 B．2 C．3 D．4【答案】B．【解析】解：①∵二次函数y＝ax2+bx+c图象的对称轴为x＝1,且开口向下,∴当x＝1时,y＝a+b+c,y取最大值,即二次函数的最大值为a+b+c,所以①正确；②当x＝﹣1时,a﹣b+c＝0,所以②错误；③图象与x轴有2个交点, b2﹣4ac＞0,所以③错误；④∵图象的对称轴为x＝1,与x轴交于点A、点B（﹣1,0）,∴A（3,0）,当y＞0时,﹣1＜x＜3,所以④正确．所以答案为：B．【例3】如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E作FE⊥AE,交CD于F点,设点E运动路程为x,FC＝y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是25,则矩形ABCD的面积是（）A ．235B ．5C ．6D ．254【答案】B .【解析】解：若点E 在BC 上时,如图∵∠EFC +∠AEB ＝90°,∠FEC +∠EFC ＝90°, ∴∠CFE ＝∠AEB , ∴△CFE ∽△BEA , ∴CF CEBE AB=, 当E 在BC 中点时,CF 有最大值,BE ＝CE ＝x ﹣52, 即2552CEBE=,∴BE ＝CE ＝1, ∴BC ＝2,AB ＝52, ∴矩形ABCD 的面积为2×52＝5；故答案为：B ．【变式3-1】如图1,则等边三角形ABC 中,点P 为BC 边上的任意一点,且∠APD ＝60°,PD 交AC 于点D ,设线段PB 的长度为x ,CD 的长度为y ,若y 与x 的函数关系的大致图象如图2,则等边三角形ABC 的面积为．【答案】．【解析】解：由题可得,∠APD＝60°,∠ABC＝∠C＝60°, ∴∠BAP＝∠CPD,∴△ABP∽△PCD,∴AB CP BP CD=,设AB＝a,则a a xx y-=,∴y＝2x axa-+=21124ax aa⎛⎫--+⎪⎝⎭,当x＝12a时,y取得最大值2,可得：a=8,即等边三角形的边长为8,∴S×82＝故答案为：．【变式3-2】如图1,四边形ABCD中,AB∥CD,∠ADC＝90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设P点的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图2所示,当P运动到BC中点时,△APD的面积为（）图1 图2A．4 B．5 C．6 D．7【答案】B．【解析】解：根据题意得：四边形ABCD是梯形,AB+BC＝6,CD＝4,12AD×CD＝8,得：AD＝4,∵12AD×AB＝2,∴AB＝1,当P运动到BC中点时,△APD的高为12（AB+CD）＝52,∴△PAD的面积＝12×52×4＝5；所以答案为：B．1.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成．为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器．设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为（）图1 图2A．A→O→B B．B→A→C C．B→O→C D．C→B→O【答案】C.【解析】解：A、从A点到O点y随x的增大而减小,从O到B是先减小后增发,观察图2,A不符合题意；B、从B到A点y随x的增大先减小再增大,在A点达到最大值,从A到C点y随x的增大先减小再增大,观察图2,B不符合题意；C、从B到O点y随x的增大先减小再增大,从O到C点y随x的增大先减小再增大,在B、C点距离最大,观察图2,C符合题意；D、从C到B点y随x的增大先减小后增大,在到达M点时y=0,与图象不符,D不符合题意；所以答案为：C．2.小明家、食堂,图书馆在同一条直线上,小明从家去食堂吃早餐,接着去图书馆读报,然后回家,如图反映了这个过程中,小明离家的距离y（km）与时间x（min）之间的对应关系,根据图象,下列说法正确的是（）A．小明吃早餐用了25minB．食堂到图书馆的距离为0.6kmC．小明读报用了30minD．小明从图书馆回家的速度为0.8km/min【答案】C．【解析】解：由图象可得,小明吃早餐用25﹣8＝17min,故选项A错误；食堂到图书馆的距离为：0.8﹣0.6＝0.2km,故选项B错误；小明读报用了58﹣28＝30min,故选项C正确；小明从图书馆回家的速度为：0.8÷（68﹣58）＝0.08km/min,故选项D错误；所以答案为：C．3.已知二次函数y＝ax2+bx+c中,函数y与自变量x的部分对应值如表所示：x…﹣5 ﹣4 ﹣3 ﹣2 ﹣1 …y…﹣8 ﹣3 0 1 0 …当y＜﹣3时,x的取值范围是．【答案】x ＜﹣4或x ＞0．【解析】解：由表可知,二次函数的对称轴为直线x ＝﹣2,抛物线的开口向下, 由x =﹣4时,y =-3得：x ＝0时,y ＝﹣3, ∴y ＜﹣3时,x 的取值范围为x ＜﹣4或x ＞0．故答案为：x ＜﹣4或x ＞0．4.如图,抛物线y ＝ax 2+bx +c （a ≠0）与x 轴交于点A （1,0）,对称轴为直线x ＝﹣1,当y ＞0时,x 的取值范围是（）A ．﹣1＜x ＜1B ．﹣3＜x ＜﹣1C ．x ＜1D ．﹣3＜x ＜1【答案】D ．【解析】解：∵抛物线y ＝ax 2+bx +c 与x 轴交于点A （1,0）,对称轴为直线x ＝﹣1, ∴抛物线与x 轴的另一交点坐标是（﹣3,0）, ∴当y ＞0时,x 的取值范围是﹣3＜x ＜1．所以答案为：D ．5.在矩形ABCD 中,AD =2AB =4,E 是AD 的中点,一块足够大的三角板的直角顶点与点E 重合,将三角板绕点E 旋转,三角板的两直角边分别交AB ,BC （或它们的延长线）于点M ,N ,设∠AEM =α（0°＜α＜90°）,给出下列四个结论：①AM =CN ； ②∠AME =∠BNE ； ③BN ﹣AM =2； ④S △EMN =22cos．上述结论中正确的个数是（）A．1 B．2 C．3 D．4【答案】C．【解析】解：①过E作EF⊥BC于点F,∵矩形ABCD,AD=2AB,E是AD的中点,∴AB=AE=EF=FC,∠MAE=∠NFE=90°,∵∠AEM+∠DEN=90°,∠FEN+∠DEN=90°, ∴∠AEM=∠FEN,∴△AME≌△FNE,∴AM=FN,∴MB=CN．∵M不一定是AB的中点,∴AM不一定等于CN,故①错误,②由Rt△AME≌Rt△FNE,得∠AME=∠BNE, 故②正确,③由①知,AM=NF,∵AD=2AB=4,∴BC=4,AB=2∴BN﹣AM=BN﹣NF =BF=AE=2,故③正确,④由①知,△AME≌△FNE,∴EM=EN,可得△EMN 为等腰直角三角形,在Rt △AEM 中,EM = cos AE α, ∴S △EMN = 212cos AE α⎛⎫ ⎪⎝⎭=22cos α, 故④正确．故答案为：C ．6.已知二次函数y =ax 2+bx +c （a ≠0）的图象如图所示,并且关于x 的一元二次方程ax 2+bx +c ﹣m =0有两个不相等的实数根,下列结论：①b 2﹣4ac ＜0；②abc ＞0；③a ﹣b +c ＜0；④m ＞﹣2,其中,正确的个数有（）A ．1B ．2C ．3D ．4【答案】B ．【解析】解：如图所示：图象与x 轴有两个交点,则b 2﹣4ac ＞0,故①错误；∵图象开口向上,∴a ＞0,∵对称轴在y 轴右侧,∴a ,b 异号,b ＜0,∵图象与y 轴交于x 轴下方,∴c ＜0,∴abc ＞0,故②正确；当x =﹣1时,a ﹣b +c ＞0,故③错误；∵由图象知,y ≥﹣2,∴关于x 的一元二次方程ax 2+bx +c ﹣m =0有两个不相等的实数根,则m ＞﹣2,故④正确．故答案为：B ．7.阅读对话,解答问题：（1）分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出（a,b）的所有取值；（2）求在（a,b）中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率．【答案】见解析．【解析】解：（1）（a,b）对应的表格为：1 2 31 （1,1）（1,2）（1,3）2 （2,1）（2,2）（2,3）3 （3,1）（3,2）（3,3）4 （4,1）（4,2）（4,3）（2）由方程x2﹣ax+2b=0有实数根,得：△=a2﹣8b≥0．由（1）中表格知：使a2﹣8b≥0的（a,b）有：（3,1）,（4,1）,（4,2）三组,∴p（△≥0）=14．8.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动（点D与点B、C不重合）,作BE⊥AD 于E,CF⊥AD于F,则BE+CF的值（）A．不变B．增大C．减小D．先变大再变小【答案】C．【解析】解：S△ABC=S△ABD+S△ACD=12×AD×BE+12×AD×CF=12×AD×(BE+ CF),∵S△ABC是定值,∴BE+ CF=2ABCSAD,由图知,AD的长逐渐变大,则BE+ CF的值逐渐减小,故答案为：C.9.如图,已知在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论：①ED⊥BC；②∠A=∠EBA；③EB平分∠AED；④ED=12AB中,一定正确的是（）A．①②③B．①②④C．①③④D．②③④【答案】B.【解析】解：由作图知,P在线段BC的垂直平分线上,而D是BC中点, ∴PD是线段BC的垂直平分线,即①正确；∴EB=CE=AE,即E是AC的中点,即∠A=∠EBA,②正确；由上可知,DE是△ABC的中位线,∴ED=12AB,④正确；只有当∠A=60°时,∠BED=∠AEB=60°,∴③错误；综上所述,答案为：B.10.一般情况下,中学生完成数学家庭作业时,注意力指数随时间x（分钟）的变化规律如图所示（其中AB、BC为线段,CD为双曲线的一部分）．（1）分别求出线段AB和双曲线CD的函数关系式；（2）若学生的注意力指数不低于40为高效时间,根据图中信息,求出一般情况下,完成一份数学家庭作业的高效时间是多少分钟？【答案】见解析.【解析】解：（1）设直线AB的解析式为：y=kx+b,将（0,30）,（10,50）代入得：b=30,10k+b=50,解得：k=2,b=30,即直线AB的解析式为：y=2x+30（0≤x≤10）；设双曲线CD的解析式为：myx =,将点C(44,50)代入得：m=2200,即双曲线CD的解析式为：2200yx=（x≥44）；（2）在y=2x+30中,当y=40时,x=5,在2200yx=中,当y=40时,x=55,55－5=50,即一般情况下,完成一份数学家庭作业的高效时间是50分钟.11.如图,正方形ABCD的边长为a,点E在边AB上运动（不与点A,B重合）,∠DAM＝45°,点F在射线AM上,且AF BE,CF与AD相交于点G,连接EC,EF,EG,则下列结论：①∠ECF＝45°；②△AEG的周长为（）a；③BE2+DG2＝EG2；④△EAF的面积的最大值18a2．其中正确的结论是．（填写所有正确结论的序号）【答案】①④.【解析】解：在BC上截取BH＝BE,连接EH,∵BE＝BH,∠EBH＝90°,∴EH BE,∵AF BE,∴AF＝EH,∵∠DAM＝∠EHB＝45°,∠BAD＝90°,∴∠FAE＝∠EHC＝135°,∵BA＝BC,BE＝BH,∴AE＝HC,∴△FAE≌△EHC,∴EF＝EC,∠AEF＝∠ECH,∵∠ECH+∠CEB＝90°,∴∠AEF+∠CEB＝90°,∴∠FEC＝90°,∴∠ECF＝∠EFC＝45°,故①正确,延长AD到H,使得DH＝BE,则△CBE≌△CDH,∴∠ECB＝∠DCH,∴∠ECH＝∠BCD＝90°,∴∠ECG＝∠GCH＝45°,∵CG＝CG,CE＝CH,∴△GCE≌△GCH,∴EG＝GH,∵GH＝DG+DH,DH＝BE,∴EG＝BE+DG,故③错误,△AEG的周长＝AE+EG+AG＝AE+AH＝AD+DH+AE＝AE+EB+AD＝AB+AD＝2a,故②错误,设BE＝x,则AE＝a﹣x,AF,∴S△AEF＝12•（a﹣x）x＝﹣12（x﹣12a）2+18a2,∴x＝12a时,△AEF的面积的最大值为18a2．故④正确,即答案为：①④．12.如图1,E为矩形ABCD边AD上的一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B 沿BC运动到点C时停止,它们运动的速度都是2 cm/s．若P,Q同时开始运动,设运动时间为t（s）,△BPQ的面积为y（cm2）,已知y与t的函数关系图象如图2,则CDBE的值为（）A3B C D图1 图2 【答案】D .【解析】解：由图2知,8≤t ≤10时,△BPQ 的面积不变,则P 在线段DE 上运动,∴BE =8×2=16cm ,DE =2×2=4cm ,t =8时,BQ =16,此时y,∴=12×BQ ×CD ,即：=12×16×CD , 解得：CD, ∴CD BE=164 即答案为：D .13.在矩形ABCD 中,AB >CD ,对角线AC ,BD 相交于点O ,动点P 由点A 出发,沿AB →BC →CD 向点D 运动．设点P 的运动路程为x ,△AOP 的面积为y ,y 与x 的函数关系图象如图②所示,则AD 边的长为（）A . 3B . 4C . 5D .6【答案】B .【解析】解：当P 点在AB 上运动时,y 逐渐增大,当P 点到达B 点时,y 最大为3． ∴12AB •12＝3,即AB •BC ＝12．当P 点在BC 上运动时,y 逐渐减小,当P 点到达C 点时,y 为0,此时结合图象可知P 点运动路径长为7, ∴AB +BC ＝7．图1图2则BC＝7﹣AB,代入AB•BC＝12,得：AB2﹣7AB+12＝0,解得：AB＝4或3,∵AB＜AD,∴AB＝3,BC＝4．即AD=BC=4,故答案为：B.14.在正方形ABCD中,点P从点D出发,沿着D→A方向匀速运动,到达点A后停止运动,点Q从点D出发,沿着D—C—B—A的方向匀速运动,到达点A后停止运动. 已知点P的运动速度为4,图②表示P、Q两点同时出发x秒后,△APQ的面积为y与x的函数关系,则点Q的运动速度可能是（）A. 2B. 3C. 8D. 12图①图②【答案】12.【解析】解：由图②知函数图象有三段,设正方形的边长为1,则点Q在线段AB上时,点P仍在运动,设点Q的速度为v,∴2134v v ≤<,∴8<v≤12,故答案为：12.15.如图,在矩形ABCD中,动点P从点B出发,沿B-C-D-A方向运动到点A停止,运动速度为1单位每秒. 设点P的运动路程为x,△ABP的面积为y,若y与x的函数关系式如图2所示,则△ABC的面积为【答案】10.【解析】解：由题意知,AB=4×1=4,BC=(9-4)×1=5,∴S△ABC=12×4×5=10,即答案为：10.16.如图,在矩形ABCD中,动点P从点A出发,沿A→B→C运动,设PA=x点D到直线PA的距离为y且y 关于x的函数图象如图所示,则当△PCD和△PAB的面积相等时,y的值为____.【答案】125.【解析】解：由题意知,AB=3,AD=4, 当x=5时,△PCD和△PAB的面积相等,此时△APD的面积为：12×3×4=6,即12xy=6,得：y=125,故答案为：125.17.如图 1,四边形ABCD 中,AB∥CD,∠B=90°,AC=AD．动点P 从点B 出发,沿折线B-A-D-C 方向以1 单位/秒的速度匀速运动,在整个运动过程中,△BCP 的面积S 与运动时间t（秒）的函数图象如图 2 所示,则AD 等于图1 图2【解析】解：过A作AE⊥CD于E,则四边形ABCE 是矩形,E 是CD 中点,由题意知,AB =3,∴CD =6,由图2知,S 最大值为15, 即12·BC ·CD =15, ∴BC =5,由勾股定理得：AC 即AD18.二次函数y =ax 2+bx +c 的大致图象如图所示,顶点坐标为（-2,-9a ）,下列结论：①4a +2b +c >0；②5a -b +c =0；③若方程a (x +5)(x -1)=-1有两个根x 1,x 2,且x 1<x 2,则-5< x 1< x 2<1；④若方程|ax 2+bx +c |=1有四个根,则这四个根的和为-4,其中正确的结论有（） A . 1个 B .2个 C . 3个 D .4个【答案】B .【解析】解：由图象知,a >0,∵顶点坐标为（-2,-9a ）,∴22b a-=-,2494ac b a a -=-, ∴b =-4a ,c =-5a ,抛物线的解析式为：y =ax 2+4ax -5a ,∴4a +2b +c =7a >0,故①正确；5a -b +c =-4a <0,故②错误；0=ax 2+4ax -5a ,解得：x =1或x =-5,即抛物线与x 轴交于点（1,0）,（-5,0）,∵方程a (x +5)(x -1)=-1有两个根x 1,x 2,且x 1<x 2,∴-5< x 1< x 2<1,故③正确；∵方程|ax 2+bx +c |=1有四个根,∴这四个根的和为：2×（b a -）=-8,故④错误；即答案为：B.19.如图1,四边形ABCD中,AB∥CD,∠ADC=90°,P从A点出发,以每秒1个单位长度的速度,按A→B→C→D的顺序在边上匀速运动,设点P的运动时间为t秒,△PAD的面积为S,S关于t的函数图象如图2所示,当P运动到BC中点时,△PAD的面积为（）A．4 B．8 C．6 D．5图1 图2【答案】D.【解析】解：由图象知,AB+BC=6,AB+BC+CD=10,∴CD=4,当点P运动到点C时S最大,最大值为8,即12AD·CD=8,∴AD=4,当点P运动到B点时,S=2,即12AB·AD=2,∴AB=1,当P运动到BC中点时,S=12×12（AB+CD）×AD=5,故答案为：D.。

决胜2021年中考数学压轴题全揭秘精品(上海专版) 专题01 创新题型(教师版含解析)

专题01创新题型模块一：定义应用例1.定义[x ]为不超过x 的最大整数，如[3.6] = 3，[ 3.6-] = 4-．对于任意实数x ，下列式子错误的是( ) A ．[x ] = x (x 为整数)B ．0[]1x x ≤-<C ．[][][]x y x y +≤+D ．[][]n x n x +=+(n 为整数)【难度】★★ 【答案】C ．【解析】由反例[][3.8 2.7] 6.56+==，[3.8][2.7]325+=+=可知C 错误．【总结】本题考查取整函数[x ]的定义及应用．例 2.在平面直角坐标系xOy 中，对于点P (x ，y )和Q (x ，'y )，给出如下定义：若()()0'0y x y y x ⎧≥⎪=⎨-<⎪⎩，则称点Q 为点P 的“可控变点”．如果点(1-，2-)为点M 的可控变点，则点M 的坐标为___________．【难度】★★ 【答案】(-1，2)【解析】由题意得，当0<x 时，'=-y y ，且x 不变，所以当1x =-，时'2=y ，即点M 坐标为(1-，2)．【总结】把握好“可控变点”的定义，找出'y 与y 两者之间存在的关系．例3.定义一种新运算：2x y x y x +*=，如2212122+⨯*==，则()()421**-=______．【难度】★★ 【答案】0．【解析】先计算()4224224+⨯*==，再计算()()2122102+-⨯*-==．【总结】根据运算法则进行运算，注意运算顺序．例4.已知1m x =+，2n x =-+，若规定()()11m n m n y m n m n ⎧+-≥⎪=⎨-+<⎪⎩，则y 的最小值为( )A ．0B ．1C ．1-D ．2【难度】★★ 【答案】B ．【解析】把1m x =+，2n x =-+代入，得到1221222⎧⎛⎫≥ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+< ⎪⎪⎝⎭⎩x x y x x ，当12≥x 时，1≥y ；当12<x 时，1>y ．所以y 的最小值是1，故选B ．【总结】考查分段函数求最值的问题．例5.定义运算“*”：规定x y ax by *=+(其中a 、 b 为常数)，若113*=，()111*-=，12*=______．【难度】★★ 【答案】4．【解析】把113*=，()111*-=代入运算法则，得31+=⎧⎨-=⎩a b a b ，解得：21=⎧⎨=⎩a b ，所以12*=2×1+1×2=4．【总结】根据新运算，求出a 、b 的值是解答本题的关键．例 6.对于实数m 、n ，定义一种运算“*”为：m n mn n *=+．如果关于x 的方程()14x a x **=-有两个相等的实数根，那么满足条件的实数a 的值是______．【难度】★★ 【答案】0．【解析】根据运算法则，()*=+a x ax x ，()()*+=+++x ax x x ax x ax x ，整理得()()211104++++=a x a x ，此方程有两个相等的实数根，则()()210110+≠⎧⎪⎨=+-+=⎪⎩a a a ，解得：1201a a ==-，(舍)，所以a=0．【总结】由运算法则整理得一元二次方程的一般形式，再结合一元二次方程根的判别式进行求解，注意二次项系数不能为零．例7.(2020黄浦区一模)定义：我们知道，四边形的一条对角线把这个四边形分成两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的相似对角线，在四边形ABCD 中，对角线BD 是它的相似对角线，∠ABC =70°，BD 平分∠ABC ，那么∠ADC =____________度【答案】145【分析】先画出示意图，由相似三角形的判定可知，在△ABD 和△DBC 中，已知∠ABD=∠CBD ，所以需另一组对应角相等，若∠A=∠C ，则△ABD 与△DBC 全等不符合题意，所以必定有∠A=∠BDC,再根据四边形的内角和为360°列式求解. 【详解】解：根据题意画出示意图，已知∠ABD=∠CBD ， △ABD 与△DBC 相似，但不全等， ∴∠A=∠BDC ，∠ADB=∠C.又∠A+∠ABC+∠C+∠ADC=360°， ∴2∠ADB+2∠BDC+∠ABC=360°， ∴∠ADB+∠BDC=145°，即∠ADC=145°.【点睛】对于新定义问题，读懂题意是关键.例8.(2020杨浦区一模).在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF ．如果△DEF 与△ABC 相似(相似比不为1)，那么△DEF 的面积为______．【答案】1；【分析】根据小正方形的边长，分别求出ABC 和DEF 三边的长，然后判断它们是否对应成比例，再用三角形面积公式求解即可. 【详解】如图，∵1AB BC ==，，AC∴:?:?AB BC AC =∵DE =2EF =，DF =∴::DE EF DF ==∴:?:?::AB BC AC DE EF DF = ∴~ABC DEF ∴12112DEFS=⨯⨯= 故答案为：1【点睛】本题考查了在网格中画与已知三角形相似的三角形、三角形全等的判定以及三角形面积公式，熟练掌握三角形全等的判定是解题的关键.例9.我们把两个三角形的外心之间的距离叫做外心距．如图，在Rt ABC ∆和Rt ACD ∆中，90ACB ACD ∠=∠=︒，点D 在边BC 的延长线上，如果BC = DC = 3，那么ABC ∆和ACD ∆的外心距是______．【难度】★★ 【答案】3．【解析】直角三角形的外心为斜边的中点，所以ABC ∆和ACD ∆ 的外心分别为AB 和AD 的中点，这两个三角形的外心距即∆ABD 的中位线，长度是132=BD ．【总结】本题考查的知识点有直角三角形的外心、三角形的中位线．例10.定义[a ，b ，c ]为函数2y ax bx c =++的“特征数”．如：函数232y x x =+-的“特征数”是[1，3，2-]，函数4y x =-+的“特征数”是[0，1-，4]．如果将“特征数”是[2，0，4]的函数图像向下平移3个单位，得到一个新函数图像，那么这个新函数的解析式是__________________．【难度】★★ 【答案】221=+y x ．【解析】由题意得“特征数”是[2，0，4]的函数解析式为224=+y x ，向下平移3个单位可得新函数的解析式为：221=+y x ．【总结】特征数[a ，b ，c ]即为二次函数的三个系数，已知特征数则可求得二次函数的解析式，再根据抛物线的平移法则“上加下减、左加右减”进行解题．例11.在平面直角坐标系xOy 中，C 的半径为r ，点P 是与圆心C 不重合的点，给出如下定义：若点'P 为射线CP 上一点，满足2'CP CP r =，则称点'P 为点P 关于C 的反演点．如图为点P 及其关于C 的反演点'P 的示意图．请写出点M (12，0)关于以原点O 为圆心，以1为半径的O 的反演点'M 的坐标．AB D【难度】★★★【答案】(2，0)．【解析】由反演点的定义可得2'=OM OM r ，即21'12=OM ，解得：'2=OM ，又点'M 在x 轴上，所以点'M 的坐标为(2，0)．【总结】掌握“反演点”的定义中，两点之间存在的关系．例12.如图1，对于平面上不大于90°的MON ∠，我们给出如下定义：如果点P 在MON ∠的内部，作PE OM ⊥，PF ON ⊥，垂足分别为点E 、F ，那么称PE + PF 的值为点P 相对于MON ∠的“点角距离”，记为d (P ，MON ∠)．如图2，在平面直角坐标系xOy 中，点P 在第一象限内，且点P 的横坐标比纵坐标大1，对于xOy ∠，满足d (P ，xOy ∠)= 5，点P 的坐标是__________．【难度】★★★ 【答案】(3，2)．x yP' CPO ENF OPM 图1yx-11-11O图2【解析】过点P 分别作PA ⊥x 轴，PB ⊥y 轴， ∵点P 在第一象限内且横坐标比纵坐标大1， ∴设PA =a ，则PB =a +1， ∵d (P ，xOy ∠)= 5，可得：PA +PB =5，即a +a +1=5，解得：a =2，所以点P 的坐标为(3,2)．【总结】本次考查“点角距离”的定义，利用定义求解相关点的坐标．模块二：阅读理解例1.一组数1，1，2，x ，5，y ，…，满足“从第三个数起，每个数都等于它前面的两个数之和”，那么这组数中y 表示的数为______．【难度】★ 【答案】8．【解析】由题得，x =1+2=3，y =3+5=8．【总结】本题难度不大，运算也比较简单．例2.四个数a 、b 、c 、d 排列成a b c d，我们称之为二阶行列式．规定它的运算法则为：a b ad bc c d=-．若331233x x x x +-=-+，则x =______．【难度】★★ 【答案】1．【解析】由运算法则得()()22333333+-=+---+x x x x x x ，整理得：1212=x ，解得：x =1．【总结】由运算法则整理，再解关于x 的方程即可．例3.对于两个不相等的实数a 、b ，我们规定符号{max a ，}b 表示a 、b 中的较大值，如：{max 2，}44=，按照这个规定，方程{max x ，}21x x x+-=的解为( )A ．1B ．2-C ．11D ．11-【难度】★★ 【答案】D ．【解析】当x >0时，{}max x x x -=，，解方程21+=x x x，得：1=±x所以1=+x 当x <0时，{}max x x x -=-，，解方程21x x x+-=，得：121==-x x ，所以1=-x ；综上，1=x 1-，故选D ．【总结】本题注意分类讨论，根据定义进行取值，再解关于x 的方程．例4.我们把三角形中最大内角与最小内角的度数差称为该三角形的“内角正度值”．如果等腰三角形的腰长为2，“内角正度值”为45°，那么该三角形的面积等于______．【难度】★★ 【答案】1或2．45x +，45，则180x =，解得：45x =，此三角形为等腰直角三角形， ∴此三角形的面积=12当顶角为x 时，则4545180x x x ++++=，解得：30x =．如图，2==AB AC ，30A ∠=，作CD ⊥AB ，在Rt ADC ，∵30A ∠=，∴112==CD AC ， 211⨯=．综上所述，该三角形的面积等于1或2．【总结】本题注意分类讨论．根据“内角正度值”的定义求出三角形各内角的度数，再进行面积的求解．例 5.如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“有趣三D CBA角形”，这条中线称为“有趣中线”．已知Rt ABC ∆，90C ∠=︒，较短的一条直角边边长为1，如果Rt ABC ∆是“有趣三角形”，那么这个三角形“有趣中线”长等于．【难度】★★【解析】“有趣中线”有三种情况：若“有趣中线”为斜边AB 上的中线，直角三角形的斜边中点到三顶点距离相等，不合题意；若“有趣中线”为BC 边上的中线，根据斜边大于直角边，矛盾，不成立；若“有趣中线”为另一直角边AC 上的中线，如图所示，BC =1，设2BD x =，则CD x =．在Rt BCD 中，勾股定理得1+()222=x x ，解得：xBD =2x．【总结】本题考查“有趣中线”的定义，注意分类讨论．例6.如果一个平行四边形一个内角的平分线分它的一边为1 : 2的两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”．当“协调边”为3时，它的周长为______．【难度】★★ 【答案】8或10．【解析】由题意可知，存在两种情况：(1)一组邻边长分别为3和1，周长=8； (2)一组邻边长分别为3和2，周长=10．【总结】本题考查“协调平行四边形”的定义及平行四边形的性质．例7.设正n 边形的半径为R ，边心距为r ，如果我们将Rr的值称为正n 边形的“接近度”，那么正六边形的“接近度”是______(结果保留根号)．DCBA【难度】★★【解析】设正六边形的边长为a ，则半径为R=a ，边心距为，所以R r．【总结】本题考查“接近度”的定义及正六边形的性质．例8.将关于x 的一元二次方程20x px q ++=变形为2x px q =--，就可将2x 表示为关于x 的一次多项式，从而达到“降次”的目的，我们称这样的方法为“降次法”．已知210x x --=，可用“降次法”求得431x x --的值是____________．【难度】★★ 【答案】1．【解析】由210x x --=，得21=+x x ，代入431x x --=()221311+--=-=x x x x ．【总结】本题运用“降次”及“整体代入”的思想进行解题．例9.在平面直角坐标系中，我们把半径相等且外切、连心线与直线y = x 平行的两个圆，称之为“孪生圆”；已知圆A 的圆心为(2-，3)A 的所有“孪生圆”的圆心坐标为_________．【难度】★★【答案】(0，5)或(-4，1)．【解析】由题意得，连心线所在直线为5=+y x ，因为两圆外切，设另一圆心为圆B ，所以圆心距=AB ，设(),5+B x x ，所以AB 解得：10=x ，24=-x ，所以圆心B 的坐标为(0,5)或(-4,1)．【总结】本题考查了“孪生圆”的定义、一次函数的图像以及圆与圆的位置关系．例10.当两个圆有两个公共点，且其中一个圆的圆心在另一圆的圆内时，我们称此两圆的位置关系为“内相交”．如果1O 、2O 半径分别3和1，且两圆“内相交”，那么两圆的圆心距d 的取值范围是___________．【难度】★★ 【答案】23<<d ．【解析】两个圆有两个公共点即两圆相交，可得24<<d ，当小圆的圆心恰好在大圆上时，3=d ，所以内相交的圆心距d 取值范围是23<<d ．【总结】本题考查圆与圆的位置关系及“内相交”的定义．模块三：规律探究例1.观察下列各数：1，43，97，1615，…，按你发现的规律计算这列数的第6个数为( )A ．2531B ．3635C ．47D ．6263【难度】★★ 【答案】C ．【解析】根据题意，可知规律为221n n -，故第6个数为：3663，化简为47，故选C ．【总结】本题考查针对给定的一列数字找规律．例2.按一定规律排列的一列数：12，22，32，52，82，132，…．若x 、y 、z 表示这列数中的连续三个数，猜测x 、y 、z 满足的解析式是____________．【难度】★★ 【答案】=xy z ．【解析】由给出的这一列数字，可得出规律：从第三个数字开始，每个数等于它两个数的乘积，所以=xy z ．【总结】本题考查针对给定的一列数字找规律．例3.在平面直角坐标系中，有三个点A (1，1-)、B (1-，1-)、C (0，1)，点P (0，2)关于点A 的对称点为1P ，1P 关于点B 的对称点为2P ，2P 关于点C 的对称点为3P ，按此规律，继续以点A 、B 、C 为对称中心重复前面的操作，依次得到点4P ，5P ，6P ，…，则点2017P 的坐标为( ) A ．(0，0) B ．(0，2)C ．(2，4-)D ．(4-，2)【难度】★★ 【答案】C ．【解析】由题意得1P (2，-4)、2P (-4，2)、3P (4，0)、4P (-2，-2)、5P (0，0)，6P (0，2)，每6个数形成一个周期，2017÷6=336……1，所以2017P 的坐标和1P 的坐标相同，故选C ．【总结】本题考查了点的对称问题及周期问题的处理．例4.如图，正方形ABCD 的边长为2，其面积标记为1S ，以CD 为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为2S ，…，按照此规律继续下去，则2017S 的值为_____________．【难度】★★★【答案】20141()2．【解析】由题意得1S =2×2=4=22，2S 12=，3S =111⨯==20，…… 由以上规律，可知2017S =2-201420141()2=．【总结】本题考查了找规律在几何图形中的应用．1.(2020松江二模)如果一个三角形中有一个内角的度数是另外两个内角度数差的2倍，我们就称这个三角形为“奇巧三角形”.已知一个直角三角形是“奇巧三角形”，那么该三角形的最小内角等于度.【分析】设直角三角形的最小内角为x ，另一个内角为y ，根据三角形的内角和列方程组即可得到结论．【解答】解：设直角三角形的最小内角为x ，另一个内角为y ，由题意得，，解得：，答：该三角形的最小内角等于22.5°，故答案为：22.5．2．(2020静安二模)如果一条直线把一个四边形分成两部分，这两部分图形的周长相等，那么这条直线称为这个四边形的“等分周长线”．在直角梯形ABCD中，AB∥CD，∠A＝90°，DC＝AD，∠B是锐角，cot B＝，AB＝17．如果点E在梯形的边上，CE是梯形ABCD的“等分周长线”，那么△BCE的周长为．【分析】作CH⊥AB于H，设BH＝5a，证明四边形ADCH为矩形，得到AD＝CH＝12a，根据题意求出a，根据勾股定理求出BC，根据“等分周长线”计算，得到答案．【解答】解：作CH⊥AB于H，设BH＝5a，∵cot B＝，∴＝，∴CH＝12a，∵AB∥CD，∴∠D＝∠A＝90°，又CH⊥AB，∴四边形ADCH为矩形，∴AD＝CH＝12a，CD＝AH，∵DC＝AD，∴AH＝CD＝12a，由题意得，12a+5a＝17，解得，a＝1，∴AD＝CD＝AH＝12，BH＝5，在Rt△CHB中，BC＝＝13，∴四边形ABCD的周长＝12+12+17+13＝54，∵CE是梯形ABCD的“等分周长线”，∴点E在AB上，∴AE＝17+13﹣27＝3，∴EH＝12﹣3＝9，由勾股定理得，EC＝＝15，∴△BCE 的周长＝14+13+15＝42，故答案为：42．3.(2020嘉定二模)定义：如果三角形的两个内角∠α与∠β满足∠α=2∠β,那么，我们将这样的三角形称为“倍角三角形”，如果一个等腰三角形是“倍角三角形”，那么这个【考查内容】新定义题型，黄金三角形【评析】中等为底角时，用内角和公式求得∠β= 36，此时为黄金三角形，腰长与底边用内角和公式求得∠β= 45，此时为等腰直角三角【答案】22或215+4.(2020长宁二模)如果一个四边形有且只有三个顶点在圆上，那么称这个四边形是该圆的“联络四边形”，已知圆的半径长为5，这个圆的一个联络四边形是边长为2的菱形，那么这个菱形不在圆上的顶点与圆心的距离是．【分析】先根据题意画出图形，连接BD 、OD ，设AM ＝x ，根据AD 2﹣AM 2＝OD 2﹣OM 2，列出方程，求出x ，再根据OC ＝OA ﹣AM ﹣CM 计算即可．【解答】解：根据题意画图如下：连接BD ，与AC 交与点M ， ∵四边形ABCD 是菱形， ∴∠AMD ＝∠DMC ＝90°，∠ACD ＝∠ACB ，CD ＝CD ，AM ＝CM ， ∴DM 2＝AD 2﹣AM 2，设AM＝x，则DM2＝(2)2﹣x2，连接OD、OB，在△OCD和△OCB中，，∴△OCD≌OCB(SSS)，∴∠OCD＝∠OCB，∴∠ACD+∠OCD＝∠ACB+∠OCB＝180°，∴OC与AC在一条直线上，∴△OMD是一个直角三角形，OM＝OA﹣AM＝5﹣x，∴DM2＝OD2﹣OM2，＝52﹣(5﹣x)2，∴(2)2﹣x2＝52﹣(5﹣x)2，x＝2，∴AM＝CM＝2，∴OC＝OA﹣AM﹣CM＝5﹣2﹣2＝1．故答案为：1．5.(2020青浦二模)小明学习完《相似三角形》一章后，发现了一个有趣的结论：在两个不相似的直角三角形中，分别存在经过直角顶点的一条直线，把直角三角形分成两个小三角形后，如果第一个直角三角形分割出来的一个小三角形与第二个直角三角形分割出来的一个小三角形相似，那么分割出来的另外两个小三角形也相似．他把这样的两条直线称为这两个直角三角形的相似分割线．如图1、图2，直线CG、DH分别是两个不相似的Rt△ABC和Rt△DEF的相似分割线，CG、DH 分别与斜边AB、EF交于点G、H，如果△BCG与△DFH相似，AC＝3，AB＝5，DE＝4，DF＝8，那么AG＝．【分析】先由勾股定理得出BC的值，再由△BCG∽△DFH列出比例式，设AG＝x，用含x 的式子表示出DH；按照相似分割线可知，△AGC∽DHE，但要先得出两个相似三角形的边或角是如何对应的，再根据相似三角形的性质列出比例式，解得x值即可．解：∵Rt△ABC，AC＝3，AB＝5，∴由勾股定理得：BC＝4，∵△BCG∽△DFH，∴＝，已知DF＝8，设AG＝x，则BG＝5﹣x，∴＝，∴DH＝10﹣2x，∵△BCG∽△DFH，∴∠B＝∠FDH，∠BGC＝∠CHF，∴∠AGC＝∠DHE，∵∠A+∠B＝90°，∠EDH+∠FDH＝90°，∴∠A＝∠EDH，∴△AGC∽DHE，∴＝，又DE＝4，∴＝，解得：x＝3，经检验，x＝3是原方程的解，且符合题意．∴AG＝3．故答案为：3．6.(2020杨浦二模) 定义：对于函数y ＝f (x )，如果当a ≤x ≤b 时，m ≤y ≤n ，且满足n ﹣m ＝k (b ﹣a )(k 是常数)，那么称此函数为“k 级函数”．如：正比例函数y ＝﹣3x ，当1≤x ≤3时，﹣9≤y ≤﹣3，则﹣3﹣(﹣9)＝k (3﹣1)，求得k ＝3，所以函数y ＝﹣3x 为“3级函数”．如果一次函数y ＝2x ﹣1(1≤x ≤5)为“k 级函数”，那么k 的值是．【分析】根据一次函数y ＝2x ﹣1(1≤x ≤5)为“k 级函数”解答即可．【解答】解：因为一次函数y ＝2x ﹣1(1≤x ≤5)为“k 级函数”，可得：k ＝2，故答案为：2．7.定义：如果二次函数2111y a x b x c =++(10a ≠，1a 、1b 、1c 是常数)与2222y a x b x c =++(20a ≠，2a 、2b 、2c 是常数)满足120a a +=，12b b =，120c c +=，那么称这两个函数互为“旋转函数”．若函数2423y x mx =-+-与22y x nx n =-+互为“旋转函数”，则()2017m n +=________．【难度】★★ 【答案】-1．【解析】由“旋转函数”的定义得42320⎧=-⎪⎨⎪-+=⎩m nn ，解得：32=-⎧⎨=⎩m n ，所以()2017m n +=(-1)2017=-1．【总结】本题考查“旋转函数”的定义．8.如果三角形有一边上的中线长恰好等于这边的长，那么称这个三角形为“好玩三角形”．在Rt ABC ∆中，90C ∠=︒，若Rt ABC ∆是“好玩三角形”，则tan A =_______．【难度】★★【解析】由于直角三角形斜边上的中线等于斜边的一半，因此斜边上的中线不满足；故只能是直角边上的中线等于此直角边的长，如图所示，设BD =2x ，CD =x ，则=BC ，在Rt ABC 中，AC =2x，=BC ．当∠A为较小锐角时，tan A =当∠A为较大锐角时，tan A =．【总结】本题考查“好玩三角形”的定义，注意分类讨论．9.我们把四边形两条对角线中点的连线段称为“奇异中位线”．现有两个全等三角形，边长分别为3cm 、4cm 、5cm ．将这两个三角形相等的边重合拼成凸四边形，如果凸四边形的“奇异中位线”的长不为0，那么“奇异中位线”的长是______cm ．【难度】★★【答案】710．【解析】如图，将两个全等的直角ABC 与DEF 的斜边AC 与DF 重合，拼成凸四边形ABCE ，AC 与BE 交于点O ，M 为AC 的中点．∵△ABC ≌△DEF ，易证AO ⊥BE ．在Rt AOB 中，AO =AB •cos ∠BAO =95，因为1522==AM AC ，所以5972510=-=-=OM AM OA ．即奇异中位线的长是710．【总结】本题考查了“奇异中位线”的定义，注意根据题目要求画出合适的图形．10.如果一个二次函数的二次项系数为1，那么这个函数可以表示为2y x px q =++，我们将[p ，q ]称为这个函数的特征数．例如二次函数242y x x =-+的特征数是[4-，2]．请根据以上的信息探究下面的问题：如果一个二次函数的特征数是[2，3]，将这个函数的图像先DCBA向左平移2个单位，再向下平移3个单位，那么此时得到的图像所对应的函数的特征数为______．【难度】★★ 【答案】[6，8]．【解析】特征数是[2，3]的二次函数为223=++y x x ，即2(1)2=++y x ，将其向左平移2个单位，再向下平移3个单位后得到的二次函数为2(3)1=+-y x ，即268=++y x x ，所以特征数为[6，8]．【总结】本题考查了“特征数”的定义及二次函数图像的平移．11.如图1，点P 是以r 为半径的圆O 外一点，点'P 在线段OP 上，若满足2'OP OP r =，则称点'P 是点P 关于圆O 的反演点．如图2，在Rt ABO ∆中，90B ∠=︒，AB = 2，BO = 4，圆O 的半径为2，如果点'A 、'B 分别是点A 、B 关于圆O 的反演点，那么''A B 的长是______．【难度】★★★【答案】5．【解析】由反演点的定义，可知：2'=OA OA r ，2'=OB OB r ，则'=OA OA 'OB OB ，即''=OA OB OB OA ，又∠=∠O O ，可证''OA B ∽OBA ， ∴'''=OB A B OA AB ，即225''=A B ，解得：''A B =5．【总结】本题考查了“反演点”的定义，以及相似三角形的判定与性质．12.正方形111A B C O ，2221A B C C ，3332A B C C ，…，按如图所示的方式放置．点1A ，2A ，3A ，…和点1C ，2C ，3C ，…，分别在直线y kx b =+(0k >)和x 轴上，已知点1B (1，1)，2B (3，2)，OPP'BOA图1 图2则点6B 的坐标是__________，点n B 的坐标是__________．【难度】★★★【答案】(63，32)，1(212)nn--，．【解析】由1A (0，1)、2A (1，2)，可求得直线解析式为1=+y x ．可求得3A (3，4)、3B (7，4)，4A (7，8)、 4B (15，8)，5A (15，16)、5B (31，16)， 6A (31，32)、6B (63，32)， ……，按照此规律可得n B 1(212)n n --，．【总结】本题考查了一次函数与几何图形背景下找出点坐标的规律．13.对于平面直角坐标系 xOy 中的点P (a ，b )，若点'P 的坐标为(ba k+，ka b +)(其中k 为常数，且0k ≠)，则称点'P 为点P 的“k 属派生点”．例如：P (1，4)的“2属派生点”为'P (412+，214⨯+)，即'P (3，6)．若点P 的“k 属派生点”'P 的坐标为(3，3)，请写出一个符合条件的点P 的坐标：____________．【难度】★★★ 【答案】(2，1)．【解析】由题意得33⎧+⎪=⎨⎪+=⎩b a k ka b ，整理得：33+=⎧⎨+=⎩ka b k ka b ，所以1=k ，只要满足3+=a b 即可，可取点P (2，1)．x yO【总结】本题考查了“派生点”的定义，关键是求出k 的值，答案不唯一．14.如图，正方形ABCD 的边长为1，以对角线AC 为边作第二个正方形ACEF ，再以对角线AE 为边作第三个正方形AEGH ，…，如此下去，第n 个正方形的边长为__________．【难度】★★★ 【答案】12-n ．【解析】第一个正方形的边长为1，第二个正方形的边长为2，第三个正方形的边长为2，依次规律，第n 个正方形的边长为12-n ．【总结】本题考查了几何图形背景下线段长度上存在的规律．A BC D E FGH。

2021中考数学压轴题专项训练有答案解析-2021中考数学压轴题

2021中考数学压轴题专项训练有答案解析:2021中考数学压轴题20XX中考压轴题专项训练训练目标1.熟悉题型结构，辨识题目类型，调用解题方法；2.书写框架明晰，踩点得分（完整、快速、简洁）。

题型结构及解题方法压轴题综合性强，知识高度融合，侧重考查学生对知识的综合运用能力，对问题背景的研究能力以及对数学模型和套路的调用整合能力。

考查要点常考类型举例题型特征解题方法问题背景研究求坐标或函数解析式，求角度或线段长已知点坐标、解析式或几何图形的部分信息研究坐标、解析式，研究边、角，特殊图形。

模型套路调用求面积、周长的函数关系式，并求最值速度已知，所求关系式和运动时间相关① 分段：动点转折分段、图形碰撞分段；② 利用动点路程表达线段长；③ 设计方案表达关系式。

坐标系下，所求关系式和坐标相关① 利用坐标及横平竖直线段长；② 分类：根据线段表达不同分类；③ 设计方案表达面积或周长。

求线段和（差）的最值有定点（线）、不变量或不变关系利用几何模型、几何定理求解，如两点之间线段最短、垂线段最短、三角形三边关系等。

套路整合及分类讨论点的存在性点的存在满足某种关系，如满足面积比为9:10 ① 抓定量，找特征；② 确定分类；.③ 根据几何特征或函数特征建等式。

图形的存在性特殊三角形、特殊四边形的存在性① 分析动点、定点或不变关系（如平行）；② 根据特殊图形的判定、性质，确定分类；根据几何特征或函数特征建等式。

三角形相似、全等的存在性① 找定点，分析目标三角形边角关系；② 根据判定、对应关系确定分类；③ 根据几何特征建等式求解。

答题规范动作1.试卷上探索思路、在演草纸上演草。

2.合理规划答题卡的答题区域：两栏书写，先左后右。

作答前根据思路，提前规划，确保在答题区域内写完答案；同时方便修改。

3.作答要求：框架明晰，结论突出，过程简洁。

23题作答更加注重结论，不同类型的作答要点：几何推理环节，要突出几何特征及数量关系表达，简化证明过程；面积问题，要突出面积表达的方案和结论；几何最值问题，直接确定最值存在状态，再进行求解；存在性问题，要明确分类，突出总结。

2021年中考数学压轴题专项训练07 综合探究类(含解析)

综合探究类1．综合与实践问题背景：综合与实践课上，同学们以两个全等的三角形纸片为操作对象，进行相一次相关问题的研究．下面是创新小组在操作过程中研究的问题，如图一，△ABC≌△DEF，其中∠ACB=90°，BC=2，∠A=30°．操作与发现：（1）如图二，创新小组将两张三角形纸片按如图示的方式放置，四边形ACBF的形状是，CF= ；（2）创新小组在图二的基础上，将△DEF纸片沿AB方向平移至图三的位置，其中点E 与AB的中点重合．连接CE，BF．四边形BCEF的形状是，CF= ．操作与探究：（3）创新小组在图三的基础上又进行了探究，将△DEF纸片绕点E逆时针旋转至DE与BC平行的位置，如图四所示，连接AF，BF．经过观察和推理后发现四边形ACBF也是矩形，请你证明这个结论．【解析】（1）如图所示：△ABC ≌△DEF ，其中∠ACB =90°，BC =2，∠A =30°，∴60,2ABC FED BC EF ∠=∠=︒==， ∴90C F FAC ∠=∠=∠=︒，∴四边形ACBF 是矩形，AB=4∴，∴AB=CF=4；故答案为：矩形，4 ；（2）如图所示：△ABC ≌△DEF ，其中∠ACB =90°，BC =2，∠A =30°，∴60,2ABC FED BC EF ∠=∠=︒==， ∴//BC EF ，∴四边形ECBF 是平行四边形，点E 与AB 的中点重合，∴CE=BE ，∴CBE △是等边三角形，∴EC=BC ，∴四边形ECBF 是菱形，∴CF 与EB 互相垂直且平分，∴OC EC ==∴CF =，故答案为：菱形，（3）证明：如图所示：∵90,3060C A ABC ∠=︒∠=︒∴∠=︒ ∵//,DE BC DEF ABC ≌ ∴60DEB DEF ABC ∠=∠=∠=︒ ∴60AEF ∠=︒∵24,2AB BC AE ==∴= ∵2EF BC AE EF ==∴= ∴AEF ∆为等边三角形 ∴60FAE ABC ∠=︒=∠ ∴//BC AF ∵AE EF BC ==∴四边形ACBF 为平行四边形 ∵90C ∠=︒∴四边形ACBF 为矩形．2．如图，在每个小正方形的边长为1的网格中，A ，B ，C 为格点，D 为小正方形边的中点.（1）AC的长等于_________；+取得最小值时，请在如图所示（2）点P，Q分别为线段BC，AC上的动点，当PD PQ的网格中，用无刻度．．．的直尺，画出线段PD，PQ，并简要说明点P和点Q的位置是如何找到的（不要求证明）.【解析】解：（1）由图可得：5=，故答案为：5；（2）如图，BC与网格线相交，得点P；取格点E，F，连接EF，与网格线相交，得点G，取格点M，N，连接MN，与网格线相交，得点H，连接GH，与AC相交，得点Q.连接PD，PQ.线段PD，PQ即为所求.如图，延长DP，交网格线于点T，连接AB，GH与DP交于点S，由计算可得：，，AC=5，∴△ABC为直角三角形，∠ABC=90°，∴tan∠ACB=2，∵tan∠BCT=PT：TC=2，∴∠ACB=∠BCT，即BC平分∠ACT，根据画图可知：GH∥BC，∴∠ACB=∠CQH，∠BCT=∠GHC，∵∠BCT=∠BCA，∴∠CQH=∠GHC，∴CQ=CH，由题意可得：BS=CH，∴BS=CQ，又∵BP=CP，∠PBS=∠PCQ，∴△BPS≌△CPQ，∴∠PSB=∠PHC=90°，即PQ⊥AC，∴PD+PQ的最小值即为PD+PT，∴所画图形符合要求.3．数学实验室：制作4张全等的直角三角形纸片（如图1），把这4张纸片拼成以弦长c为边长的正方形构成“弦图”（如图2），古代数学家利用“弦图”验证了勾股定理．探索研究：（1）小明将“弦图”中的2个三角形进行了运动变换，得到图3，请利用图3证明勾股定理；数学思考：（2）小芳认为用其它的方法改变“弦图”中某些三角形的位置，也可以证明勾股定理．请你想一种方法支持她的观点（先在备用图中补全图形，再予以证明）．【解析】（1）解：如图3所示，图形的面积表示为：2222122a b ab a b ab ++⨯=++，图形的面积也可表示：22122c ab c ab +⨯=+， ∴a 2b 2ab c 2ab ，∴a2b2c 2（2）解：如图4所示，大正方形的面积表示为：a b2，大正方形的面积也可以表示为：221422c ab c ab +⨯=+，∴22a b c ab+=+，()2∴a2b22ab c22ab，∴a2b2c2；4．综合与探究（实践操作）三角尺中的数学数学实践活动课上，“奋进”小组将一副直角三角尺的直角顶点叠放在一起，如图1，使直角顶点重合于点C．（问题发现）（1）①填空：如图1，若∠ACB＝145°，则∠ACE的度数是，∠DCB的度数，∠ECD的度数是．②如图1，你发现∠ACE与∠DCB的大小有何关系？∠ACB与∠ECD的大小又有何关系？请直接写出你发现的结论．（类比探究）（2）如图2，当△ACD与△BCE没有重合部分时，上述②中你发现的结论是否还依然成立？请说明理由．【解析】解：（1）①1459055∠=∠︒︒︒=﹣=，ACE DCB==﹣；∠∠-∠︒︒=︒ECD BCE BCD905535②结论：ACE DCB=；∠+∠︒ACB ECD∠=∠，180证明：∵90∠=∠-∠=∠-︒DCB ACB ACD ACB∠=∠-∠=∠-︒，90ACE ACB BCE ACB∴ACE DCB∠=∠∵9090180∠=∠+∠-∠=︒+︒-∠=︒-∠ACB ACD BCE ECD ECD ECD∴180=ACB ECD∠+∠︒（2）结论：当ACD与BCE没有重合部分时，上述②中发现的结论依然成立．理由：∵90∠=∠=︒，ACD ECB∴ACD DCE ECB DCE∠+∠=∠+∠，∴ACE DCB∠=∠，∵90∠=∠=︒，ACD ECB∴180=，∠+∠︒ACD ECB∵360=，ACD ECD ECB ACB∠+∠+∠+∠︒∴180ACB ECD=，∠+∠︒∴ACE DCB∠+∠︒=．ACB ECD∠=∠，180∴上述②中发现的结论依然成立．故答案为：（1）①55°，55°，35°；②∠ACE＝∠DCB，∠ACB+∠ECD＝180°；（2）当△ACD与△BCE没有重合部分时，上述②中发现的结论依然成立，理由详见解析5．操作：将一把三角尺放在如图①的正方形ABCD中，使它的直角顶点P在对角线AC 上滑动，直角的一边始终经过点B，另一边与射线DC相交于点Q，探究：=.(1)如图②，当点Q在DC上时，求证：PQ PB(2)如图③，当点Q在DC延长线上时，①中的结论还成立吗？简要说明理由.【解析】(1)证明：过点P作//BCMN，分别交AB于点M，交CD于点N，则四边形AMND和四边形BCNM都是矩形，△AMP和△CNP都是等腰直角三角形．∴NP=NC=MB∵∠BPQ=90°∴∠QPN+∠BPM=90°，而∠BPM+∠PBM=90° ，∴∠QPN=∠PBM，又∠QNP=∠PMB=90°，在△QNP和△BMP中，∠QNP=∠PMB，MB=NP，∠QPN=∠PBM∴△QNP≌△PMB（ASA），∴PQ=BP．(2)成立.过点P作PN AB⊥于N,PN交CD于点M在正方形ABCD中//AB CD,45∠=ACD∴90∠=∠=∠=PMQ PNB CBN∴CBNM是矩形，∴CM BN=，∴CMP∆是等腰直角三角形，∴PM CM BN ==，∵90PBN BPN ∠+∠=，90BPN MPQ ∠+∠=∴MPQ PBN ∠=∠，在PMQ ∆和BNP ∆中，90MPQ PBN PNB PMQ BN PM ∠=∠⎧⎪∠=∠=⎨⎪=⎩， ∴()PMQ BNP AAS ∆≅∆， ∴BP QP =；6．实践操作：第一步：如图1，将矩形纸片ABCD 沿过点D 的直线折叠，使点A 落在CD 上的点A '处，得到折痕DE ，然后把纸片展平．第二步：如图2，将图1中的矩形纸片ABCD 沿过点E 的直线折叠，点C 恰好落在AD 上的点C '处，点B 落在点B '处，得到折痕EF ，B C ''交AB 于点M ，C F '交DE 于点N ，再把纸片展平．问题解决：（1）如图1，填空：四边形AEA D '的形状是_____________________；（2）如图2，线段MC '与ME 是否相等？若相等，请给出证明；若不等，请说明理由；（3）如图2，若2cm,'4cm AC DC '==，求:DN EN 的值．【解析】（1）解：∵ABCD 是平行四边形， ∴'////AD BC EA ，'//AE DA ∴四边形'AEA D 是平行四边形∵矩形纸片ABCD 沿过点D 的直线折叠，使点A 落在CD 上的点A '处 ∴'AED A ED ≌ ∴'AE A E = ∵90A ∠=∴四边形AEA D '的形状是正方形故最后答案为：四边形AEA D '的形状是正方形；（2）MC ME '=理由如下：如图，连接EC '，由（1）知：AD AE = ∵四边形ABCD 是矩形， ∴90AD BC EAC B '=∠=∠=︒，由折叠知：B C BC B B '''=∠=∠， ∴90AE B C EAC B ''''=∠=∠=︒，又EC C E ''=， ∴Rt EC A Rt C EB '''≌ ∴C EA EC B '''∠=∠ ∴MC ME '=（3）∵Rt EC A Rt C EB '''≌，∴AC B E ''= 由折叠知：B E BE '=，∴AC BE '= ∵2(cm)4(cm)AC DC ''==， ∴()2428cm AB CD ==++=设cm DF x =，则()8cm FC FC x '==-在Rt DC F '中，由勾股定理得：2224(8)x x +=- 解得：3x =，即()3cm DF =如图，延长BA FC '，交于点G ，则AC G DC F ''∠=∠ ∴3tan tan 4AG DF AC G DC F AC DC ''∠=∠==='' ∴3(cm)2AG = ∴3156(cm)22EG =+= ∵//DF EG ，∴DNF ENG ∽ ∴152::3:25DN EN DF EG === 7．综合与实践在线上教学中，教师和学生都学习到了新知识，掌握了许多新技能．例如教材八年级下册的数学活动﹣﹣折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．实践发现：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM，把纸片展平，连接AN，如图①．（1）折痕BM（填“是”或“不是”）线段AN的垂直平分线；请判断图中△ABN 是什么特殊三角形？答：；进一步计算出∠MNE＝°；（2）继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图②，则∠GBN＝°；拓展延伸：（3）如图③，折叠矩形纸片ABCD，使点A落在BC边上的点A'处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA'交ST于点O，连接AT．求证：四边形SATA'是菱形．解决问题：（4）如图④，矩形纸片ABCD中，AB＝10，AD＝26，折叠纸片，使点A落在BC边上的点A'处，并且折痕交AB边于点T，交AD边于点S，把纸片展平．同学们小组讨论后，得出线段AT的长度有4，5，7，9．请写出以上4个数值中你认为正确的数值．【解析】解：（1）如图①∵对折矩形纸片ABCD，使AD与BC重合，∴EF垂直平分AB，∴AN＝BN，AE＝BE，∠NEA＝90°，∵再一次折叠纸片，使点A落在EF上的点N处，∴BM垂直平分AN，∠BAM＝∠BNM＝90°，∴AB＝BN，∴AB＝AN＝BN，∴△ABN是等边三角形，∴∠EBN＝60°，∴∠ENB＝30°，∴∠MNE＝60°，故答案为：是，等边三角形，60；（2）∵折叠纸片，使点A落在BC边上的点H处，∴∠ABG＝∠HBG＝45°，∴∠GBN＝∠ABN﹣∠ABG＝15°，故答案为：15°；（3）∵折叠矩形纸片ABCD，使点A落在BC边上的点A'处，∴ST垂直平分AA'，∴AO＝A'O，AA'⊥ST，∵AD∥BC，∴∠SAO＝∠TA'O，∠ASO＝∠A'TO，∴△ASO≌△A'TO（AAS）∴SO＝TO，∴四边形ASA 'T 是平行四边形，又∵AA '⊥ST ，∴边形SATA '是菱形；（4）∵折叠纸片，使点A 落在BC 边上的点A '处， ∴AT ＝A 'T ，在Rt△A 'TB 中，A 'T ＞BT ， ∴AT ＞10﹣AT ， ∴AT ＞5， ∵点T 在AB 上，∴当点T 与点B 重合时，AT 有最大值为10， ∴5＜AT ≤10，∴正确的数值为7，9，故答案为：7，9． 8．综合与实践问题情境数学活动课上，老师让同学们以“三角形平移与旋转”为主题开展数学活动，ACD 和BCE 是两个等边三角形纸片，其中，52AC cm BC cm ==,．解决问题（1）勤奋小组将ACD 和BCE 按图1所示的方式摆放(点,,A C B 在同一条直线上) ，连接,AE BD ．发现AE DB =，请你给予证明；（2）如图2，创新小组在勤奋小组的基础上继续探究，将BCE 绕着点C 逆时针方向旋转，当点E 恰好落在CD 边上时，求ABC 的面积；拓展延伸（3）如图3，缜密小组在创新小组的基础上，提出一个问题： “将BCE 沿CD 方向平移acm 得到''',B C E 连接''AB B C ,，当'AB C △恰好是以'AB 为斜边的直角三角形时，求a 的值．请你直接写出a 的值．【解析】（1）∵ACD 和BCE 是两个等边三角形， ∴AC=CD，BC=CE ，∠ACD=∠ECB=60°， ∴∠ACD+∠DCE=∠ECB+∠DCE, 即∠ACE=∠DCB， ∴△ACE≌△DCB， ∴AE=BD；（2）由题意得∠ACD=∠ECB=60°，过点B 作BF⊥AC，交AC 的延长线于F ，∴∠BCF=180°-∠ACD -∠ECB=60°，∠F=90°， ∴∠CBF=30°， ∴CF=12BC=1cm ，=cm ，∴11522ABCSAC BF =⋅=⨯；（3）由题意得∠ACD=E C B '''∠=60°， ∵∠ACB '=90°， ∴30C CB ''∠=,∵C CB C B C E C B '''''''∠+∠=∠, ∴30C B C ''∠=, ∴C C C B '''==2cm ， ∴a=2.9．动手做一做：某校教具制作车间有等腰三角形正方形、平行四边形的塑料若干，数学兴趣小组的同学利用其中7块恰好拼成一个矩形（如图1），后来又用它们拼出了XYZ等字母模型（如图2、图3、图4），每个塑料板保持图1的标号不变，请你参与：（1）将图2中每块塑料板对应的标号填上去；（2）图3中，点画出了标号7的塑料板位置，请你适当画线，找出其他6块塑料板，并填上标号；（3）在图4中，找出7块塑料板，并填上标号．【解析】（1）如下图（2）如下图（3）如下图10．已知：如图1，在O 中，弦2AB =，1CD =，AD BD ⊥．直线,AD BC 相交于点E ．（1）求E ∠的度数；（2）如果点,C D 在O 上运动，且保持弦CD 的长度不变，那么，直线,AD BC 相交所成锐角的大小是否改变？试就以下三种情况进行探究，并说明理由（图形未画完整，请你根据需要补全）．①如图2，弦AB与弦CD交于点F；②如图3，弦AB与弦CD不相交：③如图4，点B与点C重合．【解析】解：（1）连接OC、OD，如图：∵AD BD⊥∴AB是直径∴1===OC OD CD∴OCD是等边三角形∴60∠=︒COD∴30∠=︒DBE∴60∠=︒E（2）①结论：直线AD、BC相交所成锐角的大小不发生改变依然是60︒证明：连接OD、OC、AC，如图：∵1===OD OC CD∴OCD为等边三角形∴60∠=︒COD∴30DAC∠=︒∴30∠=︒EBD∵90∠=︒ADB∴903060E∠=︒-︒=︒②结论：直线AD、BC相交所成锐角的大小不发生改变依然是60︒证明：连接OC、OD，如图：∵AD BD⊥∴AB是直径∴1===OC OD CD∴OCD是等边三角形∴60∠=︒COD∴30∠=︒DBE∴903060∠=︒-︒=︒BED③结论：直线AD、BC相交所成锐角的大小不发生改变依然是60︒证明：如图：∵当点B与点C重合时，则直线BE与O只有一个公共点∴EB恰为O的切线∴90∠=︒ABE∵90CD=，2∠=︒，1ADBAD=∴30A∠=︒∴60∠=︒．E故答案是：（1）60∠=︒（2）①结论：直线AD、BC相交所成锐角的大小不发生改变，E依然是60︒；证明过程见详解．②结论：直线AD、BC相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．③结论：直线AD、BC相交所成锐角的大小不发生改变，依然是60︒；证明过程见详解．11．综合与实践：折纸中的数学问题背景在数学活动课上，老师首先将平行四边形纸片ABCD按如图①所示方式折叠，使点C与点A重合，点D落到D′处，折痕为EF．这时同学们很快证得：△AEF是等腰三角形．接下来各学习小组也动手操作起来，请你解决他们提出的问题．操作发现(1) “争先”小组将矩形纸片ABCD 按上述方式折叠，如图②，发现重叠部分△AEF 恰好是等边三角形，求矩形ABCD 的长、宽之比是多少？实践探究(2)“励志”小组将矩形纸片ABCD 沿EF 折叠，如图③，使B 点落在AD 边上的B ′处；沿B ′G 折叠，使D 点落在D ′处，且B ′D ′过F 点．试探究四边形EFGB ′是什么特殊四边形？(3)再探究：在图③中连接BB ′，试判断并证明△BB ′G的形状．【解析】解：（1）矩形ABCD证明：设BE a =，AEF ∆等边三角形，60EAF ∴∠=︒，四边形ABCD 为矩形，90BAD ABE ∴∠=∠=︒，30BAE BAD EAF ∠=∠-∠=︒．在Rt ABE ∆中，90ABE ∠=︒，30BAE ∠=︒，BE a =，2sin BEAE a BAE ∴==∠，tan BEAB BAE ==∠，AE EC =，3BC BE EC a ∴=+=，∴BCAB ．（2）四边形B EFG '是平行四边形．证明：四边形ABCD 为矩形，//AD BC ∴，B EF BFE ∴∠'=∠，EB F GFB ∠'=∠'，DB G FGB ∠'=∠'．由翻折的特性可知：BFE B FE ∠=∠'，DB G FB G ∠'=∠'，B EF B FE ∴∠'=∠'，FB G FGB ∠'=∠'，又EB F GFB ∠'=∠'，B FE FB G ∴∠'=∠'，//EF B G ∴'，又//B E FG '，∴四边形B EFG '是平行四边形．（3）△BB G '为直角三角形．证明：连接BB '交EF 于点M ，如图所示．//AD BC ，EB B FBB ∴∠'=∠'，BF B F ='，FBB FB B ∴∠'=∠'，EB B FB B ∴∠'=∠'．B EF B FE ∠'=∠'，∴△B EF '为等腰三角形，B M EF ∴'⊥，90∴∠=︒．BMFEF B G'，//∴∠'=∠=︒，90BB G BMF∴△BB G'为直角三角形．12．综合与实践问题情境：在综合与实践课上，老师让同学们以“等腰三角形的剪拼”为主题开展数学活动．如图1，在△ABC中，AB＝AC＝10cm，BC＝16cm．将△ABC沿BC边上的中线AD剪开，得到△ABD和△ACD．操作发现：（1）乐学小组将图1中的△ACD以点D为旋转中心，按逆时针方向旋转，使得A'C'⊥AD，得到图2，A'C'与AB交于点E，则四边形BEC'D的形状是．（2）缜密小组将图1中的△ACD沿DB方向平移，A'D'与AB交于点M，A'C'与AD交于点N，得到图3，判断四边形MNDD'的形状，并说明理由．实践探究：（3）缜密小组又发现，当（2）中线段DD'的长为acm时，图3中的四边形MNDD'会成为正方形，求a的值．（4）创新小组又把图1中的△ACD放到如图4所示的位置，点A的对应点A'与点D重合，点D的对应点D'在BD的延长线上，再将△A'C'D'绕点D逆时针旋转到如图5所示的位置，DD'交AB于点P，DC'交AB于点Q，DP＝DQ，此时线段AP的长是cm．【解析】解：操作发现：（1）如图1：∵AB＝AC＝10cm，BC＝16cm．∴∠B＝∠C，BD＝CD＝8cm，∠BAD＝∠CAD，∵△ACD以点D为旋转中心，按逆时针方向旋转，∴C'D＝BD，∵AD⊥BD，A'C'⊥AD，∴A'C'∥BD，∠ADC'＝90°﹣∠C'，∴∠ADC'＝90°﹣∠B，且∠BAD＝90°﹣∠B，∴∠ADC'＝∠BAD，∴AB∥C'D，∴四边形BDC'E是平行四边形，∵BD＝C'D，∴四边形BEC'D是菱形，故答案为：菱形；（2）如图3，四边形MNDD'是矩形，理由如下：∵BD＝CD，∴BD'＝CD，且∠B＝∠C'，∠MD'B＝∠NDC'∴△MDB'≌△NDC'（ASA）∴MD'＝ND，∵△ACD 沿DB 方向平移，∴MD '∥DN ，∴四边形MNDD '是平行四边形，∵∠BD 'M ＝90°，∴四边形MNDD '是矩形；（3）由图形（1）可得AB ＝10cm ，BD ＝8cm ， ∴AD6cm ，∵四边形MNDD '为正方形，∴D 'M ∥DN ，D 'M ＝D 'D ＝acm ，∴△BD 'M ∽△BDA ， ∴BD MD BD AD''=， ∴886a a -=， ∴a ＝247；（4）如图5，过点D 作DG ⊥AB 于点G ，∵DP ＝DQ ，∴∠DQP ＝∠DPQ ，QG ＝PG ，又∵∠A ＝∠PDQ ，∴△DQP ∽△AQD ，∴∠ADQ ＝∠DPQ ，2021年中考数学压轴题专项训练07 综合探究类（含解析）∴∠ADQ＝∠AQD，∴AQ＝AD＝6，∵∠A＝∠A，∠DGA＝∠BDA，∴△DGA∽△BDA，∴AG AD AD AB=，∴6 610 AG=，∴AG＝185，∴GQ＝AQ﹣AG＝6﹣185＝125，∴PG＝QG＝125，∴AP＝AG﹣PG＝185﹣125＝65，故答案为：65．。

2021年中考数学压轴题专项训练06规律问题含解析

规律问题1．某种球形病毒的直径约是0.01纳米，一个该种病毒每经过一分钟就能繁殖出9个与自己完全相同的病毒，假如这种病毒在人体内聚集到一定数量，按这样的数量排列成一串，长度达到1分米时，人体就会感到不适．（1米9=10纳米）（1）从感染到第一个病毒开始，经过5分钟，人体内改种病毒的总长度是多少纳米？（2）从感染到第一个病毒开始，经过多少分钟，人体会感到不适？【答案】（1）从感染到第一个病毒开始，经过5分钟，人体内改种病毒的总长度是1000纳米；（2）从感染到第一个病毒开始，经过10分钟，人体会感到不适．【解析】解：（1）由题意可知：经过5分钟，人体内改种病毒的总长度是0.01×1×105=1000（纳米）答：从感染到第一个病毒开始，经过5分钟，人体内改种病毒的总长度是1000纳米；（2）1分米=110米8=10纳米而810÷（0.01×1）=1010∴从感染到第一个病毒开始，经过10分钟，人体会感到不适答：从感染到第一个病毒开始，经过10分钟，人体会感到不适．2．你会求()()20182017201621?··1a a a a a a -++++++的值吗？这个问题看上去很复杂，我们可以先考虑简单的情况，通过计算，探索规律：()()2111a a a -+=-()()23111a a a a -++=-()()324111a a a a a -+++=-（1）由上面的规律我们可以大胆猜想，得到()()201920182017211a a a a a a -+++⋅⋅⋅+++=_____；（2）利用上面的结论求2019201820172222221++++++的值．（3）求201920182017255554+++⋅⋅⋅++的值【答案】（1）20201a -；（2）202021-；（3）()20201594-．【解析】（1）由题可以得到()()12211n n n a a a a a a ---++++++11n a +=-()()20192018211a a a a a ∴-+++++20201a =-（2）由结论得：2019201820172222221++++++()()2019201822122221=-⋅+++++ 202021=-（3）201920182017255554+++++()()2019201820172515555+5+1-24-+++=()202015124=-- ()20201594=- 3．计算|1﹣12|+|12﹣13|+|13﹣14|+…+|199﹣1100|．【答案】99100【解析】解：111111112233499100-+-+-++- 111111=1223499100-+--++- 1=1100-99=100． 4．观察下列等式：第1个等式：11111212a ==-⨯；第2个等式：21112323a ==-⨯；第3个等式：31113434a ==-⨯；第4个等式：41114545a ==-⨯； ……解答下列问题：（1）按以上规律写出第5个等式：5a =—————— = ——————．（2）求1232020a a a a ++++的值．（3）求111148812121620162020++++⨯⨯⨯⨯的值．【答案】（1）156⨯，1156-；（2）20202021；（3）631010．【解析】解：（1）第1个等式：11111212a ==-⨯；第2个等式：21112323a ==-⨯；第3个等式：31113434a ==-⨯；第4个等式：41114545a ==-⨯；…… 第5个等式：51115656a ==-⨯；故答案为：156⨯；1156-；（2）12320201111111112233420202021a a a a ++++=-+-+-++- 112021=- 20202021=；（3）111148812121620162020++++⨯⨯⨯⨯ 812111111144820162020⎛⎫=⨯-+-++- ⎪⎝⎭111442020⎛⎫=⨯- ⎪⎝⎭150442020=⨯ 631010=． 5．阅读材料：求2342015122222+++++⋯+的值．解：设234201420151222222S =+++++⋯++，将等式的两边同乘以2，得234201520162222222S =++++⋯++将下式减去上式得，2016221S S -=-即201621S =-．即2342015201612222221+++++⋯+=-请你仿照此法计算：（1）填空：231222+++= ．（2）求2341012222+++++…+2的值．（3）求234111111()()()()33333n +++++⋯+的值．（其中n 为正整数）【答案】（1）15；（2）2047；（3）311()223n -⨯．【解析】解：（1）由题意可得，1+2+22+23=24-1=16-1=15，故答案为：15；（2）由题意可得，2341012222+++++…+2 1121=- 20481=- 2047=；（3）设234111111()()()()33333n S =+++++⋯+，则23411111111()()()()()3333333n n S +=++++⋯++， 1111()33n S S +∴-=-， 1211()33n S +∴=-，解得，311()223n S =-⨯，即234111111()()()()33333n +++++⋯+的值是311()223n -⨯． 6．在日历上，我们可以发现其中某些数满足一定的规律，图是2020年1月份的日历，我们用如图所示的四边形框出五个数．2020年1月：（1）将每个四边形框中最中间位置的数去掉后，将相对的两对数分别相减，再相加，例如：(108)(162)16-+-=，(2119)(2713)16-+-=．不难发现，结果都是16．若设中间位置的数为n ，请用含n 的式子表示发现的规律，并写出验证过程．（2）用同样的四边形框再框出5个数，若其中最小数的2倍与最大数的和为56，求出这5个数中的最大数的值．（3）小明说：我用同样的四边形框也框出了5个数，其中最小数与最大数的积是120．请判断他的说法是否正确，并说明理由．【答案】（1）(1)(1)(7)(7)16n n n n +--++--=，见解析；（2）28；（3）正确，见解析【解析】（1）设中间位置的数为n ，左边数为1n -，右边数1n +，上面数7n -，下面数为7n +，则(1)(1)(7)(7)16n n n n +--++--=（2）2(7)(7)56n n -++=，21n =，21728∴+=．（3）正确(7)(7)120n n -+=，13n ∴=- (舍去)或者13n =，可以存在．7．材料：若一个正整数，它的各个数位上的数字是左右对称的，则称这个正整数是对称数．例如：正整数22是两位对称数；正整数797是三位对称数；正整数4664是四位对称数；正整数12321是五位对称数．根据材料，完成下列问题：（1）最大的两位对称数与最小的三位对称数的和为___________（2）若将任意一个四位对称数拆分为前两位数字顺次表示的两位数和后两位数字顺次表示的两位数，则这两个两位数的差一定能被9整除吗？请说明理由．（3）如果一个四位对称数的个位数字与十位数字的和等于10，并且这个四位对称数能被7整除，请求出满足条件的四位对称数．【答案】（1）200；（2）一定可以，理由见解析；（3）3773【解析】解：（1）最大的两位对称数是99，最小的三位对称数是101，99101200+=，故答案是：200；（2）设个位和千位上的数字是a ，十位和百位上的数字是b ，则这两位数分别是10a b +、10b a +，()101099a b b a a b +-+=-，它们的差是99a b -，这个数是9的倍数，所以这个数一定可以被9整除；（3）设这个四位数的个位数是x ，则十位数是()10x -，这个数可以表示为()()1010100101000x x x x +-+-+，化简得8911100x +，令1x =，则这个数是1991，x=，则这个数是2882，令2x=，则这个数是3773，令3……x=，则这个数是9119，令9其中只有3773能够被7整除，∴满足条件的四位数是3773．8．用棱长为2cm的若干小正方体按如所示的规律在地面上搭建若干个几何体．图中每个几何体自上而下分别叫第一层、第二层，，第n层（n为正整数)（1）搭建第④个几何体的小立方体的个数为．（2）分别求出第②、③个几何体的所有露出部分（不含底面）的面积．1cm需要油漆0.2克，求喷涂（3）为了美观，若将几何体的露出部分都涂上油漆（不含底面），已知喷涂2第20个几何体，共需要多少克油漆？【答案】（1）30；（2）第②个几何体露出部分（不含底面）面积为264cm，第③个几何体露出部分（不含132cm；（3）992克．底面）面积为2【解析】（1）搭建第①个几何体的小立方体的个数为1，搭建第②个几何体的小立方体的个数为2+=+，1412搭建第③个几何体的小立方体的个数为22149123++=++，归纳类推得：搭建第④个几何体的小立方体的个数为22212341491630+++=+++=，故答案为：30；（2）第②个几何体的三视图如下：由题意，每个小正方形的面积为2224()cm ⨯=，则第②个几何体的所有露出部分（不含底面）面积为()232324464()cm ⨯+⨯+⨯=；第③个几何体的三视图如下：则第③个几何体的所有露出部分（不含底面）面积为()2626294132()cm ⨯+⨯+⨯=；（3）第20个几何体从第1层到第20层小立方体的个数依次为221,2,,20，则第20个几何体的所有露出部分（不含底面）面积为()()2221220212202044960()cm ⎡⎤⨯++++⨯++++⨯=⎣⎦，因此，共需要油漆的克数为49600.2992⨯=（克），答：共需要992克油漆．9．阅读下列解题过程：=====请回答下列回题：（1）观察上面的解答过程，请写出= ；（2）请你用含n （n 为正整数）的关系式表示上述各式子的变形规律；（3）利用上面的解法，请化简： ......【答案】（1）10-（21=-（3）9．【解析】（1===10=-；故答案为：10-（21=-（31=-......=......=......=1-．10．先化简，再求值：(2x+x)2−(2x−x)(2x+x)−5xx，其中x=2019，x=−1.【答案】2021.【解析】原式=4x2+4xx+x2−（4x2−x2）−5xx=4x2+4xx+x2−4x2+x2−5xx，=2x2−xx，当x=2019，x=−1时，原式=2×（−1）2−2019×（−1）=202111．观察下列三行数，回答问题：-1、+3、-5、 +7、-9、 +11、……-3、 +1、-7、 +5、-11、+9、……+3、-9、 +15、-21、+27、-33、……（1）第①行第9个数是___________第②行第9个数是___________第③行第9个数是___________（2）在第②行中，是否存在连续的三个数，使其和为83？若存在，求这三个数；若不存在，说明理由．（3）是否存在第m列数（每行取第m个数），这三个数的和正好为-99？若存在，求m；若不存在，说明理由．【答案】（1）-17；-19；51．（2）存在，85，-91，89；（3）第m 列数不存在，理由见解析．【解析】（1）观察到第①行的规律是()()121n n --，第②行的规律是将第①行的数-2，第③行的规律是()()1163n n +--，因此当n=9时，第①行的数为-17∴第②行的数为-17-2=-19，第③行的数为()17351-⨯-=；（2）设第②行存在连续的三个数和为83，且第一个数为x ，若0x >，即x 在第②行中的偶数次列，满足第n 列的数为23n -（其中n 为正偶数），则()()6483x x x +--++=，得85x =，即2385,44n n -==，符合题意，x 在第②行第44列，此时，连续的三个数依次为85，-91，89．若0x <，即x 在第②行中的奇数次列，满足第n 列的数为21n --（其中n 为正奇数），则()()2483x x x +--+-=，得89x =，即2189n --=，45n =-，不符合题意，故舍去，综上所述，存在这样连续的三个数使和为83，依次为85，-91，89．（3）设存在第m 列数使三个数的和为-99，且此列第①行的数为y ，则第m 列第②行的数为2y -，第③行的数为3y ，()2399y y y +-+-=-，得97y ，又第①行中奇数次列为负，偶数次列为正，()971249+÷=，即97在第①行第49列，应为负，故假设不成立，所以，这样的第m 列数不存在．12．回答下列问题：（1）填空：()()a b a b -+=___________________；()()22a b a ab b -++=_____________________；()()3223a b a a b ab b -+++=______________________．（2）猜想：()()1221n n n n a b a a b ab b -----++++=___________________．（其中n 为正整数，且2n ≥）；（3）利用（2）猜想的结论计算：①10987322222222+++++++； ②10987322222222-+-+-+-．【答案】（1）22a b -；33a b -；44a b -；（2）n n a b -；（3）①2046；②682【解析】解：()()22a b a b a b -+=-； ()()22a b a ab b -++322223=++---a a b ab a b ab b33=-a b ；()()3223a b a a b ab b -+++4322332234=+++----a a b a b ab a b a b ab b44a b =-；故答案为：22a b -；33a b -；44a b -；（2）根据（1）中的规律，可得猜想：()()1221-----++++=-n n n n n b a b a a b ab b a b （其中n 为正整数，且2n ≥），故答案为：n n a b -；（3）①10987322222222+++++++1098732222222211=++++++++-10982733728910(21)(22121212121211)1=-+⨯+⨯+⨯++⨯+⨯+⨯+- 11211=--204811=--2046=；②10987322222222-+-+-+-1098732222222211=-+-+-+-+-109827337289101[2(1)][22(1)2(1)2(1)2(1)2(1)2(1)(1)]13=⨯--+⨯-+⨯-+⨯-++⨯-+⨯-+⨯-+--11111[2(1)]13=⨯---1=⨯-20491 3=-6831 =．682。

2021年中考数学压轴题专项训练三角形含解析2

20XX年复习资料教学复习资料班级：科目：2021年中考数学压轴题专项训练《三角形》1．已知，△ABC是等边三角形，过点C作CD∥AB，且CD＝AB，连接BD交AC于点O．（1）如图1，求证：AC垂直平分BD；（2）如图2，点M在BC的延长线上，点N在线段CO上，且ND＝NM，连接BN．求证：NB ＝NM．（1）证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠CAB＝60°，∵CD∥AB，且CD＝AB，∴CD＝CA＝BC，∠ACD＝∠ACB＝60°，∴BO＝DO，CO⊥BD，∴AC垂直平分BD；（2）由（1）知AC垂直平分BD，∴NB＝ND，∵ND＝NM，∴NB＝NM．2．等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F．（1）求证：△ADG≌△CDE．（2）若点H恰好为CE的中点，求证：∠CGF＝∠CFG．证明：（1）在等腰Rt△ABC中，∵点D为斜边AB上的中点，∴CD＝AB，CD⊥AB，∵AD＝AB，∴AD＝CD，∵CD⊥AB，∴∠ADG＝∠CDE＝90°，∵AH⊥CE，∴∠CGH+∠GCH＝90°，∵∠AGD+∠GAD＝90°，又∵∠AGD＝∠CGH，∴∠GAD＝∠GCH，在△△ADG和△CDE中∵∠ADG＝∠CDE＝90°，AD＝CD，∠GAD＝∠GCH∴△ADG≌△CDE（ASA），（2）∵AH⊥CE，点H为CE的中点，∴AC＝AE，∴∠CAH＝∠EAH，∵∠CAH+∠AFC＝90°，∠EAH+∠AGD＝90°，∴∠AFC＝∠AGD，∵∠AGD＝∠CGH，∴∠AFC＝∠CGH，即∠CGF＝∠CFG．3．如图，在△ABC中，AD⊥BC且BD＝DE，EF垂直平分AC，交AC于点F，交BC于点E．（1）若∠BAE＝32°，求∠C的度数；（2）若AC＝6cm，DC＝5cm，求△ABC的周长．解：（1）∵AD⊥BC，BD＝DE，EF垂直平分AC∴AB＝AE＝EC∴∠C＝∠CAE，∵∠BAE＝32°∴∠AED＝（180°﹣32°）＝74°；∴∠C＝∠AED＝37°；（2）由（1）知：AE＝EC＝AB，∵BD＝DE，∴AB+BD＝EC+DE＝DC，∴△ABC的周长＝AB+BC+AC，＝AB+BD+DC+AC，＝2DC+AC＝2×5+6＝16（cm）．4．如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D．（1）求证：∠AOB＝90°+∠C；（2）求证：AE+BF＝EF；（3）若OD＝a，CE+CF＝2b，请用含a，b的代数式表示△CEF的面积，S△CEF＝ab（直接写出结果）．证明：（1）∵OA，OB平分∠BAC和∠ABC，∴，，∴∠AOB＝180°﹣∠OAB﹣∠OBA＝＝＝＝（2）∵EF∥AB，∴∠OAB＝∠AOE，∠ABO＝∠BOF又∠OAB＝∠EAO，∠OBA＝∠OBF，∴∠AOE＝∠EAO，∠BOF＝∠OBF，∴AE＝OE，BF＝OF，∴EF＝OE+OF＝AE+BF；（3）∵点O在∠ACB的平分线上，∴点O到AC的距离等于OD，∴S△CEF＝（CE+CF）•OD＝•2b•a＝ab，故答案为：ab．5．如图，在△ABC中，AB＝AC，AD为BC边上的中线，DE⊥AB于点E．（1）求证：BD•AD＝DE•AC．（2）若AB＝13，BC＝10，求线段DE的长．（3）在（2）的条件下，求cos∠BDE的值．证明：（1）∵AB＝AC，BD＝CD，∴AD⊥BC，∠B＝∠C，∵DE⊥AB，∴∠DEB＝∠ADC，∴△BDE∽△CAD．∴，∴BA•AD＝DE•CA；（2）∵AB＝AC，BD＝CD，∴AD⊥BC，在Rt△ADB中，AD＝＝＝12，∵•AD•BD＝•AB•DE，∴DE＝．（3）∵∠ADB＝∠AED＝90°，∴∠BDE＝∠BAD，∴cos∠BDE＝cos∠BAD＝．6．如图，在△ABC中，AB＝AC，以AB为直径作半圆O，交BC于点D，交AC于点E．（1）求证：BD＝CD．（2）若弧DE＝50°，求∠C的度数．（3）过点D作DF⊥AB于点F，若BC＝8，AF＝3BF，求弧BD的长．（1）证明：如图，连接AD．∵AB是圆O的直径，∴AD⊥BD．又∵AB＝AC，∴BD＝CD．（2）解：∵弧DE＝50°，∴∠EOD＝50°．∴∠DAE＝∠DOE＝25°．∵由（1）知，AD⊥BD，则∠ADB＝90°，∴∠ABD＝90°﹣25°＝65°．∵AB＝AC，∴∠C＝∠ABD＝65°．（3）∵BC＝8，BD＝CD，∴BD＝4．设半径OD＝x．则AB＝2x．由AF＝3BF可得AF＝AB＝x，BF＝AB＝x，∵AD⊥BD，DF⊥AB，∴BD2＝BF•AB，即42＝x•2x．解得x＝4．∴OB＝OD＝BD＝4，∴△OBD是等边三角形，∴∠BOD＝60°．∴弧BD的长是：＝．7．阅读下面材料：数学课上，老师给出了如下问题：如图，AD为△ABC中线，点E在AC上，BE交AD于点F，AE＝EF．求证：AC＝BF．经过讨论，同学们得到以下两种思路：思路一如图①，添加辅助线后依据SAS可证得△ADC≌△GDB，再利用AE＝EF可以进一步证得∠G＝∠FAE＝∠AFE＝∠BFG，从而证明结论．思路二如图②，添加辅助线后并利用AE＝EF可证得∠G＝∠BFG＝∠AFE＝∠FAE，再依据AAS可以进一步证得△ADC≌△GDB，从而证明结论．完成下面问题：（1）①思路一的辅助线的作法是：延长AD至点G，使DG＝AD，连接BG；②思路二的辅助线的作法是：作BG＝BF交AD的延长线于点G．（2）请你给出一种不同于以上两种思路的证明方法（要求：只写出辅助线的作法，并画出相应的图形，不需要写出证明过程）．解：（1）①延长AD至点G，使DG＝AD，连接BG，如图①，理由如下：∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，，∴△ADC≌△GDB（SAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EFA，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．故答案为：延长AD至点G，使DG＝AD，连接BG；②作BG＝BF交AD的延长线于点G，如图②．理由如下：∵BG＝BF，∴∠G＝∠BFG，∵AE＝EF，∴∠EAF＝∠EFA，∵∠EFA＝∠BFG，∴∠G＝∠EAF，在△ADC和△GDB中，，∴△A DC≌△GDB（AAS），∴AC＝BG，∴AC＝BF；故答案为：作BG＝BF交AD的延长线于点G；（2）作BG∥AC交AD的延长线于G，如图③所示：则∠G＝∠CAD，∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，，∴△ADC≌△GDB（AAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EFA，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．8．如图1，直线AB分别与x轴、y轴交于A、B两点，OC平分∠AOB交AB于点C，点D为线段AB上一点，过点D作DE∥OC交y轴于点E，已知AO＝m，BO＝n，且m、n满足n2﹣8n+16+|n﹣2m|＝0．（1）求A、B两点的坐标；（2）若点D为AB中点，求OE的长；（3）如图2，若点P（x，﹣2x+4）为直线AB在x轴下方的一点，点E是y轴的正半轴上一动点，以E为直角顶点作等腰直角△PEF，使点F在第一象限，且F点的横、纵坐标始终相等，求点P的坐标．解：（1）∵n2﹣8n+16+|n﹣2m|＝0，∴（n﹣4）2+|n﹣2m|＝0，∵（n﹣4）2≥0，|n﹣2m|≥0，∴（n﹣4）2＝0，|n﹣2m|＝0，∴m＝2，n＝4，∴点A为（2，0），点B为（0，4）；（2）延长DE交x轴于点F，延长FD到点G，使得DG＝DF，连接BG，设OE＝x，∵OC平分∠AOB，∴∠BOC＝∠AOC＝45°，∵DE∥OC，∴∠EFO＝∠FEO＝∠BEG＝∠BOC＝∠AOC＝45°，∴OE＝OF＝x，在△ADF和△BDG中，，∴△ADF≌△BDG（SAS），∴BG＝AF＝2+x，∠G＝∠AFE＝45°，∴∠G＝∠BEG＝45°，∴BG＝BE＝4﹣x，∴4﹣x＝2+x，解得：x＝1，∴OE＝1；（3）如图2，分别过点F、P作FM⊥y轴于点M，PN⊥y轴于点N，设点E为（0，m），∵点P的坐标为（x，﹣2x+4），∴PN＝x，EN＝m+2x﹣4，∵∠PEF＝90°，∴∠PEN+∠FEM＝90°，∵FM⊥y轴，∴∠MFE+∠FEM＝90°，∴∠PEN＝∠MFE，在△EFM和△PEN中，，∴△EFM≌△PEN（AAS），∴ME＝NP＝x，FM＝EN＝m+2x﹣4，∴点F为（m+2x﹣4，m+x），∵F点的横坐标与纵坐标相等，∴m+2x﹣4＝m+x，解得：x＝4，∴点P为（4，﹣4）．9．在等边△ABC中，线段AM为BC边上的中线．动点D在直线AM上时，以CD为一边在CD 的下方作等边△CDE，连结BE．（1）若点D在线段AM上时（如图1），则AD＝BE（填“＞”、“＜”或“＝”），∠CAM ＝30 度；（2）设直线BE与直线AM的交点为O．①当动点D在线段AM的延长线上时（如图2），试判断AD与BE的数量关系，并说明理由；②当动点D在直线AM上时，试判断∠AOB是否为定值？若是，请直接写出∠AOB的度数；若不是，请说明理由．解：（1））∵△ABC与△DEC都是等边三角形∴AC＝BC，CD＝CE，∠ACB＝∠DC E＝60°∴∠ACD+∠DCB＝∠DCB+∠BCE∴∠ACD＝∠BCE．在△ADC和△BEC中，∴△ACD≌△BCE（SAS），∴AD＝BE；∵△ABC是等边三角形，∴∠BAC＝60°．∵线段AM为BC边上的中线∴∠CAM＝∠BAC，∴∠CAM＝30°．故答案为：＝，30；（2）①AD＝BE，理由如下：∵△ABC和△CDE都是等边三角形∴AB＝BC，DC＝EC，∠ACB＝∠DCE＝60°，∵∠ACD＝∠ACB﹣∠DCB，∠BCE＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，∴△ACD≌△BCE（SAS）∴AD＝BE．②∠AOB是定值，∠AOB＝60°，理由如下：当点D在线段AM上时，如图1，由①知△ACD≌△BCE，则∠CBE＝∠CAD＝30°，又∠ABC＝60°，∴∠CBE+∠ABC＝60°+30°＝90°，∵△ABC是等边三角形，线段AM为BC边上的中线∴AM平分∠BAC，即，∴∠BOA＝90°﹣30°＝60°．当点D在线段AM的延长线上时，如图2，∵△ABC与△DEC都是等边三角形∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°∴∠ACB+∠DCB＝∠DCB+∠DCE∴∠ACD＝∠BCE在△ACD和△BCE中，∴△ACD≌△BCE（SAS）∴∠CBE＝∠CAD＝30°，同理可得：∠BAM＝30°，∴∠BOA＝90°﹣30°＝60°．10．数学课上，王老师出示了如下框中的题目．小明与同桌小聪讨论后，进行了如下解答：（1）特殊情况•探索结论：在等边三角形ABC中，当点E为AB的中点时，点D在CB点延长线上，且ED＝EC；如图1，确定线段AE与DB的大小关系．请你直接写出结论AE ＝DB；（2）特例启发，解答题目王老师给出的题目中，AE与DB的大小关系是：AE＝DB．理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）（3）拓展结论，设计新题在△ABC中，AB＝BC＝AC＝1；点E在AB的延长线上，AE＝2；点D在CB的延长线上，ED ＝EC，如图3，请直接写CD的长1或3 ．解：（1）如图1，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠AFE＝∠ACB＝∠ABC＝60°，△AEF为等边三角形，∴∠EFC＝∠EBD＝120°，EF＝AE，∵ED＝EC，∴∠EDB＝∠ECB，∠ECB＝∠FEC，∴∠EDB＝∠FEC，在△BDE和△FEC中，，∴△BDE≌△FEC（AAS），∴BD＝EF，∴AE＝BD，故答案为：＝；（2）解答过程如下：如图2，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠AFE＝∠ACB＝∠ABC＝60°，△AEF为等边三角形，∴∠EFC＝∠EBD＝120°，EF＝AE，∵ED＝EC，∴∠EDB＝∠ECB，∠ECB＝∠FEC，∴∠EDB＝∠FEC，在△BDE和△FEC中，∴△BDE≌△FEC（AAS），∴BD＝EF，∴AE＝BD．故答案为：AE＝DB．（3）解：分为四种情况：如图3，∵AB＝AC＝1，AE＝2，∴B是AE的中点，∵△ABC是等边三角形，∴AB＝AC＝BC＝1，△ACE是直角三角形（根据直角三角形斜边的中线等于斜边的一半），∴∠ACE＝90°，∠AEC＝30°，∴∠D＝∠ECB＝∠BEC＝30°，∠DBE＝∠ABC＝60°，∴∠DEB＝180°﹣30°﹣60°＝90°，即△DEB是直角三角形．∴BD＝2BE＝2（30°所对的直角边等于斜边的一半），即CD＝1+2＝3．如图4，过A作AN⊥BC于N，过E作EM⊥CD于M，∵等边三角形ABC，EC＝ED，∴BN＝CN＝BC＝，CM＝MD＝CD，AN∥EM，∴△BAN∽△BEM，∴，∵△ABC边长是1，AE＝2，∴，∴MN＝1，∴CM＝MN﹣CN＝1﹣＝，∴CD＝2CM＝1；如图5，∵∠ECD＞∠EBC（∠EBC＝120°），而∠ECD不能大于120°，否则△EDC不符合三角形内角和定理，∴此时不存在EC＝ED；如图6，∵∠EDC＜∠ABC，∠ECB＞∠ACB，又∵∠ABC＝∠ACB＝60°，∴∠ECD＞∠EDC，即此时ED≠EC，∴此时情况不存在，答：CD的长是3或1．故答案为：1或3．11．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．（1）如图1，△ABC中，AB＝AC，∠A＝36°，求证：△ABC是倍角三角形；（2）若△ABC是倍角三角形，∠A＞∠B＞∠C，∠B＝30°，AC＝，求△ABC面积；（3）如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE＝AB，若AB+AC＝BD，请你找出图中的倍角三角形，并进行证明．（1）证明：∵AB＝AC，∴∠B＝∠C，∵∠A+∠B+∠C＝180°，∠A＝36°，∴∠B＝∠C＝72°，∴∠A＝2∠C，即△ABC是倍角三角形，（2）解：∵∠A＞∠B＞∠C，∠B＝30°，①当∠B＝2∠C，得∠C＝15°，过C作CH⊥直线AB，垂足为H，可得∠CAH＝45°，∴AH＝CH＝AC＝4．∴BH＝，∴AB＝BH﹣AH＝﹣4，∴S＝．②当∠A＝2∠B或∠A＝2∠C时，与∠A＞∠B＞∠C矛盾，故不存在．综上所述，△ABC面积为．（3）∵AD平分∠BAE，∴∠BAD＝∠EAD，∵AB＝AE，AD＝AD，∴△ABD≌△AED（SAS），∴∠ADE＝∠ADB，BD＝DE．又∵AB+AC＝BD，∴AE+AC＝BD，即CE＝BD．∴CE＝DE．∴∠C＝∠BDE＝2∠ADC．∴△ADC是倍角三角形．12．如图，在平面直角坐标系中，OA＝OB，AC＝CD，已知两点A（4，0），C（0，7），点D 在第一象限内，∠DCA＝90°，点B在线段OC上，AB的延长线与DC的延长线交于点M，AC与BD交于点N．（1）点B的坐标为：（0，4）；（2）求点D的坐标；（3）求证：CM＝CN．解：（1）∵A（4，0），∴OA＝OB＝4，∴B（0，4），故答案为：（0，4）．（2）∵C（0，7），∴OC＝7，过点D作DE⊥y轴，垂足为E，∴∠DEC＝∠AOC＝90°，∵∠DCA＝90°，∴∠ECD+∠BCA＝∠ECD+∠EDC＝90°∴∠BCA＝∠EDC，∴△DEC≌△COA（AAS），∴DE＝OC＝7，EC＝OA＝4，∴OE＝OC+EC＝11，∴D（7，11）；（3）证明：∵BE＝OE﹣OB＝11﹣4＝7 ∴BE＝DE，∴△DBE是等腰直角三角形，∴∠DBE＝45°，∵OA＝OB，∴∠OBA＝45°，∴∠DBA＝90°，∴∠BAN+∠ANB＝90°，∵∠DCA＝90°，∴∠CDN+∠DNC＝90°，∵∠DNC＝∠ANB，∴∠CDN＝∠BAN，∵∠DCA＝90°，∴∠ACM＝∠DCN＝90°，∴△DCN≌△ACM（ASA），∴CM＝CN．13．如图，在△ABC中，BD⊥AC，垂足为C，且∠A＜∠C，点E是一动点，其在BC上移动，连接DE，并过点E作EF⊥DE，点F在AB的延长线上，连接DF交BC于点G．（1）请同学们根据以上提示，在上图基础上补全示意图．（2）当△ABD与△FDE全等，且AD＝FE，∠A＝30°，∠AFD＝40°，求∠C的度数．解：（1）补全示意图如图所示，（2）∵DE⊥EF，BD⊥AC，∴∠DEF＝∠ADB＝90°．∵△ABD与△DEF全等，∴AB＝DF，又∵AD＝FE，∴∠ABD＝∠FDE，∴BD＝DE．在Rt△ABD中，∠ABD＝90°﹣∠A＝60°．∴∠FDE＝60°．∵∠ABD＝∠BDF+∠AFD，∵∠AFD＝40°，∴∠BDF＝20°．∴∠BDE＝∠BDF+∠FDE＝20°+60°＝80°．∵BD＝DE，∴∠DBE＝∠BED＝（180°﹣∠BDE）＝50°．在Rt△BDC中，∠C＝90°﹣∠DBE＝90°﹣50°＝40°．14．如图．CP是等边△ABC的外角∠ACE的平分线，点D在边BC上，以D为顶点，DA为一条边作∠ADF＝60°，另一边交射线CP于F．（1）求证．AD＝FD；（2）若AB＝2，BD＝x，DF＝y，求y关于x的函数解析式；（3）联结AF，当△ADF的面积为时，求BD的长．证明：（1）如图1，连接AF，∵∠ACB＝60°，∴∠ACE＝120°，∵CP平分∠ACE，∴∠ACP＝∠PCE＝60°，∴∠ADF＝∠ACP＝60°，∴A、D、C、F四点共圆，∴∠AFD＝∠ACB＝60°，∴∠ADF＝∠AFD＝60°，∴∠DAF＝60°，∴△ADF是等边三角形，∴AD＝FD；（2）如图2，过点A作AH⊥BC，∵△ABC是等边三角形，AH⊥BC，AB＝2，∴BH＝1，AH＝BH＝，∴HD＝BD﹣BH＝x﹣1，∵DF＝＝，∴y＝（3）∵△ADF是等边三角形，且△ADF的面积为，∴DF2＝，∴DF2＝＝x2﹣2x+4∴x＝∴BD＝或15．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN ＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．解：（1）结论BM+CN＝BD成立，理由如下：如图②，过点D作DE∥AC交AB于E，∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∵DE∥AC，∴∠BED＝∠A＝60°，∠BDE＝∠C＝60°，∴∠B＝∠BED＝∠BDE＝60°，∴△BDE是等边三角形，∠EDC＝120°，∴BD＝BE＝DE，∠EDN+∠CDN＝120°，∵∠EDM+∠EDN＝∠MDN＝120°，∴∠CDN＝∠EDM，∵D是BC边的中点，∴DE＝BD＝CD，在△CDN和△EDM中，，∴△CDN≌△EDM（ASA），∴CN＝EM，∴BD＝BE＝BM+EM＝BM+CN；（2）上述结论不成立，BM，CN，BD之间的数量关系为：BM﹣CN＝BD；理由如下：如图③，过点D作DE∥AC交AB于E，∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∴∠NCD＝120°，∵DE∥AC，∴∠BED＝∠A＝60°，∠BDE＝∠C＝60°，∴∠B＝∠BED＝∠BDE＝60°，∴△BDE是等边三角形，∠MED＝∠EDC＝120°，∴BD＝BE＝DE，∠NCD＝∠MED，∠EDM+∠CDM＝120°，∵∠CDN+∠CDM＝∠MDN＝120°，∴∠CDN＝∠EDM，∵D是BC边的中点，∴DE＝BD＝CD，在△CDN和△EDM中，，∴△CDN≌△EDM（ASA），∴CN＝EM，∴BD＝BE＝BM﹣EM＝BM﹣CN，∴BM﹣CN＝BD．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

图形规律探索题【例1】如图,在平面直角坐标系中,等腰直角三角形OA 1A 2的直角边OA 1在y 轴的正半轴上,且OA 1=A 1A 2=1,以OA 2为直角边作第二个等腰直角三角形OA 2A 3,以OA 3为直角边作第三个等腰直角三角形OA 3A 4,…,依此规律,得到等腰直角三角形OA 2017A 2018,则点A 2017的坐标为【答案】（0,2）.【解析】解：由题意知：A 1(0,1),A 2(1,1),OA 2=A 2A 3,OA 3=2,∴A 3(2,0),同理,A 4(2,－2),A 5(0,－4),A 6(－4,－4),A 7(－8,0),A 8(－8,8),A 9(0,16)……每隔8个点恰好处于同一坐标系或象限内,2017÷8=252……1,即点A 2017在y 轴正半轴上,横坐标为0,各点纵坐标的绝对值为：20,20,21,21,22,22,23,23,……2017÷2=1008……1,可得点A 2017的纵坐标为：21008, 故答案为（0,21008）.【变式1-1】如图,在一个单位为 1 的方格纸上,△A 1A 2A 3,△A 3A 4A 5,△A 5A 6A 7,…,是斜边在 x 轴上、斜边长分别为 2,4,6,…的等腰直角三角形．若△A 1A 2A 3的顶点坐标分别为A 1(2,0),A 2(1,-1),A 3(0,0),则依图中所示规律,A 2019的横坐标为（）A ．-1008B ．2C ．1D ．1011【答案】A.【解析】解：观察图形可知,奇数点在x轴上,偶数点在象限内,所以A2019在x轴上,A1,A5,A9,A13……,A4n－3在x正半轴,4n－3=2019,n=505.5,所以A2019不在x正半轴上；A3（0,0）,A7（－2,0）,A11（－4,0）,A15（－8,0）……,3=4×0+3,7=4×1+3,11=4×2+3,15=4×3+3,……,2019=4×504+3,∴－2×504=－1008,即A2019的坐标为（－1008,0）,故答案为：A.【变式1-2】如图,在平面直角坐标系中,将正方形O ABC绕点O逆时针旋转45°后得到正方形OA1B1C1,称为一次旋转,依此方式,……,绕点O连续旋转 2 019 次得到正方形O A2 019B2 019C2 019,如果点A的坐标为(1,0),那么点B2 019 的坐标为.【答案】,0）.【解析】由旋转及正方形性质可得：B(1,1),B1(0, ),B2(－1, 1),B3(－,0),B4(－1, －1),B5(0, －),B6(1, －1),B7(, 0),B8(1, 1),……∴360÷45=8,2019÷8=252……3,∴点B2019落在x轴负半轴上,即B2019(,0),故答案为：,0）.【例2】如图,在平面直角坐标系中,将△ABO绕点A顺指针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…,若点A（53,0）,B（0,4）,则点B2016的横坐标为（）A．5 B．12 C．10070 D．10080 【答案】D．【解析】解：由图象可知点B2016在第一象限,∵OA=53,OB=4,∠AOB=90°,在Rt△BOA中,由勾股定理得：AB=133,可得：B2（10,4）,B4（20,4）,B6（30,4）,…∴点B2016横坐标为10080．故答案为：D．【变式2-1】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”（如1,3,6,10…）和“正方形数”（如1,4,9,16…）,在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n 的值为（）A．33 B．301 C．386 D．571 【答案】C．【解析】解：由图形知：第n个三角形数为1+2+3+…+n＝()12n n+,第n个正方形数为n2,当n＝19时,()12n n+＝190＜200,当n＝20时,()12n n+＝210＞200,所以最大的三角形数：m＝190；当n＝14时,n2＝196＜200,当n＝15时,n2＝225＞200,所以最大的正方形数：n＝196,则m+n＝386,所以答案为：C．1.如图,边长为1的菱形ABCD中,∠DAB=60°．连接对角线AC,以AC为边作第二个菱形ACC1D1,使∠D1AC=60°；连接AC1,再以AC1为边作第三个菱形AC1C2D2,使∠D2AC1=60°；…,按此规律所作的第n个菱形的边长为．【答案】1n -．【解析】解：∵四边形ABCD 是菱形,∠DAB =60°,∴AB =BC =1,∠ACB =∠CAB =30°,∴AC ,同理可得：AC 1=2,AC 213,……第n 个菱形的边长为：1n -,故答案为：1n -．2.如图,在平面直角坐标系中,∠AOB =30°,点A 的坐标为（2,0）,过点A 作AA 1⊥OB ,垂足为点A 1,过A 1作A 1A 2⊥x 轴,垂足为点A 2；再过点A 2作A 2A 3⊥OB ,垂足为点A 3；再过点A 3作A 3A 4⊥x 轴,垂足为点A 4…；这样一直作下去,则A 2017的横坐标为（）A ．32 ）2015B ．32 ）2016C ．32 ）2017D ．32）2018 【答案】B ．【解析】解：∵∠AOB =30°,点A 坐标为（2,0）,∴OA =2,∴OA 1OA OA 2OA 1=2×2⎝⎭,OA 3OA 2=2×3⎝⎭…,∴OA n =）n OA =2）n ．∴OA 2018）2018=32）2016故答案为：B．3.如图,函数()()()4022824x x xyx x--≤<⎧=⎨-+≤<⎩的图象记为C1,它与x轴交于点O和点A1,将C1绕点A1选择180°得C2,交x轴于点A2……,如此进行下去,若点P(103,m)在图象上,则m的值是（）A. -2B. 2C. -3D. 4【答案】A．【解析】解：由图可知：横坐标每间隔8个单位,函数值相同,即函数图象重复周期为8,103÷8=12……5,当x=5时,y=－2,即m=－2,故答案为：A.4.如图,弹性小球从点P(0,1)出发,沿所示方向运动,每当小球碰到正方形DABC 的边时反弹,反弹时反射角等于入射角,当小球第 1 次碰到正方形的边时的点为P1(-2,0),第 2 次碰到正方形的边时的点为P2,……,第n 次碰到正方形的边时的点为Pn,则点P2 019的坐标是（）A．(0,1) B．(-4,1) C．(-2,0) D．(0,3)【答案】D．【解析】解：根据图象可得：P1(-2,0),P2(-4,1),P3(0,3),P4(-2,4),P5(-4,0),P6(0,1),P7（－2,0）……2019÷6=336……3,即P2019（0,3）,故答案为：D.5.如图,在坐标系中放置一菱形 OABC ,已知∠ABC =60°,点 B 在 y 轴上,OA =1,先将菱形 OABC 沿 x 轴的正方向无滑动翻转,每次翻转 60°,连续翻转2019次,点 B 的落点依次为 B 1,B 2,B 3,…,则 B 2 019 的坐标为（）A . (1010,0)B .(1310.5, 2)C . (1345, 2)D . (1346,0)【答案】D .【解析】解：连接AC ,如图所示．∵四边形OABC 是菱形,∴OA =AB =BC =OC ．∵∠ABC =60°,∴△ABC 是等边三角形．∴AC =AB ．∴AC =OA ．∵OA =1,∴AC =1．由图可知：每翻转6次,图形向右平移4．∵2019=336×6+3,∴点B 3向右平移1344（即336×4）到点B 2019．∵B 3的坐标为（2,0）,∴B 2019的坐标为（1346,0）,故答案为：D ．6.如图,在直角坐标系中,已知点A （﹣3,0）,B （0,4）,对△OAB 连续作旋转变换,依次得到△1,△2,△3,△4,…,则△2019的直角顶点的坐标为（）A．（8076,0）B．（8064,0）C．（8076,125）D．（8064,125）【答案】A．【解析】解：∵点A（﹣3,0）、B（0,4）,由勾股定理得：AB＝5,由图可知,三个三角形为一个循环,经历一次循环前进的水平距离为：12,2019÷3＝673,直角顶点在x轴上,673×12＝8076,∴△2019的直角顶点的坐标为（8076,0）．故答案为：A．7.如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1,l2,过点（1,0）作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为．【答案】（21008,21009）．【解析】解：由图可知：A1（1,2）,A2（﹣2,2）,A3（﹣2,﹣4）,A4（4,﹣4）,A5（4,8）,…,∵2017=504×4+1,∴点A2017在第一象限,∵2017=1008×2+1,∴A2n+1（（﹣2）n,2（﹣2）n）（n为自然数）．∴A2017的坐标为（（﹣2）1008,2（﹣2）1008）=（21008,21009）．故答案为：（21008,21009）．8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为（1,0）,那么点B2018的坐标为（）A．（1,1）B．（）C．（）D．（﹣1,1）【答案】D．【解析】解：∵四边形OABC是正方形,OA＝1,∴B（1,1）,连接OB,在Rt△OAB中,由勾股定理得：OB,由旋转性质得：OB＝OB1＝OB2＝OB3,∴B1（,B2（﹣1,1）,B3,0）,…,360÷45=8,每8次一循环,2018÷8＝252……2,∴点B2018的坐标为（﹣1,1）.故答案为：D．9.将直角三角形纸板OAB按如图所示方式放置在平面直角坐标系中,OB在x轴上,OB＝4,OA＝．将三角形纸板绕原点O逆时针旋转,每秒旋转60°,则第2019秒时,点A的对应点A′的坐标为（）A．（﹣3,﹣3）B．（3,﹣3）C．（﹣3,3）D．（0,2 3）【答案】A．【解析】解：360÷60=6,即每6秒一循环,2019÷6=336……3,即2019秒时, 点A与其对应点A′关于原点O对称,∵OA＝4,∠AOB＝30°,可得：A(3, 3),∴第2019秒时,点A的对应点A′的坐标为(－3, －3),故答案为：A.10.正方形ABCD的位置在坐标中如图所示,点A、D的坐标反别为（1,0）、（0,2）,延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2017个正方形的面积为【答案】4032352⎛⎫⎪⎝⎭．【解析】解：∵四边形ABCD是正方形,∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA, ∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°, ∴∠ADO=∠BAA1,∵∠DOA=∠ABA1,∴△DOA∽△ABA1,∴11 2OA BAOD AB==,由勾股定理得：AB=AD=5,∴BA1,∴第2个正方形A1B1C1C的边长A1C=A1B+BC,面积=2⎝⎭,同理,第3个正方形的面积为：232⎛⎝⎭,第4个正方形的面积为：23322⎛⨯⎝⎭,……∴第2017个正方形的面积为：4032352⎛⎫⎪⎝⎭.即答案为：4032352⎛⎫⎪⎝⎭.11.如图所示,一动点从半径为 2 的⊙O 上的A0 点出发,沿着射线A0O 方向运动到⊙O 上的点A1 处,再向左沿着与射线A1O 夹角为60°的方向运动到⊙O 上的点A2 处；接着又从A2 点出发,沿着射线A2O 方向运动到⊙O 上的点A3 处,再向左沿着与射线A3O 夹角为60°的方向运动到⊙O 上的点A4 处；……按此规律运动到点A2 017 处,则点A2 017 与点A0 间的距离是【答案】4.【解析】解：由图分析可知,A6点与A0点重合,2017÷6=336……1,即点A2 017 与A1重合,∵⊙O的半径为 2 ,∴点A2 017 与点A0 间的距离是4.12.如图,由一些点组成形如正多边形的图案,按照这样的规律摆下去,则第n（n＞0）个图案需要点的个数是．【答案】n 2+2n .【解析】解：由图知,第1个图形点数为3+0×3,第2个图形点数为4+1×4；第3个图形点数为5+2×5；第4个图形点数为6+3×6……第n 个图形点数为：（n +2）+（n －1）（n +2）=n 2+2n ,即答案为：n 2+2n .13..如图所示的坐标系中放置一菱形OABC ,已知∠ABC =60°,点B 在y 轴上,OA =1,先将菱形OABC 沿x 轴的正方形无滑动翻转,每次翻转60°,连续翻转2017次,点B 的落点分别是B 1,B 2,B 3,……,则B 2017的坐标为【答案】（.【解析】解：由题意知：OB 即B∴B 1,=32,即B 1(32),由图可知,每翻折6次,图形向右平移4个单位,2017=336×6+1,求得：B 2017（336×4+ 32,即B 2017（）,故答案为：（.14.如图,在平面直角坐标系中,点A 1,A 2,A 3,……和点B 1,B 2,B 3,……分别在直线15y x b =+和x 轴上,△OA 1B 1,△B 1A 2B 2,△B 2A 3B 3……都是等腰直角三角形,若点A 1(1,1),则点A 2019的纵坐标是【答案】201832⎛⎫ ⎪⎝⎭.【解析】解：如图,分别过A 1,A 2,A 3作x 轴的垂线,∵点A (1,1)在直线15y x b =+上, ∴b =45, 由△OA 1B 1是等腰直角三角形,得：OB 1=2,设A 2(x ,y ),则B 1C 2=x －2,y = x －2,∴x －2=1455x +,解得：x =72,y =32,即A 2的纵坐标为：32；同理可得：A 3的纵坐标为：29342⎛⎫= ⎪⎝⎭, 即A n 的纵坐标是A n －1纵坐标的32倍, 即A 2019的纵坐标为：201832⎛⎫ ⎪⎝⎭.15.在平面直角坐标系中,正方形 ABCD 的位置如图所示,点 A 的坐标为(1,0),点 D 的坐标为(0,2),延长CB 交x 轴于点A 1,作正方形 A 1CC 1B 1；延长 C 1B 1 交 x 轴于点 A 2,作正方形 A 2C 1C 2B 2；…,按照这样的规律作正方形,则点B2 019的纵坐标为．【答案】201932⎛⎫⎪⎝⎭.【解析】解：过B作BH⊥x轴于H,由一线三直角模型,可知△ADO≌△BAH,即BH=OA=1,即B点纵坐标为1,同理得：B1点纵坐标为32,B2点纵坐标为232⎛⎫⎪⎝⎭,B3点纵坐标为332⎛⎫⎪⎝⎭,……B2019点纵坐标为201932⎛⎫⎪⎝⎭,即答案为：2019 32⎛⎫⎪⎝⎭.。