高三理科数学专题复习--概率与统计
《高三数学复习教案:概率与统计分析》

《高三数学复习教案:概率与统计分析》高三数学复习教案:概率与统计分析概率与统计分析是高中数学复习中重要的一部分,也是考试中常见的考点。
通过掌握概率与统计分析的基本概念、运算方法和实际应用,能够帮助同学们提高解题能力,提升数学成绩。
一、基本概念1. 概率的定义和性质:概率是指某种事件发生的可能性大小。
在数学上,可以用一个介于0与1之间的实数表示概率。
当某个事件必然发生时,其概率为1;当某个事件不可能发生时,其概率为0。
概率具有加法法则、乘法法则和互斥事件等性质。
2. 随机变量和概率分布:随机变量是随机试验结果的函数。
离散随机变量取有限或可列无穷多个可能值,而连续随机变量则取无限多个可能值。
随机变量的概率分布由它取各个可能值及其对应的概率所构成。
二、运算方法1. 排列组合:在排列组合问题中,我们经常需要计算某些事件出现的可能性。
排列是指从n个不同元素中选取m个元素进行排序,可以用数学公式P(n,m)表示;组合是指从n个不同元素中选取m个元素,不考虑其顺序,可以用数学公式C(n,m)表示。
2. 概率计算方法:a. 事件的概率为发生该事件的样本数与总样本空间的大小之比。
b. 随机变量的期望值是每种可能取值乘以相应概率后求和得到的。
c. 随机变量的方差是每种可能取值与期望值之差的平方乘以相应概率后求和得到的。
三、实际应用1. 排列组合在实际问题中的应用:在日常生活和工作中,排列组合思想经常被用到。
比如,在组织活动时需要确定座位安排,则可以通过计算排列或组合的方法来得到不同座位安排方式的数量。
2. 概率在实际问题中的应用:概率理论广泛应用于金融、保险、医疗等领域。
比如,在投资决策中,通过对某只股票未来走势进行概率分析,可以帮助投资者做出更明智的决策。
3. 统计分析的应用:统计分析是对大量数据进行整理、分析和解释的过程。
在日常生活中,通过统计分析可以了解人口结构、收入水平、消费习惯等信息,从而为社会制定相关政策提供参考。
高三数学二轮复习建议——专题二:概率统计 PPT课件 图文

目目 录录
CCOONNTTEENNTTSS
1 历年高考分析 22 重点、热点分析 3 复习目标、方案专题 4 命题预测、优题展示
一 高考试题分析
1.1 2012——2017年高考考查内容分析
2 道 小 题
1 道 大 题
年份 题号
理科 考查 内容
题号
文科 考查 内容
2017 年
2016 年 2015 年 2014 年 2013 年 2012 年
T1 9
相关系数、统计、均值、方差、3 σ原则、概率的意义
T14 二项式定理
2016 年
T4 几何概型
T3 古典概型
从文科高考试题看,解答题一般以工农业生产和生活中的实 频数分布、频率与概率、事件的
频数分布、频率与概率、事件的
T19 独立性、互斥事件、分布列、概 T19 独立性、互斥事件、分布列、概
√√
√
古典概型
几何概型 率 随机模拟
√√√ √ √
随机变量间的函数关系
√
√
二 重点、热点分析
重点、热点、规律方法(一)二项式定理
例
1.(1)(2017▪全国卷Ⅰ理科▪T6)
(1
1 x2
)(1
x)6
展开式中
x2
的系数为
A.15
B.20
C.30
D.35
(2)(2016▪全国卷Ⅰ理科▪T14) (2x x )5 的展开式中,x3 的系数是
T1 8
分步乘法计数原理、组合
正态分布、对立事件
T3
函数、频率与概率、分布列、期 望、方差、概率的意义
T 18
数字特征及其意义 几何概型
相关系数、统计、均值、方差、3 σ原则、概率的意义
【最新】高考数学理科二轮复习课件:专题7概率与统计.1

解析:方法一:直接将(a+x)(1+x)4展开得x5+(a+4)x4+(6+ 4a)x3+(4+6a)x2+(1+4a)x+a,由题意得1+(6+4a)+(1+4a)=32, 解得a=3. r 1 方法二:(1+x)4展开式的通项为Tr+1=Cr x ,由题意可知, a (C 4 4+ 0 2 4 C3 4)+C4+C4+C4=32,解得a=3. 答案:3
2.某次联欢会要安排3个歌舞类节目、2个小品类节目和1个相声 类节目的演出顺序,则同类节目不相邻的排法种数是( ) A.72 B.120 C.144 D.168
解析:依题意,先仅考虑3个歌舞类节目互不相邻的排法种数为 3 A3 3 A 4 =144,其中3个歌舞类节目互不相邻但2个小品类节目相邻的排 2 3 法种数为A 2 2 A 2 A 3 =24,因此满足题意的排法种数为144-24=120, 选B. 答案:B
1 主干梳理· 体验高考 1.两个计数原理: (1)分类加法计数原理:完成一件事有几类不同的方案,各类方 案相互独立,每类方案中又有多种不同的方法,则完成这件事的不同 方法数是各类不同方法数的和. (2)分步乘法计数原理:完成一件事需要分成几个步骤,每一步 的完成又有多种不同的方法,则完成这件事的不同方法数是每一步中 各种不同的方法数的乘积. 2.抽样方法:有简单随机抽样、系统抽样、分层抽样三种. 3.排列数公式: n! m A n =n(n-1)(n-2)„(n-m+1)= (这里,m,n∈N*,且 n-m! m≤n).
n 1 2 n
1.(2015· 湖北卷)已知(1+x)n的展开式中第4项与第8项的二项式系 数相等,则奇数项的二项式系数和为( ) A.212 B.211 C.210 D.29
解析:因为(1+x)n的展开式中第4项与第8项的二项式系数相等, 3 7 所以C n =C n ,解得n=10,所以二项式(1+x)10的展开式中奇数项的二 1 项式系数和为 ×210=29. 2 答案:D
专题4理 概率与统计-2021届高三高考数学二轮复习PPT全文课件

● D.85和85
●
【解析】 (1)对于选项A:2019年1~4月的业务量,3月最高,2月最低,
● 差值为4 397-2 411=1 986,接近2 000万件,
● 所以A是正确的;
● 对于选项B:2019年1~4月的业务量同比增长率分别为55%,53%,62%,58%,均超过50%, 在3月最高,
专题4理 概率与统计-2021届高三高考数学二 轮复习 PPT全 文课件
专题4理 概率与统计-2021届高三高考数学二 轮复习 PPT全解决此类题目的关键是深刻理解各种抽样方法的特点和适用范
围.
(2)在系统抽样的过程中,要注意分段间隔,需要抽取n个个体,样
本就需要分成n个组,则分段间隔为
●
()
● A.15
B.16
C.17
D.18
C
专题4理 概率与统计-2021届高三高考数学二 轮复习 PPT全 文课件
●
【解析】 由系统抽样法知,按编号依次每30个编号作为一组,共分50组,
● 高二学生编号为496到985,在第17组到33组内,
● 第17组编号为16×30+23=503,为高二学生,
2.22+26.22+19.82)=307.16,
故选D.
● 关于平均数、方差的计算
● 样本数据的平均数与方差的计算关键在于准确记忆公式,要特别注意区分方差与标准差, 不能混淆,标准差是方差的算术平方根.
●
3 . ( 2 0 2 0 ·广 陵 区 校 级 模 拟 ) 某 地 区 连 续 5 天 的 最 低 气 温 ( 单 位 : ℃ ) 依 次 为 8 , - 4 , - 1 , 0 , 2 ,
考点一 抽样方法
● 抽样方法主要有简单随机抽样、系统抽样、分层抽样三种,这三种抽样方法各自适用不同 特点的总体,但无论哪种抽样方法,每一个个体被抽到的概率都是相等的,都等于样本容量和总 体容量的比值.
高中数学高考综合复习专题概率与统计(二)

高中数学高考综合复习专题概率与统计(二)一、知识网络:
二、高考考点:1.离散型随机变量的分布列、期望与方差以及运用期望与方差的意义解决实际问题;
2.抽样方法的概念与区别;3.总体分布值所用的计算;正态分布的公式以及正态分布曲线的性质应用;4.线性相关以及回归方程的意义。三、知识要点:(二)统计1、抽样方法统计的基本思想是用样本估计总体,即通常不是直接去研究总体,而是通过从总体中抽取一个样本,根据样本的情况去估计总体的相应情况。
1o 简单随机抽样设一个总体的个体数为N,如果通过逐个抽取的方法从中抽取一个样本,并且每次抽取时各个个体被抽到的概率相等,就称这样的抽样为简单随机抽样。认知:(Ⅰ)简单随机抽样的特点①总体的个体数有限;
②从总体中逐个地进行抽取;③等概率(不放回)抽样(Ⅱ)通过逐个抽取的方法从总体中抽取一个容量为n的样本,每次抽取一个样本时各个个体被抽到的概率(记为P1)相等,并且在整个抽样过程中各个个体被抽到的概率(记为P2)也相等,但这里P1≠P2。
公式:如果运用简单随机抽样从个体数为N的总体中抽取一个容量为n的样本,则(在整个
抽样过程中)每个个体被抽到的概率为。(1)抽签法将总体中所有个体编号,并把号码写在形状、大小相同的号签上,然后将这些号签放在同一个箱子里,进行均匀搅拌,抽签时,每次从中抽出一个号签,连续抽取n次,就得到一个容量为n的样本,当总体的个体数不多时,适宜采用这种方法。
(2)随机数表法事先制好随机数表,表中共随机出现0,1,2,…,9十个数字且在表中每个位置上出现各个数字的概率都是相等的,在此基础上,严格按照课本介绍的步骤进行。
2o 系统抽样(1)定义当总体中的个体数较多时,将总体分成均衡的几个部分,然后按照预先定出的规则,从每一部分抽取一个个体,得到所需要的样本,这样的抽样叫做系统抽样。系统抽样与简单随机抽样的联系在于:将总体匀分后的每一部分进行抽样时,采用的是简单随机抽样。
高三复习专题概率和统计
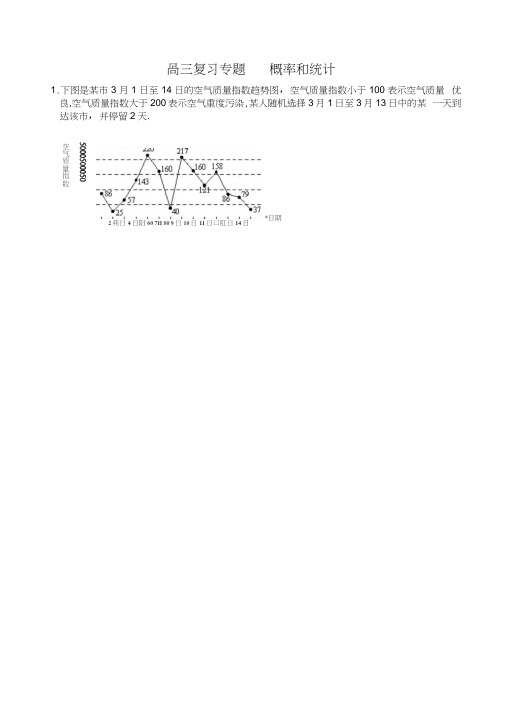
咼三复习专题 概率和统计1.下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量 优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某 一天到达该市,并停留2天.空气质量指数*日期2弗日4日阳60 7H 80 9日10日11日口肛日14日 50005000502 2 11 L3. 甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判,设各局中双方获胜的概率均为1,各局比赛的结果相互独立,第1局甲当裁2判•(I) 求第4局甲当裁判的概率;(II) X表示前4局中乙当裁判的次数,求X的数学期望.4. 现有10道题,其中6道甲类题,4道乙类题,张同学从中任取3道题解答.(I) 求张同学至少取到1道乙类题的概率;(II) 已知所取的3道题中有2道甲类题,1道乙类题.设张同学答对甲类题的概率都是-,答5 对每道乙类题的概率都是-,且各题答对与否相互独立.用X表示张同学答对题的个数,求5X的分布列和数学期望.5. 在一场娱乐晚会上,有5位民间歌手(1至5号)登台演唱,由现场数百名观众投票选出最受欢迎歌手.各位观众须彼此独立地在选票上选3名歌手,其中观众甲是1号歌手的歌迷, 他必选1号,不选2号,另在3至5号中随机选2名.观众乙和丙对5位歌手的演唱没有偏爱,因此在1至5号中随机选3名歌手.(I )求观众甲选中3号歌手且观众乙未选中3号歌手的概率;(n)X表示3号歌手得到观众甲、乙、丙的票数之和,求X的分布列和数学期望.6•经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示. 经销商为下一个销售季度购进了130t该农产品,以X (单位:t, 100乞X乞150)表示下一个销售季度内的市场需求量,T(单位:元)表示下一个销售季度内销商该农产品的利润.(I )将T表示为X的函数;(n )根据直方图估计利润T不少于57000元的概率;(川)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若X引100,110),则取X = 105 ,且X = 105的概率等于需求量落入[100,110)的概率),求利润T的数学期望.7.甲、乙两支排球队进行比赛,约定先胜3局者获得比赛的胜利,比赛随即结束,除第五局甲队获1 2胜的概率是-夕卜,其余每局比赛甲队获胜的概率都是2,假设各局比赛结果相互独立.2 3(I )分别求甲队以3:0,3:1,3:2 胜利的概率;(II)若比赛结果为3:0或3:1,则胜利方得3分,对方得0分;若比赛结果为3:2,则胜利方得2分、对方得1分.求乙队得分X的分布列及数学期望.8 •—批产品需要进行质量检验,检验方案是:先从这批产品中任取4件作检验,这4件产品中优质品的件数记为n.如果n=3,再从这批产品中任取4件作检验,若都为优质品,则这批产品通过检验;如果n=4,再从这批产品中任取1件作检验,若为优质品,则这批产品通过检验;其他情况下,这批产品都不能通过检验•假设这批产品的优质品率为50%,即取出的产品是优质品的概率都为,且各件产品是否为优质品相互独立(1)求这批产品通过检验的概率;⑵已知每件产品检验费用为100元,凡抽取的每件产品都需要检验,对这批产品作质量检验所需的费用记为X(单位:元),求X的分布列及数学期望•9. 设S 是不等式x —x —6^0的解集,m , n S 。
年高考数学二轮复习 专题七 概率与统计 第2讲 概 率课件 理.pptx

3.(2017·全国Ⅱ)一批产品的二等品率为0.02,从这批产品中每次随机取一 件,有放回地抽取100次,X表示抽到的二等品件数,则D(X)=_1_._9_6__. 解析 由题意得X~B(100,0.02), ∴D(X)=100×0.02×(1-0.02)=1.96.
1234
解析 37 答案
4.(2017·江苏)记函数f(x)= 6+x-x2 的定义域为D.在区间[-4,5]上随机取
∴E(ξ1)=p1,E(ξ2)=p2,
D(ξ1)=p1(1-p1),D(ξ2)=p2(1-p2),
又∵0<p1<p2<12,∴E(ξ1)<E(ξ2),
把方差看作函数y=x(1-x),
当 0<x<12时,y′=1-2x>0,根据 0<p1<p2<12知,D(ξ1)<D(ξ2).
1234
解析 36 答案
个上车的是女生的基本事件数m=6,所以概率P=1,故选B. 2
解析 5 答案
(2)(2017届江西省重点中学盟校联考)如图,在边长为 2的正方形ABCD中,M是AB的中点,过C,M,D三 点的抛物线与CD围成阴影部分,则向正方形内撒一 粒黄豆落在阴影部分的概率是
1 A.6
1 B.3
1 C.2
√D.23
123
押题依据 43 解答
(2)设甲、乙两人所付的租车费用之和为随机变量ξ,求ξ的分布列与期 望E(ξ).
123
46 解答
2 概率为__5__.
1234
解析 34 答案
2.(2017·浙江改编)已知随机变量ξi满足P(ξi=1)=pi,P(ξi=0)=1-pi,i=
1,2.若0<p1<p2<
1 2
,则E(ξ1)__<___E(ξ2),D(ξ1)__<___D(ξ2).(填>,<或=)
人教版高中数学高三复习《概率与统计专题》

解析 1 运动员甲得分的中位数为22,运动员乙得分的
中位数为23.
2因为x甲 14 17 15 24 22 23 32 21,
7 x乙 12 13 11 23 27 31 30 21,
7
10
s甲2
21 142
5
3.对于频率分布直方图,要注意如下关系:
1每个小矩形的面积 频率,小矩形面积之
和 1.
2
每一组的频率
频率 组距
组距;每一组的频数 样本容量
该组的频率;频率之和 1.
6
变式1.某中学为了解学生数学课程的学习 情况,在3000名学生中随机抽取200名,并统计这200 名学生的某次数学考试成绩,得到了样本的频率分布 直方图(如图).根据频率分布直方图推测3000名学生在 该次数学考试中成绩小于60分的学生数是______.
21 17 2
7
21 152
21
242
21 222 21 232 21 322 236
7
7
s乙2
21 122
21 132
7
21 112
21
232
21 272 21 312 21 302 466
17
考点3 线性相关分析
例3 某农科所对冬季昼夜温差大小与某反季节大豆新品 种发芽量之间的关系进行分析研究,他们分别记录了12 月1日至12月5日的每天昼夜温差与实验室每天每100颗种 子中的发芽数,得到如下资料:
18
该农科所确定的研究方案是:先从这五组数据中选取2 组,用剩下的3组数据求线性回归方程,再对被选取的 2组数据进行检验.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学习好资料 欢迎下载
2013届高三理数专题复习---概率与统计
班别:_________学号:________姓名:____________
1.(本题满分12分)
某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组:第
1组,第2组,第3组,第4组,第5组得到的频
率分布直方图如图所示:
(1)分别求第3,4,5组的频率;
(2)若该校决定在第3,4,5 组中用分层抽样的方法抽取6名学生进入第二轮面试,
①已知学生甲和学生乙的成绩均在第3组,求学生甲和学生乙同时进入第二轮面试的概率;
②学校决定在这6名学生中随机抽取2名学生接受考官的面试,第4组中有名学生被
考官面试,求的分布列和数学期望.
D
D
]100,95[
)95,90[)90,85[)85,80[
)80,75[
学习好资料 欢迎下载
2.某中学在高三开设了4门选修课,每个学生必须且只需选修1门选修课。对于该年级的甲、
乙、丙3名学生,回答下面的问题:
(1)求这3名学生选择的选修课互不相同的概率;
(2)某一选修课被这3名学生选修的人数的数学期望.
3.某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员
可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、
丁4名参加保险人员所在的地区附近有A,B,C三家社区医院,并且他们对社区医院的选择
是相互独立的.
(I)求甲、乙两人都选择A社区医院的概率;
(II)求甲、乙两人不选择同一家社区医院的概率;
(III)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
学习好资料 欢迎下载
4.(本小题满分12分)
甲乙两名射手互不影响地进行射击训练,根据以往的数据统计,他们设计成绩的分布列如下:
射手甲 射手乙
环数 8 9 10 环数 8 9 10
概率 13 13 13 概率
13 12 1
6
(Ⅰ)若甲乙两射手各射击两次,求四次射击中恰有三次命中10环的概率;
(Ⅱ)若两个射手各射击1次,记所得的环数之和为,求的分布列和期望.
5.(本小题满分12分)
某班从6名班干部(其中男生4人,女生2人)中选3人参加学校学生会的干部竞选.
(1)设所选3人中女生人数为,求的分布列及数学期望;
(2)在男生甲被选中的情况下,求女生乙也被选中的概率.
学习好资料 欢迎下载
2
2
()()()()()nadbcKabcdacbd
6.为了比较注射A,B两种药物后产生的皮肤疱疹的面积,选200只家兔做实验,将这200
只家兔随机地分成两组.每组100只,其中一组注射药物A,另一组注射药物B.下表1
和表2分别是注射药物A和药物B后的实验结果.(疱疹面积单位:2mm)
(1)完成下面频率分布直方图,并比较注射两种药物后疱疹面积的中位数大小;
(2)完成下面22列联表,并回答能否有99.9%的把握认为“注射药物A后的疱疹
面积与注射药物B后的疱疹面积有差异”.
附:
学习好资料 欢迎下载
1.【答案】(1)第3组的频率为 ;第4组的频率为 ;第5
组的频率为
(2)按分层抽样的方法在第3、4、5组中分别抽取3人、2人、1人。
的分布列为
0 1 2
2.【答案】解:(1) 8343341Ap;
(2) 的分布列为
0 1 2 3
p
6427 6427 649 64
1
数学期望
.43641364926427164270E
3.【答案】解:(Ⅰ) 19. (Ⅱ)2()1()3PBPB.
(Ⅲ)ξ的分布列为4444122()()()3381kkkkkPkCC,0,1,2,3,4k.即
0 1 2 3 4
P
1681 3281 2481 881 1
81
所以 14433E.
4.【答案】(Ⅰ)7162;(Ⅱ)
107
6
5.(本小题满分12分)
3215101512158115
6
0E
15115
8
15
6
P
1.0502.0
2.0504.0
3.0506.0
学习好资料 欢迎下载
(1)解:的所有可能取值为0,1,2.…………………………1分
依题意,得3436C1(0)C5P, 214236CC3(1)C5P, 124236CC1(2)C5P.
∴的分布列为
0 1 2
P
51 53 5
1
∴ 1310121555E.…………………………………………………6分
(2)解法1:设“男生甲被选中”为事件A,“女生乙被选中”为事件B,
则2536C1C2PA,1436C1C5PAB, ………………………………………10分
∴
2
5PABPBAPA
.
故在男生甲被选中的情况下,女生乙也被选中的概率为25.……………………12分
解法2:设“男生甲被选中的情况下,女生乙也被选中”为事件C,
从4个男生、2个女生中选3人,男生甲被选中的种数为25C10,……………8分
男生甲被选中,女生乙也被选中的种数为14C4,………………………………10分
∴1425C42C105PC.
故在男生甲被选中的情况下,女生乙也被选中的概率为25.………………………12分
6.解: (1)
………………4分
学习好资料 欢迎下载
图1注射药物A后皮肤疱疹面积的频率分布直方图 图2注射药物B后皮肤疱疹面积的频率分布直方图
可以看出注射药物A后的疱疹面积的中位数在65至70之间,而注射药物B后的疱疹
面积的中位数在70至75之间,所以注射药物A后疱疹面积的中位数小于注射药物B
后疱疹面积的中位数.
(2)表3
疱疹面积小于270mm 疱疹面积不小于270mm
合计
注射药物A
70a 30b 100
注射药物B
35c 65d
100
合计
105 95
200n
56.2495105100100)30356570(20022K
由于828.102K,所以有99.9%的把握认为“注射药物A后的疱疹面积与注射药物B
后的疱疹面积有差异”.
