稀疏子空间聚类算法
信号与数据处理中的低秩模型——理论、算法与应用

min rank( A), s.t.
A
( D) ( A)
2 F
,
(2)
以处理测量数据有噪声的情况。 如果考虑数据有强噪声时如何恢复低秩结构的问题,看似这个问题可以用传统的 PCA 解决,但 实际上传统 PCA 只在噪声是高斯噪声时可以准确恢复潜在的低秩结构。对于非高斯噪声,如果噪声 很强,即使是极少数的噪声,也会使传统的主元分析失败。由于主元分析在应用上的极端重要性, 大量学者付出了很多努力在提高主元分析的鲁棒性上,提出了许多号称“鲁棒”的主元分析方法, 但是没有一个方法被理论上严格证明是能够在一定条件下一定能够精确恢复出低秩结构的。 2009 年, Chandrasekaran 等人[CSPW2009]和 Wright 等人[WGRM2009]同时提出了鲁棒主元分析 (Robust PCA, RPCA) 。他们考虑的是数据中有稀疏大噪声时如何恢复数据的低秩结构:
b) 多子空间模型
RPCA 只能从数据中提取一个子空间,它对数据在此子空间中的精细结构无法刻画。精细结构 的最简单情形是多子空间模型,即数据分布在若干子空间附近,我们需要找到这些子空间。这个问 题马毅等人称为 Generalized PCA (GPCA)问题[VMS2015],之前已有很多算法,如代数法、RANSAC 等,但都没有理论保障。稀疏表示的出现为这个问题提供了新的思路。E. Elhamifar 和 R. Vidal 2009 年利用样本间相互表达,在表达系数矩阵稀疏的目标下提出了 Sparse Subspace Clustering (SSC)模型 [EV2009]((6)中 rank( Z ) 换成 Z
* 本文得到国家自然科学基金(61272341, 61231002)资助。
【国家自然科学基金】_子空间聚类_基金支持热词逐年推荐_【万方软件创新助手】_20140731

2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 2 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
k-means算法 dna微阵列数据 ap聚类
53 d-s证据理论 54 clique
推荐指数 4 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43
科研热词 子空间聚类 聚类分析 聚类 数据挖掘 支持向量机 多类分类 高雏指标 高维数据索引 高维数据 高光谱 频繁模式 非线性建模 遥感 逆系统方法 辨识 谱聚类 聚类算法 聚类树 联合基尼值 网格划分 线性判别分析 粗糙集 类别保留投影 相对熵 相似兴趣子空间 目标检测 热工过程 模糊规则 模糊c均值聚类 模拟电路 核方法 最优聚类中心 最优变换 故障诊断 投影寻踪 属性关系图 密度聚类 子空间 基因表达数据 基于内容图像检索 图像分割 可视化 可信子空间 加速遗传算法 加权ls-svm 分解聚类 分类属性 农业综合生产力 亚像素目标 二又树 k均值聚类 fp.树
【计算机应用】_稀疏性_期刊发文热词逐年推荐_20140724
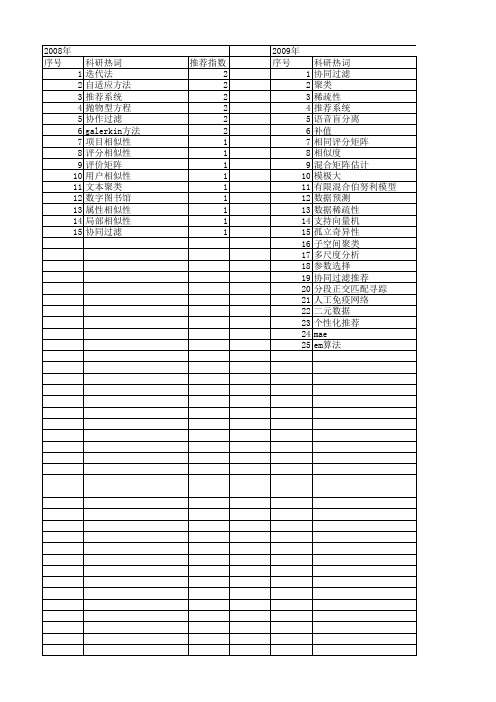
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
科研热词 协同过滤 ຫໍສະໝຸດ 类 稀疏性 推荐系统 语音盲分离 补值 相同评分矩阵 相似度 混合矩阵估计 模极大 有限混合伯努利模型 数据预测 数据稀疏性 支持向量机 孤立奇异性 子空间聚类 多尺度分析 参数选择 协同过滤推荐 分段正交匹配寻踪 人工免疫网络 二元数据 个性化推荐 mae em算法
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
推荐指数 5 4 3 3 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
主动训练策略 个性化推荐 pr算子分裂算法 pc分量 kaiser窗口 fisher准则函数
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52
科研热词 协同过滤 稀疏性 推荐系统 压缩感知 项目分类 正交匹配追踪 信号分解 高斯混合参数 项目相似性 非线性重构 非平稳信号 非参数基函数 降噪模型 重要子空间 贝叶斯 语音信号 话题模型 评分预测 自适应正则化 聚类分析 线性预测分析 稀疏性度量 稀疏去噪 磁共振成像 电子商务推荐方法 用户关注度 独立成分分量 特征提取 模糊自适应 文本聚类 文本分类 数据稀疏性 数据挖掘 支持向量机 推荐算法 微博 径向基函数 层次聚类 小波方法 多尺度几何分析 协作型过滤 冗余字典 兴趣最近邻 信息量 信息检索 信号表示 仿真 互信息 云模型 个性化推荐 web使用挖掘 sar图像
一种改进的子空间选择算法在聚类中的应用

Key words clustering ; high dimensional space; k nearest neighbors ; approximate nearest neighbors 摘 要 高维空间聚类由于其数据分布稀疏、 噪声数据多、差距趋于零现象” “ 等特征, 因而给传统的聚类 方法带来很大的阻碍. 为了解决这些问题 , 介绍了一种对于潜在子空间的选择方法. 原有方法采用 k 邻
关键词 聚类 ; 子 空间; 郁近; 近似部近 k
中图法分类号 T P3l l
聚类是数据挖掘研究 中的一个重要分析手段 , 目前的聚类算法主要分为层次方法和划分方 法. 层 次方法对给定的数据集进行层次分解, 对分解结果
题, 在处理海量数据集和高维数据上表现得尤为
明显 .
做合并或分裂形成聚簇, BIRcH[‘ ]和cu RE[2〕 是典
型的层次聚类算法 ; 分区方法利用某一个划分策略 对数据集进行分区, 得到的每个分区代表一个聚簇 ,
典型 算法包括 尔mediod[3] ,一 走 means[3〕 随着聚类 等.
在实际中的应用 越来越广泛 , 也逐 渐凸现 出一些 问
收稿 日期 :2007一 一 03 05
高维空间数据有如下特点 : 1 数据分布稀疏 、 ) 噪声数据较多; 2 维度高达一定程度时, ) 对给定数 据点、 距其最近的数据点与最远数据点间的距离随 着维度的增加渐趋于零 , 在此称为“ 差距趋零现象” . 并且 , 这些特点随着维度 的增 加更趋 明显. 为了处 理这些问题 , 通常采用将对聚簇无关或者影响不大
13 0
计算机研究与发展 200 , ( 增刊) 7 44
( 5 为 l o s ) w r ,T in动ua 协1* r it , 1咭 100084 ) o f t f a e s s y 及红
基于稀疏表示的故障敏感特征提取方法_栗茂林

运行状态信息,却使状态特征空间变得庞大,给信 号处理带来了困难。为此,提取低维敏感特征是诊 断特征提取和选择研究中的一个关键问题。 主分量分析(Principal component analysis, PCA) 是常见的多元统计方法,基于数据的二阶统计性质 来发现其内部线性结构,并通过低维主分量来反映 [5-6] 原始特征信息 。 但由于主分量包含了全部原始特 征,使其可解释性变差,无法了解主分量与特征间 的关联性。且由于权系数小的特征往往对分类贡献
1 sgn( x) 0 1 (7) 令
L2-范数下求取最大方差,主要用于重构误差度量,
在诊断特征提取中,目标是提取特征分量,且信号
T 中包含有噪声干扰,因此,采用 W X
2 2
1
代替
β ( β1 , β2 , , βd )T
则
w (t 1) β β2
W T X ,实现对噪声和野点的容忍。另外,约束
JOURNAL OF MECHANICAL ENGINEERING
DOI:10.3901/JME.2013.01.073
基于稀疏表示的故障敏感特征提取方法*
栗茂林 1, 2 梁 霖1 王孙安 1
(1. 西安交通大学机械工程学院 西安 710049; 2. 西安交通大学工程坊 西安 710049)
摘要: 针对故障诊断中的特征选择问题, 提出一种基于非负稀疏表示的低维敏感特征提取方法。 为了增强主分量的可解释性, 针对 L1-范数优化目标,通过权系数的稀疏和非负约束实现非负稀疏主分量的提取。采用主分量特征的累积方差变化率自适 应地确定稀疏度,并依据稀疏分量与原始特征少关联的需求确定稀疏分量的数目,实现敏感特征的优化提取。通过仿真数据 的分析表明,非负稀疏分量不仅提取出描述原始数据分布的敏感特征,还提高了数据的聚类性能。将该方法应用于滚动轴承 的多种故障状态识别中,在由非负稀疏主分量构成的特征空间中,数据的聚类效果优于主分量特征空间;综合分析稀疏参数 的选取和敏感特征的提取过程, 表明提出的稀疏表示方法不仅能自适应地确定稀疏度, 还能有效地获取原始特征的敏感程度, 为故障诊断特征提取提供了很好的解决方案。 关键词:稀疏表示 中图分类号:TH17 主分量分析 特征提取 故障诊断
基于局部协方差矩阵的谱聚类算法

基于局部协方差矩阵的谱聚类算法杜婷婷;文国秋;吴林;童涛;谭马龙【摘要】针对传统谱聚类算法没有解决簇划分过程中,簇间交叉区域样本点对聚类效果有影响这个问题,提出一种基于局部协方差矩阵的谱聚类算法,主要介绍了一种新的计算样本之间相似度亲和矩阵的方法,即通过计算样本点之间的欧氏距离划分出小子集,计算小子集的协方差,通过设定阈值剔除交叉点,由剩下的点构造相似矩阵,对相似矩阵进行特征值分解,用经典的k-means算法对由特征向量组成的矩阵聚类.通过在Control等真实数据集上的实验结果表明,该算法在聚类准确率、标准互信息等指标上比较对比算法获得更优秀的效果.%For the traditional spectral clustering algorithm does not solve the cluster division process, the cross-cluster cross-region sample points have an impact on the clustering effect. In this paper, a spectral clustering algorithm based on local covariance is proposed. The algorithm mainly introduces a new method for calculating the similarity affinity matrix between samples. Firstly, it divides the child by calculating the Euclidean distance between sample points. Then it calcu-lates the covariance matrix of the small subset, sets the threshold to eliminate the intersection, the remaining point con-structs a similarity matrix, and then the eigenvalue decomposition of the similarity matrix is done, and finally it uses the classical k -means algorithm for the eigenvectors matrix clustering. Experiments on real data sets such as Control show that the algorithm of this paper obtains better results in terms of clustering accuracy, standard mutual information and other indicators.【期刊名称】《计算机工程与应用》【年(卷),期】2019(055)014【总页数】8页(P148-154,176)【关键词】谱聚类;协方差矩阵;相似矩阵【作者】杜婷婷;文国秋;吴林;童涛;谭马龙【作者单位】广西师范大学广西多源信息挖掘与安全重点实验室,广西桂林541004;广西师范大学广西多源信息挖掘与安全重点实验室,广西桂林 541004;广西师范大学广西多源信息挖掘与安全重点实验室,广西桂林 541004;广西师范大学广西多源信息挖掘与安全重点实验室,广西桂林 541004;广西师范大学广西多源信息挖掘与安全重点实验室,广西桂林 541004【正文语种】中文【中图分类】TP1811 引言聚类[1-6]就是将样本空间中“相似”的对象划分为同一个簇,而“不相似”的对象划分成不同的簇。
文本聚类算法总结
⽂本聚类算法总结以下内容为聚类介绍,除了红⾊的部分,其他来源百度百科,如果已经了解,可以直接忽略跳到下⼀部分。
聚类分析⼜称群分析,它是研究(样品或指标)分类问题的⼀种统计分析⽅法,同时也是数据挖掘的⼀个重要算法。
聚类(Cluster)分析是由若⼲模式(Pattern)组成的,通常,模式是⼀个度量(Measurement)的向量,或者是多维空间中的⼀个点。
聚类分析以相似性为基础,在⼀个聚类中的模式之间⽐不在同⼀聚类中的模式之间具有更多的相似性。
在商业上,聚类可以帮助市场分析⼈员从消费者数据库中区分出不同的消费群体来,并且概括出每⼀类消费者的消费模式或者说习惯。
它作为数据挖掘中的⼀个模块,可以作为⼀个单独的⼯具以发现数据库中分布的⼀些深层的信息,并且概括出每⼀类的特点,或者把注意⼒放在某⼀个特定的类上以作进⼀步的分析;并且,聚类分析也可以作为数据挖掘算法中其他分析算法的⼀个预处理步骤。
聚类分析的算法可以分为划分法(Partitioning Methods)、层次法(Hierarchical Methods)、基于密度的⽅法(density-based methods)、基于⽹格的⽅法(grid-based methods)、基于模型的⽅法(Model-Based Methods)。
很难对聚类⽅法提出⼀个简洁的分类,因为这些类别可能重叠,从⽽使得⼀种⽅法具有⼏类的特征,尽管如此,对于各种不同的聚类⽅法提供⼀个相对有组织的描述依然是有⽤的,为聚类分析计算⽅法主要有如下⼏种:划分法划分法(partitioning methods),给定⼀个有N个元组或者纪录的数据集,分裂法将构造K个分组,每⼀个分组就代表⼀个聚类,K<N。
⽽且这K个分组满⾜下列条件:(1)每⼀个分组⾄少包含⼀个数据纪录;(2)每⼀个数据纪录属于且仅属于⼀个分组(注意:这个要求在某些模糊聚类算法中可以放宽);对于给定的K,算法⾸先给出⼀个初始的分组⽅法,以后通过反复迭代的⽅法改变分组,使得每⼀次改进之后的分组⽅案都较前⼀次好,⽽所谓好的标准就是:同⼀分组中的记录越近越好,⽽不同分组中的纪录越远越好。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
稀疏子空间聚类算法与模型建立
稀疏子空间聚类是一种基于谱聚类的子空间聚类方法,
基本思想:假设高位空间中的数据本质上属于低维子空间,能够在低维子空间中进行线性表示,能够揭示数据所在的本质子空间, 有利于数据聚类.
基
本方法是, 对给定的一组数据建立子空间表示模型,寻找数据在低维子空间中的表示系数, 然后根据表示系数矩阵构造相似度矩阵, 最后利用谱聚类方法如规范化割(Normalized cut, Ncut)[22] 获得数据的聚类结果。
基本原理
稀疏子空间聚类[32] 的基本思想是: 将数据 αS x i ∈表示为所有其他数据的线性组合, j i
j ij i x Z x ∑≠= (1)
并对表示系数施加一定的约束使得在一定条件下对所有的αS x j ∉, 对应的0=ij Z 。
将所有数据及其表示系数按一定方式排成矩阵 ,则式(1)等价于 XZ X = (2)
且系数矩阵N N R Z ⨯∈ 满足: 当i x 和j x 属于不同的子空间时, 有0=ij Z . 不同于用一组基或字典表示数据, 式(2)用数据集本身表示数据, 称为数据的自表示. 若已知数据的子空间结构, 并将数据按类别逐列排放, 则在一定条件下可使系数矩阵Z 具有块对角结构, 即
⎥⎥⎥⎥⎦
⎤⎢⎢⎢⎢⎣⎡=k Z Z Z Z 00000021 (3) 这里),,1(k Z =αα 表示子空间αS 中数据的表示系数矩阵; 反之, 若Z 具有块对角结构, 这种结构揭示了数据的子空间结构. 稀疏子空间聚类就是通过对系数矩阵Z 采用不同的稀疏约束, 使其尽可能具有理想结构, 从而实现子空间聚类.
Elhamifar 等[32] 基于一维稀疏性提出了稀疏子空间聚类(Sparse subspace clustering,SSC) 方法, 其子空间表示模型为
1min Z Z 0,..==ii Z XZ X t s (4)
该模型利用稀疏表示(SR) 迫使每个数据仅用同一
子空间中其他数据的线性组合来表示. 在数据所属的子空间相互独立的情况下, 模型(4) 的解Z 具有块对角结构, 这种结构揭示了数据的子空间属性: 块的个数代表子空间个数, 每个块的大小代表对应子空间的维数, 同一个块的数据属于同一子空间. 注意, 模型中的约束0=ii Z 是为了避免平凡解, 即每个数据仅用它自己表示, 从而Z 为单位矩阵的情形. 稀疏子空间聚类综述 王卫卫1 李小平1 冯象初1 王斯琪1
32 Elhamifar E, Vidal R. Sparse subspace clustering. In: Pro-ceedings of the 2009 IEEE Computer Society Conferenceon Computer Vision and Pattern Recognition (CVPR).Miami, FL, USA: IEEE, 2009. 2790¡2797
稀疏最优化模型
位于线性或仿射子空间集合的高维数据可以稀疏地被同一个子空间的点线性或者仿射表示。
通过文献[9]中稀疏表示技巧获得高维数据的稀疏表示。
设有N 个D 维数据{}N i i y 1=,处于D R 空间的n 个线性子空间{}n
l l S 1=中,子空间的维数分别为{}n l l d 1=,定义一个矩阵Y 为:
Γ==][][11n N Y Y y y Y 其中,l N M R Y ⨯∈矩阵。
对于每个数据点都可以被一些除它以外的数据点表示,即0,==cii ci i Y y ,其中N N N i R c c c C ⨯∈=][21 ,该表示是任意的并存在一个最稀疏的形式。
为了获得每个数据点的最稀疏的表示,选择最小化其0l 范数对其进行凸松弛处理。
稀疏最优化模型为: 0)(,..min 1==C diag YC Y t s C
将已获得的稀疏系数矩阵C应用到谱聚类算法中,从而对数据进行聚类,称为稀疏子空间聚类算法。
谱聚类算法
谱聚类[11]是建立在图谱理论基础上的一种重要的数据聚类方法,首先根据给定的样本数据集建立数据间的相似度矩阵,然后构造加权图,通过寻找图的最优划分实现数据聚类的目的。
非正则化Laplacian W D L -=
正则化Laplacian 2/12/12/12/1:-----==W D D I LD D L xym W D I L D L rw 11:---== 其中,D 度矩阵为对角矩阵,对角线上的元素为∑==n j ij n w
d d d 121,,, 。
L 对应于划分准则
RatioCut 【12】,而正则化:Laplacian 对应于划分准则Ncut [12]。
根据Laplacian 矩阵的选择不同[12],衍生出三个谱聚类算法,一种非正则化谱聚类,两种正则化谱聚类[6,13]。
谱聚类算法寻求相似加权图的最优划分,要求类间切割权值最小而类内相似权值最大。
然而非正则化
谱聚类有时不能满足类内相似权值最大这个要求,而正则化谱聚类能够很好的满足这两个条件。
因此,正则化谱聚类算法优于非正则化谱聚类算法。
一种改进的稀疏子空间聚类算法 欧阳佩佩,赵志刚,刘桂峰(青岛大学信息工程学院,青岛266071
[6] Ng A,Weiss Y,Jordan.On spectral clustering:analysis and an algorithm [J].Neural Information Processing Systems,2001:849-856.
[9] Elhamifar E,Vidal R.Sparse subspace clustering:Algorithm,theory,and applications[J].IEEE Transactions on Pattern Analysis and
Machine Intelligence,2013,35(11):2765-2781.
[11]von Luxburg U,A tutorial on spectral clustering[J].Statistics and Computing,2007,17(4):395-416.
[12]Boyd S,Parikh N,Chu E,et al.Distributed optimization and statistical learning via the alternating direction method
of multipliers[J].
Foundations and Trends in Machine Learning,2010,3(1):1-122.
[13]Shi J,Malik J.Normalized cuts and image segmentation[J].IEEE Trans.on Pattern Analysis and Machine Intelligence,2000,2(8):888-905.
以上所述的稀疏子空间聚类模型通常采用交替方向法(Alternating direction method, ADM)[74]来求解, 需要大量的迭代, 同时复杂度较高。
我们选用ADM 的改进算法,ADMM (交替方向乘子法)。
交替方向乘子法是求解分散式优化问题的方法之一,它收敛性好,鲁棒性强,且不要求子优化模型目标函数严格凸和有限,近年来越来越受关注。
其标准形式[17]如下:⎩⎨⎧=++c
Bz Ax t s z g x f ..)()(min
p m p n p m n R c R B R A R z R x ∈∈∈∈∈⨯⨯;;;; ;g f ,为凸函数。
当 g f ,函数在{}∞+→ R R n 上为凸函数时,算法能收敛到最优解[17]。
需特别注意的是
ADMM 不要求g f ,函数有限,因此g f ,除了可以表示每个子系统的目标函数外,还可以表示每个子系统的等式或不等式约束,这时,当每个子系统约束不越限时, 0,0==g f ,否则 +∞=+∞=g f ,。
[11] Chen C .Non-convex economic dispatch :A direct search approach[J].Energy Conversion and Management ,2007,48(1):219-225.
基于交替方向乘子法的动态经济调度分散式优化 李佩杰,陆镛,白晓清,韦化
求解:。
