对驻波与半波损失的认识
6-驻波

驻波
波动
驻波系统的驻波原理: 驻波系统的驻波原理: 简正模式的频率称为系统的的固有频率 简正模式的频率称为系统的的固有频率,一个 固有频率, 驻波系统有多个固有频率, 驻波系统有多个固有频率,这与弹簧振子只有 一个固有频率不同. 一个固有频率不同. 当外界驱动源以驻波系统的某个固有频率振 动时,会激起强驻波,这种现象也称为共振 共振. 动时,会激起强驻波,这种现象也称为共振. 系统究竟按哪种模式振动取决于初始条件, 系统究竟按哪种模式振动取决于初始条件,一 般驻波系统的振动频率是各种简正模式的叠 加.
y = 2 A cos2π cos2π ν t
x
λ
y
λ 2
例 x=±
λ 3λ
4 λ
4
,
为波节
o
x
x
λ2
x
4
x
λ
4
<x<
, cos2 π > 0
λ
3λ x < x < , cos2 π < 0 4 4 λ
λ
y = 2 A cos 2 π
y = 2 Acos2 π
λ
cos 2π ν t
cos(2 πν t + π)
驻波
波动
B
o
y反
驻波方程: 驻波方程:
y = y入 + y反
2π t 2π ( 3 λ x ) 4 = A cos T λ 2π t 2π x 3π = A cos( + ) T λ 2
2πt 2πx π 2πt 2πx 3π = A cos( + ) + A cos( + ) T λ 2 T λ 2 2π x 2π t π λ = 2 A cos( ) cos( + ) n = 0, x1 = λ T 2 4
大学物理第6章第4节-驻波
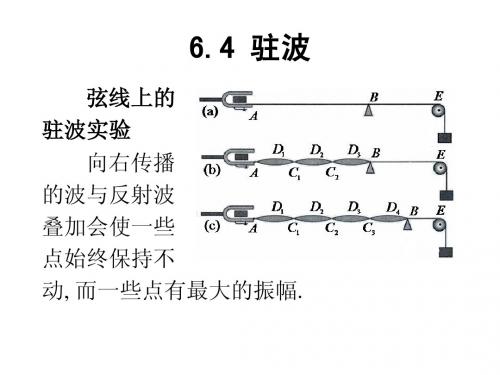
x k (m), (k 0,1, 2, 3,4,5)
波腹位置
cos x 2 1
x
2 2 1 x k (m), (k 0,1, 2,3,4) 2
2k
, k 0,1, 2,
作业: (P. 152) 6.16 习题册: (P. 6) 1, (P. 7) 5
3 L O P 2 2
u
2
2
u
L
2
5
2
反射波沿x轴负向传播, 其波动方程
x y反 0.02 cos4 (t ) O 4 x 0.02 cos4 (t ) 4 2
在两个相邻波节之间的符号相同. (1) 波节两边的相位相反; (2) 两相邻波节之间的相位相同.
x
x
三. 半波损失 波在波密介质界面反射时, 反射波在界 形成波节 面处形成波节(发生 波疏介质 波密介质 的相位突变). 称为半 波疏介质 : u小 波损失. 波密介质 : u大 波在波疏介质界 波密介质 波疏介质 形成波腹 (自由端反射 ) 面反射 (称为自由端), 反射波在界面处形成波腹 (没有相位突变).
1 3 (m) x 100 2 k 2 3
t0
x
t T 6
x
t T 4
x
方法二
y1 0.06 cos[( 2)(8.0t 0.02x)] y2 0.06 cos[( 2)(8.0t 0.02x)]
相位差
( 2)(8.0t 0.02x) ( 2)(8.0t 0.02x)
1), ( 2 ) ( x 50(2k 2 3) (m)
4.波的干涉_驻波
三、驻波能量:
⒈动能:
当各质点同时到达平衡位置时: 介质无形变,势能为零,此时驻波能量为动能。 波腹处动能最大,驻波能量集中在波腹附近。
⒉势能:
当各质点同时到达最大位移时: 动能为零,此时驻波能量为势能。 波节处形变最大,势能最大,能量集中在波节附近。
⒊结论:
动能、势能不断在波腹附近和波节附近间相互转 换,能量交替传递,无定向传播。
2 x 波腹位置: cos(2 ) 1 相邻两波腹距离 10 20 0 x x k , k 0,1,2 2 2
相邻两波节距离 x
各点相位:
y 2 A cos(2
x
) cos(2 t )
各质点作振幅为 2 A cos(2
cos(2
相位跃变(半波损失)
波 疏 介 质
波 密 介 质 较 大
u
较 小
u
当波从波疏介质垂直入射到波密介质, 被反射 到波疏介质时形成波节. 入射波与反射波在此处的相 位时时相反, 即反射波在分界处产生 的相位跃变, 相当于出现了半个波长的波程差,称半波损失.
π
当波从波密介ቤተ መጻሕፍቲ ባይዱ垂直入射到波疏介质, 被反射 到波密介质时形成波腹. 入射波与反射波在此处的相 位时时相同,即反射波在分界处不产生相位跃变.
同一直线上沿相反方向传播时叠加而形成的一种特殊
的干涉现象.
驻波的形成
特征:
1、波形不移动。 2、各质点以不同的振幅在各自的平衡位置附近振动。
3、分段振动:振幅最大的点为波腹,
振幅为零的点为波节。
二、驻波方程:
沿X 轴正、负向传播的两列平面简谐波的波动方程为: x 在任意点 x 处叠加, y1 A cos 2 ( t ) 合位移: x y y1 y2 y 2 A cos 2 ( t ) x 2 A cos(2 ) cos(2 t ) ( 设初相 10 20 0)
驻波解析

原点描写合成驻波。由于绳很长,可不考虑反射。 绳上的波速设为u 。
解 设左端的振动为y1 =Acos t,则右端的振动 为 y2=Acos ( t + )。
设右行波的波动表达式(以绳的中心为坐标原点)
y1Acos(t[ux)1]
设左行波的波动表达式(以绳的中心为坐标原点)
dE k2dV A 22co 2(2 s πx)si2 nt dE p2dV A 22si2n 2 πxco 2st
(1) cos t = ±1 各质点的位移达到最大,dEk为零,
势能dEp不为零。波节处势能最大;在波腹处势 能最小。势能集中在波节附近。
波腹处势能始终为0
(2) cos t = 0 各质点都回到平衡位置,此时所有
反射波在B点的振动方程
tl y反 BAco2 s([T)]
反射波的表达式
y 反 A co 2 (T s t [ l) 2 (l x )]
y反
Acos2( t T
212x)
Acos2(t x)
T
(2)驻波的表达式为
yy入y反
Acos2(t x)Acos2(t x)
T
T
2Asin2xsin2t
x k
2
点O 到点B 之间的波节
x 0 ,,,3 ,2 ,5 , 3 ,7 ,4 ,9 ,5
22 2 2 2
波腹的坐标
sin 2π x 1 2π x(2k1)π x (2k 1)
2
4
x ,3 ,5 ,7 ,9 ,1 ,1,3 1 ,5 1,7 19
4444444 4 4 4
例题* 两人各执长为l 的绳的一端,以相同的角 频率和振幅在绳上激起振动,右端的 ]A co (t sx [l)]
10-5驻波(1)

二、驻波方程
x y1 A cos 2 (t )
y2 A cos 2 (t )
x
y y1 y2 2 A cos 2
振幅为 A 2 A cos 2
x
x
cos 2t
振动方程
前一项表明:不同 x 处质点振幅按余弦分布
四、实际的驻波形成条件
弦 线 上 驻 波 形 成 条 件
§6.驻波 / 四.实际的驻波形成条件
•形成驻波的条件: ln
n
2
当
u
u 为 的整数倍的波才能形成驻波。 2l
§6.驻波 /四.实际的驻波形成条件
u n n , n 1,2,3 2l
•两端开口管中形成驻波的条件 •形成驻波的条件: ln
§6.驻波 /四.实际的驻波形成条件
五、半波损失
为何固定端或封闭端形成波节而开口 端或自由端形成波腹?。
•自由端没有 半波损失 •固定端有半 波损失,相 位跃变
§6.驻波 / 五 四.半波损失
波在媒质分界面上反射时:
1
2
用 Z1 1u1 和Z 2 2u2 分别表示两媒 质的特性阻抗。两种媒质比较,Z 值较大的 称为波密媒质,Z 值较小的称为波疏媒质。
2、相位特点
y 2 A cos 2 cos 2t x cos 2 0 相位为 2t
x
x
cos 2
0
相位为
2t
把相邻两波节之间的各点叫一段
波节两侧的振动相位 相反。 两波节间振动相位相同
所以驻波实际上是分段振动现象,各 段作为一个整体,同步振动。
5驻波

1
•如果 •如果
2
2u2 1u1 2u2 1u1
界面处出现半波损失;则介
质1称为波疏媒质,介质2称为波密媒质。 界面处不出现半波损失;则介 质1称为波密媒质,介质2称为波疏媒质。
2.相位突变
界面处为波节时,反射波相位突变了,相当半 个波长的波程----半波损失。
11
五、弦线上驻波形成条件
§ 5.6
驻波
1
一、驻波
1.驻波的产生 驻波是两列振幅、频率和传播速率都相同的相干 波在同一直线上沿相反方向传播时波的叠加而形成的现 象。(由于其波动看起来处于静止状态,与行波相对称 为驻波。) 当一列波遇到障碍时产生的反射波与入射波叠加 可产生驻波----波形不传播。
2
二 、驻波方程
t x 正行波(入射波) y1 A cos2 T t x 负行波(反射波) y2 A cos2 T
合成波 由三角公式:
y y1 y2
cosα+cosβ=2cos[(α+β)/2]cos[ (α-β)/2]
t x t x y A cos2 A cos2 T T
t 2 A cos 2 cos 2 T
4.波节、波腹位置 ①.波节位置
波腹
x 0
2 A cos 2
2
x
(2k 1)2x (2k 1)
4
( k 0,1,2)
5
/2
波节
②.相邻波节距离
波腹
x (2k 1)
4
x k1 x k [2( k 1) 1] (2k 1) 4 4 2 x cos 2 1 ③.波腹位置
关于光波的半波损失的教学讨论

关于光波的半波损失的教学讨论
《关于光波的半波损失的教学讨论》
光波的半波损失是光学学科中的一个重要概念,它涉及到光波在传播过程中的损耗问题。
光波的半波损失是指,当光波在介质中传播时,会发生一定的损耗,使光波的能量减少,从而影响光波的传播距离。
光波的半波损失可以通过吸收、衍射、反射和折射等物理现象来解释。
其中,吸收是指光波在介质中传播时,因为介质中的分子的存在,会吸收一部分光波的能量,从而造成损失。
衍射是指光波在介质中传播时,因为介质中的分子的存在,会发生衍射现象,从而造成损失。
反射是指光波在介质中传播时,因为介质的表面质地不同,会发生反射现象,从而造成损失。
折射是指光波在介质中传播时,因为介质的密度不同,会发生折射现象,从而造成损失。
光波的半波损失可以通过量化的方法来计算,即通过测量光波在介质中传播时的衰减程度,来估算光波的半波损失。
此外,光波的半波损失也可以通过改变介质的结构来改善,从而提高光波的传播距离。
光波的半波损失是一个重要的物理概念,我们应当加强对它的认识,以便更好地理解光学学科中的其他概念和现象。
10-5驻波

12-5 驻波1、理解驻波形成的条件和特点驻波及其形成,了解驻波和行波的区别;2、理解驻波中的相位和能量,建立半波损失的概念。
重点:驻波形成的条件和特点、驻波方程的建立、驻波中的相位和能量;难点:驻波的形成,半波损失课堂讲授(MCAI教学)1个学时干涉是特定条件下波的叠加,驻波是特定条件下波的干涉。
一、驻波的产生及特征1、产生条件:两列波:(1)满足相干条件;(2)相同振幅;(3)速度相同;(5)沿同一直线相向传播相遇而产生驻波。
2、驻波的特征(1)某些点始终不动—波节,某些点振动最大—波腹。
(2)波腹、波节等间隔稳定分布(波形没有跑动)。
(3)媒质质元分段振动,各分段步调一致,振幅不同。
二、驻波方程分析1、驻波方程:设两列平面相干波沿x轴正、负向传播,在x=0处相位相同。
右行波:1cos2πνλ⎛⎫=-⎪⎝⎭xy A t左行波:x 轴上的合振动为:122cos 2cos 2ππνλ=+=x y y y A t 2、驻波的振幅 由驻波方程2cos 2cos 2ππνλ=x y A t 与时间无关的因子为振幅分布因子,与时间有关的为谐振动因子。
振幅为:2cos 2πλxA(1) 驻波的振幅沿x 轴周期变化。
(2) 波腹——振幅最大最大振幅为2A 由22cos 22πππλλ=⇒=±xxA A k 相邻两波腹间距12λ+∆=-=k k x x x 波腹处坐标:2λ=±⋅x k (k = 0,1,2,…)(3) 波节——振幅为零 由22cos 20(21)2πππλλ=⇒=±+x x A k (21)4λ=±+x k 相邻两波节的间距12λ+∆=-=k k x x x3、驻波的相位 2cos 2πνλ⎛⎫=+ ⎪⎝⎭x y A t驻波方程2cos 2cos 2ππνλ=xy A t 可写为: 2c o s 2c o s 2(c o s 20)ππνπλλ=>x x y A t 2cos 2cos(2)(cos 20)ππνππλλ=+<x xy A t驻波的相位与坐标无关,说明不象行波随位置依次落后,即驻波的相位不向前传播。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当光从折射率大的光密介质,正入射于折射率小的 光疏介质时,反射光没有半波损失。
折射光都无半波损失。
结论
• 首先可以肯定这两种半波损失的产生机理并 不相同。我们在课本中讨论的绳波,是一种 特殊的机械波,而光波是电磁波。
• 在查阅资料后,发现对于光波的半波损失需 要借助菲涅耳公式进行证明,所以它与驻波 的半波损失不同。
如上图所示前进波(发射波) 与反射波以相反方向进行。
完全匹配,将不产生反射波, 这样,在馈线里各点的电压 振幅是恒定的 .不匹配时, 在馈线里产生驻留在馈线里 的电压波形,即驻波。
我们可以引入驻波比的概念来表示阻抗的匹配情况: 驻波比(VSWR)的值的计算公式如下:
驻波比的值在1到无穷大之间。驻波比为1,表示完全匹 配;驻波比为无穷大表示全反射,完全失配。 在移动通信系统中,一般要求驻波比小于1.5,但实际应 用中VSWR应小于1.2。过大的驻波比会减小基站的覆盖 并造成系统内干扰加大,影响基站的服务性能。
• 类比水波,对于声波,假设它在一个密闭的矩形房间里传 播。考虑两堵平行的墙壁,对于恒定的波源,特定频率的 波,某些恒定的点会成为波腹和波节。在波节的点就始终 听不到这一频率的声音,而在波腹的点声音频率特别高。
• 实际上,不管声源在什么地方,只要有二个平行平面存在 ,声音最终都会在平行的二个面之间来回反射。所以,凡 是两个平行面间的距离是某些频率的半波长或半波长的整 数倍,那么,这些频率都是这个房间的驻波频率。这些频 率在空间的各点会表现出非常不同的性质。
在无线电技术中,驻波有重要的 应用。
在发射过程中要使无线电波以尽 量大的功率传输。
只有阻抗完全匹配,才能达到最 大功率传输。这在高频更重要! 发射机、传输电缆(馈线)、天 线阻抗都关系到功率的传输。驻 波比就是表示馈线与天线匹配情 形。
不匹配时,发射机发射的电波将 有一部分反射回来,在馈线中产 生反射波,反射波到达发射机, 最终产生为热量消耗掉。接收时, 也会因为不匹配,造成接收信号 不好。
对于一般家庭的矩形房间,设一对墙面距离为d,波速 按340m/s计,那么半波长频率f=0.5×340÷d。所有半 波长的整数倍频率都有驻波发生,但波腹与波节的位 置不同,而频率为半波长频率的声音驻波反映最强, 所以一般越小的房间,音响效果越差。
半波损失
• 课本在讨论固定端反射问题时,提到了半 波损失。相比于自由端,两者的差异是由 于解微分方程后初始值的待定产生的。
k 2k
2 2 2
振幅最大,这种位置称为波腹,这时质点的振幅为分 波振幅的两倍。相邻波腹的距离为λ/2。
当X满足 x (2n 1) 2 1 (2n 1) 2 1
2k
2k
4
2 2
振幅为零,这种位置称为波节。相邻波节的距离也为 λ/2。
驻波在生活中的应用
• 首先举几个生活中常见驻波的例子: • 以弦乐器的弦来说明。当拨动琴弦,产生一个波,遇到两
音响与驻波
• 现在许多人在家庭装修时都会考虑购买音响,而音响技术 中有一个最难对付的祸害--驻波。下面我们来讨论一下音 响学中的驻波。
• 声音虽然是纵波,但它与横波一样同样存在驻波现象。波 节两边的质点在某一时刻涌向波节,使波节附近成为质点 密集区,半周期后,又向两边散开,使波节附近成为质点 稀疏区,相邻节点附近质点的密集和稀疏情况正好相反。
对于矩形房间,要考虑3对驻波:
第一种轴向驻波,是最强的驻波。是由二二相对的前 后、左右、上下六个平面形成的。
第二种切向驻波,强度次之。是在相对的棱线间发生 的。
第三种为斜向驻波,作用最弱。是对角到对角。
与驻波有关的平面越多,驻波的强度就越弱,对声场 频响的影响就越小。如果是一个球体空间,驻波就不 会发生。房间各个平面都不平行,驻波也不会发生。 这就是音乐厅和电影院都建设成扇形空间的原因 。
个固定端后发生反射,形成驻波。无论是提琴还是古筝, 它的每一根弦在特定的长度和张力下,都会有自己的固有 频率。当弦以固有频率振动时,两端被固定振幅最小,但 振动方向的张力最大(波节)。中间振幅最大,但弦最松 弛,即振动张力最小(波腹)。 • 一块石头落入水中,水波向四面散开。水波碰到硬质表面 就反射回来,反射回来的幅度和相位就象是没有阻档表面 时波原来传播下去那样的形状,但被折了回来。一般情况 这二种波是无规则的叠加的,不会使波形出现异常。但当 波源到反射表面的距离等于半波长的整数倍时,情况就不 同了。我们看到了驻波。 • 此外,能量在驻波中的分布是不均匀的,振动的能量在波 节处的分布相对更为集中。
• 而在中学时我们学过,光波在界面间发生 反射时也有半波损失。
• 这两种半波损失是否相同,有何联系?
半波损失:光从光疏介质进入光密介质,光反射后有
了量值为 的位相突变,即在反射过程中损失了半个
波长的现象。
产生条件:
i n1
n1 n2
r
n2
当光从折射率小的光疏介质,正入射或掠入射于折 射率大的光密介质时,则反射光有半波损失。
对驻波与半波损失的认识
PB05000834 华奕
驻波
介质中有反向行进的两个同频率的波存在,这两个 波叠加后将产生干涉现象。不妨设弹性弦上传播着 具有相同的振幅、相反传播方向的两波,它们的运 动方程为:
y1 Acos( t kx 1) 右行波
y2 Acos( t kx 2 )
左行波
合成后,弦上的运动为
y y1 y2 2Acos(kx
合成后的波称为驻波
2
2
1
)
cos(
t
2
2
1
)
由图可以看出:
各点离平衡位置 的距离保持不变, 经过T/4,各点 位移改变符号。
于是,我们所见 的驻波与行波不 同,没有位相的 逐点不同和逐点 传播。
驻波中,振动的振幅在空间有一定的分布规律:
当X满足 x n 2 1 n 2 1
• 这已经超出力学的范围。
• 现在仅需知道结论,以后在光学中会仔细讨 论。
参考文献: 《力学》
杨维纮
中国科学技术大学出版社.2003
本篇文章纯属个人之见。在写作过程中深感自己知识浅薄,对 物理知识只知皮毛,不知深入。对许多问题心存疑惑,却无法 给出自圆其说的解答。
