五年级下册奥数小综合思维训练
小学五年级数学思维训练(奥数)《推理问题》讲解及练习题(含答案)

推理问题专题简析:解数学题,从已知条件到未知的结论,除了计算外,更重要的一个方面就是推理。
通常,我们把主要依靠推理来解的数学题称为推理问题。
推理问题中的条件繁杂交错,解题时必须根据事情的逻辑关系进行合情推理,仔细分析,寻找突破口,并且可以借助于图表,步步深入,这样才能使问题得到较快的解决。
例1有8个球编号是(1)——(8),其中有6个球一样重,另外两个球都轻1克。
为了找出这两个轻球,用天平称了3次,结果如下:第一次:(1)+(2)比(3)+(4)重;第二次:(5)+(6)比(7)+(8)轻;第三次:(1)+(3)+(5)与(2)+(4)+(8)一样重。
那么,两个轻球分别是几号?分析与解答从第一次看,(3)、(4)两球中有一个轻;从第二次看,(5)、(6)两球中有一个轻;从第三次看,(1)、(3)、(5)中有一个轻,(2)、(4)、(8)中也有一个轻。
综合上面的分析可以推出,两个轻球的编号分别是(4)和(5)。
随堂练习:1,甲、乙、丙、丁四个人中,乙不是最高,但他比甲和丁高,而甲不比丁高。
请说出他们各是几号。
2,某商品编号是一个三位数,现有五个三位数:874,756,123,364,925,其中每一个数与商品编号恰好在同一个数位上有一个相同数字。
这个商品的编号是多少?例2一个正方体6个面上分别写着1、2、3、4、5、6。
根据下图摆放的三种情况,判断每个数字对面上的数字是几。
分析与解答如果直接思考哪个数字的对面是几,有一定的困难。
我们可以这样想:这个数字的对面不会是几。
(1)从(A)、(B)两种摆法中可以看出:4的对面不会是2、5,也不会是1、6,那么,4对面一定是3;(2)从(B)、(C)两种摆法中可以看出:1的对面不会是4、6,也不会是2、3,那么,1的对面一定是5;(3)剩下2的对面一定是6。
随堂练习:1,一个正方体的6个面分别涂着红、黄、白、黑、绿六种颜色,根据下面的三种摆法,判断哪种颜色的对面涂着哪种颜色。
五六年级奥数思维训练100题

五六年级奥数思维训练100题姓名:__________ 班级:__________ 得分:__________ 一、计算问题(15 题)1.25.6×4.2×0.252.2999+999×9993.(3.6×6+4×5)÷(6+5)4.1002×998-998×9975.4.8×(3.2÷0.6)6.890×102-8907.(5.5×8+3.5×6)÷(8+6)8.1345×8+1345 9.3.5×(4.8÷1.6)10.990×90+9011.18.5×3.6×0.12512.3999+999×99813.(4.8×7+3.2×5)÷(7+5)14.1003×997-997×99615.5.2×(4.5÷1.5)二、图形问题(15 题)16.一个平行四边形的底是 18 厘米,高是 14 厘米,求它的面积。
17.一个三角形的底是 25 厘米,高是 20 厘米,求它的面积。
18.一个梯形的上底是 10 厘米,下底是 14 厘米,高是 12 厘米,求它的面积。
19.一个正方形的边长是 15 厘米,求它的周长和面积。
20.一个长方形的长是 22 厘米,宽是 16 厘米,求它的周长和面积。
21.一个圆形的半径是 8 厘米,求它的周长和面积。
22.一个等腰梯形的上底是 8 厘米,下底是 12 厘米,高是 10 厘米,求它的面积。
23.一个直角三角形的两条直角边分别是 12 厘米和 16 厘米,求它的面积。
24.一个长方体的长、宽、高分别是 10 厘米、8 厘米、6 厘米,求它的表面积和体积。
25.一个正方体的棱长是 12 厘米,求它的表面积和体积。
五年级下册奥数思维训练:数列与数表综合 全国通用 (砍柴篇)

分数数列(★★★★)有这样一串分数:11,12,22,12,13,23,33,23,13,14,24…那么,⑴第一次出现的8998是这一串分数中的第几个分数? ⑵第500个分数是几分之几? (★★★)已知一串有规律的数:1,23,58,1321,3455那么,在这串数中,从左往右数,第10个数是多少?例1数 列 与 数 表 综 合例2(砍柴篇)数表(★★★★)如图,数阵中的数是按一定规律排列的,请问:⑴100在第几行、第几列?⑵第20行第3列的数是多少?(★★★)如果把一些自然数按下表进行排列,那么数1000应在哪个字母下面?例3例4例5(★★★★★)自然数每9个数一行进行排列,现在用2×3的小方框围出6个数,然后算出它们的和.如图,可以横着围或竖着围.若某个方框围出的6个数之和为567,那么其中最大的数为______.例6(★★★★★)如图,数表中的数字是按照一定的规律排列顺序的,那么这个数表中第50行最左边的数应该是_______.(★★★★)如图,从1开始的自然数按某种方式排列起来,请问:⑴100在第几行?100是这一行左起第几个数?⑵第25行左起第5个数是多少?例7期中考试考试时间:90分钟满分:120分(说明:本套试卷,共12题.难度和重要程度均没有大的区别,每道题都是10分)1.一个等比数列,第1项是7,第3项是175,那么第4项是________.2.计算:1111 248 (1024)2481024++++.3.(第七届“小机灵杯”数学竞赛五年级复赛)8点________分的时候,分针与时针第一次形成75︒角.4.(2007年四中分班考试真题)如图,假设某星球的一天只有6小时,每小时36分钟,那么3点18分时,时针和分针所形成的锐角是________度.5.(四中小升初选拔试题)被除数、除数、商与余数之和是2143,已知商是33,余数是52,求被除数和除数. 6.(全国小学数学奥林匹克试题)用自然数n去除63,91,129得到的三个余数之和为25,那么n=________.7.求24611356047⨯⨯除以11的余数.8.甲、乙两港之间的水路是234千米,一只船从甲港到乙港需9小时,从乙港返回甲港需13小时,问船速和水速各为多少?9.某船在静水中的速度是每小时15千米,它从上游甲地开往下游乙地共花去了8小时,水速每小时3千米,问从乙地返回甲地需要多少时间?10.有一列数:2,3,6,8,8,….从第三个数起,每个数都是前两个数乘积的个位数字,那么这一列数中的第100个数是________;11.如图所示的数表中,从左往右依次看作五列.⑴第99行右边第一个数是________;⑵2006出现在第________行,第________列;12.如图,把从1开始的自然数排成数阵.试问:能否在数阵中放入一个3×3的方框,使得它围住的几个数之和等于:⑴1997;⑵2016;⑶2349.如果可以,请写出方框中最大的数.0 2 4 12 10 8 614 16 18 26 24 22 20……答 案1.【分析】先算公比231255a q q a ⇒===,那么41755875a ⨯==. 2.【分析】把算式的整数部分和分数部分分开:()1111248102424810241023204821024102320461024⎛⎫ ⎪⎝⎭原式=+++++++++=-+=3.【分析】分针每分钟走1格,时针每分钟走112格.当它们成75︒角时,中间相差7525603602⨯=(格),需要追赶25554022-=(格).需要时间为551(1)30212÷-=(分钟).4.【分析】分针速度为:10°/分钟;时针速度为:53o/分钟;3点时分针与时针成180°,18分钟后分针追上时针518101503⎛⎫⨯ ⎪⎝⎭-=°所以此时,分针与时针所成的锐角为30°.5.【分析】(法1)被除数2143=-除数-商-余数2143=-除数3352--2058=-除数,被除数=除数⨯商+余数,所以除数33522058⨯+=-除数, 则除数(205852)3459=-÷=,被除数2058591999=-=.(法2)从被除数中减掉余数52后,被除数就是除数的33倍,所以可以得到:2143335252(331)---=+⨯除数,求得除数59=,被除数 3359521999⨯=+=.6.【分析】n 能整除639112925258++-=.因为25381÷=,所以n 是258大于8的约数.显然,n 不能大于63.符合条件的只有43.7.【分析】因为2461112238÷=,13511123÷=,6047115498÷=,根据余数性质⑤,2461135604711⨯⨯÷的余数等于83811⨯⨯÷的余数,而838192⨯⨯=,19211175÷=,所以2461135604711⨯⨯÷的余数为5.8.【分析】从甲到乙顺水速度:234926÷=(千米/时),从乙到甲逆水速度:2341318÷=(千米/时),船速是:(2618)222+÷=(千米/时),水速是:(2618)24-÷=(千米/时).9.【分析】从甲地到乙地的顺水速度为15318+=(千米/时),甲、乙两地路程为188144⨯=(千米),从乙地到甲地的逆水速度为15312-=(千米/时),返回所需要的时间为1441212÷=(小时).10.【分析】周期问题,先找出周期.2,3,6,8,8,4,2,8,6,8,8…6位一循环.()10026162-÷=,那么第100个数是循环中的第2个.第100个数是8.11.【分析】⑴首先观察规律.数表里面出现的是从0开始的连续偶数;每两行中有7个数,其中第1行有3个数,从小到大排在第3,4,5号位置;第2行有4个数,从大到小排在第1,2,3,4号位置.那么前98行中有7982343⨯÷=个数,其中第343个数是()34312684-⨯=.第99行最右边的数是该行的第3个数,它是:6846690+=.⑵2006是第2006211004÷+=个数.100471433÷=,那么第1004个数在第14321287⨯+=行的第3个数,那么就是第287行的第5列.12.【分析】左上角的数为:123891015161781++++++++=.由于每向右移动一位,即增加9,最多可向右移动4次,向下移动一位可增加63. 由于:⑴()1997811916,1916633026-=÷=, 不是9的倍数;⑵()2016811935,1935633045-=÷=,无法向右移动5次;⑶()2349812268,22686336-=÷=;所以,只有2349是可以的,应向下移动36次, 所以最大的数为:73617269⨯+=.。
五年级下册奥数思维训练:问题解决 全国通用
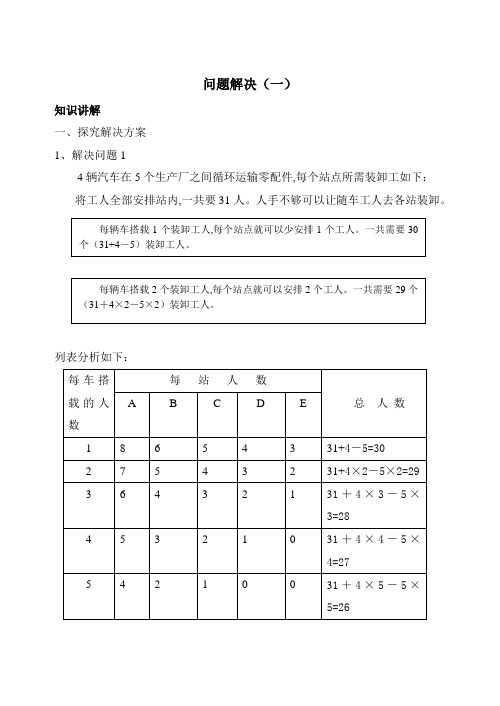
问题解决(一)知识讲解一、探究解决方案1、解决问题14辆汽车在5个生产厂之间循环运输零配件,每个站点所需装卸工如下:将工人全部安排站内,一共要31人。
人手不够可以让随车工人去各站装卸。
列表分析如下:解决这道题的过程中,你还想到了什么?选择下面的问题或自己编出类似的问题进行研究。
并在小组内交流自己的想法。
(1)如果在线路上增加一个需要10名装卸工人的站点,车的辆数保持不变,最少需要多少名工人。
(2)如果线路上的站点不变,车的辆数减少1辆,最少需要多少名工人? 学生互相讨论、交流出示交流结果,并说出解题思路。
2、模仿练习五辆汽车在7个站点之间循环运输,每个站点所需装卸工人如图所示。
怎样安排可以使运输工人人数最少?最少需要多少人?A B CGFE D 3、解决问题2AB 两地相距4a 千米,中间是荒无人烟的戈壁,只有一条公路连接,现有50辆卡车要从A 地到B 地,然后再返回A 地,已知卡车自身携带的汽油只能走3a 千米,为完成任务配备了运油车(耗油量与卡车相同),保证供油。
运油车一次● ● ● ●●●能运送一辆卡车行150a千米的汽车。
请你设计一个方案,用若干辆运油车保证任务完成?解题方案:卡车自身携带的汽油可以行3a千米,卡车从A地到B地,然后再返回A地,一共需要行8a千米的汽油,还需要性5a千米的汽油,50辆卡车一共需要行5a×50=250a千米的汽油。
要使整个任务的耗油量最少,必须使运油车的耗油量最少;要使运油车的耗油量最少,必须使运油车行尽可能少的路,尽可能利用卡车的载油量,使加油地点到B地往返的距离等于3a,因此加油地点在离B地1.5a处。
运油车携带能行150a千米的汽车,运到从A地到B地2.5a千米处停下,它为维持自身往返需要行5a千米的汽油,能为卡车提供145a千米的汽油。
一共需要行250a千米的汽油,因此,至少需要2辆运油车:一辆满载,另一辆至少载行250a -145a+5a=110a千米汽油。
五年级下册奥数思维训练:竞赛试题三 全国通用

(希望杯5年级2试第8题)如果一个自然数的各位数字中有偶数个偶数,则称之为“希望数”.例如,26,201,533是希望数,8,36,208不是希望数,那么,把所有的希望数从小到大排列,第2010个希望数是_______.(希望杯)一艘客轮在静水中的航行速度是26千米/时.往返于A 、B 两港之间,河水的流速是6千米/时,如果客轮在河中往返4趟共用13小时,那么A 、B 两港之间相距 ____千米.(客轮掉头时间不计)例1竞 赛 例2(希望 杯)试 题选 编 一例3(希望杯5年级1试)夜里下了一场大雪,早上,小龙和爸爸一起步测花园里一条环形小路的长度,他们从同一点同向行走,小龙每步长54厘米,爸爸每步长72厘米,两人各走完一圈后又都回到出发点,这时雪地上只留下60个脚印.那么这条小路长____米.例4(希望杯5年级1试)有三个自然数a,b,c,已知b除以a,得商3余3;c除以a,得商9余11.则c除以b,得到的余数是_______.例5(希望杯六年级二试)某小学的六年级有一百多名学生,若按三人一行排队,则多出一人;若按五人一行排队,则多出二人;若按七人一行排队,则多出一人.该年级的人数是_____.例6(希望杯六年级二试)如图,三角形ABC和三角形DEC都是等腰三角形,A和E是直角顶点,阴影部分是正方形.如果三角形DEC的面积是24平方米,那么三角形ABC的面积是______平方米.例7(希望杯五年级二试)如图7,梯形ABCD与正方形DEFC拼在一起,AF与DE交于点G.已知BC=CD=4,三角形AGD的面积是三角形DGF面积的2倍.⑴求梯形ABCD的面积;⑵比较三角形GEF和三角形AGD的面积大小.例8(希望杯五年级二试第7题)如图,棱长分别为1厘米、2厘米、3厘米、5厘米的四个正方体紧贴在一起,则所得到的多面体的表面积是_____平方厘米.例9(希望杯六年级二试)如图,已知长方形长是宽的2倍,对角线的长是9,则长方形的面积是_______.例10(希望杯6年级2试)两个顽皮的孩子逆着自动扶梯行驶的方向行走,从扶梯的一端到达另一端,男孩走了100秒,女孩走了300秒.已知在电梯静止时,男孩每秒走3米,女孩每秒走2米,则该自动扶梯长_____米.。
五年级下册数学奥数试题 思维训练综合卷(3) 全国通用

五年级奥数阶段检测卷(3)姓名一、计算(5分×2)1、7.8×10.1-0.782、2005×20062006-2004×20052005二、应用题(10分×14)1、甲、乙两人一共有269.5元,甲的钱数的小数点向右移动一位,他的钱数就和乙的钱数相等。
甲、乙各有钱多少元?2、两个数相除,商39余58,如果被除数、除数、商及余数相加,和是3275,求被除数和除数?3、3筐苹果和5筐梨共重138千克,9筐同样的苹果和4筐同样的梨共重216千克,每筐苹果和梨各重多少?4、甲有5盒糖,乙有4盒糕共值22元,如果甲乙两人对换一盒,则每人所有的物品价钱相等,求一盒糖,一盒糕分别值多少钱?5、小刚从家到学校,去时每分钟走40米,回来时每分钟走60米,小刚往返的平均速度是多少?6、某校安排学生住宿,若每间6人,则有20人没位置,若每间住8人,则空出一间半宿舍,求宿舍几间?学生几人?7、站在桥上用绳子测桥的高度,把绳子对折垂到水面尚余3米,把绳子三折后垂到水面,尚余1米,求桥的高度和绳长?8、小明读书,第一天读83页,第二天读74页,第三天读71页,第四天读64页,第五天读的页数比五天中平均读的页数还多3.2页,小明第五天读了多少页?9、5头牛,6匹马,2只羊每天吃草143千克;6头牛,5匹马,4只羊每天吃草133千克;3头牛,2匹马,1只羊每天吃草55千克,求1头牛,1匹马,1只羊每天各吃草多少千克?10、某校招生考试,所有考生的平均分是65分,从考生中录取了15,这些学生的平均分比录取分数线高9分,其他没被录取的学生的平均分比录取分数线低21分,那么录取分数线是多少分?11、有4个数,每次选取其中3个数,算出它们的平均数,再加上另外一个数,用这样的方法计算了4次,分别得到以下四个数:26、30、36、40,那么原来四个数分别是多少?12、小红早上步行去上学,她以每分钟60米的速度先走了2分钟,然后发现,如果照这个速度走下去,要迟到5分钟;如果每分钟多走15米,则可提前2分钟到校。
小学五年级数学思维训练(奥数)《长方体和正方体巧算表面积》讲解及练习题(含答案)
长方体和正方体巧算表面积专题简析:学了长方体和正方体后,同学们都只知道,长方体和正方体都有6个面,长方体相对的两个面的大小、形状完全一样,正方体6个面的大小、形状都完全一样。
例1 两个棱长是2厘米的小正方体可以拼成一个长方体,这个长方体的表面积是多少?分析与解答先根据题意画图:从图上可以清楚地看出:两个正方体原先各有6个正方形的面,当把它们拼起来时就少了2个正方形的面。
这时,求长方体的表面积只相当于求(12-2=)10个正方形的面积;还可以这样想:当两个正方体拼成一个长方体时,求长方体的表面积,我们可以先分别求出这个长方体的长、宽、高,再求出它的表面积。
方法总结:1.当物体拼合时表面积之和少了,可以根据用原来的面去掉减少了的面,从而求出拼合后物体的面积数量,然后求出表面积。
2.还可以求出拼成后大物体的长、宽、高,再根据物体形状直接求表面积。
随堂练习:把底面积是36平方厘米的两个正方体木块拼成一个长方体,长方体的表面积是多少?例2把一个长、宽、高分别是7厘米、6厘米、5厘米的长方体截成两个长方体,使这两个长方体表面积之和最大,这时表面积之和是多少平方厘米?分析与解答:把长方体截成两个长方体后,两个长方体表面积之和等于原长方体表面积再加上两个截面的面积。
这个长方体几个面中,上、下面的面积最大,所以要看哪个面的面积最大,于是本题就按平行于上、下面的方式去截,才使表面积之和最大。
方法总结:长方体截成两个长方体有三种截法,如图:随堂练习:把两个长3厘米、宽2厘米、高1厘米的长方体拼成一个表面积最大的长方体,这个长方体的表面积是多少平方厘米?例3求出下面立体图形的表面积。
(单位:厘米)分析与解答:从图上看出,这个图形是由一个长方体和一个正方体组成的,求它的表面积时,可以把正方体的右侧面平移到长方体上,这方体的上、下、前、后四个面的面积。
随堂练习:1.在一个棱长为5分米的正方体上放一个棱长为4分米的小正方体(如图),求这个立体图形的表面积。
小学生奥数思维训练及答案
小学生奥数思维训练及答案奥数(即奥林匹克数学竞赛)是许多小学生参与的一种数学比赛,它旨在培养学生的数学思维和解题能力。
在这里,我们将讨论一些奥数思维训练的方法,并提供一些答案以帮助小学生更好地应对这种竞赛。
一、理解问题在参加奥数比赛时,理解问题是解题的第一步。
许多竞赛问题都有一定的难度,所以正确理解问题是至关重要的。
以下是一些训练学生理解问题的方法:1. 仔细阅读问题:在阅读问题时,学生应该将注意力集中在每个细节上。
他们应该注意问题中给出的条件、要求和约束。
如果可能,学生可以在问题旁边做一些标记,以便更好地理解。
2. 弄清问题的关键点:学生应该确定问题中关键的信息和目标。
他们可以用自己的话来概括问题,以确保完全理解。
3. 解析问题:通过解析问题,学生可以从中提取有用的信息并排除不必要的内容。
他们可以使用图表、图像或其他方法来帮助他们组织思维。
二、解决问题解答奥数问题需要一定的技巧和策略。
以下是一些帮助学生解决问题的方法:1. 建立数学模型:将问题抽象为数学模型是解决问题的关键。
学生应该将问题转化为适当的数学形式,例如方程式、不等式等。
这样可以使问题更具结构性,更容易应用数学知识来解决。
2. 使用已学数学知识:奥数问题往往需要学生运用已学的数学知识来解决。
学生应该根据问题的要求来运用所学的数学概念、公式和定理。
他们也可以参考课本或在线资源以获得更多的知识。
3. 尝试不同的解题方法:对于复杂的问题,学生可以尝试不同的解题方法。
有时候,直接计算可能不是最有效的方法,使用逆向思维或试错法可能更加高效。
三、示例答案这里给出两个奥数问题的示例及其答案:问题1:某班级有30名学生,男生所占比例为3:7,女生有多少名字?解答1:设男生有3x人,女生有7x人。
根据题目条件,3x + 7x = 30,求解得到x = 3。
因此,女生共有7x = 7 * 3 = 21名。
问题2:从1到100的所有整数中,有多少个整数的个位数字是5?解答2:一共有10个个位数,分别是0, 1, 2, 3, 4, 5, 6, 7, 8, 9。
【精品奥数】五年级下册数学思维训练讲义-第二讲 盈亏问题 人教版(含答案)
第2讲盈亏问题第一部分:趣味数学盈亏问题《九章算术》第七章介绍了盈亏问题,这一类问题是把一定数量的物品平均分给若干对象,每个对象少分,则物品有余;如果每个对象多分,则物品不足。
所以分物时经常出现盈(有余)、亏(不足)、尽(恰好分完)的情况,所以古人把这类问题称为盈不足问题。
盈亏问题情况多样,解法巧妙,倍受古人重视,在许多古代算书上留下了不少好题。
下面选取其中的一个给同学欣赏:题目今有人共买物,人出八,盈三;人出七,不足四,问人数,物价各几何?题意:有一群人凑钱买一件物品。
如果每人出8枚钱币,就比物价多出3个钱币。
如果每人出7枚钱币,就比物价少4个钱币。
求人数和钱数各是多少?分析:这是属于“一盈一亏”类的问题。
当第一次每人出8枚钱币时多3枚,当第二次每人出7枚钱币时不但不多,还要少4枚,即第二次比第一次共少了4+3=7枚。
这是由于第二次比第一次每人少出了8-7=1枚钱币。
相差7枚,就说明有7÷1=7人。
这样物价也就可以算出来了。
解答:4+3=7(枚)8-7=1(枚)7÷1=7(人)7×8 – 3 = 53(枚)答:一共有7人,物价为53枚。
事实上,古代数学家发现,在计算人数(即分物对象的个数)时,还有一个简单易记、琅琅上口的口诀:“有余加不足,大减小来除”。
这种算法的绝妙之处在于它几乎可以不动脑筋,只要把几个数按口诀对号入座,马上可以得出答案。
同学们如果你学会了,有兴趣就试试下面这个题目吧!钱几何今有散钱不知其数,作七十七陌穿之,欠五十凑穿;第二部分:奥数小练盈亏问题的基本数量关系是:(盈+亏)÷两次所分之差=人数;还有一些非标准的盈亏问题,它们被分为四类:1.两盈:两次分配都有多余;2.两不足:两次分配都不够;3.盈适足:一次分配有余,一次分配够分;4,不足适足:一次分配不够,一次分配正好。
一些非标准的盈亏问题都是由标准的盈亏问题演变过来的。
解题时我们可以记住:1.“两亏”问题的数量关系是:两次亏数的差÷两次分得的差=参与分配对象总数;2.“两盈”问题的数量关系是:两次盈数的差÷两次分得的差=参与分配对象总数;3.“一盈一亏”问题的数量关系是:盈与亏的和÷两次分得的差=参与分配对象总数。
小学五年级奥数思维训练全集
小学五年级奥数思维训练全集第一周平均数(一)专题简析:把几个不相等的数,在总数不变的条件下,通过移多补少,使它们完全相等,求得的相等的数就是平均数。
平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:有4箱水果,已知苹果、梨、橘子平均每箱42个,梨、橘子、桃平均每箱36个,苹果和桃平均每箱37个。
一箱苹果多少个?分析:①:1箱苹果+1箱梨+1箱橘子=42×3=136(个);②:1箱桃+1箱梨+1箱橘子=36×3=108(个)③:1箱苹果+1箱桃=37×2=74(个)由①、②可知:1箱苹果比1箱桃多126-108=18(个),再根据等式③,用和差关系求出:1箱桃有(74-18)÷2=28(个),1箱苹果有28+18=46(个).试一试1:甲、乙、丙、丁四人称体重,乙、丙、丁三人共重120千克,甲、丙、丁三人共重126千克,丙、丁二人的平均体重是40千克。
求四人的平均体重是多少千克?例2:某3个数的平均数是2,如果把其中一个数改为4,平均数就变成了3。
被改的数原来是多少?分析:原来三个数的和是2×3=6,后来三个数的和是3×3=9,9比6多出了3,是因为把那个数改成了4。
因此,原来的数应该是4-3=1.试一试2:有五个数,平均数是9.如果把其中的一个数改为1,那么这五个数的平均数为8.这个改动的数原来是多少?例3:五一班同学数学考试平均成绩91。
5分,事后复查发现计算成绩时将一位同学的98分误作89分计算了。
经重新计算,全班的平均成绩是91。
7分,五一班有多少名同学?分析:98分比89分多9分。
多算9分就能使全班平均每人的成绩上升91。
7-91。
5=0。
2(分)。
9里面包含有几个0。
2,五一班就有几名同学。
试一试3:某班的一次测验,平均成绩是91.3分。
复查时发现把张静的89分误看作97分计算,经重新计算,该班平均成绩是91.1分.全班有多少同学?专题二平均数(二)专题简析:平均数=总数量÷总份数总数量=平均数×总份数总份数=总数量×平均数例1:小明前几次数学测验的平均成绩是84分,这次要考100分,才能把平均成绩提高到86分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
______________________________________________________________________________________________________________ 精品资料 五年级下册奥数小综合思维训练(1)
(找 规 律、包含与排除) 1:18÷11的商的小数点后面第2008位数字是几?
2:有一列数字402140214021……问第31个数字是多少?前面30个数字的和是多少? 3、17÷6的商的小数点后第123位和第124位上的数字的和是多少? 4、5÷7的商的小数部分后面第100位上的数字是几? 5、13.258小数部分第1000位上的数字是几?小数点后面前300个数字的和是多少? 6、不用计算,直接写得数 1÷7=0.142857142857…… 2÷7=0.285714285714…… 3÷7=0.428571428571…… 4÷7= 5÷7= 6÷7=
7、23÷7的商的小数点后面2000个数字之和是多少?
8、15÷52的商的小数点右边第200个数字是多少?小数点后面前200个数字的和是多少? 9、9÷7的商的小数点后第2005位数字是几? 10、18÷13的商的小数点后第2010位的数字是几? 11:五年级有96名学生都订了刊物,有64人订了少年报,有48人订了小学生报,问两种刊物都订的有多少人? 12:学校开展课外活动,共有250人参加,其中参加象棋组和乒乓球组的同学不同时活动,参加象棋组的有83人,参加乒乓球组的有86人,这两个小组都参加的有25人,问250名同学中,象棋组、乒乓球组都不参加的有多少人?
13、一个班的52人都在做语文和数学作业,有32人做完了语文作业,有35人做完了数学作业。这个班语文,数学作业都做完的有多少人?
14、某班有50名学生,在一次测验中有26人满分,在第二次测验中有21人满分。如果两次测验都没有过满分的学生有17人,那么两次测验都获满分的有多少人?
15、某班的在一次测验中有26人语文获优,有30人数学获优。其中语,数双优的有12人,另外还有8人语,数均未获优。这个班共有多少个学生? ______________________________________________________________________________________________________________ 精品资料 16、第一小组的同学们都在做两道数学思考题,做对第一题的有15人,做对第二题的有10人,两道题都做对的有7人,两道题都做错的有2人,第一小组共有多少人?
17、有122名同学参加语文,数学考试,每人至少有一门得优,已知语文65人得优,数学78人得优,求只有语文一门得优的有多少人?
18、在100位旅客中,有70人懂英语,65人懂日语,既懂英语又懂日语的有45人,那么,既不懂英语又不懂日语的有多少人?
19、老师在统计考试成绩,数学得分90分以上的有25人,语文得90分以上的有21人,两科中有一科的在90分以上有38人,问:两样都得90分以上的有多少人?
20、少年乐团学生中有170人不是五年级的,有135人不是六年级的,已知五,六年级的共有205人,小年乐团中,五,六年级以外的学生共有多少人? ______________________________________________________________________________________________________________
精品资料 五年级下册奥数小综合思维训练(2) (长方体和正方体、解决问题、分解质因数) 1:在一个长15分米,宽12分米的长方体水箱中,有10分米深的水。如果在水中沉入一个棱长为10厘米的正方体铁块,那么,水箱中水深多少分米? 2:一个长方体棱长的总和是48厘米,已知长是宽的1.5倍,宽是高的2倍,求这个长方体的体积。 3:有一个棱长是3厘米的正方体,先从它的每个顶点处挖去一个棱长是1厘米的小正方体,再在它每个面的中央粘上一个棱长是1厘米的小正方体。所得物体的表面积是多少平方厘米?体积是多少立方厘米? 5、18个边长为2厘米的小正方体堆成如图的形状, 求它的表面积。 6、把8个同样大小的小正方体拼成一个大正方体。已知小正方体的表面积是150平方厘米,大正方体的表面积是多少平方厘米?
7、图中A的面积是25平方米,B的面积是15平方米,h是4米。现在把A处的土堆到B处,使A、B两处同样高,这时B处比原来升高了多少米?
8、在一个棱长为2厘米的正方体上面的正中间向下挖一个棱长 为1厘米的正方体小洞,接着在小洞的底面再向下挖一个棱长为0.5厘米的小洞。第三个小洞的棱长为0.25厘米挖法与前两个小洞的挖法相同。现在这个立方体图形的表面积是多少?
9、用2100个棱长是1厘米的正方体木块堆成一个实心的长方体。已知长方体的高是
A B h ______________________________________________________________________________________________________________
精品资料 10厘米,并且长和宽都大于高。这个长方体的长和宽各是多少厘米? 10、在一个长20分米,宽15分米的长方体容器中,有20分米深的水。现在在水中沉入一个棱长20厘米的正方体铁块,这时容器中水深多少分米? 11、把一个长9厘米,宽7厘米,高3厘米的长方体铁块和一块棱长5厘米的正方体铁块熔铸成一个底面积是20平方厘米的长方体。求这个长方体的高。 12、有一块长方形的铁皮,长32厘米。在这块铁皮的四角各剪下一个边长为4厘米的小正方形,然后制成一个无盖的长方体盒子。已知这个盒子的容积是768厘米,求原来长方形铁皮的面积。 13:一个长方体玻璃缸,长8分米,宽6分米,高4分米,玻璃缸内水深2.8分米。把一块棱长为4分米的正方体铁块放入玻璃缸内后,水会溢出多少升?
14把一个底面积为正方形且边长是3分米,高是5分米的长方体石料尽量加工为体积最大的正方体,那么凿去的石料体积是多少立方分米?(不计损耗)
15、一个长方体的玻璃缸,最多可装水120升,已知玻璃缸里面长6分米,宽4分米,现有水深3分米。如果在玻璃缸内放入体积为15立方分米的玻璃球,里面的水会不会溢出,为什么?
16、一个棱长8分米的正方体水槽里装了490升水,把这些水倒入一个长10分米,宽7分米,高8分米的长方体水槽里,水槽里的水深是多少?
17、把一块棱长8厘米的正方体钢坯,锻造成长16厘米,宽5厘米的长方体钢板,这钢______________________________________________________________________________________________________________
精品资料 板有多厚?(损耗不计) 18、 一个长方体油桶,底面积是18平方分米,它可装43.2千克油,如果每升油重0.8千克,油桶内油高是多少? 19、 一个长方形铁皮长30cm,宽25cm,从四个角各切掉一个长为5cm的正方形,然后做成一个无盖的盒子,这个盒子用了多少铁皮?它的容积是多少? 20、把一块长26dm的长方形木板,在四个角上分别剪去边长为3dm的正方形,将它制成容积为840立方分米的长方体无盖容器,这块木板原来的宽是多少? 21、一个长方体游泳池长60米,宽30米,深2米,游泳池占地多少平方米?沿游泳池的内壁1.5米处用红漆划一条水位线,这条线的长度是多少?现在游泳池内的水正好到达水位线,求池内水的体积?
22、 一个长方体玻璃缸,从里面量长40厘米,宽25厘米,水深12厘米,把一块石头浸入水中后,水面上升到16厘米,求石块的体积?
23:李老师带领一班学生去植树,学生恰好分成4组,如果老师和每个学生植树棵数一样多,那么他们共植树539棵。这个班共有多少名学生?每人植多少颗树?
24:把40,44,45,63,65,78,99,105这8个数字分成两组,使这两组4个数的乘积相等。
25、下面的算式里“□”里的数字各不相同,求这四个数字之和 □□×□□=1995 ______________________________________________________________________________________________________________ 精品资料 25、3月12日是植树节,李老师带领同学排成两路人数相等的纵队去植树。已知李老师和同学们每人植树的棵数相等,一共植了111棵。叁加植树的同学有多少名? 26、王老师和同学们去植树,全班同学刚好可以平均分成4个小组。如果老师与学生每人植树的棵数相等,一共植了520棵,参加植树的一共有多少个学生?平均每人植多少棵? 27、有三个学生,他们的年龄一个比一个大3岁,他们三人年龄的乘积是1620,这三个学生的年龄和是多少? 28、将下面八个数分成两组,使这两组数的乘积相等 2、5、14、24、27、55、56、99
29、把30、33、42、52、65、66、77、78、105九个数字分为三组,使每组数的乘积相等。
30、将0.09、0.15、0.3、0.34、0.28、0.77、0.55、0.85八个数分成两组,使这两组数的乘积相等。
31、将下面8个数分成个数相等的两组,怎样分才能保证两组数的乘积相等? 1.4、0.33、0.35、16.9、14.3、0.75、0.39、0.3
