甘肃省张掖市高三数学一轮学案 模块1 函数与导数 第16讲 函数与方程 新人教A版
2020年高考数学一轮复习精品学案(人教版a版)函数概念与表示

2020年高考数学一轮复习精品学案(人教版a版)函数概念与表示――函数概念与表示一.【课标要求】1.通过丰富实例,进一步体会函数是描述变量之间的依靠关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念;2.在实际情境中,会依照不同的需要选择恰当的方法〔如图象法、列表法、解析法〕表示函数;3.通过具体实例,了解简单的分段函数,并能简单应用;4.通过已学过的函数专门是二次函数,明白得函数的单调性、最大〔小〕值及其几何意义;结合具体函数,了解奇偶性的含义;5.学会运用函数图象明白得和研究函数的性质二.【命题走向】函数是整个高中数学的重点,其中函数思想是最重要的数学思想方法,函数咨询题在历年的高考中都占据相当大的比例。
从近几年来看,对本部分内容的考察形势稳中求变,向着更灵活的的方向进展,关于函数的概念及表示多以下面的形式显现:通过具体咨询题〔几何咨询题、实际应用题〕找出变量间的函数关系,再求出函数的定义域、值域,进而研究函数性质,寻求咨询题的结果。
高考对函数概念与表示考察是以选择或填空为主,以解答题形式显现的可能性相对较小,本节知识作为工具和其他知识结合起来命题的可能性依旧专门大推测2018年高考对本节的考察是:1.题型是1个选择和一个填空;2.热点是函数概念及函数的工具作用,以中等难度、题型新颖的试题综合考察函数成为新的热点。
三.【要点精讲】1.函数的概念:设A、B是非空的数集,假如按照某个确定的对应关系f,使关于集合A中的任意一个数x,在集合B中都有唯独确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B 的一个函数。
记作:y=f(x),x∈A。
其中,x叫做自变量,x的取值范畴A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域。
甘肃省张掖市2013届高三数学一轮学案 模块1 函数与导数 第12讲 指数式与对数式 新人教A版

第十二讲 指数式与对数式一、知识梳理(1)指数与指数幂的运算:1.一般地,如果a x n=,那么x 叫做a 的n 次方根。
其中+∈>N n n ,1.2.当n 为奇数时,a a n n=;当n 为偶数时,aa nn =.3.我们规定: ⑴m n mna a =()1,,,0*>∈>m N n m a ; ⑵()01>=-n a a n n ;4.运算性质:⑴()Q s r a a a a s r s r ∈>=+,,0;⑵()()Q s r a a a rs sr∈>=,,0;⑶()()Q r b a b a ab r r r∈>>=,0,0(2)对数与对数运算: 1、xN N a a x =⇔=log ; 2、a aNa =log . 3、01log =a ,1log =a a .4、当0,0,1,0>>≠>N M a a 时:(1)()N M MN a a a log log log +=;(2)N M N Ma a a log log log -=⎪⎭⎫⎝⎛;(3)Mn M a n a log log =.5.换底公式:abb c c a log log log =()0,1,0,1,0>≠>≠>b c c a a .6.a b b a log 1log =()1,0,1,0≠>≠>b b a a二、同步练习1.下列运算正确的是 ( ) A (-a2)3=(-a3)2 B (-a2)3=-a2+3 C (-a2)3=a2+3 D (-a2)3=-a62.3334)21()21()2()2(---+-+---的值是 ( )A -24B -8 C437D 83.已知xx 2121-+=5,则x x 12+的值是 ( )A 5B 23C 25D 274.下列各式中成立的是 ( )A322n m +=)(32n m + Bba ab 5515)(=C2)2(2-=- D31324=5.a>0,下列各式中不成立的是 ( )Aanm nm a =Baanm nm 1=-Can a n nnnnna ===)()(1 D2)(nm nm aa=-6.化简ab b a ab b a 342141223)(3(a ,b>0)的结果是 ( )A a bB abC b aD a2b 7.设25a bm ==,且112a b +=,则m =( )AB .10C .20D .100 8.2log 的值为( )A. BC .12-D . 129.设指数函数()(0,1)xf x a a a =>≠,则下列等式不正确的是( ) A . f(x+y)=f(x)f(y) B . f((xy)n)=()()n nf x f y C. ()()()f x f x y f y -=D .()()n f nx f x =10. 下列等式成立的是( ).A .log2(8-4)=log28-log24B .log28log24=log284 C .log28=3log22 D .log2(8+4)=log28+log24 11. 设a ,b ,c 都是正数,且3a=4b=6c ,那么正确的选项是 ( )A .b a c 111+=B .b a c 122+= C .b a c 221+= D .b ac 212+= 12.已知2lg(x -2y)=lgx+lgy ,则y x的值为( )A .1B .4C .1或4D .41或413. 已知532log [log (log )]0x =,那么12x-等于( )A. 13B. 6C. 4D. 314. 式子82log 9log 3的值为 ( )A.23B.32 C.2 D.315.1123634271628---+-⨯⎛⎫ ⎪⎝⎭=16.已知12,x x -+=则1122xx -+=17.若23x x=,则=x18.235111log log log 2589⨯⨯=19.33(lg 2)3lg 2lg5(lg5)++= 20.已知log 2,log 3a a m n==,则2m na+=21. 若1249a =(a>0) ,则23log a = .22. 方程的解是___________________23. =++-3121)6427()5(lg )972(_________ __24.已知35a bc ==,且112a b +=,求c =25.142log 2112log 487log 222--+= ;11lg9lg 240212361lg 27lg 35+-+-+= 。
第八节函数与方程学案高三数学一轮复习

第八节函数与方程一、学习目标1、理解函数零点的概念以及函数的零点与方程的根之间的关系,并会求函数的零点或判断个数。
2、会根据函数的零点求参数,了解函数零点存在定理,会判断零点所在区间。
二、学习过程知识点一函数的零点1.函数零点的概念对于函数y=f(x),x∈D,我们把使f(x)=0的叫做函数y=f(x),x∈D的零点.注意:零点不是点,是满足f(x)=0的实数x.2.三个等价关系3.零点存在定理【提醒】函数零点存在定理只能判断函数在某个区间上的变号零点.自查自测1、(判断题)函数的零点就是函数的图象与x 轴的交点. ( )2、函数245y x x =--的零点为( ).A .()5,0B .()1,5-C .1-和5D .()1,0-和()5,03、(人教A 版必修①P155·T1改编)下列图象所表示的函数中不能用零点存在性定理求零点的是( ).A 、B 、C 、D 、考点一 函数零点所在区间的判断例11、设()2f x lnx x =+-,则函数f (x )的零点所在的区间为( ).1(0)A , ).(12?B , .3(2)C , .4(3)D ,变式11:()2ln 1f x x x =--的零点所在的区间是( ) A .()1,2 B .()2,3 C .()3,4 D .()4,5 变式12、(人教A 版必修①P160)已知函数x x f x +=2)(,x x x g +=2log )(,x x x h +=3)(的零点分别为a ,b ,c ,则a ,b ,c ,的大小顺序为( ).A 、c b a >>B 、a c b >>C 、b a c >>D 、c a b >>考点二 函数零点个数问题例21、已知函数()⎪⎩⎪⎨⎧>≤=0,log 0,)(221x x x x f x ,则函数g (x )=f (x )-12的零点个数为( ) A .0 B .1 C .2 D .3变式21、函数()()0.2sin log 02f x x x x π⎛⎫=-> ⎪⎝⎭的零点个数为( ) A .1 B .2 C .3 D .4交点个数为( )A 、3B 、4C 、6D 、8拓展、已知函数22,0()log ,0x x f x x x ⎧≤=⎨>⎩,函数()()g x f x x m =++,若()g x 有两个零点,则m 的取值范围是( ).A .[1,)-+∞B .(,1]-∞- C .[0,)+∞ D .[1,0)-【当堂检测】1.函数()234x f x x =+-的零点所在的区间是( ) A .()1,0- B .()0,1 C .()1,2 D .()2,32.已知函数()1,02,0x f x x x x ⎧>⎪=⎨⎪+≤⎩,则方程()30x f x -=的解的个数是( ) A .0B .1C .2D .3 3.函数()sin 4f x x π⎛⎫=- ⎪⎝⎭在[]0,8π上的所有零点之和为( )A .45πB .40πC .35πD .30π 4.(选做)若函数()2ln f x x m x =+-在区间()1,2上只有一个零点,则常数m 的取值范围为( )A .12m <<B .ln 22m <<C .11ln 2m <<+D .1ln 22m +<<【归纳总结】1、确定函数零点所在区间的常用方法2、函数零点个数的判断方法【作业】1、函数2()log f x x x =+的零点所在的区间为( )A .11,32⎛⎫ ⎪⎝⎭B .12,23⎛⎫ ⎪⎝⎭C .23,34⎛⎫ ⎪⎝⎭D .3,14⎛⎫ ⎪⎝⎭2、(多选)函数2()2x f x a x=--的一个零点在区间(1,2)内,则实数a 的可能取值是( ) A .0 B .1 C .2 D .33、函数()32,03e ,0x x x f x x x ⎧+≤=⎨-+>⎩的零点个数为___________. 4、(2024上海模拟卷改编 选做)已知函数()()()122,0,R log 1,0,x x f x a x x ⎧≤⎪=∈⎨+>⎪⎩,a x f x g +=)()(在R 上没有零点,则实数a 的取值范围是( ) A .(){},10-∞- B .(),1∞-- C .()1,-+∞ D .。
高考数学一轮复习高考大题规范解答系列一_函数与导数学案含解析新人教版

高考大题规范解答系列(一)——函数与导数考点一 利用导数解决与函数有关的极、最值问题例1 (2020·北京,19,15分)已知函数f (x )=12-x 2. (1)求曲线y =f (x )的斜率等于-2的切线方程;(2)设曲线y =f (x )在点(t ,f (t ))处的切线与坐标轴围成的三角形的面积为S (t ),求S (t )的最小值.【标准答案】——规范答题 步步得分(1)因为f (x )=12-x 2,所以f ′(x )=-2x ,1分………………………………得分点① 令-2x =-2,解得x =1,2分………………………………………………得分点② 又f (1)=11,所以所求切线方程为y -11=-2(x -1),整理得2x +y -13=0.4分……………………………………………………得分点③ (2)由(1)可知f ′(x )=-2x ,所以曲线y =f (x )在点(t ,f (t ))处的切线斜率k =-2t ,又f (t )=12-t 2,所以切线方程为y -(12-t 2)=-2t (x -t ),6分…………………………得分点④整理得2tx +y -(t 2+12)=0,当x =0时,y =t 2+12,所以切线与y 轴的交点为(0,t 2+12),7分……………………………………………………………………………得分点⑤当y =0时,x =t 2+122t ,所以切线与x 轴的交点为⎝⎛⎭⎫t 2+122t ,0.8分………得分点⑥ ①当t >0时,S (t )=12·t 2+122t ·(t 2+12)=(t 2+12)24t ,9分………………………得分点⑦则S ′(t )=3(t 2-4)(t 2+12)4t 2,10分……………………………………………得分点⑧当0<t <2时,S ′(t )<0,此时S (t )在(0,2)上单调递减; 当t >2时,S ′(t )>0,此时S (t )在(2,+∞)上单调递增,所以S (t )min =S (2)=32.11分…………………………………………………得分点⑨ ②当t <0时,S (t )=-(t 2+12)24t ;12分………………………………………得分点⑩则S ′(t )=-3(t 2-4)(t 2+12)4t 2,13分…………………………………………得分点⑪当t <-2时,S ′(t )<0,此时S (t )在(-∞,-2)上单调递减; 当-2<t <0时,S ′(t )>0,此时S (t )在(-2,0)上单调递增,所以S (t )min =S (-2)=32.14分………………………………………………得分点⑫ 综上所述,当t =±2时,S (t )取最小值,为32.15分………………………得分点⑬【评分细则】 ①求对导函数得1分. ②解对f ′(x )=-2得1分. ③写对切线方程得2分. ④写对切线方程得2分. ⑤求对与y 轴交点得1分. ⑥求对与x 轴交点得1分. ⑦分类讨论t ≥0时写对S (t )得1分. ⑧求对S (t )得1分. ⑨求对S (t )的最小值得1分. ○10分类讨论,t <0时写对S (t )得1分. ⑪求对S ′(t )得1分. ⑫求对S (t )最小值得1分. ⑬总结叙述正确得1分. 【名师点评】 1.核心素养:利用导数研究函数的极、最值问题,首先对函数求导,分解因式,分类讨论函数在给定区间的增减情况确定极最值,重点考查学生数学运算、逻辑推理及分类的数学核心素养.2.解题技巧:(1)求出切线与x 轴、y 轴交点,并写出三角形的积S (t ). (2)对S (t )分类讨论,分别求最值是本题关键点. 〔变式训练1〕(理)(2020·湖南期末统测)已知函数f (x )=ln x +1-2a -x +a x 有两个不同的极值点x 1,x 2.(1)求实数a 的取值范围.(2)求f (x )的极大值与极小值之和的取值范围.(文)(2020·长春市第二次质量监测)已知函数f (x )=(a -1)·ln x -ax -x (a ∈R ).(1)当a =2时,求曲线y =f (x )在点(2,f (2))处的切线方程; (2)若函数f (x )在[1,3]上的最大值为-2,求实数a 的值.[解析] 本题考查利用导数研究函数的单调性、极值和最值.(理)(1)f (x )定义域为(0,+∞),f ′(x )=1x -1-a x 2=-x 2+x -ax 2.因为f (x )有两个不同的极值点x 1,x 2,且x >0,所以x 2-x +a =0有两个不同的正根,所以⎩⎪⎨⎪⎧Δ=1-4a >0,x 1+x 2=1>0,x 1x 2=a >0,解得0<a <14.故实数a 的取值范围为⎝⎛⎭⎫0,14. (2)由(1)知x 1x 2=a ,x 1+x 2=1,不妨设x 1<x 2,所以f (x )极小值=f (x 1),f (x )极大值=f (x 2), 所以f (x )极小值+f (x )极大值=f (x 1)+f (x 2)=ln(x 1x 2)+2(1-2a )+a (x 1+x 2)x 1x 2-(x 1+x 2)=ln a +2-4a .令φ(a )=ln a -4a +2,则φ′(a )=1a -4,当0<a <14时,φ′(a )>0,所以φ(a )在⎝⎛⎭⎫0,14上单调递增,所以φ(a )<φ⎝⎛⎭⎫14=-2ln 2 +1. 又当a →0时,φ(a )→-∞,所以f (x )的极大值与极小值之和的取值范围是(-∞,-2ln 2+1).(文)(1)a =2时,f (x )=ln x -2x -x ,f ′(x )=1x +2x 2-1,f (2)=ln 2-3,f ′(2)=0,所以曲线在点(2,f (2))处的切线方程为y =ln 2-3. (2)f ′(x )=a -1x +a x 2-1=-(x +1)(x -a )x 2(1≤x ≤3),当a ≤1时,f ′(x )≤0,f (x )在[1,3]上单调递减, 所以f (1)=-2,a =1;当a ≥3时,f ′(x )≥0,f (x )在[1,3]上单调递增,所以f (3)=-2,a =ln 3+1ln 3-13<3,舍去;当1<a <3时,f (x )在(1,a )上单调递增,在(a,3)上单调递减, 所以f (a )=-2,a =e. 综上,a =1或a =e.考点二 利用导数解决与不等式有关的函数问题例2 (2020·课标Ⅱ,21,12分)已知函数f (x )=sin 2x sin 2x . (1)讨论f (x )在区间(0,π)的单调性; (2)证明:|f (x )|≤338; (3)设n ∈N *,证明:sin 2x sin 22x sin 24x …sin 22n x ≤3n 4n. 【标准答案】——规范答题 步步得分 (1)f ′(x )=cos x (sin x sin 2x )+sin x (sin x sin 2x )′ =2sin x cos x sin 2x +2sin 2x cos 2x=2sin x sin 3x .2分……………………………………………………………得分点① 当x ∈⎝⎛⎭⎫0,π3∪⎝⎛⎭⎫2π3,π时,f ′(x )>0;当x ∈⎝⎛⎭⎫π3,2π3时,f ′(x )<0.所以f (x )在区间⎝⎛⎭⎫0,π3,⎝⎛⎭⎫2π3,π单调递增,在区间⎝⎛⎭⎫π3,2π3单调递减.4分………………………………得分点②(2)证明:因为f (0)=f (π)=0,由(1)知,f (x )在区间[0,π]的最大值为f ⎝⎛⎭⎫π3=338,5分 …………………………………………………………………………………得分点③ 最小值为f ⎝⎛⎭⎫2π3=-338.6分…………………………………………………得分点④ 而f (x )是周期为π的周期函数,故|f (x )|≤338.7分…………………………得分点⑤ (3)证明:由于(sin 2x sin 22x …sin 22n x )32 8分…………………………………得分点⑥=|sin 3x sin 32x …sin 32n x |=|sin x ||sin 2x sin 32x …sin 32n -1x sin2n x ||sin 22n x |9分……………………………得分点⑦ =|sin x ||f (x )f (2x )…f (2n -1x )||sin 22n x |10分……………………………………得分点⑧ ≤|f (x )f (2x )…f (2n -1x )|,11分…………………………………………………得分点⑨所以sin 2x sin 22x …sin 22n x ≤⎝⎛⎭⎫3382n3=3n4n .12分……………………………得分点⑩【评分细则】①正确求得导函数并化简正确得2分. ②讨论f (x )的单调性,正确得2分. ③求对f (x )的最大值得1分. ④求对f (x )的最小值得1分. ⑤证出|f (x )|≤338得1分. ⑥变形正确得1分. ⑦合理转化得1分.⑧转化出f (x )、f (2x )、…、f (2n -1x )得1分. ⑨放缩正确得1分. ⑩证出结论得1分. 【名师点评】 1.核心素养:利用导数判断函数的单调性及解决与不等式有关的函数问题是高考命题的热点问题.本题主要考查“逻辑推理”及“数学运算”的核心素养.2.解题技巧:(1)讨论函数的单调性首先要明确函数的定义域,一般用导数的方法,对导数解不等式. (2)求出f (x )的最值是证明第2问的关键.(3)将不等式左边变形与f (x )及第2问结合起来是完成第3问的关键. 〔变式训练2〕(理)(2020·河南省郑州市高三第二次质量预测)设函数f (x )=ax 2-(x +1)ln x (a ∈R ),曲线y =f (x )在点(1,f (1))处的斜率为0.(1)求a 的值;(2)求证:当0<x ≤2时,f (x )>12x .(文)(2018·课标全国Ⅰ,21)已知函数f (x )=a e x -ln x -1,a ∈R . (1)设x =2是f (x )的极值点,求a ,并求f (x )的单调区间; (2)证明:当a ≥1e时,f (x )≥0.[分析] (文)(1)看到x =2是f (x )的极值点,想到f ′(2)=0且两边异号,看到求单调区间想到求函数定义域,并对函数求导.(2)看到证明当a ≥1e 时,f (x )≥0想到用1e 替换a 进行放缩,构造函数y =e xe -ln x -1,从而求此函数的最小值.[解析] (理)(1)f ′(x )=2ax -ln x -1-1x ,由题意可得f ′(1)=2a -2=0, ∴a =1.(2)要证f (x )>12x (0<x ≤2),只需证x -ln x x -ln x >12,即证x -ln x >ln x x +12,令g (x )=x -ln x ,h (x )=ln x x +12,由g ′(x )=1-1x=0,解得x =1,g (x )在(0,1)上单调递减,在(1,2]上单调递增, 故g (x )min =g (1)=1,由h ′(x )=1-ln xx 2可知h (x )在(0,2]上单调递增,故h (x )max =h (2)=1+ln 22<1=g (x )min ,故h (x )<g (x ),即f (x )>12x .(文)(1)f (x )的定义域为(0,+∞), f ′(x )=a e x -1x .由题设知,f ′(2)=0, 所以a =12e2.从而f (x )=12e 2e x -ln x -1,f ′(x )=12e 2e x -1x.当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.所以f (x )在(0,2)上单调递减,在(2,+∞)上单调递增. (2)当a ≥1e 时,f (x )≥e xe -ln x -1.设g (x )=e xe -ln x -1,则g ′(x )=e x e -1x .当0<x <1时,g ′(x )<0; 当x >1时,g ′(x )>0.所以x =1是g (x )的最小值点. 故当x >0时,g (x )≥g (1)=0. 因此,当a ≥1e时,f (x )≥0.考点三 利用导数解决与函数零点有关的问题例3 (2021·山东省青岛市高三模拟检测)已知函数f (x )=a e x -x -a ,e =2.718 28…是自然对数的底数.(1)讨论函数f (x )的单调性;(2)若f (x )恰有2个零点,求实数a 的取值范围. 【分析】 ①看到单调性想到求函数f (x )的导数.②看到f (x )恰有2个零点,想到f (x )=0有两解或y =f (x )图象与x 轴有两个交点. 【标准答案】——规范答题 步步得分(1)f ′(x )=a e x -1,1分……………………………………………………………得分点① 当a ≤0时,f ′(x )=a e x -1<0,所以x ∈(-∞,+∞),f ′(x )<0,故f (x )在(-∞,+∞)上单调递减,2分…得分点② 当a >0时,令f ′(x )=a e x -1=0,得x =-ln a ;所以x ∈(-∞,-ln a )时,f ′(x )<0,f (x )在(-∞,-ln a )上单调递减;x ∈(-ln a ,+∞)时,f ′(x )>0,f (x )在(-ln a ,+∞)上单调递增.4分………………………………得分点③(2)由(1)知,当a ≤0时,f (x )在(-∞,+∞)上单调递减;又知f (0)=0,所以f (x )仅有1个零点;5分……………………………………得分点④ 当0<a <1时,f (0)=0,所以f (-ln a )<0,取f (-2ln a )=1a +2ln a -a ,令函数g (a )=1a +2ln a -a ,得g ′(a )=-(a -1)2a 2<0,所以g (a )>g (1)=0,所以f (-2ln a )=1a +2ln a -a >0得f (x )在(-ln a ,-2ln a )上也有1个零点,8分……………………………………………………………………………………得分点⑤ 当a =1时,f (x )≥f (0)=0,所以f (x )仅有1个零点,9分……………………得分点⑥ 当a >1时,f (0)=0,所以f (-ln a )<0, 令函数h (a )=a -ln a ,a >1得h ′(a )=1-1a >0,所以h (a )>h (1)>0,所以a >ln a ,∴-a <-ln a ,取f (-a )=a e -a >0,得f (x )在(-a ,-ln a )上也有1个零点,综上可知:若f (x )恰有2个零点,则a ∈(0,1)∪(1,+∞).12分……………得分点⑦ 【评分细则】 ①求对导函数得1分. ②求对a ≤0单调区间得1分. ③求对a >0单调区间得2分.④求对a ≤0时f (x )只有一个零点得1分. ⑤求对0<a <1时f (x )有两个零点得3分. ⑥求对a =1时f (x )有一个零点得1分.⑦求对a >1时f (x )有两个零点,并进行综述得3分. 【名师点评】 1.核心素养:本题主要考查导数与函数单调性的关系、零点存在性定理,考查考生的数形结合能力、推理论证能力以及运算求解能力,考查的数学核心素养是直观想象、逻辑推理、数学运算.2.解题技巧:(1)通过求导,分类讨论,进而求单调区间.(2)通过(1)的分析知道函数f (x )的单调性、最值,讨论f (x )零点的个数,从而得出结论. 〔变式训练3〕(2020·全国Ⅲ,21)设函数f (x )=x 3+bx +c ,曲线y =f (x )在点⎝⎛⎭⎫12,f ⎝⎛⎭⎫12处的切线与y 轴垂直.(1)求b .(2)若f (x )有一个绝对值不大于1的零点,证明:f (x )所有零点的绝对值都不大于1. [解析] 本题考查导数的几何意义及利用导数研究函数的单调性、极值、零点. (1)f ′(x )=3x 2+b .依题意得f ′⎝⎛⎭⎫12=0,即34+b =0,故b =-34. (2)证明:由(1)知f (x )=x 3-34x +c ,f ′(x )=3x 2-34.令f ′(x )=0,解得x =-12或x =12.f ′(x )与f (x )的情况为:因为f (1)=f ⎝⎛⎭⎫-12=c +14,所以当c <-14时,f (x )只有大于1的零点. 因为f (-1)=f ⎝⎛⎭⎫12=c -14,所以当c >14时,f (x )只有小于-1的零点. 由题设可知-14≤c ≤14.当c =-14时,f (x )只有两个零点-12和1.当c =14时,f (x )只有两个零点-1和12.当-14<c <14时,f (x )有三个零点x 1,x 2,x 3,且x 1∈⎝⎛⎭⎫-1,-12,x 2∈⎝⎛⎭⎫-12,12,x 3∈⎝⎛⎭⎫12,1. 综上,若f (x )有一个绝对值不大于1的零点,则f (x )所有零点的绝对值都不大于1.。
人教A版高三一轮复习- 函数的概念与基本初等函数导学案
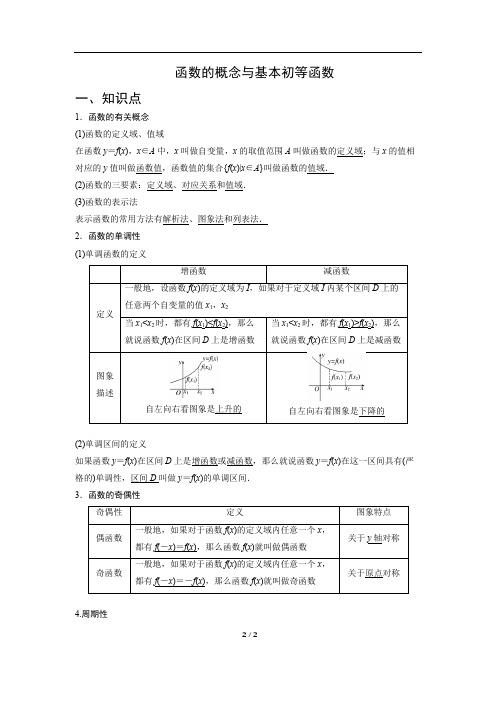
函数的概念与基本初等函数一、知识点1.函数的有关概念(1)函数的定义域、值域在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域.(2)函数的三要素:定义域、对应关系和值域.(3)函数的表示法表示函数的常用方法有解析法、图象法和列表法.2.函数的单调性(1)单调函数的定义自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数y=f(x)在区间D上是增函数或减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,区间D叫做y=f(x)的单调区间.3.函数的奇偶性4.周期性2 / 2(1)周期函数:对于函数y=f(x),如果存在一个非零常数T,使得当x取定义域内的任何值时,都有f(x+T)=f(x),那么就称函数y=f(x)为周期函数,称T为这个函数的周期.(2)最小正周期:如果在周期函数f(x)的所有周期中存在一个最小的正数,那么这个最小正数就叫做f(x)的最小正周期.基本初等函数1.幂函数(1)幂函数的定义一般地,形如y=xα的函数称为幂函数,其中x是自变量,α是常数.(2)常见的五种幂函数的图象和性质比较R R R{x|x≥0}{x|x≠0}2.二次函数的图象和性质R R2 / 22 / 2(1)我们规定正数的正分数指数幂的意义是m na =na m (a >0,m ,n ∈N *,且n >1).于是,在条件a >0,m ,n ∈N *,且n >1下,根式都可以写成分数指数幂的形式.正数的负分数指数幂的意义与负整数指数幂的意义相仿,我们规定m na-=1m na(a >0,m ,n ∈N *,且n >1).0的正分数指数幂等于0;0的负分数指数幂没有意义.(2)有理数指数幂的运算性质:a r a s =a r +s ,(a r )s =a rs ,(ab )r =a r b r ,其中a >0,b >0,r ,s ∈Q .4.指数函数的图象与性质(1)R 5.一般地,如果a x =N (a >0,且a ≠1),那么数x 叫做以a 为底N 的对数,记作x =log a N ,其中a 叫做对数的底数, N 叫做真数. 6.对数的性质与运算法则 (1)对数的运算法则如果a >0,且a ≠1,M >0,N >0,那么:①log a (MN )=log a M +log a N ;②log a MN =log a M -log a N ;③log a M n =n log a M (n ∈R ).(2)对数的性质2 / 2①log a N a = N ;②log a a N = N (a >0,且a ≠1). (3)对数的换底公式log a b =log c blog c a (a >0,且a ≠1;c >0,且c ≠1;b >0).7.对数函数的图象与性质(1)(0,+∞)函数图像和零点1.图象变换 (1)平移变换(2)对称变换①y =f (x )――――――→关于x 轴对称y =-f (x ); ②y =f (x )――――――→关于y 轴对称y =f (-x ); ③y =f (x )―――――→关于原点对称y =-f (-x );④y =a x (a >0且a ≠1)――――――→关于y =x 对称y =log a x (a >0且a ≠1). (3)伸缩变换2 / 2①y =f (x )―――――――――――――――――――――――→a >1,横坐标缩短为原来的1a倍,纵坐标不变0<a <1,横坐标伸长为原来的1a倍,纵坐标不变y =f (ax ). ②y =f (x )――――――――――――――――――――→a >1,纵坐标伸长为原来的a 倍,横坐标不变0<a <1,纵坐标缩短为原来的a 倍,横坐标不变y =af (x ). (4)翻折变换①y =f (x )――――――――――→保留x 轴上方图象将x 轴下方图象翻折上去y =|f (x )|. ②y =f (x )―――――――――――→保留y 轴右边图象,并作其关于y 轴对称的图象y =f (|x |). 2.函数的零点 (1)函数零点的定义对于函数y =f (x )(x ∈D ),把使f (x )=0的实数x 叫做函数y =f (x )(x ∈D )的零点. (2)三个等价关系方程f (x )=0有实数根⇔函数y =f (x )的图象与x 轴有交点⇔函数y =f (x )有零点. (3)函数零点的判定(零点存在性定理)如果函数y =f (x )在区间[a ,b ]上的图象是连续不断的一条曲线,并且有f (a )·f (b )<0,那么,函数y =f (x )在区间(a ,b )内有零点,即存在c ∈(a ,b ),使得f (c )=0,这个 c 也就是方程f (x )=0的根.二、高考真题练习比大小1.【2019年高考全国Ⅰ卷理数】已知0.20.32log 0.220.2a b c ===,,,则 A .a b c << B .a c b << C .c a b <<D .b c a <<【答案】B2.【2019年高考天津理数】已知5log 2a =,0.5og 2.l 0b =,0.20.5c =,则,,a b c 的大小关系为 A .a c b << B .a b c << C .b c a <<D .c a b <<【答案】A2 / 23.【2019年高考全国Ⅱ卷理数】若a >b ,则 A .ln(a −b )>0 B .3a <3b C .a 3−b 3>0 D .│a │>│b │【答案】C4.【2018年高考天津理数】已知2log e a =,ln2b =,121log 3c =,则a ,b ,c 的大小关系为A .a b c >>B .b a c >>C .c b a >>D .c a b >>【答案】D5.【2018年高考全国Ⅲ卷理数】设0.2log 0.3a =,2log 0.3b =,则A .0a b ab +<<B .0ab a b <+<C .0a b ab +<<D .0ab a b <<+ 【答案】B6.【2017年高考全国Ⅰ卷理数】设x 、y 、z 为正数,且235x y z ==,则A .2x <3y <5zB .5z <2x <3yC .3y <5z <2xD .3y <2x <5z 【答案】D7.【2017年高考天津理数】已知奇函数()f x 在R 上是增函数,()()g x xf x =.若2(log 5.1)a g =-,0.8(2)b g =,(3)c g =,则a ,b ,c 的大小关系为A .a b c <<B .c b a <<C .b a c <<D .b c a <<【答案】C8.【2017年高考山东理数】若,且,则下列不等式成立的是A .B .0a b >>1ab =()21log 2aba ab b +<<+()21log 2a b a b a b<+<+2 / 2C .D . 【答案】B 运算1.【2017年高考山东理数】设函数y =A ,函数ln(1)y x =-的定义域为B ,则AB =A .(1,2)B .(1,2]C .(-2,1)D .[-2,1)【答案】D2.【2019年高考江苏】函数y =的定义域是 .【答案】[1,7]-3.【2018年高考江苏】函数()f x =________.【答案】[2,+∞)4.【2017年高考江苏】记函数()f x =的定义域为D .在区间[4,5]-上随机取一个数x ,则x D ∈的概率是 . 【答案】595.【2019年高考北京理数】在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足m 2−m 1=2152lg E E ,其中星等为m k 的星的亮度为E k (k =1,2).已知太阳的星等是−26.7,天狼星的星等是−1.45,则太阳与天狼星的亮度的比值为 A .1010.1B .10.1C .lg10.1D .10−10.1【答案】A6.【2019年高考全国Ⅱ卷理数】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星()21log 2a ba ab b +<+<()21log 2aba b a b +<+<2 / 2“鹊桥”,鹊桥沿着围绕地月拉格朗日2L 点的轨道运行.2L 点是平衡点,位于地月连线的延长线上.设地球质量为M 1,月球质量为M 2,地月距离为R ,2L 点到月球的距离为r ,根据牛顿运动定律和万有引力定律,r 满足方程:121223()()M M M R r R r r R +=++.设rRα=,由于α的值很小,因此在近似计算中34532333(1)ααααα++≈+,则r 的近似值为ABCD【答案】D7.【2017年高考北京理数】根据有关资料,围棋状态空间复杂度的上限M 约为3361,而可观测宇宙中普通物质的原子总数N 约为1080.则下列各数中与M N最接近的是(参考数据:lg3≈0.48)A .1033B .1053C .1073D .1093【答案】D 函数图像1.【2019年高考全国Ⅰ卷理数】函数f (x )=在[,]-ππ的图像大致为A .B .C .D .【答案】D2sin cos ++x xx x2 / 22.【2019年高考全国Ⅲ卷理数】函数3222x xx y -=+在[]6,6-的图像大致为A .B .C .D .【答案】B3.【2019年高考浙江】在同一直角坐标系中,函数1x y a =,1(2log )ay x =+(a >0,且a ≠1)的图象可能是【答案】D4.【2018年高考全国Ⅱ卷理数】函数()2e e x xf x x --=的图像大致为2 / 2【答案】B5.【2018年高考全国Ⅲ卷理数】函数422y x x =-++的图像大致为【答案】D6.【2018年高考浙江】函数y =2xsin2x 的图象可能是A .B .2 / 2C .D .【答案】D 函数性质1.【2019年高考全国Ⅲ卷理数】设()f x 是定义域为R 的偶函数,且在()0,+∞单调递减,则A .f (log 314)>f (322-)>f (232-)B .f (log 314)>f (232-)>f (322-)C .f (322-)>f (232-)>f (log 314)D .f (232-)>f (322-)>f (log 314)【答案】C2.【2018年高考全国Ⅱ卷理数】已知()f x 是定义域为(),-∞+∞的奇函数,满足()()11f x f x -=+.若()12f =,则()()()123f f f ++()50f ++=A .50-B .0C .2D .50【答案】C3.【2017年高考全国Ⅰ卷理数】函数()f x 在(,)-∞+∞单调递减,且为奇函数.若(11)f =-,则满足21()1x f --≤≤的x 的取值范围是 A .[2,2]- B .[1,1]- C .[0,4] D .[1,3]【答案】D2 / 24.【2017年高考北京理数】已知函数1()3()3x xf x =-,则()f xA .是奇函数,且在R 上是增函数B .是偶函数,且在R 上是增函数C .是奇函数,且在R 上是减函数D .是偶函数,且在R 上是减函数【答案】A5.【2017年高考全国Ⅲ卷理数】设函数()π(3cos )f x x =+,则下列结论错误的是A .()f x 的一个周期为2π-B .()y f x =的图象关于直线8π3x =对称 C .(π)f x +的一个零点为π6x = D .()f x 在(π2,π)单调递减【答案】D6.【2017年高考天津理数】已知函数23,1,()2, 1.x x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩设a ∈R ,若关于x 的不等式()||2xf x a ≥+在R 上恒成立,则a 的取值范围是 A .47[,2]16-B .4739[,]1616-C.[2]- D.39[]16- 【答案】A7.【2019年高考全国Ⅱ卷理数】已知()f x 是奇函数,且当0x <时,()e ax f x =-.若(ln 2)8f =,则a =__________.【答案】3-8.【2019年高考北京理数】设函数()e e xxf x a -=+(a 为常数).若f (x )为奇函数,则a =________;若f (x )是R 上的增函数,则a 的取值范围是___________. 【答案】(]1;,0--∞9.【2018年高考北京理数】能说明“若f (x )>f (0)对任意的x ∈(0,2]都成立,则f (x )在[0,2]上是增函数”为假命题的一个函数是__________.2 / 2【答案】23()()2f x x =-- (答案不唯一)10.【2018年高考江苏】函数()f x 满足()()()4f x f x x +=∈R ,且在区间(]2,2-上,()πcos ,02,21,20,2x x f x x x ⎧<≤⎪⎪=⎨⎪+-<≤⎪⎩则()()15f f 的值为________.11.【2017年高考江苏】已知函数31()2e e xxf x x x =-+-,其中e 是自然对数的底数.若(1)f a -+2(2)0f a ≤,则实数a 的取值范围是 ▲ . 【答案】1[1,]2-12.【2017年高考全国Ⅲ卷理数】设函数10()20xx x f x x +≤⎧=⎨>⎩,,,则满足1()()12f x f x +->的x 的取值范围是_________. 【答案】1,4⎛⎫-+∞ ⎪⎝⎭13.【2017年高考山东理数】若函数e ()xf x (e 2.71828=是自然对数的底数)在()f x 的定义域上单调递增,则称函数()f x 具有M 性质.下列函数中所有具有M 性质的函数的序号为 .①()2xf x -=②()3xf x -=③3()f x x =④2()2f x x =+【答案】①④函数与导数1.【2018年高考全国Ⅰ卷理数】设函数()()321f x x a x ax =+-+,若()f x 为奇函数,则曲线()y f x =在点()0,0处的切线方程为2 / 2A .2y x =-B .y x =-C .2y x =D .y x =【答案】D2.【2017年高考浙江】若函数f (x )=x 2+ ax +b 在区间[0,1]上的最大值是M ,最小值是m ,则M – mA .与a 有关,且与b 有关B .与a 有关,但与b 无关C .与a 无关,且与b 无关D .与a 无关,但与b 有关【答案】B3.【2017年高考山东理数】已知当[0,1]x ∈时,函数2(1)y mx =-的图象与y m=的图象有且只有一个交点,则正实数m 的取值范围是 A .(0,1][23,)+∞ B .(0,1][3,)+∞ C.[23,)+∞ D.[3,)+∞ 【答案】B 函数与方程4.【2019年高考全国Ⅱ卷理数】设函数()f x 的定义域为R ,满足(1) 2 ()f x f x +=,且当(0,1]x ∈时,()(1)f x x x =-.若对任意(,]x m ∈-∞,都有8()9f x ≥-,则m 的取值范围是 A .9,4⎛⎤-∞ ⎥⎝⎦B .7,3⎛⎤-∞ ⎥⎝⎦C .5,2⎛⎤-∞ ⎥⎝⎦D .8,3⎛⎤-∞ ⎥⎝⎦【答案】B5.【2019年高考浙江】已知,a b ∈R ,函数32,0()11(1),032x x f x x a x ax x <⎧⎪=⎨-++≥⎪⎩.若函数()y f x ax b =--恰有3个零点,则2 / 2A .a <–1,b <0B .a <–1,b >0C .a >–1,b <0D .a >–1,b >0【答案】C6.【2018年高考全国Ⅰ卷理数】已知函数()e 0ln 0x x f x x x ⎧≤=⎨>⎩,,,,()()g x f x x a =++.若g (x )存在2个零点,则a 的取值范围是A .[–1,0)B .[0,+∞)C .[–1,+∞)D .[1,+∞)【答案】C7.【2017年高考全国Ⅲ卷理数】已知函数211()2(e e )x x f x x x a --+=-++有唯一零点,则a =A .12- B .13C .12D .1【答案】C8.【2019年高考浙江】已知a ∈R ,函数3()f x ax x =-,若存在t ∈R ,使得2|(2)()|3f t f t +-≤,则实数a 的最大值是___________. 【答案】439.【2019年高考北京理数】李明自主创业,在网上经营一家水果店,销售的水果中有草莓、京白梨、西瓜、桃,价格依次为60元/盒、65元/盒、80元/盒、90元/盒.为增加销量,李明对这四种水果进行促销:一次购买水果的总价达到120元,顾客就少付x 元.每笔订单顾客网上支付成功后,李明会得到支付款的80%.①当x =10时,顾客一次购买草莓和西瓜各1盒,需要支付__________元; ②在促销活动中,为保证李明每笔订单得到的金额均不低于促销前总价的七折,则x 的最大值为__________. 【答案】①130;②152 / 210.【2018年高考全国Ⅲ卷理数】函数()πcos 36f x x ⎛⎫=+ ⎪⎝⎭在[]0π,的零点个数为________.【答案】311.【2018年高考浙江】我国古代数学著作《张邱建算经》中记载百鸡问题:“今有鸡翁一,值钱五;鸡母一,值钱三;鸡雏三,值钱一。
新高考数学一轮复习 课时规范练16 导数的概念及运算 新人教A版高三全册数学试题

课时规范练16 导数的概念及运算基础巩固组1.(2019河南豫西名校联考一)已知函数f (x )在x=x 0处的导数为f'(x 0),则lim Δx →0f(x 0-m x x)-f(x 0)x x等于( )A.mf'(x 0)B.-mf'(x 0)C.-1mf'(x 0)D.1mf'(x 0)2.(多选)(2019山东临淄区月考)若函数f (x )的导函数f'(x )的图象关于y 轴对称,则f (x )的解析式可能为( )A.f (x )=3cos xB.f (x )=x 3+xC.f (x )=x+1xD.f (x )=e x+x3.(2019黑龙江哈尔滨市六中期中)设f (x )=ln x.若f'(x 0)=3,则x 0=( )A.e 3B.3C.13D.ln 34.(2019湖南湘潭期末)设函数f (x )=ax 3+1.若f'(1)=3,则a 的值为( )A.0B.1C.2D.45.(2019云南师大附中模拟)设f (x )是(-∞,0)∪(0,+∞)上的偶函数,当x>0时,f (x )=x 2-x ,则f (x )在点(-1,f (-1))处的切线方程为( )A.x-y-1=0B.x+y-1=0C.x-y+1=0D.x+y+1=06.(2019山西大学附属中学期末,5)已知函数f (x )=12e x-32e -x,则曲线y=f (x )上任意一点处的切线的倾斜角α的取值范围是( )A.(0,π3]B.(π2,2π3]C.[π3,π2)D.[π3,π)7.(2019江西赣州期末)设函数f (x )在R 上可导,f (x )=x 2f'(1)-2x+1,则f (a 2-a+2)与f (1)的大小关系是( )A.f (a 2-a+2)>f (1)B.f (a 2-a+2)=f (1)C.f (a 2-a+2)<f (1) D.不确定8.(2019贵州铜仁一中期中)已知曲线y=ln x 在点A 处的切线与直线x-y+1=0平行,则点A 的坐标为( )A.(e,1)B.(1,0)C.(1e ,-1)D.(e 2,2)9.(2019江西新八校联考二)若f (x )+3f (-x )=x 3+2x+1对x ∈R 恒成立,则曲线y=f (x )在点(1,f (1))处的切线方程为( )A.5x+2y-5=0B.10x+4y-5=0C.5x+4y=0D.20x-4y-15=010.已知函数f(x)为奇函数,当x>0时,f(x)=x3-ln x,则曲线y=f(x)在点(-1,-1)处的切线的斜率为.已知抛物线C:y2=4x的焦点为F,A(x0,y0)是C上一点,|AF|=54x0,则x0=.11.(2019河南八市重点高中联考二,15)若一直线与曲线y=eln x和曲线y=mx2相切于同一点P,则实数m=.12.若函数f(x)=12x2-ax+ln x存在垂直于y轴的切线,则实数a的取值范围是.综合提升组13.已知函数f(x)=x ln x,若直线l过点(0,-1),并且与曲线y=f(x)相切,则直线l的方程为()A.x+y-1=0B.x-y-1=0C.x+y+1=0D.x-y+1=014.下面四个图象中,有一个是函数f(x)=13x3+ax2+(a2-1)x+1(a∈R)的导函数y=f'(x)的图象,则f(-1)=()A.13B.-23C.73D.-13或5315.(2019黑龙江大庆铁人中学期末)如图,y=f(x)是可导函数,直线l:y=kx+2是曲线y=f(x)在x=3处的切线,令g(x)=xf(x),g'(x)是g(x)的导函数,则g'(3)=()A.-1B.0C.2D.416.(2019江苏,10)在平面直角坐标系xOy中,P是曲线y=x+4(x>0)上的一个动点,则点P到直线xx+y=0的距离的最小值是.创新应用组+x3+sin x,其导函数为f'(x),则f(2 020)+f'(217.(2019湖南娄底高三模拟)已知函数f(x)=4e x+1020)+f(-2 020)-f'(-2 020)的值为()A.4 040B.4C.2D.018.(2019江西南昌模拟)已知f(x)在R上连续可导,f'(x)为其导函数,且f(x)=e x+e-x-f'(1)x·(e x-e-x),则f'(2)+f'(-2)-f'(0)f'(1)=()A.4e2+4e-2B.4e2-4e-2C.0D.4e2参考答案课时规范练16导数的概念及运算1.B因为函数f(x)在x=x0处的导数为f'(x0),所以limΔx→0f(x0-m x x)-f(x0)x x=-m xxx-m x x→0x(x0-xΔx)-x(x0)-xΔx=-mf'(x0).故选B.2.BC对于A,f(x)=3cos x,其导数f'(x)=-3sin x,其导函数为奇函数,图象不关于y轴对称,不符合题意;对于B,f(x)=x3+x,其导数f'(x)=3x2+1,其导函数为偶函数,图象关于y轴对称,符合题意;对于C,f(x)=x+1x ,其导数f'(x)=1-1x2,其导函数为偶函数,图象关于y轴对称,符合题意;对于D,f(x)=e x+x,其导数f'(x)=e x+1,其导函数不是偶函数,图象不关于y轴对称,不符合题意.故选BC.3.C∵f(x)=ln x,∴f'(x)=1x.又f'(x0)=3,∴1x0=3,解得x0=13.故选C.4.B∵f(x)=ax3+1,∴f'(x)=3ax2.又f'(1)=3,∴3a=3,解得a=1.故选B.5.D 由f (x )是(-∞,0)∪(0,+∞)上的偶函数得,当x<0时,-x>0,f (x )=f (-x )=(-x )2-(-x )=x 2+x ,此时f'(x )=2x+1,f'(-1)=-1,f (-1)=0.故f (x )在点(-1,f (-1))处的切线方程为y-0=-(x+1),即x+y+1=0.故选D .6.C ∵f (x )=12e x-32e -x,∴f'(x )=12e x +32e -x =12(e x +3e -x )≥12×2√e x ·3e -x =√3,当且仅当e x =3e -x,即x=ln32时等号成立.∴tan x ≥√3.又0≤α<π,∴π3≤x <π2.故选C .7.A 由题意可知,f'(x )=2f'(1)x-2,则f'(1)=2f'(1)-2,解得f'(1)=2.故f (x )=2x 2-2x+1.所以函数f (x )在区间(12,+∞)上单调递增.因为a 2-a+2=(x -12)2+74>1>12, 所以f (a 2-a+2)>f (1).故选A .8.B 设点A 的坐标为(x 0,ln x 0),曲线y=ln x 在点A 处的切线的斜率为k.∵y=ln x ,∴y'=1x ,∴k=y'|x =x 0=1x 0.又切线与直线x-y+1=0平行,∴1x 0=1,解得x 0=1,∴ln x 0=0.故点A 的坐标为(1,0).故选B .9.B ∵f (x )+3f (-x )=x 3+2x+1,①∴f (-x )+3f (x )=-x 3-2x+1, ②联立①②,解得f (x )=-12x 3-x+14,则f'(x )=-32x 2-1.∴f (1)=-12-1+14=-54,f'(1)=-32-1=-52.故切线方程为y+54=-52(x-1),即10x+4y-5=0.故选B .10.2 4 根据题意,设x<0,则-x>0,则f (-x )=(-x )3-ln(-x )=-x 3-ln(-x ),又由函数f (x )为奇函数,则f (x )=-f (-x )=x 3+ln(-x ),当x<0时,f'(x )=3x 2+1x ,则f'(-1)=3-1=2,则曲线y=f (x )在点(-1,-1)处的切线的斜率为2.抛物线C :y 2=4x 的焦点为F (1,0),∵A (x 0,y 0)是C 上一点,|AF|=54x 0,∴54x 0=x 0+1,解得x 0=4.11.12 曲线y=eln x 的导数为y'=ex ,曲线y=mx 2的导数为y'=2mx.由ex =2mx ,x>0,m>0,得x=√e2x ,故切点P 的坐标为(√e 2x,e2).将点P 的坐标代入y=eln x 得,eln √e 2x =e 2,解得m=12.12.[2,+∞) ∵f (x )=12x 2-ax+ln x ,∴f'(x )=x-a+1x .∵f (x )的图象存在垂直于y 轴的切线,∴f'(x )存在零点,∴x+1x -a=0有解,∴a=x+1x ≥2(x>0)当且仅当x=1时取等号.13.B 设直线l 的方程为y=kx-1,直线l 与f (x )的图象相切于点(x 0,y 0),则{xx 0-1=x 0,x 0ln x 0=x 0,ln x 0+1=x ,解得{x 0=1,x 0=0,x =1.故直线l 的方程为y=x-1,即x-y-1=0. 14.D ∵f'(x )=x 2+2ax+a 2-1,∴f'(x )的图象开口向上,故②④排除.若f'(x )的图象为①,则a=0,f (-1)=53;若f'(x )的图象为③,则a 2-1=0.又对称轴x=-a>0,∴a=-1,∴f (-1)=-13.15.B 将点(3,1)的坐标代入y=kx+2得,3k+2=1,解得k=-13,所以f'(3)=k=-13.因为点(3,1)在函数y=f (x )的图象上,所以f (3)=1.因为g (x )=xf (x ),所以g'(x )=f (x )+xf'(x ),所以g'(3)=f (3)+3f'(3)=1+3×(-13)=0.故选B .16.4 当直线x+y=0平移到与曲线y=x+4x 相切位置时,切点Q 即为点P 到直线x+y=0的最小距离的点,有y'=(x +4x )'=1-4x 2=-1(x>0),得x=√2(-√2舍).此时y=√2+2=3√2,即切点Q (√2,3√2),则切点Q 到直线x+y=0的距离为d=√2+√2|=4,即为所求最小值.17.B 因为f (x )=4e x +1+x 3+sin x ,所以f (x )+f (-x )=4e x +1+4e xe x +1=4. 又f'(x )=-4e x(e x +1)2+3x 2+cos x ,所以f'(x )-f'(-x )=0.所以f (2020)+f'(2020)+f (-2020)-f'(-2020)=4.故选B .18.C 因为f (-x )=e -x +e x -f'(1)(-x )(e -x -e x)=f (x ),所以f (x )是偶函数.对f (-x )=f (x )两边求导,得-f'(-x )=f'(x ),即f'(-x )=-f'(x ),则f'(x )是R 上的奇函数,故f'(0)=0,f'(-2)=-f'(2),即f'(2)+f'(-2)=0.所以f'(2)+f'(-2)-f'(0)f'(1)=0.故选C .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
甘肃省张掖市2013届高三数学一轮学案 模块1 函数与导数 第16讲 函数与方程 新人教A
版
1 / 2
第十六讲 函数与方程
一、知识梳理
1.函数零点的概念: 。
2.函数零点的性质
如果函数xfy在区间ba, 上的图象是连续不断的一条曲线,并且有0bfaf,
那么,函数xfy在区间ba,内有零点,即存在bac,,使得0cf,这个c也
就是方程0xf的根.
3.函数零点与方程根的关系
(1)函数xfy有零点.函数xfy的图象与x轴有交点的横坐标
方程0xf有实根
(2)函数)()(xgxfy的零点可以看成是函数)(xfy与)(xgy图象交点的横坐
标。
4.用二分法求方程的近似解方法:
二、同步练习
1. 若函数)0()(bbaxxf有一个零点3,那么函数axbxxg3)(2的零点是 .
2. 在用二分法求方程0123xx的一个近似解时,现在已经将一个根锁定在区间
)2,1(
内,则下一步可断定该根所在的区间为 。
3. 已知函数axxf2log)(在区间)4,2(内有零点,则实数a的取值范围是 。
4. 函数f(x)=3ax-2a+1在[-1,1]上存在一个零点,则a的取值范围是 .
5. 若函数223fxxax有一个零点为23,则1f .
6.函数2xfxex的零点所在的一个区间是( )
A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)
7. 方程ln2xx必有一个根的区间是( )
A.1,2 B.2,3 1C.,1e
D.3,
8.已知函数f(x)为偶函数,其图象与x轴有四个交点,则该函数的所有零点之和为 .
9.已知11yxxx的图形如图所示,今考虑110.01fxxxx,
则方程0fx (填上正确性的序号)
甘肃省张掖市2013届高三数学一轮学案 模块1 函数与导数 第16讲 函数与方程 新人教A
版
2 / 2
(1)有三个实根;(2)当1x时,有且仅有一个实根
(3)当10x,恰有一个实根(4)当01x,恰有一实根,
(5)当1x,恰有一个实根;
10.已知f(x)=1-(x-a)(x-b) (a<b),m,n是f(x)的零点,且m<n,则实数a,b,m,n的大小关系
是 .
11. 已知二次函数xfy有两个相异零点21,xx,且函数xfy满足
xfxf33,则21xx
。
12.已知关于x的方程22210xmxm,根据下列条件,求m的取值范围。
(1)若方程的二根分别分布在区间(-1,0)和(1,2);
(2)若方程的二根均在区间(0,1)内。
13.已知函数32()fxaxbxcxd()xR的零点是0、1、2,且在(,0)上f(x)<0.
(1)勾画出函数的草图;
(2)根据草图直接写出不等式f(x)>0,f(x)≤0解集;
(3)试判断,ab的符号。
