八年级上册第一章 分式单元测试
八年级上册数学第一章分式单元试题附(新湘教版)

八年级上册数学第一章分式单元试题附答案(新湘教版)八年级上册数学第一章分式单元试题附答案(新湘教版)种类之一分式的见解1.若分式2a+1存心义,则a的取值范围是()A.a=0B.a=1C.a≠-1D.a≠02.当a________时,分式1a+2存心义.3.若式子2x-1-1的值为零,则x=________.4.求出使分式|x|-3(x+2)(x-3)的值为0的x的值.种类之二分式的基本性质5.a,b为有理数,且ab=1,设P=aa+1+bb+1,Q=1a+1+1b+1,则P____Q(填“gt;”、“lt;”或“=”).种类之三分式的计算与化简6.化简1x-3-x+1x2-1(x-3)的结果是()7.化简x(x-1)2-1(x-1)2的结果是______________.8.化简:1+1x÷2x-1+x2x.9.先化简:1-a-1a÷a2-1a2+2a,再采纳一个合适的值代入计算.10.先化简,后求值:x-1x+2#8226;x2-4x2-2x+1÷1x2-1,其中x2-x=0.种类之四整数指数幂11.计算:(1)(-1)2013-|- (2)(m3n)-2#8226;(2m-2n-3)- 7|+9×(7-π)0+15-1;2÷(m-1n)3.种类之五科学记数法12.在日本核电站事故时期,我国某监测点监测到极微量的人工放射性核素碘-131,其浓度为0.0000963贝克/立方米.数据“0.0000963”用科学记数法可表示为__________________.种类之六解分式方程13.分式方程12x2-9-2x-3=1x+3的解为()A.x=3B.x=-3C.无解D.x=3或-314.解方程:2x-1=1x-2.15.解方程:23x-1-1=36x-2.种类之七分式方程的应用16.李明到离家2.1千米的学校参加九年级联欢会,到学校时发现演出道具还放在家中,此时距联欢会开始还有42分钟,于是他立刻步行匀速回家,在家拿道具用了1分钟,尔后立刻匀速骑自行车返回学校,已知李明骑自行车的速度是步行速度的3倍,且李明骑自行车到学校比他从学校步行到家少用了20分钟.(1)李明步行的速度是多少米/分?(2)李明可否在联欢会开始前赶到学校?17.为了提高产品的附加值,某企业计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,企业派出有关人员分别到这两间工厂认识情况,获得以下信息:信息一:甲工厂单独加工达成这批产品比乙工厂单独加工达成这批产品多用10天;信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.依照以上信息,求:甲、乙两个工厂每天分别能加工多少件新产品.答案剖析1.C2.≠-23.34.剖析要使分式的值为0,必定使分式的分子为0,且分母不为0,即|x|-3=0且(x+2)(x-3)≠0.解:要使已知的分式的值为0,x 应知足|x|-3=0 且(x+2)#8226;(x- 3)≠0.由|x|-3=0 ,得x=3 或x=-3 ,查验知:当x=3 时,(x+2)(x-3)=0 ,当x=-3 时,(x+2)(x- 3)≠0,所以知足条件的x的值是x=-3.5.=6.B剖析原式=1x-3-1x-1(x-3)=1-x-3x-1=x-1x-1-x-3x-1=2x-1.7.1x-18.解:原式=x+1x÷x2-1x=x+1x×x(x+1)(x-1)=1x-1.9.解:原式=1-a-1a×a(a+2)(a+1)(a-1)=1-a+2a+1=-1a+1.当a=3时,原式=-13+1=-14.(a的取值为0,±1,-2外的任意值)10.剖析此题是一道含有分式乘除混淆运算的分式运算,先化简,尔后把化简后的最简结果与已知条件相结合,不难发现计算方法.解:原式=x-1x+2#8226;(x+2)(x-2)(x-1)2#8226;(x+1)(x-1)1=(x-2)#8226;(x+1)=x2-x-2.当x2-x=0时,原式=0-2=-2.11.剖析先算乘方,再算乘除.解:(1)原式=-1-7+3+5=0;(2)原式=m-6n-2#8226;2-2m4n6÷m-3n3=14m-6+4-(-3)n-2+6-3=14mn.×10-513.C剖析方程的两边同乘(x+3)(x-3),得12-2(x+3)=x-3,解得x=3.查验:当x=3时,(x+3)(x-3)=0,即x=3不是原分式方程的解,故原方程无解.14.解:方程两边都乘(x-1)(x-2),得2(x-2)=x-1,去括号,得2x-4=x-1,移项,得x=3.经查验,x=3是原方程的解,所以原分式方程的解是x=3.15.解:方程两边同时乘6x-2,得4-(6x-2)=3,化简,得-6x=-3,解得x=12.查验:当x=12时,6x-2≠0,所以x=12是原方程的解.16.剖析(1)相等关系:从学校步行回家所用的时间- 从家赶往学校所用的时间=20分钟;(2)比较回家取道具所用总时间与42分的大小.解:(1)设李明步行的速度是x米/分,则他骑自行车的速度是3x米/分,依照题意,得2100x-21003x=20,解得x=70,经查验,x=70是原方程的解,所以李明步行的速度是70米/分.(2)因为210070+21003×70+1=41(分)lt;42(分),所以李明能在联欢会开始前赶到学校.17.剖析此题的等量关系为:甲工厂单独加工达成这批产品所用天数-乙工厂单独加工达成这批产品所用天数=10;乙工厂每天加工的数量=甲工厂每天加工的数量×1.5,则若设甲工厂每天加工x件产品,那么乙工厂每天加工1.5x件产品,依照题意可分别表示出两个工厂单独加工达成这批产品所用天数,进而列出方程求解.解:设甲工厂每天加工x件产品,则乙工厂每天加工1.5x件产品,依题意,得1200x-12001.5x=10,解得x=40,经查验x=40是原方程的根,所以1.5x=60.答:甲工厂每天加工40件产品,乙工厂每天加工60件产品.八年级上册数学第一章分式单元试题到这里就结束了,希望能帮助大家提高学习成绩。
湘教版八年级数学(上)第一章《分式》测试卷
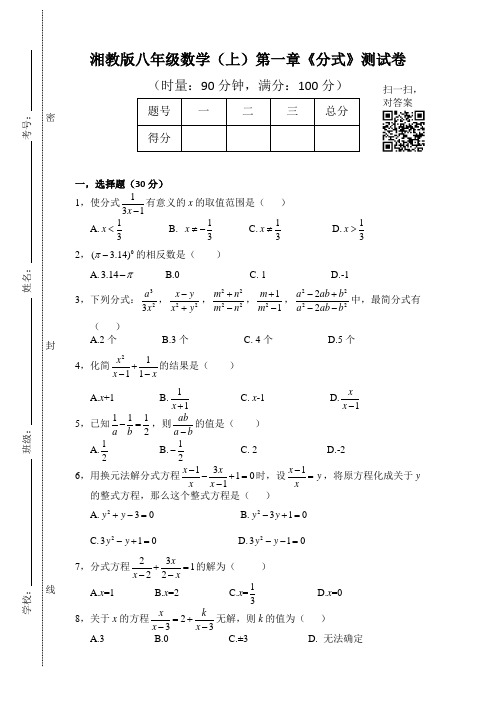
湘教版八年级数学(上)第一章《分式》测试卷(时量:90分钟,满分:100分)题号 一 二 三 总分 得分一,选择题(30分)1,使分式131x -有意义的x 的取值范围是( )A.13x <B. 13x ≠-C.13x ≠D.13x >2,0( 3.14)π-的相反数是( )A.3.14π-B.0C. 1D.-13,下列分式:323a x ,22x yx y -+,2222m n m n+-,211m m +-,222222a ab b a ab b -+--中,最简分式有 ( )A.2个B.3个C. 4个D.5个4,化简2111x x x+--的结果是( ) A.x +1 B.11x + C. x -1 D.1x x - 5,已知1112a b -=,则aba b -的值是( )A.12B.12- C. 2 D.-26,用换元法解分式方程13101x x x x --+=-时,设1x y x-=,将原方程化成关于y 的整式方程,那么这个整式方程是( )A.230y y +-=B.2310y y -+=C.2310y y -+=D.2310y y --=7,分式方程23122x x x+=--的解为( ) A.x =1 B.x =2 C.x =13D.x =08,关于x 的方程233x k x x =+--无解,则k 的值为( ) A.3 B.0 C.±3 D. 无法确定学校: 班级: 姓名: 考号:密封线扫一扫,对答案9,若22347x x ++的值为14,则21681x x +-的值是( ) A.1 B.-1 C.17- D.1510,为迎接“六一”儿童节,某儿童品牌玩具专卖店购进A ,B 两类玩具,其中A 类玩具的进价比B 类玩具的进价每个多3元,经调查:用900元购进A 类玩具与用750购进B 类玩具的数量相同,设A 类玩具的进价为m 元/个, 根据题意可列出方程是( )A.9007503m m =+B.9007503m m =+ C.9007503m m =- D.9007503m m=- 二,填空题:(24分)11,代数式13x -在实数范围内有意义,则x 的取值范围是 .12,已知分式235x x x a--+,当x =2时,分式无意义,则a = .13,当x =2时,分式11x -的值是 .14,化简221(1)(1)x x x ---的结果是 . 15,计算:11x x x -+= . 16,若分式方程1x aa x -=+无解,则a 的值为 . 17,分式方程572x x =-的解为 .18,计算222232a b aa b a b+---= .三,解答题(46分)19,(6分)化简:22()a b b a ba b a b a b---÷+-+.20、(6分)先化简,再求值:21211x x ---,其中x =-2.21、(6分)解分式方程:(1)3221x x=+(2)23111y yy y-+=-22、(8分)已知0abc≠,且0a b c++=,求111111()()()a b cb c c a a b+++++的值.23,(10分)小明解方程121xx x--=的过程如图,请指出他解答过程的错误,并写出正确的解答过程. 解:方程两边同乘以x,得:1-(x-2)=1 ①去括号,得:1-x-2=1 ②合并同类项,得:-x-1=1 ③移项,得:-x=2 ④解得:x=-2 ⑤∴原方程的解为x=-2 ⑥密24,(10分)跃壮五金商店准备从宁云机械厂购进甲,乙两种零件进行销售,若每个甲种零件的进价比每个乙种零件的进价少2元,且用80元购进甲种零件的数量与用100购进乙种零件的数量相同.(1)求每个甲种零件,每个乙种零件的进价分别为多少?(2)若该五金商店购进甲种零件的数量比购进乙种零件的数量的3倍还少5个,购进两种零件的总数量不超过95个,该五金商店每个甲种零件的售价为12元,每个乙种零件的售价为15元,则将本次购进的甲,乙两种零件全部售出后,可使销售两种零件的总利润(利润=售价-进价)超过371元,通过计算求出跃壮五金商店本次从宁云机械厂购进甲,乙两种零件有几种方案,请设计出来.。
八年级数学上册《分式》单元测试卷(含答案解析)

八年级数学上册《分式》单元测试卷(含答案解析)一.选择题1.下列各式﹣3x,,,,,,中,分式的个数为()A.1 B.2 C.3 D.42.下列各式中:①;②;③;④;⑤;⑥分式有()A.1个B.2个C.3个D.4个3.代数式中,,, +b,,分式有()A.1个B.2个C.3个D.4个4.下列约分中,正确的是()A.= B.=0 C.=x3 D.=5.把分式﹣约分结果是()A.﹣B.﹣C.﹣D.﹣6.已知=7,则的值是()A.B.2 C.D.7.下列运算中正确的是()A.= B.C.•=﹣ D.÷=8.当x=﹣2时,下列分式有意义的是()A. B.C. D.9.若分式的值为0,则x的值为()A.﹣5 B.5 C.﹣5和5 D.无法确定10.下列各式,从左到右变形正确的是()A.B. C. D.二.填空题11.当x时,分式有意义.12.约分=.13.写出一个含有字母m,且m≠2的分式,这个分式可以是.14.若分式的值为负数,则x的取值范围是.15.计算=.16.一组按规律排列的式子:,,,,,…,其中第7个式子是,第n个式子是(用含的n式子表示,n 为正整数).17.若式子的值为零,则x的值为.18.不改变分式的值,使分式的分子、分母中各项系数都为整数,=.19.化简:=.20.下列各式中中分式有个.三.解答题21.(1)=(2)=22.当x为何值时,分式的值为0?23.给定下面一列分式:,…,(其中x≠0)(1)把任意一个分式除以前面一个分式,你发现了什么规律?(2)根据你发现的规律,试写出给定的那列分式中的第7个分式.24.下列分式,当x取何值时有意义.(1);(2).25.已知实数a,b满足,6a=2010,335b=2010,求+的值.26.定义:如果一个分式能化成一个整式与一个分子为常数的分式的和的形式,则称这个分式为“和谐分式”.如==+=1+,==a﹣1+,则和都是“和谐分式”.(1)下列分式中,属于“和谐分式”的是:(填序号);①;②;③;④(2)将“和谐分式化成一个整式与一个分子为常数的分式的和的形为:=.(3)应用:已知方程组有正整数解,求整数m的值.参考答案与解析一.选择题1.解:﹣3x,,的分母中均不含有字母,因此它们是整式,而不是分式.﹣,,,分母中含有字母,因此是分式.故选:D.2.解:①分母中含有π,是具体的数,不是字母,所以不是分式;②分母中含有字母a,是分式;③是等式,不是分式;④分母中没有字母,不是分式;⑤分母中含有字母x,是分式;⑥分母中没有字母,不是分式;分式有②⑤2个,故选:B.3.解;代数式, +b的分母中含有字母,是分式,故选:B.4.解:A、=,故此选项错误;B、,无法化简,故此选项错误;C、=x4,故此选项错误;D、=,正确.故选:D.5.解:﹣=﹣=﹣.故选:C.6.解:∵=7,∴=,∴x﹣4﹣=,∴x﹣=,∵的倒数为x﹣1﹣=﹣1=,∴=,故选:C.7.解:A、=≠,不正确;B、=﹣1,正确;C、=,不正确;D、==,不正确;故选:B.8.解:A、当x=﹣2时,x+2=0,无意义;B、当x=﹣2时,有意义;C、当x=﹣2时,x2﹣4=0,无意义;D、当x=﹣2时,x2+3x+2=4﹣6+2=0,无意义.故选:B.9.解:由题意得,|x|﹣5=0,解得x=±5,当x=5时,x2﹣4x﹣5=0,分式无意义;当x=﹣5时,x2﹣4x﹣5=40≠0,分式有意义;∴x的值为﹣5.故选:A.10.解:A、2前面是加号不是乘号,不可以约分,原变形错误,故本选项不符合题意;B、原式=﹣,原变形错误,故本选项不符合题意;C、原式==,原变形正确,故本选项符合题意;D、从左边到右边不正确,原变形错误,故本选项不符合题意;故选:C.二.填空题11.解:由题意得:2x+3≠0,解得:x≠﹣,故答案为:≠﹣.12.解:=.故答案为:.13.解:含有字母m,且m≠2的分式可以是,故答案为:(答案不唯一).14.解:∵分式的值为负数,∴﹣2x+3<0,解得:x>.故答案为:x>.15.解:原式=x=.故答案为:.16.解:∵=(﹣1)2•,=(﹣1)3•,=(﹣1)4•,…∴第7个式子是,第n个式子为:.故答案是:,.17.解:∵式子的值为零,∴x2﹣1=0,(x﹣1)(x+2)≠0,解得:x=﹣1.故答案为:﹣1.18.解:分式的分子,分母同时乘以500就可得到.故答案为:.19.解:原式==,故答案为:.20.解:中分式为:、+1,﹣共3个.故答案为:3.三.解答题21.解:(1)由分式的基本性质,可得故答案为:5y.(2)分式的分子分母同时乘以﹣1,得=,故答案为2﹣x.22.解:∵分式的值为0,∴,解得x=0且x≠3,∴x=0.∴当x=0时,分式的值为0.23.解:(1)﹣÷=﹣;÷(﹣)=﹣…规律是任意一个分式除以前面一个分式恒等于;(2)∵由式子:,…,发现分母上是y1,y2,y3,…故第7个式子分母上是y7,分子上是x3,x5,x7,故第7个式子是x15,再观察符号发现第偶数个为负,第奇数个为正,∴第7个分式应该是.24.解:(1)要使分式有意义,则分母3x+2≠0,解得:x≠﹣;(2)要使分式有意义,则分母2x﹣3≠0,x≠.25.解:∵6a=2010,335b=2010,∴6ab=2010b,335ab=2010a,∴6ab×335ab═2010b+a,(6×335)ab=2010 a+b,∴ab=a+b,∴+==1.26.解:(1)①=,故是和谐分式;②=,故不是和谐分式;③=,故是和谐分式;④=,故是和谐分式;故答案为①③④;(2)===,故答案为;(3)解方程组得,∵方程组有正整数解,∴m=﹣1或﹣7.。
湘教新版八年级上册《第1章 分式》2021年单元测试卷(1)(附答案详解)

湘教新版八年级上册《第1章分式》 2021年单元测试卷(1)一、选择题(本大题共9小题,共27.0分) 1. 下列各式是分式的是( )A. 25xB. ab3C. 32xD. a2. 分式1x 2+3x 与1x 2−9的最简公分母是( )A. x(x +3)(x −3)B. x(x +1)(x +3)C. (x 2+3x)(x 2−9)D. (x +3)(x −3)3. 下列各式中,无论x 取何值,分式都有意义的是( )A. 1x 2+3B. 12x+1C.3x+1x 2D. x2x−14. 若分式|x|−3x 2−x−6的值为零,则x 的值为( )A. ±3B. 3C. −3D. 以上答案均不正确5. 下列方程中,不是分式方程的是( )A. x −2x =1 B. x 2−13=xC. xx+1+2x+2x=12D. √2x +x x 2−1=126. 已知x x 2−x+1=12,则x 2+1x 2的值为( )A. 12B. 14C. 7D. 47. 分式方程xx−1−11−x =2的解为( )A. x =2B. x =3C. x =1D. 无解8. 把方程x0.7=1.5的分母化为整数,可得方程( )A. x7=1.5B. x7=15C.10x 7=15 D.10x 7=1.59. 分式方程1x =2x+1的解是( )A. 1B. 0C. −2D. 无解二、填空题(本大题共8小题,共24.0分) 10. 化简2x+6x 2−9得______.11.当m=______时,方程mx−1=2+31−x有增根,增根是______.12.分式x3x 、3a+13a+b、m+nm2−n2、2−2x2x中,最简分式的个数是______个.13.小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等.设小明打字速度为x个/分钟,则列方程为______.14.观察下列分式:−b2a ,b5a2,−b8a3,b11a4,…,其中ab≠0,则第7个分式是______,第n个分式是______.15.某超市从我国西部某城市运进两种糖果,甲种a千克,每千克x元,乙种b千克,每千克y元,如果把这两种糖果混合后销售,保本价是______ 元/千克.16.要使分式x2−1x+1无意义,则x的取值范围是______ .17.甲乙两地相距135千米,两辆汽车从甲地开往乙地,大汽车比小汽车早出发5小时,小汽车比大汽车晚到30分钟,小汽车和大汽车的速度之比为5:2,则小汽车的速度是______千米/时.三、计算题(本大题共1小题,共10.0分)18.计算(1)y+3x+y +y−3x+y(2)a2+2a+1a2−9⋅a2+3aa+1.四、解答题(本大题共4小题,共39.0分)19.计算(x−1x −1x)÷x−2x2−x.20. 先化简,再求值:(1−1a+2)÷a 2−1a+2,其中a =3.21. 计算:x −2−y −2x −1+y −1+1y −1x .22. 是否存在x ,使得当y =5时,分式x+yx 2−y 2的值为0?若存在,求出x 的值;若不存在,请说明理由.答案和解析1.【答案】A【解析】解:25x是分式,符合题意;ab3是整式,不符合题意;32x是整式,不符合题意;a是整式,不符合题意;故选:A.分式的定义:一般地,如果A、B(B不等于零)表示两个整式,且B中含有字母,那么式子AB就叫做分式,再根据分式的定义判别选项中的每一个式子即可求解.本题考查分式的定义,熟练掌握分式的定义,能够准确判断分式是解题的关键.2.【答案】A【解析】解:∵1x2+3x =1x(x+3),1 x2−9=1(x+3)(x−3),∴1x2+3x 与1x2−9的最简公分母是x(x+3)(x−3),故选:A.把各个分母分解因式,找出各个因式的最高次幂,乘积就是分母的最简公分母.本题考查了最简公分母的找法.注意:把各个分母分解因式,找出各个因式的最高次幂,乘积就是分母的最简公分母.3.【答案】A【解析】解:A、无论x取何值,x2+3≥3,分式都有意义,故本选项符合题意;B、x=−12时,2x+1=0,分式无意义,故本选项不符合题意;C、x=0时,x2=0,分式无意义,故本选项不符合题意;D、x=12时,2x−1=0,分式无意义,故本选项不符合题意.故选:A.根据分式有意义,分母不等于0对各选项分析判断即可得解.本题考查了分式有意义的条件,从以下三个方面透彻理解分式的概念:(1)分式无意义⇔分母为零;(2)分式有意义⇔分母不为零;(3)分式值为零⇔分子为零且分母不为零.4.【答案】C【解析】解:根据题意得|x|−3=0且x2−x−6≠0,解|x|−3=0得x=3或−3,而x=3时,且x2−x−6=9−3−6=0,所以x=−3.故选:C.根据分式的值为零的条件得到|x|−3=0且x2−x−6≠0,先解解|x|−3=0得x=3或−3,然后把x的值代入x2−x−6进行计算可确定x的值.本题考查了分式的值为零的条件:分式的分子为0,分母不为0,则分式的值为0.5.【答案】B【解析】解:A、方程分母中含有未知数x,是分式方程,故本选项不符合题意;B、方程分母中不含有未知数x,不是分式方程,故本选项符合题意;C、方程分母中含有未知数x,是分式方程,故本选项不符合题意;D、方程分母中含有未知数,是分式方程,故本选项不符合题意.故选:B.根据分式方程的定义:分母中含有未知数的方程叫做分式方程进行判断.本题考查了分式方程的定义,判断一个方程是否为分式方程,主要是依据分式方程的定义,也就是看分母中是否含有未知数(注意:仅仅是字母不行,必须是表示未知数的字母).6.【答案】C【解析】[分析]先由xx2−x+1=12左右两边求倒数,得到x−1+1x=2,即x+1x=3,再根据完全平方公式可求x2+1x2的值.此题主要考查了分式的值,关键是要熟练掌握完全平方公式.[详解]解:xx2−x+1=12,x2−x+1x=2,x−1+1x =2,即x+1x=3,x2+1x2=(x+1x)2−2=9−2=7.故选C.7.【答案】B【解析】解:分式方程可变形为:xx−1+1x−1=2,去分母得:x+1=2(x−1),去括号得:x+1=2x−2,移项得:x−2x=−2−1,合并同类项得:−x=−3,把x的系数化为1得:x=3,检验:把x=3代入最简公分母x−1=3−1=2≠0,故原分式方程的解为:x=3.故选:B.首先把分式方程可变形为:xx−1+1x−1=2,两边同时乘以最简公分母x−1去分母,然后去括号、移项、合并同类项、把x的系数化为1,即可算出x的值,然后再检验.此题主要考查了分式方程的解法,关键是不要忘记检验,这是同学们最容易出错的地方.8.【答案】D【解析】解:把方程x0.7=1.5的分母化为整数,分子、分母上同时乘以10,得:10x7=1.5.故选:D.把方程的分母化为整数,方法是分子、分母上同时乘以10,化简的依据是分式的基本性质,同时在分子、分母上同时乘以或除以同一个非0的数或整式,分式的值不变.本题考查了分式的基本性质,要注意与解方程的去分母区别,去分母是依据的等式的基本性质.9.【答案】A【解析】解:去分母得:x+1=2x,解得:x=1,经检验x=1是分式方程的解.故选:A.分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.10.【答案】2x−3【解析】解:2x+6x2−9=2(x+3) (x+3)(x−3)=2x−3.故答案为:2x−3.首先分别把分式的分母、分子因式分解,然后约去分式的分子与分母的公因式即可.此题主要考查了约分问题,要熟练掌握,解答此题的关键是要明确:①分式约分的结果可能是最简分式,也可能是整式.②当分子与分母含有负号时,一般把负号提到分式本身的前面.③约分时,分子与分母都必须是乘积式,如果是多项式的,必须先分解因式.11.【答案】−3x=1【解析】解:去分母得:m=2x−2−3,由分式方程有增根,得到x−1=0,即x=1,把x=1代入整式方程得:m=−3,故答案为:−3;x=1分式方程去分母转化为整式方程,由分式方程有增根,求出x的值,代入整式方程即可求出m的值.此题考查了分式方程的增根,增根问题可按如下步骤进行:①让最简公分母为0确定增根;②化分式方程为整式方程;③把增根代入整式方程即可求得相关字母的值.12.【答案】1【解析】解:x3x=x2.3a+13a+b的分子、分母都不能再分解,且不能约分,是最简分式;m+n m2−n2=m+n(m+n)(m−n)=1m−n;2−2x 2x =2(1−x)2x=1−xx.综上所述,上述分式中,是最简分式的个数是:1.故答案是:1.最简分式的标准是分子、分母中不含有公因式,不能再约分.本题考查了最简分式.分式的化简过程,首先要把分子、分母分解因式,观察分子、分母中有无公因式.13.【答案】120x =180x+6【解析】解:设小明打字速度为x个/分钟,120 x =180x+6.故答案为:120x =180x+6.设小明打字速度为x个/分钟,根据小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等,可列出方程.本题考查理解题意的能力,设出打字速度,以时间做为等量关系列方程.14.【答案】−b20a7(−1)n×b3n−1a n【解析】解:∵−b2a ,b5a2,−b8a3,b11a4,…,∴系数为:(−1)n,分母为底数为a,次数是连续的正整数,分子是底数为b,次数是第1个是:2,第2个是3+2,第3个是:6+2,…则第7个分式是:−b20a7,第n个分式是:(−1)n×b(n−1)×3+2a n=(−1)n×b3n−1a n.故答案为:−b20a7,(−1)n×b3n−1a n.利用已知分式的系数以及分母与分子次数的变化规律,进而求出即可.此题主要考查了分式的定义,正确得出分子与分母的变化规律是解题关键.15.【答案】ax+bya+b【解析】解:甲种a千克,每千克x元,乙种b千克,每千克y元,保本价=(ax+by)÷(a+b)=ax+bya+b.保本价即要计算其平均价=总价格÷总质量=ax+bya+b.注意代数式的正确书写:出现除法写成分数线的形式.列代数式的关键是正确理解文字语言中的关键词,找到其中的数量关系.16.【答案】x=−1【解析】解:∵分式x2−1x+1无意义,∴x+1=0,解得x=−1.故答案为:x=−1.根据分式无意义,分母等于0列方程求解即可.本题考查了分式有意义的条件,从以下三个方面透彻理解分式的概念:(1)分式无意义⇔分母为零;(2)分式有意义⇔分母不为零;(3)分式值为零⇔分子为零且分母不为零.17.【答案】45【解析】解:依题意,设小汽车速度为5x千米/时,则大汽车速度为2x千米/时,则:1352x −1355x=5−12,解方程得x=9,经检验:x=9是原方程的根,5x=45,答:小汽车的速度为45千米/时.根据小汽车和大汽车的速度之比为5:2,设小汽车速度为5x千米/时,则大汽车速度为2x千米/时,由大汽车用的时间−小汽车用的时间=5−0.5,列方程求x,再表示大汽车的速度.根据比例设未知数,由时间关系,建立等量关系列方程求解,是解题的关键.18.【答案】解:(1)原式=y+3+y−3x+y=2yx+y;(2)原式=(a+1)2(a+3)(a−3)⋅a(a+3)a+1=a(a+1)a−3.【解析】(1)原式利用同分母分式的加法法则计算即可得到结果;(2)原式约分即可得到结果.此题考查了分式的乘除法,以及加减法,熟练掌握运算法则是解本题的关键.19.【答案】解:原式=x−2x ⋅x(x−1)x−2=x−1.【解析】首先计算括号里面的减法,然后再计算括号外的除法即可.此题主要考查了分式的混合运算,关键是掌握分式的混合运算顺序及注意问题1.注意运算顺序:分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.2.注意化简结果:运算的结果要化成最简分式或整式.分子、分母中有公因式的要进行约分化为最简分式或整式.20.【答案】解:原式=a+2−1a+2⋅a+2 (a+1)(a−1)=1a−1,当a=3时,原式=12【解析】【试题解析】先根据分式的混合运算法则化简.然后代入计算即可.本题考查分式的化简求值,解题的关键是记住分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的.21.【答案】解:原式=1x2−1y21x−1y+1y−1x=(1x+1y)(1x−1y)1x+1y+1y−1x=1x −1y+1y−1x=0【解析】根据分式运算的法则以及负整数指数幂的意义即可求出答案.本题考查学生的计算能力,涉及因式分解,分式约分与分式加减等知识,负整数指数幂的意义,属于中等题型22.【答案】解:不存在,理由如下:把y=5代入x+yx2−y2,得x+y x2−y2=x+5x2−52=x+5(x+5)(x−5).当x+yx2−y2=0,即x+5(x+5)(x−5)=0时,x+5=0且(x+5)(x−5)≠0,则x无解.即这样的x的值不存在.【解析】分式的值为0,分子为0且分母不为0.本题考查了分式的值为零的条件.若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.。
1数学八年级上册第一章《分式》_整章水平测试题(B)

八年级上册分式整章水平测试题一、填空: (每空3分,共18分)1. 当x ________时,分式11x x +-有意义,当x ________时,分式11x x +-的值为0. 2. 化简=-+-ab b b a a . 3. 约分:)(20)(15322b c a c b a --= 4. 如果分式x+16 的值为 -3,则x 的值为 __________. 5. 生物学家发现一种病毒的长度约为0.000043㎜,用科学记数法表示0.000043的结果 为 ㎜.二、选择:(每题3分,共15分)6. 在下列各式ma m xb a x x a ,,,,,2221x 34323--++π中,是分式的有( ) A.2个 B.3个 C.4个 D.5个7. 下列各式中,正确的是( ) A.3232-=-+x x B. 1112-=--x x x C.1=-+-b a a b D. b a b a b a b a +-=+--- 8. 下列运算,正确的是( )A. 01.01.02=- B. 8)21(3-=- C. 4)2(2=-- D. m n mn 212)(=-- 9. 当1a =-时,分式22a a a a+-( ) A.等于零 B.等于1 C.等于1- D.没有意义10 . 有游客m 人,如果每n 个人住一个房间,结果还有一个人无房住,则客房有( )间 A.n m 1- B.1-n m C.n m 1+ D.1+nm11. 4121222-+-⨯--x x x x x 12. x xx x x 224422-+++13. 200710)1()23()14.3(-+-+--π 14. 2211b a ab b a -÷⎪⎭⎫ ⎝⎛--四、先化简,再求值:(每题7分)15. xx x x x x +++÷--2221211,其中2x =-.五、解分式方程:(每题7分,共28分)16. 1215x x=- 17. x x x -=--313218. 2141.11x x x +-=--19. 1112132-=+--x x x六、列方程解应用题:(8分)同一条高速公路沿途有三座城市A 、B 、C ,C 市在A 市与B 市之间,A 、C 两市 的距离为540千米,B 、C 两市的距离为600千米.现有甲、乙两辆汽车同时分别 从A 、B 两市出发驶向C 市,已知甲车比乙车的速度慢10千米/时,结果两辆车同 时到达C 市.求两车的速度.七、附加题(10分)已知m x x =+-1,求22-+x x 的值.。
第1章 分式数学八年级上册-单元测试卷-湘教版(含答案)

第1章分式数学八年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、如果把分式中的和都扩大3倍,那么分式的值 ( )A.扩大6倍B.扩大3倍C.缩小3倍D.不变2、要使分式有意义,则x的取值范围是()A.x>2B.x<2C.x≠0D.x≠23、关于分式方程的解,下列说法正确的是()A.解是x=2B.解是x=4C.解是x=﹣4D.无解4、若代数式有意义,则实数的取值范围是()A. B. C. D.5、下列各运算中,正确的是()A.3a+2a=5a 2B.(-3a 3)2=9a 6C.a 4÷a 2=a 3D.(a+2)2=a 2+46、已知关于的分式方程的解为非正数,则的取值范围是()A. B. C. D.7、化简- 的结果为( )A. B. C. D.8、下列运算及判断正确的是()A.﹣5×÷(﹣)×5=1B.方程(x 2+x﹣1)x+3=1有四个整数解 C.若a×567 3=10 3, a÷10 3=b,则a×b= D.有序数对(m 2+1,m)在平面直角坐标系中对应的点一定在第一象限9、化简÷的结果是()A. B. C. D.2(x﹣1)10、下列运算中,正确的是()A.2xa+xa=3x 2a 2B.(a 2)3=a 6C.3a•2a=6aD.3﹣2=﹣611、函数的自变量的取值范围是()A. B. C.且 D.12、泰山风景区推出“智慧泰山”,是未来社会的基础设施,是国家战略. 网络峰值速率是网络峰值速率的10倍,在峰值速率下传输1000兆数据,;网络比网络快约90秒,求这两种网络的蜂值速率,设网络的峰值速率为每秒传输x兆数据,依题意,可列方程是()A. B. C. D.13、若分式在实数范围内有意义,则的取值范围为( )A. B. C. D.且14、计算:()A. B. C. D.15、分式的值是零,那么x的值是( )A.-1B.0C.1D.±1二、填空题(共10题,共计30分)16、若分式值为0,则________.17、已知10m=3,10n=5,则103m﹣n=________.18、若分式的值为0,则x的值是________.19、计算:+(﹣3)2=________.20、方程﹣1=1的解是________.21、已知,则________.22、关于的方程的解是正数,则的取值范围是________.23、9月25日,北京大兴机场正式投运,国庆期间,小罗一家准备自驾去北京游玩,顺便领略一下大兴国际机场的高科技及智慧.手机导航系统推荐了两条线路,线路一全程,线路二全程,汽车在线路二上行驶的平均时速是线路一平均时速的倍,线路二的用时预计比线路一用时少2小时,设汽车在线路一行驶的平均速度为,则所列方程为________.24、计算:=________25、关于x的分式方程的解是正数,则m的取值范围为________.三、解答题(共5题,共计25分)26、化简:27、化简:(1)(2a+3b)(3a﹣2b)﹣(3a+2b)2﹣a(a﹣b);(2)÷(﹣28、已知x=﹣4时,分式无意义,x=2时,此分式的值为零,求分式的值.29、计算(1)(﹣a3)2÷a2(2)|﹣3|﹣(﹣1)0÷()﹣2 .30、计算:(1)(xy﹣x2)÷(2).参考答案一、单选题(共15题,共计45分)1、D2、D3、D4、A5、B6、A7、D8、B10、B11、C12、A13、B14、C15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题,共计25分)26、27、28、29、30、。
第1章 分式数学八年级上册-单元测试卷-湘教版(含答案)
第1章分式数学八年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、下列运算正确的是()A.3a+4b=12aB.(ab 3)2=ab 6C.(5a 2﹣ab)﹣(4a 2+2ab)=a 2﹣3abD.x 12÷x 6=x 22、已知关于x的方程=3无解,则m的值是( )A.0B.2C.4D.-43、下列计算正确的是()A.a 3•a 2=a 6B.(π﹣3.14)0=1C.()﹣1=﹣2D.=±34、下列运算正确的是( )A.a².a 3=a 6B.(-a) 8÷(-a) 4=a 2C.(-2a²) 3=-6a 6D.a -2= (a≠0)5、﹣()]=中,在()内填上的数是()A. B. C. D.6、化简的结果是()A. B. a C. a﹣1 D.7、为使有意义,x的取值范围是()A.x>B.x≥C.x≠D.x≥且x≠8、下列计算正确的是()A. B. C. D.9、下列运算正确的是()A. B. C.D.10、已知,那么 ( )A.6B.7C.9D.1011、若分式的值为0,则x的值为( )A. 或B.C.D.12、下列计算正确的是()A.x 2•x=x 3B.x+x=x 2C.(x 2)3=x 5D.x 6÷x 3=x 213、把,,通分的过程中,不正确的是()A.最简公分母是(x-2)(x+3) 2B.C. D.14、使分式有意义,x的取值范围是()A.x>﹣2B.x≠﹣2C.x≠0D.x≠215、计算x6÷x2正确的结果是()A.3B.x 3C.x 4D.x 8二、填空题(共10题,共计30分)16、(﹣2)﹣1=________.17、约分:=________18、计算:=________19、计算:的结果是________.20、当x=________ 时,分式的值为0.21、分式, , 的最简公分母是________.22、若关于x的方程+ =2的解不大于8,则m的取值范围是________.23、若,则________.24、计算下列各数的值:2﹣1=________;5﹣2=________;(π﹣3)0=________.25、化简:÷=________.三、解答题(共5题,共计25分)26、计算:|﹣2|﹣2cos60°+()﹣1﹣(π﹣)0.27、甲、乙两工程队共同完成一项工程,乙队先单独做1天后,再由甲、乙两队合作2天就完成了全部工程,已知甲队单独完成这项工程所需的天数是乙队单独完成工程所需天数的2倍,则甲、乙两工程队单独完成工程各需多少天?28、先化简再求值:÷(﹣x﹣2),其中x=﹣3.29、先化简,再求值:,其中.30、小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等.求小明和小张每分钟各打多少个字?参考答案一、单选题(共15题,共计45分)1、C2、D3、B4、D5、D6、B7、D8、D9、C10、B11、C12、A13、D15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、。
第1章 分式 单元测试卷 2022-2023学年湘教版数学八年级上册
2022-2023学年湘教新版八年级上册数学《第1章 分式》单元测试卷一.选择题(共10小题,满分30分)1. 若分式2(1)(2)44x x x x +--+的值为0,则x 的值为( )A. 1-B. 2C. 2或1-D. 12. 在1x ,+m n m ,25ab ,23x π中,分式有( )A. 2个 B. 3个 C. 4个 D. 1个3. 如果把分式xy x y+中的x 和y 都扩大为原来的4倍,那么分式的值( )A. 扩大为原来的4倍B. 扩大为原来的2倍C. 不变D. 缩小为原来的124. 若将分式2223x x y -与分式2()x x y -通分后,分式2()x x y -的分母变为2(x ﹣y )(x+y ),则分式2223x x y-的分子应变为( )A. 6x 2(x ﹣y )2 B. 2(x ﹣y ) C. 6x 2 D. 6x 2(x+y )5. 分式216x 与13xy -的最简公分母是( )A. 36x y B. 26x y C. 218x y D. 318x y6. 计算a b b ac⋅的结果是( )A. ab abcB. a cC. 1cD. 07. 计算:0(20)-=( )A. 0B. 20C. 1D. 20-8. 若m -n =2,则代数式222m n m m m n-⋅+的值是( )A. -2B. 2C. -4D. 49. 给出以下方程:314x -=,32x =,3152x x +=+,132x x -=,其中分式方程的个数是( )A. 1B. 2C. 3D. 410. 已知113a b +=,114b c+=,115c a +=,则abc ab bc ca =++( )A.13 B. 14C. 15 D. 16二.填空题(共10小题,满分30分)11. 关于x 的方程2312x x x --=-的解为______.12. 已知两分式221x x -+11x +中间阴影覆盖了运算符号.(1)若覆盖了“+”,其运算结果为______;(2)若覆盖了“÷”,并且运算结果为1,则x 的值为______.13. 已知分式5x n x m ++(m ,n 为常数)满足表格中的信息:x 的取值2-0.4q 分式的值无意义03则q 的值是 _____.14. 当x ___________时,分式12x -的值为正数.15. 若关于x 的方程1222x m x x++=--有增根,则m 的值是______________.16. 若0(99)a =,1(0.1)b -=-,25()3c -=-,那么a 、b 、c 三数的大小为 ______.(用“<”连接)17. 代数式12x M x+÷+化简的结果是2x +,则整数M =______.当<2x -时,12x x++______12(填“>”“<”“=”)18. 下列四个分式:22x y x y ++、22x y x y --、22x y x y -+、22x y x y +-,其中最简分式有__________个.19. 受疫情的影响,“84”消毒液需求量猛增,某商场用4000元购进一批“84”消毒液后,供不应求,商场又用6750元购进第二批这种消毒液,所购的瓶数是第一批瓶数的1.5倍,但每瓶单价贵了1元,则该商场第一批购进“84”清毒液每瓶的单价为______元.20. 化简:2222444x y x xy y--+=_____.三.解答题(共6小题,满分90分)21. 已知分式236x x x ---.(1)当x 为何值时,此分式有意义?(2)当x 为何值时,此分式的值为零?22. 计算(1)22346()2x xy y x⋅-;(2)2221221a a a a a a-⋅-++.23. 计算:(1)2301()(48)2-÷⨯; (2)2213(3)34ab ab a b ⋅-24. 先化简,再求值:211211a a a a ⎛⎫÷- ⎪+++⎝⎭,其中1a =.25. 为做好新冠肺炎疫情防控,某学校购入了一批洗手液与消毒液.购买洗手液花费4000元,购买消毒液花费3000元,购买的洗手液瓶数是消毒液瓶数的2倍,每瓶消毒液的价格比每瓶洗手液的价格高5元.(1)求一瓶洗手液的价格与一瓶消毒液的价格分别是多少元?(2)由于疫情还未结束,学校决定再次购入一批相同质量品牌的洗手液与消毒液,洗手液和消毒液的瓶数分别都比第一次的购入量多100瓶.适逢经销商进行价格调整,每瓶洗手液的价格比第一次的价格降低5%4a,每瓶消毒液的价格比第一次的价格降低%a,最终第二次购买洗手液与消毒液的总费用只比第一次购买洗手液与消毒液的总费用多350元,求a的值.26. 已知A、B两地相距a km甲乙两人分别从A、B两地同时匀速出发,若相向而行,则经过a min后两人相遇,若同向而行,则经过b(b a>)min后甲追上乙.(1)试用含a,b的代数式表示甲、乙两人的速度v甲,v乙;(2)若73VV=甲乙,求ab的值;(3)若两人相向而行,第一次相遇后继续按原方向前进,其中甲到达B地后按原路返回.直接写出甲、乙从第一次相遇到再次相遇所需的时间.2022-2023学年湘教新版八年级上册数学《第1章 分式》单元测试卷一.选择题(共10小题,满分30分)【1题答案】【答案】A【解析】【分析】根据分式值为零且分式有意义的条件求解即可.【详解】解:∵分式2(1)(2)44x x x x +--+的值为0, ∴(x +1)(x -2)=0,且x 2-4x +4≠0,解得x =-1或x =2,且x ≠2,∴x =-1故选:A .【点睛】此题考查了分式值为零的条件,分式有意义的条件,熟记分式的知识是解题的关键.【2题答案】【答案】A【解析】【分析】根据一般地,如果A 、B 表示两个整式,并且B 中含有字母,那么式子A B叫做分式判断即可.【详解】解:在1x ,+m n m ,25ab ,23x π中,分式有:1x ,+m n m共2个,其余2个是整式,故选:A .【点睛】本题考查了分式的定义,注意π是数字,熟练掌握分式的定义是解题的关键.【3题答案】【答案】A【解析】【分析】根据分式的基本性质,进行计算即可解答.【详解】解:由题意得:44444x y xy x y x y⋅=++,∴如果把分式xy x y+中的x 和y 都扩大为原来的4倍,那么分式的值扩大为原来的4倍,故选:A .【点睛】本题考查了分式的基本性质,熟练掌握分式的基本性质是解题的关键.【4题答案】【答案】C【解析】【分析】分式2223x x y -与分式 2()x x y -的公分母是2(x+y )(x ﹣y ),据此作出选择.【详解】解:因为分式2()x x y - 与分式2223x x y- 的公分母是2(x+y )(x ﹣y ),所以分式2()x x y -的分母变为2(x ﹣y )(x+y ),则分式2223x x y- 的分子应变为6x 2故选:C .【点睛】本题考查了通分.通分的关键是确定最简公分母.①最简公分母的系数取各分母系数的最小公倍数.②最简公分母的字母因式取各分母所有字母的最高次幂的积.【5题答案】【答案】B【解析】【分析】两个分母中系数的最小公倍数为6,所有字母因式x 与y 的最高次幂分别是x 2、y ,这三者的乘积则是最简公分母.【详解】分式216x 与13xy -的最简公分母是26x y ,故选:B .【点睛】本题考查了分式的最简公分母,知道如何找最简公分母是解题的关键.【6题答案】【答案】C【解析】【分析】根据分式的乘法运算法则来求解.【详解】解:1a b ab b ac abc c⋅==.故选:C .【点睛】本题主要考查了分式乘法的运算法则,理解约分是解答关键.【7题答案】【答案】C【解析】【分析】根据零指数幂的意义计算即可.【详解】解:0(20)1-= ,故选:C .【点睛】本题考查零指数幂的意义,掌握零指数幂公式01(0)a a =≠是解题的关键.【8题答案】【答案】D【解析】【分析】先因式分解,再约分得到原式=2(m -n ),然后利用整体代入的方法计算代数式的值.【详解】解:原式m n m n m +-=()()•2m m n+=2(m -n ),当m -n =2时,原式=2×2=4.故选:D .【点睛】本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.【9题答案】【答案】B【解析】【分析】利用分式方程的定义:分母中含有未知数的方程,进行逐一判断即可.【详解】解:314x -=中分母不含未知数,不是分式方程;32x=中分母含有未知数,是分式方程;3152x x +=+中分母含有未知数,是分式方程;132x x -=中分母不含未知数,不是分式方程,共有两个是分式方程,故B 正确.故选:B .【点睛】本题主要考查的是分式方程的定义,掌握定义并进行准确判断是解题的关键.【10题答案】【答案】D【解析】【分析】先把原条件通分变形可得3,4,5,ac bc ab ac ab bc abc abc abc +++===再把三式相加,再取倒数即可得到答案.【详解】解:∵113a b +=,114b c +=,115c a +=,∴3,4,5,a b b c a c ab bc ac+++=== ∴3,4,5,ac bc ab ac ab bc abc abc abc+++===22212,ac bc ac abc++∴= 6,ac bc ab abc++∴= ∴ 1.6abc ab bc ca =++故选D【点睛】本题考查的是分式的求值,掌握“倒数法求解分式的值”是解本题的关键.二.填空题(共10小题,满分30分)【11题答案】【答案】45x =【解析】【分析】根据解分式方程的规则进行求解即可,最后必须检验.【详解】解:去分母得:2(2)(2)3x x x x ---=,整理得:54x =,解得:45x =,经检验:4424(2)(2)05525x x -=⨯-=-≠,∴45x =是原方程的解.故答案为:45x =.【点睛】本题考查了解分式方程,熟练掌握解分式方程的步骤是解题关键,注意一定要对求出来的未知数的值进行检验.【12题答案】【答案】①. 1x - ②. 【解析】【分析】根据分式的加法与解分式方程分别计算即可求解.【详解】(1)221x x -++11x +()()21121111x x x x x x +--+===-++;(2)221x x -+÷111x =+,221111x x x -+⨯=+;221x -=,x ∴=,经检验x =是原方程的解,故答案为:1x -,【点睛】本题考查了分式的混合运算,解分式方程,正确的计算是解题的关键.【13题答案】【答案】4【解析】【分析】由表格中的数据,结合分式值无意义及分式值为0的条件可求解m ,n 值,即可求解分式,利用x q =时,5232q q -=+,计算可求解.【详解】解:由表格可知:当2x =-时0x m +=,且当0.4x =时,50x n +=,解得2m =,2n =-,∴分式为522x x -+,当x q =时,5232q q -=+,解得4q =,经检验,4q =是分式的解,故答案为:4.【点睛】本题主要考查分式的值,分式有意义的条件及分式的值为零的条件,解分式方程,求解m ,n 值是解题的关键.【14题答案】【答案】2x >【解析】【分析】根据题意可知分子10>,只要分母20x ->即可求解.【详解】解:∵分式12x -的值为正数,∴20x ->,解得2x >.故答案为:2x >.【点睛】本题考查了分式的值,根据题意列出不等式是解题的关键.【15题答案】【答案】-1【解析】【分析】利用分式方程解法的一般步骤解分式方程,令方程的解为2得到关于m 的方程,解方程即可得出结果.【详解】解:去分母得:1−(x +m )=2(x −2),去括号得:1−x −m =2x −4,移项,合并同类项得:−3x =m −5,∴53m x -=.∵关于x 的方程1222x m x x ++=--有增根,∴x =2∴523m -=,∴m =−1.故答案为:−1.【点睛】本题主要考查了解分式方程,分式方程的增根,理解分式方程增根的意义解答是解题的关键.【16题答案】【答案】b<c<a【解析】【分析】利用零指数幂的意义,负整数指数幂的意义分别计算a ,b ,c 的值,再进行大小比较,即可得出答案.【详解】解:∵0(99)a =,1(0.1)b -=-,25()3c -=-,∴1a =,10b =-,925c =,又∵910125-<<,∴b<c<a ,故答案为:b<c<a .【点睛】本题考查零指数幂,负整数指数幂,解题的关键是熟练掌握:01a =,1-=m ma a .【17题答案】【答案】①. 1x +##1x + ②. >【解析】【分析】根据题意可得()122x M x x+=⋅++,即可求解;然后把12x x ++变形为112x-+,即可求解.【详解】解:根据题意得:()122x M x x +=⋅++1x =+;∵12111222x x x x x++-==-+++,∵<2x -,即20x +<∴102x<+,∴102x->+,∴1112x ->+,即112x x+>+,∴1122x x +>+.故答案为:1x +,>【点睛】本题主要考查了分式的乘法运算以及化简,熟练掌握分式的运算法则是解题的关键.【18题答案】【答案】2##两【解析】【分析】最简分式是分式的分子、分母没有非零的公因式,即不能再约分,据此判断即可解答.【详解】解:22x y x y ++是最简分式,22x y x y --()()x y x y x y -=+-1x y=+,不是最简分式,22x y +是最简分式,22x y x y +-()()x y x y x y +=+-1x y=-,不是最简分式,故最简分式有2个,故答案为:2.【点睛】本题考查最简最简分式,判断一个分式是最简分式,主要看分式的分子、分母是不是有公因式.【19题答案】【答案】8【解析】【分析】设该商场第一批购进“84”清毒液每瓶的单价为x 元,根据所购的瓶数是第一批瓶数的1.5倍列分式方程解答.【详解】解:设该商场第一批购进“84”清毒液每瓶的单价为x 元,由题意得400067501.51x x ⨯=+,解得x =8,经检验,x =8是原方程的解,故答案为:8.【点睛】此题考查了分式方程的实际应用,正确理解题意列得分式方程是解题的关键.【20题答案】【答案】22x y x y +-【解析】【分析】先根据平方差公式和完全平方公式把分子与分母进行整理,然后进行约分即可.【详解】解:原式()()()2222x y x y x y -+=-2x y=-,故答案为:22x y x y +-.【点睛】此题考查了约分,用到的知识点是平方差公式和完全平方公式,关键是把要求的式子进行变形.三.解答题(共6小题,满分90分)【21题答案】【答案】(1)x ≠3且x ≠﹣2 (2)x =﹣3【解析】【分析】(1)根据分式有意义的条件是分母不等于零列出不等式计算即可;(2)根据分式值为零的条件是分子等于零且分母不等于零列式计算.【详解】(1)由题意得:x 2﹣x ﹣6≠0,解得:x ≠3且x ≠﹣2;(2)由题意得:|x |﹣3=0且x 2﹣x =6≠0,解得:x =﹣3,则当x =﹣3时,此分式的值为零.【点睛】本题考查了是的是分式有意义和分式值为零的条件,掌握分式有意义的条件和分式值为零的条件是解题的关键.【22题答案】【答案】(1)334x y- (2)2a 1-【解析】【分析】(1)先计算乘方,再计算乘法并化简;(2)先将分子与分母分解因式,再计算乘法并化简即可.【小问1详解】原式=623468x xy y x-⋅ =334x y-;【小问2详解】原式=()()()()211211a a a a a a +-⋅+- =2a 1-.【点睛】此题考查了分式的计算,正确掌握分式的计算法则及运算顺序是解题的关键.【23题答案】【答案】(1)116;(2)233214a b a b -【解析】【分析】(1)先算乘方,再算括号,后算除法即可;(2)根据单项式与多项式的乘法法则计算即可;【详解】解:(1)原式=4(641)÷⨯=464÷=116;(2)原式=221313343ab ab ab a b ⨯⨯-=233214a b a b -.【点睛】本题考查了负整数指数幂、零指数幂的意义,以及单项式与多项式的乘法计算,熟练掌握运算法则是解答本题的关键.【24题答案】【答案】11a +,12【解析】【分析】根据分式的运算法则,先计算括号里的,再将除法转化为乘法,对分子分母因式分解后约分化简,再将1a =代入化简得代数式即可求解.【详解】解:211211a a a a ⎛⎫÷- ⎪+++⎝⎭2112111a a a a a a +⎛⎫=÷- ⎪++++⎝⎭ 2211a a a a a =÷+++()211aa aa +=⨯+11a =+,将1a =代入上式得:原式11112==+.【点睛】本题考查分式的化简求值,熟练掌握分式的运算法则及运算顺序是解决问题的关键.【25题答案】【答案】(1)一瓶洗手液的价格为 10元,一瓶消毒液的价格为15 元 (2)20【解析】【分析】(1)设一瓶洗手液的价格为x 元,则一瓶消毒液的价格为(x +5)元.根据题意可列出关于x 的分式方程,求出x 即可.(2)先求出第二次购入洗手液和消毒液各多少瓶,再结合题意列出关于a 的一元一次方程,解出a 即可.【小问1详解】解:设一瓶洗手液的价格为x 元,则一瓶消毒液的价格为(x +5)元.根据题意可列方程:4000300025x x =⨯+,解得:10x =,经检验8x =是原方程得解.∴一瓶洗手液的价格为10元,一瓶消毒液的价格为8+7=15元,答:一瓶洗手液的价格为10元,一瓶消毒液的价格为15元.【小问2详解】解:第二次购入洗手液400010050010+=瓶,购入消毒液300010030015+=瓶.根据题意可列等式:550010(1%)30015(1%)400030003504a a ⨯⨯-+⨯⨯-=++.解得:20a =.【点睛】本题考查一元一次方程和分式方程的实际应用.根据题意找准等量关系,列出相应方程是解答本题的关键.【26题答案】【答案】(1)v 甲=2a b b +,v 乙=2b a b - (2)25 (3)()b b a a b -+min【解析】【分析】(1)根据同向而行和相向而行分别列出方程,解之即可;(2)根据(1)中结果,得到73a b b a +=-,解之即可;(3)根据题意列出算式,再计算可得结果.【小问1详解】解:由已知可得()()a v v ab v v a ⎧+=⎪⎨-=⎪⎩甲乙甲乙,2a b v b +∴=甲,2b a v b-=乙;【小问2详解】73v a b v b a +==-甲乙,∴()()37a b b a +=-,∴3377a b b a +=-,∴104a b =,∴25a b =;【小问3详解】2()222b a a b b a a b a b b b-+-⋅⨯÷-=-.答:甲、乙从第一次相遇到再次相遇所需的时间为()min b a -.【点睛】本题考查了二元一次方程组,列分式及其计算,熟练运用路程公式是解题的关键.。
湘教版数学八年级上册第一章《分式》测试卷
初中数学试卷金戈铁骑整理制作湘教版八年级数学(上)第一章《分式》测试卷一、选择题(30分)1、使分式1存心义的x的取值范围是()3x1A.x1;B.x1;C.x1;D.x1;33332、(3.14)0的相反数是()A.;B.;C.1;;3、以下分式:a3,x,m2n2,m1,a22abb2中,最简分式有:3 x2x22m2n2m2a22ab b2个;B.3个;C.4个;个;4、化简x21的结果是()11xA.x+1;B.;C.x-1;D.;x x15、已知111,则ab的值是()b2a1;B.;C.;;A .26、用换元法解分式方程x13x10时,设x1y,将原方程化成对于yx1x的整式方程,那么这个整式方程是()A.y2y30;B.y23y10;C.3y2y10;D.3y2y10;7、分式方程23x1的解为()22x1A .x=1;B.;C.;D.x=0;x=2x=38、对于x的方程2无解,则k的值为()x3A .3;B.;C.±3;D.没法确立;9、若3x22的值为1,则的值是()4x746x8x1A .1;B.-1;C.1;D. 1;7510、为迎接“六一”小孩节,某小孩品牌玩具专卖店购进A、B两类玩具,此中A类玩具的进价比B类玩具的进价每个多3元,经检查:用900元购进A类玩具与用750购进B类玩具的数目同样,设A类玩具的进价为m元/个,依据题意可列出方程是()A.900750;B.900750;C.900750;D.900750;mm3m3m mm3m3m二、填空题:(24分)11、代数式1在实数范围内存心义,则x的取值范围是。
3、已知分式x,当x=2时,分式无心义,则a=。
12x25x13、当x=2时,分式的值是。
x14、化简1的结果是。
1)2(x1)2(x15、计算:x11=。
、若分式方程x a 无解,则a的值为。
16x117、分式方程7的。
5解为x23 a2b a18、计算22。
湘教版数学八年级上册第一章 分式单元测试题.docx
初中数学试卷 桑水出品第一章 分式单元测试题一、选择题1、在式子:23123510,,,,,94678xy a b c x y x a x yπ+++中,分式的个数是( ) A :2B :3C :4D :5 2、化简1x x y x÷⋅的结果是( ) A :1 B :xy C :y x D :x y 3、若把分式xy x 23+的x 、y 同时扩大10倍,则分式的值( ) A :扩大10倍B :缩小10倍C :不变D :缩小5倍 4、化简2293mm m --的结果是( ) A :3+m m B :3+-m m C :3-m m D :m m -3 5、对于分式23x -有意义,则x 应满足的条件是( ) A :3x ≥ B :3x > C :3x ≠ D :3x <6、用科学记数法表示-0.0000064记为( )A :-64×10-7B :-0.64×10-4C :-6.4×10-6D :-640×10-8 7、若分式112--x x 的值为0,则x 的取值为( ) A :1=x B :1-=x C :1±=x D :无法确定8、下列等式成立的是( )A :9)3(2-=-- B :()9132=-- C :2222b a b a ⨯=⨯-- D :b a a b b a +=--22 9、若方程342(2)a x x x x =+--有增根,则增根可能为( ) A :0 B :2 C :0或2 D :110、小明和小张两人练习电脑打字,小明每分钟比小张少打6个字,小明打120个字所用的时间和小张打180个字所用的时间相等。
设小明打字速度为x 个/分钟,则列方程正确的是( )A :x x 1806120=+B :x x 1806120=-C :6180120+=x xD :6180120-=x x 二、填空题 11、计算:=-321)(b a ;=+-203π ;12、方程xx 527=-的解是 ; 13、分式,21x xy y 51,212-的最简公分母为 ;14、约分:=-2264xyy x ;932--x x = ; 15、若关于x 的方程211=--ax a x 的解是x=2,则a= ; 16、计算ab b b a a -+-= ; 17、如果分式121+-x x 的值为-1,则x 的值是 ; 18、已知31=b a ,分式ba b a 52-+的值为 ; 19、当x 时,分式21xx -的值为正数; 20、轮船顺水航行46km 和逆水航行34km 所用的时间恰好相等,水的流速是3km/h ,设轮船在静水中的速度是xkm/h ,可列得方程为 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 分式 单元测试题
班级 姓名:
一、填空题。
(每小题3分,共30分)
1、当______x 时,分式
1-x x 有意义 2、2)(22-=-x x
x x 3、计算:=-321)(b a ___________
4、xyz
x y xy 61,4,13-的最简公分母是 5、用科学记数法表示:—0.000000108=__________________
6、计算:=•c b a a bc 222 ;=÷23342y
x y x 7、计算=+--10)20111(
)14.3(π 8、方程1233x x x
=+--的解是_________ 9、计算:=---4
4212a a 10、一件工作,甲单独做a 小时完成,乙单独做b 小时完成,则甲、乙合作 小时完成。
二、选择题。
(每小题3分,共30分)
11、下列各式:π
8,11,5,21,7,322x x y x b a a -++中,分式有( ) A 、1个 B 、2个 C 、3个 D 、4个
12、若分式1
12+-x x 的值为0,则x 的取值为( ) A 、1=x B 、1-=x C 、1±=x D 、无法确定
13、如果把分式y
x x +2中的x 和y 都扩大3倍,那么分式的值( ) A 、扩大3倍 B 、缩小3倍 C 、缩小6倍 D 、不变
14、下列各式变形正确的是( )
A .y x =xy x 2
B .a b = (a
b )2 C .y x =2y xy D .a3·a2=a6 15、下列等式中错误的是( )
A.3322b a ab =- B. ax b ab x 3434221=-- C. ()y x y x 212515=-- D.33
11=- 16、分式方程1x —1 =2x —2
( ) A 、无解 B 、有解x=1 C 、有解x=2 D 、有解x=0
17、若方程144
x m x x -=--有增根,则m 的值是( ). A 、2 B 、3 C 、-3 D 、1 18、若xy y x =+,则
y x 11+的值为( ) A 、0 B 、1 C 、-1 D 、2
19、某农场开挖一条480米的渠道,开工后,每天比原计划多挖20米,结果提前4天完成
任务,若设原计划每天挖x 米,那么求x 时所列方程正确的是( )
A 、
448020480=--x x B 、204
480480=+-x x C 、420480480=+-x x D 、204804480=--x x 20、已知:M=4a 2-4 ,N=1a+2 + 1 2-a
则 M、N 的关系是( ) A 、M=N B 、M·N=1 C 、M+N=0 D 、不能确定
三、解答题。
21、计算:(4分×4=16分)
(1)b a 522·32
a b (2)2442222++-•-+a a a a
a a
(3)
1
211222+++÷--x x x x x (4) a a a -+-21422
22、解方程:(5分×2=10分): ⑴
512552x x x +=-- ⑵283111x x x ++=--
23、已知:042=-x ,求代数式
()()
12131-+---x x x x 的值。
(4分)
24、甲、乙两地相距19千米,某人从甲地出发出乙地,先步行7千米,然后改骑自行车,
共用2小时到达乙地。
已知这个人骑自行车的速度是步行速度的4倍,求步行速度和骑自行车的速度。
(5分)
25、在建设社会主义新农村中,某乡镇决定对一段公路进行改造,已知这项工程由甲工程队单独做需要40天完成;如果由乙队先单独做10天,那么剩下的工程还需要两队合作20天才能完成,求乙工程队单独完成这项工程所需的天数;(5分)。
