总复习(图形与几何)
新人教版数学六年级下册总复习《图形与几何》课件(知识点全面)

这些计算公式是怎样推导出来的?它们之间有什么联系?
长方形和正方形是用面积单 位量出来的。
平行四边形转化成长方形。
两个完全相同的三角形或梯形 都可以拼成平行四边形。
利用割补、转化的方 法来推导图形的面积 公式。
长方形的面积是研究其它图形面积的基础。
9.三角形三边的关系
4cm
7cm
13cm
三角形其中两条线段的和大于第三条线段时,这样的三条 线段才能组成一个三角形。
30cm
上升的水的体积就是马铃薯的体积。
在方格纸上分别画出从不同方向看到左边立体图形 的形状图。
正面
左面
上面
连一连。
一个蓄水池(如下图),长10米,宽4米,深2米。 (1)蓄水池占地面积有多大?
10×4 = 40(平方米) 答:占地面积是40平方米。 (2)在蓄水池的底面和四周抹上水泥,抹水泥的面积有多大? 10×4 +(4×2+2×10)×2= 96(平方米)
三角形
锐角三角形 直角三角形
等腰三角形
(三个角都是 (有一个角是直角) 不等边三角形 (两条边相等)
锐角) 钝角三角形
(三条边都 等边三角形 不相等) (三条边都相等)
(有一个角是钝角)
1.平面图形的分类
四边形的分类
平行四边形 长方形
正方形
四边形 梯形
等腰梯形 直角梯形
2.直线、射线和线段
名称
相同点
比例尺 1∶20000
2.辨认方向
在平面图中确定方位,通常是上北、下南、左西、右东。
北
西北
东北
西
东
西南
南
东南
3.根据方向和距离,确定物体位置的一般步骤。
总复习几何与图形(教案)2023-2024学年数学三年级上册北师大版

总复习几何与图形(教案)20232024学年数学三年级上册北师大版一、教学目标1. 知识与技能:使学生进一步理解和掌握本册几何与图形的知识点,提高学生的空间想象力和图形分析能力。
2. 过程与方法:通过复习,让学生熟练掌握几何图形的基本特征和性质,培养学生运用数学知识解决实际问题的能力。
3. 情感、态度和价值观:激发学生对几何图形的兴趣,培养学生积极参与、主动探索的精神,增强学生的合作意识。
二、教学内容1. 认识平面图形:长方形、正方形、三角形、平行四边形、圆等。
2. 平面图形的对称性:轴对称图形、中心对称图形。
3. 立体图形:长方体、正方体、圆柱、圆锥等。
4. 观察物体:从不同方向观察物体,培养学生的空间观念。
5. 测量:长度、面积、体积的测量。
三、教学重点与难点1. 教学重点:平面图形和立体图形的特征及性质,图形的测量。
2. 教学难点:图形的对称性,从不同方向观察物体,体积的计算。
四、教具与学具准备1. 教具:多媒体课件、实物模型、挂图等。
2. 学具:直尺、圆规、量角器、剪刀、彩纸等。
五、教学过程1. 导入:通过提问、游戏等方式,引导学生回顾本册几何与图形的知识点。
2. 新课导入:讲解图形的特征、性质和测量方法,引导学生运用数学知识解决实际问题。
3. 案例分析:通过实例分析,让学生深入了解图形在实际生活中的应用。
4. 小组讨论:分组讨论,让学生在合作中发现问题、解决问题,培养学生的团队协作能力。
6. 课后作业:布置与课程内容相关的作业,巩固所学知识。
六、板书设计1. 总复习几何与图形2. 目录:教学目标、教学内容、教学重点与难点、教具与学具准备、教学过程、板书设计、作业设计、课后反思3. 按照教学过程逐步展示教学内容,突出重点、难点。
七、作业设计1. 基础题:巩固图形的基本特征和性质。
2. 提高题:培养学生的空间想象力和图形分析能力。
3. 拓展题:激发学生的创新思维,提高解决问题的能力。
八、课后反思2. 学生反馈:了解学生对本次课程的掌握程度,针对学生的疑问进行解答。
北师大版数学四年级下册总复习图形与几何

1、右图中有( )个直角三角形,( )个锐角三角形,投我以桃,报之以李。
《诗经·大雅·抑》原创不容易,【关注】,不迷路!( )个钝角三角形。
2、判断(1)正方形、平行四边形都是特殊的长方形。
( )(2)用4根木条钉成一个平行四边形木框,用力拉这个木框,我们会发现平行四边形容易变形。
( )(3)在一个三角形中,已知两个内角分别是86°和23°,这个三角形一定是锐角三角形。
( )(4)在三角形中,有两条边都是7分米,那么第三条边一定大于7分米。
( )(5)有一组对边平行的四边形是梯形。
( )3、一个等腰梯形,它的上底长3.4厘米,下底长6.5厘米,一条腰长3厘米。
这个等腰梯形的周长是多少?参考答案1、4 2 22、×√√××3、3.4+6.5+3+3=15.9(厘米)答:这个等腰梯形的周长是15.9(厘米。
【素材积累】岳飞应募参军,因战功累累不断升职,宋高宗亲手写了“精忠岳飞”四个字,制成旗后赐给他。
又召他到寝阁,对他说:“中兴的大事,全部委托给你了。
”金人攻打拱州、亳州,刘锜向朝廷告急,宋高宗命令岳飞火速增援,并在赐给岳飞的亲笔信中说:“设施之事,一以委卿,朕不遥度。
”岳飞于是调兵遣将,分路出战,自己率领轻装骑兵驻扎在郾城,兵锋锐气十足。
但是,后来高宗和秦桧决定与金议和,向金称臣纳贡。
就在岳飞积极准备渡过黄河收复失地的时候,高宗和秦桧却连发12道金字牌班师诏,命令岳飞退兵。
后岳飞被以“莫须有”的罪名毒死于临安风波亭,时年仅39岁。
总复习图形与几何课件六年级上册数学人教版(共25张PPT)

(2)剪完圆后,哪张白铁皮剩下的废料多些?
d=1.8m
d=(1.8÷2)m
d=(1.8÷3)m
第一张白铁皮:1.82-3.14×(1.8÷2)2=0.6966(m2) 第二张白铁皮:1.82-3.14×(1.8÷2÷2)2 ×4=0.6966(m2) 第三张白铁皮:1.82-3.14×(1.8÷3÷2)2 ×9=0.6966(m2)
巩固练习
1.一个公园是圆形布局,半径长 1km,圆心处设立了一 个纪念碑。公园共有四个门,每两个相邻的门之间有 一条直的水泥路相通,长约1.41km。
(1)这个公园的围墙有多长?
2×3.14×1= 6.28(km) 答:这个公园的围墙有6.28km。
1.一个公园是圆形布局,半径长 1km,圆心处设立了一 个纪念碑。公园共有四个门,每两个相邻的门之间有 一条直的水泥路相通,长约1.41km。 (2)北门在南门的什么方向? 距离南门有多远? 1+1= 2(km) 答:北门在南门的正北方,距 离南门2km。
2.确定某个点的位置
北 小川家
西
小白家
30° 45°
东
100m
南
学校
在练习本上 画一画。
学校在小白家的东偏 南 45° 方 向 、 距 离 小 白 家 500m , 在 图 中 标 出学校的位置。
2.确定某个点的位置
北
➢ 确定参照点、方向标和图上
小川家
单位长度代表的实际距离。
西
小白家
30° 45°
答:剪完圆后,剩下的废料同样多。
(3)根据以上的计算,你发现了什么?
d=1.8m
d=(1.8÷2)m
d=(1.8÷3)m
按这样的方式剪圆,无论怎么减,剩下的废料总是不变的。 剪掉16个圆:
北师大版五年级上册数学《 总复习图形与几何》教学设计

北师大版五年级上册数学《总复习图形与几何》教学设计一. 教材分析北师大版五年级上册数学《总复习图形与几何》教材,主要是对本册所学图形与几何知识的梳理和巩固。
内容包括平面图形的认识、图形的运动、图形的大小和形状、图形的面积和周长等。
本节课的教学设计,旨在帮助学生系统地掌握图形与几何的基本概念、性质和运算方法,提高他们的数学思维能力和解决问题的能力。
二. 学情分析五年级的学生已经学习了平面图形的认识、图形的运动、图形的大小和形状等基础知识,对图形与几何有了一定的了解。
但部分学生对一些概念和运算方法的掌握还不够扎实,需要通过复习和练习来巩固。
此外,学生们的数学思维能力和解决问题的能力参差不齐,需要在教学过程中给予不同的指导和鼓励。
三. 教学目标1.知识与技能:通过复习,使学生系统地掌握图形与几何的基本概念、性质和运算方法,提高他们的数学思维能力。
2.过程与方法:培养学生的观察、分析、归纳和总结能力,提高他们解决问题的能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养他们积极、主动的学习态度,使他们感受到数学的魅力。
四. 教学重难点1.重点:图形与几何的基本概念、性质和运算方法。
2.难点:对一些概念和运算方法的理解和应用。
五. 教学方法采用问题驱动法、案例分析法、小组合作法等多种教学方法,激发学生的学习兴趣,引导学生主动参与课堂讨论,培养他们的数学思维能力和解决问题的能力。
六. 教学准备1.课件:准备与教学内容相关的课件,以便在课堂上进行展示和讲解。
2.练习题:准备一些与教学内容相关的练习题,用于课堂练习和巩固知识。
3.教学工具:准备黑板、粉笔等教学工具,以便进行板书和讲解。
七. 教学过程1.导入(5分钟)利用课件展示一些生活中常见的图形,引导学生回顾平面图形的认识,激发学生的学习兴趣。
2.呈现(10分钟)呈现本节课的教学内容,包括图形的运动、图形的大小和形状、图形的面积和周长等,让学生对所学知识有一个整体的认识。
六年级总复习知识点——图形与几何专题
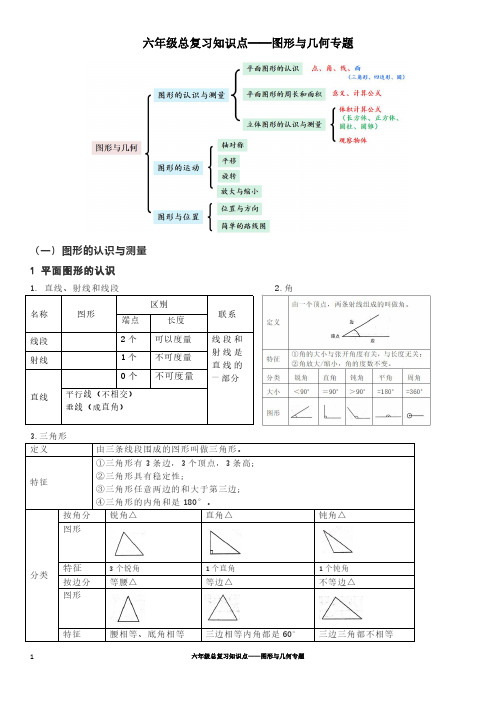
六年级总复习知识点——图形与几何专题2.角3个锐角1个直角1个钝角等腰△腰相等、底角相等三边相等内角都是三边三角都不相等、(2)四边形定义和类型定义由四条线段围成的图形叫做四边形分类名称图形特征边正方形两组对边平行,四边相等长方形两组对边平行,两组对边分别相等平行四边形两组对边分别平行,两组对边分别相等梯形只有一组对边平行5.圆定义圆是由一条曲线围成的封闭图形。
各部分名称①圆心0:圆中心一点;②半径r:圆心到圆上任意一点的线段;③直径d:通过圆心并两端都在圆上的线段。
特征①圆是一个轴对称图形,有无数条对称轴,直径所在直线是它的对称轴;②在一个圆内,有无数条半径和直径,且所有的直径、半径都相等。
③直径=半径×2(d=2r)半径=直径÷2(r=d÷2)圆周率①圆的周长与直径的比值等于圆周率,即②π是一个无限不循环小数,π≈3.14;2平面图形的周长与面积1.常见平面图形的周长和面积计算公式名称图形周长面积长方形正方形平行四边形三角形梯形圆半圆圆周长的一半r.C143=半圆的周长:r.C145=圆环外方内圆外圆内方3立体图形的认识与测量aCbbCaba+b)(aC-÷=→-÷=→=⨯+=22222{abS=aSbbSa÷=÷=hSaaSh÷=÷={ahS=2aS=hSaaSh÷⨯=÷⨯=22{2÷=ahSahSbbhSabaSh-÷⨯=-÷⨯=+÷⨯=222)({2÷+=)(baSπrπdC2==2rd÷÷=÷=→πCπC2πrS=22÷=πrSrr-22+==环宽)(环RRπS4r86.02:圆:正方形πS==2r14.12:圆:正方形πS==4÷=→CaaC4=1.长方体和正方体的特征图形名称相同点不同点展开图面棱长长方体6个面,12条棱,8个顶点一般都是长方形,可能有2个相对的面是正方形;相对的面大小相等。
三下总复习《图形与几何 》教学设计
面积的知识,并做好笔记,然后在教师的组织下进行交流。
(1)组织学生回顾关于位置与方向的知识内容,并在小组中交流。
(2)组织学生集体交流,根据学生整理的情况引导汇报并板书:整理位置与方向的相关知识。
(1)八个基本方向与相对性;(2)描述物体的位置与观测点;
(3)描述行走路线。
:
2.复习面积(面积单位、面积单位间的进率、面积的计算)。
(1)根据复习提纲整理,要求学生先独立思考,然后在小组内交流。
提纲:①学过哪些面积单位?请按单位大小的顺序排列;②整理单位之间的进率,看看有什么好办法记住它;③计算长方形和正方形的面积各需要哪些条件?如何计算?
(2)学生交流汇报,教师适时板书:
整理面积的知识。
(1)常用面积单位及进率;(2)长方形、正方形的面积计算;
(3)简单组合图形的面积。
(1)说一说学校、儿童乐园分别在明明家的哪个方向。
(2)明明从家向()走271米,又向()走430米到图书大厦。
(3)明明从家出发到医院可以怎么走?哪条路最近?
图形与几何
板
书
设
计。
部编版六年级数学下册总复习《图形与几何》授课课件
2.在一个边长为5米的大花坛外 围四周铺上宽为1米的碎石路。 碎石路的面积是多少平方米?
解题思路: 如图所示,用大正方形的面积减去小正方形
的面积,就是碎石路的面积。大正方形的边长是 5+1+1=7(米),小正方形的边长是5米。
在一个边长为5米的大花坛外围 四周铺上宽为1米的碎石路。碎 石路的面积是多少平方米?
6.小明走一步的平均长度约是6分米。他 测得一块菜地的长是25步,宽是15步。 这块菜地的面积大约是多少平方米?
解题思路: 题目中长方形菜地的长与宽没有直接给出,而
是由小明每步的长度和步数求出。计算时要注意单 位换算。
6.小明走一步的平均长度约是6分米。他 测得一块菜地的长是25步,宽是15步。 这块菜地的面积大约是多少平方米?
米到医院。271+500=771(米),771>627,路线一近。
2. 说一说1路车的行车路线。
从广场出发向( 西 ) 行 驶( 2 )站到电影院,再向 ( 北 )行驶( 1 )站到 商场,再向( 西北 )行驶 ( 4 )站到少年宫,再向 ( 西南 )行驶( 4 ) 站到动物园。
1. 看图回答问题。
西
南
北东
东
北
3.三(1)班同学排成方队进行队列表演,明明的东、 西、南、北四个方向各有3名同学,三(1)班共 有多少名同学参加队列表演? 3+3+1=7(名) 7×7=49(名) 答:三(1)班共有49名同学参加队列表演。
考 点 1 位置和方向
1.填空。 (1)小亮上学从家向东北方向走到学校,放学时他从学校
5+1+1=7(米)
7×7=49(平方米)
5×5=25(平方米)
49-25=24(平方米)
总复习—图形与几何易错题(试题)-六年级下册数学人教版
人教版数学六年级下册总复习——图形与几何易错题1.如图,一块长方形铁皮剪下图中的涂色部分正好可以围成一个圆柱。
则这个圆柱的底面周长是多少分米?高是多少分米?2.下图中,若小圆的半径是 1 cm,大圆的半径是 3 cm。
那么,让小圆沿着大圆外侧滚动一周,小圆的圆心移动的距离是多少?小圆滚动后扫过的面积是多少?3.如下图,三个半径都是2cm的圆两两相交于圆心,阴影部分的面积是多少平方厘米?4.如下图,一个直角三角形,将它的一条直角边对折到斜边上去,与斜边重合,则未被盖住的部分(图中的阴影部分)的面积是多少平方分米?(图中单位:dm)5.下面的容器倒过来后,水面的高度是多少厘米?6.要把一根长 27.9 cm的木料锯成长29 cm和4.9cm两种规格的小木料,每锯一次要损耗01cm的木料,两种规格的木料各锯几段才能使浪费最少?(列表计算各种方案)7.一个圆锥形沙堆,底面直径是 6m,高是2.5m。
用一辆载质量为 8t的汽车去运,几次可以运完?(每立方米沙约重 1.8 t)8.有一个用玻璃制成且密封的长方体水箱(如图a),从里面量得长是6 dm,宽是4 dm高是10 dm,水箱内水的高度是 8 dm,如果将水箱向后放倒(如图 b),以它的后面为底面这时水箱内水的高度是多少分米?9.从一个长方体上截下一个体积是 18 dm3的小长方体后,剩下一个棱长是 3 dm 的正方体。
原来这个长方体的表面积是多少?10.张师傅用一块边长38 cm的正方形铁皮做铁盒(铁皮厚度忽略不计),他从四个角上各剪掉一个边长是4 cm的正方形(如下图),然后用剩下的部分做成铁盒,这个铁盒的容积是多少立方厘米?11.求图中阴影部分的面积。
12.某公司准备在新建的办公楼大厅的主楼梯上铺红地毯。
已知这种红地毯每平方米的售价是40元,主楼梯宽2.5m,其侧面如下图所示(单位:m)。
请你算一算,购买这种红地毯需要多少钱?13.如图,把底面周长18.84 cm高10cm的圆柱切成若干等份,拼成一个近似的长方体这个长方体的底面积是多少?体积是多少?与这个圆柱等底等高的圆锥的体积是多少?14.如右图(单位:cm),甲圆柱形容器是空的,乙长方体容器水深6.28 cm,要将乙容器中的水全部倒人甲容器,这时水深多少厘米?15.一个圆柱沿着底面的一条直径竖直切开,表面积增加了120平方厘米,已知这个圆柱的高是10厘米,它的体积是多少立方厘米?16.一个圆锥形金属铸件的底面半径是6cm,把它完全浸没在底面半径是10cm的圆柱形玻璃水槽内,水面升高2cm(水未溢出)。
北师大版数学四年级下册总复习图形与几何
图形 ②ห้องสมุดไป่ตู้④ ⑥ 是梯形。
只有一组对边平行的四边形
第二十二页,共二十六页。
返回
图形与几何
4.听口令,搭一搭,用4个正方体搭一个(yī ɡè)立体图形。
正面
(zhè ngmi àn)
右面
上面
第二十三页,共二十六页。
返回
图形与几何
5.画出蚂蚁(mǎyǐ)进洞的线路。
2
4
1
3
5
6
等腰三角形
等边三角形 锐角三角形
⑴
5
3⑵
4
3
6
6
3+6>5
3+4>6
3+5>6
3+6>4
5+6>3
4+6>3
三角形任意(rènyì)两边之和大于第三边 。
第二十一页,共二十六页。
返回
图形与几何
3.下面(xià mian)图形中哪些是平行四边形?哪些
是梯形?找一找,填一填。
一般四边形
图形(t①úxí③ng)⑤ ⑧
是平行四边形两。组对边分别平行的四边形
锐角三角形
三角形
1个直角
1个钝角+2个锐角
3个锐角
(1zh.í任ji何ǎo一)+2个个锐三角 角形都至少有两个锐角。
2.要想判断一个三角形是什么三角形,只要看它最大的
角是什么角就可以。
3.三者呈并列关系。
第九页,共二十六页。
返回
图形与几何
并列(bìngliè)关系
钝角 (dùnjiǎo)三
角形
直角三角形
第十五页,共二十六页。
返回
图形与几何
正方形、长方形、平行四边形之间的相同点与不同点 是什么(shén me)?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)在一个三角形中,如果有两个锐角,那么这个三角形就一定是
锐角三角形。
(×)
(2)钝角三角形只有一条高。
(× )
(3)锐角三角形中任意两个锐角的和一定大于90°。
(√ )
(4)把一个大三角形剪成两个小三角形,每个小三角形的内角和是
90°。
(× )
(5)一个等腰三角形的周长是21厘米,底边长是3厘米,则腰长是
我发现从不同方向观察同一个立体 图形,看到的形状可能是不同的; 从同一方向观察不同的立体图形, 看到的形状可能是相同的。
我知道了所有三角形 的内角和都是180°, 我还知道三角形任意 两边的和一定大于第 三边。
我会画轴对称图形,还会将一个 图形向上、下、左、右方向平移。
一、知识梳理
我用表格的方式整理了第五单元三角形的知识点。
二、基础练习
1. 连一连。
从前面看
从左面看
从上面看
二、基础练习
2. 在( )里填上适当的数或文字。
(1)小明准备用图钉固定硬纸条做一个三角形。他应该准备( 3 )根 硬纸条,因为三角形有( 3 )条边,他应该准备( 3 )个图钉, 因为三角形有三个( 顶点)。
(2)红领巾按角分类属于( 钝角)三角形,按边分类属于(等腰)三角形。
2. 画出下面三角形的三条边对应的高。
9厘米。
(√)
√ (6)有一个角是60°的等腰三角形一定是一个等边三角形 。 ( )
二、基础练习
4. 先根据对称轴补全下面这个轴对称图形,再画出向右平移14格后 的图形。
先想一想怎 样能画得又 快又好。
三、综合应这道用题能直接求出
∠1的度数吗?该怎
1. 求下面各角的度数。
么Hale Waihona Puke 呢?2∠1= 90°- 60° = 30°
因为3+4=7,所以 第三边要比3大,并 且还要比11小。
答:另一条边可能是4cm或5cm或6cm 或7cm或8cm或9cm或10cm。
五、课堂总结,浅谈收获
这节课,你有什么收获?
图形与几何 1、加深对轴对称图形、三角形三边 的关系和三角形内角和的理解; 2、能熟练画出平移后的图形;
3、能正确、熟练计算三角形的内角。
人教版四年级数学下册
总复习第3课时 (空间与图形)
一、知识梳理
我会给三角形画高,
同你学能们用,自这 己学 喜期 欢“ 的图 方形 式与 把 几第何五”单部元分 三我 角们 形都 这学 部习 分了 知
还会按不同标准给三 角形分类。
哪识些整知理识一? 下吗?
第二单元学习了观察物体, 第五单元学习了三角形,第 七单元学习了图形的运动。
(3)等边三角形的每个内角都是( 60)°,等腰直角三角形的一个底 角是( 45)° 。
(4)房屋的屋架做成三角形是运用了( 三角形的稳定性 )。
(5)右图中,与线段AB对应的高是线段
C D
( A)C,与线段BC对应的高是线
段( )AD。
A
B
二、基础练习
3. 下面的说法正确吗?正确的画“√”,错误的画“×”。
四、布置作业
作业:第110页,第3题; 第112页练习二十五,第10题; 第113页练习二十五,第11~13题; 第115页练习二十五,第18题。
课堂作业
1.填空:
(1)任意三角形的内角和是( );一个直角三角形的两个锐角的和 是( )。 (2)正三角形的3条边的长度都( ),每一个内角是( ) 度。 (3)一个三角形的两个角分别是36度和44度,那么这个三角形是 ( )三角形。 (4)一个直角三角形的一个锐角是38°,另一个锐角是( )。 (5)一个等腰三角形的一个顶角是70°,它的一个底角是( )。
∠2= 180°- 90°-60° = 30°
∠2= 180°- 53° = 127°
∠1= 180°- 127°-20° = 33°
三、综合应用
2. 如果一个三角形的两条边分别是4cm和7cm,另一 条边可能是几厘米(取整数值)?
我知道三角形 任意两边的和 大于第三边。
4+7=11(cm) 3+4=7(cm) 3cm<第三条边<11cm
