高等数学第十二章单元测试题答案

合集下载

【3套试卷】人教版数学八年级上册第十二章《全等三角形》单元检测题(含答案)

人教版数学八年级上册第十二章《全等三角形》单元检测题（含答案）一、单选题（每小题只有一个正确答案）1．下列各组图形中不是全等形的是( )A ．B ．C ．D ．2．下列说法正确的是( )A ．形状相同的两个三角形全等B ．完全重合的两个三角形全等C ．面积相等的两个三角形全等D ．所有的等边三角形全等3．在ABC ∆内一点P 满足P 到AB 、BC 、AC 的距离相等，则P 一定是ABC ∆( )A ．三条线角平分线的交点B ．三条中线交点C ．三条高的交点D ．三边垂直平分线的交点4．如图，在△ABC 和△DEB 中，已知AB=DE ，还需添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是( )A ．BC=EC ，∠B=∠EB ．BC=EC ，AC=DC C ．BC=DC ，∠A=∠D D ．∠B=∠E，∠A=∠D5．如图，△ABC 的外角∠CBD 和∠BCE 的平分线相交于点F ，则下列结论正确的是（）A ．点F 在BC 边的垂直平分线上B ．点F 在∠BAC 的平分线上 C ．△BCF 是等腰三角形D ．△BCF 是直角三角形6．如图，小明把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（）A ．带①去B ．带②去C ．带③去D ．①②③都带去7．如图所示，AD 、AE 分别是△ABC 的高和角平分线，且∠B=76°，∠C=36°，则∠DAE 等于（）A ．20°B ．18°C ．45°D ．30°8．如图所示，已知∠1=∠2，下列添加的条件不能使△ADC ≌△CBA 的是( )A ．//AB DC B ．AB CD = C ．AD BC = D ．B D ∠=∠9．如图所示,点F ,A ,D ,C 在同一直线上,△ABC ≌△DEF ,AD=3,CF=10,则AC 等于( )A ．5B ．6C ．6.5D ．710．下列各组条件中，不能判断△ABC≌△DEF 的是（）A.∠A=∠D，AB=DE ，∠B=∠EB.AB=DE ，∠A=∠D，BC=EFC.AB=DE ，BC=EF ，AC=DFD.∠B=∠E=90°，AB=DE ，AC=DF11．如图，在△ABC 中，AB 、AC 的垂直平分线分别交BC 于点E 、F ，若∠BAC=110°，则∠EAF 为（）A ．35°B ．40°C ．45D ．50°12．如图，AD 是△AB C 的角平分线，DE⊥AC，垂足为E ，BF∥AC 交ED 的延长线于点F ，若BC恰好平分∠ABF，AE=2BF,给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（）A．4个B．3个C．2个D．1个二、填空题13．如图，OP平分∠AOB，PB⊥OB，PB＝2cm，则点P到OA的距离是_____cm．14．如图，∠AEC=∠ACE，∠DAB=∠CAE，要使△ABC≌△ADE，应添加的条件是_____．（添加一个条件即可）15．如图，在△ABC中，∠A=90°，AB=AC，∠ABC的平分线BD交AC于点D，CE⊥BD，交BD 的延长线于点E，若BD=8，则CE=_________．16．如图，AE=AD，∠B=∠C，BE=6，AD=4，则AC=_______________．17．如图，△ABC中，AD平分∠BAC，AB＝4，AC＝2，且△ABD的面积为2，则△ACD的面积为_____．三、解答题18．如图，已知AD、BC相交于点O，AB＝CD，AD＝CB.求证：∠A＝∠C.19．如图，有一个池塘，要到池塘两侧AB的距离，可先在平地上取一个点C，从C不经过池塘可以到达点A和B，连接AC并延长到点D，使CD=CA，连接BC并延长到点E，使CE=CB，连接DE，那么量出DE的长就是A，B的距离，为什么？20．已知:如图,点A,D,C,B在同一条直线上,AD=BC，AE=BF,CE=DF,求证:（1）AE∥FB,（2）DE=CF.21．如图，在ABC 中，90C ∠=，2AB AC =，AD 平分BAC ∠，求证：点D 在AB 的垂直平分线上．22．如图，已知AC 平分∠BAD，CE⊥AB 于E ，CF⊥AD 于F ，且BC=CD.（1）求证：△BCE≌△DCF；（2）求证：AB+AD=2AE.23．如图，BE 、CF 是△ABC 的高且相交于点P ，AQ ∥BC 交CF 延长线于点Q ，若有BP=AC ，CQ=AB ，线段AP 与AQ 的关系如何？说明理由.参考答案1．B2．B3．A4．C5．B6．C7．A8．B9．C10．B11．B12．A13．2 14．∠B=∠D （AB=AD 或∠C=∠AED ） 15．4 16．1017．118．解：若连结BD ，在ABD 和CDB 中 ∵AB＝CD ，AD ＝CB ，BD ＝DB∴ABD ≌CDB ∴∠A＝∠C19．解：量出DE 的长就等于AB 的长，理由如下：在△ABC 和△DEC 中，CB CE ACB DCE CA CD =⎧⎪∠=∠⎨⎪=⎩，∴△ABC ≌△DEC （SAS ），∴AB=DE ．20．证明：（1）∵AD=BC ，∴AC=BD ，在△ACE 和△BDF 中，AC BD AE BF CE DF ⎧⎪⎨⎪⎩＝＝＝，∴△ACE ≌△BDF （SSS ）∴∠A=∠B ，∴AE ∥BF ；（2）在△ADE 和△BCF 中，AE BF A B AD BC ＝＝＝⎧⎪∠∠⎨⎪⎩∴△ADE ≌△BCF （SAS ），∴DE=CF ．21．解：如图，过点D 作DE AB ⊥于E ，∵90C ∠=，AD 平分BAC ∠，∴CD DE =，在ADC 和ADE 中，AD AD CD DE=⎧⎨=⎩， ∴()ADC ADE HL ≅，∴AE AC =，∵2AB AC =，∴2BE AB AE AC AE AE =-=-=，∴点D 在AB 的垂直平分线上．22．（1）证明：∵AC 是角平分线，CE⊥AB 于E ，CF⊥AD 于F ，∴CE=CF，∠F=∠CEB=90°，在Rt△BCE 和Rt△DCF 中，∴△BCE≌△DCF；（2）解：∵CE⊥AB 于E ，CF⊥AD 于F ，∴∠F=∠CEA=90°，在Rt△FAC 和Rt△EAC 中，， ∴Rt△FAC≌Rt△EAC，∴AF=AE，∵△BCE≌△DCF，∴BE=DF，∴AB+AD=（AE+BE ）+（AF ﹣DF ）=AE+BE+AE ﹣DF=2AE.23．解： AQ 与AP 的关系是：相等且互相垂直，理由如下：∵BE 、CF 是△ABC 的高，∴∠BFP=∠CEP=90°，∴∠ABP+∠BPF=90°，∠ACP+∠CPE=90°，又∵∠BPF=∠CPE，∴∠ABP=∠ACP，在△ACQ 和△PBA 中：BP AC ABP ACP AB CQ ⎧⎪∠∠⎨⎪⎩＝＝＝，∴△ACQ≌△PBA（SAS ），∴AP=AQ，∠Q=∠PAF，∵∠PAF+∠APF=90°，∴∠APF+∠Q=90°，∴AP⊥AQ，即：AQ 与AP 的关系是相等且互相垂直.人教版八年级上册第十二章全等三角形单元测试一、单选题1．已知图中的两个三角形全等，则∠α的度数是（）A．80°B．60°C．90°D．50°2．如图，CE⊥AB，DF⊥AB，垂足分别为E、F，AC∥DB，且AC=BD，那么Rt△AEC≌Rt△BFD 的理由是（）A．SSS B．AAS C．SAS D．HL3．如图，某同学把一块三角形的玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，最省事的办法是（）A．带①去B．带②去C．带③去D．带①和②去4．如图，CE⊥AB，BD⊥AC，垂足分别为E、D，BD、CE交于点O，AB＝AC，∠B＝20°，则∠AOD＝（）A．20°B．40°C．50°D．55°5．两个三角形具备下列（）条件，则它们一定全等．A．两边和其中一边的对角对应相等B．两个角对应相等C ．三条边对应相等D ．两边及第三边上的高对应相等6．如图，在五边形ABCDE 中，对角线AC=AD ，AB=DE ，BC=EA ，∠CAD=65°，∠B=110°，则∠BAE 的大小是（）A ．135°B ．125°C ．115°D ．105°7．如图所示，等腰Rt ABC ∆中，90C ∠=︒，AD 平分CAB ∠，交BC 于D ，过D 作DE AB ⊥于E ，若CD b =，BD a =，那么AB 的长度是( )A ．+a bB ．2+a bC ．2a b +D ．22a b +8．如图所示，在ABC ∆和DEC ∆中，AC DC =.若添加条件后使得ABC DEC ∆≅∆，则在下列条件中，添加不正确的是( )A ．BC EC =，BCE DCA ∠=∠B ．BC EC =，AB DE = C ．B E ∠=∠，AD ∠=∠ D ．AB DE =，B E ∠=∠9．如图所示，在ABC ∆中，AC BC =，90ACB ∠=，直线MN 过点C ，并交AB 边于点D ，点A 到直线MN 的距离2AE =，点B 到直线MN 的距离5BF =，则线段EF 的长是（）A ．2B ．3C ．5D ．710．如图，OB 、OC 分别是ABC ∠、∠ACB 的平分线，80A =∠，则O ∠=（）A ．80B ．100C ．120D ．13011．射线BD 在内部，下列各式中不能说明BD 是的角平分线的是（） A.B. C. D.12．己知如图，等腰ABC ∆，AB AC =，120BAC ︒∠=，AD BC ⊥于点D .点P 是延长线上一点，点O 是线段上一点，OP OC =下面的结论： ①30APO DCO ∠+∠=︒；②APO DCO ∠=∠；③OPC ∆是等边三角形④.AB AO AP =+其中正确的是（）A ．①③④B ．①②③C ．①③D ．①②③④二、填空题 13．如图是油路管道的一部分，延伸外围的支路恰好构成一个直角三角形，两直角边分别为6m 和8m ．按照输油中心O 到三条支路的距离相等来连接管道，则O 到三条支路的管道总长（计算时视管道为线，中心O 为点）是_____．14．如图，在ABC △中，AB AC =，高BD ，CE 交于点O ，连接AO 并延长交BC 于点F ，则图中共有______________________组全等三角形．15．如图，△ABC ≌△ADE ，其中，点B 与D 、点C 与E 是对应点.若∠BAE=120°，∠BAD=40°，则∠BAC 的大小为_______.16．如图，在ABC △中，90C ∠=︒，AC BC =，AD 平分CAB ∠交BC 于D ，DE AB ⊥于E ，若6AB cm =，则DBE ∆的周长是___________cm ．三、解答题17．将两块大小相同的含30°角的直角三角板(BAC B A C ''∠=∠=30°)按图1的方式放置，固定三角板A´B´C 然后将三角板ABC 绕直角顶点C 顺时针方向旋转（旋转角小于90°）至图2所示的位置，AB 与A´C 交于点E ，AC 与A´B´交于点F ，AB 与A´B´交于点O.(1)求证：BCE B CF '≅V V ；(2)当旋转角等于30°时，AB 与A´B´垂直吗？请说明理由。

人教版八年级数学上册《第十二章全等三角形》单元检测卷及答案

人教版八年级数学上册《第十二章全等三角形》单元检测卷及答案一、单选题1．如图已知OC 平分∠AOB ，P 是距离是OC 上一点，PH∠OB 于点H ，若PH ＝5，则点P 到射线OA 的距离是（）A ．6B ．5C ．4D ．32．下列说法正确的是（）A ．全等三角形的边相等B ．全等三角形的角相等C ．全等三角形的面积相等D ．面积相等的两个三角形全等3．在正方形网格中，AOB ∠的位置如图所示，到AOB ∠两边距离相等的点应是（）A ．P 点B ．Q 点C ．M 点D ．N 点4．BP 是∠ABC 的平分线，CP 是∠ACB 的邻补角的平分线，∠ABP=20°，∠ACP=50°，则∠P=（）A ．30°B ．40°C ．50°D ．60°5．如图，AD 是∠ABC 的角平分线，DF∠AB ，垂足为F ，DE ＝DG ，∠ADG 和∠AED 的面积分别为50和38，则∠EDF 的面积为（）A ．6B ．10C ．12D ．226．在正方形方格纸中，每个小方格的顶点叫做格点，以格点的连线为边的三角形叫做格点三角形．如图是5×5的正方形方格纸，以点D ，E 为两个顶点作格点三角形，使所作的格点三角形与∠ABC 全等，这样的格点三角形最多可以画出（）A ．2个B ．4个C ．6个D ．8个7．如图，在ABC 中，点D 是BC 边上一点，已知,90,2DAC DAB CE αα∠=∠=︒-平分ACB ∠交AB 于点E ，连接DE ，则DEC ∠的度数为（）A ．2αB ．3α C ．302α︒-D ．45α︒-8．如图，Rt ABC 中90C ∠=︒．分别以AB 、AC 、BC 为边在AB 的同侧作正方形ABEF 、ACPQ 和BCMN ．四块阴影部分的面积如图所示分别记为S 、1S 和2S 、3.S 若10S =，则123S S S ++等于（）A ．10B ．15C ．20D ．309．如图，已知∠ABC 和∠DCE 均是等边三角形，点 B 、C 、E 在同一条直线上，AE 与 BD 交于点 O ，AE 与 CD 交于点 G ，AC 与 BD 交于点 F ，连接 OC 、FG ，则下列结论要：①AE ＝BD ；②AG ＝BF ；③FG∠BE ；④OC 平分∠BOE ，其中结论正确的个数有（）A ．1个B ．2个C ．3个D ．4个10．如图AF CD ，BC 平分ACD ∠，BD 平分EBF ∠，且BC BD ⊥，下列结论：①BC 平分ABE ∠；②AC BE ；③90BCD D ∠+∠=︒；④60DBF ∠=︒，其中正确的个数是（）A ．1个B ．2个C ．3个D ．4个二、填空题11．如图，已知ABD ACE ≌，53A ∠=︒和22B ∠=︒，则C ∠= ︒．12．如图，已知AB=CB ，要使四边形ABCD 成为一个轴对称图形，还需添加一个条件，你添加的条件是．（只需写一个，不添加辅助线）13．如图所示的网格是33⨯的正方形网格，点A ，B ，C ，D 均落在格点上，则BAD ADC ∠+∠= ．14．如图，在ABC 中40B ∠=︒，三角形ABC 的内角BAC ∠和BCA ∠的平分线交于点E ，则AEC ∠= ．15．如图，在平面内，两条直线l 1，l 2相交于点O ，对于平面内任意一点M ，若p 、q 分别是点M 到直线l 1，l 2的距离，则称（p ，q ）为点M 的“距离坐标”.根据上述规定，“距离坐标”是（1，1）的点共有个.16．如图， ABC 中，一内角和一外角的平分线交于点 D ，连结 24AD BDC ∠=︒，， CAD ∠=.17．已知如图，AD//BC ，BD//AE ，DE 平分ADB ∠，且ED CD ⊥，若128AED BAD ∠+∠=︒，则BCD EAB ∠-∠= 度．18．如图，BA 1和CA 1分别是∠ABC 的内角平分线和外角平分线，BA 2是∠A 1BD 的角平分线，CA 2是∠A 1CD 的角平分线，BA 3是∠A 2BD 的角平分线，CA 3是∠A 2CD 的角平分线，若∠A=64°，则∠A= ，∠A 3= ，若∠A=α，则∠A2018为。

八年级数学上册《第十二章一次函数》单元测试卷-附答案(沪科版)

八年级数学上册《第十二章一次函数》单元测试卷-附答案(沪科版)一、选择题1．利用太阳能热水器加热水的过程中，热水器里的水温随所晒时间的长短而变化，这个问题的因变量是（） A ．太阳光强弱B ．水的温度C ．所晒时间D ．热水管2．下列图象中，表示y 是x 的一次函数的是（）A ．B ．C ．D ．3．一次函数1y x =+的图象不经过（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．在同一平面直角坐标系中，若一次函数5y x =-+与31y x =+的图象交于点M ，则点M 的坐标为（）A ．()14，B ．()16-，C ．()14-，D ．()12--， 5．在物理实验课上，小明用弹簧称将铁块A 悬于盛有水的水槽中（如图），然后匀速向上提起，直至铁块完全露出水面一定高度，则能反映弹簧秤的读数y （单位：N ）与铁块被提起的高度x （单位：cm ）之间的函数关系的图象大致是（）A ．B ．C ．D ．6．如图为一次函数y=kx+b (k 和b 为常数且00)k b ≠≠，的图象，则一次函数y bx k =+的图象大致是（）A ．B ．C ．D ．7．一次函数1y mx n =+与2y kx a =+的图象如图所示，则mx n kx a +>+的解集为( )A ．2x <B ．2x >C ．1x >D ．1x <8．若直线y ＝2x＋n 与y ＝mx ﹣1相交于点（1，﹣2），则（） A ．m ＝12，n ＝﹣52 B ．m ＝12，n ＝﹣1C ．m ＝﹣1，n ＝﹣52D ．m ＝﹣3，n ＝﹣329．已知点()P a b ，在一次函数2y x =-+的图象上，且在一次函数y x =图象的下方，则符合条件的a b -值可能是（） A ．-2B ．-1C ．0D ．110．如图，直线1l y x m =+：与直线2l y x n =-+：相交于点()12P ，，则关于x y ，的方程组y x my x n =+⎧⎨=-+⎩的解为（）A ．11x y =⎧⎨=-⎩B ．12x y =⎧⎨=⎩C ．21x y =⎧⎨=⎩D ．11x y =-⎧⎨=⎩二、填空题11．饮食店里快餐每盒10元，买n 盒需付s 元，则其中因变量是． 12．已知函数1()1f x x =-，那么(2)f = ． 13．已知一次函数y kx k =-，当0k <时，图像不过第象限．14．已知一次函数3y x =-与y kx =（k 是常数，0k ≠）的图像的交点坐标是()21-，，则方程组30x y kx y -=⎧⎨-=⎩的解是 . 三、解答题15．如图，正方形ABCD 的边长为2，P 为DC 上的点（不与C ，D 点重合）．设线段DP 的长为x ，求梯形ABCP 的面积y 关于x 的函数关系式，并写出自变量x 的取值范围．16．如图，直线AB 分别与x 轴、y 轴交于点()20A -，，()03B ，直线CD 分别与x 轴、y 轴交于点()10C ，和()01D ，，与直线AB 交于点E ．求四边形AODE 的面积．17．一次函数的图象经过点(35)-，且与直线13y x =-平行，求这个函数表达式．四、综合题18．小南一家到度假村度假，小南和妈妈坐公交车先出发，爸爸自驾车沿着相同的道路后出发，爸爸到达度假村后，发现忘了东西在家里，于是立即返回家里取，取到东西后又马上驾车前往度假村，（取东西的时间忽略不计），如下图是他们离家的距离s （km ）与小南离家的时间t （h ）的关系图，请根据图回答下列问题：（1）图中的自变量是，因变量是，小南家到该度假村的距离是km（2）小南出发小时后爸爸驾车出发，爸爸驾车的平均速度为 km /h （3）小南从家里到度假村的路途中，当他与爸爸相遇时，离家的距离是多少km ？19．如图，在平面直角坐标系中，O 为坐标原点，一次函数2y kx =+（k 为常数，0)k ≠的图象经过(21)A --，，并且交x 轴于点B ，交y 轴于点C .（1）求k 的值；（2）求BOC 的面积.20．网上购物快捷、简便，受到人们的广泛喜爱．小明家装修要用某种环保装饰材料，两个商家的原价相同．购物节优惠促销，甲店打9折，乙店不超过3件不打折，实际付费金额y甲（元），y乙（元）和x（件）（x为非负整数）的关系如图所示，小明家需要这种装饰材料6件，发现两家的付费金额恰好相同．（1）写出y甲（元）与x（件）的函数关系式，并求出a的值；（2）写出y乙（元）和x（件）的函数关系式，并写出乙店实际的优惠方案；（3）小宇家也需要这种装饰材料，按照上述的优惠方案，已知甲店比乙店付费金额高60元，求小宇家购买的件数．参考答案与解析1．【答案】B【解析】【解答】根据题意可得：因变量是水的温度。

人教版八年级数学上册《第十二章全等三角形》单元测试卷及答案

人教版八年级数学上册《第十二章全等三角形》单元测试卷及答案一．选择题（共8小题，满分24分）1．根据下列条件，能画出唯一确定的三角形的是（）A．AB＝2，BC＝5，AC＝2B．AB＝6，∠B＝30°，AC＝4C．AB＝4，∠B＝60°，∠C＝75°D．BC＝8，∠C＝90°2．下列各组图形、是全等图形的是（）A．B．C．D．3．在△ABC中，∠A＝50°，∠B＝60°，若△ABC≌△DEF，则∠E与∠F的关系为（）A．∠E＜∠F B．∠E＝∠F C．∠E＞∠F D．无法确定4．如图，CD⊥AB，BE⊥AC，垂足分别为D、E，BE、CD相交于点O．如果AB＝AC，那么图中全等的直角三角形的对数是（）A．1B．2C．3D．45．如图，已知点A、D、C、F在同一条直线上，∠B＝90°，AB＝DE，AD＝CF，BC＝EF，则∠E＝（）A．90°B．45°C．50°D．40°6．如图是雨伞在开合过程中某时刻的截面图，伞骨AB＝AC，点D，E分别是AB，AC的中点，DM，EM 是连接弹簧和伞骨的支架，且DM＝EM，已知弹簧M在向上滑动的过程中，总有△ADM≌△AEM，其判定依据是（）A．ASA B．AAS C．SSS D．HL7．下列作图属于尺规作图的是（）A．用量角器画出∠AOB，使∠AOB＝60°B．借助没有刻度的直尺和圆规作∠AOB，使∠AOB＝2∠αC．用三角尺画MN＝1.5cmD．用三角尺过点P作AB的垂线8．两把相同的长方形直尺按如图所示方式摆放，记两把直尺的接触点为P，其中一把直尺边缘和射线OA 重合，另把直尺的下边缘与射线OB重合，连，接OP并延长．若∠BOP＝25°，则∠AOP的度数为（）A．12.5°B．25°C．37.5°D．50°二．填空题（共8小题，满分24分）9．长方体的直观图有很多种画法，通常我们采用画法．10．如图，AB＝AC，点D，E分别在AB与AC上，CD与BE相交于点F．只填一个条件使得△ABE≌△ACD，添加的条件是：．11．如图，在△ABC中，AD平分∠BAC，DE⊥AB，若AC＝9，DE＝4，则S＝．△ACD12．某中学计划在一块长16m，宽6m的矩形空地上修建三块全等的矩形草坪，如图所示，余下空地修建成同样宽为a的小路．（1）若a＝1.5m，则草坪总面积为平方米．（2）若草坪总面积恰好等于小路总面积，那么，此时的路宽a是米．13．如图所示，点A、B、C、D均在正方形网格格点上，则∠ABC+∠ADC＝．14．如图，小红要测量池塘A、B两端的距离，他设计了一个测量方案，先在平地上取可以直接到达A点和B点的C，D两点，AC与BD相交于点O，且测得AC＝BD＝55m，OA＝OD＝17m，△COD的周长为103m，则A，B两端的距离为m．15．如图，点E，C在BF上，BE＝CF，∠A＝∠D＝90°，请添加一个条件，使Rt△ABC≌Rt△DFE．16．我们把一条对角线是另一条对角线2倍的四边形叫“奇异四边形”．现有两个全等的直角三角形，一条直角边长是1，如果它们可以拼成对角线互相垂直的“奇异四边形”，那么直角三角形另一条直角边长是．三．解答题（共6小题，满分52分）17．如图，AD与BC相交于点O，连接AC、BD，AC＝BD，∠C＝∠D，求证：△OAC≌△OBD．18．如图，在△ABC中，点E是BC边上的一点．连接AE，BD垂直平分AE，垂足为F，交AC于点D．连接DE．（1）若△ABC的周长为19，AB为6，求△DEC的周长；（2）若∠ABC＝35°，∠C＝50°，求∠CDE的度数．19．在下列3个6×6的网格中，画有正方形ABCD，沿网格线把正方形分ABCD分割成两个全等图形，请用三种不同的方法分割，画出分割线．20．如图，△ABC≌△DEF，点B，F，C，E在同一条直线上，BC＝5，FC＝4．（1）猜想AB与DE之间的位置关系，并说明理由．（2）求BE的长．21．如图，在△ABC中，∠B＝90°，点O是∠CAB、∠ACB平分线的交点．（1）连接BO，求证：BO平分∠ABC；（不能利用“三角形三条角平分线相交于一点”直接来证明）（2）若BC＝4cm，AC＝5cm，求点O到边AB的距离．22．如图，若两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等．试说明两个滑梯的倾斜角∠ABC和∠DFE互余．参考答案与解析一．选择题（共8小题，满分24分）1．【答案】C【解答】解：A、∵2+2＜5，即AB+AC＜BC∴此时三条线段不能构成三角形，不符合题意；B、AB＝6，∠B＝30°，AC＝4，根据边边角不能确定唯一三角形，不符合题意；C、AB＝4，∠B＝60°，∠C＝75°，根据角角边可以确定唯一三角形，符合题意；D、BC＝8，∠C＝90°，只有一角和一边，不能确定唯一三角形，不符合题意；故选：C．2．【答案】D【解答】解：A、两个图形不能完全重合，不是全等图形，不符合题意；B、两个图形不能完全重合，不是全等图形，不符合题意；C、两个图形不能完全重合，不是全等图形，不符合题意；D、两个图形能够完全重合，是全等图形，符合题意；故选：D．3．【答案】A【解答】解：∵在△ABC中，∠A＝50°，∠B＝60°∴∠C＝180°﹣∠A﹣∠B＝70°∵△ABC≌△DEF∴∠A＝∠D＝50°，∠B＝∠E＝60°，∠C＝∠F＝70°∴∠E＜∠F故选：A．4．【答案】C【解答】解：∵CD⊥AB，BE⊥AC∴∠ADC＝∠AEB＝90°在△ADC和△AEB中∴△ADC≌△AEB（AAS）；∴AD＝AE，∠C＝∠B∵AB＝AC∴BD＝CE在△BOD和△COE中∴△BOD≌△COE（AAS）；∴OB＝OC，OD＝OE在Rt△ADO和Rt△AEO中∴Rt△ADO≌Rt△AEO（HL）；∴共有3对全等直角三角形故选：C．5．【答案】A【解答】证明：∵AD＝CF∴AD+DC＝CF+DC即AC＝DF在△ABC和△DEF中∴△ABC≌△DEF（SSS）∴∠E＝∠B＝90°故选：A．6．【答案】C【解答】解：∵AB＝AC，点D，E分别是AB，AC的中点∴AD＝AE在△ADM和△AEM中．∴△ADM≌△AEM（SSS）故选：C．7．【答案】B【解答】解：尺规作图是指：只利用没有刻度的直尺和圆规进行作图故选：B．8．【答案】B【解答】解：∵两把相同的长方形直尺的宽度一致∴点P到射线OA，OB的距离相等∴OP是∠AOB的角平分线∵∠BOP＝25°∴∠AOP＝∠BOP＝25°故选：B．二．填空题（共8小题，满分24分）9．【答案】斜二侧．【解答】解：长方体的直观图有很多种画法，通常我们采用斜二侧画法．故答案为：斜二侧．10．【答案】∠B＝∠C（答案不唯一）．【解答】解：∵∠B＝∠C，AB＝AC，∠A＝∠A∴△ABE≌△ACD（ASA）故答案为：∠B＝∠C（答案不唯一）．11．【答案】18．【解答】解：过点D作DF⊥AC，交AC于点F∵AD平分∠ABC，DE⊥AB，DF⊥AC∴DF＝DE＝4∵AC＝9＝AC•DF＝×94＝18∴S△ACD故答案为：18．12．【答案】（1）30；（2）1．【解答】解：（1）由图可得草坪的总面积是（16﹣4a）（6﹣2a）＝8a2﹣56a+96当a＝1.5时8a2﹣56a+96＝8×1.52﹣56×1.5+96＝8×2.25﹣56×1.5+96＝18﹣84+96＝30即a＝1.5m时，草坪总面积为30平方米故答案为：30；（2）由图可得草坪的总面积是（16﹣4a）（6﹣2a）＝8a2﹣56a+96 路的总面积是16×6﹣（8a2﹣56a+96）＝56a﹣8a2 ∵草坪总面积恰好等于小路总面积∴8a2﹣56a+96＝56a﹣8a2解得a1＝1，a2＝6（舍去）即此时的路宽a为1米故答案为：1．13．【答案】45°．【解答】解：如图所示在△ACB和△AED中∴△ACB≌△AED（SAS）∴∠ABC＝∠ADE∴∠ABC+∠ADC＝∠ADE+∠ADC＝∠CDE＝45°．故答案为：45°．14．【答案】48．【解答】解：∵AC＝BD，OA＝OD∴AC﹣OA＝BD﹣OD即OC＝OB在△COD和△BOA中∴△COD≌△BOA（SAS）∴CD＝AB∵△COD的周长为103m∴OC+OD+CD＝OC+OA+CD＝103m即AC+CD＝103m．∵AC＝55m．∴CD＝48m．∴AB＝48m．故答案为：48．15．【答案】DE＝AC（答案不唯一）．【解答】解：添加DE＝AC∵BE＝CF∴BE+EC＝CF+EC即EF＝CB在Rt△ABC与Rt△DFE中∴Rt△ABC≌Rt△DFE（HL）．故答案为：DE＝AC（答案不唯一）．16．【答案】见试题解答内容【解答】解：（1）当CD＝1时，设DO＝m，且0＜m＜1 BD＞1，如图1所示：∵Rt△ABC≌Rt△DBC∴∠BAC＝∠BDC＝90°，BA＝BD，CA＝CD ∴△ABD是等腰三角形∴AO＝DO＝m又∵BC＝2AD∴BC＝4m又∵AD⊥BC∴＝2m2又∵CD⊥BD∴＝BD∴2m2＝BD解得：BD＝4m2在Rt△DBC中，由勾股定理得：BD＝＝∴4m2＝解得：m2＝或m2＝∴4m2＝2+或4m2＝2﹣（舍去）∵BD＞1∴BD＝2+；（2）当BD＝1时，设DO＝x，且0＜x＜1CD＜1，如图1所示：同理可求得：或∴4x2＝2+（舍去），或4x2＝2﹣∵CD＜1∴CD＝2﹣；综合所述，另一条直角边的长为2+或2﹣故答案为2+或2﹣．三．解答题（共6小题，满分52分）17．【答案】证明见解析．【解答】证明：在△OAC与△OBD中∴△OAC≌△OBD（AAS）．18．【答案】（1）7．（2）45°．【解答】解：（1）∵BD垂直平分AE，AB＝6∴BA＝BE＝6，DA＝DE∵△ABC的周长为19∴AB+BC+AC＝19∴AB+BE+EC+AD+DC＝2AB+EC+DE+CD＝19∴CE+ED+DC＝19﹣2AB＝19﹣2×6＝7∴△DEC的周长为7；（2）∵∠ABC＝35°，∠C＝50°∴∠BAD＝180°﹣∠ABC﹣∠C＝180°﹣35°﹣50°＝95°∵BD垂直平分AE∴BA＝BE，DA＝DE在△BAD和△BED中∴△BAD≌△BED（SSS）∴∠BAD＝∠BED＝95°∴∠DEC＝180°﹣∠BED＝180°﹣95°＝85°∴∠CDE＝180°﹣∠DEC﹣∠C＝180°﹣85°﹣50°＝45°．19．【答案】见解析．【解答】解：如图所示：20．【答案】（1）AB∥DE，理由见解析；（2）6．【解答】解：（1）AB∥DE，理由如下：∵△ABC≌△DEF∴∠B＝∠F∴AB∥DE；（2）∵△ABC≌△DEF∴EF＝BC＝5∵FC＝4∴CE＝EF﹣FC＝1∴BE＝BC+CE＝6．21．【答案】（1）证明见解析；（2）1．【解答】（1）证明：过O作OD⊥BC于D，OE⊥AB于E，OF⊥AC于F ∵点O是∠CAB、∠ACB平分线的交点∴OD＝OF，OE＝OF∴OE＝OD∵OD⊥BC，OE⊥AB∴BO平分∠ABC；（2）解：∵BC＝4cm，AC＝5cm，∠ABC＝90°∴AB＝＝3∵△ABC的面积＝△OBC的面积+△AOB的面积+△AOC的面积∴BC•AB＝BC•OD+AB•OE+AC•OF∴3×4＝（3+4+5）×OE∴OE＝1∴点O到边AB的距离是1．22．【答案】见解析．【解答】解：∵两个滑梯长度相同∴BC＝EF∵AC＝DF，∠CAB＝∠FDE＝90°在Rt△CAB和Rt△FDE中∴Rt△CAB≌Rt△FDE（HL）∴∠ABC＝∠DEF∵∠DFE+∠DEF＝90°∴∠DFE+∠ABC＝90°即：两个滑梯的倾斜角∠ABC和∠DFE互余．。

人教版八年级数学第十二章《全等三角形》单元测试题(含答案)

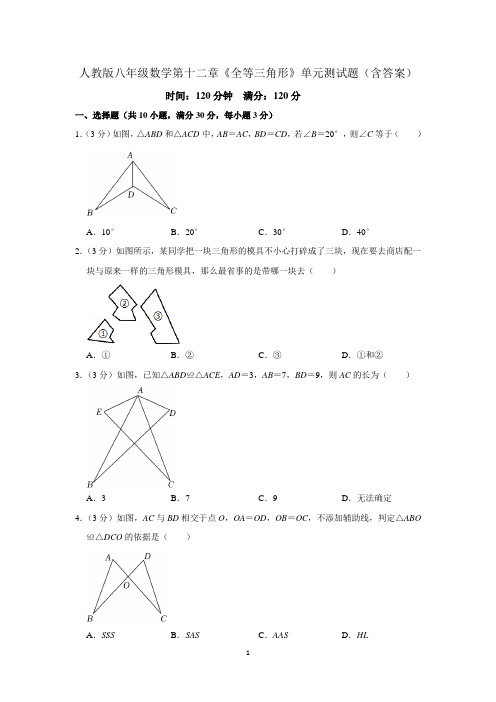
人教版八年级数学第十二章《全等三角形》单元测试题（含答案）时间：120分钟满分：120分一、选择题（共10小题，满分30分，每小题3分）1．（3分）如图，△ABD和△ACD中，AB＝AC，BD＝CD，若∠B＝20°，则∠C等于（）A．10°B．20°C．30°D．40°2．（3分）如图所示，某同学把一块三角形的模具不小心打碎成了三块，现在要去商店配一块与原来一样的三角形模具，那么最省事的是带哪一块去（）A．①B．②C．③D．①和②3．（3分）如图，已知△ABD≌△ACE，AD＝3，AB＝7，BD＝9，则AC的长为（）A．3B．7C．9D．无法确定4．（3分）如图，AC与BD相交于点O，OA＝OD，OB＝OC，不添加辅助线，判定△ABO ≌△DCO的依据是（）A．SSS B．SAS C．AAS D．HL5．（3分）如图，在△ABC和△DEF中，点A，E，B，D在同一直线上，AC∥DF，AC＝DF，只添加一个条件，能判定△ABC≌△DEF的是（）A．BC＝DE B．AE＝DB C．∠A＝∠DEF D．∠ABC＝∠D 6．（3分）如图，点E、F、C、B在同一直线上，AB＝DE，∠A＝∠D，添加下列一个条件，不能判定△ABC≌△DEF的条件是（）A．∠ACB＝∠DFE B．AC＝DF C．∠B＝∠E D．BC＝EF7．（3分）如图，∠AOB＝150°，OP平分∠AOB，PD⊥OB于点D，PE⊥OA于点E，PC ∥OB交OA于点C，若PD＝3，则OC的长为（）A．6B．5C．4D．38．（3分）如图，AB，CD相交于O，△OCA≌△OBD，AO＝6，BO＝4，则CD的长为（）A．9B．10C．11D．129．（3分）下列结论正确的是（）A．两个等边三角形全等B．有一个锐角相等的两个直角三角形全等C．有两边及一个角对应相等的两个三角形全等D．斜边和一个锐角对应相等的两个直角三角形全等10．（3分）根据语句“直线a与直线b相交，点P在直线a上，直线b不经过点P．”画出的图形是（）A．B．C．D．二、填空题（共5小题，满分15分，每小题3分）11．（3分）如图，P是∠AOB的平分线OC上一点，PD⊥OB，PE⊥OA，垂足分别为D，E，若PD＝3，则PE的长是．12．（3分）已知△ABC的三边长为x，3，6，△DEF的三边长为5，6，y．若△ABC与△DEF全等，则x+y的值为．13．（3分）如图，AD是△ABC的角平分线，DF⊥AB于点F，点E，G分别是边AB，AC 上的点，且DE＝DG，则∠AED+∠AGD＝度．14．（3分）如图，OP平分∠MON，P A⊥ON于点A，若P A＝3，则点P到射线OM的距离是．15．（3分）如图，BO平分∠ABC，OD⊥BC于点D，点E为射线BA上一动点，若OD＝5，则OE的最小值为．三、解答题（共8小题，满分75分）16．（9分）如图，已知AD平分∠BAC，AB＝AC．求证：△ABD≌△ACD．17．（9分）如图，已知△ABC和△ADC有公共边AC，且AB＝AD，请你添加一个条件（不再添加其他线段，不再标注或使用其他字母），使∠B＝∠D，并说明理由．18．（9分）如图，AB＝AD，∠C＝∠E，∠BAE＝∠DAC．求证：AC＝AE．19．（9分）如图，已知AB＝AD，AE＝AC，∠DAB＝∠EAC．求证：△ACD≌△AEB．20．（9分）已知：如图，点E、F在BC上，AF与DE交于点G，AB＝DC，GE＝GF，∠B ＝∠C．求证：AG＝DG．21．（10分）已知：如图，AC＝BD，AD＝BC，AD，BC相交于点O，过点O作OE⊥AB，垂足为E．求证：（1）△ABC≌△BAD．（2）AE＝BE．22．（10分）如图，已知AD∥BC，AD＝CB，AE＝FC．（1）求证：∠D＝∠B；（2）若∠A＝20°，∠D＝110°，求∠BEC的度数．23．（10分）如图，△ABC中，D是BC延长线上一点，满足CD＝AB，过点C作CE∥AB 且CE＝BC，连接DE并延长，分别交AC、AB于点F、G．（1）求证：△ABC≌△DCE；（2）若∠B＝50°，∠D＝22°，求∠AFG的度数．参考答案一、选择题（共10小题，满分30分，每小题3分）1．B；2．C；3．B；4．B；5．B；6．D；7．A；8．B；9．D；10．D；二、填空题（共5小题，满分15分，每小题3分）11．312．813．18014．315．5三、解答题（共8小题，满分75分）16．证明：∵AD平分∠BAC，∴∠BAD＝∠CAD，在△ABD和△ACD中，，∴△ABD≌△ACD（SAS）．17．解：添加条件：CB＝CD，理由：在△ABC和△ADC中，，∴△ABC≌△ADC（SSS），∴∠B＝∠D．（答案不唯一）18．证明：∵∠BAE＝∠DAC，∴∠BAE+∠EAC＝∠DAC+∠EAC，即∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（AAS），∴AC＝AE．19．证明：∵∠DAB＝∠EAC，∴∠DAB+∠BAC＝∠EAC+∠BAC，即∠DAC＝∠BAE，在△ACD和△AEB中，，∴△ACD≌△AEB（SAS）．20．证明：∵GE＝GF，∴△GEF为等腰三角形，∴∠GEF＝∠GFE，∵在△ABF和△DCE中，∠B＝∠C，∴∠A＝∠D，在△ABF和△DCE中，，∴△ABF≌△DCE（ASA），∴AF＝DE，又∵GF＝GE，∴AF﹣GF＝DE﹣GE，即AG＝DG．21．证明（1）在ABC和△BAD中，，∴△ABC≌△BAD（SSS）；（2）∵△ABC≌△BAD，∴∠CBA＝∠DAB，∴OA＝OB，∵OE⊥AB，∴AE＝BE．22．（1）证明：∵AD∥BC，∴∠A＝∠C，∵AE＝FC，∴AF＝CE，在△ADF和△CBE中，，∴△ADF≌△CBE（SAS），∴∠D＝∠B；（2）解：∵∠A＝20°，∠D＝110°，∴∠AFD＝50°，∵△ADF≌△CBE，∴∠BEC＝∠AFD＝50°．23．（1）证明：∵CE∥AB，∴∠B＝∠DCE，在△ABC与△DCE中，，∴△ABC≌△DCE（SAS）；（2）解：∵△ABC≌△DCE，∠B＝50°，∠D＝22°，∴∠ECD＝∠B＝50°，∠A＝∠D＝22°，∵CE∥AB，∴∠ACE＝∠A＝22°，∵∠CED＝180°﹣∠D﹣∠ECD＝180°﹣22°﹣50°＝108°，∴∠AFG＝∠DFC＝∠CED﹣∠ACE＝108°﹣22°＝86°。

高考数学(文科)异构异模复习考案撬分法习题第十二章算法初步 12 Word版含答案

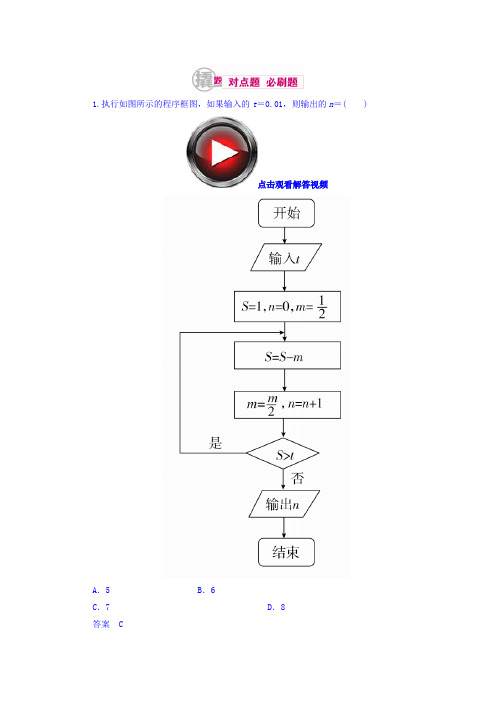
1.执行如图所示的程序框图，如果输入的t＝0.01，则输出的n＝( )点击观看解答视频A．5 B．6C．7 D．8答案 C解析由程序框图可知，S ＝1－12＝12，m ＝14，n ＝1，12>0.01； S ＝12－14＝14，m ＝18，n ＝2，14>0.01； S ＝14－18＝18，m ＝116，n ＝3，18>0.01； S ＝18－116＝116，m ＝132，n ＝4，116>0.01； S ＝116－132＝132，m ＝164，n ＝5，132>0.01； S ＝132－164＝164，m ＝1128，n ＝6，164>0.01； S ＝164－1128＝1128，m ＝1256，n ＝7，1128<0.01.故选C. 2．下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的a ，b 分别为14,18，则输出的a ＝( )A ．0B ．2C ．4D ．14答案 B解析第一次执行，输入a ＝14，b ＝18，因为a <b ，所以b ＝18－14＝4；第二次执行，因为a ＝14，b ＝4，a >b ，所以a ＝14－4＝10；第三次执行，因为a ＝10，b ＝4，a >b ，所以a ＝10－4＝6；第四次执行，因为a ＝6，b ＝4，a >b ，所以a ＝6－4＝2；第五次执行，因为a ＝2，b ＝4，a <b ，所以b ＝4－2＝2，此时a ＝b ＝2.故选B.3．执行如图所示的程序框图，若输出k 的值为8，则判断框内可填入的条件是( )点击观看解答视频A ．s ≤34？B ．s ≤56？C ．s ≤1112？D ．s ≤2524？答案 C解析第一次循环，得k ＝2，s ＝12；第二次循环，得k ＝4，s ＝12＋14＝34；第三次循环，得k ＝6，s ＝34＋16＝1112；第四次循环，得k ＝8，s ＝1112＋18＝2524，此时退出循环，输出k ＝8，所以判断框内可填入的条件是s ≤1112？，故选C.4．执行如图所示的程序框图，如果输入n ＝3，则输出的S ＝( )A.67B.37C.89D.49答案 B解析当输入n ＝3时，输出S ＝11×3＋13×5＋15×7＝12⎝ ⎛⎭⎪⎫1－13＋13－15＋15－17＝37.故选B. 5．根据下边框图，当输入x 为2006时，输出的y ＝( )A．28 B．10C．4 D．2答案 B解析因为x所有的值构成首项为2006，公差为－2的等差数列．结合题意可知，当x ＝－2时，输出y的值，此时y＝32＋1＝10.故选B.6．执行如图所示的程序框图，如果输入的t∈，则输出的S属于( )A．B．C ．D ．答案 D解析当0≤t ≤2时，S ＝t －3∈．当－2≤t <0时，2t 2＋1∈(1,9]，则S ∈(－2,6]．综上，S ∈，故选D.7．执行下面的程序框图，若输入的a ，b ，k 分别为1,2,3，则输出的M ＝( )A.203B.72C.165D.158答案 D解析当a ＝1，b ＝2，k ＝3，n ＝1时，1≤3，M ＝1＋12＝32，a ＝2，b ＝32，n ＝2；2≤3，M ＝2＋23＝83，a ＝32，b ＝83，n ＝3；3≤3，M ＝32＋38＝158，a ＝83，b ＝158，n ＝4；4>3，程序结束，输出M ＝158.8．执行下面的程序框图，如果输入的x ，t 均为2，则输出的S ＝( )A．4 B．5C．6 D．7答案 D解析第一次：1≤2成立，M＝2，S＝5，k＝2；第二次：2≤2成立，M＝2，S＝7，k＝3；第三次：3≤2不成立，输出S＝7.故输出的S＝7.9．阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为( )A．7 B．9C．10 D．11答案 B解析通过对程序框图的分析可知，该循环是一个根据判断条件不断累加的过程，∵i ＝7时，S ＝0＋lg 13＋lg 35＋lg 57＋lg 79＝lg 19>－1，i ＝9时，S ＝0＋lg 13＋lg 35＋lg 57＋lg 79＋lg 911＝lg 111<－1，∴i ＝9，故选B.10．根据框图，对大于2的整数N ，输出的数列的通项公式是( )A ．a n ＝2nB ．a n ＝2(n －1)C ．a n ＝2nD ．a n ＝2n －1答案 C解析因为N >2，所以可取N ＝3，则a 1＝2×1＝2，S ＝a 1＝2，i ＝1＋1＝2.判断2>3是否满足？否，返回运算a 2＝2S ＝4，i ＝3，S ＝a 2＝4，判断3>3是否满足？否，返回运算a 3＝2S ＝8，因此a 1＝2，a 2＝4，a 3＝8，只有C 选项符合．11．执行如图的程序框图，如果输入的x ，y ∈R ，那么输出的S 的最大值为( )点击观看解答视频A ．0B ．1C ．2D ．3答案 C解析先画出x ，y 满足的约束条件⎩⎪⎨⎪⎧x ≥0，y ≥0，x ＋y ≤1，对应的可行域如图中阴影部分：移动直线l0：y＝－2x.当直线经过点A(1,0)时，y＝－2x＋S中截距S最大，此时S max＝2×1＋0＝2.再与x≥0，y≥0，x＋y≤1不成立时S＝1进行比较，可得S max＝2.12．执行如图所示的程序框图，输出的结果为( )A．(－2,2) B．(－4,0)C．(－4，－4) D．(0，－8)答案 B解析初始值x＝1，y＝1，k＝0，执行程序框图，则s＝0，t＝2，x＝0，y＝2，k＝1；s＝－2，t＝2，x＝－2，y＝2，k＝2；s＝－4，t＝0，x＝－4，y＝0，k＝3，此时输出(x，y)，则输出的结果为(－4,0)，选B.13．执行如图所示的程序框图(算法流程图)，输出的n为________．答案 4解析各次循环中变量a，n的取值如下表所示：当a＝1.416时，跳出循环，输出的n为4.14．根据如图所示的伪代码，可知输出的结果S为________．答案7解析该伪代码运行3次，故输出的S为7.15．下图是一个算法流程图，则输出的n的值是________．答案 5解析本题实质上是求不等式2n>20的最小整数解，2n>20的整数解为n≥5，因此输出的n＝5.16．设a是一个各位数字都不是0且没有重复数字的三位数，将组成a的3个数字按从小到大排成的三位数记为I(a)，按从大到小排成的三位数记为D(a)(例如a＝815，则I(a)＝158，D(a)＝851)．阅读如图所示的程序框图，运行相应的程序，任意输入一个a，输出的结果b＝________.答案495解析不妨取a＝815，则I(a)＝158，D(a)＝851，b＝693；则取a＝693，则I(a)＝369，D(a)＝963，b＝594；则取a＝594，则I(a)＝459，D(a)＝954，b＝495；则取a＝495，则I(a)＝459，D(a)＝954，b＝495.故输出结果b＝495.。

高数第十二章习题课

n
lim
n
(n
1) 3n
2n1
lim
n
(n
3n1 1) 2n1
n 2n 3n
n 2n
lim 3 n 3 1 n 2 n 1 2
故级数发散
二、交错级数及其审敛法
设 un 0 , n 1, 2,, 则各项符号正负相间的级数
称为交错级数 . 定理7 . ( 莱布尼茨判别法 ) 若交错级数满足条件:
类似可证前面加上或改变有限项的情况 .
性质4. 收敛级数加括弧后所成的级数仍收敛,且其和不变.
推论: 若加括弧后的级数发散, 则原级数必发散.
注意: 收敛级数去括弧后所成的级数不一定收敛.
说明:(1)此性质说明收敛级数项中任意加括号，既不改变级数的收敛性，也不改变它的和.
(2)若一个级数加括号后收敛，则原级数敛散性不
因此这个级数发散.
原命题真逆命题假否命题假逆否命题真
第二节
第十二章
常数项级数的审敛法
一、正项级数及其审敛法二、交错级数及其审敛法三、绝对收敛与条件收敛
一、正项级数及其审敛法
1.定义: 如果级数 un中各项均有un 0，
n1
2.正项级数收敛的充要条件:
定理 1. 正项级数
发收散敛
使得一大类级数的收敛判定问题，转化为正项级数的收敛问题 .
注意
一般而言，由
| un |收敛，能推出
un 收敛,
i 1
i 1
但由 | un | 发散，并不能推出 un 发散.
i 1
i 1
如 (1)n 1
n1
n
1
i1 n
发散,
但
(1)n 1 收敛

《高等数学12》理工类试题与答案

《高等数学12》理工类试题一一、填空题（本题共5小题，每小题3分，满分15分，请将答案填在题中的横线上） 1、已知函数(,)y f x y xe -=，它在点(1,0)P 处的梯度等于． 2、过Z 轴和点0(2,3,4)M -的平面方程为 .3、空间曲线211x t t y t z t=+⎧⎪+⎪=⎨⎪⎪=⎩在点1t =处的切线方程为 .4、周期为2π的函数()f x 在[,)ππ-上的表达式为1,0(),0x x f x x x ππ+≤<⎧⎪=⎨-≤<⎪⎩，则它展开成傅里叶级数时的系数0a = .5、函数2222(,)2f x y x y x y =+-在区域{}22(,)4D x y x y =+≤上的最大值为．二、选择题（本题共5小题，每小题3分，满分15分，每小题给出的四个选项中，只有一个符合题目要求，把所选项前的字母填在题后的括号内） 1、设正项级数1n n u ∞=∑收敛，则下列级数一定收敛的是（）．（A ）11(1)n n n u ∞+=-∑；（B ）1n n u ∞=∑；（C ）11n nu ∞=∑ （D ）1()(0)n n u a a ∞=+>∑2、设直线l 为102x y z==-，则直线l （）. （A ）过原点且垂直于x 轴；（B ）过原点且垂直于y 轴；（C ）过原点且垂直于z 轴；（D ）不过原点也不垂直于坐标轴.3、求244x y y y xe '''-+=的特解时，应设（）． (A) *2()x y Ax B e =+； (B) *22x y Ax e =； (C) *2()x y x Ax B e =+； (D) *22()x y x Ax B e =+．4、设(,)f x y 为连续函数，则二次积分420d (,)d x xx f x y y =⎰⎰（）（A ）2414d (,)d y y y f x y x ⎰⎰；（B) 21440d (,)d y y y f x y x -⎰⎰；（C ）41104d (,)d y f x y x ⎰⎰；（D ）20144d (,)d y y y f x y x ⎰⎰.5、比较321I ()d ()d DDx y x y σσ=+=+⎰⎰⎰⎰2与I 的大小，其中积分区域D 是由圆周22(2)(1)1x y -+-=所围成,则（）(A) 12I I =； (B) 12I I ≥；(C) 12I I ≤； (D) 1I 和2I 不能比较大小.三、计算题（本题共5小题，1题6分，2、3、4题每题8分，5题10分，满分40分） 1、求向量{1,1,2}a →=--与{1,2,1}b →=-的夹角θ；2、设(,)z f x y =由方程222z x z y e -=所确定，求d z ；3、设2(2,)y z xf x x =，f 具有二阶连续偏导数，求2zx y∂∂∂.4、计算二重积分2()d d Dy x x y -⎰⎰，其中D 由曲线2y x =和 1y =所围成的平面闭区域；5、已知立体Ω是由圆柱面221x y +=内部、平面4z =下方和抛物面221z x y =--上方部分围成，求22d x y V Ω+⎰⎰⎰.四、判断题（本题8分）判定级数11(1)sin2n nn nππ-∞=-∑是否收敛？如果是收敛的，是绝对收敛还是条件收敛？五、综合题（本题共3小题，1题8分， 2、3题每题7分，满分22分）1、将函数2()4xf x x =+展开成x 的麦克劳林级数，并讨论级数的收敛域.2、求微分方程ln 2(ln 1)xy x y x x '+=+的通解.3、求微分方程(1)xxe yy e '+=满足初始条件00x y==的特解.《高等数学12》理工类试题一答案一、填空题(每题3分,共15分)1、_____i j →→-或{1,1}-_____. 2、______320x y +=______.3、_____221112x y z ---==-_____. 4、 ______1______. 5、___8或8f =最大或(0,2)8f ±=最大______.二、选择题（每小题 3分，共 15分）1、A.2、B.3、D.4、A.5、C.三、（本题共5小题，1题6分，2、3、4题每题8分，5题每题10分，共40分） 1、解：（6分）cos a b a b θ→→→→⋅=⋅………2分1221cos 266a ba bθ→→→→⋅-++===⋅………3分3πθ=………1分.2、解：（8分）222z z z x zy x x e ∂∂-=∂∂， z z xx z ye∂=∂+ ………3分 222z z z z z y y y e e ∂∂-=+∂∂， z zz e y z ye ∂-=∂+ ………3分 d z z x dx z ye =+zze dy z ye-++ ………2分. 3、解：（8分）令f 对2x 的偏导数记为1f '，对2yx的偏导数记为2f '，1f '对2y x 的偏导数记为12f ''，2f '对2y x 的偏导数记为22f ''， ………1分2212122[2()]2z y y f x f f f xf f x x x∂''''=++-=+-∂ ………4分2221222222222[][]z y y y y yf x f f f x y x x x x x∂''''''=⋅+⋅--⋅∂∂ 31222224y yf f x''''=-. ………3分. 4、解：（8分）如图所示,211221()d d ()xDy x x y dx y x dy --=-⎰⎰⎰⎰ ………4分221121241111[][]222x y x y dx x x dx --=-=-+⎰⎰351111[]2310x x x -=-+ ……2分 815=. ……2分5、解：（10分）如图所示 , ……2分221422201d r x y V d r dr dz πθ-Ω+=⎰⎰⎰⎰⎰⎰……3分1223510012(3)2[]5r r dr r r ππ=+=+⎰ ………3分 125π=………2分四、（本题8分）解：（8分）考察111(1)1sinsin 22n nnn n nnππππ-∞∞==-=∑∑，因为11sin 2nnn πππ≤(1)n ≥ ………4分而11q π=<，所以几何级数11nn π∞=∑是收敛的，故11(1)sin2n nn nππ-∞=-∑绝对收敛，原级数收敛.………4分五、（本题共3小题，1题8分， 2、3题每题7分，满分22分）1、解：（8分）因为，21()414x f x x =⋅+，又因为01(1),(11)1n n n x x x ∞==--<<+∑， ………2分所以，()f x =221100(1)()(1)444n n n n n n n x x x +∞∞+==-=-∑∑. ………3分 222321121lim (1)/(1)lim 4444n n n n n n n n x x x x ρ+++++→∞→∞=--==. 当214xρ=<，即22x -<<时，级数绝对收敛；当2x =-时，级数111000(2)441(1)(1)(1)4242n n nn n n n n n n ∞∞∞+++===-⋅-=-=-⋅∑∑∑发散，当2x =时，级数100241(1)(1)42n nn n n n ∞∞+==⋅-=-∑∑发散，级数收敛域为(22)x -<<.所以，()f x 2110(1)4n nn n x +∞+==-∑，(22)x -<< ………3分2、解：（7分）因为112(1)ln ln dy y dx x x x+=+是一阶线性微分方程，所以由 ()()[()]P x dxP x dxy e Q x e dx C -⎰⎰=+⎰ ………2分11ln ln 1[2(1)]ln dx dx x x x xy e e dx C x-⎰⎰=++⎰ln(ln )[(2ln 2)]x e x dx C -=++⎰ ……3分11[2ln 2][2(ln )2]ln ln xdx dx C x x x x C x x=++=-++⎰⎰ 2ln C x x =+.所以，通解为2ln Cy x x=+ ………2分 3、解：因为1xxe ydy dx e =+是变量可分离微分方程，所以由 1xx e ydy dx e =+⎰⎰ ………2分21ln(1)2x y e C =++ 22ln(1)x y e C =++ （其中12C C =） ……3分由00x y==，得002ln(1)e C =++2ln 2C =-特解为： 22ln(1)2ln 2xy e =+-. ……2分。

高考(新课标)数学(文)大一轮复习检测：第十二章推理与证明、算法、复数 12-2 Word版含答案

A 组专项基础训练(时间：35分钟)1．若a 、b ∈R ，则下面四个式子中恒成立的是() A ．lg(1＋a 2)>0B ．a 2＋b 2≥2(a －b －1) C ．a 2＋3ab >2b 2 D.a b <a ＋1b ＋1【解析】在B 中，∵a 2＋b 2－2(a －b －1)＝(a 2－2a ＋1)＋(b 2＋2b ＋1)＝(a －1)2＋(b ＋1)2≥0，∴a 2＋b 2≥2(a －b －1)恒成立．【答案】 B2．①已知p 3＋q 3＝2，求证p ＋q ≤2，用反证法证明时，可假设p ＋q ≥2；②已知a ，b ∈R ，|a |＋|b |＜1，求证方程x 2＋ax ＋b ＝0的两根的绝对值都小于1，用反证法证明时可假设方程有一根x 1的绝对值大于或等于1，即假设|x 1|≥1.以下正确的是()A ．①与②的假设都错误B ．①与②的假设都正确C ．①的假设正确；②的假设错误D ．①的假设错误；②的假设正确【解析】反证法的实质是否定结论，对于①，其结论的反面是p ＋q ＞2，所以①不正确；对于②，其假设正确．【答案】 D3．分析法又称执果索因法，若用分析法证明：“设a ＞b ＞c ，且a ＋b ＋c ＝0，求证b 2－ac ＜3a ”索的因应是()A ．a －b ＞0B ．a －c ＞0C ．(a －b )(a －c )＞0D ．(a －b )(a －c )＜0 【解析】由题意知b 2－ac ＜3a ⇐b 2－ac ＜3a 2⇐(a ＋c )2－ac ＜3a 2⇐a 2＋2ac ＋c 2－ac －3a 2＜0 ⇐－2a 2＋ac ＋c 2＜0 ⇐2a 2－ac －c 2＞0⇐(a －c )(2a ＋c )＞0⇐(a －c )(a －b )＞0. 【答案】 C4．若P ＝a ＋a ＋7，Q ＝a ＋3＋a ＋4(a ≥0)，则P ，Q 的大小关系是()A ．P >QB ．P ＝QC ．P <QD ．由a 的取值确定【解析】∵P 2＝2a ＋7＋2a ·a ＋7 ＝2a ＋7＋2a 2＋7a ，Q 2＝2a ＋7＋2a ＋3·a ＋4＝2a ＋7＋2a 2＋7a ＋12， ∴P 2<Q 2，∴P <Q . 【答案】 C5．设a ，b 是两个实数，给出下列条件：①a ＋b ＞1；②a ＋b ＝2；③a ＋b ＞2；④a 2＋b 2＞2；⑤ab ＞1. 其中能推出：“a ，b 中至少有一个大于1”的条件是() A ．②③ B ．①②③ C ．③ D ．③④⑤【解析】若a ＝12，b ＝23，则a ＋b ＞1，但a ＜1，b ＜1，故①推不出；若a ＝b ＝1，则a ＋b ＝2，故②推不出；若a ＝－2，b ＝－3，则a 2＋b 2＞2，故④推不出；若a ＝－2，b ＝－3，则ab ＞1，故⑤推不出；对于③，即a ＋b ＞2，则a ，b 中至少有一个大于1，反证法：假设a ≤1且b ≤1，则a ＋b ≤2与a ＋b ＞2矛盾，因此假设不成立，a ，b 中至少有一个大于1. 【答案】 C6．用反证法证明命题“a ，b ∈R ，ab 可以被5整除，那么a ，b 中至少有一个能被5整除”，那么假设的内容是__________________________________________________________________．【解析】“至少有n 个”的否定是“最多有n －1个”，故应假设a ，b 中没有一个能被5整除．【答案】a ，b 中没有一个能被5整除7．下列条件：①ab ＞0，②ab ＜0，③a ＞0，b ＞0，④a ＜0，b ＜0，其中能使b a ＋ab≥2成立的条件的序号是________．【解析】要使b a ＋a b ≥2，只需b a ＞0且a b＞0成立，即a ，b 不为0且同号即可，故①③④能使b a ＋a b≥2成立．【答案】①③④8．若二次函数f (x )＝4x 2－2(p －2)x －2p 2－p ＋1，在区间内至少存在一点c ，使f (c )＞0，则实数p 的取值范围是________．【解析】令⎩⎪⎨⎪⎧f （－1）＝－2p 2＋p ＋1≤0，f （1）＝－2p 2－3p ＋9≤0，解得p ≤－3或p ≥32，故满足条件的p 的范围为⎝ ⎛⎭⎪⎫－3，32. 【答案】⎝⎛⎭⎪⎫－3，329．已知a ≥b ＞0，求证：2a 3－b 3≥2ab 2－a 2b . 【证明】要证明2a 3－b 3≥2ab 2－a 2b 成立，只需证：2a 3－b 3－2ab 2＋a 2b ≥0，即2a (a 2－b 2)＋b (a 2－b 2)≥0，即(a ＋b )(a －b )(2a ＋b )≥0.∵a ≥b ＞0，∴a －b ≥0，a ＋b ＞0，2a ＋b ＞0，从而(a ＋b )(a －b )(2a ＋b )≥0成立， ∴2a 3－b 3≥2ab 2－a 2b .10．已知四棱锥S ABCD 中，底面是边长为1的正方形，又SB ＝SD ＝2，SA ＝1. (1)求证：SA ⊥平面ABCD ；(2)在棱SC 上是否存在异于S ，C 的点F ，使得BF ∥平面SAD ？若存在，确定F 点的位置；若不存在，请说明理由．【解析】 (1)证明由已知得SA 2＋AD 2＝SD 2， ∴SA ⊥AD .同理SA ⊥AB .又AB ∩AD ＝A ， ∴SA ⊥平面ABCD .(2)假设在棱SC 上存在异于S ，C 的点F ，使得BF ∥平面SAD . ∵BC ∥AD ，BC ⊄平面SAD . ∴BC ∥平面SAD .而BC ∩BF ＝B ， ∴平面FBC ∥平面SAD .这与平面SBC 和平面SAD 有公共点S 矛盾， ∴假设不成立．∴不存在这样的点F ，使得BF ∥平面SAD .B 组专项能力提升 (时间：30分钟)11．已知函数f (x )＝⎝ ⎛⎭⎪⎫12x，a ，b 是正实数，A ＝f ⎝ ⎛⎭⎪⎫a ＋b 2，B ＝f (ab )，C ＝f ⎝ ⎛⎭⎪⎫2ab a ＋b ，则A 、B 、C 的大小关系为()A ．A ≤B ≤C B ．A ≤C ≤B C ．B ≤C ≤AD ．C ≤B ≤A 【解析】∵a ＋b2≥ab ≥2aba ＋b，又f (x )＝⎝ ⎛⎭⎪⎫12x在R 上是减函数． ∴f ⎝⎛⎭⎪⎫a ＋b 2≤f (ab )≤f ⎝ ⎛⎭⎪⎫2ab a ＋b ，即A ≤B ≤C .【答案】 A12．如果△A 1B 1C 1的三个内角的余弦值分别等于△A 2B 2C 2的三个内角的正弦值，则() A ．△A 1B 1C 1和△A 2B 2C 2都是锐角三角形 B ．△A 1B 1C 1和△A 2B 2C 2都是钝角三角形C ．△A 1B 1C 1是钝角三角形，△A 2B 2C 2是锐角三角形D ．△A 1B 1C 1是锐角三角形，△A 2B 2C 2是钝角三角形【解析】由条件知，△A 1B 1C 1的三个内角的余弦值均大于0，则△A 1B 1C 1是锐角三角形，假设△A 2B 2C 2是锐角三角形．由⎩⎪⎨⎪⎧sin A 2＝cos A 1＝sin ⎝ ⎛⎭⎪⎫π2－A 1，sin B 2＝cos B 1＝sin ⎝ ⎛⎭⎪⎫π2－B 1，sin C 2＝cos C 1＝sin ⎝ ⎛⎭⎪⎫π2－C 1，得⎩⎪⎨⎪⎧A 2＝π2－A 1，B 2＝π2－B 1，C 2＝π2－C 1.那么，A 2＋B 2＋C 2＝π2，这与三角形内角和为180°相矛盾．所以假设不成立，又显然△A 2B 2C 2不是直角三角形．所以△A 2B 2C 2是钝角三角形．【答案】 D13．已知点A n (n ，a n )为函数y ＝x 2＋1图象上的点，B n (n ，b n )为函数y ＝x 图象上的点，其中n ∈N *，设c n ＝a n －b n ，则c n 与c n ＋1的大小关系为________．【解析】由条件得c n ＝a n －b n ＝n 2＋1－n ＝1n 2＋1＋n，∴c n 随n 的增大而减小，∴c n ＋1＜c n . 【答案】c n ＋1＜c n14．(2016·江苏)记U ＝{1，2，…，100}．对数列{a n }(n ∈N *)和U 的子集T ，若T ＝∅，定义S T ＝0；若T ＝{t 1，t 2，…，t k }，定义S T ＝at 1＋at 2＋…＋at k .例如：T ＝{1，3，66}时，S T ＝a 1＋a 3＋a 66.现设{a n }(n ∈N *)是公比为3的等比数列，且当T ＝{2，4}时，S T ＝30.(1)求数列{a n }的通项公式；(2)对任意正整数k (1≤k ≤100)，若T ⊆{1，2，…，k }，求证：S T ＜a k ＋1； (3)设C ⊆U ，D ⊆U ，S C ≥S D ，求证：S C ＋S C ∩D ≥2S D . 【解析】 (1)由已知得a n ＝a 1·3n －1，n ∈N *.于是当T ＝{2，4}时，S T ＝a 2＋a 4＝3a 1＋27a 1＝30a 1. 又S T ＝30，故30a 1＝30，即a 1＝1. 所以数列{a n }的通项公式为a n ＝3n －1，n ∈N *.(2)证明因为T ⊆{1，2，…，k }，a n ＝3n －1＞0，n ∈N *，所以S T ≤a 1＋a 2＋…＋a k ＝1＋3＋…＋3k －1＝12(3k －1)＜3k.因此，S T ＜a k ＋1. (3)证明下面分三种情况证明．①若D 是C 的子集，则S C ＋S C ∩D ＝S C ＋S D ≥S D ＋S D ＝2S D . ②若C 是D 的子集，则S C ＋S C ∩D ＝S C ＋S C ＝2S C ≥2S D .③若D 不是C 的子集，且C 不是D 的子集．令E ＝C ∩∁U D ，F ＝D ∩∁U C ，则E ≠∅，F ≠∅，E ∩F ＝∅. 于是S C ＝S E ＋S C ∩D ，S D ＝S F ＋S C ∩D ，进而由S C ≥S D 得S E ≥S F . 设k 为E 中的最大数，l 为F 中的最大数，则k ≥1，l ≥1，k ≠l . 由(2)知，S E ＜a k ＋1.于是3l －1＝a l ≤S F ≤S E ＜a k ＋1＝3k，所以l －1＜k ，即l ≤k .又k ≠l ，故l ≤k －1.从而S F ≤a 1＋a 2＋…＋a l ＝1＋3＋…＋3l －1＝3l －12≤3k －1－12＝a k －12≤S E －12，故S E ≥2S F ＋1，所以S C －S C ∩D ≥2(S D －S C ∩D )＋1，即S C ＋S C ∩D ≥2S D ＋1. 综合①②③得，S C ＋S C ∩D ≥2S D .15．(2015·北京高考节选)已知数列{a n }满足：a 1∈N *，a 1≤36，且a n ＋1＝⎩⎪⎨⎪⎧2a n ，a n ≤18，2a n －36，a n ＞18(n ＝1，2，…)．记集合M ＝{a n |n ∈N *}．(1)若a 1＝6，写出集合M 的所有元素；(2)若集合M 存在一个元素是3的倍数，证明：M 的所有元素都是3的倍数．【解析】 (1)6，12，24.(2)证明因为集合M 存在一个元素是3的倍数，所以不妨设a k 是3的倍数．由a n ＋1＝⎩⎪⎨⎪⎧2a n ，a n ≤18，2a n －36，a n ＞18可归纳证明对任意n ≥k ，a n 是3的倍数．如果k ＝1，则M 的所有元素都是3的倍数．如果k ＞1，因为a k ＝2a k －1或a k ＝2a k －1－36，所以2a k －1是3的倍数，于是a k －1是3的倍数．类似可得，a k －2，…，a 1都是3的倍数．从而对任意n ≥1，a n 是3的倍数，因此M 的所有元素都是3的倍数．综上，若集合M 存在一个元素是3的倍数，则M 的所有元素都是3的倍数．。

2023年广东开放大学高等数学(本专)单元测试及形成性考核答案

单元1练习题1、2、3、4、6、7、8、10、11、A.对B.错12、A.对B.错13、A.对B.错14、A.对B.错A.对B.错16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.D 2.A 3.D 4.D 5.C 6.A 7.A 8.C 9.D 10.D 11.A 12.A 13.A 14.A 15.A 16.B 17.B 18.A 19.A 20.B单元2练习题1、2、3、4、5、7、8、9、10、A.对B.错12、A.对B.错13、A.对B.错14、A.对B.错15、B.对 B.错16、A.对B.错A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.C 2.C 3.B 4.D 5.D 6.D 7.B 8.B 9.B 10.D 11.A 12.A 13.A 14.A 15.B 16.B 17.A 18.A 19.B 20.A单元3练习题1、2、3、4、5、6、7、8、10、11、A.对B.错12、A.对B.错13、A.对B.错A.对B.错15、C.对 B.错16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.C 2.D 3.D 4.B 5.A 6.C 7.A 8.B 9.B 10.B 11、A 12.A 13.A 14.B 15.A 16.A 17.A 18.A 19.B 20.A单元4练习题1、2、3、4、5、6、7、8、9、10、11、A.对B.错12、A.对B.错13、A.对B.错14、A.对B.错15、D.对 B.错16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.B 2.B 3.A 4.B 5.C 6.D 7.D 8.B 9.D 10.A11.A 12.A 13.A 14.A 15.A 16.A 17.A 18.A 19.B 20.A单元5练习题1、2、3、4、5、6、7、8、9、10、11、A.对B.错12、A.对B.错13、A.对B.错14、A.对B.错15、E.对 B.错16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.A 2.C 3.D 4.A 5.C 6.B 7.A 8.B 9.C 10.C 11.A 12.A 13.A 14.A 15.A 16.A 17.B 18.A 19.A 20.A单元6练习题1、2、3、4、5、6、7、8、9、10、11、A.对B.错12、A.对B.错13、A.对B.错14、A.对B.错15、F.对 B.错16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.D 2.C 3.D 4.B 5.B 6.B 7.C 8.D 9.D 10.A 11.B 12.A 13.A 14.A 15.A 16.A 17.A 18.A 19.A 20.A单元7练习题1、a.Ab.Bc.Cd.D2、3、4、5、6、7、8、9、11、12、13、A.对B.错A.对B.错15、G.对 B.错16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错A.对B.错答案：1.D 2.A 3.B 4.D 5.A 6.A 7.C 8.B 9.A 10.D 11.B 12.D 13.B 14.A 15.B 16.B 17.A 18.A 19.A 20.A形成性考核一1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错21、22、23、24、25、答案：1.C 2.B 3.B 4.A 5.C 6.B 7.B 8.D 9.B 10.B 11.C 12.A 13.C 14.A 15.D 16.A 17.A 18.A 19.B 20.A 21. A 22.B 23.A 24.A 25.B形成性考核二1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错答案：1.C 2.C 3.B 4.C 5.A 6.D 7.B 8.B 9.A 10.B 11.C 12.A 13.D 14.B 15.D 16.A 17.A 18.A 19.B 20.B形成性考核一1、2、3、4、5、6、7、8、9、10、11、12、13、14、15、16、A.对B.错17、A.对B.错18、A.对B.错19、A.对B.错20、A.对B.错21、A.对B.错22、A.对B.错23、A.对B.错24、A.对B.错25、A.对B.错答案：1.B 2.B 3.C 4.D 5.B 6.D 7.A 8.C 9.B 10.C11.A 12.A 13.A 14.A 15.A 16.B 17.B 18.A 19.A 20.A 21.A 22.A 23.A 24.A 25.A形成性考核四1、2、3、4、5、6、7、8、9、10、11、12、。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十二章单元测试题答案
班级学号姓名成绩

1、求微分方程22222(1)xydxyxxydy的通解。（5分）
解：222(1)(1)xydxyxdy

22211xydxdyxy

211(1)()1dxydyxy
所以方程的通解是：21arctanln2xxyyC
2、求方程22yyyx的通解。（10分）
解： 2xyyy，即12yyxy
它是1n的伯努力方程，设12nzyy
得方程

2222224[4][2]dxdxxxxzzxzexedxCexeeC











故同解为
2221x
yCex

3、求方程(lnln)0xxyyy的通解。（10分）

解：1ln, lnxdyydyyyydxxdxxx即

设yzx，则,dzyxzyzxdx
所以： lndzzzxdxz
ln1lndzzzzdxzx


分离变量得
ln1lnz
dzdxzzzx



111
()(1ln)dzdxzzzx



两边积分

1
ln(1ln)lnlnln1lnzzxCzCxz



故通解为
1lnyCyx

4、设0()cos2()sin1xfxxfttdtx，其中()fx为可导函数，求()fx。（10
分）

解：方程0()cos2()sin1xfxxfttdtx两边求导
()cos()sin2()sin1fxxfxxfxx
令 ()yfx
得 cossin1yxyx

即 1tancosyyxx
这是一个一阶线微分方程，求解得
cos(tan)yxxC
由 (0)1y得1C，所以()sincosfxxx
5、求微分方程(coscos)'sinsin0xyxyyxy的通解。（10分）
解：(coscos)(sinsin)0xyxdyyxydx

因为 cossinpQyxyx，所以该方程为全微分方程
重新组合得
(cossin)(cossin)0xydyydxxdyyxdx

即 (sin)(cos)0dxydyx
所以方程的通解是：sincosxyyxC
6、求微分方程369xyyyxe满足初始条件(0)0,(0)0yy的特解。
（10分）
解：特征方程为2690rr，特征根为123rr
所以对应齐次方程690yyy的通解为：312()xyecxc

原方程具有特解*23()xyxaxbe，代入原方程得1,06ab

即*3316xyxe
故原方程的通解是333121()6xxyecxcxe
由初始条件(0)0,(0)0yy得123, 1cc
所求的解是3331(31)6xxyexxe

7．对x>0,过曲线()yfx上点(,())xfx处的切线在y轴上的截距等于
0

1
()d,xftt

x


求()fx的一般表达式。（10分）
解：曲线()yfx上点(,())xfx处切线方程：()()()YfxfxXx
由于曲线()yfx上点(,())xfx处的切线在y轴上的截距等于01()d,xfttx得方程
0
1
()()()d,xfxxfxfttx


即 20()()()dxxfxxfxftt
积分方程两边求导得()()0xfxfx
令()pfx，方程()()0xfxfx化为0xpp，求解得11pcx。

解方程11()fxcx，得12()lnfxcxc
8．设曲线积分2()[2()]Lyfxdxxfxxdy在右半平面（x>0）内与路径无关，其中
()fx
可导，且(1)1, ()ffx求.（10分）
解：因为积分与路径无关，所以2(2())(())xfxxyfxxy
即 2()2()2()fxxfxxfx
令 ()yfx，得112yyx

求解上面的一次线性微分方程得：1223ycxx
因此 122()3fxcxx
由(1)1f，得13c，故 1212()33fxxx
9、设对于半空间 0x 内任意的光滑有向封闭曲面都有
2()()0x
xfxdydzxyfxdzdxezdxdy


，

其中函数()fx 在(0,)内具有连续一阶导数，且0lim()1xfx，求
()fx
。

（20分）
解：由高斯公式知：

22()()(()()())x

x
xfxdydzxyfxdzdxezdxdyfxxfxxfxedv







由2()()0xxfxdydzxyfxdzdxezdxdy 和的任意性得
2()()()0x
fxxfxxfxe

即 211()(1)()xfxfxexx
求解方程得其通解
()()xxefxecx
因为

00lim()lim()1,xxxxefxecx
所以

20lim()0xx
xece


因此 1c

故 ()(1)xxefxex