2021年新课标高中数学必修二检测题二
2021年高中数学 综合测试A(含解析)新人教B版必修2

2021年高中数学综合测试A(含解析)新人教B版必修2一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.已知点A(a,3)、B(-1,b+2)且直线AB的倾斜角为90°,则a、b的值为( )A.a=-1,b∈R且b≠1B.a=-1,b=1C.a=3,b=1 D.a=3,b=-1[答案]A[解析]∵直线AB的倾斜角为90°,∴AB⊥x轴,∴a=-1,b∈R且b≠1.2.不论m为何值,直线(m-2)x-y+3m+2=0恒过定点( )A.(3,8) B.(8,3)C.(-3,8) D.(-8,3)[答案] C[解析]直线方程(m-2)x-y+3m+2=0可化为m(x+3)-2x-y+2=0,∴x=-3时,m∈R,y=8,故选C.3.(xx·陕西西安市一中高一期末测试)垂直于同一条直线的两条直线一定( ) A.平行B.相交C.异面D.以上都有可能[答案] D[解析]如图正方体ABCD-A1B1C1D1,AD⊥AB,BC⊥AB,AD∥BC,BB1⊥AB,AD与BB1异面,AA1⊥AB,AA1与AD相交,故选D.4.对两条不相交的空间直线a与b,必存在平面α,使得( )A.a⊂α,b⊂αB.a⊂α,b∥αC.a⊥α,b⊥αD.a⊂α,b⊥α[答案] B[解析]已知两条不相交的空间直线a和b,可以在直线a上任取一点A,使得A∉b.过A作直线c∥b,则过a、b必存在平面α,且使得a⊂α,b∥α.5.若点P(a,b)在圆C:x2+y2=1的外部,则有直线ax+by+1=0与圆C的位置关系是( )A.相切B.相离C.相交D.相交或相切[答案] C[解析]∵点P(a,b)在圆C:x2+y2=1的外部,∴a2+b2>1.∴圆C的圆心(0,0)到直线ax+by+1=0的距离d=1a2+b2<1,即直线ax+by+1=0与圆C相交.6.如图,在同一直角坐标系中,表示直线y=ax与y=x+a正确的是( )[答案] C[解析]当a>0时,直线y=ax的斜率k=a>0,直线y=x+a在y轴上的截距等于a>0,此时,选项A、B、C、D都不符合;当a<0时,直线y=ax的斜率k=a<0,直线y=x+a 在y轴上的截距等于a<0,只有选项C符合,故选C.7.已知平面α外不共线的三点A、B、C到平面α的距离相等,则正确的结论是( ) A.平面ABC必平行于αB .平面ABC 必不垂直于α C .平面ABC 必与α相交D .存在△ABC 的一条中位线平行于α或在α内 [答案] D[解析] 平面ABC 与平面α可能平行也可能相交,排除A 、B 、C ,故选D.8.(xx·甘肃天水一中高一期末测试)圆O 1:x 2+y 2-4x -6y +12=0与圆O 2:x 2+y 2-8x -6y +16=0的位置关系是( )A .内切B .外离C .内含D .相交[答案] A[解析] 圆O 1的圆心O 1(2,3),半径r 1=1,圆O 2的圆心O 2(4,3),半径r 2=3.|O 1O 2|=4-22+3-32=2,r 2-r 1=2,∴|O 1O 2|=r 2-r 1,故两圆内切.9.光线沿着直线y =-3x +b 射到直线x +y =0上,经反射后沿着直线y =ax +2射出,则有( )A .a =13,b =6B .a =-13,b =-6C .a =3,b =-16D .a =-3,b =16[答案] B[解析] 由题意,直线y =-3x +b 与直线y =ax +2关于直线y =-x 对称,故直线y =ax +2上点(0,2)关于y =-x 的对称点(-2,0)在直线y =-3x +b 上,∴b =-6,y =-3x -6上的点(0,-6),关于直线y =-x 对称点(6,0)在直线y =ax +2上,∴a =-13选B.10.(xx ·福建南安一中高一期末测试)某几何体的三视图如图所示,且该几何体的体积是3,则正视图中的x 的值是( )A .2B .94C .3D .92[答案] C[解析] 由三视图可知,该几何体是底面为直角梯形的四棱锥,且直角梯形的上底长为1,下底长为2,高为2,四棱锥的高为x ,其体积为13×1+2×22·x =3,∴x =3.11.圆x 2+y 2-4x -4y +7=0上的动点P 到直线y =-x 的最小距离为( ) A .22-1 B .2 2 C . 2 D .1[答案] A[解析] 圆x 2+y 2-4x -4y +7=0可化为(x -2)2+(y -2)2=1,故圆心坐标为(2,2),半径r =1.圆心(2,2)到直线y =-x 的距离d =|2+2|2=2 2.故动点P 到直线y =-x 的最小距离为22-1.12.一个几何体的三视图如下图所示,该几何体的表面积为( )A .280B .292C .360D .372[答案] C[解析] 该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面的面积之和.S =2×(10×8+10×2+8×2)+2×(6×8+8×2)=360.二、填空题(本大题共4个小题,每小题4分,共16分,把正确答案填在题中横线上) 13.(xx·云南曲靖市陆良县二中高一期末测试)两平行直线l 1:3x +4y -2=0与l 2:6x +8y -5=0之间的距离为________.[答案]110[解析] 直线l 2的方程可化为3x +4y -52=0,故两平行直线l 1、l 2之间的距离d =|-2--52|32+42=110. 14.一个正四棱柱的侧面展开图是一个边长为4的正方形,则它的体积为__________. [答案] 4[解析] 由已知得,正四棱柱的底面边长为1,高为4,体积V =12×4=4.15.若点P 在坐标平面xOy 内,点A 的坐标为(0,0,4)且d (P ,A )=5,则点P 的轨迹方程为________.[答案] x 2+y 2=9[解析] 设P (x ,y,0),则d (P ,A )=x -02+y -02+0-42=5,即x2+y 2=9.16.设m 、n 是平面α外的两条直线,给出三个论断:①m ∥n ;②m ∥α;③n ∥α.以其中两个为条件,余下的一个为结论,构成三个命题,写出你认为正确的一个命题:__________________.[答案] ①②⇒③或(①③⇒②)三、解答题(本大题共6个大题,共74分,解答应写出文字说明,证明过程或演算步骤)17.(本题满分12分)设A (1,-2,x ),B (x,3,0),C (7,x,6),且A 、B 、C 三点能构成直角三角形,求x 的值.[解析] AB 2=2x 2-2x +26,BC 2=2x 2-20x +94,AC 2=2x 2-8x +76, 由(2x 2-2x +26)+(2x 2-20x +94)=2x 2-8x +76得x 2-7x +22=0无解;由(2x 2-2x +26)+(2x 2-8x +76)=2x 2-20x +94得x 2+5x +4=0,∴x 1=-4,x 2=-1;由(2x 2-20x +94)+(2x 2-8x +76)=2x 2-2x +26得x 2-13x +72=0无解, ∴x 的值为-4或-1.18.(本题满分12分)(xx·甘肃天水市泰安县二中高一月考)直线l 经过直线x +y -2=0和直线x -y +4=0的交点,且与直线3x -2y +4=0平行,求直线l 的方程.[解析] 解法一:由⎩⎪⎨⎪⎧x +y -2=0x -y +4=0,得⎩⎪⎨⎪⎧x =-1y =3.即直线l 过点(-1,3).∵直线l 的斜率为32,∴直线l 的方程为y -3=32(x +1),即3x -2y +9=0.解法二:由题意可设直线l 的方程为x -y +4+λ(x +y -2)=0,整理得(1+λ)x +(λ-1)y +4-2λ=0, ∵直线l 与直线3x -2y +4=0平行, ∴-2(1+λ)=3(λ-1), ∴λ=15.∴直线l 的方程为65x -45y +185=0,即3x -2y +9=0.19.(本题满分12分)如图,在底面为直角梯形的四棱锥P -ABCD 中,AD ∥BC ,∠ABC =90°,PA ⊥平面ABCD ,AC ∩BD =E ,AD =2,AB =23,BC =6,求证:平面PBD ⊥平面PAC .[解析] ∵PA ⊥平面ABCD ,BD ⊂平面ABCD ,∴BD ⊥PA . 又tan ∠ABD =AD AB =33. tan ∠BAC =BCAB= 3. ∴∠ABD =30°,∠BAC =60°, ∴∠AED =90°,即BD ⊥AC . 又PA ∩AC =A ,∴BD ⊥平面PAC . ∵BD ⊂平面PBD .所以平面PBD ⊥平面PAC .20.(本题满分12分)在△ABC 中,BC 边上的高所在的直线方程为x -2y +1=0,∠A 的平分线所在的直线方程为y =0.若B 的坐标为(1,2),求△ABC 三边所在直线方程及点C 坐标.[解析] BC 边上高AD 所在直线方程x -2y +1=0, ∴k BC =-2,∴BC 边所在直线方程为:y -2=-2(x -1)即2x +y -4=0.由⎩⎪⎨⎪⎧ x -2y +1=0y =0,得A (-1,0),∴直线AB :x -y +1=0,点B (1,2)关于y =0的对称点B ′(1,-2)在边AC 上, ∴直线AC :x +y +1=0,由⎩⎪⎨⎪⎧x +y +1=02x +y -4=0,得点C (5,-6).21.(本题满分12分)降水量是指水平地面上单位面积所降雨水的深度,用上口直径为38 cm ,底面直径为24 cm ,深度为35 cm 的圆台形容器(轴截面如图)来测量降水量,若在一次降水中,此桶盛得的雨水正好是桶深的17,则本次降雨的降水量是多少?(精确到mm)[解析] 如图,作BE ⊥CD 于点E ,交MN 于点G ,作AH ⊥CD 于H ,交MN 于点P ,则BG BE=17,四边形ABEH 、PGEH 均为矩形.∴BG =17·BE =17×35=5(cm).EH =PG =AB =24 cm.又∵四边形ABCD 为等腰梯形, ∴MN =PG +2GN .又∵EC =12(CD -AB )=12(38-24)=7(cm),∴GN =17EC =1(cm),∴MN =PG +2GN =24+2=26(cm). ∴此次降雨中雨水的体积为V =13π[(MN 2)2+(AB 2)2+(MN 2·AB2)]·BG =13π×5×(132+122+13×12) =23453(cm 3), 降雨中雨水面的面积S =π(CD2)2=361π(cm 2).∴此次降雨的降水量为h =V S =2345π3×361π≈2.2(cm)=22(mm).即本次降雨的降水量约是22 mm.22.(本题满分14分)已知⊙C :x 2+y 2+2x -4y +1=0. (1)若⊙C 的切线在x 轴、y 轴上截距相等,求切线的方程;(2)从圆外一点P (x 0,y 0)向圆引切线PM ,M 为切点,O 为原点,若|PM |=|PO |,求使|PM |最小的P 点坐标.[解析] ⊙C :(x +1)2+(y -2)2=4, 圆心C (-1,2),半径r =2. (1)若切线过原点设为y =kx , 则|-k -2|1+k2=2,∴k =0或43. 若切线不过原点,设为x +y =a , 则|-1+2-a |2=2,∴a =1±22, ∴切线方程为:y =0,y =43x ,x +y =1+22和x +y =1-2 2.(2)x 20+y 20+2x 0-4y 0+1=x 20+y 20, ∴2x 0-4y 0+1=0,|PM |=x 20+y 20+2x 0-4y 0+1=5y 20-2y 0+14∵P 在⊙C 外,∴(x 0+1)2+(y 0-2)2>4, 将x 0=2y 0-12代入得5y 20-2y 0+14>0,∴|PM |min =510.此时P ⎝ ⎛⎭⎪⎫-110,15.5 :22989 59CD 姍34320 8610 蘐}$@24328 5F08 弈31026 7932 礲34151 8567 蕧 29686 73F6 珶22096 5650 噐。
(2021年整理)高中数学必修二第一章测试题及答案

高中数学必修二第一章测试题及答案编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学必修二第一章测试题及答案)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学必修二第一章测试题及答案的全部内容。
第一章空间几何体一、选择题1.有一个几何体的三视图如下图所示,这个几何体可能是一个().主视图左视图俯视图(第1题)A.棱台B.棱锥C.棱柱D.正八面体2.如果一个水平放置的平面图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ).A.2+2B.221+C.22+2D.2+13.棱长都是1的三棱锥的表面积为( ).A.3B.23C.33D.434.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( ).A.25πB.50πC.125πD.都不对5.正方体的棱长和外接球的半径之比为( ).A.3∶1 B.3∶2 C.2∶3D.3∶36.若底面是菱形的棱柱其侧棱垂直于底面,且侧棱长为5,它的对角线的长分别是9和15,则这个棱柱的侧面积是().A.130 B.140 C.150 D.1607.如图是一个物体的三视图,则此物体的直观图是( ).(第7题)8.已知a 、b 、c 是直线,β是平面,给出下列命题: ①若c a c b b a //,,则⊥⊥; ②若c a c b b a ⊥⊥则,,//; ③若b a b a //,,//则ββ⊂;④若a 与b 异面,且ββ与则b a ,//相交;⑤若a 与b 异面,则至多有一条直线与a ,b 都垂直. 其中真命题的个数是A .1B .2C .3D .4二、填空题9.若三个球的表面积之比是1∶2∶3,则它们的体积之比是_____________.10.正方体ABCD -A 1B 1C 1D 1 中,O 是上底面ABCD 的中心,若正方体的棱长为a ,则三棱锥O -AB 1D 1的体积为_____________.11.已知一个长方体共一顶点的三个面的面积分别是2、3、6,则这个长方体的对角线长是___________,它的体积为___________.三、解答题12 .已知半球内有一个内接正方体,求这个半球的体积与正方体的体积之比.13.如图,在四边形ABCD 中,∠DAB =90°,∠ADC =135°,AB =5,CD =22,AD =2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.(第13题)15。
2021高中数学人教A版必修二(第四章+圆与方程)章节练习试题(含详细解析)

圆与方程一、单选题(共20题;共0分)1、(0分)空间直角坐标系中,O 为坐标原点,已知两点坐标为A (3,1,0),B (-1,3,0),若点C 满足 OC →=αOA →+βOB →, 其中 α , β∈R, α+ β=1,则点C 的轨迹为( )A. 平面B. 直线C. 圆D. 线段2、(0分)已知圆O: x 2+y 2=4 , 直线l 过点P (1,1),且与直线OP 垂直,则直线l 的方程为( ) A.B.C.D.3、(0分)过点A (0,2),B (﹣2,2),且圆心在直线x ﹣y ﹣2=0上的圆的方程是( )A. (x −1)2+(y +1)2=26B. (x +1)2+(y +3)2=26C. (x +2)2+(y +4)2=26D. (x −2)2+y 2=264、(0分) 表示一个圆,则的取值范围是( )A. ≤2B.C.D.≤5、(0分)圆 x 2+y 2−4x =0的圆心坐标和半径分别是( ) A. (0,2) 2 B. (2,0) 4C. (-2,0) 2D. (2,0) 26、(0分)点M (x,y )在曲线C:x 2−4x +y 2−21=0上运动,t =x 2+y 2+12x −12y −150−a ,且t 的最大值为b ,若a ,b ∈R +,则1a+1+1b 的最小值为( )A. 1B. 2C. 3D. 4 7、(0分)在空间直角坐标系中,点 ,,则( )A. 3B. 4C. 5D. 68、(0分)将一颗骰子投掷两次,第一次、第二次出现的点数分别记为a 、b ,设直线l 1:ax +by =2与l 2:x +2y =2平行的概率为P 1,相交的概率为P 2,则圆C:(x −1)2+(y −6)2=122上到直线3P 1x +2P 2y =1的距离为√1222的点有( )A. 1个B. 2个C. 3个D. 4个9、(0分)已知点A(−1,−1).若曲线T上存在两点B,C,使△ABC为正三角形,则称T为“正三角形”曲线.给定下列三条曲线:①x+y−3= 0 (0≤x≤3);②x2+y2=2(−√2≤x≤0);③y=−1x (x>0).其中,“正三角形”曲线的个数是A. 0B. 1C. 2D. 310、(0分)已知定点A(-1,0),B(1,0),动点P满足直线PA,PB的斜率之积为-1,则动点P满足的方程是( )A. x2+y2=1B. x2+y2=1(x≠±1)C. x2+y2=1(x≠0)D. y=(x≠±1)11、(0分)从圆O: x2+y2=4上任意一点P向x轴作垂线,垂足为P′,点M是线段PP′的中点,则点M的轨迹方程是( )A. 9x 216+y24=1 B. x24+y2=1 C. x2+y24=1 D. 9y216+x24=112、(0分)圆C的圆心在y轴正半轴上,且与x轴相切,被双曲线x2−y23=1的渐近线截得的弦长为√3,则圆C的方程为()A. x 2+(y-1) 2=1B. x 2+(y- ) 2=3C. x 2+(y- ) 2=D. x 2+(y-2) 2=413、(0分)过双曲线x 2a2−y2b2=1(a>0,b>0)左焦点F1的直线与以右焦点F2为圆心、|OF2|为半径的圆相切于A点,且|F1A|=2b,则双曲线的离心率为()A. √32 B.C. √2D. √314、(0分)若P(2,−1)为圆(x−1)2+y2=25的弦AB的中点,则直线AB的方程()A. x−y−3=0B. 2x+y−3=0C. x+y−1=0D. 2x−y−5=015、(0分)已知椭圆x 2a2+y2b2=1(a>b>0)的离心率e=12,右焦点为F(c,0),方程ax2+bx−c=0的两个实根x1,x2,则点P(x1,x2)()A. 必在圆x2+y2=2内B. 必在圆x2+y2=2上C. 必在圆 x 2+y 2=2外D. 以上三种情况都有可能16、(0分)经过圆x 2+2x +y 2=0的圆心C ,且与直线x +y =0垂直的直线方程是( )A. x -y +1=0B. x -y -1=0C. x +y -1=0D. x +y +1=017、(0分)已知点A(−3,1,4),则点A 关于x 轴对称的点的坐标为 A. (−3,−1,−4) B. (−3,−1,4)C. (3,1,4)D. (3,−1,−4)18、(0分)圆C:x 2+y 2-2x+2y -2=0的圆心坐标为A. (1,1)B. (1,-1)C. (-1,-1)D. (-1,1)19、(0分)已知圆M :x 2+y 2=1与圆N :(x −2)2+y 2=9,则两圆的位置关系是( )A. 相交B. 相离C. 内切D. 外切20、(0分)圆x 2+y 2−6x +4y =3的圆心坐标与半径是( ) A. (−3,2) √13 B. (3,−2) √13C. (−3,2) 4D. (3,−2) 4二、填空题(共10题;共0分) 21、(0分)直线 被曲线 截得的弦长等于_____________ .22、(0分)已知ΔABC 中,AB =AC =√3,ΔABC 所在平面内存在点P 使得PB 2+PC 2=3PA 2=3,则ΔABC 面积的最大值为 .23、(0分)已知A,B,C 是圆x 2+y 2=1上互不相同的三个点,且满足|AB →|=|AC →|,则AB →⋅AC →的取值范围是 .24、(0分)设 P 点在圆 x 2+(y +2)2=1上移动,点Q 满足条件{x +y ≤4y ≥x x ≥1,则 |PQ |的最大值是 .25、(0分)点P (1,2,3)关于y 轴的对称点为P 1 , P 关于坐标平面xOz 的对称点为P 2 , 则|P 1P 2|= _____________ .26、(0分)在平面直角坐标系中,设A 、B 、C 是曲线y= 1x−1 上三个不同的点,且D 、E 、F 分别为BC 、CA 、AB 的中点,则过D 、E 、F 三点的圆一定经过定点 _____________ . 27、(0分)实数x 、y 满足3x2+2y2=6x ,则的最大值为28、(0分)已知圆x 2+y 2+mx -14=0与抛物线y =14x 2的准线相切,则m =_________ . 29、(0分)平面内与两定点距离之比为定值的点的轨迹是 _____________.30、(0分)点 P(1,1,−2)关于 xoy 平面的对称点的坐标是 .三、解答题(共5题;共0分)31、(0分)已知直线 过点 M (﹣3,3),圆.(Ⅰ)求圆 C 的圆心坐标及直线 截圆 C 弦长最长时直线 的方程; (Ⅱ)若过点 M 直线与圆 C 恒有公共点,求实数 m 的取值范围.32、(0分)如图,已知三棱柱ABC −A 1B 1C 1的侧棱与底面垂直,AA 1=AB =AC =1,AB ⊥AC ,M 是CC 1的中点,N 是BC 的中点,点P 在直线A 1B 1上,且满足A 1P →=λA 1B 1→.(1)当λ取何值时,直线PN 与平面ABC 所成的角θ最大?(2)若平面PMN 与平面ABC 所成的锐二面角为45∘,试确定点P 的位置.33、(0分)选修4﹣4:坐标系与参数方程 已知在平面直角坐标系xOy 内,点P (x ,y )在曲线C : {x =1+cosθy =sinθ(θ 为参数,θ∈R)上运动.以Ox 为极轴建立极坐标系,直线l的极坐标方程为 ρcos(θ+π4)=0 .(Ⅰ)写出曲线C 的标准方程和直线l 的直角坐标方程;(Ⅱ)若直线l 与曲线C 相交于A 、B 两点,点M 在曲线C 上移动,试求△ABM 面积的最大值,并求此时M 点的坐标.34、(0分)在空间直角坐标系中,落在x 轴上和xoy 坐标平面内的点的坐标各有什么特点?试分别写出三个落在x 轴和xoy 平面内的点的坐标(答案不唯一)35、(0分)(2016•江苏)如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆M :x2+y 2﹣12x ﹣14y+60=0及其上一点A (2,4).(1).设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线x=6上,求圆N的标准方程;(2).设平行于OA 的直线l 与圆M 相交于B 、C 两点,且BC=OA,求直线l 的方程; (3).设点T (t,0)满足:存在圆M 上的两点P 和Q,使得 TA →+TP →=TQ →,求实数t 的取值范围。
第5章 统计与概率 单元测试-【新教材】2020-2021学年人教B版(2019)高中数学必修第二册
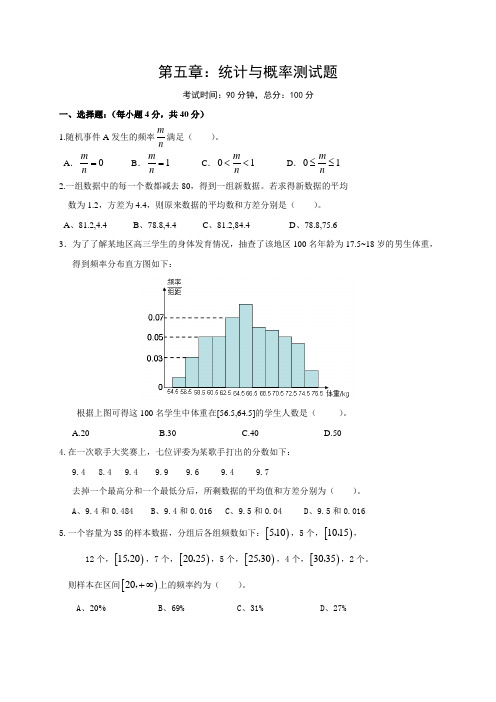
第五章:统计与概率测试题考试时间:90分钟,总分:100分一、选择题:(每小题4分,共40分) 1.随机事件A 发生的频率mn满足( )。
A .0m n = B .1m n = C .01m n << D .01m n≤≤ 2.一组数据中的每一个数都减去80,得到一组新数据。
若求得新数据的平均 数为1.2,方差为4.4,则原来数据的平均数和方差分别是( )。
A 、81.2,4.4 B 、78.8,4.4 C 、81.2,84.4 D 、78.8,75.63.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5~18岁的男生体重,得到频率分布直方图如下:根据上图可得这100名学生中体重在[56.5,64.5]的学生人数是( )。
A.20 B.30 C.40 D.50 4.在一次歌手大奖赛上,七位评委为某歌手打出的分数如下: 9.4 8.4 9.4 9.9 9.6 9.4 9.7去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )。
A 、9.4和0.484 B 、9.4和0.016 C 、9.5和0.04 D 、9.5和0.016 5.一个容量为35的样本数据,分组后各组频数如下:[)510,,5个,[)1015,,12个,[)1520,,7个,[)2025,,5个,[)2530,,4个,[)3035,,2个。
则样本在区间[)20+∞,上的频率约为( )。
A 、20% B 、69% C 、31% D 、27%6.随机抽取某中学甲、乙两班各11名同学的数学成绩,获得分数的数据茎叶图如下图。
则下列结论正确的是( )。
A 、甲班的平均水平高B 、乙班的中位数为93C 、甲班的样本方差比乙班大D 、乙班的样本方差比甲班大7. 某人将一枚硬币连掷了10次,正面朝上的情形出现了6次。
若用A 表示正面朝上这一事件,则A 的( )。
A 、概率为53 B 、频率为53C 、频率为6D 、概率接近0.6 8.从数字1,2,3,4,5中任取两个不同的数字构成一个两位数,则这个两位数大于40的概率为( )。
2021数学必修2第三章测试题和答案

10
∵两条直角边相互垂直,
∴其斜率k1,k2应满意k1k2=-1,解除A、C、D,故选B.
11[答案] A
[解析]
kPA=-4,kPB=,画图视察可知k≥或k≤-4.
12 由平面几何知,与A距离为1的点的轨迹是以A为圆心,以1为半径的⊙A,与B距离为2的点的轨迹是半径为2的⊙B,明显⊙A和⊙B相交,符合条件的直线为它们的公切线有2条.
A.(-2,1)
ﻩB.(2,1)
C.(1,-2)
ﻩD.(1,2)
6.已知ab<0,bc<0,则直线ax+by+c=0通过(
)
A.第一、二、三象限
B.第一、二、四象限
C.第一、三、四象限
D.其次、三、四象限
7.点P(2,5)到直线y=-x的距离d等于(
)
A.0
ﻩB.
C.
ﻩD.
8.与直线y=-2x+3平行,且与直线y=3x+4交于x轴上的同一点的直线方程是(
∴直线CM的方程为:=,
22[解析] (1)倾斜角为45°,则斜率为1.
∴-=1,解得m=-1,m=1(舍去)
直线方程为2x-2y-5=0符合题意,∴m=-1
(2)当y=0时,x==1,
解得m=-,或m=2
当m=-,m=2时都符合题意,
∴m=-或2。
新课标第一网系列资料www。xkb1。com
本文来源:网络收集与整理,如有侵权,请联系作者删除,谢谢!
21.(本小题满分12分)已知△ABC的三个顶点A(4,-6),B(-4,0),C(-1,4),求
(1)AC边上的高BD所在直线方程;
(2)BC边的垂直平分线EF所在直线方程;
高中数学第四章圆与方程4.1圆的方程4.1.1圆的标准方程检测新人教A版必修2(2021年整理)

2018-2019学年高中数学第四章圆与方程4.1 圆的方程4.1.1 圆的标准方程检测新人教A版必修2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018-2019学年高中数学第四章圆与方程4.1 圆的方程4.1.1 圆的标准方程检测新人教A版必修2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018-2019学年高中数学第四章圆与方程4.1 圆的方程4.1.1 圆的标准方程检测新人教A版必修2的全部内容。
4.1.1 圆的标准方程[A级基础巩固]一、选择题1.已知圆(x-2)2+(y+8)2=(-3)2,下列说法正确的是( )A.圆心是(2,-8),半径长为-3B.圆心是(-2,8),半径长为3C.圆心是(2,-8),半径长为3D.圆心是(-2,8),半径长为-3解析:由圆的标准方程(x-a)2+(y-b)2=r2,知圆心是(2,-8),半径长不可能是负数,故为3.答案:C2.圆x2+y2=1的圆心到直线3x+4y-25=0的距离是()A.5 B.3 C.4 D.2解析:圆x2+y2=1的圆心为(0,0),所以d=错误!=5。
答案:A3.点(1,1)在圆(x-a)2+(y+a)2=4的内部,则a的取值范围是( )A.(-1,1)B.(0,1)C.(-∞,-1)∪(1,+∞)D.a=±1解析:若点(1,1)在圆的内部,则(1-a)2+(1+a)2<4,化简得a2〈1,因此-1<a<1,故选A。
答案:A4.圆(x-1)2+(y-1)2=1上的点到直线x-y=2的距离的最大值是( )A.2 B.1+错误!C.2+错误!D.1+2错误!解析:圆(x-1)2+(y-1)2=1的圆心为(1,1),圆心到直线x-y=2的距离为错误!=2,圆心到直线的距离加上半径就是圆上的点到直线的最大距离,即最大距离为1+错误!.答案:B5.圆的标准方程为(x-5)2+(y-6)2=a2(a>0).若点M(6,9)在圆上,则a的值为() A。
2021学年数学人教A版必修2检测试题:第1-3章 含解析
第一章检测试题 时间:90分钟 分值:120分 第Ⅰ卷(选择题,共60分) 一、选择题(每小题5分,共60分) 1.用任意一个平面截一个几何体,各个截面都是圆面,则这个几何体一定是( C ) A.圆柱 B.圆锥 C.球体 D.圆柱、圆锥、球体的组合体 解析:当用过高线的平面截圆柱和圆锥时,截面分别为矩形和三角形,只有球满足任意截面都是圆面. 2.下列说法中,正确的个数为( B ) ①相等的角在直观图中对应的角仍然相等;②相等的线段在直观图中对应的线段仍然相等;③平行的线段在直观图中对应的线段仍然平行;④线段的中点在直观图中仍然是线段的中点. A.1 B.2 C.3 D.4 解析:③④正确. 3.如图所示为一个简单几何体的三视图,则其对应的实物是( A )
解析:根据三种视图的对角线位置关系,容易判断A是正确结论. 4.如图所示,△A′O′B′表示水平放置的△AOB的直观图,B′在x′轴上,A′O′和x′轴垂直,且A′O′=2,则△AOB的 边OB上的高为( D ) A.2 B.4 C.22 D.42 解析:由直观图与原图形中边OB长度不变,得S原图形=22S直观
图. 设△AOB的边OB上的高为h,
则12·OB·h=22×12×2O′B′. ∵OB=O′B′,∴h=42. 5.如图,有一个圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面的点B处的食物.当圆柱的高等于12 cm,底面半径为3 cm时,蚂蚁沿圆柱表面爬行的最短路程是( C )
A.12 cm B.15π cm C.144+9π2 cm D.18 cm 解析:如图,在圆柱的侧面展开图中,BC的长为底面圆周长的
一半,即BC=12×2π×3=3π(cm),蚂蚁所走路程为AB=122+3π2=144+9π2(cm).故蚂蚁沿圆柱表面爬行的最短路程是144+9π2 cm. 6.棱台上、下底面面积分别为16,81,有一平行于底面的截面,其面积为36,则截面截得两棱台高的比为( C ) A.11 B.12 C.23 D.34 解析:如图,将棱台还原为棱锥,设顶端小棱锥的高为h.两棱台
(2021年整理)高中数学必修一和必修二综合测试及参考答案A
高中数学必修一和必修二综合测试及参考答案A编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(高中数学必修一和必修二综合测试及参考答案A)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为高中数学必修一和必修二综合测试及参考答案A的全部内容。
高中数学必修一和必修二综合测试A考号 班级 姓名一、选择题(每小题5分,共10小题,共50分)1、设集合{}(,)1A x y y ax ==+,{}(,)B x y y x b ==+,且{}(2,5)AB =,则:( )A .3,2a b ==B .2,3a b ==C .3,2a b =-=-D .2,3a b =-=-2、对于一个底边在x 轴上的三角形,采用斜二测画法作出其直观图,其直观图的面积是原三角形面积的:( )A 。
2倍 B.24倍 C 。
22倍 D. 12倍 3。
已知函数2log (0)()3(0)x x x f x x >⎧=⎨≤⎩,则1[()]4f f 的值是( )A 。
8 B. 18 C 。
9 D. 194. 设1,01,x y a >><<则下列关系正确的是:( )A 。
a a y x -->B 。
ay ax <C 。
y x a a < D. y x a a log log >5. 函数()23x f x =-的零点所在区间为:( )A . (-1,0) B. (0,1) C 。
(1,2) D. (2,3)6. 函数()f x 的定义域为(,)a b ,且对其内任意实数12,x x 均有:1212()[()()]0x x f x f x --<,则()f x 在(,)a b 上是:( ) A. 增函数 B 。
高中数学8.6第八章 立体几何初步综合测试卷2021高中数学新教材配套提升训练人教A版必修第二册
第八章 《立体几何初步》 综合测试卷一、单选题1.(2021·安徽省肥东县第二中学高二期末(文))棱长为4的正方体的内切球的表面积为( ) A .4π B .12πC .16πD .20π【答案】C 【解析】由正方体的内切球直径为正方体棱长,直接求解. 【详解】由球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径, 得24r =,2r ,故表面积为2416S r ππ==,故选:C. 【点睛】与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径. 2.(2021·安徽蚌埠市·高二期末(文))阿基米德(Archimedes ,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.他推导出的结论“圆柱内切球体的体积是圆柱体积的三分之二,并且球的表面积也是圆柱表面积的三分之二”是其毕生最满意的数学发现,后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球(如图所示),该球与圆柱的两个底面及侧面均相切,圆柱的底面直径与高都等于球的直径,若球的体积为36π,则圆柱的体积为 ( )A .36πB .45πC .54πD .63π【答案】C 【解析】根据球的体积公式求出半径,根据圆柱的体积公式可求得结果. 【详解】设球的半径为R ,则343R π=36π,所以3R =, 所以圆柱的底面半径为3R =,圆柱的高为26R =, 所以圆柱的体积为232254R R R πππ⨯==. 故选:C3.(2021·湖北武汉市·高二期末)过圆柱的上,下底面圆圆心的平面截圆柱所得的截面是面积为8的正方形,则圆柱的侧面积是( )A .B .12πC .8πD .10π【答案】C 【解析】结合立体图,先由面积计算底面半径和侧棱,再利用侧面积公式计算即可. 【详解】如图所示,过圆柱的上,下底面圆圆心的平面截圆柱所得的截面是正方形ABCD ,面积为8,故边长AB AC ==12R AB ==AC =则圆柱的侧面积是228S R AC πππ=⋅==. 故选:C.4.(2021·广西钦州市·高二期末(理))直三棱柱111ABC A B C -中,1AB AC AA ==,60BAC ∠=︒,则1AC 与面11BCC B 成角的正弦值为( )ABCD【答案】A 【解析】过A 作AM BC ⊥,可证AM ⊥平面11BB C C ,连接1C M ,可知1AC M ∠即为所求线面角,计算即可求解. 【详解】如图,过A 作AM BC ⊥,连接1C M ,在直三棱柱111ABC A B C -中,因为11,B B AM BC BB B⊥=所以AM ⊥平面11BB C C ,故1AC 在平面11BB C C 上的射影为1MC ,所以1AC M ∠为直线1AC 与平面11BB C C 所成的角, 设1AB AC AA a ===,又60BAC ∠=︒所以1,2AM a AC ==故1sin AC M ∠== 故选:A5.(2021·宁夏银川市·银川一中高一期末)如图,正方体1111ABCD A B C D -的棱长为2,下面结论错误的是( )A .//BD 平面11CB D B .1AC ⊥平面11CB DC .异面直线1CB 与BD 所成角为60 D .三棱锥11D CB D -体积为23【答案】D 【解析】根据线面平行的判定定理,证明A 正确;根据线面垂直的判定定理,证明B 正确;在正方体中,作出异面直线1CB 与BD 所成角,结合题中条件,可判断C 正确;根据三棱锥的体积公式,可判断D 错. 【详解】A 选项,在正方体1111ABCD ABCD -中,11//BD B D ,又11B D ⊂平面11CB D ,BD ⊄平面11CB D ,所以//BD 平面11CB D ,即A 正确;B 选项,连接11AC ,1CD ,在正方体1111ABCD A B C D -中,1111B D A C ⊥,11DC CD ⊥,AD ⊥平面11C D DC ,1AA ⊥平面1111D C B A ,因为1CD ⊂平面11C D DC ,11B D ⊂平面1111D C B A , 所以1CD AD ⊥,111AA B D ⊥,又1DC AD D ⋂=,1DC ⊂平面1AC D ,AD ⊂平面1AC D ,所以1CD ⊥平面1AC D , 因此11CD AC ⊥; 同理111B D AC ⊥, 又1111CD B D D =,1CD ⊂平面11CB D ,11B D ⊂平面11CB D ,所以1AC ⊥平面11CB D ;即B 正确;C 选项,因为11//BD BD ,所以11CB D ∠即等于异面直线1CB 与BD 所成角,又1111CB B D CD ====11CB D 为等边三角形,即异面直线1CB 与BD 所成角为60,故C 正确;D 选项,三棱锥11D CB D -的体积为111111111142223323D CB D B CDD CDD V V S B C --==⋅=⨯⨯⨯⨯=.故D 错; 故选:D.6.(2021·安徽池州市·高三期末(文))三棱锥P ABC -中,PA PB PC ==,4ABC π∠=,AC =,则三棱锥P ABC -外接球表面积的最小值是( ) A .8π B .4πC .2πD .π【答案】B 【解析】根据正弦定理求出ABC 外接圆半径,设三棱锥P ABC -高为h ,球的半径为R ,从而可得222()R h R r -+=,再利用基本不等式求出R 的最小值即可.【详解】设底面ABC 外接圆圆心为1O ,半径为r , 则22sin ACr ABC==∠,即1r =.设三棱锥P ABC -高为h ,球的半径为R .由PA PB PC ==,得球心O 在1PO 上,且222()R h R r -+=,则111122R h h ⎛⎫=+≥⋅= ⎪⎝⎭,当且仅当1h =时等号成立,此时外接球表面积最小,则min 4S π=.故选:B7.(2021·安徽合肥市·高二期末(文))三棱锥D ABC -及其三视图中的正视图和侧视图如图所示,CD ⊥平面ABC ,则棱BD 的长为( )A .B .4C .D .2【答案】A 【解析】由已知中的三视图可得DC ⊥平面ABC ,且底面△ABC 为等腰三角形,解三角形即可求解. 【详解】由三棱锥D ABC -及其三视图中的正视图和侧视图可知, DC ⊥平面ABC ,且底面△ABC 为等腰三角形,在△ABC 中AC =4,AC 边上的高为故4BC ==,在Rt △DBC 中,由DC =4,4BC =,可得DB 22442.故选:A8.(2021·河北唐山市·高二期末)在四棱锥P -ABCD 中,//AD BC ,2AD BC =,E 为PD 中点,平面ABE 交PC 于F ,则PFFC=( ) A .1 B .32C .2D .3【答案】C 【解析】首先通过延长直线,DC AB ,交于点G ,平面BAE 变为GAE ,连结PG ,EG 交于点F ,再根据三角形中线的性质,求PFFC的值. 【详解】延长,DC AB ,交于点G ,连结PG ,EG 交PC 于点F ,//AD BC ,且2AD BC =,可得点,B C 分别是,AG DG 的中点,又点E 是PD 的中点,PC ∴和GE 是△PGD 的中线,∴点F 是重心,得2PFFC=故选:C9.(2021·安徽合肥市·高二期末(文))设有直线m ,n ,l 和平面α,β,下列四个命题中,正确的是( ) A .若//,//m n αα,则//m n B .若//,//,//l m αβαβ,则//l m C .若,m αβα⊥⊂,则m β⊥ D .若,,m m αββα⊥⊥⊄,则//m α【答案】D 【解析】在A 中,m 与n 相交、平行或异面; 在B 中,l 与m 不一定平行,有可能相交;在C 中,m ⊥β或m ∥β或m 与β相交;在D 中,由直线与平面垂直的性质与判定定理可得m ∥α. 【详解】由直线m 、n ,和平面α、β,知:对于A ,若m ∥α,n ∥α,则m 与n 相交、平行或异面,故A 错误; 对于B ,若//,//,//l m αβαβ,l 与m 不一定平行,有可能相交,故B 错误;对于C ,若α⊥β,m ⊂α,则m ⊥β或m ∥β或m 与β相交,故C 错误;对于D ,若α⊥β,m ⊥β,m ⊄α,则由直线与平面垂直的性质与判定定理得m ∥α,故D 正确. 故选:D .10.(2021·江苏淮安市·高二期末)蹴鞠,又名蹴球,筑球等,蹴有用脚踢、踏的含义,鞠最早系外包皮革、内实含米糠的球.因而蹴鞠就是指古人以脚踢、踏皮球的活动,类似现在的足球运动.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.3D 打印属于快速成形技术的一种,它是一种以数字模型为基础,运用粉末状金属或塑料等可粘合材料,通过逐层堆叠积累的方式来构造物体的技术.过去常在模具制造、工业设计等领域被用于制造模型,现正用于一些产品的直接制造,特别是一些高价值应用(比如人体的髋关节、牙齿或飞机零部件等).已知某蹴鞠的表面上有四个点A .B .C .D ,满足任意两点间的直线距离为6cm ,现在利用3D 打印技术制作模型,该模型是由蹴鞠的内部挖去由ABCD 组成的几何体后剩下的部分,打印所用原材料的密度为31g/cm ,不考虑打印损耗,制作该模型所需原材料的质量约为( )(参考数据)π 3.14≈ 1.41≈ 1.73≈ 2.45≈. A .101g B .182gC .519gD .731g【答案】B【解析】由题意可知所需要材料的体积即为正四面体外接球体积与正四面体体积之差,求出正四面体体积、外接球体积,然后作差可得所需要材料的体积,再乘以原料密度可得结果. 【详解】由题意可知,几何体ABCD 是棱长为6cm 的正四面体,所需要材料的体积即为正四面体外接球体积与正四面体体积之差,设正四面体的棱长为a =,设正四面体外接球半径为R ,则2222()()332R R a =-+⨯,解得R =,所以3D 打印的体积为:3233411343223812V a a a a ππ⎛⎫=-⋅⋅⋅=- ⎪ ⎪⎝⎭, 又336216a ==,所以207.71125.38182.331182V =-≈-=≈, 故选:B 二、多选题11.(2020·沙坪坝区·重庆一中高三月考)设m 、n 是两条不同的直线,α、β是两个不同的平面,下列命题中错误..的是( ) A .若,,//m n m n αβ⊂⊂,则//αβ B .若,m n m α⊂⊥,则n α⊥ C .若,mn αα,则m n ⊥D .若//,,m n αβαβ⊂⊂,则//m n【答案】ABD 【解析】根据空间线、面关系,结合空间关系相关图例以及线线、线面、面面间的平行、垂直判定与性质,即可知选项的正误. 【详解】A :,,//m n m n αβ⊂⊂,α、β不一定平行,错误.B :,m n m α⊂⊥,n 不一定垂直于α,错误.C :由线面垂直的性质:,m n αα,则必有m n ⊥,正确.D ://,,m n αβαβ⊂⊂,m 、n 不一定平行,错误.故选:ABD12.(2020·全国高三月考)在直三棱柱111ABC A B C -中,90ABC ∠=︒,2AB BC ==,12AA =,M 是BC 的中点,N 是11A C 的中点,点P 在线段1B N 上,点Q 在线段AM 上,且23AQ AM =,S 是1AC 与1A C 的交点,若//PS 面1B AM ,则( )A .1//PSB Q B .P 为1B N 的中点C .AC PS ⊥D .三棱锥1P B AM -的体积为23【答案】ACD 【解析】连接交NS 交AC 于G 点,连接BG ,利用线面平行的性质定理判断A ;根据三角形相似判断B ;由线面垂直的判定定理及性质定理判断C ;由11P AB M B ABM V V --=计算可得,从而判断D ;【详解】解:对于选项A :连接交NS 交AC 于G 点,连接BG ,则由AB BC =,23AQ AM =,可得BG 必过点Q ,且23BQ BG =,因为PS ⊂面1BB NG ,//PS 面1AMB ,面1AMB 面11BB NG B Q =,所以1//PS B Q ,故A 正确;对于选项B :1//PS B Q ,1NPS NBQ B QB ∴∠=∠=∠,1Rt Rt PNS QBB ∴∽△△,112PN NS BQ BB ∴==,即111212233PN BQ BG B N ==⋅=, P ∴为靠近N 的三等分点,故B 错误;对于选项C :AC NG ⊥,AC BG ⊥,,NG BG ⊂面1BB NG ,NG BG G =AC ∴⊥面1BB NG ,PS ⊂面1BB NG ,AC PS ∴⊥,故C 正确;对于选项D :1//B P BQ ,且1B P BQ =,1BB PQ ∴是矩形,111112221323P AB M B AB M B ABM V V V ---∴===⋅⋅⋅⋅=,故D 正确. 故选:ACD13.(2020·全国高三专题练习)如图所示,矩形ABCD 中,E 为边AB 的中点,将ADE 沿直线DE 翻转成1A DE △,若M 为线段1A C 的中点,则在ADE 翻转过程中,则下列命题正确的是( )A .||BM 是定值B .点M 在球面上运动C .一定存在某个位置,使1DE A C ⊥D .一定存在某个位置,使//MB 平面1A DE【答案】ABD【解析】取CD 中点N ,连接MN 、NB ,则1//MN A D 、//NB DE ,由平行线性质得1A DE MNB ∠=∠,可判断A ,这时可得出平面//MNB 平面1A DE ,从而判断D ,利用BM 长为定值可判断B ,结合1A C 在平面ABCD 内的射影可判断C .A 对,取CD 中点N ,连接MN 、NB ,则1//MN A D 、//NB DE ,1A DE MNB ∠=∠,112MN A D ==定值,NB DE ==定值,根据余弦定理得,2222cos MB MN NB MN NB MNB =+-⋅⋅∠,∴||BM 是定值,B 对,B 是定点,∴M 是在以B 为球心,MB 为半径的球面上,C 错,当矩形ABCD 满足AC DE ⊥时存在,其他情况不存在,否则若AC DE ⊥不成立,作CF DE ⊥于F ,连接1A F ,可得DE ⊥平面1A CE ,从而有1DE A F ⊥,因此有原图形中,,A F C 共线,AC DE ⊥,矛盾.D 对,取CD 中点N ,连接MN 、NB ,则1//MN A D 、//NB DE ,∴平面//MNB 平面1A DE ,∵MB ⊂平面MNB ,∴//MB 平面1A DE .故选ABD.14.(2021·湖北黄石市·黄石二中高二期末)在矩形ABCD 中,4AB =,3BC =,沿矩形对角线BD 将BCD △折起形成四面体ABCD ,在这个过程中,现在下面四个结论其中所有正确结论为( )A .在四面体ABCD 中,当DA BC ⊥时,BC AC ⊥B .四面体ABCD 的体积的最大值为245C .在四面体ABCD 中,BC 与平面ABD 所成角可能为3π D .四面体ABCD 的外接球的体积为定值.【答案】ABD【解析】 A.根据线面垂直判定定理证明BC ⊥平面ACD 进而有BC AC ⊥;B.当平面ABD ⊥平面BCD 时,四面体ABCD 的体积最大,根据体积公式计算即可;C.当平面ABD ⊥平面BCD 时BC 与平面ABD 所成的角CBD ∠最大,计算得3CBD π∠<; D.斜边BD 中点到,,,A B C D 距离相等,所以四面体ABCD 的外接球的半径为定值52,其题意奕为定值.解:对于A.当DA BC ⊥时,又因为,,,BC CD CD DA D CD DA ⊥=⊂平面ACD ,所有BC ⊥平面ACD ,所以BC AC ⊥,故A 正确;对于B.当平面ABD ⊥平面BCD 时,四面体ABCD 的体积最大在BCD △中根据等面积法可得C 到平面ABD 的距离满足125345h h =⨯⇒=所以11112243433255A BCD ABD V S h -⎛⎫=⋅=⨯⨯⨯⨯= ⎪⎝⎭,故B 正确; 对于C. 当平面ABD ⊥平面BCD 时BC 与平面ABD 所成的角CBD ∠最大,此时4tan 3CBD ∠=<3CBD π∠<,故C 错误; 对于D.因为BAD 和BCD △都是直角三角形且共斜边,所以斜边BD 中点到,,,A B C D 距离相等,所以四面体ABCD 的外接球的半径1522R BD ==,所以四面体ABCD 的外接球的体积为定值34532π⎛⎫⨯ ⎪⎝⎭故选:ABD三、填空题15.(2021·周至县第二中学高一期末)如图所示,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化后正好盛满杯子,则杯子高h =_______cm .【答案】8【解析】根据题意半球的体积等于圆锥的体积,根据等体积法化简即可.解:由题意得半球的半径和圆锥底面圆的半径4r =,如果冰淇淋融化后正好盛满杯子,则半球的体积等于圆锥的体积 所以()32141448233h h ππ⨯⨯=⨯⨯⇒= 故答案为:816.(2021·安徽蚌埠市·高二期末(理))正方体1111ABCD A B C D -中,点P 是1CC 的中点,则异面直线AP 与1BC 所成角的大小为_________. 【答案】4π 【解析】设正方体1111ABCD A B C D -的棱长为2,连接11,AD D P ,在正方体1111ABCD A B C D -中,11//AD BC ,所以1D AP ∠(或其补角)为异面直线AP 与1BC 所成角,即可求解.【详解】设正方体1111ABCD A B C D -的棱长为2,连接11,AD D P在正方体1111ABCD A B C D -中,11//AD BC所以1D AP ∠(或其补角)为异面直线AP 与1BC 所成角113,AD AP D P ====所以2221111cos 22AP AD D PD AP AP AD +-∠===⨯⨯ 所以14D AP π∠=故答案为:4π17.(2021·海南高三二模)如图,位于山西省朔州市应县佛宫寺内的释迦塔,俗称应县木塔,是我国现存最高最古老的木结构塔式建筑,木塔顶部可以近似地看成一个正八棱锥,其侧面和底面的夹角大小为30︒,则该正八棱锥的高和底面边长之比为________.(参考数据:tan 22.51︒=)【解析】 设底面边长为a ,根据正八棱锥底边所对的圆心角为45,求得圆心到底边的距离,再由侧面与底面成30︒求解.【详解】如图所示:点P 是正八棱锥的顶点,点O 是底面的中心,AB 是底面的一条边,M 是AB 的中点,根据题意知22.5BOM ︒∠=,因为tan 22.51︒=,设AB a ,则1tan 22.52BM OM a ︒+==, 又因为二面角P AB O --的大小为30︒,即30PMO ︒∠=,所以tan306OP OM ︒+==,故答案为:6四、双空题 18.(2020·浙江杭州市·高一期末)一圆台的母线长为20cm ,母线与轴的夹角为30,上底面半径为15cm ,则下底面半径为____,圆台的高为_______.【答案】25【解析】根据题意画出图形,结合图形求出圆台的高和下底面圆的半径和高.【详解】解:如图所示,圆台的母线长为20l cm =,母线与轴的夹角为30,上底面的半径为15r cm =,所以圆台的高为cos3020)h l cm =︒==, 则1sin3020102R r l -=︒=⨯=, 所以底面圆的半径为151025()R cm =+=,故答案为:25;19.(2020·浙江省杭州第二中学高二期中)如图,在四面体ABCD 中, AB CD =,M 、N 、P 、Q 分别是BC 、AD 、AC 、BD 的中点,则MN 和PQ 所成角为_________,若AB 与CD 所成角为30︒,则MN 和CD 所成角为_________.【答案】90 15或75.【解析】(1)连接,,,MP PN NQ MQ ,可证明四边形MPNQ 是菱形,即可得出;(2)可得PMQ ∠即为AB 与CD 所成角(或其补角),且30PMQ 或150,继而得出MN 和CD 所成角为15NMQ ∠=或75.【详解】(1)连接,,,MP PN NQ MQ ,M 、N 、P 、Q 分别是BC 、AD 、AC 、BD 的中点,11,22MQ CD PN CD ∴,MQ PN ∴, ∴四边形MPNQ 是平行四边形, 12MP AB =,AB CD =,12MP CD ∴=,MP MQ ∴=,故四边形MPNQ 是菱形,MN PQ ∴⊥,故MN 和PQ 所成角为90;//,//MP AB MQ CD ,PMQ ∴∠即为AB 与CD 所成角(或其补角),30PMQ ∴∠=或150,而NMQ ∠为MN 和CD 所成角,且15NMQ ∠=或75,即MN 和CD 所成角为15或75.故答案为:90;15或75.20.(2020·全国高二单元测试)设P A ⊥Rt △ABC 所在的平面α,∠BAC=90°,PB 、PC 分别与α成45°和30°角,P A=2,则P A 与BC 的距离是___________;点P 到BC 的距离是___________.【解析】作AD ⊥BC 于点D ,连接PD ,根据P A ⊥面ABC ,易得AD 是P A 与BC 的公垂线,BC ⊥平面P AD 求解.【详解】如图所示:作AD ⊥BC 于点D ,因为P A ⊥面ABC ,所以P A ⊥AD ,所以AD 是P A 与BC 的公垂线.因为PB 、PC 分别与α成45°和30°角,P A=2,所以AB=2,AC=BC=4,,连接PD ,由,,BC AD BC PA PA AD A ⊥⊥⋂=则BC ⊥平面P AD ,则PD ⊥BC ,所以点P 到BC 的距离.21.(2021·浙江杭州市·高二期末)在正方体1111ABCD A B C D -中,棱1AA 与面对角线1BC 所成角的大小是____;面对角线1BC 与体对角面11ACC A 所成角的大小是_____.【答案】45︒ 30︒【解析】连接1BC ,11A C ,AC ,BD ,记AC 与BD 交点为O ,连接1C O ,根据异面直线所成角,以及线面角的概念,得到11B BC ∠等于棱1AA 与面对角线1BC 所成的角,1BC O ∠即为面对角线1BC 与体对角面11ACC A 所成角,再根据正方体的结构特征,即可得出结果.【详解】连接1BC ,11A C ,AC ,BD ,记AC 与BD 交点为O ,连接1C O , 在正方体1111ABCD A B C D -中,侧棱相互平行,即11//AA BB , 所以11B BC ∠等于棱1AA 与面对角线1BC 所成的角(或所成角的补角), 因为在正方形11BCC B 中,1145B BC ∠=︒,异面直线所成角大于0︒且小于等于90︒, 所以棱1AA 与面对角线1BC 所成角的大小是45︒; 又在正方体1111ABCD A B C D -中,侧棱垂直于底面,所以1AA ⊥平面ABCD , 因为BD ⊂平面ABCD ,所以1AA BD ⊥,又底面ABCD 为正方形,所以AC BD ⊥,因为1AC AA A =∩,1AA ⊂平面11AAC C ,AC ⊂平面11AAC C ,所以BD ⊥平面11AAC C ,因此1BC O ∠即为面对角线1BC 与体对角面11ACC A 所成角, 所以111112sin 2BD BO BC O BC BC ∠===, 因为1BC O ∠显然为锐角,所以130BC O ∠=︒.故答案为:45︒;30︒.五、解答题22.(2020·陕西西安市·高一期末)如图,在三棱锥P ABC -中,,PA PC AB BC ==,O 是AC 的中点,PO BO ⊥,2,3PO AC BO ===.(1)证明:AC PB ⊥;(2)求三棱锥A PBC -的体积.【答案】(1)证明见解析;(2)2【解析】(1)通过,PO AC BO AC ⊥⊥得出AC ⊥平面POB ,即可证明;(2)先证明PO 是三棱锥的高,再直接求出三棱锥体积.【详解】(1),PA PC AB BC ==,O 是AC 的中点,,PO AC BO AC ∴⊥⊥,PO BO O =,AC ∴⊥平面POB ,∴AC PB ⊥;(2),PO AC PO BO ⊥⊥,AC BO O ⋂=,PO ∴⊥平面ABC ,即PO 是三棱锥的高,1112322332A PBC ABC V S PO -∴=⋅=⨯⨯⨯⨯=. 23(2020·陕西西安市·西安一中高一月考)一个透明的球形装饰品内放置了两个具有公共底面的圆锥,且这两个圆锥的顶点和底面圆周都在这个球面上,如图,已知圆锥底面面积是这个球的表面积的316,设球的半径为R ,圆锥底面半径为r .(1)试确定R 与r 的关系,并求出大圆锥与小圆锥的侧面积的比值.(2)求出两个圆锥的总体积(即体积之和)与球的体积之比.【答案】(1)2r R =;(2)3:8. 【解析】(1)求出球的表面积和圆锥底面积,即可得出r R =,根据几何特征表示出圆锥的高和母线长,即可求出侧面积之比;(2)根据体积公式计算出,即可得出比值.【详解】解:(1)球的表面积为24R π,∴圆锥的底面积为223416r R ππ=⨯,解得2r R =, 由几何体的特征知球心到圆锥底面的距离,球的半径以及圆锥底面的半径三者可以构成一个直角三角形;由此可以求得球心到圆锥底面的距离是:112OO R ==,所以小圆锥的高为:1122R R R -=R =;同理可得大圆锥的高为:1322R R R +==; 又由这两个圆锥的底面半径相同,:R =.(2)由(1)可得两个圆锥的体积和为:321232R r R ππ⋅⋅⋅=, 球的体积为:343R π, 故两个圆锥的体积之和与球的体积之比为:334:3:823R R ππ=.24.(2021·浙江嘉兴市·高二期末)如图,在直三棱柱111ABC A B C -中,底面ABC 为正三角形,1AB 与1A B 交于点O ,E ,F 是棱1CC 上的两点,且满足112EF CC =.(1)证明://OF 平面ABE ;(2)当1CE C F =,且12AA AB =,求直线OF 与平面ABC 所成角的余弦值.【答案】(1)证明见解析;(2 【解析】 (1)取AB 中点G ,连结OG 、EG ,可证明四边形OGEF 为平行四边形,则 OF EG ∥,由线面平行的判定定理即可求证;(2)由(1)可知,OF EG ∥,则直线OF 与平面ABC 所成角即为直线EG 与平面ABC 所成角,EC ⊥平面ABC ,则EGC ∠即为直线EG 与平面ABC 所成的角,在EGC 中即可求EGC ∠的余弦值.【详解】(1)取AB 中点G ,连结OG 、EG ,在直三棱柱111ABC A B C -中,1OG BB ∥,则OG EF ∥, 又112EF CC =,则OG EF =, 所以四边形OGEF 为平行四边形,则 OF EG ∥,又EG ⊂平面ABE ,OF ⊄平面ABE , 故//OF 平面ABE .(2)由(1)可知,OF EG ∥,则直线OF 与平面ABC 所成角即为直线EG 与平面ABC 所成角, 连接CG ,由直三棱柱111ABC A B C -可得EC ⊥平面ABC ,则EGC ∠即为直线EG 与平面ABC 所成的角,设2AB =,则114AA CC ==,又1CE C F =,则1CE =,CG =2EG =,所以,直线EG 与平面ABC故直线OF 与平面ABC 方法点睛:证明直线与平面平行的常用方法(1)定义法:证明直线与平面没有公共点,通常要借助于反证法来证明;(2)判定定理:在利用判断定理时,关键找到平面内与已知直线平行的直线,常考虑利用三角形中位线、平行四边形的对边平行或过已知直线作一平面,找其交线进行证明;(3)利用面面平行的性质定理:直线在一平面内,由两平面平行,推得线面平行;直线在两平行平面外,且与其中一平面平行,这这条直线与另一个平行.25.(2021·六盘山高级中学高一期末)如图,AB是O的直径,P A垂直于O所在的平面,C是圆周上不同于A,B的一动点.(1)证明:BC⊥面P AC;(2)若P A=AC=1,AB=2,求直线PB与平面P AC所成角的正切值.【答案】(1)证明见解析;(2)2【解析】(1)证明AC⊥BC和P A⊥BC,BC⊥面P AC即得证;BC PC即得解.(2)先证明∠BPC为PB与平面P AC所成的角,再通过解三角形求出,【详解】证明:(1)AB为圆O直径∴∠ACB=90°即AC⊥BCP A⊥面ABC,∴P A⊥BCAC P A=A∴BC⊥面P AC.(2)BC⊥面P AC,∴∠BPC为PB与平面P AC所成的角,在直角三角形ABC 中,BC在直角三角形PAC 中,PC ==,在直角三角形PBC 中,tan ∠BPC2=.故直线PB 与平面P AC 方法点睛:求线面角常用几何法求解,其步骤为:找→作→证(定义)→指→求(解三角形). 26.(2021·安徽宿州市·高二期末(文))如图,四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥底面ABCD ,E 为PD 的中点.(1)证明://PB 平面AEC ;(2)设1AP =,AD =P ABCD -的体积为1,求证:平面PAC ⊥平面PBD .【答案】(1)证明见解析;(2)证明见解析.【解析】( 1)设BD 与AC 的交点为O ,连接EO ,通过直线与平面平行的判定定理证明//PB 平面AEC ; ( 2)通过体积得到底面为正方形,再由线面垂直得到面面垂直即可.【详解】(1)连接BD 交AC 于点O ,连结EO ,因为ABCD 为矩形,所以O 为BD 的中点,又E 为PD 的中点,所以//EO PB ,EO ⊂平面AEC ,PB ⊄平面AEC ,所以//PB 平面AEC .(2)因为113P ABCD V AB AD AP -=⨯⨯⨯=,所以AB =ABCD 为正方形,所以BD AC ⊥,因为PA ABCD ⊥,所以BD PA ⊥,且AC PA A ⋂=,所以BD ⊥平面PAC ,又BD ⊂平面PBD ,所以平面PAC ⊥平面PBD .27.(2021·陕西西安市·高三一模(文))如图在四棱锥P ABCD -中,底面ABCD 为菱形,PAD △为正三角形,平面PAD ⊥平面ABCD E F ,、分别是AD CD 、的中点.(1)证明:BD PF ⊥;(2)若M 是棱PB 上一点,三棱锥M PAD -与三棱锥P DEF -的体积相等,求M 点的位置.【答案】(1)证明见解析;(2)M 点在PB 上靠近P 点的四等分点处.【解析】(1)连接AC ,由//AC EF ,可证明BD EF ⊥,BD PE ⊥,从而得BD ⊥平面PEF ,得证线线垂直; (2)设设PM MB λ=,则1PM PB λλ=+,根据棱锥的体积公式,利用体积法得出结论,由11M PAD B PAD P ABD V V V λλλλ---==++,1144P DEF P ACD P ABD V V V ---==,可得λ值. 【详解】(1)连接AC PA PD =,且E 是AD 的中点,PE AD ⊥∴.又平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD PE =⊂,平面PAD .PE ∴⊥平面ABCD BD ⊂,平面ABCD BD PE ∴⊥,.又ABCD 为菱形,且E F 、分别为棱AD CD 、的中点,//EF AC ∴. BD AC BD EF ⊥∴⊥,,又BD PE PE EF E BD ⊥⋂=∴⊥,,平面PEF ;PF ∴⊂平面PEF BD PF ∴⊥,. (2)如图,连接MA MD 、, 设PM MB λ=,则1PM PB λλ=+, 11M PAD B PAD P ABD V V V λλλλ---∴==++, 14DEF DAC S S =△△,则1144P DEF P ACD P ABD V V V ---==,又M PAD P DEF V V --=. 114λλ∴=+. 解得13λ=,即M 点在PB 上靠近P 点的四等分点处.。
2021学年人教版高中数学必修2检测:第3章直线与圆课后提升作业213.2.3版含解析
课后提升作业二十一直线的一般式方程(30分钟60分)一、选择题(每题5分 ,共40分)1.直线2x +ay +3 =0的倾斜角为120° ,那么a的值是( ) A.【解析】° ,所以直线的斜率k = - ,即 - = - ,所以 a =.【补偿训练】平面直角坐标系中 ,直线x +y +2 =0的斜率为( )A. C.【解析】选B.将直线化为斜截式y = -x -.故斜率为 -. 2.(2021·海淀高一检测)直线l经过点P(2 ,1) ,且与直线2x -y +2 =0平行 ,那么直线l的方程是( )A.2x -y -3 =0B.x +2y -4 =0C.2x -y -4 =0D.x -2y -4 =0【解析】选A.由题意可设所求的方程为2x -y +c =0 ,代入点 (2 ,1) ,可得4 -1 +c =0 ,即c = -3 ,故所求直线的方程为2x -y -3 =0.3.直线3x +4y +5 =0的斜率和它在y轴上的截距分别为( )A. , , -, - D. ,【解析】选C.根据斜率公式k = - = - ,令x =0 ,那么y = - ,即在y轴上的截距为 -.l1:2x +3y +8 =0 ,l2:x -y -1 =0 ,l3:x +ky +k + =0能围成三角形 ,那么k不等于( )A.C. , -1D. , -1 , -【解析】得交点P( -1 , -2) ,假设P在直线x +ky +k + =0上 ,那么k = - ,此时三条直线交于一点;k =时 ,直线l1与l3平行;k = -1时 ,直线l2与l3平行 ,综上知 ,要使三条直线能围成三角形 ,应有k≠ - ,和 -1.5.(2021·杭州高一检测)直线l:ax +y -2 -a =0在x轴和y轴上的截距相等 ,那么a的值是( )【解析】选D.当截距都为0时 , -2 -a =0即a = -2;当截距都不为0即a≠ -2时 ,直线方程可变形为: + =1 ,由有=a +2 ,得a =1.6.(2021·北京高一检测)直线ax +by +c =0的图象如图 ,那么( )A.假设c>0 ,那么a>0 ,b>0B.假设c>0 ,那么a<0 ,b>0C.假设c<0 ,那么a>0 ,b<0D.假设c<0 ,那么a>0 ,b>0【解析】选D.由ax +by +c =0 ,得斜率k = - ,直线在x ,y轴上的截距分别为 - , -.如题图 ,k<0 ,即 -<0 ,所以ab>0 ,因为 ->0 , ->0 ,所以ac<0 ,bc<0.假设c<0 ,那么a>0 ,b>0;假设c>0 ,那么a<0 ,b<0.7.(2021·威海高一检测)直线l过点( -1 ,2)且与直线2x -3y +4 =0垂直 ,那么l的方程是( )A.3x +2y -1 =0B.3x +2y +7 =0C.2x -3y +5 =0D.2x -3y +8 =0【解析】l与直线2x -3y +4 =0垂直 ,可知直线l的斜率是 - ,由点斜式可得直线l的方程为y -2 = -(x +1) ,即3x +2y -1 =0. 【补偿训练】过点(1 ,0)且与直线x -2y -2 =0平行的直线方程是( )A.x -2y -1 =0B.x -2y +1 =0C.2x +y -2 =0D.x +2y -1 =0【解析】选A.设所求直线的方程为x -2y +m =0 ,把点(1 ,0)代入 ,得m = -1 ,应选A.≠0 ,直线ax +3my +2a =0在y轴上的截距为2 ,那么直线的斜率为( )【解析】选A.令x =0 ,得y = - ,因为直线在y轴上的截距为2 ,所以 - =2 ,所以a = -3m ,原直线化为 -3mx +3my -6m =0 ,所以k =1.【延伸探究】把题中的 "在y轴上的截距为2〞改为 "在两坐标轴上的截距之和为2〞 ,那么直线的斜率为( )A.1【解析】选D.令x =0 ,得y = - ,令y =0 ,得x = -2 ,因为在两坐标轴上的截距之和为2 ,所以 - +( -2) =2 ,所以a = -6m ,原直线化为 -6mx +3my -12m =0 ,所以k =2.二、填空题(每题5分 ,共10分)9.(2021·广州高一检测)垂直于直线3x -4y -7 =0 ,且与两坐标轴围成的三角形的面积为6的直线在x轴上的截距是________.【解析】设直线方程是4x +3y +d =0 ,分别令x =0和y =0 ,得直线在两坐标轴上的截距分别是 - , -.所以6 =×× =.所以d =±12 ,那么直线在x轴上的截距为3或 -3.答案:3或 -310.假设方程(2m2 +m -3)x +(m2 -m)y -4m +1 =0表示一条直线 ,那么实数m的取值范围是______________.【解题指南】求x ,y的系数不同时为0的m值即可 ,即先求出x与y 的系数均为零时m的值 ,再取补集即可.【解析】由得m =1 ,故要使方程表示一条直线 ,需2m2 +m -3与m2 -m不同时为0 ,故m≠1.答案:m≠1三、解答题11.(10分)求与直线3x -4y +7 =0平行 ,且在两坐标轴上截距之和为1的直线l的方程.【解析】方法一:由题意知:可设l的方程为3x -4y +m =0 ,那么l在x轴 ,y轴上的截距分别为 - ,.由 - + =1知 ,m = -12.所以直线l的方程为:3x -4y -12 =0.方法二:设直线方程为 + =1 ,由题意得解得所以直线l的方程为: + =1.即3x -4y -12 =0.【补偿训练】(2021·大连高一检测)直线2x +(t -2)y +3 -2t =0 ,分别根据以下条件 ,求t的值.(1)过点(1 ,1).(2)直线在y轴上的截距为 -3.【解析】(1)因为直线2x +(t -2)y +3 -2t =0过点(1 ,1) ,所以2 +(t -2) +3 -2t =0 ,即t =3.(2)令x =0 ,得y = = -3 ,解得t =.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修2检测题二
一、选择题
1、下列命题为真命题的是()
A.平行于同一平面的两条直线平行;B.与某一平面成等角的两条直线平行;
C.垂直于同一平面的两条直线平行;D.垂直于同一直线的两条直线平行。
D.
2、下列命题中错误的是:()
A.如果α⊥β,那么α内一定存在直线平行于平面β;
B.如果α⊥β,那么α内所有直线都垂直于平面β;
C.如果平面α不垂直平面β,那么α内一定不存在直线垂直于平面β;
D.如果α⊥γ,β⊥γ,α∩β=l,那么l⊥γ.
3、右图的正方体ABCD-A’B’C’D
’
中,异面直线AA’与BC所成的角是()
A. 300B.450C.600D.90
0
4、右图的正方体ABCD- A’B’C’D
’
中,
二面角D
’
-AB-D的大小是(B )
A. 300B.450C.600D.90
0
5、直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则()
A.a=2,b=5; B.a=2,b=5; C.a=2,b=5; D.a=2,b=5.
6、直线2x-y=7与直线3x+2y-7=0的交点是()
A (3,-1) B (-1,3) C (-3,-1) D (3,1)
7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是()
A 4x+3y-13=0 B 4x-3y-19=0
C 3x-4y-16=0 D 3x+4y-8=0
8、正方体的全面积为a,它的顶点都在球面上,则这个球的表面积是:()
A.3a; B.2a; C.a2; D.a3.
9、已知一个铜质的五棱柱的底面积为16cm2,高为4cm,现将它熔化后铸成一个正方体的铜块(不
计损耗),那么铸成的铜块的棱长是()
A. 2cm; B.cm34; C.4cm; D.8cm。
10、圆x2+y2-4x-2y-5=0的圆心坐标是:()
A B
D
A’B’
D’
C
C’
A.(-2,-1); B.(2,1); C.(2,-1); D.(1,-2).
11、直线3x+4y-13=0与圆
1)3()2(
22
yx
的位置关系是:()
A. 相离; B. 相交; C. 相切; D. 无法判定.
12、圆C1: 1)2()2(22yx与圆C2:16)5()2(22yx的位置关系是()
A、外离 B 相交 C 内切 D 外切
二、填空题
13、底面直径和高都是4cm的圆柱的侧面积为cm
2
。
14、两平行直线0962043yxyx与的距离是。
15、、已知点M(1,1,1),N(0,a,0),O(0,0,0),若△OMN为直角三角形,则a=____________;
16、若直线08)3(1myxmyx与直线平行,则m。
17,半径为a的球放在墙角,同时与两墙面和地面相切,那么球心到墙角顶点的距离为________________;
三、解答题
18、(10分)已知点A(-4,-5),B(6,-1),求以线段AB为直径的圆的方程。
19、(10分)已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点。(1)求
AB边所在的直线方程;(2)求中线AM的长。
20、(15分)如图,在边长为a的菱形ABCD中,
ABCDPCABC面,60
,E,F是PA和AB的中点。
(1)求证:EF||平面PBC
;
(2)求E到平面PBC的距离。
21、(15分)已知关于x,y的方程C:04222myxyx.
(1)当m为何值时,方程C表示圆。
(2)若圆C与直线l:x+2y-4=0相交于M,N两点,且MN=
5
4
,求m的值。
A
B
C
D
P
E
F
